近年来随着天文观测技术的不断发展，有关致密星的研究成为国际前沿的热点之一。对大质量中子星 PSR J1614-2230($ 1.908 \pm 0.016M_{\odot} $)^[1−2]，PSR J0348+0432($ 2.01 \pm 0.04M_{\odot} $)^[3] 和 PSR J0740+6620($ 2.08 \pm 0.07M_{\odot} $)^[4]的质量的精确测量，将中子星的最大质量限制在$ 2 {M_{\odot}} $以上。2017 年第一次观测到双中子星并合的引力波信号，即GW170817事件，为$ 1.4 {M_{\odot}} $的中子星的半径和潮汐形变带来严格的限制^[5−8]。2019 年探测到的GW190814事件涉及一个22.2~24.3$ {M_{\odot}} $的黑洞和一个质量为2.50~2.67$ {M_{\odot}} $的致密星^[9]。这个$ \sim 2.6M_{\odot} $的致密星可能为目前最重的中子星或者最轻的黑洞^[10−13]。

大质量中子星的核心密度可达5~10倍饱和密度，为研究强子在低温高密处的退禁闭相变行为提供了良好的实验环境。许多工作使用有效模型对中子星内部的强子退禁闭相变进行了研究^[14−18]。目前认为在低温、高密度状态下，退禁闭相变可能属于一级相变，在相变过程中系统可能处于混杂相。常见的研究强子-夸克混杂相的方法为Gibbs结构(GC)^[19−20] 和Maxwell结构(MC)^{[16, 21]}。Gibbs结构满足全局电中性条件，Maxwell结构满足局域电中性条件。一般认为Maxwell结构和Gibbs结构分别对应于强子-夸克分界面的表面张力的两种极端情况，即Gibbs结构对应表面张力为零的情况；Maxwell结构对应表面张力很大的情况。这两种结构中均没有考虑有限尺度效应和电荷屏蔽效应，即在混杂相的能量密度中仅包含了强子相和夸克相的能量贡献，没有考虑表面能和库仑能的贡献。研究表明，有限尺度效应对于理解真实的强子-夸克相变过程具有重要的影响^[22−23]。当在强子-夸克混杂相中考虑有限尺度效应时，混杂相可能以具有一定对称性的结构呈现，即pasta结构^[24−25]。随着密度的增加，混杂相可能出现液滴形(droplet)，柱形(rod)，片形(slab)，圆筒形(tube)和气泡形(bubble)等几何结构。同时研究表明电荷屏蔽效应会影响混杂相中带电粒子的分布，对强子-夸克混杂相的性质和密度范围有显著的影响^[26−27]。

近几十年，基于多种能量密度泛函的RMF理论在研究多种核物理现象取得了巨大成功^[28−29]。在RMF理论中，重子通过交换同位旋标量-标量介子($\sigma$)、同位旋标量-矢量介子($\omega$)和同位旋矢量-矢量介子($\rho$)发生相互作用。模型中的耦合参数通过拟合核物质饱和性质和有限核的基态性质得到。在本篇工作中选取两组的RMF参数，即BigApple模型和 NL3 模型。BigApple和 NL3 模型参数均可以很好地重现核素图中有限核的基态性质，并且都预言了一个较大的中子星最大质量。BigApple模型得出的中子星半径和潮汐变形与GW170817引力波事件观测以及NICER的观测结果相符。众所周知，核物质对称能及其斜率在理解中子星性质方面起着至关重要的作用，且对称能斜率L与中子星半径之间存在正相关关系^[30]。BigApple模型中包含了$\omega$-$\rho$的耦合项，具有相对较小的对称能斜率。相比而言，NL3模型具有较大的对称能斜率L，这导致对于1.4$ M_\odot $的中子星而言，预测出的半径和潮汐变形性相比于天体物理观测的估计值而言偏大。本文研究的重点在于对称能斜率对强子相变及其混杂相结构性质的影响，NL3模型可作为一个良好的对照组。此前许多工作对$ \omega $-$ \rho $的耦合项在改变对称能的密度依赖性以及对中子星性质的影响进行了研究^[31−32]。

对于夸克物质的描述，本文采用 MIT 袋模型，该模型包含了矢量相互作用，通常被称为vMIT模型^[33−34]。文献表明，在夸克间加入矢量相互作用可以显著硬化高密度下物质的状态方程(EOS)，并有助于产生与天文观测相符的大质量中子星^[35]。vMIT 模型中的矢量相互作用通过交换一种类似于 Walecka 模型中$\omega$介子的矢量介子引入^[36]。在Han等^[34]和Gomes等^[33]的研究中，利用Gibbs和Maxwell结构研究了矢量相互作用对致密星性质的影响，但未考虑可能的几何结构。本工作中，我们旨在通过EM方法探讨夸克间的矢量相互作用如何影响强子-夸克pasta相的特性。

在EM方法中，强子-夸克pasta相是通过 Wigner-Seitz 元胞近似来描述。这种近似方法将整个空间分割成多个等效的元胞，每个元胞都具有一定的几何对称性。元胞内部强子相和夸克相由明显的分界面隔开，元胞整体呈电中性。文献[27]提出，在强子相和夸克相中间可能存在一个薄层，这导致两相之间的电势存在差异，使得强子相和夸克相中电子密度不相等，但化学势保持相等。据此观点，尽管两相中的电子密度不同，Maxwell结构仍可能是稳定的。两相间电子密度的差异可以理解为电荷屏蔽效应的结果。本研究将在EM方法中考虑电荷屏蔽效应，进一步研究电荷屏蔽效应对强子-夸克pasta 相影响。

本文将主要研究两部分内容，一是讨论在满足现有观测约束的同时，大质量中子星核心中出现强子-夸克混杂相的可能性以及夸克间矢量相互作用的影响。第二，旨在扩展EM方法以描述考虑电荷屏蔽效应的强子-夸克混杂相。通过允许强子相和夸克相拥有不同的电子密度，在Wigner-Seitz元胞内实现局部$ \beta $平衡，计算电荷屏蔽效应的影响，帮助我们理解强子-夸克混杂相从Gibbs结构(GC)到Maxwell结构(MC)的转变。

我们采用RMF模型描述强子物质，强子物质包含中子，质子，电子和$ \mu $轻 子。均匀核物质的拉氏密度表示为

其中$ W^{\mu\nu} $和$ R^{a\mu\nu} $分别为$\omega^{\mu}, \ \rho^{a\mu}$介子的反对称张量算符。在RMF模型中，核子通过交换不同的介子传递强相互作用。同位旋标量-标量介子$\sigma$反映核子之间的中程吸引力，同位旋标量-矢量介子$\omega$反映核子间的短程排斥力，同位旋矢量-矢量介子$ \rho $反映同位旋相关性，即质子和中子之间的区别。我们采用BigApple和NL3参数组计算强子物质，它们可以很好地描述核素图中原子核的 基态性质。BigApple和NL3参数组的饱和性质在表 1中给出。通过计算系统的能动量张量，我们可以得到强子物质的能量密度和压强。

对于夸克相的描述，我们采用vMIT口袋模型，即在MIT口袋模型的基础上加入夸克间的矢量相互作用。在vMIT模型中，夸克间通过交换一个质量为$ m_V $的矢量介子发生相互作用。夸克物质中包括u，d，s夸克和e，μ轻子。在平均场近似下，夸克物质的拉氏密度为

B代表口袋常数；$ \varTheta $是阶梯函数。矢量场$ V_{0} $的数值通过求解矢量介子的运动方程获得，

$ n_i $是夸克$ i $的粒子数密度。夸克$ i $的化学势为

矢量相互作用$ G_V $的加入，提高了夸克$ i $的化学势。均匀夸克物质的能量密度和压强为

式中$ \varepsilon^i_{\rm{FG}} $和$ P^i_{\rm{FG}} $分别为自由费米气体的能量密度和压强。夸克物质中矢量相互作用对中子星高密处的EOS有重要的影响。在本章的计算中，我们将通过改变耦合常数$ G_V=(g_V/m_V)^2=0 \sim 0.3 $fm²，讨论夸克间矢量相互作用对强子-夸克混杂相的影响。

对于强子-夸克混杂相，我们采用Wigner-Seitz(WS)元胞近似，即系统被分为许多相同的具有特定对称性的元胞。在元胞内部，强子相和夸克相由一个分界面隔开。此分界面具有一定的表面张力。关于表面张力的取值，有很大的不确定性^{[18, 37]}。文章基于 MIT 口袋模型使用 MRE 方法计算表面张力，得到强子-夸克混杂相中表面张力范围为43~48 MeV/fm^2[22]。在本文计算中，我们采用相同量级的常数值$ \sigma =40 $ MeV/fm²。我们采用共存相(CP)方法和 EM 方法计算强子-夸克混杂相。CP方法符合Gibbs结构的平衡条件，将表面能和库仑能作为微扰相添加在系统能量密度中。EM 方法中我们不仅将表面能和库仑能自洽加在混杂相能量密度中，还考虑了电荷屏蔽效应带来的影响，即强子相和夸克相拥有不同的电子密度，从而引入库仑相互作用。库仑相互作用的引入会改变混杂相中带电粒子的分布^[23]，影响强子-夸克混杂相的结构性质。对比 EM 方法和CP方法，我们得到电荷屏蔽效应对强子-夸克混杂结构性质的影响。

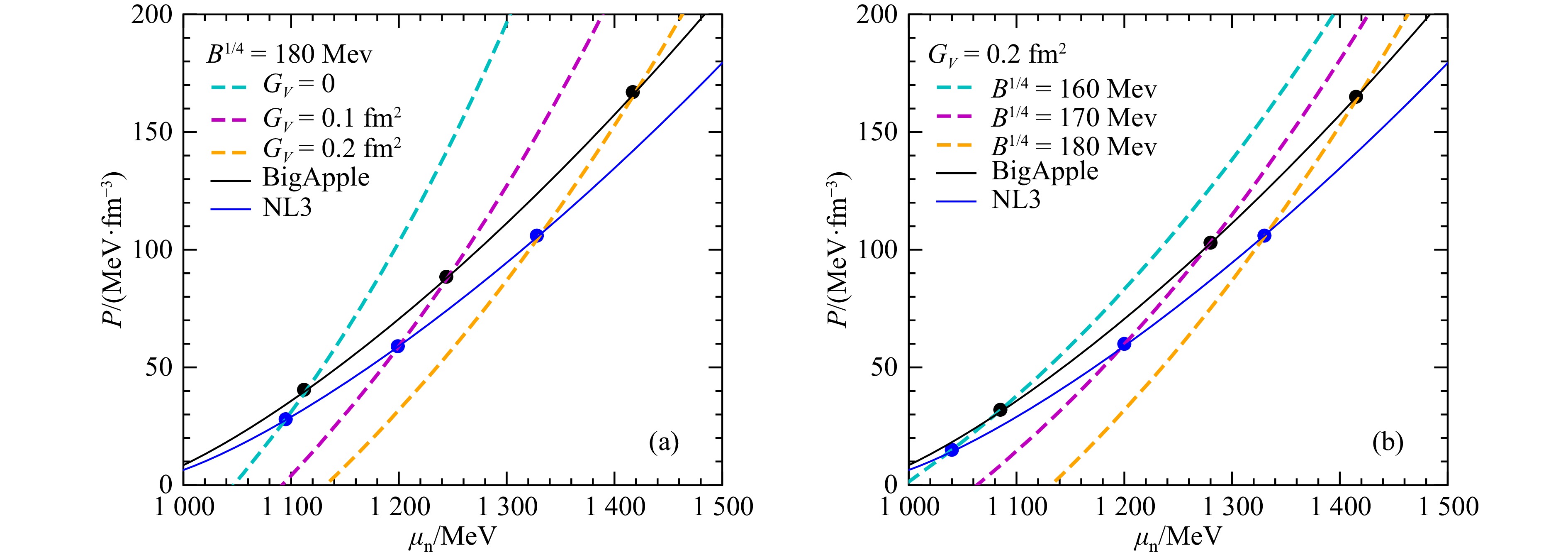
在研究强子-夸克相变中通常采用的方法是Maxwell结构。Maxwell结构满足局域电中性条件，强子相与夸克相具有相同的压强和重子化学势。因此Maxwell结构的相变点为强子物质与夸克物质的压强随化学势变化曲线的交叉点处。图1(a)和(b)分别展示了在不同的矢量相互作用$ G_V $和口袋常数B的情况下，压强随中子化学势的变化，图中黑色实线是BigApple参数组的结果，蓝色实线为 NL3 的结果。Maxwell相变发生在强子物质和夸克物质的 EOS 曲线的交叉点。由图1(a) 可以发现，$ G_V $越大，相变点的压强越大，相变密度越大。图1(b) 可以看出，口袋常数B越大，相变点压强越大，相变密度越大。相比于 NL3 参数组，BigApple 模型预言了一个更大的压强，导致相变密度更大。我们得到矢量相互作用$ G_V $和口袋常数B越大，会推迟强子-夸克相变过程的发生。

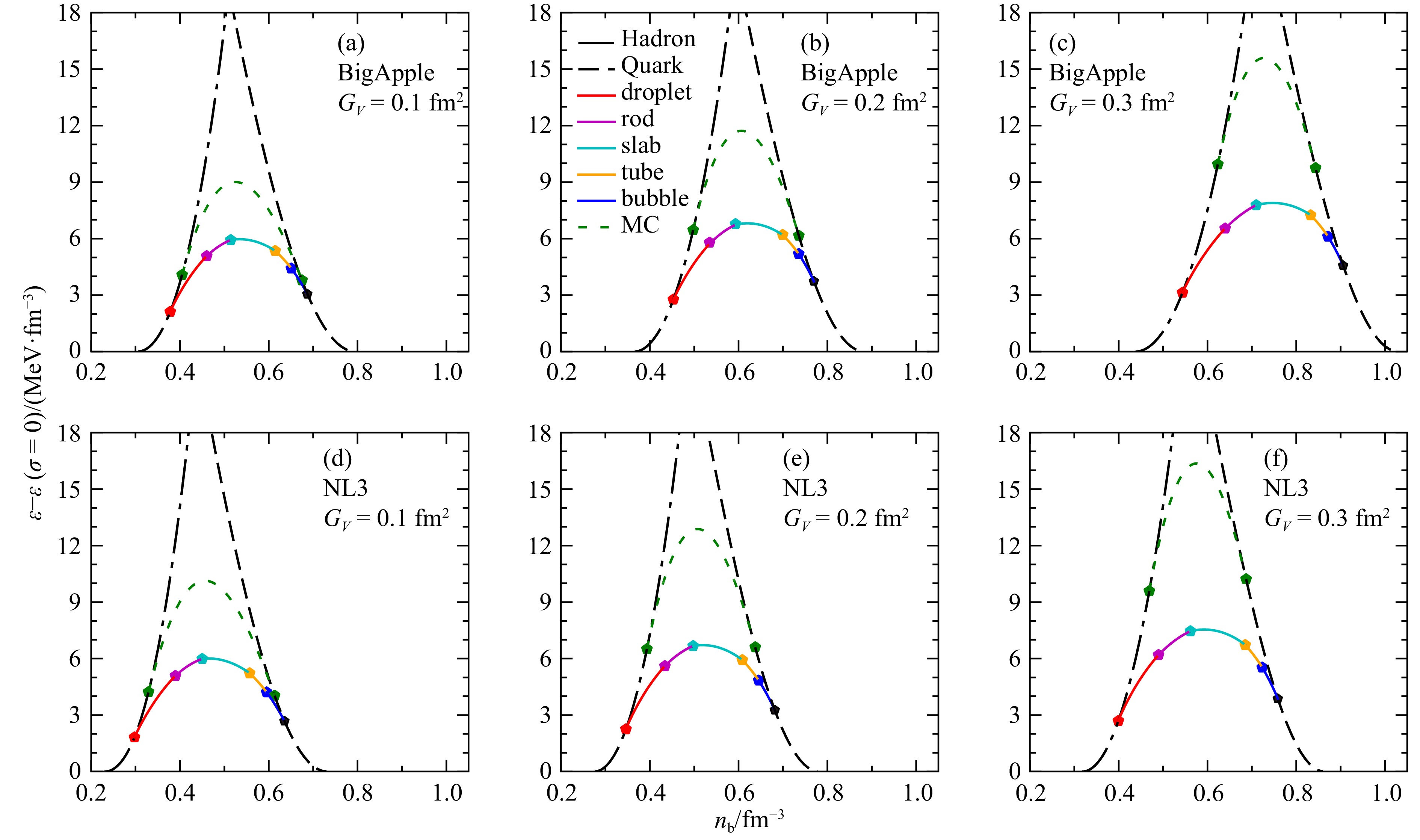
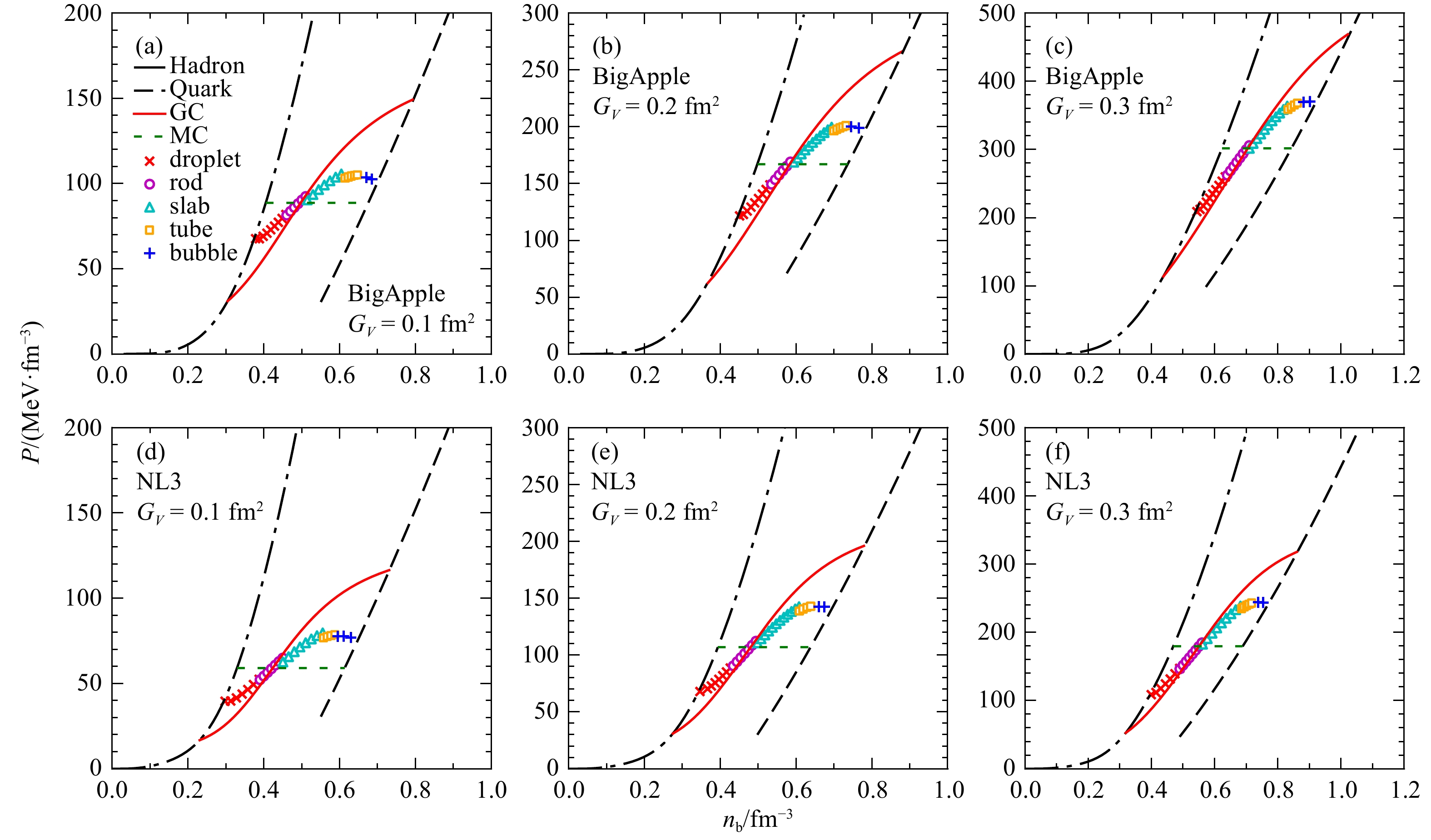
我们使用EM方法计算了强子-夸克混杂相的性质，并与Gibbs的结果进行了比较。EM方法中自洽地将有限尺度效应，即表面能和库仑能的贡献，考虑在系统能量密度中。图2展示了口袋常数$ B^{1/4}=180 $ MeV，表面张力$ \sigma=40 $ MeV/fm²情况下，EM方法计算得到的pasta相与Gibbs$(\sigma =0) $结构的能量密度差值随着重子数密度的变化曲线。实心圆点代表pasta相变点，纯强子相和纯夸克相的能量密度分别用黑点划线和虚线表示，Maxwell结构用绿色虚线表示。由图2看出，强子-夸克pasta相结构随着重子数密度的增加，由droplet逐渐变为rod，slab，tube，bubble，最后相变为纯夸克相。EM方法的结果始终高于Gibbs的结果，说明库仑能和表面能对系统总能量的贡献为正。Maxwell结构一直高于pasta相的结果，表明此时pasta结构更稳定。对比第一行和第二行，可以看到强子物质的EOS的变化对强子-夸克相变的影响。结果表明NL3模型发生相变的密度点早于BigApple模型发生相变的密度点，这与图1的结果一致。对比$ G_V=0.1, \ 0.2, \ 0.3 $ fm²的结果，可以看到随着$ G_V $的增加，混杂相向高密处移动，且其覆盖的密度范围更宽，这与图1(a)中Maxwell结构的变化趋势一致。

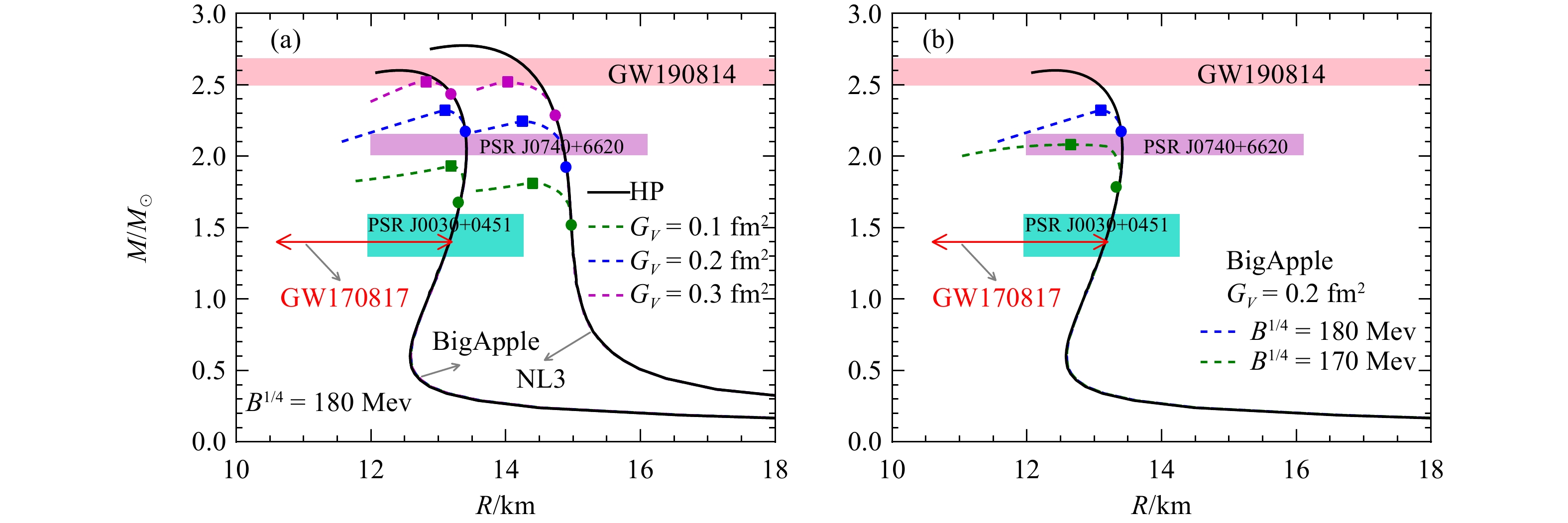
图3展示了压强随重子数密度的变化曲线，其中vMIT模型中口袋常数为$ B^{1/4}=180 $ MeV。Maxwell结构在相变过程中保持压强不变，Gibbs结构在相变过程中压强随重子数密度的增加而增加。随着矢量相互作用$ G_V $的增加，可以看到强子-夸克混杂相出现在更高的密度处。其中$ G_V $对强子-夸克混杂相结束的密度点影响较为明显，这是因为随着重子数密度增大，夸克相的体积分支比逐渐增加，夸克间的相互作用在混杂相中逐渐占据主导地位。对比图3中第一行和第二行，发现在给定重子数密度$ n_{\rm{b}} $时，NL3模型相比于BigApple模型预言了一个更小的压强，导致NL3模型描述的强子物质更早地发生相变，这与图2的结果一致。

在图4中，我们展示了中子星质量-半径关系，以及一些来自天体物理观测的约束条件。我们发现与纯强子EOS(实线)的结果相比，夸克自由度的出现明显降低了中子星的最大质量$ M_{\rm max} $。对比NL3和BigApple模型的质量-半径关系曲线，发现NL3模型预言了一个较大的中子星半径，这是因为NL3模型具有一个较大的对称能斜率$ L $。根据现有的天文观测给出的限制，我们更倾向于一个较小的对称能斜率$ L $。相比之下，BigApple模型参数组预言的$ R_{1.4} $满足GW170817和NICER对PSR J0030+0451的测量给出的限制。从图4(a)可以看到矢量相互作用$ G_V $对中子星的最大质量影响非常明显。矢量耦合越强，即$ G_V $越大，中子星的最大质量也越大，混杂相出现越晚。对于$ 1.4\ M_\odot $中子星，中心密度尚未达到混杂相出现的条件，此时中子星核心仍为强子物质，这和文章结果一致^[38]。图4(b)中包括$ B^{1/4}=180 $ MeV和$ B^{1/4}=170 $ MeV两种情况的结果，可以看到口袋常数$ B $对中子星最大质量的影响。口袋常数$ B $越小，中子星的最大质量越小。这是因为$ B $越小，强子-夸克混杂相出现的越早，中子星的EOS变软导致。为了详细地分析强子-夸克混杂相对中子星的影响，我们在表 2中展示了在BigApple和NL3模型中，分别使用EM和CP方法计算得到的中子星最大质量的结构性质。对比表 2中第一、二、三行，可以看到矢量耦合作用$ G_V $越强，中子星中心密度越大，所支持中子星最大质量越大，但混杂相的半径在减小。在口袋常数$ B^{1/4}=180 $ MeV时，无论是BigApple模型还是NL3模型，中子星内部都只出现了强子-夸克混杂相核心没有纯夸克相的出现。采用同样的口袋常数$ B $，对比EM方法和CP方法的计算结果，可以发现EM方法因为考虑了电荷屏蔽效应，得到的中子星的最大质量小于CP方法的结果。此外我们发现口袋常数为$ B^{1/4}=170 $MeV时，此时中子星的中心密度大于纯夸克相的出现密度，出现了纯夸克相核心。

在本文工作中，我们采用了基于RMF模型BigApple参数和NL3参数计算强子物质，包含矢量相互作用的MIT口袋(vMIT)模型计算夸克物质。我们发现在同等重子数密度下，相比NL3模型，BigApple模型预言了一个更高的压强，导致混杂相的出现密度大于NL3模型。通过对比夸克物质中矢量相互作用$ G_V=0.1, \ 0.2, \ 0.3 $ fm²三种情况的结果，我们发现矢量相互作用越强，即$ G_V $越大，高密处的中子星EOS越硬，从而导致中子星的最大质量更大。同时矢量相互作用强度越高，强子-夸克混杂相的出现越晚，对纯夸克相的出现密度影响最为显著。我们对比了口袋常数$ B^{1/4}=180 $ MeV和$ B^{1/4}= 170 $ MeV两种情况的结果，以及矢量相互作用$ G_V= 0.1, \ 0.2, \ 0.3 $ fm²三种情况的结果，结果表明口袋常数$ B $越小，中子星最大质量越小；$ G_V $越大，夸克相出现引起的中子星质量减小的幅度越小。在本文的模型框架中，夸克自由度的出现明显地软化了中子星的EOS，降低了中子星的最大质量。基于本文模型，强子-夸克混杂相可能会出现在大质量中子星的内部，$ 1.4M_\odot $质量的中子星不支持夸克自由度的出现。