相对论重离子碰撞不仅会产生具有强集体性的夸克-胶子等离子体^[1−7]，而且还会产生目前人类所知的最强磁场，这是由于弹核和靶核中不参与碰撞的带电质子以接近光速相互穿越^[8−13]。这恰好为研究QCD(Quantum Chromodynamics)真空的拓扑特性和强磁场下的反常输运现象提供了实验场所^[14−17]。一种众所周知的反常输运现象是手征磁效应(Chiral Magnetic Effect, CME)，它导致了在手性不平衡的系统中的电荷沿磁场方向的分离^[18−20]。

文献[21]中电荷相关的方位角关联首次被提出来作为检测CME是否存在的观测量，即$ \gamma_{\alpha \beta}=\langle \cos(\phi_{\alpha}+ \phi_{\beta}-2\psi_{\rm RP}) \rangle $，其中$ \phi_{\alpha(\beta)} $是带电粒子$ \alpha(\beta) $的方位角，$ \psi_{\rm RP} $是反应平面的方位角，$ \varDelta \gamma=\gamma_{{\mathrm{OS}}}-\gamma_{{\mathrm{SS}}} $表示异号电荷和同号电荷之间的差异。电荷相关方位角的首次测量结果来自美国布鲁克海文国家实验室(BNL)相对论重离子对撞机(RHIC)的STAR合作组^[22−25]，欧洲核子研究中心(CERN)的大型强子对撞机(LHC)的ALICE合作组^[26]也进行了测量，结果均与CME的预期一致，即$ \varDelta \gamma>0 $。然而不幸的是，由于存在强集体运动，一些背景效应对测量的结果有贡献，特别是来自椭圆流的贡献^[27−31]。最近RHIC-STAR给出了一个严格的约束结果，即在200 GeV的Au+Au碰撞中提取的CME信号是相当小的，应小于10%^[32−35]。目前已经提出了许多不同的方法或方案^{[34, 36]}将可能存在的CME信号从主要的背景中区分出来。最重要的方案之一是RHIC-STAR合作组进行质心碰撞能量为200 GeV的同质异位素碰撞^[37−38]，因为两个同质异位素系统$ ({}_{44}^{96}{\mathrm{Ru}}+ {}_{44}^{96}{\mathrm{Ru}} $和$ {}_{40}^{96}{\mathrm{Zr}}+{}_{40}^{96}{\mathrm{Zr}}) $具有相同的核子数，但质子数不同^[39]，预计在类似的椭圆流背景下，CME信号可能有20%的差异^[40−43]。

由于CME信号与磁场强度呈正相关，理论上预测来自Ru+Ru碰撞的CME信号与Zr+Zr碰撞的CME信号之比要大于1，然而，STAR新发布的实验结果观察到的各种方法均显示CME信号的观测量比值都小于1^[38]。这表明，背景效应在观测量中占主导地位，CME信号在同质异位素碰撞中要么没有，要么非常小。例如，不同的核结构或核形变被用来解释两个同质异位素系统之间的粒子多重性和集体流的差异^[44−52]。考虑到晕型中子皮结构，我们已经证明，如果在同质异位素碰撞中CME强度较弱，在CME的观测结果中很难区分CME是否存在^[53]。同时，根据最近在AVFD模型中的发现，同质异位素碰撞的实验结果倾向于存在有限的CME信号贡献，大小约为(6.8±2.6)%^[54]。

许多实验观测方法已经被用来探测Au+Au和同质异位素碰撞中的CME信号。在文献[50, 55]中提出了一种利用相对于旁观者平面(SP)和参与者平面(PP)的电荷方位角相关性的双平面测量方法，出发点是背景效应和CME信号对这两个平面的灵敏度或相关性是不同的^[56]。STAR合作组已经使用该方法检测了在Au+Au和同质异位素碰撞$ \varDelta \gamma $关联子中CME信号的比例。对于在$ \sqrt{s_{_{\rm NN}}}=200 \;{\mathrm{GeV}}$的Au+Au碰撞，STAR的结果显示，CME诱发的电荷分离的比例在周边碰撞和中心碰撞接近零，但在偏中心碰撞中可能存在有限的CME信号^[57]，而在$\sqrt{s_{_{\rm NN}}}=200 \;{\mathrm{GeV}}$的同质异位素碰撞中没有观察到明显的CME信号。这个方法可以消除背景效应中集体流的大部分影响，但一些非流的背景效应有待进一步研究^[58]。在文献[57]中，假定了椭圆流相对于不同反应平面的比值a(背景透射率)与CME信号相对于不同反应平面的比值b(CME信号透射率)相同，然而，这两个比值可能是不同的，目前测量中的a与b相等的假设是由于缺乏对比值b的理论研究^[57−59]。为了解决这个问题，需从理论上研究CME信号相对于不同反应平面之间的比值b，这促使我们在$\sqrt{s_{_{\rm NN}}}=200 \;{\mathrm{GeV}}$的同质异位素碰撞中通过使用带有初始CME信号的多相输运(AMPT)模型来计算比值b，以便为CME的实验测量提供一些理论支持。

本文组织如下，在第1节，我们介绍了AMPT模型，该模型有一个初始CME信号用于同质异位素碰撞，以及计算比值b的方法和如何用双平面方法来提取$ \varDelta \gamma $中包含的CME信号。第2节中，我们比较了我们的模型结果和STAR实验的测量结果，并讨论了我们的发现对实验结果的影响和可能的物理来源。最后一节给出了一个总结。

AMPT模型是一个混合输运模型，有四个子模型模拟相对论重离子碰撞的四个主要阶段^[60−62]：1) HIJING模型提供了初始条件：碰撞核的横向密度分布由Woods-Saxon分布给出。2) 采用Bin Zhang的部分子级联模型(ZPC)模拟部分子级联阶段：描述了两体弹性散射下的部分子相互作用，用胶子-胶子相互作用的领头阶pQCD计算了部分子碰撞截面。3) 夸克聚合模型将两个或三个最接近的部分子组合成强子来模拟强子化。4) 相对论输运(ART)模型模拟了强子重散射阶段，包括重子-重子、重子-介子和介子-介子相互作用的弹性和非弹性散射的共振衰减和所有强子反应。许多先前的研究表明，AMPT模型可以很好地描述RHIC和LHC能量下大系统和小系统碰撞中的各种实验观测结果^[60−69]。

为了模拟同质异位素碰撞，根据球坐标系下的Woods-Saxon公式可以给出静止坐标系下${}_{44}^{96}{\mathrm{Ru}} $和${}_{40}^{96}{\mathrm{Zr}} $的内部的核子空间分布：

其中：ρ₀为核密度；a₀为表面扩散系数；R₀为核半径；β₂和β₃为核的四极形变和八极形变。在文献[53]中我们发现，在18种不同抽样分布中晕型中子皮的结构得到的模型计算结果最符合带电粒子多重数分布、平均带电粒子数和椭圆流的实验比值结果。因此，我们在研究中也选择了晕型中子皮的结构，其中${}_{44}^{96}{\mathrm{Ru}} $和${}_{40}^{96}{\mathrm{Zr}} $没有形变，即$ \beta_2=\beta_3=0 $，但在${}_{44}^{96}{\mathrm{Ru}} $内质子和中子的$ R_0=5.085 $，$ a_{0}=0.523 $，而${}_{40}^{96}{\mathrm{Zr}} $内质子的$ R_0=5.021 $，$ a_{0}=0.523 $，中子的$ R_0=5.021 $，$ a_{0}=0.592 $，这是由于${}_{40}^{96}{\mathrm{Zr}} $可能存在晕型中子皮。在文献[70]中，类似CME的电荷分离已经被引入AMPT模型的初始部分子阶段，通过调整参与电荷分离的夸克的比例p，可以控制CME的强度。p的定义是：

其中：N为给定的(u或d或s)的夸克数；+和−表示夸克的正电荷和负电荷；↑和↓表示夸克沿磁场的运动方向。考虑到Ru+Ru和Zr+Zr碰撞的磁场是不同的^[56]，我们实际上是根据磁场的大小和方向，通过计算每个事件的磁场来设定初始电荷分离，若$p_{{\mathrm{Ru}}+{\mathrm{Ru}}}^{}$表示为Ru+Ru碰撞中的CME强度，则要保持$p_{\rm Ru+Ru}^{}/p_{\rm Zr+Zr}^{}=1.15$，例如，$ p=2 \text{%} $表示$p_{\rm Ru+Ru}^{}=2 \text{%}$而$p_{\rm Zr+Zr}^{}=2 \text{%} /1.15=1.74 \text{%}$。

在双平面方法中，椭圆流的背景效应被认为与参与者平面(PP)更相关，但CME信号与旁观者平面(SP)更相关^{[50, 55]}。为了与实验的情况相符合，本文的椭圆流和观测量$ \varDelta \gamma $的计算中用末态强子的事件平面(EP)来代替参与者反应平面(PP)，需要注意的是椭圆流和观测量$ {\varDelta}\gamma $的计算中需要进行修正^[71−72]。关于使用参与者反应平面(PP)和旁观者反应平面(SP)的相关计算方法和结果，在文献[73]中进行了详细的讨论。下面用式(4)来重构旁观者反应平面$ \psi_\mathrm{ S P} $，式(5)用来重构事件平面$ \psi_\mathrm{EP} $，

式(4)中，$ r_{{\mathrm{ne}}} $和$ \phi_{{\mathrm{ne}}} $分别是AMPT模型中初态的旁观者中子在横平面上的半径和方位角。式(5)中，n的值为2，$ w_i $和$ \phi_i $分别是满足$ 0.2<p_T<2.0 \; \mathrm{GeV} / c $和$ |\eta|<1 $内的末态中性强子在横平面的动量和方位角，这里用末态中性强子而不是带电粒子来重建事件平面(EP)是为了避免与计算椭圆流$ v_2\{\mathrm{EP}\} $时使用的带电粒子产生自关联，M则表示满足上述范围内的末态中性强子的总数目。两个不同的平面相应的椭圆流$ v_2\{\mathrm{SP}\} $和$ v_2\{\mathrm{EP}\} $，可以分别用下面的公式计算：

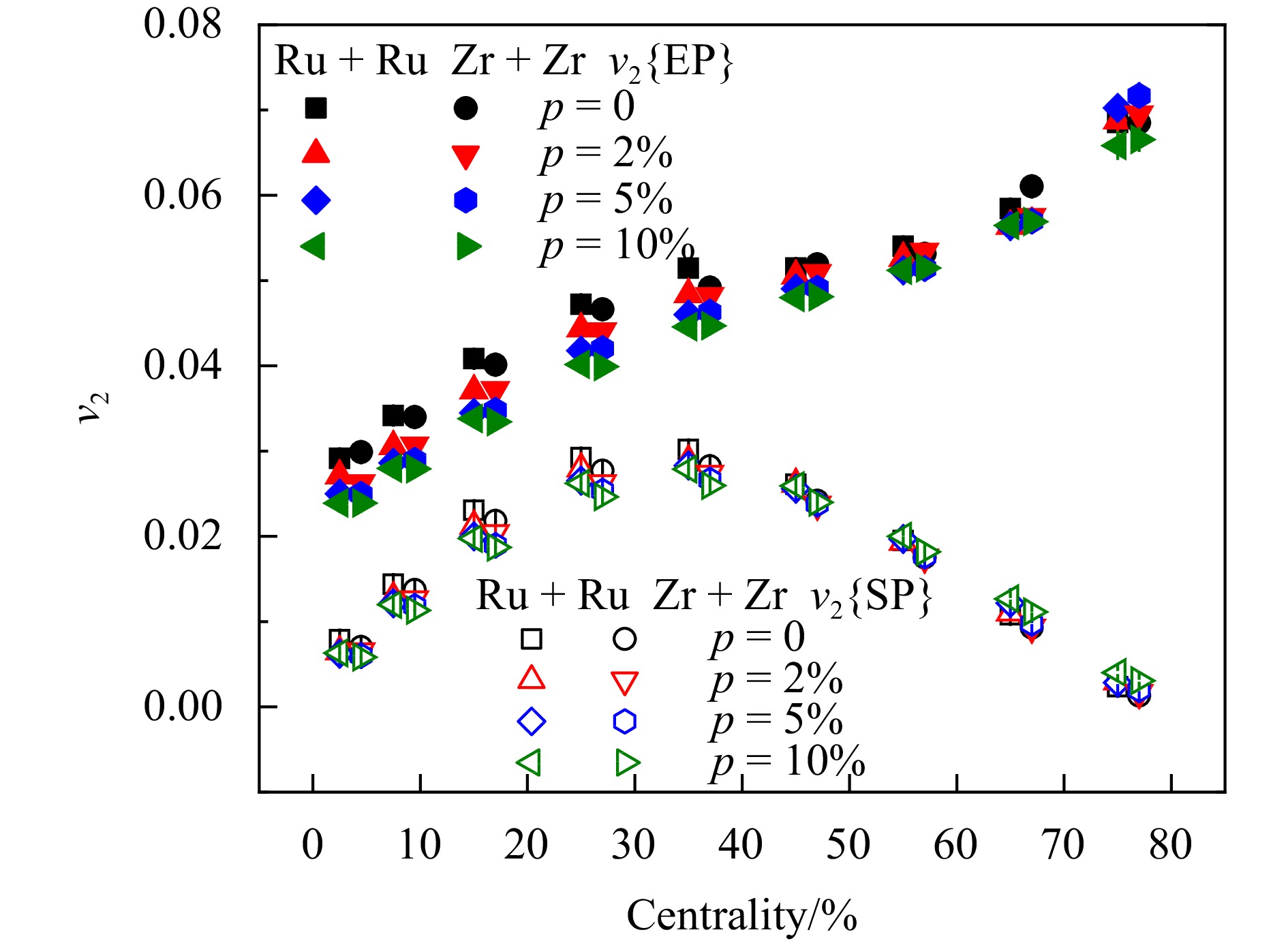
式(6)中ϕ是末态带电强子的方位角；$ \psi_{ \rm SP} $来自式(4)。式(7)中ϕ也是末态带电强子的方位角；$ \psi_{ \rm EP} $来自式(5)，此外还需要考虑分辨率的修正R^[71]。

图1表示来自不同CME强度的AMPT模型中范围为$ 0.2<p_T<2.0\; \mathrm{GeV}/c $和$ |\eta|<1 $末态带电强子的$ v_2\{\mathrm{EP}\} $和$ v_2\{\mathrm{SP}\} $的中心度依赖关系。可以看到，在所有情况下，$ v_2\{\mathrm{EP}\} $都大于$ v_2\{\mathrm{SP}\} $，因为椭圆流与参与者平面的相关性要大于旁观者平面(事件平面)。另一方面，对于0~50%的中心度，$ v_2\{\mathrm{EP}\} $和$ v_2\{\mathrm{SP}\} $都随着CME信号强度的增加而略有下降。对于50%~80%的中心度，$ v_2\{\mathrm{EP}\} $和$ v_2\{\mathrm{SP}\} $对CME信号的强度都不敏感。

在本小节中，首先介绍检测CME信号的双平面方法，然后讨论如何利用AMPT模型改进双平面方法。

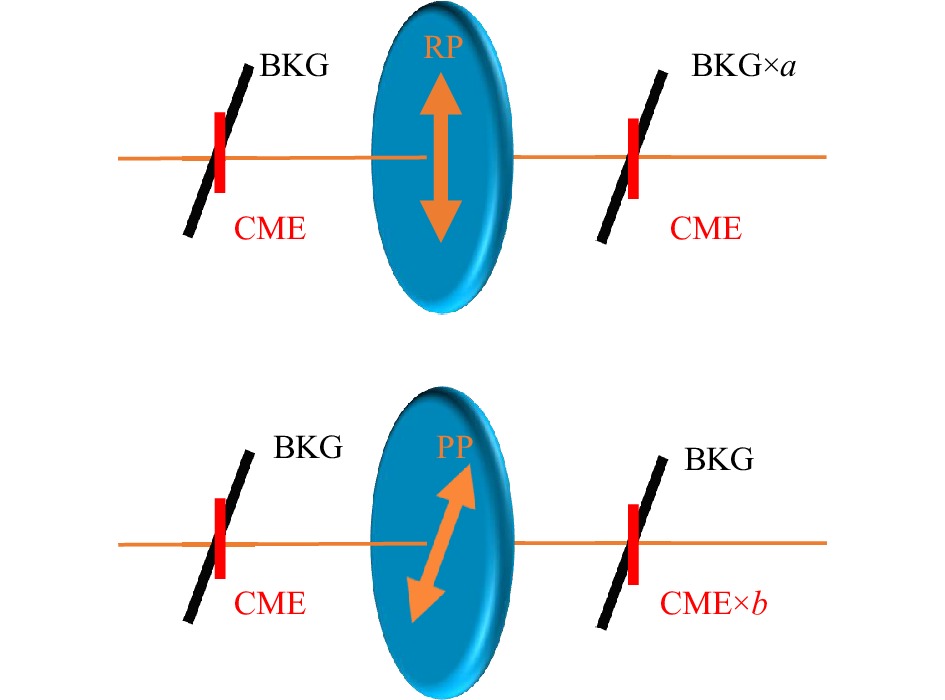
图2展示了椭圆流相对于不同反应平面的比值a(背景透射率)和CME信号相对于不同反应平面的比值b(CME信号透射率)的情形。背景效应不能完全透射RP平面(或SP平面)，需要通过背景透射率 a进行修正；而CME信号也不能全部透射PP平面，需要通过CME信号透射率b进行修正。实验测量的CME观测值$ \varDelta \gamma $包含了CME信号和主要由椭圆流和非流效应产生的背景效应，因此，CME观测值$\varDelta \gamma $相对于不同的反应平面可以分为以下两部分：

其中ψ代表$ \psi_{\rm PP} $或$ \psi_{\rm SP} $两种不同平面的椭圆流和观测量的比值可以分别用a和A来定义，如下所示：

其中a遵循两个平面的相关系数，即$ a = \langle\cos 2\left(\varPsi_{\mathrm{PP}}- \varPsi_{\mathrm{SP}}\right)\rangle $^{[55, 74−75]}。由于CME信号在实验中不能直接测量，通常认为不同反应平面的CME信号之比是a的倒数，因此，可以得到以下关系：

经过简单的变换，CME信号在观测量内的百分比$ f_{\mathrm{CME}} $可通过以下方式获得：

式 (12)表明，通过计算A和a可以得到CME观测量内CME信号的百分比。然而，参考文献[58−59]中指出，CME信号的比例和椭圆流的反比可能是不同的。若假设以下关系成立：

其中b代表CME信号相对于不同平面的比值。通过替换式(11)中的相应部分，可以得到一个新的关系式，如下所示：

因此，当考虑b后，更真实的CME信号在可观测值内的百分比可通过以下公式计算：

其中：a来自式(9)；A来自式(10)；还需要计算b值。在AMPT模型中，CME信号是通过影响初始状态下的一定比例的部分子来模拟的，CME影响的部分子的比例在本文中用p表示。在我们的模型中，b的值可以通过使用以下公式得到：

其中分子和分母分别表示相对于参与者和旁观者平面的观测量内的CME信号。

在这一节中，我们介绍AMPT关于带电粒子相对于旁观者和参与者平面的电荷相关方位角的计算结果，并将其与STAR同质异位素碰撞的实验结果进行了比较。我们选取的末态带电强子范围与STAR实验一致，为$ 0.2<p_T<2.0 \mathrm{\; GeV} / c $和$ |\eta| < 1 $。为了与实验的情况相符合，下面的结果是用末态强子的事件平面(EP)代替了式(9)~(16)中的参与者反应平面(PP)，同时要注意$ {\Delta} \gamma \{\mathrm{EP}\} = \gamma_{{\mathrm{OS}}} \{\mathrm{EP}\} - \gamma_{{\mathrm{SS}}} \{\mathrm{EP}\} $，$ \gamma \{\mathrm{EP}\} = \langle \cos \left(\phi_{\alpha}+\phi_{\beta}- 2 \psi_{\mathrm{EP}}\right) \rangle / R $，其中R与式(7)中的R是相同的，而$ \varDelta \gamma\{\mathrm{SP}\} $的计算不需要进行修正。

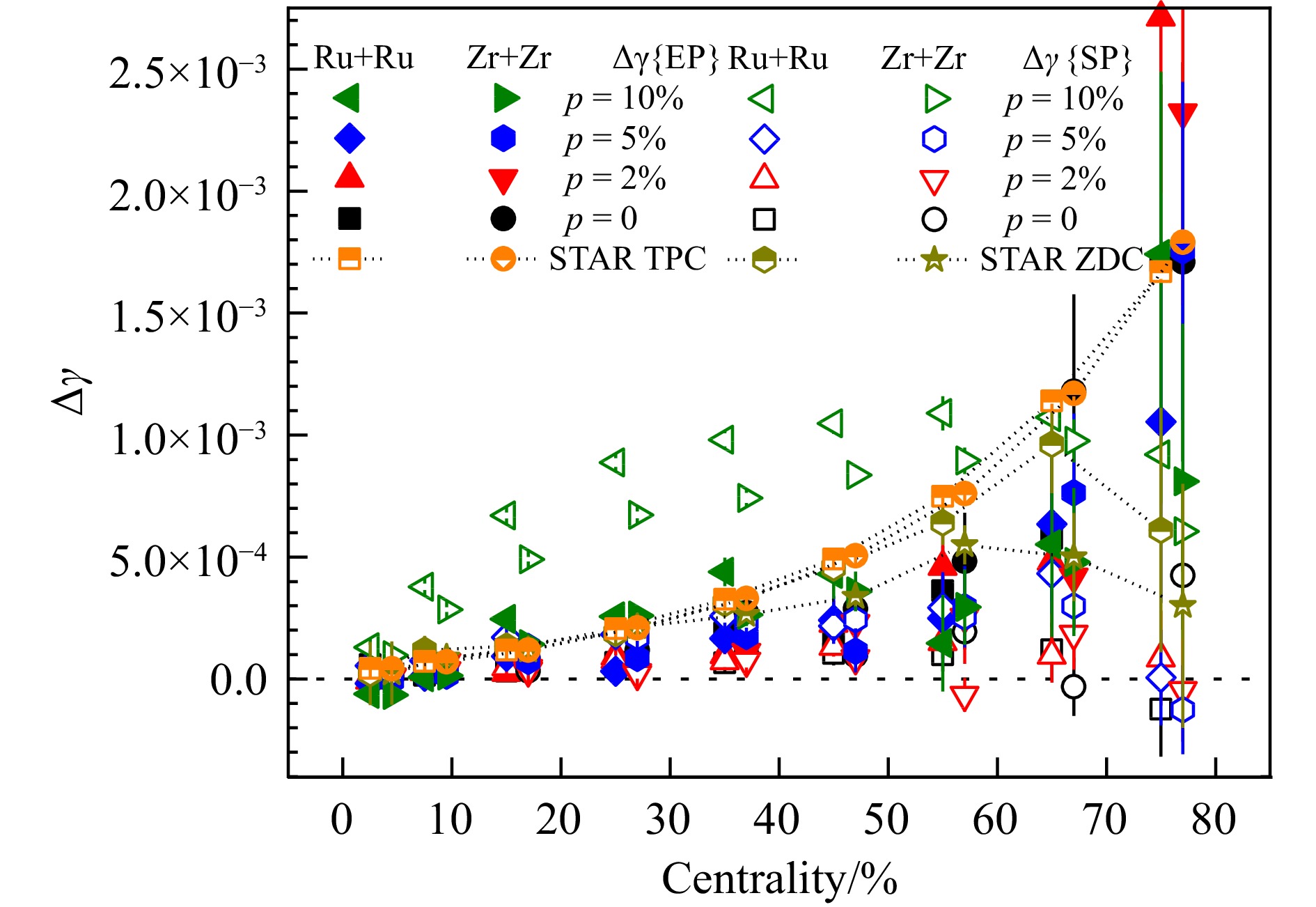
图3展示了$ \varDelta \gamma\{\mathrm{EP}\} $和$ \varDelta \gamma\{\mathrm{SP}\} $的中心度依赖，在$ \sqrt{s_{_{\rm NN}}} = 200 \;{\mathrm{GeV}}$的Ru+Ru和Zr+Zr碰撞中$ \varDelta \gamma\{\mathrm{EP}\} $和$ \varDelta \gamma\{\mathrm{SP}\} $的中心度依赖来自不同强度CME的AMPT模型的结果。当模型中CME的强度大于5%后，$ \varDelta \gamma\{\mathrm{SP}\} $大于$ \varDelta \gamma\{\mathrm{EP}\} $，这表明$ \varDelta \gamma\{\mathrm{SP}\} $对CME比$ \varDelta \gamma\{\mathrm{EP}\} $更敏感，因为旁观者平面与磁场方向的相关性比参与者平面(事件平面)更强。

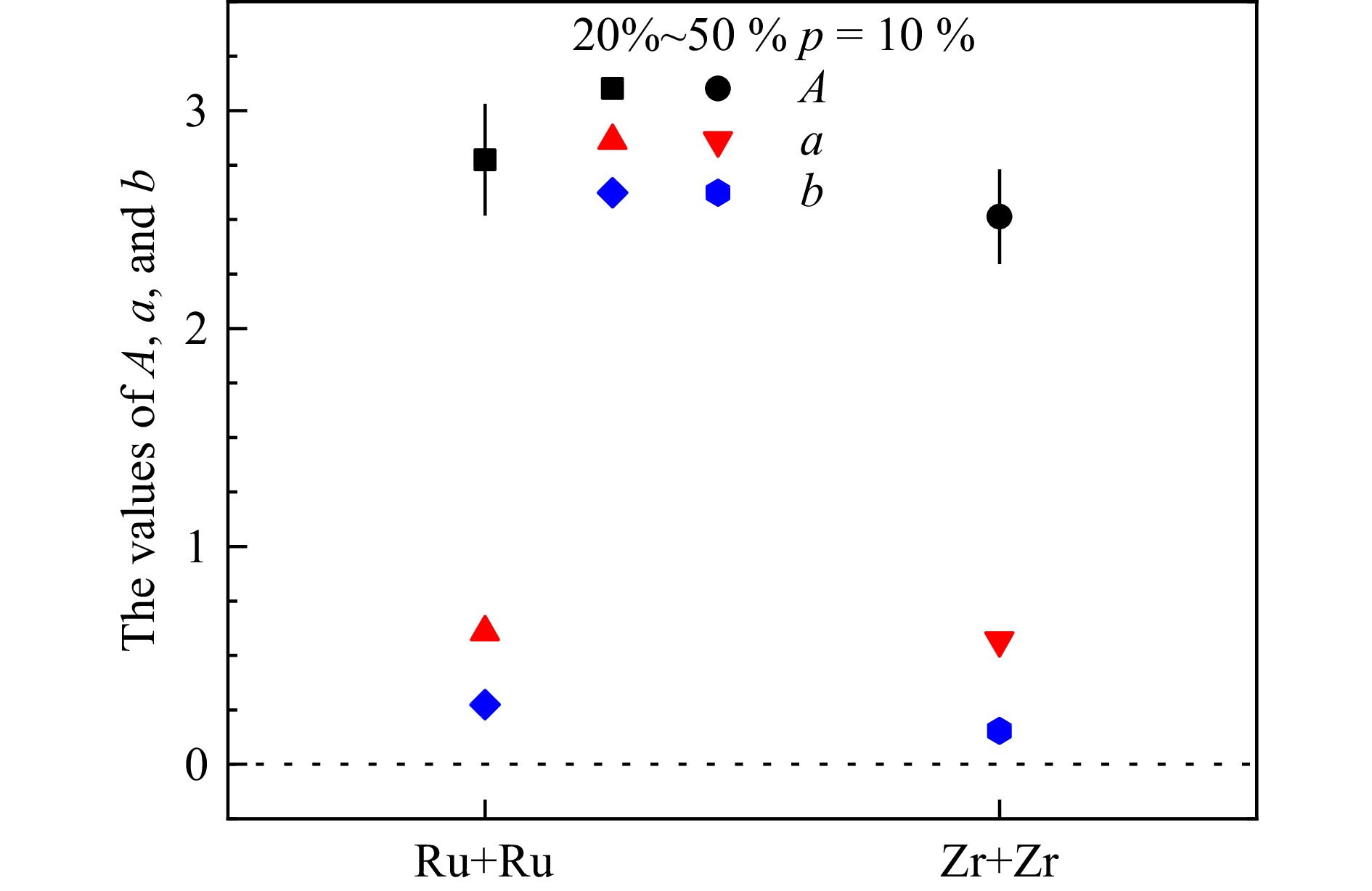
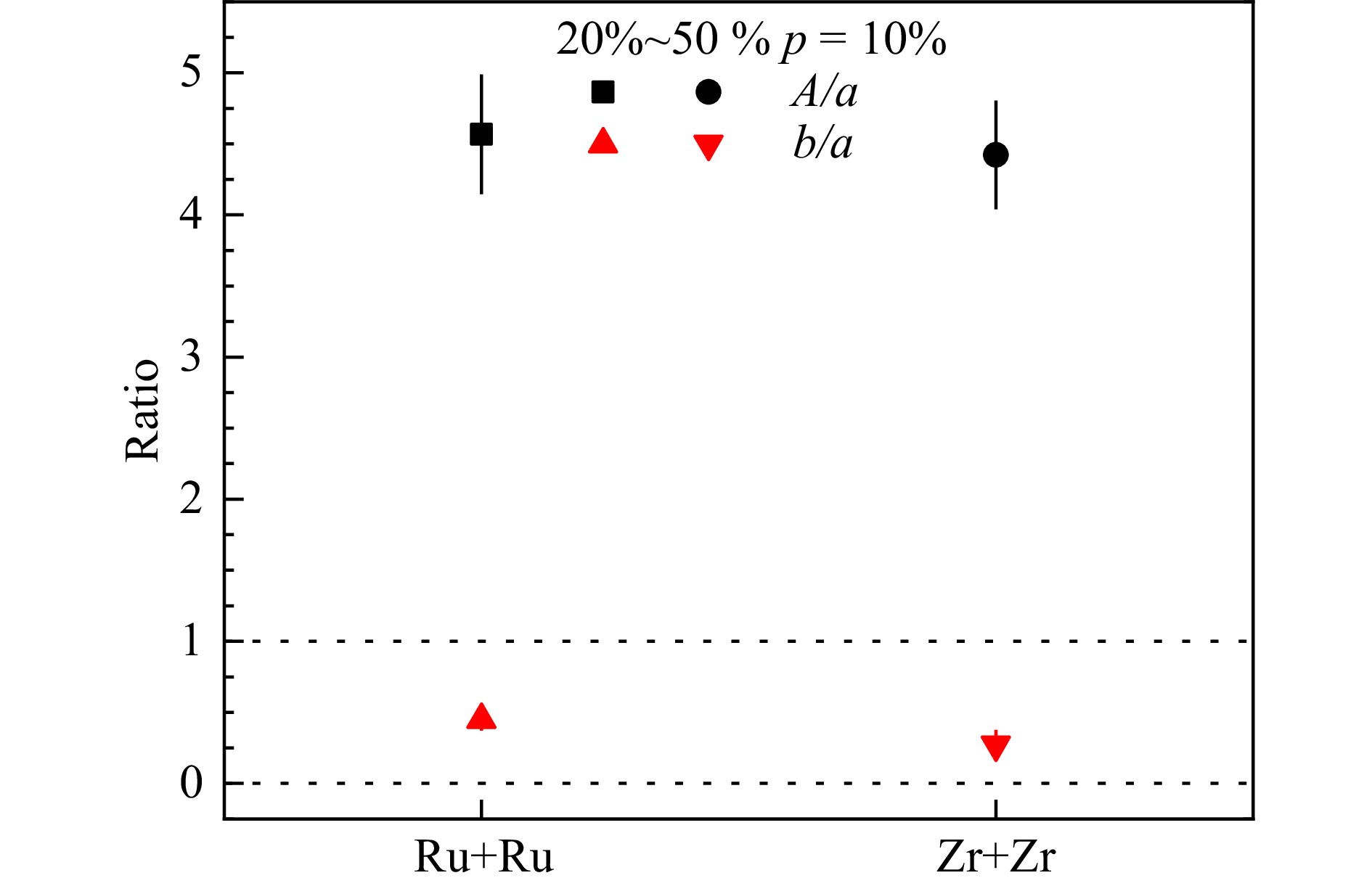
实验结果^[38]表明中心度为20%~50%时更有可能测得CME信号。后面我们通过CME的强度$ p=10 \text{%} $，中心度取20%~50%为例给出相应的计算结果。图4中，横轴分别表示Ru+Ru和Zr+Zr碰撞，纵轴表示的数值结果来自比值公式，A可以通过式(10)计算得到，要注意$ \varDelta \gamma\{\mathrm{PP}\} $用修正后的$ \varDelta \gamma\{\mathrm{EP}\} $代替，a可通过式(9)得到，其中用$ v_2\{\mathrm{EP}\} $代替$ v_2\{\mathrm{PP}\} $，式(16)中$ \varDelta \gamma\{\mathrm{PP}\} $也是用修正后的$ \varDelta \gamma\{\mathrm{EP}\} $代替。可以发现，A的值比a大，b的值比a小。

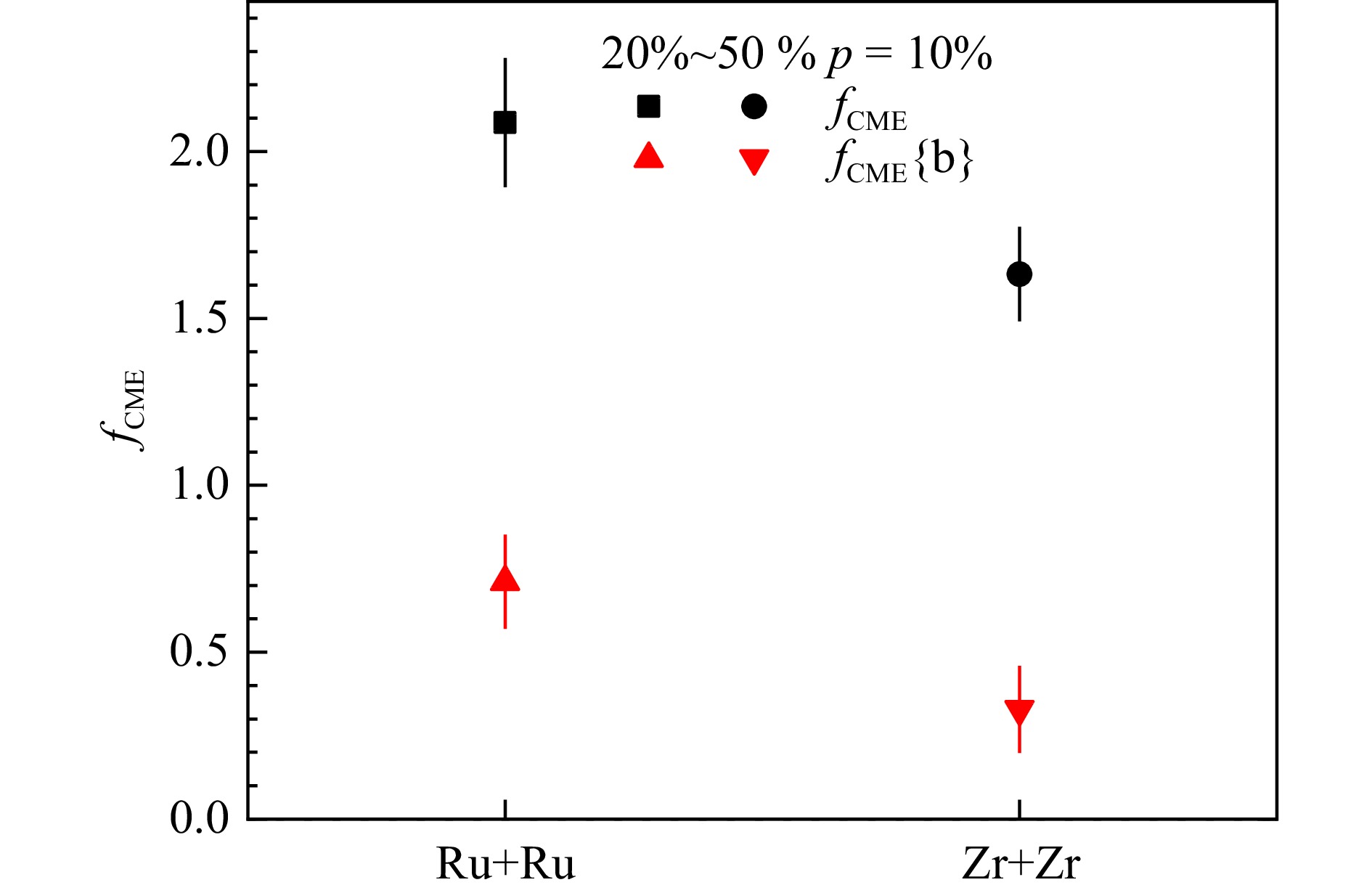
图5来源于图4中A与a和b与a的比值结果，通过式(12)和式(15)可以发现，a与b均大于0，当$ A/a $的值大于1时，表明观测量$ \varDelta \gamma\{\mathrm{PP}\} $($ \varDelta \gamma\{\mathrm{EP}\} $)中存在CME信号。

在图6中可以发现，同质异位素碰撞中心度为20%~50%，$ p=10 \text{%} $时，$ f_{\mathrm{CME}}\{\mathrm{b}\} $的值均小于$ f_{\mathrm{CME}} $的值。这表明，如果假定$ b=a $，CME信号在可观测量$ \varDelta \gamma $内的比例将被高估。同时，结合图3也可以发现，提取自Ru+Ru碰撞的CME信号($\varDelta \gamma\{\mathrm{EP}\} $和$ f_{\mathrm{CME}} $或$ f_{\mathrm{CME}}\{\mathrm{b}\} $的值相乘的结果)与提取自Zr+Zr碰撞的CME信号之比要大于1，这表明实验上观测不到理论上预测来自Ru+Ru碰撞的CME信号与Zr+Zr碰撞的CME信号之比要大于1的情况的可能原因之一是CME的强度太小。出现$ f_{\mathrm{CME}} $大于1的情况可能是由于式(12)定义的$ f_{\mathrm{CME}} $是基于“相对于两平面的CME信号比例与$ v_2 $的比例成反比”的条件下成立，但是我们通过加入CME后的AMPT模型模拟发现这个条件是不成立的，因此只能通过式(15)定义的$ f_{\mathrm{CME}}\{\mathrm{b}\} $才能更准确得到观测量中信号的比例。在文献[73]中，我们也证明使用$ f_{\mathrm{CME}}\{\mathrm{b}\} $计算观测量$ \varDelta \gamma $中CME信号的比例更加合理。

在图7中可以发现，b的值随演化的进行而减小。这表明相对于不同平面的CME信号之间的相关性越来越小，可以理解为重离子碰撞演化过程中末态相互作用产生的退关联的结果^{[53, 70, 76]}，部分子级联后b的值出现大于1的情况可能是由于存在非流效应的影响。

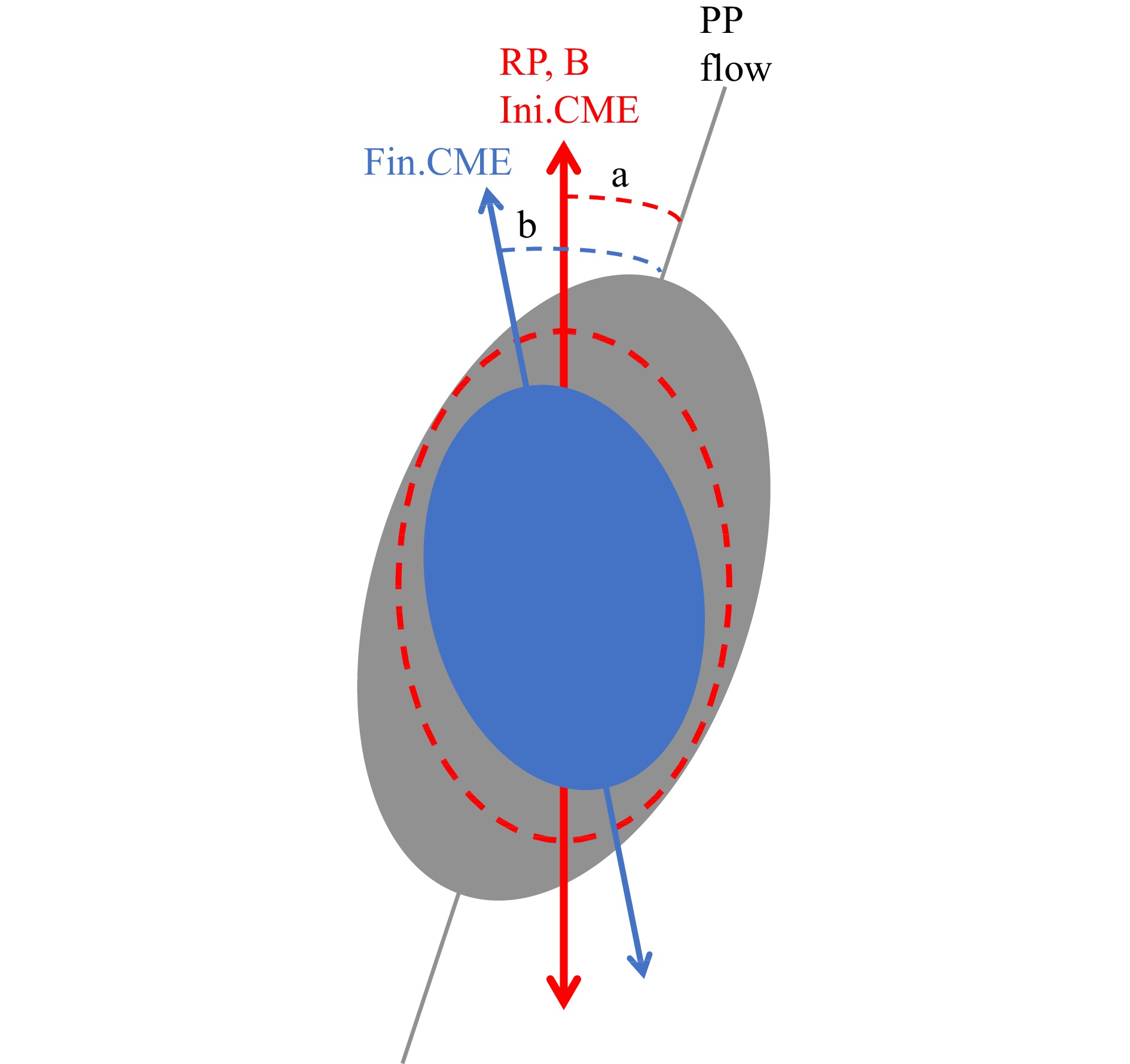
可能有两个原因导致b和a值的不同，示意图为图8。一是在参考文献[70]中，已经发现了相对论重离子碰撞中电荷分离通过演化后其强度显著降低，这种减弱可高达一个数量级，即末态相互作用会大大减少最终幸存下来的CME信号；二是沿磁场方向(靠近重叠区长轴)的CME信号比其他地方的信号有更大的阻尼，这导致幸存信号从初始磁场方向向短轴背景方向旋转，但CME信号仍然存在。如果假设CME仍然沿着磁场方向一样，取$ b=a $可以用来提取这部分的CME信号。因此，实验提取的CME信号是受末态演化影响后的CME信号的上限。同时，非流效应的影响也值得关注^[58]。

基于具有不同强度CME的多相输运模型，用重新考量了的双平面方法确定了$ \sqrt{s_{_{\rm NN}}} = 200 \;{\mathrm{GeV}} $的同质异位素碰撞中$ \varDelta \gamma $中的CME信号的比例。我们计算了相对于旁观者平面和参与者平面的椭圆流$ v_2 $和CME观测值$ \varDelta \gamma $，发现了CME信号相对于两个不同平面的比值b与同质异异位素碰撞中椭圆流相对于两个不同平面的比值a不同。结果表明，在目前的实验研究中假定a和b相等，可能会导致末态CME信号的比例被高估。同时，随着AMPT模型模拟碰撞的演化阶段不同，末态的b的值有所下降，这表明相对于旁观者和参与者平面的手征磁效应的退关联可能是由同质异位素碰撞中末态相互作用引起的。我们期望我们的研究能够为将来准确测量相对论重离子碰撞中的手征磁效应信号的比例提供理论参考。

致谢 感谢王福强教授和廖劲峰教授的讨论，这些讨论对本文的工作产生了重要的启发。