高级搜索

飞机目标在爆炸冲击波作用下的毁伤效应评估方法

,  , 

downloadPDF

上一篇

下一篇

冯晓伟, 卢永刚, 李永泽. 飞机目标在爆炸冲击波作用下的毁伤效应评估方法[J]. 高压物理学报, 2019, 33(4): 045101-1. doi: 10.11858/gywlxb.20180687
引用本文: 冯晓伟, 卢永刚, 李永泽. 飞机目标在爆炸冲击波作用下的毁伤效应评估方法[J]. 高压物理学报, 2019, 33(4): 045101-1. doi: 10.11858/gywlxb.20180687
shu
Xiaowei FENG, Yonggang LU, Yongze LI. Damage Assessment Method of Aircraft Targets under Blast Wave[J]. gaoyawli, 2019, 33(4): 045101-1. doi: 10.11858/gywlxb.20180687
Citation: Xiaowei FENG, Yonggang LU, Yongze LI. Damage Assessment Method of Aircraft Targets under Blast Wave[J]. gaoyawli, 2019, 33(4): 045101-1. doi: 10.11858/gywlxb.20180687
shu

飞机目标在爆炸冲击波作用下的毁伤效应评估方法

  • 中国工程物理研究院总体工程研究所，四川 绵阳　621999

    • 作者简介: 冯晓伟（1984－），男，博士，副研究员，主要从事武器毁伤效能评估研究. E-mail：414fengxw@caep.cn .
    通讯作者: 卢永刚（1973－），男，博士，研究员，主要从事武器毁伤效能评估研究. E-mail：lygcaep@263.net; 

  • 中图分类号: O383; TJ410.3

Damage Assessment Method of Aircraft Targets under Blast Wave

  • Institute of Systems Engineering, China Academy of Engineering Physics, Mianyang 621999, China

    • Corresponding author: Yonggang LU, lygcaep@263.net ; 

  • MSC: O383; TJ410.3

  • 摘要: 从飞机结构强度设计角度出发，研究了大当量爆炸冲击波作用下飞机目标毁伤效应评估方法。根据飞机结构强度设计准则，确定了典型飞机目标的失效判据。通过有限元分析，获得了典型飞机目标机翼在均布冲击波作用下完全失效的超压值，与试验数据对比表明，该方法具有较好的合理性。在此基础上，考虑动态加载下的结构响应，通过计算不同工况下飞机目标失效的超压值和相应的持续时间，获得了飞机失效的冲击波超压-冲量准则，为后继冲击波对飞机整体毁伤效应评估提供了更为合理的方法。
    Abstract: A new damage assessment method of aircraft targets under blast wave was studied based on the strength of aircraft structures. The failure criterion of typical aircraft targets was determined according to the strength design criterion of aircraft structure. Further, the critical blast wave overpressure causing the aircraft failure was obtained by the finite element analysis. It shows that the simulation results were consistent with the previous experimental results and the method was proved to be reasonable. Based on the method, the structural response under dynamic loading was further investigated. A series of blast wave overpressures and corresponding durations causing the aircraft failure were studied by the numerical simulations. Consequently, the overpressure-impulse damage criterion of typical aircraft target under blast wave was established. The results were considered to be a more reasonable method for assessing the aircraft overall damage effects under blast wave loading.
  • 加载中

  • 图 1  机翼载荷示意图[9]

    Figure 1.  Schematic of aircraft wing loads[9]

    下载: 全尺寸图片 幻灯片

    图 2  翼面形状及主要尺寸（单位：mm）

    Figure 2.  The shape and main sizes of aircraft wing (Unit: mm)

    下载: 全尺寸图片 幻灯片

    图 3  1/4椭圆形载荷分布曲线

    Figure 3.  Quarter elliptic loading distribution curve

    下载: 全尺寸图片 幻灯片

    图 4  三角形载荷分布曲线

    Figure 4.  Triangular loading curve

    下载: 全尺寸图片 幻灯片

    图 5  机翼的等效有限元模型

    Figure 5.  The equivalent finite element model of the aircraft wing

    下载: 全尺寸图片 幻灯片

    图 6  边界条件及加载条件示意图

    Figure 6.  Schematic of the boundary conditions and loading conditions

    下载: 全尺寸图片 幻灯片

    图 7  飞机毁伤的超压-冲量准则

    Figure 7.  Overpressure-impulse criterion of aircraft targets

    下载: 全尺寸图片 幻灯片
  • [1] 蒋浩征, 周兰庭, 蔡汉文. 火箭战斗部设计原理[M]. 北京: 国防工业出版社, 1982.
    [2] BALL R E. The fundamentals of aircraft combat survivability analysis and design [M]. 2nd ed. Reston: American Institute of Aeronautics and Astronautics Inc., 2003.
    [3] 刘彤. 防空战斗部杀伤威力评估方法研究[D]. 北京: 北京理工大学, 2004.
    [4] 裴扬, 宋笔锋, 石帅. 飞机作战生存力分析方法研究进展与挑战 [J]. 航空学报, 2016, 37(1): 216–234. PEI Y, SONG B F, SHI S. Analysis method of aircraft combat survivability: progress and challenge [J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(1): 216–234.
    [5] 司凯, 李向东, 郭超, 等. 破片式战斗部对飞机类目标毁伤评估方法研究 [J]. 弹道学报, 2017, 29(4): 52–57. doi: 10.3969/j.issn.1004-499X.2017.04.009 SI K, LI X D, GUO C, et al. Research on damage assessment method of fragmentation warhead against airplane targets [J]. Journal of Ballistics, 2017, 29(4): 52–57. doi: 10.3969/j.issn.1004-499X.2017.04.009
    [6] 梁斌, 冯高鹏, 周婕群, 等. 离散杆和EFP组合战斗部对飞机毁伤效应研究 [J]. 弹箭与制导学报, 2017, 37(1): 39–45. L1ANG B, FENG G P, ZHOU J Q, et al. Research on the damage effect of EFP combined warhead and discrete rod to battleplane [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2017, 37(1): 39–45.
    [7] KONOKMAN H E, KAY A M. Analysis of aircraft survivability against fragmenting warhead threat: AIAA-2014.0355 [R]. Reston: AIAA, 2014.
    [8] 黄季墀, 汪海. 飞机结构设计与强度计算[M]. 上海: 上海交通大学出版社, 2012.
    [9] 陶梅贞. 现代飞机结构综合设计[M]. 西安: 西北工业大学出版社, 2014.
    [10] 张森林. 在核爆炸冲击波环境中飞行飞机的结构动力响应分析 [J]. 航空学报, 1992, 13(9): A510–A515. ZHANG S L. Analysis of structural dynamic response for aircraft to petrating in the environment of nuclear explosion shock waves [J]. Acta Aeronautica et Astronautica Sinica, 1992, 13(9): A510–A515.
    [11] 刘杨, 陆浦. 一种机翼弯剪载荷包线近似计算方法 [J]. 航空工程进展, 2013, 4(2): 241–246. doi: 10.3969/j.issn.1674-8190.2013.02.018 LIU Y, LU P. Approximation method for calculating the wing load envelope of bending moment and shear force [J]. Advances in Aeronautical Science and Engineering, 2013, 4(2): 241–246. doi: 10.3969/j.issn.1674-8190.2013.02.018
    [12] 隋树元, 王树山. 终点效应学[M]. 北京: 国防工业出版社, 2000.
  • 加载中
图( 7)
计量
  • 文章访问数:  4670
  • HTML全文浏览数:  4670
  • PDF下载数:  90
  • 施引文献:  0
出版历程
  • 收稿日期:  2018-11-13
  • 网络出版日期:  2019-08-25
  • 刊出日期:  2019-08-01

飞机目标在爆炸冲击波作用下的毁伤效应评估方法

    通讯作者: 卢永刚（1973－），男，博士，研究员，主要从事武器毁伤效能评估研究. E-mail：lygcaep@263.net; 
    作者简介: 冯晓伟（1984－），男，博士，副研究员，主要从事武器毁伤效能评估研究. E-mail：414fengxw@caep.cn
  • 中国工程物理研究院总体工程研究所，四川 绵阳　621999
  • 收稿日期:  2018-11-13
  • 网络出版日期:  2019-08-25

摘要: 从飞机结构强度设计角度出发，研究了大当量爆炸冲击波作用下飞机目标毁伤效应评估方法。根据飞机结构强度设计准则，确定了典型飞机目标的失效判据。通过有限元分析，获得了典型飞机目标机翼在均布冲击波作用下完全失效的超压值，与试验数据对比表明，该方法具有较好的合理性。在此基础上，考虑动态加载下的结构响应，通过计算不同工况下飞机目标失效的超压值和相应的持续时间，获得了飞机失效的冲击波超压-冲量准则，为后继冲击波对飞机整体毁伤效应评估提供了更为合理的方法。

English Abstract

    全文HTML

  • 在现代战争中，空中打击已经成为十分重要的战争手段，是迅速获取战争主动权，甚至决定整场战争胜负的关键因素。飞机一直是执行空中打击任务的主要作战平台，因此也成为反空袭作战中防空武器的重点攻击对象。开展防空武器对飞机目标的毁伤效应评估，在战斗部研制领域，将有助于把握防空弹药毁伤能力，提升和优化防空战斗部毁伤效能；而在飞机设计领域，可为提高飞机在防空弹药打击下的生存能力提供重要依据。

    军用飞机在空战或者对地攻击过程中，往往遭受大口径高射武器及大多数地空、空空导弹等外爆型战斗部的威胁。根据威胁终端产物类型的不同，防空战斗部对飞机目标的毁伤元素通常包括破片（含普通破片、射弹、离散杆等）和爆炸冲击波[1-3]。高速破片侵彻毁伤飞机目标结构被认为是防空武器的主要毁伤方式，得到了广泛研究[4-6]；冲击波超压随着距离的增加衰减很快，特别是大脱靶量武器，往往作为次级威胁采用绘制冲击波易损性包线方式进行毁伤判定[2, 7]。随着导弹制导技术的飞速发展以及大型中远程防空导弹的研制，防空战斗部的爆炸冲击波作用逐渐占据主要地位，将来有可能成为杀伤目标的主要元素。目前，关于爆炸冲击波对飞机目标的整体毁伤效应研究鲜有报道，如何从飞机目标结构失效特性出发获得相应的冲击波毁伤准则及判据值得进一步探讨。

    本研究从飞机结构强度设计角度出发，将机翼等典型易损部件的失效设计准则作为其在冲击波作用下的毁伤准则及判据，结合冲击波载荷作用特征，获得飞机结构在不同冲击波作用下的最终毁伤效应。

1.   飞机结构强度设计准则简述

  • 强度设计是飞机设计中传统的设计准则，设计基础是保证飞机结构在服役过程中遭遇最大外载荷时仍具有保持安全工作的能力。飞机飞行过程中，外界作用于飞机的载荷主要有：升力Y、阻力X、发动机推力T、飞机重力G及飞行中的惯性力N。在不考虑旋转的情况下，其受力平衡方程为

    式中：下标x、y分别代表水平方向和垂直方向，g为重力加速度，ay为垂直方向的加速度。（1）式表明，飞机在做机动动作时所需的升力等于重力乘以一个系数，称之为载荷系数（即过载系数，简称过载），飞机的载荷大小可由其来确定[8-9]。若飞机重心处的载荷系数已知，则结合对应载荷系数的其他飞行参数（如高度、质量、速度、气动力分布等），可求得飞机结构各部分所受实际载荷大小及方向。从毁伤角度上看，当作用于飞机上的冲击波载荷产生的应力高于基于极限载荷系数设计的结构强度时，飞机结构发生失效。因此，若已知飞机的设计载荷系数，可反推出导致其失效的冲击波强度，进而为获得冲击波毁伤飞机准则及判据奠定基础。目前确定载荷系数的主要因素是驾驶员生理上的抗负荷能力。通常，最大载荷系数为nmax=8，最小载荷系数为nmin=–4[8-9]。

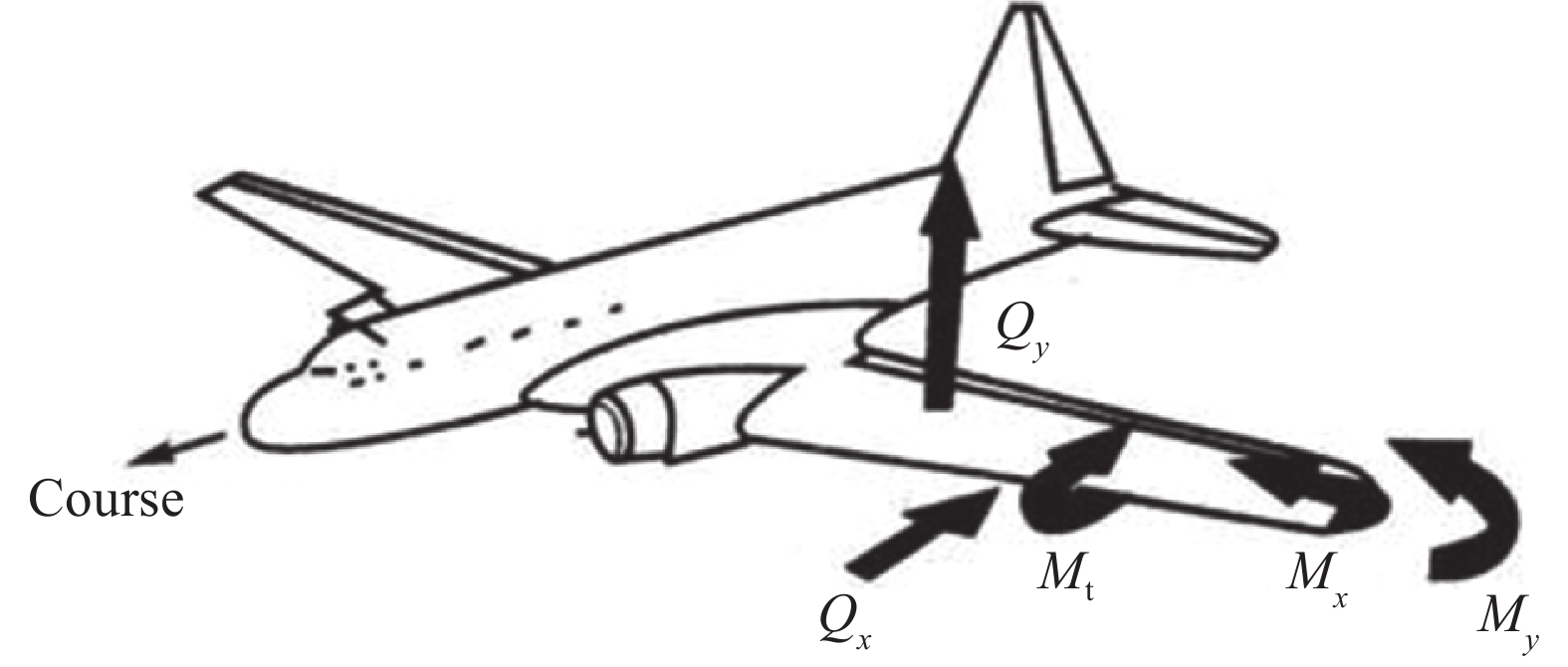
    机翼是飞机的主要承力机构，为飞机飞行提供升力。此外，机翼受载面积大，是爆炸环境中受冲击波毁伤的主要关键部件[10]。因此，可通过机翼结构强度设计特性确定爆炸冲击波毁伤飞机目标的临界载荷强度。飞机飞行过程中，机翼的设计载荷主要是由气动载荷、质量力及集中载荷等外载荷所引起的剪力Q、弯矩M和扭矩Mt，见图1[9]，其中：x为沿航向的飞机轴线，y为垂直飞机平面向上，z为右手定则决定的飞机侧向，Qy为垂直方向剪力，Mx为沿航向的弯矩，Mt为绕机翼展向的扭矩，Qx为沿航向的剪力，My为沿垂直轴y向的弯矩。由于机翼的${M_x} \gg {M_y}$，因此Mx引起的应力远高于My引起的应力，可重点考虑Q（Qy）、M（Mx）和Mt。

2.   典型飞机目标机翼总体载荷计算

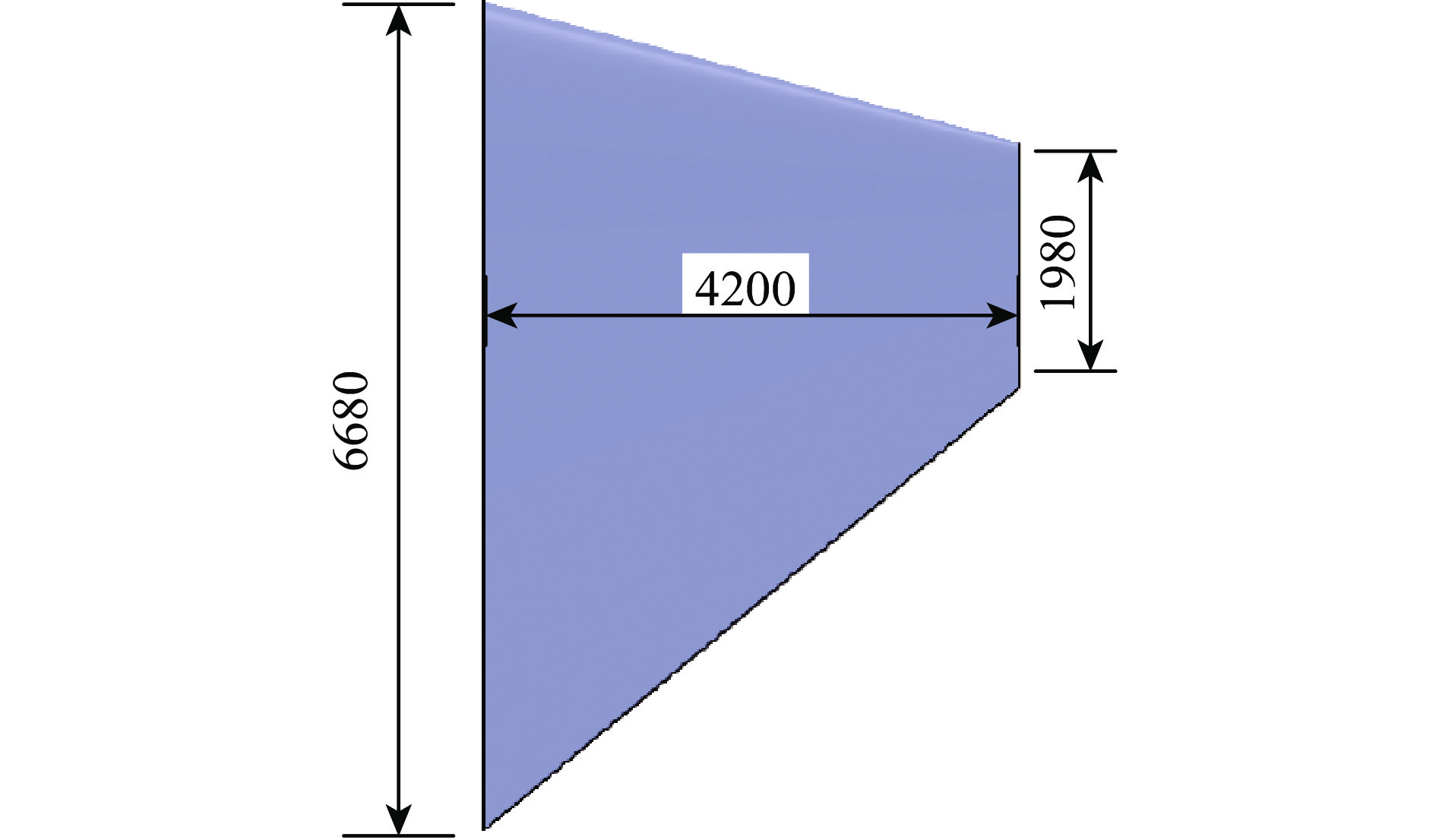
  • 以某典型战斗机为研究对象，根据上述设计准则计算机翼上的总载荷，作为冲击波对飞机目标毁伤效应评估的依据。典型战斗机设计质量m=2.8×104 kg，机动设计过载n=8，安全系数为1.5，重力加速度g=9.8 m/s2；机翼形状见图2，半翼展b1/2=4.2 m，根弦长c1=6.68 m，尖弦长c2=1.98 m。

    机翼载荷分布方程一般有两种[11]：1/4椭圆形分布和三角形分布，以下对两种分布方式分别进行计算对比。

    （1）1/4椭圆形分布

    采用1/4椭圆形分布时，不同展向位置y对应的分布载荷大小w(y)为

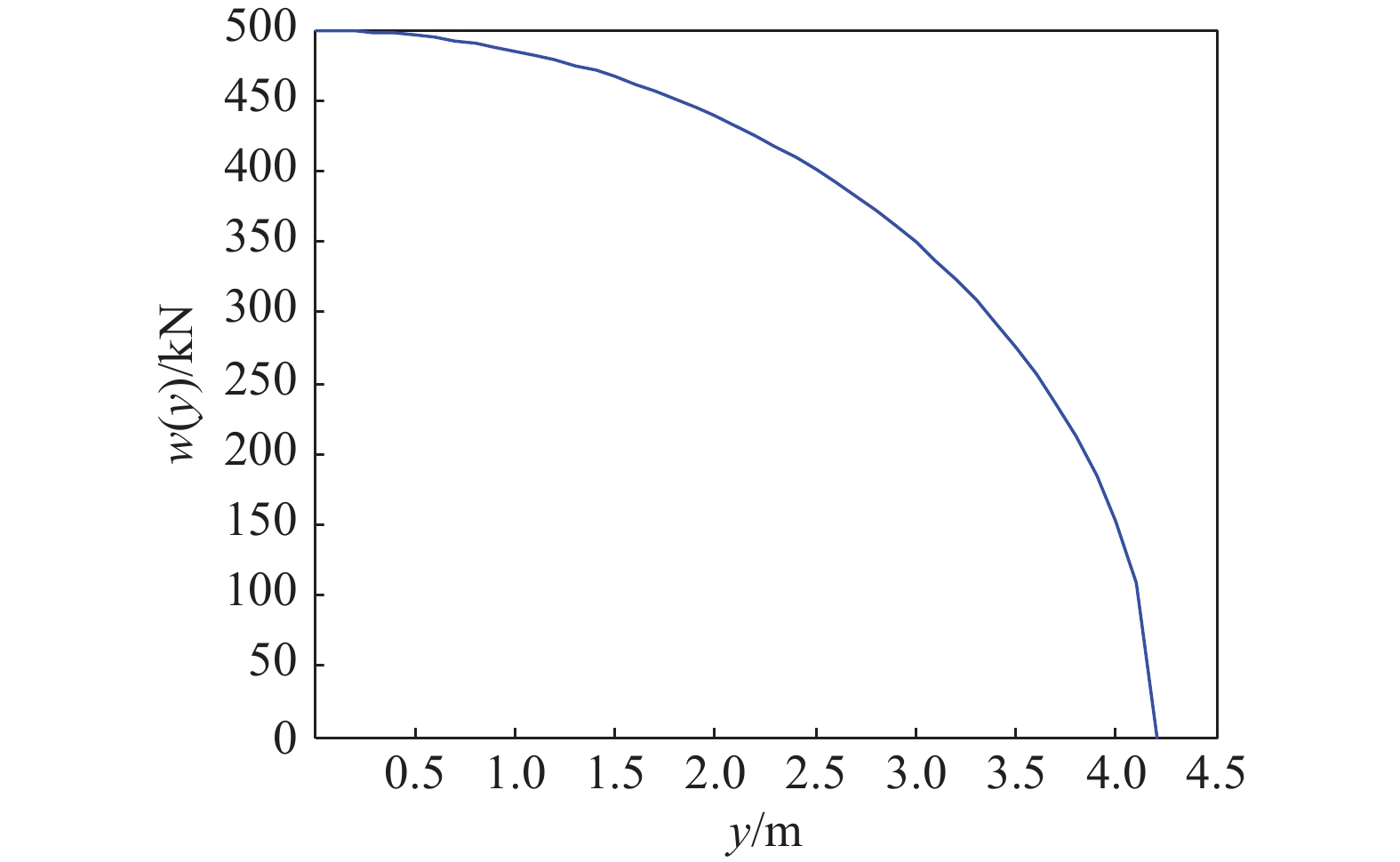
    式中：w(y)为机翼上分布载荷，y为机翼展向坐标，F为机翼某分布载荷的总载荷，Fw为单个机翼上的总载荷，b为翼展。代入具体数值得到载荷沿展向分布为

    式中：w(y)的单位为N，y的单位为mm，对应的分布曲线如图3所示。

    经积分验算总载荷为1.6472×106 N。在此基础上对翼根进行弯矩积分，总弯矩M的计算公式为

    代入具体数值得到

    （2）三角形分布

    采用三角形分布时，不同展向位置y对应的分布载荷大小w(y)为

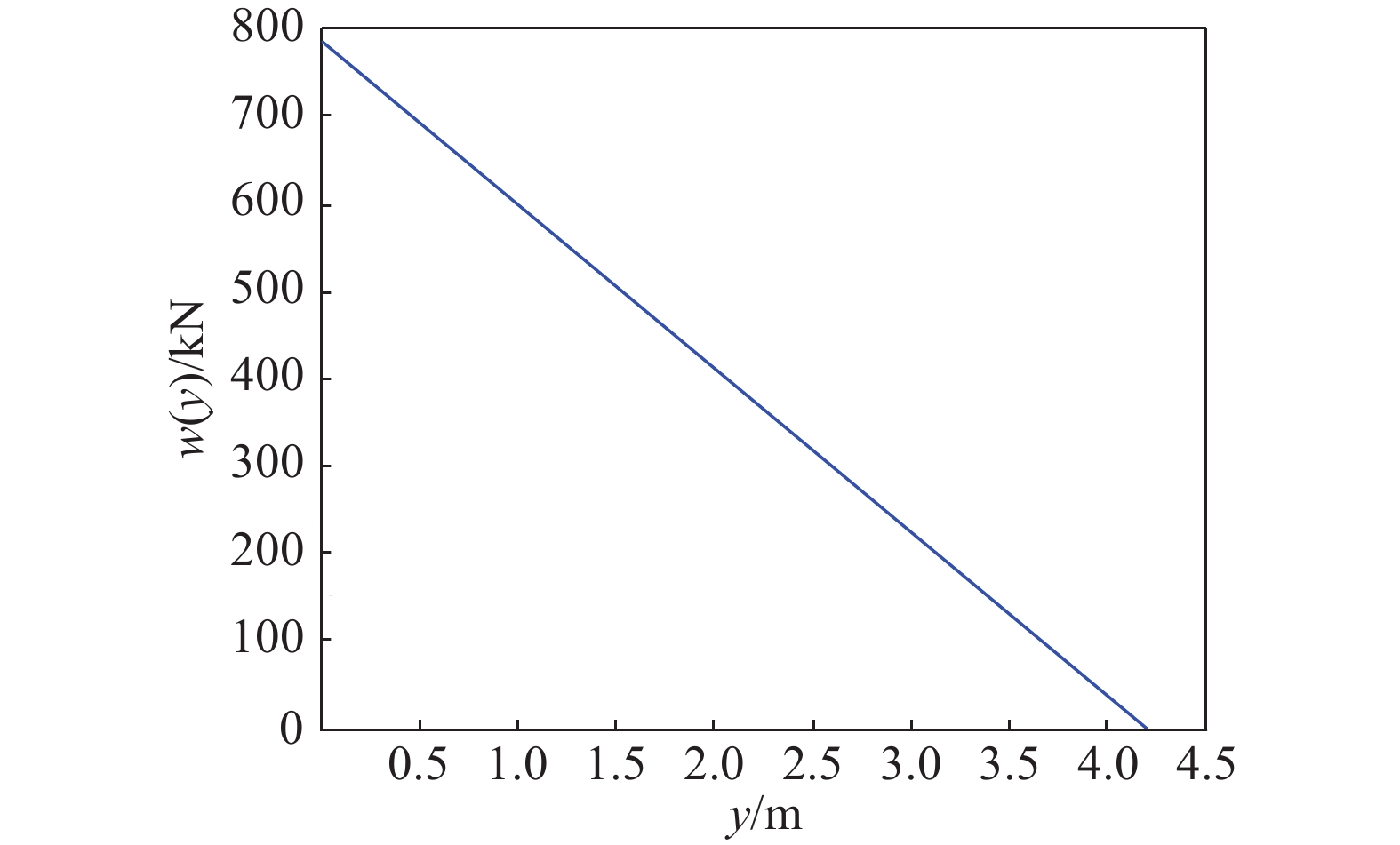
    代入具体数值得到载荷沿展向分布

    式中：w(y)的单位为N，y的单位为mm，对应的分布曲线如图4所示。

    经积分验算总载荷为1.6464×106 N，与椭圆形分布基本一致。在此基础上对翼根进行弯矩积分，总弯矩M的计算公式为

    代入具体数值得到

    对比两种分布方式，在剪力载荷分布一致的情况下，1/4椭圆形分布的总弯矩比三角形分布大，在计算中弯矩采用2.9×106 N·m较为保守。

3.   爆炸冲击波对典型飞机目标毁伤效应的数值模拟

  • 根据飞机目标的尺寸特性，建立机翼的等效有限元模型，如图5所示，其中机翼受载面积及质量与真实情况完全相同。分析机翼设计载荷可知，在翼根部产生的剪力和弯矩最大，故以该位置的载荷为重点研究对象，忽略机翼内部的复杂结构形式，仅以质量和刚度进行等效。

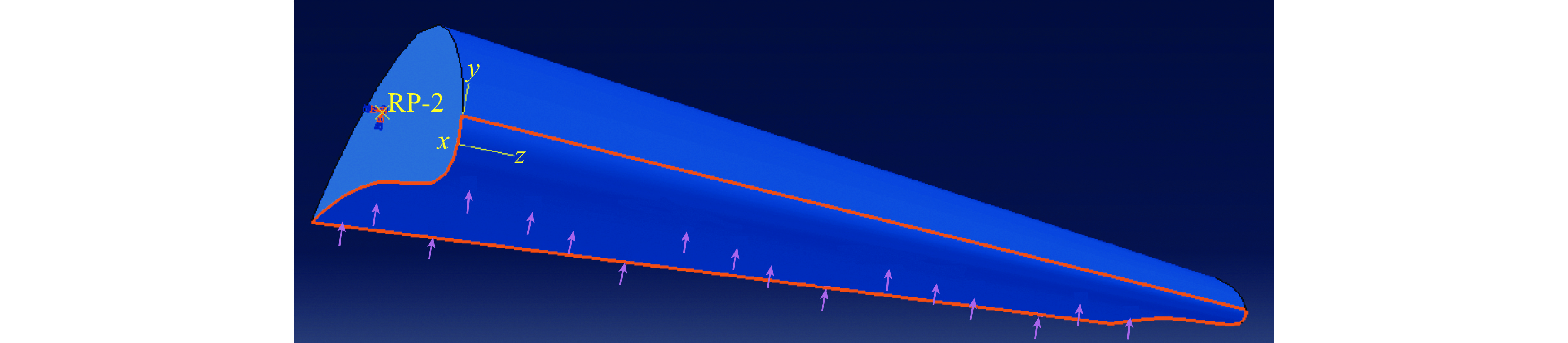
    把机翼看作固定在机身上的悬臂梁。模型中取一半机翼为研究对象，将翼根面与一个参考点进行运动耦合，并将该耦合点进行固支来模拟机翼的边界条件。考虑到大当量爆炸时冲击波作用范围较广，将冲击波简化为均布载荷施加在整个翼面上，如图6所示。

    目前，飞机目标的毁伤超压阈值多基于核爆试验，当超压大于0.1 MPa时，各类飞机目标完全破坏[12]。考虑到核爆情况下，冲击波持续时间较长，故可近似用静态工况进行模拟。本研究采用ABAQUS中的静态分析步进行冲击波作用下典型飞机目标机翼的力学响应模拟。计算结果表明，当冲击波压力为0.09 MPa时，翼根处的剪力和弯矩分别为1.6×106 N和2.9×106 N·m，与理论计算值基本吻合。结合核爆试验结果，其失效判据与数值结果基本一致，证明了本研究方法具有一定的合理性。

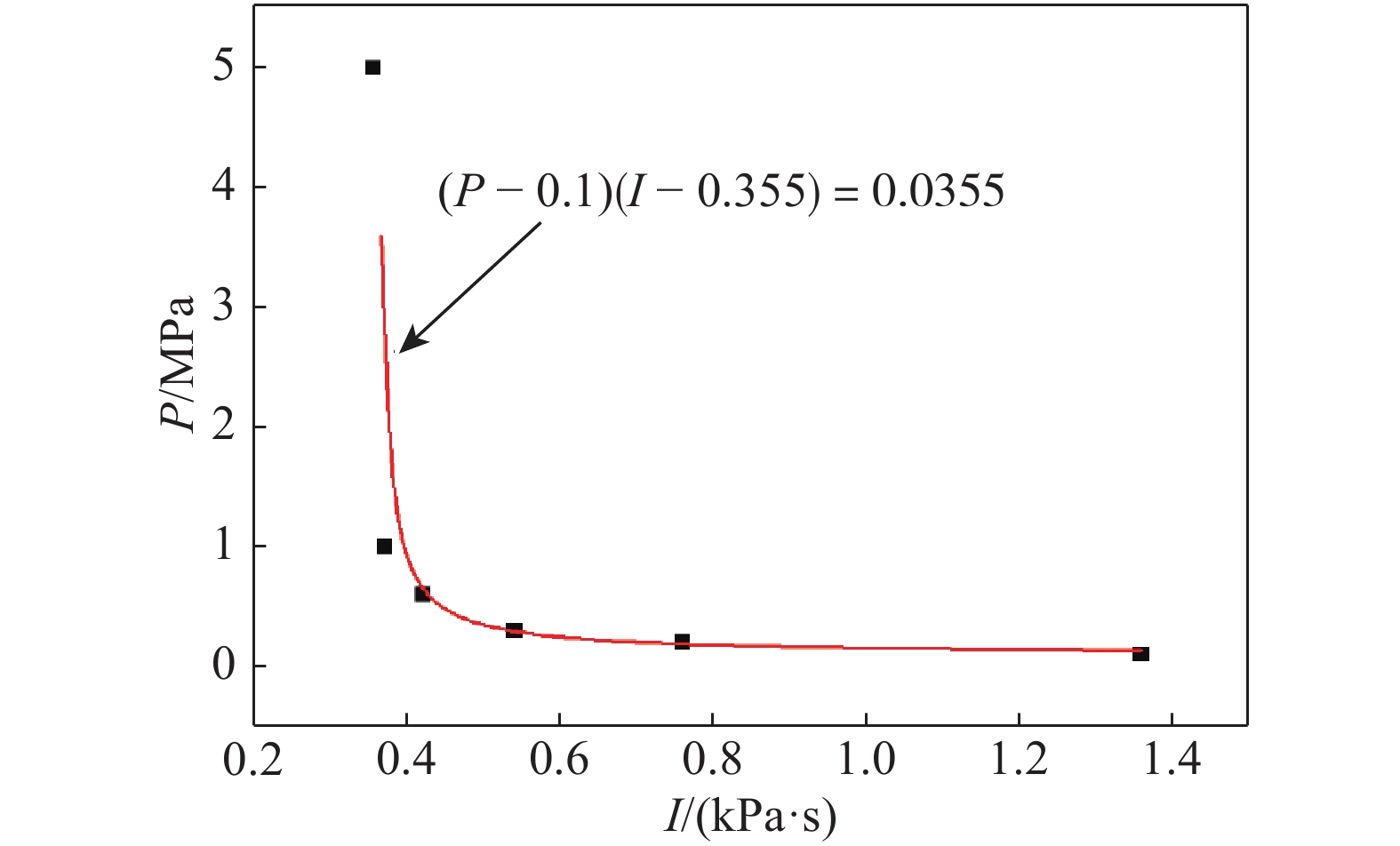
    冲击波毁伤准则通常有超压准则、冲量准则和超压-冲量准则（P-I准则）。不同目标在冲击波作用下的动态响应不同，所适用的毁伤准则也不尽相同。通常而言，当冲击波正压的持续时间远大于目标结构本身的振动周期时，目标的破坏作用取决于冲击波超压；反之，当冲击波正压的持续时间远小于目标结构本身的振动周期时，则主要取决于冲击波的冲量。其他情况则建议使用超压-冲量准则。相比于超压准则和冲量准则，超压-冲量准则具有考虑全面、评价准确、适用广泛的优点。为不失一般性，本研究采用超压-冲量准则研究冲击波对机翼的毁伤效应。

    通过计算显示，在动态加载条件下，机翼中存在明显的结构响应，其弯矩的响应较剪力具有明显的滞后性，剪力通常先于弯矩达到临界值，故采用剪力作为失效判据更为合理。在计算中，假设冲击波为矩形波，随着加载时间的延长，机翼根部的剪力将达到其破坏临界值，提取相应的临界时间与超压值相乘，可获得相应的冲击波冲量。计算了0.1、0.2、0.3、0.6、1.0以及5.0 MPa超压下，机翼达到破坏状态时的冲击波冲量，分别为1.36、0.76、0.54、0.42、0.37和0.355 kPa·s，对这些数据进行拟合获得P-I准则，如图7所示。随着超压值P的增大，机翼破坏对应的冲击波冲量I逐渐减小并趋于稳定值，表明：低于此冲量时，无论超压多大，结构都不会破坏；反之，随着超压减小，冲量将趋于无穷大，当低于某个超压值时，无论冲量多大，结构都不会发生破坏。

4.   结　论

  • 依据飞机结构强度设计准则，分析了飞机结构强度设计的关键因素。在此基础上，根据飞机强度设计载荷准则，计算得到机翼发生失效的剪力和弯矩值。通过有限元分析，结合核爆作用下飞机目标完全失效的试验结果，验证了该方法的的合理性。进而考虑动态加载下的结构响应，获得了飞机失效的冲击波超压-冲量准则，为后继冲击波对飞机的毁伤效应评估提供了较为合理的方法。

参考文献 (12)

目录

/

返回文章
返回