The JC constitutive model including failure criterion are commonly used in the numerical simulations of the response and failure of a metal structure subjected to dynamic loadings. The constitutive equation represents the equivalent stress of the metal as the product of the terms of strain, strain rate and temperature. It has a simple form and the parameters in the model can be obtained easily through laboratory material tests. The equivalent stress ${\sigma _{\rm{eq}}}$ in the JC constitutive model can be expressed by the following equation^[1–2]

where A, B, C, n, m are material constants, ${\varepsilon _{\rm{p}}}$ is the equivalent plastic strain, ${\dot \varepsilon ^*}_{\rm{p}} = {{{{\dot \varepsilon }_{\rm{p}}}} /{{{\dot \varepsilon }_0}}}$ with ${\dot \varepsilon _0}$ being a reference strain rate (in this paper it is taken as the strain rate employed in the quasi-static tensile tests), and $T^*$=(T–T_r)/(T_m–T_r) is the homologous temperature with T, T_r, T_m being the current temperature, the room temperature, the melting temperature, respectively.

The JC failure criterion is based on equivalent plastic strain and it is assumed that the damage of materials accumulates with plastic deformation. In the JC failure criterion a damage parameter D can be defined as

where $\Delta {\varepsilon _{\rm{p}}}$ is the increment of the equivalent plastic strain，${\varepsilon _{\rm{f}}}$ is the equivalent plastic strain to fracture. Eq.(2) means that when D reaches 1 the material will fail, that is to say, the accumulation of equivalent plastic strain reaches the equivalent plastic strain to fracture. ${\varepsilon _{\rm{f}}}$ is defined as the product of the terms of stress triaxiality, strain rate and temperature, which can be written in the following form

where D₁, D₂, D₃, D₄, D₅ are material constants, $\eta = {\sigma _{\rm{H}}}/{\sigma _{{\rm{eq}}}}$ is stress triaxiality with ${\sigma _{\rm{H}}}$ being hydrostatic pressure.

In addition, the numerical model implemented in this work takes into account the temperature evolution due to heat equation assuming adiabatic conditions, the temperature increment $\Delta T$ can be defined as

where $\rho $ is material density, C_p is material specific heat, $\chi $ is the proportion coefficient of plastic work conversion into heat usually taken to be 0.9. The equation of state is Grüneisen EOS (Equation of State) as follows

where P is hydrostatic pressure, C₀, s₁ and ${\varGamma _0}$ are material constants, E_m is material specific internal energy and $\mu=1-V/V_0 $ (V and V₀ are current volume and initial volume, respectively).

In this section the accuracy of the JC constitutive model including failure criterion is critically assessed by comparing the model predictions with the material test data for some metals under different loading conditions in terms of stress-strain relationships, strain rate effects, temperature effects and failure criterion as well as ballistic perforation data.

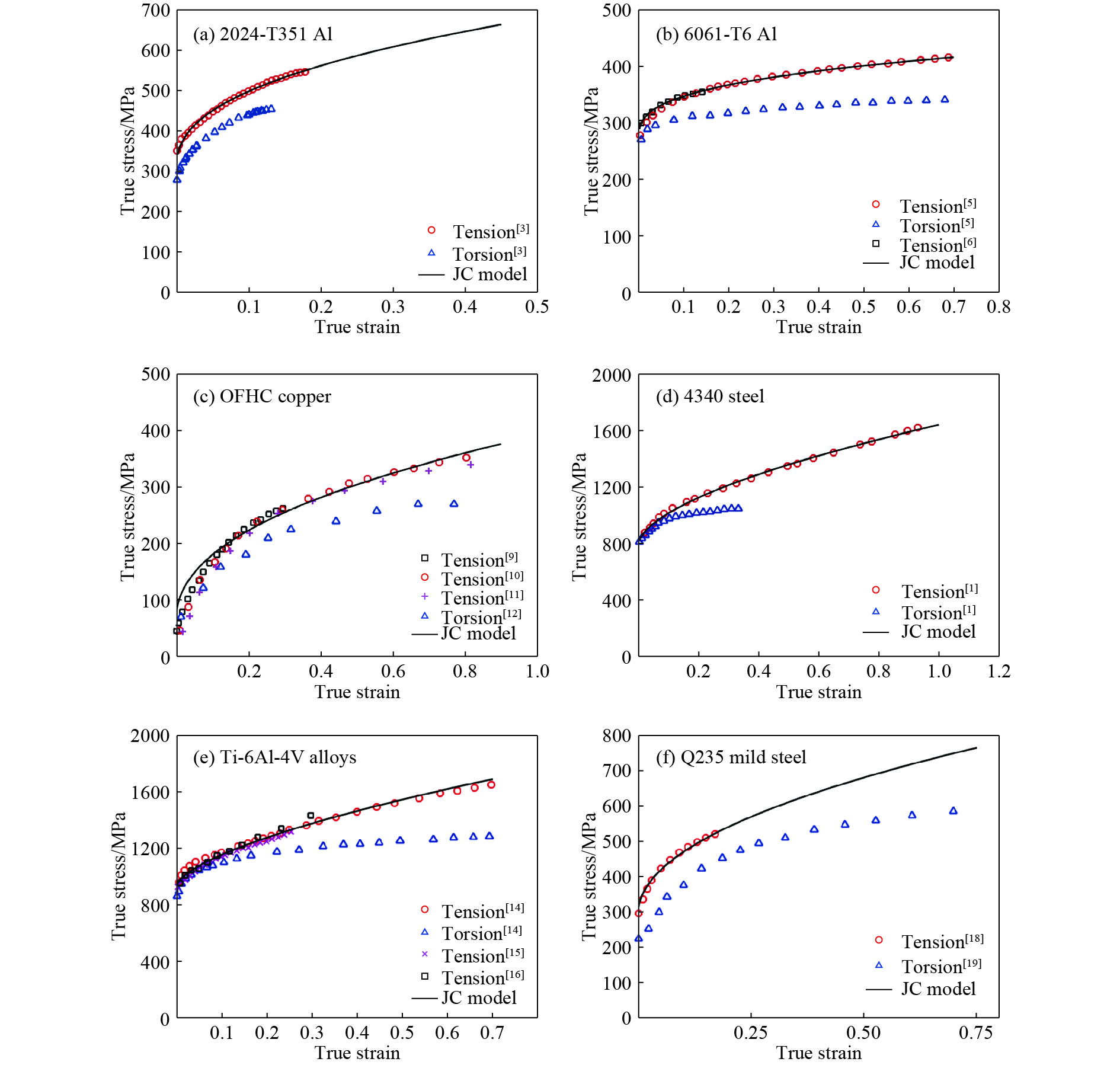
Fig.1 shows the quasi-static true stress-true strain curves both in tension and shear for 2024-T351 aluminum alloy^[3], 6061-T6 aluminum alloy^[5–6], OFHC copper^[9–12], 4340 steel^[1], Ti-6Al-4V alloys^[14–16] and Q235 mild steel^[18–19]. The values of $A,B$ and $n$ are shown in Table 1. The quasi-static true stress-true strain relationships in shear in Fig.1 are obtained from the torsion data by using the von Mises flow rule, i.e., tensile stress is $\sigma = \sqrt 3 \tau $ and corresponding tensile strain is $\varepsilon = {\gamma /{\sqrt 3 }}$.

It is clear from Fig.1 that the mechanical behavior of the materials examined does not obey the von Mises flow rule and its associated flow rule as the true stress-true strain curves both in tension and shear are not identical. In other words, the mechanical behavior of metals examined is sensitive to the state of stress and the JC constitutive model has failed to capture this phenomenon as it does not take into consideration the effects of Lode angle.

As mentioned before strain rate effects are very important in the formulation of a constitutive model for materials and the JC constitutive model is no exception. In this section, the accuracy of the term of strain rate in the model will be assessed in terms of dynamic increase factor (DIF) and dynamic true stress-true strain curves.

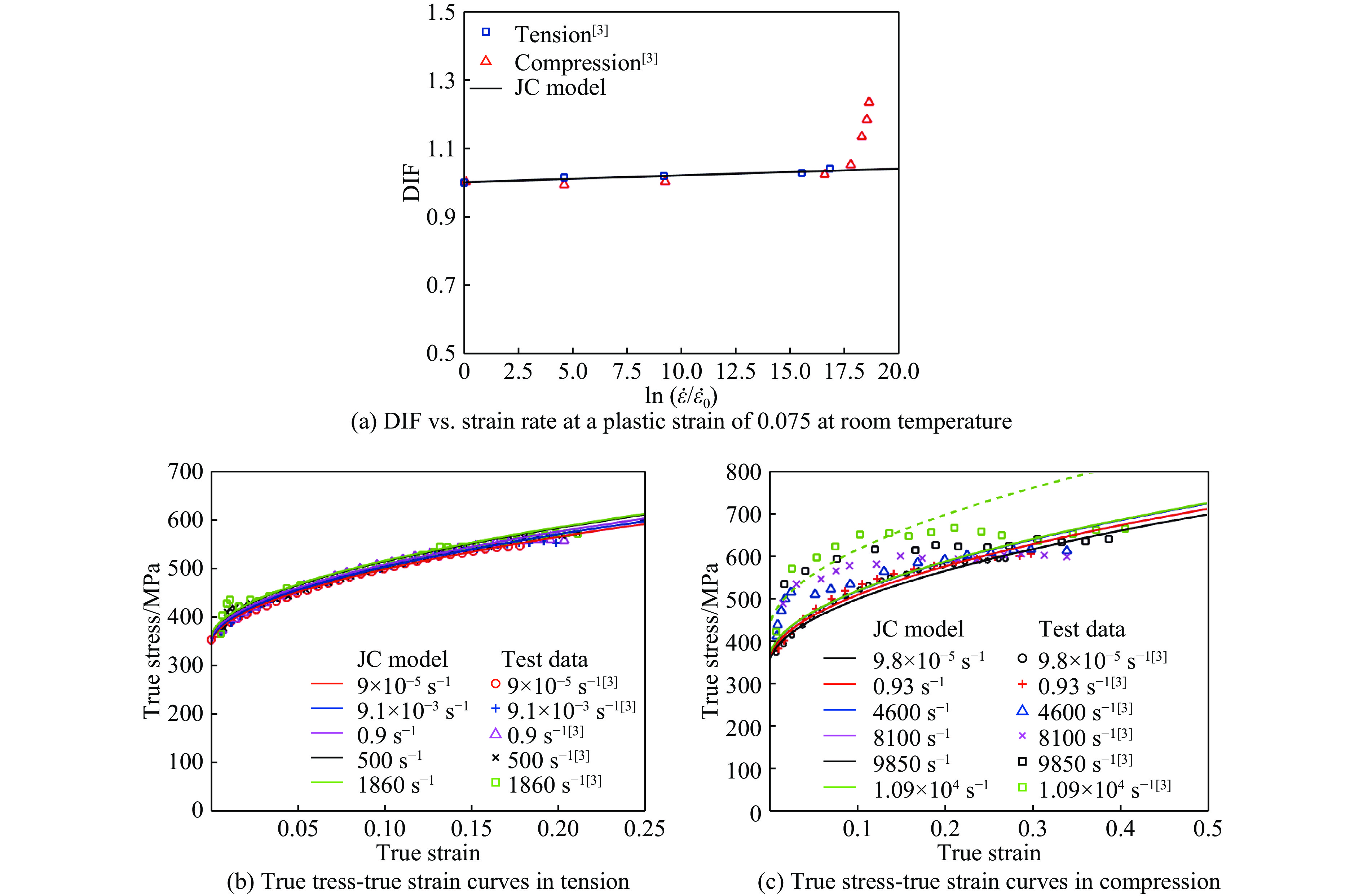
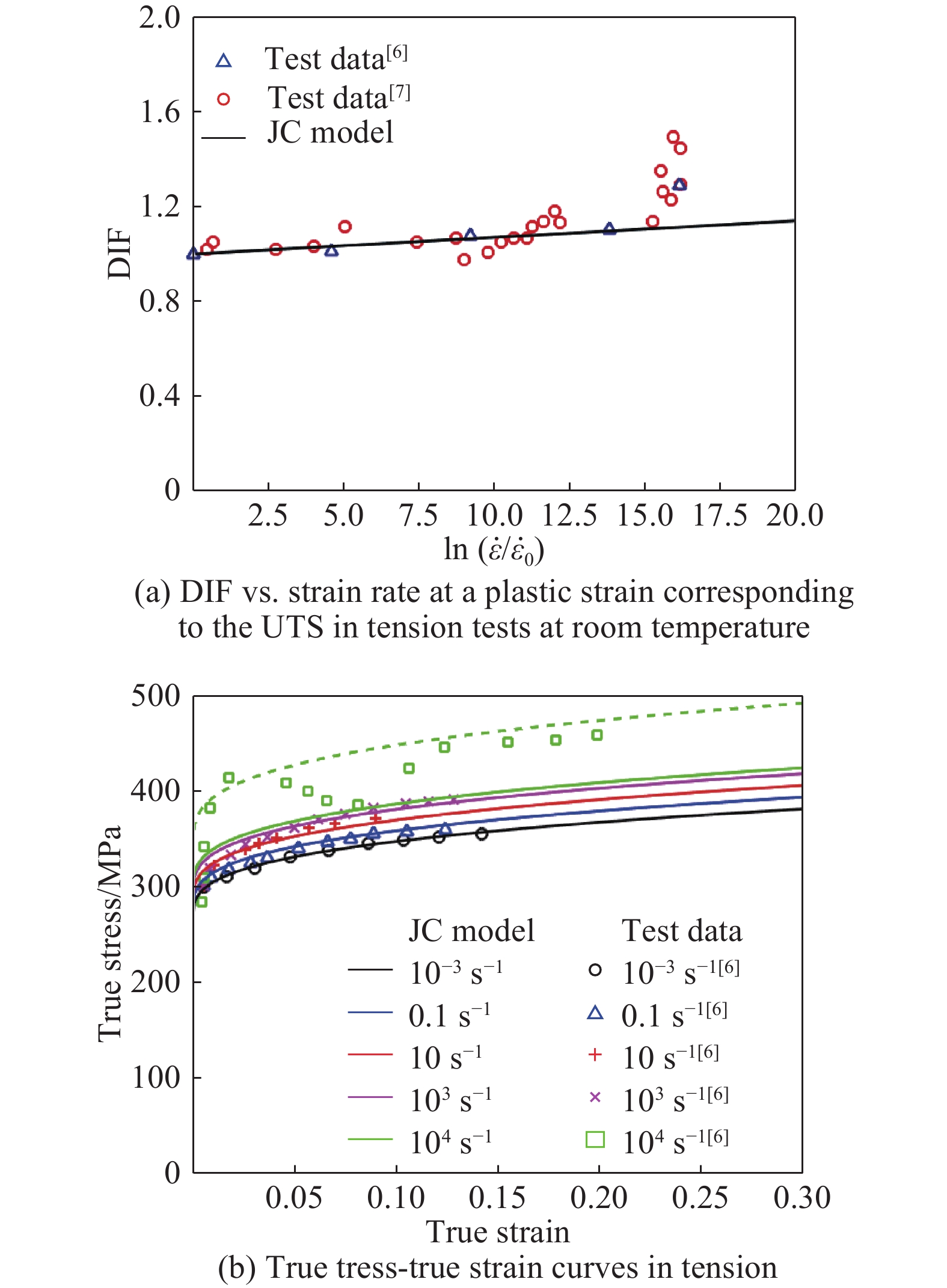
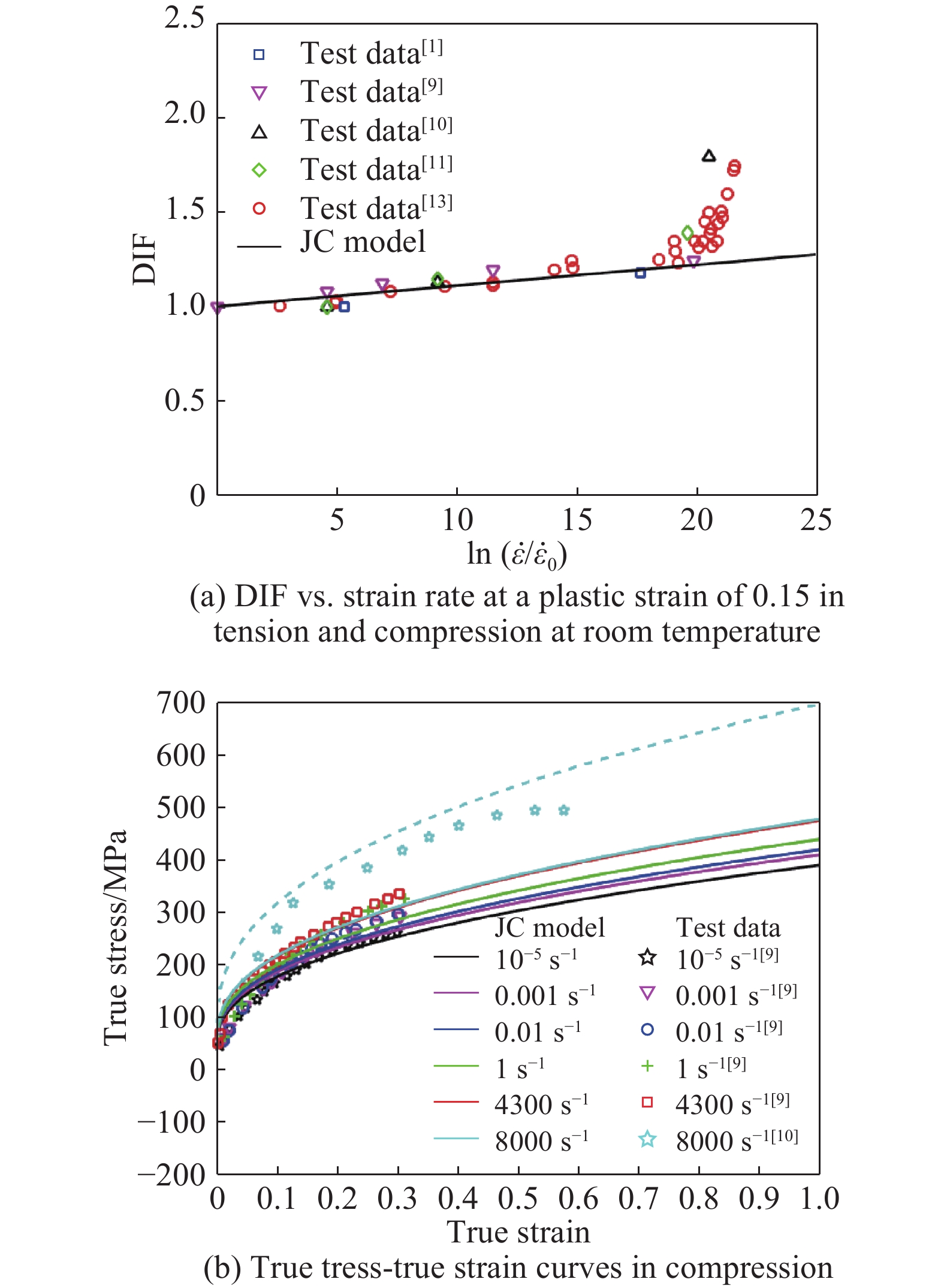
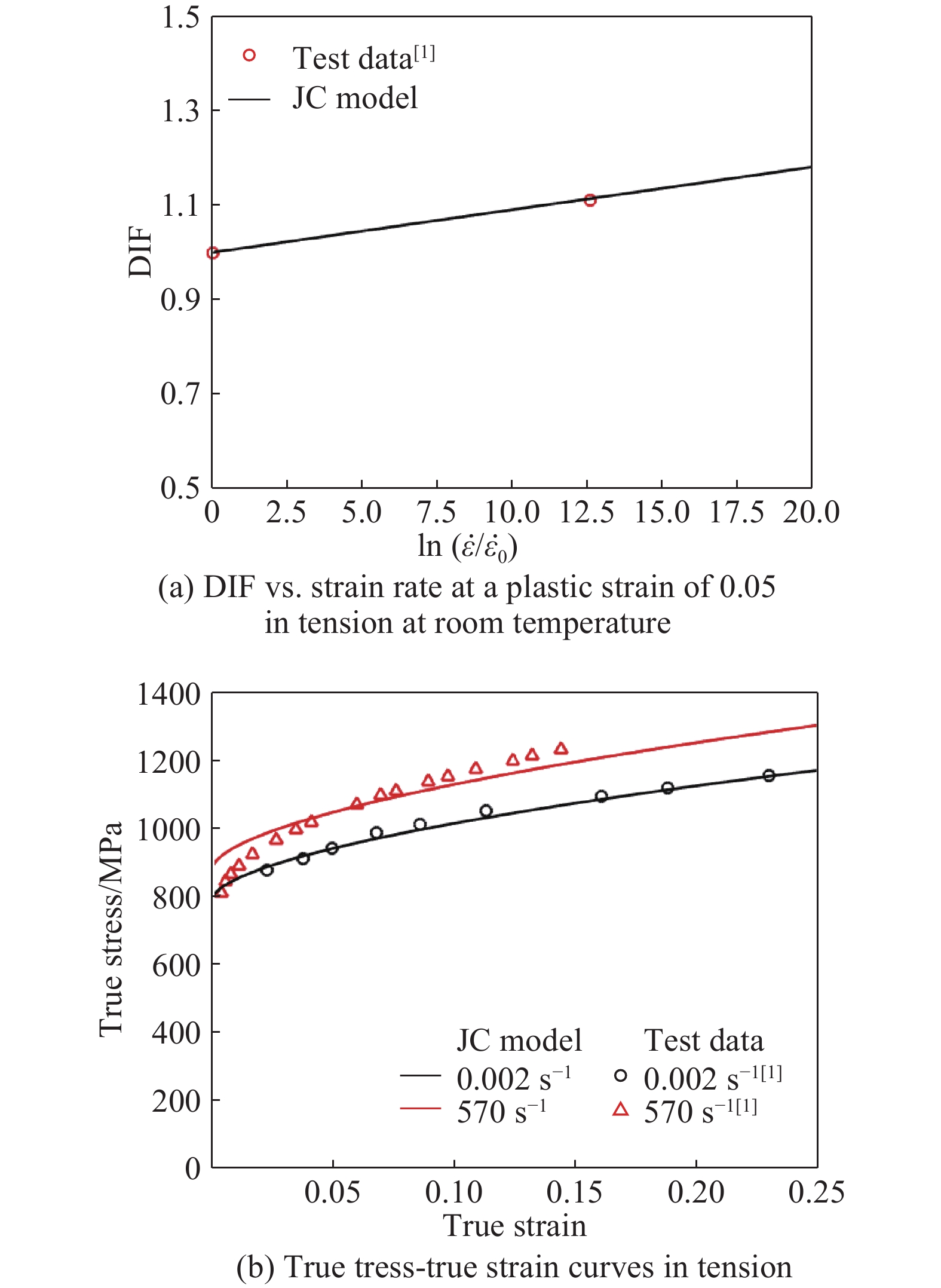
Fig.2–Fig.7 show comparisons of the JC model predictions with the test data for 2024-T351 aluminum alloy^[3], 6061-T6 aluminum alloy^[6–7], OFHC copper^{[1, 9–11, 13]}, 4340 steel^[1], Ti-6Al-4V alloys^[15–16] and Q235 mild steel^[18]. The values of $C$ and ${\dot \varepsilon _0}$ are shown in Table 1. In this paper, DIF is mainly employed to characterize the rate sensitive behavior of metallic materials.

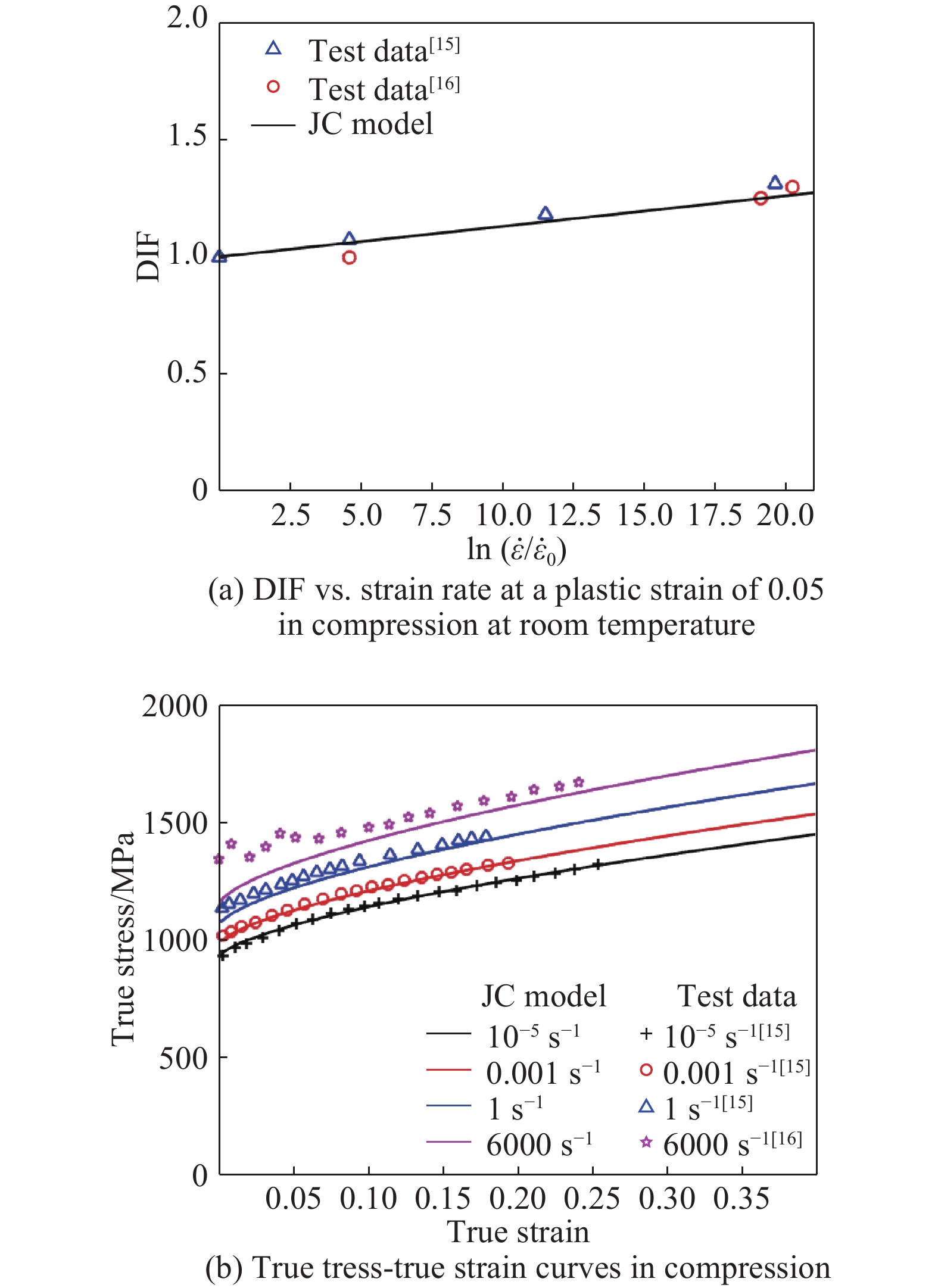
It is evident from Fig.2(a) that the term of strain rate, namely, $(1 + C\dot \varepsilon _{\rm{p}}^*)$ in the JC constitutive model can be used to describe the relationship between the DIF and the strain rate for 2024-T351 aluminum alloy at strain rates less than 4600 s^–1 and for strain rates greater than this value the DIF increases rapidly with increasing strain rate and the JC model fails to predict it. As a matter of fact, it significantly under-estimate the strain rate effects for 2024-T351 aluminum alloy at higher strain rates as can be seen from Fig.2(a). It is also evident from Fig.2(b) and Fig.2(c) that the true stress-true strain relationships both in tension and compression can be reasonably described by the JC model for strain rates less than 4600 s^–1 whilst for strain rates larger than this value the agreement between the JC model predictions and the experimental data are poor. Similar results are also observed for 6061-T6 aluminum alloy and OFHC copper as can be seen from Fig.3 and Fig.4, respectively.

Fig.5 and Fig.6 show comparisons of the JC constitutive model predictions with the test data for 4340 steel and for Ti-6Al-4V alloys, respectively. It is clear from the figures that reasonable agreement is obtained within the ranges of the strain rates examined (for 4340 steel the highest strain rate achieved in reference is only 570 s^–1 whilst for Ti-6Al-4V alloys the strain rates of up to 6000 s^–1). It should be mentioned here that in some situations (e.g. ballistic impact) where much higher strain rates can be involved, and the uncertainty of the accuracy of the JC model still remains due to lack of test data at even higher strain rates both for 4340 steel and Ti-6Al-4V alloys.

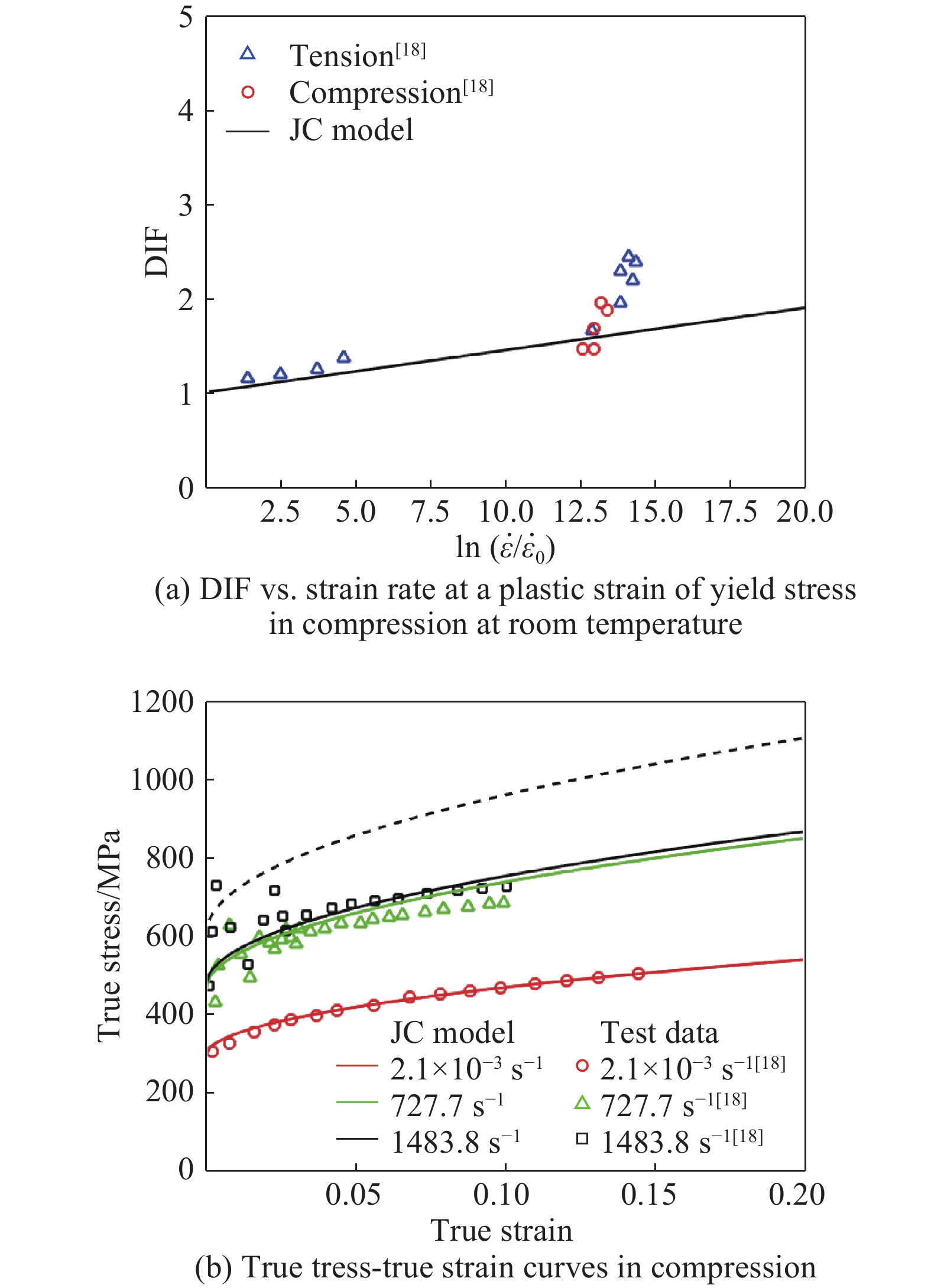
Fig.7 shows comparison between the JC model predictions and the test results for Q235 mild steel. As can be seen from Fig.7(a) that the JC model has failed to describe the strain rate effects for strain rates greater than 727.7 s^–1 accurately, although it seemingly describes reasonably well the dynamic stress-strain response as can be seen from Fig.7(b).

To further investigate the accuracy of the JC constitutive model the true stress-true strain curves predicted by the quasi-static stress-strain curve multiplied by the experimentally determined DIF at the highest strain rates for 2024-T351, 6061-T6, OFHC copper and Q235 mild steel are also shown in Fig.2(c), Fig.3(b), Fig.4(b) and Fig.7(b) as indicated by the dashed lines. It is found from Fig.2(c), Fig.3(b) and Fig.4(b) much better agreements are obtained for 2024-T351, 6061-T6 and OFHC copper whilst from Fig.7(b) much worse agreement is achieved for Q235 mild steel. In other words, the JC model has failed to produce consistent results for different materials, implying the form of its equation, i.e. 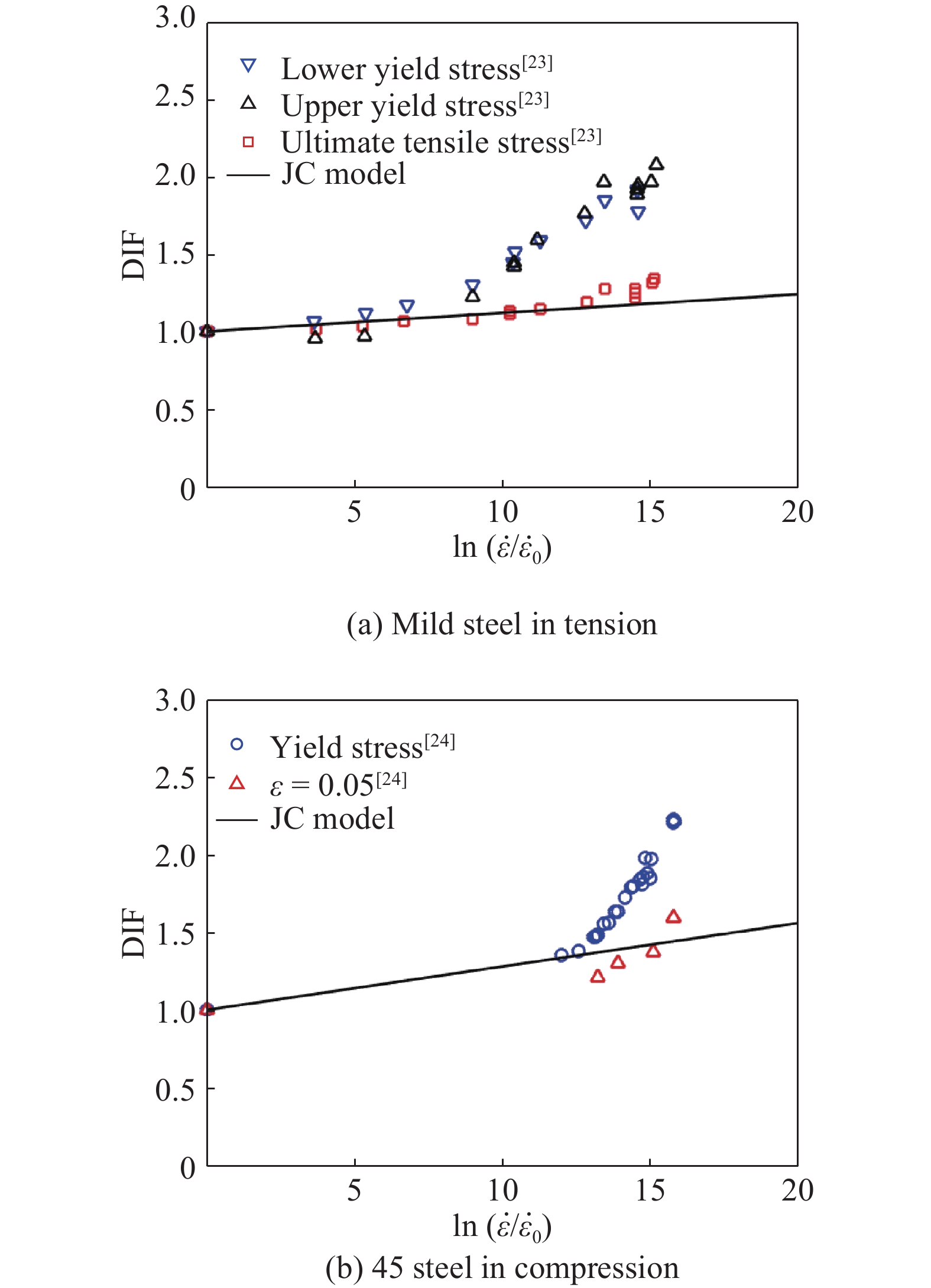$\left( {A + B\varepsilon _{\rm{p}}^n} \right)\left( {1 + C \ln\,{{\dot \varepsilon }^*}_{\rm{p}}} \right)$, may be inadequate.

Moreover, it should be borne in mind here that the test data presented in Fig.2(a), Fig.3(a), Fig.4(a), Fig.5(a), Fig.6(a) and Fig.7(a) were taken at different plastic strains, for example, DIF at a plastic strain of 0.075 for 2024-T351, DIF at a plastic strain corresponding to UTS for 6061-T6, DIF at a plastic strain of 0.05 both for 4340 steel and Ti-6Al-4V alloy, DIF at a plastic strain of 0.15 for OFHC copper and DIF at yield stress for Q235 mild steel. Generally speaking, the strain rate effects in terms of DIF for a particular material at different plastic strains are different as observed experimentally by Campbell and Cooper^[22] and highlighted by Jones^[23] for mild steel which is redrawn in Fig.8(a) in terms of DIF vs. strain rate and by Chen et al.^[24] which is presented in Fig.8(b) for 45 steel. In other words, as can be clearly seen from Fig.8 that the experimentally determined DIF according to different plastic strains can lead to different results. Hence, the choice of DIF at different plastic strains may add further uncertainty to the accuracy of the JC constitutive model.

Temperature effect is also very important in the situations where high strain rates, large plastic strains are involved which lead to temperature rise due to (quasi) adiabatic conditions and it should be considered in the formulation of a constitutive model for materials. In this section, the accuracy of the term of temperature effect in the JC constitutive model will be assessed in terms of ratio of true stress at elevated temperature to that at room temperature and true stress-true strain curves at elevated temperature.

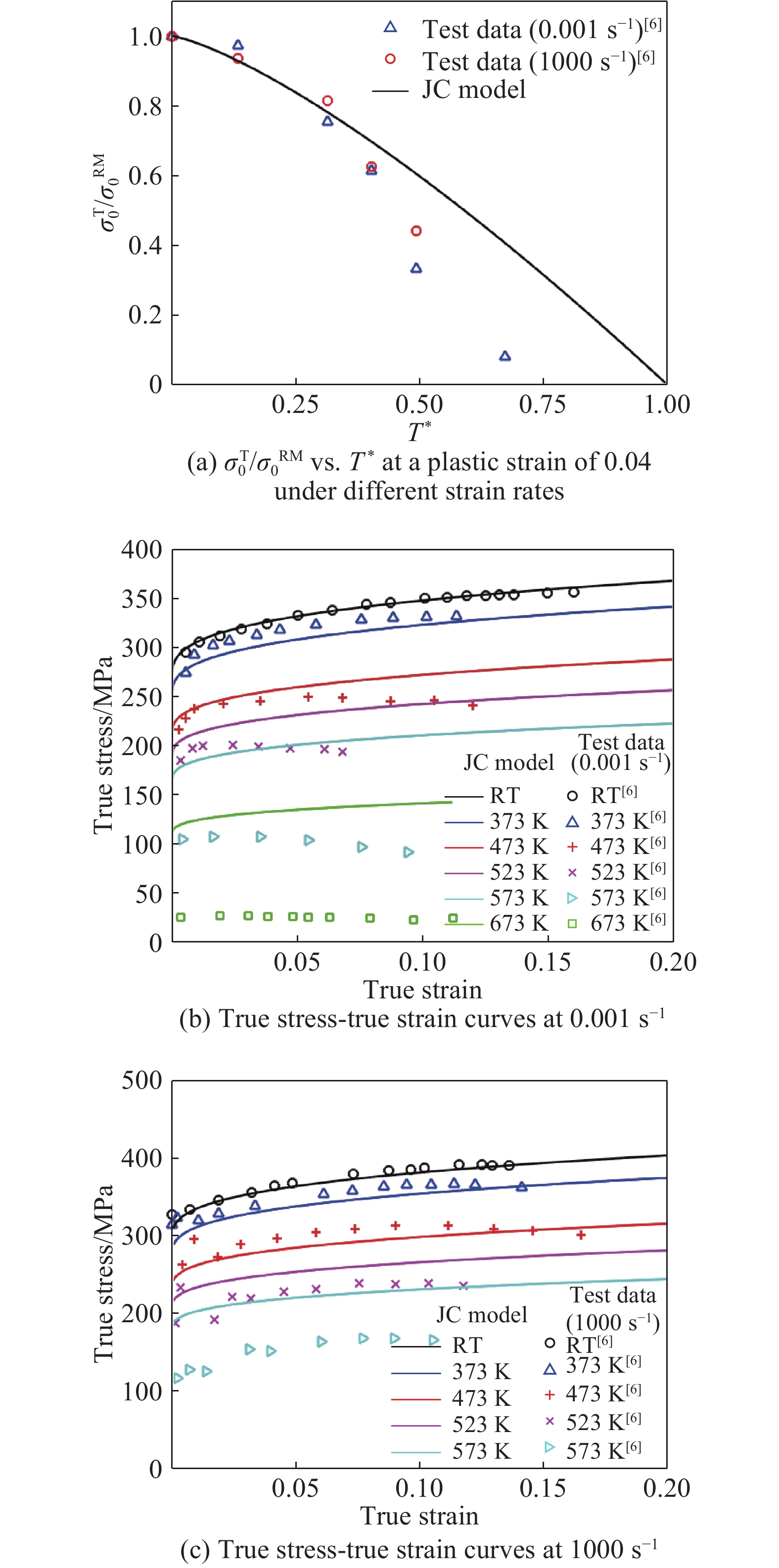
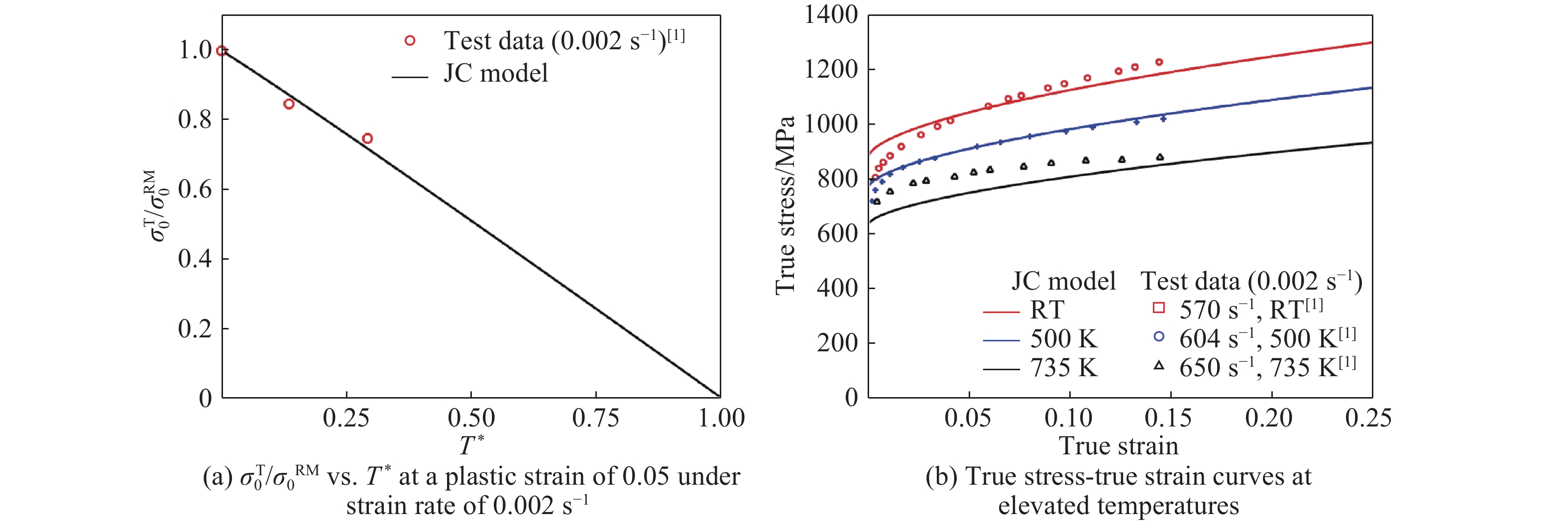
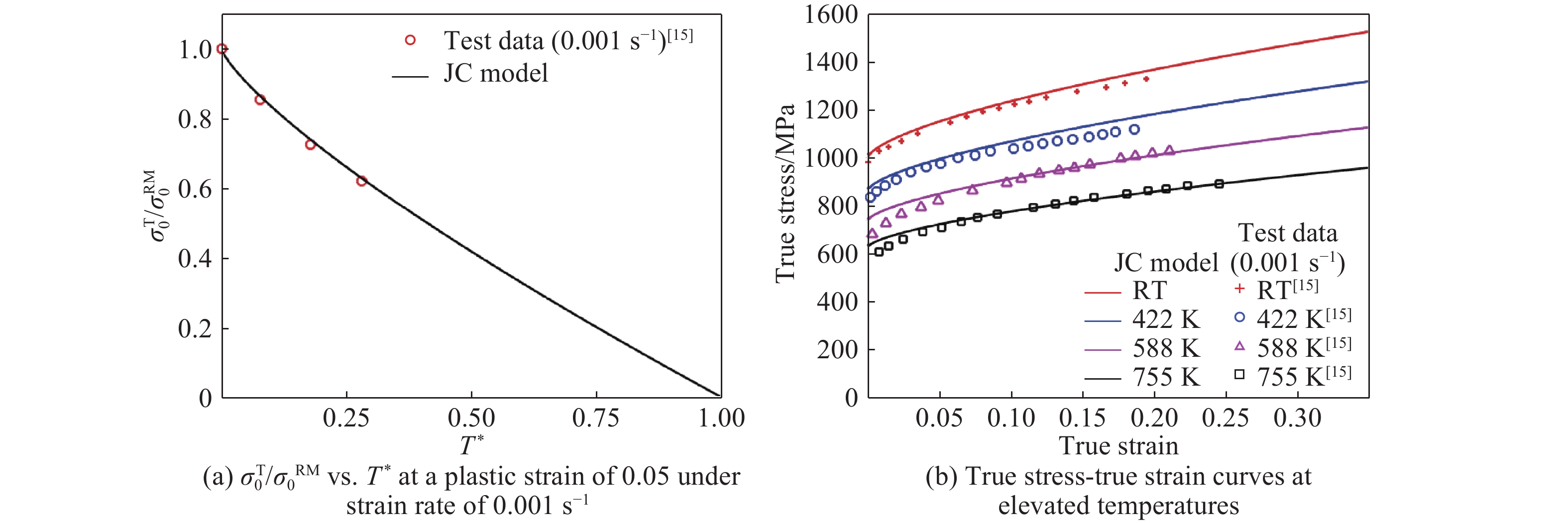
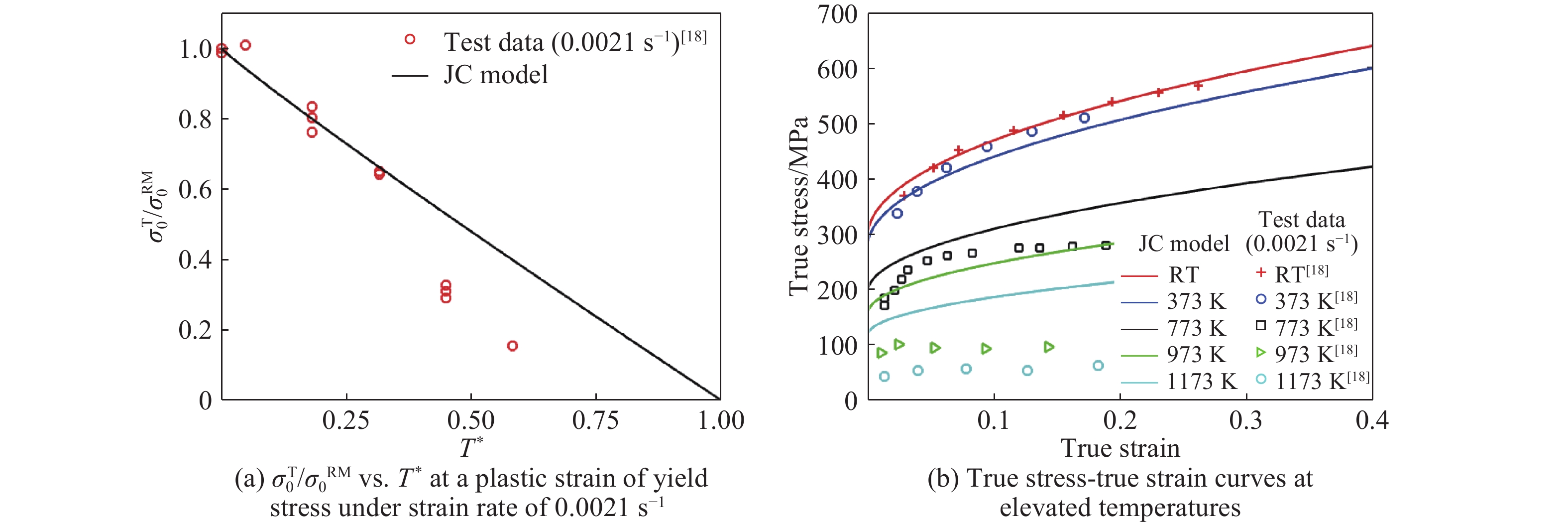
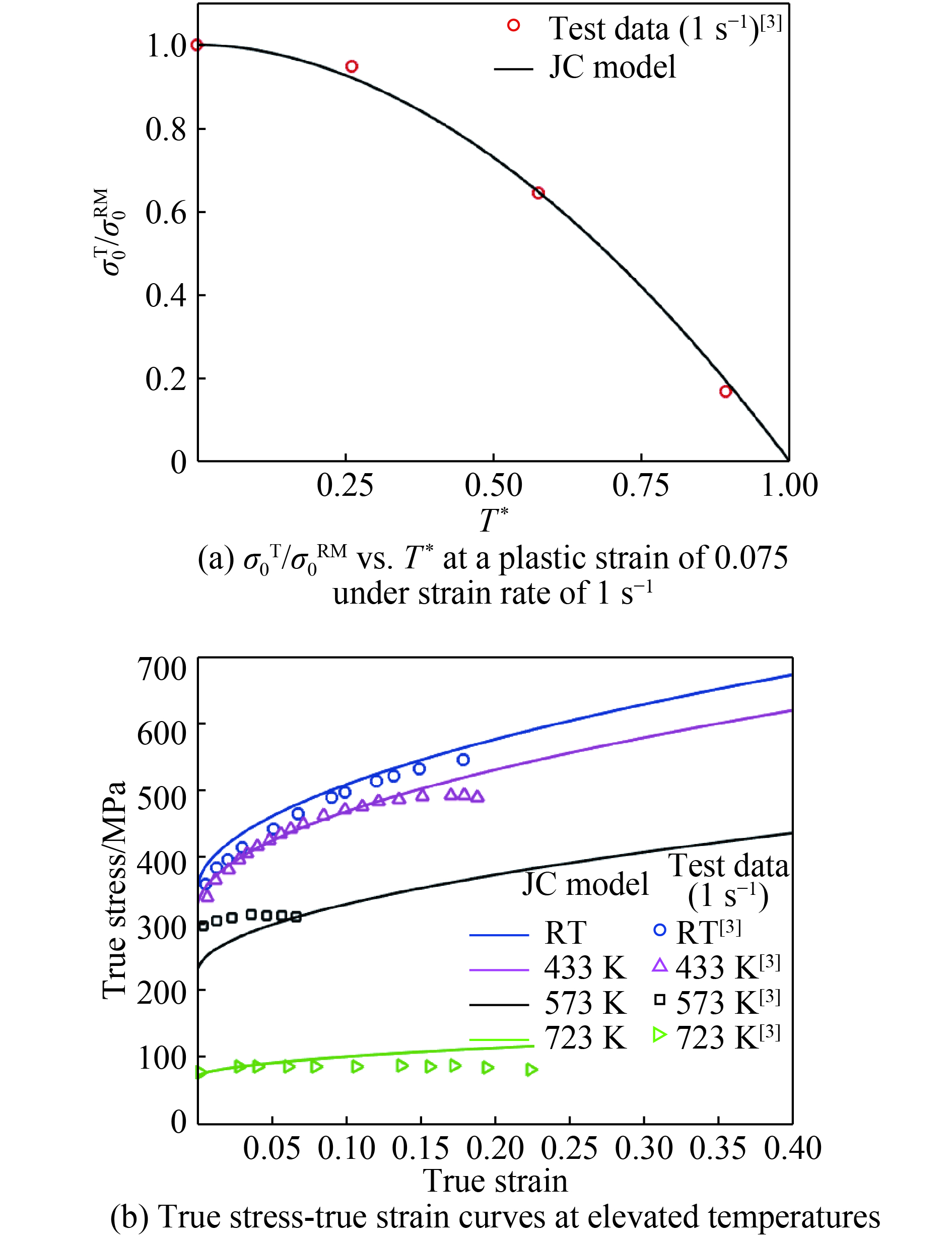
Fig.9–Fig.14 show comparisons of the JC model predictions with the test data for 2024-T351 aluminum alloy^[3], 6061-T6 aluminum alloy^[6], OFHC copper^{[9, 11]}, 4340 steel^[1], Ti-6Al-4V alloys^[15] and Q235 mild steel^[18]. The values of $m$ and ${T_{\rm{m}}}$ are shown in Table 1. In this paper, ratio of (yield) stress at elevated temperature to that at room temperature ($\sigma _0^{\rm{T}}/\sigma _0^{{\rm{RM}}}$) is normally employed to characterize the effect of temperature on the behavior of metallic materials.

It can be seen from Fig.9(a) that the term of temperature, namely, $(1 - {T^*}^m)$ in the JC constitutive model can be used to describe the relationship between the ratio of stress at elevated temperature to that at room temperature ($\sigma _0^{\rm{T}}/\sigma _0^{{\rm{RM}}}$) and dimensionless temperature (T^*) for 2024-T351 aluminum alloy when T_m is taken to be 775 K^{[3, 21]}. Similarly, the true stress-true strain relationships in tension can be also reasonably described by the JC model as can be seen from Fig.9(b). However, it is evident from Fig.10(a), Fig.11(a) and Fig.14(a) that the term of temperature, namely, $(1 - {T^*}^m)$ in the JC constitutive model can be used to describe the relationship between the ratio of stress at elevated temperature to that at room temperature ($\sigma _0^{\rm{T}}/\sigma _0^{{\rm{RM}}}$) and dimensionless temperature (T^*) for 6061-T6 aluminum alloy, OFHC copper and Q235 mild steel at T^* less than 0.4, and for T^* greater than this value the ratio decreases rapidly with increasing T^* and the JC model fails to predict it. As a matter of fact, it significantly over-estimate the temperature effects for 6061-T6 aluminum alloy, OFHC copper and Q235 mild steel at higher T^* as can be seen from Fig.10(a), Fig.11(a) and Fig.14(a). It is also evident from Fig.10(b), Fig.10(c), Fig.11(b) and Fig.14(b) that the true stress-true strain relationships in tension can be reasonably described by the JC model for T^*< 0.4, whilst for temperature larger than this value the agreement between the JC model predictions and the experimental data are poor.

Fig.12 and Fig.13 show comparisons of the JC constitutive model predictions with the test data for 4340 steel and Ti-6Al-4V alloys, respectively. It is clear from these figures that reasonable agreement is obtained within the ranges of the temperatures examined (i.e. T^* < 0.3).

Failure is extremely important in the safety calculations and assessment of structures subjected to large loads which produce large plastic deformations leading to rupture, and it should be taken into account in the formulation of a constitutive model for materials. In this section, the accuracy of the JC failure criterion will be assessed by comparing it with the test data for the fracture of different metallic materials under different loading conditions.

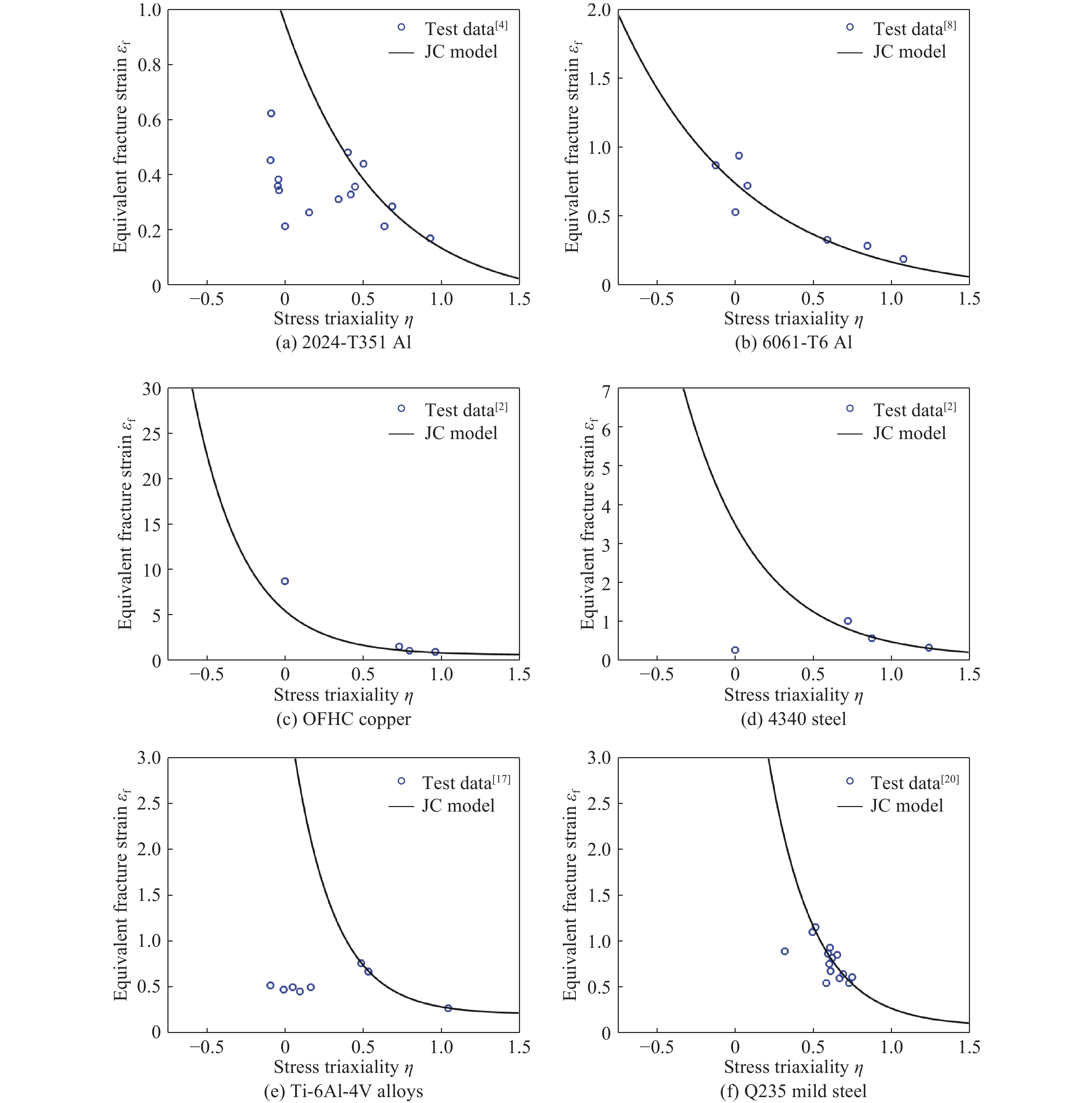
Fig.15 shows the dependence of the equivalent strain to fracture on the stress triaxiality for 2024-T351 aluminum alloy^[4], 6061-T6 aluminum alloy^[8], OFHC copper^[2], 4340 steel^[2], Ti-6Al-4V alloys^[17] and Q235 mild steel^[20]. The values of ${D_1},{D_2}$ and ${D_3}$ are shown in Table 1. It is demonstrated from Fig.15(a) that for 2024-T351 aluminum alloy the JC fracture criterion can describe the relationship between the fracture strain and the stress triaxiality for the smooth and notched tension tests reasonably well. Nonetheless, as can be seen from Fig.15(a), the JC fracture criterion has failed to predict the fracture strains of 2024-T351 specimens under other loading conditions such as shear loading. Similar results are also obtained for 4340 steel, Ti-6Al-4V alloys, Q235 mild steel as can be seen from Fig.15(d)–Fig.15(f). For 6061-T6 aluminum alloy and OFHC copper the JC fracture criterion is in reasonable agreement with the available test data as can be seen from Fig.15(b) and Fig.15(c) .

It is also demonstrated from Fig.15(a), Fig.15(d)–Fig.15(f) that the critical fracture strains at shear are much lower than those at tension for 2024-T351 aluminum alloy, 4340 steel, Ti-6Al-4V alloys and Q235 mild steel. Moreover, the experimental results in Fig.15(a) does not show that the fracture strain decreases monotonically with increasing stress triaxiality as the JC fracture criterion implies. It is no surprising since the JC fracture criterion does not take into account the effect of Lode angle on the rupture of materials subjected to different loadings. Bai and Wierzbicki^[25] conducted a comparative study of 16 fracture models and pointed out that the JC fracture criterion has not taken into consideration the effect of the third deviatoric stress invariant. Wang and Qu^[26] performed an analysis of ductile fracture by the way of an extended unified strength theory which catered for the effects of the stress triaxiality and the normalized Lode angle parameter.

In Section 2.1 a critical assessment of the accuracy of the JC constitutive model has been made by comparing its predictions with the material test data available for some metals. It is clear that JC constitutive model is applicable to Mises materials at quasi-static to intermediate strain rates and low to moderate temperature and that its accuracy deceases with increasing strain rate and temperature. In order to assess further the accuracy of the JC constitutive model and the suitability of its application in situations where higher strain rates and temperatures are involved, the following numerical simulations are carried out for the ballistic perforation of metal plates made of 2024-T351 aluminum alloy by flat-ended projectiles using the JC constitutive model.

Rodriguez-Millan et al.^[21] recently conducted an experimental investigation into the ballistic perforation of 2024-T351 aluminum alloy plates. The diameter of the flat-ended cylindrical projectile was 5.5 mm and its length 7 mm. The maraging steel projectile had a mass of 1.1 g. The aluminum alloy target was fully clamped with a square window of 100 mm×100 mm and its thickness 4 mm. Fig.16 shows the finite element model used in the numerical simulations. In order to achieve computational efficiency as well as accuracy, the target plate adopts transition grid from the impact center to the boundary. The target plate area around the impact point, which has a radius of 1.8 times the projectile one, has the smallest mesh size (i.e. 0.1 mm×0.1 mm×0.1 mm). Due to symmetry boundary conditions only 1/2 of finite element model is built to save computing time. In the numerical simulations no friction is considered and the projectile is assumed to remain rigid.

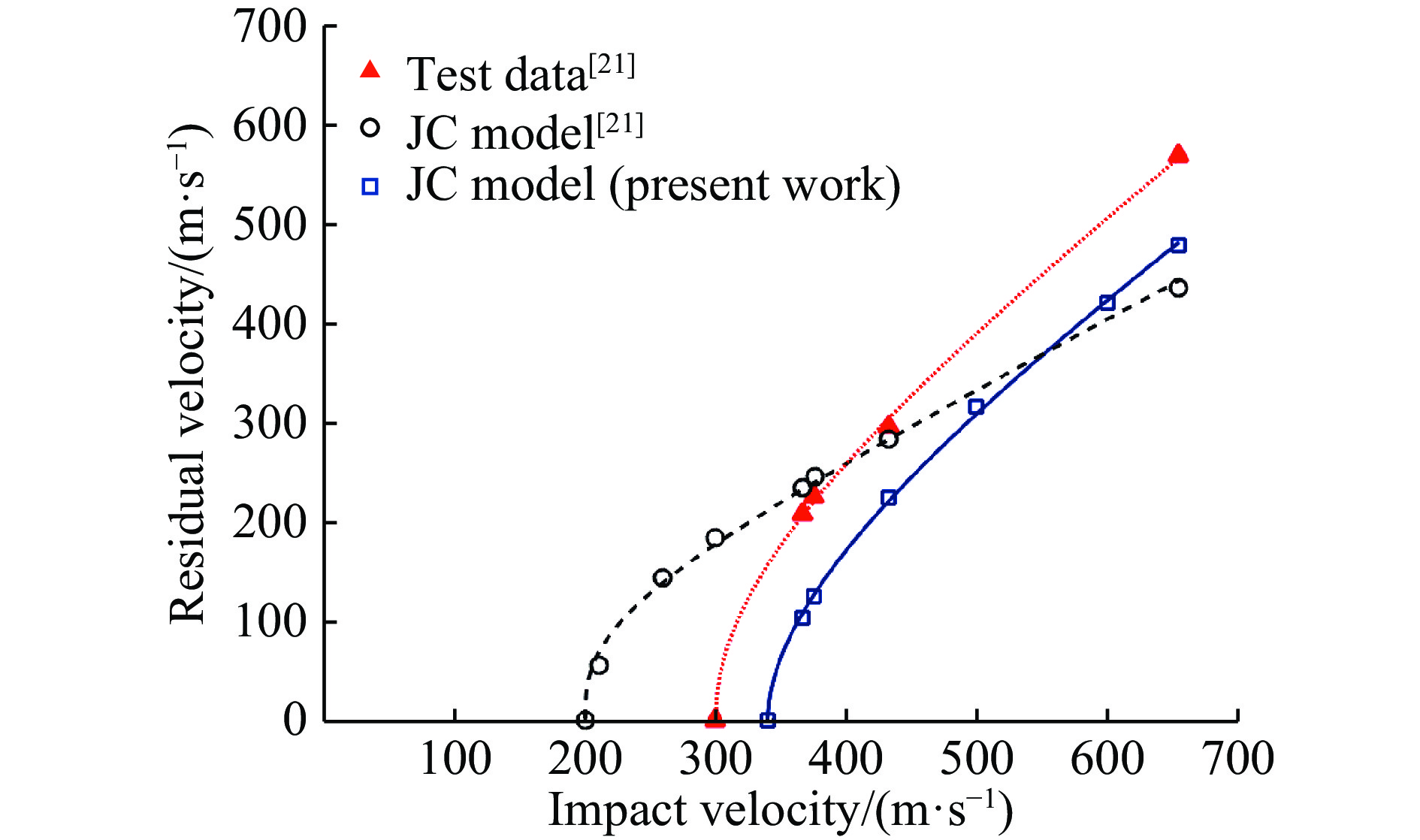
Table 2 lists two sets of the values of various parameters in the JC constitutive model for 2024-T351 aluminum alloy employed in the numerical simulations. One set is directly quoted from Ref.[21] and the other obtained from Section 2.1. To illustrate the difference of these two sets of parameters values Fig.17 shows the comparison of them in terms of quasi-static stress-strain curves, DIF vs. strain rate, $\sigma _0^{\rm{T}}/\sigma _0^{{\rm{RM}}}$ vs. T^*, and equivalent strain to fracture vs. the stress triaxiality curves. It can be seen from Table 2 and Fig.17 that the two sets of data differ a lot in terms of strain rate effect and fracture strain effect.

Fig.18 shows comparison of the numerically predicted residual velocities with the test results for the perforation of the 2024-T351 aluminum alloys plates struck by the flat-faced projectile^[21]. Also shown in the figure are the numerical results obtained by Rodriguez-Millan et al.^[21]. It is clear from Fig.18 that the numerical results using both sets of parameters values in the JC constitutive model are in poor agreement with the experimental data. The numerical results using the set of parameter values obtained in Section 2.1 are generally lower than the test data; the numerical results obtained by Rodriguez-Millan et al.^[21] using the other set of parameter values are higher than the test data for impact velocities less than 400 m/s, whilst for impact velocities greater than 400 m/s the numerical results are lower than the experimental data. All these results as presented in Fig.17 and Fig.18 have demonstrated that the JC constitutive model is incapable to describe the response of metals at higher strain rates and at fracture. This is due to the facts that the linear term of $\left( {1 + C\,{\rm {ln}}\,{{\dot \varepsilon }^*}_{\rm{p}}} \right)$ in the JC constitutive model cannot reflect the non-linearity of the strain rate sensitivity of metals at higher loading rates as involved in ballistic perforation; and that its failure criterion is a monotonically decreasing function of the stress triaxiality and takes no account the effect of Lode angle.

A critical assessment has been made in this paper about the accuracy of the JC constitutive model including failure criterion based on the analysis of the material test data for different metals under different loading conditions. To assess further its accuracy the model predictions have been also made with the experimental data for the perforation of 2024-T351 aluminum alloy plates struck normally by a flat-ended projectile. The main conclusions are as follows:

(1) The JC constitutive model is applicable to Mises materials at quasi-static to intermediate strain rates and low to moderate temperature;

(2) The agreement between the model predictions and the experimental results is poor for non-Mises materials in terms of shear stress-shear strain curve;

(3) The JC fracture criterion can describe reasonably well the fracture of metals in axisymmetric stress state (i.e. tensile loading) but fail to predict the failure of the metals in plane strain state (i.e. shear loading) as it takes no account of Lode angle effect;

(4) Its accuracy decreases with increasing strain rate and temperature;

(5) The form of the model’s equation (namely, quasi-static stress-strain curve multiplied by DIF) may be inadequate at least for the scenarios where high strain rates are involved.