高级搜索

爆炸驱动亚毫米级金属颗粒群的飞散特性

,  ,  , 

downloadPDF

上一篇

下一篇

冯吉奎, 皮爱国, 刘源, 景莹琳. 爆炸驱动亚毫米级金属颗粒群的飞散特性[J]. 高压物理学报, 2019, 33(6): 065104-1. doi: 10.11858/gywlxb.20190741
引用本文: 冯吉奎, 皮爱国, 刘源, 景莹琳. 爆炸驱动亚毫米级金属颗粒群的飞散特性[J]. 高压物理学报, 2019, 33(6): 065104-1. doi: 10.11858/gywlxb.20190741
shu
Jikui FENG, Aiguo PI, Yuan LIU, Yinglin JING. Scattering Characteristics of Sub-Millimeter Metal Particle Group Driven by Explosion[J]. gaoyawli, 2019, 33(6): 065104-1. doi: 10.11858/gywlxb.20190741
Citation: Jikui FENG, Aiguo PI, Yuan LIU, Yinglin JING. Scattering Characteristics of Sub-Millimeter Metal Particle Group Driven by Explosion[J]. gaoyawli, 2019, 33(6): 065104-1. doi: 10.11858/gywlxb.20190741
shu

爆炸驱动亚毫米级金属颗粒群的飞散特性

  • 北京理工大学爆炸科学与技术国家重点实验室，北京　100086

    • 作者简介: 冯吉奎（1993－），男，硕士，主要从事结构与冲击动力学研究. E-mail: 18810998871@163.com .
    通讯作者: 皮爱国（1977－），男，博士，副教授，主要从事爆炸冲击研究. E-mail: aiguo_pi@bit.edu.cn; 

  • 中图分类号: O347.1; TJ55

Scattering Characteristics of Sub-Millimeter Metal Particle Group Driven by Explosion

  • State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China

    • Corresponding author: Aiguo PI, aiguo_pi@bit.edu.cn ; 

  • MSC: O347.1; TJ55

  • 摘要: 采用试验与数值模拟相结合的方法，研究了爆炸驱动下亚毫米级WC颗粒群的飞散特性及其影响因素。首先对重金属嵌层碳纤维复合材料（CFRP）壳体开展静爆试验研究，测得距爆心一定距离处颗粒速度；然后基于离散元方法（DEM），依据实体情况对WC颗粒层的颗粒进行无序建模与数值模拟，分析了颗粒无序排列时不同颗粒、装填比及长径比对颗粒速度的影响规律。结果表明：在相同装填比下，颗粒粒径越大，单个颗粒所获得的速度越小；端部附近内外层颗粒速度相同，相对轴向位置X/L=0.62附近速度差最大；长径比在0.5～1.5范围内时，随着长径比的增加，颗粒的速度及速度差增大，起爆端相对于非起爆端颗粒速度增加较小。
    Abstract: Under the implosion of the carbon fiber composite (CFRP) shell embedded in dense inert metal particle, the damage elements dominated by dense inert metal particles will be formed. Thus, accurately acquiring and predicting the scattering performance of heavy metal particle cluster driven by internal-burst is of great significance for the design and evaluation of damage capability of low collateral damage munitions. In this paper, both the experimental study and numerical simulation are adopted to investigate the scattering characteristics and influencing factors of the sub-millimeter WC particle group under explosion. Based on the discrete element method (DEM), the disordered model and numerical simulation of particles in WC particle layer are carried out according to the entity condition, the effects of different particles, loading ratio and length-to-diameter ratio on particle velocity are analyzed. The results show that the larger size of a particle can result in a lower velocity under the condition of the same loading ratio. The outer layer particle velocity at the end is the same, but the velocity difference near the relative axial position X/L=0.62 is the largest. When the ratio of length to diameter is in the range of 0.5–1.5, both the particle velocity and velocity difference increase with the ratio of length to diameter, and the incremental velocity of the particles at the detonating end is smaller than that at the non-initiating end.
  • 加载中

  • 图 1  颗粒速度测试装置原理图

    Figure 1.  Schematic diagram of particle velocity test device

    下载: 全尺寸图片 幻灯片

    图 2  战斗部结构

    Figure 2.  Warhead structure

    下载: 全尺寸图片 幻灯片

    图 3  试验现场布局

    Figure 3.  Experimental field arrangement

    下载: 全尺寸图片 幻灯片

    图 4  不同时刻颗粒飞散图

    Figure 4.  Particle scattering diagram at different times

    下载: 全尺寸图片 幻灯片

    图 5  距爆心不同位置处颗粒速度历史

    Figure 5.  Velocity history of particle at different distance away from the charge center

    下载: 全尺寸图片 幻灯片

    图 6  颗粒速度-相对轴向位置曲线

    Figure 6.  Particle velocity vs. relative axial position curve

    下载: 全尺寸图片 幻灯片

    图 7  试验和理论公式计算得到的颗粒速度-位移曲线

    Figure 7.  Particle velocity vs. displacement obtained from experiments and empirical formula

    下载: 全尺寸图片 幻灯片

    图 8  内外层颗粒初速与相对轴向位置关系

    Figure 8.  Initial velocity of inner and outer particles vs. relative axial position

    下载: 全尺寸图片 幻灯片

    图 9  不同装填比颗粒初速与相对轴向位置的关系

    Figure 9.  Particle initial velocity vs. relative axial position under different filling ratios of charge

    下载: 全尺寸图片 幻灯片

    图 10  不同长径比颗粒初速与相对轴向位置的关系

    Figure 10.  Initial particle velocity vs. relative axial position for different aspect ratios of charge

    下载: 全尺寸图片 幻灯片

    表 1  装药参数

    Table 1.  Charge parameters

    $ \rho $/(g·cm−3)R/mmL/mmCFRP thickness/mmThickness of particle layer/mm
    Inner caseOuter case
    1.692050233
    下载: 导出CSV

    表 2  试验结果

    Table 2.  Experimental results

    No.DistanceMeasured velocity/(m·s–1)Fixed velocity/(m·s–1)
    137.5d705757
    240.0d685743
    362.5d635697
    下载: 导出CSV

    表 3  钨颗粒参数设置

    Table 3.  Parameters of tungsten particle

    $ \rho $/(g·cm–3)G/GPaA/GPaB/GPaNCMTM/KTR/K${ {{\dot \varepsilon }_0}}$/s–1cp/(J·g-1·K-1)
    17.62501.371.51×10–20.120.0161.01 4982941.01.35×10–3
    PCSpallITD1D2D3D4D5c0/(m·s–1)S1${\gamma_0}$
    –1.753.00.02.01.77–3.4003 8001.441.58
    下载: 导出CSV

    表 4  空气的状态方程参数

    Table 4.  Equation-of-state parameters of air

    $ \rho $/(g·cm–3)${C_0}$${C_1}$${C_2}$${C_3}$${C_4}$${C_5}$${C_6}$
    1.293×10–300000.40.40
    下载: 导出CSV

    表 5  炸药的JWL状态方程参数

    Table 5.  JWL equation-of-state parameters of explosive

    $ \rho $/(g·cm–3)AE/GPaBE/GPaR1R2$ \omega $pCJ/GPaDCJ/(m·s–1)e0/GPa
    1.69669.912.9014.31.20.3368 60010
    下载: 导出CSV

    表 6  炸药爆炸驱动不同颗粒的初速

    Table 6.  Maximum driving speed of different particles

    Granularity/mm$ \rho $/(g·cm–3)vmax/(m·s–1)Average velocity/(m·s–1)
    0.217.61 2491 060
    0.517.6984823
    0.717.6806686
    0.519.3574476
    下载: 导出CSV
  • [1] 刘意. 高密度惰性金属炸药爆轰与粒子流形成过程研究[D]. 北京: 北京理工大学, 2015: 7–37. LIU Y. Detonation of dense inert metal explosive and the formation of particles flow [D]. Beijing: Beijing Institute of Technology, 2015: 7–37.
    [2] FROST D L, ORNTHANALAI C, ZAREI Z, et al. Particle momentum effects from the detonation of heterogeneous explosives [J]. Journal of Applied Physics, 2007, 101(11): 113529. doi: 10.1063/1.2743912
    [3] GARDNER D R. Near-field dispersal modeling for liquid fuel-air explosives: SAND-90-0686 [R]. USA: New Mexico, Sandia National Laboratories, 1990.
    [4] GLASS M W. Far-field dispersal modeling for liquid fuel-air explosive: SAND90-0687 [R]. USA: New Mexico, Sandia National Laboratories, 1990.
    [5] BORISOV A A. Research on the explosive dispersion of FAE [R]. Bulawayo, Naweed Zaman, 1996.
    [6] ZHANG F, FROST D L, THIBAULT P A, et al. Explosive dispersal of solid particles [J]. Shock Waves, 2001, 10(6): 431–443. doi: 10.1007/PL00004050
    [7] 申超. 重金属粉末嵌层CFRP壳体内爆下低附带毁伤特性表征[D]. 北京: 北京理工大学, 2015: 9–22. SHEN C. The low collateral damage characterization of CFRP shell structure with heavy mental powder embedded as a layer under implosion [D]. Beijing: Beijing Institute of Technology, 2015: 9–22.
    [8] 白春华, 陈亚红, 李建平, 等. 爆炸抛撒金属颗粒群的装药方式 [J]. 爆炸与冲击, 2010, 30(6): 652–657. doi: 10.11883/1001-1455(2010)06-0652-06 BAI C H, CHEN Y H, LI J P, et al. Charge forms for explosion dispersal of metal particles [J]. Explosion and Shock Waves, 2010, 30(6): 652–657. doi: 10.11883/1001-1455(2010)06-0652-06
    [9] CUNDALL P A. A computer model for simulating progress, large scale movements in blocky rock systems [C]//Proceedings of the Symposium of the International Society for Rock Mechanics. Nancy, France, 1971.
    [10] CUNDALL P A, STRACK O D L. Discussion: a discrete numerical model for granular assemblies [J]. Géotechnique, 1980, 30(3): 331–336. doi: 10.1680/geot.1980.30.3.331
    [11] LIU T, FLECK N A, WADLEY H N G, et al. The impact of sand slugs against beams and plates: coupled discrete particle/finite element simulations [J]. Journal of the Mechanics and Physics of Solids, 2013(61): 1798–1821.
    [12] OWEN P J, CLEARY P W. Prediction of screw conveyor performance using the discrete element method (DEM) [J]. Powder Technology, 2009, 193(3): 274–288. doi: 10.1016/j.powtec.2009.03.012
    [13] SAWAMOTO Y, TSUBOTA H, KASAI Y, et al. Analytical studies on local damage to reinforced concrete structures under impact loading by discrete element method [J]. Nuclear Engineering and Design, 1998, 179(2): 157–177. doi: 10.1016/S0029-5493(97)00268-9
    [14] CLEARY P W. Industrial particle flow modelling using discrete element method [J]. Engineering Computations, 2009, 26(6): 698–743. doi: 10.1108/02644400910975487
    [15] 薛琨, 许俊彪, 白春华. 爆炸驱动颗粒射流形成与演化的试验研究 [J]. 振动与冲击, 2014, 33(7): 126–132. XUE K, XU J B, BAI C H. Tests for formation and evolement of particle jets driven by and explosion [J]. Journal of Vibration and Shock, 2014, 33(7): 126–132.
    [16] 宋玉江, 周涛, 沈飞, 等. 双层预制破片爆炸驱动早期行为研究 [J]. 火炸药学报, 2018, 41(3): 308–313. SONG Y J, ZHOU T, SHEN F, et al. Research on the behavior of initial stage about explosively-driven double-layered premade fragments [J]. Chinese Journal of Explosives & Propellants, 2018, 41(3): 308–313.
    [17] 黄长强, 朱鹤松. 球形破片对靶板极限穿透速度公式的建立 [J]. 弹箭与制导学报, 1993(2): 58–61. HUANG C Q, ZHU H S. Establishment of the formula for the ultimate penetration speed of spherical fragments on the target plate [J]. Journal of Projectiles and Guides, 1993(2): 58–61.
    [18] 熊冉, 高欣宝, 许兴春, 等. 破片侵彻金属薄板后的剩余速度研究 [J]. 爆破, 2013, 30(4): 41–44. doi: 10.3963/j.issn.1001-487X.2013.04.009 XIONG R, GAO X B, XU X C, et al. Research on residual velocity of fragment after penetrating metallic sheet [J]. Blasting, 2013, 30(4): 41–44. doi: 10.3963/j.issn.1001-487X.2013.04.009
    [19] 倪妍. CFRP壳体战斗部低附带毁伤特征表征[D]. 北京: 北京理工大学, 2014: 30–56. NI Y. Characterization of low incidental damage of CFRP shell warhead [D]. Beijing: Beijing Institute of Technology, 2014: 30–56.
    [20] BABU V, KULKARNI K, KANKANALAPALLI S, et al. Sensitivity of particle size in discrete element method to particle gas method (DEM_PGM) coupling in underbody blast simulations [C]//Ravi Thyagarajan 14th International LS-DYNA Conference. USA: Sanjay, 2016: 191–212.
    [21] 楼建锋, 王政, 洪滔, 等. 钨合金杆侵彻半无限厚铝合金靶的数值研究 [J]. 高压物理学报, 2009, 23(1): 65–71. doi: 10.11858/gywlxb.2017.03.001 LOU J F, WANG Z, HONG T, et al. Numerical study on penetration of seni-infinite aluminum-alloy targets by tungsten-alloy rod [J]. Chinese Journal of High Pressure Physics, 2009, 23(1): 65–71. doi: 10.11858/gywlxb.2017.03.001
    [22] 张世林. 轴向预制破片战斗部破片飞散特性影响因素分析[D]. 太原: 中北大学, 2012: 35–46. ZHANG S L. Analyze on the factors of dispersion characteristic of axial prefabricated fragments [D]. Taiyuan: North University of China, 2012: 35–46.
    [23] 谭多望, 温殿英, 张忠斌, 等. 球形破片长距离飞行时速度衰减规律研究 [J]. 高压物理学报, 2002, 16(4): 271–275. doi: 10.3969/j.issn.1000-5773.2002.04.006 TAN D W, WEN D Y, ZHANG Z B, et al. Long-distance flight performances of spherical fragments [J]. Chinese Journal of High Pressure Physics, 2002, 16(4): 271–275. doi: 10.3969/j.issn.1000-5773.2002.04.006
    [24] 印立魁, 蒋建伟. 多层球形预制破片战斗部破片初速场的计算模型 [J]. 含能材料, 2014, 22(3): 300–305. doi: 10.3969/j.issn.1006-9941.2014.03.006 YIN L K, JIANG J W. Calculation model of initial velocity on multilayered spherical fragments warhead [J]. Chinese Journal of Energetic Materials, 2014, 22(3): 300–305. doi: 10.3969/j.issn.1006-9941.2014.03.006
  • 加载中
图( 10) 表( 6)
计量
  • 文章访问数:  2474
  • HTML全文浏览数:  2474
  • PDF下载数:  34
  • 施引文献:  0
出版历程
  • 收稿日期:  2019-03-14
  • 网络出版日期:  2019-12-25
  • 刊出日期:  2019-12-01

爆炸驱动亚毫米级金属颗粒群的飞散特性

    通讯作者: 皮爱国（1977－），男，博士，副教授，主要从事爆炸冲击研究. E-mail: aiguo_pi@bit.edu.cn; 
    作者简介: 冯吉奎（1993－），男，硕士，主要从事结构与冲击动力学研究. E-mail: 18810998871@163.com
  • 北京理工大学爆炸科学与技术国家重点实验室，北京　100086
  • 收稿日期:  2019-03-14
  • 网络出版日期:  2019-12-25

摘要: 采用试验与数值模拟相结合的方法，研究了爆炸驱动下亚毫米级WC颗粒群的飞散特性及其影响因素。首先对重金属嵌层碳纤维复合材料（CFRP）壳体开展静爆试验研究，测得距爆心一定距离处颗粒速度；然后基于离散元方法（DEM），依据实体情况对WC颗粒层的颗粒进行无序建模与数值模拟，分析了颗粒无序排列时不同颗粒、装填比及长径比对颗粒速度的影响规律。结果表明：在相同装填比下，颗粒粒径越大，单个颗粒所获得的速度越小；端部附近内外层颗粒速度相同，相对轴向位置X/L=0.62附近速度差最大；长径比在0.5～1.5范围内时，随着长径比的增加，颗粒的速度及速度差增大，起爆端相对于非起爆端颗粒速度增加较小。

English Abstract

    全文HTML

  • 在未来反恐作战及城市战争场景下，减少对平民的附带杀伤及非军事目标的毁伤成为目前研究的热点[1]。亚毫米级高密度惰性金属颗粒在近场范围内具有较高的比动能，远场速度又能快速衰减，故采用亚毫米级高密度金属颗粒作为毁伤元是实现低附带毁伤的主要技术途径之一[2]，开展亚毫米级颗粒在爆炸驱动下的飞散特性研究对低附带毁伤弹药的研制具有重要意义。

    为研究爆炸驱动亚毫米级颗粒的能力，早在20世纪初，Gardner[3]、Glass[4]、Borisov[5]对爆炸抛撒液体燃料成雾（尤其是近场情况）进行了数值模拟和试验研究，给出了近场爆炸结束时云雾半径随装置外径的变化关系，奠定了低附带毁伤研究的基础。Zhang等[6]借助气固二相流理论模拟了爆炸驱动颗粒群飞散过程，初步分析了不同初始装药条件对颗粒群、爆炸产物、冲击波三者时程关系的影响。随后，申超[7]在Zhang等[6]研究的基础上对爆炸驱动作用下冲击波、颗粒及爆炸产物前沿进行了数值计算，分析得到相同装药条件下颗粒追赶爆炸产物前沿的距离随着密度的增加而增加。为了研究分装式和混装式装药驱动颗粒飞散特点，白春华等[8]通过设计等装填比静爆试验，证明了分装加飞散剂型装药在空间数密度、颗粒对靶板的侵彻能力、工艺和安全方面优于混装式。但是由于试验中缺少对亚毫米级颗粒速度进行测试的装置，因此对亚毫米颗粒在爆炸驱动下的加速过程研究较少，且很少对大量亚毫米颗粒群的爆炸驱动过程进行三维数值模拟研究。Cundall[9]提出了有别于光滑粒子流体动力学（SPH）的离散元方法（Discrete Element Method, DEM），并成功应用于岩石力学。在DEM中，单元的质量都赋予到颗粒的质心上，且每个单元都单独存在，随后Strack等[10]将其应用于颗粒材料。在近期研究中，Liu等[11]采用DEM和有限元方法（FEM）耦合对沙粒冲击三明治靶板结构进行数值模拟，证实了可以采用等效泡沫弹体替代沙粒对三明治结构进行冲击研究。Owen等[12]应用DEM研究了螺旋传送机传送颗粒类材料时（不同运行条件下）颗粒的速度、质量流量、能量耗散和功耗，为螺旋传送机的设计提供了技术支持。Sawamoto等[13]采用DEM研究了钢筋混凝土在冲击下的局部损伤，并通过试验进行了验证，证明了可以采用DEM模拟材料由连续到离散的过程。Cleary[14]使用DEM对工业粒子流进行粒子尺度模拟，更好地理解了粒子动力学，从而改善设备的设计及操作。

    由于亚毫米级颗粒尺寸太小，用传统的光学或者电学测试难以准确获取其飞散速度、速度衰减规律等量化的特征参量，而这是低附带毁伤武器设计、评估的重要依据。本研究设计了爆炸驱动亚毫米级碳化钨颗粒的速度测试设备，在重金属钨颗粒嵌层碳纤维复合材料（CFRP）壳体静爆试验中测量距爆心不同位置处的颗粒速度；并利用DEM对钨粉层进行数值建模，通过数值模拟研究不同装填比、颗粒及长径比对颗粒初速的影响规律。

1.   亚毫米碳化钨颗粒爆炸驱动试验

    1.1.   亚毫米级金属颗粒速度测试原理

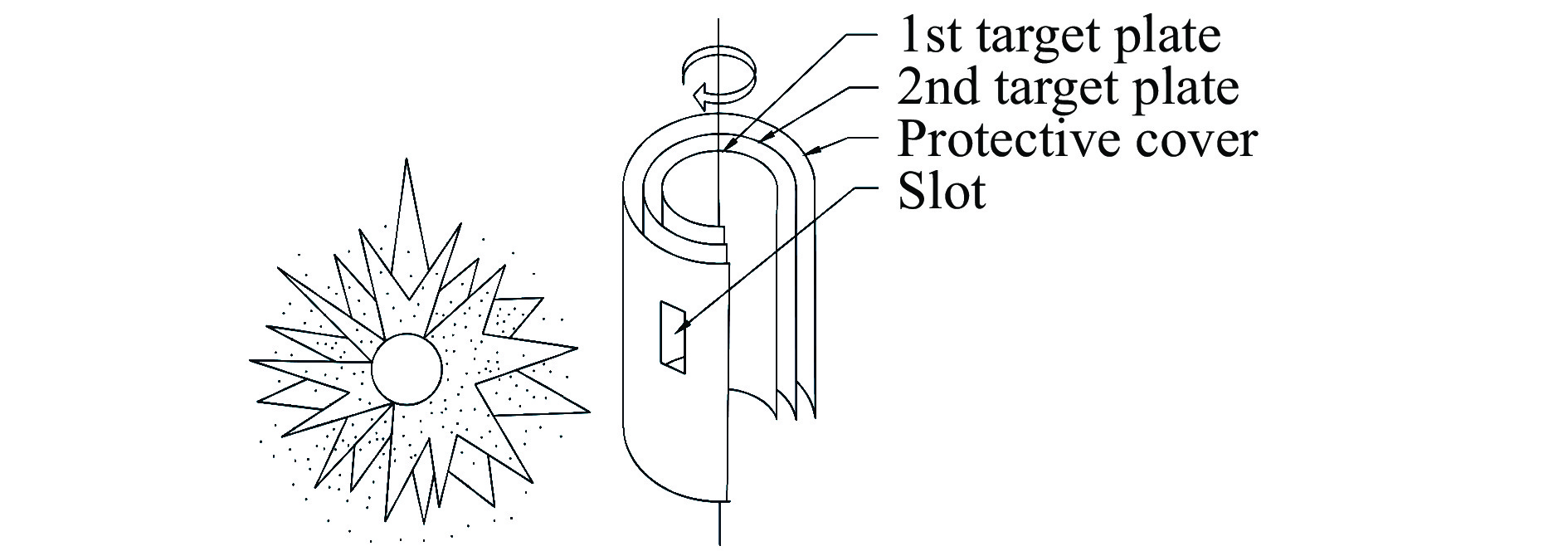
  • 现有的颗粒场轨迹、速度及爆炸产物轨迹测试装置，基本上是利用高速摄影仪、X射线相机等光学测试仪器对爆炸过程中颗粒及爆炸产物的飞散过程进行高速录像[15-16]。但是，由于试验中飞散颗粒对高速摄影仪等设备具有一定的毁伤危险，高速摄影仪等光学设备只能放置在安全距离处，所拍摄到的颗粒轨迹图像受清晰度影响，测量结果与真实结果之间的误差较大。因此，本研究基于一种新型的爆炸驱动金属颗粒群速度梯度测试方法，参考转镜式高速相机的原理，将颗粒场的直线运动转换成测试装置的旋转运动，进而可测量距爆心不同位置处的颗粒群速度，测速装置原理如图1所示。测速装置由效应板、带条形槽的保护罩及转轴组成。为避免颗粒速度较大时对穿第1层效应板影响试验结果，在第1层效应板中间加装圆柱形泡沫材料。试验过程中，第1、2层效应板始终以相同的角速度转动。爆炸驱动后，颗粒场以一定的速度梯度穿过保护罩上的条形槽，击穿第2层效应板，并最终到达第1层效应板，在两层效应板的不同位置形成弹孔。

    颗粒速度测速装置中，第1层效应板的半径为R，第2层效应板半径为$ R + \Delta r$，效应板与转轴以相同的角速度$ \omega $转动。炸药爆炸后驱动颗粒加速，假设颗粒穿过第1层效应板与第2层效应板间的夹角为$ \Delta \gamma $，则颗粒穿过第1层靶板到达第2层靶板所用的时间间隔$ \Delta t $为

    颗粒速度为

    本研究通过连轴器实现内、外效应板以相同的速度转动，利用电位控制器实现试验过程中效应板以恒定转速8 637 r/min转动。两层靶板两端用圆形固定环固定，保证靶板定位及外形。两层固定环之间放置间距为5 cm的定位环，用来确定两层靶板的间距。

    • 1.2.   亚毫米级金属颗粒速度测试试验布置

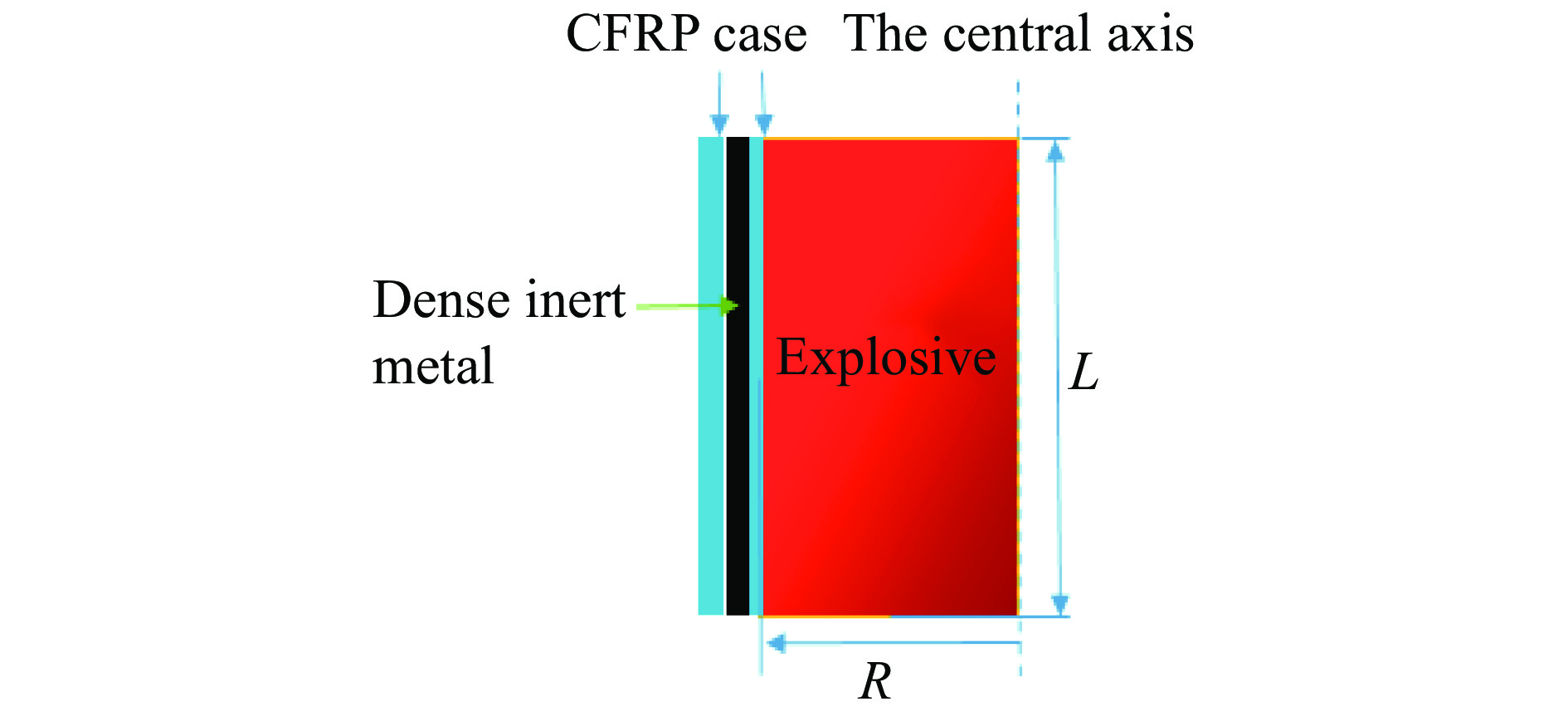
  • 战斗部结构如图2所示。战斗部主要由内层和外层CFRP壳体、钨颗粒层和炸药组成，内层CFRP壳体主要用来分隔炸药与钨颗粒，外层CFRP壳体主要用于保证战斗部结构强度。各结构具体尺寸如表1所示，其中ρ为密度，L为炸药长度。炸药采用压装圆柱形8701装药，装药量约为106 g。

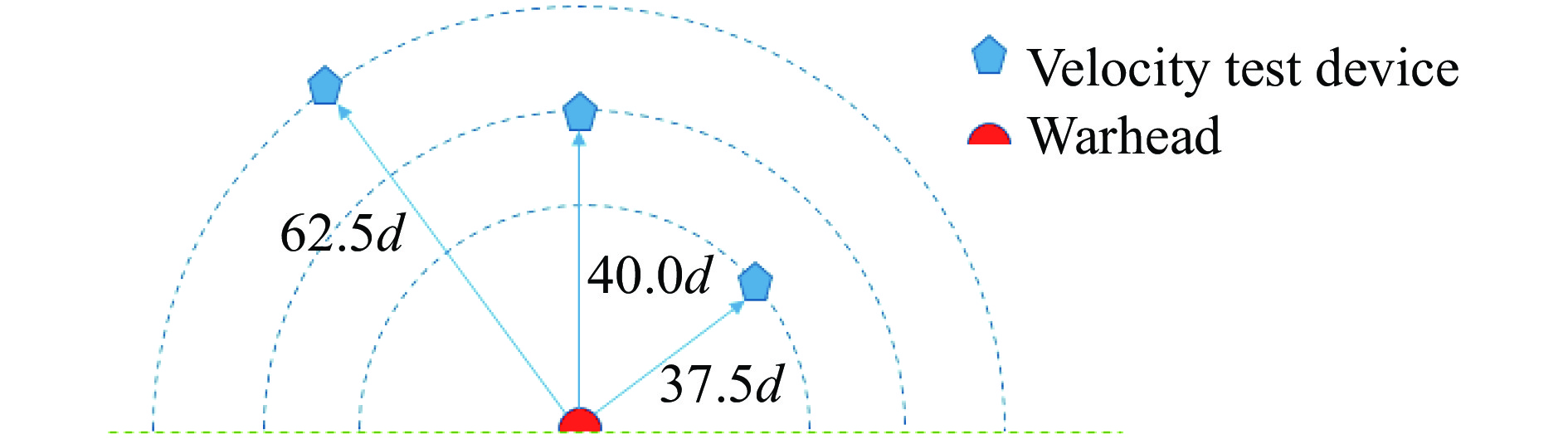
    战斗部两层壳体内填充直径为0.5 mm的碳化钨颗粒，金属颗粒质量约为175 g。为减小地面反射波对颗粒飞散的影响，设置炸药中心距地面0.5 m。为避免测速装置保护罩在冲击波和颗粒耦合作用下遭到破坏而影响测试结果，将速度测试装置分别放置在距爆心37.5d、40.0d、62.5d处(d为炸药直径)，并保证装置中心与炸药中心平齐。试验布局见图3。

    • 1.3.   亚毫米级金属颗粒结果与分析

  • 由试验可得，距爆心37.5d处靶板的穿孔数为55，40.0d处靶板穿孔数为31。距爆心62.5d处速度测试装置效应板回收结果显示：穿孔数为16，尺寸集中在55 mm×115 mm范围内；大部分穿孔集中在条形槽对应效应板的轴向位置，两侧颗粒数目较少，说明由爆心位置飞散的颗粒弹道垂直于效应板面，测得速度为颗粒的有效速度。通过对比测速装置效应板可以发现，距爆心距离越远的测速装置效应板上穿孔数目越少，穿孔沿轴向的分布宽度也随距离的增加而减少。

    回收效应板时，沿同一周向位置剪开。在数据处理时，规定以效应板转动方向为正方向，测量得到所有弹孔沿周向位置坐标并取平均值，以此计算试验中WC颗粒穿过两层靶板间的平均角度差，并根据（1）式、（2）式得到距爆心37.5d、40.0d、62.5d处颗粒的测试速度。由于颗粒在穿透第1层效应板时损失部分动能，由文献[17-18]中的经验公式可得到动能损失。

    颗粒的极限贯穿速度为

    式中：a、b为常数，分别取4.24、0.75；${\rho _{\rm{t}}}$为效应板密度；${\rho _{\rm{p}}}$为颗粒密度；${\sigma _{\rm{t}}}$为效应板强度极限。通过（3）式可以计算出颗粒在测量点处不受测速装置靶板阻碍作用时的速度，即颗粒的修正速度，结果如表2所示。

2.   数值仿真

    2.1.   仿真模型建立

  • 数值模拟结果可以对爆炸驱动颗粒试验结果进行补充。参考倪妍[19]的试验研究结果，静爆砂箱回收的残片表明，CFRP壳体在爆炸所产生的高温高压下完全燃烧，且壳体变形能及破裂能较爆炸过程中产生的能量很小，因此对数值模型进行简化，忽略壳体，仅针对重金属颗粒嵌层的爆炸驱动过程进行数值模拟分析。建立$\varnothing 40$ mm×50 mm的炸药模型，在距炸药表面2～5 mm内排列粒径为0.5 mm的球形钨颗粒，并建立$\varnothing 400$ mm×120 mm空气域。

    炸药驱动钨颗粒的有限元模型中，炸药和空气采用Euler网格，颗粒采用DEM颗粒。利用有限元前处理软件Ls-Prepost在给定区域内填充粒径为0.5 mm的球形离散单元，该单元以球心质点形式表现，当两球心之间的距离小于半径之和时，则认为存在接触力。炸药和颗粒之间通过定义耦合（关键字为*ALE_COUPLING _NODAL_ CONSTRAINT）进行相互作用，颗粒之间的相互作用力通过关键字*CONTROL_DISCRETE _ELEMENT定义[20]。起爆方式为端面点起爆。由于模型具有对称性，为了简化计算，采用1/4对称模型进行建模。

    数值模型中，不考虑钨球破碎，假设颗粒间碰撞为弹性碰撞。参考文献[21]对钨合金材料的试验分析及本构研究，得到WC颗粒材料的*MAT_Johnson_Cook材料模型及*EOS_Grüneisen状态方程参数，如表3所示。表3中：G为剪切模量，A为初始屈服应力，B为应变硬化常数，C为应变率硬化系数，M为温度软化指数，N为应变率硬化指数，TM、TR分别为室温和熔化温度，$ {{\dot \varepsilon }_0}$为参考应变率，cp为等压比热容，D1～D5为材料的损伤常数，c0、S1、γ0为Grüneisen状态方程参数。

    空气采用理想气体状态方程进行描述

    式中：C0、C1、C2、C3、C4、C5、C6均为常数；$\mu {\rm{ = }}\dfrac{1}{V} - 1$，$V$表示相对体积；$E$为初始内能。空气的材料参数见表4。

    炸药采用高能炸药模型和JWL状态方程进行描述

    式中：pE为任意时刻炸药单元所释放的压力，AE、BE、R1、R2和$ \omega $为常数，e为单位体积的内能密度。本研究选择8701炸药，依据文献[22]，其本构模型和状态方程参数如表5所示，其中：pCJ为炸药爆轰CJ压力，DCJ为炸药爆轰速度，e0为初始比内能。

    • 2.2.   计算结果与讨论

  • 爆炸驱动亚毫米金属颗粒数值模拟结果如图4所示。起爆后，起爆面端颗粒最先开始加速，但由于端部效应，相同时刻端部颗粒的位置落后于靠近中点的颗粒。爆炸完成后，颗粒飞散形状呈现鼓形。产生这种现象的主要原因是：炸药点起爆后，爆炸产物与内层球形颗粒最先作用，然后内层颗粒推动外层加速，颗粒层开始变薄；当颗粒层减至1～2层颗粒厚度时，颗粒间出现缝隙，爆炸产物通过间隙向外扩散；当颗粒群所受阻力大于驱动力时，颗粒开始减速。

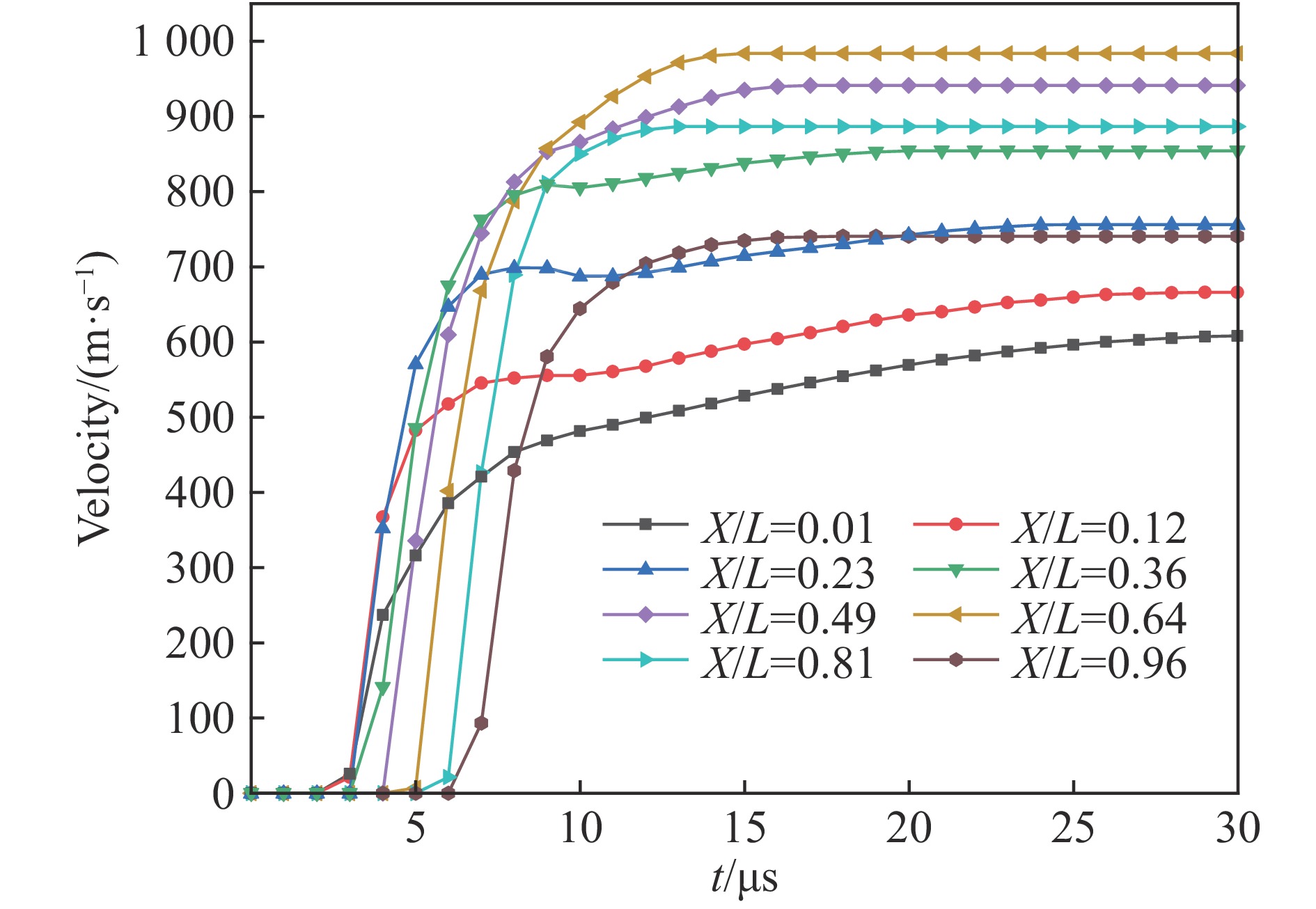
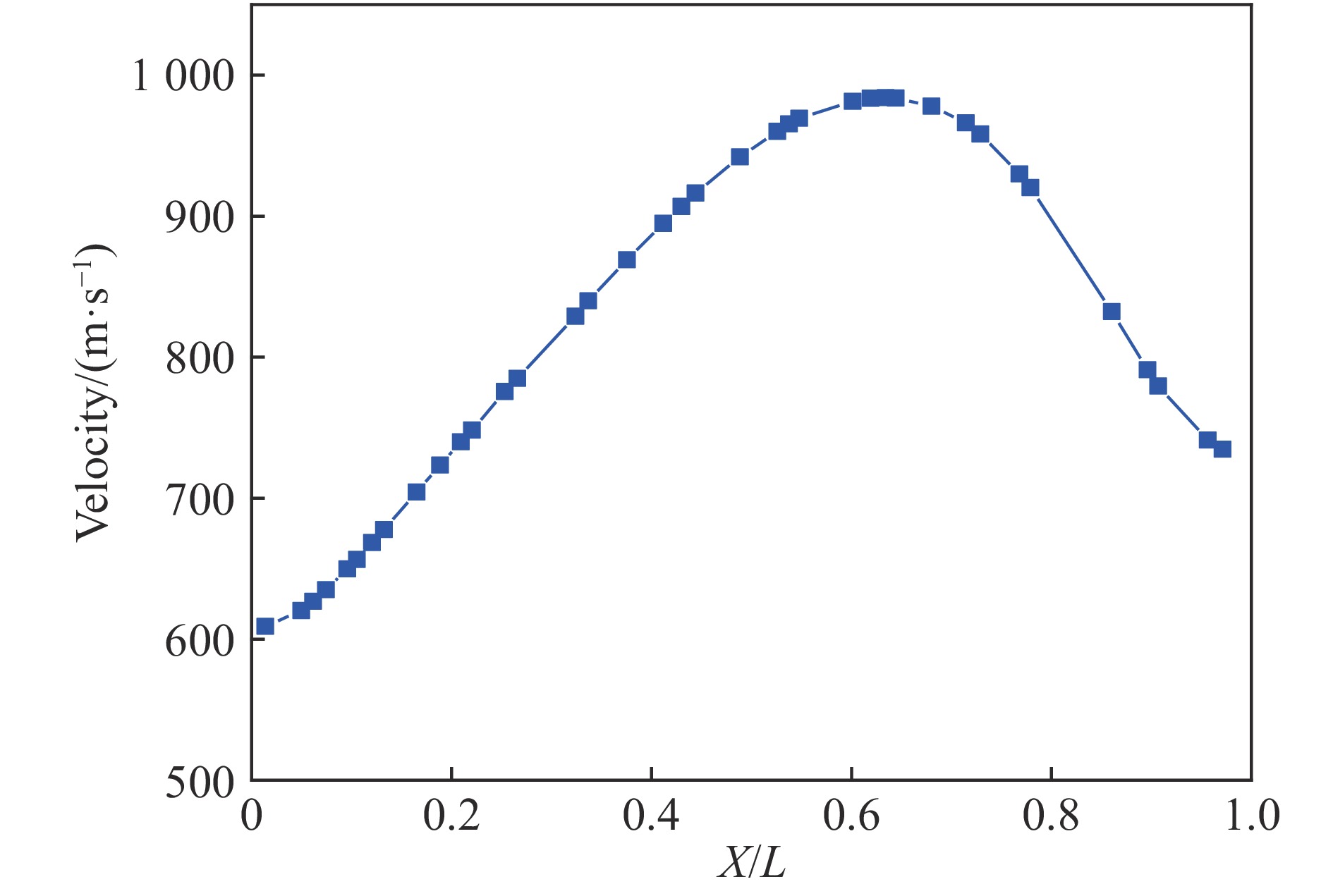
    图5为不同轴向位置颗粒速度与时间的关系。由图5可知，$ 2 \;{\text{μ}}{\rm s}$ 时，靠近起爆端的颗粒在爆炸产物作用下最先开始加速，其速度急剧增加，之后受到爆炸传播方向的影响，速度增长趋势变缓。与非起爆端相比，其颗粒加速时间较长。相对轴向位置（颗粒距起爆点轴向距离X与炸药长度L的比值）X/L为0.12、0.23、0.36的颗粒出现速度回落现象，颗粒速度下降，然后进一步加速。这种现象的产生主要是由于炸药爆炸之后的负压作用，导致在距爆心一定距离内颗粒的速度出现回落，然后进一步加速。

    图6所示是颗粒速度与相对轴向位置的关系。从图6中可知：随着相对轴向位置的增大，颗粒初速度从609 m/s开始增大；当相对轴向位置为0.62时，颗粒初速达到最大值，约为984 m/s；当相对轴向位置进一步增大后，速度开始下降，直至非起爆端面处速度为735 m/s。这种现象产生的原因是端部存在稀疏波效应，颗粒速度呈现中间大、两端小的特点。

    由数值模拟得到炸药中心位置颗粒初速，由于颗粒在爆炸驱动下的加速距离较小，故忽略加速阶段颗粒位移，根据文献[23]中球形破片速度衰减公式，可得到颗粒减速过程中速度与位移的关系

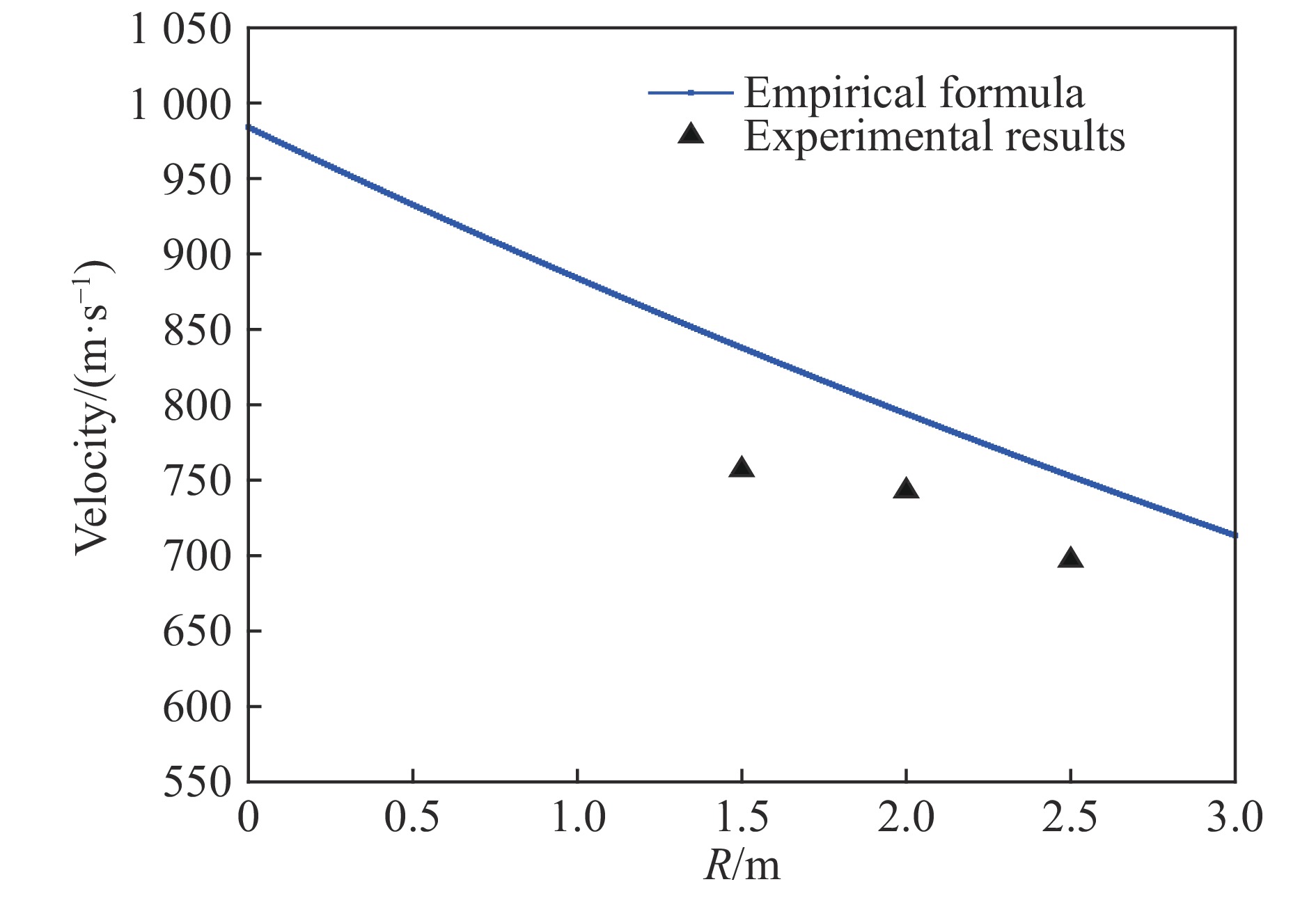
    式中：${v_{\rm{P}}}$为颗粒在位置$X$处的速度，${v_0}$为颗粒的初速，ρA为空气密度，${k_{\rm d}}$为颗粒所受的阻力系数，${S_{\rm f}}$为颗粒的迎风面积，m为颗粒的质量。

    将(6)式计算结果与试验修正后的数据进行对比，如图7所示。可见，试验结果与经验公式反映的颗粒减速趋势一致；但经验公式所得颗粒速度值大于试验数据，主要是由于经验公式中没有考虑颗粒周围流场密度的变化对颗粒阻力的增强效应。

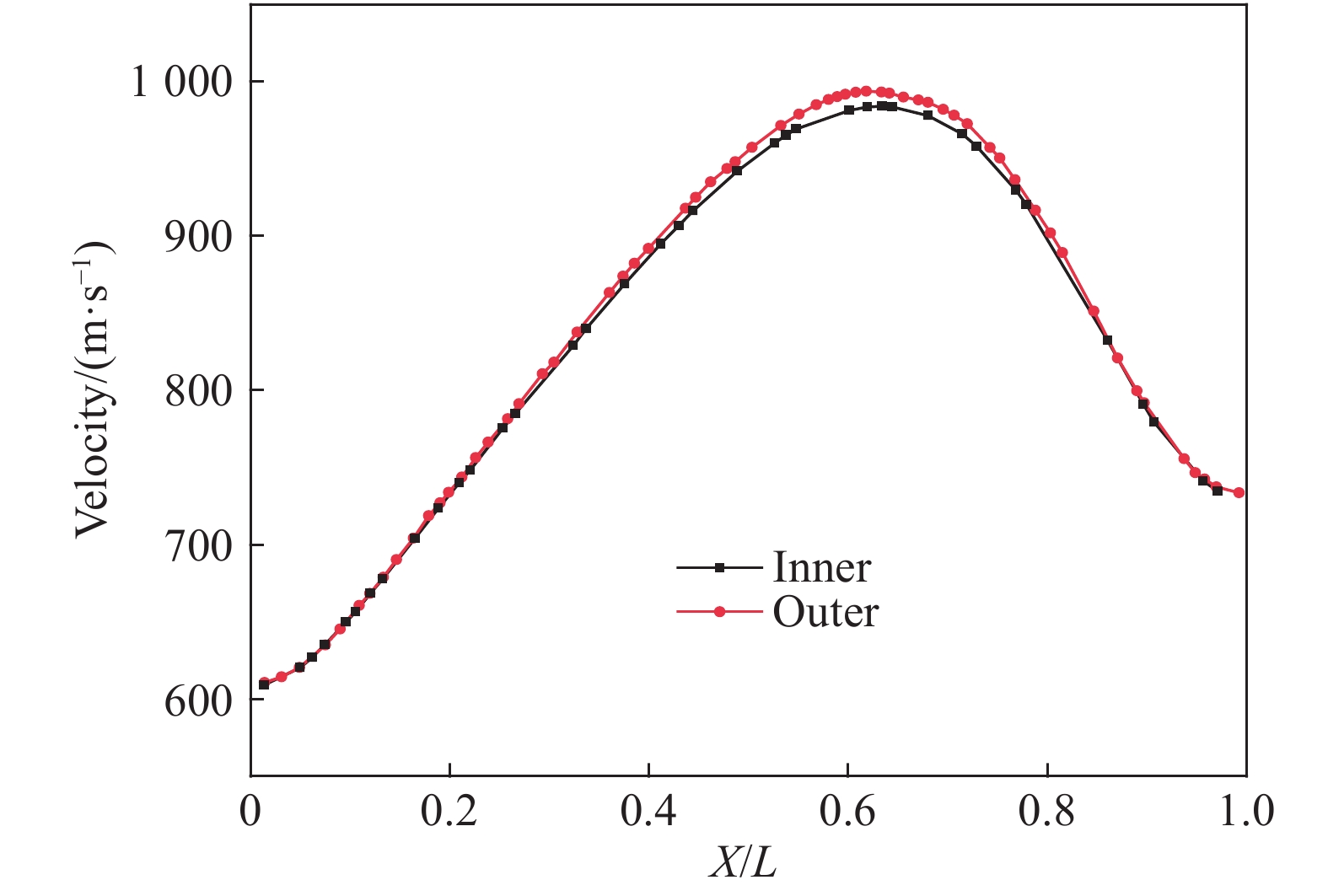
    为研究颗粒层不同径向位置对颗粒速度的影响，取最内层和最外层颗粒速度，得到最内层及最外层颗粒速度与轴向位置的关系，如图8所示。可以得出，与传统毫米级排列规则的预制破片初速[24]相比，亚毫米级颗粒无序排列时，在距离端部一定范围内最内层与最外层颗粒速度相同，在相对轴向位置0.35～0.83范围内存在速度差，最大速度差为2%。这说明当亚毫米级颗粒无序排列时，由于爆炸波传播方向和稀疏波效应，端部颗粒初速不受径向位置影响，内层颗粒与外层颗粒的初速相同；但战斗部中部的颗粒内外层存在一定的速度差，导致颗粒在飞散过程中形成一定厚度的颗粒群。

3.   影响爆炸驱动颗粒初速的因素分析

    3.1.   装填比对颗粒初速的影响

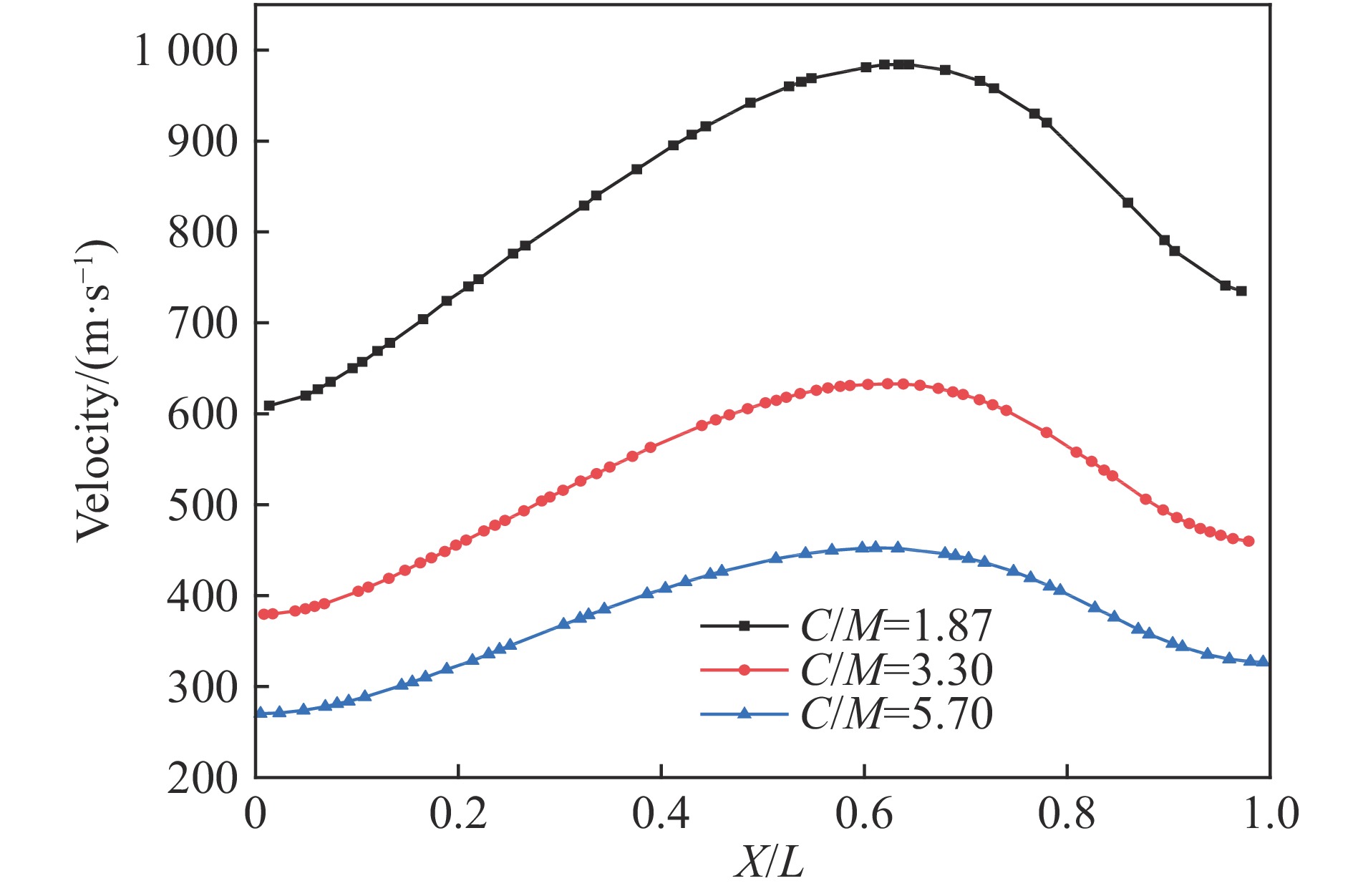
  • 为了研究不同装填比C/M（颗粒层质量与炸药质量之比）对颗粒速度的影响规律，在长径比与粒径相同的情况下，计算了装填比分别为1.87、3.30、5.70时炸药爆炸驱动颗粒的速度，得到了不同装填比下相对轴向位置与颗粒速度的关系，如图9所示。随着装填比的增大，颗粒速度有所减小，颗粒最大速度与起爆端颗粒速度之差由375 m/s减小至182 m/s。这主要是因为在炸药尺寸及种类一定时，炸药爆炸所产生的能量相同，随着装填比的增大，颗粒数量增多，单个颗粒获得的动能减小，相同轴向位置处颗粒的最大速度减小。相比于装填比为1.87的工况，装填比为5.70的颗粒速度与不同轴向位置的关系曲线起伏逐渐变缓。

    • 3.2.   不同颗粒对颗粒速度的影响

  • 为了研究不同颗粒粒度、密度对颗粒速度的影响规律，在装药质量与装填比相同的情况下，计算了粒径为0.2、0.5、0.7 mm（密度均为17.6 g·cm–3）和密度为17.6、9.3 g·cm–3（粒度均为0.5 mm）的颗粒速度随相对轴向位置的变化关系，结果如表6所示。由表6可知：随着颗粒粒径的增大，炸药爆炸驱动颗粒速度减小；粒径为0.2 mm的颗粒速度最大值为1 249 m/s，而粒径为0.7 mm的速度相比于粒径0.2 mm颗粒速度下降了40%；与密度为17.6 g·cm–3的颗粒相比，密度为19.3 g·cm–3的颗粒在起爆端速度减小10.0%，非起爆端减小9.8%，而最大速度由673 m/s减至633 m/s，减小了9.4%。这主要是因为在装药条件相同的情况下，炸药爆炸所产生的能量相同，颗粒密度或粒度越大，颗粒质量越高，单个颗粒所获得的能量越小，因而不同密度或粒度的颗粒在相同装药情况下被驱动加速获得的速度不同。

    • 3.3.   长径比对颗粒速度影响

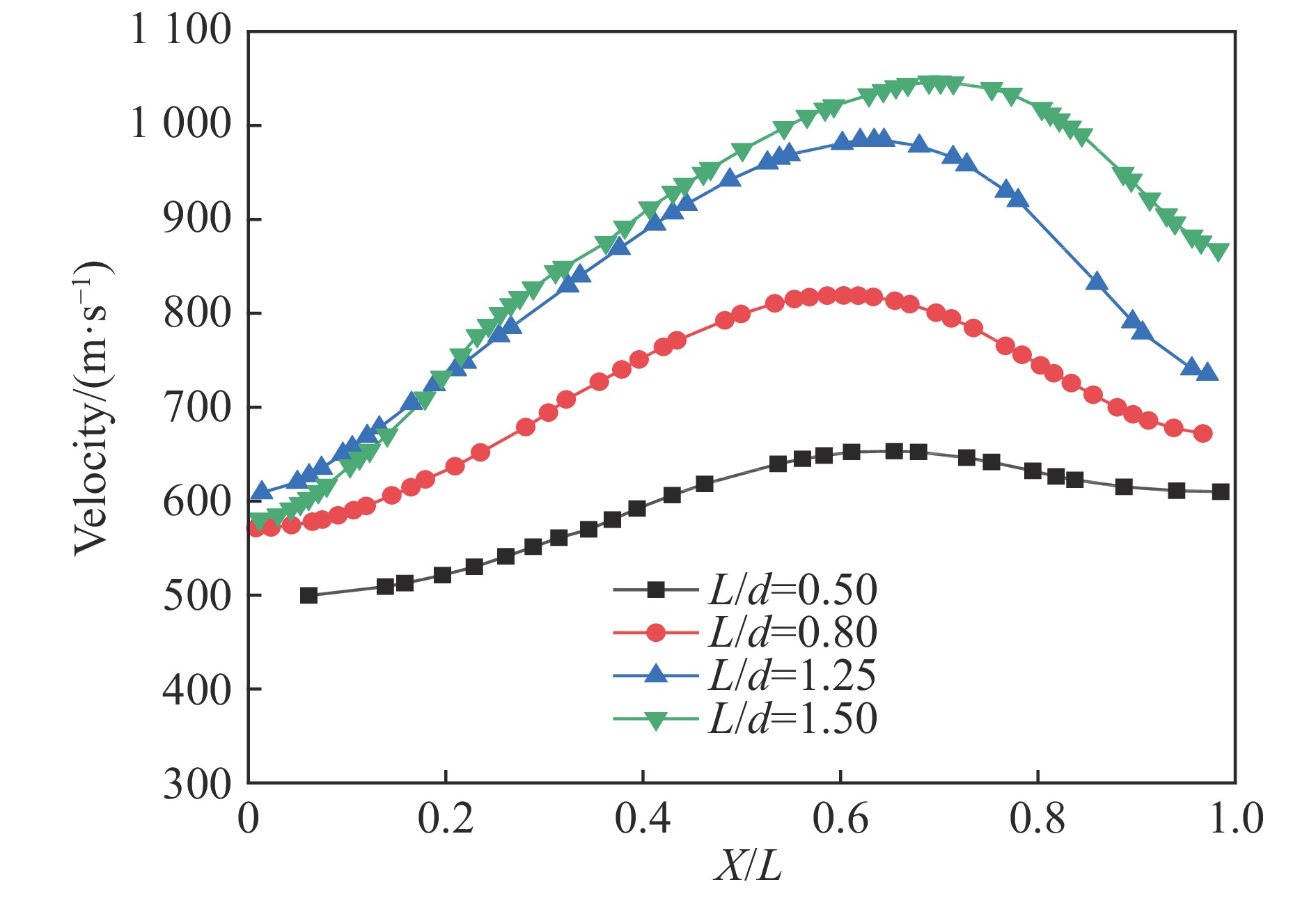
  • 为研究不同长径比L/d（炸药长度与炸药直径的比值）低附带毁伤战斗部在爆炸作用下对钨颗粒层颗粒速度的影响，在保证装填比及颗粒粒径不变的情况下，开展了4种不同长径比（0.50、0.80、1.25、1.50）下爆炸驱动重金属颗粒群的数值计算，得到不同长径比的相对轴向位置与颗粒速度的关系，如图10所示。可以看出：长径比在0.50～1.50时，随着长径比的增加，相同相对轴向位置颗粒的速度增加；起爆端颗粒速度随长径比的变化小于非起爆端。长径比为0.50时，由于端部效应，炸药在爆炸后，冲击波几乎同时达到颗粒内层表面，对不同轴向位置颗粒的加速效果基本相同，导致颗粒速度差较小。

    • 3.4.   小　结

  • 基于上述数值模拟分析，对比装填比、颗粒密度和长径比对爆炸驱动亚毫米级金属颗粒飞散的影响程度，得到在爆炸作用下颗粒初速强烈依赖于颗粒质量与炸药质量的比值，并且相同条件下颗粒密度对颗粒初速的影响大于粒径对颗粒的影响。另外，为保证试验效果，在试验过程中，长径比应该不小于1.25。

4.   结　论

  • （1）针对爆炸驱动亚毫米级颗粒速度大、粒径小的特点及传统测试方法的局限，建立了一种较准确的高速颗粒速度测试方法及装置，通过静爆试验成功测得距爆心37.5、40.0、62.5倍装药直径处粒径为0.5 mm的WC颗粒群平均速度。

    （2）利用DEM实现了对爆炸驱动亚毫米级颗粒群特性的数值模拟，模型可体现试验样品中钨颗粒层颗粒的非规则排列特性，计算所得的颗粒飞散形态以及颗粒最大速度等与试验结果吻合较好。

    （3）颗粒速度受长径比、装填比、颗粒粒度等影响。当长径比小于2时，爆炸完成之后，颗粒呈鼓形飞散。随着装填比的增加，颗粒速度有所减小；随着长径比的增加，相同相对轴向位置颗粒的速度增加；起爆端颗粒初速随长径比的变化小于非起爆端；随着颗粒粒径的增大，炸药爆炸驱动颗粒速度减小；最大初速均出现在相对轴向位置X/L=0.62附近；在相同装填比下，粒径为0.7 mm的颗粒初速相比粒径0.2 mm的颗粒下降了40%；相比于17.6 g·cm–3的颗粒，密度为19.3 g·cm–3的颗粒初速减小10%左右。

参考文献 (24)

目录

/

返回文章
返回