高级搜索

球形破片侵彻多层板弹道极限的量纲分析

,  ,  , 

downloadPDF

上一篇

下一篇

王雪, 智小琦, 徐锦波, 范兴华. 球形破片侵彻多层板弹道极限的量纲分析[J]. 高压物理学报, 2019, 33(6): 065102-1. doi: 10.11858/gywlxb.20190757
引用本文: 王雪, 智小琦, 徐锦波, 范兴华. 球形破片侵彻多层板弹道极限的量纲分析[J]. 高压物理学报, 2019, 33(6): 065102-1. doi: 10.11858/gywlxb.20190757
shu
Xue WANG, Xiaoqi ZHI, Jinbo XU, Xinghua FAN. Dimensional Analysis of Ballistic Limit of Spherical Fragments Penetrating Multi-Layer Plate[J]. gaoyawli, 2019, 33(6): 065102-1. doi: 10.11858/gywlxb.20190757
Citation: Xue WANG, Xiaoqi ZHI, Jinbo XU, Xinghua FAN. Dimensional Analysis of Ballistic Limit of Spherical Fragments Penetrating Multi-Layer Plate[J]. gaoyawli, 2019, 33(6): 065102-1. doi: 10.11858/gywlxb.20190757
shu

球形破片侵彻多层板弹道极限的量纲分析

  • 1.

    中北大学机电工程学院，山西 太原　030051

  • 2.

    晋西工业集团，山西 太原　030027

    • 作者简介: 王　雪（1994－），女，硕士研究生，主要从事弹药工程与毁伤技术研究. E-mail：271976366@qq.com .
    通讯作者: 智小琦（1963－），女，博士，教授，主要从事武器毁伤与装药技术研究. E-mail：zxq4060@sina.com; 

  • 中图分类号: TJ410.3

Dimensional Analysis of Ballistic Limit of Spherical Fragments Penetrating Multi-Layer Plate

  • 1.

    College of Mechatronic Engineering, North University of China, Taiyuan 030051, China

  • 2.

    Shanxi West Group, Taiyuan 030027, China

    • Corresponding author: Xiaoqi ZHI, zxq4060@sina.com ; 

  • MSC: TJ410.3

  • 摘要: 为了研究Q235钢多层板的抗侵彻性能，进行了直径为9.45 mm的钨合金球形破片侵彻7.2 mm和(3.6+3.6)mm厚Q235钢双层板试验，获得了相应的弹道极限。在此基础上，建立数值仿真模型，研究了钨合金球侵彻接触式等厚3层、4层、5层、6层板的弹道极限。通过量纲分析方法，分析了分层数对靶板弹道极限的影响。结果表明：对于球形破片，总厚度为7.2 mm的等厚双层板的抗侵彻性能高于单层板；当分层数大于2时，接触式多层等厚靶板的弹道极限随着层数的增加而减小，即分层数越多，靶板的抗侵彻性能越低，通过量纲分析方法得到了靶板分层数与破片弹道极限的关系。研究结果可为未来装甲防护设计提供一定的参考。
    Abstract: In order to study the anti-penetration performance of Q235 steel multi-layer plate, we carried out a $\varnothing $9.45 mm spherical fragment of tungsten alloy to penetrate the 7.2 mm and (3.6+3.6) mm Q235 steel double-layer plates, and obtained the corresponding ballistic limits. On this basis, we established a numerical simulation model to study the ballistic limits of the laminated contact plates with three, four, five, and six layers of equal thickness penetrated by the tungsten ball. Through the dimensional method, we analyzed the effect of the number of layers on the ballistic limit of the target. The results show that for spherical fragments, the anti-penetration performance of the double-layer plate with a total thickness of 7.2 mm is higher than that of the single-layer plate; when the number of layers is greater than 2, the ballistic limit of the multi-layer target decreases with the increase of the number of layers. The relationship between the number of layers of the target and the ballistic limit of the fragment is obtained by the dimensional method. The results can provide a guidance for the design of armor protection in the future.
  • 加载中

  • 图 1  试验原理图

    Figure 1.  Experimental schematic

    下载: 全尺寸图片 幻灯片

    图 2  弹托、破片及小药筒

    Figure 2.  Sabot, fragments and small cartridge

    下载: 全尺寸图片 幻灯片

    图 3  单层板冲击试验后破片与冲塞状态

    Figure 3.  Fragmentation and plug after single layer impacting experiment

    下载: 全尺寸图片 幻灯片

    图 4  试验后的单层板状态

    Figure 4.  Single-layer plate after experiment

    下载: 全尺寸图片 幻灯片

    图 5  试验后的双层板状态

    Figure 5.  Double-layer plate after the test

    下载: 全尺寸图片 幻灯片

    图 6  有限元模型

    Figure 6.  Finite element model

    下载: 全尺寸图片 幻灯片

    图 7  数值模拟和试验得到的残余速度的比较

    Figure 7.  Comparison of residual velocity obtained by numerical simulation and experiment

    下载: 全尺寸图片 幻灯片

    图 8  仿真结果

    Figure 8.  Simulation results

    下载: 全尺寸图片 幻灯片

    图 9  多层板的数值模拟结果

    Figure 9.  Numerical simulation of multi-layer plate

    下载: 全尺寸图片 幻灯片

    图 10  多层板残余速度的数值模拟

    Figure 10.  Numerical residual velocity of multi-layer plate

    下载: 全尺寸图片 幻灯片

    表 1  破片侵彻试验结果

    Table 1.  Experimental results of fragment penetrating plate

    Target typeInitial velocity/(m∙s−1)Residual velocity/(m∙s−1)Phenomenon
    Single layer plate
    7.2 mm    		494.3Embedment
    598.8248.6Penetration
    662.0350.2Penetration
    718.5413.3Penetration
    726.4423.0Penetration
    734.1454.3Penetration
    766.1479.2Penetration
    787.3504.9Penetration
    837.0558.9Penetration
    Double layer plate
    (3.6+3.6) mm    		455.3Embedment
    532.7Embedment
    604.0 194.2Penetration
    619.0224.4Penetration
    631.4246.1Penetration
    652.5281.8Penetration
    738.0400.7Penetration
    819.0493.2Penetration
    下载: 导出CSV

    表 2  钨合金球的材料模型参数

    Table 2.  Material model parameters of tungsten alloy ball

    Density/(g·cm–3)Young modulus/GPaPoisson’s ratioYield stress /MPaETAN/MPa
    18.23570.3031 506762
    BETASRCSRPFSVP
    13.961.20
    下载: 导出CSV

    表 3  Q235钢靶板的材料模型参数

    Table 3.  Material model parameters of Q235 steel plate

    Density/(g·cm–3)G/GPaA/MPaB/MPacmn
    7.877.33003470.10.550.08
    Tm/KTr/KD1D2D3D4D5
    1 7953000.30.92.800
    下载: 导出CSV

    表 4  破片侵彻靶板的仿真结果

    Table 4.  Simulation results of fragmentation penetrating the plate

    Target typeInitial velocity/(m∙s−1)Residual velocity/(m∙s−1)Relative error/%Phenomenon
    SimulationExperiment
    Single-layer plate
    7.2 mm    		494.3Embedment
    598.8243.8248.61.93Penetration
    662.0340.3350.22.83Penetration
    718.5408.9413.31.06Penetration
    726.4410.7423.02.91Penetration
    734.1435.8454.34.07Penetration
    766.1467.3479.22.48Penetration
    787.3487.8504.93.39Penetration
    837.0541.5558.93.11Penetration
    Double-layer plate
    (3.6+3.6) mm    		532.7Embedment
    604.0189.5194.22.42Penetration
    619.0217.4224.43.12Penetration
    631.4237.4246.13.54Penetration
    652.5270.5281.84.01Penetration
    738.0383.2400.74.37Penetration
    819.0470.7493.24.56Penetration
    下载: 导出CSV

    表 5  破片侵彻靶板的仿真结果

    Table 5.  Simulation results of fragmentation penetrating the plate

    Target typeInitial velocity/(m∙s−1)Residual velocity/(m∙s−1)Phenomenon
    Three-layer plate
    (2.4+2.4+2.4) mm    		550115Penetration
    600228Penetration
    630267Penetration
    680342Penetration
    700360Penetration
    750417Penetration
    Four-layer plate
    (1.8+1.8+1.8+1.8) mm    		52064Penetration
    550157Penetration
    600250Penetration
    650318Penetration
    700381Penetration
    750434Penetration
    Five-layer plate
    (1.44+1.44+1.44+1.44+1.44) mm    		550168Penetration
    600258Penetration
    650325Penetration
    700389Penetration
    750441Penetration
    Six-layer plate
    (1.2+1.2+1.2+1.2+1.2+1.2) mm    		550184Penetration
    600265Penetration
    650332Penetration
    700394Penetration
    750450Penetration
    下载: 导出CSV

    表 6  相关物理量与无量纲量

    Table 6.  Related physical quantities and dimensionless quantities

    H/m${{v_{{\rm{50}}}}}$/(m∙s−1)n${\dfrac{H}{{{d_{\rm{p}}}}}}$${\dfrac{{{v_{50}}\sqrt {{\rho _{\rm{t}}}} }}{{\sqrt {{\sigma _{{\rm{st}}}}} }}}$
    0.002 40527.930.254 00.003 041
    0.001 80512.740.190 50.002 954
    0.001 44507.250.152 40.002 922
    0.001 20500.760.127 00.002 885
    下载: 导出CSV

    表 7  破片侵彻靶板的仿真结果

    Table 7.  Simulation results of fragment penetrating the plate

    Target typeInitial velocity /(m∙s−1)Residual velocity/(m∙s−1)Phenomenon
    Eight-layer plate
    (0.9+0.9+0.9+0.9+0.9+0.9+0.9+0.9) mm    		550196Penetration
    600284Penetration
    650356Penetration
    700410Penetration
    750472Penetration
    下载: 导出CSV
  • [1] 赵旭东, 高兴勇, 刘国庆. 装甲防护材料抗侵彻性能研究现状 [J]. 包装工程, 2017, 38(11): 117–122. ZHAO X D, GAO X Y, LIU G Q. Research status of anti-penetration performance of armor protective materials [J]. Packaging Engineering, 2017, 38(11): 117–122.
    [2] IQBAL M A, CHAKRABARTI A, BENIWALA S, et al. 3D numerical simulations of sharp nosed projectile impact on the ductile plates [J]. International Journal of Impact Engineering, 2010, 37(2): 185–195. doi: 10.1016/j.ijimpeng.2009.09.008
    [3] DURMUS A, GUDEN M, GULCIMEN B, et al. Experimental investigations on the ballistic impact performances of cold rolled sheet metals [J]. Materials and Design, 2011, 32(2): 1356–1366.
    [4] GUPTA N K, IQBAL M A, SEKHON G S. Effect of projectile nose shape, impact velocity and plate thickness on deformation behavior of aluminum plates [J]. International Journal of Solids and Structures, 2007, 22(10): 3411–3439.
    [5] 邓云飞, 李剑峰, 孟凡柱. Q235钢单层及接触式多层板对卵形头弹抗侵彻特性 [J]. 机械工程学报, 2015, 51(17): 66–71. DENG Y F, LI J F, MENG F Z. Q235 anti-penetration characteristics of steel single-layer and contact-type multilayer boards against oval heads [J]. Journal of Mechanical Engineering, 2015, 51(17): 66–71.
    [6] 任善良, 文鹤鸣, 周琳. 平头弹穿透接触式双层金属板的理论研究 [J]. 高压物理学报, 2018, 32(3): 1–7. REN S L, WEN H M, ZHOU L. Theoretical study on penetrating contact double-layer metal plate [J]. Chinese Journal of High Pressure Physics, 2018, 32(3): 1–7.
    [7] 邓云飞, 张伟, 曹宗胜. 叠层顺序对双层A3钢薄板抗侵彻性能的影响 [J]. 爆炸与冲击, 2013, 33(3): 263–268. doi: 10.3969/j.issn.1001-1455.2013.03.007 DENG Y F, ZHANG W, CAO Z S. Effect of lamination sequence on the anti-penetration performance of double-layer A3 steel sheet [J]. Explosion and Shock Waves, 2013, 33(3): 263–268. doi: 10.3969/j.issn.1001-1455.2013.03.007
    [8] RECH R F, IPSON T W. Ballistic perforation dynamics [J]. Journal of Applied Mechanics, 1963, 30(3): 384–390. doi: 10.1115/1.3636566
    [9] 钱伟长.穿甲力学 [M]. 北京: 国防工业出版社, 1984: 170–208. QIAN W C.Piercing mechanics [M]. Beijing: National Defense Industry Press, 1984: 170–208.
    [10] 马晓青. 冲击动力学 [M]. 北京: 北京理工大学出版社, 1992: 307–342. MA X Q. Impact dynamics [M]. Beijing: Beijing Institute of Technology Press, 1992: 307–342.
    [11] 马红磊, 胡更开, 李树奎. 97钨合金力学性能研究 [J]. 兵器材料学与工程, 2005, 26(9): 39–41. MA H L, HU G K, LI S K. Study on mechanical properties of 97 tungsten alloy [J]. Weapon Materials Science and Engineering, 2005, 26(9): 39–41.
    [12] 周捷, 智小琦, 徐锦波. 小尺寸破片对单兵防护装备的侵彻研究 [J]. 爆炸与冲击, 2019, 39(2): 81–87. doi: 10.11883/bzycj-2018-0023 ZHOU J, ZHI X Q, XU J B. Research on the penetration of small size fragments on individual protective equipment [J]. Explosion and Shock Waves, 2019, 39(2): 81–87. doi: 10.11883/bzycj-2018-0023
    [13] 陈刚, 陈小伟, 陈忠富. A3钢钝头弹撞击45钢板破坏模式的数值分析 [J]. 爆炸与冲击, 2007, 27(5): 390–397. doi: 10.3321/j.issn:1001-1455.2007.05.002 CHEN G, CHEN X W, CHEN Z F. Numerical analysis of failure mode of 45 steel plate impacted by A3 steel blunt head [J]. Explosion and Shock Waves, 2007, 27(5): 390–397. doi: 10.3321/j.issn:1001-1455.2007.05.002
    [14] СЕДОВ Л И. 力学中的相似方法与量纲理论 [M]. 沈青, 倪锄非, 李维新, 译. 北京: 科学出版社, 1982. СЕДОВ Л И. Similar methods and dimensional theory in mechanics [M]. Translated by SHEN Q, NI C F, LI W X. Beijing: Science Press, 1982.
  • 加载中
图( 10) 表( 7)
计量
  • 文章访问数:  3552
  • HTML全文浏览数:  3552
  • PDF下载数:  48
  • 施引文献:  0
出版历程
  • 收稿日期:  2019-04-10
  • 网络出版日期:  2019-12-25
  • 刊出日期:  2019-12-01

球形破片侵彻多层板弹道极限的量纲分析

    通讯作者: 智小琦（1963－），女，博士，教授，主要从事武器毁伤与装药技术研究. E-mail：zxq4060@sina.com; 
    作者简介: 王　雪（1994－），女，硕士研究生，主要从事弹药工程与毁伤技术研究. E-mail：271976366@qq.com
  • 1. 中北大学机电工程学院，山西 太原　030051
  • 2. 晋西工业集团，山西 太原　030027
  • 收稿日期:  2019-04-10
  • 网络出版日期:  2019-12-25

摘要: 为了研究Q235钢多层板的抗侵彻性能，进行了直径为9.45 mm的钨合金球形破片侵彻7.2 mm和(3.6+3.6)mm厚Q235钢双层板试验，获得了相应的弹道极限。在此基础上，建立数值仿真模型，研究了钨合金球侵彻接触式等厚3层、4层、5层、6层板的弹道极限。通过量纲分析方法，分析了分层数对靶板弹道极限的影响。结果表明：对于球形破片，总厚度为7.2 mm的等厚双层板的抗侵彻性能高于单层板；当分层数大于2时，接触式多层等厚靶板的弹道极限随着层数的增加而减小，即分层数越多，靶板的抗侵彻性能越低，通过量纲分析方法得到了靶板分层数与破片弹道极限的关系。研究结果可为未来装甲防护设计提供一定的参考。

English Abstract

    全文HTML

  • 在现代高科技战场中，武器装备的不断发展对装甲防护提出了更高的要求[1]。装甲防护技术从单层开始向多层发展，因此，对于防护材料的分层设计研究成为十分重要的课题，国内外已有一些关于多层金属板抗侵彻性能的研究报道。例如：Iqbal等[2]利用ABAQUS/EXPLICIT建立了锥头弹体和靶板的三维模型，发现了单层板的抗侵彻性能高于接触式双层板；Durmus等[3]利用标准卵形头子弹对单层和接触式双层钢板进行了撞击试验，发现单层板比双层板的抗侵彻性能好；Gupta等[4]利用平头、半球形和卵形弹对单层和双层薄铝板进行了撞击试验，发现单层板和双层板的抗侵彻性能接近，靶体对卵形头弹的弹道极限最低，其次是平头弹和半球形弹；邓云飞等[5]利用卵形头杆弹正撞击单层板和等厚接触式3层板的试验，探讨了靶板结构对其抗侵彻特性的影响；任善良等[6]基于单层金属板的穿透理论和试验研究，提出了平头弹侵彻等厚接触式双层金属板的穿透模型，模型预测结果与试验数据吻合较好；邓云飞等[7]利用卵形头、平头及半球形头杆弹正撞击等厚接触式双层板试验，发现叠层顺序对双层靶体抗侵彻性能的影响与弹体头部形状相关。

    综合上述研究结果可以发现，目前对于多层板的抗侵彻性能研究，侵彻体大多采用弹丸，靶板最多分3层，研究结果依据靶体结构、分层方法及侵彻体形状而各异。然而对于飞机、轻型装甲车辆，毁伤破片是主要的毁伤元，因此，研究破片对于多层板的侵彻以及靶板的分层情况对抗侵彻性能的影响具有重要的意义。

    本研究选用钨合金球形破片，对Q235钢单层板和接触式等厚双层板进行冲击试验研究，以获得两种防护结构的弹道极限。在此基础上，建立数值仿真模型，开展接触式等厚3层、4层、5层和6层Q235钢板的数值仿真，通过量纲分析方法，得到分层数与弹道极限之间的关系，以期为未来装甲防护设计提供参考。

1.   弹道极限试验

    1.1.   试验装置

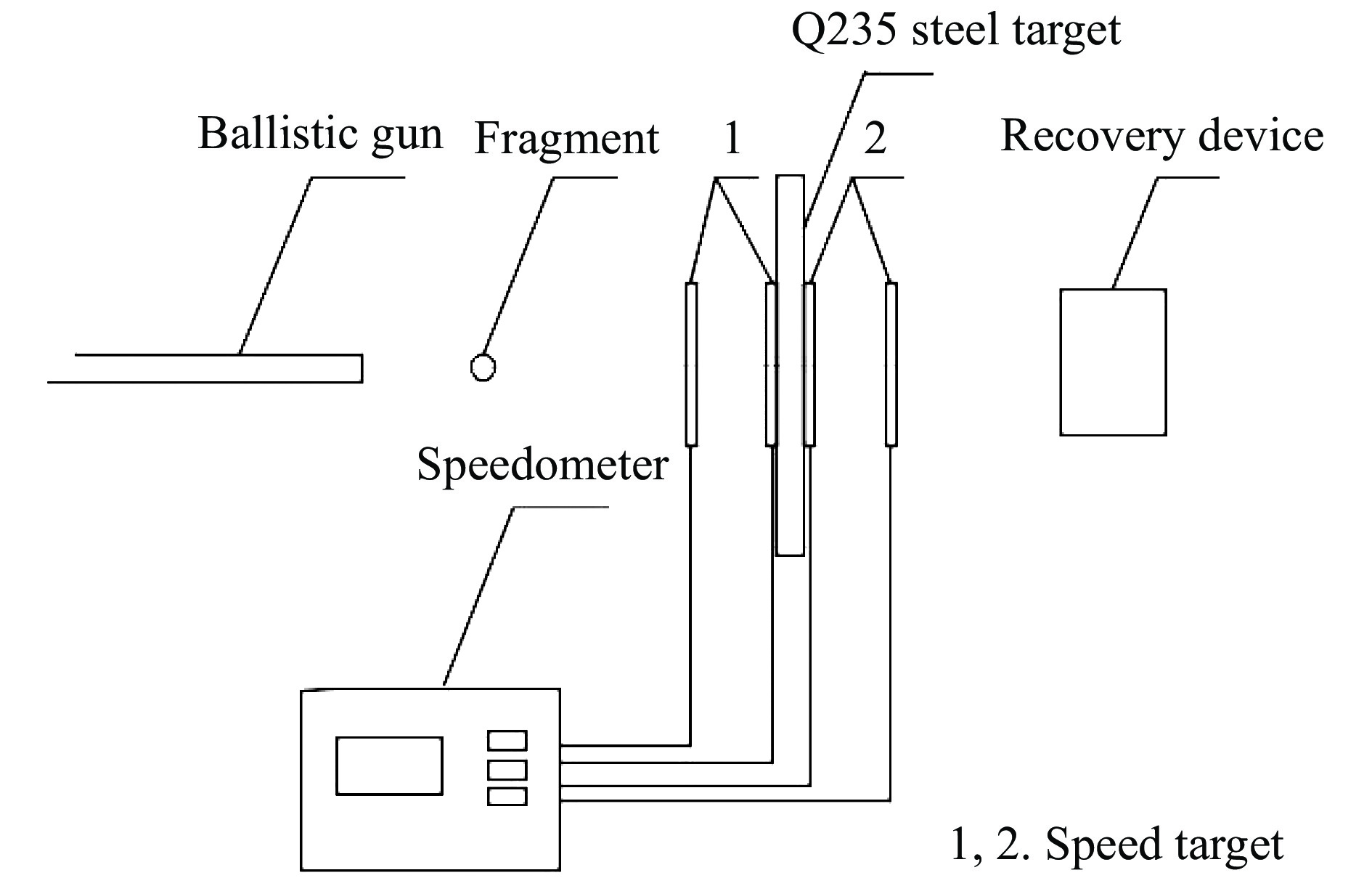
  • 使用口径为12.7 mm的弹道枪发射破片，破片速度由装药量以及弹托与子弹药筒配合的紧密程度控制。采用通断靶测速法，利用NGL202-Z型六通道测速仪的测速装置进行靶前速度与靶后速度的测试。选用直径为9.45 mm、质量为8.05 g的钨合金球形破片，对7.2 mm和(3.6+3.6) mm厚Q235钢板进行冲击试验。试验原理如图1所示，图2为弹托、破片及小药筒照片。

    • 1.2.   试验结果及分析

  • 钨合金球侵彻7.2 mm和(3.6+3.6) mm厚Q235钢板的试验结果见表1。

    通过比较弹道极限来评估靶板的抗侵彻性能。利用能量守恒和动量定理的R-I公式[8]，获得弹靶系统的弹道极限，具体表达式为

    式中：${v_0}$为初始速度（m/s）；${v_1}$为残余速度（m/s）；${v_{50}}$为弹道极限（m/s）；$\alpha = {m_{\rm{p}}}/\left( {{m_{\rm{p}}} + {m_{{\rm{pl}}}}} \right)$，${m_{\rm{p}}}$和${m_{{\rm{pl}}}}$分别为子弹质量和冲塞质量；$\alpha $和p可通过对试验数据进行最小二乘法拟合得到。

    根据冲击试验结果（见表1），通过（1）式拟合得到球形破片侵彻7.2 mm厚Q235钢单层板的弹道极限为523.7 m/s，侵彻(3.6+3.6) mm厚Q235钢多层板的弹道极限为555.6 m/s。在总厚度相等的情况下，对于钨合金球，接触式等厚双层板的抗侵彻性能高于单层板。

    • 1.3.   失效模式分析

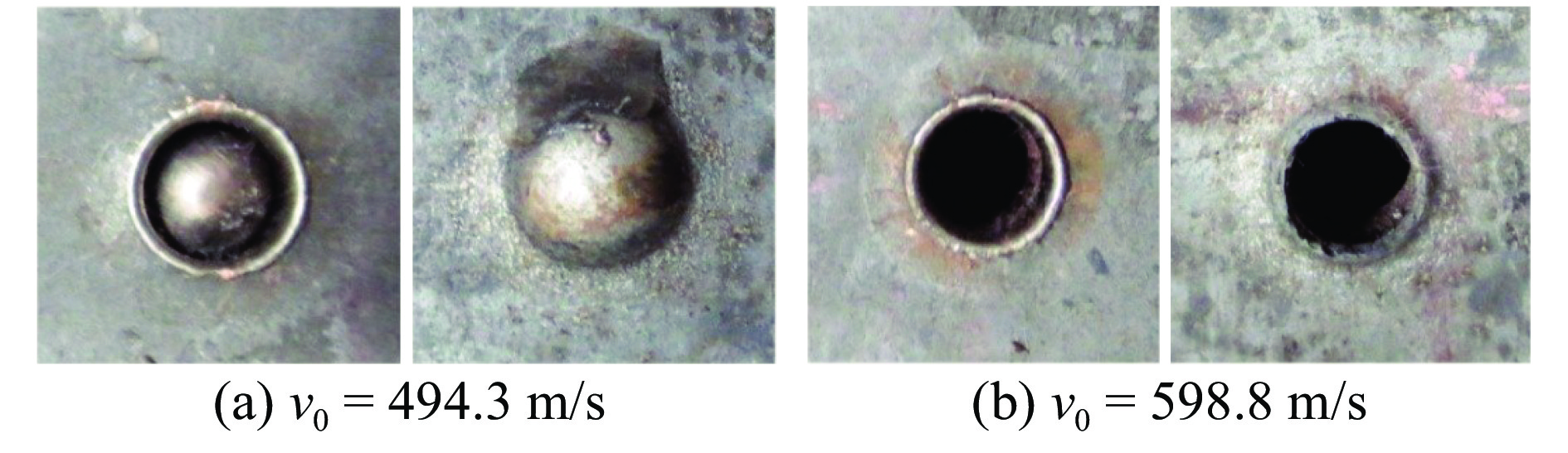
  • 图3为单层板冲击试验后破片与冲塞状态。可以看出，以598.8 m/s的速度撞击靶板时，破片只有轻微的变形；随着侵彻速度的增加，破片的变形增大；当侵彻速度为837.0 m/s时，破片发生碎裂。

    钨合金球侵彻单层板的过程中，当初始速度小于穿透速度时，单层板的主要失效模式是隆起和盘形凹陷。在撞击过程中，破片挤压靶板，靶板产生与破片形状相同的隆起变形。受撞击的靶板部分，由于靶板弯曲而造成较小的盘形凹陷变形[9]，如图4（a）所示。当初始速度大于穿透速度时，单层板的主要失效模式是绝热剪切冲塞破坏。在撞击过程中，破片挤压靶板，靶板表面因塑性变形向外翻起，出现翻唇现象[10]。当破片侵入靶板时，靶板发生较大的应变。当这种应变超过靶板的许可应变时，靶板在该处发生断裂。由于撞击过程进展很快，局部断裂产生的热不能及时散出，使这部分材料急速升温，从而降低该处的抗剪强度，发生绝热剪切现象。当绝热剪切延伸到靶板背面时，塞块脱离靶板，完成冲塞，结束侵彻，冲塞与破片以相同的速度向前运动。试验后单层板的状态如图4所示。

    钨合金球侵彻双层板的过程中，当初始速度小于穿透速度时，双层板与单层板的主要失效模式相同，即隆起和盘形凹陷。在撞击过程中，破片挤压第1层板，第1层板受挤压产生向下的压力，挤压第2层板，两层板同时产生与破片形状相同的隆起变形。受撞击的靶板部分，由于靶板弯曲而造成较小的盘形凹陷变形，如图5（a）所示。当初始速度大于穿透速度时，双层板中第1层板的失效模式与单层板相似。撞击过程中，破片挤压靶板，靶板发生应变。由于撞击过程进展很快，发生绝热剪切，形成冲塞，冲塞与破片以相同的速度向前运动。由于受破片和冲塞的共同作用，第2层板被压缩变薄，出现隆起破坏，并形成一个塞块。试验后双层板的状态如图5所示。

    为了进一步研究多层板的抗侵彻性能，对钨合金球侵彻接触式等厚3层、4层、5层、6层板进行数值模拟，并通过量纲分析方法，分析分层数对靶板弹道极限的影响。

2.   数值模拟及分析

    2.1.   仿真模型建立

  • 根据试验内容，建立数值仿真所需的有限元模型。根据模型的对称性，为减少计算时间，简化运算，建立破片及靶板的1/4有限元模型。为提高计算精确度，采用六面体单元进行网格划分，靶板和破片直接作用区域进行网格局部加密。在对称边界施加对称约束，靶板边界处施加非反射边界，定义破片与靶板的接触算法为面面侵蚀算法，靶板与靶板间的接触算法为自由接触算法。有限元模型如图6所示。

    • 2.2.   破片与靶板材料模型的确定

  • 由于钨合金具有明显的应变率特征[11]，选用PLASTIC_KINEMATIC材料模型，其参数如表2所示，ETAN表示切线模量，BETA表示硬化参数，SRC、SRP表示应变率参数，FS表示失效应变。

    破片侵彻靶板属于高速冲击问题，冲击过程伴随着高应变率、高温、高压和冲击波的传播，使用Johnson-Cook本构模型进行描述。对于涉及冲击波的行为，可以用Grüneisen 状态方程表征[12]。参考文献[13]的相关参数，根据实际试验进行微调，主要参数如表3所示。

    • 2.3.   基于试验的数值仿真

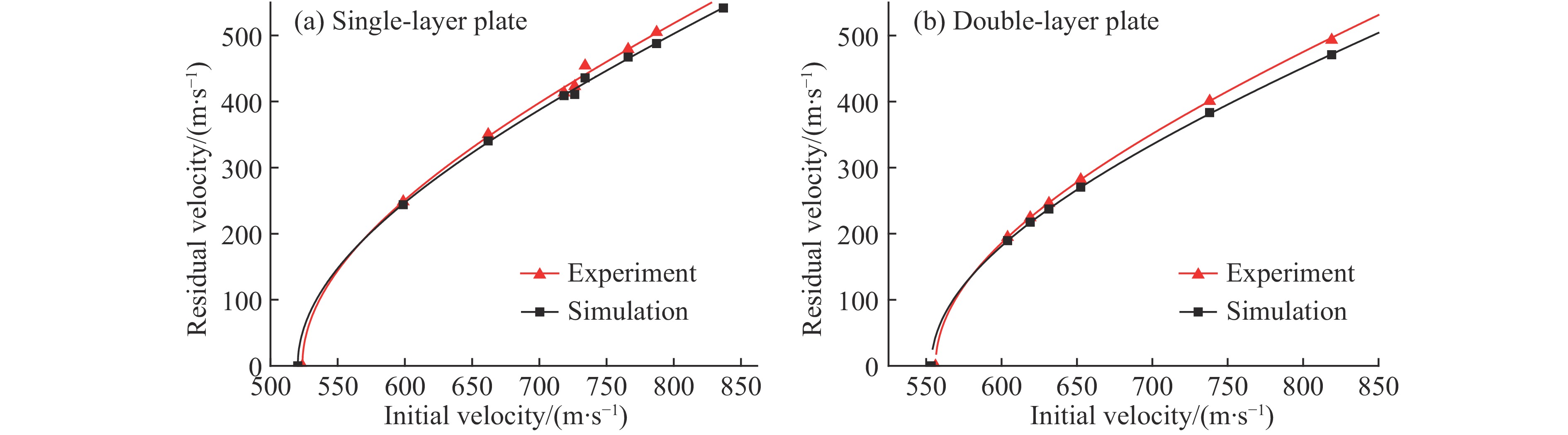
  • 利用上述仿真模型进行钨合金球侵彻7.2 mm厚Q235钢单层板和(3.6+3.6) mm厚双层板的数值模拟，结果列于表4。将数值模拟与试验结果进行对比，如图7所示。

    从表4可以看出，在试验速度的间隔范围内，数值模拟得到的速度与试验数据吻合较好，最大相对误差在5%以内。通过数值模拟得到钨合金球侵彻7.2 mm厚Q235钢单层板和(3.6+3.6) mm厚Q235钢多层板的弹道极限分别为520.3 m/s和552.7 m/s，与试验弹道极限的相对误差分别为0.65%和0.52%。破片侵彻靶板从即将穿透靶板到完全穿透靶板的速度是弹道极限范围。因此，对试验得到的弹道极限附近速度进行仿真，预估其弹道极限范围，仿真结果如图8所示。从图8（a）可以看出，钨合金球侵彻单层板的弹道极限范围为520～524 m/s。从图8（b）可以看出，钨合金球侵彻双层板的弹道极限范围为552～557 m/s。因此，仿真结果与试验结果吻合。

    • 2.4.   钨合金球侵彻多层靶的数值模拟

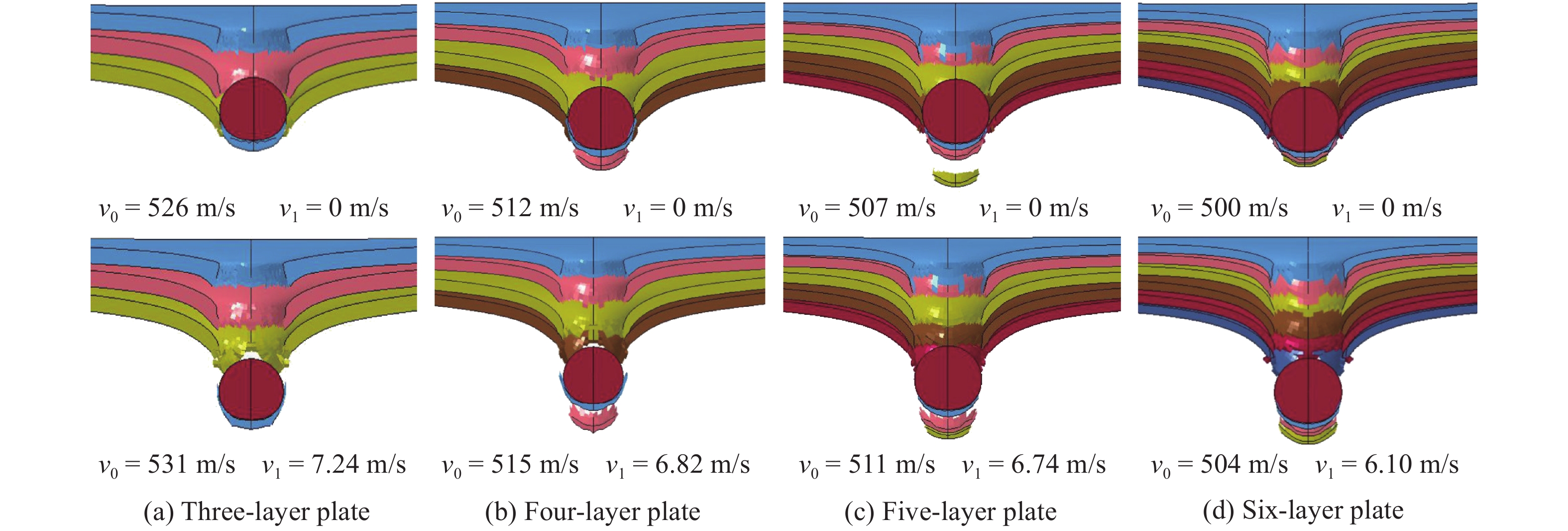
  • 根据数值模拟结果（见表5），通过（1）式拟合得到钨合金球侵彻接触式等厚3层、4层、5层、6层板的弹道极限，分别为527.9、512.7、507.2、500.7 m/s。

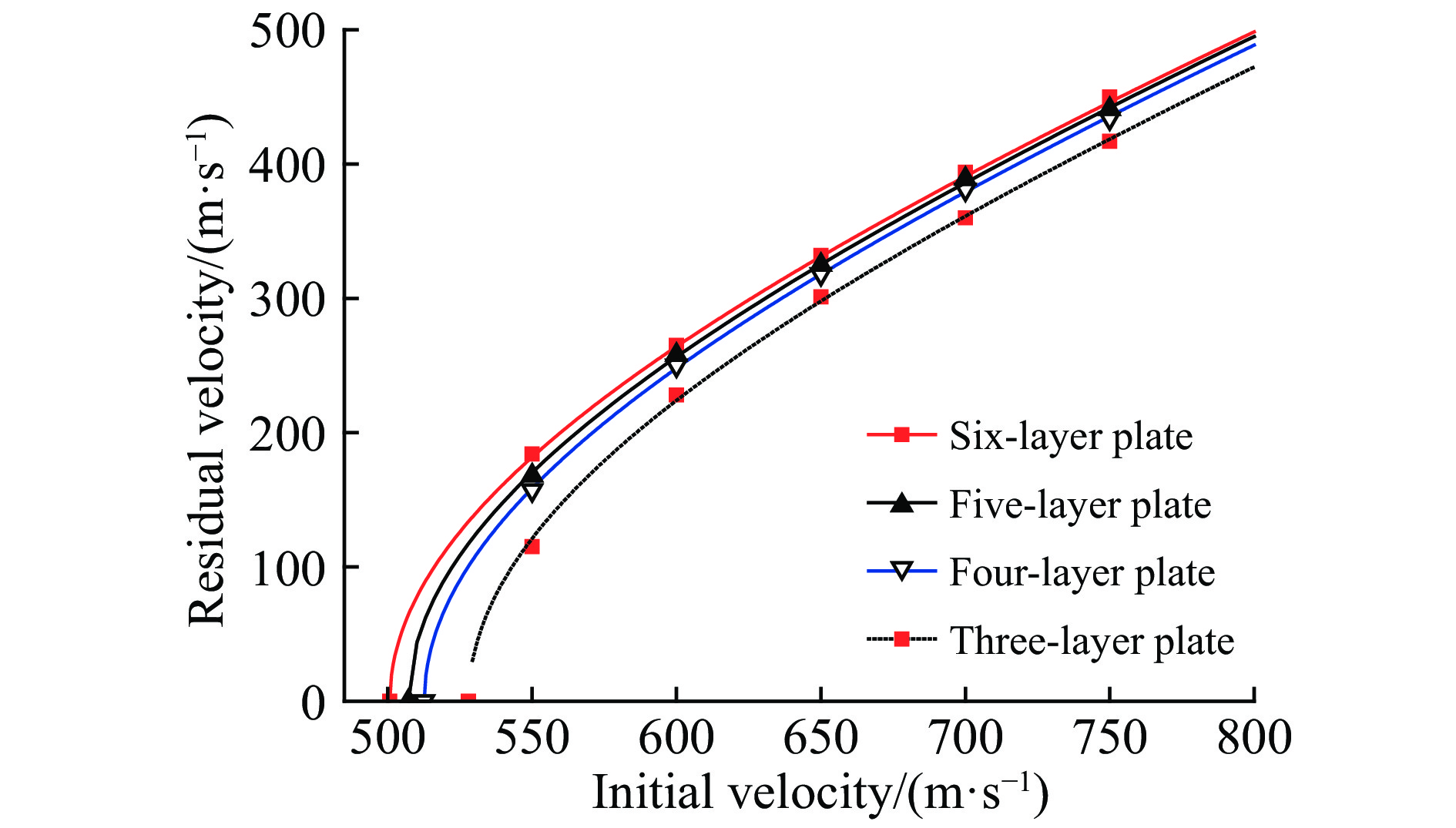
    对拟合得到的弹道极限附近速度进行仿真，仿真结果如图9所示。钨合金球侵彻接触式等厚3层、4层、5层、6层板的弹道极限范围分别为526～531、512～515、507～511和500～504 m/s。在图10中给出不同分层数等厚接触式多层板的数值拟合曲线。从图10中可以看出，分层数越多，弹道极限越小，靶板的抗侵彻性能越差。此外，侵彻速度越大，分层数对靶板抗侵彻性能的影响越小。

    为了实现对不同分层的多层板弹道极限的预估，通过量纲分析，定量地研究分层数对多层板弹道极限的影响，获得分层数与弹道极限之间的关系，以期为未来装甲防护设计提供参考。

3.   分层数对弹道极限的影响

    3.1.   分层数对弹道极限的影响的量纲分析

  • 破片垂直侵彻多层叠合板过程中，影响其弹道极限的因素包括破片和靶板两方面，相关因素主要有：（1）破片参数，即密度${\rho _{\rm{p}}}$、杨氏模量${E_{\rm{p}}}$、屈服极限${\sigma _{{\rm{sp}}}}$、直径${d_{\rm{p}}}$、质量${m_{\rm{p}}}$；（2）靶板参数，即密度${\rho _{\rm{t}}}$、杨氏模量${E_{\rm{t}}}$、屈服极限${\sigma _{{\rm{st}}}}$、抗剪强度${\sigma _{{\text{τ}}{\rm{t}}}}$、抗拉强度${\sigma _{{\rm{ft}}}}$、靶板层数n、每层靶板的厚度H。下标“p”表示弹，下标“t”表示靶板。

    弹道极限${v_{{\rm{50}}}}$与影响因素之间的函数关系为

    取${d_{\rm{p}}}$、${\rho _{\rm{t}}}$、${\sigma _{{\rm{st}}}}$作为量纲独立变量，根据柏金汉定理[14]得

    （2）式可改写成

    弹体结构、材料和靶板的材料不变，则$\dfrac{{{\rho _{\rm{p}}}}}{{{\rho _{\rm{t}}}}}$、$\dfrac{{{E_{\rm{p}}}}}{{{\sigma _{{\rm{st}}}}}}$、$\dfrac{{{\sigma _{{\rm{sp}}}}}}{{{\sigma _{{\rm{st}}}}}}$、$\dfrac{{{m_{\rm{p}}}}}{{d_{\rm{p}}^3{\rho _{\rm{t}}}}}$、$\dfrac{{{E_{\rm{t}}}}}{{{\sigma _{{\rm{st}}}}}}$、$\dfrac{{{\sigma _{{\text{τ}}{\rm{t}}}}}}{{{\sigma _{{\rm{st}}}}}}$、$\dfrac{{{\sigma _{{\rm{ft}}}}}}{{{\sigma _{{\rm{st}}}}}}$均为常数，则（3）式可简化为

    利用钨合金球侵彻等厚接触式多层板的5组数据，得到（4）式中所需的数据，见表6。

    将表6中的数据代入（4）式进行回归，得出弹道极限与靶板分层数目的无量纲关系式

    当使用与模型相同的破片结构、材料及靶板材料时，由（5）式可得到不同厚度靶板、大于2层的不同分层数所对应的弹道极限，进而预估不同分层情况靶板的抗侵彻能力，也可对给定弹道极限与层数，确定与模型材料相同的靶板厚度，为装甲防护设计提供参考。

    • 3.2.   基于无量纲关系式的验证计算

  • （1）将钨合金球侵彻双层板试验所得到的结果带入无量纲关系式（（5）式），计算得出的弹道极限为556.2 m/s，与试验所得的弹道极限555.6 m/s相比，相对误差为0.112%，可看出（5）式的计算结果与试验吻合较好。

    （2）为了更好地验证关系式（（5）式）的可靠性，进行$\varnothing $9.45 mm钨合金球侵彻7.2 mm厚Q235钢接触式等厚8层板的仿真，结果列于表7。通过拟合，确定其弹道极限为496 m/s。由（5）式计算获得的对应的弹道极限为495.3 m/s，与仿真结果进行对比，相对误差为0.141%。因此，无量纲关系（5）式具有一定的可靠性。

4.   结　论

  • （1）直径为9.45 mm、质量为8.05 g的钨合金球侵彻7.2 mm厚 Q235钢单层板的弹道极限为523.7 m/s，侵彻(3.6+3.6) mm厚Q235钢叠合板的弹道极限为555.6 m/s。在靶板总厚度不变的情况下，接触式等厚双层板抗钨合金球破片的侵彻性能高于单层板。

    （2）靶板的失效模式与靶板厚度、靶板性能及破片侵彻速度有关。对于确定的靶板而言，破片的侵彻速度以弹道极限为分水岭，即无论对于单层板还是接触式双层板，破片侵彻速度小于弹道极限时靶板的失效模式与侵彻速度大于弹道极限时是不同的，且当破片的侵彻速度大于弹道极限时，双层靶的第1层和第2层的失效模式也不同。

    （3）对于确定厚度的靶板，当等厚靶的分层数大于2层，随着分层数的增加，靶板的抗侵彻性能降低。用量纲分析方法得到的靶板分层数与破片弹道极限的关系，可对相关研究提供预估计算，也可为装甲防护设计提供参考。

参考文献 (14)

目录

/

返回文章
返回