高级搜索

铝弹丸超高速撞击防护结构的研究进展

,  ,  ,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

林健宇, 罗斌强, 徐名扬, 宋卫东, 柏劲松, 裴晓阳, 于继东, 李平. 铝弹丸超高速撞击防护结构的研究进展[J]. 高压物理学报, 2019, 33(3): 030112-1. doi: 10.11858/gywlxb.20190774
引用本文: 林健宇, 罗斌强, 徐名扬, 宋卫东, 柏劲松, 裴晓阳, 于继东, 李平. 铝弹丸超高速撞击防护结构的研究进展[J]. 高压物理学报, 2019, 33(3): 030112-1. doi: 10.11858/gywlxb.20190774
shu
Jianyu LIN, Binqiang LUO, Mingyang XU, Weidong SONG, Jingsong BAI, Xiaoyang PEI, Jidong YU, Ping LI. Progress of Aluminum Projectile Impacting on Plate with Hypervelocity[J]. gaoyawli, 2019, 33(3): 030112-1. doi: 10.11858/gywlxb.20190774
Citation: Jianyu LIN, Binqiang LUO, Mingyang XU, Weidong SONG, Jingsong BAI, Xiaoyang PEI, Jidong YU, Ping LI. Progress of Aluminum Projectile Impacting on Plate with Hypervelocity[J]. gaoyawli, 2019, 33(3): 030112-1. doi: 10.11858/gywlxb.20190774
shu

铝弹丸超高速撞击防护结构的研究进展

  • 1.

    中国工程物理研究院流体物理研究所，四川 绵阳　621999

  • 2.

    北京理工大学爆炸科学与技术国家重点实验室，北京　100081

    • 作者简介: 林健宇（1987－），男，博士，助理研究员，主要从事多介质力学计算研究. E-mail：linjiany@mail.ustc.edu.cn .
    通讯作者: 宋卫东（1975－），男，博士，教授，主要从事材料与结构冲击动力学研究. E-mail：swdgh@bit.edu.cn; 

  • 中图分类号: O347; V423

Progress of Aluminum Projectile Impacting on Plate with Hypervelocity

  • 1.

    Institute of Fluid Physics, CAEP, Mianyang 621999, China

  • 2.

    State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China

    • Corresponding author: Weidong SONG, swdgh@bit.edu.cn ; 

  • MSC: O347; V423

  • 摘要: 以空间碎片防护为背景，回顾了超高速铝弹丸正撞击单层和双层铝合金防护结构的研究进展，讨论了目前针对超高速撞击的弹丸发射技术和数值模拟方法（如Euler方法、无网格方法等）的优缺点。数值模拟不仅建立在离散方法上，还需要提供准确的材料本构模型和状态方程。介绍了常用材料模型（包括Johnson-Cook、Steinberg-Guinan模型）和状态方程（包括Tillotson、ANEOS、SESAME、GRAY三相状态方程）。基于实验和数值模拟，目前对7 km/s以下的超高速撞击物理过程已经认识得比较清楚。对单层板，重点讨论了板的穿孔特征和孔径模型；对双层板，除了前板的穿孔外，还讨论了碎片云的分布特征、材料相变、碎片云的相态分布、弹丸形状的影响、碎片云的散布模型以及碎片云对后板造成的破坏特征。最后介绍了工程防护中较为重要的防护结构的弹道极限方程。单层板和双层板的弹道极限方程研究近年来取得了较大进展。本文回顾了国内外常用的弹道极限方程以及近年来新提出的理论模型和基于人工神经网络的模型等。
    Abstract: This paper focuses on the protection of debris clouds in space and the progress of the studies of Al projectile impacting on single shield and Whipple shields are discussed. The advantages and drawbacks of the widely used experimental method for launching hypervelocity projectile and numerical methods for hypervelocity impact such as Euler methods and meshfree methods are introduced. The numerical simulation is usually based on the constitutive laws and the equation of states. In this paper we have reviewed the constitutive law including Johnson-Cook and Steinberg-Gruinan, while for the equation of states we include the Tillotson, ANEOS, SESAME, GRAY. The mechanics and physics for the hypervelocity impact below 7 km/s are now well understood based on the progresses made by the experiments and numerical simulations. Then, for the single shield we mainly focus on the perforation by the projectile and the models predicting the hole size. For the Whipple shield we have discussed the characteristics of the debris clouds evolution, the phase states of the materials, the models predicting the evolution of the debris clouds and damage features of the second wall of the Whipple structure induced by the debris clouds. Finally we discussed the ballistic limit equations which are very important to the protection in the engineering. Great progresses have been achieved for the ballistic equations for the single and double shields structures based on the experiments and numerical simulations. We have discussed the commonly used ones and the models which are newly developed recently including theoretical models and the models from artificial intelligence.
  • 加载中

  • 图 1  横截面图和孔洞形状[154]（左侧横截面图的上方为撞击侧，箭头为横截面图放大的位置）

    Figure 1.  Cross-sections and the shape of the hole[154]（Cross sections are shown with the impacted side toward the top of the page. Arrow in hole indicates where material in micrograph was obtained.）

    下载: 全尺寸图片 幻灯片

    图 2  Rosenberg公式[161]与实验[154]的对比（虚线斜率分别为0.95和1.05）

    Figure 2.  Comparison between Rosenberg’s model[161] and experiments[154] (The slopes of dashed lines are separately 0.95 and 1.05.)

    下载: 全尺寸图片 幻灯片

    图 3  数值模拟[76]和实验[62]对比（v=6.15 km/s，撞击时间分别是8.1 ${\text{μ}}{\rm{s}}$、23.2 ${\text{μ}}{\rm{s}}$，初始弹丸形状叠加在图中）

    Figure 3.  Comparison of debris from calculation （top）[76] and experiment （bottom）[62] （v=6.15 km/s, time at 8.1 ${\text{μ}}{\rm{s}}$ and 23.2 ${\text{μ}}{\rm{s}}$, the initial shape of the projectile is also shown in the left picture.）

    下载: 全尺寸图片 幻灯片

    图 4  二阶Euler数值模拟和实验[62]对比（v=6.15 km/s，撞击时间是8.1 ${\text{μ}}{\rm{s}}$）

    Figure 4.  Comparison of 2nd Eulerian simulation and experiment[62]（v=6.15 km/s, time at 8.1 ${\text{μ}}{\rm{s}}$）

    下载: 全尺寸图片 幻灯片

    图 5  不同厚度下碎片云的变化[166]

    Figure 5.  Debris clouds of different thicknesses of the plate[166]

    下载: 全尺寸图片 幻灯片

    图 6  碎片云随弹丸速度变化[166]（t/D=0.049）

    Figure 6.  Debris clouds for different velocities of the projectile[166] （t/D=0.049）

    下载: 全尺寸图片 幻灯片

    图 7  （a）（b） Mo和Pb弹丸高速撞击碎片云形态对比[169, 171]；（c） Pb弹丸数值模拟密度云图[136]；（d） MPM数值模拟结果[110]；（e） 铝弹丸的数值模拟相态分布[153]（红色为气态，绿色为液态，淡蓝色为固态）

    Figure 7.  （a）（b） Comparison of the debris clouds of Mo and Pb projectiles[169, 171]; （c） density clouds from the simulation of Pb projectile[136]; （d） results from MPM simulation; （e） phase clouds from the simulation of Al projectile[153]（ red for gases, green for liquids and cyan for solids）

    下载: 全尺寸图片 幻灯片

    图 8  弹丸质量相同但形状不同的碎片云分布

    Figure 8.  The distribution of debris cloud generated by hypervelocity impact of projectiles with the same mass and different shapes

    下载: 全尺寸图片 幻灯片

    图 9  三维SPH模拟柱状弹丸撞击刚性壁的温度云图

    Figure 9.  The temperature cloud diagram of the cylindrical projectile impacting rigid wall by 3D SPH simulation

    下载: 全尺寸图片 幻灯片

    图 10  六种不同速度下三维模拟得到的电荷数随时间变化

    Figure 10.  The charges change with time at six different impact velocities by 3D simulation

    下载: 全尺寸图片 幻灯片

    图 11  相同速度、不同角度碰撞产生的等离子体电量

    Figure 11.  Plasma charges generated along different impacting angles under the same impact velocity

    下载: 全尺寸图片 幻灯片

    图 12  相同碰撞速度、不同撞击角度下产生等离子体引发的磁感应强度随时间变化曲线

    Figure 12.  The time-depedent magnetic induction intensity generated by hypervelocity impacts at different impact angles under the same impact velocity

    下载: 全尺寸图片 幻灯片

    图 13  直径为6.35 mm的铝弹丸以5 km/s撞击1 mm厚铝板碎片云模型[184]与SPH模拟对比

    Figure 13.  Comparison between the model and the simulation of SPH[184] （The diameter of the Al projectile is 6.35 mm, the velocity is 5 km/s and the thickness of the Al plate is 1 mm.）

    下载: 全尺寸图片 幻灯片

    图 14  中低速后撞击板损伤破坏特征：（a）（b）取自文献[185]；（c）取自文献[184]

    Figure 14.  The damage patterns impacted by low and medium velocity: （a）（b） are from Ref.[185] and （c） is from Ref.[184]

    下载: 全尺寸图片 幻灯片

    图 15  高速撞击后板损伤破坏特征[186]

    Figure 15.  The damage patterns for high speed projectile[186]

    下载: 全尺寸图片 幻灯片

    图 16  数值模拟结果与二级轻气炮实验结果的比较

    Figure 16.  Comparions between simulation and two-stage light gas gun experiment

    下载: 全尺寸图片 幻灯片

    图 17  ANN的弹道极限曲线与JSC模型（BLE）的比较

    Figure 17.  Comparison between ANN model and JSC （BLE） ballistic model

    下载: 全尺寸图片 幻灯片

    表 1  实验加载方式和典型克/亚克级发射参数

    Table 1.  Experimental methods and typical parameters for projectile with mass in gram or sub-gram

    MethodsYearMaterialVelocity/（km·s–1）ShapeMass/gComments and sources
    Three-stage light gas gun1993Al9.52Flyer plate0.78Sandia National Laboratories[48]
    2017Al10.1Flyer plate0.22Institute of Fluid Physics[49]
    Magnetically driven device2011Al45Flyer plate0.79Z accelerator, Sandia National Laboratories[50]
    2014Al8.7Flyer plate0.12CQ-4, Institute of Fluid Physics[51]
    2014Al11.5Flyer plate0.15PTS, Institute of Fluid Physics[52]
    Electric gun2019Mylar10Flyer plate0.30Institute of Fluid Physics
    ISCL （Inhibited Shaped Charge Launcher）1995Al11.16Cylinder1.02Southwest Research Institute[53]
    下载: 导出CSV

    表 2  铝平面对称碰撞时相变对应的速度和压力

    Table 2.  The velocity of the Al projectile and the pressure from impacting

    Source/Phase
    change    		Incipient melting
    due to release    		Complete melting
    due to release    		Incipient vaporization
    due to release    		Complete vaporization
    due to release
    Hopkins et al.[169]2.7 km/s, 65 GPa3.38 km/s, 89 GPa
    Anderson et al.[170]2.85 km/s, 71 GPa3.45 km/s, 94 GPa5.2 km/s, 174 GPa
    Bjork[171]6.2 km/s, 225 GPa2700 GPa
    Shockey et al.[172]2.6–3.6 km/s3.3–4.6 km/s5.5–7.5 km/s12.5–16.5 km/s
    Pierazzo et al.[173]73 GPa106 GPa315 GPa
    Source/Phase
    change    		Incipient melting
    due to shock    		Complete melting
    due to shock
    Tang[153]125 GPa160 GPa
    下载: 导出CSV

    表 3  弹丸质量相同、形状不同所得到碎片云的参数

    Table 3.  The parameters of debris cloud generated by hypervelocity impact of projectiles with the same mass and different shapes

    Shape of projectileDimensionsMass/gAxial length/mmRadical length/mm
    Sphere$\varnothing $5.02 mm0.180 8944.540.5
    Cylinder$\varnothing $5.02 mm×4.6 mm0.182 6146.544.0
    Disk$\varnothing $5.02 mm×1.0 mm0.181 0645.532.2
    下载: 导出CSV
  • [1] 张庆明, 黄风雷. 超高速碰撞动力学引论[M]. 北京: 科学出版社, 2000: 1. ZHANG Q M, HUANG F L. Introduction to dynamics of hypervelocity impact [M]. Beijing: Science Press, 2000: 1.
    [2] 曲广吉, 韩增尧. 空间碎片超高速撞击动力学建模与数值仿真技术 [J]. 中国空间科学技术, 2002(5): 26–30. doi: 10.3321/j.issn:1000-758X.2002.05.005 QU G J, HAN Z Y. Dynamical modeling and numerical simulation of hypervelocity space debris impact [J]. Chinese Space Science and Technology, 2002(5): 26–30. doi: 10.3321/j.issn:1000-758X.2002.05.005
    [3] WHIPPLE F L. Meteorites and space travel [J]. Astronomical Journal, 1947, 1161: 131–147.
    [4] WICKLEIN M, RYAN S, WHITE D M, et al. Hypervelocity impact on CFRP: testing, material modelling, and numerical simulation [J]. International Journal of Impact Engineering, 2008, 35(12): 1861–1869. doi: 10.1016/j.ijimpeng.2008.07.015
    [5] HUANG J, MA Z, REN L, et al. A new engineering model of debris cloud produced by hypervelocity impact [J]. International Journal of Impact Engineering, 2013, 56: 32–39. doi: 10.1016/j.ijimpeng.2012.07.003
    [6] CHRISTIANSEN E L. Design and performance equations for advanced meteoroid and debris shields [J]. International Journal of Impact Engineering, 1993, 14(1): 145–156.
    [7] 龚自正, 杨继云, 张文兵, 等. 航天器空间碎片超高速撞击防护的若干问题 [J]. 航天器环境工程, 2007, 24(3): 125–130. doi: 10.3969/j.issn.1673-1379.2007.03.001 GONG Z Z, YANG J Y, ZHANG W B, et al. Spacecraft protection from the hypervelocity impact of space meteoroid and orbital debris [J]. Spacecraft Environment Engineering, 2007, 24(3): 125–130. doi: 10.3969/j.issn.1673-1379.2007.03.001
    [8] SCHONBERG W P. Characterizing secondary debris impact ejecta [J]. International Journal of Impact Engineering, 2001, 26(1): 713–724.
    [9] FAHRENTHOLD E P, HORBAN B A. An improved hybrid particle-element method for hypervelocity impact simulation [J]. International Journal of Impact Engineering, 2001, 26(1): 169–178.
    [10] CORVVONATO E, DESTEFANIS R, FARAUD M. Integral model for the description of the debris cloud structure and impact [J]. International Journal of Impact Engineering, 2001, 21: 115–128.
    [11] COHEN L J. A debris cloud cratering model [J]. International Journal of Impact Engineering, 1995, 17(1/2/3): 229–240.
    [12] MAIDEN C J, MCMILLAN A R. An investigation of the protection afforded a spacecraft by a thin shield [J]. AIAA Journal, 1964: 1992–1998.
    [13] PIEKUTOWSKI A J. Fragmentation-initiation threshold for spheres impacting at hypervelocity [J]. International Journal of Impact Engineering, 2003, 29: 563–574. doi: 10.1016/j.ijimpeng.2003.10.005
    [14] PIEKUTOWSKI A J. Characteristics of debris clouds produced by hypervelocity impact of aluminum spheres with thin aluminum plates [J]. International Journal of Impact Engineering, 1993, 14(1): 573–86.
    [15] BASHUROV V V, BEBENIN G V, BELOV G V, et al. Experimental modeling and numerical simulation of high- and hypervelocity space debris impact to spacecraft shield protection [J]. International Journal of Impact Engineering, 1997, 20(1): 69–78.
    [16] COUR-PALAIS B G. The shape effect of non-spherical projectiles in hypervelocity impacts [J]. International Journal of Impact Engineering, 2001, 26: 129–143. doi: 10.1016/S0734-743X(01)00075-6
    [17] IYER K A, POORMON K L, DEACON R M, et al. Hypervelocity impact response of Ti-6Al-4V and commercially pure titanium [J]. Procedia Engineering, 2013, 58: 127–137. doi: 10.1016/j.proeng.2013.05.016
    [18] FRIICHTENICHT J F, SLATTERY J C. Ionization associated with hypervelocity impact: D-2091 [R]. USA: NASA, 1963.
    [19] CRAWFORD D A, SCHULTZ P H. Laboratory observation of impact-generated magnetic fields [J]. Nature, 1988, 336(6194): 50–52. doi: 10.1038/336050a0
    [20] CRAWFORD D A, SCHULTZ P H. Laboratory investigation of impact-generated plasma [J]. Journal of Geophysical Research: Planets, 1991, 96: 18807–18817. doi: 10.1029/91JE02012
    [21] CRAWFORD D A, SCHULTZ P H. The production and evolution of impact-generated magnetic fields [J]. International Journal of Impact Engineering, 1993, 14: 205–216. doi: 10.1016/0734-743X(93)90021-X
    [22] GRUN D E, KISSEL J. The ion-composition of the plasma produced by impacts of fast dust particles [J]. Planetary and Space Science, 1977, 25(2): 135–147. doi: 10.1016/0032-0633(77)90017-4
    [23] DIETZEL H, EICHORN G, FECHTIG H, et al. The HEOS2 and HELIOS micrometeoroid experiments [J]. Journal of Physics E: Scientific Instruments, 1973, 6(3): 209–217. doi: 10.1088/0022-3735/6/3/008
    [24] GRÜN E, FECHTIG H, HANNER M S, et al. The Galileo dust detector [J]. Space Science Reviews, 1992, 60: 317–340.
    [25] RATCLIFF P R, MC DONNELL J A M, FIRTH J G, et al. The cosmic dust analyser [J]. Journal of the British Interplanetary Society, 1992, 45: 355–358.
    [26] CRAWFORD D A, SCHULTZ P H. Electromagnetic properties of impact-generated plasma, vapor and debris [J]. International Journal of Impact Engineering, 1999, 23: 169–180. doi: 10.1016/S0734-743X(99)00070-6
    [27] RATCLIFF P R, REBER M, COLE M J, et al. Velocity thresholds for impact plasma production [J]. Advances in Space Research, 1997, 20(8): 1471–1476. doi: 10.1016/S0273-1177(97)00419-5
    [28] RATCLIFF P R, ALLAHDADI F. Characteristics of the plasma from a 94 km/s micro-particle impact [J]. Advances in Space Research, 1996, 17(12): 87–91. doi: 10.1016/0273-1177(95)00763-5
    [29] GAULT D E, HEITOWOT E D. The partition of energy for hypervelocity impact craters formed in rocks [C]//Proceedings of the 6th Hypervelocity Impact Symposium, 1963, 2: 419.
    [30] 柳森, 谢爱民, 黄洁, 等. 超高速碰撞碎片云的激光阴影照相技术 [J]. 实验流体力学, 2005, 19(2): 35–39. doi: 10.3969/j.issn.1672-9897.2005.02.007 LIU S, XIE A M, HUANG J, et al. Laser shadowgraph for the visualization of hypervelocity impact debris cloud [J]. Journal of Experimnets in Fluid Mechanics, 2005, 19(2): 35–39. doi: 10.3969/j.issn.1672-9897.2005.02.007
    [31] 柳森, 李毅, 黄洁, 等. 用于验证数值仿真的Whipple屏超高速撞击试验结果 [J]. 宇航学报, 2005, 26(4): 505–508. doi: 10.3321/j.issn:1000-1328.2005.04.024 LIU S, LI Y, HUANG J, et al. Hypervelocity impact test results of Whipple shield for the validation of numerical simulation [J]. Journal of Astronautics, 2005, 26(4): 505–508. doi: 10.3321/j.issn:1000-1328.2005.04.024
    [32] 马兆侠, 黄洁, 石安华, 等. 铝球超高速撞击铝板反溅碎片云团辐射特性研究 [J]. 实验流体力学, 2014, 28(2): 90–94. MA Z X, HUANG J, SHI A H, et al. Study on radiation characteristics of ricochet debris cloud form aluminum plate subjected to hypervelocity impacts by aluminum projectile [J]. Journal of Experimnets in Fluid Mechanics, 2014, 28(2): 90–94.
    [33] 兰胜威, 柳森, 覃金贵, 等. 不同密度弹丸对水冰的超高速撞击成坑实验 [J]. 宇航学报, 2018, 39(9): 1054–1059. LAN S W, LIU S, QIN J G, et al. Hypervelocity impact cratering in water ice by projectiles with different densities [J]. Journal of Astronautics, 2018, 39(9): 1054–1059.
    [34] 庞宝君, 林敏, 张凯, 等. 丝网防护屏碎片云特性数值模拟研究 [J]. 高压物理学报, 2013, 27(3): 391–397. doi: 10.11858/gywlxb.2013.03.012 PANG B J, LIN M, ZHANG K, et al. Numerical simulation of debris cloud characteristics of the mesh shields [J]. Chinese Journal of High Pressure Physics, 2013, 27(3): 391–397. doi: 10.11858/gywlxb.2013.03.012
    [35] 龚自正, 杨继运, 代福, 等. CAST空间碎片超高速撞击试验研究进展 [J]. 航天器环境工程, 2009, 26(4): 301–306. doi: 10.3969/j.issn.1673-1379.2009.04.001 GONG Z Z, YANG J Y, DAI F, et al. M/OD hypervelocity impact tests carried out in CAST [J]. Spacecraft Environment Engineering, 2009, 26(4): 301–306. doi: 10.3969/j.issn.1673-1379.2009.04.001
    [36] 冉宪文, 张若棋, 徐志宏, 等. 超高速碰撞条件下铝靶熔化临界速度的理论估算及Grüneisen参数的影响[C]//第四届全国空间碎片专题研讨会. 南京, 2007.
    [37] 裴晓阳, 唐蜜, 钟敏, 等. 超高速撞击下碎片云相分布的数值模拟研究[C]//第十四届全国物理力学学术会议缩编文集, 2016: 228.
    [38] 李宝宝. 超高速碰撞下相变效应的数值模拟研究[D]. 长沙: 国防科学技术大学, 2010. LI B B. The numerical simulation study on effect of phase transition in hypervelocity impacting [D]. Changsha: University of Defense Technology, 2010.
    [39] TANG E L, WANG H L, XIA J, et al. Experimental study on plasma discharge induced by high-velocity impact solar array associated with projectile incidence angles [J]. International Journal of Applied Electromagnetics and Mechanics, 2016, 51(2): 107–117. doi: 10.3233/JAE-150119
    [40] 唐恩凌, 张庆明, 张健. 超高速碰撞LY12铝靶产生等离子体的特征参量测量 [J]. 弹箭与制导学报, 2008, 28(4): 110–112. doi: 10.3969/j.issn.1673-9728.2008.04.034 TANG E L, ZHANG Q M, ZHANG J. Characteristic parameter measurement of plasma generated during hypervelocity impact on LY12 Aluminum target [J]. Jounral of Projectiles, Rochets, Missiles and Guidance, 2008, 28(4): 110–112. doi: 10.3969/j.issn.1673-9728.2008.04.034
    [41] 马月芬, 张庆明, 吴碧, 等. 超高速碰撞产生等离子体的电磁场测量方法 [J]. 北京理工大学学报, 2011, 31(9): 1118–1121. MA Y F, ZHANG Q M, WU B, et al. Measurement method of electromagnetic fields of plasma produced by hypervelocity impact [J]. Transactions of Beijing Institute of Technology, 2011, 31(9): 1118–1121.
    [42] 马月芬, 张庆明, 李一磊, 等. 超高速碰撞产生的电磁场对通信电路的干扰 [J]. 北京理工大学学报, 2011, 31(7): 859–862. MA Y F, ZHANG Q M, LI Y L, et al. Interference on communication circuits due to electromagnetic fields generated by hypervelocity impact [J]. Transactions of Beijing Institute of Technology, 2011, 31(7): 859–862.
    [43] SONG W D, LV Y T, LI J Q, et al. Influence of impact conditions on plasma generation during hypervelocity impact by aluminum projectile [J]. Physics of Plasmas, 2016, 23: 073506. doi: 10.1063/1.4956440
    [44] 栗建桥, 宋卫东, 宁建国. 超高速撞击产生的等离子体特性研究 [J]. 高压物理学报, 2011, 27(4): 542–548. doi: 10.11858/gywlxb.2013.04.012 LI J Q, SONG W D, NING J G. A study on characteristics of plasma generated by hypervelocity impact [J]. Chinese Journal of High Pressure Physics, 2011, 27(4): 542–548. doi: 10.11858/gywlxb.2013.04.012
    [45] 宁建国, 栗建桥, 宋卫东. 超高速碰撞产生等离子体的毁伤特性研究 [J]. 力学学报, 2014, 46(6): 853–861. NING J G, LI J Q, SONG W D. Investigation of plasma damage properties generated by hypervelocity impact [J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(6): 853–861.
    [46] SONG W, LÜ Y, WANG C, et al. Investigation on plasma generated during hypervelocity impact at different impact velocities and angles [J]. Physics of Plasmas, 2015, 22(12): 123519. doi: 10.1063/1.4938516
    [47] 李怡勇, 沈怀荣, 李智. 超高速撞击动力学及航天器防护研究进展 [J]. 力学与实践, 2009, 31(2): 11–16. LI Y Y, SHEN H R, LI Z. Advances in hypervelocity impact dynamics and spacecraft protection research [J]. Mechanics in Engineering, 2009, 31(2): 11–16.
    [48] BOSLOUGH M B, ANG J A, CHHABLLDAS L C, et al. Hypervelocity testing of advanced shielding concepts for spacecraft against impacts to 10 km/s [J]. International Journal of Impact Engineering, 1993, 14: 95–106. doi: 10.1016/0734-743X(93)90012-V
    [49] 王翔, 王青松, 彭建祥, 等. 三级炮超高速发射技术在空间碎片防护研究中的初步应用 [J]. 高能量密度物理, 2017(4): 115–122. WANG X, WANG Q S, PENG J X, et al. The application of three-stage gun in the study of space debris [J]. High Energy Density Physics, 2017(4): 115–122.
    [50] LEMKE R W, KNUDSON M D, DAVIS J P. Magnetically driven hyper-velocity launch capability at the Sandia Z accelerator [J]. International Journal of Impact Engineering, 2011, 38(6): 480–485. doi: 10.1016/j.ijimpeng.2010.10.019
    [51] ZHANG X, WANG G, ZHAO J, et al. High velocity flyer plates launched by magnetic pressure on pulsed power generator CQ-4 and applied in shock Hugoniot experiments [J]. Review of Scientific Instruments, 2014, 85(5): 055110. doi: 10.1063/1.4875705
    [52] 王贵林, 郭帅, 沈兆武, 等. 基于聚龙一号装置的超高速飞片发射实验研究进展 [J]. 物理学报, 2014, 63(19): 196201. doi: 10.7498/aps.63.196201 WANG G L, GUO S, SHEN Z W. Recent advances in hyper-velocity flyer launch experiments on PTS [J]. Acta Physica Sinica, 2014, 63(19): 196201. doi: 10.7498/aps.63.196201
    [53] WALKER J D, GROSCH D J, MULLIN S A. A hypervelocity fragment launcher based on an inhibited shaped charge [J]. International Journal of Impact Engineering, 1993(14): 763–774.
    [54] 杨继运. 二级轻气炮模拟空间碎片超高速碰撞试验技术 [J]. 航天器环境工程, 2006, 23(1): 16–22. doi: 10.3969/j.issn.1673-1379.2006.01.003 YANG J Y. Simulation of space debris hypervelocity impact using two stage light gas gun [J]. Spacecraft Environment Engineering, 2006, 23(1): 16–22. doi: 10.3969/j.issn.1673-1379.2006.01.003
    [55] SEILER F, LGRA O. Hypervelocity lauchers [M]. Springer, 2016: 23–52.
    [56] CANNING T N, SEIFF A, JAMES C S. Ballistic range technology [M]. North Atlantic Treaty Origanization, 1970: 9–54.
    [57] EXOW B L, WICKERT M, THOMA K, et al. The extra-large light-gas gun of the Fraunhofer EMI: applications for impact cratering research [J]. Meteoritics & Planetary Science, 2013, 48(1): 3–7.
    [58] 王金贵. 气体炮原理与技术 [M]. 北京: 国防工业出版社, 2001: 198–202. WANG J G. Principle and technology of gas gun [M]. Beijing: National Defense Industry Press, 2001: 198–202.
    [59] CHHABILDAS L C, KMETYK, L N, REINHART W D, et al. Enhanced hypervelocity launcher-capabilities to 16 km/s [J]. International Journal of Impact Engineering, 1995, 17: 183–194. doi: 10.1016/0734-743X(95)99845-I
    [60] OSHER J E, HENRY G B, CHAU H, et al. Operating characteristics and modelling of the LLNL 100-kV electric gun [J]. IEEE Transactions on Plasma Science, 1989, 17(3): 392–402. doi: 10.1109/27.32247
    [61] 张文兵, 龚自正, 杨继运, 等. 用于模拟空间碎片超高速撞击的激光驱动飞片系统 [J]. 空间碎片研究, 2007, 7(1): 26–30. ZHANG W B, GONG Z Z, YANG J Y, et al. The laser-driven flyer system for space debris hypervelocity impact simulations [J]. Space Debris Research, 2007, 7(1): 26–30.
    [62] PIEKUTOWSKI A J. Effects of scale on debris cloud properties [J]. International Journal of Impact Engineering, 1997, 20: 639–50. doi: 10.1016/S0734-743X(97)87451-9
    [63] PIEKUTOWSKI A J, POORMON K L. Effects of scale on the performance of Whipple shields for impact velocities ranging from 7 to 10 km/s [J]. Procedia Engineering, 2013, 58: 642–652. doi: 10.1016/j.proeng.2013.05.074
    [64] 贾祖朋, 张树道, 蔚喜军. 多介质流体动力学计算方法[M]. 北京: 科学出版社, 2014: 1–25. JIA Z P, ZHANG S D, WEI X J. Numerical methods for dynamics of multi-material [M]. Beijing: Science Press, 2014: 1–25.
    [65] PEERY J S, CARROLL D E. Multi-material ALE methods in unstructured grids [J]. Computer Methods in Applied Mechanics and Engineering, 2000, 187(3/4): 591–619.
    [66] WINGATE C A, STELLINGWERF R F, DAVIDSON R F, et al. Models of high velocity impact phenomena [J]. International Journal of Impact Engineering, 1993, 14: 819–830. doi: 10.1016/0734-743X(93)90075-I
    [67] FREY J D, JANICOT F, GARAUD X, et al. The validation of hydrocodes for orbital debris impact simulation [J]. International Journal of Impact Engineering, 1993, 14: 255–265. doi: 10.1016/0734-743X(93)90025-3
    [68] BURKETT M W, CLANCY S P, MAUDLIN P J, et al. Coupled plasticity and damage modeling and their applications in a three-dimensional Eulerian hydrocode [J]. International Journal of Impact Engineering, 2006, 33: 126–132. doi: 10.1016/j.ijimpeng.2006.09.068
    [69] HORNER J K. A comparison of ballistic limit with adaptive-mesh Eulerian hydrocode predictions of one- and two-plate aluminum shielding protection against millimeter-sized Fe-Ni space debris [J]. International Journal of Impact Engineering, 2008, 35(12): 1602–1605. doi: 10.1016/j.ijimpeng.2008.07.039
    [70] TRUCANO T G, MC GLAUN J M. Hypervelocity impact calculations using CTH: case studies [J]. International Journal of Impact Engineering, 1990, 10: 601–613. doi: 10.1016/0734-743X(90)90092-A
    [71] GRIMALDI A, SOLLO A, GUIDA M, et al. Parametric study of a SPH high velocity impact analysis–a birdstrike windshield application [J]. Composite Structures, 2013, 96: 616–630. doi: 10.1016/j.compstruct.2012.09.037
    [72] MICHEL Y, CHEVALIER J M, DURIN C, et al. Hypervelocity impacts on thin brittle targets: experimental data and SPH simulations [J]. International Journal of Impact Engineering, 2006, 33: 441–451. doi: 10.1016/j.ijimpeng.2006.09.081
    [73] SHAW A, REID S R. Heuristic acceleration correction algorithm for use in SPH computations in impact mechanics [J]. Computer Methods in Applied Mechanics and Engineering, 2009, 198(49/50/51/52): 3962–3974.
    [74] LIU X, OSHER S, CHAN T. Weighted essentially non-oscillatory schemes [J]. Journal of Computational Physics, 1994, 115(1): 200–212. doi: 10.1006/jcph.1994.1187
    [75] COCKBURN B. Discontinuous Galerkin methods [J]. Zeitschrift fur Angewandte Mathematik und Mechanik, 2003, 83(11): 731–754. doi: 10.1002/(ISSN)1521-4001
    [76] BEISSEL S R, GERLACH C A, JOHNSON G R. Hypervelocity impact computations with finite elements and meshfree particles [J]. International Journal of Impact Engineering, 2006, 33: 80–90. doi: 10.1016/j.ijimpeng.2006.09.047
    [77] KOKH S, LAGOUTIÈRE F. An anti-diffusive numerical scheme for the simulation of interfaces between compressible fluids by means of a five-equation model [J]. Journal of Computational Physics, 2010, 229(8): 2773–2809. doi: 10.1016/j.jcp.2009.12.003
    [78] SHUKLA R K. Nonlinear preconditioning for efficient and accurate interface capturing in simulation of multicomponent [J]. Journal of Computational Physics, 2014, 276: 508–540. doi: 10.1016/j.jcp.2014.07.034
    [79] XIAO F, LI S, CHEN C. Revisit to the THINC scheme: a simple algebraic VOF algorithm [J]. Journal of Computational Physics, 2011, 230(19): 7086–7092. doi: 10.1016/j.jcp.2011.06.012
    [80] SAMBASIVAN S K, UDAYKUMAR H S. A sharp interface method for high-speed multi-material flows: strong shocks and arbitrary material pairs [J]. International Journal of Computational Fluid Dynamics, 2011, 25(3): 139–162. doi: 10.1080/10618562.2011.558011
    [81] KIPP M E, GRADY D E. High-pressure shock compression of solids II dynamic fracture and fragmentation [M]. Springer, 1996: 238.
    [82] MCGLAUN J M, THOMPSON S L, ELRICK M G. CTH: A three-dimensional shock wave physics code [J]. International Journal of Impact Engineering, 1990, 10: 351–360. doi: 10.1016/0734-743X(90)90071-3
    [83] 王言金, 刘军. Whipple防护结构超高速碰撞的欧拉数值模拟: GF-A 23030504 [R]. 北京: 北京应用物理与计算数学研究所, 2014. WANG Y J, LIU J. Eulerian numerical study of hypervelocity impacts on Whipple shields: GF-A 23030504 [R]. Beijing: Institute of Applied Physics and Computational Mathematics, 2014.
    [84] 梁仙红, 李征, 何长江, 等. 多介质流体力学两步欧拉方法的模型封闭性方法 [J]. 计算物理, 2010, 27(5): 658–664. doi: 10.3969/j.issn.1001-246X.2010.05.004 LIANG X H, LI Z, HE C J, et al. Closing relations in two-step Eulerian method for multifluid dynamics [J]. Chinese Journal of Computational Physics, 2010, 27(5): 658–664. doi: 10.3969/j.issn.1001-246X.2010.05.004
    [85] THOMPSON S L, MCGLAUN J L. CSQIII-an Eulerian finite difference program for two-dimensional material response: user’s manual: Sandia Report SAND87-2763 [R]. Albuquerque: Sandia National Laboratories, 1988.
    [86] HERTEL E S, MCINTOSH R L, PATTERSON B C. A comparison of phase change phenomena in CTH experimental data [J]. International Journal of Impact Engineering, 1995, 17: 399–408. doi: 10.1016/0734-743X(95)99865-O
    [87] POVARNITSYN M E, KHISHCHENKO K V, LEVASHOV P R. Simulation of melting and vaporization of metals at hypervelocity impact [J]. Journal of Physics: Conference Series, 2008(98): 042025.
    [88] CHEN J, MICHAEL H, CHI S. Meshfree methods: progress made after 20 years [J]. Journal of Engineering Mechanics, 2017, 143(4): 04017001. doi: 10.1061/(ASCE)EM.1943-7889.0001176
    [89] GINGOLD R A, MONAGHAN J J. Smoothed particle hydrodynamics: theory and application to non-spherical stars [J]. Monthly Notices Royal Astronomy Society, 1977, 181(3): 375–389. doi: 10.1093/mnras/181.3.375
    [90] GUAN P C, CHI S W, CHEN J S. Semi-Lagrangian reproducing kernel particle method for fragment-impact problems [J]. International Journal of Impact Engineering, 2011(38): 1033–1047.
    [91] SULSKY D, CHEN Z, SCHREYER. A particle method for history-dependent materials [J]. Computer Methods in Applied Mechanics and Engineering, 1994, 118: 179–196. doi: 10.1016/0045-7825(94)90112-0
    [92] LI B, HABBAL F, ORTIZ M. Optimal transportation meshfree approximation schemes for fluid and plastic flows [J]. International Journal for Numerical Methods in Engineering, 2010(83): 1541–1579.
    [93] LUCY L B. A numerical approach to the testing of the fission hypothesis [J]. The Astronomical Journal, 1977, 82: 1013–1024. doi: 10.1086/112164
    [94] MONAGHAN J J. An introduction to SPH [J]. Computer Physics Communications, 1988, 48(1): 89–96. doi: 10.1016/0010-4655(88)90026-4
    [95] LIBERSKY L D, PETSCHEK A G. Smooth particle hydrodynamics with strength of materials [M]//Advances in the Free-Lagrange Method Including Contributions on Adaptive Gridding and the Smooth Particle Hydrodynamics Method. Heidelberg: Springer Berlin Heidelberg, 1991: 248–257.
    [96] LIU M B, LIU G R. Smoothed particle hydrodynamics (SPH): an overview and recent developments [J]. Archives of Computational Methods in Engineering, 2010, 17(1): 25–76. doi: 10.1007/s11831-010-9040-7
    [97] 乐莉, 闫军, 钟秋海. 超高速撞击仿真算法分析 [J]. 系统仿真学报, 2014, 16(9): 1941–1943. YUE L, YAN J, ZHONG Q H. Simulations of debris impacts using three different algorithms [J]. Journal of System Simulation, 2014, 16(9): 1941–1943.
    [98] HIERMAIER S, KONKE D, STILP A J, et al. Computational simulation of the hypervelocity impact of Al-spheres on thin plates of different materials [J]. International Journal of Impact Engineering, 1997, 20(1): 363–374.
    [99] 王林, 胡秀章, 李永池, 等. 基于LS-DYNA的超高速撞击SPH数值模拟研究 [J]. 防护工程, 2010, 32(2): 32–38. WANG L, HU X Z, LI Y C, et al. Numerical simulation of hypervelocity impact by smoothed particle hydrodynamics using LS-DYNA [J]. Protective Engineering, 2010, 32(2): 32–38.
    [100] 徐英, 时家明, 林志丹. 撞击物形状和速度对高速撞击结果的影响 [J]. 弹箭与制导学报, 2010, 30(2): 106–110. doi: 10.3969/j.issn.1673-9728.2010.02.032 XU Y, SHI J M, LIN Z D. On the shape and velocity of impact bodies in hypervelocity impact [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2010, 30(2): 106–110. doi: 10.3969/j.issn.1673-9728.2010.02.032
    [101] LIBERSKY L D, PETSCHEK A G, CARNEY T C, et al. High strain Lagrangian hydrodynamics: a threedimensional SPH code for dynamic material response [J]. Journal of Computational Physics, 1993, 109(1): 67–75. doi: 10.1006/jcph.1993.1199
    [102] ZHOU C E, LIU G R, LOU K Y. Three-dimensional penetration simulation using smoothed particle hydrodynamics [J]. International Journal of Computational Methods, 2007, 4(4): 671–691. doi: 10.1142/S0219876207000972
    [103] MEDINA D F, CHEN J K. Three-dimensional simulations of impact induced damage in composite structures using the parallelized SPH method [J]. Composites: Part A, 2000, 31(8): 853–860. doi: 10.1016/S1359-835X(00)00031-2
    [104] HIERMAIER S, KÖNKE D, STILP A J, et al. Computaional simulation of the hypervelocity impact of Al-spheres on thin plates of different materials [J]. International Journal of Impact Engineeringn, 1997, 20(1): 363–374.
    [105] GROENENBOOM P H L. Numerical simulation of 2D and 3D hypervelocity impact using the SPH option in PAM-SHOCK [J]. International Journal of Impact Engineering, 1997, 20: 309–323. doi: 10.1016/S0734-743X(97)87503-3
    [106] FARAUD M, DESTEFANIS R, PALMIERI D, et al. SPH simulations of debris impacts using two different computer codes [J]. International Journal of Impact Engineering, 1999, 23: 249–260. doi: 10.1016/S0734-743X(99)00077-9
    [107] HARLOW F H. The particle-in-cell computing method for fluid dynamics [J]. Methods for Computational Physics, 1964, 3: 319–343.
    [108] BRACKBILL J U, RUPPEL H M. FLIP: a method for adaptively zoned, particle-in-cell calculations of fluid flows in two dimensions [J]. Journal of Computational Physics, 1986, 65: 314–343. doi: 10.1016/0021-9991(86)90211-1
    [109] 廉艳平, 张帆, 刘岩, 等. 物质点的理论和应用 [J]. 力学进展, 2013, 43(2): 237–264. LIAN Y P, ZHANG F, LIU Y, et al. Material point method and its applications [J]. Advaced in Mechanics, 2013, 43(2): 237–264.
    [110] 黄鹏. 金属及岩土冲击动力学问题的物质点法研究[D]. 北京: 清华大学, 2010: 69–70. HUANG P. Material point method for metal and soil impact dynamics problems [D]. Beijing: Tsinghua University, 2010: 69–70.
    [111] LIU P, LIU Y, ZHANG X, et al. Investigation on high-velocity impact of micron particles using material point method [J]. International Journal of Impact Engineering, 2015, 75: 241–254. doi: 10.1016/j.ijimpeng.2014.09.001
    [112] ZHANG C, KALIA R K, NAKANO A, et al. Hypervelocity impact induced deformation modes in α-alumina [J]. Applied Physics Letters, 2007, 91: 071906. doi: 10.1063/1.2753092
    [113] SAMELA J, KAI N. Atomistic simulation of the transition from atomistic to macroscopic cratering [J]. Physical Review Letters, 2008, 101(2): 027601. doi: 10.1103/PhysRevLett.101.027601
    [114] ANDERS C, BRINGA E M, URBASSEK H M. Crater production by energetic nanoparticle impact on Au nanofoams [J]. Applied Physics Letters, 2016, 108(11): 113108. doi: 10.1063/1.4944420
    [115] 巨圆圆, 张庆明, 龚良飞, 等. 球形弹丸超高速撞击铝靶的分子动力学模拟 [J]. 航天器环境工程, 2018, 35(2): 153–157. doi: 10.3969/j.issn.1673-1379.2018.02.009 JU Y Y, ZHANG Q M, GONG L F, et al. Molecular dynamics simulation for hypervelocity impact of spherical projectile to aluminum target [J]. Spacecraft Environment Engineering, 2018, 35(2): 153–157. doi: 10.3969/j.issn.1673-1379.2018.02.009
    [116] JARAMILLO-BOTERO A, AN Q, THEOFANIS P L, et al. Large-scale molecular simulations of hypervelocity impact of materials [J]. Procedia Engineering, 2013, 58: 167–176. doi: 10.1016/j.proeng.2013.05.020
    [117] 李毅, 柳森. 航天器铝合金面板的超高速撞击数值模拟 [J]. 载人航天, 2004(6): 52–55.
    [118] 冯春, 李世海, 刘晓宇. 一种基于颗粒接触的二维无网格方法及其在高速冲击模拟中的应用 [J]. 爆炸与冲击, 2014, 34(3): 292–299. doi: 10.11883/1001-1455(2014)03-0292-08 FENG C, LI S H, LIU X Y. A 2D particle contact-based meshfree method and its application to hypervelocity impact simulation [J]. Explosion and Shock Waves, 2014, 34(3): 292–299. doi: 10.11883/1001-1455(2014)03-0292-08
    [119] JOHNSON G R, STRYK R A. Conversion of 3D distorted elements into meshless particles during dynamic deformation [J]. International Journal of Impact Engineering, 2003, 28(9): 947–966. doi: 10.1016/S0734-743X(03)00012-5
    [120] JOHNSON G R, BEISSEL S R, GERLACH C A. Another approach to a hybrid particle-finite element algorithm for high-velocity impact [J]. International Journal of Impact Engineering, 2011, 38(5): 397–405. doi: 10.1016/j.ijimpeng.2011.01.002
    [121] JOHNSON G R, BEISSEL S R, STRYK R A. A generalized particle algorithm for high velocity impact computations [J]. Computational Mechanics, 2000, 25(2/3): 245–256.
    [122] JOHNSON G R, COOK W H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures [J]. Engineering Fracture Mechanics, 1985, 21(1): 31–48. doi: 10.1016/0013-7944(85)90052-9
    [123] JOHNSON G R, COOK W H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures [C]//Seventh International Symposium on Ballistics. The Hague, Netherlands, 1983.
    [124] STEINBERG D J, COCHRAN S G, GUINAN M W. A constitutive model for metals applicable at high-strain rate [J]. Journal of Applied Physics, 1980, 51(3): 1498–1504. doi: 10.1063/1.327799
    [125] SELYUTINA N S, PETROV Y V. Structural and temporal features of high-rate deformation of metals [J]. Doklady Physics, 2017, 62(2): 102–105. doi: 10.1134/S1028335817020136
    [126] SCHÄFER F K. An engineering fragmentation model for the impact of spherical projectiles on thin metallic plates [J]. International Journal of Impact Engineering, 2006, 33: 745–762. doi: 10.1016/j.ijimpeng.2006.09.067
    [127] STEINBERG D J, LUND C M. A constitutive model for strain rates from 10-4 to 106 s-1 [J]. Journal of Applied Physics, 1989, 65(4): 1528–1533. doi: 10.1063/1.342968
    [128] 张伟, 庞宝君, 贾斌, 等. 弹丸超高速撞击防护屏碎片云数值模拟 [J]. 高压物理学报, 2004, 18(1): 47–52. doi: 10.3969/j.issn.1000-5773.2004.01.009 ZHANG W, PANG B J, JIA B, et al. Numerical simulation of debris cloud produced by hypervelocity impact of projectile on bumper [J]. Chinese Journal of High Pressure Physics, 2004, 18(1): 47–52. doi: 10.3969/j.issn.1000-5773.2004.01.009
    [129] MCQUEEN R G, MARSH S P, FRITZ J N. Ultrabasic rocks and the composition of the upper mantle [J]. Journal of Geophysical Research: Planets, 1967, 72: 4999. doi: 10.1029/JZ072i020p04999
    [130] BJORK R L, OLSHAKER A E. The role of melting and vaporization in hypervelocity impact: RM-3490-PR [R]. USA: USA Air Force, 1965.
    [131] TANG E L, ZHANG Q M, ZHANG J. Preliminary study on diagnostic techniques for transient plasma generated by hypervelocity impact [J]. Plasma Science and Technology, 2008, 10(6): 735–738. doi: 10.1088/1009-0630/10/6/16
    [132] KRAUS R G, STEWART S T, SWIFT D C, et al. Shock vaporization of silica and the thermodynamics of planetary impact events [J]. Journal of Geophysical Research, 2012, 117(E9): 371–387.
    [133] HORNUNG K, MICHEL K W. Equation-of-state data of solids from shock vaporization [J]. Journal of Chemical Physics, 1971, 56(5): 2072–2078.
    [134] HORNUNG K, MALAMA Y G, THOMA K. Modeling of the very high velocity impact process with respect to in-situ ionization measurements [J]. Advances in Space Research, 1996, 17(12): 77–86. doi: 10.1016/0273-1177(95)00762-4
    [135] HORNUNG K. Impact vaporization and ionization of cosmic dust particles [J]. Astrophysics and Space Science, 2000, 274: 355–363. doi: 10.1023/A:1026553502542
    [136] POVARNITSYN M E, KHISHCHENKO K V, LEVASHOV P R. Hypervelocity impact modeling with different equations of state [J]. International Journal of Impact Engineering, 2006, 33: 625–633. doi: 10.1016/j.ijimpeng.2006.09.078
    [137] BRUNDAGE A L. Implementation of Tillotson equation of state for hypervelocity impact of metals, geologic materials, and liquids [J]. Procedia Engineering, 2013, 58: 461–470. doi: 10.1016/j.proeng.2013.05.053
    [138] BERGH M, GARCIA V. A computational models for assessing high-velocity debris impact in space applications [J]. Shock Waves, 2017, 27(4): 675–684. doi: 10.1007/s00193-017-0709-9
    [139] TILLOTSON J H. Metallic equations of state for hypervelocity impact: General Atomic Report GA-3216 [R]. San Diego, CA: General Atomic, 1962.
    [140] SCHONBERG W P. Characterizing material states in orbital debris impacts [J]. Proceedings of SPIE -The International Society for Optical Engineering, 1995, 2483: 31–39.
    [141] THOMPSON S L, LAUSON H S. Improvements in the Chart D radiation-hydrodynamic CODE III: revised analytic equations of state: SC-RR-71-0714 [R]. Albuquerque, New Mexico: Sandia National Laboratories, 1972.
    [142] MELOSH H J. A hydrocode equation of state for SiO2 [J]. Meteoritics & Planetary Science, 2007, 42(12): 2079–2098.
    [143] LITTLEFIELD D L. ANEOS extensions for modeling hypervelocity impact [J]. International Journal of Impact Engineering, 1997, 20: 533–544. doi: 10.1016/S0734-743X(97)87442-8
    [144] COLLINS G S, MELOSH H J. Improvments to ANEOS for multiple phase transitions [C]//45th Lunar and Planetary Science Conference, 2014: 2664.
    [145] JOHNSON J D. The SESAME databse [C]// 12th Symposium on Thermophysical Properties Boulder. Colorado, 1994: LA-UR-9401451.
    [146] LYON P, JOHNSON J D. SESAME: the Los Alamos national laboratory equation of state database: LA-UR-92-3407 [R]. USA: Los Alamos national laboratory, 1992.
    [147] 唐蜜, 刘仓理, 李平, 等. 超高速撞击产生碎片云相分布数值模拟 [J]. 强激光与粒子束, 2012, 24(9): 2203–2206. TANG M, LIU C L, LI P. Numerical simulation of phase distribution of debris cloud generated by hypervelocity impact [J]. High Power Laser and Particle Beams, 2012, 24(9): 2203–2206.
    [148] CHHABILDAS L C, REINHART W D, THORNHILL T F, et al. Debris generation and propagation phenomenology from hypervelocity impacts on aluminum from 6 to 11 km/s [J]. International Journal of Impact Engineering, 2003, 29: 185–202. doi: 10.1016/j.ijimpeng.2003.09.016
    [149] ROYCE E B. A three-phase equation of state for metals: UCRL-51121 [R]. USA: Lawrence Livermore Lab, 1971.
    [150] GROVER R. Liquid metal equation of state based on scaling [J]. Journal of Chemical Physics, 1971, 55(7): 3435–3441. doi: 10.1063/1.1676596
    [151] YOUNG D A, ALDER B J. Critical point of metals from the van der Waals model [J]. Physics Review A, 1971, 3(1): 364–371. doi: 10.1103/PhysRevA.3.364
    [152] 于继东, 李平, 王文强, 等. 金属铝固液气完全物态方程研究 [J]. 物理学报, 2014, 63(11): 116401. doi: 10.7498/aps.63.116401 YU J D, LI P, WANG W Q, et al. A solid-liquid-gas three phase complete equation of state of aluminum [J]. Acta Physica Sinica, 2014, 63(11): 116401. doi: 10.7498/aps.63.116401
    [153] 唐蜜. 基于欧拉方法的超高速撞击程序研制及碎片云相分布数值模拟 [D]. 绵阳: 中国工程物理研究院, 2015: 85–98. TANG M. Development of hypervelocity impact codes based on Euler method and numerical study of the phase distribution in debris cloud [D]. Mianyang: China Academy of Engineering Physics, 2015: 85–98.
    [154] PIEKUTOWSKI A J, POORMON K L. Holes formed in thin aluminum sheets by spheres with impact velocities from 2 to 10 km/s [J]. Procedia Engineering, 2015, 103: 482–489. doi: 10.1016/j.proeng.2015.04.063
    [155] PIEKUTOWSKI A J. Formation and description of debris clouds produced by hypervelocity impact: NASA-CR-201000 [R]. USA: NASA, 1995.
    [156] MESPOULET J, HÉREIL P L, ABDULHAMID H, et al. Experimental study of hypervelocity impacts on space shields above 8 km/s [J]. Procedia Engineering, 2017, 204: 508–515. doi: 10.1016/j.proeng.2017.09.748
    [157] HILL S A. Determination of an empirical model for the prediction of penetration hole diameter in thin plates from hypervelocity impact [J]. International Journal of Impact Engineering, 2004, 30(3): 303–321. doi: 10.1016/S0734-743X(03)00079-4
    [158] DE CHANT L J. A high velocity plate penetration hole diameter relationship based on late time stagnation point flow concepts [J]. Applied Mathematics and Computation, 2005, 170(1): 410–424. doi: 10.1016/j.amc.2004.12.047
    [159] HOSSEINI M, ABBAS H. Growth of hole in thin plates under hypervelocity impact of spherical projectiles [J]. Thin-Walled Structures, 2006, 44(9): 1006–1016. doi: 10.1016/j.tws.2006.08.024
    [160] ABBAS H, ALSAYED S H, ALMUSALLAM T H, et al. Characterization of hole-dameter in thin metallic plates perforate by spherical projectiles using genetic algorithms [J]. Archive of Applied Mechanics, 2011, 81(7): 907–924. doi: 10.1007/s00419-010-0459-y
    [161] ROSENBERG Z, KOSITSKI R. The hole diameter in metallic plates impacted by hypervelocity projectiles [J]. International Journal of Impact Engineering, 2017, 102: 147–155. doi: 10.1016/j.ijimpeng.2016.12.015
    [162] SHINAR G I, BARNEA N, RAVID M, et al. An analytical model for the cratering of metallic targets by hypervelocity long rods [C]// 15th International Symposium on Ballistics. Jerusalem, 1995: 59-66.
    [163] JOLLY W H, SCHONBERG W P. Analytical prediction of hole diameter in thin plates due to hypervelocity impact of spherical projectiles [J]. Shock and Vibration, 1997, 4(5/6): 379–390.
    [164] 迟润强, 庞宝君, 何茂坚, 等. 球形弹丸超高速正撞击薄板破碎状态实验研究 [J]. 爆炸与冲击, 2009, 29(3): 231–236. doi: 10.3321/j.issn:1001-1455.2009.03.002 CHI R Q, PANG B J, HE M J, et al. Experimental investigation for deformation and fragmentation of spheres penetrating sheets at hypervelocity [J]. Explosion and Shock Waves, 2009, 29(3): 231–236. doi: 10.3321/j.issn:1001-1455.2009.03.002
    [165] 汪庆桃, 吴克刚, 陈志阳. 圆柱形长杆超高速正碰撞薄板结构破碎效应 [J]. 振动与冲击, 2017, 36(5): 54–60. WANG Q T, WU K G, CHEN Z Y. Fragmentation effect of a long cylindrical rod with a hypervelocity normally impacting a thin plate structure [J]. Journal of Vibration and Shock, 2017, 36(5): 54–60.
    [166] PIEKUTOWSKI A J. Formation and description of debris cloud produced by hypervelocity impact: NASA-CR-201000 [R]. USA: NASA, 1995.
    [167] SCHMIDT R M, HOUSEN K R, BJORKMAN M D, et al. Advanced all-metal orbital debris shield performance at 7 to 17 km/s [J]. International Journal of Impact Engineering, 1995, 17: 719–730. doi: 10.1016/0734-743X(95)99894-W
    [168] POORMON K L, PIEKUTOWSKI A J. Comparisions of cadmium and aluminum debris clouds [J]. International Journal of Impact Engineering, 1995, 17: 639–648. doi: 10.1016/0734-743X(95)99887-W
    [169] HOPKINS A K, LEE T W, SWIFT H F. Materials phase transformation effects upon performance of spaced bumper systems [J]. Journal of Spacecraft and Rockets, 1970, 9(5): 342–345.
    [170] ANDERSON C E JR, TRUCANO T G, MULLIN S A. Debris cloud dynamics [J]. International Journal of Impact Engineering, 1990, 9(1): 89–113. doi: 10.1016/0734-743X(90)90024-P
    [171] BJORK R L. The physics of hypervelocity lethality [J]. International Journal of Impact Engineering, 1987, 5: 129–154. doi: 10.1016/0734-743X(87)90034-0
    [172] SHOCKEY D A, CURRAN D R, OSHER J E, et al. Disintegration behavior of metal rods subjected to hypervelocity impact [J]. International Journal of Impact Engineering, 1987, 5: 585–593. doi: 10.1016/0734-743X(87)90073-X
    [173] PIERAZZO E, VICKERY A M, MELOSH H J. A reevaluation of impact melt production [J]. Icarus, 1997, 127(2): 408–423. doi: 10.1006/icar.1997.5713
    [174] QUINTANA S N, CRAWFORD D A, SCHULTZ P H. Analysis of impact melt and vapor production in CTH for planetary applications [J]. Procedia Engineering, 2015, 103: 499–506. doi: 10.1016/j.proeng.2015.04.065
    [175] POVARNITSYN M E, KHISHCHENKO K V, LEVASHOV P R. Simulation of shock-induced fragmentation and vaporization in metals [J]. International Journal of Impact Engineering, 2008, 35(12): 1723–1727. doi: 10.1016/j.ijimpeng.2008.07.011
    [176] 宋卫东, 吕旸涛, 栗建桥. 超高速碰撞产生等离子体的电磁特性研究[C]// 第十四届全国物理力学学术会议缩编文集, 2016.
    [177] 龙仁荣, 张庆明. 超高速弹丸碰撞薄板产生碎片云的运动模型分析 [J]. 北京理工大学学报, 2009, 29(3): 193–196. LONG R R, ZHANG Q M. Dynamic model for debris clouds produced from impacts of hypervelocity projectiles with thin sheets [J]. Transactions of Beijing Institute of Technology, 2009, 29(3): 193–196.
    [178] SWIFT H F. Impact dynamics [M]. New York: John Wiley & Sons, 1982.
    [179] PIEKUTOWSKI A J. A simple dynamic model for the formation of debris clouds [J]. International Journal of Impact Engineering, 1990, 10(1): 453–471.
    [180] BLESS S J. Bumper debris cloud structure estimated by shock calculations [J]. Journal de Physique III, 1991, 1(3): 903–908.
    [181] 郑建东, 龚自正, 席爽, 等. 超高速撞击碎片云模型研究综述[C]//第六届全国空间碎片学术交流会, 2011: 671–682. ZHENG J D, GONG Z Z, XI S, et al. Review of debris cloud models produced by hypervelocity impact of space debris [C]// 6th Symposium on debris in space, 2011: 671–682.
    [182] NEBOLSINE P E, GELB A, LEGNER H H, et al. Simple model for the debris velocity and distribution due to a catastrophic impact [C]// AIAA Space Programs and Technologies Conference and Exhibit. USA: AIAA, 1994
    [183] SCHONBERG W P, WILLIAMSEN J E. Empirical hole size and crack length models for dual-wall systems under hypervelocity projectile impact [J]. International Journal of Impact Engineering, 1997, 20(6): 711–722.
    [184] 迟润强. 弹丸超高速撞击薄板碎片云建模研究[D]. 哈尔滨: 哈尔滨工业大学, 2010: 100–120. CHI R Q. Research and modeling of debris cloud produced by hypervelocity impact of projectile with thin plate [D]. Harbin: Harbin Institute of Technology, 2010: 100–120.
    [185] 管公顺, 朱耀, 迟润强, 等. 铝双层板结构撞击损伤的板间距效应实验研究 [J]. 材料科学与工艺, 2008, 16(5): 692–695. doi: 10.3969/j.issn.1005-0299.2008.05.025 GUAN G S, ZHU Y, CHI R Q, et al. Experimental investigation of space effect on damage of aluminum dual-wall structure by hypervelocity impact [J]. Materials Science & Technology, 2008, 16(5): 692–695. doi: 10.3969/j.issn.1005-0299.2008.05.025
    [186] PIEKUTOWSKI A J, POORMON K L, CHRISTIANSEN E L, et al. Performance of Whipple shields at impact velocities above 9 km/s [J]. International Journal of Impact Engineering, 2011, 38(6): 95–503.
    [187] COUR-PALAIS B G. Hypervelocity impact in metals, glass and composites [J]. International Journal of Impact Engineering, 1987, 5: 221–237. doi: 10.1016/0734-743X(87)90040-6
    [188] PIEKUTOWSKI A J. Debris clouds generated by hypervelocity impact of cylindrical projectiles with thin aluminum plates [J]. International Journal of Impact Engineering, 1987, 5: 509–518. doi: 10.1016/0734-743X(87)90066-2
    [189] VERMA P N, DHOTE K D. Characterising primary fragment in debris cloud formed by hypervelocity impact of spherical stainless steel projectile on thin steel plate [J]. International Journal of Impact Engineering, 2018, 120: 118–125. doi: 10.1016/j.ijimpeng.2018.05.003
    [190] SCHONBERG W P. Concise history of ballistic limit equations for multi-wall spacecraft shielding [J]. REACH-Reviews in Human Space Exploration, 2016(1): 46–54.
    [191] 袁俊刚, 曲广吉, 闫军. 国外空间碎片防护结构弹道极限方程分析 [J]. 空间碎片, 2007, 7(7): 21–25. YUAN J G, QU G J, YAN J. Analysis for development of ballistic limit equations of space debris shield configurations from other countries [J]. Space Debris Research, 2007, 7(7): 21–25.
    [192] 闫军, 曲广吉, 郑世贵. 空间碎片超高速撞击弹道极限方程的研究评述 [J]. 航天器工程, 2005, 14(2): 42–46. YAN J, QU G J, ZHENG S G. Comments on the ballistic limit equations of space debris with hypervelocity [J]. Spacecraft Engineering, 2005, 14(2): 42–46.
    [193] HAYASHIDA K B, ROBINSON J H. Double-plate penetration equations: NASA/TM-2000-209907 [R]. USA: NASA Marshall Space Flight Cener, 2000.
    [194] LI W. The relationship between Brinell hardness and strength of material [J]. Heavy Cast Forg, 1994, 65(3): 48–51.
    [195] ZHANG X, JIA G, HUANG H. An approach for constituting double/multi wall BLE by single wall BLE of spacecraft shield [J]. International Journal of Impact Engineering, 2014, 69: 114–121. doi: 10.1016/j.ijimpeng.2014.02.009
    [196] FISH R H, SUMMERS J L. The effect of material properties on threshold penetration [C]// Proceedings of the Seventh Hypervelocity Impact Symposium. Tampa, 1965.
    [197] FROST V C. Meteoroid damage assessment: NASA SP-8042 [R]. USA: NASA, 1970.
    [198] CORONADO A R, GIBBINS M N, WRIGHT M A, et al. Space station integrated wall design and penetration damage control: NAS8-36426 [R]. USA: NASA, 1987.
    [199] HOLSAPPLE K A, SCHMIDT R M. On the scaling of crater dimensions 2 impact process [J]. Journal of Geophysical Research, 1982, 87: 1849–1870. doi: 10.1029/JB087iB03p01849
    [200] COUR-PALAIS B G. Hypervelocity impact investigations and meteoroid shielding experience related to Apollo and Skylab: NAS-S-82-05009 [R]. USA: NASA, 1984.
    [201] HAYASHIDA K B, ROBINSON J H. Single wall penetration equations: NASA TM-103565 [R]. USA: NASA, 1991.
    [202] CHRISTIANSEN E L. Shield sizing and response equations: NASA-SN3-91-42 [R]. USA: NASA, 1991.
    [203] LEE M, CHO Y J. Characterization of the ballistic limit curve for hypervelocity impact of sphere onto single plate [J]. Journal of Mechanical Science and Technology, 2011, 25(9): 2457–2463. doi: 10.1007/s12206-011-0716-1
    [204] 贾斌, 盖芳芳, 马志涛, 等. 5A06铝合金单层板超高速撞击弹道极限分析 [J]. 材料科学与工艺, 2007, 15(5): 636–639. doi: 10.3969/j.issn.1005-0299.2007.05.011 JIA B, GAI F F, MA Z T. Ballistic limit analysis of aluminum 5A06 single wall plate subjected to hypervelocity impact [J]. Materials Science & Technology, 2007, 15(5): 636–639. doi: 10.3969/j.issn.1005-0299.2007.05.011
    [205] 徐小刚, 贾光辉, 黄海. 单层板超高速撞击弹道极限方程综合建模 [J]. 弹箭与制导学报, 2007, 15(5): 636–639. XU X G, JIA G H, HUANG H. Integrated modeling of ballistic limit equations of single plate under hypervelocity impact [J]. Journal of Projectiles, Rockets, Missiles and Guidance, Materials Science & Technology, 2007, 15(5): 636–639.
    [206] 张晓天, 谌颖, 贾光辉. 航天器单层板结构弹道极限的支持向量机预测模拟 [J]. 宇航学报, 2014, 35(3): 298–305. doi: 10.3873/j.issn.1000-1328.2014.03.008 ZHANG X T, CHEN Y, JIA G H. Support vector machine model for spacecraft single wall ballistic limit prediction [J]. Journal of Astronautics, 2014, 35(3): 298–305. doi: 10.3873/j.issn.1000-1328.2014.03.008
    [207] COUR-PALAIS B G. Meteoroid protection by multi-wall structures [C]//AIAA Hypervelocity Impact Conference. Cincinnati, 1969: 69–372.
    [208] REIMERDES H G, NLKE D, SCHÄFER F. Modified Cour-Palais/Christiansen damage equations for double-wall structures [J]. International Journal of Impact Engineering, 2006, 33: 645–654. doi: 10.1016/j.ijimpeng.2006.09.036
    [209] CHRISTIANSEN E L, KERR J H. Ballistic limit equations for spacecraft shielding [J]. International Journal of Impact Engineering, 2001, 26(1): 93–104.
    [210] 贾光辉, 张平, 李轩, 等. 双层板弹道极限方程的速度区间修正方法 [J]. 空间碎片研究与应用, 2012, 12(4): 25–30. JIA G H, ZHANG P, LI X, et al. Whipple ballistic limit equations optimization method via correcting the velocity region [J]. Space Debris Research and Application, 2012, 12(4): 25–30.
    [211] RYAN S, CHRISTIANSEN E L. A ballistic limit analysis programme for shielding against micrometeroids and orbital debris [J]. Acta Astronautica, 2011, 69(5/6): 245–257.
    [212] RYAN S, THALER S. Artificial neural networks for characterizing Whipple shield performance [J]. International Journal of Impact Engineering, 2013, 56: 61–70. doi: 10.1016/j.ijimpeng.2012.10.011
    [213] MILLER J E, BJORKMAN M D, CHRISTIANSEN E L, et al. Analytic ballistic performance model of Whipple shields [J]. Procedia Engineering, 2015, 103: 389–397. doi: 10.1016/j.proeng.2015.04.037
    [214] 袁俊刚, 曲广吉, 韩增尧, 等. 空间碎片防护结构弹道极限方程综合建模研究 [J]. 空间碎片研究, 2008, 8(2): 14–19. YUAN J G, QU G J, HAN Z Y, et al. Modeling ballistic limit of M/OD Whipple shield [J]. Space Debris Research, 2008, 8(2): 14–19.
    [215] 郑建东, 龚自正, 童靖宇, 等. 新型高精度Whipple防护结构弹道极限方程的精度对比 [J]. 空间碎片研究与应用, 2012, 12(1): 28–32. ZHENG J D, GONG Z Z, TONG J Y. Accuracy comparison of a new type with high accuracy Whipple shield ballistic limit equations [J]. Space Debris Research and Application, 2012, 12(1): 28–32.
    [216] 贾光辉, 欧阳智江, 蒋辉, 等. Whipple防护结构弹道极限方程的多指标修正 [J]. 宇航学报, 2013, 34(12): 1651–1656. doi: 10.3873/j.issn.1000-1328.2013.12.016 JIA G H, OU Y Z Z, JIANG H, et al. Multiple indicator correction for Whipple shield ballistic limit equation [J]. Journal of Astronautics, 2013, 34(12): 1651–1656. doi: 10.3873/j.issn.1000-1328.2013.12.016
  • 加载中
图( 17) 表( 3)
计量
  • 文章访问数:  11703
  • HTML全文浏览数:  11703
  • PDF下载数:  120
  • 施引文献:  0
出版历程
  • 收稿日期:  2019-05-13
  • 刊出日期:  2019-06-01

铝弹丸超高速撞击防护结构的研究进展

    通讯作者: 宋卫东（1975－），男，博士，教授，主要从事材料与结构冲击动力学研究. E-mail：swdgh@bit.edu.cn; 
    作者简介: 林健宇（1987－），男，博士，助理研究员，主要从事多介质力学计算研究. E-mail：linjiany@mail.ustc.edu.cn
  • 1. 中国工程物理研究院流体物理研究所，四川 绵阳　621999
  • 2. 北京理工大学爆炸科学与技术国家重点实验室，北京　100081
  • 收稿日期:  2019-05-13

摘要: 以空间碎片防护为背景，回顾了超高速铝弹丸正撞击单层和双层铝合金防护结构的研究进展，讨论了目前针对超高速撞击的弹丸发射技术和数值模拟方法（如Euler方法、无网格方法等）的优缺点。数值模拟不仅建立在离散方法上，还需要提供准确的材料本构模型和状态方程。介绍了常用材料模型（包括Johnson-Cook、Steinberg-Guinan模型）和状态方程（包括Tillotson、ANEOS、SESAME、GRAY三相状态方程）。基于实验和数值模拟，目前对7 km/s以下的超高速撞击物理过程已经认识得比较清楚。对单层板，重点讨论了板的穿孔特征和孔径模型；对双层板，除了前板的穿孔外，还讨论了碎片云的分布特征、材料相变、碎片云的相态分布、弹丸形状的影响、碎片云的散布模型以及碎片云对后板造成的破坏特征。最后介绍了工程防护中较为重要的防护结构的弹道极限方程。单层板和双层板的弹道极限方程研究近年来取得了较大进展。本文回顾了国内外常用的弹道极限方程以及近年来新提出的理论模型和基于人工神经网络的模型等。

English Abstract

    全文HTML

  • 超高速撞击是指撞击产生的冲击压力远大于弹丸和靶的强度的撞击过程[1–2]。在研究超高速碰撞问题的初期，人们在研究超高速碰撞对飞行器的破坏时关注的重点是超高速碰撞产生的力学毁伤效应。Whipple[3]提出了一种双层板结构用于防护太空垃圾对航天器的超高速碰撞，Whipple防护屏至今仍然在航天器中得到广泛使用，一些有关超高速碰撞结构响应的工程模型也不断被提出和发展[4–5]。本文重点关注人造航天器防护领域中的超高速撞击问题。空间碎片和微流星体均会对人造航天器造成损坏。空间碎片的最大速度可以超过14 km/s，平均速度约10.3 km/s，而微流星体速度介于11～72 km/s之间[6]。对于厘米级的空间碎片，航天器一般采取主动规避的方法，而对于毫米级的碎片只能采取防护措施[7]。防护结构中最简单的是单层防护结构和双层防护结构（即Whipple防护结构）。虽然航天器现大量采用多层防护结构，且材料除铝合金外还有新型陶瓷和复合材料，但单层板和双层板依然被使用和大量研究，其相关研究可以揭示空间碎片防护中的基本现象和物理机理，为更复杂的防护结构研究提供借鉴。

    国外对超高速碰撞的研究起步较早，在理论、数值模拟和实验方面都开展了大量工作。超高速碰撞过程较为复杂，因此理论必须做大量简化。如Schonberg[8]将复杂的超高速碰撞模型简化为一维问题，从一维冲击波理论的角度对碎片云特征参数进行了研究。该模型形式简单，且容易得到所需的碎片云特征参数，因而具有很好的易用性，是目前应用最广的理论模型；但其也存在模型过于简化，所得参数精度低等问题。Fahrenthold等[9]基于Grady-Kipp碎片理论，从能量守恒、熵增理论出发，提出了超高速碰撞的热力学连续损伤和断裂模型。Fahrenthold模型经过严格的理论推导得到特征碎片尺寸和塑性断裂表面积等参数，其结果可信，但是由于理论体系较为复杂，且应用范围狭小，因此未能得到推广应用。此外，Corvvonato等[10]和Cohen[11]也对超高速碰撞碎片云提出了各自的理论模型。Maiden等[12]运用波传播理论对超高速弹体正撞击薄板时的破碎过程进行了定性描述，认为弹靶材料的破碎是由于稀疏波导致材料中某一位置处的净拉伸应力超过材料的动态断裂强度而引起的。目前，理论方法仅能得到某些特定物理量的大致估计值，不能全面求解超高速碰撞问题所涉及的诸多参数，无法就超高速碰撞问题给出一个合理且方便应用的解。

    超高速碰撞的实验研究为理解超高速碰撞提供了大量的数据。Piekutowski[13]采用实验方法对不同材料、弹丸形状、碰撞倾角、撞击速度以及弹径靶厚比值的超高速碰撞问题作了深入研究。他依据拍摄所得碎片云的图片对其内部结构作了细致的分析，结果表明碎片尺寸越大，破坏能力越强，且圆盘形弹丸和柱状弹丸的破坏能力明显强于球形弹丸。Piekutowski[14]还对铝球超高速撞击铝靶产生的孔洞作了研究。Bashurov等[15]对钢球超高速正碰撞和45°斜碰撞钢或铝合金单层靶板的实验研究表明，随着碰撞速度的增加，碰撞碎片的数量明显增加，而碎片尺寸则明显减小。Cour-Palais[16]通过分析锌、镉和铝3种材料的弹丸超高速碰撞实验，研究了超高速碰撞的弹丸形状效应，结果表明：碎片云的局部或全部发生了熔化和汽化；柱状弹丸更容易造成防护屏的破坏，而多层防护屏和填充式防护结构能起到很好的防护效果。Lyer等[17]研究了直径为2.35 mm的2017-T4铝球以7 km/s的速度撞击Ti-6Al-4V防护屏，结果表明弹坑底部损伤方式包括微裂纹、剪切带、大晶粒变形和再结晶作用。

    相对于超高速碰撞对结构的影响，其电磁效应的研究进行得较少，尚处于探索阶段，并且相关研究主要以实验为主。超高速碰撞引起电磁效应的研究大体可分成两类：对超高速碰撞过程中产生的等离子体的研究、对超高速碰撞中产生的闪光现象的研究。对超高速碰撞产生等离子体的研究，国外很早就开展了，最早由Friichtenicht和Slattery[18]报道。他们认为产生的等离子体电量正比于入射能量，且与速度有关，提出一种与速度相关的函数来表示超高速碰撞产生等离子体的电量，即

    式中：Mpro为弹丸的质量，K1为常数，vimp为弹丸速度，$f\left( {{v_{\rm imp}}} \right)$是速度相关的函数。后来很多人针对超高速碰撞等离子体进行了更深入的研究，均以实验室观察现象为主[19–21]，其研究目的是通过检测等离子体的方法原位检测宇宙尘埃颗粒[22–25]。随后人们开始关注碰撞所产生的等离子体的特性和参数，Crawford和Schultz[26]通过实验拟合得到一个经验公式，用于计算一定质量和速度的弹丸碰撞靶板之后蒸气云中所带电荷的总量和形成的磁场大小

    式中：xdis为测量距离。对于电离机制的研究，在很早之前就有相关工作，很多人通过实验与数值模拟及理论研究相对比的方法试图找出碰撞电离机制并实现理论预测和数值仿真分析。Ratcliff等[27]在质谱仪上做了一系列尘埃粒子超高速碰撞特定材质靶板产生等离子体的实验。在一些实验中他们得到了不同速度下不同类型离子的密度，同时将分子动力学和流体代码结合进行数值模拟，假设所有等离子体都处于蒸气中，并且电离的发生是由于蒸气原子自由碰撞引起的，以随机的弹性碰撞过程中转移的能量为依据给出超高速碰撞产生离子数的理论和数值模拟结果。Ratcliff等[28]在另外一些实验里分析了更高速度的碰撞，70 nm的碳化硼微粒以94 km/s的速度超高速碰撞掺银铝靶板。这组实验也在质谱仪上进行，利用质谱仪区分收集到的离子的数量和种类，结合追踪到的靶板碰撞后喷射的体积和微粒体积，得到某一种元素的蒸气体积，再考虑到元素的电离能和汽化热，综合得到了微粒入射动能在喷射物和等离子体中的分配：在这个碰撞速度下，入射微粒动能的4%分配到产生的等离子体和蒸气云中。质谱仪无法捕捉蒸气云的含量，但是Ratcliff认为如果假设产生的等离子体处于热平衡状态，应用Saha方程得到的电离度基本为100%，于是就算等离子体未处于热平衡状态，喷射物中存在的中性蒸气含量也是稀少的，可以近似认为全部动能的4%都用来使喷射物电离。但是这种能量分配与入射速度有关，对于较低速度入射情况[29]，如当入射速度约为6 km/s时，这部分能量要小于1%。

    我国近年来越来越多的科研人员对超高速碰撞问题开展了广泛研究。中国空气动力研究与发展中心超高速研究所的柳森等[30]在超高速碰撞靶上建立了激光阴影照相系统，研究了超高速碰撞过程中所产生碎片云的特性，获得了撞击速度为6 km/s时清晰的碎片云图像，也对球形弹丸超高速撞击Whipple屏进行了实验研究，得到撞击速度、碰撞倾角、靶孔直径、后墙损伤情况等，实验结果表明，在实验所达到的范围内，弹丸撞击速度越高，Whipple屏的防护效果越好[31]。马兆侠、黄洁等[32]通过超高速撞击实验，获得了铝球撞击铝板反溅粒子云团在250～340 nm波段的辐射特征光谱，结合所得超高速撞击反溅粒子云团温度经验公式推导出基态原子数与撞击参数之间的关系。兰胜威等[33]开展了水冰的超高速撞击成坑实验，获得了水冰撞击坑特征随撞击参数的变化规律。哈尔滨工业大学空间碎片高速撞击研究中心的庞宝君等[34]通过实验和数值模拟方法研究了Whipple防护结构和丝网防护屏的超高速撞击特性，获得了铝合金Whipple防护结构在0.5～5.5 km/s撞击速度区间内的撞击极限曲线，丝网防护屏的防护特性体现在有效地切割、粉碎弹丸，但不能有效地扩散碎片云，碎片云动量分布较为集中。北京卫星环境工程研究所的龚自正等[35]开展了二级轻气炮超高速撞击地面模拟试验技术、典型防护结构防护性能的超高速撞击试验验证，以及载人航天器外露材料超高速撞击特性等方面的研究。冉宪文等[36]选用不同的Mie-Grüneisen参数表达形式，从理论上计算得到了超高速碰撞条件下铝弹撞击铝靶使其发生冲击熔化和卸载熔化所对应的临界速度，并且指出有必要研究适合于超高速碰撞条件下的物态方程和所涉及的物性参数。裴晓阳等[37]重点围绕多介质数值计算方法和固-液-气多相完全物态方程构建开展研究工作，给出了不同速度下碎片云的相分布特点和演化趋势。李宝宝[38]研究了超高速碰撞中相变效应产生的影响，在自编光滑粒子流体动力学（Smooth Particle Hydrodynamics，SPH）程序中引入GRAY三相物态方程，对超高速碰撞问题进行数值模拟研究，并与常用的Tillotson物态方程进行对比分析，探讨了Whipple防护结构的防护性能问题，分析表明材料的相变效应和热软化效应对于防护结构的防护性能影响较大。北京理工大学爆炸科学与技术国家重点实验的张庆明、唐恩凌等[39–42]构建了扫描Langmuir探针等离子体特征参量诊断的实验系统，自行设计螺旋形线圈建立磁场测量系统，用二级轻气炮加载技术进行超高速碰撞实验，测量了实验中空间某个位置处产生等离子体电导率、电子温度和密度以及电磁场等特征参量，证实超高速碰撞产生的磁场对通信电路产生了明显的干扰。宋卫东、栗建桥等[43–46]采用理论分析和数值模拟方法，建立热电离物理模型，给出了热平衡等离子体电离度及等离子体电导率与温度的关系，并利用SPH方法模拟了超高速碰撞产生等离子体的总电荷量，修正了传统的经验公式。

    本文重点关注铝球正撞铝合金单层板和双层板防护结构的问题。在空间碎片的防护问题中，由于航天器发射的有效载荷的限制，防护板厚不可能太大，故涉及的板厚一般属于薄板或中厚板。弹丸撞击薄板可能会形成碎片云，而弹丸撞击中厚板可能会形成层裂[47]，本文主要讨论薄板的情况，涉及的弹丸速度一般大于1 km/s。超高速撞击过程涉及很多物理和力学问题，受篇幅限制，不可能涵盖所有方面。首先，回顾用于超高速碰撞的弹丸发射方法、数值模拟方法和模型；其次，重点讨论空间碎片防护结构研究领域较为关注的几个问题，包含防护板的穿孔、碎片云的演化、靶板的破坏和相变等；最后介绍基于实验和数值模拟的超高速弹道极限方程。由于空间碎片防护问题的研究超过半个世纪，产生了大量的文献，本文不求包含所有文献结果，只涉及该方向的主要和最新研究结果。

1.   超高速撞击的弹丸发射实验技术

  • 从20世纪50年代左右起，对超高速撞击开展了大量的实验研究，为超高速撞击的机理认识和工程建模提供了大量数据。目前用于弹丸/飞片超高速发射的主要技术手段有二级/三级轻气炮、金属箔电爆炸（电炮）、磁驱动装置、激光驱动装置等。表1列出了一些发射速度大于8 km/s、发射质量为克/亚克级的典型实验加载方式及相关参数。

    二级轻气炮由压缩级和发射级组成[54]，压缩级由火药或高压气体驱动活塞压缩二级轻质气体（氢气或者氦气），发射级由轻质气体驱动弹丸运动，其发射速度一般在8 km/s以下。虽然理论上二级轻气炮能达到10 km/s以上的发射速度[55]，例如NASA的AMES实验室发射0.94 g弹丸的速度高达9.54 km/s[56–57]，但各实验室通常操作的速度均小于8 km/s，因为在更高的速度下高温高压气体会对设备管壁产生破坏[55]。

    在二级轻气炮基础上改进的三级炮可以实现更高的发射速度。三级炮有各种形式，例如在二级炮后接轨道炮[58]、使用二级轻气炮发射阻抗梯度飞片撞击次级飞片等，本文中三级炮指的是后者。使用阻抗梯度飞片可以实现准等熵加载，与直接冲击加载相比，降低了熵增，使冲击能量更多转化为飞片的动能，从而实现更高速度的发射，同时降低飞片的温升而使其不易熔化。美国Sandia国家实验室的Chhabildas等[59]在三级炮管中将$\varnothing $10 mm×1.0 mm的铝（0.21 g）和钛飞片（0.34 g）分别发射到13.8 km/s和13.4 km/s的高速，并将$\varnothing $6 mm×0.56 mm的钛飞片（0.068 g）驱动到15.8 km/s的高速。国内流体物理研究所采用密度梯度飞片，不仅成功将铝、钛宏观金属飞片发射至10～15 km/s，而且将克级重金属钽飞片发射至10 km/s以上[49]。

    金属箔电爆炸驱动高速飞片技术利用金属箔电爆炸产生的高压气体/等离子体膨胀驱动高速飞片。受限于金属箔的电爆炸过程，其发射飞片为塑料等非导电材料。美国劳伦斯利弗莫尔国家实验室[60]的100 kV电炮装置将10 mm×10 mm×0.3 mm的Kapton膜（约43 mg）发射至18 km/s，而中国工程物理研究院流体物理研究所的98 kJ电炮装置可以将$\varnothing$10 mm×0.2 mm的Kapton圆柱形飞片（约19 mg）驱动至11 km/s。

    磁驱动超高速飞片是近十年发展起来的一种新的飞片驱动技术，其原理是采用脉冲大电流产生的洛伦兹力发射金属飞片。美国Sandia国家实验室的ZR装置将初始尺寸为38 mm×11 mm×0.9 mm的铝飞片驱动至45 km/s的高速；国内流体物理研究所也建立了磁驱动装置，如CQ-4、PTS（见表1）。

    激光驱动高速飞片技术适用于亚毫米量级尺寸的飞片发射，其原理是通过激光烧蚀飞片后部镀的金属膜产生等离子体推动飞片高速发射。我国北京卫星环境工程研究所详细研究了激光驱动微型高速飞片的发射参数[61]，实现了8.4 km/s的$\varnothing $1 mm×0.007 mm铝飞片发射，$\varnothing $1 mm×0.003 mm铝飞片达到10.4 km/s的最高速度。

    虽然近年来实验发射技术取得了较大进展，但实验发射能力仍然有一定局限性，例如对弹丸形状和质量的限制：磁驱动和电炮往往只适用于飞片的发射；ISCL技术适用于中空柱形弹丸；三级炮在超高速发射球形弹丸时，如何防止弹丸变形和破碎也是难点。由于当前发射能力的限制，对超高速研究常采用缩比结构，但由于率相关效应、非尺度化物性参数等因素的存在[62–63]，当采用缩比结构时，物理现象并不与全尺寸结构等价或简单地按比例缩放。为了研究全尺寸防护结构，在高速段（例如大于7 km/s），基于中低速实验验证的数值模拟提供了另外一种研究手段。

2.   超高速撞击的数值模拟方法和模型

    2.1.   数值方法

  • 在超高速碰撞研究中，数值模拟因其花费少、具有可重复性而受到越来越多的关注。弹丸超高速撞击靶板属于典型的可压缩多介质问题，模拟此类问题的方法一般分为Lagrange方法、ALE方法[64–67]、Euler方法[68–70]、无网格方法[71–73]等。由于在薄板超高速撞击过程中会产生物质破碎，如产生大面积的碎片云，基于传统有限元的Lagrange方法和ALE方法并不能很好地胜任，故本文主要介绍Euler方法和无网格方法。

    • 2.1.1.   Euler方法

  • 在Euler方法中，网格固定在空间位置处，不随时间变化。在物质发生变形时，网格不会发生畸变，故适合于大变形问题，特别是流体问题。基于守恒律的Euler方法已经成为流体研究领域的最主流方法，特别是随着WENO[74]、DG[75]等高精度算法的出现，Euler方法在流体研究中得到了大规模应用。

    在超高速撞击过程中，随着弹丸速度增加到一定程度后，弹丸和靶板发生熔化和汽化，此时Euler方法的优势将得到体现。但在这之前，物质的强度不可忽略，而Euler方法在计算物质导数时对流项的离散误差较大[76]。另外，在处理多物质问题时，数学上线性退化的物质界面会受到数值黏性的影响。因此，基于混合物思想（如按各物质体积分数加权计算网格变量）的界面处理方法（又作扩散界面法）会造成界面厚度随时间扩散，导致物质界面的解析度下降，特别是长距离、长时间的输运过程会造成较大的数值误差。最近几年，Euler方法中物质界面扩散的问题受到了大量研究人员的重视。解决该问题基本有两条思路。一条思路是在全Euler框架下阻止数值扩散。如在多相流中反扩散[77]、人工压缩[78–79]等方法对控制界面扩散取得了很好效果。但目前上述方法只在多相流中得到一些应用，在多介质连续介质问题中的应用有待开展。另外，如果摒弃扩散界面法而采用尖锐界面处理方法，例如基于Level-Set的GFM（Ghost Fluid Method）[80]，那么可以完全克服混合物方法的界面扩散问题，但算法的守恒性不能得到满足，并且其算法和程序开发难度相应上升。另外一条思路是通过引入拉氏思想来处理对流项。例如美国有名的CTH[81–82]程序即采用“Lagragian+VOF （Volume of Fluid）+Remmap” （LVR）的方法，由于Lagragian步不存在数值扩散，而Remmap步可以通过VOF在单元内部重构的界面来进行变量从拉氏网格到欧拉网格的映射，从而克服数值扩散，类似的方法在我国北京应用物理与计算数学研究所的MEPH程序[83–84]中得到应用。但需要注意的是，该类方法多基于分裂方法，即每个空间维度的处理均按一维处理。基于LVR的程序在处理率相关材料本构时，仍然面临较大误差。引入拉氏思想还包括后文中要提到的物质点法（Material Point Method，MPM）。跟LVR相比，物质点法不仅可以解决对流项的离散误差，更重要的是可以准确处理率相关本构方程。基于Euler方法的代表性的程序有CTH、CSQIII[85]等。虽然全Euler方法在计算高速撞击时具有一定缺陷，但仍然被国内外较多研究者采用。如Hertel等[86]使用CTH程序在锌球超高速撞击锌薄靶的过程中考虑了材料相变，结果表明碎片云尺度以及碎片云动量的数值结果与实验结果相符。Povarnitsyn等[87]利用流体力学程序数值模拟了材料熔化、汽化等相变现象。

    • 2.1.2.   无网格方法

  • 鉴于有限元方法（Finite Element Method，FEM）在模拟涉及材料剧烈变形、破碎等问题时存在一定的缺陷，从20世纪90年代开始国际计算力学界兴起了无网格方法的研究热潮。无网格方法将求解区域的模型离散成若干个粒子，并借助这些离散点构造近似函数求解具有不同边界条件的偏微分方程或积分方程组，进而得到精确且稳定的数值解。无网格方法（Meshfree Method）种类很多，Chen等[88]的综述中至少提到超过28种无网格方法，常见的方法如SPH[89]、RKPM[90]、MPM[91]、OTM[92]等。无网格方法一般分为两大类：一类是基于偏微分方程（PDE）强形式的配置类方法（Collocation Methods），另一类是基于PDE的弱形式的Galerkin类方法。以下以SPH和MPM为例，简单介绍其基本思想。

    SPH作为无网格方法的典型代表，是无网格方法中发展最早的一种，是由Lucy[93]、Gingold和Monaghan[89]在1977年提出的一种无网格化拉格朗日算法，最先应用于求解三维空间的天体物理学问题。随后Monaghan[94]在SPH方法的研究与应用中进行了大量的工作，并将该方法广泛应用于固体力学和流体力学中。20世纪90年代初，Libersky等[95]率先将材料强度引入SPH方法中，成功模拟了高速碰撞问题。随后国内外学者对SPH方法进行了大量的研究工作，使其理论不断得到发展与完善。跟拉氏有限元相比，SPH更适合处理大变形问题，且更容易推广至小尺度/多尺度计算、非连续介质计算和多维计算[96]；缺点是效率和精度低，稳定性差[97]。SPH的基本原理是通过核函数来近似场函数及其导数。例如，对于场函数f（x），核函数近似<f（x）>为

    式中：$\varOmega $为积分域，W为核函数，h为光滑长度。在W为偶函数的前提下，核函数近似可以达到二阶精度。对核函数近似在粒子上离散后，代入拉格朗日形式连续介质方程即可得到SPH的离散形式，但离散后达不到二阶精度（例如边界效应导致降阶）。近年来，学者们对该方法在核函数的选取、一致性、稳定性等方面进行了大量研究，相关工作可参见Liu的综述[96]。SPH代表性的程序有SOPHIA[98]及商用程序LS-DYNA-SPH、AUTODYN-SPH[99–100]等。目前SPH方法已被广泛应用到天体物理学、爆炸力学、流体力学、冲击动力学等涉及大变形问题的领域且取得了巨大的成功，并被大量研究者应用到高速撞击领域[101–102]。Medina等[103]采用基于SPH算法的MAGI并行程序对冲击诱导的复合材料结构损伤进行了三维模拟。Hiermaier等[104]在SPH方法中引入Tillotson物态方程和Johnson-Cook本构模型，对铝球超高速碰撞不同材料的薄靶进行了数值模拟，各模型得到的孔洞直径、碎片云形状和碎片云速度等结果与实验结果很好地吻合。Groenenboom[105]利用PAM-SHOCK中的SPH求解器对超高速碰撞问题进行了二维和三维数值模拟，给出了弹丸和靶板的密度和速度分布，比较了由不同物态方程得到的动能时程曲线，并研究了光滑长度和物态方程对计算结果的影响。Faraud等[106]采用PAM-SHOCK 3D和AUTODYN 2D中的SPH求解器模拟了碎片超高速碰撞多层防护结构，由两种软件给出的碎片云形状与实验图像吻合得较好。

    MPM方法起源于流体领域的PIC（Particle in Cell）[107]和FLIP（Fluid Implicit Particle）方法[108]。在PIC方法中，控制方程被分裂为不含对流项的拉氏步计算，计算完成后通过物质点在网格间输运模拟对流项，PIC方法中粒子本身只记录位置和质量。而在FLIP方法中，粒子本身还记录动量和能量。Sulsky等[91]在1994年将其核心思想推广至弹塑性固体的计算，物质点本身携带所有物质信息，通过弱形式建立动量方程的离散形式。在MPM中，背景网格上的量由物质点插值得到，并在背景网格上求解动量方程，通过背景网格返回的速度和加速度更新物质点的位置和速度。MPM从欧拉方法继承而来，由于在背景网格进行辅助计算，通常只需要对8个（三维）节点求和，故计算量小于SPH等无网格方法[109]。另外该方法的时间步长取决于背景网格而不是粒子间距，故不会出现很小的时间步长。在MPM中即使不采用接触算法，也不会出现物质间的相互穿透。同有限元方法比，MPM的积分建立在物质点上，而FEM的积分建立在高斯点上，故在精度上MPM低于FEM，但MPM更适合计算大变形问题。MPM在超高速撞击问题中得到了较多应用。黄鹏[110]用MPM对铅弹丸撞击靶板的高速撞击过程开展了数值模拟研究，其质点数量达到了千万量级，碎片云形态同实验吻合较好（见后文对碎片云的讨论）。Liu等[111]通过物质点法模拟单个铝粒子和粒子群以不同速度和角度超高速碰撞铝靶板，分析了粒子流密度、碰撞角度和速度对弹坑形貌的影响，并提出粒子群超高速碰撞靶板形成弹坑的坑深经验公式。

    从不采用网格这个角度看，分子动力学模拟也可看作是对于小尺度计算的无网格方法。近年来在高速撞击的模拟方面，采用分子动力学方法取得了一些进展。如Zhang等[112]利用分子动力学方法对超高速碰撞条件下Al2O3的变形机制进行大规模并行计算，原子数目达到540×106个。Samela等[113]通过分子动力学模拟发现，具有1000～10 000个原子的金弹丸超高速撞击金靶板时，靶板上会出现宏观碰撞中的成坑现象，弹坑体积与宏观经验公式的计算结果基本一致。Anders等[114]利用分子动力学技术对纳米尺度的球形金弹丸撞击密实金靶和多孔金靶进行研究，分析了弹丸动能对靶板损伤特性的影响。巨圆圆等[115]采用分子动力学程序LAMMPS模拟弹丸以10 km/s的速度超高速撞击靶板，获得了超高速碰撞靶板的物理过程及靶板损伤特性。Jaramillo-Botero等[116]利用大规模分子动力学数值模拟了材料的电离现象。

    • 2.1.3.   混合类方法

  • 混合方法一般采用欧拉或者无网格方法与拉格朗日方法耦合，欧拉或无网格方法对变形剧烈区域的模拟较好，而拉格朗日方法对变形小的区域的模拟精度较高。例如可在撞击核心区域采用无网格方法，在边缘区域采用拉氏有限元[97, 117]。又如Groenenboom[105]尝试FEM-SPH耦合建模方法，减少了模型中的SPH粒子数。冯春等[118]提出了一种自适应有限元，根据材料变形程度自动选择有限元或粒子类算法。Johnson等[119–120]提出的混合方法在变形不剧烈时采用高精度的拉氏有限元计算，在变形剧烈时从单元转化为适合破碎的GPA（Generalized Particle Algorithm）方法[121]。Beissel等[76]将混合方法应用到弹丸高速（最高速度6.47 km/s）正碰和斜碰靶板的问题中，结合JC损伤模型，得到了碎片云中相分布和损伤分布，同实验吻合较好。

    • 2.2.   本构模型

  • 在超高速数值模拟研究中多采用Johnson-Cook（JC）模型[122–123]和Steinberg-Guinan（SG）模型[124]。由于两者被广泛应用，故本文不再给出其具体形式。JC模型由应变硬化、应变率硬化和热软化3项相乘组成，但该模型不适用于超高应变率情况，一般认为不超过105 s–1。从Selyutina等[125]的结果看，对铝来说该应变率极限小于104 s–1。在超高速碰撞模拟中，最大应变率可以用下式进行估计[126]

    式中：Vp为弹丸速度，Dp为弹丸直径。在空间碎片防护问题中，弹道极限对应的弹丸直径约为1 mm量级，弹丸速度10 km/s量级，故最大应变率估计为106 s–1量级，显然超过了JC模型的使用范围；但是另一方面，由于JC模型的广泛研究，对应的材料库比较全，因此也有大量工作采用该模型。SG模型同样包含应变硬化项，热软化项通过剪切模量随温度的变化引入；后来加入的应变率效应（SGL模型）[127]使得该模型比JC模型更适合高应变率（如106 s–1量级）情况，然而SGL模型针对大量材料的应变率相关参数依然较为缺乏。在超高速撞击时，固体会流体化，本构模型的影响随撞击速度增加而减弱。哈尔滨工业大学的张伟等[128]使用AUTODYN中的SPH模块对比了不同本构方程（JC、SG、流体模型）在6.71 km/s速度下的表现，发现本构模型对碎片云的径向碰撞、颗粒大小影响不大。但是本研究组在测试中发现，对于弹道极限，防护板本构模型的影响较大。

    • 2.3.   状态方程

  • 对于超高速碰撞问题的理论分析和数值模拟，物质在高温高压下的状态方程研究是一个关键。在这方面，国内外都进行了很多研究。McQueen等[129]对强冲击作用下材料发生的一级相变进行了比较详细的分析。Bjork和Olshaker[130]论述了超高速碰撞作用下材料熔化和汽化的冲击波加热机制，认为超高速碰撞下材料的熔化和汽化是由等熵卸载后保留在材料中的剩余比内能决定的，如果剩余比内能高于材料的熔化比内能，材料就熔化，如果高于材料的气化比内能，材料就气化[131]。Kraus等[132]利用激光加载冲击波，研究了几百吉帕冲击作用下二氧化硅的熔化和汽化，精确测量了二氧化硅的冲击温度。在超高速碰撞过程中熔化和汽化现象很重要。Hornung和Michel[133]通过分光镜技术研究了金属受冲击波作用后蒸气种类总量，并发现汽化度依赖于冲击波熵，这点有可能决定压力大于20 GPa情况下的状态方程。Hornung等[134]在相关方面开展了工作：利用统计力学方法给出了冲击压缩汽化部分的温度，并与理想气体状态方程所描述的温度相比较，发现理想气体状态方程得到的温度远远高于其结果；使用二维Godunov格式进行数值模拟，给出了飞片超高速碰撞平板产生膨胀蒸气云的电离度。Hornung[135]还公布了一项理论成果，可以帮助深入理解超高速碰撞汽化和电离过程，他们使用Godunov方法模拟碰撞，碰撞速度为80 km/s，状态方程采用Thomas-Fermi（TF）模型，给出了从靶板上飞出物中气体和液体的总量，并计算出电离度。Povarnitsyn等[136]发现采用不包含材料相变的状态方程计算得到的碎片最大，采用考虑材料液化和汽化的热力学完全状态方程计算的相态分布较准确，其中考虑亚稳态相态情况的状态方程的计算结果最准确。

    在已发表的弹丸速度低于7 km/s的数值模拟中，多采用Mie-Grüneisen（MG）状态方程，但该方程的缺点是[137]：基于Hugoniot参考状态的MG状态方程不适用于极高压（例如压力高于100 GPa时与实验和SESAME数据库出现差异[138]），也不适用于气体和膨胀状态的液体；当解离和电离发生后，Grüneisen系数不再仅仅是密度的函数。而对于超高速碰撞，能描写相变的状态方程对数值模拟极其重要。下面介绍的状态方程被广泛用于超高速撞击的模拟。

    • 2.3.1.   Tillotson状态方程

  • Tillotson状态方程由Tillotson[139]于1962年提出，它假设Grüneisen系数是密度和内能的函数。在低压缩区，Tillotson状态方程恢复为Hugoniot关系；在高压缩区，渐近于Thomas-Fermi（TF）模型，通过TF方程获得高温高压高密度气体的温度与内能关系是一种很有效的手段，其压力和温度的适用范围很大；在膨胀区，则趋近于低密度的理想气体模型。Tillotson方程在能量低于升华能时，可以处理气-固混合区，但仍然不包含气-液、固-液和固-固共存模型[137]。在处理高压下的大变形及多相态共存问题时，用Tillotson状态方程非常方便，它不但能够描述材料在高压下的冲击压缩问题，而且对于材料的熔化和汽化也能够很好地描述[140]。在高速撞击应用方面，张伟等[128]使用AUTODYN中的SPH模块对比了不同的状态方程（Tillotson、MG）在12 km/s速度撞击下薄板的表现，发现与MG方程相比，使用Tillotson状态方程时碎片云的径向膨胀更大，颗粒更小。

    • 2.3.2.   ANEOS状态方程

  • ANEOS状态方程是由Sandia国家实验室的Thomson等[141]开发的解析形式的状态方程（后制为列表形式作为其他Hydrocode状态方程的输入），采用Helmholtz自由能F（T，$\rho$）的形式，由冷能、热能和电离能量组成。金属冷能部分采用Morse势能曲线描述。热能部分采用连接Deybe固体模型和单原子理想气体的近似关系式[142–143]，Melosh后来把该关系式推广至分子团[142]。ANEOS状态方程能处理固、液、气及其混合物，但其只能利用对冷能的修改来处理单个固-固相变[144]，意味着相变的压力随温度的变化很小，违背真实情况[142]。另外，虽然原始形式的ANEOS状态方程对高压区域的Hugoniot曲线描述较好，但对气-液相变线的描述不够准确；后来Littlefield[143]建议调整冷能曲线中的参数以及改进热能部分的插值函数形式，从而更好地符合实验结果。

    • 2.3.3.   SESAME状态方程

  • SESAME状态数据库[145]是由美国Los Alamos国家实验室的Barnes和Kerley于1971年开发的列表式状态方程数据库。SESAME包含单质、化合物、金属、矿物、高分子材料、混合物和多孔材料等[146]，同ANEOS一样，也采用Helmholtz自由能F$\left( {T, \rho } \right)$的形式，也包含压力P$\left( {T, \rho } \right)$和内能E$\left( {T, \rho } \right)$，某些物质包含汽化、熔化和剪切列表。SESAME覆盖的密度范围为10–6～104 g/cm3，温度高至105 eV。SESAME在不同的热力学区域使用不同的理论模型，并用热力学自洽的方式在不同热力学区域之间进行插值连接。将自由能分为3部分，即

    式中：${\phi_0}\left( \rho \right)$为冷能贡献，${F_{{\rm{ion}}}}\left( {\rho , T} \right)$为热离子贡献（包含离子零点能），${F_{{\rm{el}}}}\left( {\rho , T} \right)$为热电子贡献。不同部分采用的理论有多种不同的形式，例如：对于${F_{{\rm{el}}}}\left( {\rho , T} \right)$采用有限温度Thomas-Fermi-Dirac理论及其他理论[146]；固体晶格振动部分包含Einstein模型、Debye模型、Chart-D模型等，熔化线通过Lindemann熔化定律确定；液体采用Hard-Sphere模型；气体分子振动采用谐振模型，转动采用刚性转子模型等。SESAME也包含其他方法，如分子动力学模拟结果、经验性拟合公式等。在高速撞击应用方面，流体物理研究所的唐蜜等[147]将SESAME库与AUTODYN-SPH结合，研究了15 km/s铝弹丸撞击薄板的相态分布，发现碎片云头部处于气态，中心处于液态，而尾部靠近靶板处为固态。美国Sandia国家实验室的Chhabildas等[148]利用CTH和SESAME数据库对比了用三级炮驱动的钛飞片以6.5～11.2 km/s速度撞击铝靶的实验，碎片云后面的接收板的自由面速度模拟结果与实验吻合较好，说明了SESAME数据库的准确性。

    • 2.3.4.   GRAY三相状态方程

  • 传统的GRAY三相状态方程由Royce[149]于1971年提出，该方程建立在Grover[150]的液态状态方程以及Young和Alder[151]的修正范德瓦尔斯方程的基础上，固相采用Grüneisen状态方程，在不同的相区进行衔接。原始的GRAY三相状态方程形式是非完全形式的状态方程，流体物理研究所的于继东等[152]提出了完全形式的基于Helmholtz自由能的GRAY三相状态方程，并给出了Al的相图。在高速撞击应用方面，唐蜜[153]将其与一阶欧拉程序结合，研究了8～17 km/s撞击速度下铝质球形弹丸和飞片撞击产生的碎片云相分布情况。

3.   超高速撞击过程和弹道

    3.1.   前板的破坏

  • 经过Piekutowski多年对铝质球形弹丸撞击薄板穿孔的系统研究[154–155]，已将速度极限提升至9.9 km/s。图1给出了直径为9.53 mm的Al-2017-T4弹丸以6.7 km/s的速度撞击厚度为t的靶板（Al-6061-T6）的孔口形态。当弹丸速度高于5 km/s时，在板两侧均出现“唇口”结构。穿孔特征受无量纲板厚t/D的影响极大，当t/D逐渐增大时，将依次发生以下现象：“唇口”结构增大并翻转，产生孔洞和裂纹；材料从板两侧分离，楔状结构通过板中心的细网结构连接；楔状结构从板分离。孔洞多呈现圆形，但随速度增大而逐渐不规则，其尺寸随着t/D或弹丸速度的增大而增大。该规律同样在Mespoulet等[156]的实验中被发现，只不过Mespoulet的板厚更大，t/D最大约为1.3。

    对孔径的半经验性公式多为以下形式[157–159]

    式中：DH为孔径，Dp为弹丸直径，ρp为弹丸密度，ρt为板密度，C1、C2、p1～p5为拟合参数。例如，对于Hill[157]提出的模型，有：C1=3.309，C2=0，p1=0.022，p2=0.298，p3=0.033，p4=0.359，p5=0。通过遗传算法，Abbas等[160]提出了以下改进形式的模型

    以上方程的各常系数通过遗传算法得到。虽然该模型的精度与Hill模型相当，但该模型满足一些渐进特性，例如当防护板厚度或密度趋于零时，孔直径趋于弹丸直径；而当弹丸速度趋于弹道极限时，孔径趋于零。这意味着该模型的适用范围更广。

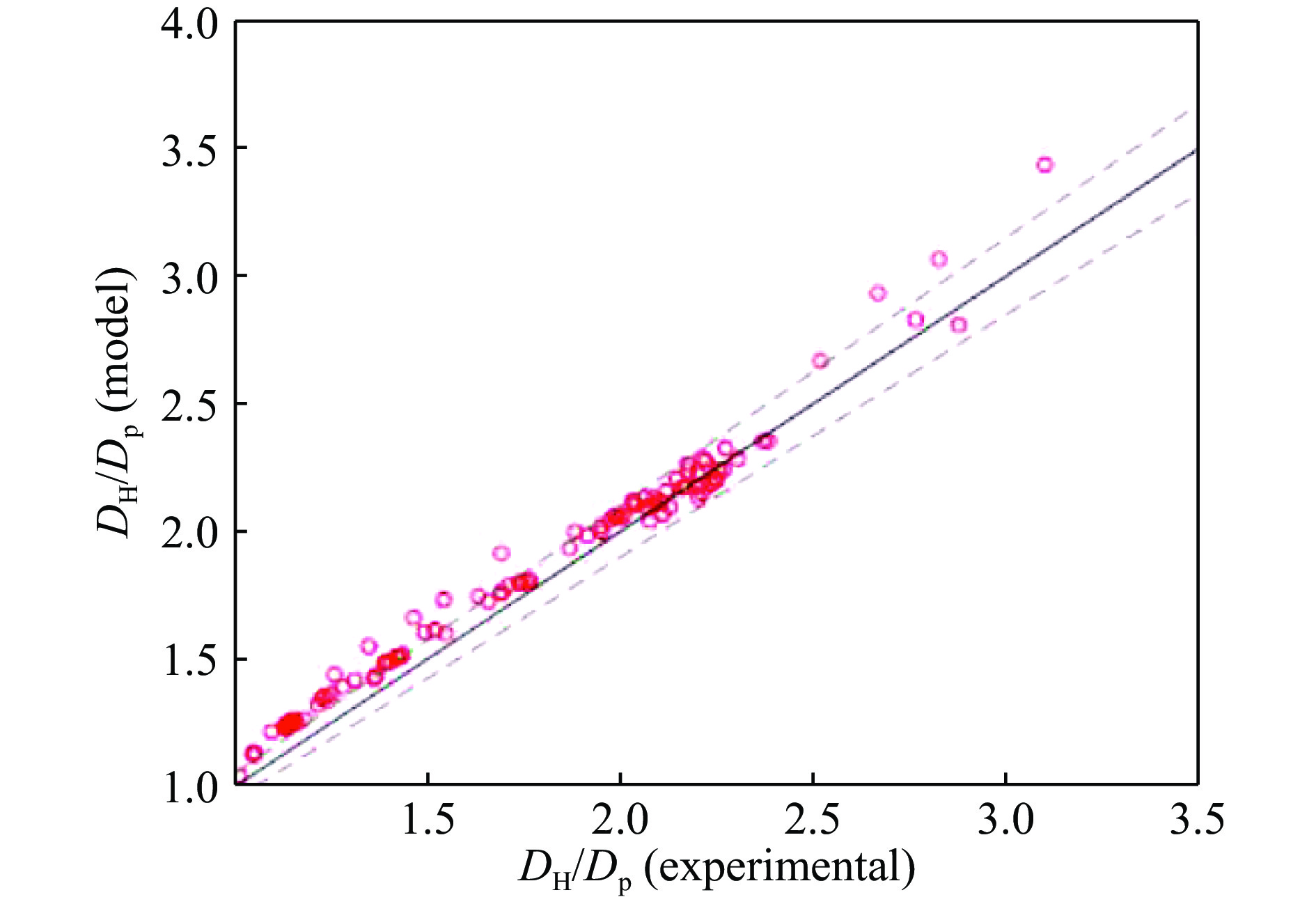
    Piekutowski的实验为孔径的理论研究提供了基础数据。Rosenberg等[161]在Euler数值模拟的基础上，考虑到无限板厚的孔径关系，给出了半经验性的最终孔径表达式

    式中：Q为无限板厚的无量纲孔径；t为板厚；$\sigma$为板强度；$\alpha$为基于数值模拟的经验性常数，这里取1。该模型在板厚趋于无穷小时，孔径等于弹丸直径；而在板厚趋于无穷大时，孔径等于Shinar模型[162]。该表达式同Piekutowski的实验吻合度较好（见图2）；但是对产生汽化的镉的撞击实验误差较大，因为该模型未进一步考虑汽化现象。

    纯理论方面的模型有Jolly模型[163]。Jolly在研究平板撞击侧表面时建立了稀疏波对冲击波卸载的一维理论，当卸载后的压力降到临界压力以下时，孔洞将不再继续扩张。通过特定实验，可以标定该临界压力。同实验的对比表明，该理论模型的预测精度对于99%的数据而言，误差可以达到20%以内（Jolly提到较大的误差可能与实验本身的精度较差有关）。

    • 3.2.   碎片云特性

  • 当弹丸穿过前薄板后，弹丸材料和防护板材料会形成碎片云，本节将介绍碎片云的分布特征、相态和散布模型。

    • 3.2.1.   碎片云的分布特征

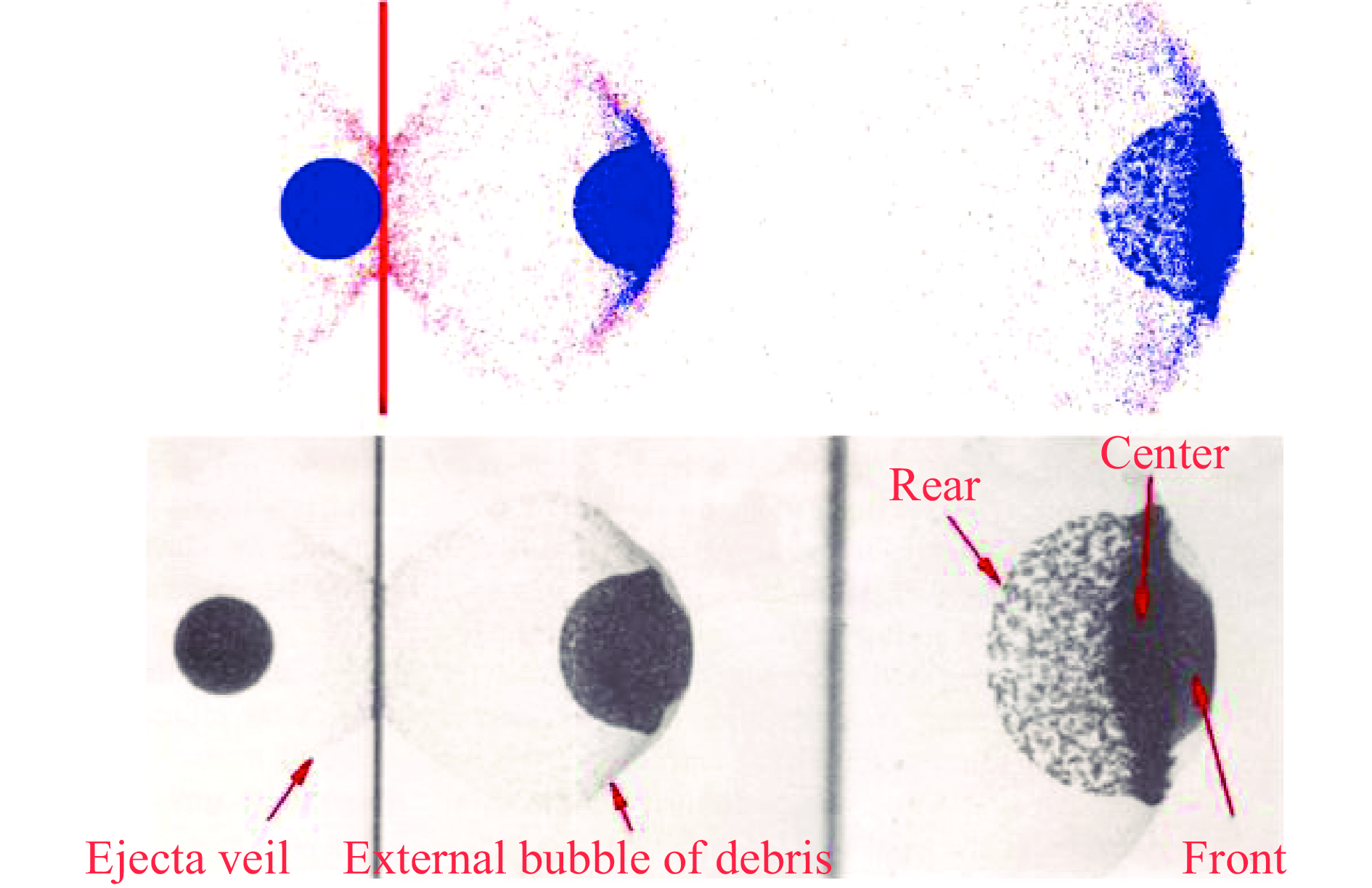
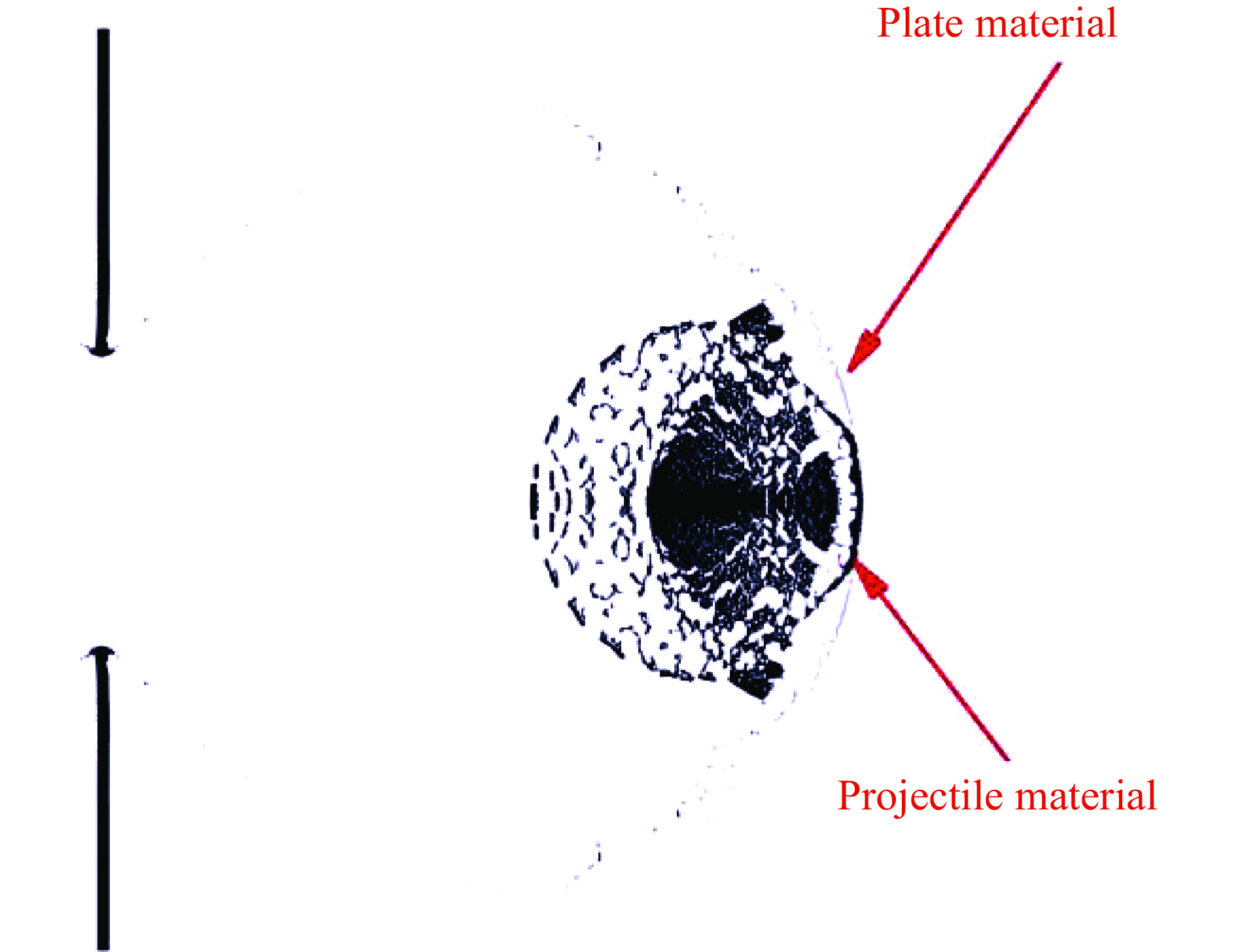
  • 当弹丸穿过薄板破碎后，会形成碎片云。图3中给出了速度v=6.15 km/s的2017-T4铝弹丸撞击6061-T6铝薄靶的碎片云分布，弹丸直径为15.88 mm，靶板厚度为0.772 mm。上半彩图为Beissel等[76]采用有限元-无网格混合方法的计算结果，下半彩图为Piekutowski[62]的实验结果。实验结果显示：前板撞击侧存在喷溅碎片云；穿过靶板的碎片云主要分布在轴线附近，其具体结构可以分为“前部”、“中部”和“尾部”（加起来称为主体碎片云）；也存在向四周扩散的泡状碎片云。喷溅碎片云由靶板物质组成，泡状碎片云也主要由靶板物质组成，而“尾部”半圆状碎片层主要来自于弹丸后半部分的破碎。经过Piekutowski[62]、迟润强等[164]等的实验对照研究，在弹丸速度、弹丸直径和板厚度变化时，碎片云的变化规律已经比较清晰，但碎片云的组成和来源依然需要数值结果进行辅助确认。在主要结构上，数值模拟较好地反映了碎片云的组成和来源。轴线附近碎片云主要结构的模拟结果与实验有一定差别，主要反映在“前部”结构不如实验明显，该现象在采用一阶Euler方法[153]、SPH方法[165]模拟中也存在。产生该差异的原因可能与状态方程和网格解析度相关，因为按照Piekutowski的分析，该部分碎片云由靶板和弹丸物质组成，且在该速度下存在熔化现象。然而模拟中采用的MG状态方程不能很好地刻画相变。值得一提的是，基于LS-DYNA SPH模块的模拟[99]却很好地捕捉了该结构。我们采用二阶Euler方法结合SESAME状态方程的模拟结果见图4，结果表明前部的物质来源于弹丸，而且位于弹丸前方的一层靶板物质与实验吻合较好。从图3的数值模拟结果看，“前部”、“中部”和“尾部”结构均为弹丸材料占主导。Beissel简单地通过熔化温度判断“前部”结构的最前端存在熔化现象，而基于Johnson-Cook的损伤破坏模型揭示了“中部”结构存在大块的碎片，这两点均与实验一致，表明数值模拟在模拟中速段时有较高的可信度。

    板厚是影响碎片云分布的一个重要因素。板厚会影响冲击波在板背面的卸载时间，从而影响弹丸中的冲击波强度和作用时间[164]。增加防护板的厚度时，碎片云的变化如图5所示。可以看到：随着板厚增加，碎片云的粒子尺度逐渐减小，“尾部”扩展增大；碎片云“中部”被压缩从而向径向扩展，形态逐渐后弯；而“前部”厚度减小，逐渐变形为圆弧状，并最终消失。值得一提的是，图5中t/D=0.163时的碗状结构为三维图，从Piekutowski[62]后续采用狭缝过滤碎片云得到的准二维平面图可以推断，此时碎片云仍然属于双层结构，即有“前部”的存在。

    弹丸速度是影响碎片云分布的另一个重要因素。弹丸速度决定了冲击波的初始强度，其压力大小直接决定是否发生冲击熔化或冲击汽化。碎片云随弹丸速度增加的变化见图6。当弹丸速度增加时，塑性变形区从弹丸前端逐渐扩展至后端；随着弹丸速度进一步增大，弹丸尾部因冲击波卸载产生破碎，当速度超过5.45 km/s时，形成“前部”，逐渐形成“前部”、“中部”、“尾部”的典型形态；当速度更大时，碎片云的粒子尺度进一步减小。Piekutowski等[63]对更高速度区间（7～10 km/s）进行了研究，其碎片云特征与在中速段发现的规律没有明显的不同，如9.19 km/s时的碎片云仍然具有前部的双层结构。速度更高的实验尚未系统性地开展，特别是针对全尺寸的Whipple结构，这主要是由于实验发射弹丸能力的限制。对于更高速度铝弹丸撞击铝板可以采用低速镉弹丸撞击镉板替代，镉具有低熔点和高密度，可以在二级炮上开展相应的实验。Schmidt等[167]的量纲分析表明，镉弹丸速度乘以3.1即可得到相应铝弹丸撞击铝板的等效结果；不过后来对比镉和铝在实验中的碎片云形态表明，该系数约为2[168]。

    • 3.2.2.   碎片云的相态

  • 当前，理论分析相态多基于从冲击波波后压力开始的等熵卸载过程。当然如果冲击压力足够高，冲击本身也会造成冲击熔化。各研究预测的铝的相变速度和（或）压力见表2，可以看到对于卸载熔化的分析结果较为接近，但对于卸载汽化开始的压力和速度有一定差别。

    很多程序本身即便采用多相完全状态方程，也并不提供相态的判断。根据程序的计算结果判断相态一般有两种方法[174]：一种称为压力法，即通过冲击波到达的最高压力判断，因为从该高压等熵卸载可能导致相变；另一种通过卸载后的温度判断，称为温度法。研究表明压力法不适用于相对低速碰撞（如5 km/s），此时材料强度比较重要，卸载过程也非完全等熵卸载，故采用温度法较为合适。Povarnitsyn等[175]给出了Al在温度-密度空间内的完全相图，除了稳定相外，还包含亚稳相，也可以直接与其对比，从而进行相态的判断。

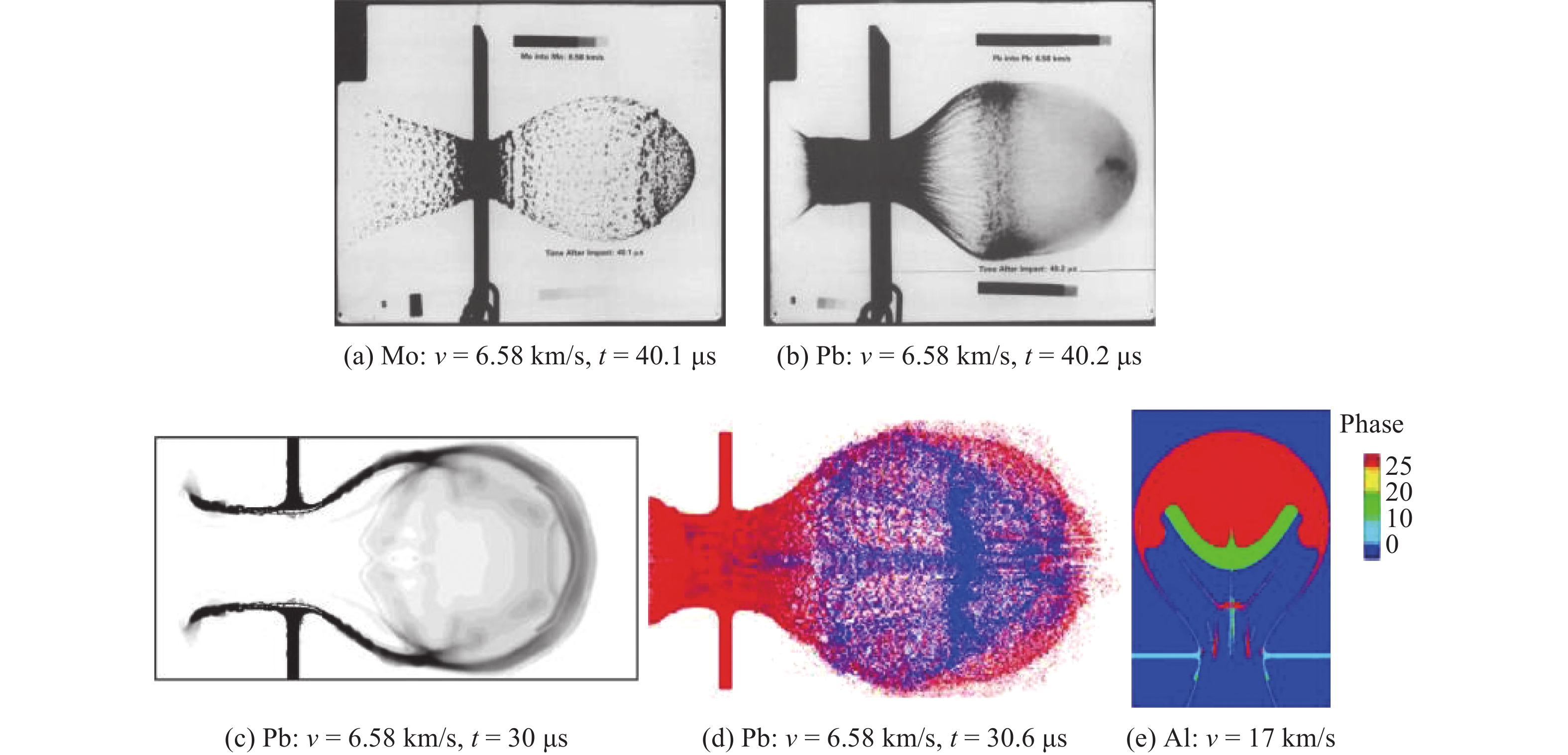
    由于铝的汽化需要较高的撞击速度，如产生30%汽化时需要弹丸速度超过10 km/s[166, 171]，故人们往往采用低熔点、低汽化温度的材料替代研究状态方程的影响，例如Pb。Bjork[171]对比了高熔点的Mo（密度10.2 g/cm3）和低熔点的Pb（密度11.3 g/cm3）弹丸以6.58 km/s速度分别撞击Mo和Pb靶板的实验结果，发现两者碎片云的组成完全不同，其结果见图7（a）和图7（b）。由于Mo和Pb的密度相近，几何参数和撞击速度一致，故其差异主要来自材料的状态方程。可以看到，对于Mo碎片云，碎片云由细小固体颗粒组成。虽然Anderson等[170]的理论分析预测Mo在速度为3.45 km/s时就会完全熔化，但实验中在6.58 km/s时仍然以固体颗粒为主；原因是稀疏波的卸载作用导致大量材料未能冲击加载到足够高的压力。理论分析和实验的差异表明以上简单的理论分析具有较大的局限性。对于Pb的碎片云，没有发现固体颗粒的特征，碎片云前半部分呈弥散形态，后半部分的飘带状流动结构暗示为液体状态。Anderson认为该飘带状流动结构来自靶板孔洞颈部材料，由于稀疏波卸载效应导致靶板材料不能达到很高的压力，故呈液态。Povarnitsyn等[136]采用3种状态方程对该实验进行了模拟，其中含亚稳态的状态方程的密度模拟见图7（c），可以看到不论是碎片云形态（如碎片云两侧的凹陷）还是密度对比度（碎片云前端密度小，靠近靶板密度大），实验中发现的特征基本都具备。唐蜜[153]对铝弹丸以17 km/s速度撞击铝靶的欧拉数值模拟基本上反应了类似的相分布（见图7（e）），也印证了以上分析的正确性。

    • 3.2.3.   弹丸形状对碎片云分布的影响

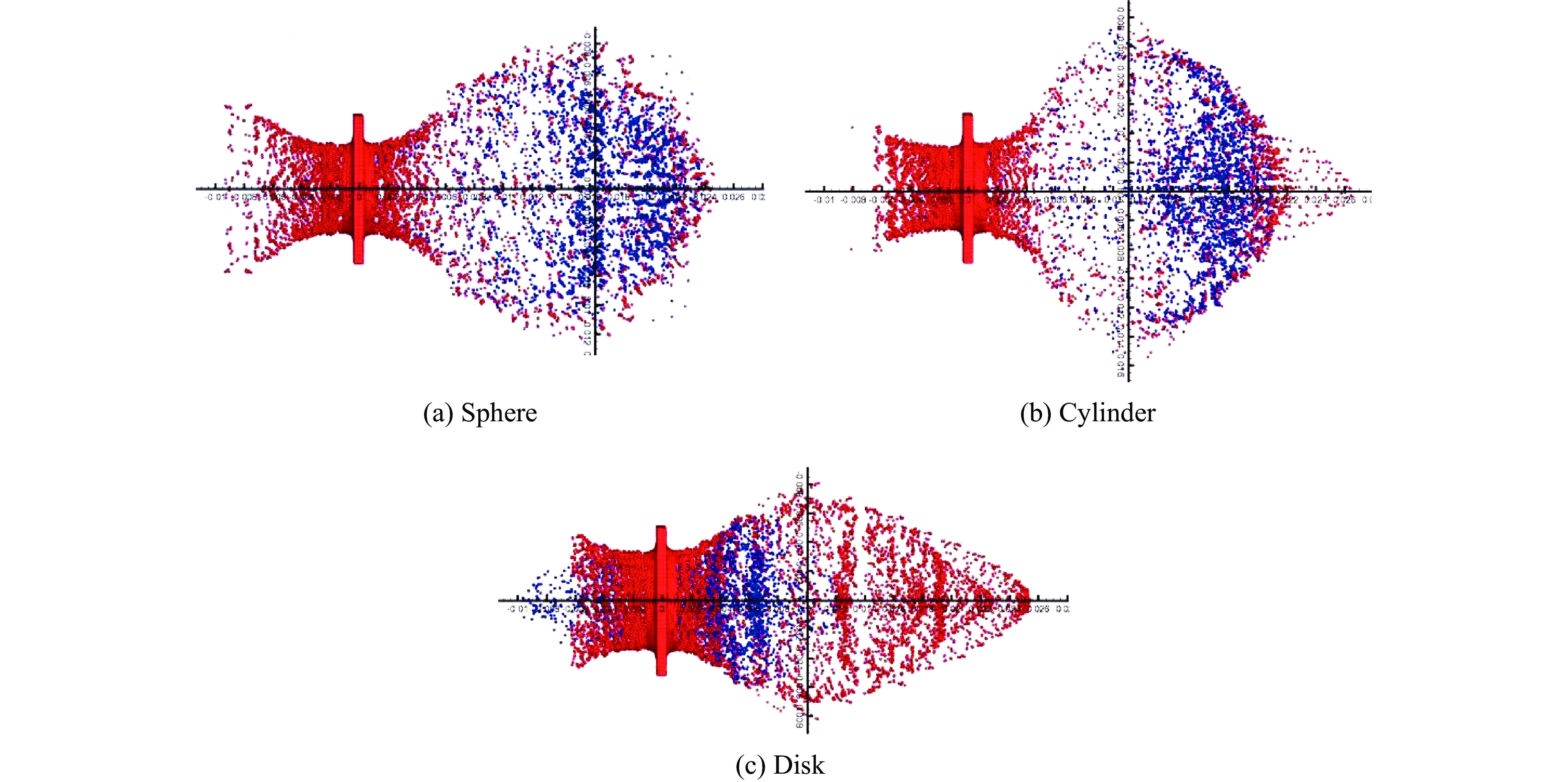
  • 为了得到相同质量、不同形状的弹丸的毁伤能力，宋卫东等采用SPH方法模拟了球形、圆柱形和圆盘形3种弹丸。图8中3种弹丸的质量大致相等，碰撞速度均为18 km/s，碰撞角度为90°，靶板厚度为0.5 mm，球形、圆柱形、圆盘形弹丸的碰撞时刻分别为1.46、1.41、1.46 ${\text{μ}}{\rm{s}}$，得到的碎片云轴向长度和径向长度如表3所示。由碎片云分布及相应数据可以看出：球形弹丸碰撞所形成碎片云的前端呈半球形分布；圆盘形弹丸碰撞所形成碎片云的前端为圆盘形，碎片云分布的轴向膨胀与其他两种弹丸差别不大，但径向膨胀明显更小；圆柱形弹丸所形成碎片云的前端有一锥状突起，弹丸没有完全破碎，弹丸尾部仍部分存在，沿轴向的碎片云膨胀程度略大于其他两种弹丸，但相差不大，而径向碎片云膨胀程度最大。球形和圆柱形弹丸所形成的碎片云都集中在碎片云的前端，圆盘形弹丸所形成的碎片却集中在中间部位，且碎片云破碎情况较好，碎片云内部由弹丸材料和靶板材料的碎片组成孔隙柱；在超高速碰撞条件下，圆柱形弹丸的破坏能力明显强于其他两种弹丸，破坏能力最强。

    • 3.2.4.   超高速碰撞条件对等离子体产生的影响

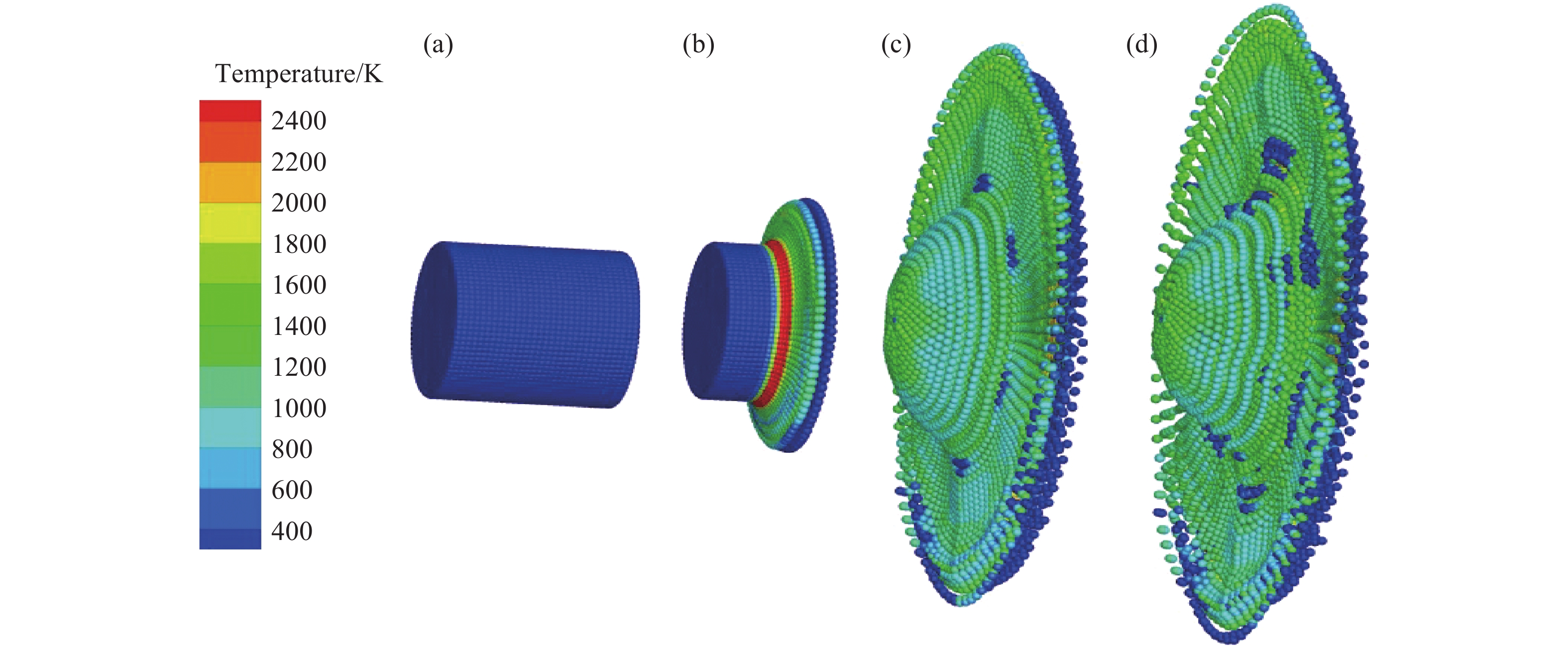
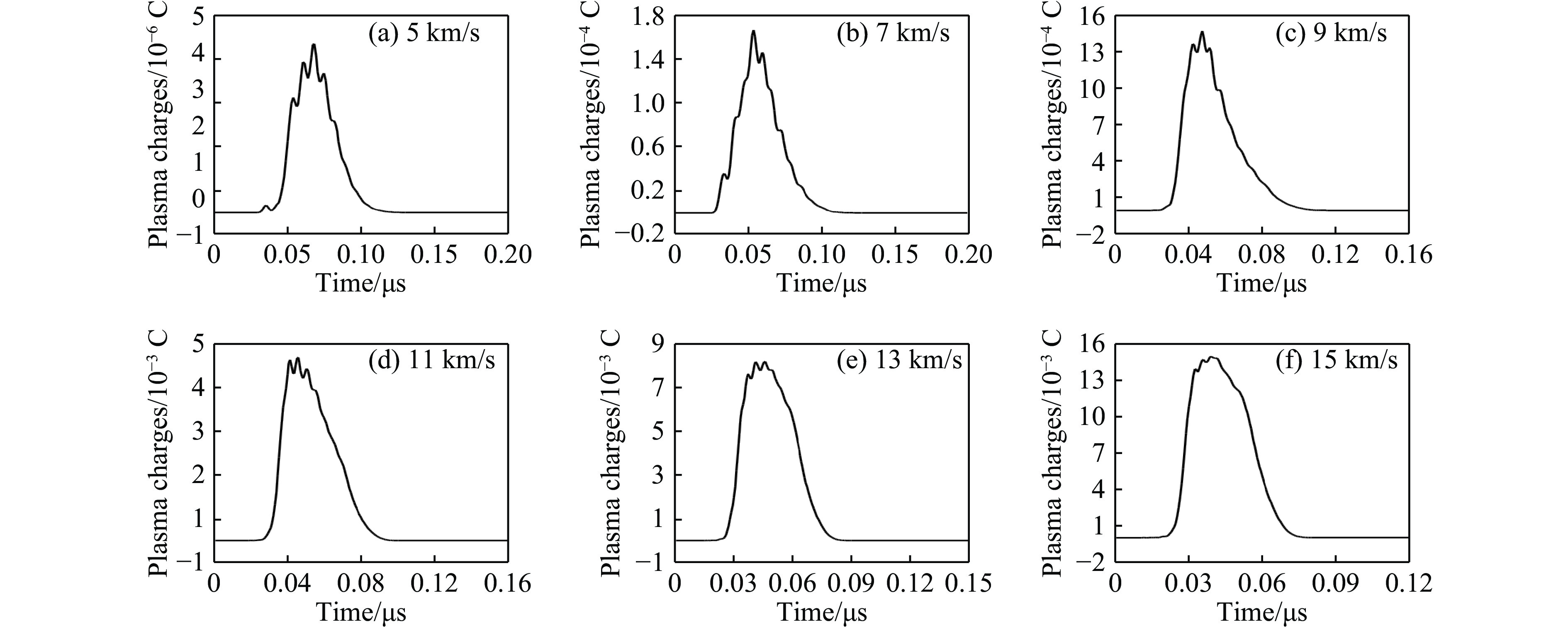
  • 宋卫东等[43, 46]通过数值模拟研究了超高速碰撞产生等离子体的特征。采用三维SPH程序对铝柱体以5、7、9、11、13和15 km/s速度碰撞刚性壁进行数值模拟，铝柱的直径和长度均为1 mm，其中9 km/s的碰撞结果如图9所示。4个时刻共用同一个图例描述，因此图9中红色区域的实际温度远高于2400 K。图10给出了6种不同速度下模拟得到的总电荷随时间的变化。

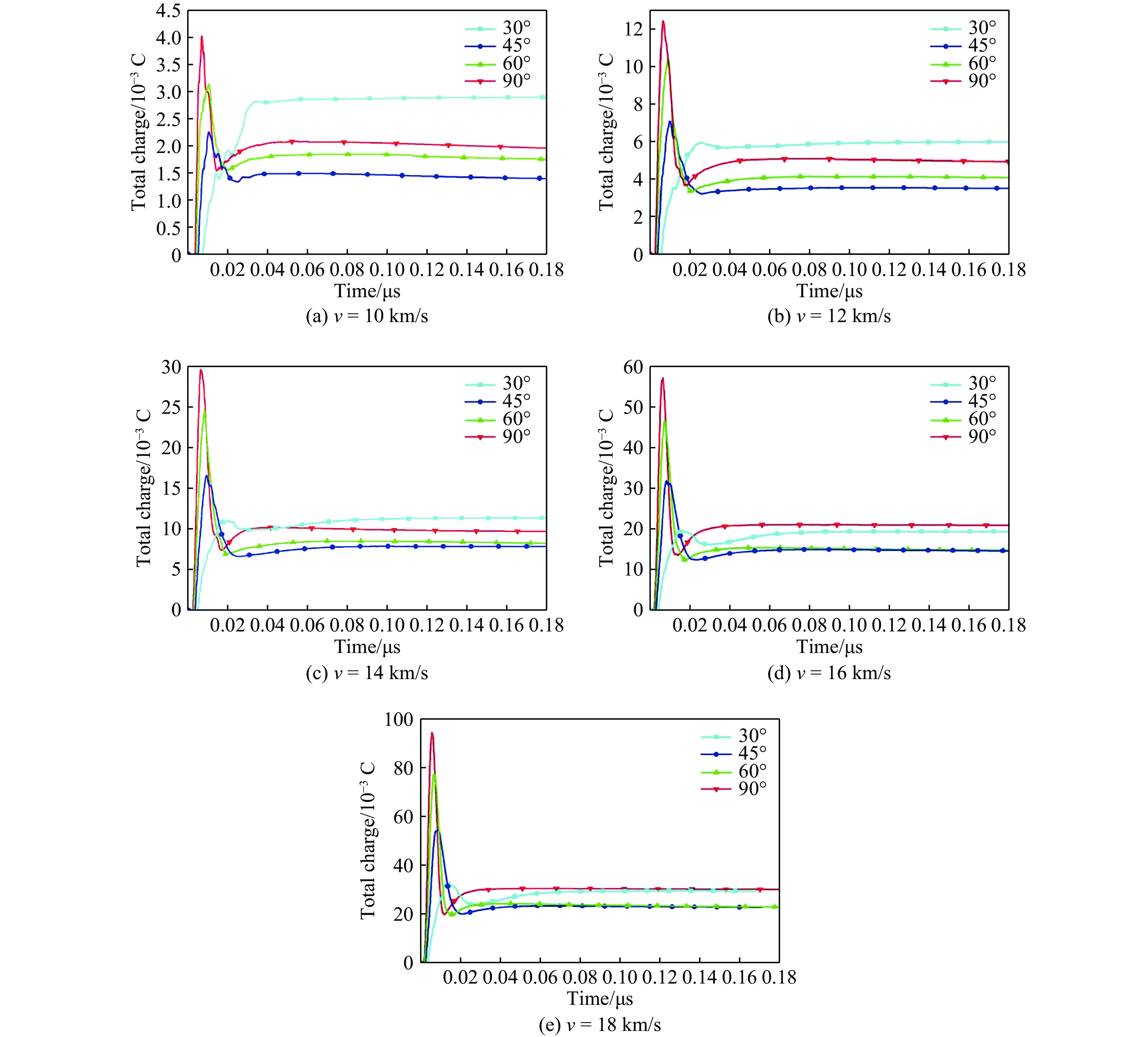
    通过3D SPH程序数值模拟了不同碰撞速度和不同碰撞角度下的超高速碰撞过程，获得了等离子体总电量随时间的变化。相同碰撞速度、不同碰撞角度下超高速碰撞产生的等离子体电量对比如图11所示。在图11中，随着碰撞角度的变化，等离子体电量的峰值变化显著。对于较高速度的碰撞，随着碰撞角度减小，等离子体电量的峰值快速减小。

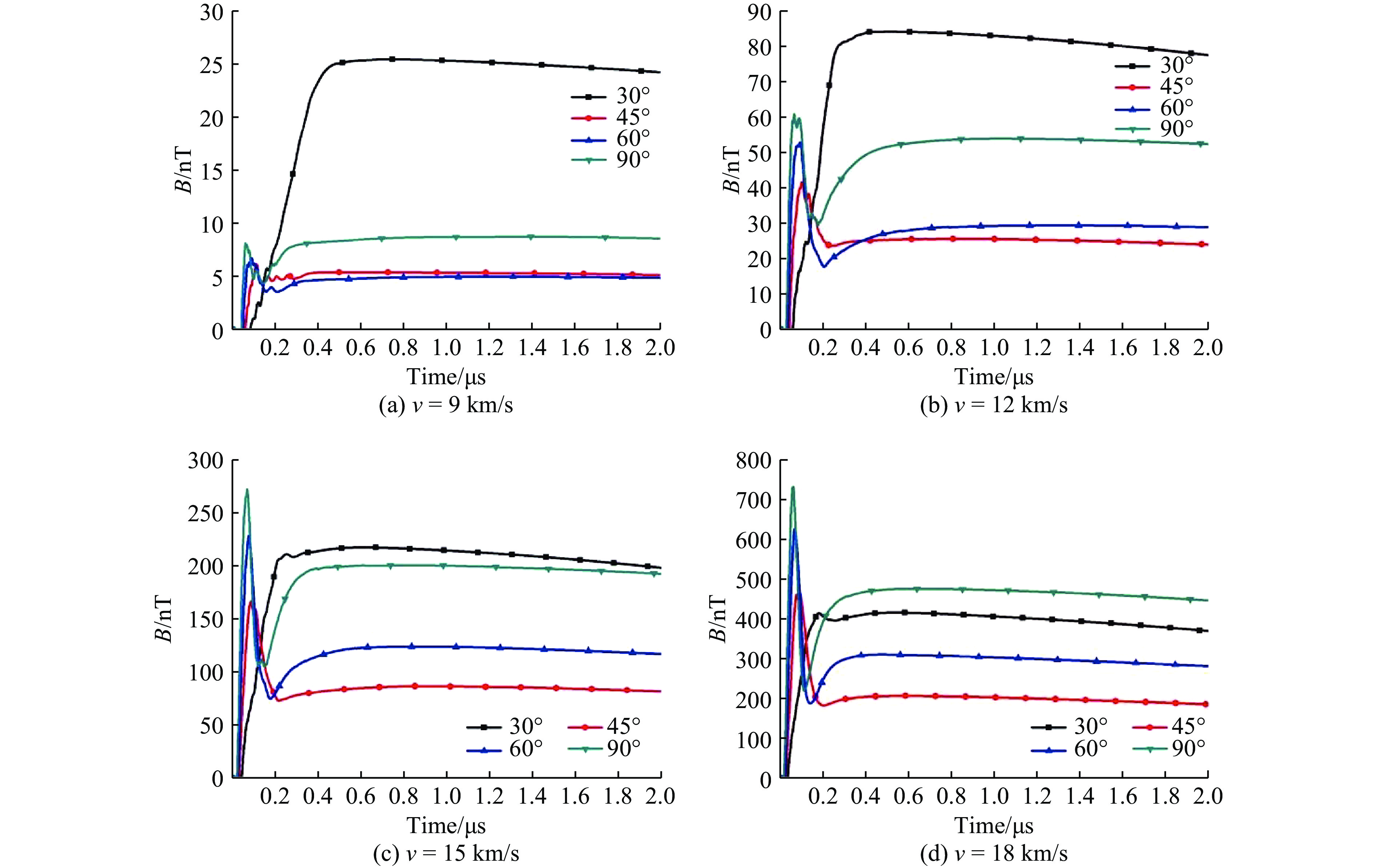
    图12给出了碰撞速度分别为9、12、15和18 km/s时不同碰撞角度下产生等离子体引发的磁感应强度随时间变化的曲线[176]。从图12中得知，碰撞产生的磁感应强度在弹丸与靶板接触后极短的时间内达到峰值，而此时碎片云还未膨胀散开，因此在该时间段内产生的磁感应强度大小差异主要归因于碰撞角度，与观测点所处的空间位置关系不大。

    • 3.2.5.   碎片云的散布理论分析

  • 碎片云的散布直接同Whipple防护结构后板的破坏相关。我国许多科研人员总结了多种碎片云分布模型，例如：龙仁荣和张庆明[177]回顾了Swift（1982）[178]（为方便起鉴，本文中模型命名均采用第一作者加年份的方式）、Piekutowski（1990）[179]和Bless（1991）[180]3种模型，就其在球形弹丸撞击飞片不同工况下的表现与SPH数值模拟进行了对比；郑建东等[181]回顾了Nebolsine（1994）[182]、Schonberg（1997）[183]、Corvvonato（2001）[10]、Schäfer（2006）[126]模型等。为尽量避免重复，以下重点回顾近几年来国内外文献中提出的模型。

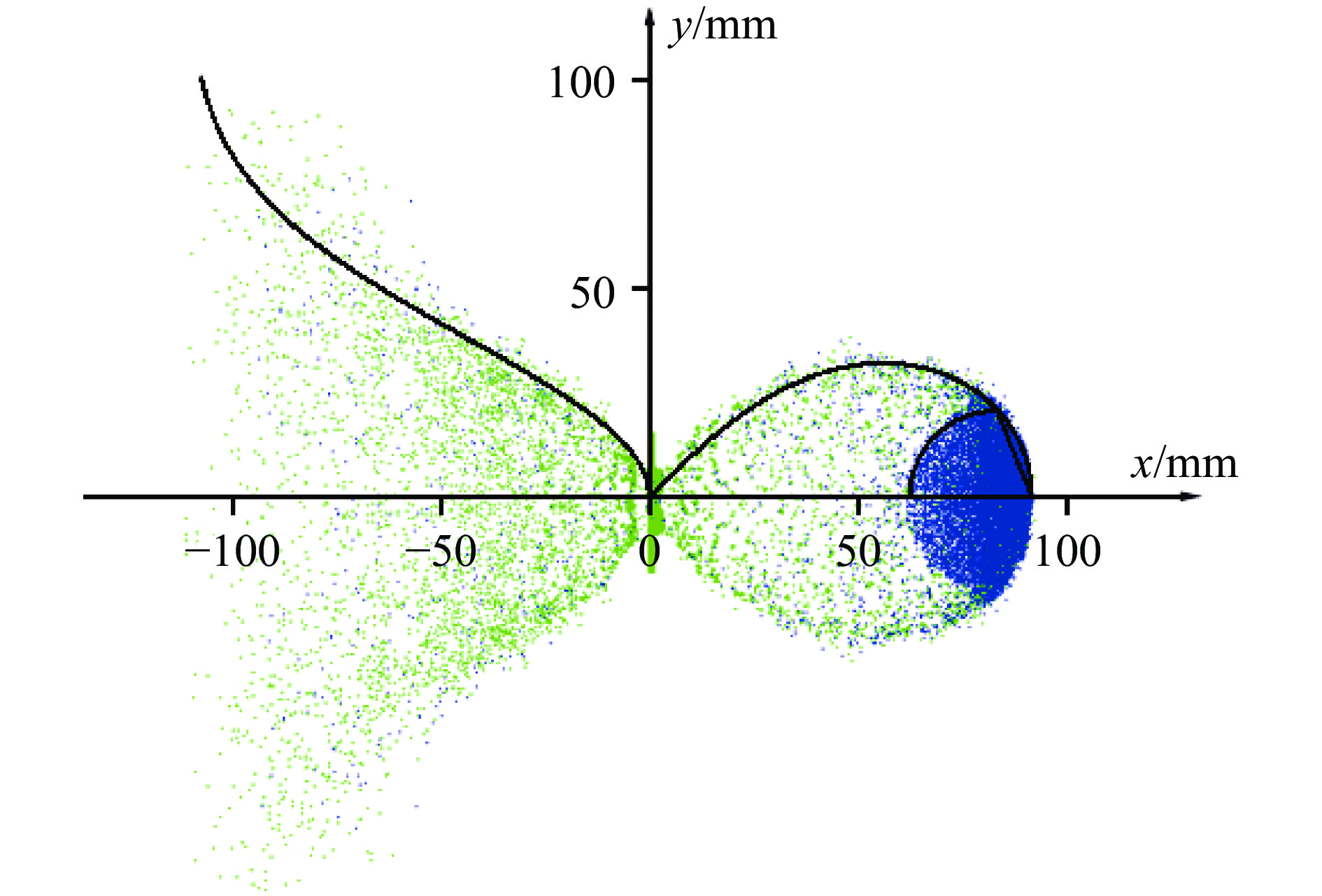
    迟润强[184]通过实验和SPH模拟，对5 km/s以下铝弹丸正撞铝靶的碎片云分布情况进行了系统的建模工作。其基本思路是对碎片云的特征点速度和质量分布进行拟合，数据来源以数值模拟为主、实验为辅。以直线描述主碎片云、圆弧描述剥落碎片云、双纽线描述外泡碎片云、高斯曲线描述反溅碎片云，在假设碎片云自相似演化的基础上，通过质量、动量和能量守恒方程求解以上拟合式中未决定的系数。从该模型与数值模拟的对比来看，它很好地描述了碎片云分布（见图13）。

    在SPH模拟的基础上，Huang（2013）模型[5]首先对碎片云前端的速度进行拟合，然后对碎片云的质量、速度和角度分布函数进行拟合，最后给出了各分布函数的限制关系。在此基础上，通过蒙特卡罗算法进行碎片云的模拟，得到碎片云的分布形态。该方法不仅可以用于正撞击，也可以用于斜撞击。其得到的碎片云质量和数目同SPH数值模拟相比，误差在10%以内。

    • 3.3.   板的损伤和破坏特性

  • Whipple结构的后板破坏特征与碎片云直接相关，由后板破坏特征可以反推碎片云的某些特性，而目前后板破坏特征研究主要通过实验。后板的破坏形式一般包括成坑、产生鼓包、层裂、剥落和穿孔[185]。

    图14（a）、图14（b）给出了弹道区（v=2.58 km/s）和破碎区（v=4.35 km/s）后板的损伤形式，图中还显示了Whipple结构参数以及后板的正面照和背面照。可以看到，在低速弹道区，后板只出现了一个大孔，且孔背面周围有材料剥落。在中速破碎区，后板中心出现穿孔，在该穿孔周围存在一个中心弹坑区和环形弹坑区，同时两者之间还叠加了许多微小弹坑，板背面伴随有鼓包和剥落。迟润强[184]对比了碎片云与后板损伤情况，如图14（c）所示，分析表明中心弹坑和环形弹坑区同主体碎片云相关，而两者之间的微型弹坑同剥落碎片云相关（即图3中的“尾部”碎片云）。

    图15给出了使用0.46倍缩比的Whipple防护结构时，速度更高的铝弹丸碎片云撞击后板产生的损伤情况[186]，其特征与中低速情况有较大差异。例如7.28 km/s和9.29 km/s两种撞击速度下均出现放射状结构，Piekutowski分析其为熔化的小铝液滴从中心往外运动导致的，该放射状特征已被其他研究者印证[187–188]。从7.28 km/s正面图片可以明显看到由弹丸碎片颗粒和防护板碎片构成的圆形界线，而9.29 km/s正面图片显示存在同心圆状纹理。通过显微镜发现在9.29 km/s结果中a、b区存在熔化的铝，而c区不存在。a区结构表明碎片云多次正向撞击；b区弹坑较少，熔化的弹丸、防护板、后板材料的径向外移造成了放射状结构；在c区可见防护板碎片造成的弹坑，并有熔化材料外移的踪迹。9.29 km/s速度以下，熔化的材料会在后板表面凝固，形成倒胡须状结构，而更高速度下熔化材料来不及凝固。在7.28 km/s速度下的背面照可以看到，损伤特征为产生鼓包和裂纹，并产生环状层裂；而在9.29 km/s的背面照中出现了剥落和不完整的环状层裂结构。

    Verma和Dhote[189]使用AUTODYN软件的SPH方法数值模拟了球形不锈钢弹丸超高速撞击薄钢板，二级轻气炮实验结果验证了数值模拟的有效性，提出了无量纲经验公式，估算出弹丸撞击靶板形成的主要碎片的特征。数值模拟与实验结果的对比如图16所示，描述主碎片质量、速度和飞行角度的无量纲经验公式分别为

    式中：M为质量，V为速度，$\theta $为碎片和弹丸的飞行速度与靶板法线的夹角，Dp为弹丸直径，ct为靶板材料声速，Tt为靶板厚度，C1、C2、P1～P3为参数。

    • 3.4.   弹道极限方程

  • 弹道极限方程一般表述为弹丸造成最后一层防护板失效的临界弹丸直径与其他参数（弹丸和板参数）的关系。20世纪90年代以前方程形式多为固定弹丸直径，给出临界板厚-弹丸速度的关系（Sizing Equation）；近年来则通常固定防护结构参数，以弹丸穿透的临界直径-弹丸速度图的形式给出弹道极限[190]。这两种形式一般可以相互转化，本文讨论后一种。弹道极限方程（Ballistic Limit Equation，BLE）一般同弹丸密度、速度、直径、强度和靶板厚度及强度等因素相关，已发表文献中各种形式的弹道极限方程不一定包含以上所有提到的参数，因为很多形式是通过实验拟合得到的，只在一定参数范围内适用。一般而言，弹道极限方程均基于铝球撞击铝板进行描述，因为空间碎片多为人造航天器产生，而人造航天器以铝合金材料为主。有关失效的定义也很多，例如后板发生剥落、发生光学穿孔、气体穿透、达到无法承受一定压力/压差的状态[187]等。本文采用Christiansen[6]的建议，在后文中如未加特别说明，则临界弹丸直径一般定义为后板发生剥落或穿孔所对应的弹丸直径。由于有关弹道极限的综述很多，例如袁俊刚[191]、闫军[192]、Hayashida[193]等，因此本文只回顾一些基本方程，以及近年来最新提出的模型。考虑到国外的弹道极限方程发展较早，而我国起步较晚，故主要介绍国外的弹道极限方程研究进展。

    • 3.4.1.   单层板弹道极限方程

  • 单层板弹道极限方程一般与板厚tw、弹丸密度${\rho _{\rm{p}}}$、弹丸正碰速度Vn、靶板声速Cw等相关，文献中给出的表达式也可能含靶板强度或Brinell硬度H，对于金属，工程上可近似认为强度与H成正比[194–195]。

    （1）Fish-Summers（1965）模型[187, 196–197]

    Fish-Summers（1965）模型是基于弹丸速度低于8.5 km/s的实验的经验公式，球形弹丸的临界直径dc为

    式中：tw为板厚（cm）；${\rho _{\rm{p}}}$为弹丸密度（g/cm3）；Vn为弹丸正碰速度（km/s）；K1为材料相关的拟合系数，部分材料如铝合金和不锈钢见文献[197]，对于铝K1=0.57。（13）式已经将原文献给出的临界板厚换算成弹丸临界直径的形式。这里“临界”的定义是靶板达到无法承受超过105 Pa压力差的状态，否则会发生气体泄露[187]。实验表明该模型不适用于超薄板（如0.01 mm量级）[197]。根据Coronado等[198]的建议当采用剥落判据时，K2=0.7，否则K2=1。

    （2）Holsapple-Schmidt（1982）模型[199]

    Holsapple-Schmidt（1982）模型形式为

    式中：${\sigma _{\rm{t}}}$为拉伸破坏强度。当采用剥落判据时，K=0.7，否则K=1。

    （3）JSC（Cour-Palais（1984））模型[200]

    在Appllo计划中，由美国JSC的Cour-Palais开发的经验性模型中，在无限厚板的基础上，通过引入系数修正来预测有限厚度板，临界弹丸直径为

    式中：E为靶板杨氏模量（GPa）。在剥落为临界失效的判据下，K1=3。

    Rockwell模型[201]同JSC模型极为相似，不过两者是独立开发的。Rockwell模型形式为

    （4）修正的JSC（Modified Cour-Palais（1991））模型[6, 202]

    修正的JSC模型的临界弹丸直径为

    当${\rho _{\rm{p}}}< 1.5{\rho _{\rm{t}}}$时，K2=0.5，否则取2/3；K1的取值依据临界条件的定义给出，在本文的临界条件判断方式下K1=2.2，其他条件下的取值见文献[6]。修正 JSC 模型与FS（1965）模型的主要区别在于Vn的指数。

    （5）模型的评估和我国模型的发展

    各种形式的单层板弹道极限方程有一些相同的尺度关系，Lee等[203]通过简单的能量分析认为dc∝（1/Vn）2/3， dc∝tw，对比以上弹道方程的具体形式可以看出其有一定合理性。同时Lee进行了各种模型与SPH模拟的对比，其结论与闫军等[192]获得的结论类似，且各个模型预测的趋势一致，即随着弹丸速度的增加，临界直径单调下降，Schmidt-Holsapple（1982）方程的预测值相对偏高，其他方程的预测值接近。同样Hayashida和Robinson[201]对各模型计算结果与实验数据进行了对比，结果表明对于防护结构设计Schmidt-Holsapple（1982）方程是最安全的，没有一个模型能完全准确地预测所有实验数据，因为这些模型都是根据自己的数据构造的经验性公式。

    可见，针对我国航天器在用单层板建立相应的弹道极限方程具有重要意义。近年来我国学者主要依托数值计算构建单层板的弹道方程。哈尔滨工业大学的贾斌等[204]对我国在用5 mm厚单层板进行了数值模拟，并与JSC模型进行了对比，速度在3 km/s以内时数值模拟和实验得到的弹道极限的相对误差在5%以内，而在1 km/s时JSC模型的误差达41%，为此他们根据自己的数据重新拟合了JSC模型参数，得到的形式为

    另外北京航空航天大学的徐小刚等[205]采用LS-DYNA的SPH模块进行了单层板的弹道极限建模工作，通过改变密度和强度进行了参数研究，结合相似律的无量纲分析，通过线性回归方法得到“综合建模弹道方程”

    式中：${\sigma _{\rm{Y}}}$为靶板屈服强度。与实验的对比表明，综合建模弹道方程优于JSC模型和修正的JSC模型。徐小刚等的工作给出了较为标准的建立单层板弹道极限方程的半理论方法。

    将机器学习应用到基于数据的方程拟合过程也是当前的发展趋势。北京航空航天大学的张晓天等[206]提出了一种基于非线性不可分支持向量机（SVM）方法，利用已发表的实验数据对SVM进行训练，可以对单层板弹道极限方程进行求解。研究表明，SVM方法的精度高于JSC模型。

    • 3.4.2.   双层板弹道极限方程

  • 一般双层板弹道极限方程为三段式，即低速弹道区、中速破碎区、高速熔化区，完整的弹道极限方程应该包含所有速度区间，一般进行分段建模。双层防护结构与单层结构相比，主要对中高速段（高于3 km/s）的防护性能有明显的提升[192]。值得一提的是，更多模型只针对高速段提出，即未进行分段。

    （1）Christiansen（1993）模型[6]

    Christiansen（1993）模型使用较为广泛，也称NNO（New Non-Optimum）模型，其中Non-Optimum表示弹丸和防护板并未完全熔化或者汽化。当Vn≤3 km/s时，弹丸保持未破碎状态，临界直径随弹丸速度的增加而增加

    式中：tb为防护板厚度（cm），$\theta$为撞击角度，V为撞击速度。当正撞速度Vn>3 km/s时，弹丸发生破碎，在3≤Vn≤7 km/s速度区间

    式中：S为板间距（cm）。该表达式为Vn<3 km/s区间和Vn>7 km/s区间的线性插值。

    对于高速段，即Vn>7 km/s区间，Christiansen根据高速撞击实验数据对Cour-Palais（1969）[207]方程进行修正，提出的临界直径为

    （22）式与Cour-Palais（1969）模型相比，Christiansen发现其对失效实验的预测精度提高了35%，但对非失效实验的预测精度降低。上述模型中高速段默认前板厚度足够大使得弹丸完全破坏[208]，与tb无关。这限制了该弹道极限方程的适用范围，即只能应用于前板厚度比0.20dp～0.25dp（弹丸直径）（S/dp>30时取0.20，否则取0.25）大的情况。

    Christiansen（1993）模型为后来许多模型提供了参考。张晓天等[206]从单层板弹道极限出发，基于实验并参考Christiansen（1993）模型构造了高速段弹道方程，提高了对实验的预测精度。另外Christiansen[209]在2001年对该三段式方程做了细微调整（Christiansen（2001）），以适应更广泛的参数空间，限于篇幅原因不再介绍其具体形式。

    （2）Reimerdes（2006）模型[208]

    Reimerdes等[208]对Christiansen的三段式弹道方程做了修正。在低速段，Reimerdes利用球形弹丸撞击有限厚度前板的临界板厚与半无限板的关系，以及相同弹丸和撞击速度下Whipple防护结构与半无限板的贯穿深度一致的结论，得到低速段的表达式为

    式中：对于本文的临界判据k=2.2，对于铝质弹丸K∞=0.42。Christiansen（1993）模型中的低速段临界速度VnL（弹丸破碎）是固定值，而该模型中VnL是通过对实验的拟合得到的

    北京航空航天大学的贾光辉等[210]也尝试对临界速度界限进行修正，他们利用遗传算法修正了Christiansen（1993）模型的分区速度极限值和方程系数，提高了该模型的预测精度。

    Reimerdes同样认为Vn=7 km/s是高速段的分界点，为了改进Christiansen（1993）模型中高速段弹丸临界直径与前板厚度无关的缺陷，Reimerdes在Christiansen（1993）模型中增加一个因子$F_2^{* - 2/3}$，即

    其中

    （tb–dp）crit为最优前板厚度，即使后板不失效且前后板总厚度最小时的前板厚度，Christiansen（1993）模型高速段前板厚度必须比该最优前板厚度大，对铝质弹丸撞击Whipple防护结构，该最优前板厚度约为0.25。比率rS/D为弹丸速度7 km/s条件下，无前板时需要的后板厚度与最优前板厚度下的后板厚度之比。因子$F_2^{* - 2/3}$能够保证在前板厚度趋于零时回归到单层板情况，在趋于最优前板厚度时回到Christiansen（1993）模型。在中速段（VnL≤Vn≤7 km/s），同样采用直线连接低速段和高速段得到。Reimerdes修正模型在7 km/s左右的弹道极限与实验对比优于Christiansen（1993）模型，而在低速段还需要更多实验验证。后来Ryan等[211]提出的JSC（2011）模型在低速段采用Christiansen（1993）模型的方法，在高速段采用Reimerdes（2006）模型的方法，JSC（2011）模型对后板失效的预测精度（80%）被证明比Reimerdes（2006）模型高5%左右[212]。

    （3）ANN（2013）模型[212]

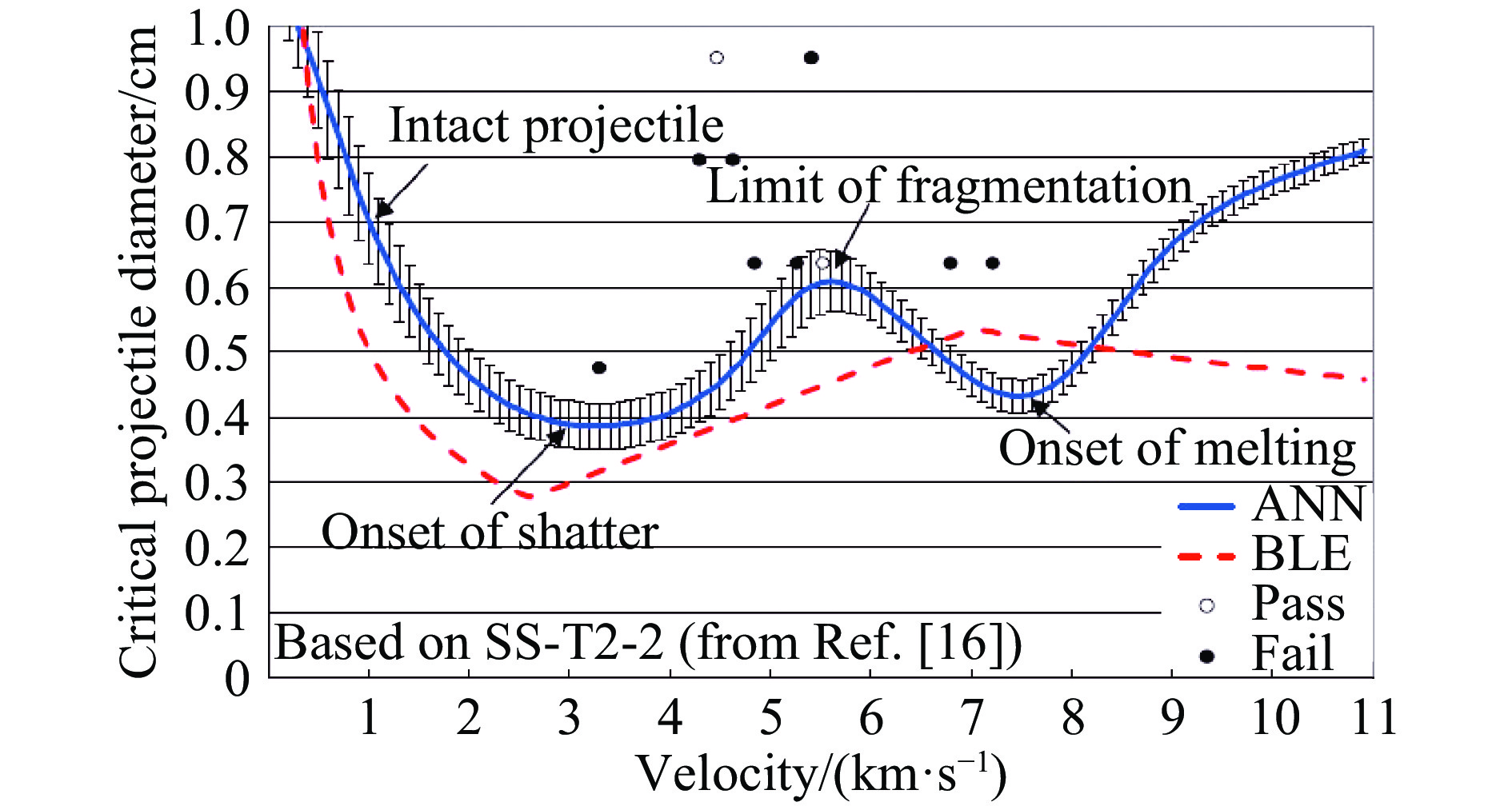
    到目前为止，已发表了大量关于防护结构弹道曲线的实验结果，较为公认的基于经验公式的预测精度在70%左右。为进一步提高预测精度，Ryan等[212]利用文献中发表的大量数据进行了人工神经网络（ANN）训练。该神经网络包含输入层、隐藏层和输出层。输入层为影响结果的参数，包含弹丸、防护板和靶板的热力学等参数（总共57个参数，远远大于目前其他文献中发表的模型）。隐藏层采用14个人工神经单元，输出层为1个布尔节点，即靶板击穿或者不击穿。Ryan发现对比384次后板失效的实验，ANN的预测精度超过95%。ANN的弹道极限优于JSC模型，在开始熔化前，又预测了另外的拐点（见图17）。虽然Ryan并没有给出解析的表达式，但原则上，可以通过ANN得到的加权系数得到最终的弹道极限方程。值得一提的是，虽然建立在大量实验数据上的ANN模型在有实验数据的速度范围内是目前所有模型中精度最高的，但是在超出有实验数据的速度范围后，由于缺乏数据来训练ANN，故其给出的弹道极限曲线的可信度降低。另外，ANN的求解方式掩盖了物理本质。此时，根据物理规律分析得到的纯理论模型或者基于经验的半理论模型的优势大于ANN模型。

    （4）Miller（2015）模型[213]

    基于实验的经验性模型的缺陷使其在外推至更高速度时可能不适用。Miller（2015）模型属于纯理论模型，相较于经验性模型，理论性模型可以更好地揭示内在力学机理，但往往与实验的对比差于经验性模型。Miller（2015）模型建立在前板一维冲击波理论、碎片云的扩展和后板的一维冲击波理论基础上，其临界直径为

    式中：${\bar m_{\rm b}}$、${\bar m_{\rm w}}$分别为前、后板面密度，$\rho _{\rm b}^*$为前板冲击波压缩后的密度，${\omega _{\rm p}}$、${\omega _{\rm b}}$分别为弹丸和前板物质的扩展比，${S_{\rm FP}}$为碎片云飞散距离，${\hat R_{\rm w}}'$为后板阻抗参数，$\hat u'$为碎片云撞击后板相关的速度参数，${\hat R_{\rm w}}'$与$\hat u'$的表达式见文献[213]。Miller（2015）模型同超过1500次的实验数据进行对比后，其预测失效（层裂）的精度为90%，未失效的精度为85%。

    （5）模型的评估和我国模型的发展

    国外基于人工智能的ANN模型和基于理论分析的Miller（2015）模型均达到了较高的预测精度，而我国模型相对来说在精度上仍处于落后阶段，且主要是对三段式弹道方程的修正。袁俊刚等（2008）[214]给出了Whipple结构综合建模过程的详细步骤：分析相关参数；利用量纲理论得到无量纲变量；参考已有弹道方程的形式（多为幂次相关）给出弹道方程形式，其中含大量系数；利用实验和数值模拟提供的数据进行系数确认。该方法提供了从已有实验和数值模拟得到有无量纲理论支撑的弹道极限方程的路径，对比基于人工神经网络等暴力拟合方法，其物理意义更为明确。袁俊刚等建立的三段式类Christiansen方程比Christiansen方程的精度略有提高。另外，郑建东等[215]也对三段式方程进行了改进，与1175发实验数据的对比表明，其新的三段式方程精度达78%，略高于Christiansen（2001）方程的72%。贾光辉等[216]在Reimerdes（2006）方程前面增添因子，并与针对我国航天器防护结构进行的实验进行对比，对我国107发实验的预测率接近90%。

4.   超高速撞击的挑战和展望

  • 本文首先回顾了空间碎片防护过程中实验发射方法、数值模拟方法及数值模拟中采用的本构模型及状态方程。然后针对铝弹丸正撞击单层板和双层板结构的防护问题，基于数值模拟和实验研究，在前板穿孔破坏、碎片云扩展、后板破坏和弹道极限方程方面的进展进行了介绍。总的来说7 km/s以下的实验研究较为充分，但对更高速度的球形弹丸的研究相对缺乏，主要受限于实验发射能力。目前的实验发射方式中很多方法只适用于飞片形式的弹丸，不适用于球形弹丸，从而限制了对球形弹丸超高速撞击靶板的研究。如何在实验发射设备上实现大质量（至少克级）的球形弹丸发射并保持弹丸的初始形状，仍然需要进一步研究。目前对更高速度的球形弹丸的实验研究主要采用缩比结构，但研究结论不能简单地推广到全尺寸防护结构。不过实验为数值模拟程序提供了大量数据，至少可以对程序在中低速弹丸撞击靶板的工况进行验证。

    超高速撞击过程涉及多介质、大变形、相变等复杂的物理过程，目前的数值模拟方法比较适用的是Euler方法和无网格方法。Euler方法经过几十年的发展，国内外均建立了较为成熟的程序。对于Euler方法固有的界面扩散问题，已有大量的解决方法，但当求解率相关本构方程时其较大的计算误差目前还未看到有效的方法予以改善。以SPH为代表的无网格方法正迅速发展，它不存在Euler方法的缺陷，但在算法的精度、稳定性、健壮性、效率等方面仍然存在许多不足。无网格方法具有极大的应用前景，相信未来会成为超高速碰撞模拟的最主流方法。对于计算模拟而言，材料的本构方程和状态方程具有极其重要的地位。超高速碰撞涉及超高应变率，需要建立适用于高应变率的本构方程或针对前人提出的适用于高应变率的本构模型（如SGL模型）进行材料参数的确定，这需要大量细致的实验。在状态方程方面，目前国外已经建立较为齐全的多相状态方程库，如SESAME，涵盖多种常用物质，但我国尚见系统的数据库发表。因此，建议我国相关单位系统地建立自己的状态方程数据库，并向其他科研单位开放。

    弹丸撞击单层板和双层板的研究涉及多个方面的内容。从前板（或单层薄板）看，存在前板破坏特征和穿孔建模两个关注点。实验结果对穿孔特征已经揭示得较为清楚，可以为数值模拟提供很好的验证数据。而在孔洞建模方面，纯理论公式的误差仍然偏大，需要进一步改进。铝球弹丸正撞击单层薄板板后的碎片云在低速段和中速度段以下（约7 km/s）的分布特征和破碎机理已经比较清晰，弹丸速度和板厚变化对碎片云的影响也已经揭示清楚。在更高速度下，虽然有零星的实验报道，但相关研究还不充分。另外，数值模拟可以对碎片云的相分布进行补充说明，但目前数值模拟并未对所有碎片云分布有精确的刻画。未来在碎片云相态的研究中数值模拟将会发挥重要作用。关于碎片云的散布模型，基于实验拟合的工程模型已经能够较好地刻画碎片云的散布，下阶段是加强理论模型对碎片云散布的预测精度，以从物理角度提升对碎片云散布的认识。碎片云的散布与Whipple防护结构后板的穿孔情况密切相关，而目前在中低速度段的实验已经将后板损伤破坏情况揭示得较为清楚，可以为数值模拟的验证提供较好的数据。

    在弹道极限方程研究方面，对于铝球弹丸正碰情况，虽然国外弹道极限方程较为成熟，但仍然需要建立适用于我国实际使用结构的弹道极限方程。我国学者提出的弹道极限方程大多是对国外模型的修正。鉴于国外新涌现的基于人工神经网络模型取得了极大成功，建议采用ANN模型在具有大量实验数据的中低速段对我国在用防护结构建立相应的弹道极限方程，而在没有实验数据或实验数据极少的高速段，基于数值模拟和理论模型建立纯理论或半理论经验公式的弹道极限方程。当前，对于更复杂的防护结构、非球形弹丸和非正碰的研究不够充分，以上所有研究内容都可以向这些方面扩展。

参考文献 (216)

目录

/

返回文章
返回