高级搜索

Fe-3.24%Si的状态方程和声速的第一性原理计算：地球内核Si元素的约束

,  , 

downloadPDF

上一篇

下一篇

李佩芸, 黄海军, 李艳丽. Fe-3.24%Si的状态方程和声速的第一性原理计算：地球内核Si元素的约束[J]. 高压物理学报, 2019, 33(6): 060101-1. doi: 10.11858/gywlxb.20190781
引用本文: 李佩芸, 黄海军, 李艳丽. Fe-3.24%Si的状态方程和声速的第一性原理计算：地球内核Si元素的约束[J]. 高压物理学报, 2019, 33(6): 060101-1. doi: 10.11858/gywlxb.20190781
shu
Peiyun LI, Haijun HUANG, Yanli LI. First-Principles Calculations of the Equation of State and Sound Velocity of Fe-3.24%Si: Implications for the Composition of Earth’s Inner Core[J]. gaoyawli, 2019, 33(6): 060101-1. doi: 10.11858/gywlxb.20190781
Citation: Peiyun LI, Haijun HUANG, Yanli LI. First-Principles Calculations of the Equation of State and Sound Velocity of Fe-3.24%Si: Implications for the Composition of Earth’s Inner Core[J]. gaoyawli, 2019, 33(6): 060101-1. doi: 10.11858/gywlxb.20190781
shu

Fe-3.24%Si的状态方程和声速的第一性原理计算：地球内核Si元素的约束

  • 武汉理工大学理学院，湖北 武汉　430070

    • 作者简介: 李佩芸（1994－），女，硕士研究生，主要从事第一性原理计算研究. E-mail：lipeiyun@whut.edu.cn .
    通讯作者: 李艳丽（1977－），女，博士，副教授，主要从事第一性原理研究.E-mail：liyanli128@whut.edu.cn

  • 中图分类号: O521.2

First-Principles Calculations of the Equation of State and Sound Velocity of Fe-3.24%Si: Implications for the Composition of Earth’s Inner Core

  • School of Science, Wuhan University of Technology, Wuhan 430070, China

    • Corresponding author: Yanli LI, liyanli128@whut.edu.cn

  • MSC: O521.2

  • 摘要: 硅（Si）被认为是地球内核的主要轻元素，但其在内地核中的含量仍然存在争议。为了探索内地核中Si的含量，应用第一性原理方法对Fe-3.24%Si（Si的质量分数为3.24%）进行了研究。构造了4种Fe-3.24%Si的超晶胞，研究了不同的晶胞大小和自旋对优化结构的影响。结果表明：在100 GPa以上，自旋对Fe-3.24%Si的密度无影响；而在100 GPa以下，考虑自旋时的计算结果更接近实验值。基于0 K下的声速、状态方程和相关热力学参数，计算了Fe-3.24%Si在内地核条件下的密度和声速。研究发现：Fe-3.24%Si的密度低于纯铁的密度，略高于内地核的密度；纵波声速及剪切波声速与纯铁的声速很接近，但均明显高于内地核声速，因此排除了内地核含有大量Si元素的可能性。
    Abstract: Silicon (Si) is considered as one major light element in Earth’s inner core, but its content is still controversy. In order to constrain its content in the inner core, using first-principles calculation method, we constructed four different supercells of Fe-3.24%Si and investigated the effects of cell size and spin on geometry optimization. It is found that the spin doesn’t affect the equation of state of Fe-3.24%Si above 100 GPa, and below 100 GPa, the calculated results with the spin are closer to the experimental data. Based on the equation of state, the sound velocity at 0 K and the corresponding thermodynamic parameters, the density and sound velocity of Fe-3.24%Si are obtained under the conditions of the inner core. The density of Fe-3.24%Si is lower than that of pure iron and slightly higher than that of the inner core. The sound velocities of longitudinal wave and shear wave for Fe-3.24%Si are very close to that of pure iron, but both are significantly higher than that of the inner core. Therefore, we could exclude the possibility that Earth’s inner core contains a large amount of Si.
  • 加载中

  • 图 1  hcp-Fe-3.24%Si的结构

    Figure 1.  Structure of hcp-Fe-3.24%Si

    下载: 全尺寸图片 幻灯片

    图 2  单位体积内的能量e随压力的变化

    Figure 2.  Variation of the energy per unit volume e versus pressure

    下载: 全尺寸图片 幻灯片

    图 3  Fe-3.24%Si的压力随密度的变化

    Figure 3.  Calculated density vs. pressure for Fe-3.24%Si

    下载: 全尺寸图片 幻灯片

    图 4  0 K状态下Fe-3.24%Si的声速与密度的关系

    Figure 4.  Sound velocity of Fe-3.24%Si versus density at 0 K

    下载: 全尺寸图片 幻灯片

    图 5  内地核条件下Fe-3.24%Si的密度、纵波声速vp、体波声速vb和横波声速vs与铁和内地核的数据比较

    Figure 5.  Comparison of the density, longitudinal sound velocity vp, bulk sound velocity vb and shear velocity vs of Fe-3.24%Si with those of Fe and the data of the inner core

    下载: 全尺寸图片 幻灯片
  • [1] RINGWOOD A E. On the chemical evolution and densities of the planets [J]. Geochimica et Cosmochimica Acta, 1959, 15(4): 257–283. doi: 10.1016/0016-7037(59)90062-6
    [2] BIRCH F. Density and composition of mantle and core [J]. Journal of Geophysical Research, 1964, 69(20): 4377–4388. doi: 10.1029/JZ069i020p04377
    [3] TAKAFUJI N, HIROSE K, MITOME M, et al. Solubilities of O and Si in liquid iron in equilibrium with (Mg, Fe)SiO3 perovskite and the light elements in the core [J]. Geophysical Research Letters, 2005, 32(6).
    [4] FISCHER R A, CAMPBELL A J, REAMAN D M, et al. Phase relations in the Fe-FeSi system at high pressures and temperatures [J]. Earth and Planetary Science Letters, 2013, 373: 54–64. doi: 10.1016/j.jpgl.2013.04.035
    [5] FISCHER R A, CAMPBELL A J, CARACAS R, et al. Equations of state in the Fe-FeSi system at high pressures and temperatures [J]. Journal of Geophysical Research: Solid Earth, 2014, 119(4): 2810–2827. doi: 10.1002/2013JB010898
    [6] TATENO S, KUWAYAMA Y, HIROSE K, et al. The structure of Fe-Si alloy in Earth’s inner core [J]. Earth and Planetary Science Letters, 2015, 418: 11–19. doi: 10.1016/j.jpgl.2015.02.008
    [7] OZAWA H, HIROSE K, YONEMITSU K, et al. High-pressure melting experiments on Fe-Si alloys and implications for silicon as a light element in the core [J]. Earth and Planetary Science Letters, 2016, 456: 47–54. doi: 10.1016/j.jpgl.2016.08.042
    [8] KNITTLE E, JEANLOZ R. Earth’s core-mantle boundary: results of experiments at high pressures and temperatures [J]. Science, 1991, 251(5000): 1438–1443. doi: 10.1126/science.251.5000.1438
    [9] DUBROVINSKY L, DUBROVINSKAIA N, LANGENHORST F, et al. Iron-silica interaction at extreme conditions and the electrically conducting layer at the base of Earth’s mantle [J]. Nature, 2003, 422(6927): 58. doi: 10.1038/nature01422
    [10] LIN J F, CAMPBELL A J, HEINZ D L, et al. Static compression of iron-silicon alloys: implications for silicon in the Earth’s core [J]. Journal of Geophysical Research: Solid Earth, 2003, 108(B1).
    [11] ASANUMA H, OHTANI E, SAKAI T, et al. Static compression of Fe0.83Ni0.09Si0.08 alloy to 374 GPa and Fe0.93Si0.07 alloy to 252 GPa: implications for the Earth’s inner core [J]. Earth and Planetary Science Letters, 2011, 310(1/2): 113–118. doi: 10.1016/j.jpgl.2011.06.034
    [12] BADRO J, FIQUET G, GUYOT F, et al. Effect of light elements on the sound velocities in solid iron: implications for the composition of Earth’s core [J]. Earth and Planetary Science Letters, 2007, 254(1/2): 233–238.
    [13] ANTONANGELI D, SIEBERT J, BADRO J, et al. Composition of the Earth’s inner core from high-pressure sound velocity measurements in Fe-Ni-Si alloys [J]. Earth and Planetary Science Letters, 2010, 295(1/2): 292–296.
    [14] MAO Z, LIN J F, LIU J, et al. Sound velocities of Fe and Fe-Si alloy in the Earth’s core [J]. Proceedings of the National Academy of Sciences, 2012, 109(26): 10239–10244. doi: 10.1073/pnas.1207086109
    [15] LIU J, LIN J F, ALATAS A, et al. Seismic parameters of hcp-Fe alloyed with Ni and Si in the Earth’s inner core [J]. Journal of Geophysical Research: Solid Earth, 2016, 121(2): 610–623. doi: 10.1002/2015JB012625
    [16] SAKAIRI T, SAKAMAKI T, OHTANI E, et al. Sound velocity measurements of hcp Fe-Si alloy at high pressure and high temperature by inelastic X-ray scattering [J]. American Mineralogist, 2018, 103(1): 85–90. doi: 10.2138/am-2018-6072
    [17] ANTONANGELI D, MORARD G, PAOLASINI L, et al. Sound velocities and density measurements of solid hcp-Fe and hcp-Fe-Si (9 wt.%) alloy at high pressure: constraints on the Si abundance in the Earth’s inner core [J]. Earth and Planetary Science Letters, 2018, 482: 446–453. doi: 10.1016/j.jpgl.2017.11.043
    [18] TSUCHIYA T, FUJIBUCHI M. Effects of Si on the elastic property of Fe at Earth’s inner core pressures: first principles study [J]. Physics of the Earth and Planetary Interiors, 2009, 174(1): 212–219.
    [19] CÔTÉ A S, VOČADLO L, DOBSON D P, et al. Ab initio lattice dynamics calculations on the combined effect of temperature and silicon on the stability of different iron phases in the Earth’s inner core [J]. Physics of the Earth and Planetary Interiors, 2010, 178(1/2): 2–7.
    [20] MARTORELL B, WOOD I G, BRODHOLT J, et al. The elastic properties of hcp-Fe1− xSi x at Earth’s inner-core conditions [J]. Earth and Planetary Science Letters, 2016, 451: 89–96. doi: 10.1016/j.jpgl.2016.07.018
    [21] HOHENBERG P, KOHN W. Inhomogeneous electron gas [J]. Physical Review, 1964, 136(3B): B864. doi: 10.1103/PhysRev.136.B864
    [22] PERDEW J P. Exchange and correlation in atoms, molecules, and solids: the density functional picture [M]//Electron Correlations and Materials Properties. Boston: Springer, 1999: 287–298.
    [23] GROSS E K U, DREIZLER R M. Density functional theory: an approach to the quantum many-body problem [M]. Berlin: Springer, 1990.
    [24] KOHN W, SHAM L J. Quantum density oscillations in an inhomogeneous electron gas [J]. Physical Review, 1965, 137(6A): A1697. doi: 10.1103/PhysRev.137.A1697
    [25] LANGRETH D C, PERDEW J P. Theory of nonuniform electronic systems. I. analysis of the gradient approximation and a generalization that works [J]. Physical Review B, 1980, 21(12): 5469. doi: 10.1103/PhysRevB.21.5469
    [26] PERDEW J P, CHEVARY J A, VOSKO S H, et al. Atoms, molecules, solids, and surfaces: applications of the generalized gradient approximation for exchange and correlation [J]. Physical Review B, 1992, 46(11): 6671. doi: 10.1103/PhysRevB.46.6671
    [27] SEGALL M D, LINDAN P J D, PROBERT M J, et al. First-principles simulation: ideas, illustrations and the CASTEP code [J]. Journal of Physics: Condensed Matter, 2002, 14(11): 2717. doi: 10.1088/0953-8984/14/11/301
    [28] VOIGT W. The relation between the two elastic moduli of isotropic materials [J]. Annals of Physics (Leipzig), 1889, 33: 573.
    [29] REUSS A. Calculation of the flow limits of mixed crystals on the basis of the plasticity of monocrystals [J]. Zeitschrift für Angewandte Mathematik und Mechanik, 1929, 9: 49–58. doi: 10.1002/zamm.19290090104
    [30] HILL R. The elastic behaviour of a crystalline aggregate [J]. Proceedings of the Physical Society Section A, 1952, 65(5): 349. doi: 10.1088/0370-1298/65/5/307
    [31] WANG C S, KLEIN B M, KRAKAUER H. Theory of magnetic and structural ordering in iron [J]. Physical Review Letters, 1985, 54(16): 1852. doi: 10.1103/PhysRevLett.54.1852
    [32] ASADA T, TERAKURA K. Cohesive properties of iron obtained by use of the generalized gradient approximation [J]. Physical Review B, 1992, 46(20): 13599. doi: 10.1103/PhysRevB.46.13599
    [33] COHEN R E, MUKHERJEE S. Non-collinear magnetism in iron at high pressures [J]. Physics of the Earth and Planetary Interiors, 2004, 143: 445–453.
    [34] BROWN J M, FRITZ J N, HIXSON R S. Hugoniot data for iron [J]. Journal of Applied Physics, 2000, 88(9): 5496–5498. doi: 10.1063/1.1319320
    [35] 冯磊. 高压下温度对Fe-8.6Si声速的影响 [D]. 武汉: 武汉理工大学, 2017: 72–83. FENG L. Effect of temperature on Fe-8.6Si sound velocity at high pressure [D]. Wuhan: Wuhan University of Technology, 2017: 72–83.
    [36] 经福谦. 实验物态方程导引 [M]. 2版. 北京: 科学出版社, 1999: 188–197. JING F Q. Introduction to experimental equation of state [M]. 2nd ed. Beijing: Science Press, 1999: 188–197.
    [37] BROWN J M, MCQUEEN R G. Phase transitions, Grüneisen parameter, and elasticity for shocked iron between 77 GPa and 400 GPa [J]. Journal of Geophysical Research: Solid Earth, 1986, 91(B7): 7485–7494. doi: 10.1029/JB091iB07p07485
    [38] BONESS D A, BROWN J M, MCMAHAN A K. The electronic thermodynamics of iron under Earth core conditions [J]. Physics of the Earth and Planetary Interiors, 1986, 42(4): 227–240. doi: 10.1016/0031-9201(86)90025-7
    [39] FEI Y, MURPHY C, SHIBAZAKI Y, et al. Thermal equation of state of hcp-iron: constraint on the density deficit of Earth’s solid inner core [J]. Geophysical Research Letters, 2016, 43(13): 6837–6843. doi: 10.1002/2016GL069456
    [40] ANDERSON O L. The power balance at the core-mantle boundary [J]. Physics of the Earth and Planetary Interiors, 2002, 131(1): 1–17. doi: 10.1016/S0031-9201(02)00009-2
    [41] BIRCH F. Elasticity and constitution of the Earth’s interior [J]. Journal of Geophysical Research, 1952, 57(2): 227–286. doi: 10.1029/JZ057i002p00227
    [42] HIROSE K, LABROSSE S, HERNLUND J. Composition and state of the core [J]. Annual Review of Earth and Planetary Sciences, 2013, 41: 657–691. doi: 10.1146/annurev-earth-050212-124007
    [43] ZHANG Y, SEKINE T, LIN J F, et al. Shock compression and melting of an Fe-Ni-Si alloy: implications for the temperature profile of the Earth’s core and the heat flux across the core-mantle boundary [J]. Journal of Geophysical Research: Solid Earth, 2018, 123(2): 1314–1327. doi: 10.1002/2017JB014723
    [44] ANTONANGELI D, KOMABAYASHI T, OCCELLI F, et al. Simultaneous sound velocity and density measurements of hcp iron up to 93 GPa and 1100 K: an experimental test of the Birch’s law at high temperature [J]. Earth and Planetary Science Letters, 2012, 331: 210–214.
    [45] ANTONANGELI D, OHTANI E. Sound velocity of hcp-Fe at high pressure: experimental constraints, extrapolations and comparison with seismic models [J]. Progress in Earth and Planetary Science, 2015, 2(1): 3. doi: 10.1186/s40645-015-0034-9
    [46] LIN J F, STURHAHN W, ZHAO J, et al. Sound velocities of hot dense iron: Birch’s law revisited [J]. Science, 2005, 308(5730): 1892–1894. doi: 10.1126/science.1111724
    [47] SAKAMAKI T, OHTANI E, FUKUI H, et al. Constraints on Earth’s inner core composition inferred from measurements of the sound velocity of hcp-iron in extreme conditions [J]. Science Advances, 2016, 2(2): e1500802. doi: 10.1126/sciadv.1500802
    [48] CHEN B, LAI X, LI J, et al. Experimental constraints on the sound velocities of cementite Fe3C to core pressures [J]. Earth and Planetary Science Letters, 2018, 494: 164–171. doi: 10.1016/j.jpgl.2018.05.002
    [49] GAO L, CHEN B, WANG J, et al. Pressure-induced magnetic transition and sound velocities of Fe3C: implications for carbon in the Earth’s inner core [J]. Geophysical Research Letters, 2008, 35(17).
  • 加载中
图( 5)
计量
  • 文章访问数:  3870
  • HTML全文浏览数:  3870
  • PDF下载数:  39
  • 施引文献:  0
出版历程
  • 收稿日期:  2019-05-22
  • 网络出版日期:  2019-12-25
  • 刊出日期:  2019-12-01

Fe-3.24%Si的状态方程和声速的第一性原理计算：地球内核Si元素的约束

    通讯作者: 李艳丽（1977－），女，博士，副教授，主要从事第一性原理研究.E-mail：liyanli128@whut.edu.cn
    作者简介: 李佩芸（1994－），女，硕士研究生，主要从事第一性原理计算研究. E-mail：lipeiyun@whut.edu.cn
  • 武汉理工大学理学院，湖北 武汉　430070
  • 收稿日期:  2019-05-22
  • 网络出版日期:  2019-12-25

摘要: 硅（Si）被认为是地球内核的主要轻元素，但其在内地核中的含量仍然存在争议。为了探索内地核中Si的含量，应用第一性原理方法对Fe-3.24%Si（Si的质量分数为3.24%）进行了研究。构造了4种Fe-3.24%Si的超晶胞，研究了不同的晶胞大小和自旋对优化结构的影响。结果表明：在100 GPa以上，自旋对Fe-3.24%Si的密度无影响；而在100 GPa以下，考虑自旋时的计算结果更接近实验值。基于0 K下的声速、状态方程和相关热力学参数，计算了Fe-3.24%Si在内地核条件下的密度和声速。研究发现：Fe-3.24%Si的密度低于纯铁的密度，略高于内地核的密度；纵波声速及剪切波声速与纯铁的声速很接近，但均明显高于内地核声速，因此排除了内地核含有大量Si元素的可能性。

English Abstract

    全文HTML

  • 基于地球物理、地球化学和冶金学的研究，现已确定地核由铁和少量轻元素组成，如氧（O）、硫（S）、硅（Si）、碳（C）和氢（H）[1]。由于Si在地球中的含量非常高[1-2]，高温高压下在铁中的溶解度也很高[3-7]，并且铁与硅酸盐反应会生成硅铁合金[8-9]，因此Si被认为是地核中的主要轻元素。

    目前，有关Si元素在内地核中的含量（以下如无特别说明，均为质量分数）仍然存在争议。例如：Lin等[10]测量了300 K下Fe-Si体系的状态方程，认为内核中存在约4%的Si；Asanuma等[11]分别测量了hcp-Fe0.93Si0.07在374 GPa和hcp-Fe0.83Ni0.09Si0.08在252 GPa压力下的状态方程，并由此预测内地核中含有3.9%～5.8%的Si；基于实验数据和第一性原理计算结果，Fischer等[5]认为内地核中Si的含量为6%～8%；Tateno等[6]根据实验测量结果推测内核中含有约7%的Si。

    地核中的候选轻元素除了满足密度约束条件外，还应满足声速的约束条件。2007年，Badro等[12]采用非弹性X射线散射技术(Inelastic X-ray Scattering，IXS)对FeSi在78 GPa下的声速进行研究，预测内地核中Si的含量为2.8%。Antonangeli等[13]使用相同的技术对Fe0.89Ni0.04Si0.07在108 GPa下的声速进行研究，认为内地核中Si的含量为1%～2%。2012年，Mao等[14]采用IXS和X射线衍射(X-Ray Diffraction，XRD)技术对hcp-Fe和hcp-Fe0.85Si0.15的声速进行研究，估测内地核中Si的含量为8%。Liu等[15]分别测量了206 GPa以内hcp-Fe和136 GPa以内hcp-Fe86.8Ni8.6Si4.6的声速，认为内地核中Si的含量为2.3%。最近，Sakairi等[16]通过高压实验研究了hcp-Fe0.89Si0.11（Fe-6%Si）的声速，指出内核中存在3%～6%的Si。Antonangeli等[17]测量了300 K下hcp-Fe和hcp-Fe-9%Si在高压下的声速，认为内核的Si不超过(3±2)%。受实验技术的限制，上述声速测量所能达到的温度和压强条件远小于内地核的温压环境，因此在外推过程中不可避免地引入了误差。

    基于密度泛函的第一性原理计算方法将不受上述条件的约束。Tsuchiya等[18]应用第一性原理方法计算了Fe-3.24%Si在0 K时的弹性常数，发现fcc (面心立方）结构和hcp（六方密堆积）结构的密度-速度关系与内地核数据一致。同样，运用第一性原理计算方法，Côté等[19]发现Fe-Si合金的结构与Si的含量有关：当Si的含量小于7%时，Fe-Si合金的结构为hcp结构；当Si的含量超过7%且温度高于4 000 K时，Fe-Si合金为fcc结构。Martorell等[20]计算了360 GPa时不同温度下的声速，认为Si不可能是内地核中的主要轻元素。综上所述，内地核中Si元素的含量还存在较大的争议，需要进一步开展理论和实验研究。

1.   计算方法

  • 本研究采用第一性原理计算方法对Fe-3.24%Si（Si的质量分数为3.24%）的状态方程和声速进行研究。计算中，将密度泛函理论（DFT）[21]的第一性原理计算方法与赝势平面波法相结合，交换关联能（XC）[22-23]采用Perdew-Burke-Ernzerh（PBE）的广义梯度近似（GGA）[24-25]。采用超软赝势（USPP）[26]，其中截断能为380 eV，k点的设定为7×7×4。能量收敛精度为1.0×10–5 eV/atom，原子间作用力的收敛精度为0.03 eV/Å，原子间应力收敛精度为0.05 GPa，原子的最大允许位移为0.001 Å。基于上述参数，计算了0 K时不同压力下hcp-Fe-3.24%Si的密度和弹性常数。

    本研究基于应力和应变的关系获得了弹性常数[27]。根据晶体弹性力学相关理论，应力和应变之间的关系为

    弹性常数矩阵有36个弹性常数。根据晶体的对称性，弹性常数矩阵可以简化为

    设零压p0下的晶体体积为V0。在本工作中，铁硅合金为六角立方结构。Voigt[28]认为体积模量KV和剪切模量GV可表示为

    Reuss[29]提出的体积模量KR和剪切模量GR分别为

    式中：M和C分别表示为

    而Hill[30]认为晶体中应力和应变分布不均匀，其体积模量KH和剪切模量GH应为Voigt和Reuss建议的平均值，即

    在固体中，横波声速vs、纵波声速vp及体波声速vb与体积模量和剪切模量的关系为

    式中：$ \rho$为密度。

2.   结果与讨论

  • 优化了4种不同结构的hcp-Fe-3.24%Si，通过比较能量，得到最接近实际值的结构(II-64-atoms)。基于第一性原理计算的状态方程和声速，计算了内核温压条件下的密度和声速，以此限定内核中Si的含量。

    • 2.1.   几何结构优化

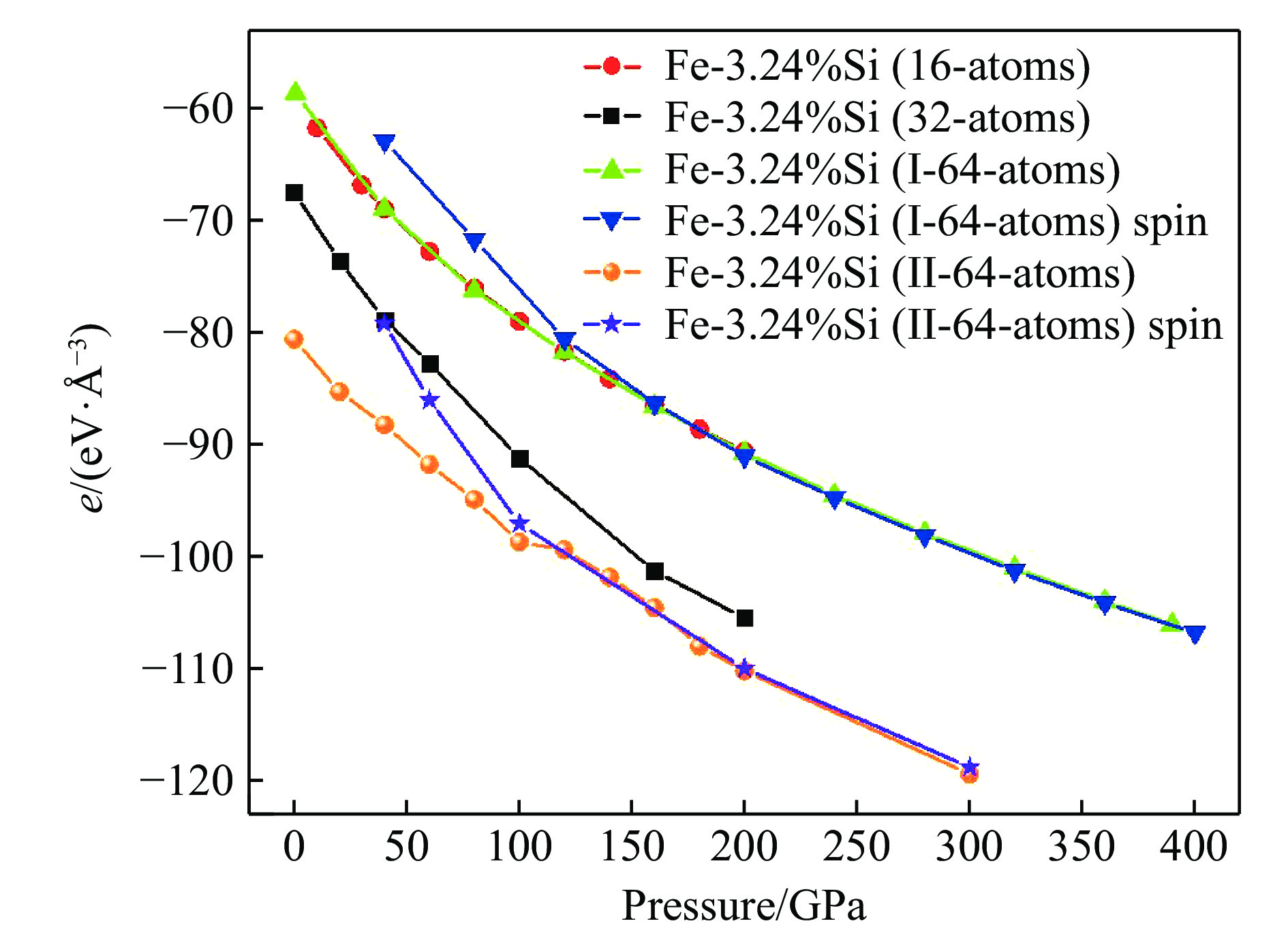
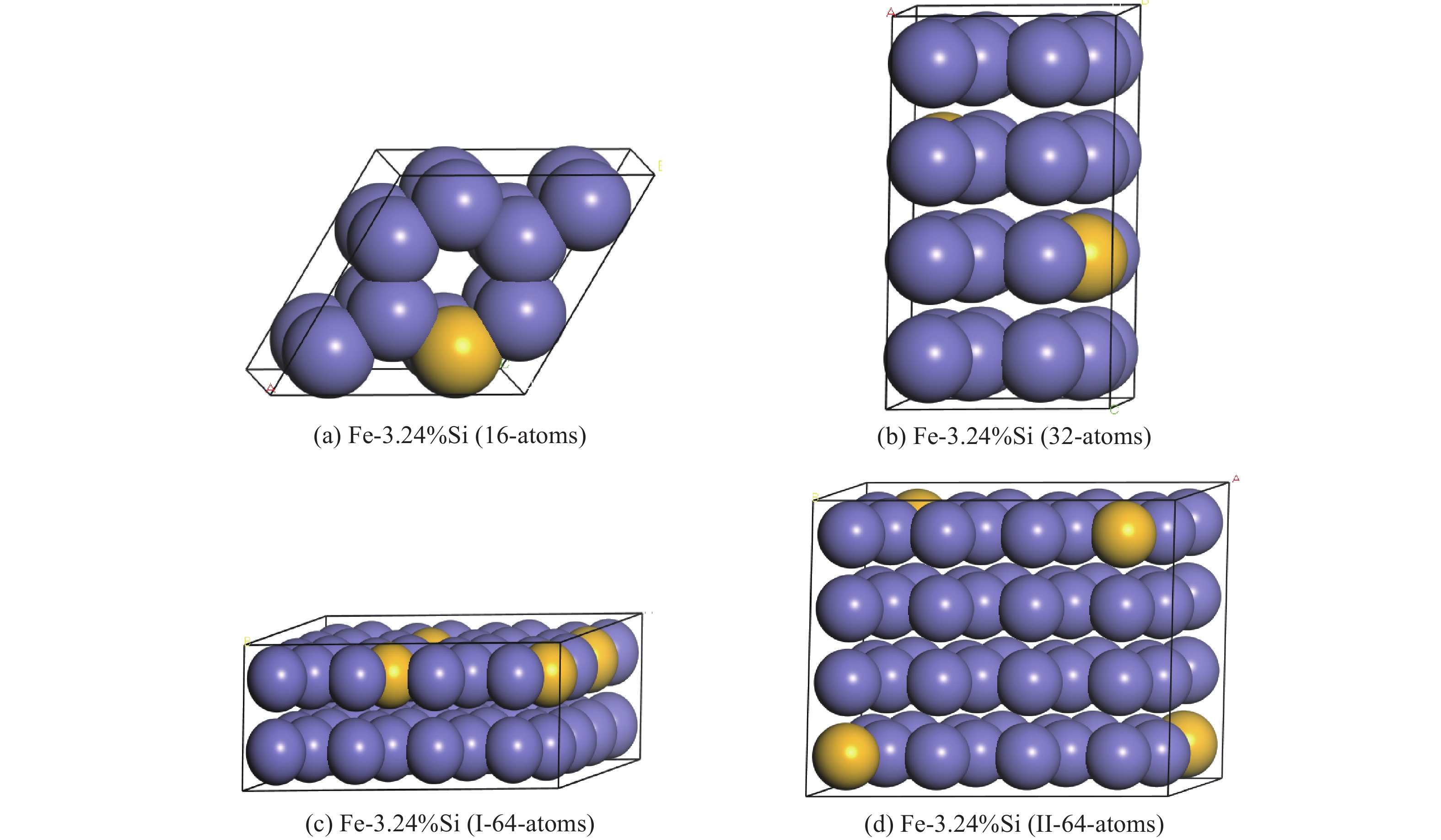
  • 考虑4种不同结构的hcp-Fe-3.24%Si（Fe0.937 5Si0.062 5），即2×2×2（16-atoms）、2×2×4（32-atoms）、4×2×4（I-64-atoms）和4×2×4（II-64-atoms），如图1所示，其中：4×2×4（I-64-atoms）的超晶胞是4个Si原子均匀分散在64个Fe原子内，4×2×4（II-64-atoms）结构是4个Si原子处于64个Fe原子中最分散的位置。这4种Fe-3.24%Si结构均在基态下进行了优化，并考虑了自旋的影响。根据每一单位体积的能量，可以选出最稳定的结构，如图2所示。当压强低于100 GPa时，II-64-atoms具有最低能量；当压强高于100 GPa时，自旋对II-64-atoms结构的能量无影响，因此单位体积内II-64-atoms具有最低的能量，即此结构最稳定。

    • 2.2.   0 K下hcp-Fe-3.24%Si的密度

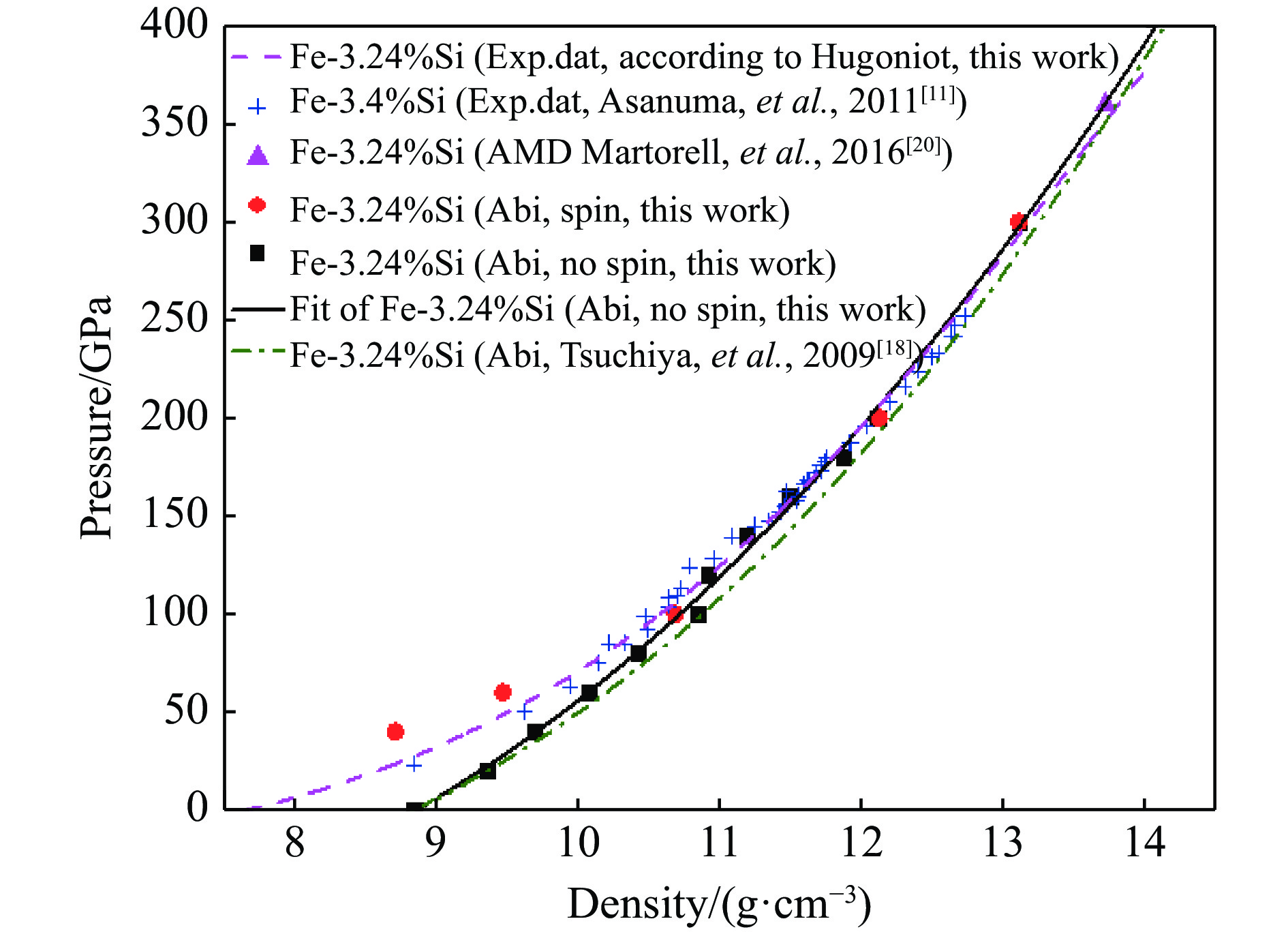
  • 沿0 K等温线，用第一性原理方法计算得到状态方程，如图3所示，其中红色实心圆和黑色实心方块分别代表Fe-3.24%Si有自旋和无自旋计算结果。当压强低于100 GPa时，Fe-3.24%Si有自旋时的密度高于无自旋时的密度，并且更接近实验数据，表明低压时必须考虑电子自旋的影响。其他研究工作[31-33]也表明，当压强低于约60 GPa时，有自旋状态比无自旋状态更稳定。当压强高于100 GPa时，与Asanuma等[11]通过实验测量的Fe-3.4%Si的实验数据一致，并且有无自旋对计算结果无影响。将不考虑自旋的Fe-3.24%Si的计算结果用三阶Birch-Murnaghan状态方程（其中初始密度$ {\rho _0}$=(8.87±0.09) g/cm3）拟合

    得到零压下的体积模量K0=(368±38) GPa，其压力导数为${K'_0}$=3.72±0.31。将计算结果外推至330 GPa，与Martorell等[20]采用第一性原理分子动力学模拟的Fe-3.24%Si结果一致，但却略高于Tsuchiya等[18]用第一性原理计算方法得到的结果。

    图3也给出了根据Hugoniot数据计算的Fe-3.24%Si的300 K状态方程，计算方法如下。Mie-Grüneisen方程表示为

    式中：${p_{\rm{H}}}(V)$为Hugoniot状态方程。

    式中：C0和$ \lambda $为Hugoniot参数。到目前为止，还未见发表Fe-3.24%Si的Hugoniot数据。为此，由纯铁的Hugoniot参数C0=3.935 km/s和$ \lambda $=1.578，纯铁的初始密度$ {\rho _0}$=7.85 g/cm3[34]，以及Fe-9%Si的Hugoniot参数C0=(4.603±0.101) km/s，$ \lambda $=1.505±0.037，Fe-9%Si的初始密度$ {\rho _0}$=7.386 g/cm3[35]，根据可加性原理[36]得到Fe-3.24%Si的Hugoniot数据

    式中：下标i代表i组分，wi是组分i的质量分数，V0为基态体积。根据（15）式，计算得到Fe-3.24%Si的Hugoniot参数为C0=4.182 km/s，$ \lambda $=1.551，以及0 K密度$ {\rho _0}$=7.668 g/cm3。（13）式中的冲击温度可以通过下式估算

    式中：CVl代表晶格对定容比热容的贡献，简称晶格比热，在高温下CVl=3R/$ \mu $，其中R为理想气体常数，摩尔质量$ \mu $=54.11 g/mol；$ {C_{V{\rm{e}}}} = {\beta _0}{\left( {{\rho _{0\varepsilon }}/\rho } \right)^\kappa }T$[37]为电子对定容比热容的贡献，简称电子比热。由于Fe-3.24%Si中Si的含量很小，因此假设其电子比热的参数和铁一致，即$ {\beta _0}$=0.091 J·kg–1·K–2和$\kappa = 1.34$[38]。另外，在本研究中还假设Fe-3.24%Si晶格和电子的Grüneisen参数都近似等于铁的相关参数$ {\gamma _{\rm l}} = 1.74{({\rho _{0\varepsilon }}/\rho )^{0.78}}$[39]和$ {\gamma _{\rm e}}=2$[40]。基于hcp-Fe-9%Si[6]在室温下的密度$ {{\rho _{0\varepsilon }}}$=7.578 g/cm3和hcp-Fe[39]的密度$ {{\rho _{0\varepsilon }}}$=8.269 g/cm3，通过内插法可估计出hcp-Fe-3.24%Si在室温下的密度$ {{\rho _{0\varepsilon }}}$=7.995 g/cm3。将这些参数代入（13）式，计算得到Fe-3.24%Si在室温下的状态方程，如图3中品红色虚线所示，与Fe-3.4%Si的静高压数据一致[11]，也与100 GPa以上的第一性原理计算结果一致。

    • 2.3.   高压下hcp-Fe-3.24%Si的声速

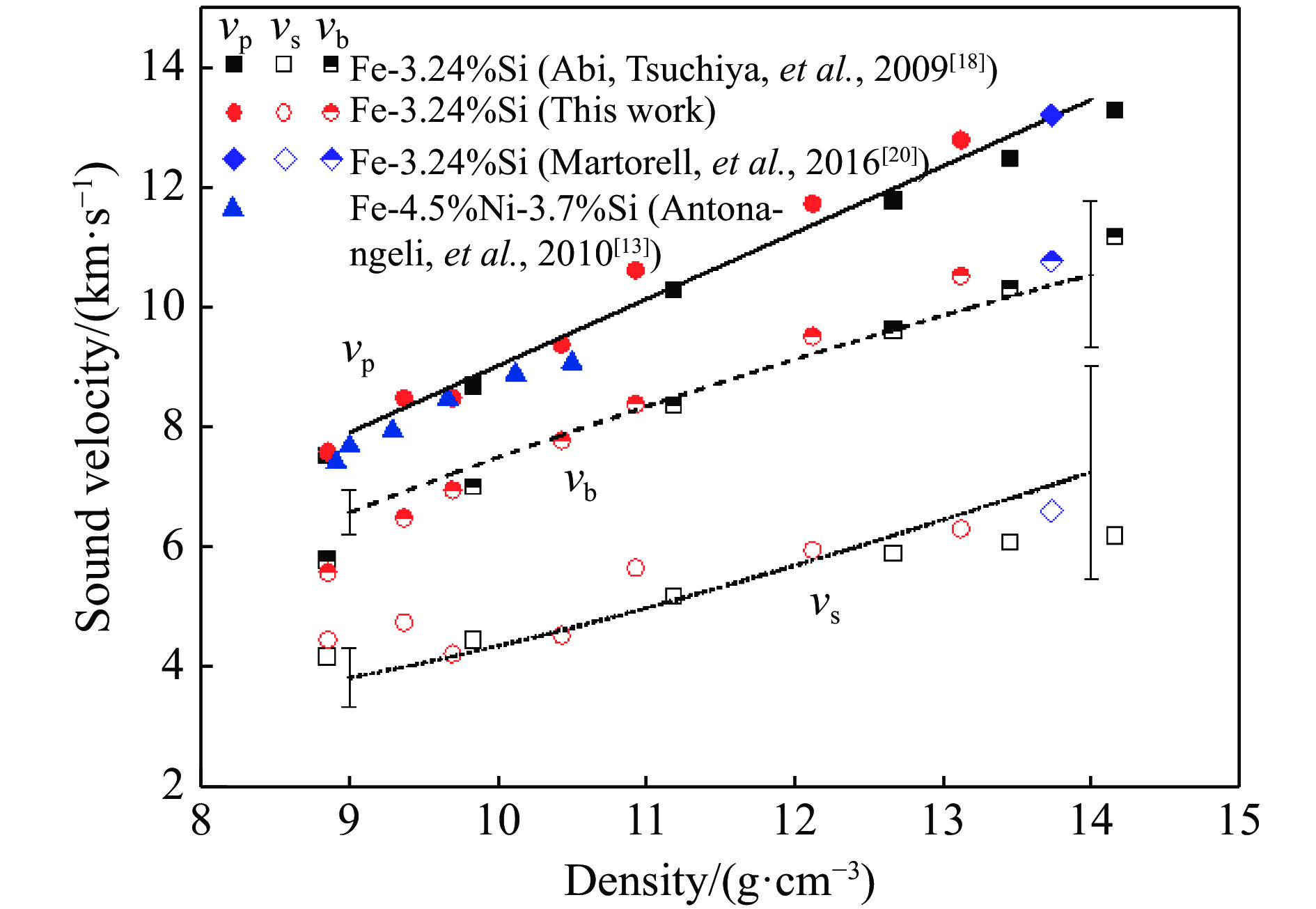
  • 由前面对比分析可知，当压强在100 GPa以上时，有无自旋对Fe-3.24%Si的状态方程无影响。考虑计算资源的问题，本研究假设自旋对声速亦无影响，在此仅计算II-64-atoms结构在高压零温下的声速。Fe-3.24%Si[18, 20]的纵波声速vp与密度呈线性关系（见图4）

    也就是说，Fe-3.24%Si的纵波声速vp在室温下满足Birch定律[41]。在低压下，所有Fe-3.24%Si的计算结果与实验测量的Fe-4.5%Ni-3.7%Si的纵波声速vp一致[13]。对于体波声速vb，本研究通过第一性原理得到的计算结果与Tsuchiya等[18]和Martorell等[20]计算的体波速度vb比较吻合。基于之前计算Fe-3.24%Si状态方程的方法，还可以根据热力学方法估算体波速度

    0 K下，根据（20）式计算的体波速度vb在低压下略高于根据（11）式得到的vb，并且两者的差异在误差范围内，高压下计算得到的vb一致。因此，可以用（20）式估算内核高温高压条件下的体波速度vb。由（19）式和（20）式，计算得到的横波声速vs如下

    在误差范围内，由（21）式计算的横波声速与由（10）式得到的横波声速相近。根据状态方程和纵波声速的拟合结果，vb和vs的相对误差分别约为11%和24%。

    • 2.4.   内地核中Si含量的限定

  • 根据0 K的状态方程和相应的热力学参数，可以通过下式计算内核条件下Fe-3.24%Si的密度

    内地核温度剖面$ {T_{\rm{E}}} = {T_{{\rm{ICB}}}}{\left( {\rho /{\rho _{{\rm{ICB}}}}} \right)^{1.5}}$可根据内外核边界处的温度TICB=(5 400±300) K[42-43]计算。对于纵波声速，前面的计算结果表明Fe-Si体系的纵波声速在室温下满足Birch定律，在高温高压下是否依然呈线性关系还存在争论[44]。Antonangeli等[45]在低于93 GPa、不高于1 100 K的温压范围内测量了Fe的声速，结果表明Fe的纵波声速在1100 K下仍然满足Birch定律。然而，Lin等[46]、Mao等[14]和Sakamaki等[47]的研究结果表明Fe的纵波声速在高温下与密度不再呈线性关系，意味着Birch定律在高温条件下并不成立。2017年，冯磊[35]应用动高压实验技术研究了Fe-9%Si在216 GPa、4 420 K时的纵波声速，测量数据与300 K下Fe-9%Si[17]的纵波声速非常一致，表明Fe-9%Si的纵波声速在高温高压下仍然满足Birch定律。在内地核高温高压条件下，假设Fe-3.24%Si的纵波声速仍然满足Birch定律，则其体波声速和横波声速可由（20）式和（21）式计算，结果如图5所示。为了研究Si对Fe的密度和声速的影响，还计算了内核条件下铁的密度和声速。铁的密度可由（13）式计算，其体积模量为K0=(172.7±1.4) GPa，${K'_0}$=4.79±0.05，初始密度$ {\rho _0}$=8.269 g/cm3[39]；铁的纵波声速$ {v_{\rm{p}}} = (1.206\rho - 4.000)$ km/s[17]。在内核条件下，Fe-3.24%Si的密度低于Fe的密度，略高于内核的密度，表明Si降低了铁的密度。Fe-3.24%Si的纵波声速与铁的纵波声速接近，表明Si对铁的纵波声速的影响很小。Martorell等[20]的计算结果也支持这一结论，尽管他们认为温度会降低Fe和Fe-Si合金的纵波声速。Fe-3.24%Si的体波速度与PREM数据一致，并且高于铁；而Fe-3.24%Si的横波声速略低于Fe，但是均明显高于内地核的横波声速。由此可见，Si对铁的纵波声速和横波声速的影响较小。由于纯铁的声速明显高于内地核的声速，因此内地核中不可能含有大量的Si，而应含有能明显降低Fe的密度和声速的轻元素，如C[48-49]。

3.   结　论

  • 研究了0 K下Fe-3.24%Si的状态方程，并将其与静态高压实验数据、理论计算和动态高压实验数据进行了比较，研究发现：当压强高于100 GPa时，自旋对计算结果没有影响；在低压条件下考虑自旋时，其计算结果更接近实验值。通过计算弹性常数，得到了Fe-3.24%Si的纵波声速、横波声速和体波声速，发现根据第一性原理计算的纵波声速与Fe-4.5%Ni-3.7%Si的实验测量结果一致，并且满足Birch定律。

    基于由第一性原理方法计算的状态方程和声速，利用热力学方法，计算了内地核温压环境下Fe-3.24%Si的密度和声速，并与内地核的密度和声速进行对比，发现：Fe-3.24%Si的密度高于PREM模型给出的内地核密度，但明显低于纯铁的密度；Fe-3.24%Si的纵波和横波声速接近Fe的声速，但是明显高于内地核的声速。由此排除了内地核含有大量Si元素的可能性。

参考文献 (49)

目录

/

返回文章
返回