高级搜索

小钨球对防弹衣加松木靶的侵彻研究

,  ,  , 

downloadPDF

上一篇

下一篇

唐昌州, 智小琦, 徐锦波, 陈志斌. 小钨球对防弹衣加松木靶的侵彻研究[J]. 高压物理学报, 2020, 34(5): 055101-1. doi: 10.11858/gywlxb.20200506
引用本文: 唐昌州, 智小琦, 徐锦波, 陈志斌. 小钨球对防弹衣加松木靶的侵彻研究[J]. 高压物理学报, 2020, 34(5): 055101-1. doi: 10.11858/gywlxb.20200506
shu
Changzhou TANG, Xiaoqi ZHI, Jinbo XU, Zhibin CHEN. Research on Small Tungsten Spheres Penetrating into Pine Target with Body Armor[J]. gaoyawli, 2020, 34(5): 055101-1. doi: 10.11858/gywlxb.20200506
Citation: Changzhou TANG, Xiaoqi ZHI, Jinbo XU, Zhibin CHEN. Research on Small Tungsten Spheres Penetrating into Pine Target with Body Armor[J]. gaoyawli, 2020, 34(5): 055101-1. doi: 10.11858/gywlxb.20200506
shu

小钨球对防弹衣加松木靶的侵彻研究

  • 1.

    中北大学机电工程学院，山西 太原　030051

  • 2.

    晋西工业集团，山西 太原　030027

    • 作者简介: 唐昌州（1996－），男，硕士研究生，主要从事弹药工程与毁伤技术研究.　E-mail：562870134@qq.com .
    通讯作者: 智小琦（1963－），女，博士，教授，主要从事武器毁伤与装药技术研究.　E-mail：zxq4060@sina.com; 

  • 中图分类号: TJ012.4

Research on Small Tungsten Spheres Penetrating into Pine Target with Body Armor

  • 1.

    College of Mechatronics Engineering, North University of China, Taiyuan 030051, Shanxi, China

  • 2.

    Jinxi Industrial Group, Taiyuan 030027, Shanxi, China

    • Corresponding author: Xiaoqi ZHI, zxq4060@sina.com ; 

  • MSC: TJ012.4

  • 摘要: 为获得小钨球对防弹衣加人体等效靶的侵彻性能，对小钨球侵彻Ⅲ级软体防弹衣加25 mm厚红松靶进行了试验研究。在此基础上，结合小钨球侵彻LY-12硬铝靶试验与数值模拟，研究了LY-12硬铝靶与Ⅲ级软体防弹衣加25 mm厚红松靶之间的等效关系，并通过量纲分析方法建立了小钨球侵彻Ⅲ级软体防弹衣加25 mm厚红松靶的弹道极限预测公式，分析了小钨球质量变化对其侵彻性能影响的规律。结果表明：对于小钨球的侵彻，Ⅲ级软体防弹衣加25 mm厚红松靶可等效为6.2 mm厚LY-12硬铝靶；弹道极限预测公式的预测值与试验值吻合良好，并且随着钨球质量的增加，弹道极限近似服从幂函数递减规律。研究结果对单兵破片战斗部的改进设计具有一定的参考价值。
    Abstract: In order to study the penetration performance of small tungsten spheres on the human equivalent target with body armor, the test of small tungsten spheres penetrating 25 mm thick pine target with Class Ⅲ soft body armor is carried out. On this basis, the equivalent relationships between 25 mm thick pine target with Class Ⅲ soft body armor and LY-12 hard aluminum target are studied by combining the experiment and numerical simulation of small tungsten spheres penetrating LY-12 hard aluminum target. According to the method of dimensional analysis, the ballistic limit prediction formula of small tungsten spheres penetrating 25 mm thick pine target with Class Ⅲ soft body armor is established and the influence of the mass change of small tungsten spheres on the penetration performance is studied. The experimental results reveal that for the penetration of small tungsten spheres, a 25 mm thick pine target with Class Ⅲ soft body armor can be equivalent to a 6.2 mm thick LY-12 hard aluminum target. The predicted value of ballistic limit prediction formula is in good agreement with the test value. And with the increase of the mass of tungsten spheres, the ballistic limit approximately obeys the law of decreasing power function. The research results have certain reference value for the improvement and design of individual fragment warhead.
  • 加载中

  • 图 1  钨球及弹托

    Figure 1.  Tungsten spheres and sabots

    下载: 全尺寸图片 幻灯片

    图 2  试验布置示意图

    Figure 2.  Schematic of experimental set-up

    下载: 全尺寸图片 幻灯片

    图 3  试验后的防弹衣和红松木

    Figure 3.  Body armor and pine after the experiment

    下载: 全尺寸图片 幻灯片

    图 4  防弹纤维的典型损伤

    Figure 4.  Typical damage of bulletproof fiber

    下载: 全尺寸图片 幻灯片

    图 5  试验后LY-12硬铝靶状态图

    Figure 5.  States of LY-12 hard aluminum target after the experiment

    下载: 全尺寸图片 幻灯片

    图 6  钨球侵彻靶板的剩余速度-着靶速度曲线

    Figure 6.  Residual velocity-initial velocity curves of tungsten spheres penetrating targets

    下载: 全尺寸图片 幻灯片

    图 7  有限元模型

    Figure 7.  Finite element model

    下载: 全尺寸图片 幻灯片

    图 8  仿真值与试验值的对比

    Figure 8.  Comparison between simulation results and experimental results

    下载: 全尺寸图片 幻灯片

    表 1  R-I模型参数

    Table 1.  R-I model parameters

    Target type$ a $vbl/(m·s−1)$ p $
    Body armor + Pine composite target0.73692.92
    8 mm thick LY-12 hard aluminum target0.77850.12
    下载: 导出CSV

    表 2  弹靶材料模型参数

    Table 2.  Material model parameters of projectile and target

    Materialρ/(g·cm−3)E/GPaμSIGY/MPaETAN/MPaSRCSRPFS
    Tungsten alloy18.13670.3031506 7923.961.2
    LY-12 hard aluminum 2.78 710.3 3751000000.8
    下载: 导出CSV

    表 3  钨球侵彻不同厚度LY-12硬铝靶的仿真结果

    Table 3.  Simulation results of tungsten sphere penetrating LY-12 hard aluminum target with different thicknesses

    Initial velocity/(m·s−1)Thickness of target/mmResidual velocity/(m·s−1)Penetration result
    692.96.1063.0Penetration
    6.2021.4Penetration
    6.210Embedment
    6.250Embedment
    6.300Embedment
    下载: 导出CSV

    表 4  钨球侵彻原型靶与等效靶弹道极限的对比

    Table 4.  Comparison of ballistic limits between tungsten spheres penetrating prototype target and the equivalent target

    Type of tungsten sphereTarget typeBallistic limit/(m·s−1)Relative error/%
    0.21 g, $ \varnothing $2.8 mmBody armor + Pine composite target692.91.8
    6.2 mm thick LY-12 hard aluminum target705.2
    0.17 g, $ \varnothing $2.6 mmBody armor + Pine composite target742.32.2
    6.2 mm thick LY-12 hard aluminum target758.7
    下载: 导出CSV

    表 5  确定弹道极限的主要物理量

    Table 5.  Main physical quantities for determining ballistic limit

    MaterialPhysical quantityDimension
    Tungsten sphereDensity ρp/(kg·m−3)ML−3
    Diameter Dp/PaL
    Elastic modulus $ {E}$p/PaL−1MT−2
    Yield strength $ {\sigma }$sp/PaL−1MT−2
    Characteristic strain $ {\varepsilon } $p1
    Sound velocity $ {C}$p/(m·s−1)LT−1
    Body armorDensity ρf /(kg·m−3)ML−3
    Thickness $ {h}$f /mL
    Elastic modulus $ {E}$f /PaL−1MT−2
    Compressive strength $ {\sigma }$sf /PaL−1MT−2
    Shear strength $ {\sigma }_{\tau}$f /PaL−1MT−2
    Tensile strength $ {\sigma } $ff /PaL−1MT−2
    Characteristic strain $ {\varepsilon }$f 1
    Sound velocity $ {C} $f /(m·s−1)LT−1
    PineDensity ρs/(kg·m−3)ML−3
    Thickness $ {h} $s/mL
    Elastic modulus $ {E} $s/PaL−1MT−2
    Failure stress $ {\sigma }$ss/PaL−1MT−2
    Characteristic strain $ {\varepsilon }$s1
    Sound velocity $ {C}$s/(m·s−1)LT−1
    下载: 导出CSV

    表 6  不同方法计算的弹道极限的比较

    Table 6.  Comparison of ballistic limits calculated by different methods

    Mass of tungsten sphere/gDiameter of tungsten sphere/mmBallistic limit/(m·s−1)Relative error/%
    Calculated Simulated
    0.263.02643.8649−0.8
    0.313.20609.9623−2.1
    0.363.36582.8599−2.8
    0.413.52558.1580−3.9
    0.463.64540.9561−3.7
    下载: 导出CSV

    表 7  0.20 g钨球侵彻防弹衣+红松木复合靶的弹道极限的试验值与计算值的对比

    Table 7.  Comparison between experimental and calculated values of ballistic limits of tungsten spheres with mass of 0.20 g penetrating body armor and pine composite target

    Type of tungsten sphereBallistic limit/(m·s−1)Relative error/%
    Experimental valueCalculated value
    0.20 g，$\varnothing$2.8 mm709.4702.5−1.0
    下载: 导出CSV
  • [1] 程可. 轻武器杀伤元对明胶靶标侵彻的数值仿真研究 [D]. 南京: 南京理工大学, 2012: 1–2. CHEN K. Numerical simulation research of small arms lethal-element penetrating gelatin target [D]. Nanjing: Nanjing University of Science and Technology, 2012: 1–2.
    [2] LIDEN E, BERLIN R, JANZON B, et al. Some observations relating to behind-body armour blunt trauma effects caused by ballistic impact [J]. The Journal of Trauma: Injury, Infection, and Critical Care, 1988, 28(Supplement): S145–S148. doi: 10.1097/00005373-198801001-00029
    [3] ROBERTS J C, O’CONNOR J V, WARD E E. Modeling the effect of nonpenetrating ballistic impact as a means of detecting behind-armor blunt trauma [J]. Journal of Trauma and Acute Care Surgery, 2005, 58: 1241–1251. doi: 10.1097/01.TA.0000169805.81214.DC
    [4] ROBERTS J C, MERKLE A C, BIERMANN P J, et al. Computational and experimental models of the human torso for non-penetrating ballistic impact [J]. Journal of Biomechanics, 2007, 40(1): 125–136. doi: 10.1016/j.jbiomech.2005.11.003
    [5] MERKLE A C, WARD E E, O’CONNOR J V, et al. Assessing behind armor blunt trauma (BABT) under NIJ Standard-0101.04 conditions using human torso models [J]. The Journal of Trauma: Injury, Infection, and Critical Care, 2008, 64(6): 1555–1561. doi: 10.1097/TA.0b013e318160ff3a
    [6] SHEN W, NIU Y, BYKANOVA L, et al. Characterizing the interaction among bullet, body armor, and human and surrogate targets [J]. Journal of Biomechanical Engineering, 2010, 132(12): 121001. doi: 10.1115/1.4002699
    [7] 罗少敏, 徐诚, 陈爱军, 等. 步枪弹侵彻带软硬复合防护明胶靶标的数值模拟 [J]. 兵工学报, 2014, 35(8): 1172–1178. doi: 10.3969/j.issn.1000-1093.2014.08.006 LUO S M, XU C, CHEN A J, et al. Numerical simulation of bullets penetrating into gelatin target with hard/soft composite armor [J]. Acta Armamentarii, 2014, 35(8): 1172–1178. doi: 10.3969/j.issn.1000-1093.2014.08.006
    [8] 孙非, 马力, 朱一辉, 等. 手枪弹对带UHMWPE软防护明胶靶标冲击效应的数值分析 [J]. 振动与冲击, 2018, 37(13): 20–26. SUN F, MA L, ZHU Y H, et al. Numerical analysis for impact effects of a pistol bullet on a gelatin target covered with UHMWPE fiber armor [J]. Journal of Vibration and Shock, 2018, 37(13): 20–26.
    [9] 唐刘建, 温垚珂, 薛本源, 等. 手枪弹侵彻有防护仿生人体躯干靶标试验研究 [J]. 振动与冲击, 2019, 38(4): 250–254. TANG L J, WEN Y K, XUE B Y, et al. Pistol bullet impact soft body armor covered bionic human torso [J]. Journal of Vibration and Shock, 2019, 38(4): 250–254.
    [10] 刘坤, 吴志林, 宁建国, 等. 手枪弹对带软防护的明胶靶标侵彻机理与实验研究 [J]. 兵工学报, 2018, 39(1): 1–17. doi: 10.3969/j.issn.1000-1093.2018.01.001 LIU K, WU Z L, NING J G, et al. Investigation on the mechanism and experiment of pistol cartridge penetrating into gelatin target with soft body armor [J]. Acta Armamentarii, 2018, 39(1): 1–17. doi: 10.3969/j.issn.1000-1093.2018.01.001
    [11] 黄拱武. 弹体撞击带纤维软防护明胶靶标的数值仿真研究 [D]. 南京: 南京理工大学, 2013: 41–43. HUANG G W. Numerical simulation research of projectile impacting gelatin target with fiber armor [D]. Nanjing: Nanjing University of Science and Technology, 2013: 41–43.
    [12] RECHT R F, IPSON T W. Ballistic perforation dynamics [J]. Journal of Applied Mechanics, 1963, 30(3): 384–390. doi: 10.1115/1.3636566
    [13] 米双山, 张锡恩, 陶贵明. 钨球侵彻LY-12铝合金靶板的有限元分析 [J]. 爆炸与冲击, 2005, 25(5): 477–480. doi: 10.3321/j.issn:1001-1455.2005.05.015 MI S S, ZHANG X E, TAO G M. Finite element analysis of spherical fragments penetrating LY-12 aluminum alloy target [J]. Explosion and Shock Waves, 2005, 25(5): 477–480. doi: 10.3321/j.issn:1001-1455.2005.05.015
    [14] 曹兵. 不同材质靶板抗破片侵彻等效关系实验研究 [J]. 弹箭与制导学报, 2006(4): 113–114. doi: 10.3969/j.issn.1673-9728.2006.04.034 CAO B. An experimental investigation on the equivalent relation between different armour plates penetrated by fragments [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2006(4): 113–114. doi: 10.3969/j.issn.1673-9728.2006.04.034
    [15] 曹兵. 靶板等效方法研究 [J]. 弹箭与制导学报, 2003(Suppl 4): 122–123. CAO B. Study on equivalent target experimental methods [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2003(Suppl 4): 122–123.
    [16] 李学林, 项鑫, 黄广炎, 等. 钨球破片对相控阵雷达典型部件的侵彻特性研究 [J]. 兵工学报, 2010(Supp 1): 51–54. LI X L, XIANG X, HUANG G Y, et al. Penetration characteristics of tungsten sphere fragment to typical components of phased array radar [J]. Acta Armamentarii, 2010(Supp 1): 51–54.
    [17] 宫能平. LY12CZ铝合金棒料的拉伸实验研究 [J]. 淮南工业学院学报, 2002(1): 62–65. GONG N P. Tensile mechanics property of aluminium LY12CZ under different strain rates [J]. Journal of Huainan Institute of Technology, 2002(1): 62–65.
    [18] 王雪, 智小琦, 徐锦波, 等. 球形破片侵彻多层板弹道极限的量纲分析 [J]. 高压物理学报, 2019, 33(6): 157–165. WANG X, ZHI X Q, XU J B, et al. Dimensional analysis of ballistic limit of fragments penetrating multi-layer plate [J]. Chinese Journal of High Pressure Physics, 2019, 33(6): 157–165.
    [19] 朱耀, 庞宝君, 盖秉政. 一种用于动态拉伸试验装置的新型试件装卡方式 [J]. 实验力学, 2009(5): 55–60. ZHU Y, PANG B J, GAI B Z. A new specimen fastener for dynamic tensile testing apparatus [J]. Journal of Experimental Mechanics, 2009(5): 55–60.
    [20] 米双山, 何剑彬, 张锡恩, 等. 战斗损伤仿真中的等效靶与破片终点速度研究 [J]. 兵工学报, 2005(5): 605–608. doi: 10.3321/j.issn:1000-1093.2005.05.007 MI S S, HE J B, ZHANG X E, et al. Equivalent target and terminal velocity of fragments in battle damage simulation [J]. Acta Armamentarii, 2005(5): 605–608. doi: 10.3321/j.issn:1000-1093.2005.05.007
    [21] 谈庆明. 量纲分析 [M]. 合肥: 中国科学技术大学出版社, 2005: 1–2. TAN Q M. Dimensional analysis [M]. Hefei: University of Science and Technology of China Press, 2005: 1–2.
    [22] 毛亮, 王华, 姜春兰, 等. 钨合金球形破片侵彻陶瓷/DFRP复合靶的弹道极限速度 [J]. 振动与冲击, 2015, 34(13): 1–5. MAO L, WANG H, JIANG C L, et al. Ballistic limit velocity of tungsten alloy spherical fragment penetrating ceramic/DFRP composite target plates [J]. Journal of Vibration and Shock, 2015, 34(13): 1–5.
  • 加载中
图( 8) 表( 7)
计量
  • 文章访问数:  2988
  • HTML全文浏览数:  2988
  • PDF下载数:  25
  • 施引文献:  0
出版历程
  • 收稿日期:  2020-01-13
  • 刊出日期:  2020-10-05

小钨球对防弹衣加松木靶的侵彻研究

    通讯作者: 智小琦（1963－），女，博士，教授，主要从事武器毁伤与装药技术研究.　E-mail：zxq4060@sina.com; 
    作者简介: 唐昌州（1996－），男，硕士研究生，主要从事弹药工程与毁伤技术研究.　E-mail：562870134@qq.com
  • 1. 中北大学机电工程学院，山西 太原　030051
  • 2. 晋西工业集团，山西 太原　030027
  • 收稿日期:  2020-01-13

摘要: 为获得小钨球对防弹衣加人体等效靶的侵彻性能，对小钨球侵彻Ⅲ级软体防弹衣加25 mm厚红松靶进行了试验研究。在此基础上，结合小钨球侵彻LY-12硬铝靶试验与数值模拟，研究了LY-12硬铝靶与Ⅲ级软体防弹衣加25 mm厚红松靶之间的等效关系，并通过量纲分析方法建立了小钨球侵彻Ⅲ级软体防弹衣加25 mm厚红松靶的弹道极限预测公式，分析了小钨球质量变化对其侵彻性能影响的规律。结果表明：对于小钨球的侵彻，Ⅲ级软体防弹衣加25 mm厚红松靶可等效为6.2 mm厚LY-12硬铝靶；弹道极限预测公式的预测值与试验值吻合良好，并且随着钨球质量的增加，弹道极限近似服从幂函数递减规律。研究结果对单兵破片战斗部的改进设计具有一定的参考价值。

English Abstract

    全文HTML

  • 大量研究数据表明，在现代战争中，70%以上的士兵伤亡是因破片和枪弹所致[1]。自从单兵防护装备出现以后，随着防护装备材料的不断发展，防护能力的不断增强，士兵的伤亡率大大降低。为此，单兵武器对毁伤元提出了更高的要求。如何设计合适的毁伤元使其贯穿单兵防护装备后对人员造成严重伤害或致命伤害成为单兵破片战斗部设计的重点。

    破片是主要的毁伤元，对于不同目标，破片质量要求不同。单兵破片战斗部对付的主要目标是人员，为提高单位面积的破片数量且保持良好的机动性，小质量钨合金破片是未来发展的主要方向之一。目前对带有软体防护装备的人体等效靶的侵彻研究，大多以标准枪弹为对象，如Liden等[2]利用9 mm子弹侵彻带有软防护的活体麻醉猪，研究了软防护后的非贯穿损伤，结果表明非贯穿子弹可对软防护后的胸膛造成严重伤害；Roberts[3-4]、Merkle[5]等建立了人体躯干的有限元模型，并模拟计算了9 mm手枪弹侵彻带有软质防弹衣的拟人上身躯干，研究了人体内部器官在非贯穿损伤下的压力分布情况，研究结果为确定胸部对弹道冲击的反应提供了参考；Shen等[6]通过试验和数值模拟研究了9 mm子弹对带有软防护人体模拟靶的侵彻，并对撞击后10～1000 $ {\text{μ}}{\rm{s}}$内的侵彻过程进行了量化；罗少敏等[7]利用数值模拟研究了7.62 mm步枪弹侵彻带软硬复合防护明胶靶的侵彻过程及其机理；孙非[8]、唐刘建[9]等分别研究了带UHMWPE软防护明胶靶在7.62 mm和9 mm手枪弹侵彻作用下的动态响应特性；刘坤等[10]研究了9 mm全铜弹和5.8 mm手枪弹对带软防护的明胶靶标的侵彻机理。而关于小尺寸破片对带有软体防护装备的人体等效靶的侵彻研究却鲜有报道。

    本工作以国际标准25 mm厚红松木靶为人体等效靶，对小钨球侵彻Ⅲ级软体防弹衣加25 mm厚红松靶展开试验研究；为方便今后对防弹衣+人体等效靶侵彻进行研究，作等效靶代换，即利用数值模拟分析计算LY-12硬铝靶与Ⅲ级软体防弹衣加红松靶之间的等效关系，并依据量纲分析方法建立小钨球侵彻Ⅲ级软体防弹衣加红松靶的弹道极限预测公式，以期为单兵破片战斗部的设计提供参考。

1.   试验研究

    1.1.   试验布置

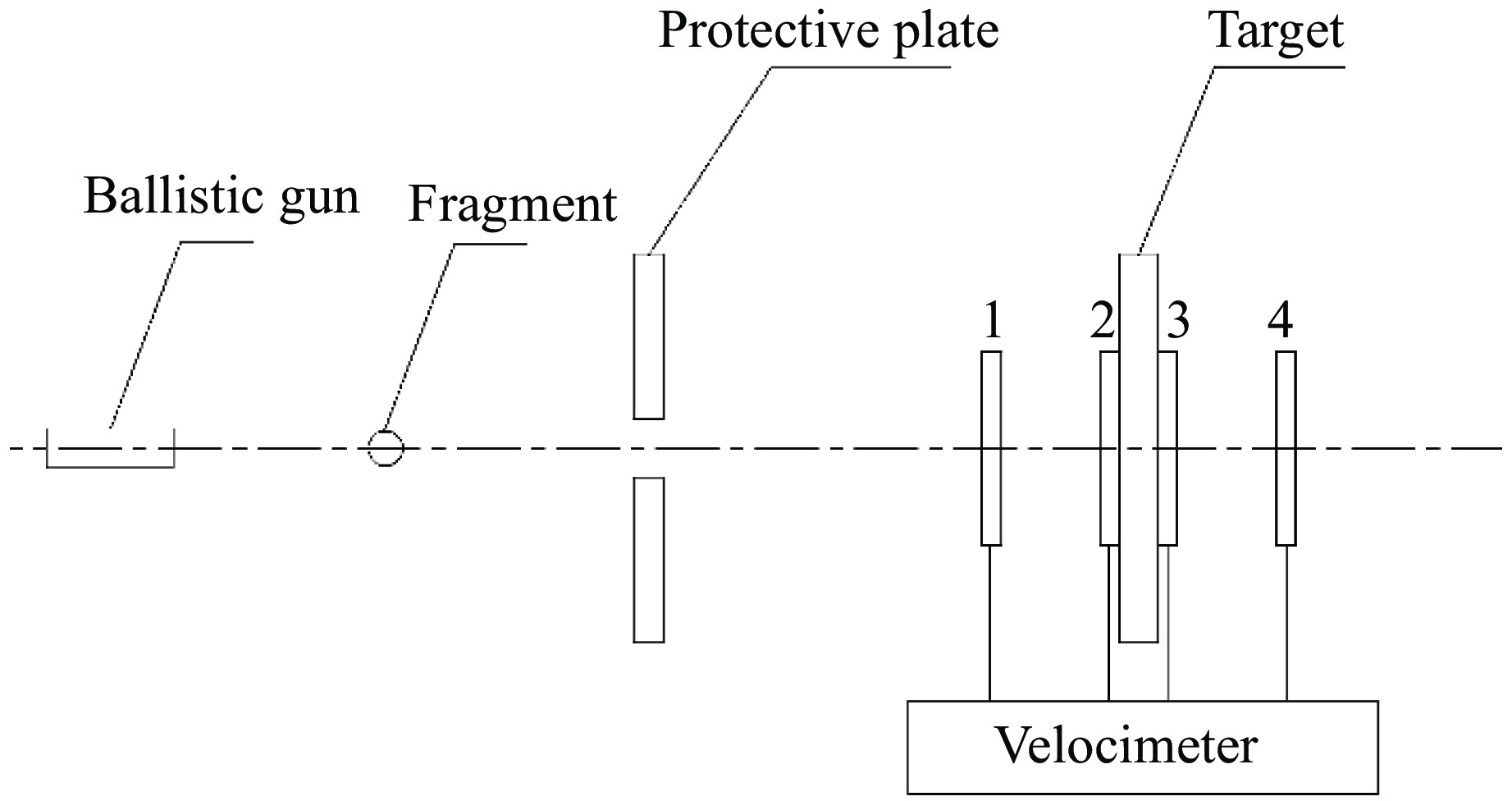
  • 试验采用12.7 mm弹道枪加载小钨球，钨球置于尼龙弹托中，钨球质量为0.21 g，直径为2.8 mm。发射时，钨球随弹托飞出，并在空气阻力作用下与弹托分离。靶板前有防护板，防护板上有比弹托小的孔，弹托挡在防护板前面无法进入靶板。图1为试验所用的钨球及弹托。靶板分别为紧密贴合的FDY3R-01型Ⅲ级防弹衣加25 mm厚红松木及8 mm厚LY-12硬铝靶。防弹衣由衣套和防弹层构成，衣套为涤纶，防弹层为凯夫拉材料，采用0°/90°正交铺层结构。所有靶板均用专用夹具固定在靶架上。为测量着靶前钨球速度及穿透靶后的剩余速度，靶前及靶后分别放置通断靶，测速装置采用南京理工大学机械工程学院设计的 NLG202-Z型六路测速仪，精度为0.1 $ {\text{μ}}{\rm{s}}$。试验布置示意图如图2所示。本次试验中的侵彻均为正侵彻。

    • 1.2.   试验结果及分析

  • 图3为试验后的防弹衣和红松木靶，图4给出了防弹衣纤维的典型损伤状态。防弹衣受到破片冲击时，冲击区域表面的纤维与树脂脱粘，并在破片剪切作用下产生剪切破坏，形成一个与破片直径近似的孔洞，如图4(a)所示。随着侵彻的进行，破片冲击产生的应力波沿纤维轴向(如图4(c)所示)及靶体纵向两个方向传播。在靶体纵向上，除了剪切破坏，纤维还会产生拉伸变形破坏，形成背部鼓包，如图4(b)、图4(d)所示。这是由于在侵彻过程中破片部分动能会转化为纤维内能，主要是弹性势能[11]，宏观表现为纤维的拉伸变形。在破片穿透防弹衣后，由于红松木材质较脆，屈服极限较低，松木靶仅在弹孔附近发生剪切破坏，且弹孔直径与破片直径相近，如图3(c)所示。

    图5为试验后LY-12硬铝靶状态图。由图5可知，LY-12硬铝靶主要发生的是剪切破坏。当破片高速撞击靶板时，靶板表面由于局部应力集中产生塑性变形，形成凹坑。随着破片侵彻的深入，靶板内部材料发生较大塑性变形。并且由于局部畸变产生的热量来不及散出，塑性变形加剧，绝热剪切带逐渐形成，铝靶在破片侵彻作用下发生剪切冲塞破坏。当破片着靶速度低于弹道极限时，靶板背面产生与破片形状相同的局部隆起变形，并伴有径向裂纹生成，如图5(d)所示。当破片着靶速度高于弹道极限时，靶板背面产生轻微的圆形延性冲塞破坏并形成圆形断口，在断口周围存在轻微的径向裂纹，如图5(b)所示。

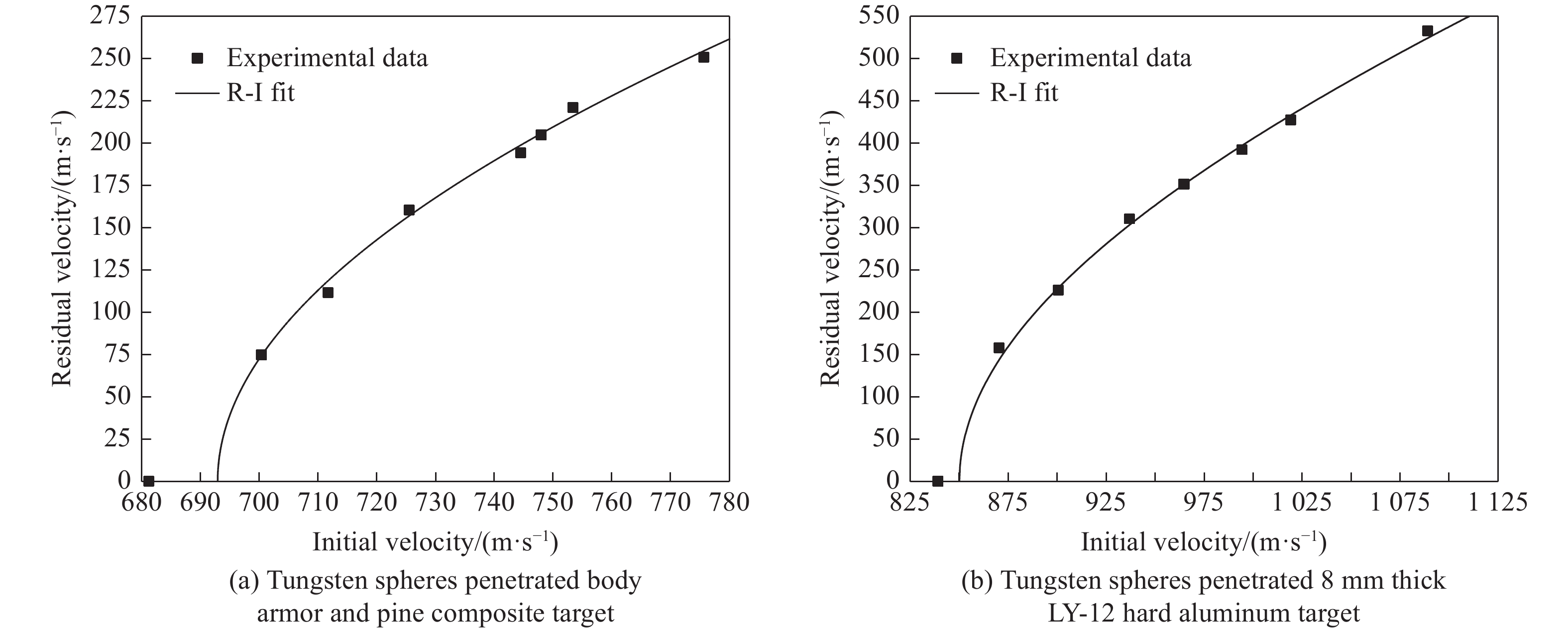
    利用Recht等[12]提出的R-I公式处理钨球剩余速度与着靶速度关系以获得弹道极限，该公式为

    式中：$ {v}_{\rm i} $为破片着靶速度，m/s；$ {v}_{\rm r} $为破片剩余速度，m/s；$ {v}_{\rm bl} $为弹道极限，m/s；$ a $、$ p $为模型参数，可利用试验数据并通过最小二乘法拟合得到。

    图6给出了钨球侵彻靶板的剩余速度-着靶速度曲线，表1给出了由式(1)拟合得到的R-I模型参数。

2.   数值模拟研究

  • 由于LY-12硬铝合金在兵器、航空等领域应用较广，尤其在近年来开展的战斗损伤研究中，大都将各类材料等效为LY-12硬铝合金来研究装备的损伤情况[13-16]。为方便以后对防弹衣+人体等效靶的侵彻研究，作等效靶代换。本研究将利用数值模拟分析在小钨球侵彻作用下LY-12硬铝靶与防弹衣+红松木复合靶之间的等效关系，

    • 2.1.   仿真模型及其参数

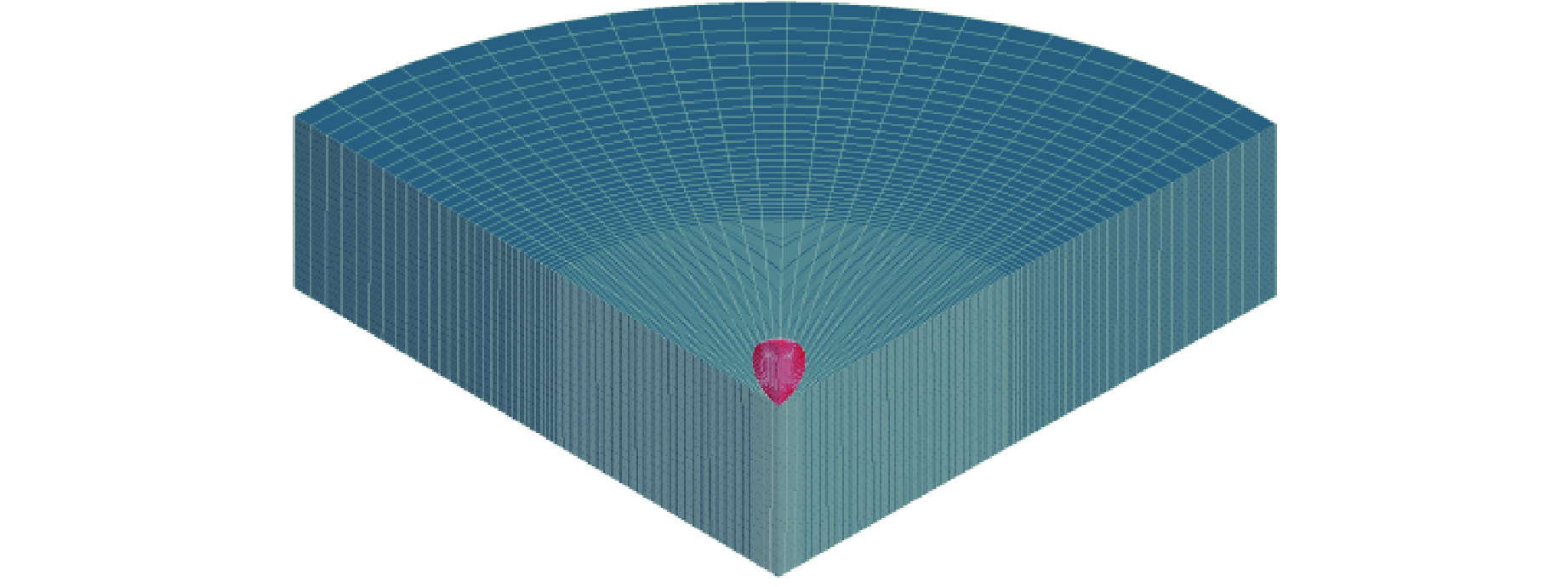
  • 采用TrueGrid软件进行建模与网格划分，考虑到模型的对称性，为节约计算时间，模型简化为1/4模型。钨球尺寸及靶板厚度与试验状态一致，靶板采用圆形靶，半径取为钨球直径的11倍，以尽量减小边界效应对侵彻过程的影响。为保证计算的连续性与高精度，网格采用渐进式。弹靶相互作用的主要区域加密，密集区网格尺寸控制在0.10～0.15 mm；其余区域采用稀疏网格，网格尺寸控制在0.15～0.90 mm；钨球最小网格尺寸为0.01 mm。有限元模型如图7所示。

    数值模拟采用LSDYNA-3D软件，单位制为cm-g-$ {\text{μ}}{\rm{s}}$，算法采用Lagrange算法。根据结构的对称性，在模型对称面添加对称边界条件，在靶板边缘添加无反射边界条件。弹靶之间的接触定义为面面侵蚀接触。

    钨球和LY-12硬铝靶均采用塑性随动硬化材料模型(MAT_PLASTIC_KINEMATIC)。由于LY-12硬铝合金为应变率不敏感材料[17]，故不考虑其应变率效应。参考文献[18-19]并根据实际试验结果对模型参数进行微调，弹靶材料模型参数如表2所示，其中：ρ为密度，E为杨氏模量，μ为泊松比，SIGY为屈服应力，ETAN为切线模量，SRC、SRP为应变率参数，FS为失效应变。

    • 2.2.   仿真模型的验证

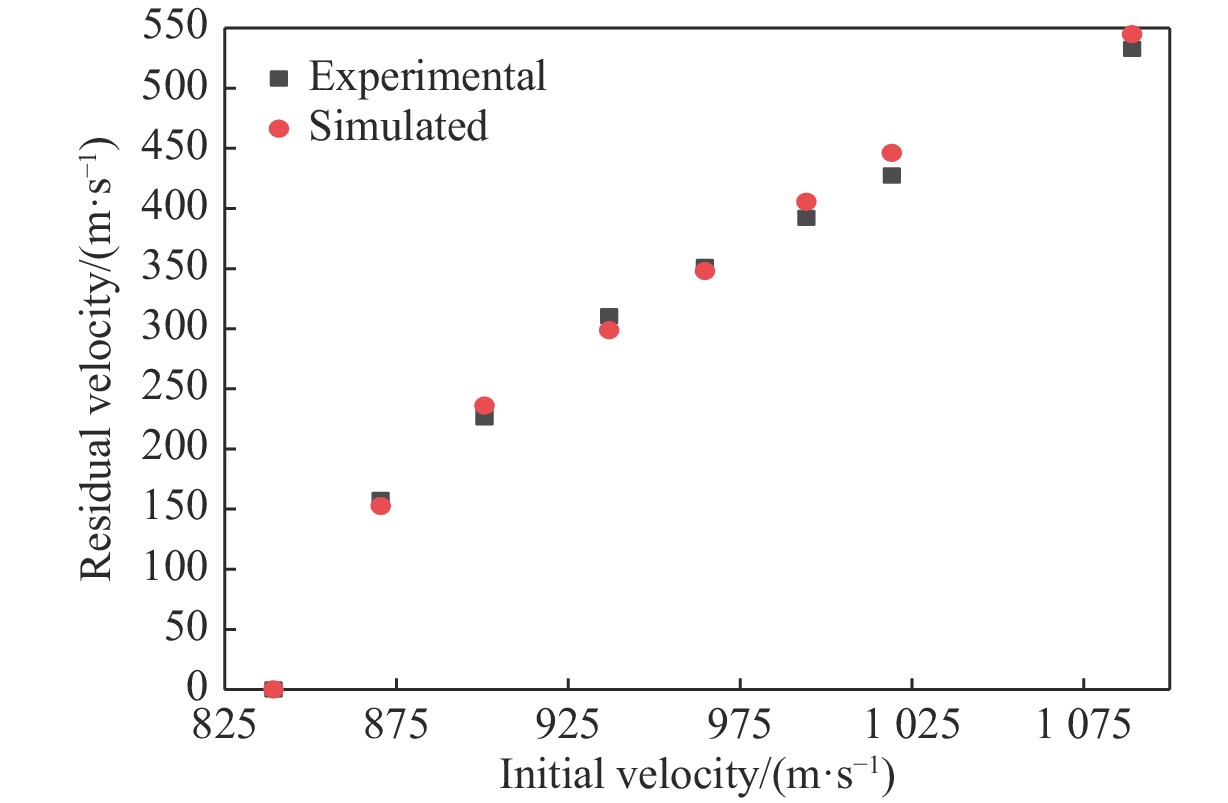
  • 利用试验数据对仿真模型进行验证，验证结果如图8所示。通过R-I公式处理仿真得到的剩余速度与着靶速度的关系可得：钨球侵彻8 mm厚LY-12硬铝靶的弹道极限为854.4 m/s，与试验所得的弹道极限的相对误差为0.5%。可见，该模型的仿真结果与试验结果接近，即仿真模型及其参数具有可靠性。

    • 2.3.   等效靶板厚度的确定

  • 根据能量等效原则[20]，钨球以692.9 m/s的速度侵彻不同厚度的LY-12硬铝靶，其仿真结果如表3所示。

    由表3可知，当着靶速度为692.9 m/s时，0.21 g的钨球能穿透6.20 mm厚LY-12硬铝靶(剩余速度为21.4 m/s，剩余动能仅为0.05 J)，而不能穿透6.21 mm厚的LY-12硬铝靶。综合考虑靶板的实际做工精度，可认为6.2 mm是该钨球以692.9 m/s的速度侵彻LY-12硬铝靶的极限穿透厚度，即防弹衣+红松木复合靶可等效为6.2 mm厚LY-12硬铝靶。

    • 2.4.   等效靶板厚度的验证

  • 利用0.21 g、直径2.8 mm以及0.17 g、直径2.6 mm两种钨球对等效6.2 mm厚LY-12硬铝靶进行弹道极限对比试验，试验对比结果如表4所示。由表4可知，钨球侵彻防弹衣+红松木复合靶与侵彻6.2 mm厚LY-12硬铝靶弹道极限的相对误差小于5%，等效靶与原型靶抗破片侵彻能力相当，即对于小钨球的侵彻，防弹衣+红松木复合靶可等效为6.2 mm厚LY-12硬铝靶。不过，由于研究的钨球质量有限，等效靶板仅适用于质量较小的钨球，而对大质量钨球的适用性有待进一步研究。

3.   量纲分析

  • 由于防弹衣和红松木材料结构复杂，很难用现有的数学模型去描述钨球侵彻防弹衣+红松木复合靶的过程及现象。而对于这类复杂问题，量纲分析法能避开复杂的内部因素变化过程从而建立物理现象基本关系[21]。因此，为进一步研究钨球质量变化对其侵彻防弹衣+红松木复合靶侵彻性能的影响，本研究依据量纲分析建立小钨球侵彻防弹衣+红松木复合靶的弹道极限预测公式。

    通过理论分析，确定钨球侵彻防弹衣+红松木复合靶弹道极限的主要物理量如表5所示[22]。

    可见，弹道极限$ {v}_{\rm bl} $是关于这些物理量的函数

    选取$ {\rho }_{\rm p} $、$ {D}_{\rm p} $和$ {\sigma }_{\rm sp} $为量纲独立变量，则根据量纲齐次原则，其他导出量可写成以下无量纲形式

    根据$ {\textit{Π}} $定理，式(2)可写为

    在钨球、防弹衣和红松木材料不变的条件下，除了$ {\textit{Π}} $、$ {\textit{Π}}_{\rm 5} $和$ {\textit{Π}}_{\rm 13} $外，其余导出量均为常数，因此式(3)可简化为

    式中：$ {c}_{\rm 0} $、$ \alpha $、$ \beta $为待定常数。

    由于本试验中的防弹衣和红松木厚度不变，令$ {c}_{\rm 1}={c}_{\rm 0}\left({{h}_{\rm f})}^{\alpha }\right({{h}_{\rm s})}^{\beta } $，$ \gamma =\alpha +\beta $，则式(4)为

    式中：$ {c}_{\rm 1} $、$ \gamma $为待定常数。

    由上述分析可知，在防弹衣和红松木材料及其厚度不变的情况下，对于不同材料的钨球，均满足

    式中：$ {c}_{i} $、$ \gamma _i $为待定常数。

    为预测不同材料的不同尺寸钨球侵彻防弹衣+红松木复合靶的弹道极限，令

    式中：$ m $、$ n $为待定常数。

    为便于求解，将式(7)两端同时取对数

    令$ y=\ln\dfrac{{v}_{\rm bl}}{\sqrt{{\sigma }_{\rm sp}/{\rho }_{\rm p}}} $，$ x=\ln\dfrac{1}{{D}_{\rm p}} $，$ k=\ln m $，则式(8)变换为

    由于试验所用钨球材料性能近似，因此$ {\sigma }_{\rm sp} $均可取1.506 GPa。利用试验数据对式(9)进行一元线性回归拟合，可得

    将$ n $、$ k $回代至式(9)，有

    为验证式(11)的有效性，利用数值模拟和式(11)分别计算不同质量钨球侵彻的弹道极限，结果如表6所示。由表6可知，钨球侵彻防弹衣+红松木复合靶的预测结果与侵彻等效6.2 mm厚LY-12硬铝靶的仿真结果比较吻合。定量地来看，当钨球质量小于0.46 g时，预测结果与仿真结果的最大相对误差小于5%，因此利用式(11)预测小钨球侵彻防弹衣+红松木复合靶的弹道极限具有较高的可信度。

    为进一步验证式(11)的可靠性，对0.20 g、直径2.8 mm的钨球侵彻防弹衣+红松木复合靶进行了侵彻试验。表7对比了0.20 g钨球侵彻防弹衣+红松木复合靶的弹道极限试验值和计算值。由表7可知，0.20 g钨球侵彻防弹衣+红松木复合靶弹道极限的试验值和计算值相对误差不超过5%，满足工程应用要求。故式(11)可用于预测小钨球侵彻防弹衣+红松木复合靶的弹道极限，适用范围为：钨球质量小于0.46 g。同时，由式(11)可以看出，随着钨球直径的增加，其质量增加，弹道极限近似服从幂函数递减规律。

4.   结　论

  • (1) 0.21 g直径2.8 mm、0.20 g直径2.8 mm以及0.17 g直径2.6 mm的小钨球侵彻Ⅲ级软体防弹衣加25 mm厚红松靶的弹道极限分别为692.9、709.4、742.3 m/s；0.21 g直径2.8 mm及0.17 g直径2.6 mm的小钨球侵彻6.2 mm厚LY-12硬铝靶的弹道极限分别为705.2、758.7 m/s；0.21 g直径2.8 mm的小钨球侵彻8.0 mm厚LY-12硬铝靶的弹道极限为850.1 m/s。

    (2)为方便今后研究，根据能量守恒原则建立了Ⅲ级软体防弹衣加25 mm厚红松靶与LY-12硬铝靶的等效关系，即前者可等效为6.2 mm厚LY-12硬铝靶；利用量纲分析建立了小钨球侵彻Ⅲ级软体防弹衣加25 mm厚红松靶的弹道极限预测公式，预测值与试验值吻合良好。

参考文献 (22)

目录

/

返回文章
返回