首页
登录
注册
-
鸟撞航空器是影响航空安全的重大问题，会带来巨大的经济损失[1]。据统计，鸟撞发生于起飞、初始爬升、航路飞行、进近及着陆等各个阶段，撞击速度在75～260 m/s区间，速度范围的跨度大[2]。各国适航规章均要求在航空器部件设计中完成抗鸟撞验证。
相比于传统鸟撞试验使用的真鸟，人工明胶鸟弹具有环保、可重复性好、与真鸟试验结果的一致性高等优点，逐渐被应用于非验证性试验，并形成了较为成熟的制备工艺[3–4]。目前，基于真鸟试验的本构模型已有较多研究[5–9]。在明胶鸟弹方面，Lavoie等[4]开展了明胶鸟弹以95 m/s的速度正/斜冲击钢板试验，采用弹塑性水动力材料结合多项式状态方程，运用任意拉格朗日-欧拉（arbitrary Lagrangian-Euler, ALE）算法和光滑粒子流体动力学（smoothed particle hydrodynamics, SPH）算法进行仿真，验证了模型的准确性。Zakir等[10]开展了明胶鸟弹以70～180 m/s速度冲击铝和钢平板试验，发现SPH方法得到的冲击力峰值和动态形貌与试验结果具有较好的一致性，但试件位移与试验测量值相差较大。冯振宇等[11]进行了明胶鸟弹冲击铝合金平板试验，对于80 m/s工况，使用拉格朗日弹塑性本构，对于130 m/s工况，使用SPH结合Murnaghan流体状态方程本构，得到了与试验相似的结果。Aslam等[12]采用Mooney-Rivlin超弹性材料结合拉格朗日离散，对比了122 m/s的明胶鸟撞试验，试验数据与数值预测结果基本相同。Pernas-Sánchez等[13]进行了在较宽速度范围（70～200 m/s）内明胶鸟弹冲击霍普金森杆试验，结果表明，低速工况下SPH鸟体无法很好地再现鸟体的径向膨胀和流动。综上所述，在目前的鸟撞研究中，对于不同速度区间采用不同的鸟体本构模型，低速下SPH模型无法较好地描述鸟体运动。基于此，本研究开展宽速域下多角度明胶鸟撞刚性平板试验，旨在通过结构动态响应（冲击力和冲量）等效方法，结合优化分析软件以及自适应FEM-SPH（finite element method-smoothed particle hydrodynamics）转换技术进行本构参数反演，建立一种适用于较宽速度范围的明胶鸟弹数值模型，为人工明胶鸟冲击试验的仿真研究提供一定的参考。
-
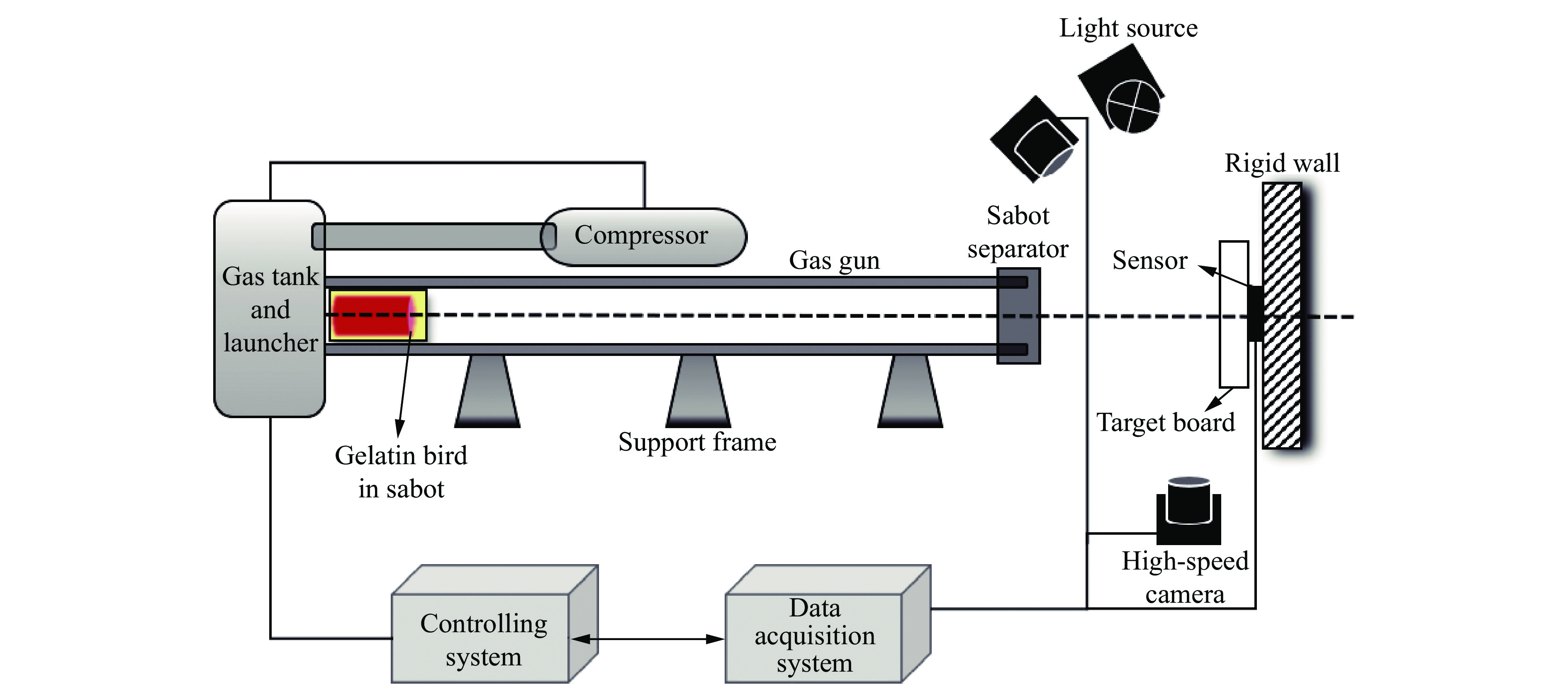
试验所用的空气炮试验设备如图1所示。将明胶鸟弹装入弹托，通过压缩空气将鸟弹射出，击中靶板正面中心。力传感器向数据采集系统传递冲击力数据，靶板侧面的高速摄像机用于测量鸟弹飞行速度，侧前方的高速摄像机用于记录鸟弹冲击过程中的变形、碎裂、飞溅等。
-
明胶鸟弹的制备工艺参考刘小川等[14]的研究，鸟弹为长径比为2∶1的圆柱体，底面半径为30.24 mm，高度为120.96 mm，质量为(330 ± 6) g，目标密度为950 kg/m3，孔隙率为10%。
鸟弹以不同速度、与靶板正面呈60°或90°入射。对于60°冲击试验，首先进行了110～190 m/s撞击试验。采用双传感器并联方式扩大传感器量程。在先进行的110、120、150 m/s试验中，除了110 m/s工况中因前2发试验的冲击力相差较大而补做了第3发试验以外，其余数据均具有较好的重合度，因此，后续的160～190 m/s工况均进行1次试验。在70～100 m/s工况中，改用单个传感器测量。在首先进行的70 m/s工况中，2组试验得到的冲击力数据的重合度较高，因此，后续的90和100 m/s工况均只进行1次试验。
本试验通过压力传感器测量靶板法向压力，为避免传感器损坏，90°工况的冲击速度范围较60°工况的冲击速度范围窄，为70～160 m/s。同样，受传感器量程的限制，在110～160 m/s的试验中使用双传感器并联，为确保试验的重复性，每种工况进行2次试验；对于70和80 m/s工况，改用单个传感器测量，首先进行的80 m/s的2组试验中所获得的冲击力数据的重合度较高，故70 m/s工况只进行1次试验。
为便于安装传感器，对于双传感器并联试验（对应的鸟撞速度较高），使用面积较大的长方形和梯形靶板；同时，考虑到60°撞击工况中鸟体在靶板上的滑移范围更大，采用面积相对较大的长方形靶板。对于单传感器测量试验（对应的鸟撞速度较低），考虑到传感器安装的便捷性和鸟体滑移面积较小，统一采用面积相对较小的正方形靶板。忽略圆角及螺孔，不同形状的靶板尺寸如图2所示。表1列出了18组共计28次人工鸟弹冲击试验结果，其中：u0为鸟弹的撞击速度，θ为撞击角度，m为鸟弹的质量。
-
受篇幅限制，选取工况12（110 m/s，90°）作为90°典型撞击工况、工况1（110 m/s，60°）作为60°典型撞击工况进行分析。
-
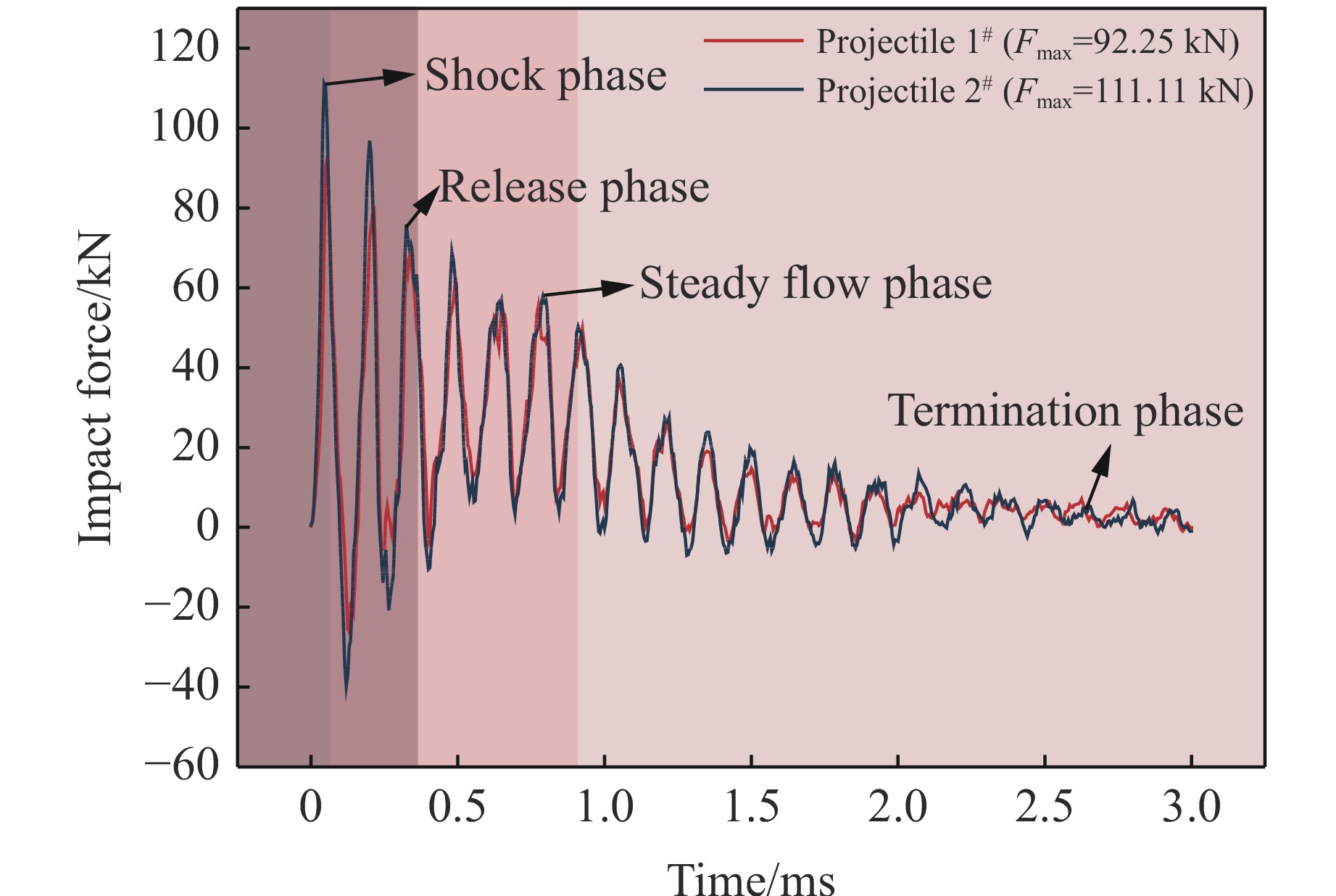
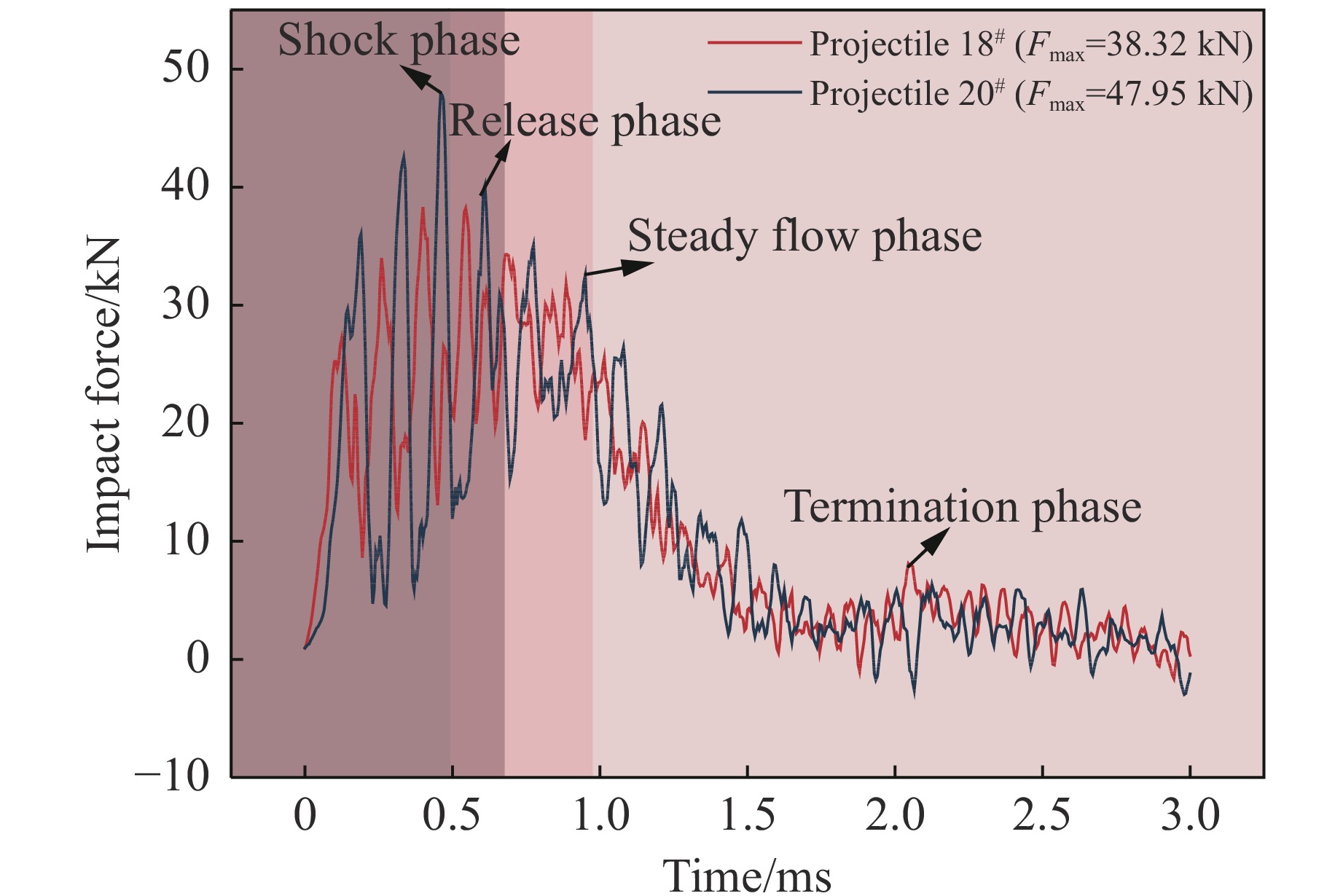
首先对重复试验结果的一致性进行验证。以相同工况下的冲击力作为对照，图3为典型90°撞击工况（工况12）下鸟弹飞行方向的冲击力时程曲线。可见，冲击力吻合得较好，可观察到初始冲击阶段、压力衰减阶段、稳态流动阶段和冲击结束阶段。图4为典型60°撞击工况（工况1）下垂直于靶板方向上的冲击力时程曲线。可见，冲击力也吻合得较好，载荷峰值（Fmax）的出现相对于90°工况滞后，平稳流动阶段缩短。
-
本试验中，用于测速的高速摄像机的帧率为44 kHz，用于观测形貌的高速摄像机的帧率为28 kHz。图5为鸟弹1#的高速摄影照片。0 ms时，鸟弹撞击靶板，鸟弹前端开始发生变形，沿靶板表面径向扩散；0.25 ms时，鸟弹的初始冲击过程结束，最外端开始发生裂解，冲击区域的压力开始衰减；随后，进入平稳流动阶段，1.00 ms时，平稳流动阶段基本结束，该时间约等于鸟弹长度除以鸟弹撞击速度；3.00 ms时，弹体完全碎裂，冲击过程结束。图6为鸟弹18#的高速摄像照片。鸟弹在0.20 ms出现边缘碎裂现象，在0.50 ms出现载荷峰值，3.00 ms冲击过程结束。相比于鸟弹1#，鸟弹18#出现了更大的碎块。
图7显示了90°撞击工况下鸟弹以不同速度撞击靶板时3.00 ms时的形貌对比。不同冲击速度下，鸟弹均发生彻底的碎裂；u0=74.7 m/s时，鸟弹出现了回弹以及互相粘连的较大碎块；u0=112.9 m/s时，碎块变小，中间夹杂着大碎块，飞溅距离增加；u0=158.5 m/s时，碎块更小，基本全部为小碎块。
-
采用有限元软件LS-DYNA建立靶板和人工鸟弹的有限元模型。选用六面体单元划分靶板和人工鸟弹，鸟弹的单元数为
9700 ，梯形、长方形及正方形靶板的单元数分别为23192 、33480 、30016 ，通过调节鸟弹密度控制鸟弹质量，对靶板底面实施固支约束。靶板材料选择7075铝合金，其材料参数列于表2，采用双线性随动强化材料模型描述。 -
鸟撞是涉及大变形、破碎、侵蚀和流固耦合的复杂软体高速冲击行为。当材料接触界面发生较大变形时，传统的FEM如拉格朗日法、欧拉法、ALE算法等易发生网格畸变，且删除失效单元会导致系统质量不守恒，带来计算误差及形貌失真。以SPH方法为代表的无网格数值方法采用离散粒子表示连续体，不会发生由大变形引起的畸变，但存在拉伸不稳定、精度较差的问题[15]。
-
根据Liu等[6, 16]的研究：当撞击速度较低时，鸟体破碎成较大的碎片，其本构模型应采用带失效模式的弹塑性模型；当撞击速度较高时，鸟体破碎较为细碎，表现为流体特征，其本构模型应采用描述流体行为的状态方程。定义失效应变的弹塑性拉格朗日模型最适于模拟低速鸟撞（69 m/s），各向同性弹塑性水动力拉格朗日模型最适于模拟中速鸟撞（116 m/s），SPH粒子结合Murnaghan状态方程最适于模拟高速鸟撞（172 m/s）。冯振宇等[11]在低速（80 m/s）工况下使用拉格朗日弹塑性本构，在高速 （130 m/s）工况下使用SPH结合Murnaghan流体状态方程本构，较好地描述了鸟撞动态响应，但是不同速度下的鸟体本构参数不能通用。
基于LS-DYNA有限元软件的自适应FEM-SPH转换方法可以结合FEM和无网格方法的优点，避免其局限性[17]。该方法使用LS-DYNA中的关键字*DEFINE_ADAPTIVE_SOLID_TO_SPH，此时需要明确参与转换的有限元实体部件ID、每个有限元单元转换成SPH粒子数量、转换后的SPH部件ID、SPH粒子截面属性以及SPH粒子与固体单元之间的耦合算法。该方法需要先定义拉格朗日实体单元的材料截面属性、初始条件、失效准则和接触算法，并定义SPH粒子的材料截面属性、状态方程以及接触算法。本研究将每个实体单元转换为1个SPH粒子，赋予其相同的密度。在运动初期，SPH粒子跟随实体单元同步运动，但未激活参与计算，在有限元单元失效并删除时，自动将失效单元转换为SPH粒子，并继承原单元的速度。设置耦合算法相关参数ICPL和IOPT为1，表示新生成的SPH粒子需计算其与附近实体单元之间的耦合作用，且该粒子在对应单元失效删除后才被激活，从而避免了因单元删除而导致的质量不守恒和网格畸变。冲击结束后，用尚未失效的实体单元表征较大的鸟体碎块。
-
低速时明胶鸟弹展现出弹塑性属性，带损伤破坏的弹塑性本构采用LS-DYNA中的*MAT_ISOTROPIC_ELASTIC_FAILURE和拉格朗日单元表征，弹性变形阶段的应力-应变关系由剪切模量G和体积模量K表征
式中：E为杨氏模量，ν为泊松比。设σs为初始屈服应力，则塑性变形阶段的应力-应变关系为
式中：σy为塑性应力，εp为有效塑性应变，Ep为塑性硬化模量。设Et为切线模量，则Ep为
设εf为单元失效的最大塑性应变，以描述材料的失效行为，即当εp>εf时，单元失去承载能力，偏应力为零，材料表现为流体，拉格朗日单元转换成SPH粒子。接触算法采用关键字*CONTACT_ERODING_SURFACE_TO_SURFACE，将拉格朗日鸟体定义为从段，靶板定义为主段。待反演关键参数为G、K、σs、Et和εf。
-
明胶鸟弹在高速下呈现流体性质，因此，选择SPH粒子表征，采用状态方程（equation of state, EOS）控制SPH粒子的流体行为，从而有效地避免了拉格朗日网格单元在高速下发生畸变和沙漏现象。流体本构采用Murnaghan状态方程表征
式中：p为压强，p0为初始压强，ρ为流体瞬时密度，ρ0为流体初始密度，B为状态方程参数，γ为无量纲系数。LS-DYNA中Murnaghan状态方程的表达式为
反演关键参数为状态方程参数k0和指数γ。材料选择MAT_NULL空材料，该材料没有屈服强度，表现为流体性质，材料参数见表3。接触算法采用关键字*CONTACT_AUTOMATIC_NODES_TO_SUR-FACE定义，从段为SPH粒子鸟体，主段为靶板。
-
采用集成优化软件Isight，首先在90°和60°撞击工况下每个速度区间中选取1个模型，其次将所有模型输入第1个Simcode组件中，识别反演关键参数，并调用LS-DYNA运行k文件。通过第2个Simcode组件调用后处理软件LS-Prepost输出载荷时程曲线，其中某时刻载荷等于拉格朗日单元与SPH粒子在该时刻的瞬时冲击力的线性和。将试验载荷和数值分析载荷的时程曲线输入Data Matching组件，计算2条曲线的绝对差值之和。使用试验设计DOE（design of experiment） 组件，通过优化拉丁超立方方法抽样，在参数取值范围内均匀取
1500 组参数，优化目标为使所有工况中2条曲线的绝对差值之和最小。表4列出了本构参数的取值范围及优化结果。 -
为验证本构参数的有效性，对比了数值模拟与试验得到的冲击力、冲量和动态形貌。采用SPH方法，选取空材料及Murnaghan状态方程参数k0 = 282 MPa，γ = 7.95[10]，采用带损伤破坏的弹塑性模型参数G = 261.6 MPa，K = 188 MPa，σs = 1.249 MPa，Et = 3.017 MPa，εf = 0.81[11]，分别建立明胶鸟弹数值模型，SPH粒子数为
10104 ，拉格朗日单元数为9700 。在相同工况下，将传统本构模型与自适应FEM-SPH模型进行对比。 -
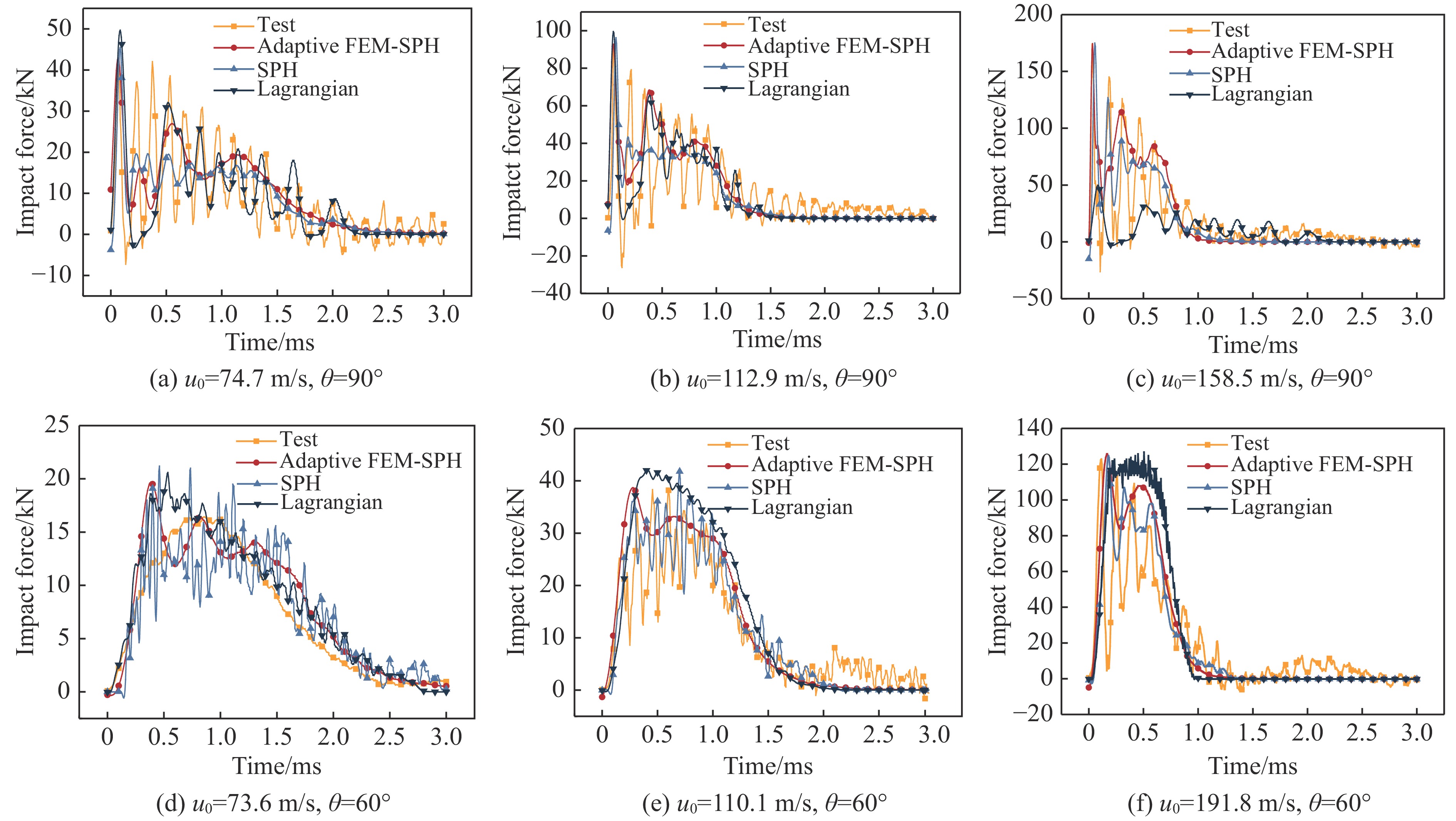
有限元分析表明，鸟撞冲击力及破坏形貌与不同形状的靶板几乎不具有相关性，相同撞击速度下3种靶板得到几乎相同的冲击力结果和形貌结果，因此，取90°撞击条件下鸟弹36#、1#、11#分别代表90°低、中、高速典型撞击工况，取60°撞击条件下鸟弹40#、18#、27#分别代表60°低、中、高速典型撞击工况。载荷时程曲线对比如图8所示。对于90°撞击工况，自适应本构和弹塑性本构在u0=74.7 m/s和u0=112.9 m/s的条件下得到的模拟载荷曲线走势与试验曲线较一致，在平稳流动阶段，SPH本构得到的载荷水平较低；在u0=158.5 m/s的条件下，弹塑性本构得到的载荷水平与试验结果相差较大，自适应本构则能较好地模拟冲击力。对于60°撞击工况，在u0为73.6、110.1、191.8 m/s的条件下自适应本构和SPH本构的模拟结果均与试验数据吻合得较好，弹塑性本构模拟结果则偏高。与模拟曲线相比，试验曲线的振荡更明显，推测为传感器与靶板的连接处在高速冲击下出现振荡所致。
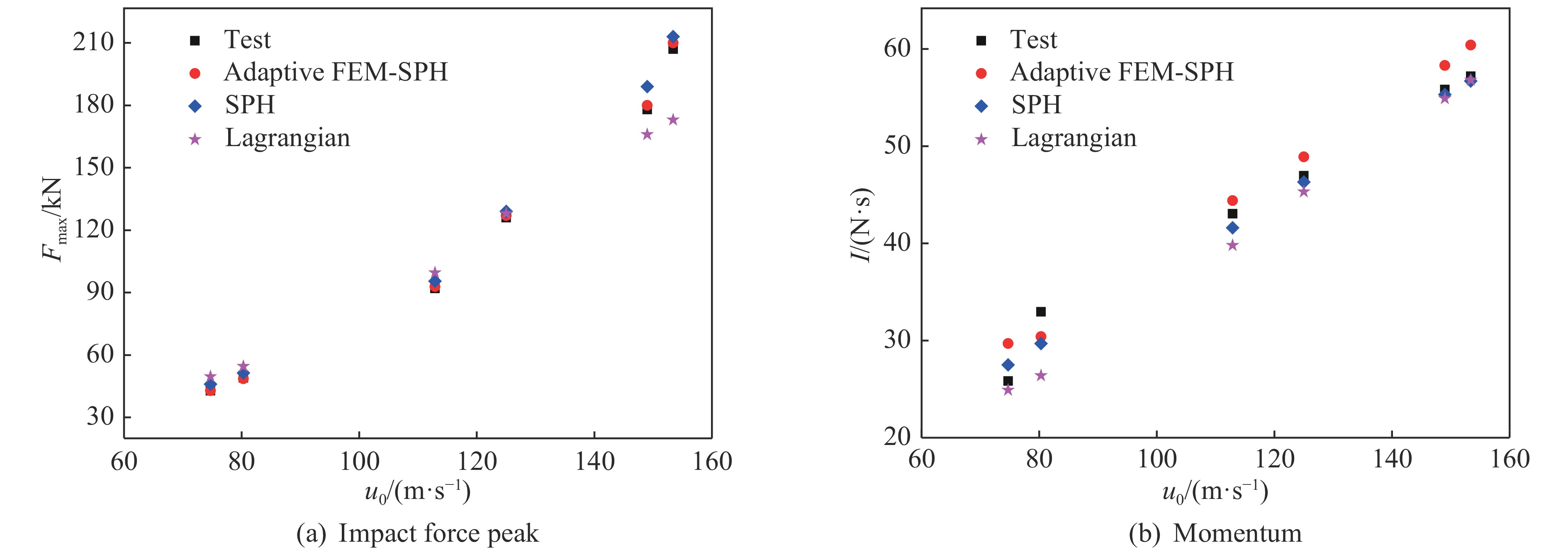
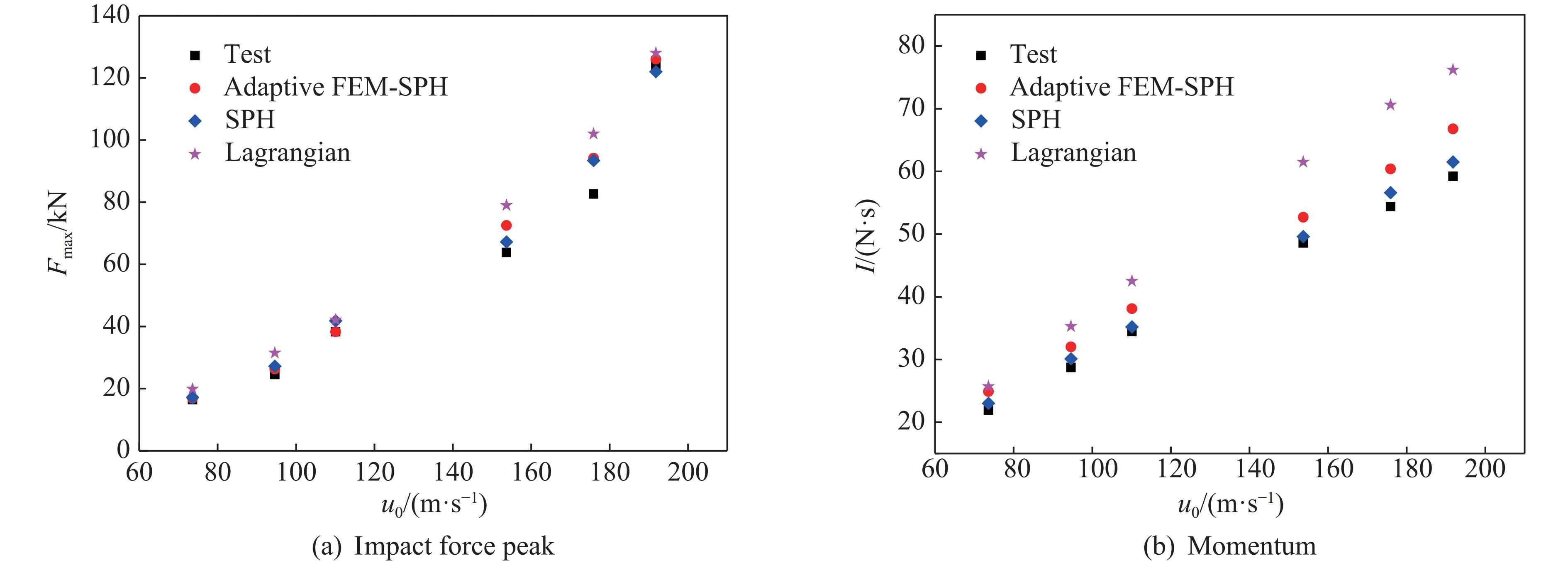
图9和图10给出了90°和60°工况下数值模拟与试验得到的载荷峰值Fmax及冲量I的对比。对于90°工况，自适应FEM-SPH模型得到的载荷峰值与试验值的相对误差在2%以内，冲量的相对误差基本在10%以内，相比于SPH和拉格朗日模型，具有更高的精度。对于60°工况，自适应FEM-SPH模型得到的载荷峰值及冲量与试验结果的相对误差均在10%左右，SPH模型和自适应FEM-SPH模型均具有较高的模拟精度，拉格朗日模型的模拟结果与实验结果的相对误差较大。
-
图11、图12和图13显示了低、中、高速典型工况下数值模拟与试验得到的鸟弹形貌对比。可以看出：低速（74.7 m/s）时，自适应FEM-SPH模型存在相互粘连的、较大的拉格朗日单元碎块；中速 （112.9 m/s）时，碎块逐渐减小，SPH粒子占比增多；高速（158.5 m/s）时，碎块完全消失，只保留了SPH粒子。对比3种本构模型，可以看出：SPH模型无法较好地反映低速下的大碎块和弹体粘连状态，无法体现中速下的较大碎块；拉格朗日模型的结果显示，低速下鸟弹未能完全碎裂，中速和高速下由于失效单元被删除，导致严重的形貌失真，无法准确表现鸟弹的碎裂及碎块飞溅过程；自适应FEM-SPH模型能够更好地模拟鸟弹碎裂形貌。
-
采用自适应FEM-SPH鸟弹模型计算了90°撞击工况下初始冲击激波区域的Hugoniot压强及稳态流动的滞止压强，并与不同学者得到的研究数据及理论值进行对比。
对于高速鸟撞，由于鸟体的屈服应力远小于冲击产生的应力，可将其视为流体力学行为，且鸟体的密度通常接近水的密度，因此，鸟撞力学理论通常近似为水的冲击[18]。根据Wilbeck[19]的理论，鸟弹90°正撞刚性平板可视为伴随激波的一维绝热不可逆流动过程，初始冲击压强（Hugoniot压强，pH）可表示为
式中：ρ1为波前物质密度，us为激波速度。
明胶鸟弹可简化为空气与明胶体的混合物，设空气的体积分数（即孔隙率）为x，则有
式中：ρave为明胶鸟弹的平均密度，ρair为空气密度，ρbody为明胶体的密度。在标准大气压、20 ℃下，ρair = 1.204 kg/m3，ρbody =
1060 kg/m3。本试验所用的人工明胶鸟弹的平均密度为951.78 kg/m3，经计算，孔隙率约为0.1。根据式 (7)，ρ1 =ρave = 951.78 kg/m3。对于多孔材料中的激波速度，有
式中：k为材料的相关常数，这里采用水的常数，即k = 2；水中声速
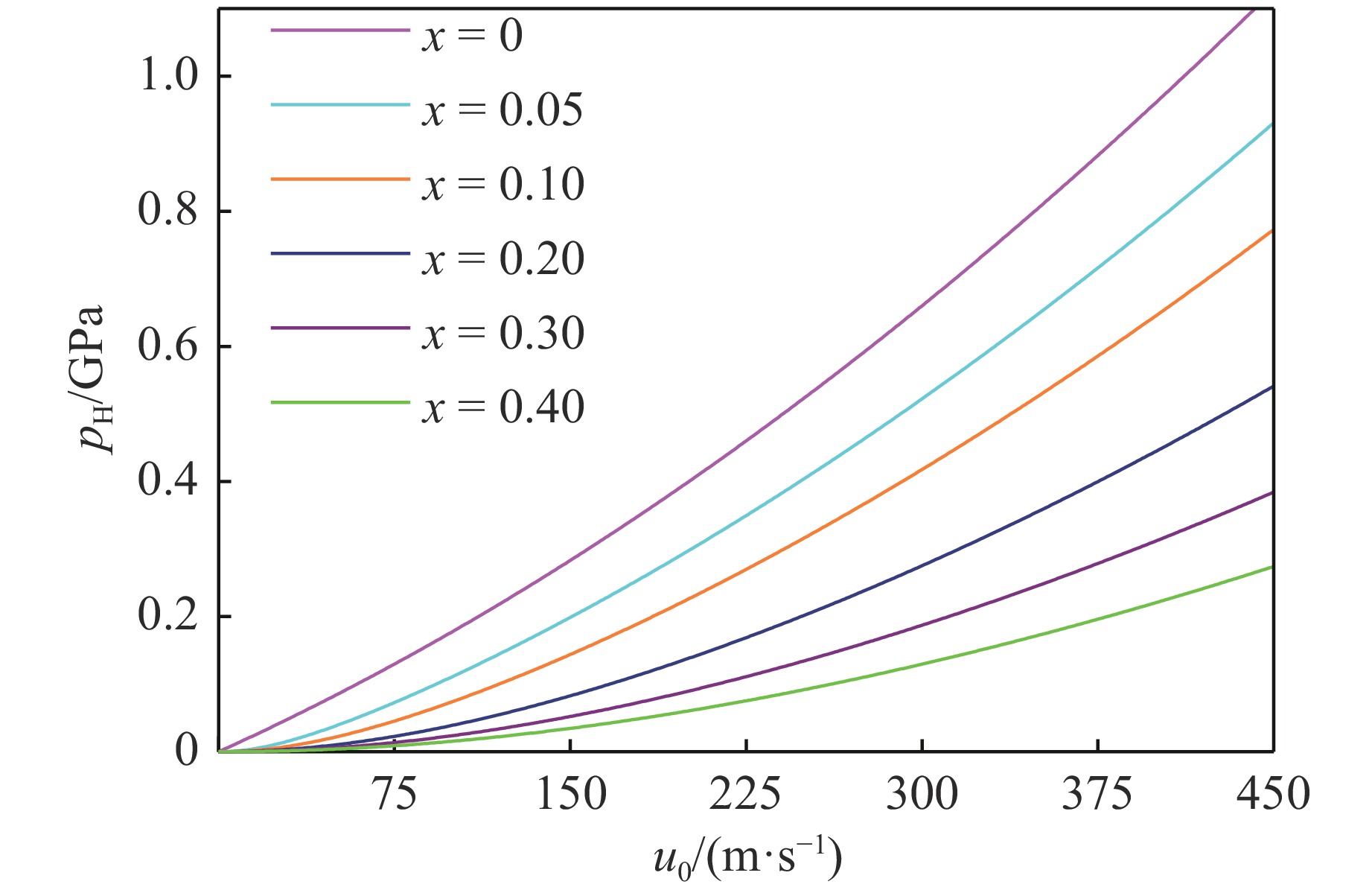
$ {c_0} $ =1482.9 m/s。通过式 (9) 解出us之后，代入式 (7) 可计算出Hugoniot压强。图14显示了明胶孔隙率x对Hugoniot压强的影响。在150 m/s撞击速度下，x=0.10的明胶鸟弹的Hugoniot压强仅为x=0时的1/2。
明胶鸟弹冲击刚性靶板瞬间，激波在鸟弹边缘处产生释放波，释放波与激波接触后，激波的压强和速度大幅衰减，释放波多次反射后，形成了稳定流动态[1]。对于不可压缩流体，滞止压强ps为
在LS-Prepost中提取鸟弹与靶板初始撞击中心的拉格朗日单元和SPH粒子，读取压强数据，仅选取初始冲击区域中心的单元/粒子，读取拉格朗日单元和SPH粒子的压强时程曲线。可以发现：对于拉格朗日实体单元，压强最大值与冲击力极值基本在同一时刻获取，而SPH粒子则由于初始时刻未被激活，极大值点出现的时间滞后约1 ms。本研究取拉格朗日单元压强的极大值作为Hugoniot压强，并与x=0.10的明胶材料的理论Hugoniot压强进行对比。
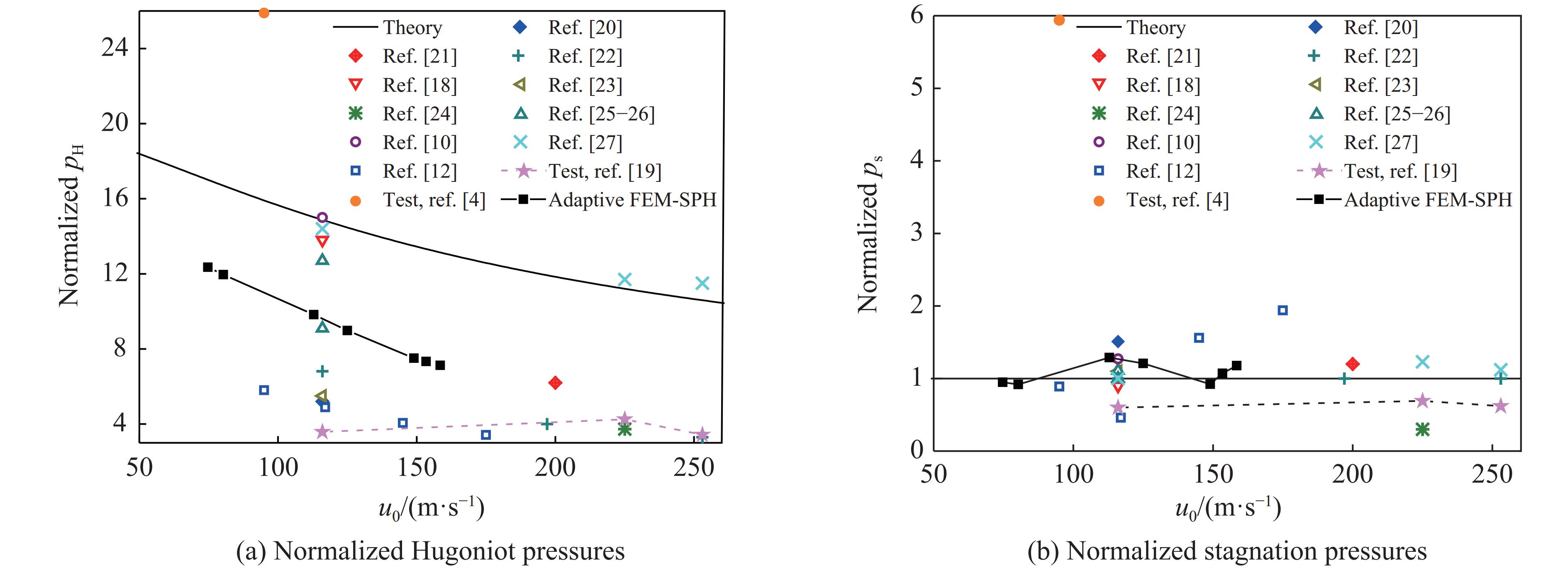
平稳流动状态在激波经过后才发生，读取90°工况模拟得到的压强云图，发现在鸟弹中部撞击靶板时刻，各工况均达到平稳流动状态，因此，读取鸟弹弹体中部与靶板接触的几何中心位置单元的压强时程曲线，取接触时刻的压强作为滞止压强，滞止压强的理论解可由式 (10) 得到，其中ρ = 951.78 kg/m3。图15和表5显示了不同学者[10, 12, 18, 20–27]通过数值模拟得到的Hugoniot压强和滞止压强，为方便对比，本研究计算了归一化Hugoniot压强和滞止压强，即均除以
$ \rho u_0^2/2 $ ，此外图15还标出了Wilbeck[19]和Lavoie等[4]的试验测量值和自适应FEM-SPH模型的数值计算值。从图15可以看出，Hugoniot压强的理论值与试验值相差甚远，特别是在低速（小于100 m/s）和中速（约110 m/s）条件下。数值计算值处于试验值与理论值之间，Hedayati等[27]在116、225、253 m/s的条件下均获得了与理论值接近的数值计算值，Aslam等[12]在145、175 m/s的条件下得到的数值计算值与Wilbeck[19]的试验值接近。本研究的自适应FEM-SPH模型的数值计算值随撞击速度的变化趋势与理论值一致。对于稳态滞止压强，除Lavoie等[4]在u0=95 m/s下得到的试验数据过大外，包括本研究在内的所有研究结果并没有很大的差异，自适应FEM-SPH模型的归一化滞止压强约为1。
-
(1) 在人工鸟弹撞击铝合金刚性平板试验中，随着撞击速度的增大，鸟弹碎裂得越充分，低速下会出现较大的回弹碎块和粘连现象，高速下基本为小碎块，相同撞击速度下，60°撞击工况比90°撞击工况出现更多的大碎块。
(2) 自适应FEM-SPH本构模型能够有效模拟低、中、高速撞击下90°和60°撞击角度下的鸟撞形貌，且冲击力时程曲线与试验曲线具有很好的一致性，载荷峰值及冲量与试验结果的相对误差基本在10%以内。
(3) 相比于单独使用SPH状态方程本构模型和拉格朗日弹塑性本构模型，自适应FEM-SPH本构模型可以根据失效判据自动分配拉格朗日单元和SPH粒子占据的比例，同一组本构参数适用于所有工况，能够更好地反映弹体的碎裂形貌，避免高速下的网格畸变现象，并具备更高的计算精度。
(4) Hugoniot压强的试验值与理论值相差较大，不同学者得到的数值计算值的离散性较大，自适应FEM-SPH模型得到的Hugoniot压强变化趋势与理论值的变化趋势一致，滞止压强的数值计算值与理论值基本相同。
一种适用宽速域冲击的明胶鸟弹数值建模方法
A Numerical Modeling Method of Gelatin Bird Projectile Suitable for Wide-Speed-Range Impact
-
摘要: 明胶鸟弹在不同撞击速度下表现出不同的响应特性。为解决传统明胶鸟弹本构表征方法在不同速度范围内不能通用的问题，开展了330 g明胶鸟弹以70～190 m/s速度、60°或90°入射刚性铝合金平板试验，记录了冲击力数据及撞击形貌。结果表明，随着撞击速度的提高，鸟弹碎裂得更充分，碎块体积减小。利用LS-DYNA建立了自适应FEM-SPH（finite element method-smoothed particle hydrodynamics）鸟体模型。依据试验结果反演得到一组鸟体本构参数：切线模量为1.33 MPa，剪切模量为115.95 MPa，Murnaghan状态方程参数γ为10.49，k0为69.77 MPa，体积模量为246.4 MPa，失效塑性应变为1.15，初始屈服应力为0.21 MPa。仿真结果与试验结果具有很好的一致性，冲击力峰值的相对误差在2%以内，冲量的相对误差在10%以内。自适应FEM-SPH鸟体模型具有比SPH模型和拉格朗日模型更高的精度。由自适应模型得到的Hugoniot压强与理论结果具有相同的变化趋势，滞止压强与理论值较接近。Abstract: Previous studies revealed that gelatin birds show different mechanical behaviors at different impact velocities. In order to solve the problem that the traditional constitutive methods of gelatin bird cannot be universal in different velocity ranges, the tests of 330 g gelatin birds impacting rigid aluminum alloy plate at 60° and 90° incident angles, covering a velocity range of 70−190 m/s were carried out to record the impact force data and impact morphology. With the increase of velocity, the birds were broken more fully and smaller fragments were observed. The adaptive FEM-SPH (finite element method-smoothed particle hydrodynamics) model of bird was established in LS-DYNA, and a set of constitutive parameters were inverted according to the test results: tangent modulus equals to 1.33 MPa, shear modulus equals to 115.95 MPa, the parameters of Murnaghan equation of state γ equals to 10.49, k0 equals to 69.77 MPa, bulk modulus equals to 246.4 MPa, failure plastic strain is 1.15, yield stress is 0.21 MPa. The simulation results were in good agreement with the test results, and had higher accuracy compared to the SPH models and the Lagrangian models. The Hugoniot pressure of the adaptive model had the same change trend as the theoretical value, and the stagnation pressure was close to the theoretical value.
-
-
图 3 90°撞击工况（工况12）的冲击力对比
Figure 3. Comparison of the impact forces in Case 12 with the impact angle of 90°
图 4 60°撞击工况（工况1）的冲击力对比
Figure 4. Comparison of the impact forces in Case 1 with the impact angle of 60°
图 7 不同冲击速度下的高速摄像图像对比（θ=90°）
Figure 7. Comparison of high-speed camera photos at different impact velocities (θ=90°)
图 8 不同工况下试验与数值模拟得到的冲击力对比
Figure 8. Comparison of the test and numerical impact forces in different cases
图 9 90°工况下数值模拟得到的峰值载荷及冲量与试验结果的对比
Figure 9. Comparison of the numerical and test impact force peak and momentum under 90° impact
图 10 60°工况下数值模拟得到的峰值载荷及冲量与试验结果的对比
Figure 10. Comparison of the numerical and test impact force peak and momentum under 60° impact
图 11 74.7 m/s撞击速度下数值模拟和试验得到的撞击过程对比
Figure 11. Comparison of the numerical and test impact processes at the impact velocity of 74.7 m/s
图 12 112.9 m/s撞击速度下数值模拟与试验得到的撞击过程对比
Figure 12. Comparison of the numerical and test impact processes at the impact velocity of 112.9 m/s
图 13 158.5 m/s撞击速度下数值模拟与试验得到的撞击过程对比
Figure 13. Comparison of the numerical and test impact processes at the impact velocity of 158.5 m/s
图 14 具有不同孔隙率的圆柱明胶鸟弹的理论Hugoniot压强随撞击速度的变化
Figure 14. Hugoniot pressure vs. impact velocity for cylindrical gelatin bird projectiles with various porosities
图 15 归一化Hugoniot压强和归一化滞止压强的数值计算结果与试验结果及理论值的对比
Figure 15. Comparison of normalized Hugoniot pressures and normalized stagnation pressures between the theoretical values, test values and numerical results
表 1 不同工况下鸟撞试验结果
Table 1. Test results of bird impact under various impact conditions
Case u0/(m·s−1) θ/(°) Plate shape Bird projectile No. (m, actual impact velocity) 1 110 60 Rectangular 18# (334 g, 110.1 m/s), 20# (329.5 g, 107.0 m/s) 2 110 60 Rectangular 29# (326 g, 114.7 m/s) 3 120 60 Rectangular 21# (327 g, 124.6 m/s), 22# (328 g, 124.1 m/s) 4 150 60 Rectangular 23# (331 g, 150.1 m/s), 24# (330 g, 153.7 m/s) 5 160 60 Rectangular 25# (331 g, 166.6 m/s) 6 170 60 Rectangular 26# (328 g, 175.9 m/s) 7 180 60 Rectangular 28# (331 g, 185.3 m/s) 8 190 60 Rectangular 27# (332 g, 191.8 m/s) 9 70 60 Square 39# (328 g, 75.2 m/s), 40# (328 g, 73.6 m/s) 10 90 60 Square 37# (328 g, 94.6 m/s) 11 100 60 Square 38# (327 g, 99.6 m/s) 12 110 90 Trapezoidal 1# (336 g, 112.9 m/s), 2# (328 g, 113.1 m/s) 13 120 90 Trapezoidal 5# (333 g, 125.0 m/s), 12# (334 g, 121.8 m/s) 14 150 90 Trapezoidal 6# (332 g, 149.0 m/s), 7# (328 g, 148.8 m/s) 15 150 90 Trapezoidal 8# (332 g, 153.4 m/s), 9# (333 g, 148.8 m/s) 16 160 90 Trapezoidal 10# (325 g, 165.3 m/s), 11# (329 g, 158.5 m/s) 17 80 90 Square 34# (330 g, 84.9 m/s), 35# (329 g, 80.3 m/s) 18 70 90 Square 36# (330.5 g, 74.7 m/s) 
下载: 导出CSV
表 2 铝合金的材料参数
Table 2. Material parameters of aluminum alloy
Density/(kg·m−3) Young’s modulus/GPa Poisson’s ratio Yield stress/MPa Tangent modulus/GPa 2796 71 0.33 450 5
下载: 导出CSV
表 3 SPH鸟体材料参数
Table 3. Material parameters of SPH bird model
Density/(kg·m−3) Cut-off pressure/MPa Dynamic viscosity/(Pa·s) 950 −1 0.001
下载: 导出CSV
表 4 自适应FEM-SPH模型的本构参数优化结果
Table 4. Optimization results of constitutive parameters for adaptive FEM-SPH model
Value Et/MPa G/MPa γ K/MPa k0/MPa εf σs/MPa Range 0.01−2.00 1−300 1−20 1−300 1−300 0.01−1.20 0.01−1.00 Optimal value 1.33 115.95 10.49 246.4 69.77 1.15 0.21
下载: 导出CSV
表 5 不同学者通过数值模拟得到的归一化Hugoniot压强和滞止压强[10, 12, 18, 20–27]
Table 5. Numerical results of normalized Hugoniot and stagnation pressures calculated by different researchers[10, 12, 18, 20–27]
Ref. u0/(m·s−1) Normalized pH Normalized ps m/kg Density/(kg·m−3) Bird model geometry [20] 116 5.2 1.5 1.8 938 Hemispherical-ended [21] 200 6.2 1.2 0.6 930 Cylinder [22] 116 6.8 1.0 1.8 934 Hemispherical-ended [22] 197 4.0 1.0 1.8 934 Hemispherical-ended [22] 253 3.3 1.0 1.8 934 Hemispherical-ended [18] 116 13.8 0.9 1.0 950 Hemispherical-ended [23] 116 5.5 1.1 1.8 950 Hemispherical-ended [24] 225 3.7 0.3 1.8 934 Cylinder [25] 116 12.7 1.1 1.8 938 Hemispherical-ended [26] 116 9.1 1.0 1.7 950 Hemispherical-ended [10] 116 15.0 1.3 0.2 1019 Cylinder [27] 116 14.4 1.0 0.8 938 Hemispherical-ended [27] 225 11.7 1.2 0.8 938 Hemispherical-ended [27] 253 11.5 1.1 0.8 938 Hemispherical-ended [12] 95 5.8 0.9 1.3 968 Cylinder [12] 117 4.9 0.5 1.3 968 Cylinder [12] 145 4.1 1.6 1.3 968 Cylinder [12] 175 3.4 1.9 1.3 968 Cylinder
下载: 导出CSV
-
[1] GUIDA M, MARULO F, BELKHELFA F Z, et al. A review of the bird impact process and validation of the SPH impact model for aircraft structures [J]. Progress in Aerospace Sciences, 2022, 129: 100787. doi: 10.1016/j.paerosci.2021.100787 [2] 张迎春, 陆晓华, 张柱国. 运输类飞机鸟撞适航要求解析及审定实践 [M]. 北京: 科学出版社, 2023: 39–40. ZHANG Y C, LU X H, ZHANG Z G. Transport category airplane bird-strike airworthiness regulations interpretation and certification practice [M]. Beijing: Science Press, 2023: 39–40. [3] 刘小川, 王计真, 白春玉. 人工鸟研究进展及在飞机结构抗鸟撞中的应用 [J]. 振动与冲击, 2021, 40(12): 80–89. doi: 10.13465/j.cnki.jvs.2021.12.011 LIU X C, WANG J Z, BAI C Y. Overview on artificial bird and application on the structural bird-strike [J]. Journal of Vibration and Shock, 2021, 40(12): 80–89. doi: 10.13465/j.cnki.jvs.2021.12.011 [4] LAVOIE M A, GAKWAYA A, ENSAN M N, et al. Bird’s substitute tests results and evaluation of available numerical methods [J]. International Journal of Impact Engineering, 2009, 36(10/11): 1276–1287. doi: 10.1016/j.ijimpeng.2009.03.009 [5] 王富生, 李立州, 王新军, 等. 鸟体材料参数的一种反演方法 [J]. 航空学报, 2007, 28(2): 344–347. doi: 10.3321/j.issn:1000-6893.2007.02.018 WANG F S, LI L Z, WANG X J, et al. A method to identify bird’s material parameters [J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(2): 344–347. doi: 10.3321/j.issn:1000-6893.2007.02.018 [6] LIU J, LI Y L, GAO X S. Bird strike on a flat plate: experiments and numerical simulations [J]. International Journal of Impact Engineering, 2014, 70: 21–37. doi: 10.1016/j.ijimpeng.2014.03.006 [7] 王计真, 刘小川. 鸟撞平板试验与鸟体本构参数识别方法 [J]. 航空学报, 2017, 38(Suppl 1): 721550. doi: 10.7527/S1000-6893.2017.721550 WANG J Z, LIU X C. Test of bird striking on panel and identification method for bird constitutive parameters [J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(Suppl 1): 721550. doi: 10.7527/S1000-6893.2017.721550 [8] ZHANG Y L, ZHOU Y D. Evaluating constitutive models of smoothed particle hydrodynamics for bird-strike simulation [J]. International Journal of Crashworthiness, 2023: 1–10. doi: 10.1080/13588265.2023.2258650 [9] YU P, YU S L, HE S, et al. Inversion for constitutive model parameters of bird in case of bird striking [J]. Shock and Vibration, 2022: 2456777. doi: 10.1155/2022/2456777 [10] ZAKIR S M, LI Y L. Dynamic response of the leading edge wing under soft body impact [J]. International Journal of Crashworthiness, 2012, 17(4): 357–376. doi: 10.1080/13588265.2012.661239 [11] 冯振宇, 霍雨佳, 裴惠, 等. 明胶鸟弹撞击力传感器试验及数值建模方法研究 [J]. 振动与冲击, 2019, 38(12): 206–212. doi: 10.13465/j.cnki.jvs.2019.12.029 FENG Z Y, HUO Y J, PEI H, et al. An experiment and numerical modeling method of gelatin bird striking on force sensors [J]. Journal of Vibration and Shock, 2019, 38(12): 206–212. doi: 10.13465/j.cnki.jvs.2019.12.029 [12] ASLAM M A, RAYHAN S B, KE Z G, et al. Ballistic gelatin Lagrange Mooney-Rivlin material model as a substitute of bird in finite element bird strike case studies [J]. Latin American Journal of Solids and Structures, 2020, 17(6): e298. doi: 10.1590/1679-78256215 [13] PERNAS-SÁNCHEZ J, ARTERO-GUERRERO J, VARAS D, et al. Artificial bird strike on Hopkinson tube device: experimental and numerical analysis [J]. International Journal of Impact Engineering, 2020, 138: 103477. doi: 10.1016/j.ijimpeng.2019.103477 [14] 刘小川, 郭军, 孙侠生, 等. 用于鸟撞试验的仿真鸟弹研究 [J]. 实验力学, 2012, 27(5): 623–629. LIU X C, GUO J, SUN X S, et al. Investigation on the artificial bird projectile used in bird strike test [J]. Journal of Experimental Mechanics, 2012, 27(5): 623–629. [15] YANG X F, LIU M B, PENG S L. Smoothed particle hydrodynamics modeling of viscous liquid drop without tensile instability [J]. Computers & Fluids, 2014, 92: 199–208. doi: 10.1016/j.compfluid.2014.01.002 [16] 刘军, 李玉龙, 郭伟国, 等. 鸟撞45#钢平板动响应试验研究 [J]. 振动与冲击, 2013, 32(4): 15–20. doi: 10.3969/j.issn.1000-3835.2013.04.004 LIU J, LI Y L, GUO W G, et al. Tests for bird striking on a plate made of 45# steel [J]. Journal of Vibration and Shock, 2013, 32(4): 15–20. doi: 10.3969/j.issn.1000-3835.2013.04.004 [17] HE Q G, CHEN X W, CHEN J F. Finite element-smoothed particle hydrodynamics adaptive method in simulating debris cloud [J]. Acta Astronautica, 2020, 175: 99–117. doi: 10.1016/j.actaastro.2020.05.056 [18] LAVOIE M A, GAKWAYA A, ENSAN M N, et al. Validation of available approaches for numerical bird strike modeling tools [J]. International Review of Mechanical Engineering, 2007, 1(4): 380–389. [19] WILBECK J S. Impact behavior of low strength projectiles [D]. College Station: Texas A&M University, 1977. [20] JOHNSON A F, HOLZAPFEL M. Modelling soft body impact on composite structures [J]. Composite Structures, 2003, 61(1/2): 103–113. doi: 10.1016/S0263-8223(03)00033-3 [21] AIROLDI A, CACCHIONE B. Modelling of impact forces and pressures in Lagrangian bird strike analyses [J]. International Journal of Impact Engineering, 2006, 32(10): 1651–1677. doi: 10.1016/j.ijimpeng.2005.04.011 [22] JENQ S T, HSIAO F B, LIN I C, et al. Simulation of a rigid plate hit by a cylindrical hemi-spherical tip-ended soft impactor [J]. Computational Materials Science, 2007, 39(3): 518–526. doi: 10.1016/j.commatsci.2006.08.008 [23] THO C H, SMITH M R. Accurate bird strike simulation methodology for BA609 tiltrotor [J]. Journal of the American Helicopter Society, 2011, 56(1): 12007. doi: 10.4050/JAHS.56.012007 [24] MEGUID S A, MAO R H, NG T Y. FE analysis of geometry effects of an artificial bird striking an aeroengine fan blade [J]. International Journal of Impact Engineering, 2008, 35(6): 487–498. doi: 10.1016/j.ijimpeng.2007.04.008 [25] SMOJVER I, IVANČEVIĆ D. Numerical simulation of bird strike damage prediction in airplane flap structure [J]. Composite Structures, 2010, 92(9): 2016–2026. doi: 10.1016/j.compstruct.2009.12.006 [26] SMOJVER I, IVANČEVIĆ D. Advanced modelling of bird strike on high lift devices using hybrid Eulerian-Lagrangian formulation [J]. Aerospace Science and Technology, 2012, 23(1): 224–232. doi: 10.1016/j.ast.2011.07.010 [27] HEDAYATI R, SADIGHI M, MOHAMMADI-AGHDAM M. On the difference of pressure readings from the numerical, experimental and theoretical results in different bird strike studies [J]. Aerospace Science and Technology, 2014, 32(1): 260–266. doi: 10.1016/j.ast.2013.10.008 -
计量
- 文章访问数: 114
- HTML全文浏览数: 114
- PDF下载数: 3
- 施引文献: 0