本研究中的理论计算均基于密度泛函理论（density functional theory，DFT），在Materials Studio中的量子力学模块—Castep^[14]中完成。采用超软膺势（ultrasoft pseudopotential）描述离子-电子相互作用，PBE（perdew burke ernzerhof）^[15]和GGA（generalized gradient approximation）^[16]作为交换关联泛函。所采用的MoS₂单胞的晶格常数a = b = 3.185 Å，石墨烯单胞的晶格常数a = b = 2.46 Å^[17]。计算过程中，引入Grimme^[18]的DFT-D2方法进行色散校正。平面波基组的截断能选取为400 eV。结构优化和性质计算时，以Г为中心的二维布里渊区K点的采样间隔分别为0.020和0.015 Å⁻¹。几何优化中，原子经过弛豫，其能量收敛精度小于10⁻⁶ eV，原子间的相互作用力收敛精度小于0.01 eV/Å。在Z方向上设置20 Å的真空层，以避免该方向上相邻异质结之间的相互作用。

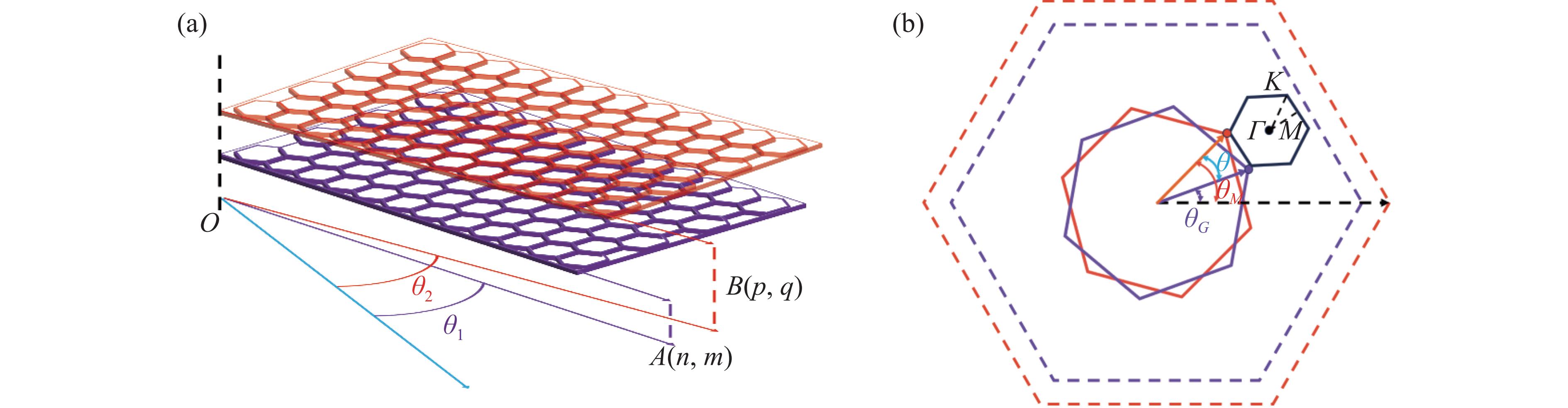
图1(a)为石墨烯/MoS₂异质结的三维示意图，通过将孤立的单层MoS₂置于孤立的单层石墨烯上，从而得到石墨烯/MoS₂异质结。如图1(b)所示，布里渊区路径为Г→M→K→Г。

根据Li等^[19]的研究，单层石墨烯和单层MoS₂存在基向量

式中：a₀和b₀分别为单层石墨烯和单层MoS₂的晶格常数，则单层石墨烯超胞结构中的基向量

单层MoS₂超胞结构中的基向量

式中：n、m、p和q为常数。

利用向量夹角公式，石墨烯/MoS₂相对转角定义为

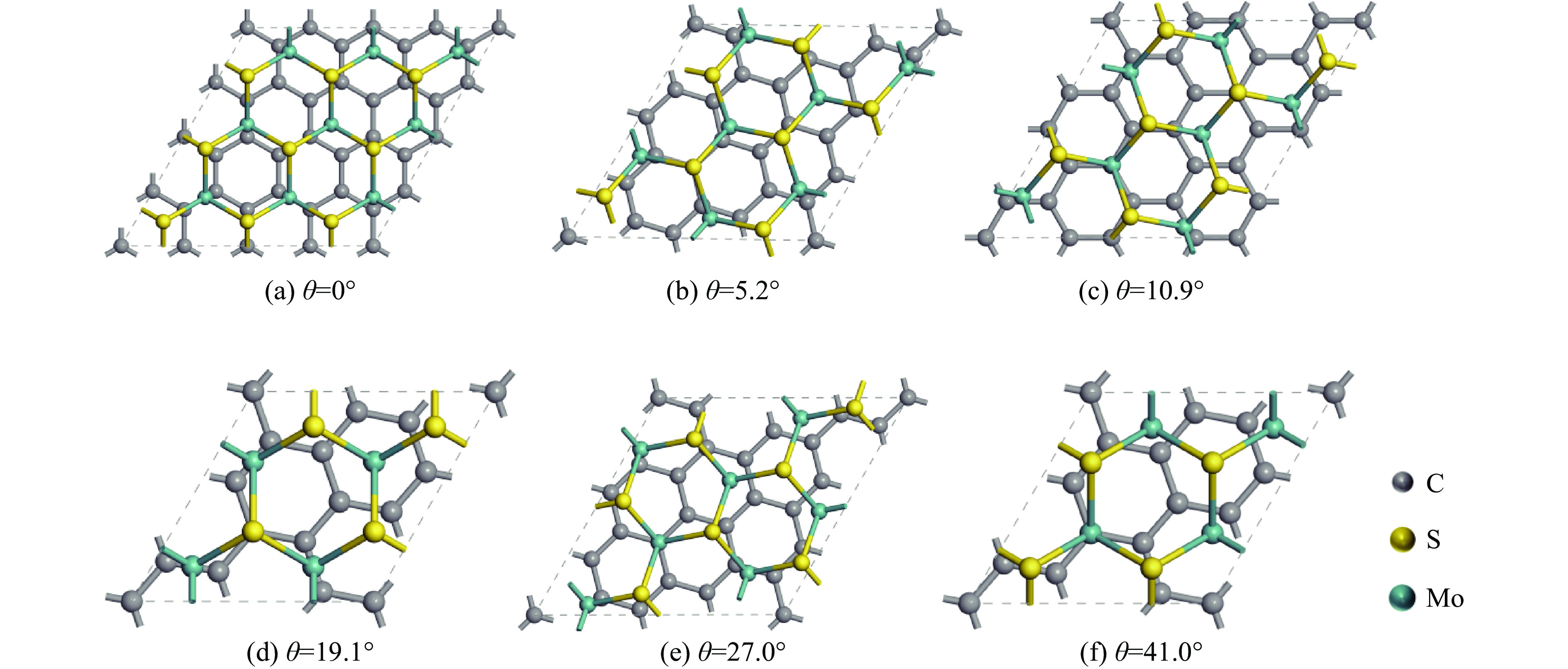
超胞中原子数目N=2(n²+m²+nm)+3(p²+q²+pq)，晶格长度为a₀$ \sqrt{{n}^{2}+{m}^{2}+nm} $，失配度σ=(a_Mo−a_G)/a_G，其中a_Mo为单层MoS₂的晶格常数，a_G为单层石墨烯的晶格常数。本研究根据上述石墨烯/MoS₂相对转角的定义，构建了6种不同石墨烯/MoS₂异质结的转角结构，计算了这些转角结构的电子结构与光学性质。图2给出了6种转角石墨烯/MoS₂异质结构，表1列出了这6种异质结的结合能（E_b）、层间距（D）和失配度σ。从表1可以看出，失配度均小于5%，满足计算要求。

为了确定石墨烯与MoS₂之间的层间作用类型，基于转角为19.1°匹配结构的异质结模型，测试了异质结在不同层间距D下的结合能E_b

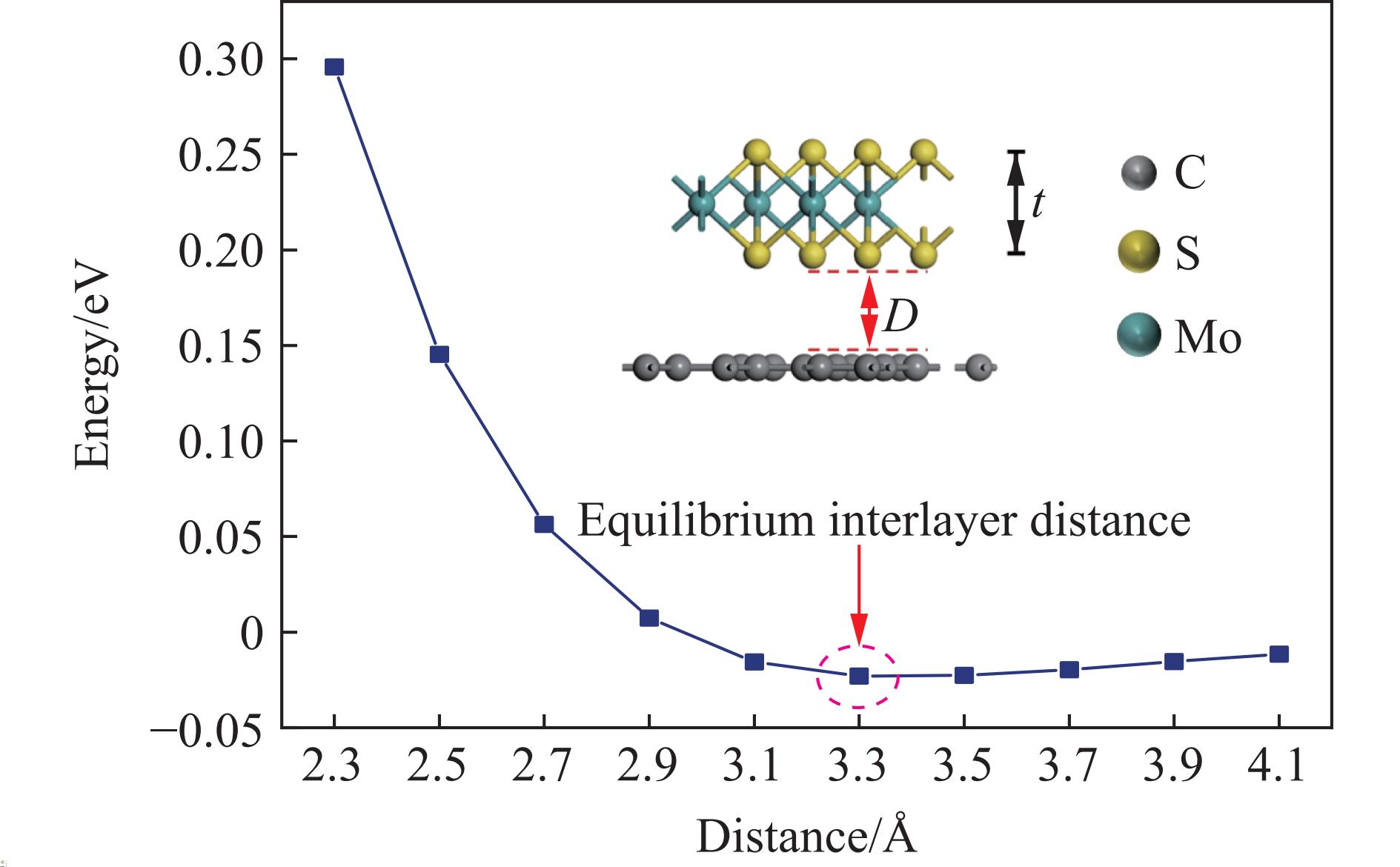
式中：$ {E}_{\mathrm{G}/\mathrm{M}} $、$ {E}_{\mathrm{G}}$、${E}_{\mathrm{M}} $分别为石墨烯/MoS₂异质结、孤立的单层石墨烯、孤立的单层MoS₂的总能量，${N}_{\mathrm{c}} $为每个模型中石墨烯的原子数目。

图3给出了界面结合能E_b与层间距D的关系曲线，图中t为单层MoS₂的厚度。从图3可以看出，最稳定的层间距为3.3 Å，与实验得到的石墨烯/MoS₂异质界面之间最稳定的层间距为(3.4±0.1) Å基本一致^[20]。层间距D为2.3～3.3 Å时，结合能E_b随层间距的增大而显著减小，并且由正值转变为负值，结构趋于稳定。此时层间相互作用主要表现为斥力，随层间距增大，斥力逐渐步减小，结构趋于稳定；层间距D为3.3～4.1 Å时，结合能缓慢增加，结构稳定性降低。此时层间相互作用主要表现为引力，随着层间距增大，引力减弱，结构稳定性降低。因此，对于6种转角结构，初始层间距D₀均设为3.3 Å。

石墨烯/MoS₂的界面相互作用力为典型的范德瓦尔斯力。石墨烯/MoS₂异质结的稳定性也可通过不同转角下的界面结合能E_b确定，充分弛豫后，得到了相应的结合能E_b和层间距D。未转角时石墨烯/MoS₂的结合能E_b为37.2 meV，如表1所示，6种转角异质结构的结合能均为负。相对于其他结构，转角为10.9°时失配度较小，结合能最低，结构更稳定。由于层与层之间原子匹配的位置发生改变，导致层间距随异质结界面间的旋转明显增加，从3.17 Å增大到约3.48 Å，从而改变了双层之间的范德华瓦尔斯力相互作用以及体系的电子结构。

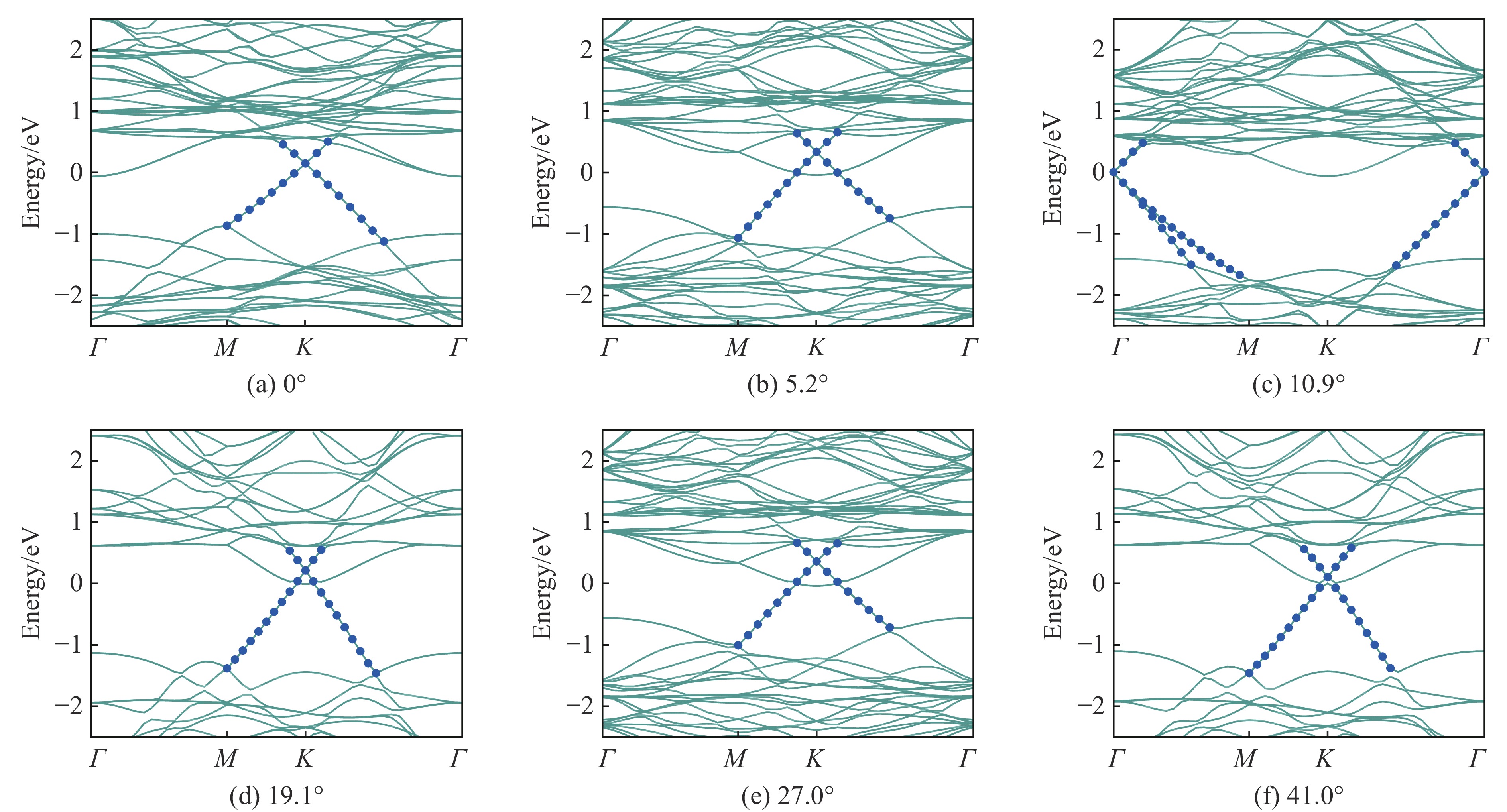
界面间的转角能够调节异质结的电子结构^[21]，图4给出了不同转角下的能带结构。得益于弱范德瓦尔斯力，石墨烯的电子结构基本保持不变，能够观察到清晰的狄拉克锥，而MoS₂的电子结构由直接带隙转变为间接带隙。在不同的扭转角度下，石墨烯中狄拉克锥与MoS₂导带底的相对排列有明显的变化。当界面间的旋转角度为0°和10.9°时，狄拉克锥远离MoS₂导带底；而当旋转角度为5.2°、19.1°、27.0°和41.0°时，狄拉克锥靠近MoS₂导带底，分别位于费米能级上方0.331、0.210、0.355和0.098 eV处。

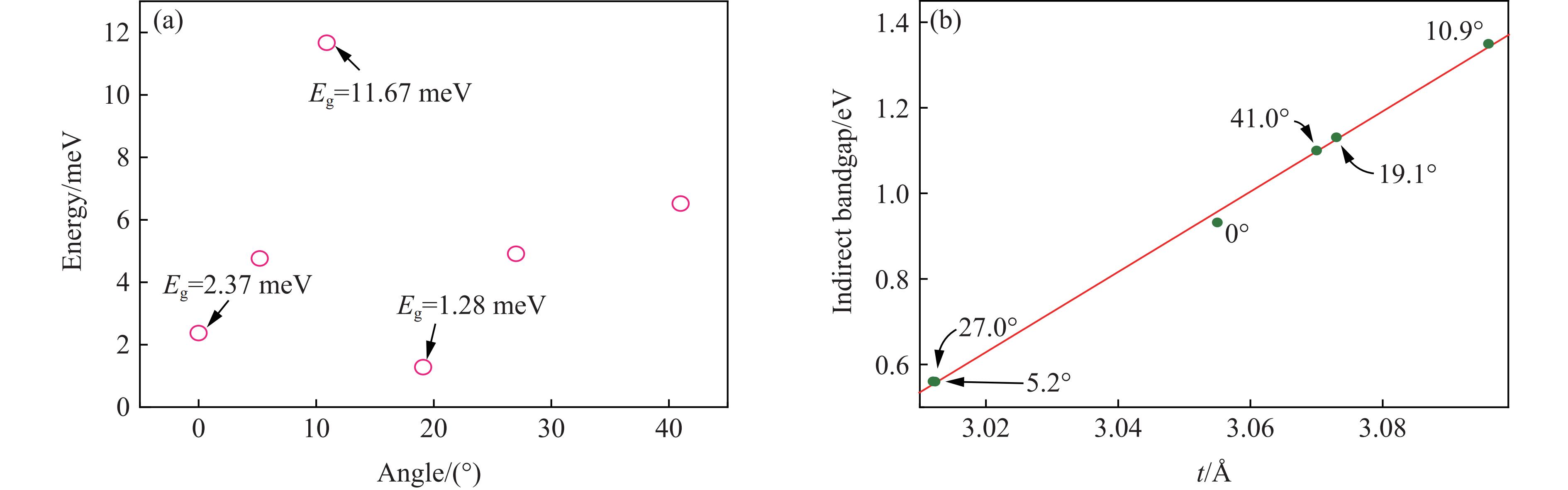
值得注意的是，由于晶格对称性遭到破坏，石墨烯打开了一个小的带隙。图5(a)显示了不同角度下狄拉克点处带隙的变化，未旋转时带隙为2.37 meV，与考虑SOC（spin-orbit coupling）效应后所得结果^[11]基本相当。当扭转角为10.9°时，狄拉克锥转移至Г点，带隙最大，相比未旋转时提高了9.3 meV，此时E_g的最大值为11.67 meV。而转角继续增大至19.1°时，狄拉克锥转移至K点，最小带隙为1.28 meV。

异质结构中，石墨烯与MoS₂的相对取向会影响MoS₂的带隙，这可以归因于单层MoS₂带隙对层厚度的高度敏感性，石墨烯与MoS₂之间的相对取向变化伴随着界面电子转移，影响了Mo―S键长，从而影响了能带结构^[22]。图5(b)给出了不同扭转角下MoS₂层厚t与其间接带隙的关系曲线，可以看出，在异质结中，MoS₂的电子结构保留了单层结构时的部分特点，随着厚度t的增加，间接带隙呈线性递增。

转角为0°时，与单层石墨烯相比，石墨烯/MoS₂异质结能带结构中狄拉克点的位置发生变化，向费米能级上方移动，导致石墨烯导带存在未填充的能级。因此，形成了p型体系，且具有较小的带隙。由于石墨烯中狄拉克点的位置高于MoS₂导带底，两者间存在电势差。因此，当石墨烯与MoS₂形成异质结时，处于较高位置的石墨烯中的电子将流入MoS₂，即MoS₂表面聚集负电荷，石墨烯表面聚集正电荷。随着界面旋转角度的改变，石墨烯中狄拉克点与MoS₂导带底的相对位置发生了变化。其中，转角为27.0°时，狄拉克点的位置远远高于MoS₂的导带底，意味着更明显的电荷转移以及更强的电负性差异。

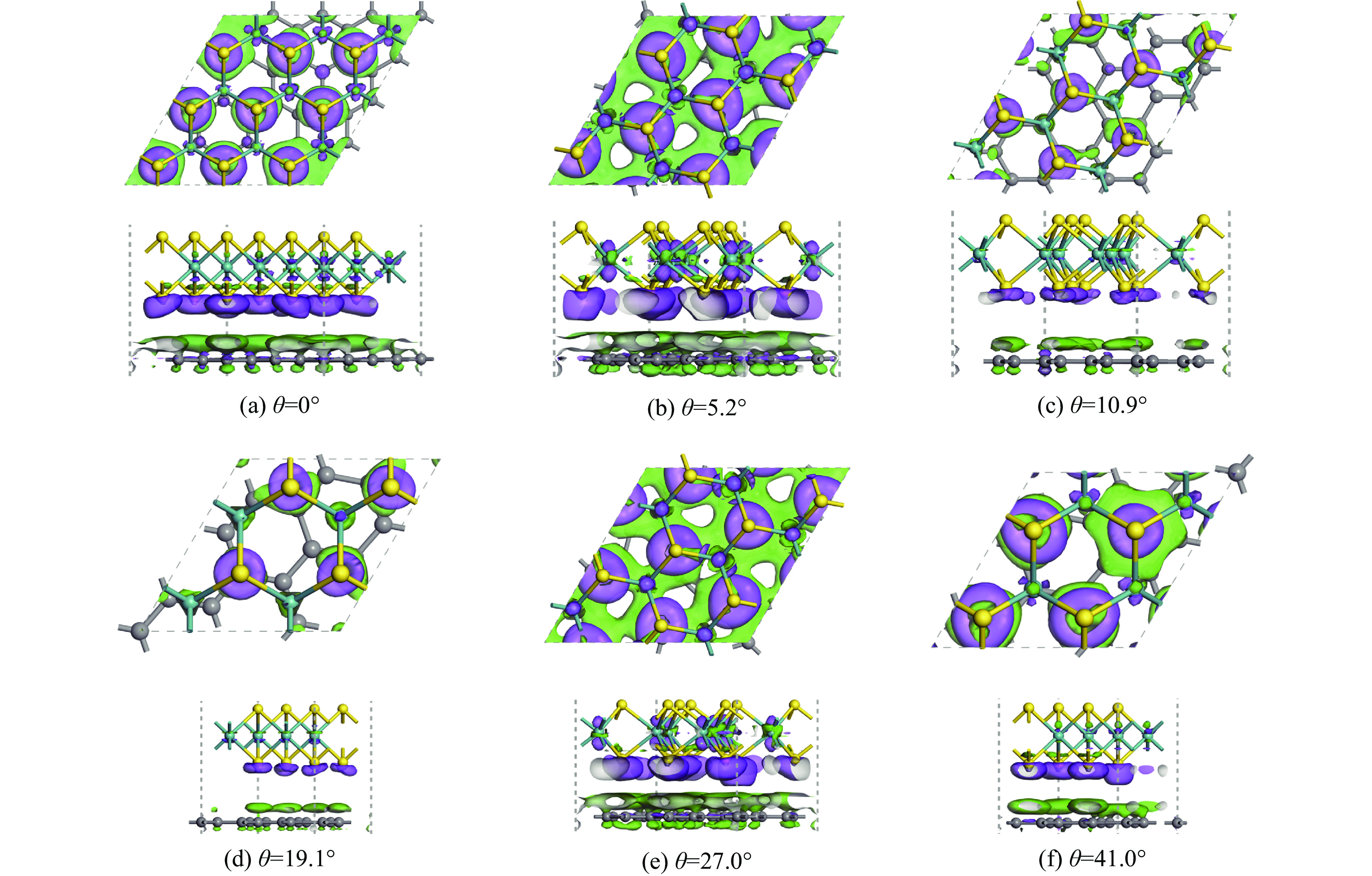
研究光电性质时，异质结的界面状态至关重要，因此，需要分析异质结界面处电荷的转移及其分布状态。图6给出了优化后6种转角异质结的差分电荷密度，上侧为俯视图，下侧为侧视图，其中紫色和绿色分布区域分别表示负电荷聚集引起的电子增加以及电子减少引起的正电荷聚集。由于层间的结合作用导致界面内的电荷重新分布，电子-空穴对有明显的分离，石墨烯层电荷耗尽，界面处的硫原子层发生电荷积累，电子从石墨烯转移至单层MoS₂。界面间的电荷会随着转角重新分布，其中转角为27.0°时石墨烯的损耗电荷较高。可以发现，在不同的旋转角度中，MoS₂层中Mo-S之间的电子转移发生了变化，这种变化引起了Mo―S键长的变化^[22]：当旋转角度为5.2°和27.0°时，异质结构Mo-S之间的电子转移最明显。对于Mo―S键长，当旋转角度为0°时，MoS₂层中Mo―S平均键长为2.32 Å；而当旋转角度为5.2°与27.0°时，Mo―S平均键长分别为2.46和2.456 Å；当转角为10.9°时，Mo―S平均键长最小，为2.42 Å。因此，Mo-S之间的电子转移使Mo―S键长发生变化，从而导致S-S层间距发生改变。

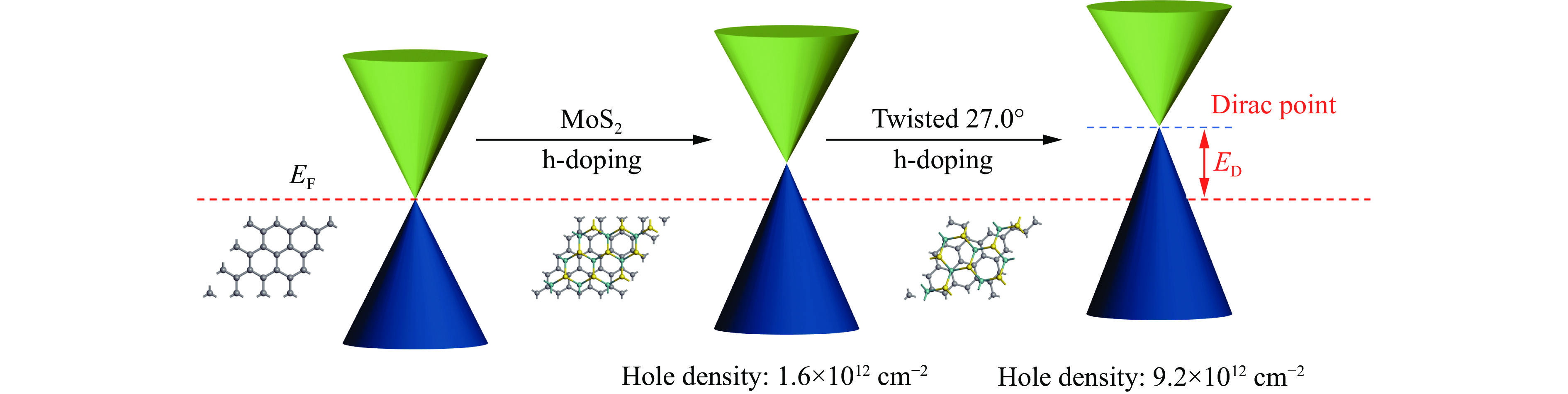
如图7所示，结合能带结构与差分电荷密度，可以发现，异质结构中狄拉克锥位置除了在外加电场下可调以外，也受界面间旋转的影响。由于电子的转移使两者间产生电负性差异，导致界面处发生自发极化，使狄拉克锥向费米能级以上移动，因此，石墨烯/MoS₂为明显的空穴掺杂（h-doping）。基于石墨烯狄拉克锥周围的线性色散，石墨烯中空穴掺杂浓度$ {N}_{\rm{h}} $可以通过下式得到^[7]

式中：$ {E}_{\mathrm{F}} $和$ {E}_{\mathrm{D}} $分别为费米能级和狄拉克锥位置的能量，石墨烯中狄拉克点的费米速度$ {v }_{\mathrm{F}} $≈10⁶ m/s ，ћ为普朗克常数除以2π（$ 1.055\times 1{0}^{-34}\,\mathrm{J}\cdot \mathrm{s} $）。转角为27.0°时，空穴载流子密度进一步提高，约为9.2×10¹² cm⁻²，远高于室温下石墨烯的载流子浓度（6×10¹⁰ cm⁻²）^[23]。因此，在由石墨烯与其他二维材料堆叠形成的异质结中，亦可利用界面间的转角有效调节石墨烯中的空穴掺杂。

石墨烯作为一种具有独特物性的二维材料，具有零能隙的特点。这意味着石墨烯在常温下不能禁止电荷传导，限制了石墨烯在电子学和光电子学等领域的应用。随着石墨烯/MoS₂异质结界面旋转角度的变化，石墨烯中狄拉克锥打开的直接带隙在1.28～11.67 meV之间变化。因此，研究界面间旋转角度的变化对石墨烯/MoS₂光学性质的影响很有必要。

光吸收曲线可以直观地反映异质结构在红外光区、可见光区和紫外光区的响应情况。吸收系数α(ω)可以表示为^[24]

损失函数L(ω)表示为

式中：$ {\varepsilon }_{1}\left(\mathrm{\omega }\right)$为介电函数实部，${\varepsilon }_{2}\left(\mathrm{\omega }\right) $为介电函数虚部。虚部${\varepsilon }_{2}\left(\mathrm{\omega }\right) $由下式给出

式中：M为跃迁矩阵元（电子跃迁过程中的激发或退激发的强度），e为电子电荷，i和j为跃迁初态和终态，$ {f}_{i} $为第i态费米分布函数，$ {E}_{i} $为第i态电子能量，k为波矢，ω为频率。在可见光范围内，石墨烯/MoS₂异质结的吸收光谱主要受介电常数虚部的影响。实部$ {\varepsilon }_{1}\left(\mathrm{\omega }\right)$可以由虚部${\varepsilon }_{2}\left(\mathrm{\omega }\right) $利用Kramers-Kronig得到

式中：P为积分主值。

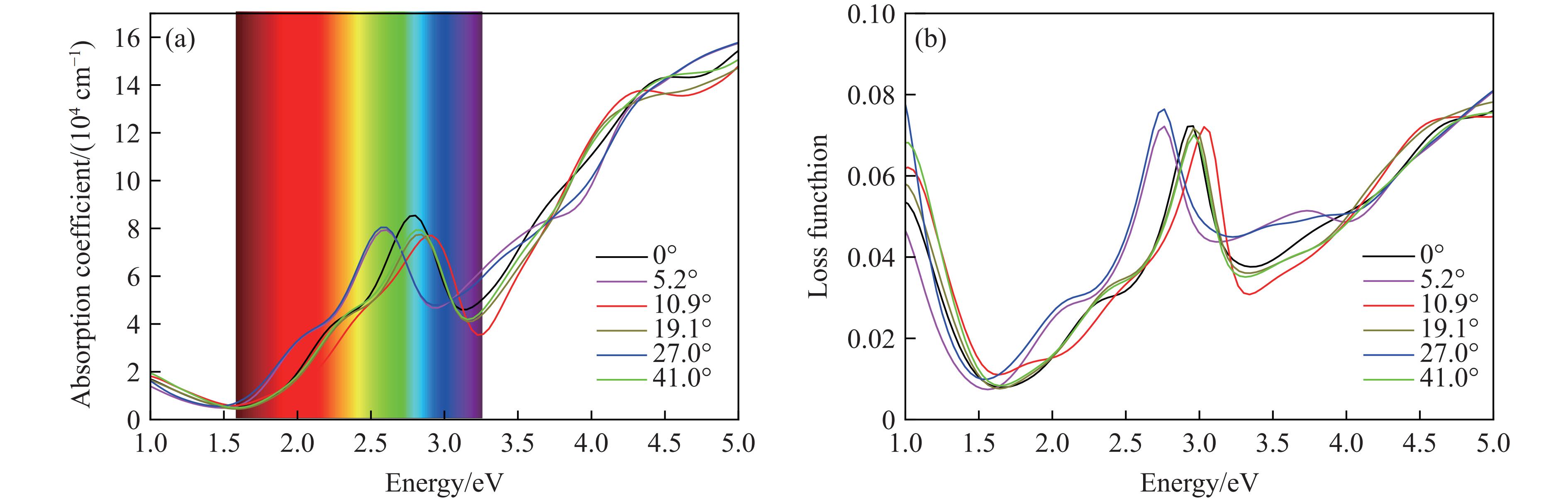
根据Yang等^[25–26]的研究，在此过程中考虑真空层厚度变化对介电常数虚部的影响，以得到异质结构的本征光学性质。图8给出了考虑真空层影响后的光学性质，图8(a)为不同转角下石墨烯/MoS₂异质结的吸收光谱随能量变化。在可见光区和紫外光区均出现吸收峰，表明对可见光（1.59～3.26 eV）和紫外光（3.26～5 eV）都有很高的响应强度，其中27.0°异质结在远紫外光区（4.56～5 eV）的光吸收最高；可见光区域内，所有转角的石墨烯/MoS₂异质结相对于未转角异质结的吸收峰值均略有下降。在27.0°的旋转角度下，石墨烯/MoS₂的吸收边发生了明显的红移，向低能区移动了大约0.233 eV；而在10.9°的旋转角度下，石墨烯/MoS₂的吸收边发生了较小的蓝移，向高能区移动了大约0.116 eV。旋转角度为5.2°的异质结的吸收边向低能区移动，发生略微红移；旋转角度为19.1°与41.0°的异质结的吸收边向高能区移动，发生略微蓝移。在红外光区（1～1.59 eV），相比于未转角结构，扭转结构的光学响应均有提升。

不同转角石墨烯/MoS₂异质结的能量损失函数如图8(b)所示。对于未转角结构，在不可见光区，随着能量的增加，能量损失持续减少；进入可见光区后，在光子能量为1.641 eV时，能量损失最低为0.007 6，随后在2.958 eV出现高达0.072 3的能量损失峰；在紫外光区内，随着能量的增加，能量损失也在持续增加。对于其他转角结构，着重讨论在可见光区域内的能量损失情况。在吸收光谱中，转角的施加使异质结在可见光中的吸收强度略微下降；而通过损失函数可知，在紫光区内，旋转角度为10.9°、19.1°和41.0°的异质结构的损失函数均降低，特别地，当旋转角度为10.9°、光子能量为3.303 eV时，能量损失最低为0.031，与未转角时相比下降了0.007。这说明通过界面间转角能够有效地调控体系的能量损失。因此，石墨烯/MoS₂异质结结构在界面旋转角度调制下所表现出的能带结构变化、光谱响应范围以及能量损失函数的改变，使其在半导体光学器件中具有潜在的应用价值。

基于第一性原理计算，对不同扭转角下石墨烯/MoS₂异质结构的电子结构和光学特性进行了研究，得到以下主要结论。

(1) 随着厚度增加，MoS₂的间接带隙持续增大。石墨烯在费米能级附近依旧保持其特殊的线性色散能带结构，并且在旋转角度为10.9°时，狄拉克锥的最大直接带隙为11.67 meV。

(2) 异质结构中石墨烯层具有更高的载流子密度，其界面间的旋转可作为调节石墨烯层掺杂载流子密度的有效措施。转角为27.0°时，石墨烯层空穴掺杂的载流子密度最高，空穴掺杂载流子浓度相比未转角时提高了6倍，约为9.2×10¹² cm⁻²。

(3) 异质结构的光学性质可以通过界面间旋转进行有效调制。转角为27.0°时，吸收边向低能区移动0.233 eV；转角为10.9°时，吸收边向高能区移动0.116 eV。可见光范围内，转角为10.9°时，能够有效地控制体系的能量损失，损失函数下降0.007。