首页
登录
注册
-
高速侵彻战斗部在攻击多层目标时，装药受高频循环脉冲载荷作用而产生损伤积累，影响弹药侵彻能力和装药安定性。李媛媛等[1]开展了装药侵彻安定性试验，通过回收试验弹，发现内部装药没有发生点火反应，含能颗粒未产生明显的破碎和穿晶断裂等微观损伤。陈文等[2]对侵彻试验后的回收装药开展了冲击起爆隔板试验，发现严重损伤区域主要分布于装药的头部和尾部，中间区域几乎不发生损伤，装药损伤越严重，冲击感度越高。Li等[3–4]基于Visco-SCRAM损伤模型和热点模型开展了钻地战斗部侵彻混凝土的数值模拟，由于钻地弹头部主要承受三轴压缩载荷，裂纹处于自锁状态，因此，钻地弹的头部损伤不严重，装药尾端承受拉-压反复载荷，裂纹易发生扩展，尾部装药损伤严重。赵生伟等[5]通过逆弹道试验测试和数值模拟，得到了弹体侵彻的应力波峰值和等效脉宽。成丽蓉等[6]基于微裂纹摩擦和孔洞塌缩机制，开展了钻地战斗部侵彻单层和多层靶板数值模拟，发现严重损伤区域主要分布于装药头部和尾部，并解释了相应的试验现象。此外，不同学者也采用内聚力方法对不同工况下装药侵彻靶板时装药的损伤开展了研究，获得了不同工况下装药的损伤模式[7–10]。
准确掌握侵彻战斗部装药在循环脉冲载荷作用下的损伤演化机制，是预测其攻击多层目标安全性的关键。当前，循环脉冲载荷作用下战斗部装药的损伤演化机制研究缺乏实验数据，尚无准确的理论模型，大多数研究都是通过宏观实验和计算粗略地估计发生损伤的位置，并不能分析炸药在循环脉冲载荷作用下的细观变形机制和局部响应。主要原因是侵彻战斗部装药的损伤行为具有多尺度的特点，需要从细观至宏观多个层次上进行关联分析，单一尺度的模拟方法只能对一定尺度范围内的损伤问题进行研究。因此，本研究将对PBX装药侵彻双层靶板过程中的宏-细观损伤进行数值模拟，建立弹体侵彻双层靶板的内聚力模型，探讨弹体侵彻双层靶板时PBX装药的损伤演化规律，结合PBX装药细观损伤模型，分析PBX装药侵彻双层靶板过程中的细观损伤演化特征。
-
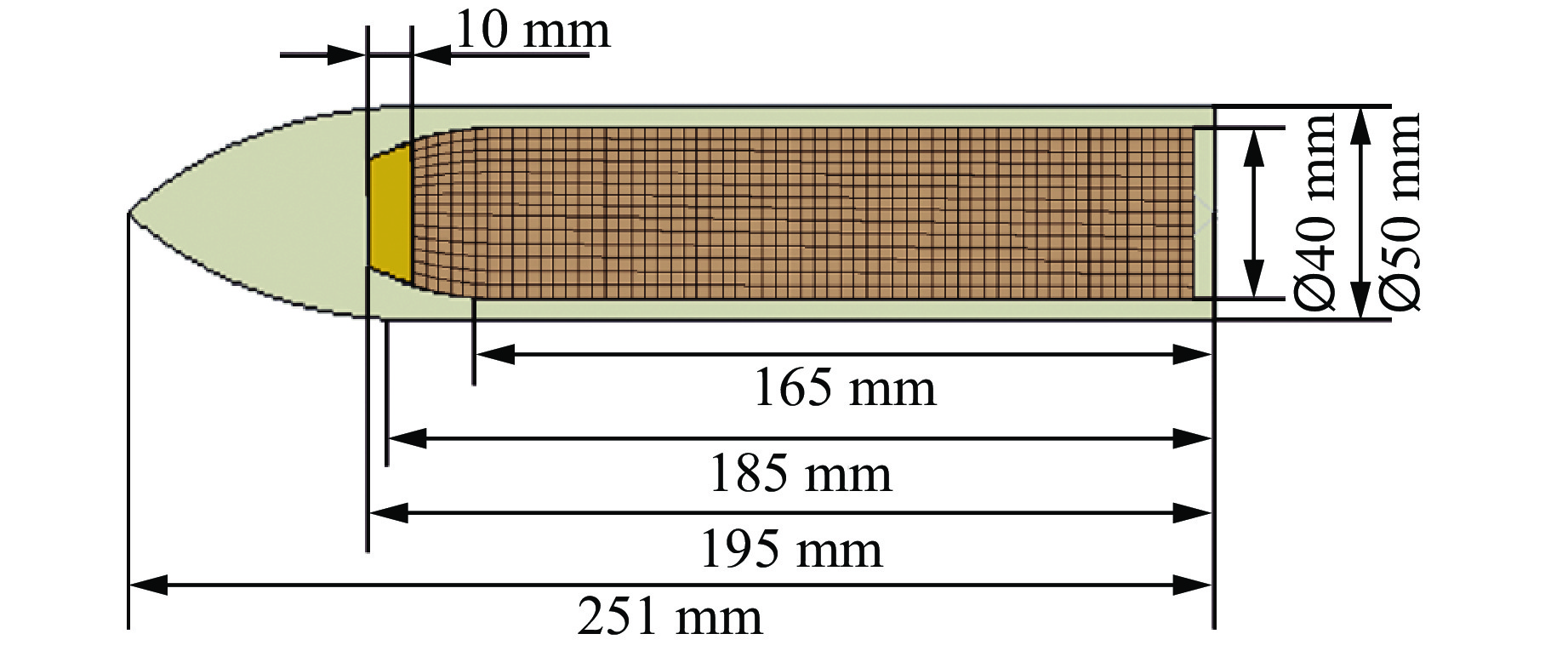
图1为建立的弹-靶仿真分析有限元模型。图2给出了弹体尺寸，弹头曲径比（caliber radius head, CRH）约为2.5。靶板为2层，厚度为10 mm，宽度为600 mm，靶板间隔为250 mm，靶板宽度与弹体外径之比大于10，可以忽略侵彻过程中靶板边界效应的影响[11–12]。
弹-靶有限元模型中所有单元类型均为C3D8。弹壳网格尺寸为2.5 mm，缓冲层和装药网格尺寸均为2 mm，靶板中心区域为侵彻接触区，网格尺寸约为1 mm，非侵彻接触区域的网格自然过渡，逐渐增大。采用自编的内聚力单元插入程序，在每个装药的实体单元之间全部插入零厚度内聚力单元，用以模拟侵彻过程中裂纹的萌生和扩展，并验证所有网格的收敛性。在不影响零厚度内聚力单元对损伤模拟的条件下，为提升计算效率，在计算模型中采用了缩减积分，导致出现微小的沙漏现象。
-
弹壳、靶板和缓冲层材料分别为35CrMnSi钢、45钢和聚碳酸酯，采用Johnson-Cook模型描述其在不同应变率下的力学性能，表达式为
式中：σy为屈服应力，A、B、n、C和m为材料的常数，
$ \varepsilon _{\rm p}^{} $ 为等效塑性应变，$ \dot \varepsilon^* $ 为无量纲的等效塑性应变率，$ T^* $ 为无量纲温度。弹壳[13]、靶板[14]、缓冲层[15]的主要材料参数见表1，其中：ρ为密度，μ为泊松比，E为弹性模量，$ {\dot \varepsilon _0} $ 为参考应变率。靶板的损伤参数D与等效塑性应变增量dεp之间的关系采用Johnson-Cook损伤模型描述
式中：εf为失效应变。
式中：
$ {d_1} $ 、$ {d_2} $ 、$ {d_3} $ 、$ {d_4} $ 和$ {d_5} $ 为材料的损伤参数，分别为0.10、0.76、1.57、0.005和−0.84；$ {\sigma _{\text{p}}} $ 为静水压力。采用各向同性弹塑性模型描述PBX装药的力学性能，其密度、泊松比、弹性模量、屈服强度和硬化模量分别为
1650 kg/m3、0.3、4.5 GPa、49 MPa和1 GPa。另外，采用双线性内聚力模型描述PBX装药的损伤产生与演化过程，结合文献[7, 16–18]得到侵彻条件下PBX装药的内聚力单元参数，结果见表2，其中：Kcoh为内聚力单元刚度，$ \sigma $ 为内聚力单元强度，G为内聚力单元断裂能。 -
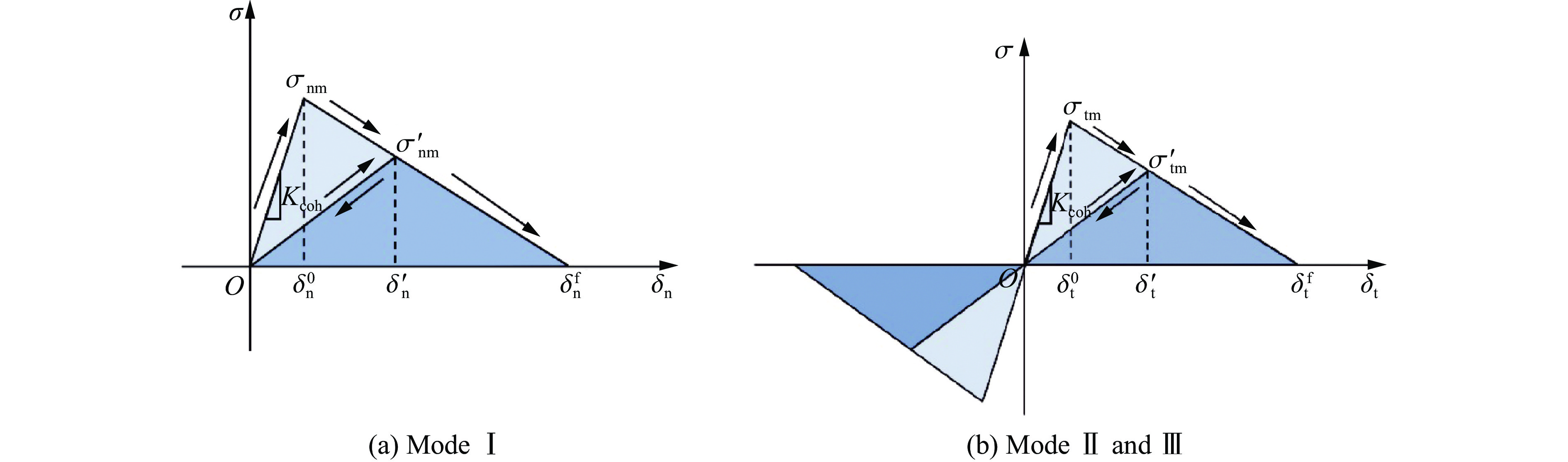
从宏观模型中提取危险位置信息作为边界条件施加到细观模型上，根据侵彻靶板过程中载荷传递特点[1]，将细观模型一端固定，并在固定端的对边施加提取到的载荷，如图3所示[19]，在细观模型中2个相邻网格单元表面之间插入内聚力单元。由于PBX装药是一种高颗粒填充材料，通常采用双线性牵引-分离规律描述黏性模型中牵引与分离之间的非线性关系[20–22]。图4为双线性内聚力法则的示意图，其中：
$ \delta _{\rm n}^0 $ 和$ \delta _{\rm t}^0 $ 分别为法向和切向临界张开位移，$ \delta _{\rm n}^{\rm f} $ 和$ \delta _{\rm t}^{\rm f} $ 分别为法向和切向失效位移，δn和δt分别为法向和切向位移，σnm和σtm分别为内聚力单元的法向和切向临界强度。在驱动力作用下，相对的单元面逐渐分离，正应力和剪应力线性增长，其斜率就是内聚力单元刚度，当应力达到临界强度$ {\sigma _{\rm {nm}}} $ 和$ {\sigma _{\rm {tm}}} $ 时，单元开始产生损伤，损伤的起始法则为式中：
$ {\sigma _{\rm n}} $ 和$ {\sigma _{\rm t}} $ 分别为内聚力单元的法向和切向应力；“⟨ ⟩”为Macaulay括号，定义为内聚力单元的分离过程由如下方程控制
当张开位移达到失效位移
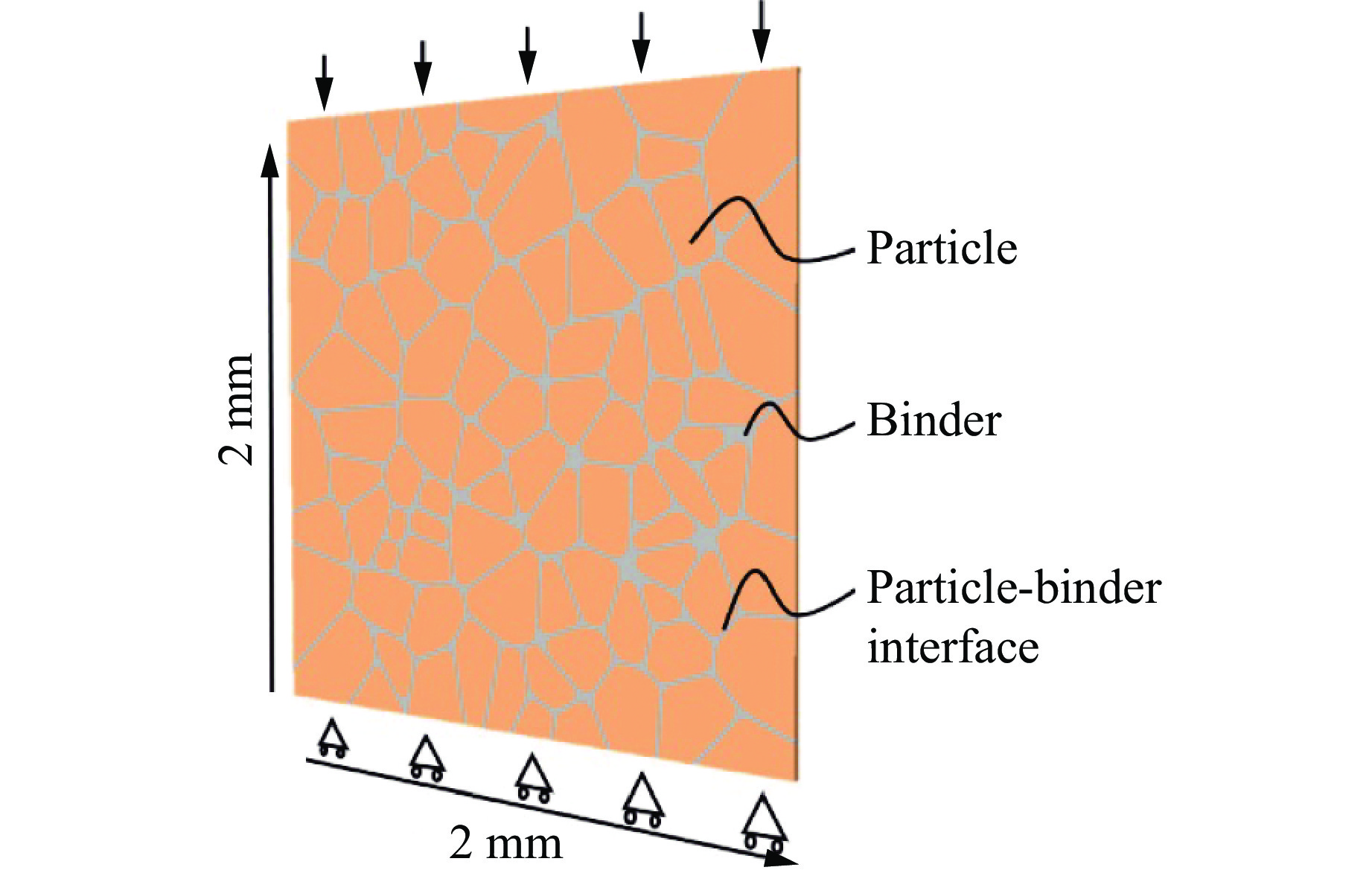
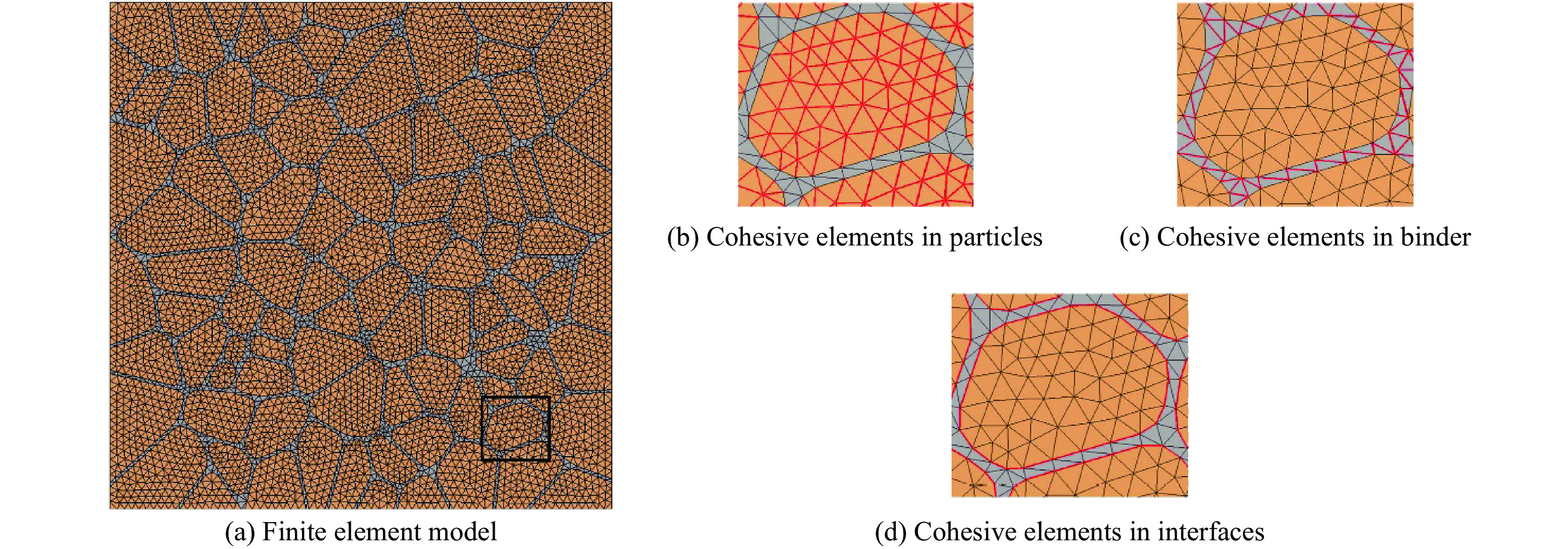
$ \delta _{\rm n}^{\rm f} $ 和$ \delta _{\rm t}^{\rm f} $ 后，内聚力单元完全失效。针对PBX装药颗粒的细观形貌特征，通过Voronoi方法生成的泰森多边形构建细观几何模型，如图5所示，其中，颗粒含量为87.39%，粒径在50～300 μm之间。采用线弹性模型描述含能颗粒的力学性质，其杨氏模量和泊松比分别为18.4 GPa和0.25，聚合物黏结剂采用线黏弹性本构模型[14]描述。RVE模型的长和宽均为2 mm，为了解决单元入侵问题，设定其厚度为0.02 mm[19]。图5(b)、图5(c)和图5(d)显示了嵌在PBX装药颗粒单元边界、黏结剂单元边界及颗粒-黏结剂界面上的内聚力单元模型，其中：红色表示插入不同区域的零厚度内聚力单元。
PBX装药的黏结性能强烈依赖于黏结参数。在双线性模型中，每个界面都包括黏结强度、临界位移和初始刚度3个参数，对于3个界面，则共有9个参数。因此，需要一种适应性强、收敛速度快、精度高的逆算法来获取PBX装药的内聚参数。常用的内聚力单元参数获取方法包括L-M算法[23]、梯度优化算法[24]、反演分析法[25]、分子动力学模拟法[26]，然而，这些方法都仅针对某一种加载条件，具有一定的局限性。改进后的卡尔曼滤波（Kalman filter，KF）算法是一种适应性较强的最优递归算法，Xu等[27]对其进行了详细的描述，但是KF算法在处理复杂的非线性问题时难以保证精度。Hook-Jeeves算法是一种直接搜索方法[28–30]，具有很高的收敛速度和计算精度，但前提是初始参数接近准确值。结合2种算法的优点，可以得到一种杂交反演方法[19]，能够确保模型在相应的应变率范围内体现PBX装药的力学性能。
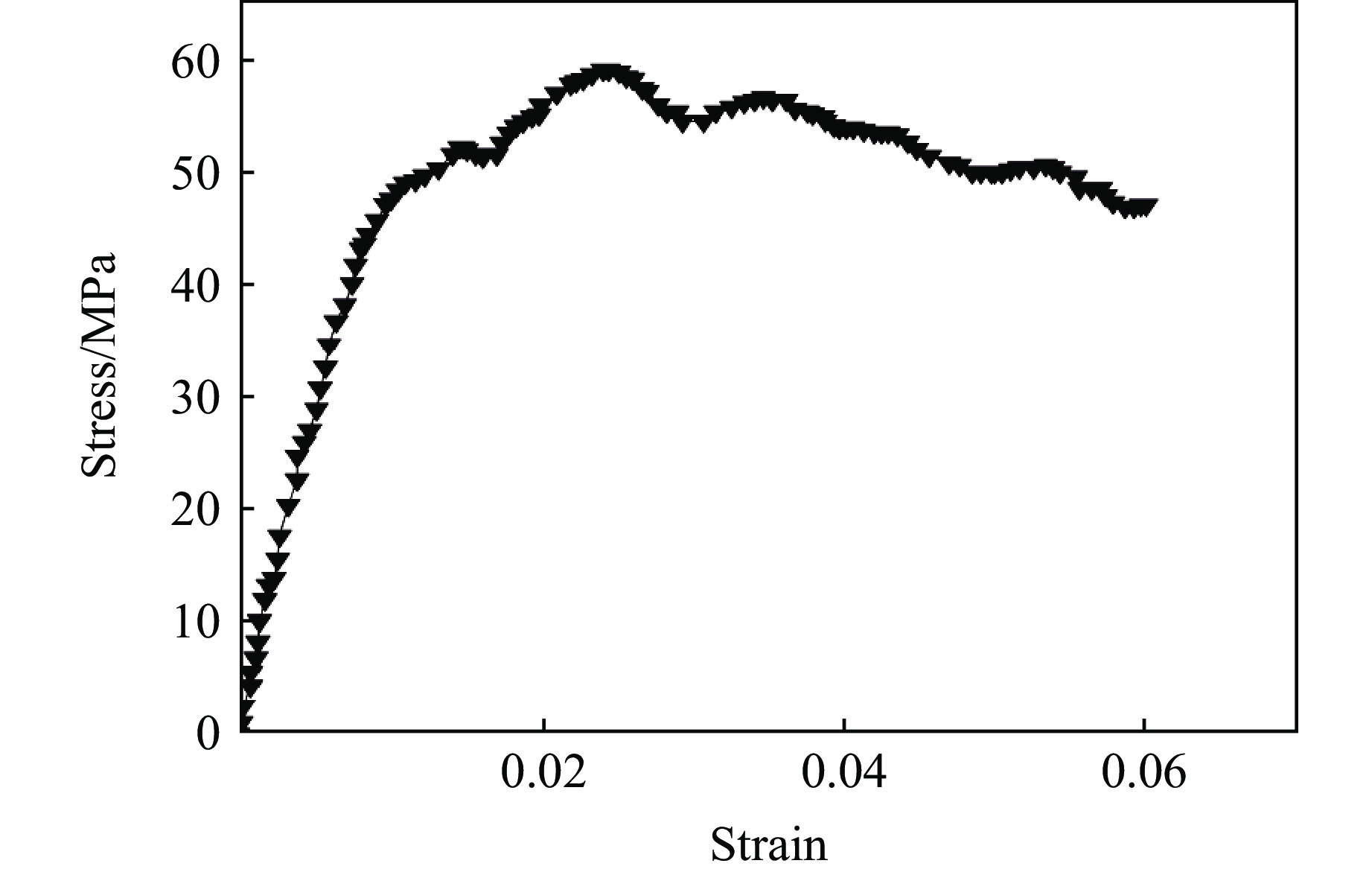
图6显示了PBX装药在
2000 s−1应变率下的应力-应变曲线。以该曲线为目标函数，采用KF与Hook-Jeeves杂交算法[19]进行优化求解，表3列出了优化后PBX装药的内聚力单元参数。 -
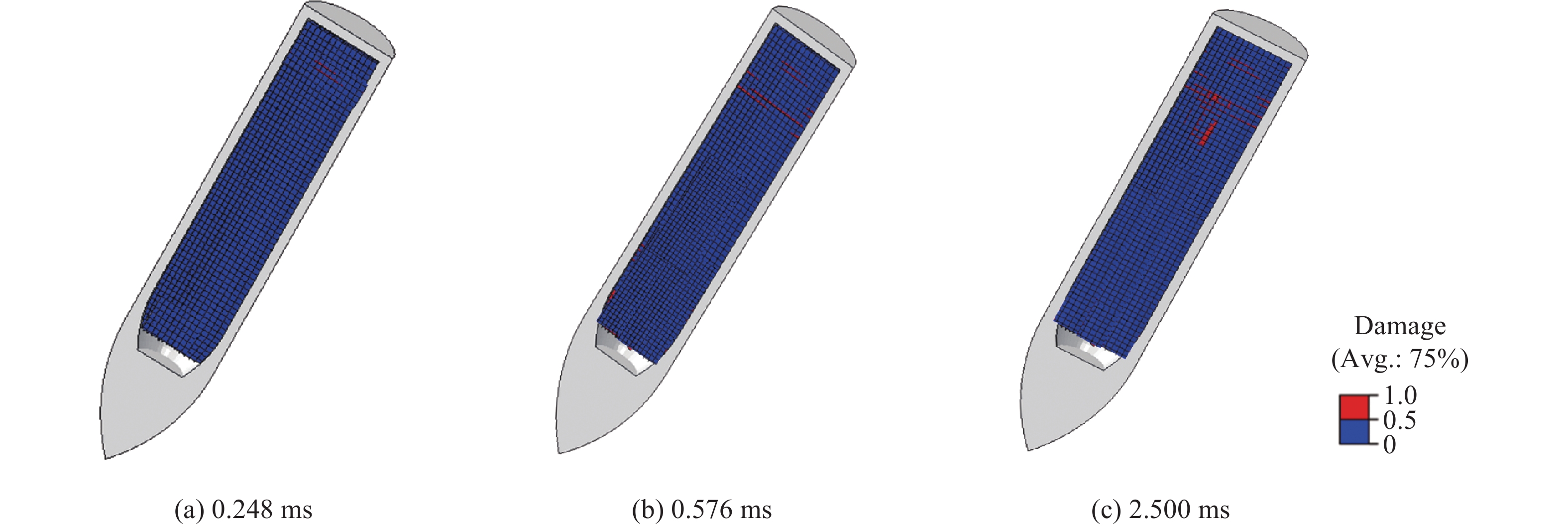
基于内聚力单元的弹体侵彻双层靶板数值模拟可以准确得到侵彻过程中裂纹的扩展位置、时间历程等信息。图7给出了以400 m/s的速度垂直侵彻双层靶板时装药损伤区域随时间的演化，损伤度为1.0时代表完全损伤。弹体撞击靶板会形成压缩波，并以不同的速度在壳体和装药中传播；当装药中的压缩波到达弹体尾部时，将在装药与壳体界面处发生反射形成拉伸波进入装药，拉伸波在装药中会衰减，因此，装药尾部的拉伸波强度最大，当拉伸应力超过装药内聚力单元强度时开始出现裂纹，最终在装药尾部出现2道垂直轴向的贯穿裂纹。
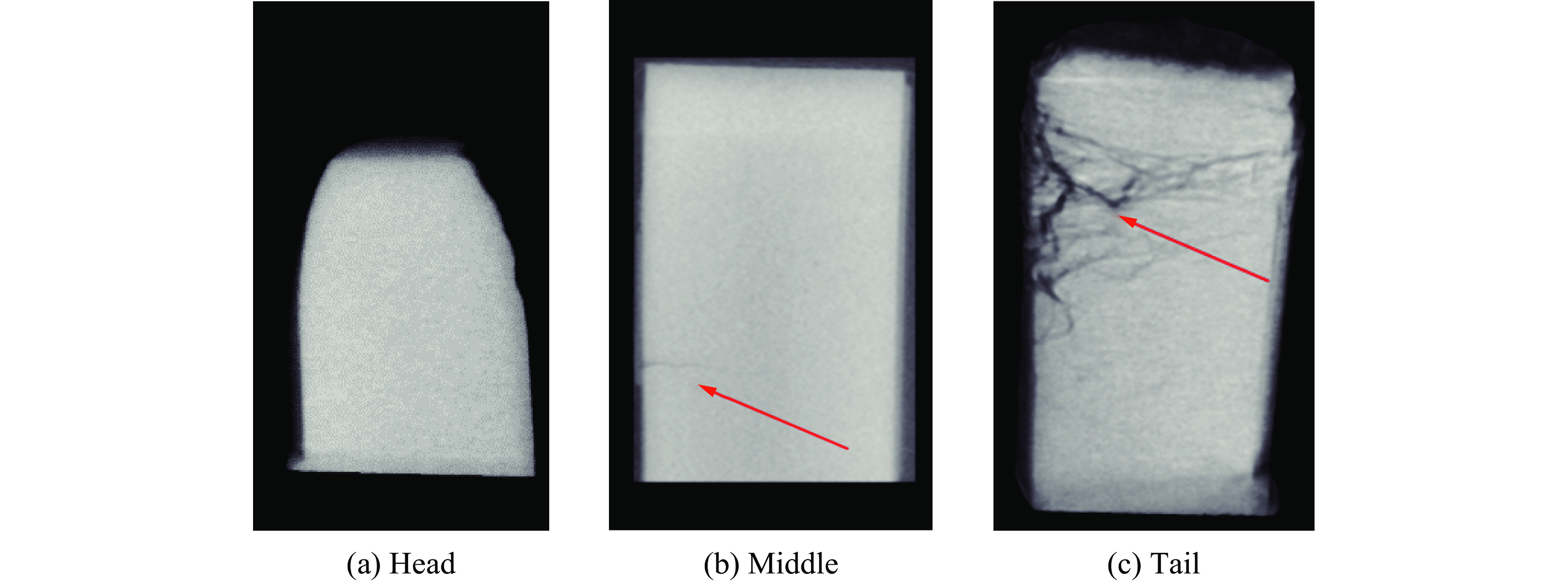
图8给出了侵彻实验结束后装药的CT扫描重构图像[8]。可以发现，装药尾部存在与加载方向垂直的裂纹，并且装药头部因挤压而发生变形和损伤，同时，在药柱中心位置出现了裂纹。这些损伤结果与数值模拟结果一致，验证了弹体侵彻靶板模型及参数的正确性，确保了后续模拟结果的准确性。
-
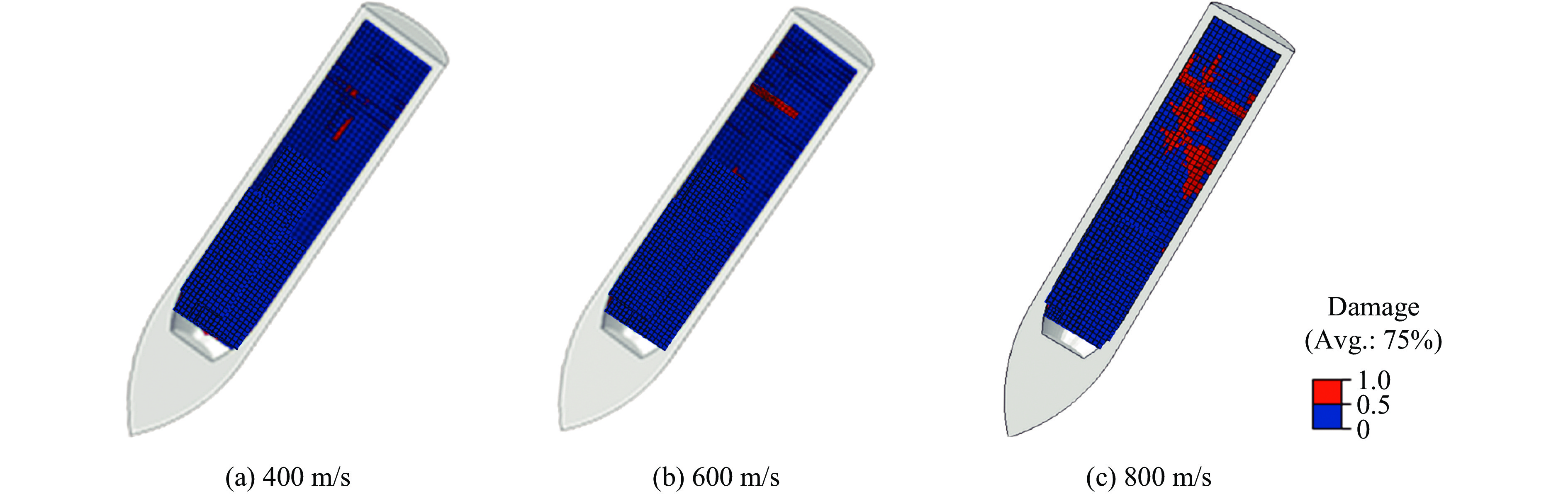
为了探究侵彻速度对装药损伤的影响，开展了侵彻速度分别为400、600和800 m/s时装药弹体侵彻双层靶板数值模拟。如图9所示，当侵彻速度从400 m/s增大到800 m/s时，拉伸和压缩载荷反复作用形成的垂直于轴向的贯穿裂纹明显增多。通过损伤比（内聚力单元损伤失效数与总内聚力单元数的比值）定量表征装药损伤。当侵彻速度分别为400、600和800 m/s时，损伤比分别为3.7%、5.9%和11.6%，显然，侵彻速度增大，损伤比明显增大。
-
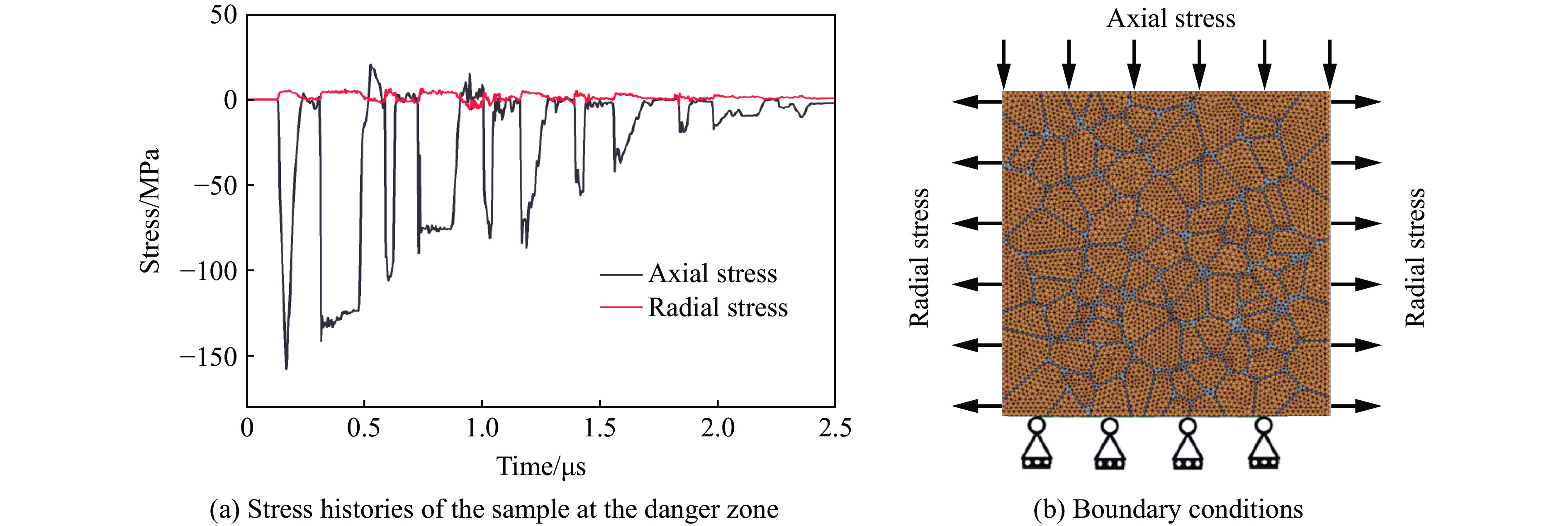
为进一步分析侵彻双层靶板过程中PBX的细观损伤特征，对以400 m/s的速度侵彻靶板时装药尾部易损伤区域的边界载荷进行提取，将其作为细观模型的加载载荷。为提高数值计算效率，并获取直观的损伤形式和分布，采用二维细观模型。
图10(a)为提取到的轴向和径向应力时程曲线，以图10(b)所示方式施加于细观模型，其中，下边界将加载方向的自由度进行约束以消除刚体位移。图11给出了不同时刻细观模型中主应变的分布情况。可见，应变主要分布于黏结剂中，且在颗粒边角处出现应变集中区域。虽然PBX装药中黏结剂的占比很少，但是黏结剂对材料整体宏观力学性能的影响非常大，而且PBX的应变率效应正是来自于黏结剂的黏弹性。
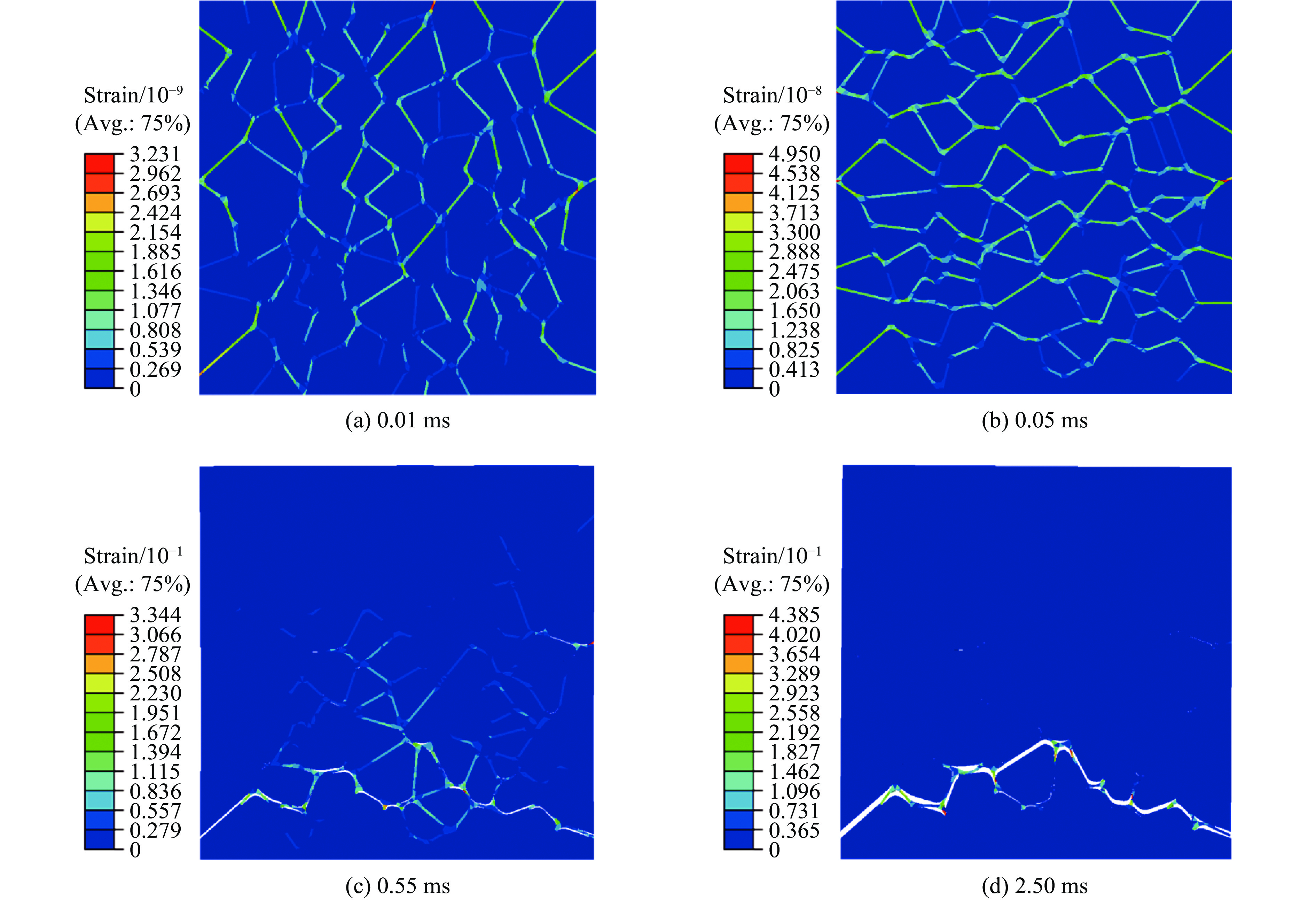
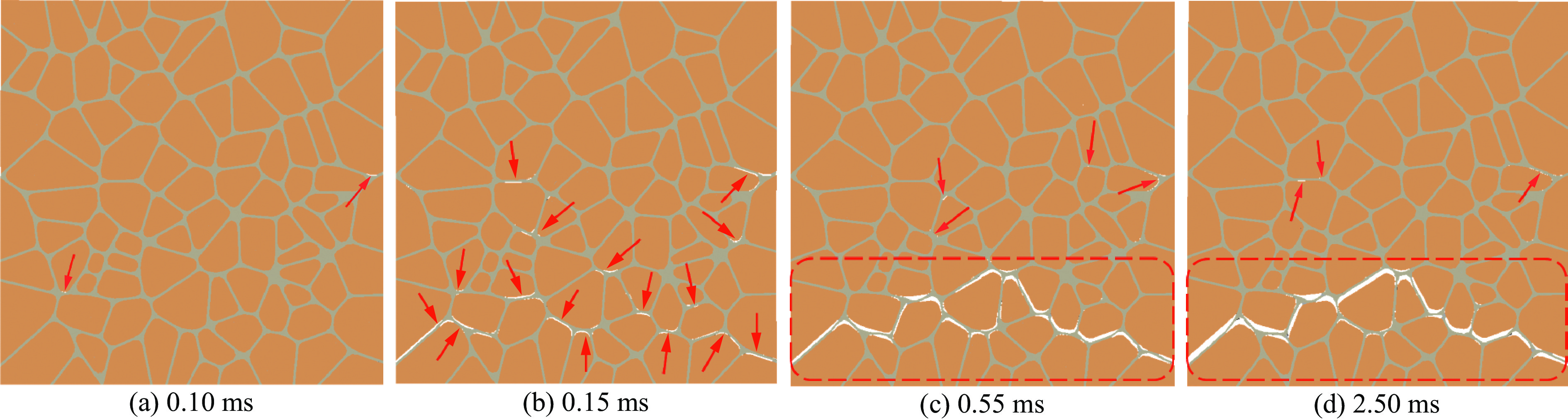
图12给出了细观模型的损伤演化过程。脱粘产生的微裂纹（图12中红色箭头）最先出现在颗粒边角处，并且逐渐增多，之后微裂纹沿着颗粒-黏结剂界面扩展，并逐渐汇聚形成贯穿的主裂纹（图12中红色方框），而非主裂纹区域的微裂纹在压缩与拉伸载荷的反复作用下出现重新黏结现象，最终形成了一条与轴向加载方向垂直的贯穿裂纹。
PBX装药侵彻双层靶板过程中，其细观损伤可分为3个阶段。在第1阶段，装药细观结构发生弹性变形，由于黏结剂的弹性模量较小，PBX装药结构的压缩变形一般由黏结剂承担，晶体几乎不变形。在第2阶段，结构发生非线性响应，此时，晶体仍基本不变形，当黏结剂颗粒表面的应力超过其脱粘强度时，微裂纹开始成核，结构刚度开始退化。同时，应变能开始向微裂纹尖端流动，剪切应变和拉伸应变也开始向裂纹尖端附近集中，剪切滑移带逐渐形成。黏结剂柔性链之间的相对剪切滑移会导致塑性变形和应变软化[31]，因此，结构的刚度进一步降低。在第3阶段，黏结剂无法承受塑性变形，微裂纹失稳扩展并汇聚为连续的主裂纹，最终使结构失去刚度。
-
基于内聚力单元建立了装药弹体侵彻双层靶板的有限元模型，研究了弹体侵彻双层靶板过程中PBX装药的损伤特征，分析了不同侵彻速度下装药的损伤演化和损伤比的变化趋势，并对侵彻载荷作用下PBX装药细观损伤进行了分析，得到如下主要结论：
(1) 弹体以不同速度侵彻靶板时，装药损伤程度随着侵彻速度的增大而增大，在拉伸和压缩载荷的反复作用下，装药尾部形成了垂直于轴向的贯穿裂纹；
(2) 弹体侵彻双层靶板过程中，PBX装药的主要损伤模式是界面脱粘，界面脱粘而产生的微裂纹最先出现在颗粒边角处，随后逐渐增多，接着微裂纹沿着颗粒-黏结剂界面扩展，并逐渐汇聚形成贯穿的主裂纹。
侵彻双层靶板过程中PBX装药的宏-细观损伤数值模拟研究
Numerical Simulation Study on Macro-Microscopic Damage of PBX Charge during Penetration of Double-Layer Targets
-
摘要: 针对高速战斗部侵彻双层目标时装药的损伤问题，基于内聚力模型开展了PBX装药战斗部侵彻双层靶板的数值模拟研究。采用内聚力模型计算装药损伤的出现与演化，分析了侵彻速度与损伤发生的关系，通过损伤比对侵彻结束后PBX装药的损伤进行了量化，建立了PBX装药细观损伤仿真模型，研究了侵彻双层靶板过程中PBX装药细观损伤机制。结果表明：当弹体垂直侵彻双层靶板时，在压-拉反复作用下，装药尾部形成了垂直于加载方向的贯穿裂纹，且装药的损伤程度随着侵彻速度的增大而增大；在侵彻双层靶板过程中，PBX装药的主要损伤模式是界面脱粘，微裂纹最先出现在颗粒边角处，并且逐渐增多，最终界面微裂纹失稳扩展并汇聚为连续的主裂纹。Abstract: To study the charge damage evolution process when a high-velocity warhead penetrated a double-layer target, a numerical simulation study was conducted using a cohesive zone model to investigate the penetration of double-layer target. The cohesive zone model was utilized to calculate the occurrence and evolution of PBX damage, as well as to analyze the relationship between the penetration velocity and damage evolution. The quantification of damage was conducted by means of the damage ratio. Furthermore, a micro-damage finite element model for PBX was established to examine the microscopic damage mechanisms during penetration into a double-layer target. The results show that when the projectile penetrates the target plate vertically, the extent of damage of the charge increases with the increase of penetration velocity. From a microscopic perspective, it was observed that cyclic tensile and compressive loads induced the formation of vertical cracks perpendicular to the loading direction. The primary mechanism of damage in PBX charge penetration into double-layer target is interface debonding. Additionally, the microcracks destabilize, propagate, and converge into a continuous main crack.
-
-
图 4 内聚力单元的双线性力-位移定律模型
Figure 4. Bilinear traction-separation law model of cohesive element
图 6 PBX在
2000 s−1应变率下的应力-应变曲线Figure 6. Stress-strain curves of PBX at the strain rate of
2000 s−1
图 7 数值模拟得到的装药内部损伤演化历程
Figure 7. Damage evolution contour of explosive charge obtained from numerical simulation
图 8 侵彻结束后装药CT扫描重构图像
Figure 8. Reconstruction of CT scan of the charge after penetration
图 9 不同侵彻速度侵彻后装药的损伤
Figure 9. Damage contour of explosive charge after penetration at different velocities
图 10 装药尾部易损伤区域的轴向和径向应力时程曲线及边界条件
Figure 10. Axial and radial stress histories and boundary conditions at the danger zone of the charge tail region
图 11 侵彻双层靶板过程中PBX装药细观结构的主应变分布
Figure 11. Principal strain distributions for microscopic model during the penetration of double-layer target
图 12 侵彻双层靶板过程中PBX装药的损伤演化
Figure 12. Damage evolution process of PBX during penetration of double-layer target
表 1 弹壳、靶板和缓冲层的材料参数
Table 1. Parameters of projectile shell, target, and buffer layer
Material $ \rho $ /(kg·m−3)μ E/GPa A/MPa B/MPa n C m $ {\dot \varepsilon _0} $ /s−135CrMnSi steel 7830 0.30 204 1440 1501 0.4403 0.039 0.404 10−3 45 steel 7830 0.33 210 496 434 0.2600 0.014 1.030 1.0 Polycarbonate 1190 0.38 3.6 84 3228 3.1456 0.089 1.010 0.1 
下载: 导出CSV
表 2 PBX装药的内聚力单元参数
Table 2. Cohesive elements parameters of PBX charge
Kcoh/(GPa·m−1) $ \sigma $ /MPaG/(kN·m−1) 1700 23 0.17
下载: 导出CSV
表 3 PBX装药颗粒、黏结剂和界面内聚力单元参数
Table 3. Cohesive elements parameters of particle, binder and interface
Cohesive element Kcoh/(GPa·m−1) $ \sigma $ /MPaG/(kN·m−1) Particle 1800 6.00 0.010 Binder 900 7.50 0.150 Particle-binder interface 800 2.75 0.012
下载: 导出CSV
-
[1] 李媛媛, 高立龙, 李巍, 等. 抗过载炸药装药侵彻安全性试验研究 [J]. 含能材料, 2010, 18(6): 702–705. doi: 10.3969/j.issn.1006-9941.2010.06.021 LI Y Y, GAO L L, LI W, et al. Experiment research on security of insensitive explosive charge during penetration [J]. Chinese Journal of Energetic Materials, 2010, 18(6): 702–705. doi: 10.3969/j.issn.1006-9941.2010.06.021 [2] 陈文, 张庆明, 胡晓东, 等. 侵彻过程冲击载荷对装药损伤实验研究 [J]. 含能材料, 2009, 17(3): 321–325. doi: 10.3969/j.issn.1006-9941.2009.03.017 CHEN W, ZHANG Q M, HU X D, et al. Experimental study on damage to explosive charge by impact load in the process of penetration [J]. Chinese Journal of Energetic Materials, 2009, 17(3): 321–325. doi: 10.3969/j.issn.1006-9941.2009.03.017 [3] LI X, LIU Y Z, SUN Y. Dynamic mechanical damage and non-shock initiation of a new polymer bonded explosive during penetration [J]. Polymers, 2020, 12(6): 1342. doi: 10.3390/polym12061342 [4] 李晓. 侵彻过程中PBX装药的损伤与点火机制研究 [D]. 哈尔滨: 哈尔滨工业大学, 2020. LI X. Investigations on damage and initiation mechanism of PBX charge during penetration [D]. Harbin: Harbin Institute of Technology, 2020. [5] 赵生伟, 初哲, 李明. 抗侵彻过载战斗部装药安定性实验研究 [J]. 兵工学报, 2010, 31(Suppl 1): 284–287. ZHAO S W, CHU Z, LI M. Experiment investigation on stability of explosive in anti-overload warhead [J]. Acta Armamentarii, 2010, 31(Suppl 1): 284–287. [6] 成丽蓉, 汪德武, 贺元吉. 侵彻单层和多层靶时战斗部装药损伤及热点生成机理研究 [J]. 兵工学报, 2020, 41(1): 32–39. doi: 10.3969/j.issn.1000-1093.2020.01.004 CHENG L R, WANG D W, HE Y J. Research on the damage and hot-spot generation in explosive charges during penetration into single- or multi-layer target [J]. Acta Armamentarii, 2020, 41(1): 32–39. doi: 10.3969/j.issn.1000-1093.2020.01.004 [7] 毕超, 郭翔, 屈可朋, 等. 斜侵彻靶板过程中装药损伤的数值模拟 [J]. 火炸药学报, 2022, 45(3): 383–387. doi: 10.14077/j.issn.1007-7812.202201009 BI C, GUO X, QU K P, et al. Numerical simulation of charge damage during oblique penetration [J]. Chinese Journal of Explosives & Propellants, 2022, 45(3): 383–387. doi: 10.14077/j.issn.1007-7812.202201009 [8] 崔云霄. 冲击载荷作用下PBX炸药的损伤破坏研究 [D]. 北京: 北京理工大学, 2017. CUI Y X. Research on damage and destruction of PBX explosive under impact load [D]. Beijing: Beijing Institute of Technology, 2017. [9] 石啸海, 戴开达, 陈鹏万, 等. 战斗部侵彻过程中PBX装药动态损伤数值模拟 [J]. 中国测试, 2016, 42(10): 138–142. doi: 10.11857/j.issn.1674-5124.2016.10.026 SHI X H, DAI K D, CHEN P W, et al. Numerical simulation of dynamic damage of PBX charge during the warhead penetration process [J]. China Measurement & Test, 2016, 42(10): 138–142. doi: 10.11857/j.issn.1674-5124.2016.10.026 [10] 石啸海, 余春祥, 戴开达, 等. 侵彻过程中弹头形状对PBX炸药损伤的影响 [J]. 弹箭与制导学报, 2019, 39(3): 81–85, 89. doi: 10.15892/j.cnki.djzdxb.2019.03.019 SHI X H, YU C X, DAI K D, et al. The influence of nose shape to dynamic damage of PBX charge during the penetration process [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2019, 39(3): 81–85, 89. doi: 10.15892/j.cnki.djzdxb.2019.03.019 [11] 张学伦, 汪衡, 谭正军, 等. 混凝土靶边界效应与弹丸长径比关联性的研究 [J]. 兵器装备工程学报, 2018, 39(4): 11–13, 18. doi: 10.11809/bqzbgcxb2018.04.003 ZHANG X L, WANG H, TAN Z J, et al. Relevance between aspect ratio of projectile and boundary effect of concrete target [J]. Journal of Ordnance Equipment Engineering, 2018, 39(4): 11–13, 18. doi: 10.11809/bqzbgcxb2018.04.003 [12] 孙宝平, 段卓平, 万经伦, 等. 基于Visco-SCRAM模型的侵彻装药点火研究 [J]. 爆炸与冲击, 2015, 35(5): 689–695. doi: 10.11883/1001-1455(2015)05-0689-07 SUN B P, DUAN Z P, WAN J L, et al. Investigation on ignition of an explosive charge in a projectile during penetration based on Visco-SCRAM model [J]. Explosion and Shock Waves, 2015, 35(5): 689–695. doi: 10.11883/1001-1455(2015)05-0689-07 [13] 李硕. 强冲击载荷下35CrMnSi动态力学行为与断裂机理研究 [D]. 太原: 中北大学, 2015. LI S. Study on dynamic mechanical behavior and fracture mechanism of 35CrMnSi under impact loads [D]. Taiyuan: North University of China, 2015. [14] 赵丽俊, 郝永平, 黄晓杰, 等. 杆式射流侵彻45钢靶数值分析及试验研究 [J]. 兵器装备工程学报, 2023, 44(8): 147–153. doi: 10.11809/bqzbgcxb2023.08.021 ZHAO L J, HAO Y P, HUANG X J, et al. Numerical simulation and experimental research on jetting projectile charge penetrating 45 steel target [J]. Journal of Ordnance Equipment Engineering, 2023, 44(8): 147–153. doi: 10.11809/bqzbgcxb2023.08.021 [15] 于鹏. 航空聚碳酸酯动态力学性能及本构关系研究 [D]. 广州: 华南理工大学, 2014. YU P. Investigation on the dynamic characteristics and constitutive model of polycarbonate of aircraft [D]. Guangzhou: South China University of Technology, 2014. [16] XIAO Y C, ZHANG Q, FAN C Y, et al. Numerical analysis of the damage and failure behavior of polymer-bonded explosives using discrete element method [J]. Computational Particle Mechanics, 2024, 11(2): 579–598. doi: 10.1007/s40571-023-00640-8 [17] XIAO Y C, ZHANG Q, GONG T Y, et al. Experimental analysis and multi-scale simulation of the fracture behavior of polymer-bonded explosives based on the dynamic notched semi-circular bend method [J]. International Journal of Solids and Structures, 2024, 291: 112690. doi: 10.1016/j.ijsolstr.2024.112690 [18] BI C, GUO X, WANG A H, et al. Strain-rate-dependent cohesive zone modelling of charge damage behavior when a projectile penetrates multilayered targets [J]. Acta Mechanica, 2023, 234(7): 2869–2887. doi: 10.1007/s00707-023-03541-2 [19] XIAO Y C, GONG T Y, ZHANG X W, et al. Multiscale modeling for dynamic compressive behavior of polymer bonded explosives [J]. International Journal of Mechanical Sciences, 2023, 242: 108007. doi: 10.1016/j.ijmecsci.2022.108007 [20] YANG Z, KANG G, LIU R, et al. Predicting the mechanical behaviour of highly particle-filled polymer composites using the nonlinear finite element method [J]. Composite Structures, 2022, 286: 115275. doi: 10.1016/j.compstruct.2022.115275 [21] BARUA A, KIM S, HORIE Y, et al. Prediction of probabilistic ignition behavior of polymer-bonded explosives from microstructural stochasticity [J]. Journal of Applied Physics, 2013, 113(18): 184907. doi: 10.1063/1.4804251 [22] HARDIN D B, ZHOU M. Effect of viscoplasticity on ignition sensitivity of an HMX based PBX [J]. AIP Conference Proceedings, 2017, 1793(1): 080005. doi: 10.1063/1.4971611 [23] CHEN X, DENG X M, SUTTON M A, et al. An inverse analysis of cohesive zone model parameter values for ductile crack growth simulations [J]. International Journal of Mechanical Sciences, 2014, 79: 206–215. doi: 10.1016/j.ijmecsci.2013.12.006 [24] AIROLDI A, DÁVILA C G. Identification of material parameters for modelling delamination in the presence of fibre bridging [J]. Composite Structures, 2012, 94(11): 3240–3249. doi: 10.1016/j.compstruct.2012.05.014 [25] VALOROSO N, SESSA S, LEPORE M, et al. Identification of mode-Ⅰ cohesive parameters for bonded interfaces based on DCB test [J]. Engineering Fracture Mechanics, 2013, 104: 56–79. doi: 10.1016/j.engfracmech.2013.02.008 [26] YAMAKOV V, SAETHER E, GLAESSGEN E H. Multiscale modeling of intergranular fracture in aluminum: constitutive relation for interface debonding [J]. Journal of Materials Science, 2008, 43(23/24): 7488–7494. doi: 10.1007/s10853-008-2823-7 [27] XU Y J, ZHAO S, JIN G H, et al. Ductile fracture of solder-Cu interface and inverse identification of its interfacial model parameters [J]. Mechanics of Materials, 2017, 114: 279–292. doi: 10.1016/j.mechmat.2017.08.013 [28] FENG T, XU J S, HAN L, et al. Modeling and simulation of the debonding process of composite solid propellants [J]. IOP Conference Series: Materials Science and Engineering, 2017, 220: 012020. [29] CUI J Y, QIANG H F, WANG J X. Experimental and simulation research on microscopic damage of HTPB propellant under tension-shear loading [J]. AIP Advances, 2022, 12(8): 085214. doi: 10.1063/5.0101388 [30] CUI H R, SHEN Z B, LI H Y. A novel time dependent cohesive zone model for the debonding interface between solid propellant and insulation [J]. Meccanica, 2018, 53(14): 3527–3544. doi: 10.1007/s11012-018-0894-3 [31] 胡静. Janus粒子对硅胶类热力学不相容体系相容性的影响及其应用研究 [D]. 北京: 北京化工大学, 2021. HU J. The effect and application of Janus particles on the compatibility of inherent immiscible blends composed of silicone rubber [D]. Beijing: Beijing University of Chemical Technology, 2021. -
图( 12) 表( 3)
计量
- 文章访问数: 361
- HTML全文浏览数: 361
- PDF下载数: 5
- 施引文献: 0