KPCA是基于核方法的主成分分析方法，旨在克服传统主成分分析算法在处理非线性可分数据特征时的局限，充分保留数据特征信息^[10]。KPCA通过核函数将数据映射至高维空间，增强数据在该空间的线性可分性，避免了非线性映射的显式表达，实现了指标数量的压缩和数据复杂度的简化，降低了模型预测所需的时间成本。本研究对KPCA采用5倍交叉验证，确定最优核参数σ的取值，利用KPCA对岩爆数据预处理，消除指标间的相关性并降维，提取主要特征。

假设有n个样本，每个样本有m个特征，建立初始样本矩阵$ {{\boldsymbol{X}}}'_{{{{n}}}\times {{{m}}}} $，归一化后得样本矩阵$ {{{\boldsymbol{X}}}}_{{{{n}}}\times {m}} $。

首先，通过映射函数$ \boldsymbol {\phi} $将样本数据$ \boldsymbol{x}_i\in{\mathbf{R}}^{n} $映射至高维特征空间$ {\mathbf{R}}^{F} $中，得到输入变量$ {\boldsymbol x}_{i} $的中心非线性映射$ {\boldsymbol \phi} \left({\boldsymbol x}_{i}\right) $，若映射的均值为零，则$ {\mathbf R}^{F} $空间中协方差矩阵为

所对应的特征方程为

式中：$ \lambda $和$ {{\boldsymbol{v}}} $分别为协方差矩阵的特征值和特征向量，且所有$ \lambda \geqslant 0 $的解$ {{\boldsymbol{v}}} $都在$ {\boldsymbol \phi} \left({\boldsymbol x}_{i}\right) $中。

然后，由式(1)～式(2)可得特征向量$ {{\boldsymbol{v}}} $

映射$ \boldsymbol \phi $通常不是显式的，$ \boldsymbol{v} $的计算较困难，因此，引入核函数$ {\boldsymbol k}({{\boldsymbol x}_i},{{\boldsymbol x}_j}) $进行处理

最后，计算核矩阵，将式(1)、式(3)分别代入式(2)，并对等式两边进行内积运算，同时将式(5)引入运算后的式(2)中，求得

式中：K为k对应的核矩阵，$ {{\boldsymbol{\alpha}} }=({{{\boldsymbol{\alpha}} }}_{1},{{{\boldsymbol{\alpha}} }}_{2},\cdots, {{{\boldsymbol{\alpha}} }}_{{{\boldsymbol{n}}}}) $。

通过式(6)得特征值$ {\lambda }_{1}\geqslant {\lambda }_{2}\geqslant \cdot \cdot \cdot\geqslant {\lambda }_{n} $及其对应的特征向量$ {{{\boldsymbol{\alpha}} }}_{1},{{{\boldsymbol{\alpha}} }}_{2},\cdots, {{{\boldsymbol{\alpha}} }}_{{{\boldsymbol{n}}}} $。选取的l（l≤n）个特征值需满足累计贡献率大于85%

当累计贡献率达到设定要求时，计算的新样本$ {\boldsymbol \phi} \left({\boldsymbol x}_{j}\right) $投影后的第$ j(j=\mathrm{1,2},\cdot \cdot \cdot ,p) $维坐标为

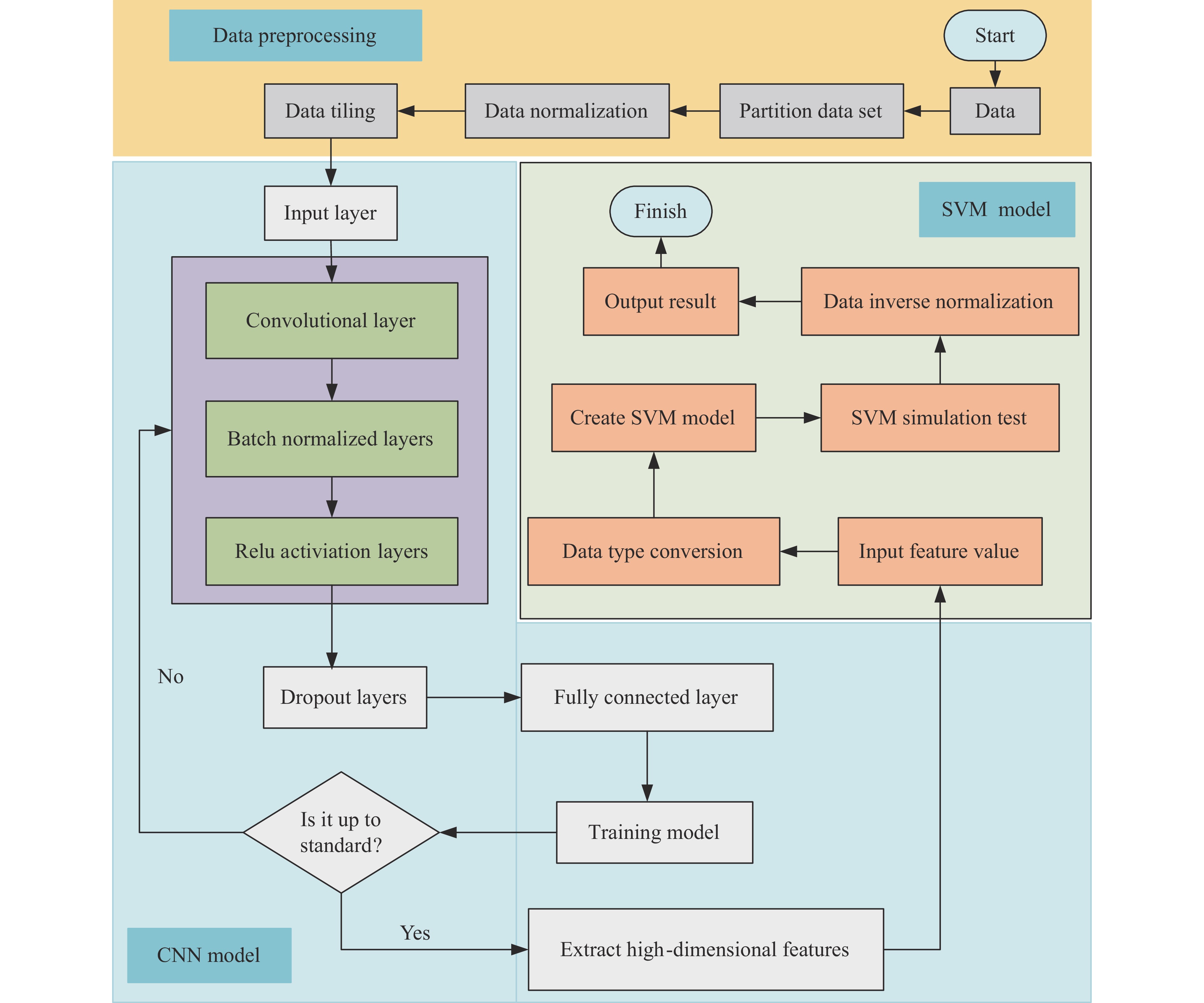
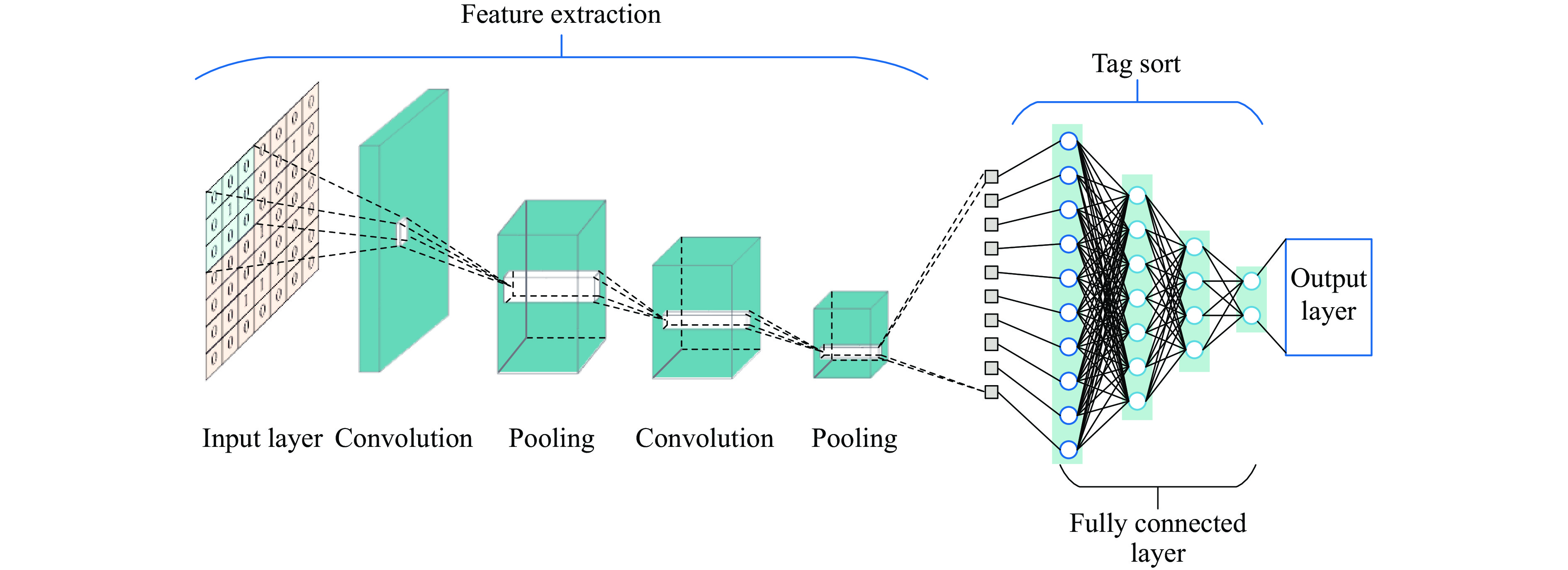
CNN属于深度学习领域的一种先进的前馈神经网络架构，通过局部连接和权值共享的方式显著提高网络模型的优化效率，降低过拟合的风险。如图1所示，CNN的结构包括输入层、卷积层、池化层、全连接层和输出层^[12–13]。输入层是网络的初始数据输入层，通过特征提取将图像传递到卷积层。卷积层线性抽取局部范围内的神经元信息与特征，运用非线性激活函数对神经元进行激活，利用卷积核在输入数据上滑动实现卷积运算，提取特征参数并反馈至池化层^[9]。池化层用于下采样，减少特征图尺寸，实施数据降维，并与全连接层相连。全连接层能够将所得到的多维特征图平铺为一维向量，实现数据高维至低维的转换，同时学习各种组合特征。CNN通过卷积、池化等操作提取并汇总特征，然后解释分类，从而提高模型的表达能力，减少模型参数和计算量。

SVM是一种基于统计学理论和结构风险最小化原则的机器学习方法，通过运用核函数定义的非线性变换将输入空间变换到高维空间，以寻找输入与输出之间的非线性映射关系，具有结构简单、泛化能力强、计算难度小、样本空间维数低等优点，可以更好地处理非线性、高维数和小样本问题^[14]。关于SVM的工作原理，已有大量文献进行了详细阐述，这里不再赘述。

传统CNN中的池化层可实现对高维冗余数据的降维，但经KPCA处理后的岩爆数据特征维数较低。鉴于使用池化层可能导致信息丢失，本研究中的CNN采用卷积层—批归一化层—Relu激活层—丢弃层—全连接层的结构设计，不采用堆叠到模型结构中的池化层。批归一化层可以在不丢失数据特征的前提下加速收敛；Relu激活层可以增强模型的收敛性，并预防过拟合现象；丢弃层则可进一步提升模型的泛化能力。SVM是一种高效的分类算法，特别适合处理小样本数据集，同时，其对缺失数据具有较强的不敏感性，能够在一定程度上规避维度灾难问题^[15]。基于此，采用SVM替代传统的CNN分类器在理论上是可行的，并且在实际预测中也表现出较高水准^[16]。本研究将堆叠CNN和SVM，建立CNN-SVM集成模型，进行分类预测。

CNN-SVM集成模型将特征提取与分类步骤分离，其中，CNN作为特征提取器，提取原始数据中的特征，输入至SVM分类器进行分类^[17]。CNN-SVM集成模型利用SVM的优化能力，并融合卷积操作和SVM的核函数，提升了模型在分类任务中的性能表现和适应性，具体流程见图2。

BKA是模拟黑翅鸢在攻击和迁徙中表现出的高度适应性和智能行为提出的群智能优化算法^[17]。该算法集成了柯西突变策略和领导者策略，增强了算法的全局寻优能力，提高了算法的收敛速度。该算法主要包括3个阶段：初始化、攻击行为和迁徙行为。

创建一组随机解，矩阵中的每个元素表示每只黑翅鸢的位置

式中：p为潜在解决方案的个数，d为给定问题的维度大小，$ B_{i,j} $为第i个黑翅鸢的第j个维度。均匀分配每只黑翅鸢的位置

式中：i为1～p之间的整数，$ B_{l,b} $和$ B_{u,b} $分别为第i个黑翅鸢在第j维的下界和上界，r在[0, 1]区间随机选值。

在种群初始化中，黑翅鸢选择适应度最好的个体作为初始种群的领导者，亦认为是最优位置。其初始领导者$ {X}_{\rm L} $的数学表示为

该策略包括不同的攻击行为，用于全局探索。以下是黑翅鸳攻击行为的数学模型

式中：$ {y}_{t}^{i,j} $和$ {y}_{t+1}^{i,j} $分别为第i只黑翅鸢在第t步和第t+1步迭代中第j维的位置，p为0.9，T为总迭代次数。

自然界中迁移通常由种群的领导者引领，因而该算法假设：若当前种群的适应度值小于随机种群的适应度值，则更换领导者；反之，则确定领导者并引导种群到达目的地。这种策略可以动态地选择优秀的领导者，确保迁移成功。以下是黑翼鸢迁徙行为的数学模型

式中：$ {L}_{t}^{j} $为迄今为止第t次迭代的第j维黑翅鸢的领先得分者，即最优解；F_i为任一黑翅鸢在第t次迭代中得到的第j维当前位置；F_ri为第t次迭代中任意黑翼鸢在第j维随机位置的适应度值；C(0, 1)为柯西突变。一维柯西分布是具有2个参数（$ \delta $和$ \mu $）的连续概率分布，概率密度函数为

当$ \delta $ =1，$ \mu $ =0时，式(17)变为标准概率密度函数

岩爆发生机理十分复杂且影响因素众多，呈现出明显的随机性、突发性和复杂性等特征^[18]。其主要影响因素包括岩性条件、地质构造、开挖扰动、围岩初始应力状态等。研究表明，相较于单一指标，多指标岩爆预测方法可以更为全面地揭示岩爆机理的复杂性，避免单一指标的岩爆判据在高精度预测方面的局限性^[8]。本研究借鉴前人成果，基于岩石的性质和岩爆影响因素，选取3个反映岩石力学主要特征的参数，即单轴抗压强度（uniaxial compressive strength，UCS）、单轴抗拉强度（uniaxial tensile strength，UTS）、围岩最大切应力（maximum tangential stress，MTS），以及3个反映围岩性质的指标，即岩体应力系数（Biot’s coefficient of friction，BCF）、脆性系数（stress concentration factor，SCF）和弹性能量指数（elastic energy index，EEI），作为岩爆预测特征指标。为探究选取的6个指标之间的相关性，对以下岩爆预测评价指标组合进行研究：(1) UTS、BCF、SCF，(2) UCS、UTS、BCF、SCF、EEI，(3) MTS、UCS、UTS、BCF、SCF、EEI。

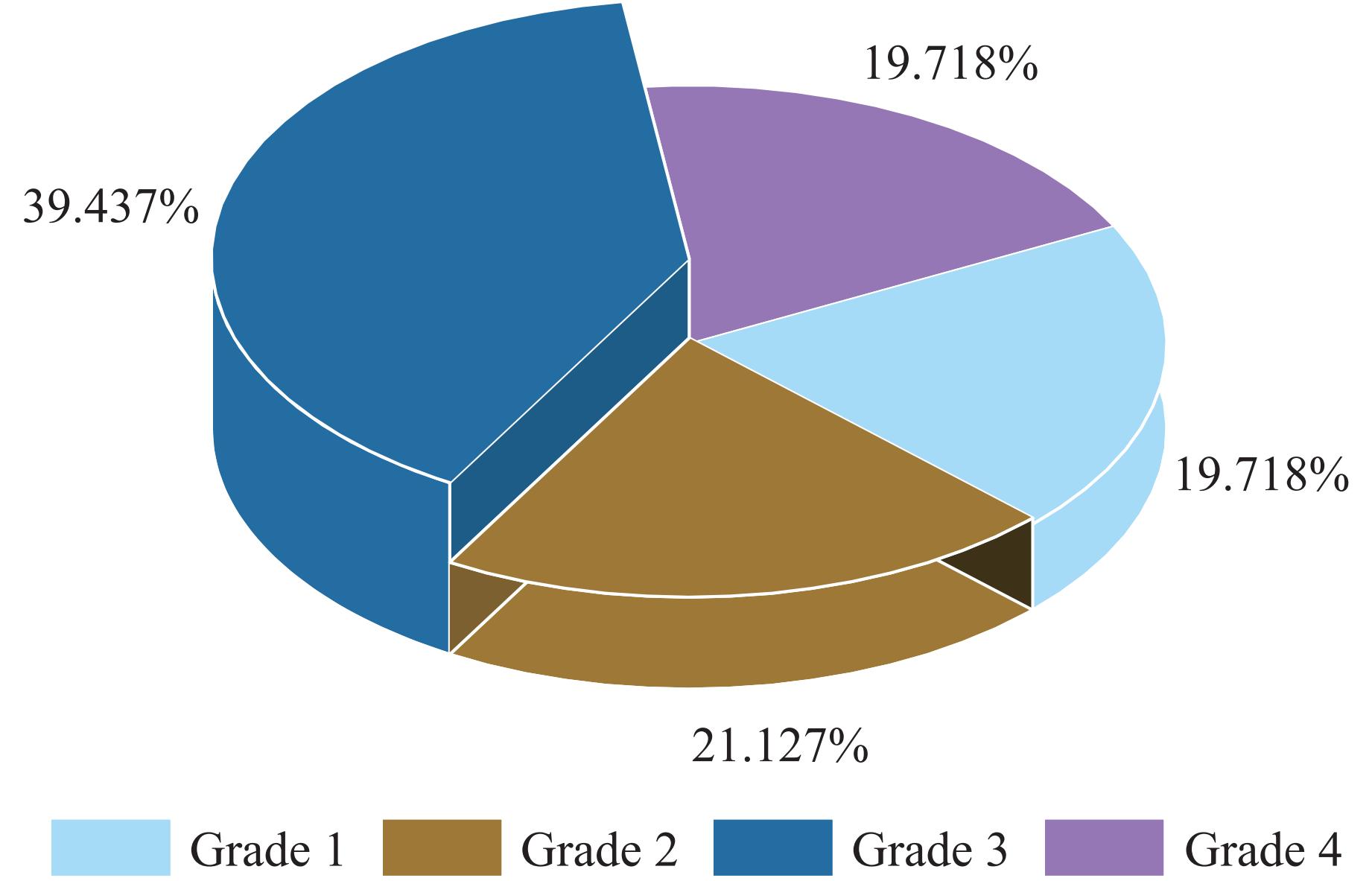
模型可靠性受岩爆案例数量和数据质量的双重影响，多数研究因预测模型基于少量案例构建，普遍存在泛化性能不足的问题。因此，本研究收集了284例国内外岩爆工程实例，部分数据见表1^[19–21]，岩爆预测结果以岩爆等级表示。目前，一般按岩爆烈度将岩爆分为4级：无岩爆（1）、轻微岩爆（2）、中等岩爆（3）、强烈岩爆（4）。本研究收集的284个案例的岩爆等级分布如图3所示。

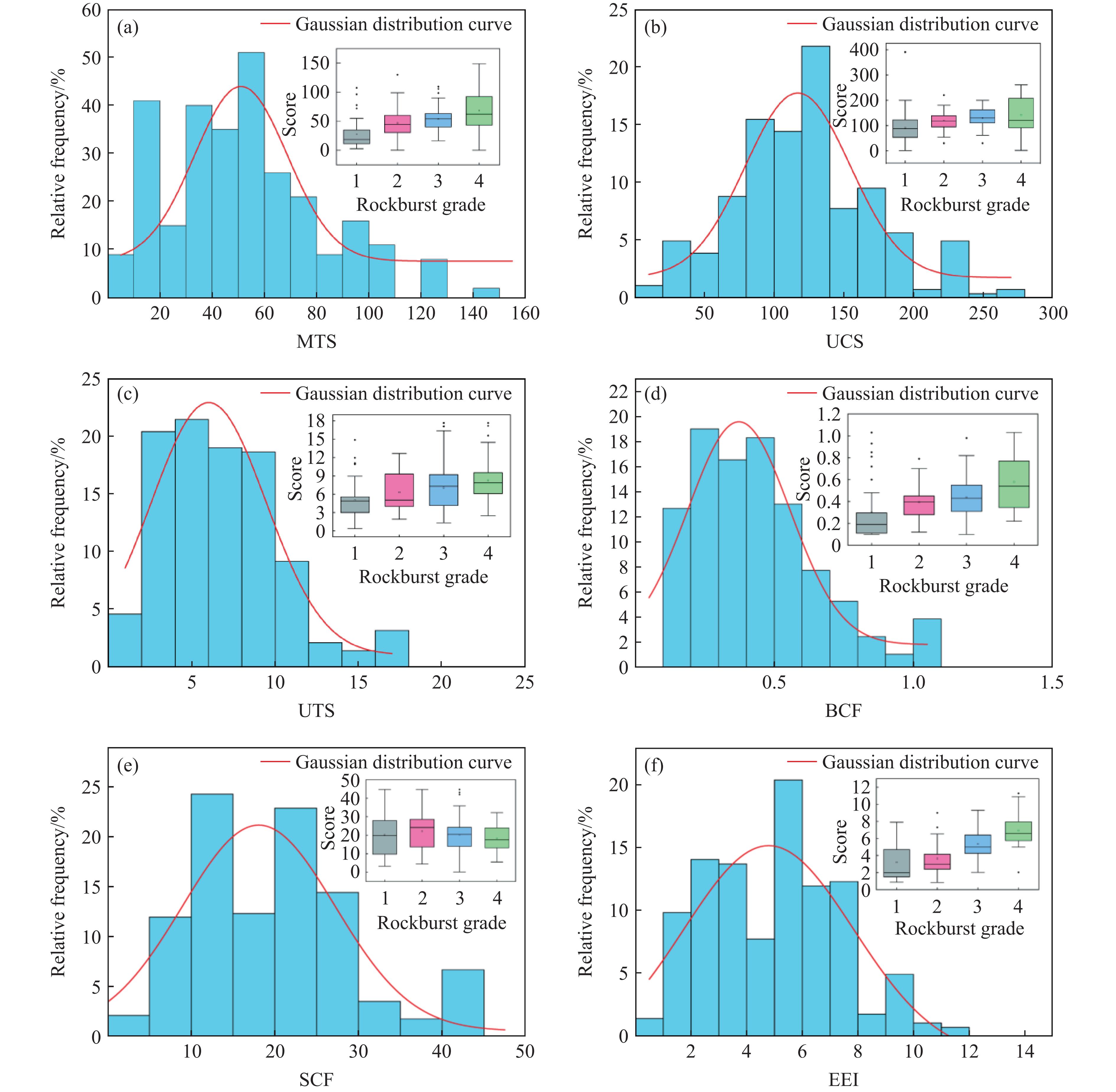
为实现较高的预测准确率，需对原始数据进行预处理。依据岩爆烈度等级对284个样本案例的基本特征情况进行汇总，结果如表2所示。由表2可知：MTS的最大值为148.81 MPa，四分位数为30.79 MPa，最小值为2.60 MPa，呈现明显的右偏现象；UTS的最大值为17.68 MPa，四分位数为4.05 MPa，最小值为0.38 MPa，也呈现出明显的右偏分布；其余数据同样具有一定的右偏特征。因表2所列数据有限，为更直观地描述样本的分布情况，绘制了6个特征的高斯函数分布曲线及不同特征中4个岩爆等级的箱型图，如图4所示。

指标特征数据在采集和测量过程中可能受到人工操作或采动因素的干扰，导致数据存在误差，因而，若个别样本值与大多数测量值不同，则为异常数据或离群值^[22]。为消除离群值对模型预测精度的影响，本研究采用拉依达准则对数据进行甄别，剔除离群值，然后用1.5倍四分位差对离群值进行替换，以确保数据的稳定性和预测模型的可靠性。拉依达准则表示为

式中：$ \beta $为标准偏差，$ {q}_{a} $和$ {\nu }_{a} $分别为数据集中第a个数据及其剩余误差，$ \overline{q} $为数据集的均值。

将收集的284组地下工程和矿山岩爆案例作为原始数据，按7∶3的比例将数据集随机分为训练集和测试集。

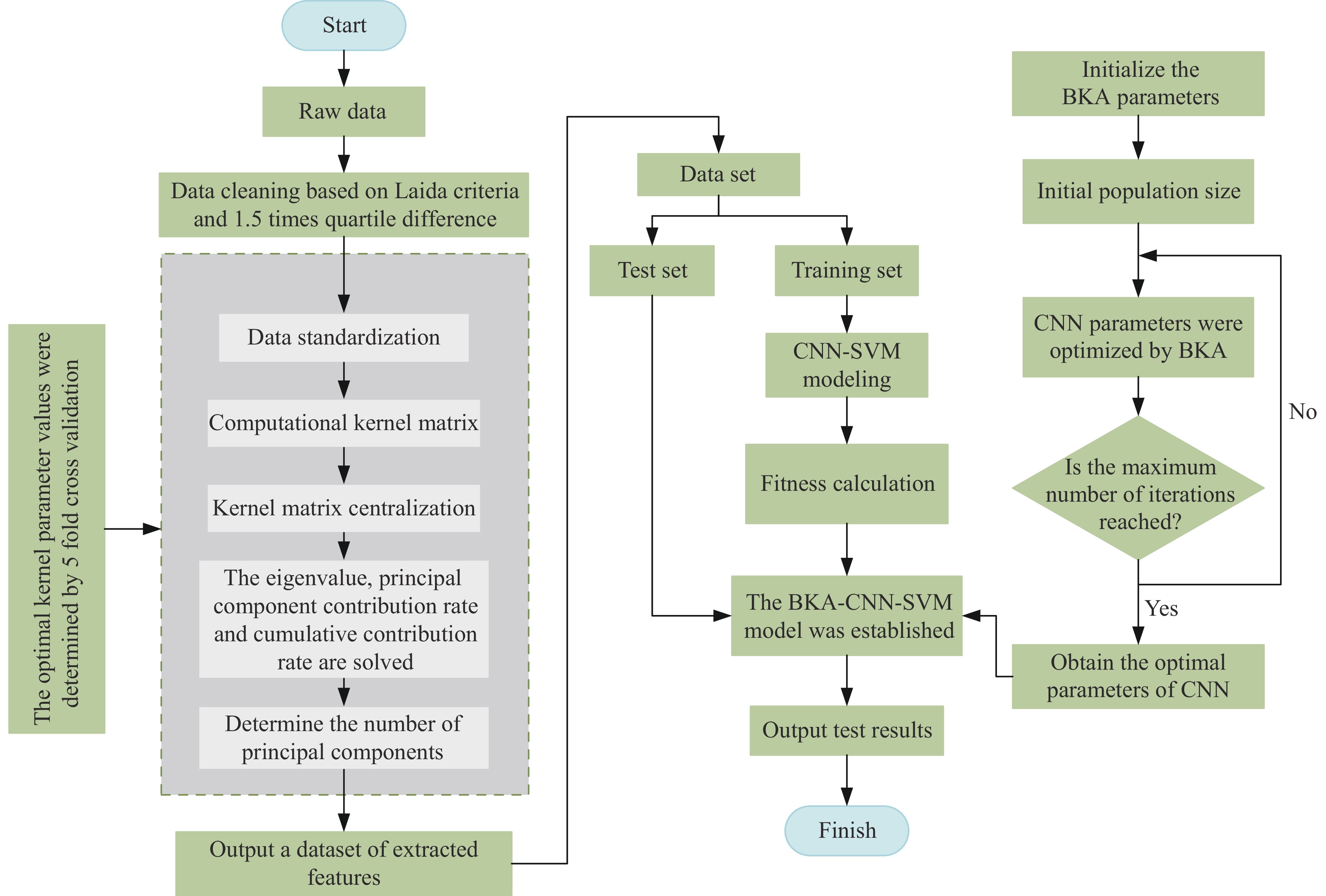
模型构建流程主要包括以下步骤：

(1) 根据选定指标搜集岩爆案例数据，基于拉依达准则将原始数据中的异常值替换成1.5倍四分位差；

(2) 将预处理后的原始数据标准化，以消除不同指标间量纲和数量级的差异；

(3) 采用五折交叉验证确定KPCA的最优核参数σ，并利用KPCA对岩爆数据预处理，消除指标间的相关性并降维，提取主要特征；

(4) 采用堆叠技术将SVM替代传统的CNN分类器，构建CNN-SVM集成模型，并应用于岩爆预测，为避免模型参数对预测精度的影响，引入黑翅鸢优化算法优化预测模型，以规避局部最优陷阱，增强模型的收敛速度和稳定性；

(5) 输入提取的特征，根据建立的BKA-CNN-SVM模型获得预测结果，并与其他模型预测结果进行比较，测试准确率。

BKA-CNN-SVM模型预测岩爆烈度的流程见图5。

KPCA是利用核函数将原始数据映射至高维空间进行主成分分析进而对数据进行降维处理，其充分保留了数据的特征信息。为消除指标间的相关性，基于KPCA对岩爆预测评价指标组合进行相关性探究，结果见表3。

由表3可知：组合1与组合2的指标间相关系数均小于0.28，呈现出微弱的相关性。组合3中，MTS与BCF的相关系数为0.6545，说明两者有较为明显的相关性，会影响岩爆预测最终结果。因此，组合3需采用KPCA进行数据处理，消除指标间相关性。

选用高斯核函数对标准化的284组岩爆案例数据进行KPCA数据处理。高斯核函数参数经五折交叉验证得到最优值为9，其特征提取步骤如1.1节所述，特征提取结果见表4。

由表4可知，前3个主成分的累计贡献率达88.19%，即前3个主成分共包含88.19% 的原始信息。前3个主成分的特征值均大于1，满足特征值大于1且累计贡献率大于85%的条件，因此，选取这3个主成分。建立数据压缩后的矩阵F₁、F₂、F₃作为BKA-CNN-SVM的输入数据。

由于CNN相关参数的取值往往影响模型的准确度，因此，采用BKA算法对CNN模型中的参数（包括学习率、每次训练样本个数、正则化系数）进行优化。算法其他相关参数设置如下：种群规模数为30，优化参数搜索范围分别取[1×10⁻³, 5 ×10⁻²]、[64, 512]、[1×10⁻⁵, 1×10⁻²]。全局寻优后获得的最优参数见表5。

为进一步验证模型的可靠性，选用CNN、SVM、CNN-SVM、ELM预测模型对同一组数据进行训练测试，并采用F₁值、准确率、精确率、召回率对比分析模型的预测性能。将86组经KPCA特征提取的测试样本输入各模型，各模型预测性能见表6。相应的混淆矩阵见图6，其中，对角线元素（从左上到右下）表示被正确分类的样本数量，非对角线元素表示错误分类的样本数量。

由表6可知：BKA-CNN-SVM的预测准确率可达95.35%，与CNN-SVM模型相比，预测准确率增长了12.79%，与CNN模型相比，预测精度亦提升了22.09%。BKA-CNN-SVM的F₁值、精确率、召回率均明显优于其他模型。综合考虑模型的准确率及相关评价指标，本研究建立的BKA-CNN-SVM模型在岩爆烈度预测分级方面表现出较好的预测性能，证明其在岩爆预测应用中的合理性和可行性。

锦屏二级水电站位于我国西南高地应力区，共有7条隧道，包括4条引水隧道、2条平行交通辅助洞以及1条施工排水隧道。洞线平均长度约为16.67 km，开挖洞径约为13 m，引水隧洞之间的间距为60 m；2条辅助洞间隔35 m，平行布置在引水隧洞南侧。辅助洞围岩岩性主要为大理岩，其饱和单轴抗压强度为65～90 MPa，抗拉强度为3～6 MPa，隧洞埋深大体处于1500～2000 m，最大埋深约为2525 m，由于隧洞地质复杂、埋深大，加之高地应力等特性，导致岩爆灾害发生率较高^[23–25]。收集锦屏二级水电站岩爆实例数据20组^[26]，将BKA-CNN-SVM模型应用于锦屏二级水电站岩爆烈度预测。将收集的284例岩爆数据作为训练集，完成BKA-CNN-SVM模型训练后，将20组岩爆实例数据作为测试集代入预测模型。为检验BKA-CNN-SVM模型对锦屏二级水电站岩爆预测的准确率，在相同的训练集和测试集条件下，将其与CNN、SVM、CNN-SVM、ELM预测模型进行对比，结果见表7。

由表7可知，ELM模型在岩爆实例判断中出现了5例误判，CNN模型误判了3例，CNN-SVM集成模型表现出较优的特征提取与泛化能力，仅发生1次误判。BKA-CNN-SVM模型预测结果与实际情况一致，证实了该模型在实际工程应用中的可靠性与实用价值，可为实际工程提供一定的参考。

(1) 采用拉依达准则和1.5倍四分位差对数据进行清洗，消除样本中异常值对模型精度的干扰。同时，引入KPCA进行数据降维，保留主要特征，去除数据中的冗余信息，从而减小了模型输入参数，避免了维度灾难，提高了模型收敛速度及预测可靠性。

(2) 建立了CNN-SVM集成模型并应用于岩爆预测，利用CNN进行数据特征提取，并采用SVM替代传统的CNN分类器进行分类预测。相较于CNN模型，CNN-SVM集成模型的预测精度提高了9.3%，显示出集成模型对不平衡岩爆数据的较高预测性能。为降低人为设置参数的影响，引入黑翅鸢优化算法，建立了BKA-CNN-SVM预测模型，有效提升了模型的全局寻优能力，避免陷入局部最优，进一步提高了预测精度。

(3) 对锦屏二级水电站岩爆实例进行预测，BKA-CNN-SVM的预测结果与实际情况符合得较好，证明该模型具有较强的工程适用性。相较于CNN、CNN-SVM、ELM岩爆预测模型，BKA-CNN-SVM岩爆预测模型具有更高的岩爆预测精度和稳定性。鉴于岩爆实例数据偏少，且未考虑地质条件、岩体质量、开挖断面尺寸等因素，因此，BKA-CNN-SVM模型在其他工程应用中的预测性能还需进一步研究。