For completeness, the theoretical model proposed by Yang et al.^[22] is provided below. The perforation energy can be written as

in which E_p is the perforation energy, comprising the energies absorbed by the initial inelastic impact (E_im), the local indentation (E_id), the local shear failure (E_sf), and the global deformations (E_gd).

E_im is determined by

in which v₀ is the impact velocity; M is the projectile mass; m is the plug mass, which can be written approximately as $m = {\text{π}}{a^2}H{\rho _{\text{t}}}$, with ${\rho _{\text{t}}}$ being the plate density, a the radius of projectile, and H the plate thickness.

E_id is determined by

in which K is the bulk modulus of plate material; $\psi $ is the ratio of the ultimate local indentation to the plate thickness; $ {\varepsilon _{\text{m}}} $ is the final compressive strain when the local indentation ends, $ {\varepsilon _{\text{m}}} = \ln \left[ {{1 \mathord{\left/ {\vphantom {1 {\left( {1 - \psi } \right)}}} \right. } {\left( {1 - \psi } \right)}}} \right] $; $ \sigma \left( {{\varepsilon _X}} \right) $ denotes the yield stress when strain in the compression direction is ${\varepsilon _X}$. ${\varepsilon _X}$ can be estimated by the following formula^[17]

in which τ₀, n and α are material constants; χ is the Taylor-Quinney coefficient, which is taken to be 0.9; c_p is the specific heat capacity of plate at constant pressure; D_m is the dynamic increase factor during perforation.

E_sf is determined by

in which $\gamma $ is the shear strain; ${\gamma _{\text{f}}}$ is the failure shear strain when shear plugging failure occurs; $\tau $ is the shear stress; $ \delta $ is the half-width of shear band; d is the diameter of projectile.

E_gd is determined by

in which W_o is the transverse displacement at the periphery of impact area; K_m and F_c are the membrane stiffness and the static collapse load of plate, respectively, whose expressions can be found in Refs. [7, 22].

The dimensionless empirical equation describing the relationship between the global deformations and the impact velocity for the localized shear plugging with global deformations (Mode Ⅱ) is proposed by Yang et al.^[22]

in which p₁, p₂, and p₃ are empirical constants determined by curve fitting; W_os is the critical transverse displacement of plate when shear failure occurs in Wen-Jones model^[7]

in which $\lambda = {{{\sigma _{\text{u}}}} / {{\sigma _{\text{y}}}}}$, with ${\sigma _{\text{u}}}$ and ${\sigma _{\text{y}}}$ being the ultimate tensile strength and the yield strength of plate material, respectively; R is the radius of target plate. The dimensionless parameter Φ is expressed as

in which v_m is the common velocity of projectile and the impact area, determined by

Φ_c is the critical value of Φ at which the transition of failure modes occurs. For plates perforated in Mode Ⅰ (i. e., simple shear failure with global deformation), W_o/W_os = 1.

Thus, the residual velocity can be obtained according to energy conservation

By letting ${v_{\text{r}}} = 0$ in Eq. (11), one obtains the equation of ballistic limit

And according to Eq. (9), a critical impact velocity v_0c can be derived

where v_mc is the critical velocity independent of plate geometry, and v_0c is the corresponding critical impact velocity when v_m equals to v_mc. Thus, the critical thickness H_c at which the transition of failure modes takes place can be determined as the thickness corresponding to the ballistic limit equals to v_0c.

In this section, the model predictions are compared with available experimental data for the perforation of Weldox 460E steel plates by a flat-nosed projectile^[18–21]. To further understand the perforation mechanisms, discussions on energy absorption are made, with a particular focus on the experimentally observed “plateau” phenomenon.

Various parameters in the present model for Weldox 460E plates as studied by Børvik et al.^[18–21] are listed in Table 1. It should be noted that the local indentation right after the initial inelastic impact is admittedly difficult to determine from experiments, but can be determined through numerical simulations^[22]. Based on previous studies^{[13–14, 17]}, the local indentation ψ can be approximated in the following formula as a first-order approximation

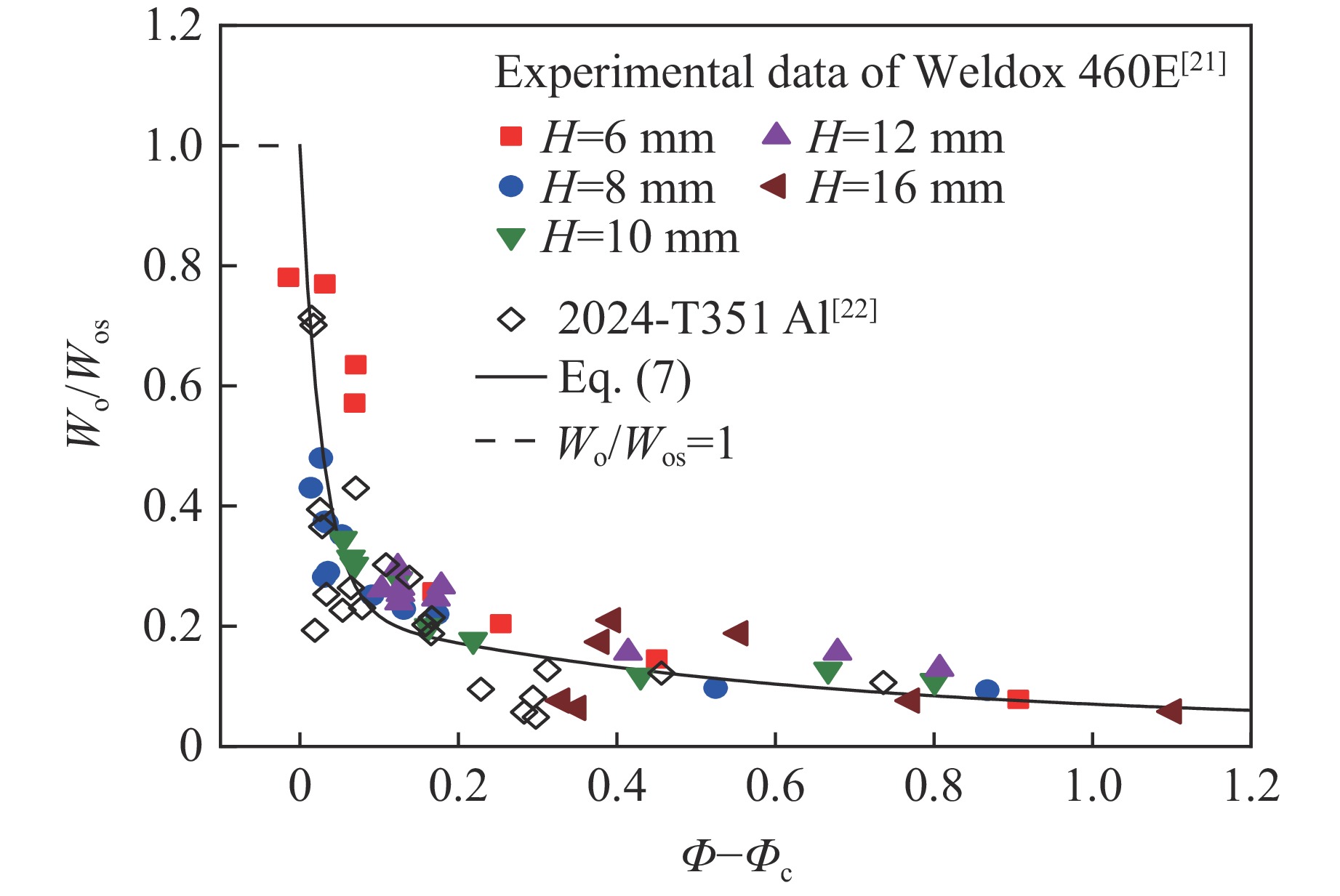
Fig.1 compares Eq. (7) with the experimental data of W_o/W_os versus Φ−Φ_c^[21] for Weldox 460E steel plates perforated by a 20 mm diameter flat-nosed projectile. Fig.1 includes as well W_o/W_os versus Φ−Φ_c for 2024-T351 aluminium plates from Ref. [22]. It is clear that good agreement is achieved between Eq. (7) and the experimental data. It should be noted here that the values of parameters p₁, p₂ and p₃ are maintained the same as in Ref. [22], which demonstrates the general applicability of Eq. (7).

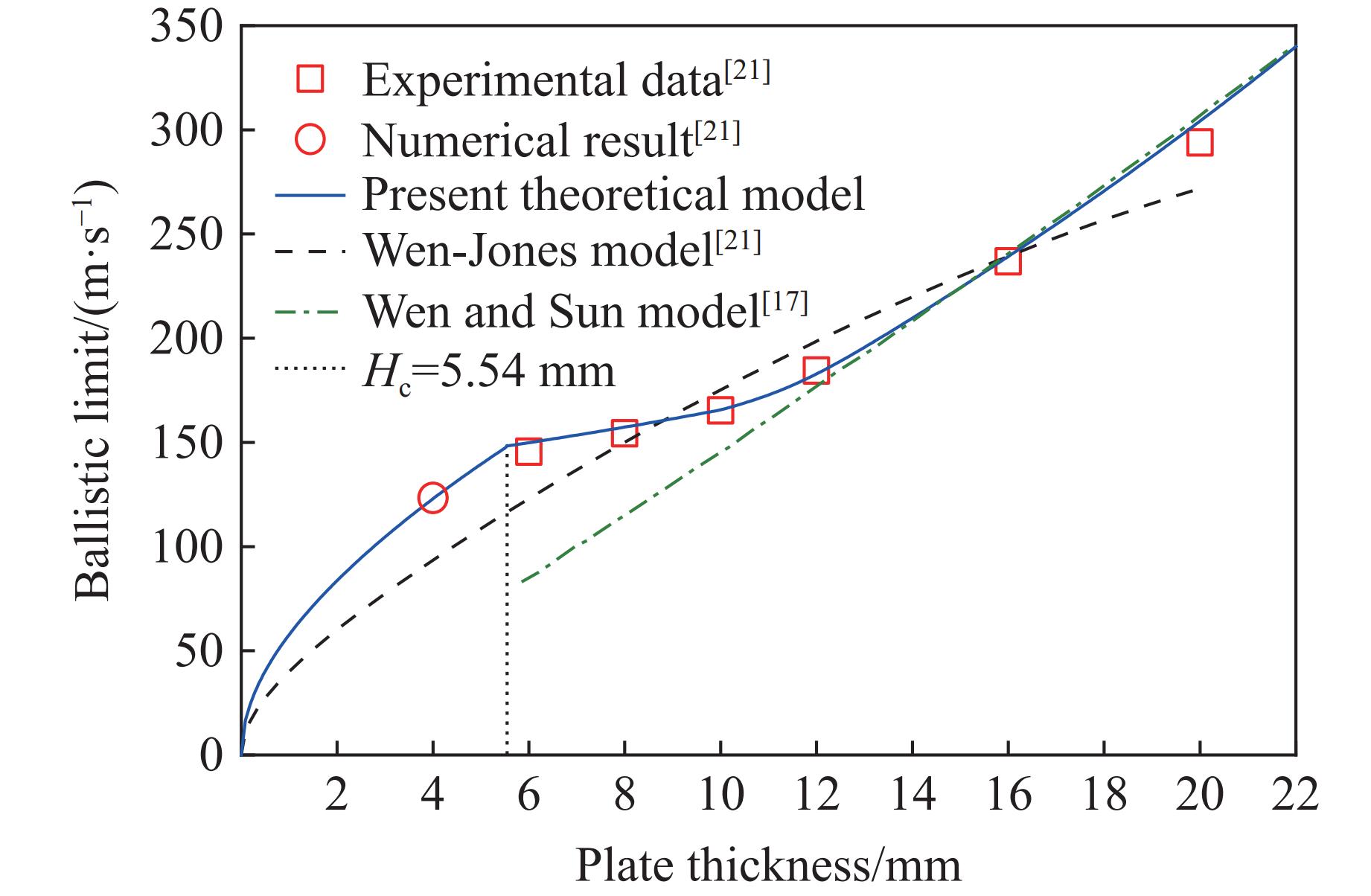
Fig.2 compares the theoretically predicted ballistic limits with the experimental data for Weldox 460E steel plates impacted by a 20 mm diameter flat-nosed projectile. It presents as well the numerically predicted ballistic limit for the 4 mm thick plate as reported by Børvik et al. ^[21] and the theoretically predicted ballistic limits given by Wen-Jones model^[21] and Wen and Sun model^[17]. By comparing the experimental data with the numerical result in Fig.2, it is evident that the present model gives more consistent results than Wen-Jones model and Wen and Sun model. It is as well evident that the present model can predict the “plateau” phenomenon observed experimentally for plate thicknesses between 6 mm and 10 mm. It should be noted here that, for the 20 mm flat-ended projectile impacting Weldox 460E steel plates, the critical thickness H_c for the transition of failure modes is 5.54 mm, which agrees well with the experimental observation.

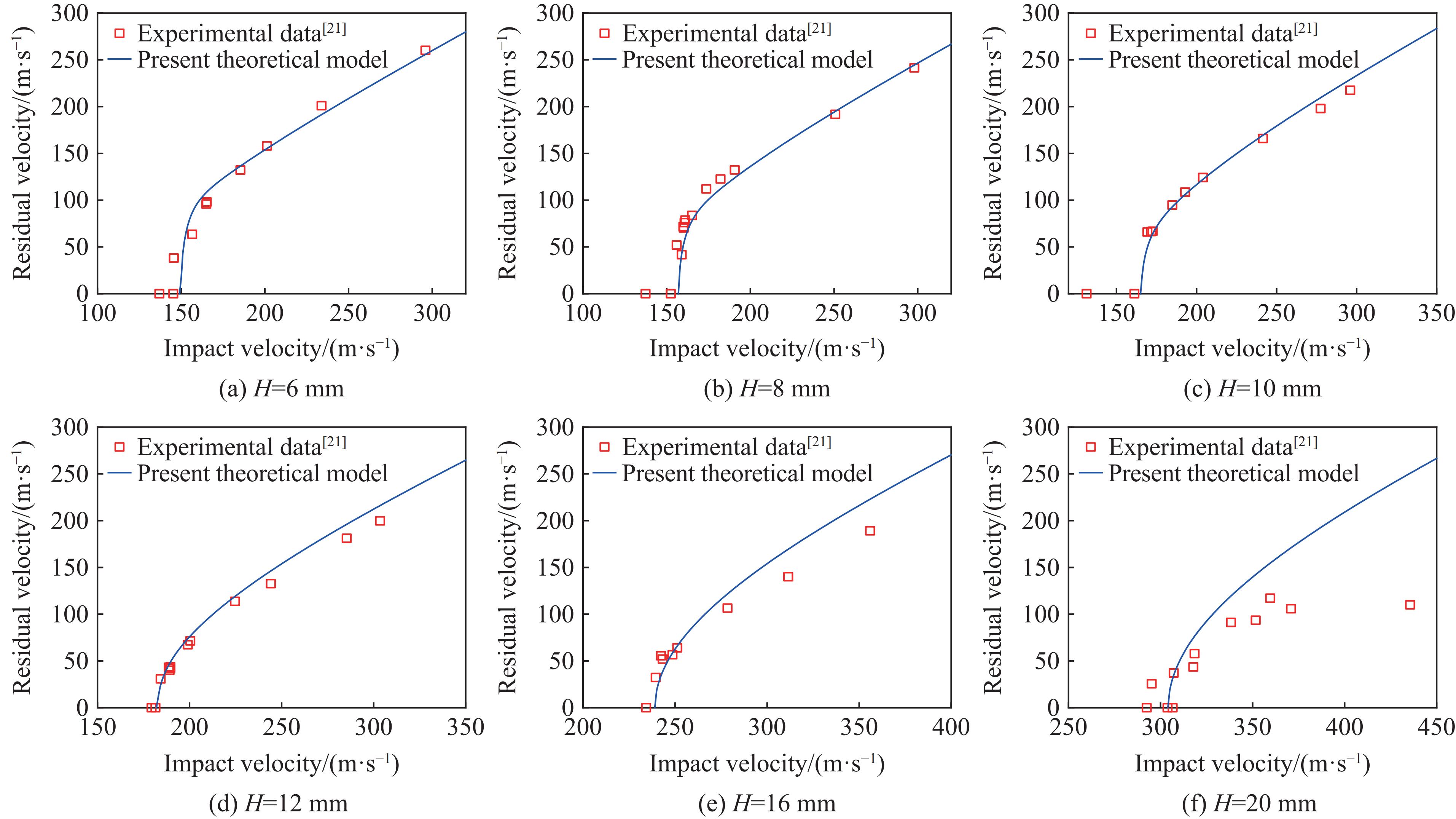
Fig.3 compares theoretically predicted residual velocities with experimental data for Weldox 460E plates with different thicknesses impacted by a 20 mm diameter flat-ended projectile^[21]. It can be seen from Fig.3 that the predictions given by the present model are in good agreement with the experimental data for the plates with thicknesses less than 12 mm. For plate thicknesses of 16 mm and 20 mm, the difference between the theoretically predicted residual velocities and the test data increases as the impact velocity rises. It is reasonable to assume that plastic deformations of the projectiles become more severe at higher impact velocities and more energies are absorbed during this process^[13–14]; however, this effect is not considered in the present model. This implies that the present model can give satisfactory predictions only when the projectile plastic deformation is negligible. Notably, the sharp increases in residual velocities close to the ballistic limits (termed “jump” by Børvik et al.^{[19, 21]}) observed in the experiments are also well predicted by the present model. This is partly due to the fact that the global deformation drops suddenly (as shown in Fig.1), which leads to a considerable decline in energy absorption and a jump in residual velocity.

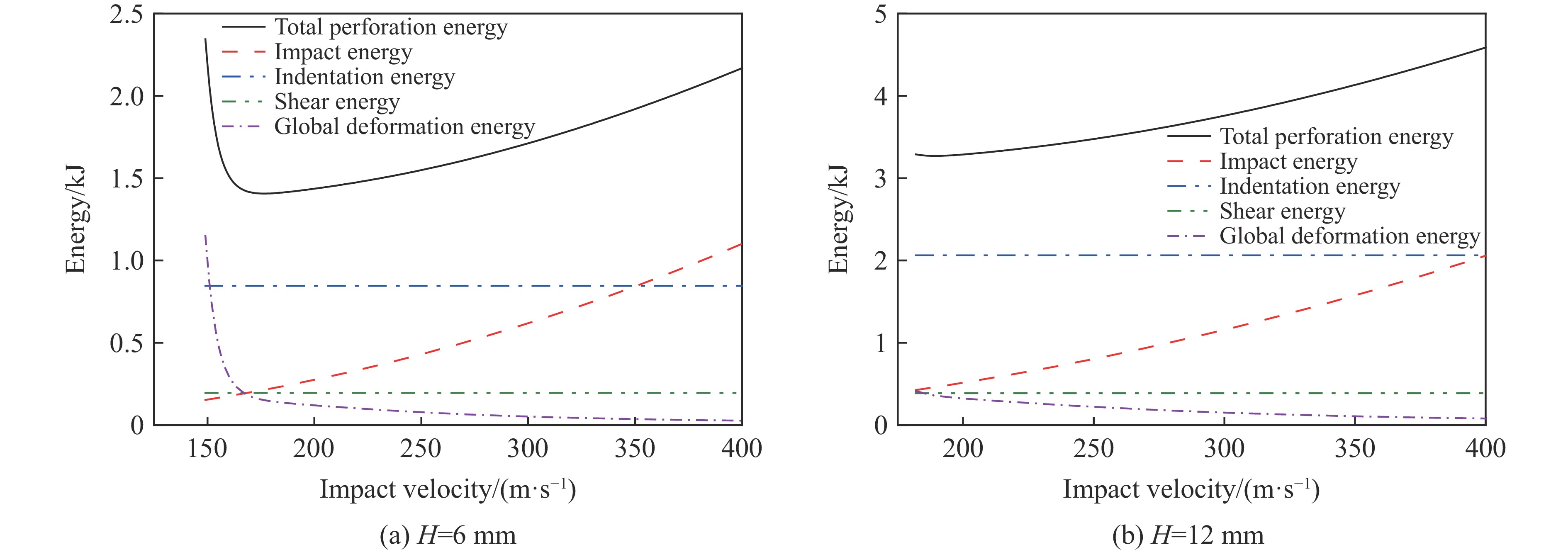
Fig.4 shows the relationships between the four parts of energy absorption of Weldox 460E steel plates and impact velocity of the 20 mm diameter flat-ended projectile. It is clear that the perforation energy first decreases and then increases with impact velocity, which is similar to the behavior of 2024-T351 plates^[22]. Meanwhile, similar to the 2024-T351 plates, the impact energy of Weldox 460E steel plates increases with impact velocity, while the indentation and the shear failure energies remain unchanged within the impact velocity range examined.

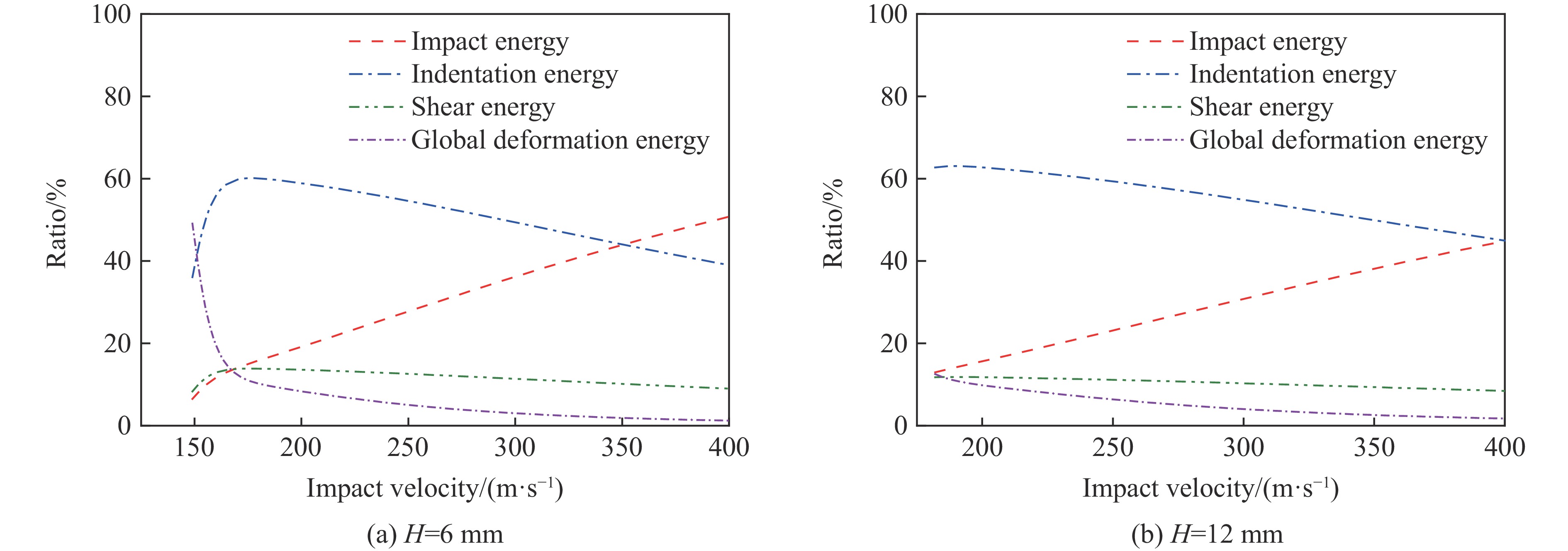
Fig.5 shows the relationship between the ratios of these four parts (i. e., impact energy, indentation energy, shear energy and global deformation energy) to the total perforation energy with the impatct velocity. For the 6 mm thick Weldox 460E plate (Fig.5(a)), it is evident that the global deformation energy at the ballistic limit accounts for a large proportion (approximately 49%) of the total perforation energy. As the impact velocity increases, the ratio of global deformation energy decreases rapidly, leading to the “jump” phenomenon in residual velocity as the 2024-T351 plates^[22]. The indentation energy accounts for a large proportion of the total perforation energy when the impact velocity is less than 350 m/s. For impact velocity greater than 350 m/s, the impact energy accounts for the largest proportion of total perforation energy. For the 12 mm thick Weldox 460E plate (Fig.5(b)), the proportion of the global deformation energy remains small even at ballistic limit, and it decreases further as the impact velocity increases. It should be mentioned here that the proportions of shear deformation energy in both plates are relatively small, which is about 10% for the impact velocity range examined. The proportion of indentation energy of Weldox 460E plates is much greater than that of 2024-T351 plates^[22], which may be due to the high yield strength and the large local indentation of Weldox 460E steel.

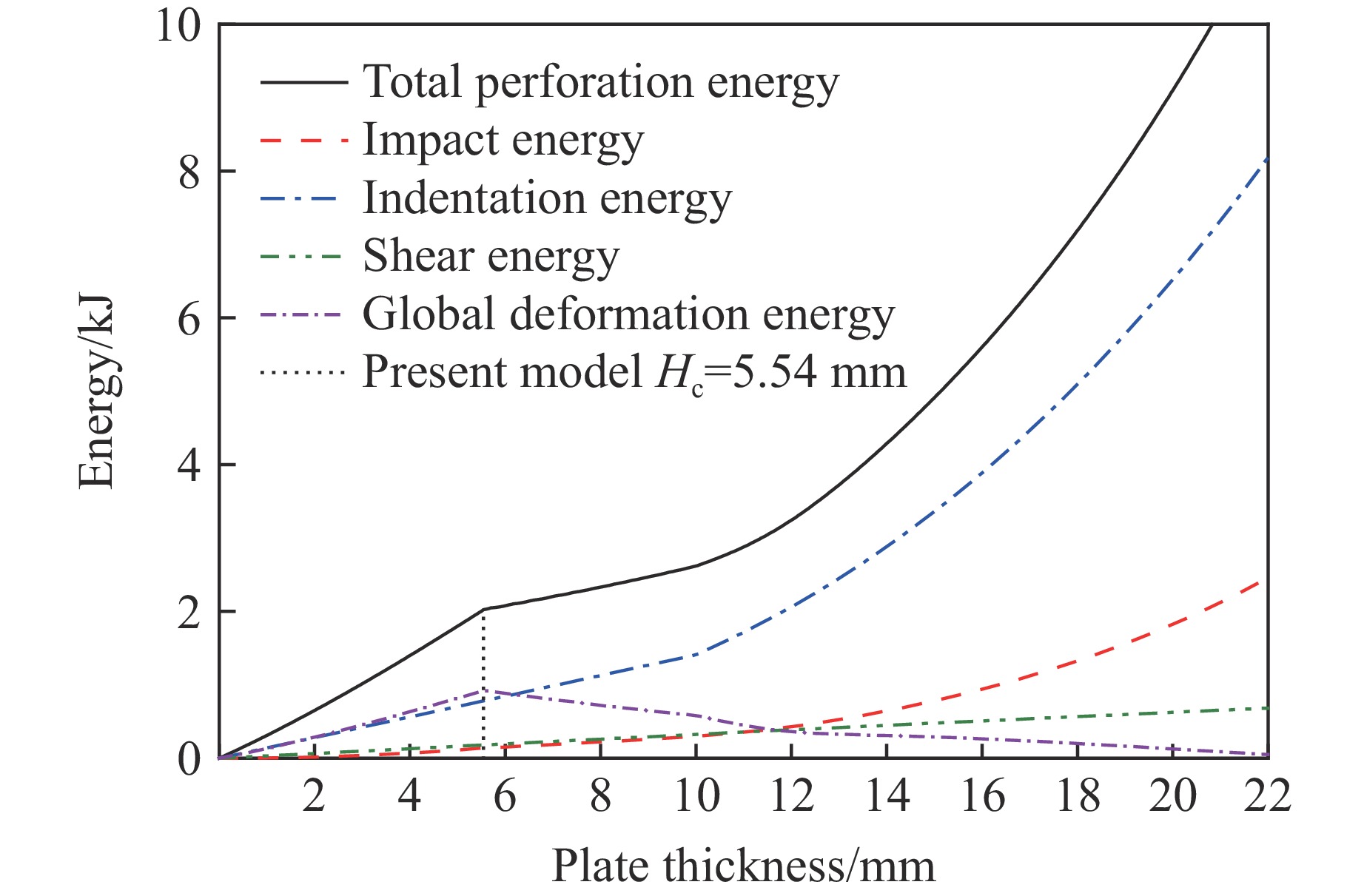
Fig.6 shows the variations of total perforation energy and its four parts at the ballistic limit with respect to thickness for the Weldox 460E plates impacted by the 20 mm diameter flat-nosed projectile. It can be seen from Fig.6 that the impact energy, indentation energy and shear energy at the ballistic limit increase with plate thickness. However, the global deformation energy first increases with plate thickness when H≤H_c, and then decreases with thickness when H>H_c, which is significantly different from that of the 2024-T351 plates (for which the global deformation energy increases with thickness when H>H_c^[22]). This is because the ballistic limit of Weldox 460E steel plates increases faster than that of 2024-T351 plates when H>H_c, resulting a faster decrease of the global deformation of Weldox 460E steel plates. Moreover, it can be seen from Fig.6 that the slope of indentation energy gets larger when H>10 mm, which corresponds to the change of the ψ-H relationship as described by Eq. (15).

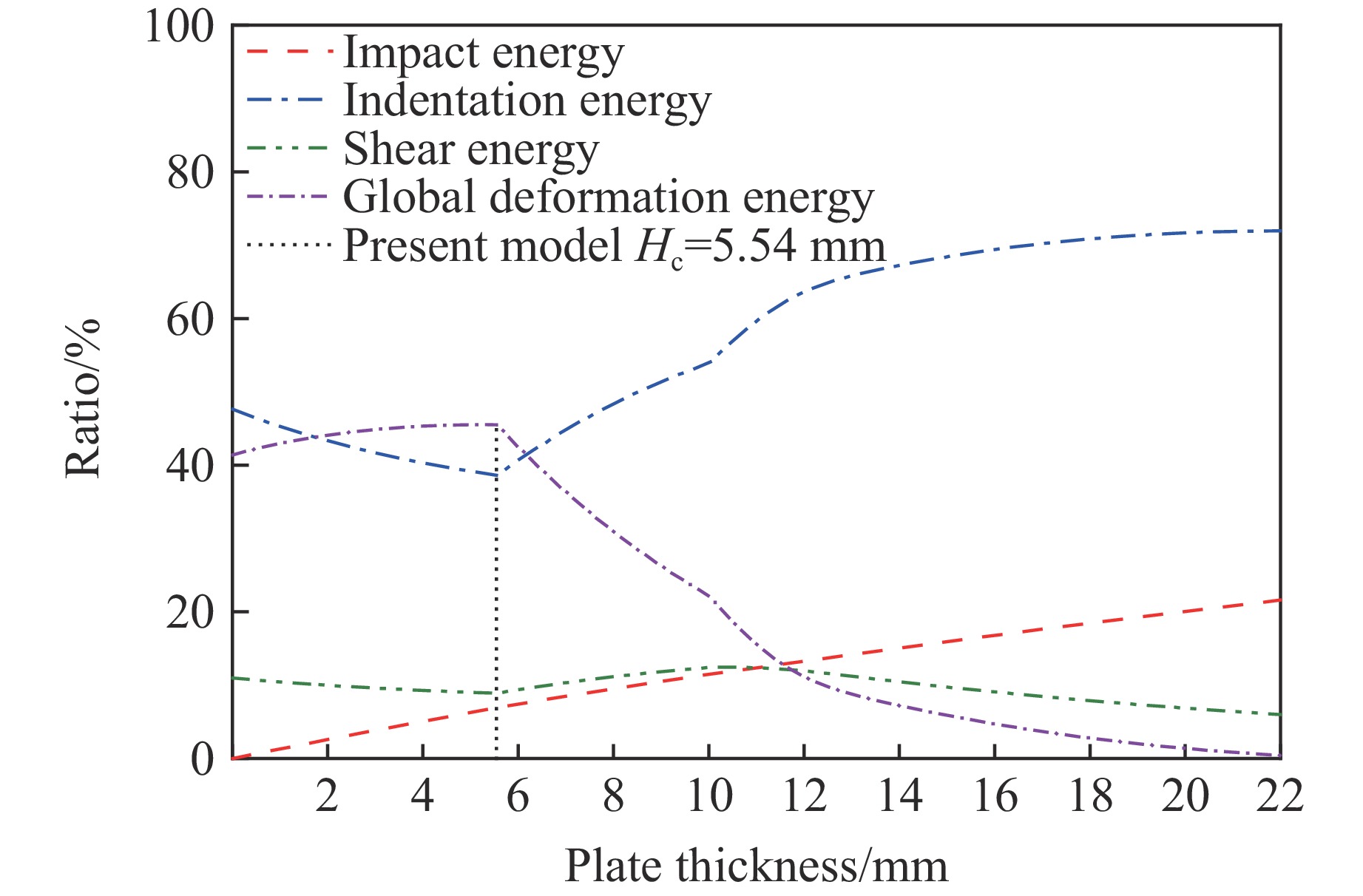
Fig.7 shows the ratio variation of the four parts to the total perforation energy at the ballistic limit with plate thickness for Weldox 460E steel plates impacted by the 20 mm diameter flat-nosed projectile. It can be clearly seen from Fig.7 that the indentation energy at the ballistic limit accounts for a large proportion of the total perforation energy for Weldox 460E steel plates, particularly when H>H_c, which can be attributed to the high yield strength and the large local indentation of the Weldox 460E steel. Correspondingly, the global deformation energy accounts for only a small proportion of the total perforation energy at the ballistic limit for plates thicker than 12 mm. Therefore, it is reasonable to assume that global deformations for thick steel plates can be neglected as done in some existing theoretical models.

In this study, the perforation of Weldox 460E steel plates impacted by a flat-nosed projectile has been investigated through a previously proposed theoretical model. The main conclusions are drawn as follows:

(1) The previously proposed empirical equation on the relationship between global deformation and impact velocity can effectively describe the experimental data of Weldox 460E steel plates, which lends further support to the accuracy and generality of the model.

(2) The predictions given by the model are in good agreement with the experimental and numerical results of Weldox 460E steel plates, including ballistic limit, residual velocity, the critical conditions for transition of failure modes, and the “plateau” phenomenon in the intermediate plate thickness range examined.

(3) The energy absorption mechanisms of Weldox 460E steel plates are analyzed and discussed using the theoretical model. Compared with 2024-T351 aluminium plates, the indentation energy of Weldox 460E plates takes more significant proportion of the total perforation energy, which can be attributed to the high yield strength and large local indentation of Weldox 460E steel.

(4) For Weldox 460E steel plates, the energies absorbed by indentation and global deformations at ballistic limit are nearly equal for thin plates which are failed by Mode Ⅰ (simple shear failure with global deformations). For thick plates failed by Mode Ⅱ (localized shear plugging), the indentation energy increases significantly with plate thickness, whereas the global deformation energy decreases sharply.