高级搜索

光学元件双面抛光加工面型预测模型

,  ,  , 

downloadPDF

上一篇

下一篇

米智恺, 聂凤明, 黄思玲, 薛枫. 光学元件双面抛光加工面型预测模型[J]. 强激光与粒子束, 2024, 36(9): 091001-1. doi: 10.11884/HPLPB202436.240068
引用本文: 米智恺, 聂凤明, 黄思玲, 薛枫. 光学元件双面抛光加工面型预测模型[J]. 强激光与粒子束, 2024, 36(9): 091001-1. doi: 10.11884/HPLPB202436.240068
shu
Zhikai Mi, Fengming Nie, Siling Huang, Feng Xue. Predictive modeling of the surface pattern of double-sided polishing process of optical components[J]. High Power Lase and Particle Beams, 2024, 36(9): 091001-1. doi: 10.11884/HPLPB202436.240068
Citation: Zhikai Mi, Fengming Nie, Siling Huang, Feng Xue. Predictive modeling of the surface pattern of double-sided polishing process of optical components[J]. High Power Lase and Particle Beams, 2024, 36(9): 091001-1. doi: 10.11884/HPLPB202436.240068
shu

光学元件双面抛光加工面型预测模型

  • 1.

    中国兵器科学研究院宁波分院，浙江 宁波 315103

  • 2.

    南京理工大学 机械工程学院，南京 210094

    • 作者简介: 米智恺，3117330394@qq.com .
    通讯作者: 聂凤明，nfm2006@sina.com。; 

  • 中图分类号: TH706

Predictive modeling of the surface pattern of double-sided polishing process of optical components

  • 1.

    Ningbo Branch of Chinese Academy of Ordnance Science, Ningbo 315103, China

  • 2.

    School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China

    • Corresponding author: Fengming Nie, nfm2006@sina.com ; 

  • MSC: TH706

  • 摘要: 针对双面抛光难以建立稳定去除函数进行加工面型预测这一问题，基于双面抛光加工原理，采用坐标变换法推导出元件上下表面相对速度分布方程，然后运用ANSYS软件仿真元件上下表面静态压力分布，采用多项式拟合法将仿真数据导入Matlab软件拟合出元件上下表面压力分布随时间变化公式。根据Preston方程推导修正系数K表达式，通过4组抛光实验数据计算出修正系数K值为2.588×10−15，构建双面抛光加工面型预测模型。最后通过加工实验验证该预测模型，实验结果表明预测PV值误差占元件实际加工后面型PV值的1.07%～7.4%，预测模型与实际加工后的面型吻合。
    Abstract: To address the challenge of establishing a stable removal function for double-sided polishing to predict the finished surface profile, we use the coordinate transformation method to derive the relative velocity distribution equations for the upper and lower surfaces of the component. Subsequently, static pressure distributions on both surfaces are simulated using ANSYS software. The simulation data is then imported into Matlab and fitted with a polynomial method to determine the time-varying pressure distribution formulas for the component's surfaces. Based on the Preston equation, an expression for the correction coefficient K is derived. The value of the correction coefficient K is calculated to be 2.588×10−15 from four sets of polishing experimental data, enabling the construction of a predictive model for the surface pattern in double-sided polishing processes. The predictive model is ultimately validated through machining experiments. The experimental results indicate that the error in predicting the PV (Peak-to-Valley) value accounts for 1.07% to 7.4% of the actual PV value after processing, demonstrating good agreement between the predicted model and the actual post-processing surface pattern.
  • 加载中

  • 图 1  双面抛光结构简图

    Figure 1.  Sketch of double-sided polishing structure

    下载: 全尺寸图片 幻灯片

    图 2  下抛光盘与元件的运动关系简图

    Figure 2.  Sketch of the relationship between the motion of the down-throwing disc and the element

    下载: 全尺寸图片 幻灯片

    图 3  上抛光盘与元件的运动关系简图

    Figure 3.  Sketch of the relationship between the movement of the up-throwing disc and the element

    下载: 全尺寸图片 幻灯片

    图 4  上盘来回摆动的位置与时间关系示意图

    Figure 4.  Schematic diagram of the position of the upper disk swinging back and forth versus time

    下载: 全尺寸图片 幻灯片

    图 5  直径300 mm上抛光盘元件下表面应力分布图

    Figure 5.  Stress distribution on the lower surface of the upper polishing disk element of 300 mm diameter

    下载: 全尺寸图片 幻灯片

    图 6  元件下表面应力分布

    Figure 6.  Stress distribution on the lower surface of the component

    下载: 全尺寸图片 幻灯片

    图 7  不同时刻下元件表面压力分布

    Figure 7.  Distribution of pressure on the surface of the element at different moments

    下载: 全尺寸图片 幻灯片

    图 8  线性拟合Preston系数K的计算

    Figure 8.  Preston coefficient K calculation

    下载: 全尺寸图片 幻灯片

    图 9  实验加工后与预测面型PV值对比图

    Figure 9.  Comparison between the predicted and the experimentally processed surface patterns

    下载: 全尺寸图片 幻灯片

    图 10  预测与加工面型误差分布图

    Figure 10.  Distribution of prediction and machined surface pattern errors

    下载: 全尺寸图片 幻灯片

    表 1  压力分布方程的系数

    Table 1.  Coefficients of pressure distribution equation

    p00 p10 p01 p20 p11 p02 p30 p21
    0.1528 −0.002813 −0.002813 2.042×10−5 5.041×10−5 2.044×10−5 −6.455×10−8 −1.173×10−7
    p12 p03 p40 p31 p22 p13 p04
    −1.172×10−7 −6.47×10−8 7.503×10−11 3.041×10−14 2.727×10−10 −1.021×10−13 7.528×10−11
    下载: 导出CSV

    表 2  修正实验中的抛光工艺参数

    Table 2.  Polishing process parameters in the modified experiment

    experimental group
    number    		 element, upper plate,
    lower plate/(r·mm−1)    		 oscillation speed/
    (mm·s−1)    		 time/s swing distance/
    mm    		 distance from the center of the element
    to the center of the lower plate/mm
    1 10.1，10.9，10 5/6 2700 10 1260
    2 12.1，12.9，10 5/6 1800
    3 12.1，12.9，10 1/3 300
    4 10.1，10.9，10 1/3 420
    下载: 导出CSV

    表 3  预测验证实验工艺参数及实验数据与预测数据对比

    Table 3.  Prediction-validated expermental process parameters and comparsion between experimental data predicted data

    experimental
    group
    number    		 element, upper
    plate, lower
    plate/(r·mm−1)    		 oscillation
    speed/
    (mm·s−1)    		 time/s swing
    distance/
    mm    		 distance from the center of
    the element to the center of
    the lower plate/mm    		 experimental PV
    values/μm    		 predicted PV
    values/μm
    1# 12.1, 12.9, 10 5/6 2700 80 0, 1160 2.145 2.122
    2# 12.1, 12.9, 10 2 900 10 0, 1160 1.149 1.122
    3# 10.1, 10.9, 8 1/3 600 10 0, 1260 0.527 0.566
    4# 10.1, 10.9, 10 1/3 1800 10 0, 1260 0.962 0.947
    5# 10.1, 10.9, 10 2 3600 10 110, 1160 1.720 1.746
    下载: 导出CSV
  • [1] Campbell J H, Hawley-Fedder R A, Stolz C J, et al. NIF optical materials and fabrication technologies: an overview[C]//Proceedings of SPIE 5341, Optical Engineering at the Lawrence Livermore National Laboratory II: The National Ignition Facility. 2004: 84-101.
    [2] Satake U, Enomoto T, Fujii K, et al. Optimization method for double-sided polishing process based on kinematical analysis[J]. Procedia CIRP, 2016, 41: 870-874. doi: 10.1016/j.procir.2015.12.043
    [3] Hashimoto Y, Ozaki R, Furumoto T, et al. A calculation method for workpiece profile variation during double-sided lapping by considering workpiece elastic deformation[J]. Precision Engineering, 2022, 73: 457-469. doi: 10.1016/j.precisioneng.2021.09.016
    [4] 王春阳, 帅闻, 肖博, 等. 基于环摆式双面抛光法加工预测模型的去除均匀性研究[J]. 光学学报, 2023, 43:0914001 doi: 10.3788/AOS221863 Wang Chunyang, Shuai Wen, Xiao Bo, et al. Uniformity removal based on processing prediction model of ring-pendulum double-sided polishing method[J]. Acta Optica Sinica, 2023, 43: 0914001 doi: 10.3788/AOS221863
    [5] 李振兴, 柏伟, 王琰璋, 等. 大尺寸非规则碲锌镉晶片双面抛光技术[J]. 人工晶体学报, 2023, 52(2):244-251 Li Zhenxing, Bai Wei, Wang Yanzhang, et al. Study on double sided polishing technology of large size irregular CdZnTe wafer[J]. Journal of Synthetic Crystals, 2023, 52(2): 244-251
    [6] 陈庚豪. 3英寸AT切石英晶圆抛光片内非均匀性研究[D]. 武汉: 华中科技大学, 2022 CHEN Genghao. Research on non-uniformity of polishing 3-inch AT-cut quartz crystal wafer[D]. Wuhan: Huazhong University of Science and Technology, 2022
    [7] 林涛. 基于磨粒磨损机制的光学元件快速抛光关键技术研究[D]. 厦门: 厦门大学, 2017 Li Tao. Research on the optical element fast polishing key technology based on the abrasive wear mechanism[D]. Xiamen: Xiamen University, 2017
    [8] 徐雳, 刘冰, 吴石, 等. 双面研磨/抛光机磨削轨迹研究[J]. 哈尔滨理工大学学报, 2018, 23(4):43-50 Xu Li, Liu Bing, Wu Shi, et al. Double-sided lapping/polishing machine grinding trajectory studies[J]. Journal of Harbin University of Science and Technology, 2018, 23(4): 43-50
    [9] 郭磊, 明子航, 靳淇超, 等. 弹性基体磨具的磨抛轨迹与表面加工质量研究[J]. 表面技术, 2022, 51(12):255-268 Guo Lei, Ming Zihang, Jin Qichao, et al. Polishing trajectory and surface machining quality of elastic matrix abrasive tool[J]. Surface Technology, 2022, 51(12): 255-268
    [10] 陈真, 杨炜, 郭隐彪. 快速抛光技术接触压力建模与仿真[J]. 厦门大学学报(自然科学版), 2012, 51(2):215-218 Chen Zhen, Yang Wei, Guo Yinbiao. Modeling and simulation for contact pressure of fast polishing process[J]. Journal of Xiamen University (Natural Science), 2012, 51(2): 215-218
    [11] 卢跃. 基于磨粒运动轨迹的端面磨削热力耦合过程分析[D]. 沈阳: 东北大学, 2019 Lu Yue. Analysis of thermal mechanical coupling process of face grinding based on the movement trajectory of abrasive grains[D]. Shenyang: Northeastern University, 2019
    [12] 王鹏里, 董志国, 轧刚, 等. 基于软性磨料流的Preston方程kp参数的修正与测定[J]. 科学技术与工程, 2018, 18(2):232-236 Wang Pengli, Dong Zhiguo, Ya Gang, et al. Modification and determination of the Preston equation kp parameter based on soft abrasive flow[J]. Science Technology and Engineering, 2018, 18(2): 232-236
    [13] Hashimoto Y, Furumoto T, Sato T, et al. Novel method to visualize Preston’s coefficient distribution for chemical mechanical polishing process[J]. Japanese Journal of Applied Physics, 2022, 61: 116502. doi: 10.35848/1347-4065/ac916b
    [14] 樊成. 光学曲面确定性抛光的面型精度控制研究[D]. 长春: 吉林大学, 2014 Fan Cheng. Investigation on control of surface form accuracy for deterministic polishing of optical part surfaces[D]. Changchun: Jilin University, 2014
    [15] Wang Lijuan, Hu Zhongwei, Fang Congfu, et al. Study on the double-sided grinding of sapphire substrates with the trajectory method[J]. Precision Engineering, 2018, 51: 308-318. doi: 10.1016/j.precisioneng.2017.09.001
    [16] Bai Yifan, Xiao Bo, Wang Chunyang, et al. Polishing uniformity analysis and process optimization based on the kinematic model of ring pendulum double-sided polisher[J]. The International Journal of Advanced Manufacturing Technology, 2023, 126(11/12): 5689-5701.
  • 加载中
图( 10) 表( 3)
计量
  • 文章访问数:  885
  • HTML全文浏览数:  885
  • PDF下载数:  9
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-02-29
  • 录用日期:  2024-05-09
  • 刊出日期:  2024-09-15

光学元件双面抛光加工面型预测模型

    通讯作者: 聂凤明，nfm2006@sina.com。; 
    作者简介: 米智恺，3117330394@qq.com
  • 1. 中国兵器科学研究院宁波分院，浙江 宁波 315103
  • 2. 南京理工大学 机械工程学院，南京 210094
  • 收稿日期:  2024-02-29
  • 录用日期:  2024-05-09

摘要: 针对双面抛光难以建立稳定去除函数进行加工面型预测这一问题，基于双面抛光加工原理，采用坐标变换法推导出元件上下表面相对速度分布方程，然后运用ANSYS软件仿真元件上下表面静态压力分布，采用多项式拟合法将仿真数据导入Matlab软件拟合出元件上下表面压力分布随时间变化公式。根据Preston方程推导修正系数K表达式，通过4组抛光实验数据计算出修正系数K值为2.588×10−15，构建双面抛光加工面型预测模型。最后通过加工实验验证该预测模型，实验结果表明预测PV值误差占元件实际加工后面型PV值的1.07%～7.4%，预测模型与实际加工后的面型吻合。

English Abstract

    全文HTML

  • 在激光聚变、天文及航天等领域重大项目中，对高精密光学元件的需求日益剧增，以激光聚变装置为例，其中需要大约7000片大口径光学元件，并且面型精度要求非常高[1]，这对现有的光学制造加工效率和技术水平提出了巨大的挑战。目前常使用的子口径抛光技术，如小工具抛光、气囊抛光、离子束抛光等，在加工大口径光学元件时存在加工周期长、加工成本高、加工环境要求严格等缺点，极大限制了超精密大口径平面元件的应用。作为一种全口径加工技术，双面抛光技术具有加工效率高、加工面型精度高等优点，但其加工缺乏完善加工预测模型，现阶段还需依靠加工经验反复抛光得到加工面型。因此建立双面抛光面型预测模型对完善抛光工艺、进一步提高抛光效率有着重要意义。

    近几年，国内外学者已经开展了有关双面抛光轨迹、压力、预测模型等方面的研究。U. Satake等人研究了元件与抛光垫之间的精确摩擦系数，利用摩擦系数建立了磨粒轨迹模型[2]。Y. Hashimoto等人采用有限元法（FEM）软件模拟变形中的弹簧单元工件与抛光盘的接触，计算了抛光盘接触压力分布[3]。王春阳等人运用了有限元法，计算出元件表面上每个方格内磨粒划过的相对速度和抛光时间，代入Preston方程，从而得出元件表面去除预测模型[4]。目前的研究问题在于构建双面抛光面型预测模型时将压力当作一个常数，会导致预测模型不够准确。

    本文针对双面抛光工艺目前缺少较为完善的面型预测模型的问题，根据双面抛光加工机理分析出影响加工的主要因素，对元件上下抛光盘磨粒进行运动学分析，进而建立元件上下表面相对速度分布方程，使用有限元分析软件ANSYS计算元件表面静态压力分布，采用Matlab仿真软件拟合表面压力与位置的关系式，建立压力分布模型，根据Preston方程建立修正系数K的表达式，通过实验数据求取K值，并建立双面抛光面型预测模型，最后开展双面抛光熔石英光学元件实验，验证面型预测模型的准确性。

1.   双面抛光机理

  • 双面抛光机床结构简图如图1所示。在抛光过程中，抛光压力通过气缸施加给上盘，然后传递到元件表面。同时上盘进行旋转和摆动，元件盘带动元件旋转，下抛光盘绕轴旋转。通过上述这种运动形式带动磨粒磨削去除材料[5-7]。

    双面抛光加工过程十分复杂，除了元件与磨粒的机械作用，还有抛光液与元件之间的化学作用。由于双面抛光去除本质是抛光液中磨粒受压力和运动速度的影响下去除材料，因此本文采用Preston方程作为预测模型，即

    式中：dz/dt表示单位时间材料去除量，K为修正系数，p(x, y, t)表示元件上某一点的瞬时压力，v(x, y, t)表示元件上某一点的瞬时相对速度。

2.   磨粒轨迹建模

    2.1.   元件下表面相对速度分布建模

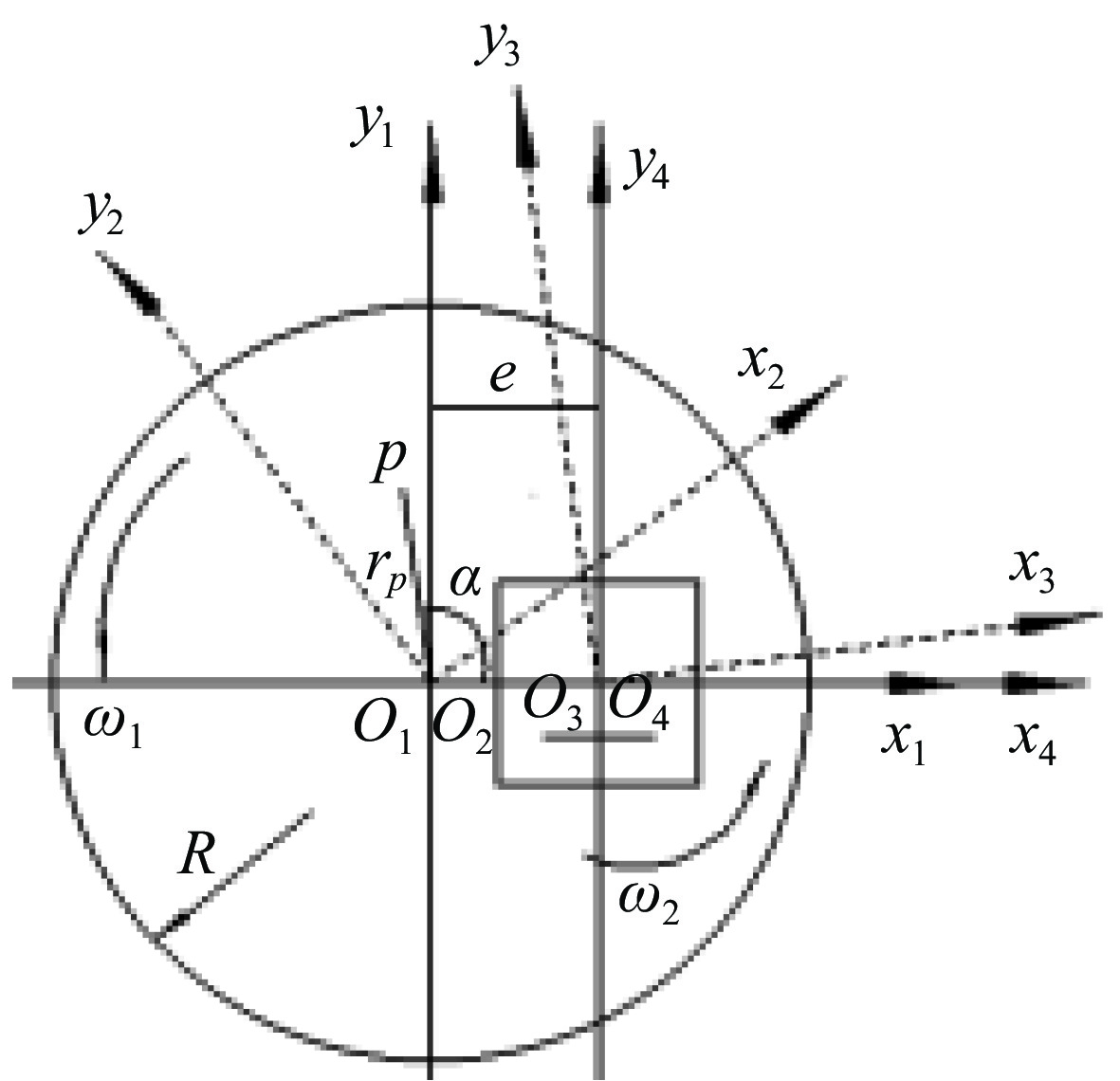
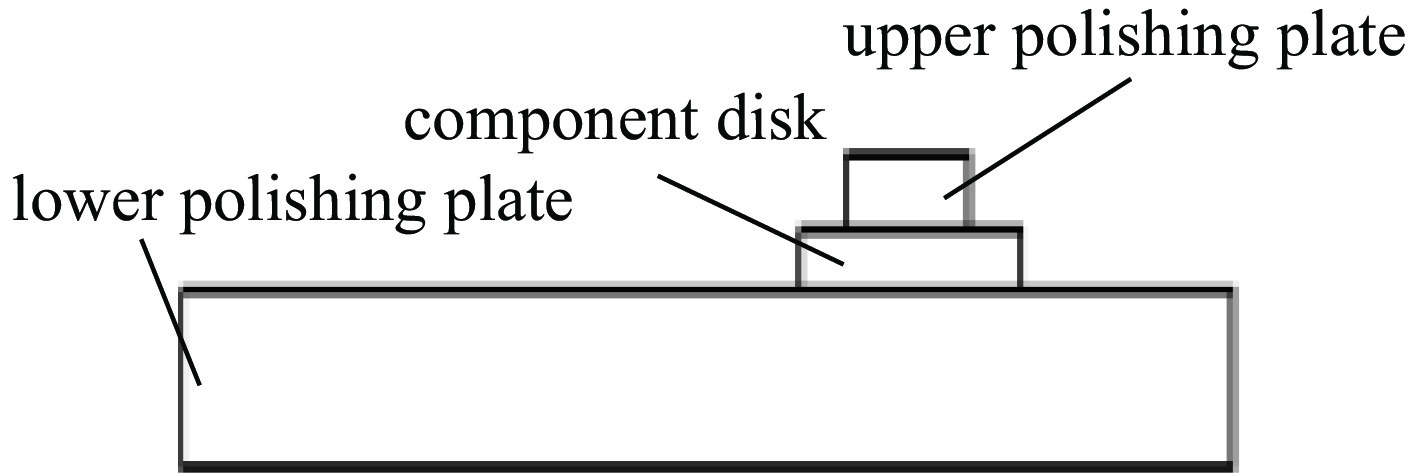
  • 图2为抛光机下盘与元件之间的运动关系简图，根据抛光过程中抛光盘与元件之间的相对运动情况，将抛光盘简化成一个半径为R的圆，元件简化成一个正方形。下抛光盘以角速度ω1绕圆心O1做旋转运动，元件以角速度ω2绕圆心O3做旋转运动。O1和O3之间的距离e为元件中心相对于抛光盘中心的偏心距，以O1和O3为中心建立4个坐标系[8-9]：（1）下抛光盘相对静止的坐标系x1O1y1；（2）随下抛光盘旋转的坐标系x2O2y2；（3）随元件旋转的坐标系x3O3y3；（4）元件相对静止的坐标系x4O4y4。

    本文以磨粒为研究对象进行运动学建模，在下盘上任取一点p距点O1的距离为rp，初始角为α。p点在坐标系X1O1Y1的坐标为

    p点通过坐标旋转变换，可得式（3），p点在下抛光盘旋转坐标系X2O2Y2的运动轨迹如式（4）所示。其中x′p和y′p分别表示p点在下抛光盘旋转坐标系的位置坐标。

    此时p点在通过坐标平移变换和坐标旋转变换，结果见式（5），可得在元件相对静止坐标系X4O4Y4的运动轨迹如式（6），其中x″p和y″p分别表示p点在元件相对静止坐标系的位置坐标

    为了得到抛光过程中任一点的相对速度，对式（6）中的时间进行求导，可得在x轴和y轴的速度分量vx和vy。

    则p点合成相对元件速度表示为

    • 2.2.   元件上表面相对速度分布模型

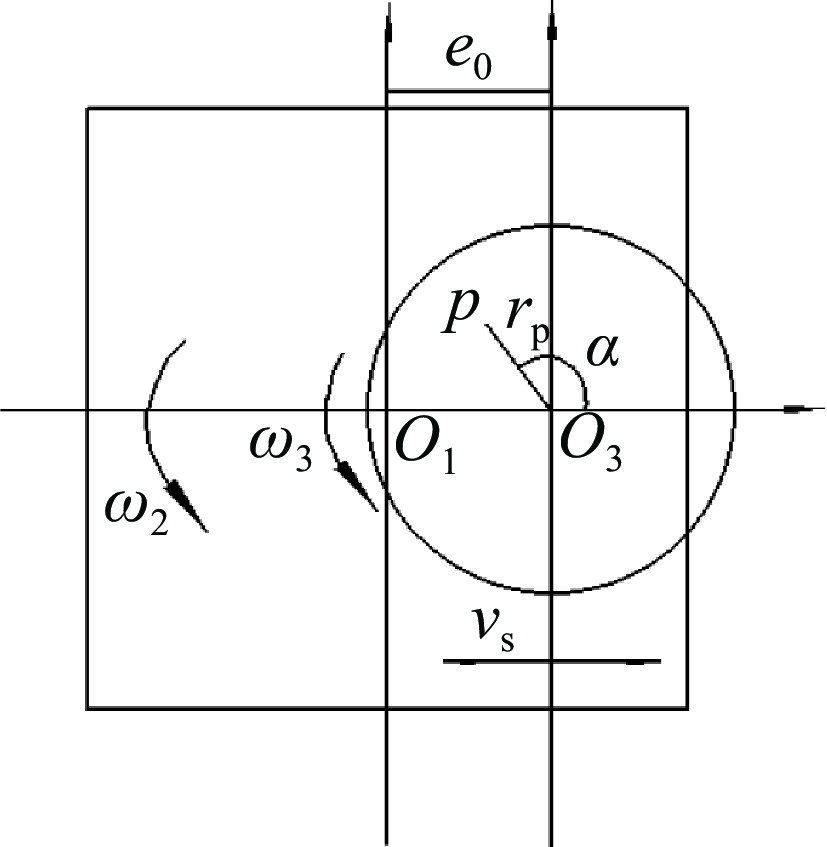
  • 元件上下表面相对速度分布建模相似，区别在于上表面存在上盘摆动，所以上表面偏心距是一个周期变换的函数。如图3所示，在上盘取一点p距上盘中心O3为rp，初始角为α，元件转角为ω2，上盘转角为ω3，上盘摆动速度为vs，上盘初始偏心距为e0。

    p点通过2次旋转变换和平移变换，见式（9），可得在元件相对静止坐标系下的运动轨迹方程如式（10）所示。

    则p点合成相对元件速度为

    上盘中心偏离元件中心的偏心距e为周期变换的函数，表示为

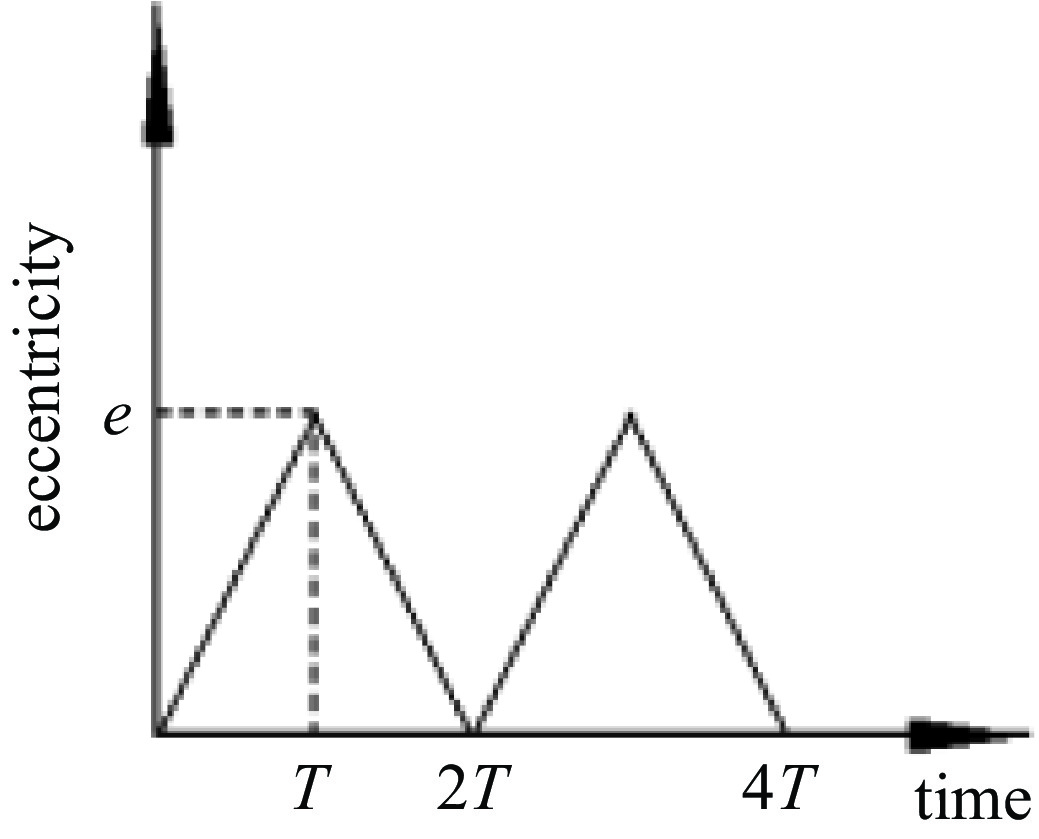
    式中：Sawtooth是锯齿波或三角波的函数，L是摆动距离，e0是初始摆动时元件中心的偏心距，vs是摆动速度，L/vs是摆动周期T。光学元件来回移动的位置与抛光时间关系如图4所示。

3.   元件下表面压力分布

  • 抛光过程中，受多种因素的影响，抛光盘与光学元件之间的作用非常复杂，很难对两者之间的力学作用进行具体分析[10-11]。本文首先只考虑元件受压力和自重的影响，采用ANSYS软件仿真元件下表面静态压力分布，提取元件下表面压力值导入Matlab软件，使用多项式拟合法，拟合出元件下表面静态压力分布方程，然后考虑元件旋转和抛光盘旋转和摆动的影响，采用坐标变换法，得出元件表面动态压力分布方程。

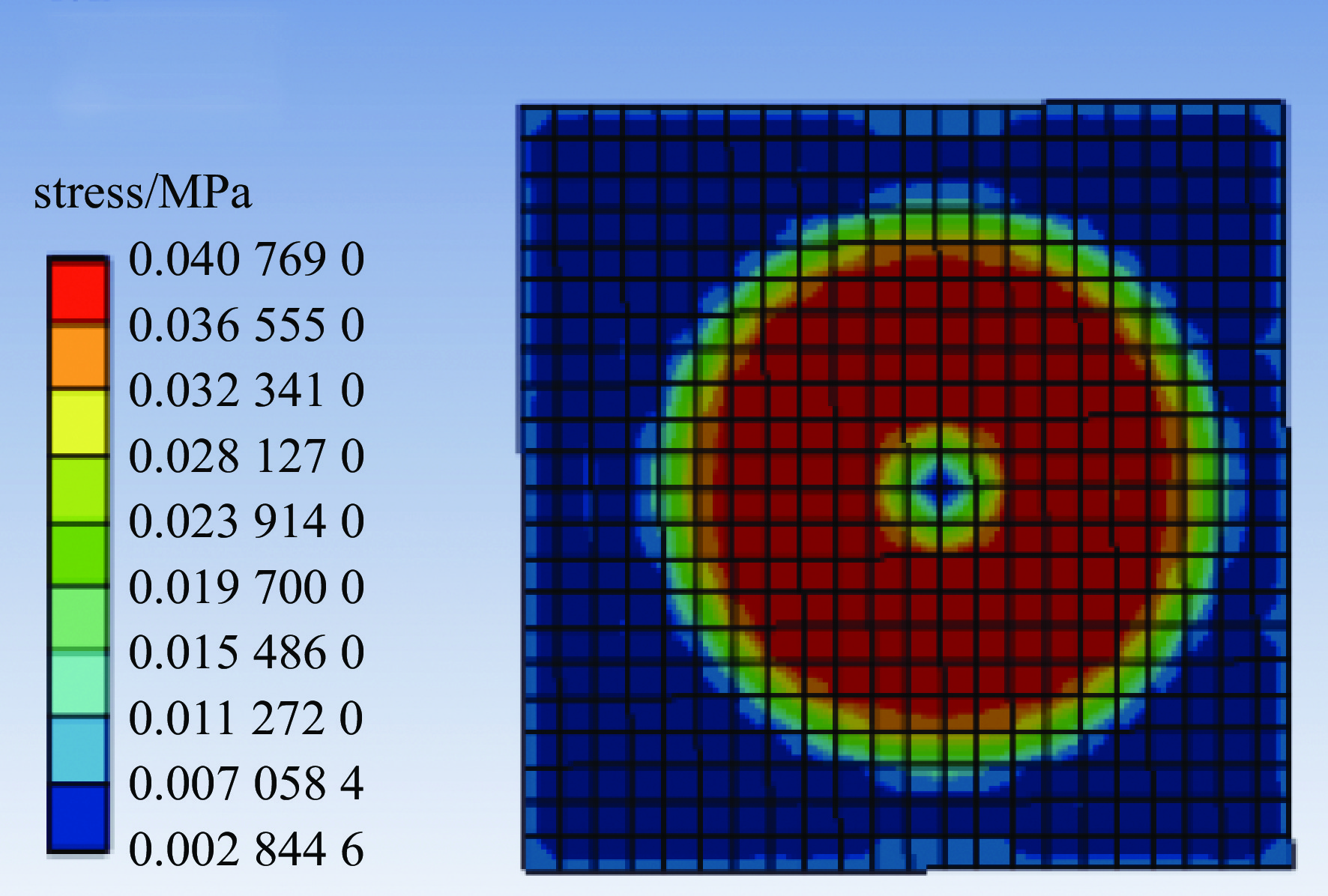
    建立直径300 mm、中心孔洞直径50 mm的抛光盘和边长430 mm的正方形元件3维模型，对3维模型进行静态模拟分析，首先对熔石英元件和大理石抛光盘的材料属性和网格分布进行设置，其次设置物体重力和下压压力为100 N，最后仿真观察结果，如图5所示。可以看出，在上抛光盘覆盖区域应力分布比较均匀，应力比较大，中心区域应力比较小，抛光盘边缘区域应力小于覆盖区域，且距离抛光盘越远应力越小。提取元件表面每个节点的应力值，并且以元件左下顶点为原点建立坐标系。

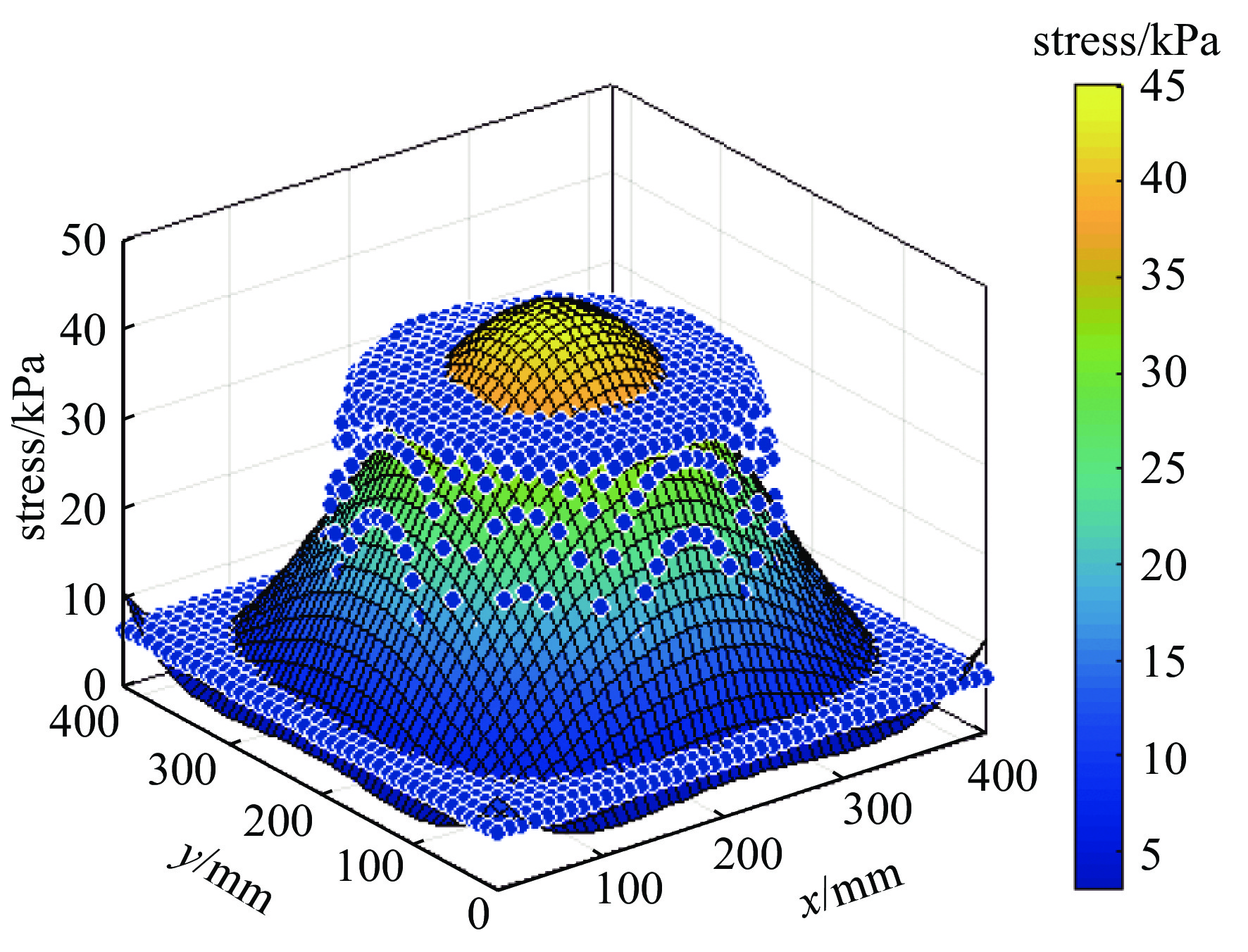
    使用Matlab软件采用多项式拟合算法寻找一个多项式函数来近似表示离散数据的趋势，拟合出应力与位置之间的关系，如图6所示。图6中的点为输入的应力点，曲面图是拟合出来的应力分布。从图中可以看出拟合出来的应力分布与ANSYS仿真的应力分布非常接近，本次拟合函数为4次多项式，拟合优度为0.7901、 拟合误差为0.0646，结果表明拟合的函数比较贴合数据，拟合效果很好。

    由于元件只受压力和自身重力，其元件表面应力为法向应力垂直于元件表面，应力大小等效于元件表面压力，拟合的函数其表达式如公式（13）所示。p（x，y）表示元件表面压力，x和y分别为元件表面横纵坐标，p00、p10、p01等为系数，数值见表1。

    在上抛光盘取一点b（xb,yb）通过2次旋转变换和平移变换，即

    可得元件上b点随时间变化的方程，将上抛光盘上许多的点以同样的方法带入静态压力分布方程，可以得出在旋转摆动状态下的压力分布方程。求解元件上表面压力分布与下表面压力分布的方法相同。为了验证我们所拟合的压力分布模型的准确性，我们把压力分布公式导入Matlab软件仿真直径300 mm抛光盘的压力分布，摆动距离为60 mm，摆动速度为2 mm/s，偏心距为0，转速比为0.99，上抛光盘转速10 r/min，仿真时间60 s，仿真步长1 s，通过拟合100个磨粒点的压力拟合出元件表面的压力分布，分别取一个周期内1、11、15、21、31、41、45、51、61 s等时刻的压力分布图，如图7所示。由图可知，当时间等于1 s时，压力分布在元件的中心位置；随着时间的改变，抛光盘覆盖的位置也会相应改变，从而导致压力分布区域的改变；当时间等于61 s时抛光盘摆动一个周期完成，抛光盘回到元件的中心，压力分布也回到了元件的中心。由此可以看出，拟合的压力方程准确地反映了实际加工过程中上抛光盘左右摆动导致元件表面压力分布改变这一现象，验证了压力分布与元件表面位置关系的正确性，由于压力大小无法测量本文不考虑拟合值与真实值之间的误差，通过修正系数K来弥补之间的误差。

4.   去除函数修正实验

  • Preston抛光系数K是对抛光材料去除轮廓预测中的一个修正参数，需要基于实验结果来计算。根据Preston方程所述，抛光点的材料去除深度与接触压力、相对线速度和抛光时间成正比。对其时间进行积分，有[12-14]

    系数K可以表示成

    式中：h (x, y)为元件表面去除深度，p(x, y)和v(x, y)是上述的元件表面压力分布和速度分布。通过抛光实验来确定系数K，实验中的抛光参数见表2。

    本次实验采用课题组自研的双面抛光机床抛光，实验对为430 mm（长）×430 mm（宽）×10 mm（高）石英平面元件进行双面抛光，抛光垫材料为网格状聚氨酯。将水与氧化铈抛光液以3∶1的比例稀释，加工完成后使用太科的INF600-LP-WM激光平面干涉仪测量熔石英光学元件透射面型。

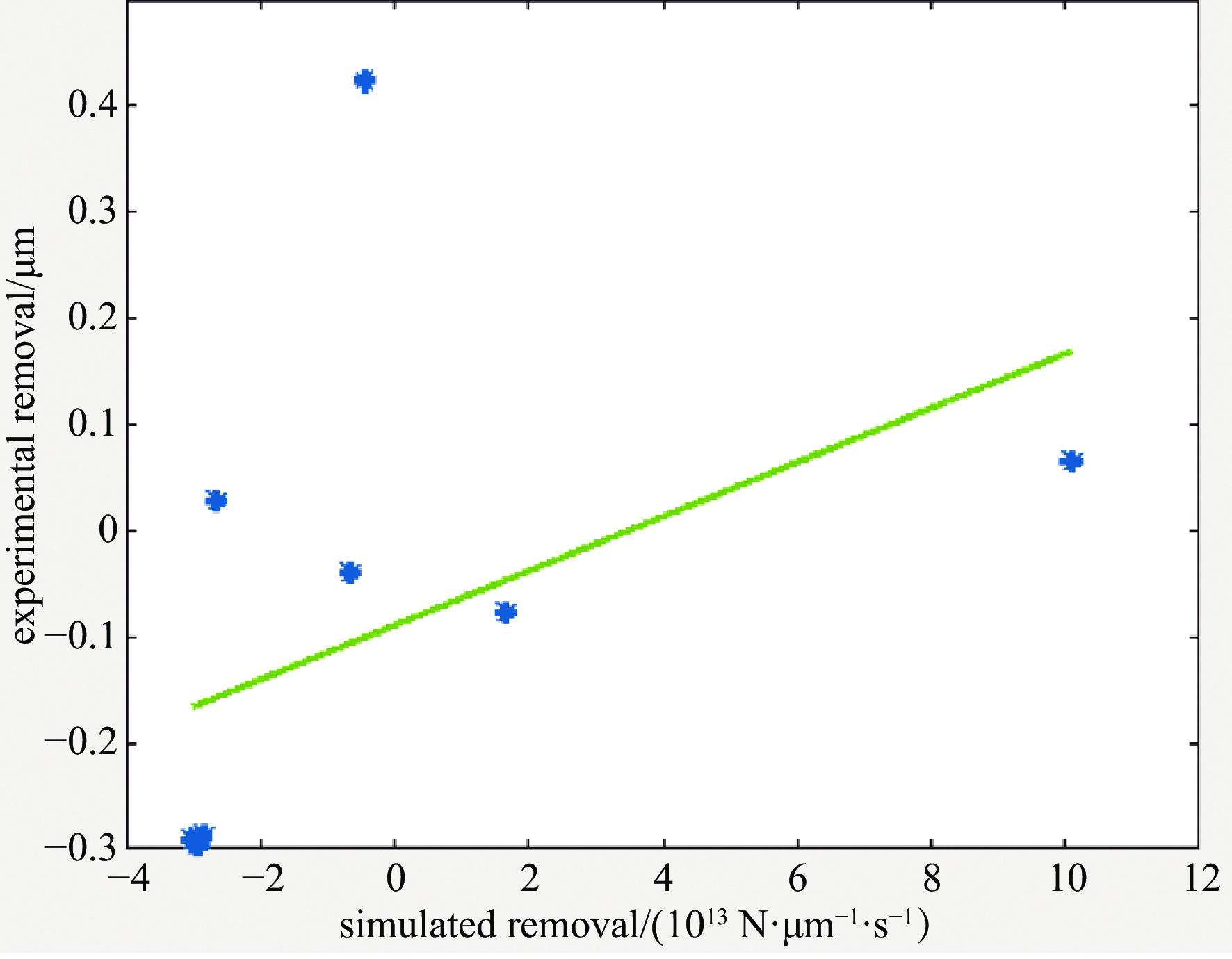
    在元件表面任意取一点材料去除深度，通过这一点的材料去除求取修正系数K，根据式（16）所示，可以通过对实验去除量和仿真去除量进行线性拟合，拟合后的直线斜率就是修正系数，如图8所示，通过实验数据的线性拟合，在本文所示的抛光实验条件下，Preston系数K约为2.558×10−15。

5.   面型预测模型验证

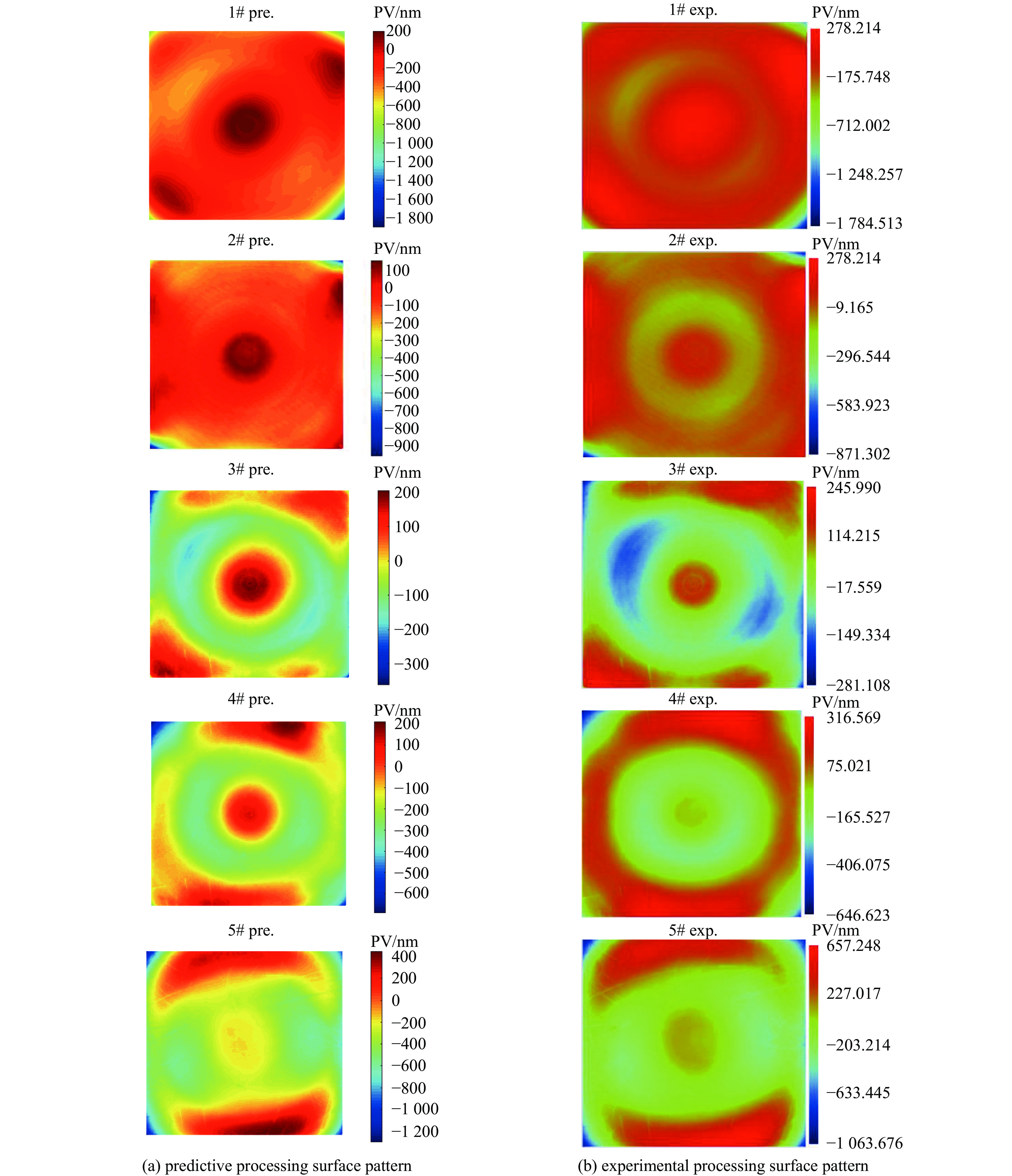
  • 将元件表面某一时刻的磨粒速度和压力分布及K值代入Preston方程，便可以得出瞬时的材料去除分布，然后将0到t时刻的材料去除进行累加，便可以得出t时间内的材料去除量分布[15-16]。本文采用Matlab软件对不同加工工艺参数进行预测模型验证，工艺参数及实验数据与预测数据对比如表3所示。将加工前的面型减去材料去除分布便可以得出预测的加工面型，如图9所示。

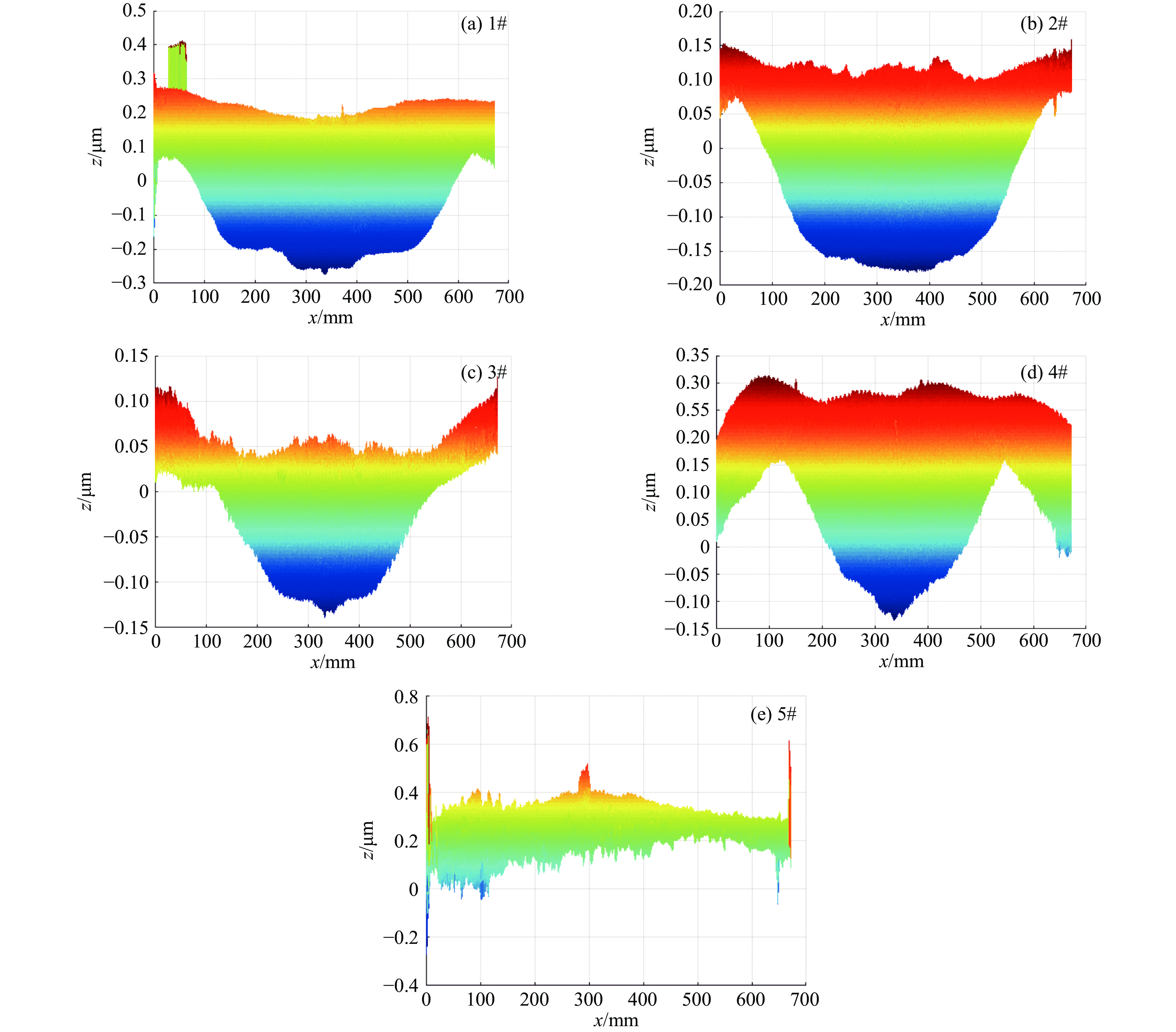
    图9（a）为预测加工后元件表面面型，图9（b）为实际加工后元件表面面型。第1#组实验实际加工后面型呈现中间低、四个角高、四条边低，其中左下角和右上角更低，预测加工后的面型也呈现中间低四角高，元件边缘左下角和右上角有低点，与实际加工后面型PV值差0.023 μm。第2#组实验实际加工后面型左下角和右上角比较高、左右两边较低，预测加工后的面型左下角和右上角比较高左右两边和中间比较低，与实际加工后面型PV值差0.027 μm。第3#组实验实际加工后面型左上角和右下角高，中间低中心旁边有一圈高点，预测加工后的面型左上角和右下角高，中间低中心旁边有一圈高点，与实际加工后面型PV值差0.039 μm。第4#组实验实际加工后面型呈现元件表面中心低中心周围有一圈高点，四条边形成了一圈低点圆环，预测加工后的面型呈现元件表面中心低中心周围有一圈高点，上下边较低，与实际加工后面型PV值差0.015 μm。第5#组实验实际加工后面型呈现元件表面中心低中心周围有一圈高点，上下边为低点，四个角为高点，预测加工后的面型呈现元件表面中心周围有一圈高点，上下边较低，与实际加工后面型PV值差0.049 μm。五组不同工艺参数的实验面型与预测面型相比较，得出预测面型PV值与实际加工面型PV值误差较小，预测PV值误差占元件实际加工后面型PV值的1.07%～7.4%左右，预测面型与实验面型基本相同。为了更好的显示预测模型的效果，将实验加工后的面型减去预测加工后的面型，得出面型误差分布图。

    图10为5组实验的误差分布图。从图中可以看出，5组实验的误差范围主要在0.15～0.4 μm之间，说明预测面型与实验加工面型误差非常小。由于双面抛光加工技术常常用于加工面型1 μm以上的光学元件，因此误差在允许范围内，表明本文构建的双面抛光加工预测模型能够比较好地预测熔石英光学元件加工后的面型。此外，针对其他性能不同的光学材料，构建预测模型时仅需要改变元件表面压力模型和修正系数K即可，因此本文的建模过程也适用于其他光学元件的双面抛光面型预测。

6.   结　论

  • 本文针对双面抛光工艺，建立基于Preston公式的双面抛光加工预测模型，并且推导了磨粒轨迹方程和拟合了压力分布方程，对预测模型进行实验验证，得出以下结论：（1）基于双面抛光加工机理，采用坐标变换法，建立磨粒轨迹方程，从而得出磨粒相对速度方程；（2）通过多项式拟合法，拟合出抛光压力与位置的关系公式，并且通过实验求取了抛光系数K等于2.558×10−15；（3）通过5组不同加工工艺参数的双面抛光加工面型预测与加工实验结果对比，研究表明预测PV值误差占元件实际加工后面型PV值的1.07%～7.4%，验证了双面抛光预测模型能够较好的预测实验加工后的面型。

参考文献 (16)

目录

/

返回文章
返回