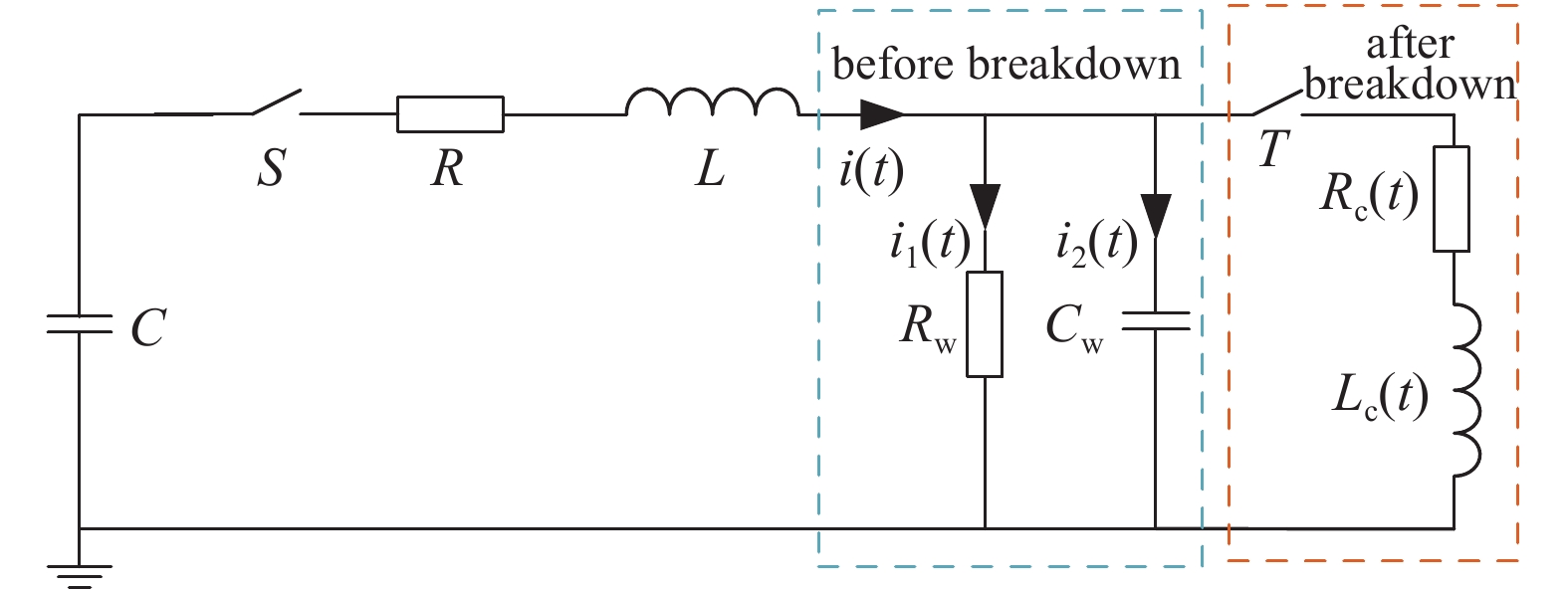
高电压脉冲放电破岩系统电路等效模型如图1所示，其中C为驱动源储能电容，其工作电压为U_cm；L为回路电感；R为回路电阻；R_w、C_w分别为电极泄漏电阻和分布电容；S为控制电压脉冲输出的开关；T为模拟岩石击穿的开关；R_c(t)、L_c(t)分别为等离子体通道时变电阻和时变电感。

高电压脉冲放电破岩等离子体通道形成前，电极等效为泄漏电阻与分布电容组成的并联负载；等离子体通道形成后，电极等效为等离子体通道时变电阻与电感组成的串联负载。通道形成前负载特性影响负载电压的上升特性，决定岩石能否击穿；通道形成后的负载特性影响通道内能量沉积与应力波的强度，决定岩石能否破碎。

在等离子体通道形成前，令电容两端电压为U_c(t)，负载两端电压为U₀(t)，回路总电流为i(t)，经过R_w的电流为i₁(t)，经过C_w的电流为i₂(t)，回路的方程可以表示为

该工况下系统输出电压处于上升阶段，破碎电极的负载阻抗较大，回路处于过阻尼状态。而电源回路电阻较小，输出电压上升时间主要取决于回路电感与破碎电极的负载阻抗。高电压脉冲放电破岩液体工作介质需具备环保、易获取等特点，常采用具有高电导率与高介电常数的自来水^[16]。破碎电极设计显著影响负载阻抗，对于复杂的爪状电极，可采用有限元分析计算电极的分布电容与泄漏电阻。

等离子体通道形成后，电极阻抗为泄漏电阻、分布电容以及通道阻抗并联，电极阻抗会在极短的时间内迅速下降，通道阻抗远小于击穿前电极的分布电容容抗与泄漏电阻，故击穿后可忽略分布电容和泄漏电阻的影响^[17]。系统负载由图1红色框线中等离子体通道时变电阻与时变电感串联组成。

等离子体通道中电感分量约为电阻分量的20%，故分析时对其进行忽略^[18]。岩石击穿后的回路方程可以表示为

岩石中等离子体通道作为电能向机械能转化的工具。基于通道发展过程中的能量平衡方程，可建立等离子体通道的时变电阻模型^[9]。

式中W_in(t)为等离子体通道内能；W_m(t)为通道膨胀对外做功；W_rad(t)为对外辐射能量；E_c(t)为通道沉积能量；n(t)为通道中粒子数；r(t)为通道半径；σ_s为斯忒藩-玻尔兹曼常数，σ_s=5.67×10⁻⁸ W·m⁻²·K⁻⁴；f为通道周围液体薄层吸收的电磁辐射分数，f=0.2；T(t)为通道温度；ε_s为介质转换为等离子体的能量，ε_s=9.74×10⁻¹⁹ J；α、β为试验系数，针对花岗岩α=300.1 MPa，β=300 MPa；ρ₀为固体密度；p(t)为通道压强。

该模型基于能量平衡方程与回路电压方程，考虑了等离子体通道发展过程中温度、辐射等影响，将等离子体通道等效为径向均匀膨胀的圆柱体，有

式中，V(t)为等离子体通道体积。对于圆柱形通道，V(t)=πr(t)²l_ch，l_ch为通道长度；γ是有效绝热系数，γ=1.12；p(t)为通道压强。利用理想气体描述电弧等离子体有

式中，k为玻尔兹曼常数，k=1.380649×10⁻²³ J/K。考虑时变电导率σ(t)，等离子体通道电阻为

式中ε为常数，对于花岗岩，ε=0.00385 K^−1.5Ω⁻¹m⁻¹。

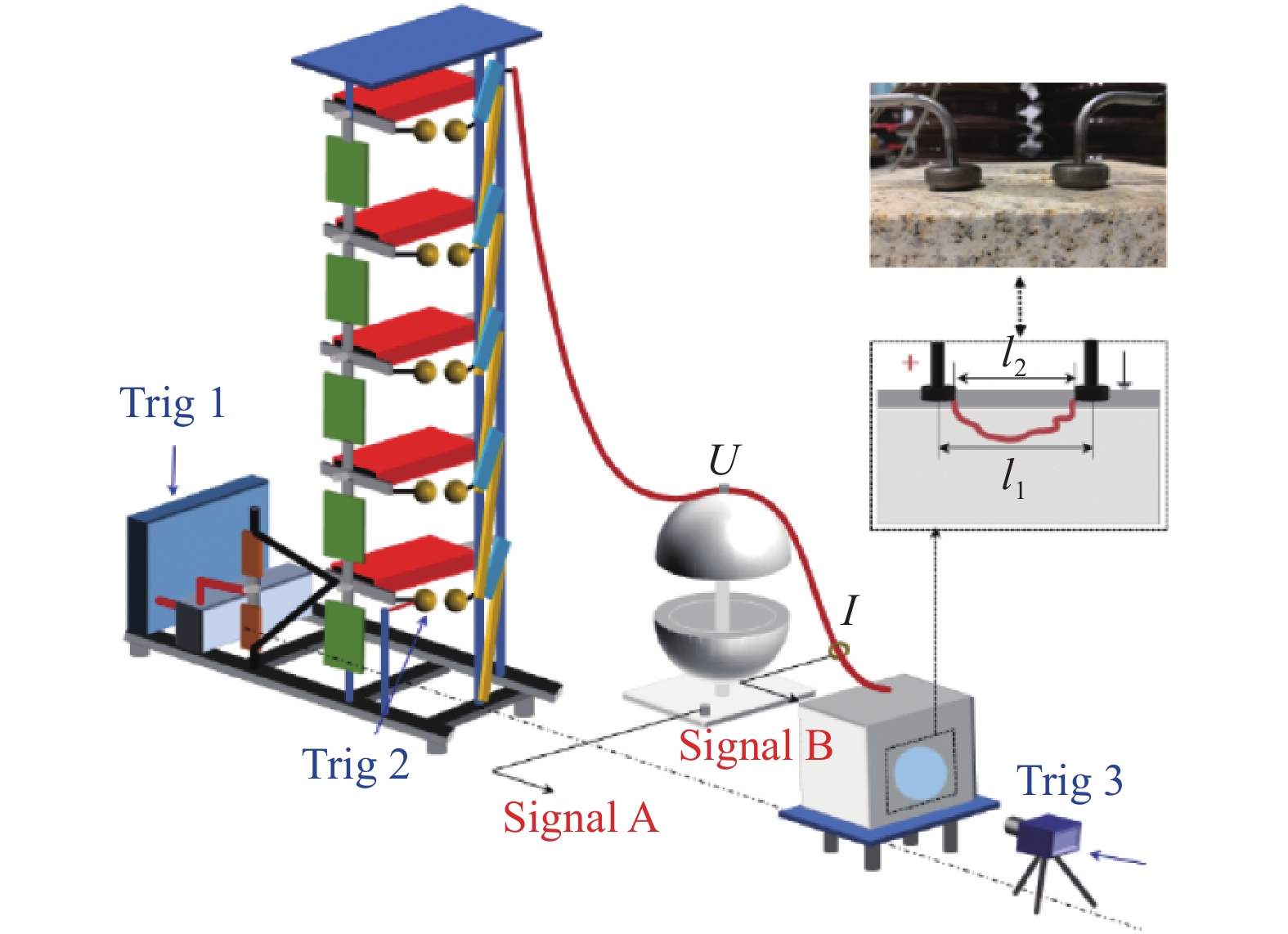
构建的高电压脉冲破岩试验平台如图2所示，驱动源采用额定输出电压为500 kV、额定储能为5 kJ的Marx发生器。放电容器为500 mm×500 mm ×500 mm的不锈钢箱体，两侧留有直径为190 mm圆形玻璃观测窗口。利用配有18-200 mm焦距镜头的高速相机（Phantom V1612）记录放电过程中的图像。相机采样速度设置为3.93 μs/帧，曝光时间为0.76 μs。岩石放置在水箱底部，通过升降平台调节岩石与电极之间的垂直距离。液体介质采用电导率34.7 mS/m的自来水。放电电极为直径30 mm、高度15 mm的圆形平板电极，电极材料为钨含量90%的钨铜合金。分别采用高压分压器（North Star VD-200）和电流线圈（Pearson 1330）测量岩石破碎过程中放电通道的电压和电流信号，利用示波器（Tektronix MSO54）进行记录。考虑到脉冲大电流放电会引起强烈的电磁干扰，测量设备均采用不间断电源独立供电，上位机与高速相机之间进行光电隔离通信。

针对花岗岩-自来水介质组合，在破碎电极间距3 cm工况下，岩石多次破碎效果如图3所示，其中n为脉冲个数。高压电脉冲作用下，岩石的破碎具有累积性。岩石破碎依赖于等离子体通道，在等离子体通道上方，等离子体通道膨胀产生的应力波以及固液分界面反射的应力波共同作用为拉剪应力；在等离子体通道下方，等离子体通道膨胀产生的应力为压剪应力^[19]。岩石的抗拉强度远小于其抗压强度，等离子体通道上方岩石发生塑性破坏，岩层剥离形成空腔，等离子体通道下方的岩层被压剪破碎，在破碎空腔内形成最深的破碎路径，而等离子通道下方岩层破坏较小，故破碎空腔最深路径的长度与等离子体通道长度接近。

岩石为多种介质组成的混合物且内部存在孔隙，等离子体通道的形成与发展存在分散性，破碎空腔内部的最深路径长度难以直接测量。利用石膏对破碎空腔进行脱模处理，不同电极间距与脉冲作用下破碎空腔脱模结果如图4所示。通过脱模结果利用游标卡尺测量破碎空腔最深路径的长度，结果如表1所示。岩石破碎空腔最深路径的长度随电压脉冲个数增加以及电极间距增大而增大。破碎空腔最深路径的长度大于电极间距，原因为破碎电极位于岩石同侧，等离子体通道经过岩石内部时，等离子体通道发生弯曲，随着脉冲次数增加，破碎深度提高，岩石击穿时等离子体通道弯曲程度与等离子体通道长度会进一步增大。

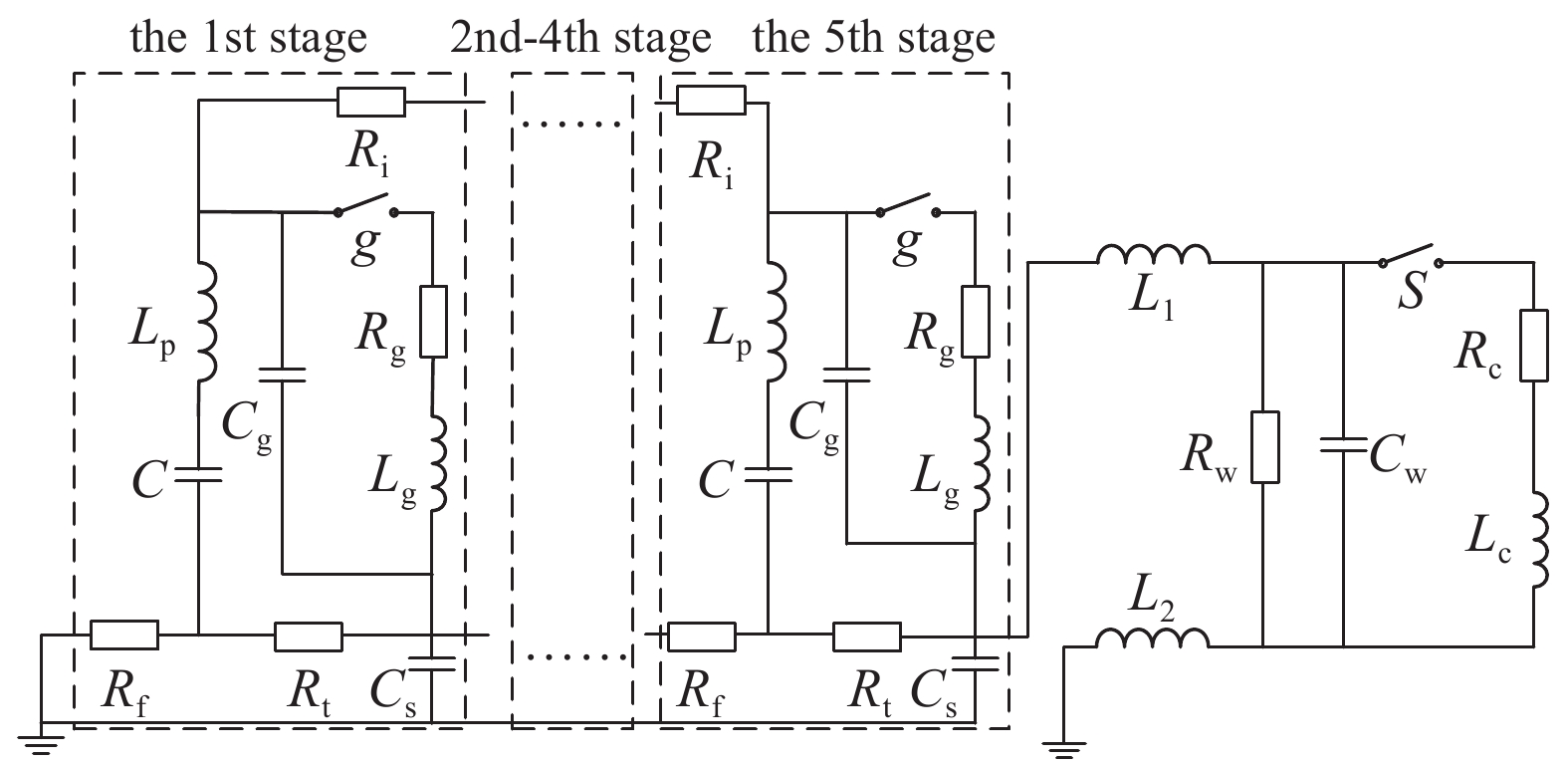
针对高电压脉冲放电破岩试验平台，为考虑系统分布参数、岩石击穿前后不同工况的转换以及岩石击穿过程中的时变阻抗特性，准确地对系统输出特性进行预测，在Pspice搭建高电压脉冲放电破岩系统仿真模型，如图5所示。C为储能电容；R_f为波前电阻；R_t为波尾电阻；R_i为充电电阻；L_g为火花开关导通通道电感与结构电感之和；C_g代表火花开关电极之间的极间分布电容；R_g为火花开关导通电阻；g为球隙火花开关，其导通时间为T₁；由于分压器难以直接对破碎电极两端电压进行测量，分压器测量电压包括部分输出回路电感的电压，令L₁为驱动源结构电感与未接入分压器的输出回路电感之和；L₂为接入分压器的输出回路电感；L_p为电容器分布电感；C_s为对地分布电容；R_w为放电电极之间的泄漏电阻；C_w为放电电极之间的分布电容；利用开关S的通断来模拟岩石的击穿，开关导通时间即为岩石实际击穿时间T₂；R_c为岩石击穿后等离子体通道电阻；L_c为岩石击穿后等离子体通道的电感。高电压脉冲破岩系统电气参数如表2所示。

电极设计对破碎电极负载阻抗影响显著，在不同电极间距下，将破碎电极导杆视为长直导线，岩石击穿前破碎电极分布电容与泄漏电阻如表3所示。

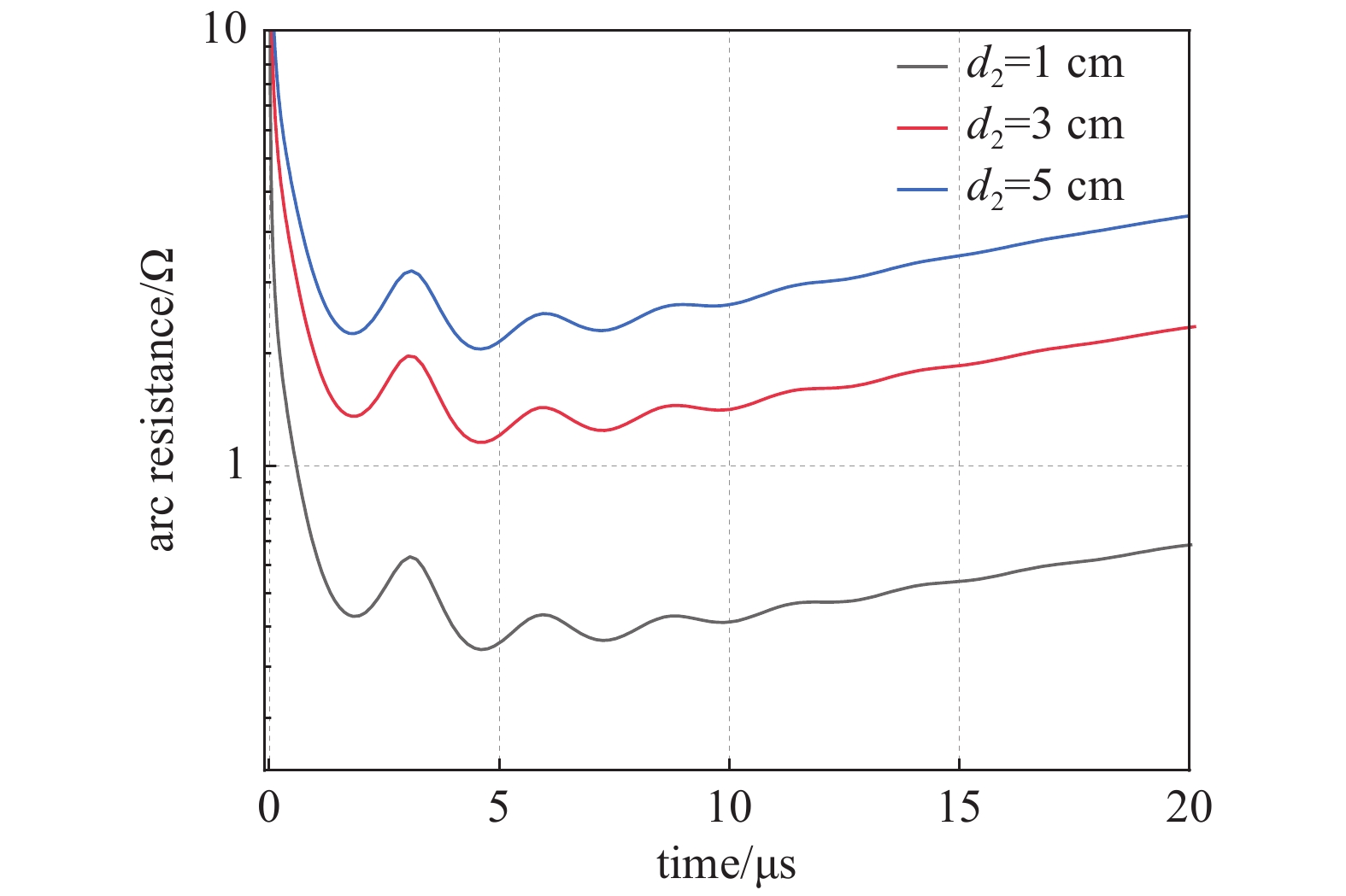
由于电弧通道长度无法直接测量，由试验脱模结果估计电弧长度，对于1，3与5 cm电极间距，电弧通道长度分别为1.4，4.5与7.2 cm，通道阻抗模型中变量的初值为r(0)=2.2×10⁻⁴ m、n(0)=5×10²⁴/m³、T(0)=19000 K。1 ，3与5 cm电极间距下，岩石中通道电阻随时间变化如图6所示，通道电阻稳定值分别为0.4，1.6，2.8 Ω，电弧通道稳定时单位长度电阻约为28.6，35.6，38.8 mΩ/mm。岩石击穿后等离子体通道迅速膨胀，温度上升，通道电阻由绝缘状态下降到稳定值；维持稳定值一段时间后，通道膨胀速度与温度下降，通道电阻逐渐上升，绝缘逐渐恢复。随着电极间距的增加，岩石击穿前后破碎电极的负载等效阻抗均会增大，而岩石击穿后等离子体通道阻抗下降速度减缓。

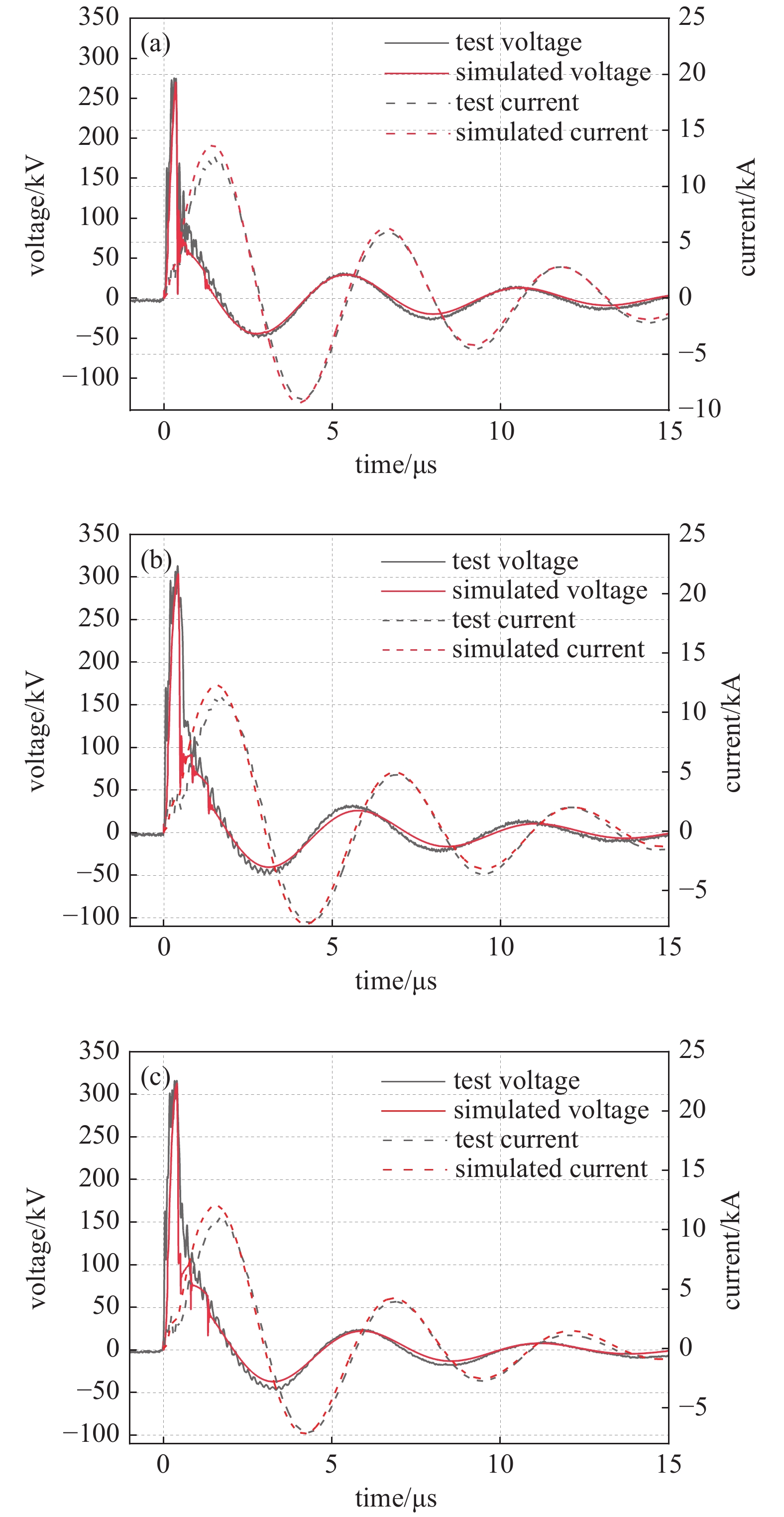
不同电极间距下，仿真模型的输出特性与试验结果对比如图7所示,定义电流峰值与次波峰值之比为衰减比，关键参数的仿真计算值与试验值对比如表4所示。考虑负载工况转换、系统分布参数以及电弧通道阻抗时变特性的影响，建立的电路仿真模型仿真结果符合实际岩石破碎工况，能够与试验结果较好的吻合。

输出电压下降沿的跌落是岩石击穿后通道阻抗的迅速下降引起的，考虑通道时变阻抗模型能够较好地反映该过程。试验中等离子体通道长度与膨胀速度的不同，会导致不同的电压下降沿特性。通道膨胀速度越快，通道阻抗下降越迅速，导致输出电压下降沿的跌落幅度越大。岩石击穿，电路工作于欠阻尼状态，输出电流峰值会随通道阻抗的上升而下降，故间隙距离的增大会降低输出电流的幅值。岩石击穿后，影响电流峰值的主要因素为回路电感，试验与仿真的电流峰值存在较大的误差，原因可能有两点：一是实际放电回路并不是规则的平面矩形，利用平面矩形回路计算回路电感导致回路电感较小；二是由于仿真时忽略了岩石击穿通道电感的变化，岩石内部通道较气、液介质中膨胀更加困难，通道半径较小，电感的影响增大。等离子体通道膨胀将会使得通道下方的岩石发生破碎，实际电弧长度小于破碎空腔最深路径长度，根据空腔脱模结果选取的通道长度可能略大于实际电弧长度，导致阻抗模型计算结果偏大。球隙开关击穿时间的随机性以及电极烧蚀对开关特性的改变，会导致相同试验条件下的输出电压波前特性发生变化，目前电路建模分析过程难以考虑其影响^[20-21]。

高电压脉冲破岩过程中负载阻抗存在较大范围的变化，在等离子体通道形成前，负载为破碎电极分布电容与泄漏电阻组成的RC并联负载；在等离子体通道形成后，负载为等离子体通道中时变电阻与时变电感组成的RL串联负载。本文针对不同的负载工况分别进行分析，建立电弧通道阻抗模型，通过石膏脱模测取破碎空腔最深破碎路径长度选取电弧通道长度，计算获得350 kV电压脉冲作用下，1，3以及5 cm电极间距的花岗岩电弧通道单位长度电阻为28.6，35.6以及38.8 mΩ/mm，电弧通道单位长度电阻随电极间距增大。考虑负载工况转换、系统分布参数以及电弧通道阻抗时变特性，建立高电压脉冲放电破岩系统的电路仿真模型，仿真结果与试验结果吻合良好，能够准确地预测高电压脉冲破岩系统的输出特性。建模时仅考虑了通道电阻的时变特性，而忽略了通道电感随时间的变化，考虑到岩层中通道更细，电感的影响较空气、液中影响要大，在后续研究中将探究通道发展过程中电感的时变特性。