本章首先求解齿背处正弦螺旋线及其共轭曲线的矩阵方程，并建立爪尖处椭圆弧修正方程，最后构建截面型线方程，完成对截面型线的求解。

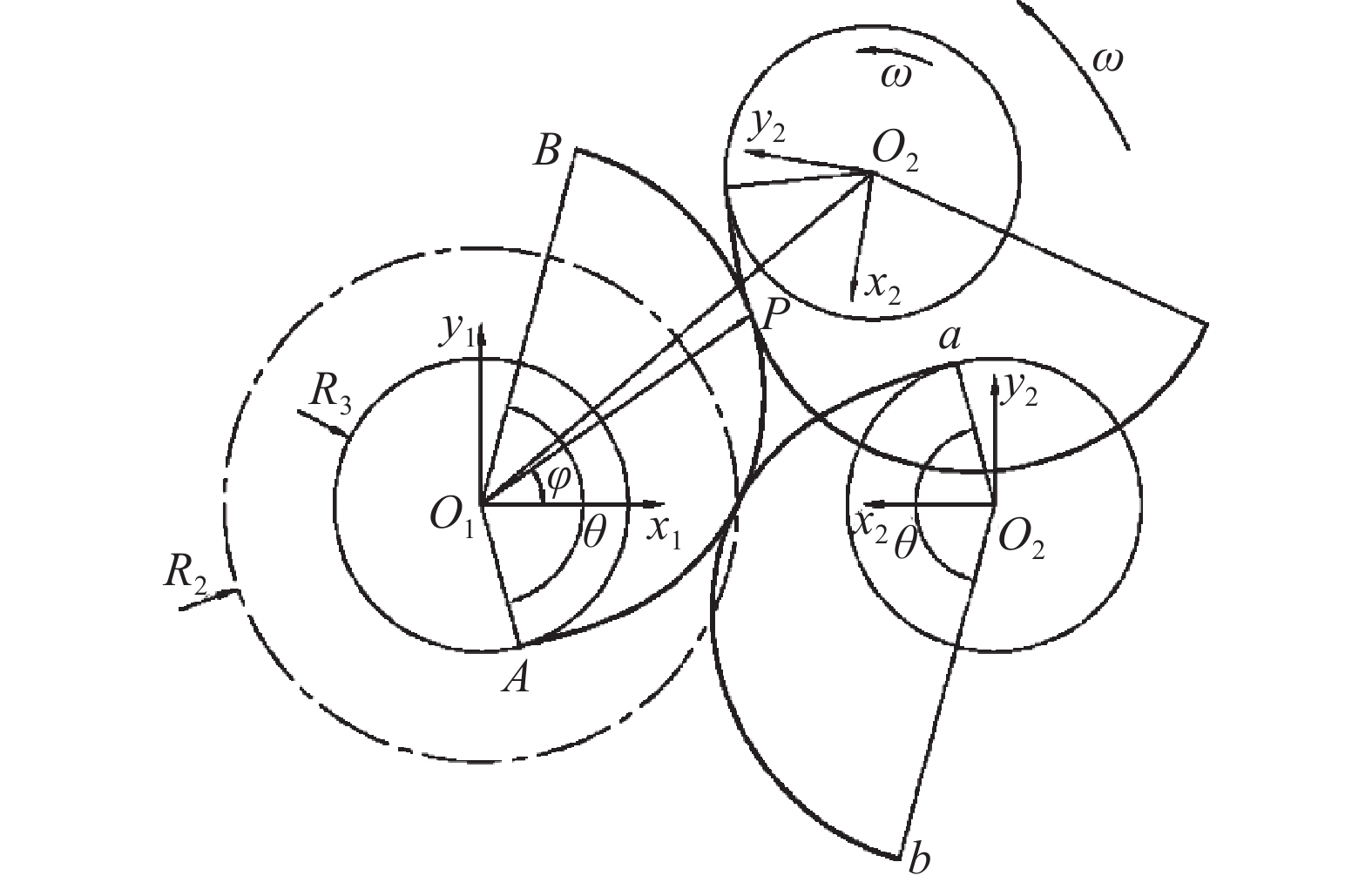
如图1所示，在左截面型线齿根圆弧取点作为点P的初始位置，绕中心点做匀速圆周运动，同时在O₁P的方向做变速直线运动，当旋转角度为θ时，此时点P在齿顶圆弧上。由点P在射线O₁P上的运动规律，以正弦函数设为速度分量，可得该方向位移分量为：

代入R(0)=R₃，R(θ)=R₁，可得P点的极坐标运动轨迹方程：

正弦螺旋线AB的矩阵方程为：

动坐标系xO₁y上坐标点在动坐标系xO₂y上的对应坐标值可表示为：

坐标变换矩阵如下：

式中：φ为截面型线的旋转角；

共轭曲线的包络条件为：

将式（6）带入坐标变换公式（4），消去φ，即可得到正弦螺旋线对应共轭曲线ab的方程。

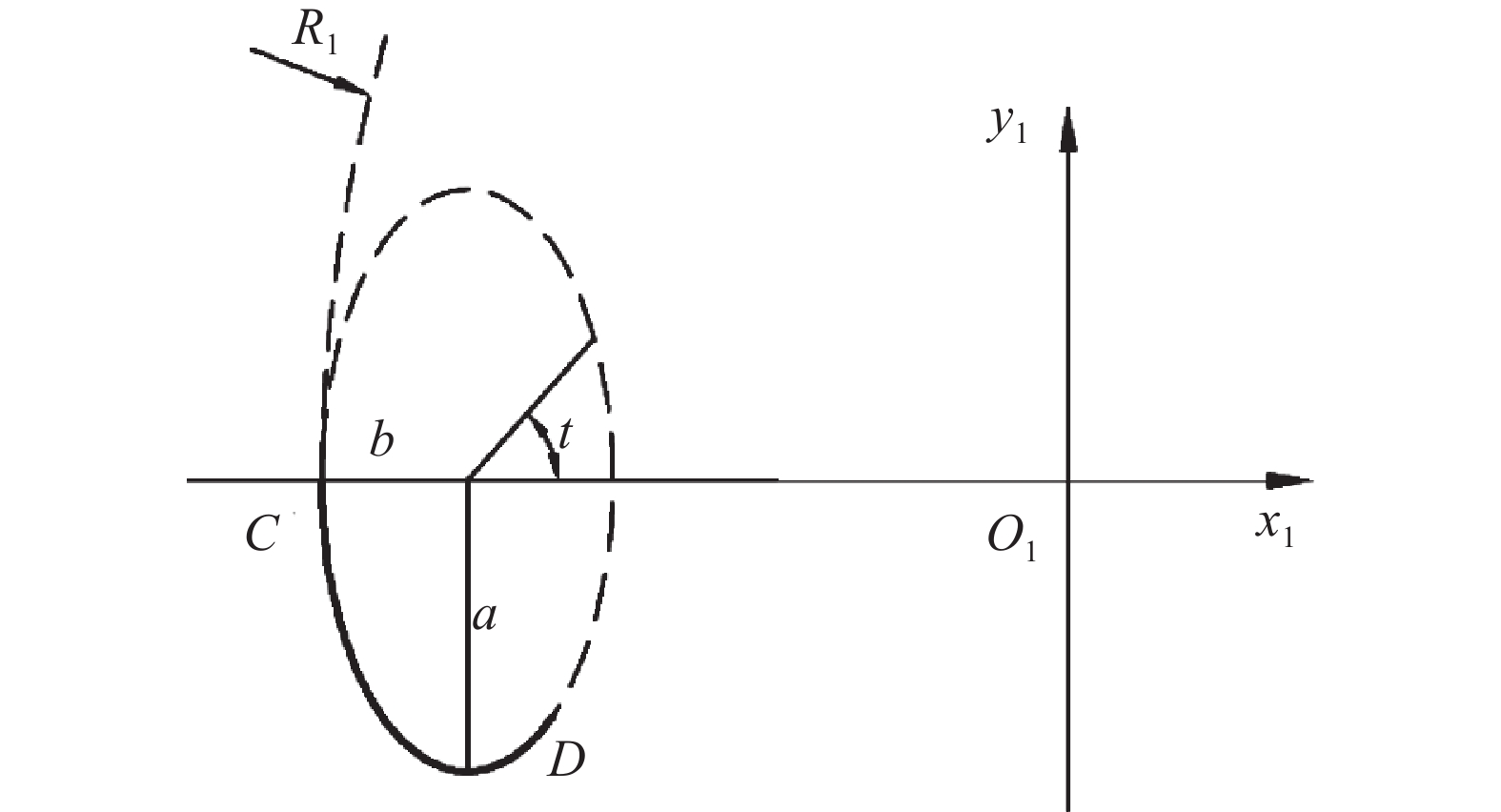
如图2所示，椭圆长半轴为a，短半轴为b，短半轴与齿顶圆R₁的半径方向一致，C点与齿顶圆R₁相切，即椭圆中心距离齿顶圆圆心为R₁−b，t为参数角。

椭圆弧方程如下：

同样根据齿廓法线法得到曲线共轭啮合条件：

得到

将φ带入M₁₂中，得到椭圆弧的共轭曲线:

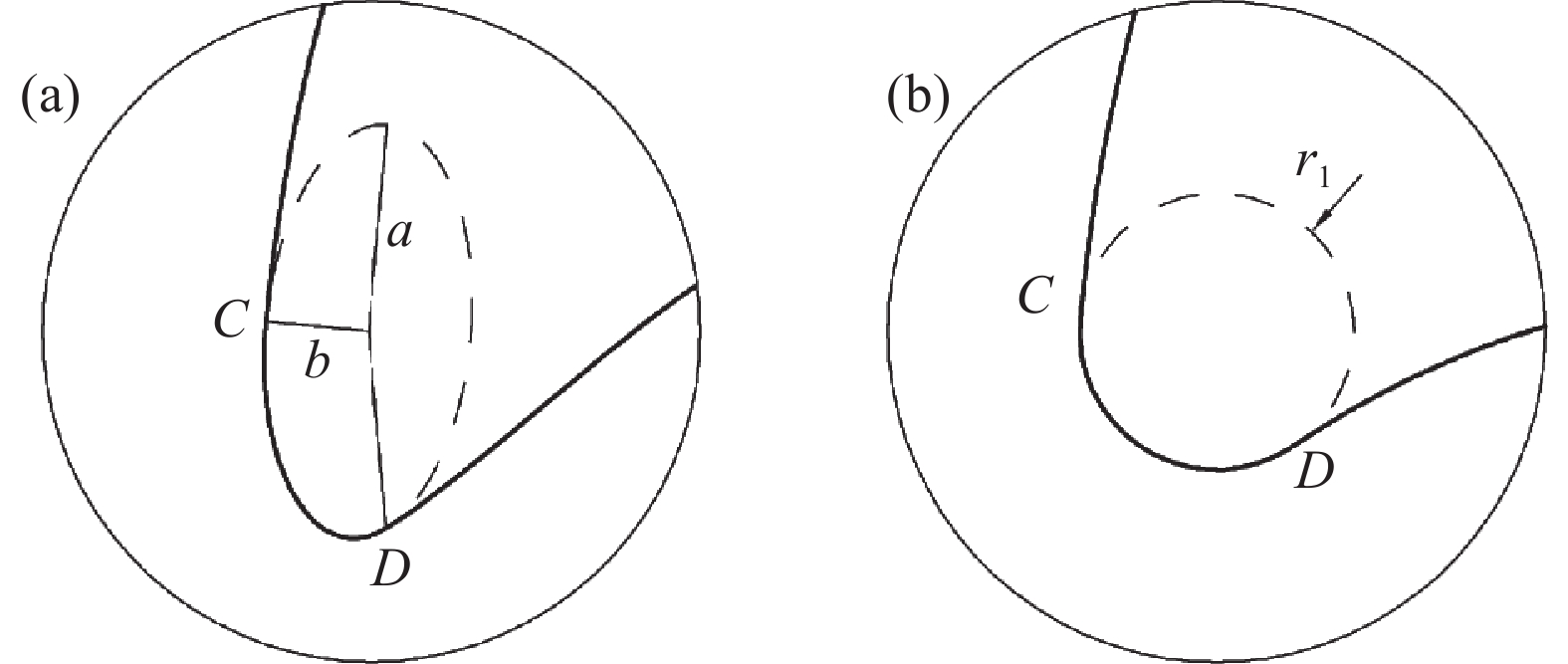
a、b比值不同时修正椭圆弧有不同的形式，a>b时为长半轴修正如图3（a）所示，a=b时为现有的圆弧修正，如图3（b）所示。

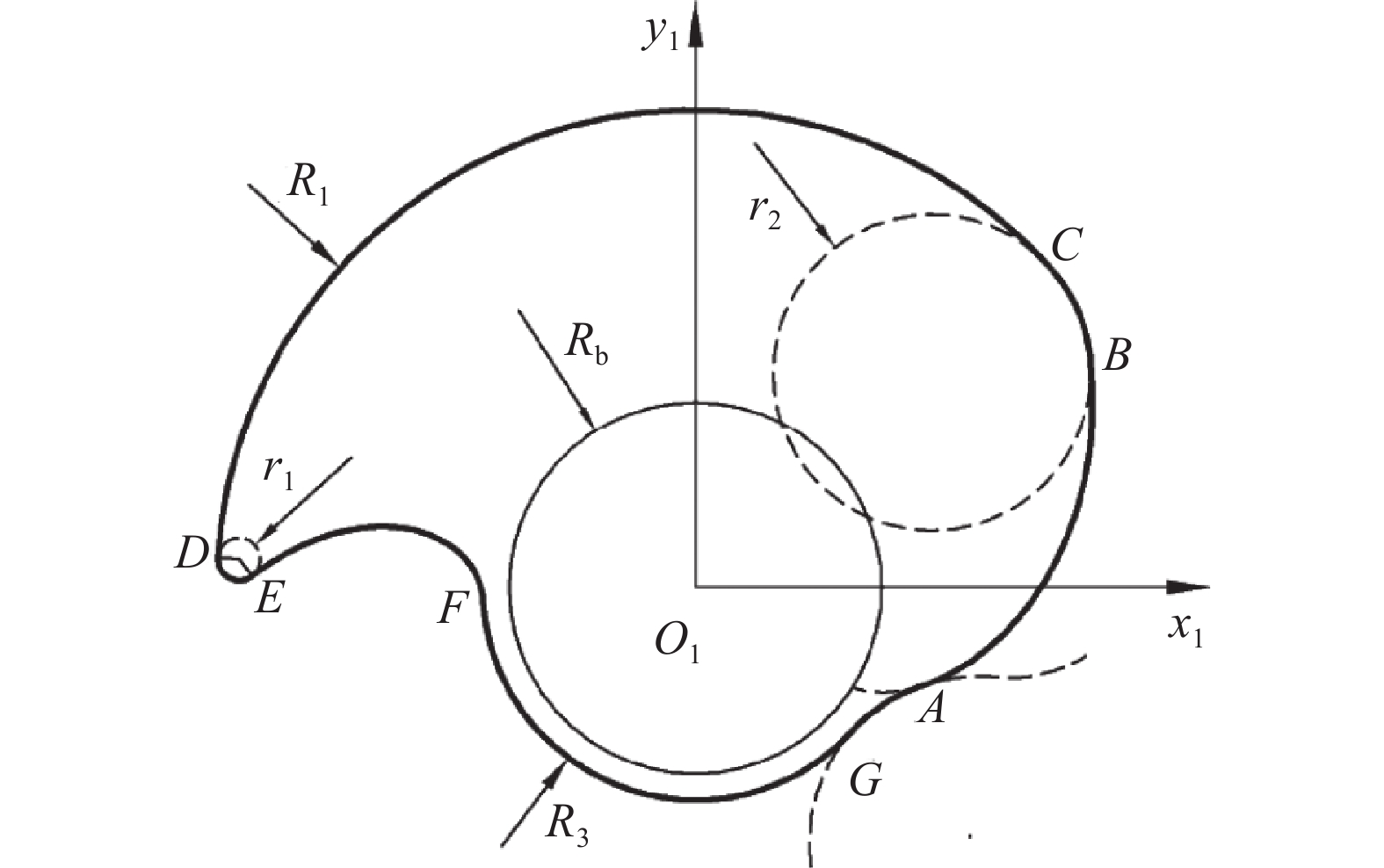
现有螺杆转子如图4所示。使用一段正弦螺旋线替代渐开线、圆弧和摆线等距曲线光滑的连接齿根圆弧和齿顶圆弧，采用椭圆弧长半轴修正替代圆弧修正，由此构建了一种正弦螺旋线-椭圆弧型转子截面型线。

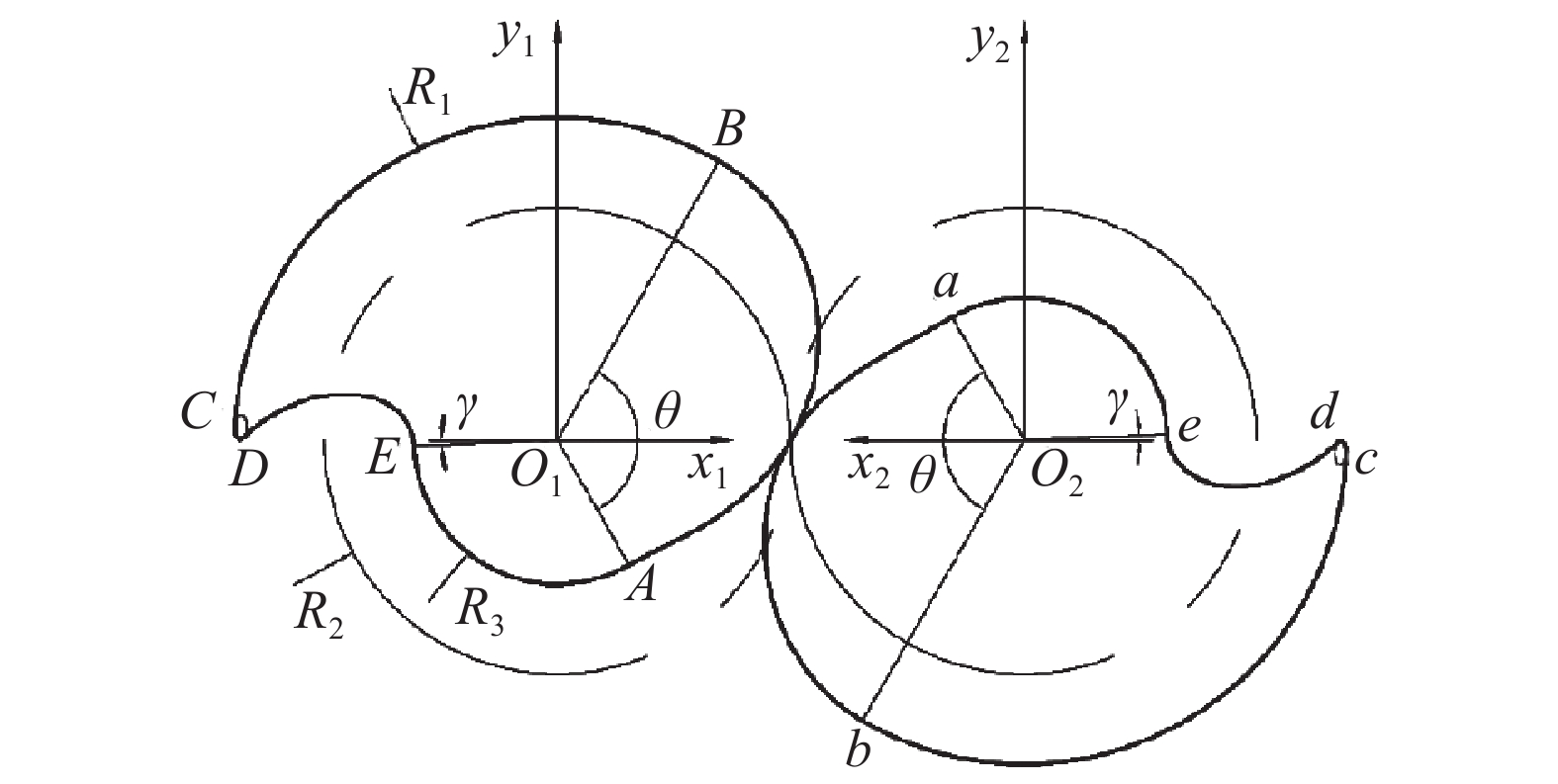
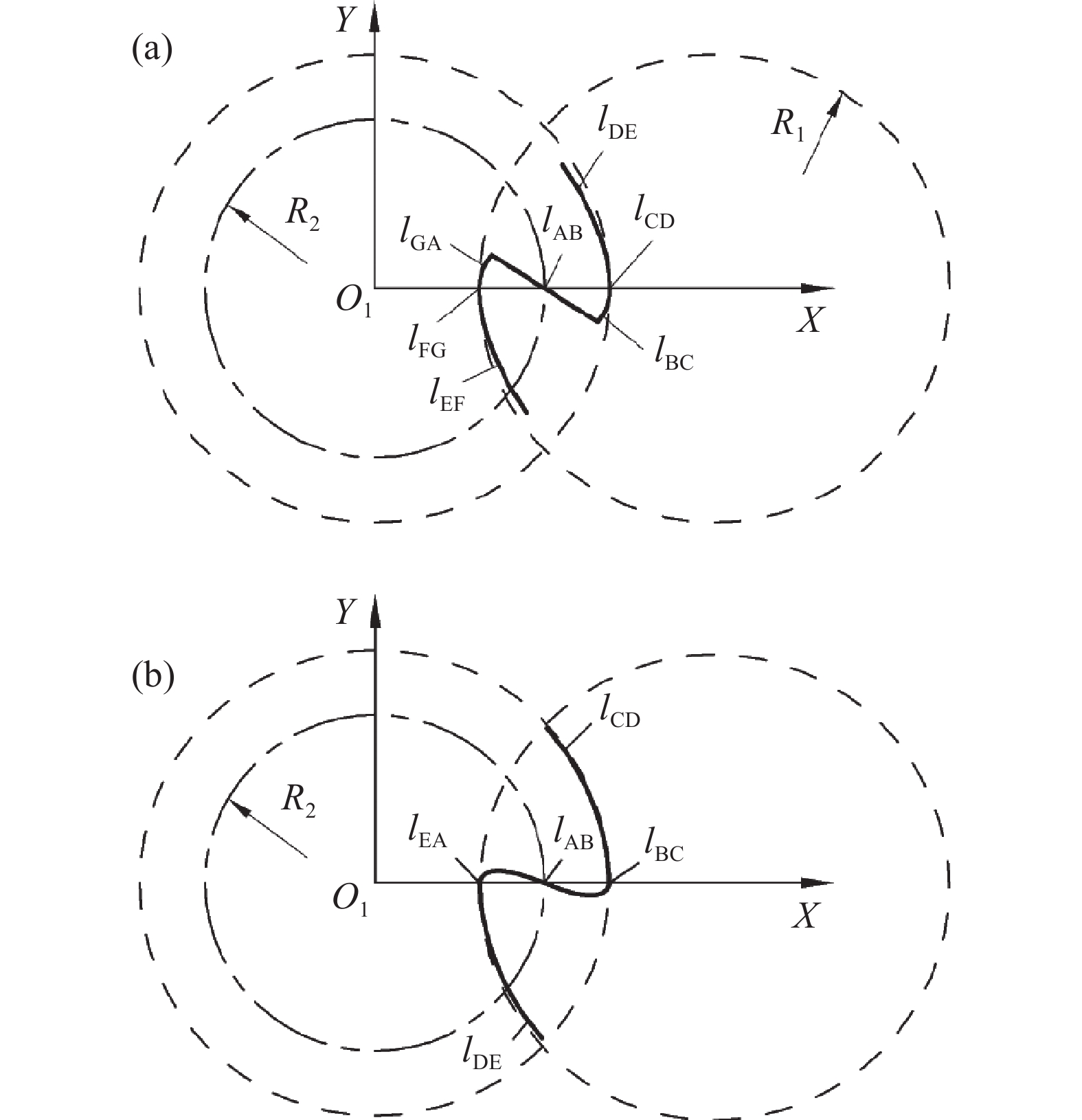
如图5所示，主动轴转子截面型线曲线由正弦螺旋线、齿顶圆弧、椭圆弧、椭圆弧对应包络线以及齿根圆弧构成，分别对应图中AB、BC、CD、DE、EA，确定方法如下：

式（3）顺时针旋转θ/2可得正弦螺旋线AB的矩阵方程：

式中M₃表示旋转变换，变换矩阵如下：

齿尖椭圆弧CD的矩阵方程为：

式中：$ \gamma $—旋转角度，可由下式确定：

即椭圆弧与其共轭曲线光滑连接的条件，交点处导数相等。

椭圆弧包络线DE的方程为$ {\mathbf{r}}_1^{CD}\left( t \right) $的包络线方程。

主动轴转子截面型线绕中点中心对称可得从动轴转子截面型线对应曲线。

本章分析对比了传统截面型线和本文新提出的截面型线的几何特性，分别从端面啮合特性、空间接触线以及泄漏三角形三个方面进行。

分析全光滑的螺杆转子型线的啮合特性，并且求解各个组成曲线的啮合线:

其中M₀₁表示从动坐标系x₁O₁y₁到静坐标系XO₁Y的变换方程：

假定爪尖修正均从C点开始，也就是齿顶和齿背对应的圆心角相等，得到圆弧-摆线型端面啮合线，如图6（a）所示，正弦螺旋线-椭圆弧型啮合线如图6（b）所示。

啮合线可以直接反映出空间接触线的最高点，从图中可以看出正弦螺旋线-椭圆弧型的啮合点更高，更接近气缸孔交线。

双螺杆真空泵加工时存在预留间隙，在运行时，高压腔气体向低压腔泄漏主要有两个通道：周向泄漏和沿侧向泄漏，在其他条件相同时，螺杆转子齿厚越厚，空间接触线越短，密封性能越好。

对接触线长度影响最大的是齿背曲线，提出的新型转子采用正弦螺旋线替代圆弧、渐开线、摆线等距曲线。取齿顶圆弧R₁=100 mm，齿根圆弧R₃=40 mm，螺距P=120 mm，控制渐开线生成圆半径和螺旋线中心角，使两种转子具有相同的转子齿厚，对比结果如表1和图7所示，图7（a）表示圆弧-摆线等距曲线型转子的空间接触线，图7（b）表示正弦螺旋线-椭圆弧型转子的空间接触线。

可见，采用正弦螺旋线比圆弧渐开线具有更短的空间接触线，长度缩短了2.54%，圆弧-摆线等距曲线型转子空间接触线长且不光滑，正弦螺旋线-椭圆弧型转子具有光滑且较短的空间接触线，具有更好的级间密封效果，减少泄漏。

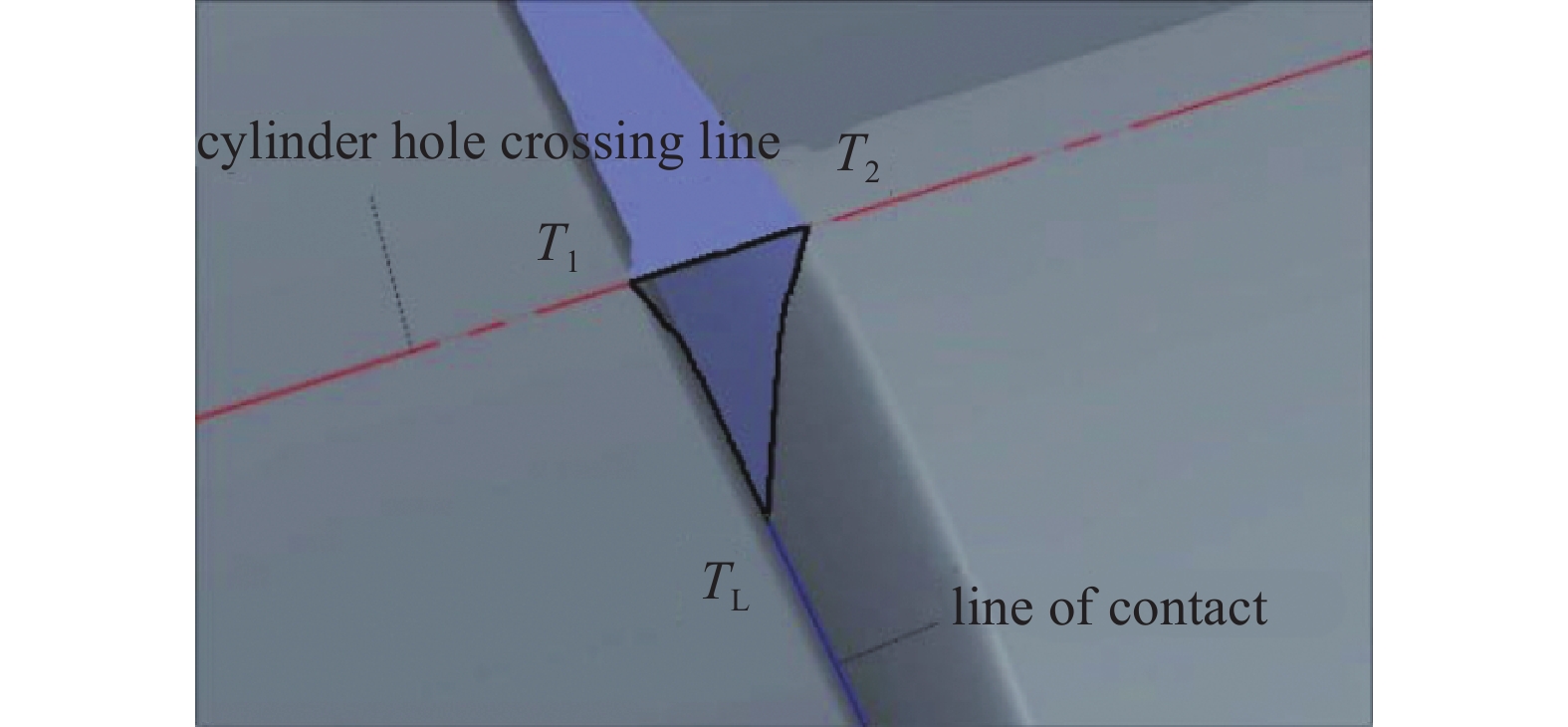
如图8所示，两个螺杆转子在发生啮合时，螺旋齿面和内壁之间会产生泄漏三角形；泄漏三角形会导致气体从高压腔泄漏到相邻的低压腔，泄漏三角形会严重影响双螺杆真空泵的运行效率和级间泄漏。

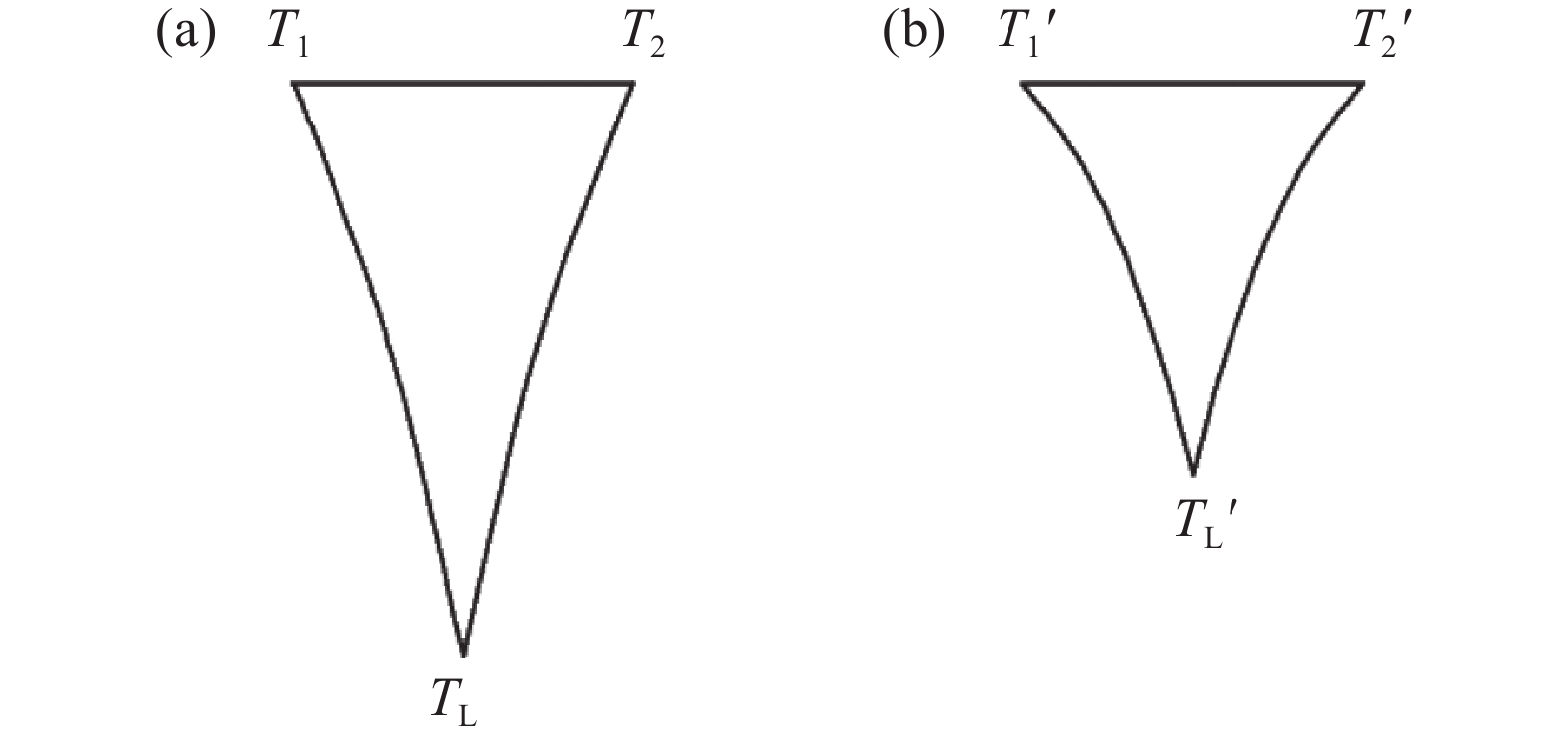
影响气体泄漏量的主要因素是气体流线垂直泄漏三角形形成的面积。图8中T₁、T₂为气缸孔交线与阴阳两转子形成的相交点，T_L则是空间接触线的最高位置。图9（a）和图9（b）分别为传统螺杆转子和本文新型的泄漏三角形对应的垂直面积。

由图9可以看出椭圆弧爪尖的接触线更靠近泵腔交线，T_L的位置更高，泄漏三角形面积如表2所示，椭圆弧修正后泄漏三角形面积为圆弧修正的72.23%，有效减小了泄漏量。

本章对螺杆转子和泵腔进行网格划分，并验证其网格无关性，最终得出内部流场的压力分布，对比分析新型螺杆转子和传统螺杆转子的泄漏情况。

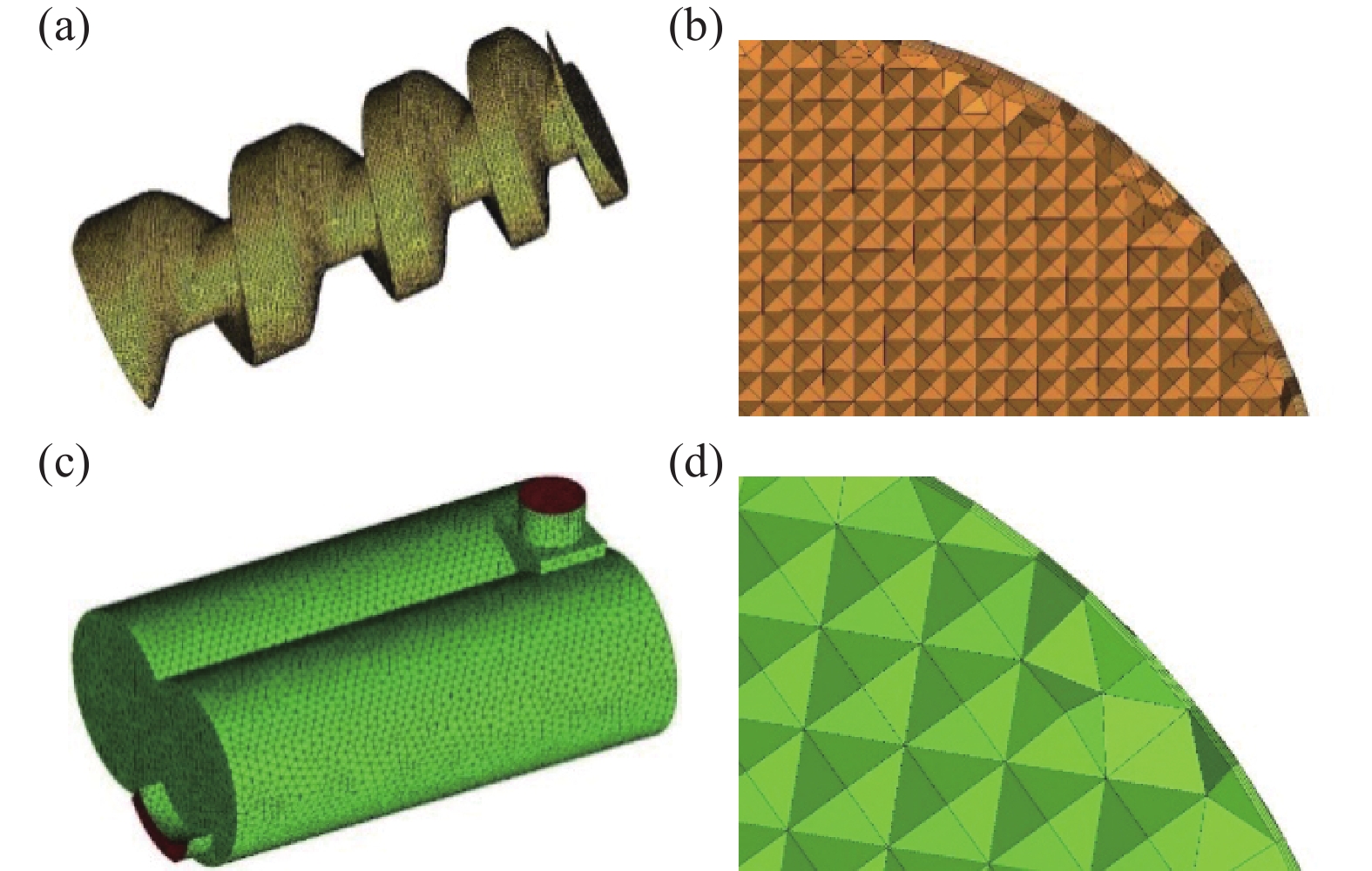
对螺杆转子进行体网格划分，网格最大尺寸选为2 mm，网格种类选择四面体网格，并在转子最外层生成5层棱柱网格来提高转子描述精度，最大尺寸设成2 mm，第一层网格高度取0.1 mm，厚度比取1.1，生成5层网格，如图10（a），（b）所示。对泵腔流体域设置出入口相关条件方便计算，泵腔网格最大尺寸选择3 mm，并在泵腔最外层继续生成3层棱柱网格以提高精度，网格最大尺寸2 mm，将第一层网格高度取为0.1 mm，厚度比1.1，生成3层网格如图10（c），（d）所示。

泵腔流体域选用k-Epsilon湍流模型，材料选择25℃空气，连续流体，无浮力，域运动为静止。边界条件操作环境设为绝压状态，入口压力20 kPa，出口压力100 kPa，流体性质为亚声速，流动方向为垂直于出入口边界。

分别尝试243657、603547和956214数量的网格对流场进行模拟，检测出口处平均质量流量。平均质量流量分别为2.254×10⁻² kg/s、3.785×10⁻² kg/s和3.955×10⁻² kg/s，网格数为603547和956214时，质量流量误差为4.491%，由此得出网格尺寸对模拟结果影响较小的结论。使用网格数量为603547模拟数据作为最终结果。

通过内部流场的数值模拟，对正弦螺旋线-椭圆弧螺杆转子和传统圆弧-摆线等距曲线型螺杆转子进行对比，来验证新型螺杆转子的密封性能。

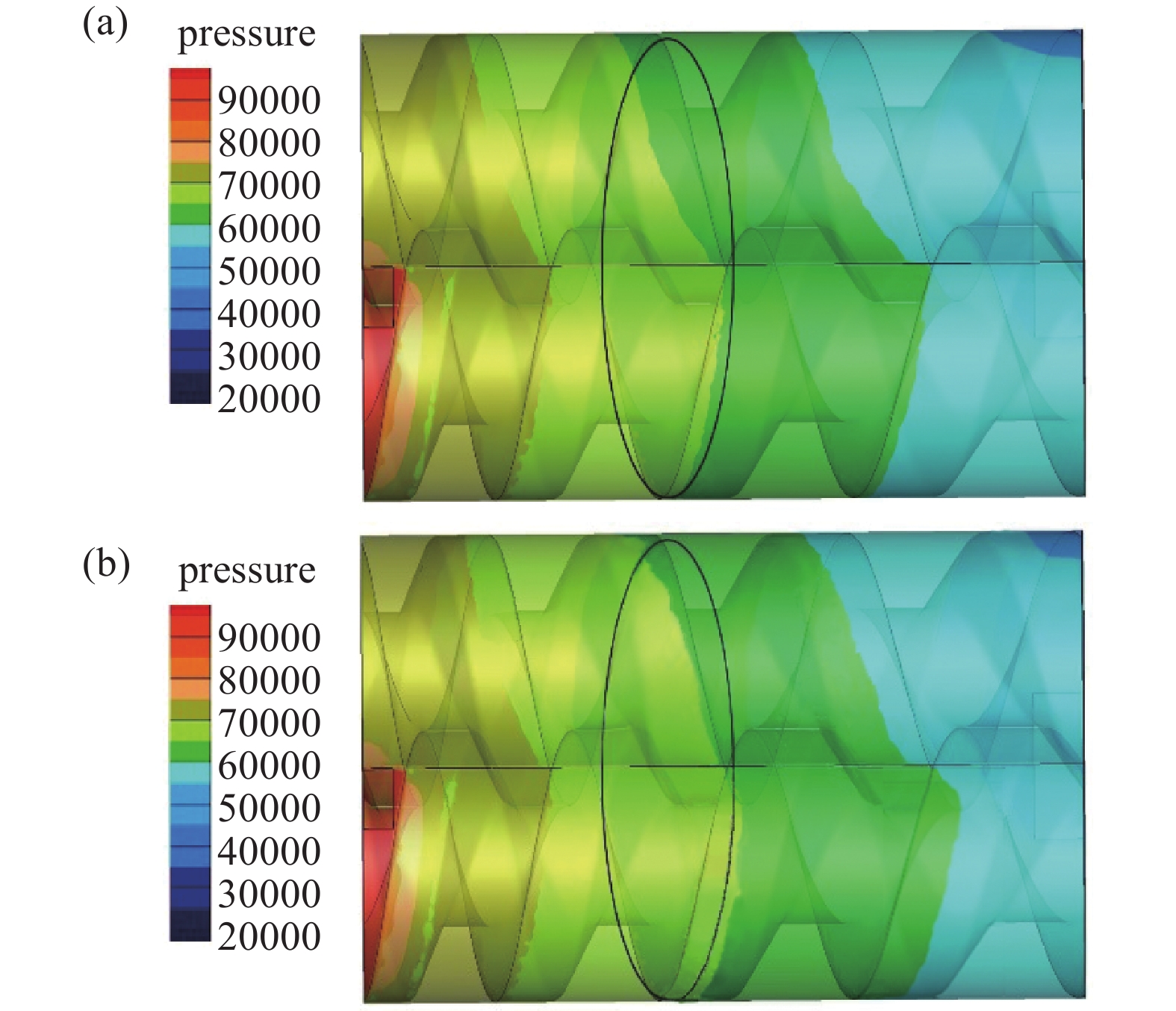
如图11所示，为内部流场的压力分布。螺杆转子进行同步异向双回转运动，吸入口吸气至工作腔吸满，工作腔向排气口逐渐移动；在运送过程中，压缩工作腔容积，压力升高；当工作腔与排气口接通时，螺杆转子排出气体，从而实现了双螺杆真空泵的一个运行循环。

图11（a）为正弦螺旋线-椭圆弧螺杆转子 内部流场的压力分布，图11（b）为传统圆弧-摆线等距曲线型螺杆转子内部流场的压力分布；由图可知，加工过程预留间隙会导致严重的级间泄漏，图11（a）中标记位置处高压气体泄漏深度远小于图11（b），出现该情况是由于新型螺杆转子采用椭圆弧优化，减小泄漏三角形面积，提高了齿顶面处的密封性能。

（1）设计了一种正弦螺旋线-椭圆弧转子，建立正弦螺旋线及其共轭曲线的啮合模型，采用该曲线解决了传统圆弧渐开线型齿背曲线构成空间接触线长的问题；建立了爪尖椭圆弧修正模型，解决了现有圆弧爪尖修正泄漏三角形面积过大的问题。

（2）分别比较了正弦螺旋线-椭圆弧转子和现有圆弧-摆线等距曲线型转子的空间接触线长度、泄漏三角形面积，空间接触线缩短2.54%，泄漏三角形面积减小了27.77%，；构建的正弦螺旋线-椭圆弧转子具有连续光滑，空间接触线短，泄漏三角形面积小等优点。

（3）对所提出的正弦螺旋线-椭圆弧转子和现有圆弧-摆线等距曲线型转子进行流场压力分布对比，提出的新型转子具有较小的齿顶压力泄漏深度，齿顶面处具有更优良的密封性能。