-
电推进技术因其高比冲、高效率、姿轨控制精度高、发射重量轻、应用模式灵活多样、在轨寿命长、综合成本低等优势,已成为先进卫星平台的重要配置[1],目前已在欧美及日本等国家实现了空间中的应用[2-4]。基于未来航天任务对离子推力器的要求,采用离子推力器完成所有在轨任务所需要的时间达上万小时[5],而空心阴极的寿命是是制约系统寿命和可靠性的最主要因素[6]。在空心阴极的几种失效模式中[7-9],发射体殆尽失效对空心阴极的寿命有着至关重要的影响。威布尔分析方法[10-14]适用于发射体不断蒸发损耗这一累计磨损的过程,并具有适用于非零起点、极小子样、无失效等情况的优点。之前的研究中提出了一种LaB6空心阴极工作在额定发射电流下时发射体耗尽的基本寿命模型[15],应用基本寿命模型及威布尔分析方法定量评估了20 A额定发射电流下空心阴极的工作寿命及可靠性。
前面研究提出的基本寿命模型是一个比较保守的寿命模型,因为发射体的失效判据为发射体下游顶端径向损耗殆尽时工作寿命终止。但就空心阴极实际工作及其工程应用实践而言,地面试验结果表明空心阴极工作寿命终止的发射体耗尽状态还可以进一步向上游扩展。基本模型的计算分析结果也表明[15]:当发射体失效时,发射体顶层四周未消耗完的部分仍处于较高温度,具备继续维持正常工作性能的电子发射能力。为此提出了一种新的发射体殆尽失效的判据寿命模型,为区别于基本模型而称之为扩展寿命模型。本文在建立扩展寿命模型的基础上,应用扩展模型和威布尔分析方法,对20 A空心阴极的工作寿命及可靠性进行了重新评估,并比较和讨论了两种模型定量评估的结果。
-
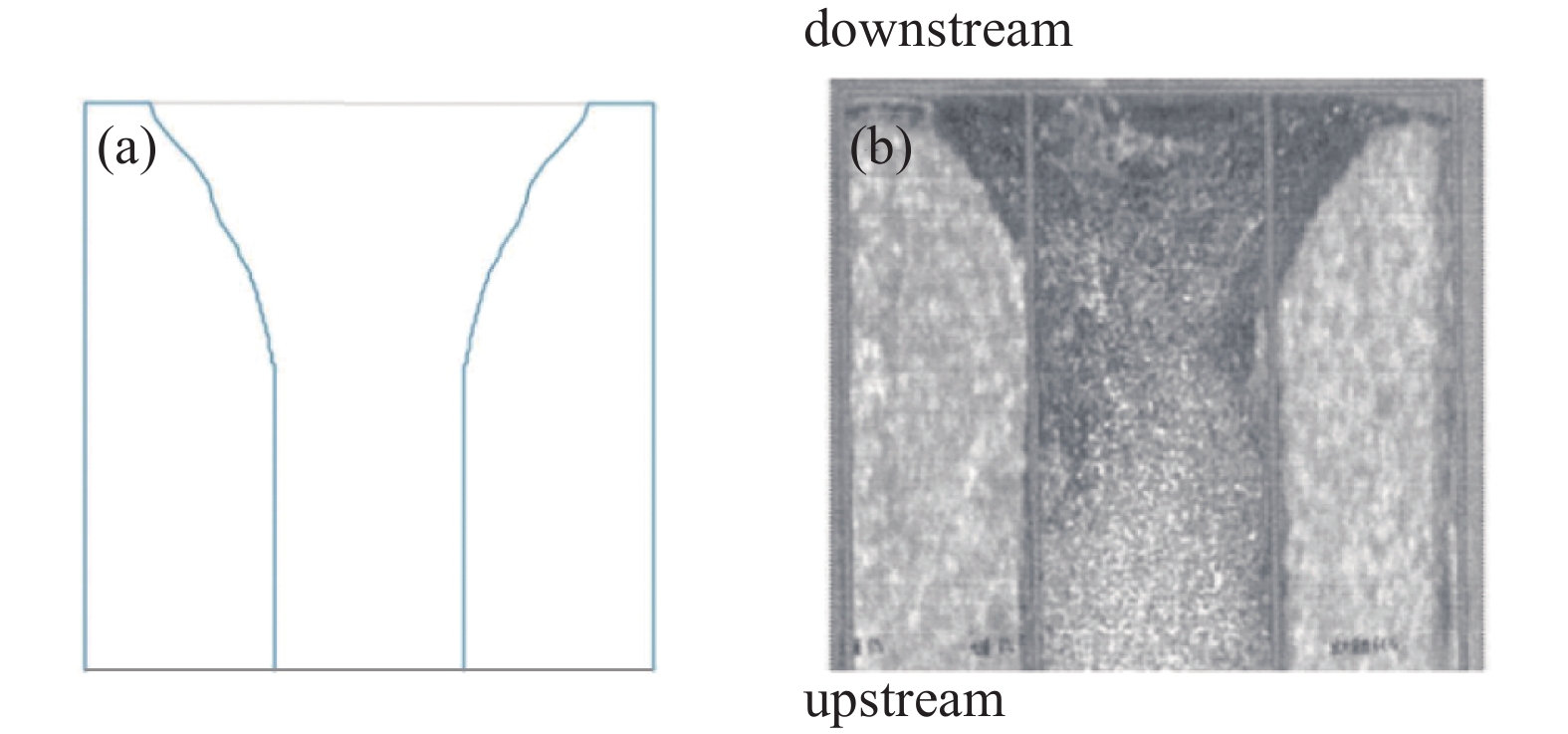
扩展寿命模型的发射体工作损耗机理模型完全继承基本寿命模型。LaB6空心阴极的工作机理及基本寿命模型在文献[15]中已进行详细介绍,概括来说,LaB6发射体发射电子的原理是高温下热电子发射,且电子发射密度满足Richardson-Dushman方程;基于国外对空心阴极内部的研究[16-18],对发射体工作损耗模型的温度分布进行假设,如图1所示,简单描述为:从发射体下游顶端开始,温度在不同的区域内按照不同的梯度下降。利用此模型计算了发射体工作15 kh后的损耗形态,如图2(a)所示,与LIPS-200离子推力器寿命试验中15 kh后的发射体形态[19]进行对比,如图2(b)所示,初步证明了此模型的合理性。
-
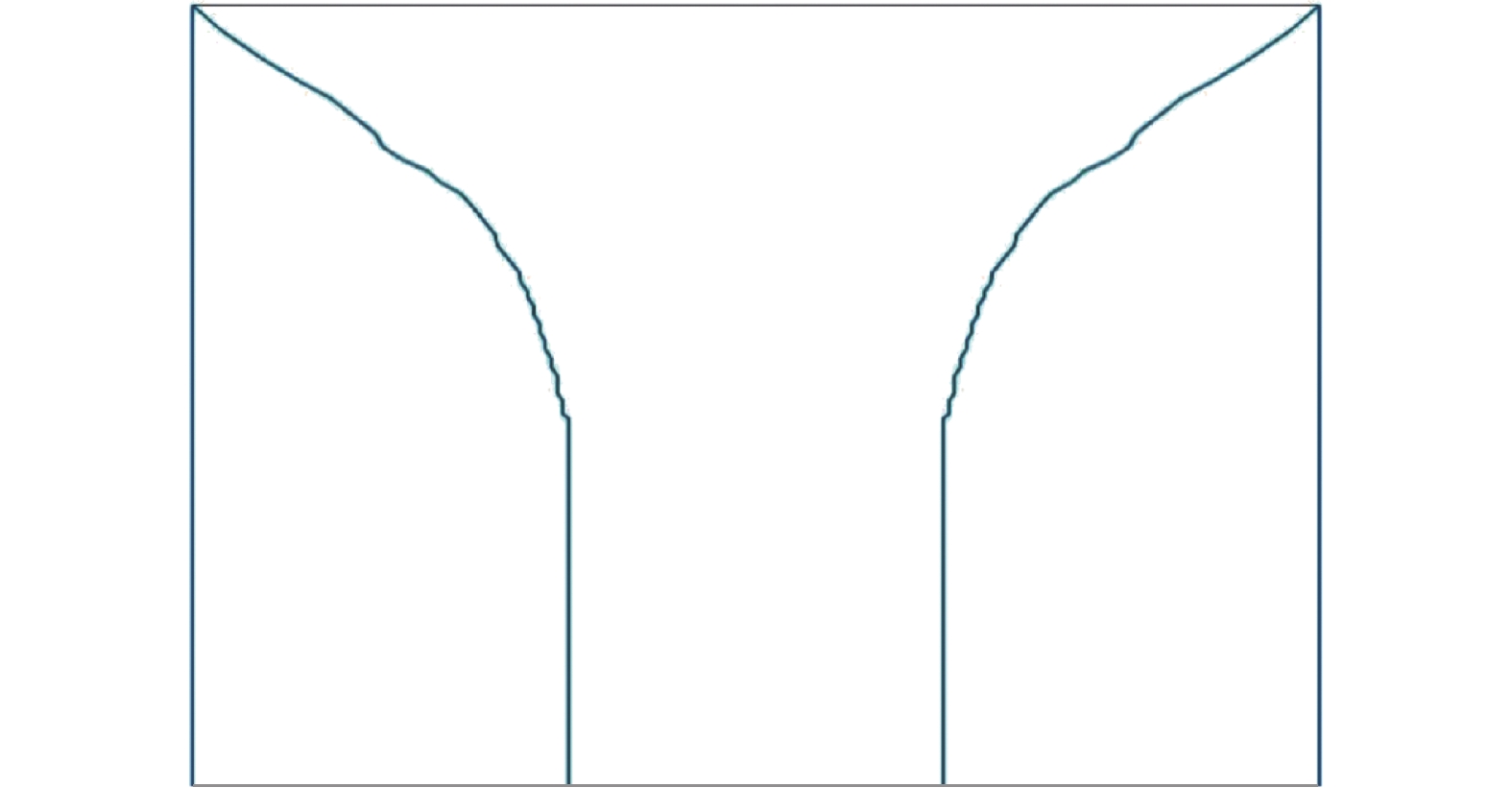
基本模型中,发射体的失效判据为:发射体下游顶端径向损耗殆尽,此时发射体寿命终止。按照此失效判据计算发射体寿命,即当发射体下游顶端径向损耗殆尽时发射体形态如图3所示。
国内外模拟实际工作的地面寿命试验结果表明:空心阴极工作寿命终止的发射体耗尽状态还可以进一步向上游扩展;国外Mikellides I、Ioannis G等[20-24]学者对钡钨发射体空心阴极内部的等离子体密度及电势分布进行了仿真分析,其仿真结果表明,在发射体下游顶端区域内具有较高密度的等离子体分布及较高的鞘层电位,这导致了这一区域具有较高的温度,尽管这些研究主要基于钡钨发射体展开,但是对LaB6空心阴极的研究仍具有意义。此外,基本模型的计算分析结果也表明[15]:当发射体失效时,发射体顶层四周未消耗完的部分仍处于较高温度,具备继续维持正常工作性能的电子发射能力。
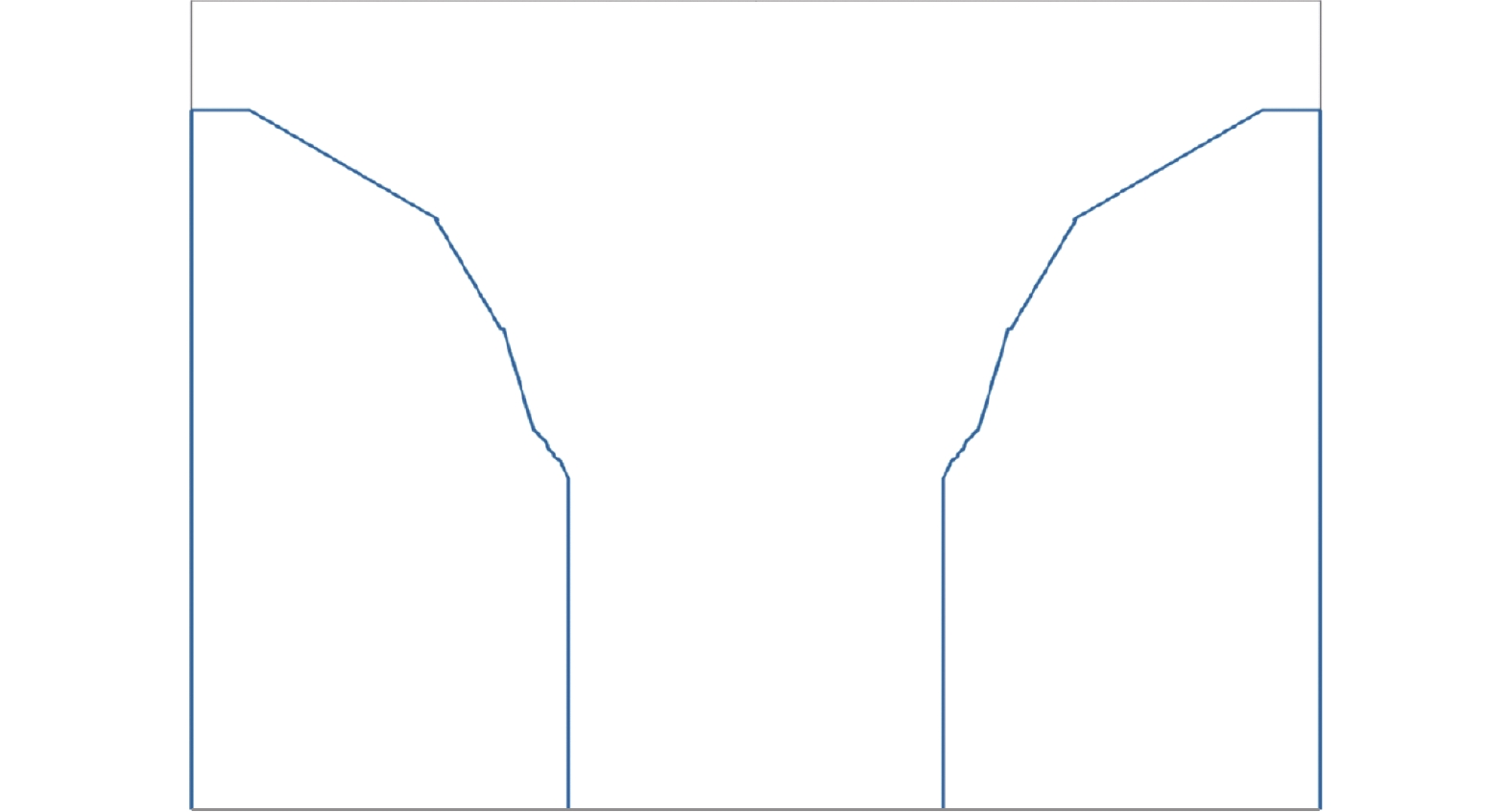
由此可见,国内外地面寿命试验、仿真分析、以及前面研究提出的发射体基本失效模型均表明发射体在顶层消耗完全的基础上具有进一步发射电子的能力,但由于对发射体失效判据的研究目前仍较少,本文提出假设,即发射体耗尽的失效判据为:假设发射体下游顶端1 mm处径向消耗90%时,发射体寿命终结,此时发射体耗尽时的发射体形态如图4所示,此形状对发射体时效时其形态的预期。
-
空心阴极发射体失效扩展基本模型中,其失效判据假定为:发射体下游顶端径向消耗完全视为发射体失效;在扩展模型中,将基本模型中的失效判据修正为:发射体下游顶端1 mm处径向消耗90%时发射体寿命终结。扩展模型的寿命分为两个阶段进行计算:(1)发射体顶层径向消耗完全所需时间
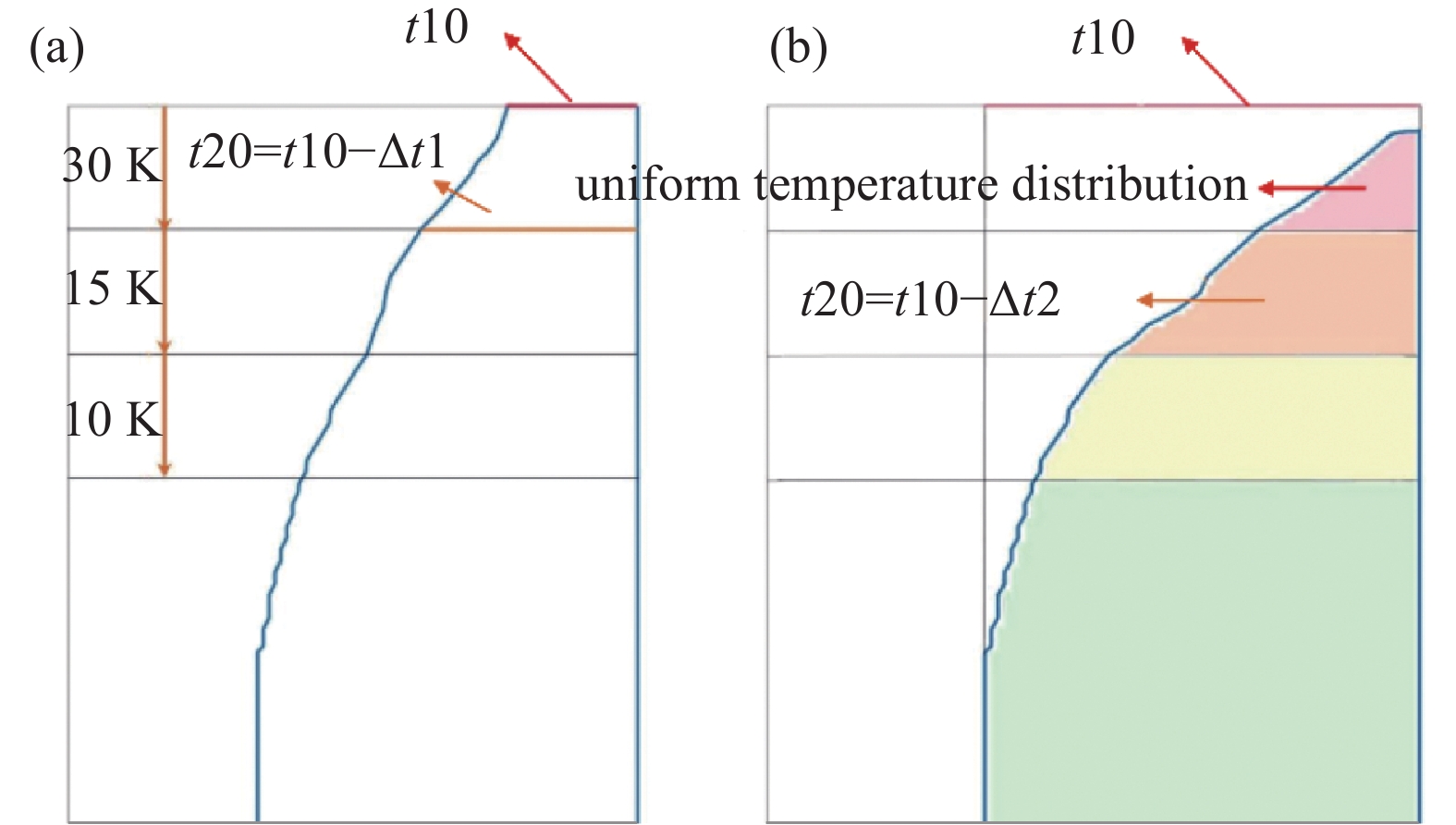
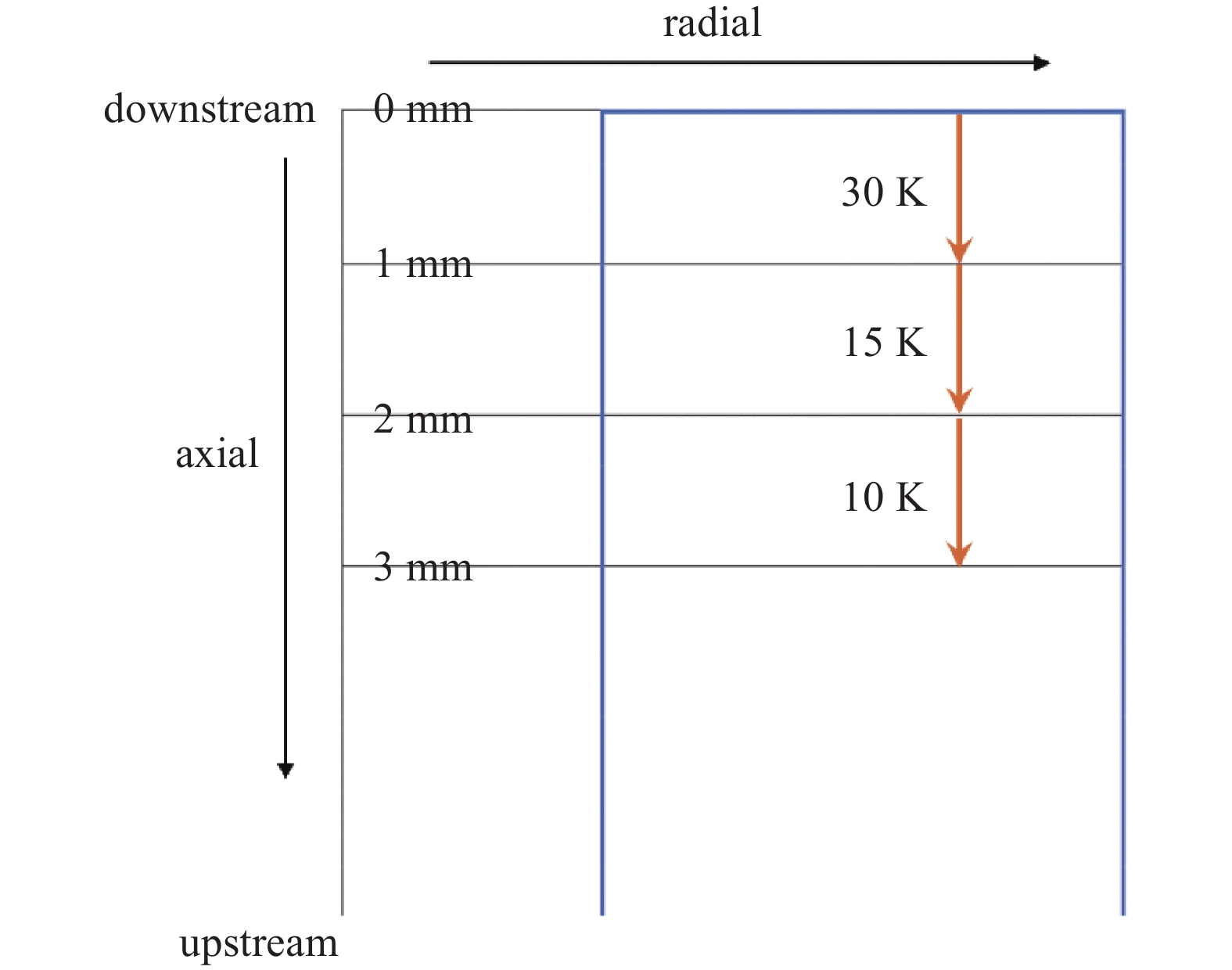
$ {t}_{1} $ ;(2)$ {t}_{1} $ 之后发射体下游1 mm处径向消耗90%所需时间$ {t}_{2} $ 。$ {t}_{1} $ 即为第二节提出的发射体寿命模型的寿命,新的模型中,发射体寿命为$ {T=t}_{1}+{t}_{2} $ 。$ {t}_{1} $ 即为基本模型中寿命计算方法。考虑$ {t}_{2} $ 阶段的消耗情况,如图5(a)所示:在$ {0-t}_{1} $ 阶段,将发射体按照距下游顶端距离分成发射体下游0~1 mm、1~2 mm、2~3 mm和剩余部分,共四部分,假设每部分顶端较上一部分顶端温度分别下降30 K、15 K、10 K、5 K。而在$ {t}_{1}-{t}_{2} $ 阶段,为了便于计算,此阶段对于温度分布重新进行假设,如图5(b)所示。假设四部分内部温度依然均匀分布,考虑到发射体不断消耗,其下游顶端区域内的等离子体密度、电势等较发射体消耗前有不同程度的降低,导致发射体表面温度有一定下降,因此对此阶段温度分布进行调整,出于相对保守的估计,假设四部分温度分别为1890 K、1875 K、1865 K、1855 K。$ {t}_{2} $ 的计算思路即为:工作$ {t}_{1} $ 时间后,发射体下游1 mm处的剩余厚度继续以新的温度分布模式进行消耗,直至下游1 mm处径向消耗完全,所用时间即为$ {t}_{2} $ 。基于此扩展模型,对发射体耗尽失效的寿命模型表达式进行推导。Richardson-Dushman方程表征了发射电流密度与温度的关系,根据肖特基效应考虑逸出功减少量[25],对Richardson-Dushman方程进行修正,如式(1)所示:
式中,
${J}_{{\rm{e}}}$ 为发射电流密度,$ \mathrm{A}/{\mathrm{c}\mathrm{m}}^{2} $ ;$ \varphi $ 为发射体材料的功函,$ \mathrm{e}\mathrm{V} $ ;$ {\varphi }_{\mathrm{s}} $ 为由肖特基效应引起的逸出功降低量,取0.05 eV;$ T $ 为加热温度,$ \mathrm{K} $ ;$ A $ 为发射常数,此模型中取90A/(cm2·K2);$ k $ 为玻尔兹曼常数,取$ 1.38\times {10}^{-23} \; \mathrm{J}/\mathrm{K} $ 。文献[15]基于Richardson-Dushman方程以及LaB6发射体蒸发率与温度的关系[26],推导了LaB6发射体蒸发速率与发射电流密度的关系,如式(2)所示:
式中,
$ v $ 为发射体蒸发速率,μm/(kh);D、B、C为拟合得到的常数,分别取66.26 µm/(kh)、 0.02477 cm2/A、−88.66 µm/(kh)。按照失效判据计算发射体寿命表达式,省略计算过程,发射体寿命扩展模型的寿命表达式如下
对其中各参数的解释如下:
$ {T}_{10} $ 为发射体下游顶端的温度,$ {(T}_{10}-{ \Delta T}_{1}) $ 为$ {0-t}_{1} $ 阶段,发射体下游1 mm处的温度,$ \left({T}_{10}-{ \Delta T}_{2}\right) $ 为$ {t}_{1}-{t}_{2} $ 阶段,发射体下游1−2 mm处这一区域温度;${J}_{{\rm{e}}10}$ 、${J}_{{\rm{e}}20}$ 、${J}_{{\rm{e}}2}$ 分别为这三个温度下的对应的发射电流密度;其他参数的含义与第二节一致,即$ \varphi $ 为LaB6材料的逸出功;$ {\varphi }_{S} $ 为肖特基效应影响下的逸出功减少量;A为发射常数;R为发射体外径;r为发射体内径;B、C、D为拟合得到的参数。各参数取额定值的情况下,计算得到寿命41.3 kh。 -
根据式(3)~(6),空心阴极的寿命由10个输入参数共同决定,分别为:
$ \varphi $ 、$ {\varphi }_{S} $ 、$ {T}_{10} $ 、$ { \Delta T}_{1} $ 、$ { \Delta T}_{2} $ 、R、r、B、C、D,即发射体寿命是这10个输入参数的函数。首先利用敏感度的评估方法[27]对各输入参数的敏感度和不确定度进行评估,其中R和r的不确定度与发射体的设计参数有关,保守估计取±0.1 mm,温度的不确定度依据工程实际假设得到;其余参数的的不确定度按照其额定值的5%进行假设,评估结果如表1所示。计算可知,10个参数中,对寿命不确定度的影响从大到小依次为:
$ {T}_{10} $ 、D、$ \varphi $ 、B、C、$ { \Delta T}_{1} $ 、$ { \Delta T}_{2} $ 、R、r、$ {\varphi }_{S} $ ,由于10个参数引起的寿命不确定度均超过1.2 kh,因此认为这些参数的取值变化对发射体寿命均有明显影响,均为重要参数,抽样计算对10个参数同时进行。 -
利用蒙特卡洛抽样法对10个参数在其各自的不确定度范围内进行抽样,共抽取12000个寿命数据,用威布尔统计函数对其进行分析,结果如下:
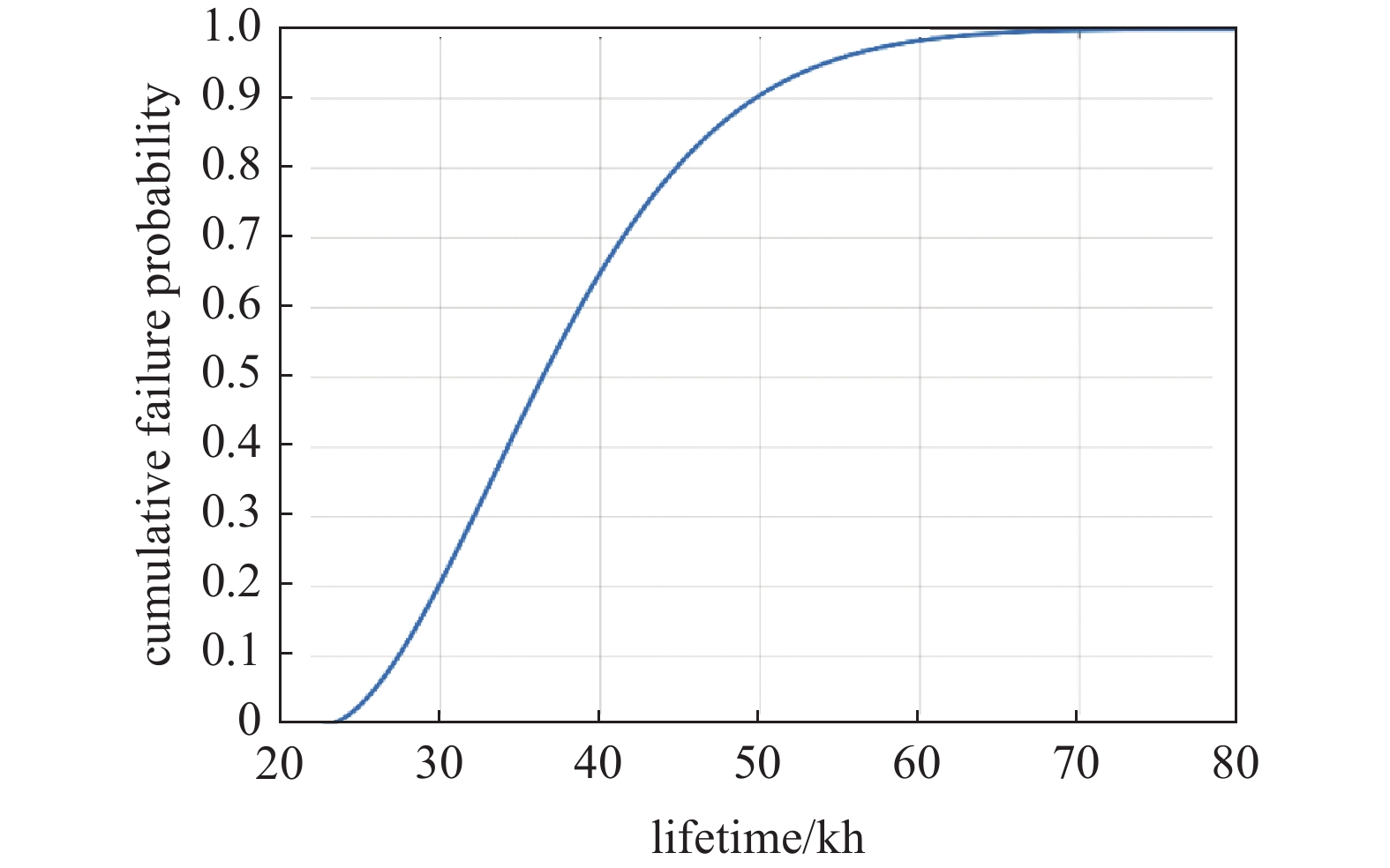
威布尔描述如式(7)所示,累计失效概率函数如图6所示。
形状参数
$ \beta $ 为$ 1.777 $ ,表示故障率明显随着时间增加,与发射体不断消耗直至失去电子发射能力的事实相符。进一步计算特定失效概率下的推力器寿命,如表2所示,当工作到44.76 kh的时候,发射体有80%的概率失效。 -
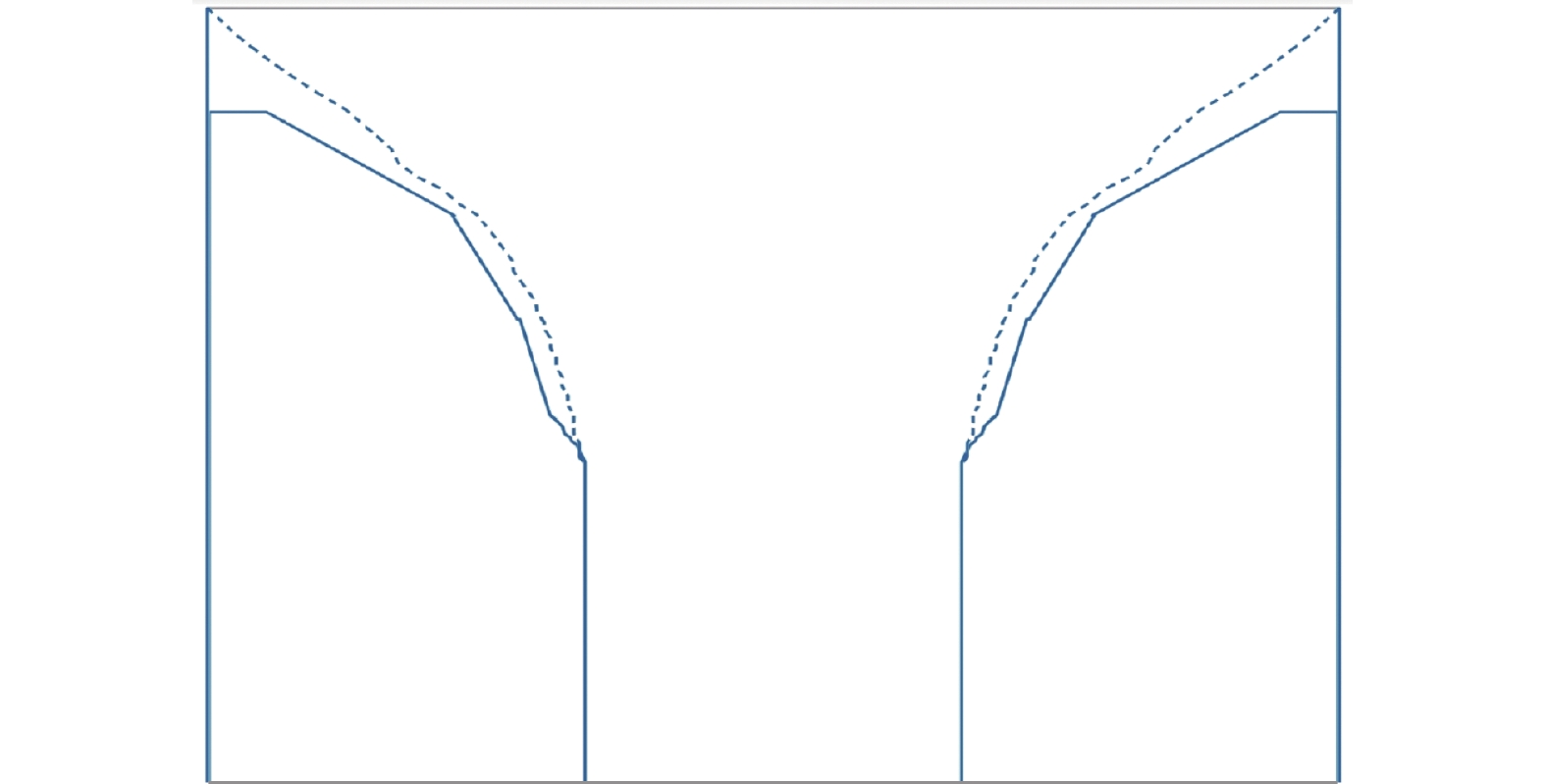
在基本模型发射体寿命23 kh相比,更改失效判据后,寿命扩展模型计算所得的寿命明显提高,约为41.3 kh,提高了将近80%。两种失效判据下,即基础模型和扩展模型中,发射体寿命终结时的形态对比图如图7所示,其中,虚线是基本模型发射体耗尽失效后的形态,实线是扩展模型中发射体失效后的形态,从图中可见,发射体寿命的延长是由于发射体体积的进一步消耗,在寿命扩展模型中,发射体在顶层消耗结束之后进一步消耗发射体下游顶端的高温区域,使得发射体寿命得以延长。
-
空心阴极发射体失效基本模型中计算得到空心阴极可靠度[15]表达式如式(8)所示:
基于当前航天任务对LIPS-300离子推力器15 kh的工作需求和未来航天任务对LIPS-300离子推力器25 kh的工作需求,分别计算空心阴极发射体失效基本模型和扩展寿命模型在工作15 kh及25 kh后的可靠度。其中,
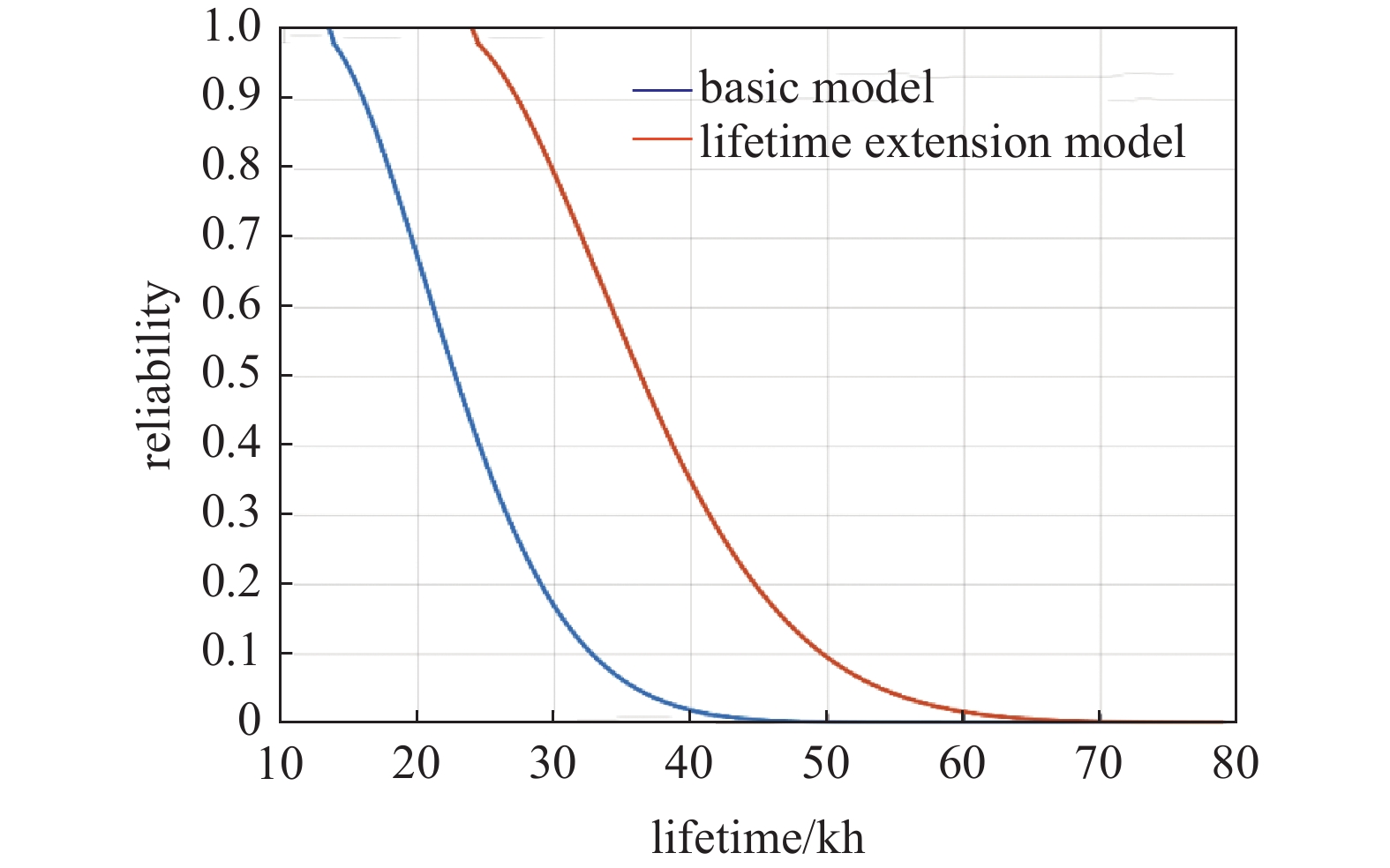
$ {P}_{1} $ 为基本模型中空心阴极的可靠度,$ {P}_{2} $ 为扩展模型中空心阴极的可靠度。计算结果如式(9)~(12)所示。计算结果表明,在基础模型中,空心阴极完成15 kh任务的可靠度为0.945,完成25 kh任务的可靠度为0.377;在扩展模型中,空心阴极完成15 kh任务的可靠度为1,完成25 kh任务的可靠度为0.969,在同样时长的任务需求下,扩展模型中空心阴极的可靠度显著高于基础模型中空心阴极的可靠度。进一步分析不同工作时间下基本模型和扩展模型的可靠度,其结果如表3所示。同时绘制了两种模型中可靠度随工作时间的关系,如图8所示。
由此可见,对于基本模型而言,在前12.5 kh内,空心阴极可靠性较好;对于扩展模型而言,在前22.6 kh内,空心阴极可靠性较好,这一阈值反应在位置参数的差异上。在12.5 kh之后,随着工作时间的增加,相同工作时间下,寿命扩展模型的可靠度明显增加,但两种模型中空心阴极的可靠度均出现不同程度的下降,曲线的下降速率反应在形状参数
$ \beta $ 的差异上。与基本模型相比,扩展模型中的形状参数$ \beta $ 并无明显变化。此外,2.1节中对各输入参数的敏感度及不确定度分析表明,模型中对温度最大的几个因素分别为$ {T}_{10} $ 、$ \varphi $ 、$ { \Delta T}_{1} $ 、$ { \Delta T}_{2} $ ,可见温度分布对空心阴极可靠度有重要影响(此处不考虑参数B、C、D的影响,此三个参数通过拟合得到,可以通过更换拟合函数或者进一步缩小其不确定度来降低拟合参数对空心阴极可靠度的影响)。此外,通过控制变量,将扩展模型中三个温度输入参数视为固定值,即不考虑$ {T}_{10} $ 、$ { \Delta T}_{1} $ 、$ { \Delta T}_{2} $ 的不可靠度,重新计算了空心阴极累计失效概率的表达式,如式(13)所示:形状参数的变化进一步证明了温度分布对离子推力器的可靠性影响,位置参数的显著增大表明减小温度分布的不确定度可以使得推力器在工作初期可靠度显著提升,因此,减小温度分布的不确定度是提高推力器可靠性的重要途径。
-
本文针对兰州空间技术物理研究所研制的LaB6空心阴极,在之前研究中提出的LaB6空心阴极工作在额定发射电流下时发射体寿命预测基本模型基础上提出了一种寿命扩展模型,即在基本模型的基础上发射体进一步消耗下游顶层高温区域,直至具顶层1 mm处径向消耗90%。由于发射体体积进一步消耗,利用寿命扩展模型计算发射体寿命约为41.3 kh,较基本寿命模型中计算寿命得到的23 kh来说有较大提高,可靠度也有明显提高。通过对扩展模型中输入参数中温度变量进行控制,比较分析了温度参数取固定值和非固定值情况下形状参数
$ \beta $ 、位置参数γ的变化,发现发射体的温度分布对发射体寿命有很大影响,通过进一步优化温度分布,可以进一步提高空心阴极的可靠度。
LaB6空心阴极发射体失效的拓展寿命模型及可靠性定量评估
Reliability Quantitative Evaluation of LaB6 Hollow Cathode Based on a Lifetime Extension Model under Insert Depletion Failure Mode
-
摘要: 空心阴极的寿命是制约离子推力器寿命及可靠性的关键因素之一,而发射体殆尽失效又是制约空心阴极寿命及可靠性的关键因素。在前面工作中,已建立了LaB6空心阴极工作在额定发射电流下时发射体的损耗过程及工作寿命预测模型,文章在此寿命预测模型的基础上提出了一种发射体寿命扩展模型,即发射体进一步消耗发射体下游顶端高温区域,利用扩展模型重新计算了发射体耗尽失效模式下空心阴极的寿命,并用威布尔统计规律及分析方法定量分析了空心阴极的可靠性,较基本模型而言,扩展模型中空心阴极的寿命及可靠性均得到明显提升。并且发射体温度分布对发射体寿命及可靠性有重要影响。Abstract: Hollow cathode’s lifetime is one of the key factors restricting ion thruster’s lifetime and reliability, and insert depletion is the key factor restricting hollow cathode’s lifetime and reliability. In the previous work, an insert consumption model and lifetime prediction method under rated emission current are established. Based on that model, this paper proposes an insert lifetime extension model, in which the emitter further consumes the high-temperature region around the downstream top area. Hollow cathode’s lifetime is predicted based on the new model and under insert depletion failure mode, and the Weibull distribution method is used to give the quantitative evaluation of hollow cathode reliability. Compared with the basic model, the lifetime and reliability of the hollow cathode in the extended model were significantly improved. And the temperature distribution of the emitter plays an important role.
-
Key words:
- Hollow cathode /
- LaB6 /
- Life prediction /
- Weibull distribution /
- Quantitative reliability evaluation .
-

-
图 2 模型中工作15 kh之后发射体形态与寿命试验15kh之后发射体形态对比。(a) 模型中工作15 kh之后发射体形态, (b) LIPS-200推力器寿命试验15 kh之后发射体形态
Figure 2. Comparison of the insert shape after working for 15000 hours of the model and experiment. (a) Insert shape after working for 15000 hours in the model, (b) insert shape after working for 15000 hours in experiment
表 1 寿命模型的参数及其敏感度和不确定度
Table 1. Parameter and the sensitivity and uncertainty for the lifetime in the model
输入参数 额定值 参数不确定度 敏感度 寿命不确定度/k $ \varphi $ 2.66/eV ±0.01/eV 507.5693 kh/eV 5.076 $ {\varphi }_{S} $ 0.05/eV ±0.0025/eV −507.5693 kh/eV 1.269 $ {T}_{10} $ 1923/K ±20/K −0.7928 kh/K 15.857 $ { \Delta T}_{1} $ 30/K ±5/K 0.6068 kh/K 3.034 $ { \Delta T}_{2} $ 48/K ±5/K 0.3621 kh/K 1.810 R 4.5/mm ±0.1/mm 13.7652 kh/mm 1.377 r 1.5/mm ±0.1/mm −13.7652 kh/mm 1.376 D 66.26/ $ ({\rm{c}\rm{m}}^{2}/\rm{A}) $ ±3.313/ $ ({\text{μm}}/\rm{k}\rm{h}) $ −1.5659 $ \text{kh}/({\text{μm}}/\rm{k}\rm{h}) $ 5.188 B 0.02477/ $ ({\text{μm}}/\rm{k}\rm{h}) $ ±0.00124/ $ ({\rm{c}\rm{m}}^{2}/\rm{A}) $ −3317.5 $ \text{kh}/({\rm{c}\rm{m}}^{2}/\rm{A}) $ 3.981 C −88.66/ $ ({\text{μm}}/\rm{k}\rm{h}) $ ±4.433/ $ ({\text{μm}}/\rm{k}\rm{h}) $ −0.7045 $ \text{kh}/({\text{μm}}/\rm{k}\rm{h}) $ 3.123 表 2 特定失效概率下推力器寿命
Table 2. Thruster’s lifetime under specific cumulative failure probability
累计失效概率 寿命/(kh) 0.001 22.93 0.05 25.77 0.1 27.37 0.5 36.39 0.8 44.76 表 3 特定工作时间下两种模型的可靠度
Table 3. Thruster’s reliability under specific working time
工作时间/kh 基本模型可靠度 扩展模型可靠度 10 1 1 15 0.927 1 20 0.677 1 25 0.385 0.969 30 0.171 0.795 35 0.059 0.563 40 0.016 0.351 -
[1] Zhang T P,Zhang X E. Application practices and realizations of the ion electric propulsion on spacecraft[J]. Vacuum and Cryogenics,2019,25(2):73−81 (张天平,张雪儿. 离子电推进的航天器应用实践及启示[J]. 真空与低温,2019,25(2):73−81(in chinese) Zhang T P, Zhang X E. Application practices and realizations of the ion electric propulsion on spacecraft[J]. Vacuum and Cryogenics, 2019, 25(2): 73-81 (in chinese) [2] Chien K R, Hart S L, Tighe W G, et al. L-3 communications ETI electric propulsion overview[C]//Proceedings of the 29th International Electric Propulsion Conference, Princeton: Princeton University, 2005 [3] Kajiwara K, Ikeda M, Kohata H, et al. ETS-Ⅷ ion engine and its operation on orbit[C]//31st International Electric Propulsion Conference, Ann Arbor: University of Michigan, 2009 [4] Killinger R, Leiter H, Kukies R. RITA ion propulsion systems for commercial and scientific applications[C]//43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference Exhibit, Cincinnati: AIAA, 2007 [5] Chen J J,Zhang T P,Jia Y H,et al. Numerical study on lifetime of LIPS-300 ion thruster ion optics[J]. Journal of Solid Rocket Technology,2016,39(1):44−49 (陈娟娟,张天平,贾艳辉,等. LIPS-300离子推力器双栅极寿命的数值分析[J]. 固体火箭技术,2016,39(1):44−49(in chinese) Chen J J, Zhang T P, Jia Y H, et al. Numerical study on lifetime of LIPS-300 ion thruster ion optics[J]. Journal of Solid Rocket Technology, 2016, 39(1): 44-49 (in chinese) [6] Van Noord J L, Kamhawi H, McEwen H K. Characterization of a high current, long life hollow cathode[C]//29th International Electric Propulsion Conference, Princeton: Princeton University, 2006 [7] Yim J T, Soulas G C, Shastry R, et al. Update of the NEXT ion thruster service life assessment with post-test correlation to the long duration test[C]//Proceedings of the 35th International Electric Propulsion Conference, Atlanta, Georgia: Georgia Institute of Technology, 2017 [8] Clark S, Randall P, Lewis R, et al. BepiColombo-solar electric propulsion system test and qualification approach[C]//Proceedings of the 36th International Electric Propulsion Conference, Vienna, Austria: University of Vienna, 2019 [9] Brophy J R, Polk J E, Randolph T M, et al. Lifetime qualification of electric thrusters for deep-space missions[C]//Proceedings of the 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Hartford, CT: AIAA, 2008 [10] Evans J W, Johnson R A, Green D W. Two-and three-parameter weibull goodness-of-fit tests[R]. Madison: United States Department of Agriculture, 1989 [11] Raju G, Katebian A, Jafri S Z. Application of Weibull distribution for high temperature breakdown data[C]//Proceedings of 2001 Annual Report Conference on Electrical Insulation and Dielectric Phenomena, Kitchener, ON, Canada: IEEE, 2001 [12] Lambrigger M. Alternative scaling of cumulative Weibull failure probability distribution functions[J]. Journal of Materials Science Letters,1997,16(19):1537−1539 doi: 10.1023/A:1018539611942 [13] Carrasco J M F,Ortega E M M,Cordeiro G M. A generalized modified Weibull distribution for lifetime modeling[J]. Computational Statistics & Data Analysis,2008,53(2):450−462 [14] Shimokawa T,Liao M. Goodness-of-fit tests for type-I extreme-value and 2-parameter Weibull distributions[J]. IEEE Transactions on Reliability,1999,48(1):79−86 doi: 10.1109/24.765931 [15] Li X,Zhang T P,Zhang X E. Lifetime prediction and reliability quantitative evaluation of LaB6 hollow cathode under cathode insert depletion failure mode[J]. Vacuum and Cryogenics,2023,29(4):392−398 (李璇,张天平,张雪儿. LaB6空心阴极发射体失效的工作寿命预测及可靠性定量评估[J]. 真空与低温,2023,29(4):392−398(in chinese) doi: 10.3969/j.issn.1006-7086.2023.04.010 Li X, Zhang T P, Zhang X E. Lifetime prediction and reliability quantitative evaluation of LaB6 hollow cathode under cathode insert depletion failure mode[J]. Vacuum and Cryogenics, 2023, 29(4): 392-398 (in chinese) doi: 10.3969/j.issn.1006-7086.2023.04.010 [16] Capece A M,Polk J E,Shepherd J E. Decoupling the thermal and plasma effects on the operation of a xenon hollow cathode with oxygen poisoning gas[J]. IEEE Transactions on Plasma Science,2015,43(9):3249−3255 doi: 10.1109/TPS.2015.2465845 [17] Becatti G,Goebel D M,Polk J E,et al. Life evaluation of a lanthanum hexaboride hollow cathode for high-power Hall thruster[J]. Journal of Propulsion and Power,2017,34(4):893−900 [18] Ortega A L, Mikellides I G, Goebel D M. Numerical simulations for life assessments of the BaO and LaB6 cathode options in the Hall effect rocket with magnetic shielding (HERMeS)[C]//Proceedings of the 35th International Electric Propulsion Conference, Atlanta, GA: Georgia Institute of Technology, 2017 [19] Jie F, Liu M Z, Tang F J, et al. Destructive evaluation of a xenon hollow cathode after 15, 000 hour life test[C]//International Astronautical Congress, 2019 [20] Katz I, Polk J E, Mikellides I G, et al. Combined plasma and thermal hollow cathode insert model[C]//Proceedings of the 29th International Electric Propulsion Conference, 2005 [21] Katz I, Mikellides I G, Goebel D M. Model of the plasma potential distribution in the plume of a hollow cathode[C]//Proceedings of the 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Fort Lauderdale, Florida: AIAA, 2004 [22] Mikellides I G, Goebel D M, Snyder J S, et al. Neutralizer hollow cathode simulations and validation with experiments[C]//Proceedings of the 45th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Denver, Colorado: AIAA, 2009 [23] Mikellides I G, Katz I, Goebel D M, et al. Theoretical model of a hollow cathode insert plasma[C]//Proceedings of the 40th AIAA/ASME/SAE/ASEE Joint Propulsion Confe-rence and Exhibit, Fort Lauderdale, Florida: AIAA, 2004: 3817 [24] Mikellides I G, Katz I, Goebel D M, et al. Theoretical modeling of a hollow cathode plasma for the assessment of insert and keeper lifetimes[C]//Proceedings of the 41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Tucson, Arizona: AIAA, 2005: 4234 [25] 张世良,胡永年. 离子镀膜用长寿命阴极电子枪[J]. 真空与低温,1991,10(3):25−28 [26] Lin Z L. A study of LaB6 cathode is used in RF electron gun[J]. High Power Laser and Particle Beams,1997,9(4):591−595 (林祖伦. 射频电子枪中LaB6阴极的研究[J]. 强激光与粒子束,1997,9(4):591−595(in chinese) Lin Z L. A study of LaB6 cathode is used in RF electron gun[J]. High Power Laser and Particle Beams, 1997, 9(4): 591-595 (in chinese) [27] Helton J C. Quantification of margins and uncertainties: conceptual and computational basis[J]. Reliability Engineering & System Safety,2011,96(9):976−1013 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: