首页
登录
注册
-
大气压气体放电技术较传统的低气压气体放电技术而言因无需大尺寸昂贵的真空设备等优点，被广泛应用于材料表面改性、高质量薄膜合成以及刻蚀技术中[1-4]。在这些应用中，往往需要在追求较高的等离子体密度的同时，努力降低离子能量，以减少对介质材料或基底的损伤[5]。对此，大气压双频调制技术应运而生。因为其可以通过高低频电源的相互配合，可以单独控制等离子体的参数，更好地满足上述应用需求。因此，大气压双频调制技术也被更广泛的应用于工业、材料、医疗中[6-10]。
如今，国内外学者越来越重视将大气压气体放电与双频调制技术相结合[11-14]，并对此展开了大量的研究。王一男等[15]利用一维流体力学模型，对双频调制大气压He放电的特性进行讨论，结果表明，高频源电压及频率对放电特性的影响要大于低频源电压和频率；张仲麟等[16]利用一维自洽流体模型并耦合半动力学方法以Ar为工质探索了大气压双频介质阻挡放电频率组合对等离子体参数的影响，结果表明当双频间存在非线性协同效应并引起耦合增益时，鞘层位置的电子碰撞激发数明显减小，但激发强度更强；Liu等[17]利用一维流体力学模型对大气压双频容性耦合He放电进行研究，发现等离子体中的电子主要由高频电场加热，而在等离子体鞘层中的电子则分别由低频电场和直流电场加热和冷却。Neill等[18]采用基于流体动力学方程和电子半动力学处理的多尺度数值模型，研究了双频激励对射频驱动大气压等离子体He/N2中有效电子能量分布函数(EEDF)的影响，研究发现功率密度、电压比和相位关系的变化提供了对电子密度和平均电子能量的单独控制。Jiang等[19]利用四极杆质谱仪研究了Ar/O2混合气体放电的离子能量分布和平均能量，结果表明随着低频功率的增加，鞘层电位增大，离子通过鞘层获得更高的能量，高能峰向高能区移动，能量宽度增大。综上可以看出，尽管国内外学者对大气压双频调制技术已经有一定的研究，但是对其反应器以及气体的选择也各有不同，其中容性耦合反应器因其设计简单，调节方便，放电均匀而更被认可[20-21]。
在大气压射频容性耦合等离子体放电中，主要存在三种电子加热模式：电子温度较高但电压较低，并且等离子体密度虽然随着电压增加而变化但增幅较小时，称这种放电模式为α模式放电；当气体为电负性气体时，电子从漂移电场和双极电场中获得能量使等离子体区和鞘层边界处的电子与中性粒子频繁发生碰撞的放电模式为DA（Drift-Ambipolar)模式；若电压较高时，电子温度较低，并且等离子体密度随电压的增加而增幅较大，则此时的放电模式为γ模式，其放电主要由二次电子维持。本文采用电压较小，故忽略二次电子发射效应，放电模式只存在α模式和DA模式[22-23]。
此外，Ar能够产生大量高能粒子并且作为惰性气体加入O2后变成含氧混合放电工作气体，可以生成许多活性粒子，其中较为常见的臭氧在医疗上常有消炎，抗氧化和镇痛的作用[24]，在环境保护上是有机废水污染物分子化学键断裂的关键粒子[25],可以降低循环冷却水的污染。综上，本文研究大气压双频容性耦合Ar/O2放电，重点关注双频源电压和频率对电子加热模式、等离子体密度、正离子总通量以及离子能量的影响，以期对工业应用有参考意义。
-
文中采用二维流体力学模型对Ar/O2放电进行研究，表1为模型中包含的粒子，模型中涉及的主要反应详见附录A，模型中的粒子j (电子、离子、中性粒子)的密度和通量分布通过连续性方程和动量守恒方程可以给出
式中
${n_{\rm{j}}}$ 与${{\varGamma }_{\rm{j}}}$ 分别为粒子j的密度和通量，${S_{\rm{j}}}$ 是粒子产生和损失项，即反应源项，${\mu _{\rm{j}}}$ 与${D_{\rm{j}}}$ 为粒子的迁移率及扩散系数(由文献[26-30]给出）。中性粒子不带电，因此不会受到电场作用，故其只有扩散项（漂移项为0）。离子因其质量很大，无法响应瞬时电场。因此引入有效电场
$ {E_{{\text{eff,i}}}} $ 来代替式(2)中电场，则式中
$ {\nu _{{\text{m,i}}}} = e{\text{/}}{m_{\text{i}}}{\mu _{\text{i}}} $ 表示离子的动量输运频率，$ {\mu _{\text{i}}} $ 是离子的迁移率，$ {m_{\text{i}}} $ 代表离子的质量。本文中的电子温度由如下能量守恒方程来计算
$ {{\mathbf{\varGamma }}_{\text{w}}} $ 代表电子的能流密度，$ {S_{\text{w}}} $ 表示电子与中性气体分子间碰撞引起的能量损失项，$ {D_{\text{e}}} $ 是电子的扩散系数。由于电子温度远大于离子和中性粒子的温度，故采用“冷流体”模型来描述离子及中性粒子的运动，令其温度等于背景气体温度，则无需求解能量守恒方程。最后，由泊松方程得出电势
$ \varphi $ 及瞬时电场E：$ {n_ + } $ 表示正离子密度、$ {\varepsilon _0} $ 为真空介电常数，$ {n_ - } $ ,$ {n_{\text{e}}} $ 分别表示负离子和电子密度。 -
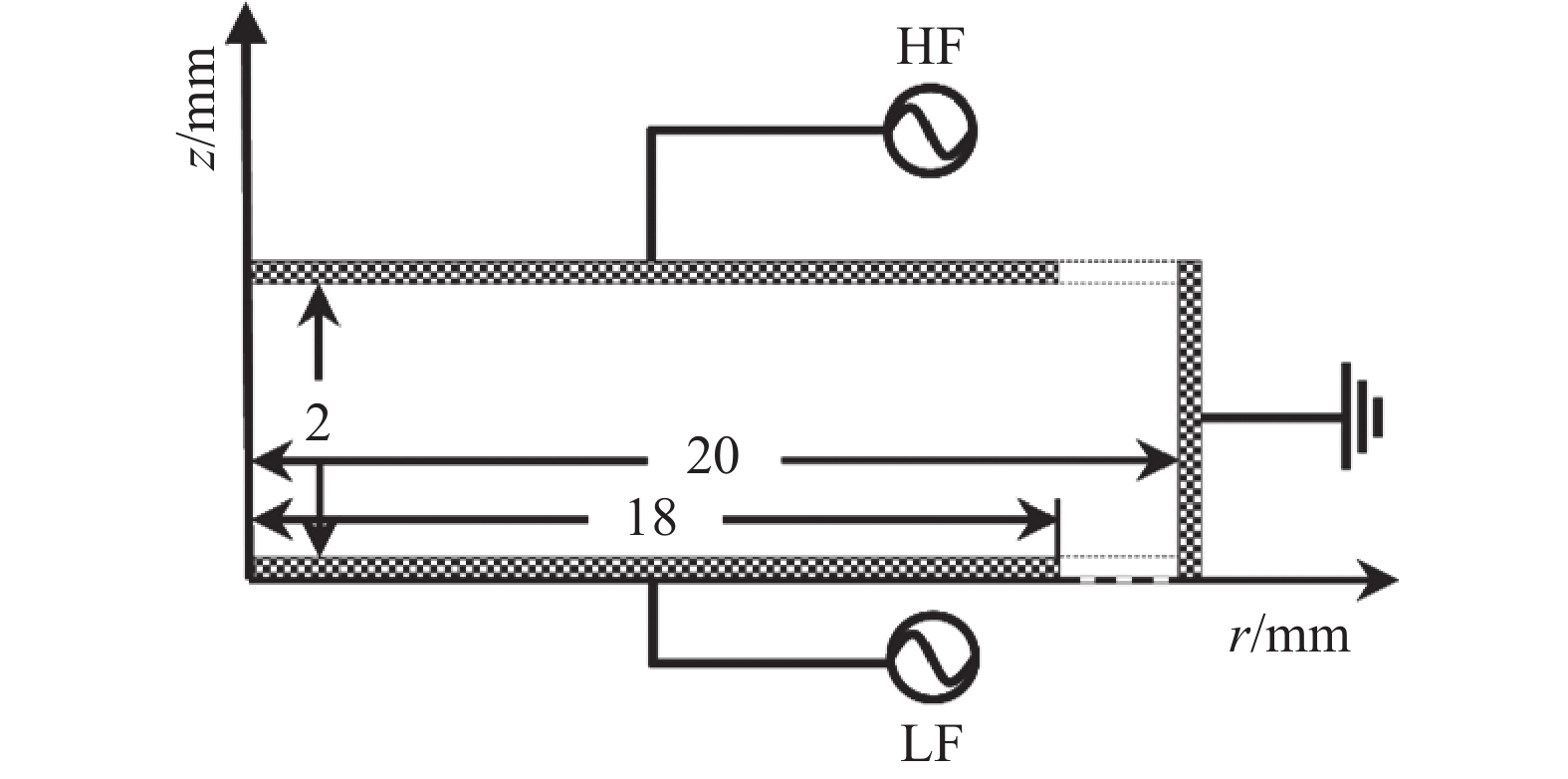
图1为本文采用的PECVD装置，其中上极板电压为
$ V = {V_{\text{H}}}\sin (\omega t) $ ，侧壁接地，下极板电压为$ V = {V_{\text{L}}}\sin (\omega t) $ ，电极与器壁间隙处的电压通过线性插值得出。当电子在极板和器壁处时，其通量为
式中
$ {u_{{\text{th,e}}}} $ 为电子的热运动速度，$ \Theta $ =0.25。能流密度当负离子在极板和器壁处时，其通量为0；正离子通量在极板和器壁处连续。中性粒子在极板和器壁处的通量为
$ {u_{{\text{th,n}}}} $ 为中性粒子热运动速度，$ {s_{\text{n}}} $ 为粘附系数。本文借助于粘附系数来近似复杂的表面反应过程（如溅射、复合以及氧化）。在表面反应过程中，假定气体分子碰到器壁后会反射回原气体中，所以设其粘附系数为0；当激发态粒子在器壁处变为去激发态时，其粘附系数设为1；其余自由基粒子粘附系数由文献[31-33]给出。 -
本文利用二维流体力学模型研究双频容性耦合Ar/O2放电特性，重点讨论高频源频率为13.56 MHz时，高低频电压及低频源频率对电子加热模式、电子和中性粒子密度、正离子能量及总通量的影响。根据稳定性条件，设时间步长为3.7×10−11 s，该模型计算了3000个周期，相邻周期等离子体密度几乎不变，基本达到稳定。
-
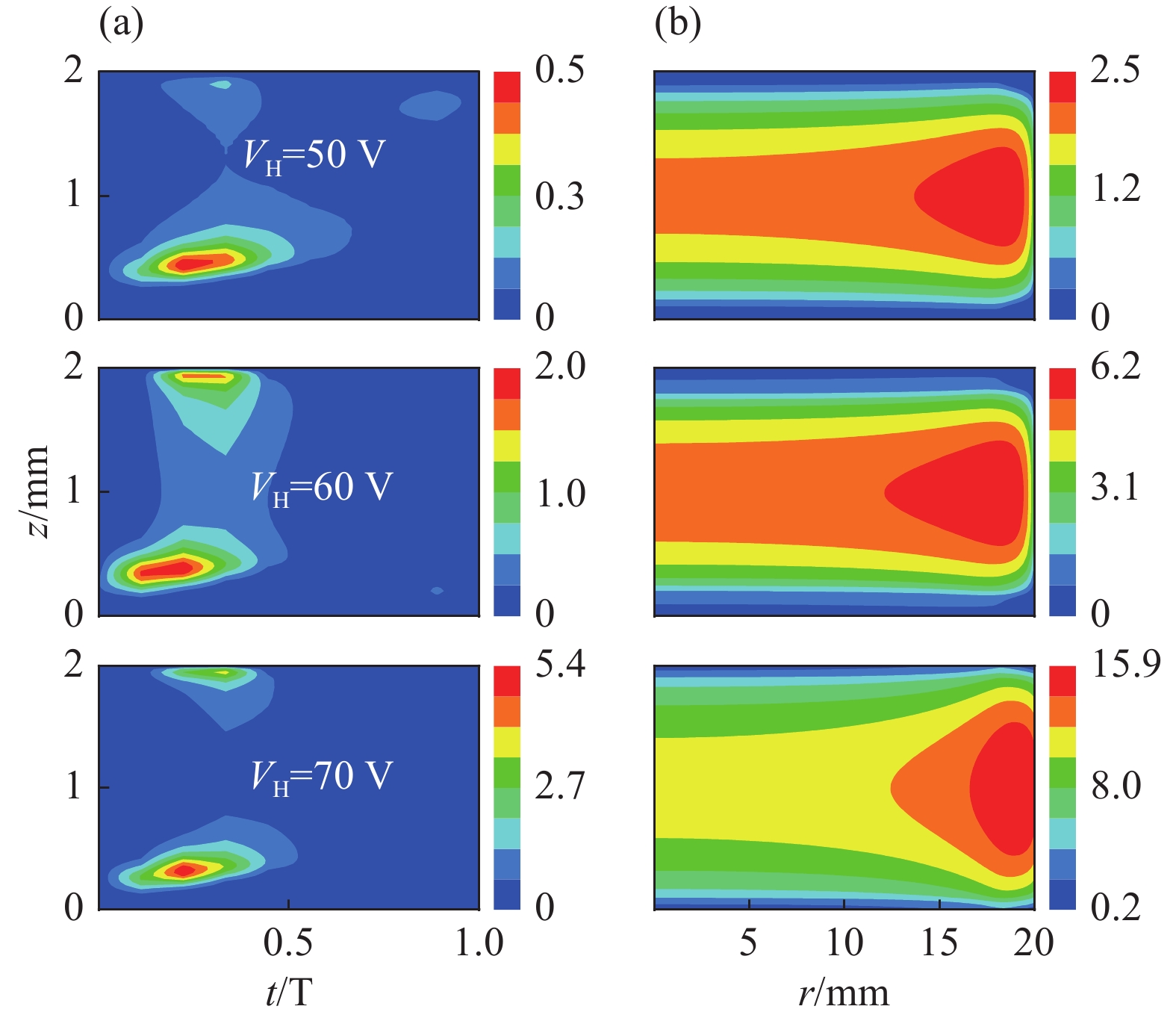
本文首先保持低频源频率fL =40 kHz与低频源电压VL=70 V不变，对不同高频源电压VH（50, 60, 70 V）体系的放电进行了模拟。图2给出了不同高频源电压下电离率的时空分布图和电子密度的空间分布，由图2(a)可以看出，当VH=50 V时，该体系放电由α模式主导，此时DA模式虽然存在，但其强度较低；随着高频源电压不断上升，其DA 模式强度也在逐渐增大，但放电模式依旧为混合模式。然而，当高频源电压VH继续增大到70 V时，DA 模式在总电离率中的占比却随之降低，总电离率仍保持上升趋势；
图2(b)给出了不同高频源电压下电子密度的空间分布，可以看出，等离子体区电子密度明显高于鞘层区密度，在侧壁附近密度取得最大值，出现明显的边缘效应。同时，随着高频源电压的增加，电子密度迅速上升，且边缘效应愈加明显。这是由于随着高频源电压的升高，其随机加热速率增强，导致生成了更多的高能电子，电离碰撞增强，因此电离率增大，电子密度升高。同时，高频源电压增大导致极板边缘处的电场得到增强，提高了电子的加热速率，使电极边缘处等离子体密度升高，边缘效应增强。
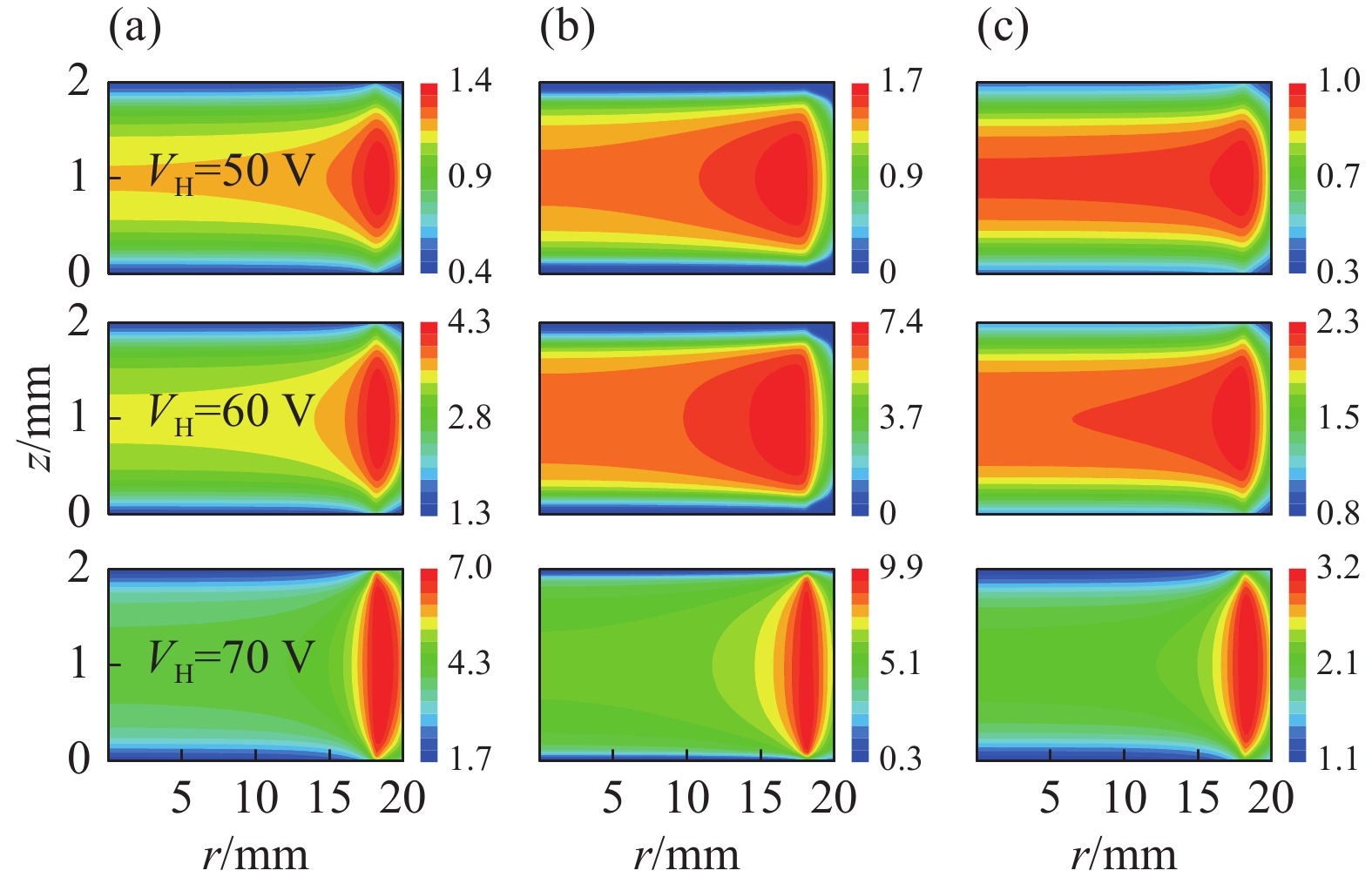
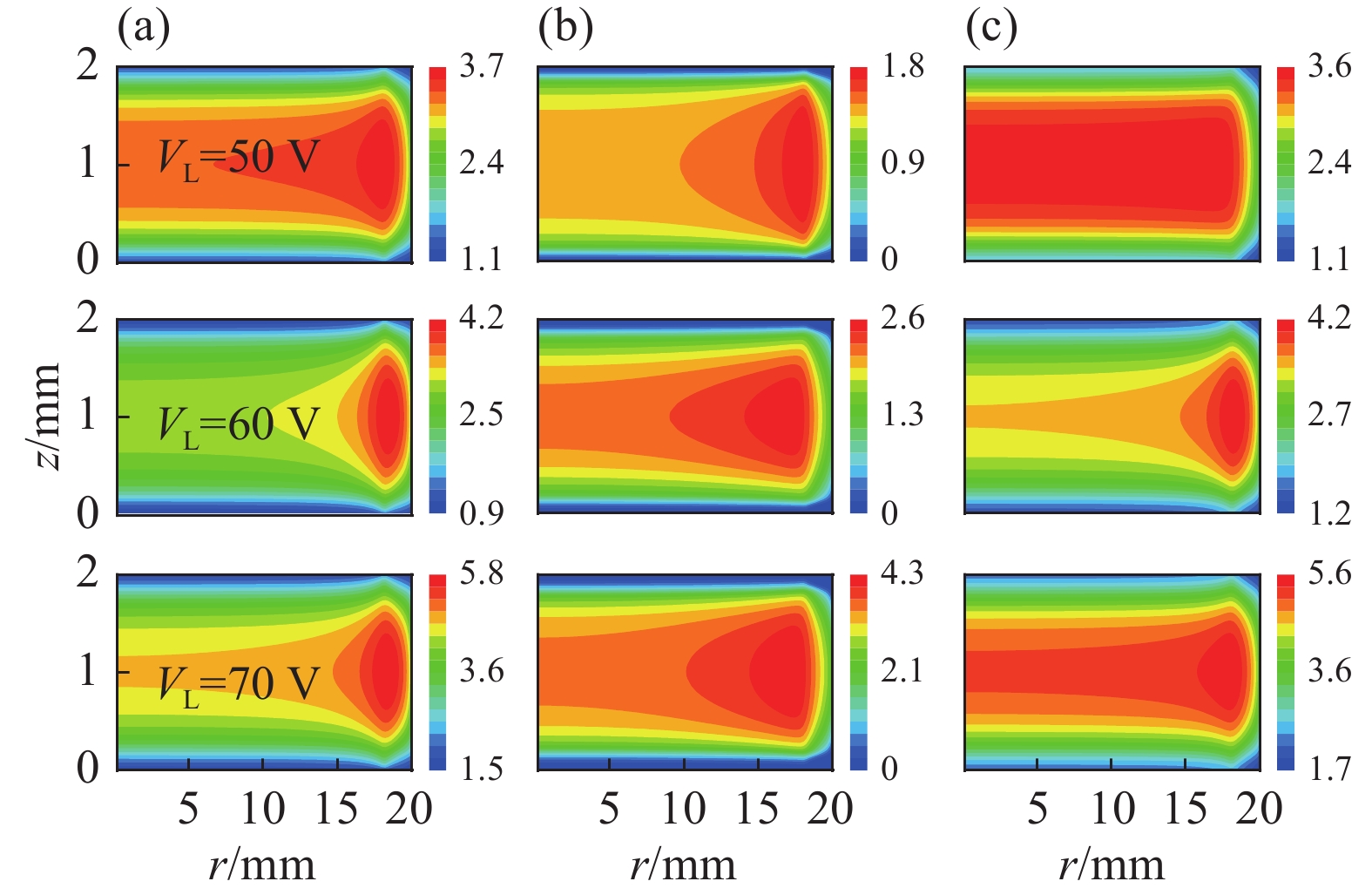
在大气压Ar/O2放电反应生成的诸多粒子中，中性粒子基态氧原子O、激发态氧原子O(1D)、臭氧O3等活性粒子被公认为在一些生物医学、工业生产、环境治理等方面有着重要作用（如：消毒、做强氧化剂、除臭和缓蚀等），通常是学者关注的重点。对此，本文也选取了这三种中性粒子，并给出了不同高频源电压下其密度的空间分布，如图3所示。可以看出，在同一高频源电压下，在这三种粒子中密度数值最大的为O粒子，其次为O3粒子，O(1D)粒子密度数值最小。同时，随着高频源电压的不断升高，这三种中性粒子的密度也随之增大，且在VH=70 V时均出现了明显的边缘效应。中性粒子密度这种变化是因为电子密度增大，电子和背景气体发生碰撞的概率增大，生成了更多的中性粒子。同时电子密度在VH=70 V时出现明显边缘效应也使得反应后生成的中性粒子也出现了边缘效应。
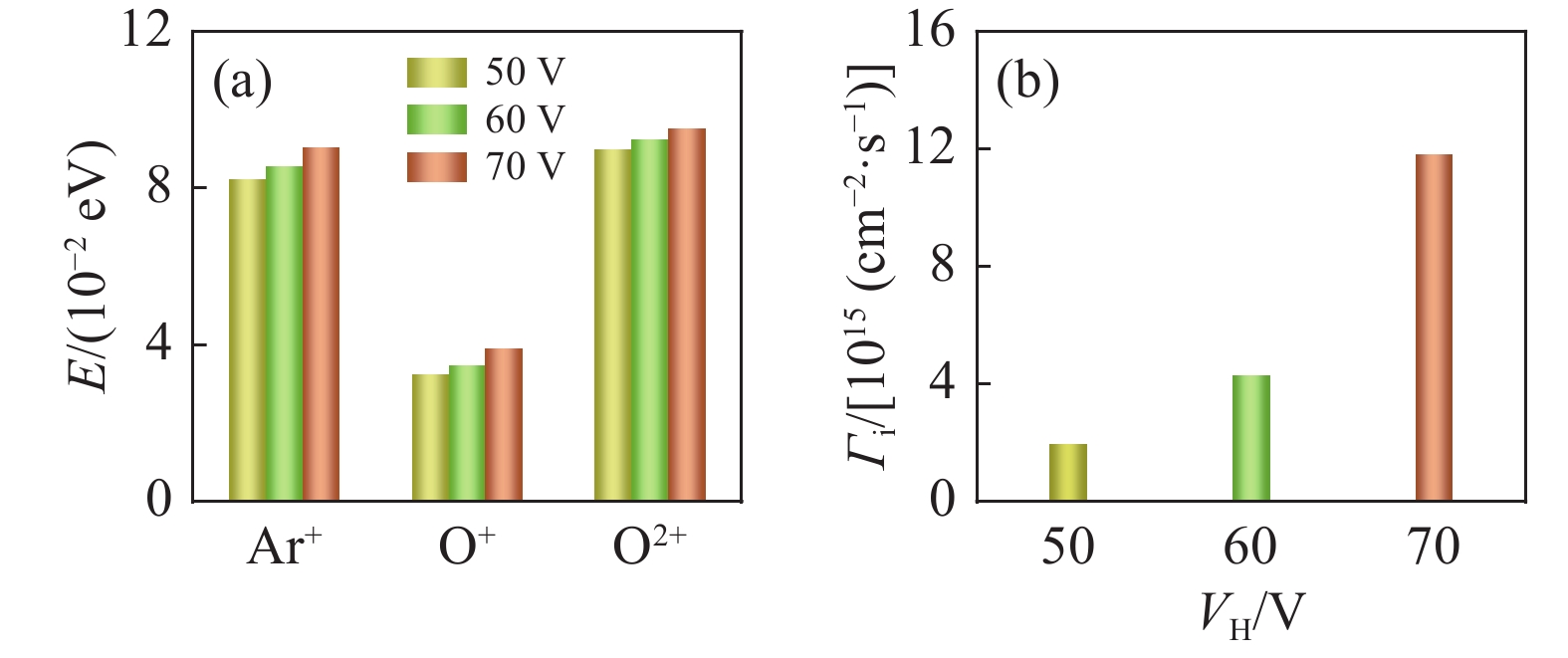
大气压Ar/O2放电等离子体也常被应用于半导体刻蚀等方面，在刻蚀技术中，离子能量往往受到了人们的重点关注。因为其大小对于是否会造成基片损伤起着决定性作用。对此，本文给出了不同高频源电压下下极板r=1 mm处主要正离子的能量变化图。由图4可以看出，在同一高频源电压下，O+的能量数值明显较小，而Ar+和O2+的能量相差不大。随着高频源电压的不断增加，三种正离子的能量均随之略微增大，且量级均在10−2 eV。离子能量的这种变化是因为随着高频源电压的增大，馈入功率变大，进而使得离子获得的能量逐渐升高，但与等离子体密度相比其变化幅度较小。
离子通量对电场、电导率均有着不同程度的作用，对此本文给出下极板r=1 mm处正离子总通量随高频源电压的变化图，可以看到总通量随着高频源电压的增大呈现出较明显的上升趋势，这是以下两方面导致的：一方面是高频源电压对离子的运动起到了加速作用，因此总通量会在高频源电压增大时随之升高；另一方面电子密度的不断增大也使得腔内电子与背景气体碰撞概率增大，导致更多的离子被生成，因此其通量增大。
综上，高频源电压主要对等离子体密度影响较大，但对离子能量产生的影响却较小。离子能量在刻蚀中起着重要的作用，为了进一步明晰大气压双频容性耦合等离子体放电特性，本文在此基础上进一步考虑了低频源电压和频率对放电参数的影响。
-
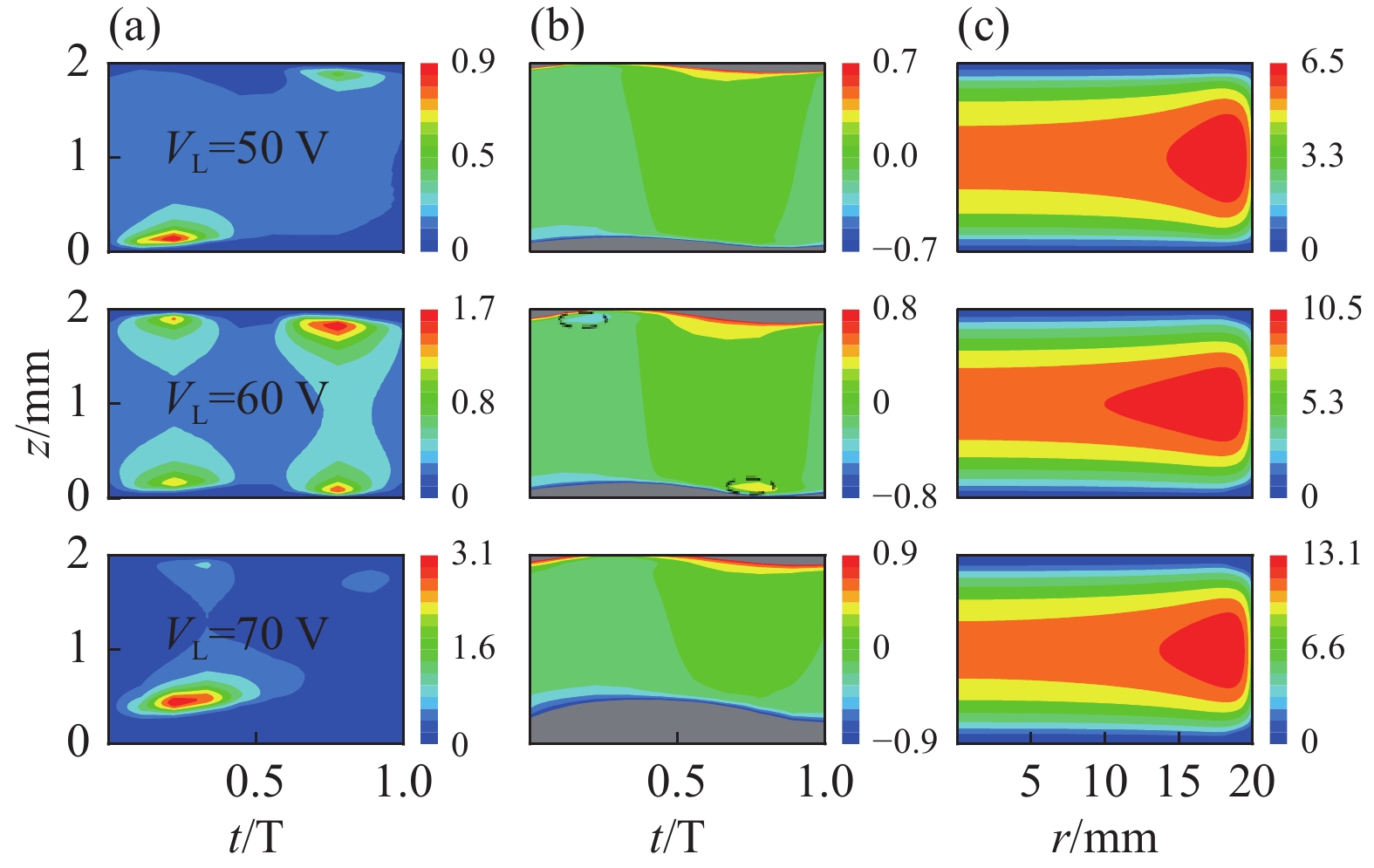
为了探究低频源电压对放电的影响，保持低频源频率fL=40 kHz、高频源电压VH=45 V不变，仅改变低频源电压 VL（50，60，70 V）。图5给出了不同低频源电压下电离率和电场的时空分布图及电子密度的空间分布图。由图5(a)可以看出，当VL=50 V时，该放电模式为单一α模式；当低频源电压增加到60 V时，DA模式强度逐渐加强，该放电由α模式与DA模式共同维持；当VL增加到70 V时，DA模式减弱，α模式又重新占据主导地位。由图5(b）也可以看出，当VL=60 V时，电场中明显出现了双极电场（图中已标出），这恰好与图5(a)中出现DA模式现象是相符的，当VL=70 V时，双极电场明显减弱，再次与电离率图像相符，再次印证了上述对模式转变的讨论。
由图5(c)可以看出当低频源电压的升高时，电子密度线性增大。这种变化是因为低频电压的增加使得输入功率增加，馈入的能量增加，进而电离出更多的电子，因此电子密度随低频源电压的增加而增大。但与高频源电压相比，等离子体密度增大的幅度较小。
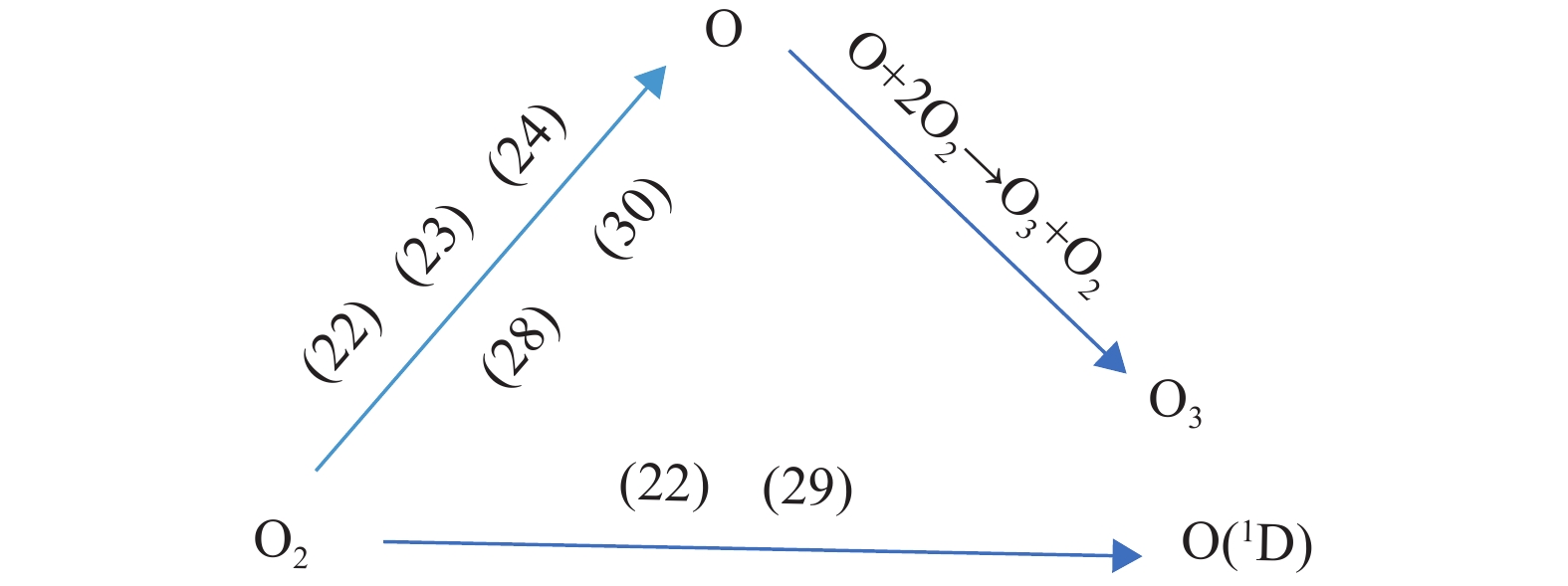
图6为不同低频源电压下O、O(1D)、O3的密度空间分布图，可以看出，随着低频源电压的增大，三种中性粒子密度均呈现出明显的上升趋势，这是因为电子密度的升高（如图5(c)）增大了电子和背景气体的碰撞概率。但值得注意的是，三种粒子中O与O3的量级明显大于O(1D)。这是由于从图7可以看出，O的主要产生项有五种（图中序号为附录A中反应）[34-37]，O(1D)的主要生成项仅有两种，并且产生O的能量阈值远小于O(1D)，因此在其他参数一致时，O的密度远大于O(1D)，而O为O3的主要产生项，因此O3的密度同样远大于O(1D)。O和O3在工业、医疗、环境处理等方面均有着重要作用，因此在实际应用中，可以考虑适当升高低频源电压，以制备更多的O3。
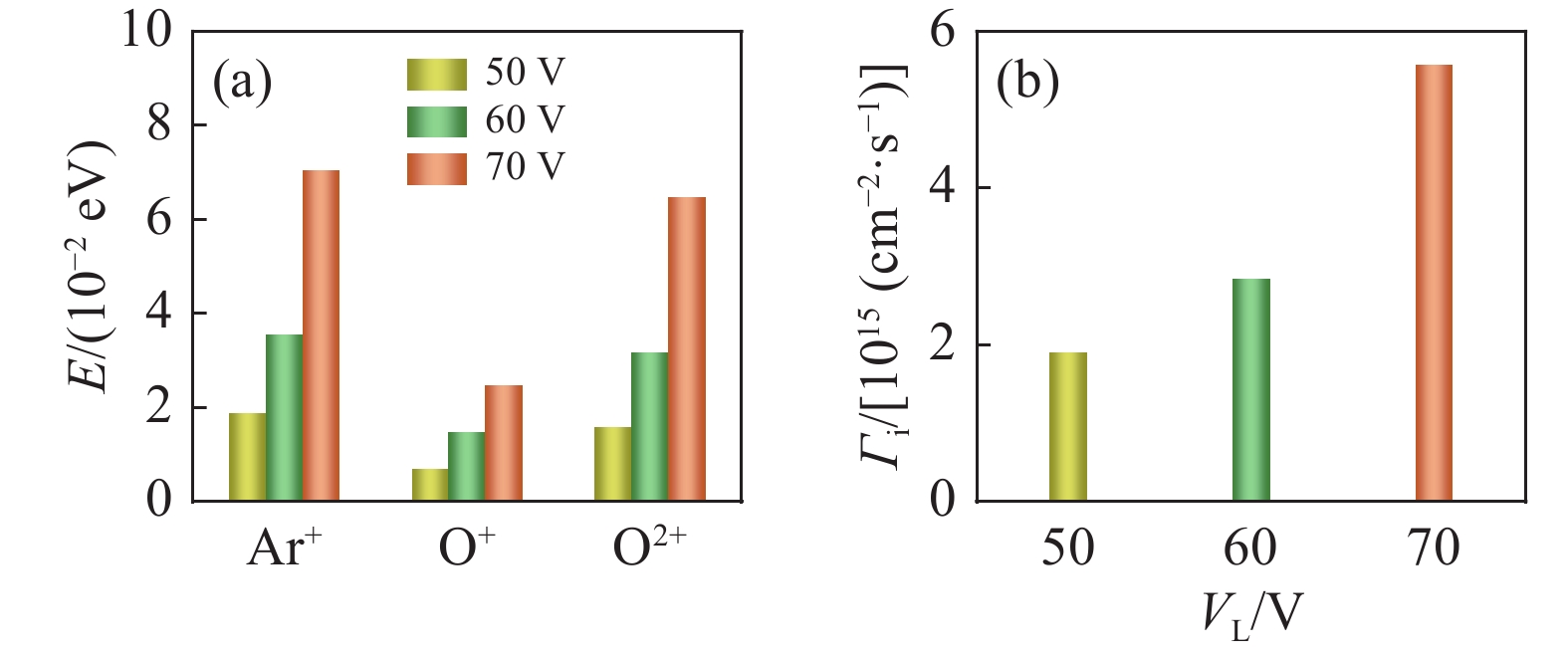
图8给出不同低频源电压下下极板r=1 mm处正离子能量和正离子总通量的变化情况。从图8(a)可以看出，所选三种正离子的能量在低频源电压增加时增幅较大，这说明低频源电压对离子能量影响很大。图8(b)为不同低频源电压下正离子总通量变化图，可以看到，随着低频源电压的增大，正离子总通量上升。这是因为离子通量主要是离子密度和离子速度发生变化导致的。由图5(c)可知，随着低频源电压的增加，电子密度呈现出增大的趋势，进而导致离子密度也随之增大；通过离子能量的变化可知离子速度随低频源电压的增加而增大，因此离子总通量随着低频源电压的升高而变大。值得注意的是，低频源电压的增加使得等离子体密度和离子能量均发生大幅度增大，这是因为改变低频源电压时发生了解耦现象。
-
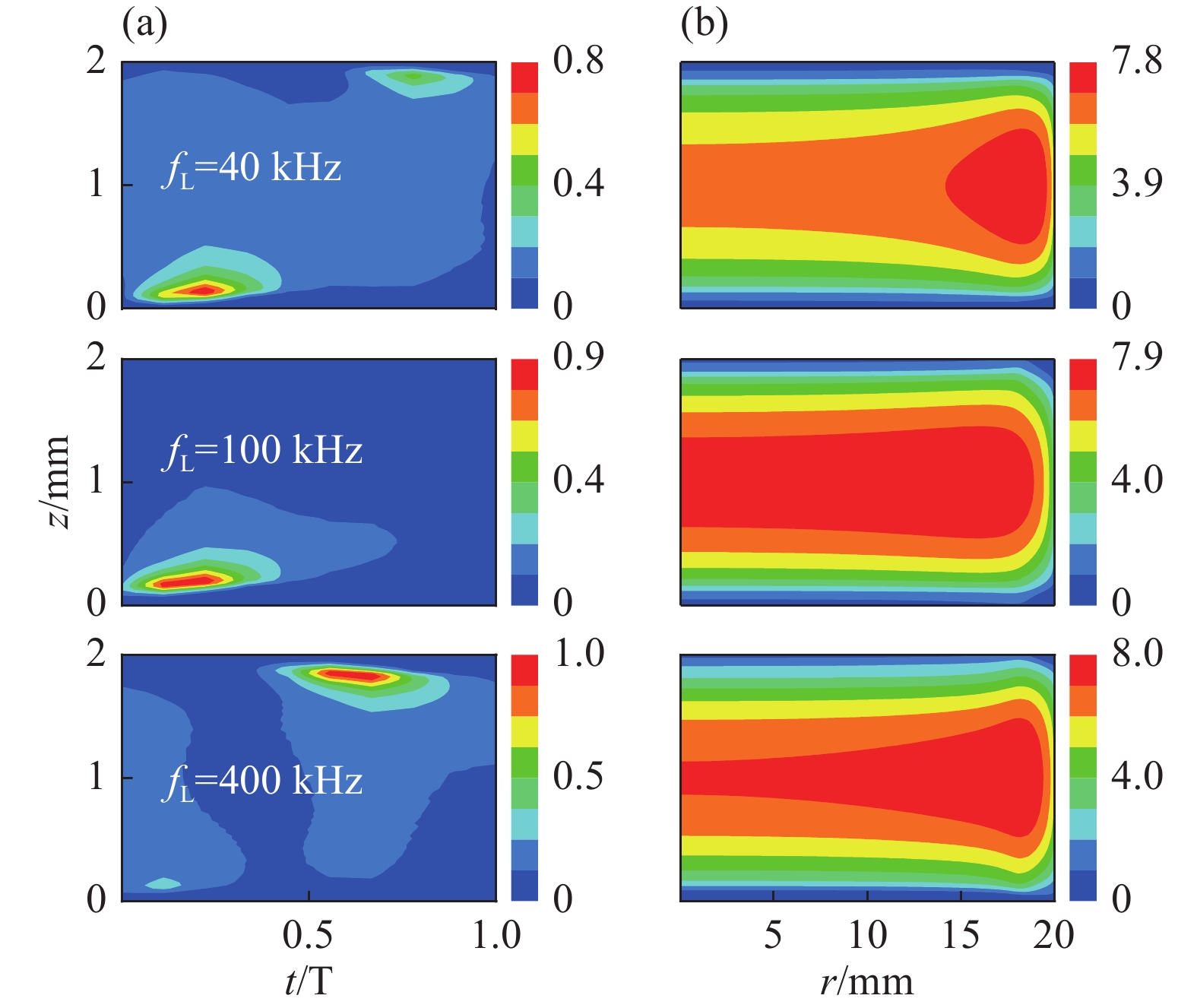
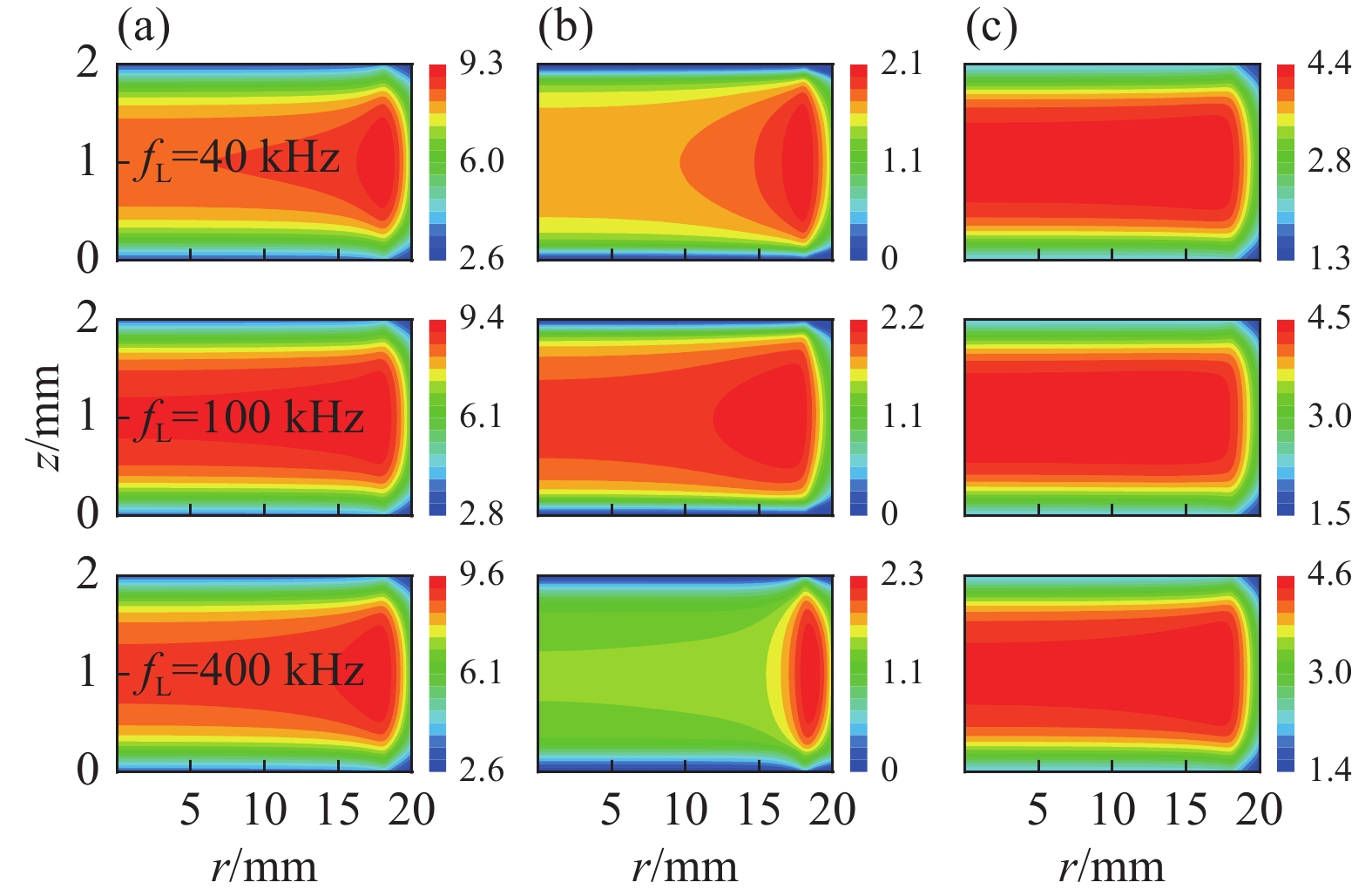
为了探究低频源频率对放电的影响，本文保持高频源电压VH =50 V，低频源电压VL=50 V不变，仅改变低频源频率 fL（40，100，400 kHz）。图9给出了不同低频源频率下电离率的时空分布图和电子密度的空间分布图。由图9(a)可以看出，该体系放电模式始终为单一的α模式，这意味着低频源频率对放电模式不产生影响。同时，在图9(b)中可以看出，当低频源频率增加时，电子密度也随之增大，但增幅较小。这说明低频源频率对电子密度几乎不产生影响。
图10给出了不同低频源频率下中性粒子密度的空间分布。可以看出，在同一低频源频率下，O(1D)生成的最少，O生成的最多，并且三种中性粒子的密度均随着低频源频率的增大而略微升高。这是因为随着低频源频率的增加，电子与背景气体碰撞频率增大，进而生成的中性粒子升高。同时，与图8相比也可以看出，低频源频率的变化对中性粒子密度的影响远小于低频源电压变化对中性粒子密度的影响，由此可知，要想改变中性粒子密度，可以选择低频源电压这一参数对其进行调控。
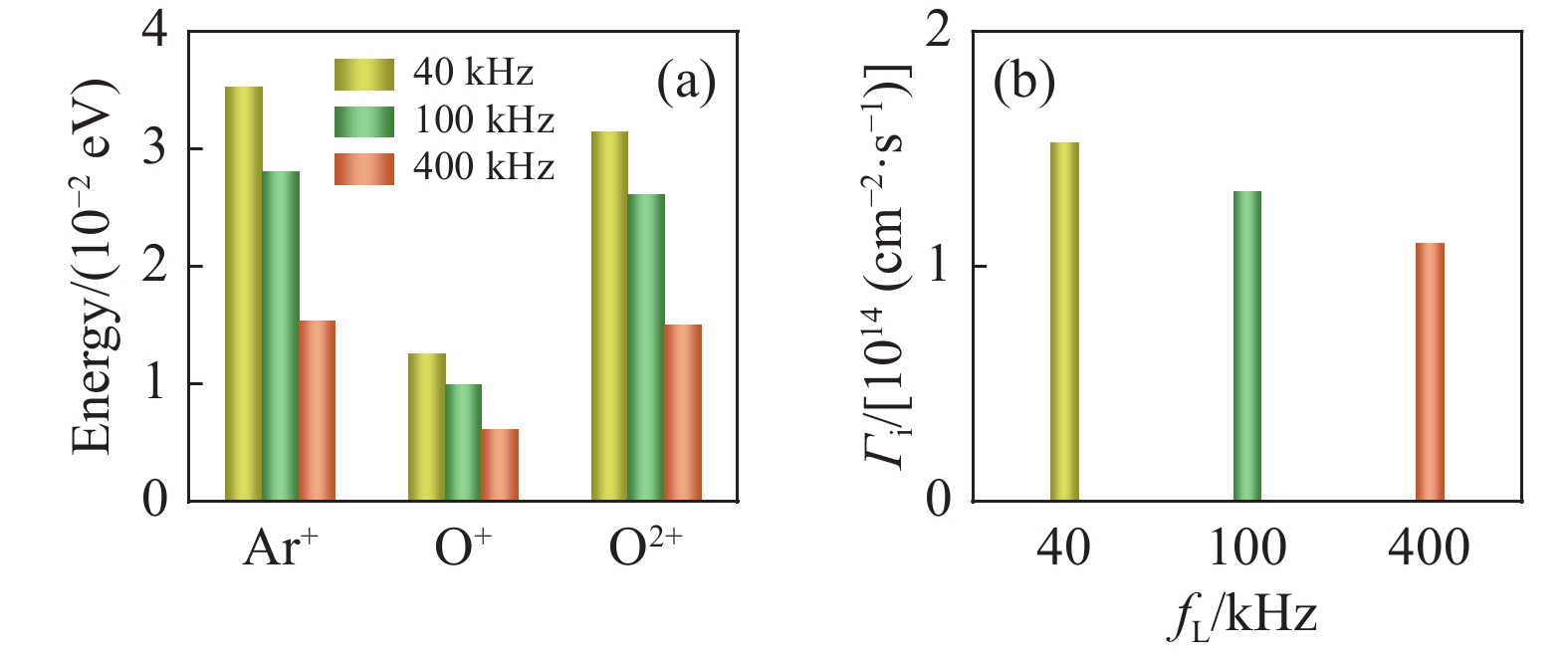
图11给出了不同低频源频率下下极板r=1 mm处正离子的能量图及正离子总通量变化图。由图可以看出，三种正离子的能量均随着低频源频率的增大而大幅下降，其中Ar+离子能量变化幅度尤为明显。这是因为低频源频率的增加，使得碰撞增多，离子能量损失增多，但输入功率不变，因此其离子能量随低频源的增大而减小。与此同时，正离子的总通量在随着低频源频率的增大而减小，这是因为离子通量由离子密度和离子速率来决定，离子能量随着低频源频率的增加而大幅度减小，而等离子体密度几乎不变，因此离子通量与离子能量均呈下降趋势。
-
本文利用二维流体力学模型对大气压容性耦合Ar/O2放电进行研究，重点关注高低频电压及低频源频率对电子加热模式、电子密度、中性粒子密度(O、O(1D)、O3)、离子能量及离子总通量的影响。结果表明：
(1)当改变高频源电压时，放电处于α和DA混合模式。电子密度、中性粒子密度以及正离子总通量均随着高频源电压的增加大幅度增大，但离子能量的增幅较小。在刻蚀工艺中常需要较小的离子能量和较高的离子通量，因此可以考虑适当增加高频源电压以达到工业生产的要求；
(2)当改变低频源电压时，电子加热模式由α模式转变为DA/α混合模式。电子密度、中性粒子密度、正离子总通量及离子能量均随着低频源电压的增加大幅度增大，产生了解耦现象；
(3)当改变低频源频率时，放电处于α模式。电子密度、中性粒子密度均随低频源频率的升高而略微升高，正离子总通量随低频源频率略微降低，但是离子能量降幅很大，符合刻蚀工业的需求。
综上所述，高频源电压和低频源频率的改变对刻蚀工艺是非常有意义的，一方面未发生模式转变现象；另一方面实现了等离子体密度和离子能量的单独控制。反之，低频源电压的改变对刻蚀工艺来说是应避免的，这是由于既发生模式转变现象又出现了解耦现象。
附录A
大气压双频容性耦合Ar/O2等离子体特性研究
The Characteristics of Ar/O2 Plasma with Dual Frequency Capacitive Coupling at Atmospheric Pressure
-
摘要: 文章利用二维流体模型对双频调制大气压Ar/O2放电特性进行了研究，着重讨论高低频电压、低频频率等不同匹配方式对等离子体参数的影响，并且通过对电子加热模式、电子密度、中性粒子密度、正离子能量以及正离子总通量等分析了大气压Ar/O2放电双频调控机制。结果表明，低频源电压的改变使得电子加热模式由α模式转变为DA/α混合模式，且等离子体密度、正离子总通量及离子能量均随着低频电压的升高而增大，发生了解耦现象。与低频源电压不同，高频源电压和低频源频率对电子加热模式不产生影响。此外，高频源电压对等离子体密度及正离子总通量影响较大，对刻蚀工业中易对材料造成损伤的离子能量影响很小；而低频源频率对工业中影响影响较大的离子能量和离子总通量影响较大，对等离子体密度影响较小，实现了等离子体密度和离子能量的独立控制。Abstract: In this paper, the characteristics of Ar/O2 discharge driven by dual frequency at atmospheric pressure are studied by using a two-dimensional fluid model. We mainly focus on the influences of different matching methods, such as high and low-frequency source voltage and low-frequency source frequency, on the plasma parameters. The dual frequency control mechanism of atmospheric pressure Ar/O2 discharge is analyzed by electron heating mode, electron density, neutral particle density, positive ion energy, and total positive ion flux. The results show that when the low-frequency source voltage increases, the electron heating mode changes from α mode to DA/α mode, and the plasma density, the total flux of positive ions, as well as the ion energy increase with the low-frequency voltage; this means that decoupling occurs. Different from the low-frequency source voltage, the high-frequency source voltage and the low-frequency source frequency have little effect on the electron heating mode. Furthermore, it is shown that the voltage of the high-frequency source can greatly influence the plasma density and the total positive ion flux, while the ion energy which damages the material in the etching industry changes little. The frequency of the low-frequency source has a great influence on the ion total flux and the energy of the positive ions, which easily affects the reaction in the industry but has little effect on the plasma density. Therefore, the independent control of plasma density and ion energy is realized.
-
Key words:
- Dual frequency capacitive coupling /
- Ar/O2 discharge /
- Atmospheric pressure plasma .
-
-
图 2 不同高频源电压下电离率的时空分布图及电子密度的空间分布图。(a) 电离率 / 1019 cm−3s−1， (b) ne / 1012 cm−3
Figure 2. Spatial and temporal distribution of ionization rate and the spatial distribution of electron density at different high-frequency source voltages. (a) ionization rate / 1019 cm−3s−1 , (b) ne/ 1012 cm−3
图 3 不同高频源电压下中性粒子密度的空间分布。(a) O /1016 cm−3，(b) O(1D) / 1014 cm−3，(c) O3 / 1015 cm−3
Figure 3. Spatial distribution of neutral particle density at different high-frequency source voltages. (a) O /1016 cm−3, (b) O(1D) / 1014 cm−3, (c) O3 / 1015 cm−3
图 4 不同高频源电压下离子能量(a)及总通量(b)变化图
Figure 4. The variation of ion energy(a) and total ion flux(b) at different high-frequency source voltages
图 5 不同低频源电压下电场、电离率的时空分布及电子密 度的空间分布图。(a) 电离率 / 1018 cm−3s−1， (b) Ez / 102 Vcm−2， (c)ne / 1011 cm−3
Figure 5. The spatial and temporal distribution of ionization rate and the spatial distribution of electron density at different low-frequency source voltages. (a) ionization rate / 1018 cm−3s−1, (b) Ez / 102 Vcm−2, (c) ne / 1011 cm−3
图 6 不同低频源电压下中性粒子密度的空间分布图。(a) O /1015 cm−3， (b) O(1D) / 1012 cm−3， (c) O3 / 1014 cm−3
Figure 6. Spatial distribution of neutral particle density at different low-frequency source voltages. (a) O /1015 cm−3, (b) O(1D) / 1012 cm−3, (c) O3 / 1014 cm−3
图 8 不同低频源电压下正离子的能量(a)和总通量(b)变化图
Figure 8. The variation of energy (a) and total flux of positive ions (b) under different low-frequency source voltages
图 9 不同低频源频率下电离率的时空分布图及电子密度的空间分布图。(a) 电离率 / 1018 cm−3s−1， (b) ne / 1011 cm−3
Figure 9. The spatial and temporal distribution of ionization rate and the spatial distribution of electron density at different low-frequency source frequencies. (a) ionization rate / 1018 cm−3s−1, (b) ne / 1011cm−3
图 10 不同低频源频率下中性粒子密度的空间分布。(a) O /1015 cm−3， (b) O(1D) / 1013 cm−3， (c) O3 / 1014 cm−3
Figure 10. Spatial distribution of neutral particle density at different low-frequency source frequencies. (a) O /1015 cm−3, (b) O(1D) / 1013 cm−3, (c) O3 / 1014 cm−3
图 11 不同低频源频率下离子能量(a)和总通量(b)变化图
Figure 11. The variation of ion energy (a) and total flux (b) at different low-frequency source frequencies
表 1 模型中的粒子
Table 1. Particles in the model
电子 离子 中性粒子 e $ {{\text{O}}^ + } $ 、$ {{\text{O}}^ - } $ 、$ {\text{O}}_{\text{2}}^{\text{ + }} $ $ {\text{O}}{{\text{(}}^{\text{1}}}{\text{D)}} $ 、$ {\text{A}}{{\text{r}}^{\text{*}}} $ $ {\text{A}}{{\text{r}}^{\text{ + }}} $ 、$ {\text{O}}_{{2}}^{{ - }} $ 、$ {\text{O}}_{\text{3}}^{{ - }} $ $ {\text{A}}{{\text{r}}_{\text{m}}} $ 、$ {\text{Ar}}_{\text{r}}^{} $ ${ {\rm{O} }_{\rm{2} } }{ {\rm{(} }^{\rm{1} } }{ {{\Delta } }_{\rm{g} } }{\rm{)} }$ 、O$ {{\text{O}}_{\text{2}}} $ 、$ {{\text{O}}_{\text{3}}} $ Ar 
下载: 导出CSV
序号 反应 反应速率 文献 1 $ {\text{Ar + e}} \to {\text{A}}{{\text{r}}^{\text{ + }}}{\text{ + 2e}} $ $ 2.3 \times {10^{ - 8}}{T_{\text{e}}}^{0.68}\exp ( - 15.76/{T_{\text{e}}})\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{ - 1}} $ [34-35] 2 $ {\text{Ar + e}} \to {\text{A}}{{\text{r}}_{\text{m}}}{\text{ + e}} $ $ 2.5 \times {10^{ - 9}}{T_{\text{e}}}^{0.74}\exp ( - 11.56/{T_{\text{e}}})\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34-35] 3 $ {\text{Ar + e}} \to {\text{A}}{{\text{r}}_{\text{r}}}{\text{ + e}} $ $ 2.5 \times {10^{ - 9}}{T_{\text{e}}}^{0.74}\exp ( - 11.56/{T_{\text{e}}})\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34-35] 4 $ {\text{Ar + e}} \to {\text{A}}{{\text{r}}^*}{\text{ + e}} $ $ 1.4 \times {10^{ - 8}}{T_{\text{e}}}^{0.71}\exp ( - 13.2/{T_{\text{e}}})\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34-35] 5 $ {\text{A}}{{\text{r}}_{\text{r}}}{\text{ + e}} \to {\text{A}}{{\text{r}}^{\text{ + }}}{\text{ + 2e}} $ $ 6.8 \times {10^{ - 9}}{T_{\text{e}}}^{0.67}\exp ( - 4.2/{T_{\text{e}}})\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34-35] 6 $ {\text{A}}{{\text{r}}_{\text{r}}}{\text{ + e}} \to {\text{Ar + e}} $ $ 4.3 \times {10^{ - 10}}{T_{\text{e}}}^{0.74}\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34-35] 7 $ {\text{A}}{{\text{r}}_{\text{r}}}{\text{ + e}} \to {\text{A}}{{\text{r}}_{\text{m}}}{\text{ + e}} $ $ 3 \times {10^{ - 7}}\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34-35] 8 $ {\text{A}}{{\text{r}}_{\text{r}}}{\text{ + e}} \to {\text{A}}{{\text{r}}^{\text{*}}}{\text{ + e}} $ $ 8.9 \times {10^{ - 7}}{T_{\text{e}}}^{0.51}\exp ( - 1.59/{T_{\text{e}}})\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34-35] 9 $ {\text{A}}{{\text{r}}_{\text{m}}}{\text{ + e}} \to {\text{A}}{{\text{r}}^{\text{ + }}}{\text{ + 2e}} $ $ 6.8 \times {10^{ - 9}}{T_{\text{e}}}^{0.67}\exp ( - 4.2/{T_{\text{e}}})\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34,35] 10 $ {\text{A}}{{\text{r}}_{\text{m}}}{\text{ + e}} \to {\text{Ar + e}} $ $ 4.3 \times {10^{ - 10}}{T_{\text{e}}}^{0.74}\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34-35] 11 $ {\text{A}}{{\text{r}}_{\text{m}}}{\text{ + e}} \to {\text{A}}{{\text{r}}_{\text{r}}}{\text{ + e}} $ $ 2 \times {10^{ - 7}}\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34-35] 12 $ {\text{A}}{{\text{r}}_{\text{m}}}{\text{ + e}} \to {\text{A}}{{\text{r}}^{\text{*}}}{\text{ + e}} $ $ 8.9 \times {10^{ - 7}}{T_{\text{e}}}^{0.51}\exp ( - 1.59/{T_{\text{e}}})\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34-35] 13 $ {\text{A}}{{\text{r}}^{\text{*}}}{\text{ + e}} \to {\text{A}}{{\text{r}}^{\text{ + }}}{\text{ + 2e}} $ $ 1.8 \times {10^{ - 7}}{T_{\text{e}}}^{0.61}\exp ( - 2.61/{T_{\text{e}}})\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34-35] 14 $ {\text{A}}{{\text{r}}^{\text{*}}}{\text{ + e}} \to {\text{Ar + e}} $ $ 3.9 \times {10^{ - 10}}{T_{\text{e}}}^{0.71}\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34-35] 15 $ {\text{A}}{{\text{r}}^{\text{*}}}{\text{ + e}} \to {\text{A}}{{\text{r}}_{\text{r}}}{\text{ + e}} $ $ 1.5 \times {10^{ - 7}}{T_{\text{e}}}^{0.51}\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34-35] 16 $ {\text{A}}{{\text{r}}^{\text{*}}}{\text{ + e}} \to {\text{A}}{{\text{r}}_{\text{m}}}{\text{ + e}} $ $ 1.5 \times {10^{ - 7}}{T_{\text{e}}}^{0.51}\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34-35] 17 $\mathrm{Ar}_{\mathrm{r} } \rightarrow \mathrm{Ar}+\mathrm{h}{\rm{\nu }}$ $ 2 \times {10^6}{{\text{s}}^{{{ - 1}}}} $ [34,36] 18 $\mathrm{Ar}_{\mathrm{m} } \rightarrow \mathrm{Ar}+\mathrm{h} {\rm{\nu }}$ $ 2 \times {10^6}{{\text{s}}^{{{ - 1}}}} $ [34,36] 19 ${\rm{A}}{{\rm{r}}^{\rm{*}}} \to {\rm{A}}{{\rm{r}}_{\rm{r}}}{\rm{ + h\nu }}$ $ 3 \times {10^7}{{\text{s}}^{{{ - 1}}}} $ [34,36] 20 ${\rm{A}}{{\rm{r}}^{\rm{*}}} \to {\rm{A}}{{\rm{r}}_{\rm{m}}}{\rm{ + h\nu }}$ $ 1 \times {10^{ - 11}}\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34,36] 21 $ {\text{e + }}{{\text{O}}_{\text{2}}} \to {{\text{O}}_{\text{2}}}{{\text{(}}^{\text{1}}}{{{\Delta }}_{\text{g}}}{\text{) + e}} $ $ 1.7 \times {10^{ - 9}}\exp ( - 3.1/{T_{\text{e}}})\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34,37] 22 $ {\text{e + }}{{\text{O}}_{\text{2}}} \to {\text{O + O}}{{\text{(}}^{\text{1}}}{\text{D) + e}} $ $ 1.7 \times {10^{ - 9}}\exp ( - 3.1/{T_{\text{e}}})\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34,37] 23 $ {\text{e + }}{{\text{O}}_{\text{2}}} \to {\text{2O + e}} $ $ 4.2 \times {10^{ - 9}}\exp ( - 5.6/{T_{\text{e}}})\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34,37] 24 $ {\text{e + }}{{\text{O}}_{\text{2}}} \to {{\text{O}}^{{ - }}}{\text{ + O}} $ $ 8.8 \times {10^{ - 11}}\exp ( - 4.4/{T_{\text{e}}})\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34,37] 25 ${\rm{e + }}{{\rm{O}}_{\rm{2}}}{{\rm{(}}^{\rm{1}}}{{\rm{\Delta }}_{\rm{g}}}{\rm{)}} \to {{\rm{O}}_{\rm{2}}}{\rm{ + e}}$ $ 5.6 \times {10^{ - 9}}\exp ( - 2.2/{T_{\text{e}}})\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34,37] 26 $ {\text{e + }}{{\text{O}}_{\text{2}}} \to {\text{O}}_{\text{2}}^{\text{ + }}{\text{ + 2e}} $ $ 9 \times {10^{ - 10}}{T_{\text{e}}}^{0.5}\exp ( - 12.6/{T_{\text{e}}})\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34,37] 27 $ {\text{e + }}{{\text{O}}_{\text{2}}} \to {{\text{O}}^{{ - }}}{\text{ + }}{{\text{O}}^{\text{ + }}}{\text{ + e}} $ $ 7.1 \times {10^{ - 11}}{T_{\text{e}}}^{0.5}\exp ( - 17/{T_{\text{e}}})\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34,37] 28 $ {\text{e + }}{{\text{O}}_{\text{2}}} \to {\text{O + }}{{\text{O}}^{\text{ + }}}{\text{ + 2e}} $ $ 5.3 \times {10^{ - 10}}{T_{\text{e}}}^{0.9}\exp ( - 20/{T_{\text{e}}})\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34,37] 29 $ {\text{e + O}} \to {\text{O}}{{\text{(}}^{\text{1}}}{\text{D) + e}} $ $ 4.2 \times {10^{ - 9}}\exp ( - 2.25/{T_{\text{e}}})\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34,37] 30 $ {\text{e + O}}{{\text{(}}^{\text{1}}}{\text{D)}} \to {\text{O + e}} $ $ 8 \times {10^{ - 9}}\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34,37] 31 $ {\text{e + O}}{{\text{(}}^{\text{1}}}{\text{D)}} \to {{\text{O}}^{\text{ + }}}{\text{ + 2e}} $ $ 9 \times {10^{ - 9}}{T_{\text{e}}}^{0.7}\exp ( - 11.6/{T_{\text{e}}})\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34,37] 32 $ {\text{e + O}} \to {{\text{O}}^{\text{ + }}}{\text{ + 2e}} $ $ 9 \times {10^{ - 9}}{T_{\text{e}}}^{0.7}\exp ( - 13.6/{T_{\text{e}}})\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34,37] 33 $ {\text{e + }}{{\text{O}}_{\text{3}}} \to {\text{O}}_{\text{2}}^{{ - }}{\text{ + O}} $ $ 1 \times {10^{ - 9}}\; {\text{c}}{{\text{m}}^{\text{3}}}{{\text{s}}^{{{ - 1}}}} $ [34,37]
下载: 导出CSV
-
[1] Wang X Q, Li X, Zhou R W, et al. Degradation of high-concentration simulated organic wastewater by DBD plasma[J]. Water Science Technology,2019,80(8):1413−1420 doi: 10.2166/wst.2019.389 [2] 牛宇锋. 气体放电与等离子体领域经典之作——《大气压气体放电及其等离子体应用》[J]. 高压电器,2016,52(01):67(in chinese) Niu Yu feng. A classic work in the field of gas discharge and plasma: Atmospheric pressure gas discharge and its plasma application[J]. High Voltage Electrical Apparatus,2016,52(01):67 [3] 侯世英, 罗书豪, 刘坤, 等. 双环电极大气压氦气等离子体射流的特性及其影响因素[J]. 高电压技术,2013,39(07):1569−1576(in chinese) Hou Shiying, Luo Shuhao, Liu Kun, et al. Characteristics and influencing factors of atmospheric pressure helium plasma Jets with Double Ring Electrode[J]. High Voltage Technology,2013,39(07):1569−1576 [4] 石峰, 王昊. 气体放电等离子体及应用的研究进展[J]. 真空与低温,2018,24(02):80−85(in chinese) Shi Feng, WANG Hao. Research progress of gas discharge plasma and its application[J]. Vacuum and Cryogenics,2018,24(02):80−85 [5] Silva W D , Belmonte T , Duday D ,et al. Interaction Mechanisms between Ar/O2 Post-discharge and Biphenyl[J]. Plasma Processes & Polymers,2012,9(2):207−216. [6] Kuo C M, Wang S M, Huang C. Improved CoQ10 production of rhodobacter sp. treated by atmospheric pressure capacitive coupled radio frequency plasma jet[J]. High Energy Chemistry,2022,56(6):461−467 doi: 10.1134/S0018143922060042 [7] Kitajima T, Takeo Y. Dual frequency PECVD silicon nitride for fabrication of CMUTs’ membranes[J]. Appl Phys Lett,2000,77:489 doi: 10.1063/1.127020 [8] Boyle P C, Ellingboe A R. Electrostatic modelling of dual frequency rf plasma discharges[J]. Plasma Sources Sci Technol,2004,13:493 doi: 10.1088/0963-0252/13/3/016 [9] Graves D B, Jensen K. L A continuum model of DC and RF discharges[J]. IEEE Trans Plasma Sci,1986,14(2):78−91 doi: 10.1109/TPS.1986.4316510 [10] Myung S W, Lee C M, Jung S C, et al. Au nanoparticles grafting on polyethylene by using atmospheric pressure gas discharge[J]. Journal of Nanoscience and Nanotechnology,2016,16(11):11448−11452 doi: 10.1166/jnn.2016.13527 [11] Lee J K , Kim H C , Babaeva N ,et al. Simulations of capacitively coupled single- and dual-frequency RF discharges[J].IEEE Transactions on Plasma Science, 2003, 32(1) DOI:10.1109/PLASMA.2003.1230050 [12] Booth J P, Curley G, Marić D, et al. Dual-frequency capacitive radiofrequency discharges: effect of low-frequency power on electron density and ion flux[J]. Plasma Sources Science and Technology,2010,19(1) : 015005 doi: 10.1088/0963-0252/19/1/015005 [13] 吴良超, 殷桂琴, 孟祥国, 等. 气压对于低气压双频容性耦合Ar/O2等离子体放电特性影响的研究[J]. 核聚变与等离子体物理,2020,40(04):372−378(in chinese) Wu Liangchao, Yin Guiqin, Meng Xiangguo, et al. Study on the effect of air pressure on the discharge characteristics of low pressure dual-frequency capacitatively coupled Ar/O2 plasma[J]. Nuclear Fusion and Plasma Physics,2020,40(04):372−378 [14] 王一男, 孟晓东, 李帅星, 等. 大气压双频氦气放电等离子体特性的数值研究[J]. 核聚变与等离子体物理,2019,39(04):373−378(in chinese) Wang Yinan, Meng Xiaodong, Li Shuaixing, et al. Numerical study of characteristics of atmospheric Pressure dual-frequency helium discharge plasma[J]. Nuclear Fusion and Plasma Physics,2019,39(04):373−378 [15] 王一男, 李帅星, 刘悦, 等. 大气压双频氦气放电特性的数值模拟研究[J]. 真空科学与技术学报,2018,38(07):590−597(in chinese) Wang Yinan, Li Shuaixing, Liu Yue, et al. Numerical simulation of atmospheric pressure dual-frequency helium discharge characteristics[J]. Journal of Vacuum Science and Technology,2018,38(07):590−597 [16] 张仲麟, 聂秋月, 王志斌, 等. 大气压介质阻挡放电双频调制技术数值模拟研究[J]. 电工技术学报,2017,32(08):48−54(in chinese) Zhang Zhonglin, Nie Qiuyue, Wang Zhibin, et al. Numerical simulation of dual-frequency modulation technique for dielectric barrier discharge at atmospheric pressure[J]. Transactions of China Electrotechnical Society,2017,32(08):48−54 [17] Liu D, Yang A, Wang X, et al. Electron heating and particle fluxes in dual frequency atmospheric-pressure helium capacitive discharge[J]. Journal of Physics D:Applied Physics,2016,49(49):49LT01 doi: 10.1088/0022-3727/49/49/49LT01 [18] Neill C O, Waskoenig J, Gans T. Tailoring electron energy distribution functions through energy confinement in dual radio-frequency driven atmospheric pressure plasmas[J]. Applied Physics Letters,2012,101(15):154107 doi: 10.1063/1.4758463 [19] Jiang X Z, Li W, Wumaier T, et al. Diagnostic study of argon and oxygen mixtures in dual-frequency capacitively coupled plasmas using quadrupole mass spectrometer[J]. Chemical Physics Letters,2019,730:472−477 doi: 10.1016/j.cplett.2019.06.044 [20] Wu Jidun, Zheng Hao, Wang Yanfei, et al. Experimental diagnosis of electron density and temperature in capacitively coupled argon plasmas: Triple-frequency discharges and two-dimensional spatial distributions[J]. Physics of Plasmas,2021,28(9):093501 doi: 10.1063/5.0044844 [21] Casaleiro J, Oliveira L B, Filanovsky I M. A quadrature RC-oscillator with capacitive coupling[J]. Integration, the VLSI Journal,2016,52:260−271 doi: 10.1016/j.vlsi.2015.06.006 [22] Liu G H, Liu Y X, Wen D Q, et al. Heating mode transition in capacitively coupled CF4 discharges: Comparison of experiments with simulations[J]. Plasma Sources Science and Technology,2015,24(3):034006 doi: 10.1088/0963-0252/24/3/034006 [23] Liu G H, Liu Y X, Bai LS, et al. Experimental investigation of mode transitions in asymmetric capacitively coupled radio-frequency Ne and CF4 plasmas[J]. Physics of Plasmas,2018,25(2):023515 DOI:10.1063/1.5000950. [24] 赵旭, 傅志俭. 医用臭氧临床应用和安全性研究进展[J]. 中国疼痛医学杂志,2018,24(07):489−492 (in chinese) doi: 10.3969/j.issn.1006-9852.2018.07.002 Zhao Xu, Fu Zhijian. Research progress on clinical application and safety of medical ozone[J]. Chinese Journal of Pain Medicine,2018,24(07):489−492 doi: 10.3969/j.issn.1006-9852.2018.07.002 [25] 徐卫东, 谈娟娟, 赵振华, 等. 臭氧/过氧化氢处理高浓有机废水的研究[J]. 精细化工中间体,2023,53(01):83−87 (in chinese) Xu Wei dong, Tan Juan juan, Zhao Zhen hua, et al. Study on the treatment of high concentration organic wastewater by ozone/hydrogen peroxide[J]. Fine Chemical Intermediates,2023,53(01):83−87 [26] Aman-ur-Rehman, Kwon H C, Park W T, et al. A study of the role of various reactions on the density distribution of hydrogen, silylene, and silyl in SiH4/H2 plasma discharges[J]. Physics of Plasmas,2011,18(9):A431 DOI:10.1063/1.3630933 [27] Bleecker K D , Herrebout D , Bogaerts A , et al. One-dimensional modelling of a capacitively coupled RF plasma in Silane/Helium, Including small concentrations of O2 and N2[J]. Journal of Physics D: Applied Physics, 2003, 36(15): 1826- 1833 DOI:10.1088/0022-3727/36/15/313 [28] Lymberopoulos D P. Fluid simulation of a pulsed power inductively coupled argon plasma[J]. Journal of Vacuum Science and Technology A: Vacuum, Surfaces, and Films, 1998, 16(2): 564- 571 DOI:10.1116/1.581072 [29] Park Q, Lee H, Kim G, et al. Global model of He/O2 and Ar/O2 atmospheric pressure glow discharges[J]. Plasma Processes and Polymers,2008,5(6):569−576 doi: 10.1002/ppap.200800019 [30] ,Lieberman M A, Lichtenberg A J. Principles of plasma discharges and materials processing [M]. New York: Wiley-Interscience, 2005,796 [31] Kushner M J. Plasma chemistry of He/O2/SiH4 and He/N2O/SiH4 mixtures for remote plasma activated chemical vapor deposition of silicon dioxide[J]. Journal of Applied Physics,1993,74(11):6538 doi: 10.1063/1.355115 [32] Jia W Z, Liu R Q, Wang X F, et al. Two-dimen- sional fluid simulation of a radio frequency Ca-pacitively coupled plasma in SiH4/N2/O2[J]. Physics of Plasmas,2018,25:093501 doi: 10.1063/1.5008586 [33] Rauf S, Kushner M J. Nonlinear dynamics of ra- dio frequency plasma processing reactors pow- ered by multifrequency sources[J]. IEEE Trans- actions on Plasma Science,1999,27(5):1329−1338 doi: 10.1109/27.799809 [34] 潘光胜, 谭震宇, 王晓龙, 等. 高氧浓度下大气压Ar/O2脉冲介质阻挡放电频率特性数值研究[J]. 电工技术学报,2017,32(20):71−81 (in chinese) Pan Guangsheng, Tan Zhenyu, Wang Xiaolong et al. Numerical study on frequency Characteristics of Ar/O2 pulse dielectric barrier discharge at atmospheric pressure under high oxygen concentration[J]. Electrotechnical journal,2017,32(20):71−81 [35] Lee M H, Chung C W. Self-consistent global model with multi-step ionizations in inductively coupled plasmas[J]. Physics of Plasmas, 2005, 12(7): 073501(5) DOI:10.1063/1.1935407 [36] Bogaerts A, Gijbels R. Modeling of metastable argon atoms in a direct-current glow discharge[J]. Physical Review A,1995,52(5):3743−3751 doi: 10.1103/PhysRevA.52.3743 [37] Golubovskii Y B, Maiorov V A, Behnke J, et al. Influence of interaction between charged particles and dielectric surface over a homogeneous barrier discharge in nitrogen[J]. Journal of Physics D: Applied Physics,2002,35(8):751−761 doi: 10.1088/0022-3727/35/8/306 -
图( 11) 表( 2)
计量
- 文章访问数: 193
- HTML全文浏览数: 193
- PDF下载数: 3
- 施引文献: 0