-
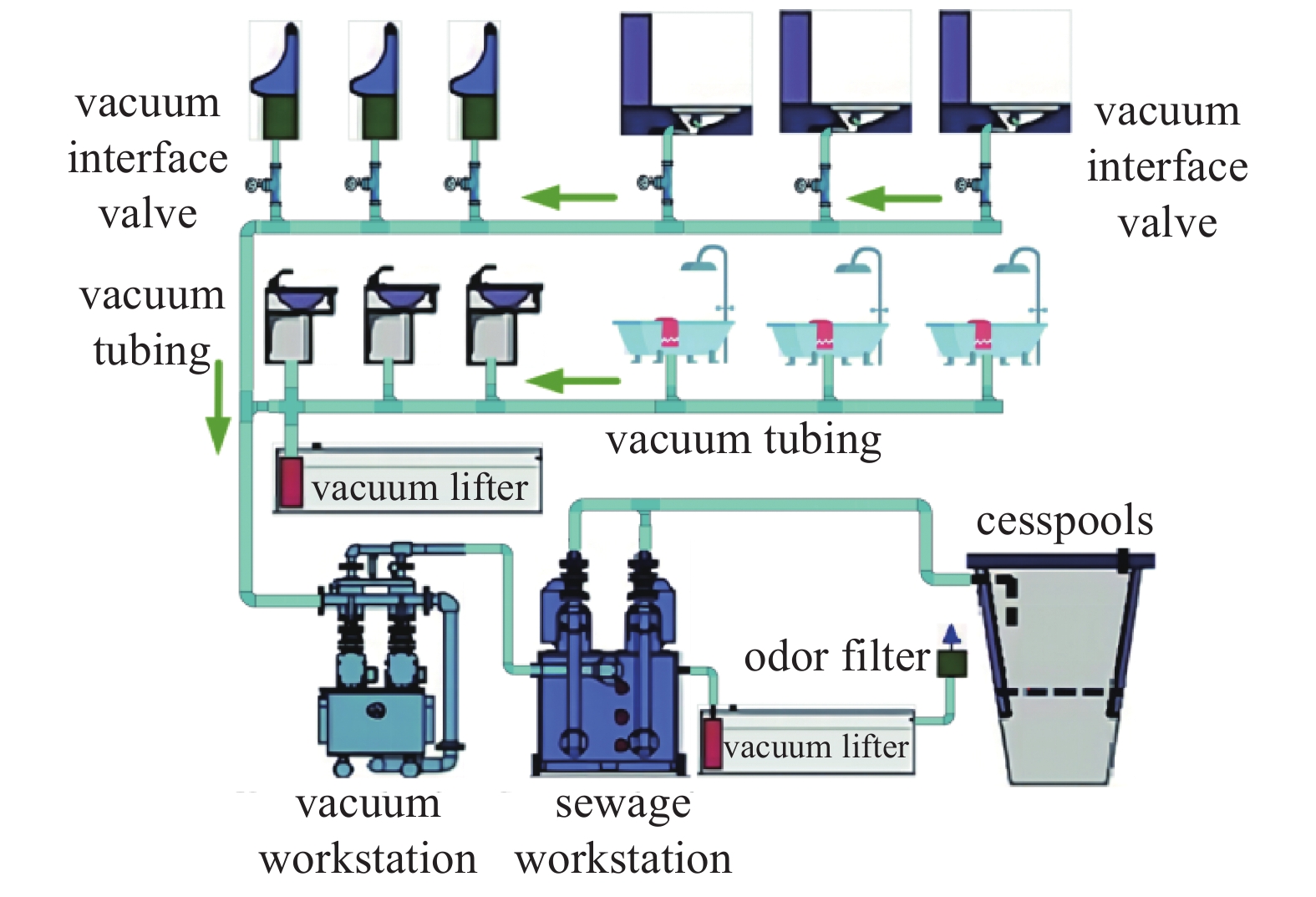
真空排污系统作为一种现代化的污水处理系统,通过利用真空泵等设备将管道两端抽吸成负压对污水进行处理收集[1]。图1为船舶真空排污流程示意图。当前,中国船舶业正处于转型升级的关键期[2],随着国际市场竞争的加剧和国内市场需求变化,传统船舶制造业面临巨大的升级和挑战。
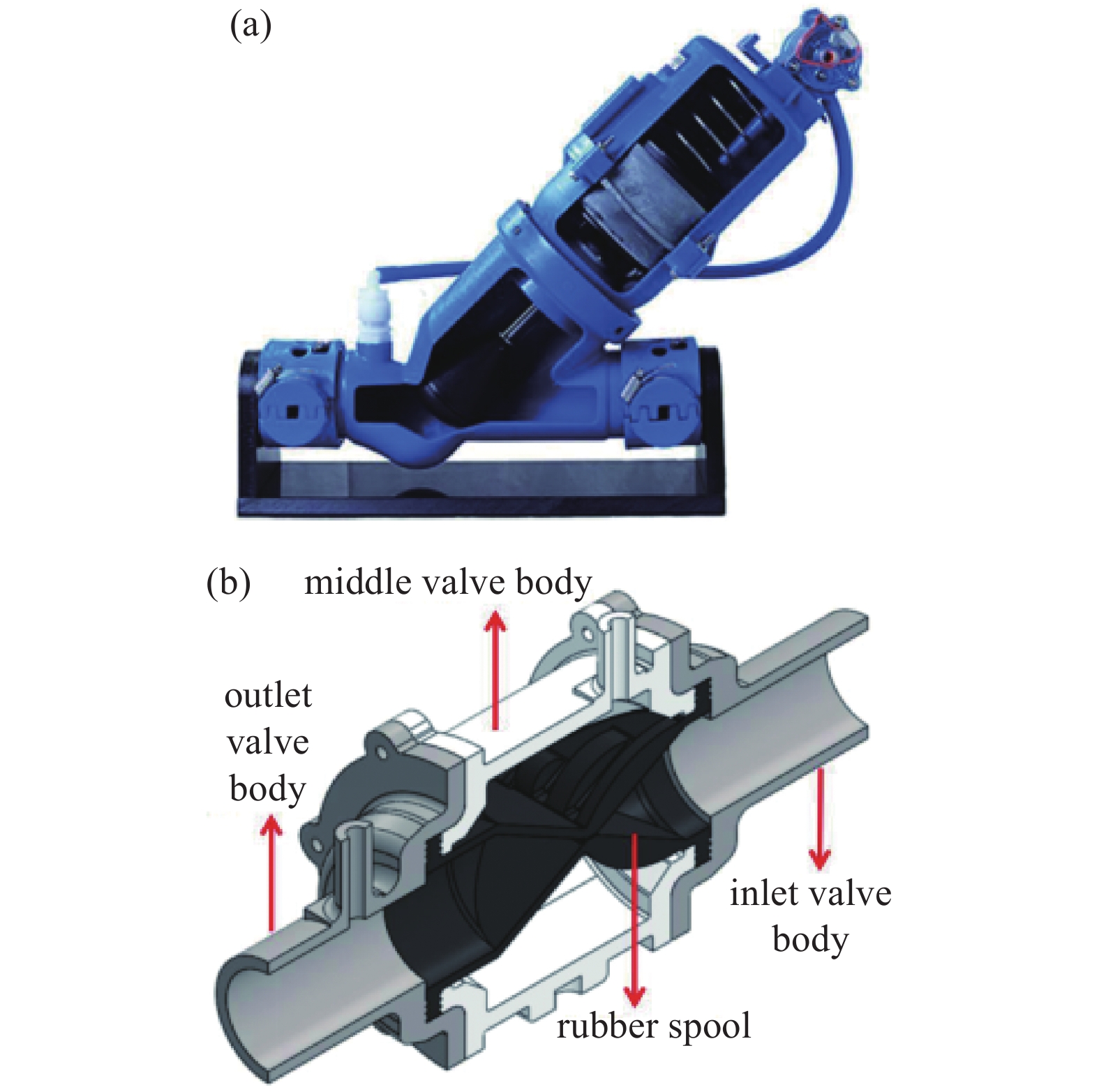
在真空排污系统中,界面阀的作用就是将负压环境与大气环境隔离[3],控制污水由大气压排入负压环境,界面阀的性能直接影响到排污系统的有效性[4],因此其气密性、稳定性、流通性直接决定了整个排污系统的正常运行,因此设计一款通过性强,结实耐用的真空界面阀极为重要。国内外学者对于界面阀做了各方面的研究,Reinhold Betz及其团队[5]研发了一种气动控制的夹管型界面阀,并对由橡胶材料制成的装置就行了强化处理,既提高了气密性,又增强了可靠性。德国Roediger、日本Fuji等[6]公司从事真空界面阀以及真空排污系统的相关研究时间较长,基本上主导垄断了真空排污以及界面阀相关产品;华中科技大学周敬宣团队[7]自主设计的VAJM44型隔膜界面阀采用了负压驱动压缩杆的方式,通过压缩杆使隔膜发生形变,以实现阀门的开关功能。孙金风、李志成等[8]设计的通过负压驱动夹管界面阀,经过有限元分析,使用仿真软件来研究橡胶阀体的壁厚和形变过程中所受的应力,以确保符合材料结构强度,并通过实验验证了结构合理性。Michael T.Rose等[9]对真空界面阀的噪声进行了试验探究,得出对界面阀结构修改有利于噪声的降低。
-
阀芯采用橡胶材料注塑而成,橡胶是一种由高分子化合物组成的材料,由于橡胶具有良好的拉伸性、抗撕裂性,能够承受较大的拉伸剪切力,同时还具有耐化学性,能够在恶劣的环境下保持其性能,因此被广泛用于汽车制造、阀门工业等领域。
橡胶材料受到外界载荷作用下产生弹性形变[11],解除外界载荷恢复原形,称为超弹性形变,这种材料称为超弹性材料。超弹性材料力学性能描述通常分为五大类[12],分别为应力−应变关系、材料参数、应力能量函数、应变能密度曲线、剪切模量的渐进行为。现如今最常用的本构模型有Yeoh模型和Ogden三阶模型等[13],利用橡胶材料实验数据[14]结合数值分析可确定橡胶材料本构模型参数。
-
Yeoh模型高度非线性的材料模型,其应变能密度公式为:
式中,Ci0和Di均为模型的待定材料参数,J为弹性体积比,
$\overline {{I_1}}$ 为应变不变量,表达式为$ \overline {{I_1}} = \overline {\lambda _1^2} + \overline {\lambda _2^2} + \overline {\lambda _3^2} $ ,λ1,λ2和λ3为主伸长率,$ \overline {{\lambda _{\text{i}}}} = J{}^{ - \frac{1}{3}}{\lambda _{\text{i}}} $ ,当材料可看作不可压缩体积时,此时J=1,因此$ \overline {{\lambda _{\text{i}}}} = {\lambda _{\text{i}}} $ 。当处于材料形变量较小的情况下,C10代表初始剪切模量;当i=2时C20为负,在中等变形下可反映橡胶材料的软化情况;当i=3时C30为正,可描述在大变形情况下材料的硬化现象。 -
Ogden模型应变能密度函数为:
其中αi为描述材料非线性参数,μi是与每个αi相关的材料参数,λ1,λ2和λ3为主应变。N为模型中的参数数量,当N=1时,代入式(2)可得到Mooney-Rivlin模型。
-
橡胶阀芯采用橡胶磨具浇筑而成,橡胶浇筑材料采用DPI8400,DPI8400是一种粘度低,流动性好,固化快,对硅胶磨具腐蚀性小,DPI8400由A、B、C三种液体构成,通过调节C液的分量,能够调节三液型真空聚氨酯橡胶的硬度,具体材料参数由下表1所示。
根据重量比精确称重,将C液倒入A液中,搅拌均匀分别将A、B二液在真空箱中进行真空脱泡处理,调整三种液体比例,浇铸成型不同硬度的三液型真空聚氨酯橡胶硬度,下表2为三种材料样本具体物性参数。
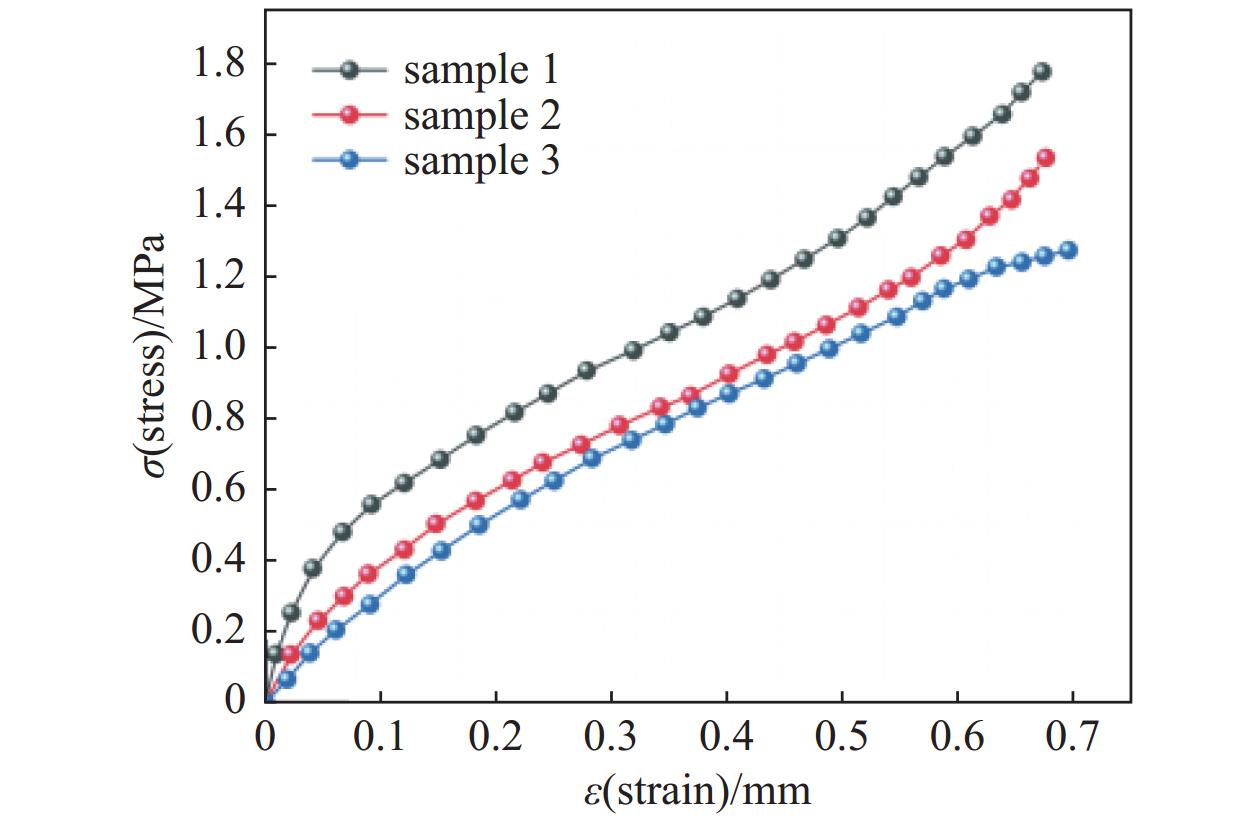
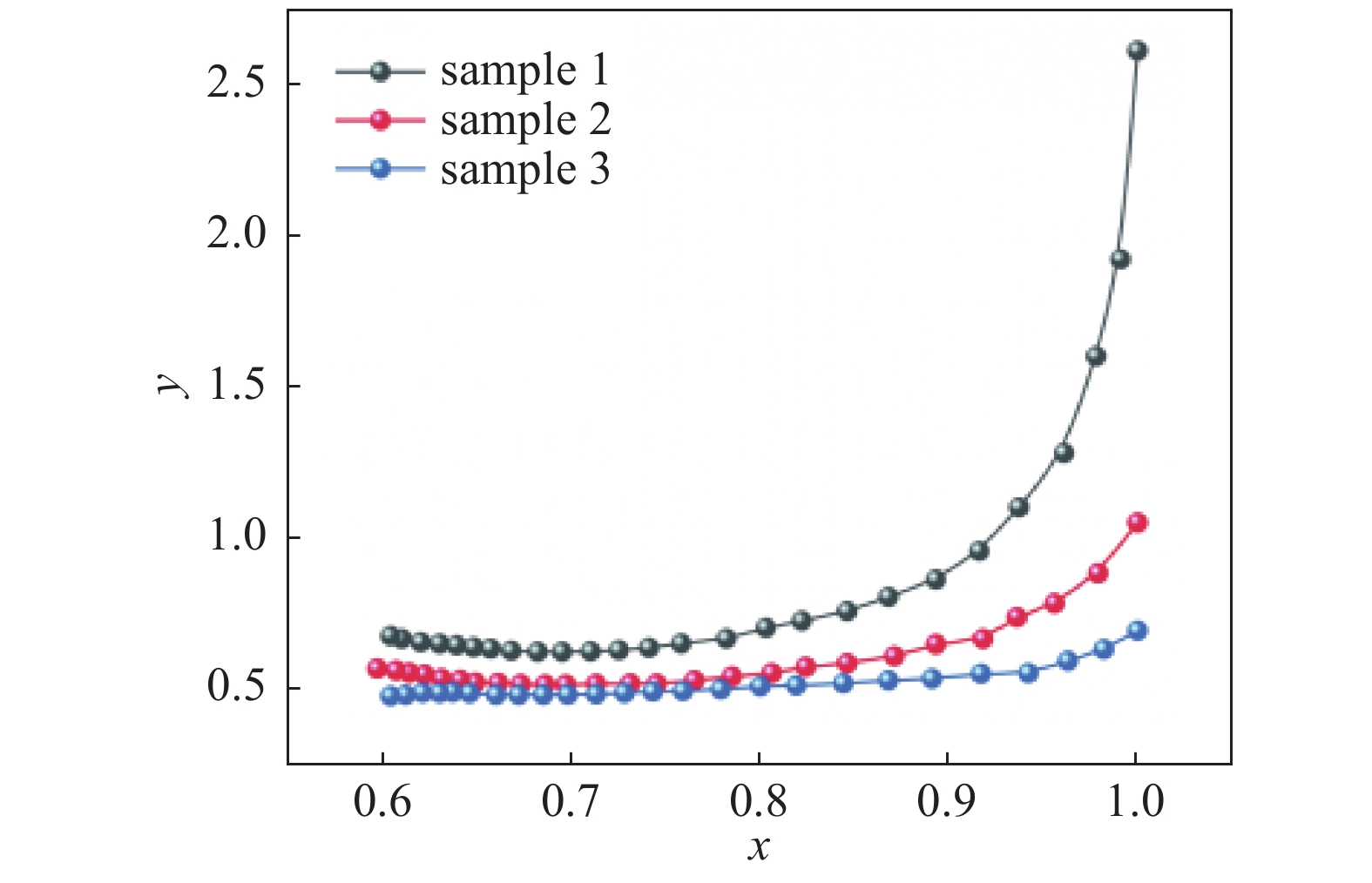
将橡胶材料样本1、2、3进行室温情况下单轴拉伸实验,得到应力−应变关系如下图3所示。
-
在单轴拉伸试验条件下i=1,因此将Yeoh模型的应变能密度函数可化为:
根据Piola-Kirchhoff应力和Cauchy-Green应变间的关系,将本构非线性橡胶材料进行线性化拟合,即可求得
$ \sigma $ i与$ \lambda $ i之间的关系式(4):式中
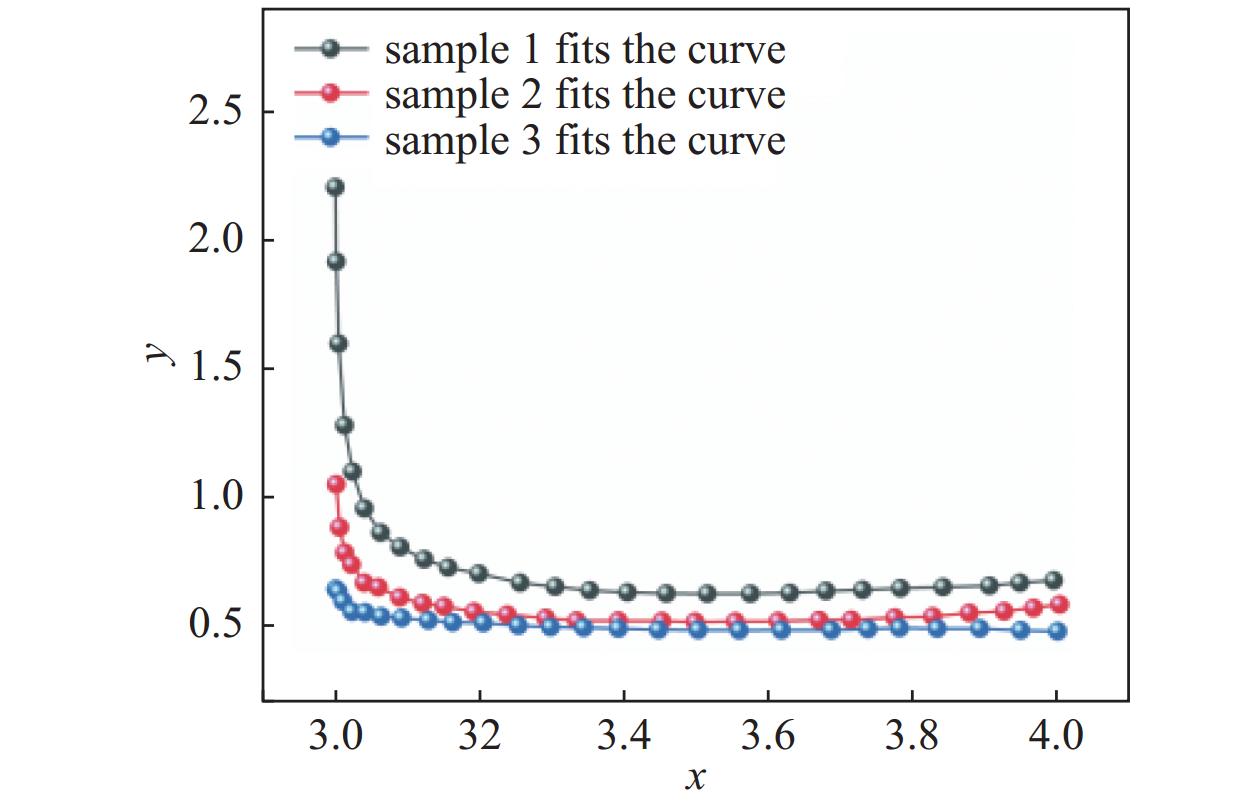
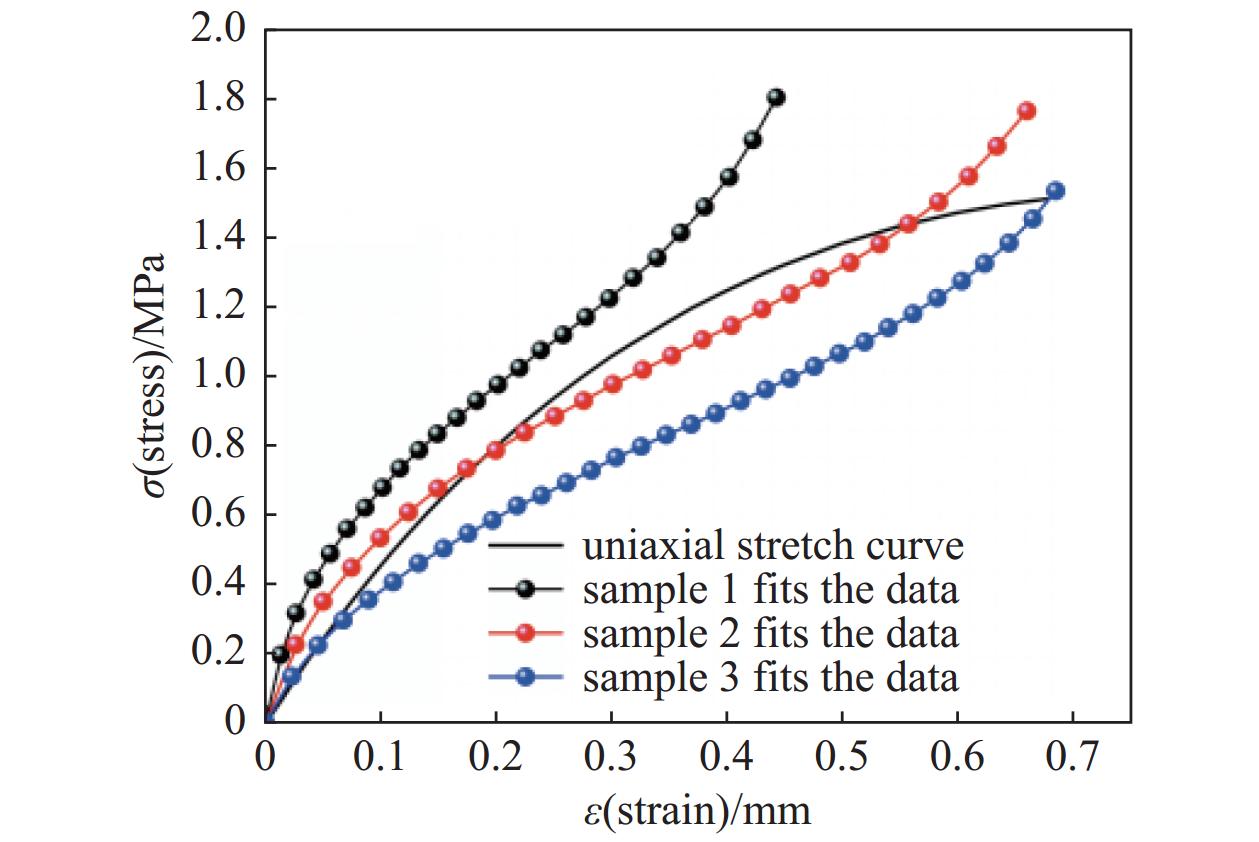
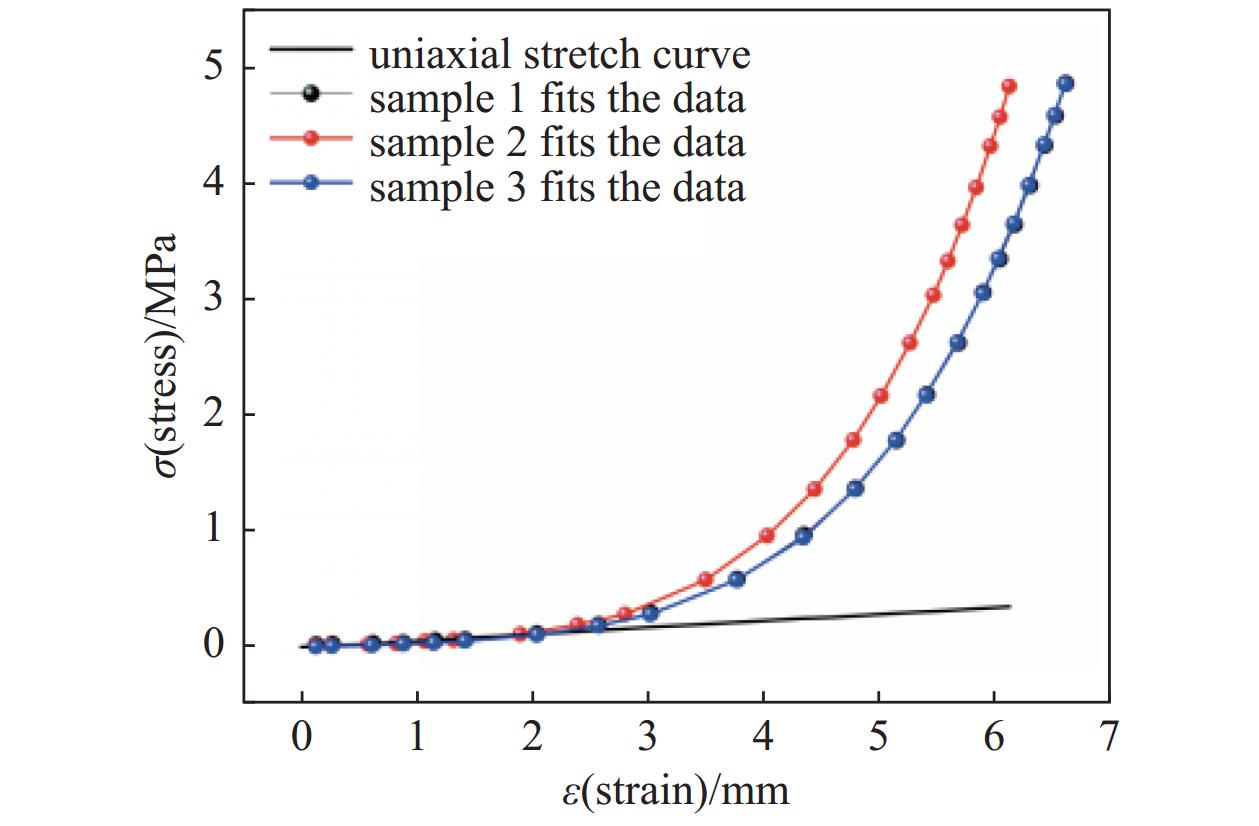
$ {\lambda _i} = 1 + {\varepsilon _i} $ ,$ \varepsilon $ i为拉伸方向的应变,将式(3)带入式(4)可得:$\lambda _1^2 + \dfrac{2}{{{\lambda _1}}}$ 为横坐标x,$\dfrac{{{\sigma _1}}}{{2({\lambda _1} - \dfrac{1}{{\lambda _1^2}})}}$ 为纵坐标y,将数据进行拟合得到下图4。因此由yeoh模型拟合曲线可得出C10=0.50231,C20=0.09331。将单轴拉伸试验数据与ANSYS材料库中的数据进行拟合得下图5,可知C10=0.53782,C20=0.89371。由此可见样本2实验数据与yeoh模型较吻合。
-
当N=1时,Ogden模型可简化为Mooney-Rivlin模型,其应变能密度函数为:
式中C10和C01为模型中的材料参数,I1和I2是应变不变量,拟合曲线如图6,C10为其截距值,C01为其斜率,可得到样本1的C10=0.1789,C01=0.9047,样本2的C10=0.3589,C01=0.8047,样本3的C10=0.5039,C01=0.3047,对其进行拟合,结果图下图7。由于与模型的曲线所给出的单轴拉伸曲线相差过大,因此,Mooney-Rivlin模型不适合该三种材料。
-
真空界面阀橡胶阀芯在真空泵站所产生的真空度下,可以正常开启和关闭,对真空界面阀的流通性能有着决定性作用,真空界面阀橡胶阀芯开启真空度为15~70 kPa[15]。
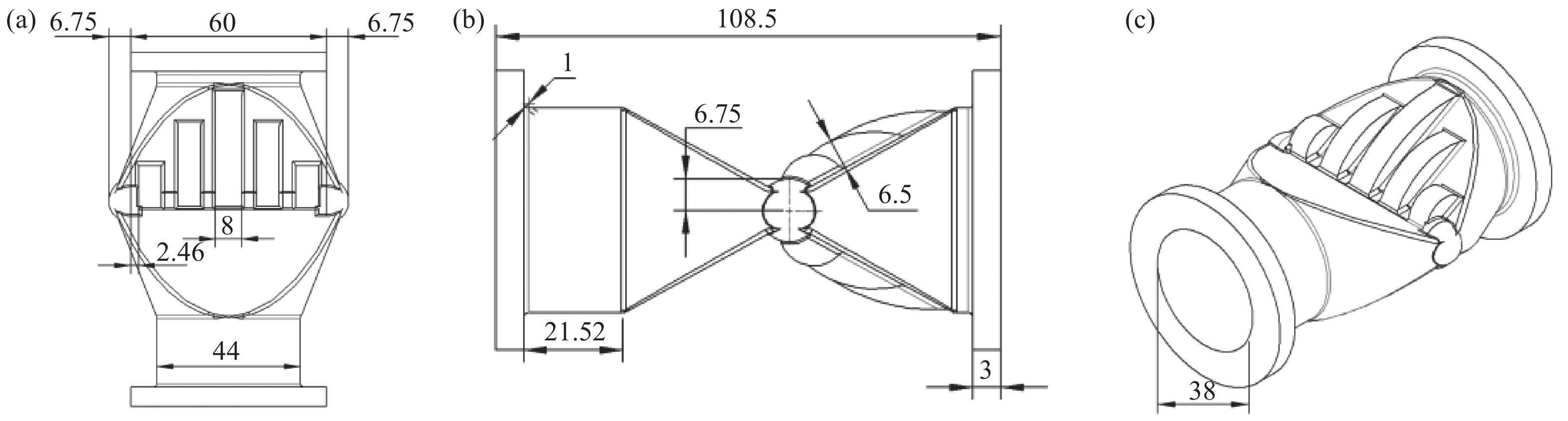
受到阀体外壳以及一般橡胶阀芯厚度的影响,将橡胶阀芯厚度定为3 mm;阀芯长度为108.5 mm,阀芯进出口直径为38 mm,阀芯外径为60 mm,阀芯形变过程中,形变张开量由阀芯宽度所决定,阀体内壁尺寸为76 mm,将阀芯宽度设为73.5 mm,如图8(a)所示;同时保证阀门在全开状态下正常开合,将中部及两侧加强筋高度设为6.5 mm,宽度设为8 mm,既能保证加强筋对阀门闭合时提供地下压力,又能防止橡胶阀芯形变过程中与壳体内壁接触,如图8(a)、8(b)所示。在阀芯形变过程中为了防止两侧破损,因此加入了半径为6.75 mm的半球形加固结构,并且延长2.46 mm与最外侧加强筋相连,最大程度保证了阀芯强度,如图8(a)所示。具体阀芯结构如下图8所示。
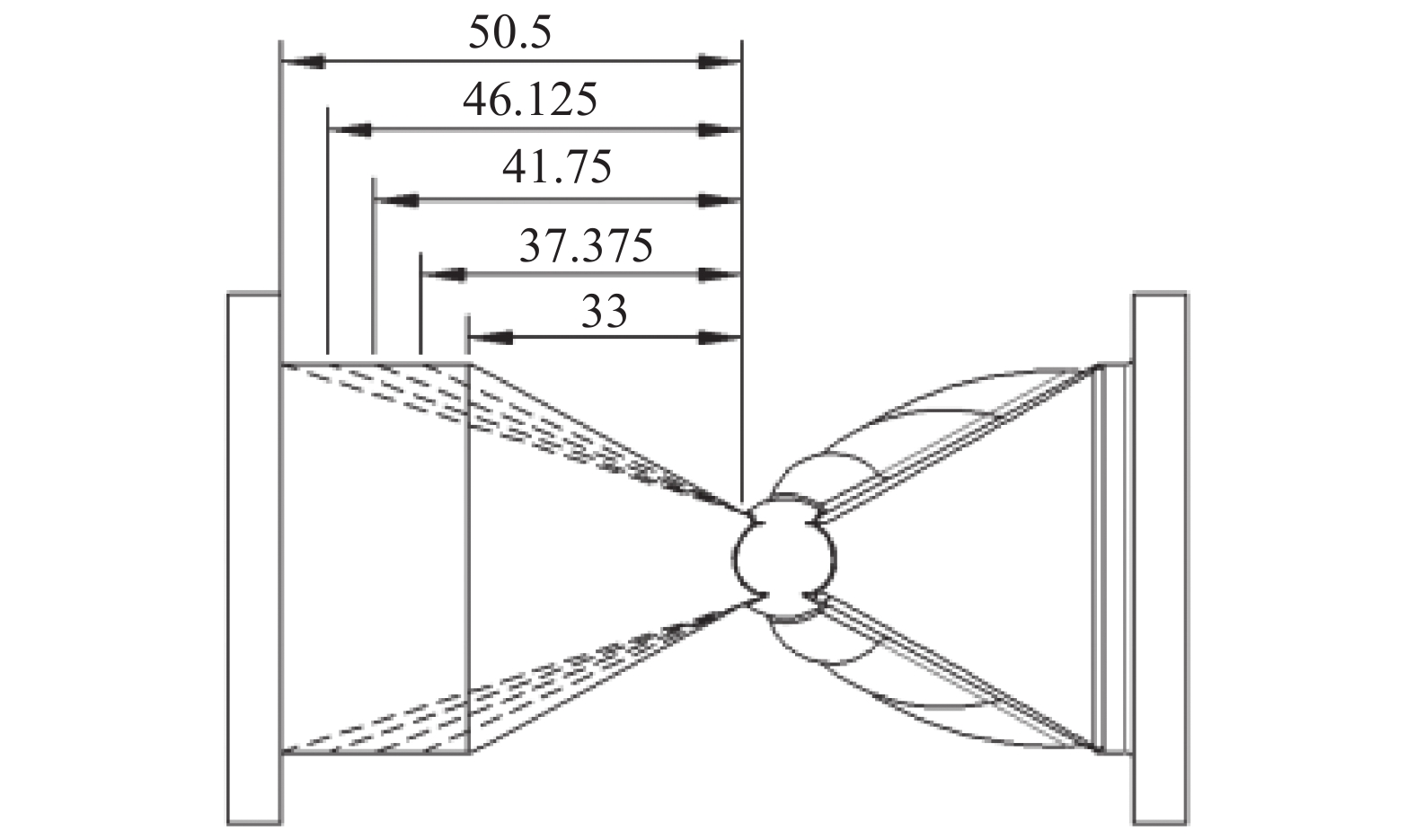
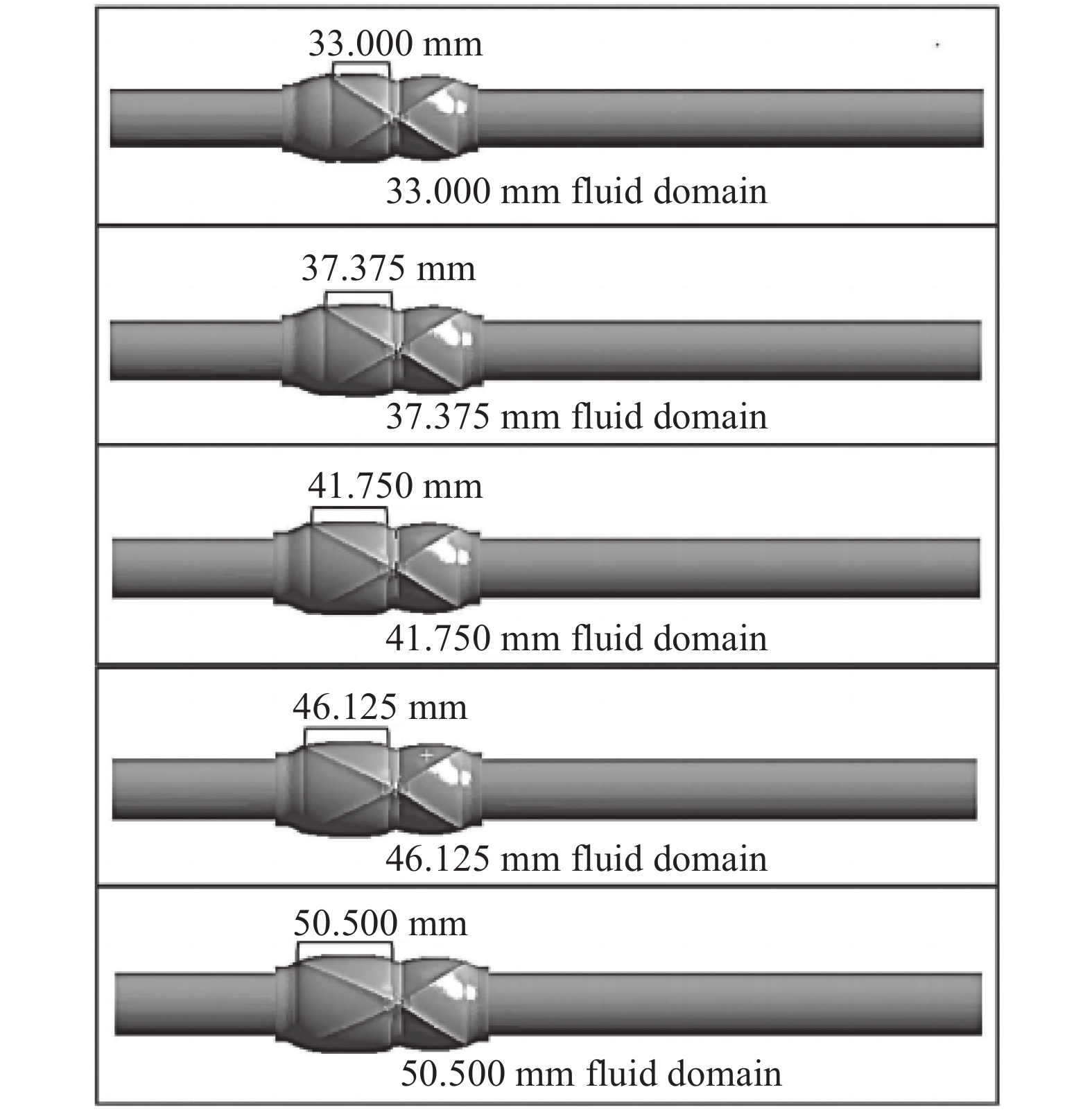
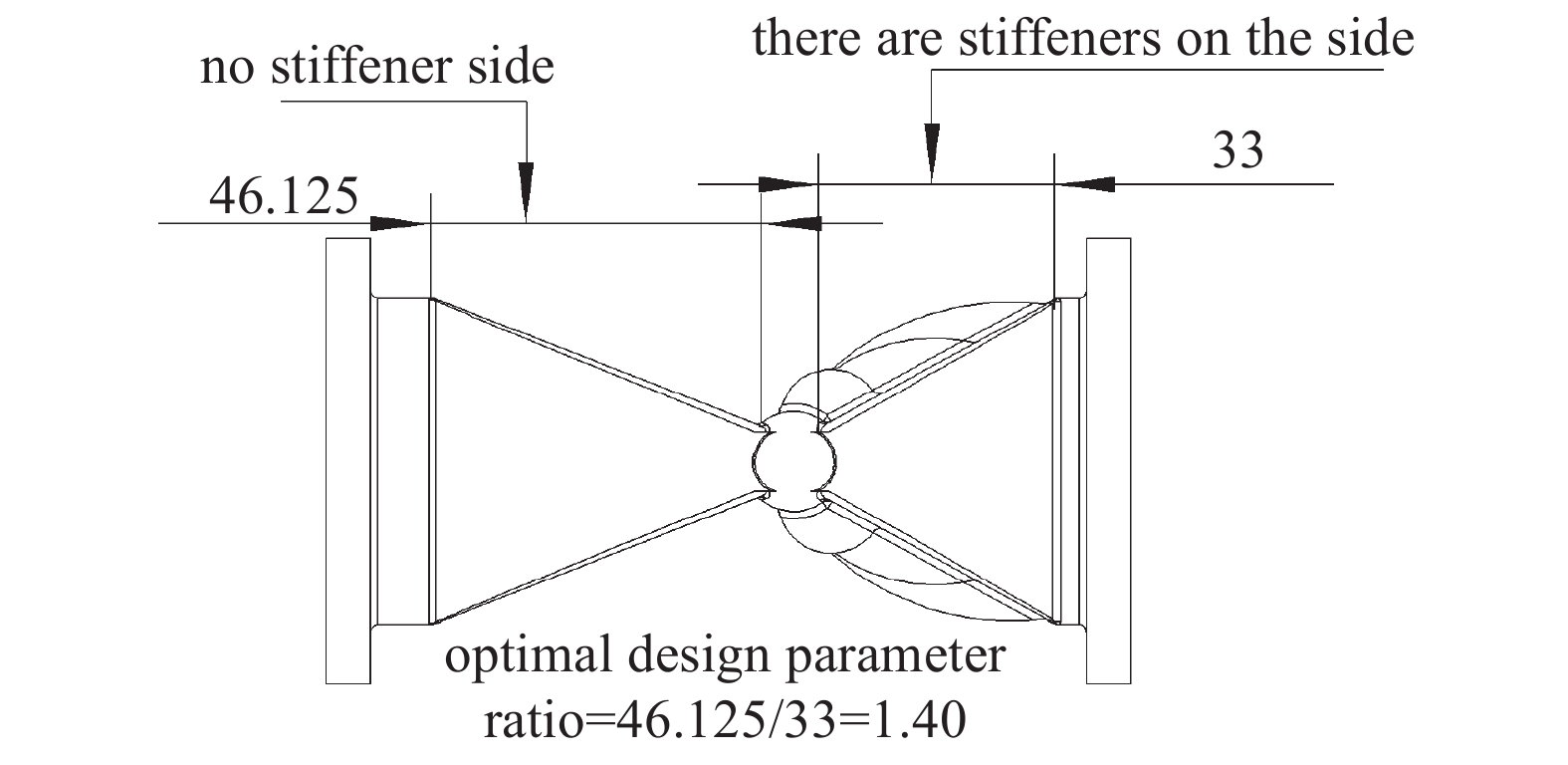
夹管式真空界面阀的阀门优化原则主要包括密封性能优化、耐久性优化、维护便捷性优化、通过性优化四点,由于阀体采用图2(b)所示三段式结构,阀芯采用橡胶材料,保证了其密封性、耐久性、维护便捷性,因此对阀门通过性进行优化。探究阀芯的结构对其形变量产生的影响,改变非加强筋一侧的斜面尺寸,水平端面尺寸示意图如图9,端面水平距离分别为33 mm,37.375 mm,41.75 mm,46.125 mm,50.5 mm五种结构。
将模型导入ANSYS中进行非结构化网格划分,为了网格尺寸对仿真结果影响。以33 mm模型,开度为100%为例,完成网格无关性验证。从表3中可知,在网格尺寸小于等于3 mm时,最大形变量基本不变,考虑到计算资源与计算精确,因此将网格尺寸设置为3 mm。
-
CFD是一门研究流体力学现象及其数值计算方法的学科,基于数学模型和计算方法,通过数值模拟来研究流体在不同条件下的运动、变形和相互作用。利用该技术可以更好地理解和优化流体系统的行为与性能,并且在描述橡胶等超弹性材料的变形行为时,通过流体力学的理论和实验方法,可以了解橡胶材料在不同应力和应变条件下的行为,为橡胶等超弹性材料制品的设计和应用提供基础。
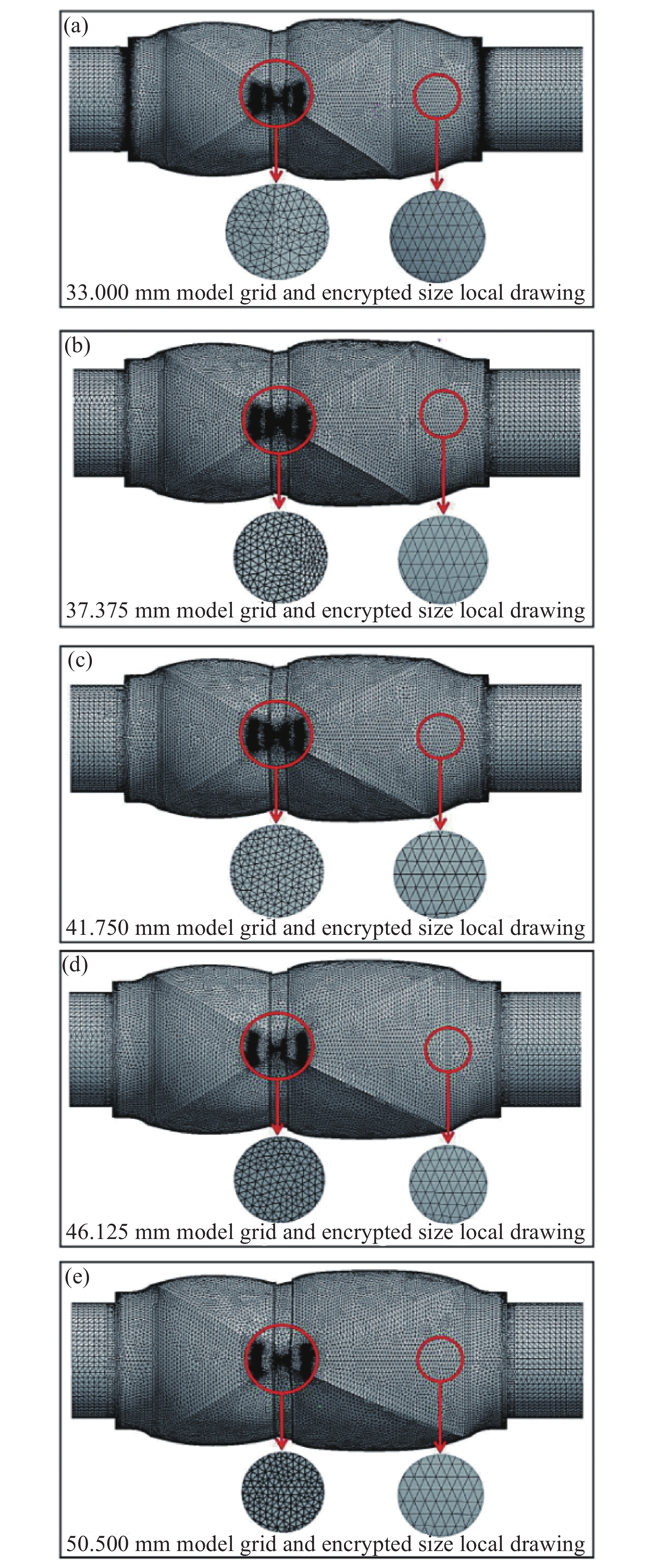
为探究五种结构模型在全开状态下的通过性,利用CFD对各模型进行稳态流场分析,结合DPM粒子模型,检测出口各尺寸粒子所占百分比,验证阀芯通过性。在前处理中抽取阀门流体域,由于进、出口管长较短,为了提高计算精度,得到稳定流场,对流体域进、出口进行适当处理拉伸,因此将进口端管长取3d,出口端管长为5d;d为真空界面阀阀门直径,数值为32 mm。对不同结构模型在70 kPa下全开状态进行流场域的抽取,其流场域模型如下图10所示。整体计算域采用非结构化四面体划分,以网格单元尺寸为自变量划分网格,观察模拟结果中出口质量流率的变化,以33 mm模型为例完成网格独立性验证,具体如下表4所示。当网格尺寸为1.5 mm时,出口的质量流率基本不变,因此网格尺寸设置为1.5 mm,为了提高流场模型的网格质量,对流场域模型两侧网格质量低的特征进行局部网格加密,加密尺寸为0.1 mm,具体网格如下图11所示。
-
阀芯开启最大真空度为70 kPa,设置压强变化分别15 kPa、42 kPa、70 kPa,阀芯两端为固定。
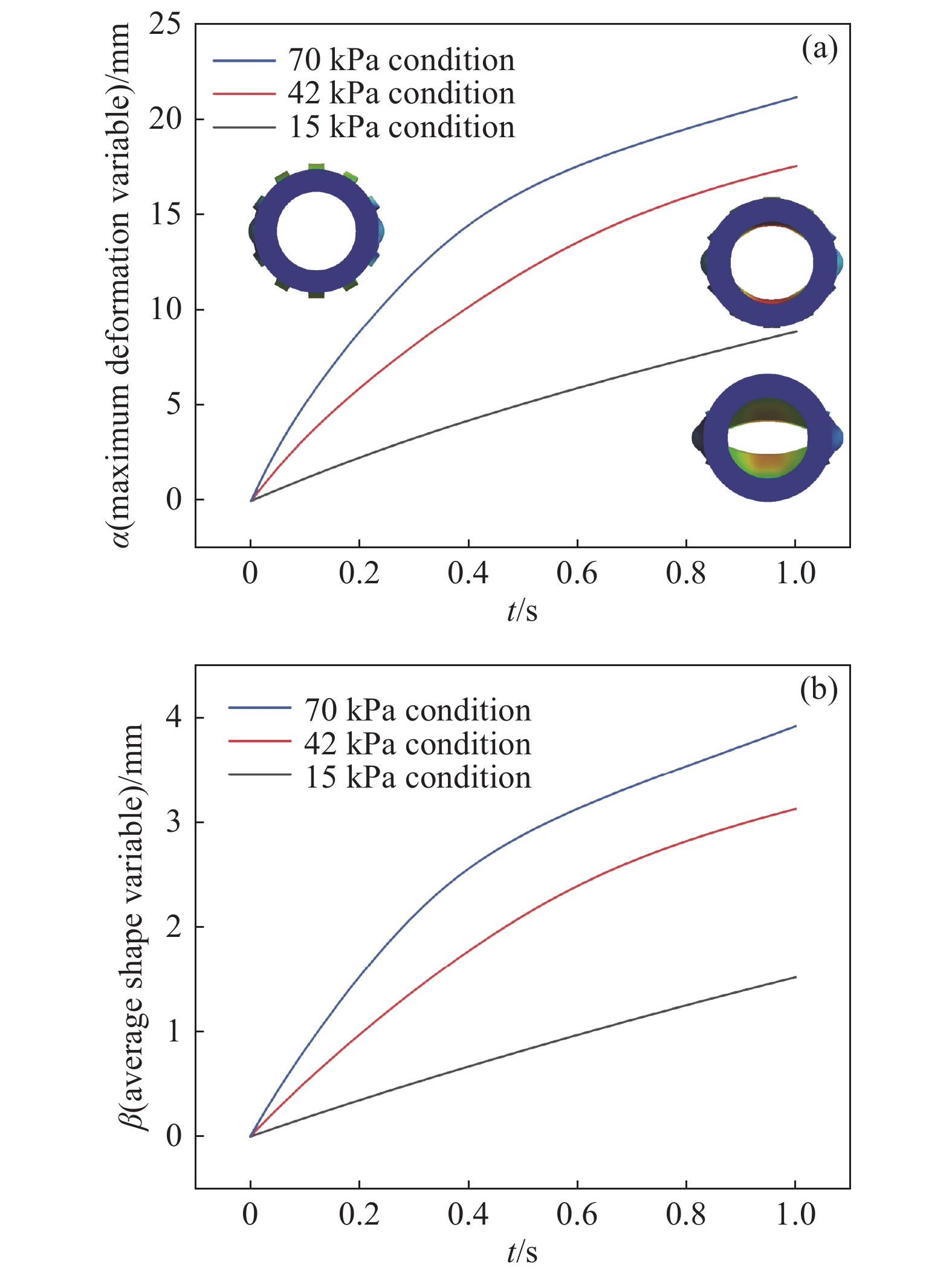
以原始模型33 mm的橡胶阀芯为探究对象,在压强不同的情况下,橡胶阀芯形变曲线如下图12所示。负压由0逐渐增大时,阀芯形变逐渐增大,根据图12(a)阀芯最大形变曲线所示,随着压强不同,阀芯最大形变曲线α不同,在15 kPa的压强下,曲线增加较缓慢,斜率较小,单位时间下α最小,随着时间增大,曲线斜率变化不大;压强42 kPa的情况下,曲线斜率相较于压强15 kPa工况下增大,随着时间增大,曲线斜率逐渐减小,单位时间下α逐渐减小;压强70 kPa下,曲线斜率最大,在0.4 s时,曲线有明显转折,这是橡胶材料的硬化作用导致的,由于70 kPa工况下形变较大,此时较接近于材料屈服点,塑性应变的增加,材料变得更强、更难以形变。
在不同压强下,橡胶阀芯平均形变曲线如下图12(b)所示。阀芯平均形变量β与最大形变规律相似,随着压强的增大,曲线斜率逐渐增大,单位时间下β逐渐增加;同一工况压强条件下,随着时间推移,曲线斜率减小,单位时间下β减小。
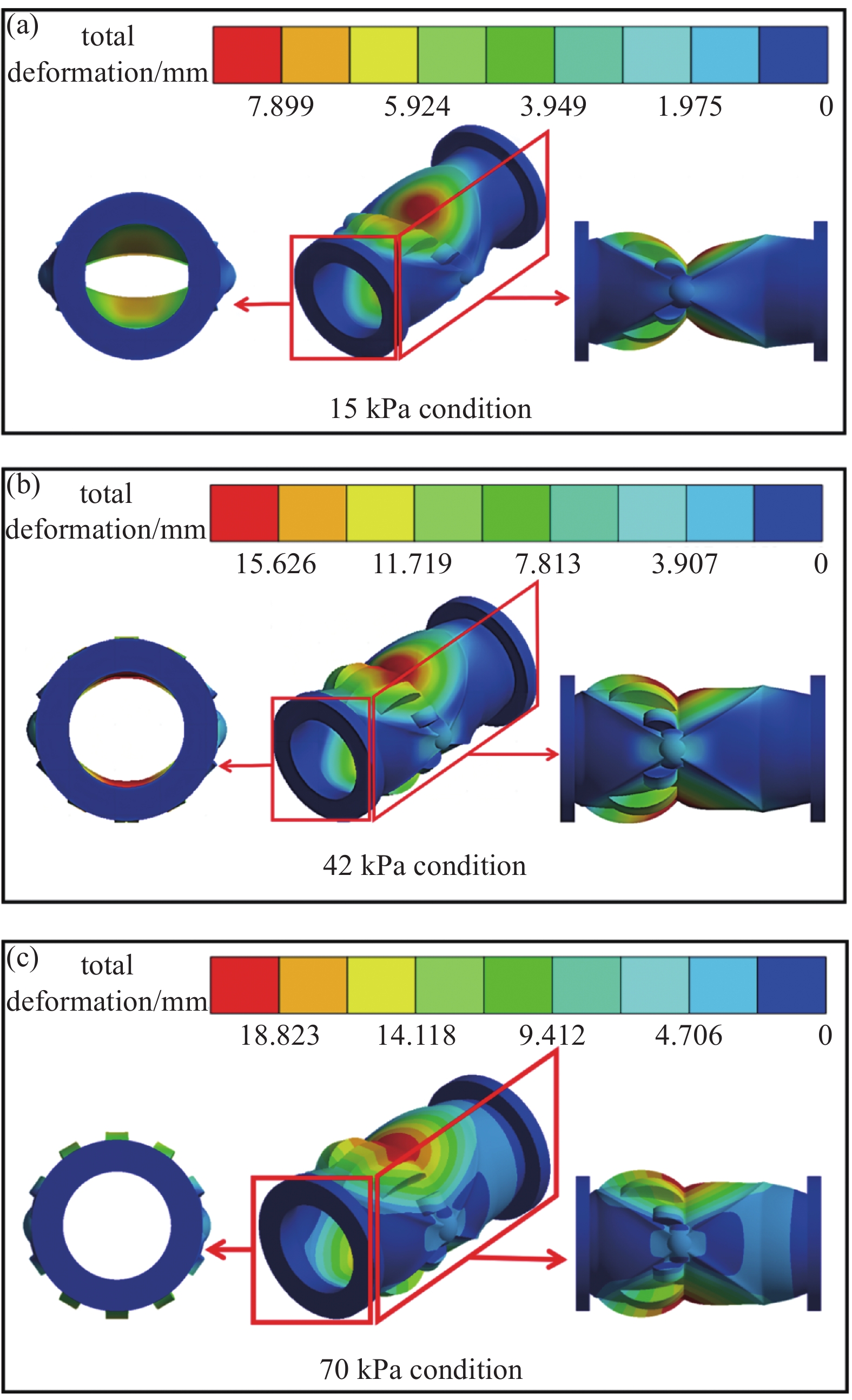
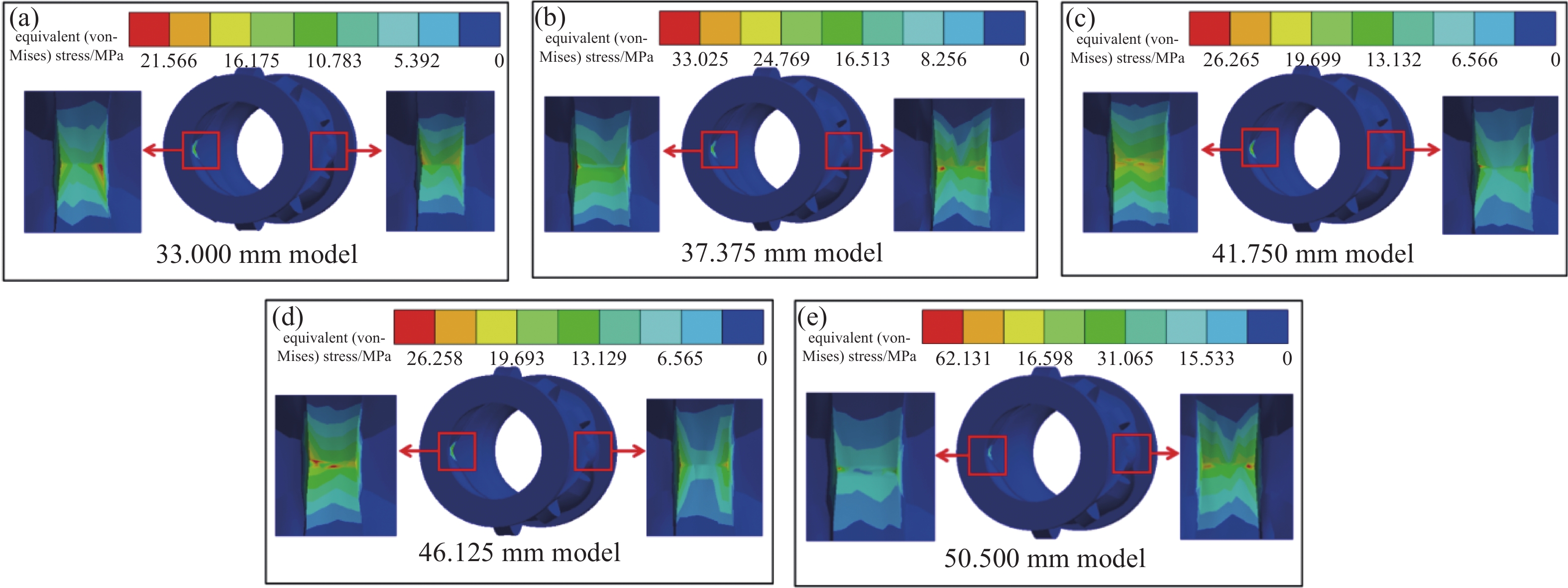
对于不同压强下阀门的形变状态,仿真形变云图如图13所示。从云图可以看出最大形变处都位于阀芯中部,在15 kPa、42 kPa、70 kPa下,最大形变量分为8.886 mm、17.579 mm、21.176 mm,并且最大形变处都位于阀芯中部,并且越靠近阀芯两端,阀门形变量越小。从云图正面看,15 kPa压强较小,阀门的开度较小,由于真空界面阀橡胶阀芯开启真空度为15~70 kPa,在15 kPa条件下,阀门能够正常开启,因此该结构满足真空界面阀橡胶阀芯开启真空度要求。
-
真空界面阀开启真空度最大为70 kPa,边界条
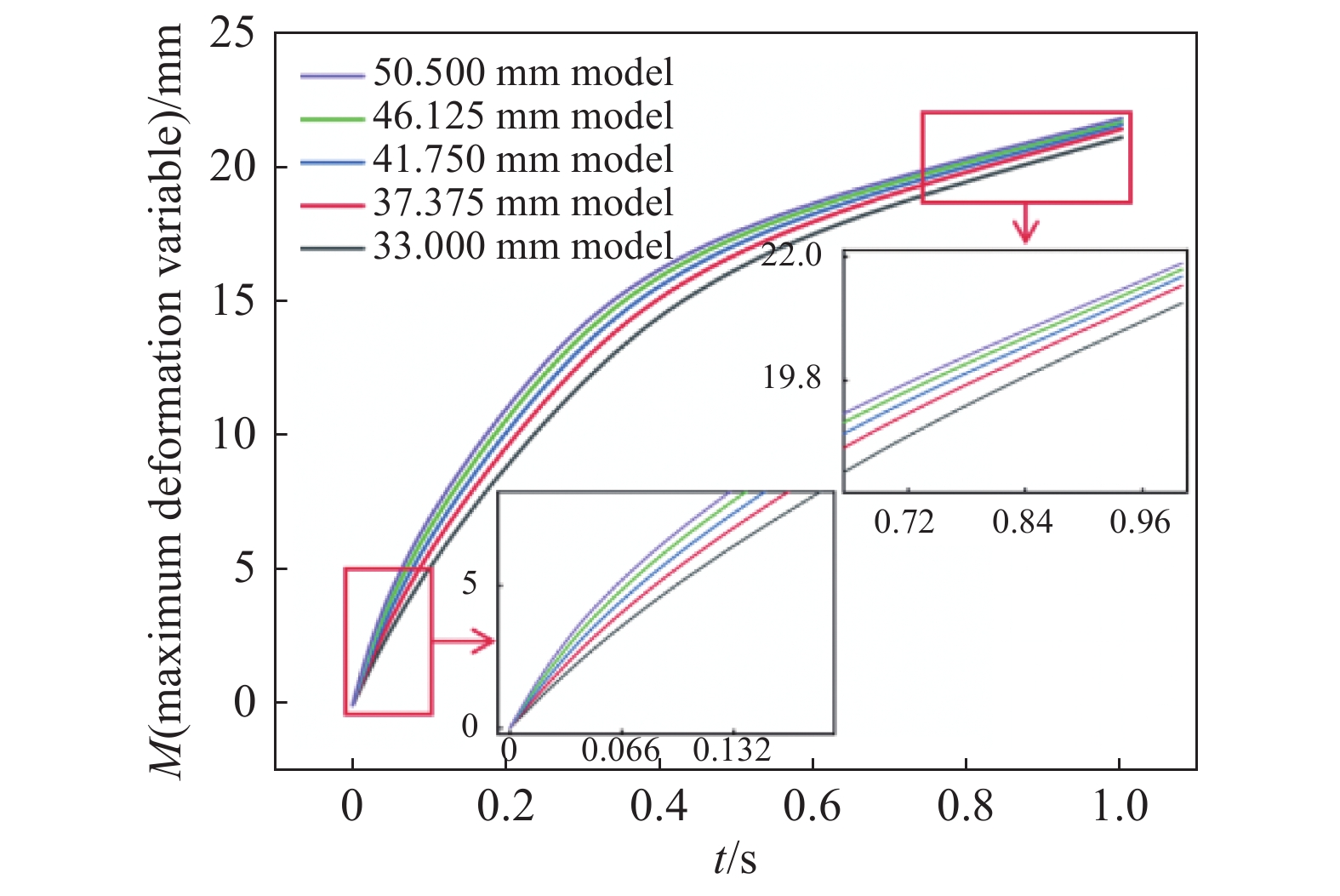
件设置阀芯受到的内外压强差为70 kPa,阀芯两端为固定。具体全开状态最大形变量M数据如图14所示。随着时间的推移,模型形变量增大,在同一时刻下的各模型M差值减小,对应最大形变量分别为21.176 mm、21.49 mm、21.652 mm、21.749 mm、21.887 mm。水平端面距离越大的模型最大形变量M越大,并且在形变过程中,水平端面距离越大的模型在任意时刻的M始终大于水平端面距离小的,因此阀门能够通过的污物的最大体积越大,阀门抗堵塞能力也越强。
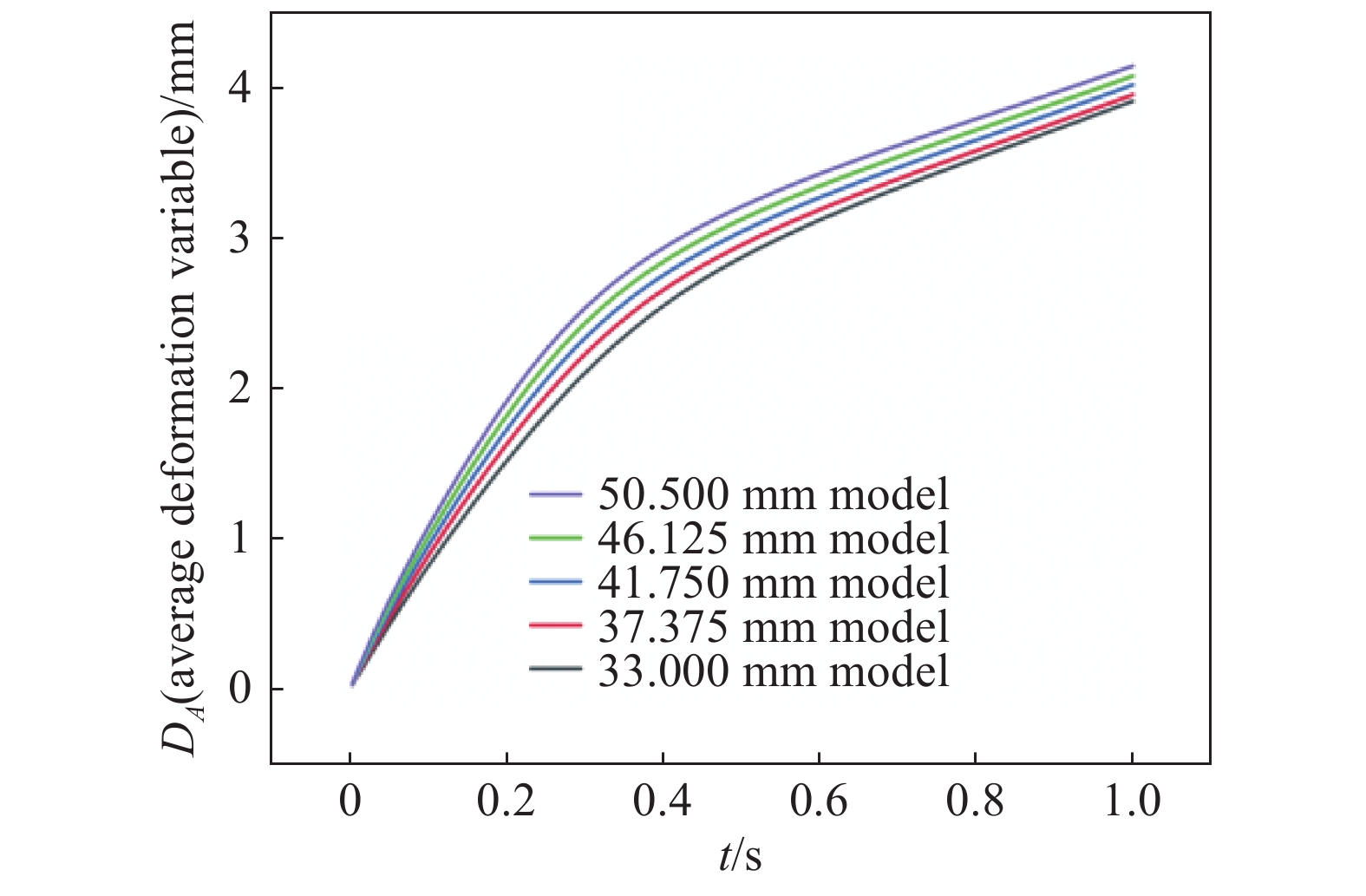
阀芯在开启过程中的平均形变量反映出阀芯整体结构的形变程度。具体平均形变量DA数据如图15所示。与最大形变量规律相同,水平端面距离越大的模型DA始终大于水平端面距离小的模型,33 mm、37.375 mm、41.75 mm、46.125 mm、50.5 mm模型在全开度下平均形变量分别为3.9173 mm、3.9595 mm、4.0246 mm、4.0841 mm、4.1515 mm,因此对于五个不同模型,50.5 mm阀芯模型在任意阶段下,最大形变量与平均形变量均优于其他四个模型,在相同时间排污情况下,50.5 mm的阀芯能够通过污物的体积更大。
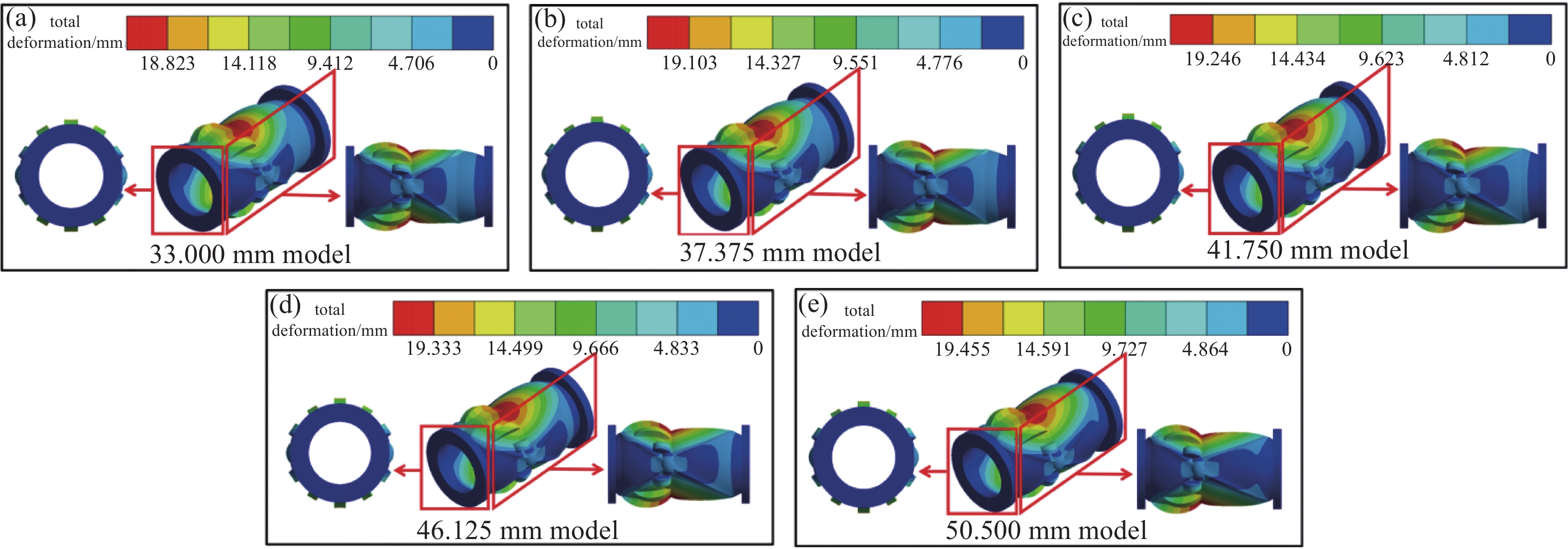
对于阀门70 kPa工况下各模型的形变状态,仿真形变云图如图16所示。从云图可以看出,模型的最大形变处都位于阀芯中部,并且越靠近阀芯两端,阀门形变量越小,这是由于阀芯采用鸭嘴形的结构导致。在形变过程中,中部与两侧斜面逐渐形变张开,两端向中部收缩,使得阀芯获得最大的容积,保证进出口尺寸不变的情况下,阀门的流通效率得到保障。结合图16中图例,50.5 mm模型由于水平端面距离最大,因此形变范围以及形变尺寸均优于其他模型。
-
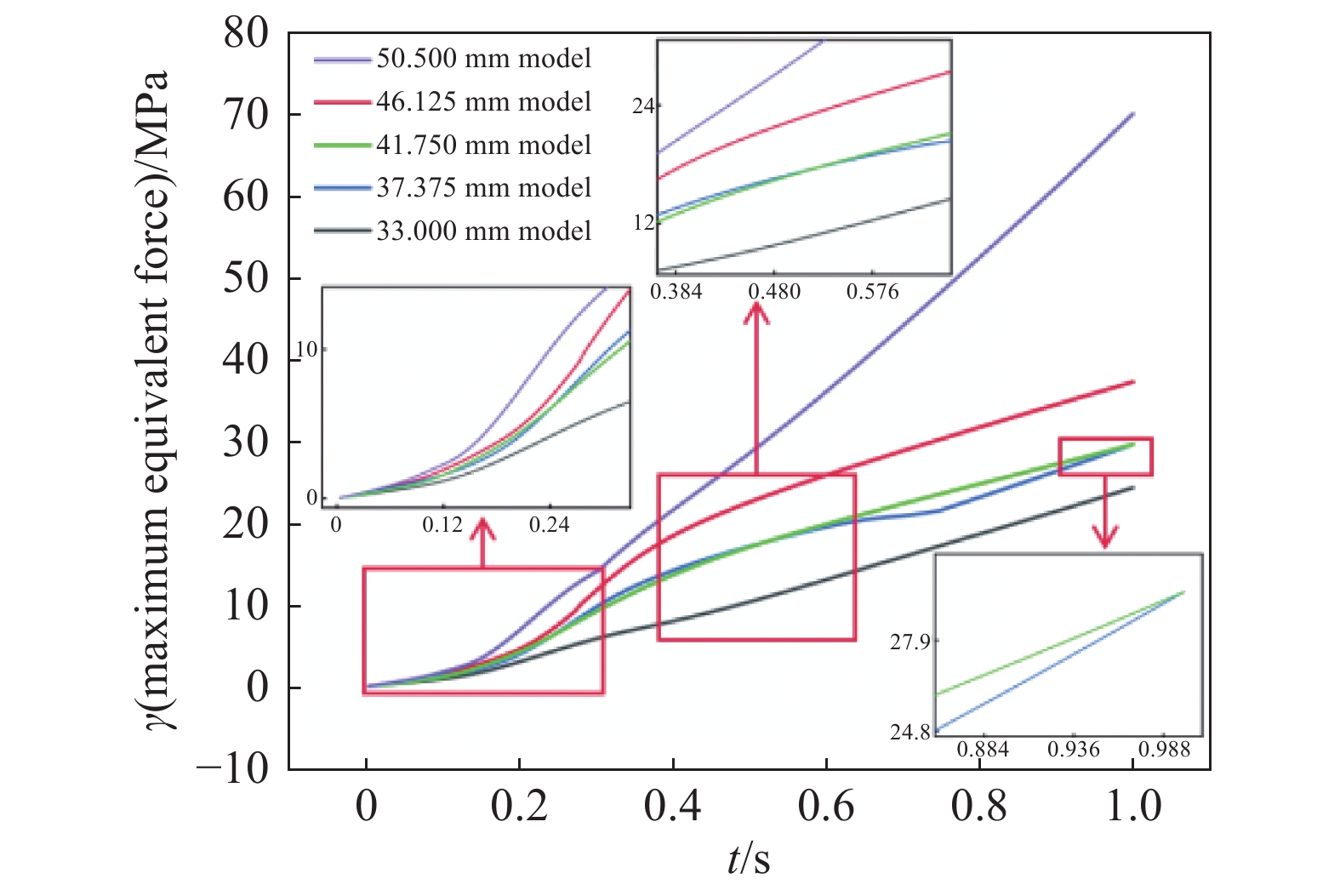
在阀门形变过程中,橡胶会发生塑性变形[16],各模型橡胶阀芯所受最大等效应力γ如下图17所示。50.5 mm模型全过程应力始终大于其余四种模型,在达到全开工况下时,50.5 mm模型γ为69.897 MPa。33 mm模型应力始终最小,在全开工况下时,γ为24.262 MPa。在形变初期,37.375 mm、46.125 mm、41.750 mm三种模型所受应力相差不大,在0.3 s之后37.375 mm模型较另外两种模型应力变化较大,在达到全开工况下时,其γ为37.153 MPa。46.125 mm、41.750 mm两种模型在形变过程中,应力曲线变化规律相似,在两者都达到全开工况下,41.750 mm、46.125 mm模型γ分别为29.548 MPa、29.54 MPa。因此可知水平端面距离增大,其γ变化为先增后减,在50.5 mm模型下其应力又剧增。
对于阀门全开状态下所受应力状态。各模型等效应力云图如图18所示。从各模型云图中可知,模型的最大应力都集中于橡胶阀芯内壁两侧狭窄处,这往往也是阀门失效破损处。已知样本2的拉伸强度为137.2 MPa,所受应力最大的50.5 mm模型应力为69.897 MPa,远远小于样本2的拉伸强度,符合设计要求。
-
流场模拟设置为单相流稳态计算,湍流模型采用SST k-omega模型,流体设置为水,重力设置为−9.81 m/s2,设置压力入口,压力出口,入口压强设置为大气压,压力出口负压设置为70 kPa,水力直径为32 mm。管壁设置为wall,壁面DPM离散相模型条件设置为trap,用以模拟污水流经阀门管道时,壁面对污水颗粒的粘附作用。离散相DPM粒子喷射源类型为surface,从入口释放,直径分布为rosin-rammler,总流量为1 kg/s。根据污水悬浮物粒径标准解析[17],城市污水处理设备一体化,水中的悬浮物质是颗粒直径约在1~10 mm。因此设置DPM最小直径为1 mm,最大直径为10 mm,平均直径设为5 mm,采用压力速度耦合Coupled算法。本次计算收敛结果较为理想,迭代计算230次达到设计残差值,从而收敛计算。
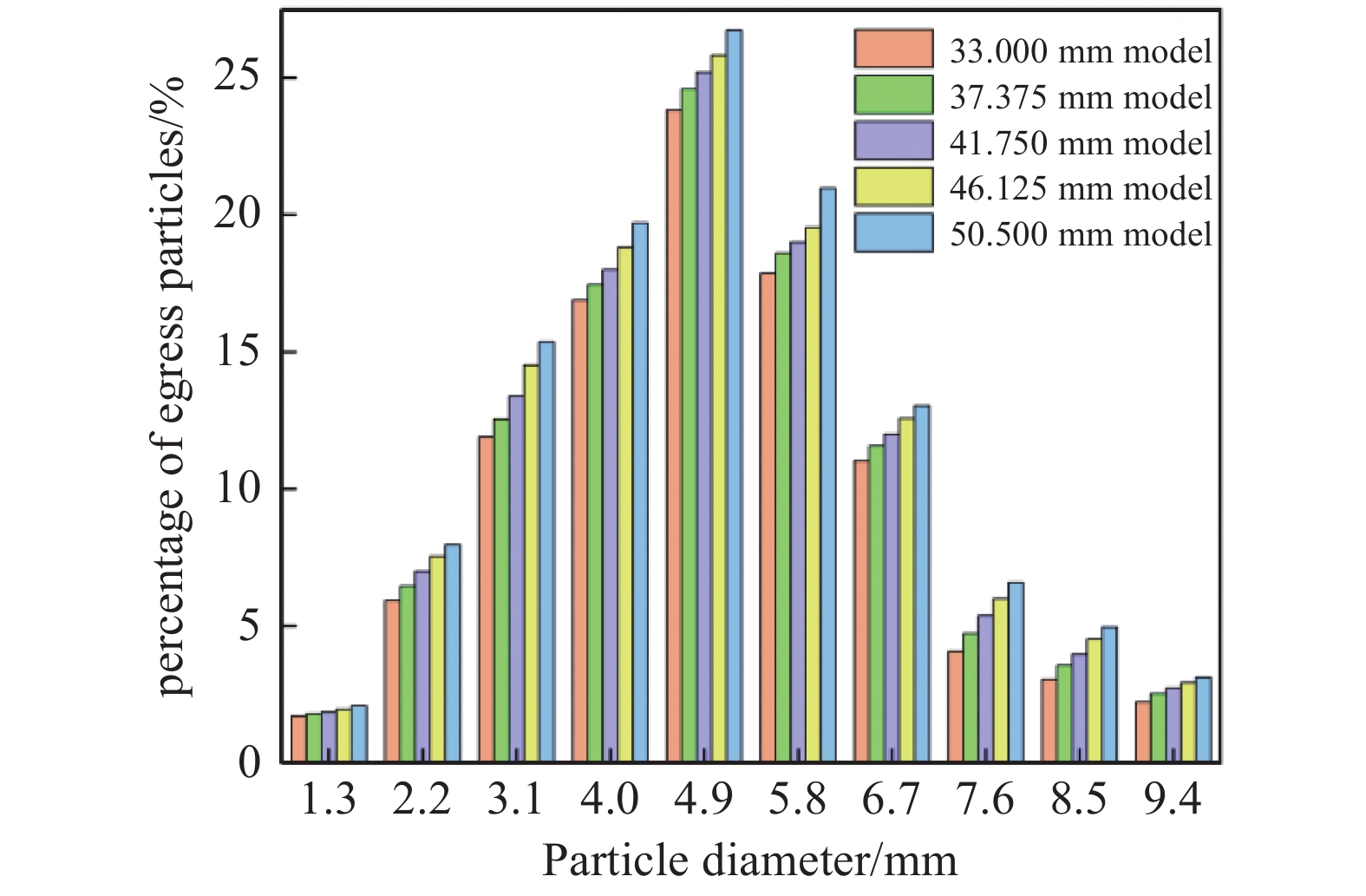
离散相采样边界选出口边界,监测出口处不同尺寸粒子所占百分比,具体数据如图19所示。由图19可知,水平端面距离与各尺寸粒子在出口粒子所占百分比成正比,并且粒子的直径与出口粒子百分比呈现正态分布的趋势,具体表现为直径4.9 mm的颗粒所占百分比均接近于25%,随着粒子直径增大或减小,出口粒子百分比均降低。出口粒子中任意粒子直径所占百分比,均为50.5 mm模型最大。考虑到阀门结构优化,不仅要保证其通过性,还要保证橡胶阀芯应力较小,以33 mm模型所受应力为基准,其余模型应力的增加量与33 mm模型所受应力的比值为应力增大率。具体阀门出口粒子所占百分比与应力增大率如下表5所示,50.5 mm模型通过性最佳,但其所受应力相较于33 mm模型,应力增大率为188%,综合考虑最优结构为46.125 mm模型。该模型相较于除了50.5 mm以外模型而言,出口平均粒子直径所占百分比和出口最大粒子直径所占百分比均为最大,与50.5 mm模型相比,出口平均粒子直径所占百分比和出口最大粒子直径所占百分比相差不大,但应力幅值得到大幅度减小。因此将阀芯通过性强且所受应力较小的结构模型无加强筋一侧水平端面距离与有加强筋一侧水平端面距离的比值定义为最佳设计参数比,该最佳设计参数比1.40:1,具体如下图20所示。
-
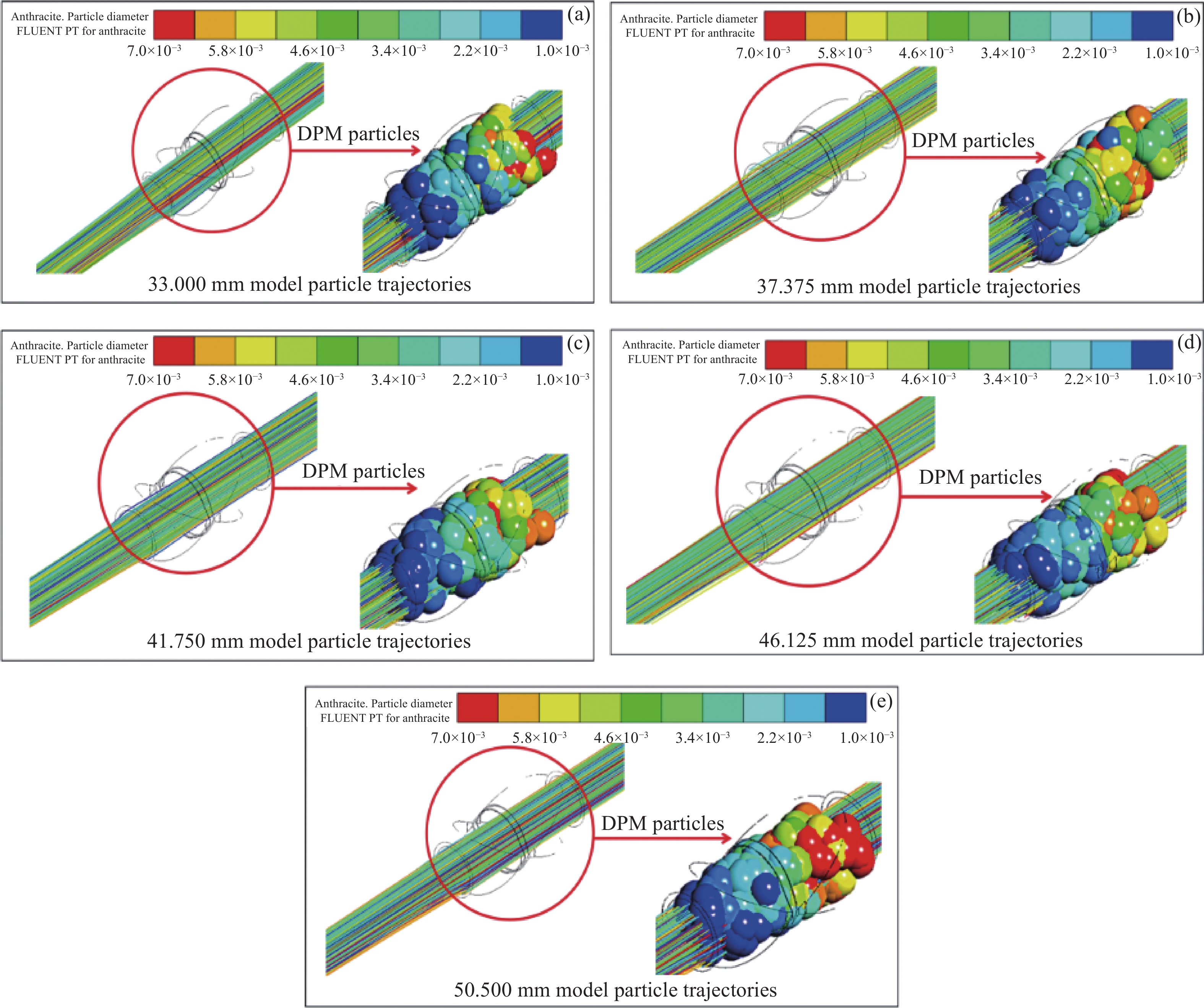
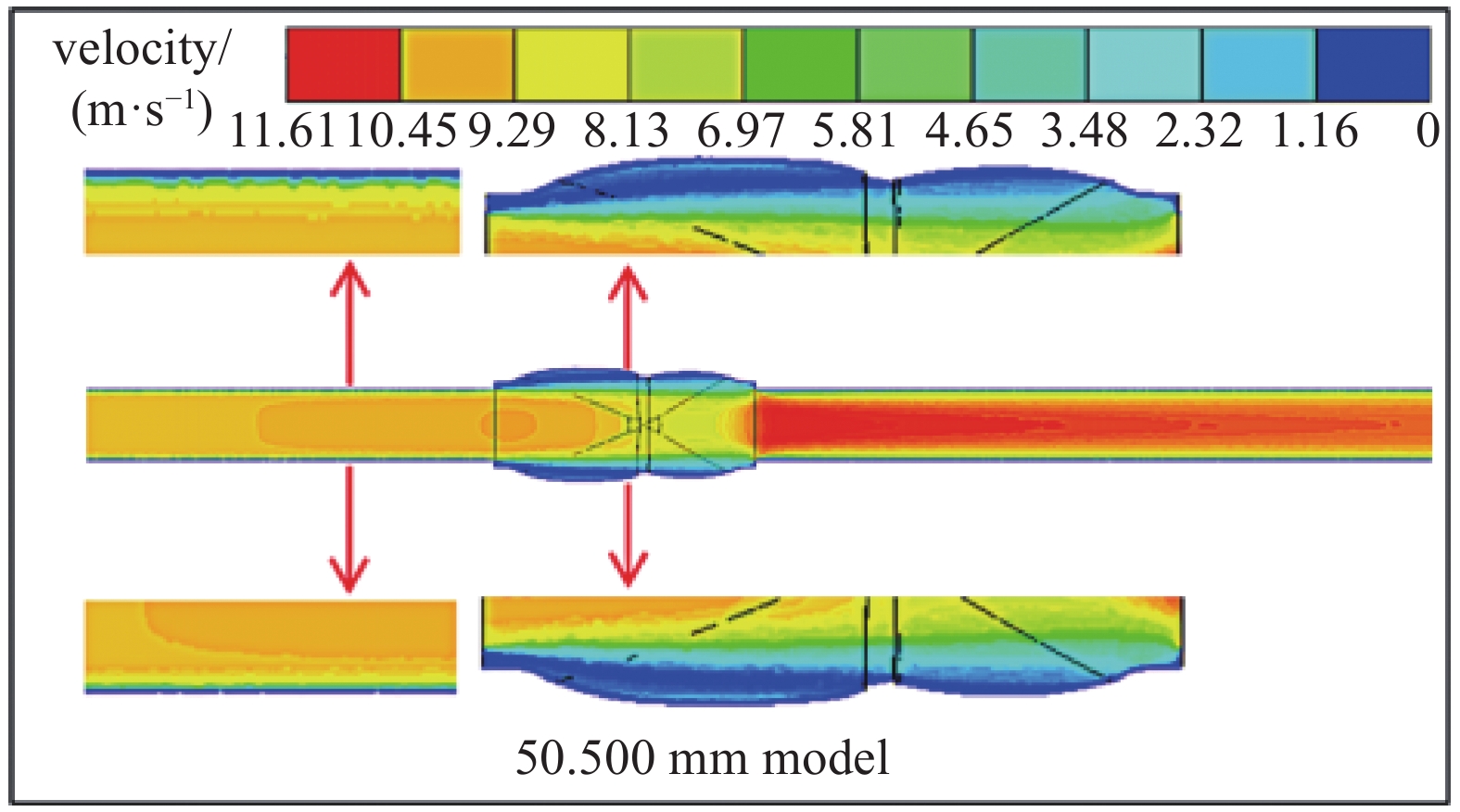
为探究出口粒子的直径与出口粒子百分比呈现正态分布的原因,壁面采用trap,颗粒有一部分会吸附于壁面,造成粒子损耗。图21为不同模型颗粒图,由图可知,污水颗粒在阀门内的分布情况与其直径有关,离出口越远的颗粒直径越大,直径越大粒子质量越大。由于壁面对于粒子的捕捉,33 mm模型捕捉粒子为912,37.375 mm模型捕捉粒子为807,41.75 mm模型捕捉粒子为716,46.125 mm模型捕捉粒子为695,50.5 mm模型捕捉粒子为541。随着模型水平端面距离结构的增大,壁面粒子捕捉的数目逐渐减少。这是阀门的平均形变量以及最大形变量所导致的,33 mm模型平均形变量以及最大形变量均为最小,直径大的粒子在进入阀门时,相对于直径小的粒子,速度较小,考虑萨夫曼剪切提升力[18]的影响,其公式为:
其中Flift为剪切提升力的矢量,表示颗粒所受的力,a为颗粒半径,
$ \eta $ 是流体的动力粘度,u是流体速度矢量,$ \nabla $ 表示梯度运算。重力大于萨夫曼剪切提升力,粒子做类抛物线运动,由于形变较小,粒子相对壁面距离更近,壁面所捕捉的粒子最多。其余模型同理,因此可知阀门形变量与壁面对直径大粒子捕捉数目成反比,同时说明图19中直径越大的粒子在出口占比越小的原因。在给水管道中,如果颗粒的速度小于流体的速度,萨夫曼升力会推动颗粒向管心运动,因此直径在中等程度的粒子被壁面捕捉较少。速度分布结果如下图22所示。污水在经过管道及阀门时,流体速度是呈现正态分布的趋势,具体表现为,管道以及阀门内部中间的污水速度最大,由于受到液体粘度影响,在靠近壁面两端速度逐渐变小,当污水由管道进入阀门的瞬间,阀门内部空间较管道而言,空间较大,因此越靠近壁面的污水在进入阀门时,速度衰减较快,以50.5 mm模型为例,当污水位于管道时,靠近管道壁面的污水流速为8.58 m/s,进入阀门的瞬间,速度衰减为3.48 m/s,并且越靠近阀门壁面时,速度梯度越大,由于受到靠近壁面污水速度衰减的影响,中间部分的污水速度也有一定程度的衰减;当靠近出口时,阀门空间较出口管道而言较大,因此当污水进入出口管道时中间部分的污水速度梯度呈现射流状,速度最大时达到11.61 m/s。当阀门尺寸不同时由于阀门形变量不同,因此相对应的阀门内部空间不同,所导致的污水速度有所差异。随着速度的变化,受到萨夫曼剪切提升力影响,颗粒的惯性产生与流体不同的速度,加强颗粒向管壁处运动,由图21可知,粒子直径较小的颗粒,速度越大,由图22速度云图可知,直径较小的颗粒受到萨夫曼剪切提升力作用,朝着壁面运动,结合图19中直径越小的粒子在出口占比越小,因此粒子直径越小的颗粒被壁面所捕捉越多。由此结合图21与图22分析,较好的说明粒子的直径与出口粒子百分比呈现正态分布趋势的原因。
-
将设计的真空界面阀进行3D打印,具体零件如图23所示。由图13可知33 mm模型在不同压强下开度不同,因此对33 mm模型进行开度实验测试,将阀门导气管与真空源相连,工况与仿真边界条件对应,实验原理及实物图如下图24所示,将真空源的负压值分别设置为15 kPa、42 kPa、70 kPa,测试阀门在不同压强下的变形程度,具体比较结果如图25所示,实验测绘阀门最大形变量分别为17 mm、34.3 mm、41.1 mm,可知实验与仿真结果相差不大。
为校验材料强度,结合图18可知,50.5 mm所受应力最大,因此对其进行压强70 kPa下的形变实验,具体实验结果如图26所示,由图可知在形变最大工况下,阀门并未发生破损,该材料强度符合设计要求。
-
本文以橡胶界面阀为研究对象,通过探究不同压强下对阀芯的形变影响、不同结构对阀芯的形变和应力影响,以及阀芯结构对阀通过性的影响规律,现得出以下结论:
(1)通过在不同压强下对33 mm阀门进行数值模拟可知,压强不同情况下,单位时间下的最大形变量和平均形变量逐渐增加;随着时间推移,塑性应变的增加,单位时间下的最大形变量和平均形变量逐渐减小。
(2)通过在70 kPa下,对不同结构橡胶阀芯进行数值模拟,水平端面距离越大的模型最大形变量和平均形变量始终大于水平端面距离小的模型。50.5 mm模型形变范围以及形变尺寸均优于其余模型,并且五个模型中,50.5 mm模型应力最大,其应力值为69.897 MPa,小于材料样本2的拉伸强度为137.2 MPa,符合设计要求。
(3)通过对全开状态下不同结构模型进行流场分析,比较各尺寸粒子在出口所占百分比的大小来验证其通过性的同时,综合考虑应力及通过性情况,确定最优结构为46.125 mm模型,最佳设计参数比为1.40:1。
(4)颗粒直径越大,重力越大,粒子速度越小,萨夫曼剪切提升力减小,粒子朝着壁面运动被捕捉。随着颗粒直径减小,重力减小,粒子速度增大,萨夫曼剪切提升力增大,逃逸壁面捕捉的粒子较多,因此中等粒子大小在出口所占百分比最大。在粒子直径进一步减小,此时速度进一步增大,萨夫曼剪切提升力大于重力,直径小的粒子被壁面所捕捉,出口所占百分比减小。
夹管式真空界面阀设计与通过性模拟研究
Vacuum Interface Valve Design and Pass-through Simulation
-
摘要: 船舶上的真空排污系统中作为阻隔大气与真空的核心部件真空界面阀,设计一款可靠实用的真空界面阀对整个真空排污系统至关重要。文章设计了一款真空界面阀,利用ANSYS Workbench对橡胶阀芯进行有限元分析,探究压强不同、阀芯结构不同情况下形变量与应力规律,利用DPM粒子模型检测出口粒子所占百分比模拟通过性,得出界面阀的最佳设计参数比例为1.40:1。通过出口粒子呈现正态分布现象,结合粒子轨迹云图、速度云图,分析出口粒子呈现正态分布原因在于直径不同的粒子,质量速度不同,粒子受到重力以及萨夫曼剪切提升力作用不同,解释了出口粒子分布原因。由于阀芯结构导致的形变量不同,使得粒子离壁面的距离不同,因此不同结构模型壁面对粒子的吸收程度也不同,这就使得出口粒子所占百分比不同,由此分析解释了真空界面阀结构不同所导致的阀门通过性差异。Abstract: As the core component of the vacuum interface valve that separates the atmosphere and vacuum in the vacuum sewage system on ships, the design of a reliable and practical vacuum interface valve is crucial to the whole vacuum sewage system. In this paper, a vacuum interface valve is designed, using ANSYS Workbench to carry out finite element analysis on the rubber spool on the rubber spool, to explore the shape variable and stress law under different pressure and spool structure, and to simulate the passability by utilizing the DPM particle model to detect the percentage of exported particles, and to conclude that the optimal ratio of the interface valve's design parameter is 1.40:1, and that the exported particles show a normal distribution phenomenon. Combined with the particle trajectory cloud map and velocity cloud map, we analyze that the reason for the normal distribution of the exit particles is that particles with different diameters have different mass velocities, and the particles are subject to different gravitational forces as well as different Saffman's shear lifting forces, which explains the reason for the distribution of the exit particles. Due to the different shape variables caused by the spool structure, the distance of the particles from the wall surface is different, so the wall surface of different structural models absorbs particles to a different extent, which makes the percentage of exported particles different, and this analysis explains the differences in the passage of the valve caused by the different structures of the vacuum interface valve.
-
Key words:
- Vacuum interface valve /
- Constitutive models /
- Structural deformation /
- DPM particle model /
- Passability .
-

-
图 11 网格及加密尺寸局部图。(a) 33 mm模型网格图,(b) 37.375 mm网格图,(c) 41.75 mm网格图,(d) 46.125 mm网格图,(e) 50.5 mm网格图
Figure 11. Partial view of grid and encryption dimensions. (a) 33 mm model grid view, (b) 37.375 mm model grid view, (c) 41.75 mm model grid view, (d) 46.125 mm model grid view, (e) 50.5 mm model grid view
图 16 不同结构下橡胶阀芯形变云图。(a) 33 mm模型形变云图,(b) 37.375 mm模型形变云图,(c) 41.75 mm模型形变云图,(d) 46.125 mm模型形变云图,(e) 50.5 mm模型形变云图
Figure 16. Cloud diagram of rubber spool deformation under different structures. (a) 33 mm model deformation contour, (b) 37.375 mm model deformation contour, (c) 41.75 mm model deformation contour, (d) 46.125 mm model deformation contour, (e) 50.5 mm model deformation contour
图 18 不同结构下阀芯等效应力云图。(a) 33 mm模型应力云图,(b) 37.375 mm模型应力云图,(c) 41.75 mm模型应力云图,(d) 46.125 mm模型应力云图,(e) 50.5 mm模型应力云图
Figure 18. Iso-effect force cloud diagram of valve core under different structures. (a) 33 mm model stress contour diagram, (b) 37.375 mm model stress contour diagram, (c) 41.75 mm model stress contour diagram, (d) 46.125 mm model stress contour diagram, (e) 50.5 mm model stress contour diagram
图 21 不同模型颗粒图。(a) 33 mm模型颗粒图,(b) 37.375 mm模型颗粒图,(c) 41.75 mm模型颗粒图,(d) 46.125 mm模型颗粒图,(e) 50.5 mm模型颗粒图
Figure 21. Particle maps of different models. (a) Particle plot of the 33 mm model, (b) particle plot of the 33 mm model, (c) particle plot of the 33 mm model, (d) particle plot of the 33 mm model, (e) particle plot of the 33 mm model
表 1 DPI8400材料参数
Table 1. DPI8400 material parameters
项目 技术参数 材料成分 A液 黑色 多元醇 B液 无色 异氰酸酯 C液 乳白色 氢气二甲基硅氧烷,二甲基硅醇 表 2 三种材料样本物性参数
Table 2. Physical property parameters of three material samples.
参数 单位 样本1 样本2 样本3 混合比 A:B:C 100:100:0 100:100:50 100:100:150 硬度 ShoreA 90 80 60 拉伸强度 kg/cm2 180 140 70 伸度 % 200 240 280 扯裂强度 kg/cm 70 60 30 回跳弹性 % 50 52 56 收缩率 % 0.6 0.5 0.4 表 3 网格独立性验证
Table 3. Grid independence verification
网格尺寸/mm 单元数 节点数 最大形变量/mm 2 131859 358661 21.38 2.5 116214 282934 21.49 3 93200 192553 21.49 3.5 90799 177741 21.73 表 4 网格独立性验证
Table 4. Grid independence verification
网格尺寸/mm 单元数 节点数 出口流量/kg·s−1 0.5 8704600 2156969 0.033 1 3261684 628431 0.035 1.5 2016819 386252 0.035 2 1706193 332858 0.041 表 5 模型应力增大率以及出口粒子百分比
Table 5. The rate of stress increase in the model and the percentage of particles egress
水平端面距离/mm 33 37.375 41.750 46.125 50.5 出口平均粒子直径
所占百分比/%24.221 24.491 24.749 24.918 25.031 出口最大粒子直径
所占百分比/%2.229 2.532 2.729 2.930 3.130 应力增大率/% 0 53 21 21.8 188 -
[1] 邵佳, 单立军. 真空排污系统的选型分析[J]. 能源与节能,2017,127(5):105−106(in chinese) doi: 10.3969/j.issn.2095-0802.2017.05.051 Shao Jia, Shan Lijun. The selection and analysis of the vacuum drainage systems[J]. Energy and Energy Conservation,2017,127(5):105−106 doi: 10.3969/j.issn.2095-0802.2017.05.051 [2] 范顺治. 物联网的舰船内部真空排污系统设计与应用[J]. 舰船科学技术,2021,43(10):199−201(in chinese) doi: 10.3404/j.issn.1672-7649.2021.5A.067 Fan Shunzhi. Design and application of vacuum sewage system inside ships of the internet of things[J]. Ship science and technology,2021,43(10):199−201 doi: 10.3404/j.issn.1672-7649.2021.5A.067 [3] 苏凌茹, 蓝思东. 中远海客滚船真空污水系统设计[J]. 广船科技,2022,42(1):26−30(in chinese) doi: 10.3969/j.issn.2095-4506.2022.01.006 Su Lingru, Lan Sidong. Design of vacuum sewage system for cosco passenger ropa vessel[J]. Guangzhou Shipbuilding Technology,2022,42(1):26−30 doi: 10.3969/j.issn.2095-4506.2022.01.006 [4] 余清洲, 李斌, 王飞, 等. 角座式真空排污界面阀的设计与模拟研究[J]. 真空科学与技术学报,2021,41(10):986−992(in chinese) Yu Qingzhou, Li Bin, Wang Fei, et al. Design and simulation study of angle seat vacuum sewage interface valve[J]. Journal of Vacuum Science and Technology,2021,41(10):986−992 [5] Reinhold B, Tostedt(DE). Interface valve for vacuum sewer systems[P]. US, US6575425 B1, 2003−6−10 [6] 余子成. 真空排污系统界面阀及排污方式研究[D]. 武汉: 华中科技大学, 2009(in chinese) Yu Zicheng, Research on interface valve and sewage discharge method of vacuum sewage system[D]. Wuhan: Huazhong University of Science and Technology, 2009 [7] 尹户生. 真空排水系统新型界面阀的研究[D]. 武汉: 华中科技大学, 2012(in chinese) Yin Husheng. Research on a new interface valve for vacuum drainage system[D]. Wuhan: Huazhong University of Science and Technology, 2012 [8] 孙金风, 李志成, 胡龙, 等. 夹管型橡胶真空界面阀的设计及流通性能分析[J]. 真空科学与技术学报,2019,39(12):1047−1053(in chinese) Sun Jinfeng, Li Zhicheng, Hu Long, et al. Design and flow performance analysis of pinch rubber vacuum interface valve[J]. Journal of Vacuum Science and Technology,2019,39(12):1047−1053 [9] Rose M T, Pielstick B D, Jones Z T, et al. Case study: noise reduction of a vacuum-assisted toilet[J]. Noise Control Engineering Journal,2020,68(4):294−302 doi: 10.3397/1/376825 [10] 褚向前, 朱武, 何磊. 铁路列车真空厕所系统设计[J]. 真空,2011,48(6):54−57(in chinese) Chu Xiangqian, Zhu Wu, He Lei. Design of the vacuum toilet system for passenger train[J]. Vacuum,2011,48(6):54−57 [11] Romi D, Dattatraya R H, Anil K, et al. A hyper-viscoelastic constitutive model for elastomers: a case study of hydrogenated nitrile butadiene rubber and polychloroprene rubber[J]. Journal of Elastomers & Plastics, 2023 [12] Majid S, Ali K, Muhammad Z S, et al. Mechanical characterization and FE modelling of a hyperelastic material[J]. Materials Research,2015,18:918−924 doi: 10.1590/1516-1439.320414 [13] Yu C K, Peng F, Zong Z D, et al. Research on Yeoh-revised hyperelastic constitutive model considering the volume almost incompressible premise for rubber materials[J]. Journal of Elastomers & Plastics, 2023 [14] Hüsnü D, Kemal A, Yashar B. On the performance of isotropic hyperelastic constitutive models for rubber-like materials: A state of the art review[J]. Applied Mechanics Reviews,2021,73(2):020802 [15] 韩彦召, 程世昆, 严巾堪, 等. 负压排水真空便器冲水噪声的影响因素[J]. 环境工程学报,2022,16(4):1400−1406(in chinese) doi: 10.12030/j.cjee.202106065 Han Yanzhao, Cheng Shikun, Yan Jinkan, et al. Negative pressure drainage vacuum toilet flushing noise influencing factors[J]. Journal of Environmental Engineering,2022,16(4):1400−1406 doi: 10.12030/j.cjee.202106065 [16] Qiu X W, Yin H S, Xing Q C, et al. Developemt of fatigue life model for rubber materials based on fracture mechanics[J]. Polymers,2023,15(12):27−46 [17] 张远, 林佳宁, 王慧等. 中国地表水环境质量标准研究[J]. 环境科学研究,2020,33(11):2523−2528(in chinese) Zhang Yuan, Lin Jianing, Wang Hui, et al. Research on environmental quality standards for surface water in China[J]. Environmental Science Research,2020,33(11):2523−2528 [18] Rousta F, Lessani B, Ahmadi G. Particle dispersion and deposition in wall-bounded turbulentflow[J]. International Journal of Multiphase Flow,2023,158:104−307 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: