首页
登录
注册
-
真空旁路开关以其长寿命、小型化与介质环保等优势在新型电力系统保护中具有新的应用前景[1]。旁路开关的结构与性能研究主要包括配用灭弧系统的结构与绝缘性能、以及配用机构系统的结构与快速关合动作性能。由于旁路开关长期服役在分闸状态，绝缘性能对其运行可靠性具有重要影响。研究表明，采用电场物理数学模型建模与数值模拟手段进行绝缘性能影响因素分析是评估旁路开关长期运行性能的有效途径之一。旁路开关绝缘性能主要取决于其所配用的真空灭弧室，其内部以真空作为绝缘介质，其结构组成主要包括绝缘外壳、动静触头、波纹管、屏蔽罩以及动静导电杆等部件。动静触头结构以及屏蔽罩型面对真空灭弧系统的绝缘性能具有直接影响[2-4]。马士奇等[5]以12 kV/1250 A/31.5 kA真空灭弧室为对象，将水平可视图法拓展至轴对称场域中，分析电场影响因素，并以最大场强最小化为目标，实现了绝缘结构优化设计。董增波等[6]在对真空灭弧室静态绝缘性能分析中，采用非支配排序多目标遗传算法实现了电场均匀度的优化设计。
近年来，将不确定性量化方法与实际应用相结合，为解决工程可靠性问题提供了新思路[7-10]。不确定性量化是一种针对系统内各参数可能存在的误差或变化，分析其对系统整体性能影响的方法，即采用数学方法将不确定性问题转化为多个确定性问题，定量化描述系统随机过程，分析在不同因素影响下系统发生变化的概率[11]。常用不确定性量化方法主要有蒙特卡罗模拟法[12]、混沌多项式展开（Polynomial Chaos Expansion, PCE）法[13]、代理模型法、降维法等。其中，PCE法通过将不确定性问题进行有限阶数的展开，将其转化为确定性问题求解。PCE法能够简化复杂系统的计算，使用方便，但也存在不能处理过多变量的问题。
综上，本文以3.6 kV/2500 A旁路开关真空灭弧室为研究对象，构建其三维电场物理数学模型，采用有限元数值模拟手段，定量分析静态耐压下绝缘性能以及触头沿面宏观增强因子分布规律。此外，聚焦触头电极中心开槽圆角区域（在此记作De）这一场强集中区域，为研究触头电极中心开槽圆角半径（re）对于极间电场的影响，采用PCE法，对其进行不确定性分析，找到合理的参数范围，为工程设计和制备提供理论基础。
-
灭弧室电场数值模拟满足麦克斯韦方程组[14]：
式中，ρ为体电荷密度，D为电位移矢量，ε为介电常数，E为电场强度。
采用有限元法进行电场求解，边界条件如下：
式中，τ1为满足狄利克里条件的表面，τ2为满足诺伊曼条件的表面，φ0为边界条件τ1的电位，q0为边界条件τ2的电荷量。
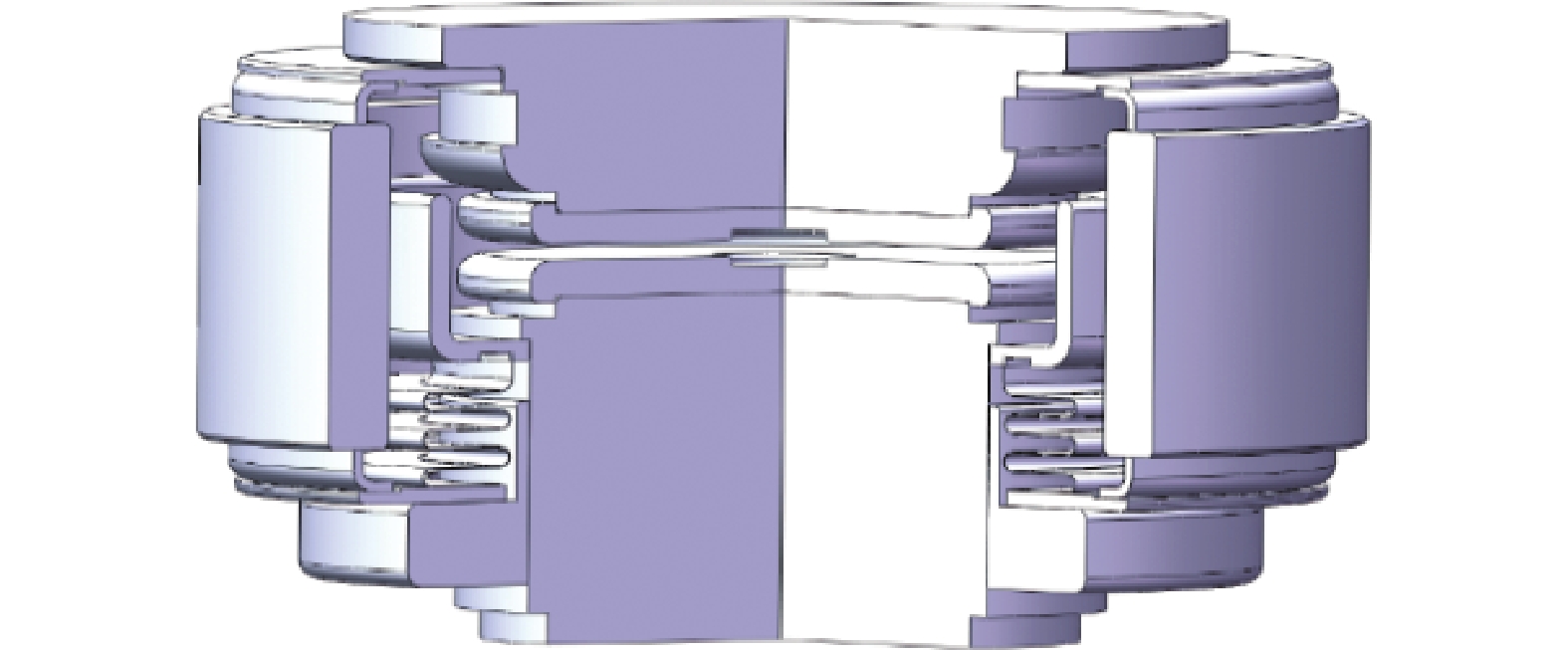
建立真空旁路开关灭弧系统三维电场仿真模型如图1所示。
灭弧室三维电场有限元数值模拟过程中，考虑真空旁路开关结构特点，首先构建等效无限远电场计算域。其次，在前处理剖分中，考虑屏蔽罩薄壁结构，为保证精细化求解精度，采用最小网格单元质量为0.00602的自由四面体网格进行全场域剖分。
静态绝缘计算条件：考虑最恶劣情况，依据《GB/T 11022-2011》标准雷电冲击耐受峰值电压(Basic impulse level, BIL)，静触头及其金属连接件施加46 kV；动触头及其金属连接件施加地电位。
材料属性：绝缘外壳材料为陶瓷(相对介电常数取值5.0)；动静触头选用铜；灭弧室内介质为真空。
-
真空灭弧室绝缘特性主要是指在承受BIL电压条件下绝缘性能可靠，其绝缘强度主要取决于真空灭弧室全场域电场分布的均匀程度。其中，典型子区域的电场均匀程度值得关注（如动静触头极间隙、触头与屏蔽罩间隙，以及屏蔽罩与屏蔽罩间隙）。
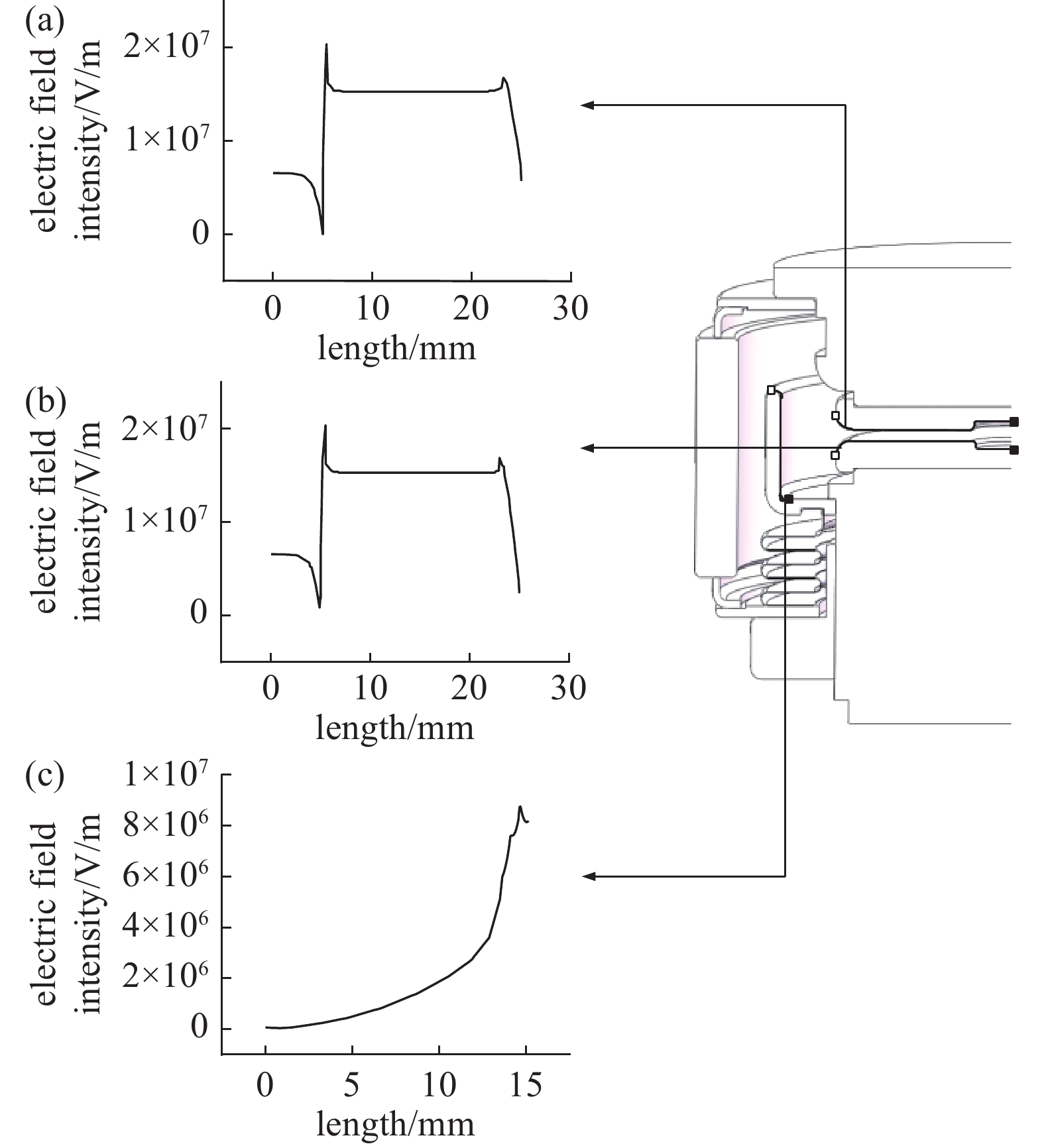
基于上述分析，针对3.6 kV/2500 A旁路开关真空灭弧室绝缘问题，定量分析触头电极在满开距下承受BIL电压条件下真空灭弧室电场分布情况，如图2所示，并对绝缘薄弱点场强进行分析；图中实心矩形和空心矩形分别表示沿面场强采样点的起点和终点。
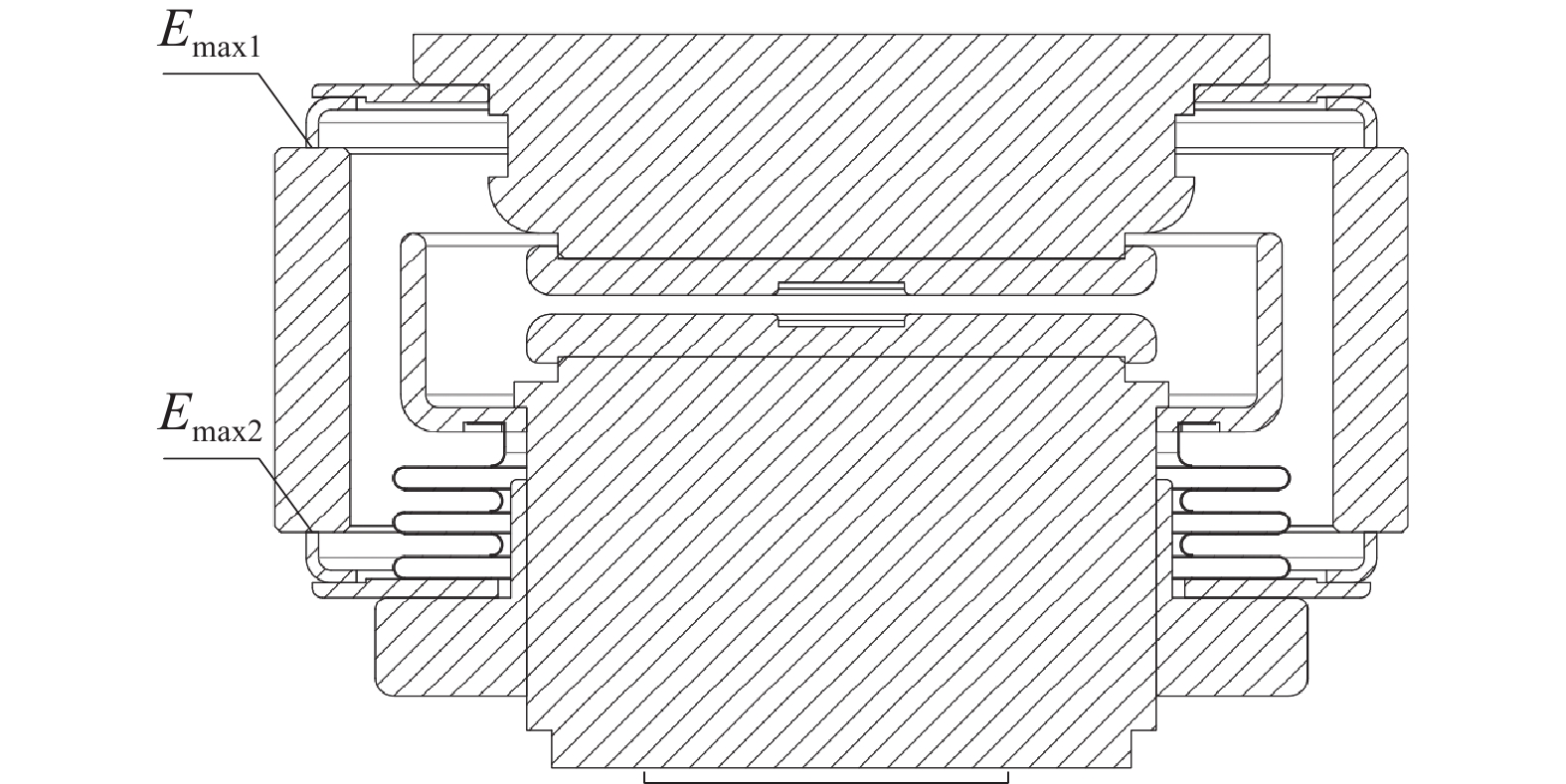
研究表明：在满开距下，真空旁路开关灭弧室场强主要集中在动静触头表面以及屏蔽罩端部区域。动静触头表面电场强度最大值分别为2.064×107 V/m和2.156×107 V/m，均位于触头电极中心开槽处圆角区域；屏蔽罩内表面电场强度最大值为9.850×106 V/m，位于屏蔽罩端部。断口区域场强最大值点位于静触头中心开槽圆角区域，同时也是灭弧室内部场强最大值点，即绝缘薄弱点。
-
真空灭弧室内部电场尤其是断口区域电场属于稍不均匀电场[15]，其电场强度由宏观增强因子与微观增强因子决定：
式中，Eg为电场强度，U为高电位电极施加电位值，d为触头行程，βg为触头结构宏观增强因子，与边缘曲率半径等几何参数相关；βm为触头表面结构微观增强因子，与触头电极微观结构有关。
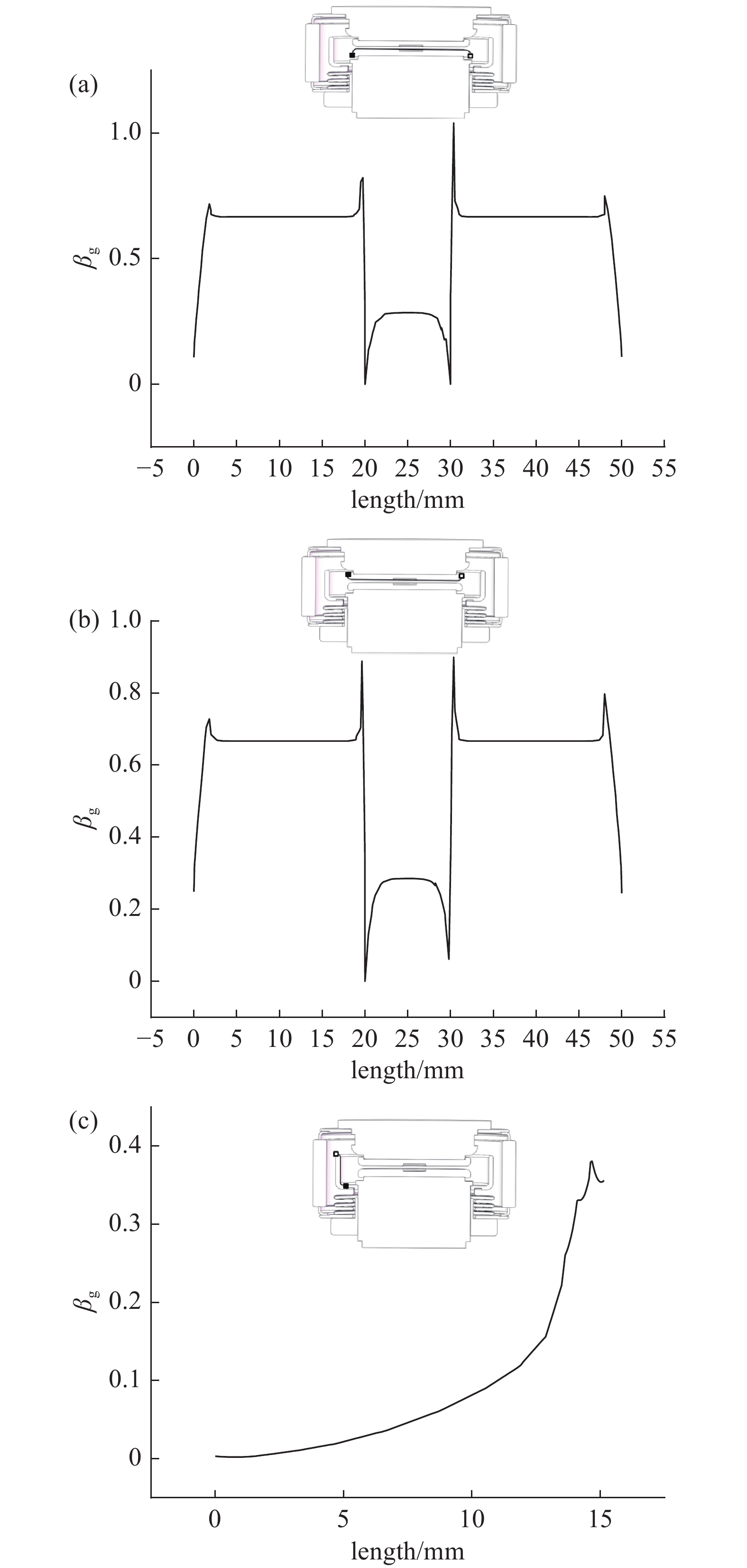
当βg和βm趋近于1时，表示灭弧室内部各区域电场强度无限接近于断口中心区域场强，即灭弧室绝缘设计的目标。其中，βm主要受电极表面组织结构以及微观蚀坑的影响。在真空灭弧室绝缘结构设计中，βm值既难以测定也难以控制。但可通过真空灭弧室的老炼过程降低βm值。而βg反映触头宏观结构参数对电场分布的影响，可通过对灭弧室内部结构型面优化实现对其进行调控，进而改善电场分布均匀度。文中，忽略βm对电场畸变与劣化的影响，求得动静触头表面以及屏蔽罩内表面满开距下βg分布，如图3所示，图中实心矩形和空心矩形分别表示触头中心平面沿线βg采样点的起点和终点。
分析表明，在动静触头沿面区域，高βg值点集中在触头中心开槽边缘圆角区域和触头外侧圆角区域，最大值均出现在触头电极中心开槽圆角区域，分别为1.074和0.929；在屏蔽罩内表面区域，βg最大值点位于屏蔽罩端部区域，其值为0.393。
-
研究表明真空灭弧室场域内场强最大值位于触头电极中心开槽圆角区域（即De），为分析触头电极中心开槽圆角半径（re）对于场强最大值的影响，并给出合理的取值，采用PCE法进行分析。
PCE法是一种新兴的不确定性量化算法，采用多项式组合形成随机空间来描述和传播随机变量的不确定性。对于混沌多项式展开模型，描述如下：
式中，θ为随机变量，α0为常系数，n为展开阶数，Hn(ε)为n阶的Hermite正交多项式。
PCE法是利用正交多项式的优异性能，对随机问题进行有限阶数展开，通过对随机变量输入到响应的映射过程建立代理模型，进而分析不确定性问题。技术路线如下：
Step1：确定变量个数以及Hermite展开阶数。
Step2：定义随机变量分布，确定变量取值范围的平均值与方差，基于正交变换确定其相关系数。
Step3：选择配点个数，基于获取的x空间配点输入相应的外部计算结果。
Step4：设置抽样次数并输入所需求解的界限值。
Step5：求解大于所设定界限值的概率，形成概率密度分布曲线。
-
在真空灭弧室制备和使用过程中，存在影响绝缘性能的多种不确定性因素，如环境、材料、加工工艺等。本文针对由加工工艺可能产生的误差对于真空灭弧室绝缘性能的影响因素进行分析。由于场强最大值主要集中在极间区域，而触头电极表面场强主要集中在De区域。也就是说，re是真空灭弧室场强的敏感参数之一。
在此，定义触头电极表面最大场强与平均场强之比为不确定性变量，分析动静触头在不同触头电极表面及屏蔽罩区域下不确定性变量的概率密度分布，提出不确定性变量表达式：
式中，η为不确定性变量，Emax为触头电极表面场强最大值，Ei为触头电极表面采样点的场强值。
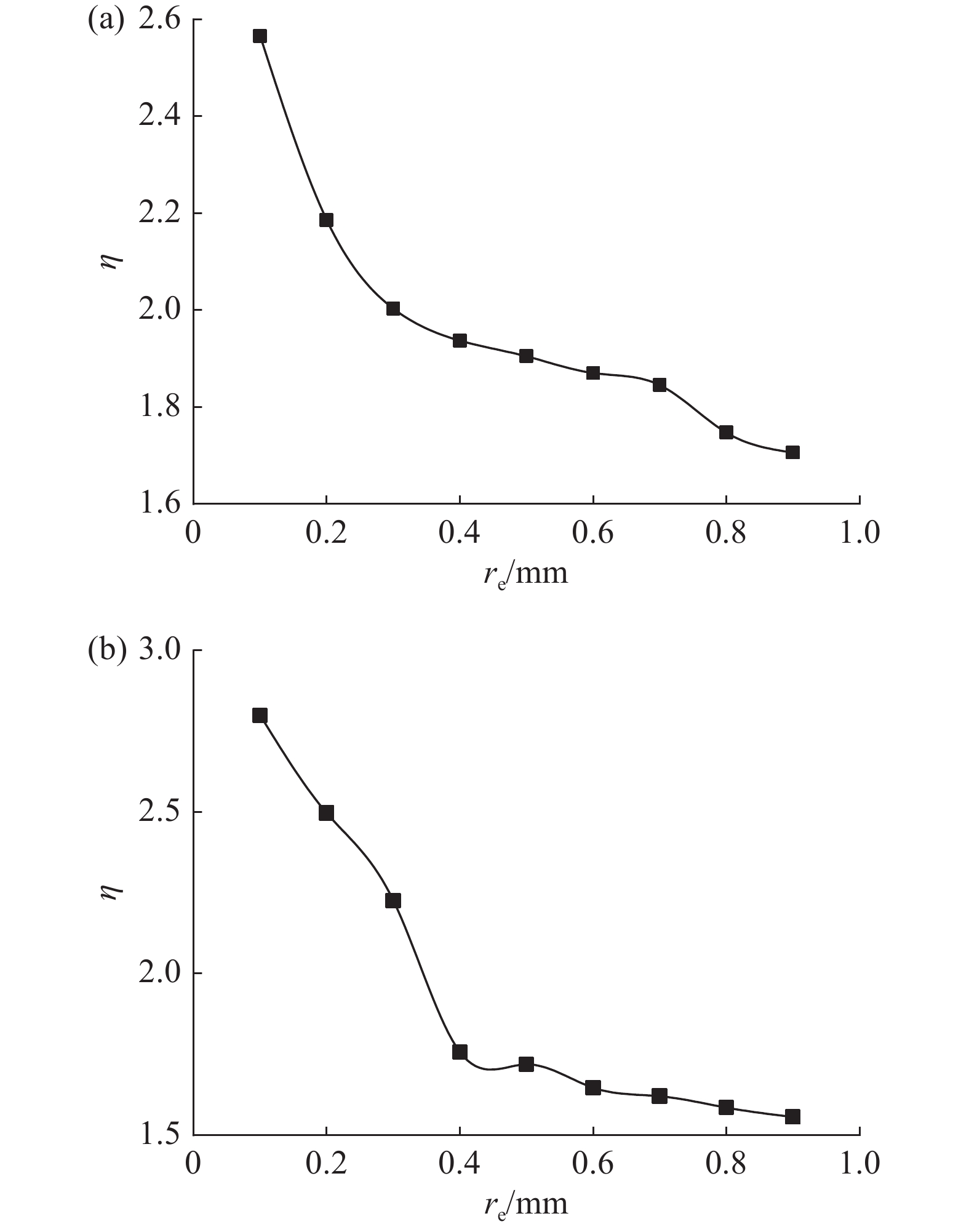
为了给不确定性分析提供参考指标，首先对于动静触头在不同re下η值进行确定性分析，由于触头电极中心开槽深度为1.0 mm，将re取值范围设定在0.1～0.9 mm之间，分析结果如图5所示。
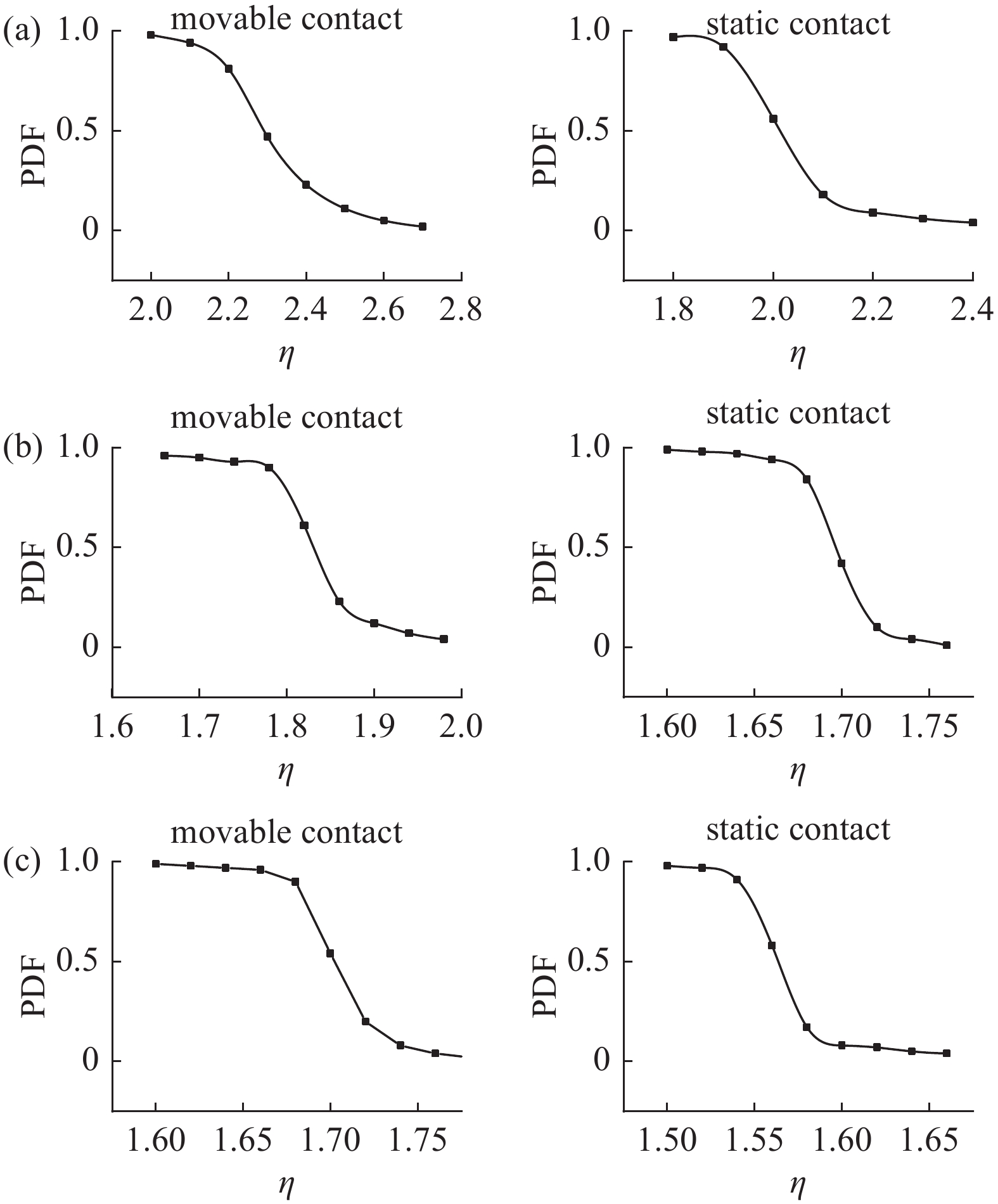
考虑实际加工过程中可能存在的误差，将re取值范围分为三组，分别为0.1~0.3 mm、0.4~0.6 mm和0.7~0.9 mm。对不确定性仿真进行设置，定义变量为2个，分别为动触头中心开槽圆角半径re1和静触头中心开槽圆角半径re2，且两个变量均服从于正态分布，Hermite展开阶数设定为3阶，相关系数为默认设置，配点个数设置15，抽样次数设置100万次，通过设置不同临界值，求得不确定性变量的概率密度函数（Probability Density Function，PDF）的曲线，不确定性分析结果如图6所示，图6(a)和(b)分别表示不确定性变量η随着re变化的PDF曲线。
研究表明：动静两侧触头随着re变化其η概率密度函数变化趋势基本相同，当re取值范围为0.1~0.3 mm时，η变化范围较大，触头电极击穿概率较大；当re取值范围为0.7~0.9 mm时，与确定性分析结果相比较，η大于确定性分析结果的概率在90%以上，对实际加工过程要求较高。基于上述分析，re取值范围应在0.4~0.6 mm内。
-
采用有限元方法，对3.6 kV/2500 A真空旁路开关灭弧室静态绝缘性能进行数值模拟与可视化分析。研究表明，在满开距下，绝缘薄弱点（即电场强度最大值点）位于触头电极中心开槽圆角区域及屏蔽罩端部区域。
为研究灭弧室内绝缘影响因素和电场分布均匀程度，引入表面电场宏观增强因子βg，并定量分析其在不同子区域的分布情况。
为探究触头电极中心开槽圆角半径（re）对于场域内场强最大值的影响机理，采用PCE法分析在不同re取值范围下，动静触头表面不确定变量的概率密度分布，进而提出合理的re取值阈。
当re取值范围在0.4~0.6 mm时，兼顾绝缘性能和加工难度，本文所选取的re的值在该范围之内，满足工程需要。
真空旁路开关灭弧室绝缘仿真及不确定性分析
Insulation Simulation and Uncertainty Analysis of Vacuum Interrupter for Bypass Switch
-
摘要: 真空旁路开关在直流系统中作为重要的保护器件长期工作在分闸状态下。针对真空旁路开关绝缘可靠性问题，文章以3.6 kV/2500 A真空旁路开关灭弧室为研究对象，采用有限元分析手段，建立三维电场物理数学模型，分析其在标准雷电冲击耐受峰值电压作用下的电场分布情况；并引入表面电场宏观增强因子，对电场集中区域的场域分布均匀程度进行定量分析。此外，采用混沌多项式展开法，对灭弧室触头电极中心开槽圆角半径进行不确定性分析，以确保其绝缘性能和加工制备的可靠性。Abstract: As an important protection device in the DC power system, the bypass switch usually works under open circuit conditions. In order to analyze the insulation reliability of the vacuum bypass switch, a three-dimensional physical mathematical model of the electric field is established by using the finite element method to illustrate the distribution of the electric field under standard lightning impulse to withstand peak voltage. The macroscopic enhancement factor of surface electric field intensity is introduced to quantitatively describe the uniformity of the electric field concentration region. Moreover, the chaotic polynomial expansion method is applied to analyze the uncertainty of the center slot fillet radius of the contact electrode to ensure the reliability of insulation performance and manufacturing processes.
-
Key words:
- Bypass switch /
- Insulation performance /
- Polynomial Chaos Expansion /
- Uncertainty analysis .
-
-
图 2 动静触头表面及屏蔽罩内表面场强分布。（a）静触头表面场强分布，（b）动触头表面场强分布，（c）屏蔽罩内表面场强分布
Figure 2. Field intensity distribution along the surface of movable and static contact and inner surface of shielding cover. (a) Field intensity distribution along the surface of static contact, (b) field intensity distribution along the surface of movable contact, (c) field intensity distribution along the inner surface of shielding cover
图 3 动静触头表面及屏蔽罩内表面βg。（a）动触头表面βg分布，（b）静触头表面βg，（c）屏蔽罩内表面βg
Figure 3. βg curves along the surface of movable and static contacts and inner surface of the shielding cover. (a) βg curves along the surface of movable contacts, (b) βg curves along the surface of static contacts, (c) βg curves along the surface of inner surface of shielding cover
图 5 动静触头在不同re下确定性分析。（a）动触头在不同re下确定性分析，（b）静触头在不同re下确定性分析
Figure 5. Deterministic analysis of movable and static contact under different re. (a) Deterministic analysis of movable contact under different re, (b) deterministic analysis of static contact under different re
图 6 动静触头在不同re下不确定性分析。（a）re=0.1~0.3 mm，（b）re=0.4~0.6 mm，（c）re=0.7~0.9 mm
Figure 6. Uncertainty analysis of movable and static contact under different re. (a) re=0.1~0.3 mm, (b) re=0.4~0.6 mm, (c) re=0.7~0.9 mm
表 1 真空灭弧室各区域场强最大值
Table 1. The maximum field strength in each region of vacuum bypass switch interrupter
场强最大值 Emaxd Emaxp Emax1 Emax2 参数值/×106 V/m 21.6 9.8 12.9 3.2 
下载: 导出CSV
-
[1] 邹积岩, 陈军平, 刘晓明, 等. 真空开关技术[M]. 北京: 机械工业出版社, 2021 (in Chinese) Zou J Y, Chen J P, Liu X M, et al. Vacuum switch technology[M]. Beijing: China Machine Press, 2021 [2] 王章启, 何俊生, 邹积岩, 等. 电力开关技术[M]. 武汉: 华中科技大学出版社, 2003 (in Chinese) Wang Z Q, He J S, Zou J Y, et al. Power switching technology[M]. Wuhan: Huazhong University of Science And Technology Publishing, 2003 [3] 刘威. 基于改进神经网络的真空灭弧室电磁场联合优化设计[D]. 天津工业大学, 2020 (in Chinese) Liu W. Electromagnetic field joint optimization design of vacuum interrupter based on improved neural network[D]. Tianjin Polytechnic University, 2020 [4] Suzuki S, Matsuo T, Sakuma R, et al. Diffusion of metal vapor from electrodes to the vacuum interrupter shield and its dependence on electrode construction[J]. IEEE Transactions on Plasma Science,2006,34(2):485−489 doi: 10.1109/TPS.2006.872452 [5] 马士奇, 刘晓明, 陈海, 等. 基于平面域水平可视图的真空灭弧室静态绝缘优化设计与分析[J]. 真空科学与技术学报,2022,42(2):118−124 (in Chinese) Ma S Q, Liu X M, Chen H, et al. Optimal design and analysis of static insulation of vacuum interrupter based on horizontal viewable plane domain[J]. Chinese Journal of Vacuum Science and Technology,2022,42(2):118−124 [6] 董增波, 杨鹏, 范辉, 等. 基于NSGA-Ⅱ的真空断路器灭弧室静态绝缘优化设计与分析[J]. 真空科学与技术学报,2021,41(12):1198−1202 (in Chinese) Dong Z B, Yang P, Fan H, et al. Optimal design and analysis of static insulation of vacuum circuit breaker interrupter based on NSGA-II[J]. Chinese Journal of Vacuum Science and Technology,2021,41(12):1198−1202 [7] 谢仕炜, 胡志坚, 王珏莹, 等. 基于不确定随机网络理论的主动配电网多目标规划模型及其求解方法[J]. 电工技术学报,2019,34(5):1038−1054 (in Chinese) Xie S W, Hu Z J, Wang Y Y, et al. A multi-objective planning model of active distribution network based on uncertain random network theory and its solution algorithm[J]. Transactions of China Electrotechnical Society,2019,34(5):1038−1054 [8] 李幸芝, 韩蓓, 李国杰, 等. 考虑非高斯耦合不确定性的交直流配电网两阶段概率状态估计[J]. 电工技术学报,2020,35(23):4949−4960 (in Chinese) Li X Z, Han B, Li G J, et al. Two-stage probabilistic state estimation for AC/DC distribution network considering non-Gaussian coupling uncertainties[J]. Transactions of China Electrotechnical Society,2020,35(23):4949−4960 [9] Zhang X L, Xiao H, Gomez T, et al. Evaluation of ensemble methods for quantifying uncertainties in steady-state CFD applications with small ensemble sizes[J]. Computers and Fluids,2020,203(1):104530 [10] Chen Y L, Ma W M. Uncertainty quantification for trace simulation of fix-II no. 5052 test[J]. Annals of Nuclear Energy,2020,143(1):107490 [11] 赵营鸽, 李颖, 王灵月, 等. 基于均值点展开的单变元降维法在EIT不确定性量化研究中的应用[J]. 电工技术学报,2021,36(18):3776−3786 (in Chinese) Zhao Y G, Li Y, Wang L Y, et al. The application of univariate dimension reduction method based on mean point expansion in the research of electrical impedance tomography uncertainty quantification[J]. Transactions of China Electrotechnical Society,2021,36(18):3776−3786 [12] 方斯顿, 程浩忠, 徐国栋, 等. 基于Nataf 变换含相关性的扩展准蒙特卡洛随机潮流方法[J]. 电工技术学报,2017,32(2):255−263 (in Chinese) Fang S D, Cheng H Z, Xu G D, et al. A nataf transformation based on extended quasi monte carlo simulation method for solving probabilistic load flow problems with correlated random variables[J]. Transactions of China Electrotechnical Society,2017,32(2):255−263 [13] 于全毅, 刘长英, 吴定超, 等. 基于广义混沌多项式法的多导体传输线辐射敏感度分析方法[J]. 电工技术学报,2020,35(17):3591−3600 (in Chinese) Yu Q Y, Liu C Y, Wu D C, et al. Radiation sensitivity analysis of multiconductor trans-mission Lines based on generalized polynomial chaos method[J]. Transactions of China Electrotechnical Society,2020,35(17):3591−3600 [14] 吴其, 刘晓明, 邹积岩, 等. 采用响应面法-几何特征模拟电荷法的电场数值求解及精度验证[J]. 高电压技术,2018,44(6):2060−2066 (in Chinese) Wu Q, Liu X M, Zou J Y, et al. Numerical solution and accuracy validation of electric field using response surface methodology and geometric feature charge simulation method[J]. High Voltage Engineering,2018,44(6):2060−2066 [15] Paul G S. The vacuum interrupter theory, design, and application[M]. Boca Raton: CRC Press, 2008 -
计量
- 文章访问数: 143
- HTML全文浏览数: 143
- PDF下载数: 3
- 施引文献: 0