高级搜索

混合沉积有机分子区域选择性生长的动力学蒙特卡罗模拟研究

,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

汪长超, 聂青苗, 石亮, 陈乃波, 胡来归, 鄢波. 混合沉积有机分子区域选择性生长的动力学蒙特卡罗模拟研究[J]. 物理学报, 2024, 73(12): 126801-1. doi: 10.7498/aps.73.20231779
引用本文: 汪长超, 聂青苗, 石亮, 陈乃波, 胡来归, 鄢波. 混合沉积有机分子区域选择性生长的动力学蒙特卡罗模拟研究[J]. 物理学报, 2024, 73(12): 126801-1. doi: 10.7498/aps.73.20231779
shu
Chang-Chao Wang, Qing-Miao Nie, Liang Shi, Nai-Bo Chen, Lai-Gui Hu, Bo Yan. Kinetic Monte Carlo simulation of selective area growth of mix deposited organic molecules[J]. Acta Physica Sinica, 2024, 73(12): 126801-1. doi: 10.7498/aps.73.20231779
Citation: Chang-Chao Wang, Qing-Miao Nie, Liang Shi, Nai-Bo Chen, Lai-Gui Hu, Bo Yan. Kinetic Monte Carlo simulation of selective area growth of mix deposited organic molecules[J]. Acta Physica Sinica, 2024, 73(12): 126801-1. doi: 10.7498/aps.73.20231779
shu

混合沉积有机分子区域选择性生长的动力学蒙特卡罗模拟研究

  • 1.

    浙江工业大学理学院, 杭州　310023

  • 2.

    复旦大学信息科学与工程学院, 上海　200433

    • 作者简介: 汪长超: wangchangchao0809@163.com .
    通讯作者: E-mail: nieqingmiao@zjut.edu.cn.;  E-mail: boyan@zjut.edu.cn.

  • 中图分类号: 68.47.-b, 68.43.Jk, 68.55.A-, 68.55.am

Kinetic Monte Carlo simulation of selective area growth of mix deposited organic molecules

  • 1.

    College of Science, Zhejiang University of Technology, Hangzhou 310023, China

  • 2.

    School of Information Science and Engineering, Fudan University, Shanghai 200433, China

    • Corresponding authors: E-mail: nieqingmiao@zjut.edu.cn.;  E-mail: boyan@zjut.edu.cn

  • MSC: 68.47.-b, 68.43.Jk, 68.55.A-, 68.55.am

  • 摘要: 由区域选择性生长方法(即分子在预图案表面的自组装技术)制备的有机微纳米图案有望在光电和全彩显示方面发挥巨大作用. 而制备多色图案薄膜的有机器件依赖于两种及多种有机分子的成核分配, 特别是混合沉积方法的应用有效提高了多色薄膜成核的效率. 本文利用动力学蒙特卡罗方法研究了两种分子间的结合能强弱对混合沉积两种分子以实现相分离式生长的影响. 结果表明: 当分子间结合能较弱时, 两种分子表现出完全不同的相分离生长行为, 绝大部分的非平面和平面分子分别沉积在电极顶部和侧面; 当分子间结合能较强时, 电极顶部及侧面都出现了两类分子的掺杂生长, 导致了分子相分离生长的失效. 研究证明了分子间的结合能会影响多种有机分子选区生长分离的效果, 因此混合沉积两种有机分子时, 通过适当调整分子间的结合能, 在电极顶部和侧面可分别获得较纯结晶的单色薄膜, 从而促进了多色有机微纳米图案在微显示等领域的进一步应用.
    Abstract: The selective area growth approach (namely the self-assembly of molecules on pre-patterned surfaces) that takes into account the properties of organic molecular materials and traditional lithography techniques, is expected to play a significant role in manufacturing organic micro-nano patterns for photoelectric and full-color display. The manufacture of organic devices with tunable multicolor patterned films depends on the control of nucleation distribution of two or more organic molecules by using a selective area growth approach, particularly through the application of mixed deposition growth that can enhance the nucleation efficiency of multicolor thin films. However, till now the issue of mixed deposition growth of two kinds of organic molecules has been rarely reported, owing to the complexity in experimental operation. In this work, the selective area growth of mixed deposition of two kinds of molecules is studied by molecular kinetic Monte Carlo approach in order to find the experimental conditions for separating two kinds of molecular growth. In the simulation, the interaction energy between the two molecules is adjusted and controlled to study its influence on the separately selective area growth of the two molecules. The results show that when the intermolecular interaction energy is weak, the planar molecules and the non-planar molecules exhibit completely different growth behaviors. The most of non-planar molecules gather at the top of the electrode in an island mode, while planar molecules mainly accumulate in a layer-by-layer mode on the sides of the electrode. On the contrary, when the intermolecular interaction energy is strong, the number of non-planar particles on the tops decreases and a large number of planar particles appear. Moreover, on the sides of the electrode, the doping nucleation of planar molecules and non-planar molecules also exists, resulting in the failure of molecular phase separation growth. It proves that the intermolecular interaction energy can affect separately area-selective growth of various organic molecules. Therefore, when several different kinds of molecules are mixed and deposited, relatively pure crystalline monochromatic films can be obtained at the top and on the sides of the electrode, respectively, by appropriately adjusting the intermolecular interaction energy, which can further facilitate the application of multi-color organic micro-nano pattern in display and other fields.
  • 加载中

  • 图 1  (a)模拟系统结构图, 其中大的灰色和小的黄色方块分别代表二氧化硅基底和金电极, 沉积的非平面(平面)粒子用蓝色(红色)的球表示, 衬底的尺寸为80a×80a×2a, 方形电极(20a×20a×4a)以40a的周期布置在基板上, a是晶格常数, 设为1; (b)平面分子的各向异性分子间相互作用的示意图

    Figure 1.  (a) Set-up of the simulation system. The large gray and small yellow squares represent the SiO2 substrate and the gold electrode, respectively. The deposited non-planar (planar) particles are represented by blue (red) balls. The size of the substrate is 80a×80a×2a. Square electrodes (20a×20a×4a) are arranged on the substrate with a 40a period. Here a is the lattice constant and set to 1. (b) Schematic diagram of anisotropic intermolecular interactions of planar molecules.

    下载: 全尺寸图片 幻灯片

    图 2  当非平面分子(蓝色)和平面分子(红色)垂直面间(沿着面内方向)结合能为0.4kBT (0.2kBT )时, 预图案表面沉积粒子形貌的截面快照随粒子数的演化　(a) 5000; (b) 15000; (c) 30000; (d) 50000

    Figure 2.  Evolution of the section snapshots of the morphology after (a) 5000, (b) 15000, (c) 30000 and (d) 50000 particles deposited on the surface of the pre-pattern. Here the out-plane (in-plane) interaction energy between the molecules of non-planar (blue) and planar (red) is 0.4kBT (0.2kBT ).

    下载: 全尺寸图片 幻灯片

    图 3  当非平面分子和平面分子垂直面间(沿着面内方向)结合能为0.4kBT (0.2kBT )时　(a)非平面分子(平面分子)在电极顶部、侧面的沉积粒子数随入射总粒子数的变化; (b)沉积在电极顶部(侧面)非平面分子(平面分子)的粒子数占顶部(侧面)总粒子数的比率随入射总粒子数的变化

    Figure 3.  (a) Variation of the number of deposited non-planar (planar) particles on (at) the tops (sides) of the electrodes with the number of incident particles; (b) the variation of the ratio of the number of deposited non-planar (planar) particles on (at) the tops (sides) of the electrodes to the total number of particles with the number of incident particles. Here the out-plane (in-plane) interaction energy between the molecules of non-planar and planar is 0.4kBT (0.2kBT ).

    下载: 全尺寸图片 幻灯片

    图 4  当非平面分子(蓝色)和平面分子(红色)垂直面间(沿着面内方向)结合能分别为(a) 0.4$ {k}_{{\mathrm{B}}}T $(0.2$ {k}_{{\mathrm{B}}}T $), (b) 1.2$ {k}_{{\mathrm{B}}}T $(0.8$ {k}_{{\mathrm{B}}}T $), (c) 2$ {k}_{{\mathrm{B}}}T $(1.4$ {k}_{{\mathrm{B}}}T $)以及(d) 2.8$ {k}_{{\mathrm{B}}}T $(2$ {k}_{{\mathrm{B}}}T $)时, 预图案表面沉积50000个粒子(非平面分子和平面分子各25000个)的最终形貌的截面快照

    Figure 4.  Section snapshots of the final morphology after 50000 particles deposited on the pre-patterned surface (25000 each for the molecule of non-planar and planar) by varying the out-plane (in-plane) interaction energies between the molecules of non-planar (blue) and planar (red) from (a) 0.4$ {k}_{{\mathrm{B}}}T $(0.2$ {k}_{{\mathrm{B}}}T $), (b) 1.2$ {k}_{{\mathrm{B}}}T $(0.8$ {k}_{{\mathrm{B}}}T $), (c) 2$ {k}_{{\mathrm{B}}}T $(1.4$ {k}_{{\mathrm{B}}}T $) to (d) 2.8$ {k}_{{\mathrm{B}}}T $(2$ {k}_{{\mathrm{B}}}T $).

    下载: 全尺寸图片 幻灯片

    图 5  当非平面分子和平面分子垂直面间(沿着面内方向)结合能分别为0.4$ {k}_{{\mathrm{B}}}T $(0.2$ {k}_{{\mathrm{B}}}T $), 1.2$ {k}_{{\mathrm{B}}}T $(0.8$ {k}_{{\mathrm{B}}}T $), 2$ {k}_{{\mathrm{B}}}T $(1.4$ {k}_{{\mathrm{B}}}T $)以及2.8$ {k}_{{\mathrm{B}}}T $(2$ {k}_{{\mathrm{B}}}T $)时, (a)非平面分子在电极顶部、侧面的沉积粒子数随入射粒子总数的变化; (b)沉积在电极顶部(侧面)非平面分子(平面分子)的粒子数占顶部(侧面)总粒子数的比率随入射总粒子数的变化

    Figure 5.  (a) Variation of the number of deposited particles of non-planar on (at) the tops (sides) of the electrodes with the number of incident particles; (b) the variation of the ratio of the number of deposited particles of non-planar (planar) on (at) the tops (sides) of the electrodes to the total number of particles with the number of incident particles. Here the out-plane (in-plane) interaction energy between the molecules of non-planar and planar is 0.4$ {k}_{{\mathrm{B}}}T $(0.2$ {k}_{{\mathrm{B}}}T $), 1.2$ {k}_{{\mathrm{B}}}T $(0.8$ {k}_{{\mathrm{B}}}T $), 2$ {k}_{{\mathrm{B}}}T $(1.4$ {k}_{{\mathrm{B}}}T $) and 2.8$ {k}_{{\mathrm{B}}}T $(2$ {k}_{{\mathrm{B}}}T $), respectively.

    下载: 全尺寸图片 幻灯片
  • [1] Shaw J M, Seidler P F 2001 IBM J. Res. Dev. 45 3 doi: 10.1147/rd.451.0003
    [2] Kippelen B, Brédas J L 2009 Energy Enviro. Sci. 2 251 doi: 10.1039/b812502n
    [3] Baek S, Kim K, Sung Y, Jung P, Ju S, Kim W, Kim S J, Hong S H, Lee H 2020 Nanotechnology 31 125301 doi: 10.1088/1361-6528/ab5d42
    [4] Tian P F, Bulovic V, Burrows P E, Gu G, Forrest S R, Zhou T X 1999 J. Vac. Sci. Technol. A 17 2975 doi: 10.1116/1.581969
    [5] Saba M H, Mukherjee S, Dutta S, Mallisetty P K, Murmu N C 2021 Mater. Today: Proc. 46 1749 doi: 10.1016/j.matpr.2020.07.570
    [6] Spiegel I A, Sammons P, Barton K 2020 IEEE Trans. Control Syst. Technol. 28 2322 doi: 10.1109/TCST.2019.2939963
    [7] Wang W C, Chi L F 2012 Acc. Chem. Res. 45 1646 doi: 10.1021/ar200299w
    [8] Bardotti L, Prevel B, Jensen P, Treilleux M, Mélinon P, Perez A, Mailly D 2002 Appl. Surf. Sci. 191 205 doi: 10.1016/S0169-4332(02)00178-2
    [9] Wang W C, Zhong D Y, Zhu J, Kalischewski F, Dou R F, Wedeking K, Chi L F 2007 Phys. Rev. Lett. 98 225504 doi: 10.1103/PhysRevLett.98.225504
    [10] Speth R L, Lauga E 2009 New J. Phys. 11 075024 doi: 10.1088/1367-2630/11/7/075024
    [11] Hopp S F, Heuer A 2010 J. Chem. Phys. 133 204101 doi: 10.1063/1.3506898
    [12] Lied F, Mues T, Wang W C, Chi L F, Heuer A 2012 J. Chem. Phys. 136 024704 doi: 10.1063/1.3676257
    [13] Zhang H, Liu G, Wang W C, Chi L F, Yuan S L 2014 RSC Adv. 4 25005 doi: 10.1039/C4RA01756K
    [14] Kotelyanskii M, Theodorou D N 2004 Simulation Methods for Polymers (Boca Raton: CRC Press
    [15] Neurock M, Hansen E W 1998 Comput. Chem. Eng. 22 S1045 doi: 10.1016/S0098-1354(98)00210-5
    [16] Liu G, Zhang H, Liu G K, Yuan S L 2016 Colloids Surf. A Physicochem. Eng. Asp. 494 186 doi: 10.1016/j.colsurfa.2016.01.033
    [17] Liu G, Zhang H, Liu G K, Yuan S L, Zhu Q Z 2016 Colloids Surf. A Physicochem. Eng. Asp. 509 401 doi: 10.1016/j.colsurfa.2016.09.029
    [18] Blel S, Hamouda A B H 2019 Results Phys. 12 1475 doi: 10.1016/j.rinp.2019.01.050
    [19] Jiang Y, Shi L, Chen N B, Hu L G, Wang W C, Nie Q M, Yan B 2023 Results Phys. 44 106145 doi: 10.1016/j.rinp.2022.106145
    [20] Wang W C, Du C, Zhong D Y, Hirtz M, Wang Y, Lu N, Wu L X, Ebeling D, Li L Q, Fuchs H, Chi L F 2009 Adv. Mater. 21 4721 doi: 10.1002/adma.200901091
    [21] Kalischewski F, Heuer A 2009 Phys. Rev. B 80 155421 doi: 10.1103/PhysRevB.80.155421
    [22] Kalischewski F, Zhu J, Heuer A 2008 Phys. Rev. B 78 155401 doi: 10.1103/PhysRevB.78.155401
    [23] Klawtanong M, Srinitiwarawong C, Chatraphorn P 2018 Thin Solid Films 645 431 doi: 10.1016/j.tsf.2017.11.020
    [24] Huitema H E A, van der Eerden J P 1999 J. Chem. Phys. 110 3267 doi: 10.1063/1.478192
    [25] Larsson M I 2001 Phys. Rev. B 64 115428 doi: 10.1103/PhysRevB.64.115428
    [26] Michely T, Krug J 2004 Islands, Mounds and Atoms (Vol. 42) (Berlin: Springer
    [27] Liu G, Zhang H, Wang W, Yuan S L 2015 Chem. Phys. Lett. 628 54 doi: 10.1016/j.cplett.2015.04.007
  • 加载中
图( 5)
计量
  • 文章访问数:  129
  • HTML全文浏览数:  129
  • PDF下载数:  2
  • 施引文献:  0
出版历程
  • 收稿日期:  2023-11-09
  • 刊出日期:  2024-06-20

混合沉积有机分子区域选择性生长的动力学蒙特卡罗模拟研究

    通讯作者: E-mail: nieqingmiao@zjut.edu.cn.; 
    通讯作者: E-mail: boyan@zjut.edu.cn.
    作者简介: 汪长超: wangchangchao0809@163.com
  • 1. 浙江工业大学理学院, 杭州　310023
  • 2. 复旦大学信息科学与工程学院, 上海　200433
  • 收稿日期:  2023-11-09

摘要: 由区域选择性生长方法(即分子在预图案表面的自组装技术)制备的有机微纳米图案有望在光电和全彩显示方面发挥巨大作用. 而制备多色图案薄膜的有机器件依赖于两种及多种有机分子的成核分配, 特别是混合沉积方法的应用有效提高了多色薄膜成核的效率. 本文利用动力学蒙特卡罗方法研究了两种分子间的结合能强弱对混合沉积两种分子以实现相分离式生长的影响. 结果表明: 当分子间结合能较弱时, 两种分子表现出完全不同的相分离生长行为, 绝大部分的非平面和平面分子分别沉积在电极顶部和侧面; 当分子间结合能较强时, 电极顶部及侧面都出现了两类分子的掺杂生长, 导致了分子相分离生长的失效. 研究证明了分子间的结合能会影响多种有机分子选区生长分离的效果, 因此混合沉积两种有机分子时, 通过适当调整分子间的结合能, 在电极顶部和侧面可分别获得较纯结晶的单色薄膜, 从而促进了多色有机微纳米图案在微显示等领域的进一步应用.

English Abstract

    全文HTML

    1.   引　言

    • 有机电子因具有环保、柔性可弯曲、成本低、生物兼容性好等优点, 数十年来获得了快速的发展[1]. 至今已被广泛应用于电子和光电器件中, 例如有机薄膜晶体管、发光二极管、太阳能电池和传感器等[2]. 大多数情况下, 电子产品需要在一定范围内达到高性能和高集成度, 由此引发了对微图案化器件与阵列的需求. 对于无机材料, 微图案化是通过自上而下的光刻技术实现的, 涉及紫外光和有机溶剂. 然而, 有机材料由于易受紫外线、溶剂和高温的影响, 难以将现有光刻技术直接用于实现有机微电子系统, 而已经开发的软印迹[3]、阴影掩模[4]、真空沉积和喷墨打印[5,6]等技术仍然存在分辨率不足、可扩展性差和复杂的多步骤处理等问题. 研究发现, 一种基于真空沉积自组装的技术可自下而上地选择性生长有机半导体分子薄膜图案[7–9]. 该技术先使用光刻技术对基底进行预图案化, 利用形成的微/纳米图案在基底上产生表面能的差异分布, 可在物理气相沉积(physical vapor deposition, PVD)过程中, 使有机分子可以沿着表面随机扩散, 并倾向于在结合能更强的地方成核, 即结构化基底上的区域选择性生长(area selective growth, ASG)[10]. 在理论模拟方面, 动力学蒙特卡罗(kinetic Monte Carlo, kMC)方法作为一种有效的模拟工具[11–13], 其可以在微观尺度上解释系统的动态演化过程, 已被广泛用来研究聚合物物理[14]和表面化学[15]中的生长动力学. 尤其在有机分子材料的ASG方面, kMC方法已成功复现了其实验过程并解析了主要的生长模式[16–19].

      为了实现红-绿-蓝全彩有机薄膜阵列, 一些实验研究发现彩色的图案可由几种不同有机分子混合来实现, 且需要将成核控制策略扩展到一种以上的分子, 由此可以实现可调的单色、双色和三色模式. 例如同时沉积不同混合比的N, N'-双[(N-(3, 6-二叔丁基-氨基甲酰基))-正癸基]喹吖啶酮(N, N'-Di[(N-(3, 6-di-tert-butyl-carbazyl))-n-decyl] quinacridone, DTCDQA)和N, N'-双-(1-萘基)-N, N'-二苯基–1, 1'-联苯–4, 4'-二胺(N, N'-bis-(1-naphthyl)-N, N'-diphenyl-1, 1'-biphenyl-4, 4'-diamine, NPB)分子在金点阵列的二氧化硅表面上, 能够得到具有不同发光特性的有机薄膜[7]. 此外通过依次沉积在紫外光激发下发出红色荧光的平面分子N, N-二辛基–3, 4, 9, 10-苝四羧酸二亚胺(N, N-dioctyl-3, 4, 9, 10-perylene tetracarboxylic diimide, PTCDI-C8)和发出蓝色荧光的非平面分子NPB, 这两类有机分子由于性能的差异会以不同的成核机制在电极顶部和台阶进行ASG聚集成膜, 从而实现两种不同颜色分子的分离生长[7,19,20]. 然而, 对于同时沉积平面分子PTCDI-C8和非平面分子NPB的实验研究却未曾有报道. 虽然分批次沉积两种分子在实验上可以实现相分离, 但是为了提高沉积效率和节约成本, 需要混合沉积且能成功实现相分离. 由于两种及以上分子混合沉积研究对制备多色薄膜的有机器件至关重要, 本文从理论模拟角度出发, 使用kMC方法探究同时沉积这两类分子在基底表面上区域选择性生长的行为, 并找出实现相分离的关键影响因素.

      为了探究平面分子和非平面分子之间的结合能跟相分离行为的相关性, 本文设置了4组从小到大不同的结合能来研究其对相分离的影响. 研究结果表明, 两种不同分子之间的结合能确实会影响分子间相分离的效果. 当分子间相互作用较弱时, 非平面分子主要成核聚集在电极顶部, 而平面分子则聚集在电极侧面进行阶梯边缘诱导的横向生长. 因此, 分子间结合能较弱时可以很好地实现两种不同类型分子的ASG, 从而达到分子分离. 相反, 当两种分子间相互作用较强时, 以非平面分子沉积为主的电极顶部出现了平面分子数量的增加. 同时以平面分子聚集为主的电极侧面也沉积了较多的非平面分子, 最终导致分子分离的失效. 因此, 同时混合沉积两种不同类型的有机分子进行ASG, 分子间适当的相互作用力可能是实现相分离的关键因素.

    2.   模拟方法

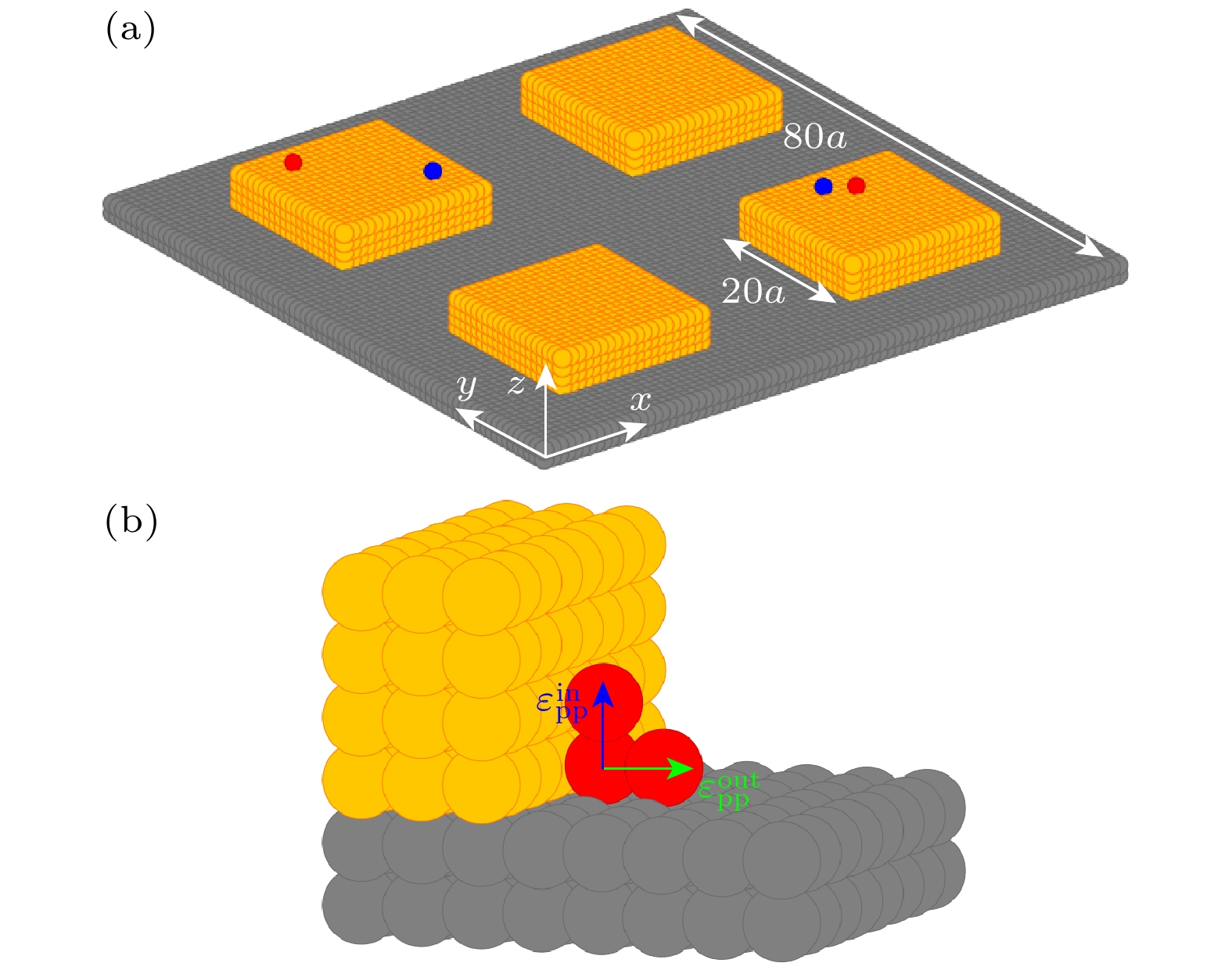
    • 模拟系统采用了ASG中常用的带有金图案的二氧化硅基底, 其可行性已被许多其他实验模拟验证[12,13], 且使用了立方晶格进行简化模拟. 如图1(a)所示, 模拟中采用80a×80a×2a (依次为x, y, z方向, 其中a为晶格常数)的三维周期性网格来构建实验中的SiO2基底, 为了模拟一个大尺寸的基底平面, 在x和y方向上采用了周期性边界条件. 接着在基底上按周期为20a均匀地构建长、宽各为20a, 高度为4a的矩阵块用来模拟实验中的金电极. 为了提高模拟效率, 体系中所有分子采用了粗粒化模型, 即采用不同的球形粒子代替基底(s)、模板(g)和有机分子(p). 虽然大多数的有机半导体分子具有各向异性, 但很多典型的实验模拟并未考虑分子的微观结构[7,13,17,21–23]. 对于入射粒子在z方向的定义范围为20a, 即如果沉积粒子扩散到z$ > $20a的空间, 则认为该粒子已经从模拟体系中溢出, 将不再考虑此溢出粒子对体系的影响.

      为了提高计算效率, 模拟中设置截止半径为$ \sqrt{3} a$, 即只考虑一个中心粒子与其周围26个粒子之间的相互作用, 而忽略了截断半径以外的粒子与中心粒子之间的相互作用, 仅考虑相邻粒子之间的相互作用. 由于将预先制备的基底和金电极视为固定不动的粒子, 因此模拟中仅考虑3种类型的相互作用: 沉积粒子之间的$ {\varepsilon }_{{\mathrm{p}}{\mathrm{p}}} $、沉积粒子与金电极之间的$ {\varepsilon }_{{\mathrm{p}}{\mathrm{g}}} $和沉积粒子与基底之间的$ {\varepsilon }_{{\mathrm{p}}{\mathrm{s}}} $. 则任意两个粒子之间的相互作用能为

      式中$ {r}_{ij} $表示粒子i和j之间的距离, $ f\left({r}_{ij}\right) $表示粒子间距离的函数. 由于采用了简立方的晶格点阵模型和近邻相互作用的截断, 分子间的相互作用能非连续变化, 仅考虑当$ {r}_{ij}\leqslant \sqrt{2}a $时, $ f\left({r}_{ij}\right) $= 1; $ {r}_{ij}= \sqrt{3}a $时, $ f\left({r}_{ij}\right)= 0.5 $; $ {r}_{ij} > \sqrt{3}a $时, $ f\left({r}_{ij}\right) $= 0. 所有分子采用粗粒化模型而忽略了具体细节, 因此分子之间的相互作用力通常用Lennard-Jones对势模拟[24,25]. 模拟中考虑到相互作用$ {\varepsilon }_{{\mathrm{p}}{\mathrm{g}}} $通常大于$ {\varepsilon }_{{\mathrm{p}}{\mathrm{s}}} $, 平面(非平面)分子和电极、基底之间的相互作用分别设置为3.1kBT (1.7kBT), 0.9kBT (0.3kBT)[12,13]. 此外, 如图1(b)所示, 考虑到平面分子间相互作用力的各向异性[7,20], 分别设置沿平面分子面内$ \varepsilon _{{\text{pp}}}^{{\text{in}}} $和垂直面外$ \varepsilon _{{\text{pp}}}^{{\text{out}}} $的范德瓦耳斯力为1.5kBT和2.0kBT. 由于非平面分子之间的相互作用力各向同性, 则统一设置为1.8kBT. 对于系统中同时沉积的两种粒子间相互作用, 为了探讨其对沉积效果的影响, 尝试了四种不同强度作用力, 即将非平面分子对平面分子面内和垂直面外方向上的相互作用力分别设置为0.2kBT和0.4kBT; 0.8kBT和1.2kBT; 1.4kBT和2kBT; 2kBT和2.8kBT. 这里$ {k}_{{\mathrm{B}}} $为玻尔兹曼常数, $ T $为绝对温度. 则系统中所有粒子之间的总势能$ {E}_{{\mathrm{o}}} $为

      在模拟过程中的一个蒙特卡罗步内, 所选择的粒子只能在相邻的6个方向中的某一个方向上扩散一个晶格长度1a, 并且新的可能扩散位置必须是未占据状态. 由(2)式可计算出可能扩散事件的总能量, 根据 Larsson能垒模型, 粒子扩散过程中所需要克服的能垒为

      式中, $ {E}_{{\mathrm{o}}} $和$ {E}_{{\mathrm{q}}} $分别表示沉积粒子扩散前、后位置的总能量; $ \alpha$为加权系数, 由分子表面扩散过程的解析计算结果可设为0.25886[11,26]. 此外, 当粒子在电极顶角位置移动时, 需要克服依赖于系统晶格结构的Ehrlich-Schwoebel的能量势垒[25]. 为了模拟连续系统, 当粒子从电极侧面扩散至其顶表面时, 将沉积粒子与电极之间的相互作用从$ 2{\varepsilon }_{{\mathrm{p}}{\mathrm{g}}} $增大到$3 {\varepsilon }_{{\mathrm{p}}{\mathrm{g}}} $[17,27].

      而某个扩散事件发生的概率可由Arrhenius公式

      计算, 其中D为粒子的有效振动频率, 在模拟过程中设置为1013 s–1 [12]. 通过(4)式可以获得体系中所有扩散事件的发生概率, 从而建立起完整的扩散事件列表. 再利用 0—1之间的随机数$ {R}_{{\mathrm{o}}} $(通过随机数发生器得到), 按照Gillespie规则从N个扩散事件中随机选择一个扩散方向n:

      式中$\displaystyle \sum\nolimits _{i=0}^{N}{P}_{i} $表示N个扩散事件概率的总和. 如果随机数$ {R}_{{\mathrm{o}}} $满足(5)式的判断标准, 则认为事件n是从N个扩散事件列表中被选取的待执行事件. 事件n被选取之后, 再按照Metropolis规则判断事件n是否被执行. 如果事件被拒绝, 则重新运行一个新的蒙特卡罗循环, 对扩散事件进行重新选取; 如果扩算事件被接受, 则完成一个蒙特卡罗步, 系统中粒子位置及扩散列表将进行更新. 此外模拟中假设每个入射粒子的时间间隔为10–8 s. 当每个入射粒子的总扩散时间大于这个间隔时, 系统中自动加入一个新粒子. 一旦所有的粒子都沉积下来, 则本次模拟结束. 由于蒙特卡罗法模拟中不同事件的发生具有其随机性, 因此本工作中显示的所有统计数据都是10个独立的实现样本的平均结果.

    3.   结果和讨论

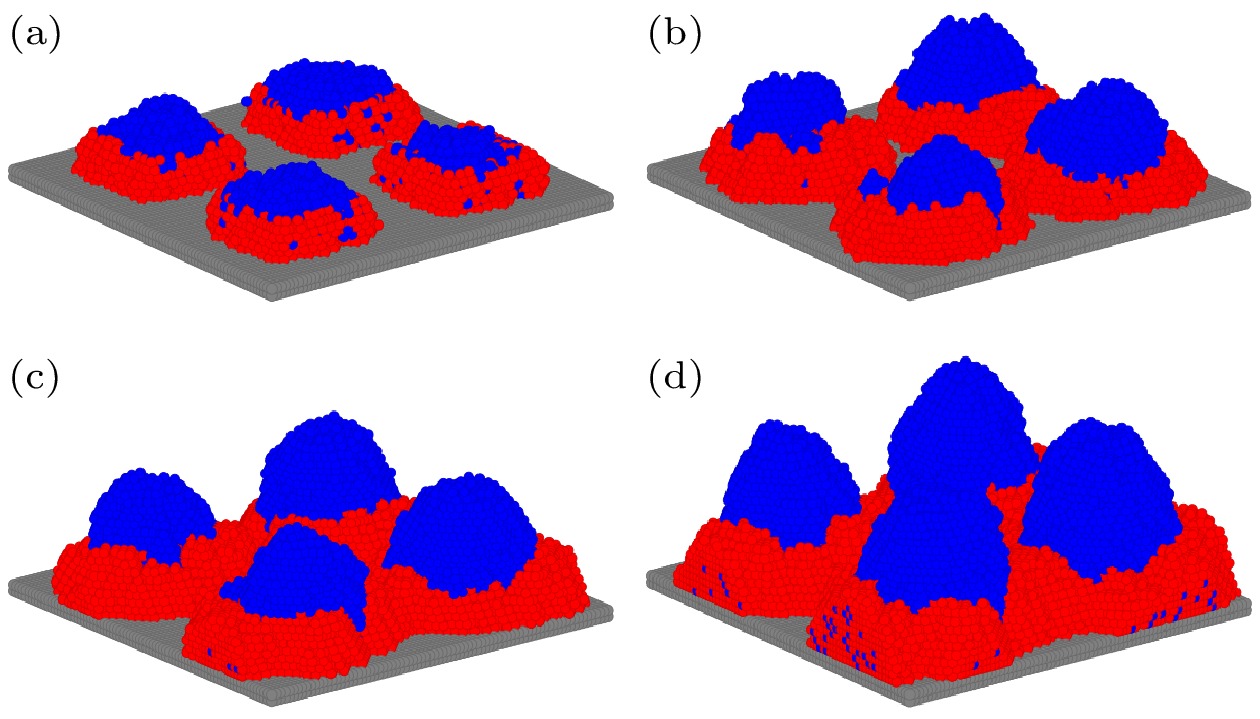
    • 首先研究了混合沉积两种不同类型分子相互作用较弱时在预图案化模板上的自组装行为. 由于平面分子间结合能存在各向异性, 因此非平面分子和平面分子之间的相互作用也应该表现出方向依赖性, 即将非平面分子与平面分子垂直面间和沿着面内方向的结合能分别设置为0.4kBT和0.2kBT. 模拟发现超过50000个粒子的沉积形貌大致相似, 因此选择沉积50000个粒子来演示模拟结果, 此外为了清楚地显示两种不同类型分子成核聚集的生长趋势, 非平面分子和平面分子各沉积25000个粒子. 模拟过程中选择性地记录了四个不同成核阶段(即5000, 15000, 30000, 50000个粒子)的沉积形貌, 如图2所示, 图中的蓝、红色球形粒子分别代表非平面分子和平面分子. 沉积初始阶段时(入射粒子数为5000个, 非平面和平面粒子各约2500个), 图2(a)中电极顶部沉积的粒子总数明显多于电极侧面的粒子总数. 这是由于粒子与电极间强相互作用的存在, 两种不同类型的分子都会优先成核聚集在电极的上表面. 随着入射粒子数量的不断增加, 从图2(b), (c)可以看出, 非平面分子主要在电极顶部岛状成核, 只有极少部分非平面分子与平面分子相互作用在电极的侧面聚集. 而平面分子主要在电极间隙处以阶梯边缘诱导方式成核而聚集生长. 如图2(d), 当入射粒子数达到50000时(非平面和平面粒子各约25000个), 4个方形电极顶部的非平面粒子保持完美地向上聚集生长且高度相当, 而平面分子由于强的垂直面间相互作用继续在4个方形电极间隙处阶梯诱导聚集直至在衬底上连成一片. 虽然有少量可见非平面分子粒子掺杂生长在电极侧面, 但是由于非平面分子与平面分子存在着较弱的相互作用力, 因此无论在电极顶部还是在侧壁只会出现极少量的两种分子的掺杂生长. 由图2可以直观地看出整个模拟过程中这两种粒子在电极顶部和侧面的生长趋势, 即非平面分子主要生长于电极的顶部, 而平面分子主要在电极的侧面聚集.

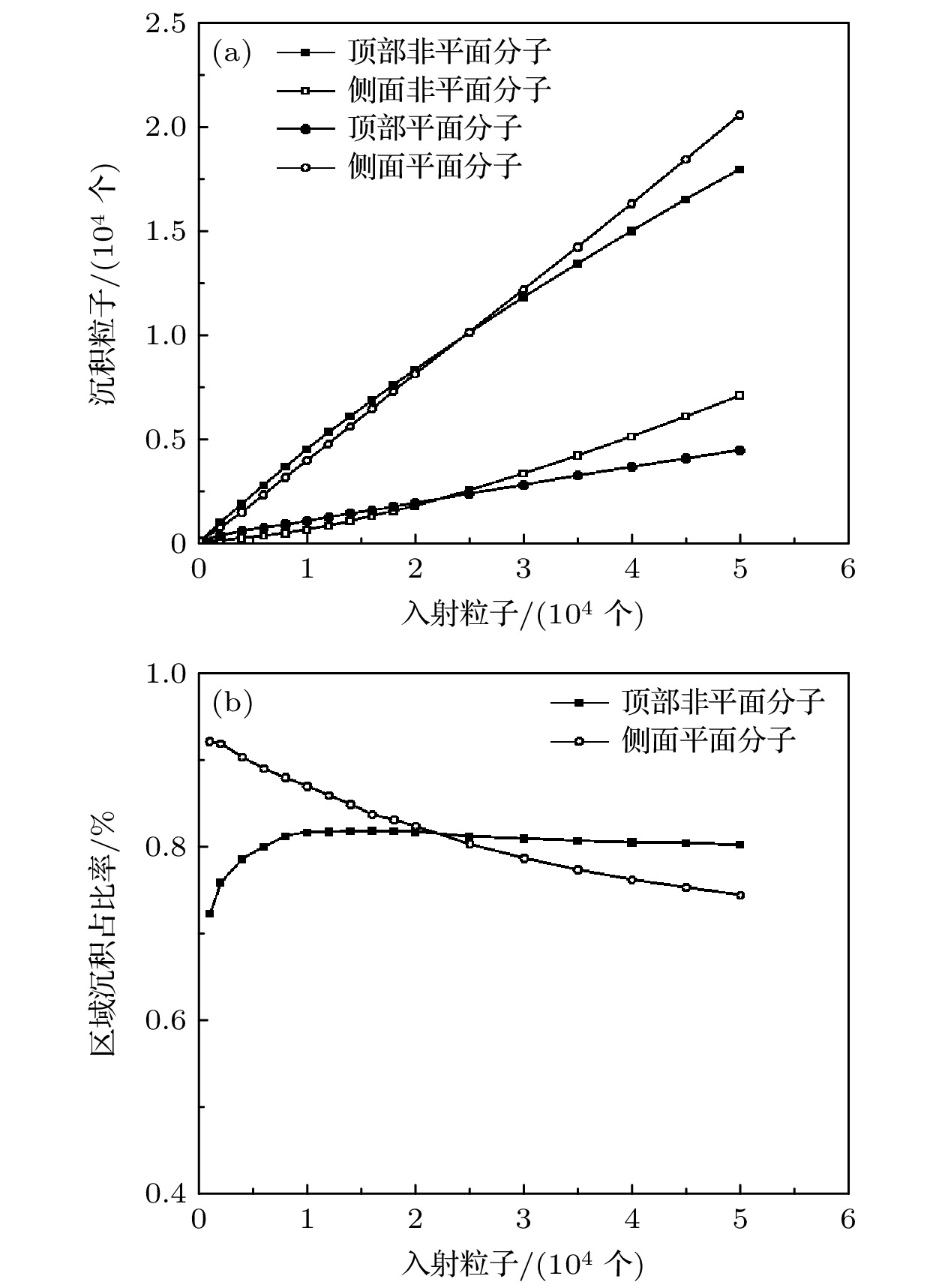
      此外模拟中还统计了非平面分子(平面分子)在电极顶部和侧面沉积数量以及占比率, 其随入射总粒子数变化的趋势如图3所示. 由图3(a)可见: 沉积前期阶段随着入射粒子数从0增至10000个左右, 电极顶部非平面粒子数量以较快的速度增加, 而电极侧面非平面粒子数则增长缓慢; 平面分子则反之, 侧面区域的粒子数量快速增加, 而电极顶部数量则缓慢地增加. 这种不同的增长趋势致使非平面(平面)分子主要成核聚集于电极的顶部(侧面). 随着入射粒子数的增加, 电极顶部的总粒子数逐渐多于侧面的总粒子数, 并且差距不断拉大. 结合图3(b)所示, 在此期间(沉积0—10000个粒子)非平面分子(平面分子)占电极顶部(侧面)总粒子数的比率呈现出相反的变化, 非平面分子占比率不断递增的同时电极侧面平面分子占比率则不断下降, 但电极顶部非平面分子的占比率却始终小于平面分子在侧面的占比率. 统计当入射10000个粒子时(非平面和平面粒子各约5000个), 电极顶部的非平面和平面分子数量分别为4487和1009个左右(总粒子数约5496个), 侧面则约为587和3917个粒子数(总粒子数约4504个), 并且非平面粒子(平面粒子)占电极顶部(侧面)总粒子数的比率分别约为81.6%和86.9%. 由此可以看出整个沉积前期阶段非平面(平面)分子主要沉积在电极的顶部(侧面), 并且初期两种不同类型的分子都会优先在电极上表面成核聚集, 导致顶部总粒子数多于侧面的同时电极顶部非平面分子的占比率却始终小于平面分子在侧面的占比率.

      当入射粒子数从10000增至50000个, 由图3(a)可见, 随着入射粒子数的增多, 电极顶部非平面粒子数继续增长的同时也有越来越多的非平面分子成核于电极侧面; 平面分子在电极侧面数量也持 续增长, 而在电极顶部则缓慢上升. 图3(b)中顶 部非平面分子的占比率基本保持不变, 而侧面平面分子的占比率持续下降, 造成了两种占比率的反超. 由于平面分子和非平面分子之间的作用力非常弱, 因此平面分子依然会保持单独沉积时类似特点: 优先在电极侧面成核, 而各向异性相互作用的性能以及电极顶部参差不齐的沉积表面限制了其在顶部的后续沉积[19,20]. 而不受此限制的各向同性非平面粒子在后续沉积过程中会倾向于掺杂沉积在电极侧面, 从而导致了电极侧面与顶部的总粒子数差距的逐渐缩减并最终反超, 而且侧面区域沉 积纯度的持续下降. 因此为了在顶部和侧面区域都获得较好沉积纯度, 应控制好沉积的非平面粒子的数目.

      总之在这种情况下平面和非平面分子分别主要沉积在电极的间隙和顶部, 表明这两类分子可以进行良好的独立自组装, 在两个区域内沉积纯度可以同时高达81.6%. 由此当混合沉积两种不同类型的分子时, 可以通过选择有机分子(如各向异性和各向异性、各向异性和各向同性)使其具有适当的分子作用力或结合能, 并且混合沉积一定数量的粒子数可以完美地实现高纯度有机分子的相分离生长.

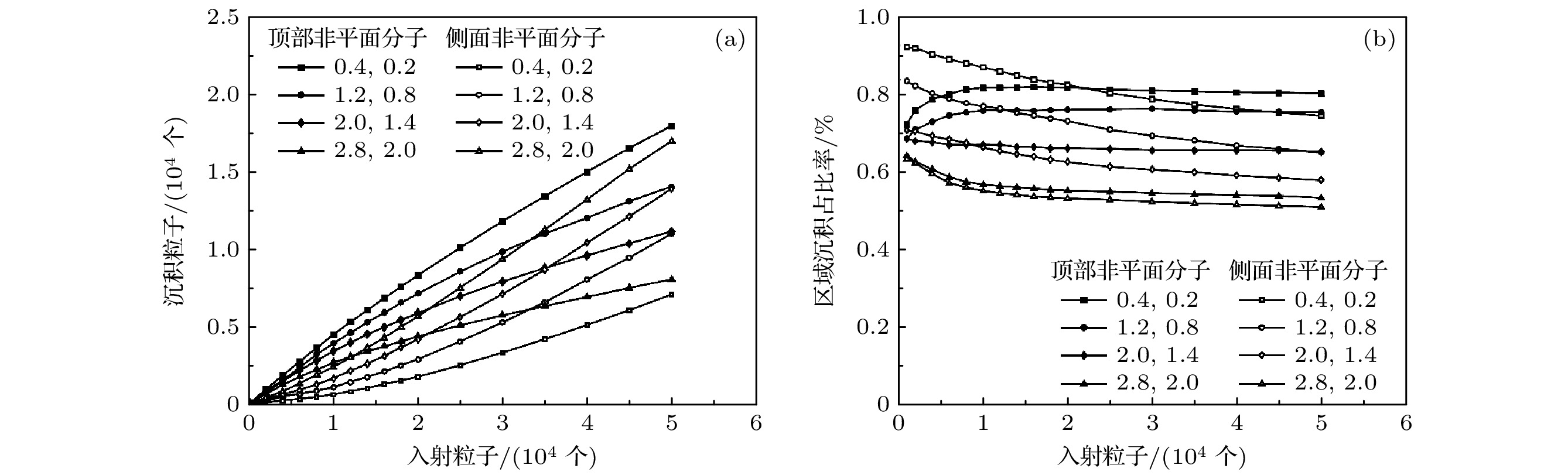
      由上述的模拟结果可知两种不同类型的有机分子在相互作用力较弱的情况下能够很好地实现各自在不同成核位点处的ASG, 实现了彼此间的相互分离, 从而产生了明显的沉积形貌: 即非平面分子主要成核聚集于电极的上表面, 而平面分子则主要横向堆积生长在电极的侧壁处. 为了进一步研究两种分子之间相互作用力多大程度上能够控制彼此间的分离生长, 将非平面分子与平面分子垂直面间和沿着面内方向之间的结合能从弱到强, 依次设置为0.4kBT和0.2kBT; 1.2kBT和0.8kBT; 2kBT和1.4kBT; 2.8kBT和2kBT. 而平面(非平面)分子和电极、基底之间的相互作用仍分别设置为3.1kBT (1.7kBT), 0.9kBT (0.3kBT). 随着两种类型分子间的结合能递增, 混合沉积非平面分子和平面分子的最终形貌(沉积50000个粒子)如图4所示. 由上述分析并结合图4(a)可知, 当平面和非平面分子之间的相互作用较弱时能够很好地引导彼此间的分离, 最终实现各自的独立自组装. 然而, 图4(b), (c)发现, 随着两种粒子间结合能的不断增强, 非平面分子较难占据电极的顶部区域, 而会在平面分子相互作用力的牵引下倾向于在电极的间隙处与横向生长的平面分子随意聚集. 同时电极顶部沉积的平面分子数也在逐渐增多. 如图4(d)所示, 当平面与非平面分子的结合能增加至2.8kBT (2kBT), 对比图4(a)可知, 沉积粒子的聚集形貌发生了巨大的变化, 无论是电极顶部还是侧面都混合沉积了大量的平面和非平面粒子, 从而导致了分子相分离和颜色分区的失效. 此外从非平面分子在电极顶部以及侧面沉积粒子具体数量随入射粒子总数变化(见图5(a))也可得知, 电极顶部的粒子数目随结合能增大而减少, 而侧面的粒子数则反之. 顶部和侧面粒子数量的差距随着结合能增大而减少, 即随着结合能的增强原先非平面分子主导沉积的顶部区域不复存在, 两个区域的粒子分布逐步趋向均匀. 平面分子沉积数量变化的图跟非平面分子的情况非常相似, 故将其略去. 图5(b)的电极顶部(侧面)非平面分子(平面分子)的占比率曲线也进一步佐证了上述变化. 随着两种分子之间结合能的逐渐增强, 占比率曲线整体向下平移. 表明两种分子在电极顶部或侧面的混合度都在逐渐上升, 即随着平面和非平面分子相互作用能的增大, 两种分子分流生长的难度在逐渐上升并最终导致分离失效, 占比率都低至51%左右. 同时, 电极顶部的非平面分子和侧面的平面分子占比率完全相同的情况也随着分子间结合能的递增逐渐提前且占比率不断下降, 甚至很难通过控制粒子数目来选择最优占比率. 这些结果表明, 对于混合沉积两种不同类型分子的ASG, 分子间结合能的大小是导致有机半导体分子以不同的生长机制产生不同的薄膜形貌的主要因素之一. 为了实现两种粒子分离在电极不同位点处成核聚集, 需要选择具有弱相互作用的合适的两类分子: 平面分子与非平面分子, 或者调控两类分子之间相互作用力[19].

    4.   结　论

    • 本文首次利用kMC模拟方法研究了两种不同类型分子混合沉积的ASG问题, 分析了分子间结合能对非平面分子和平面分子共同沉积生长形貌的影响. 从模拟结果可知分子间结合能的强弱会对两种分子分离的ASG行为产生很大的影响: 当分子间结合能较弱时, 非平面分子在电极顶部主要以岛状生长方式成核聚集, 而平面分子则有序的逐层堆积在金属电极的间隔处横向生长. 即这两种分子混合沉积时能够很好地实现分离的ASG; 当两种分子间结合能较强时, 原先以非平面分子成核聚集为主的电极顶部上的非平面粒子数量减少而平面分子聚集于顶部数量的增加. 同时以平面分子沉积为主的电极间隙处也同样出现大量掺杂非平面分子的沉积, 从而导致了分子分离生长的失效. 因此, 通过适当调整不同分子间的相互作用能并适当混合沉积一定数量的粒子数, 在电极顶部和侧面可以分别获得较纯结晶的非平面分子和平面分子薄膜, 并且将这种结构进一步应用于半导体器件中. 对于其他种类的有机半导体材料, 控制分子间适当的相互作用是实现相分离生长的关键因素之一, 但是定量的数值和细节更多依赖于与材料分子具体性能相关的计算.

    参考文献 (27)

目录

/

返回文章
返回