高级搜索

双组分玻色-爱因斯坦凝聚体中PT对称势下的异步量子Kármán涡街

,  ,  ,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

邵凯花, 席忠红, 席保龙, 涂朴, 王青青, 马金萍, 赵茜, 石玉仁. 双组分玻色-爱因斯坦凝聚体中PT对称势下的异步量子Kármán涡街[J]. 物理学报, 2024, 73(11): 110501-1. doi: 10.7498/aps.73.20232003
引用本文: 邵凯花, 席忠红, 席保龙, 涂朴, 王青青, 马金萍, 赵茜, 石玉仁. 双组分玻色-爱因斯坦凝聚体中PT对称势下的异步量子Kármán涡街[J]. 物理学报, 2024, 73(11): 110501-1. doi: 10.7498/aps.73.20232003
shu
Kai-Hua Shao, Zhong-Hong Xi, Bao-Long Xi, Pu Tu, Qing-Qing Wang, Jin-Ping Ma, Xi Zhao, Yu-Ren Shi. Asynchronous quantum Kármán vortex street in two-component Bose-Einstein condensate with PT symmetric potential[J]. Acta Physica Sinica, 2024, 73(11): 110501-1. doi: 10.7498/aps.73.20232003
Citation: Kai-Hua Shao, Zhong-Hong Xi, Bao-Long Xi, Pu Tu, Qing-Qing Wang, Jin-Ping Ma, Xi Zhao, Yu-Ren Shi. Asynchronous quantum Kármán vortex street in two-component Bose-Einstein condensate with PT symmetric potential[J]. Acta Physica Sinica, 2024, 73(11): 110501-1. doi: 10.7498/aps.73.20232003
shu

双组分玻色-爱因斯坦凝聚体中PT对称势下的异步量子Kármán涡街

  • 1.

    西北师范大学物理与电子工程学院, 兰州　730070

  • 2.

    甘肃民族师范学院物理与水电工程系, 合作　747000

  • 3.

    四川文理学院智能制造学院, 达州　635000

    • 通讯作者: Email: shiyr@nwnu.edu.cn

  • 中图分类号: 05.30.Jp, 03.75.Mn, 03.75.Kk, 11.30.Er

Asynchronous quantum Kármán vortex street in two-component Bose-Einstein condensate with PT symmetric potential

  • 1.

    College of Physics and Electronic Engineering, Northwest Normal University, Lanzhou 730070, China

  • 2.

    College of Physics and Hydropower Engineering, Gansu Normal College for Nationalities, Hezuo 747000, China

  • 3.

    College of Intelligent Manufacturing, Sichuan University of Arts and Science, Dazhou 635000, China

    • Corresponding author: Email: shiyr@nwnu.edu.cn

  • MSC: 05.30.Jp, 03.75.Mn, 03.75.Kk, 11.30.Er

  • 摘要: 数值研究了相混合态双组分玻色-爱因斯坦凝聚体(Bose-Einstein condensate, BEC)中PT (parity-time)对称势下的动力学. 在障碍势不同的宽度和速度下发现了异步量子Kármán涡街、斜向漂移涡旋偶极子、V字形涡旋对、无规则量子湍流以及各种尾迹的组合模式. 研究了作用在移动障碍势上的拖拽力, 分析了涡旋对产生的力学机理. 在不同障碍势宽度和速度下, 系统地模拟了异步量子Kármán涡街和其他尾迹模式的参数区域. 同样分析了PT对称势中具有增益-损耗强度的虚部对异步量子Kármán涡街稳定性的影响. 最后, 提供了一个实现异步量子Kármán 涡街的实验方案.
    Abstract: The dynamics of a miscible two-component Bose-Einstein condensate (BEC) with PT (parity-time) symmetric potential are investigated numerically. The dynamical behaviors of the system is described by Gross-Pitaevskii (GP) equations under the mean-field theory. Firstly, the ground state of the system is obtained by the imaginary-time propagation method. Then dynamical behaviors are numerically simulated by the time-splitting Fourier pseudo-spectral approach under periodic boundary conditions. By adjusting the width and velocity of the obstacle potential, various patterns such as no vortex, oblique drifting vortex dipole, V-shaped vortex pairs, irregular quantum turbulence and combined modes are studied. It is noted that the shedding vortex pairs in components 1 and 2 are staggered, which is called “the asynchronous quantum Kármán vortex street”. Here, the ratio of the distance between two vortex pairs in one row to the distance between vortex rows is approximately 0.18, which is less than the stability criterion 0.28 of classical fluid. We calculated the drag force acting on the obstacle potential during generation of the asynchronous quantum Kármán vortex street. It is found that periodical oscillation of the drag force is generated via drifting up or down of the vortex pairs. Meanwhile, we analyzed the influence of the imaginary part of the PT symmetric potential with gain-loss for wake. The trajectory and frequency of the vortex are changed, due to the imaginary part breaks the local symmetry of the system. In addition, the imaginary part affects the stability of the asynchronous quantum Kármán vortex street. Lots of numerical simulations are carried out to determine the parameter regions of various vortex shedding modes. We also proposed an experimental protocol to realize the asynchronous quantum Kármán vortex street in the miscible two-component BEC with PT symmetric potential.
  • 加载中

  • 图 1  PT对称势下异步量子Kármán涡街的密度分布$ {|\psi_1 |}^2 $, $ {|\psi_2 |}^2 $, $ {|\psi_1 |}^2+{|\psi_2 |}^2 $, $ {|\psi_2 |}^2-{|\psi_1 |}^2 $ 和相位分布 arg$ \psi_1 $, arg$ \psi_2 $. 障碍势的宽度和速度为$ (d, \upsilon)=(1.9, 0.46) $. 黑色虚线箭头表示障碍势的移动方向

    Figure 1.  Density $ {|\psi_1 |}^2 $, $ {|\psi_2 |}^2 $, $ {|\psi_1 |}^2+{|\psi_2 |}^2 $, $ {|\psi_2 |}^2-{|\psi_1 |}^2 $ and phase arg$ \psi_1 $, arg$ \psi_2 $ distributions of asynchronous quantum Kármán vortex street with PT symmetric potential. The width and velocity of the obstacle potential is $ (d, \upsilon)=(1.9, 0.46) $. The dashed black arrow indicates the direction of the moving obstacle potential.

    下载: 全尺寸图片 幻灯片

    图 2  PT对称势下不同尾迹的密度分布$ {|\psi_1 |}^2 $和相位分布arg$ \psi_1 $. 黑色虚线箭头表示障碍势的移动方向　(a) $ d=0.7, \upsilon=0.56 $; (b) $ d=1.1, \upsilon=0.51 $; (c) $ d=2.1, \upsilon=0.53 $

    Figure 2.  Density $ {|\psi_1 |}^2 $ and phase arg$ \psi_1 $ distributions of various wakes with PT symmetric potential. The dashed black arrow indicates the direction of the moving obstacle potential: (a) $ d=0.7, \upsilon=0.56 $; (b) $ d=1.1, \upsilon=0.51 $; (c) $ d=2.1, \upsilon=0.53 $.

    下载: 全尺寸图片 幻灯片

    图 3  异步量子Kármán涡街形成过程中作用在移动障碍势上的拖拽力随时间的演化. 蓝色实线和红色虚线表示$ f_x $和$ f_y $. F1+F2代表双组分中产生的拖拽力. 参数与图1所取参数一致

    Figure 3.  Time evolution of the drag force acting on the moving obstacle potential during the formation of asynchronous quantum Kármán vortex street. Solid blue lines and dotted red lines represent $ f_x $ and $ f_y $. F1+F2 denotes drag force of the two-component. The parameters are consistent with Fig. 1.

    下载: 全尺寸图片 幻灯片

    图 4  PT对称势下组合模式的密度分布$ {|\psi_1 |}^2 $和相位分布arg$ \psi_1 $. 黑色虚线箭头表示障碍势的移动方向　(a) $ d=0.7, \upsilon=0.57 $; (b) $ d=2.3, \upsilon=0.43 $; (c) $ d=1.3, \upsilon=0.55 $

    Figure 4.  Density $ {|\psi_1 |}^2 $ and phase arg$ \psi_1 $ distributions of combined modes with PT symmetric potential. The dashed black arrow indicates the direction of the moving obstacle potential: (a) $ d=0.7, \upsilon=0.57 $; (b) $ d=2.3, \upsilon=0.43 $; (c) $ d=1.3, \upsilon=0.55 $.

    下载: 全尺寸图片 幻灯片

    图 5  作用在移动障碍势上的拖拽力随时间的演化. (a)—(c）参数与图4(b)一致和(d)—(f)参数与图4(c)一致

    Figure 5.  Time evolution of the drag force acting on the moving obstacle potential. The parameters of (a)–(c) and (d)–(f) are consistent with Figs. 4(b) and (c), respectively

    下载: 全尺寸图片 幻灯片

    图 6  各种典型尾迹模式与移动障碍势的宽度d和速度$ \upsilon $的关系. 紫色区域表示稳定的层流, 蓝色、浅蓝色、红色、绿色和橙色区域对应图2(a)—(c)、图1和图4

    Figure 6.  Dependence of the various wake patterns on the width d and velocity $ \upsilon $ of moving obstacle potential. The purple area is consistent with the stable laminar flow. The blue, light blue, red, green and orange areas correspond to the wake patterns shown in Figs. 2(a)-(c), Fig. 1 and Fig. 4

    下载: 全尺寸图片 幻灯片

    图 7  障碍势后异步量子Kármán涡街形成的动力学演化过程. $ d=1.9,\; \upsilon=0.48 $

    Figure 7.  Dynamics evolution process of the asynchronous quantum Kármán vortex street formation behind the obstacle potential. $ d=1.9,\; \upsilon=0.48 $.

    下载: 全尺寸图片 幻灯片
  • [1] Bose V 1924 Zeitschrift für Physik 26 178 doi: 10.1007/BF01327326
    [2] Anderson M H, Ensher J R, Matthews M R, Wieman C E, Cornell E A 1995 Science 269 198 doi: 10.1126/science.269.5221.198
    [3] Edwards M, Dodd R J, Clark C W, Ruprecht P A, Burnett K 1996 Phys. Rev. A 53 R1950 doi: 10.1103/PhysRevA.53.R1950
    [4] Davis K B, Mewes M O, Andrews M R, van Druten N J, Durfee D S, Kurn D M, Ketterle W 1995 Phys. Rev. Lett. 75 3969 doi: 10.1103/PhysRevLett.75.3969
    [5] Jackson B, McCann J F, Adams C S 1998 Phys. Rev. Lett. 80 3903 doi: 10.1103/PhysRevLett.80.3903
    [6] Zhu Q L, Pan L 2021 J. Low Temp. Phys. 203 392 doi: 10.1007/s10909-021-02588-6
    [7] Sasaki K, Suzuki N, Saito H 2010 Phys. Rev. Lett 104 150404 doi: 10.1103/PhysRevLett.104.150404
    [8] Schoepe W 2015 JETP Lett. 102 105 doi: 10.1134/S0021364015140106
    [9] Li X L, Yang X Y, Tang N, Song L, Zhou Z K, Zhang J, Shi Y R 2019 New J. Phys. 21 103046 doi: 10.1088/1367-2630/ab4d06
    [10] 王力, 刘静思, 李吉, 周晓林, 陈向荣, 刘超飞, 刘伍明 2020 物理学报 69 010303 doi: 10.7498/aps.69.20191648 Wang L, Liu J S, Li J, Zhou X L, Chen X R, Liu C F, Liu W M 2020 Acta Phys. Sin. 69 010303 doi: 10.7498/aps.69.20191648
    [11] Zhang T F, Li C X, Liu W M 2023 Chin. Phys. B 32 090501 doi: 10.1088/1674-1056/acd922
    [12] 文林, 梁毅, 周晶, 余鹏, 夏雷, 牛连斌, 张晓斐 2019 物理学报 68 080301 doi: 10.7498/aps.68.20182013 Wen L, Liang Y, Zhou J, Yu P, Xia L, Niu L B, Zhang X F 2019 Acta Phys. Sin. 68 080301 doi: 10.7498/aps.68.20182013
    [13] Nore C, Huepe C, Brachet M E 2000 Phys. Rev. Lett. 84 2191 doi: 10.1103/PhysRevLett.84.2191
    [14] Aftalion A, Du Q, Pomeau Y 2003 Phys. Rev. Lett. 91 090407 doi: 10.1103/PhysRevLett.91.090407
    [15] Qi W, Guo X G, Dong L W, Zhang X F 2023 Chin. Phys. B 32 030502 doi: 10.1088/1674-1056/ac891a
    [16] Okulov V L, Fukumoto Y 2021 J. Appl. Mech. Tech. Phys. 62 519 doi: 10.1134/S0021894421030196
    [17] Abo-Shaeer J R, Raman C, Vogels J M, Ketterle W 2001 Science 292 476 doi: 10.1126/science.1060182
    [18] Kim Ildoo, Wu X L 2015 Phys. Rev. E 92 043011 doi: 10.1103/PhysRevE.92.043011
    [19] Ponta F L, Aref H 2004 Phys. Rev. Lett. 93 084501 doi: 10.1103/PhysRevLett.93.084501
    [20] Finne A P, Araki T, Blaauwgeers R, Eltsov V B, Kopnin N B, Krusius M, Skrbek L, Tsubota M, Volovik G E 2003 Nature 424 1022 doi: 10.1038/nature01880
    [21] Sasaki K, Suzuki N, Saito H 2011 Phys. Rev. A 83 033602 doi: 10.1103/PhysRevA.83.033602
    [22] Kwon W J, Kim J H, Seo S W, Shin Y 2016 Phys. Rev. A 117 245301 doi: 10.1103/PhysRevLett.117.245301
    [23] Bender C M, Boettcher S 1998 Phys. Rev. Lett. 117 5243 doi: 10.1103/PhysRevLett.80.5243
    [24] Single F, Cartarius H, Wunner G, Main J 2014 Phys. Rev. A 90 042123 doi: 10.1103/PhysRevA.90.042123
    [25] Hussain J, Nouman M, Saif F, Akram J 2020 Physica B 587 412152 doi: 10.1016/j.physb.2020.412152
    [26] Guo P, Gasparian V, Jódar E, Wisehart, C 2023 Phys. Rev. A 107 032210 doi: 10.1103/PhysRevA.107.032210
    [27] Bender C M, Boettcher S, Meisinger P N 1999 J. Math. Phys. 40 2201 doi: 10.1063/1.532860
    [28] Rüter C E, Makris K G, El-Ganainy R, Christodoulides D N, Segev M, Kip Dm 2010 Nat. Phys. 6 192 doi: 10.1038/nphys1515
    [29] Bender C M, Gianfreda M, Özdemir S K, Peng B, Yang L 2013 Phys. Rev. A 88 062111 doi: 10.1103/PhysRevA.88.062111
    [30] Guo A, Salamo G J, Duchesne D, Morandotti R, Volatier-Ravat M, Aimez V, Siviloglou G A, Christodoulides D N 2009 Phys. Rev. Lett. 103 093902 doi: 10.1103/PhysRevLett.103.093902
    [31] Wilkey A, Suelzer J, Joglekar Y, Vemuri G 2019 Photonics 6 122 doi: 10.3390/photonics6040122
    [32] Schwarz L, Cartarius H, Musslimani Z H, Main J, Wunner G 2017 Phys. Rev. A 95 053613 doi: 10.1103/PhysRevA.95.053613
    [33] Haag D, Dast D, Löhle, A, Cartarius H, Main J, Wunner G 2014 Phys. Rev. A 89 023601 doi: 10.1103/PhysRevA.89.023601
    [34] Kato M, Zhang X F, Saito H 2017 Phys. Rev. A 95 043605 doi: 10.1103/PhysRevA.95.043605
    [35] Cui X L 2022 Phys. Rev. Res. 4 013047 doi: 10.1103/PhysRevResearch.4.013047
    [36] Wang L X, Dai C Q, Wen L, Liu T, Jiang H F, Saito H, Zhang S G, Zhang, X F 2018 Phys. Rev. A 97 063607 doi: 10.1103/PhysRevA.97.063607
    [37] Zhang X F, Du Z J, Tan R B, Dong R F, Chang H, Zhang S G 2014 Ann. Phys. 346 154 doi: 10.1016/j.aop.2014.04.015
    [38] Hu X H, Zhang X F, Zhao D, Luo H G, Liu W M 2009 Phys. Rev. A 79 023619 doi: 10.1103/PhysRevA.79.023619
    [39] Fujiyama S, Tsubota M 2009 Phys. Rev. B 79 094513 doi: 10.1103/PhysRevB.79.094513
    [40] Williamson C H K 1996 Annu. Rev. Fluid Mech. 28 477 doi: 10.1146/annurev.fl.28.010196.002401
    [41] Mason P 2013 Phys. Rev. A 88 043608 doi: 10.1103/PhysRevA.88.043608
    [42] Barenghi C F 2008 Physica D 237 2195 doi: 10.1016/j.physd.2008.01.010
    [43] Papp S B, Wieman C E 2006 Phys. Rev. Lett. 97 180404 doi: 10.1103/PhysRevLett.97.180404
    [44] Papp S B, Pino J M, Wieman C E 2008 Phys. Rev. Lett. 101 040402 doi: 10.1103/PhysRevLett.101.040402
    [45] Kwon W J, Moon G, Choi J, Seo S W, Shin Y 2014 Phys. Rev. A 90 063627 doi: 10.1103/PhysRevA.90.063627
    [46] Werner J, Griesmaier A, Hensler S, Stuhler J, Pfau T 2005 Phys. Rev. Lett. 94 183201 doi: 10.1103/PhysRevLett.94.183201
    [47] Robins N P, Figl C, Jeppesen M, Dennis G R, Close J D 2008 Nat. Phys. 4 731 doi: 10.1038/nphys1027
    [48] Li J, Harter A K, Liu J, Melo L, Joglekar Y N, Luo L 2019 Nature 10 855 doi: 10.1038/s41467-019-08596-1
  • 加载中
图( 7)
计量
  • 文章访问数:  147
  • HTML全文浏览数:  147
  • PDF下载数:  2
  • 施引文献:  0
出版历程
  • 收稿日期:  2023-12-22
  • 刊出日期:  2024-06-05

双组分玻色-爱因斯坦凝聚体中PT对称势下的异步量子Kármán涡街

    通讯作者: Email: shiyr@nwnu.edu.cn
  • 1. 西北师范大学物理与电子工程学院, 兰州　730070
  • 2. 甘肃民族师范学院物理与水电工程系, 合作　747000
  • 3. 四川文理学院智能制造学院, 达州　635000
  • 收稿日期:  2023-12-22

摘要: 数值研究了相混合态双组分玻色-爱因斯坦凝聚体(Bose-Einstein condensate, BEC)中PT (parity-time)对称势下的动力学. 在障碍势不同的宽度和速度下发现了异步量子Kármán涡街、斜向漂移涡旋偶极子、V字形涡旋对、无规则量子湍流以及各种尾迹的组合模式. 研究了作用在移动障碍势上的拖拽力, 分析了涡旋对产生的力学机理. 在不同障碍势宽度和速度下, 系统地模拟了异步量子Kármán涡街和其他尾迹模式的参数区域. 同样分析了PT对称势中具有增益-损耗强度的虚部对异步量子Kármán涡街稳定性的影响. 最后, 提供了一个实现异步量子Kármán 涡街的实验方案.

English Abstract

    全文HTML

    1.   引　言

    • 玻色-爱因斯坦凝聚体(Bose-Einstein condensate, BEC)是一种宏观量子现象, 指当系统的温度低于临界温度时所有原子都聚集在最低能级上的现象[1]. 自1995年实验实现以来[2–4], BEC为研究超流体现象提供了一个精确调控的平台. 许多研究者也对BEC进行了大量的研究并发现了各种各样的现象, 如捕获系统中产生的涡旋[5,6]、Kármán 涡街[7–9]、孤子[10–12]和三维动力学[13–16]等. 其中Kármán涡街现象是指在移动障碍势后两侧脱落出旋转方向相反、涡旋间的距离不变且排列规则的两列涡旋[17–20]. 2010 年, Sasaki等[7]理论上研究了单组分BEC中移动障碍势后产生周期性交替脱落的涡旋对, 并最终形成Kármán涡街的现象. 随后, Sasaki等[21]在相分离的双组分BEC中发现, 当一个分量中的气泡穿过另一个分量时, 圆形气泡演化为椭圆形并分裂为涡旋碎片, 最后在移动气泡的尾流中形成Kármán涡街. 此外, 2016 年, Kwon等[22]实验上观测到移动的排斥高斯激光束后会周期性脱落出涡旋簇, 这些涡旋簇规则分布并形成量子Kármán涡街.

      此外, 许多学者致力于PT (parity-time)对称在BEC中的研究. 1998年, Bender和Boettcher[23]提出PT对称非厄米系统中仍然存在完全实本征谱. 通常, 非厄米哈密顿量可以描述开放量子系统, 用于考虑外部边界条件或用外势的虚部提供增益和损耗[24–26]. PT对称势是一个必要非充分条件, 其实部是偶函数, 虚部是奇函数[27–29]. 在实验上, 利用光波导通道可以实现具有增益-损耗效果的复势能[30,31]. 2017年, Schwarz等[32]在具有PT对称势的BEC中研究涡旋激发. Haag等[33]研究了满足PT对称双势阱的非线性量子动力学. 目前据我们所知, 对BEC中PT对称势下的Kármán涡街研究很少. 因此, 我们想知道BEC中PT对称势下是否可以形成Kármán涡街以及该势对尾迹的影响.

      本文对相混合态双组分BEC中PT对称势下的量子Kármán涡街进行了研究. 在障碍势宽度和速度合适的情况下发现了涡旋对交错排布的异步量子Kármán涡街, 并且具有增益-损耗强度的虚部对障碍势后涡旋对的稳定性具有一定的影响. 同样研究了涡旋脱落时作用在障碍势上的拖拽力以及各种尾迹模式的参数区域. 最后, 提供了一个实现异步量子Kármán涡街的实验方案.

    2.   理论模型

    • 根据平均场理论, 双组分BEC中PT对称势下的哈密顿量可以写为[34,35]

      其中$ {\boldsymbol{\varPsi}}({{\boldsymbol{r}}})={[ {\psi_1({{\boldsymbol{r}}}), {\psi _2}({{\boldsymbol{r}}})}]^{\rm T}} $是波函数, T和r分别表示转置和笛卡尔坐标; m是原子质量;$ V({{{\boldsymbol{r}}}}) $表示PT对称势; $ g_{jj} $和$ g_{jl} $表征组内和组间相互作用强度. $ {g_{jl}}=4\pi\hbar ^2{a_{jl}}/m$, 这里$ a_{jl} $ $ (j, l=1, 2) $ 代表s波散射长度. 实验中, BEC通常被束缚在谐振子势$ V({{\boldsymbol{r}}})_{{\mathrm{har}}}=\dfrac{1}{2}m(\omega_x^2 x^2+\omega_y^2 y^2+\omega_z^2 z^2) $中, $ \omega_x $, $ \omega_y $和$ \omega_z $分别是x, y 和z方向的角频率. 假设z方向的约束非常强, $ \hbar\omega_z $远大于$ \hbar\omega_x $和$ \hbar\omega_y $时[36–38], BEC在x-y平面上呈圆盘状. 波函数表示为$ {\psi_j}({{\boldsymbol{r},t}})= \varphi_{j}(x, y,t){\phi_{0}}(z){{\mathrm{e}}^{-{\mathrm{i}}{\omega_z}t/2}} $, 原子在z方向的运动被冻结为基态$ {\phi _{0}}(z)={({{m}{\omega _z}/\pi \hbar) }^{1/4}} {{\mathrm{e}}^{- {m}{\omega _z}{z^2}/(2\hbar)}} $. 此时三维系统近似为准二维. 引入无量纲量 $ \tilde t=\omega_0 t $, $ \tilde x=x/a_{\rm h0} $, $ \tilde y= y/ a_{\rm h0} $, $ \tilde\psi_j= \psi_{j}(x, y,t)/\sqrt{n_0/a_{\rm h0}^2} $, $\tilde g_{jl}=4\pi{n_0}{a_{jl}}/(\sqrt{2\pi}{l_z}) $, 其中, $ \omega_0=\min(\omega_x, \omega_y) $, $ l_z=\sqrt{\hbar/(m{\omega _z})} $以及$ a_{\rm h0}= \sqrt{\hbar/(m{\omega _0})} $. $ n_0 $表示粒子数密度的单位. 总粒子数为$ N={n_0} \displaystyle \int{|\psi|^2}{\mathrm{d}}x{\mathrm{d}}y $. 为方便, 省略变量上的“$ \sim $”, 得到准二维无量纲Gross-Pitaevskii (GP)方程:

      数值计算时, 设无量纲相互作用参数 $ g_{11}= 1,\; g_{22}=0.9 $和$ g_{12}=g_{21}=0.3 $以满足相混合条件 $ g_{11}g_{22} > g_{12}^2 $. 将$ [-256, 256]a_\mathrm{{h0}}\otimes[-64, 64]a_\mathrm{{h0}}$的空间离散为$ 2048\times 512 $网格点进行计算. 选取初始波函数为$ \psi_1=\psi_2=1 $. 通过虚时演化法得到系统的基态, 并将该基态作为系统的初始状态. 然后采用时间劈裂Fourier谱方法在周期性边界条件下进行非线性动力学演化, 加入少量扰动打破系统的对称性. t > 0 时, 障碍势以速度$ \upsilon $移动, 从而研究系统的动力学.

    3.   数值结果

    • 考虑PT对称势为$ V=V_{\rm R}+{\mathrm{i}}V_{\rm I} $, 其中势的实部$ V_{\rm R} $是偶函数, 势的虚部$ V_{\rm I} $为奇函数, 以满足势的PT对称性. 本文中势的实部为高斯障碍势, 实验上采用排斥的高斯激光束实现, 表达式为[34]

      其中$ (\pm x_{0 {\mathrm{r}}},\; \pm y_{0 {\mathrm{r}}})=(\pm409.6, \;\pm60) $表示t = 0时刻高斯障碍势的初始位置. 峰值强度$ V_0=100 $, d是障碍势的宽度. PT对称势的虚部表示为

      在进行动力学演化时, 势的虚部的位置固定在$ (\pm x_{0{\mathrm{ i}}}, \pm y_{0{\mathrm{ i}}})=(0, \pm70) $以实现局部粒子的增益或损耗. 但整个系统的粒子数守恒. 其中Γ表征增益-损耗强度, d代表$ V_{\rm I} $的宽度, 且与$ V_{\rm R} $的宽度相同.

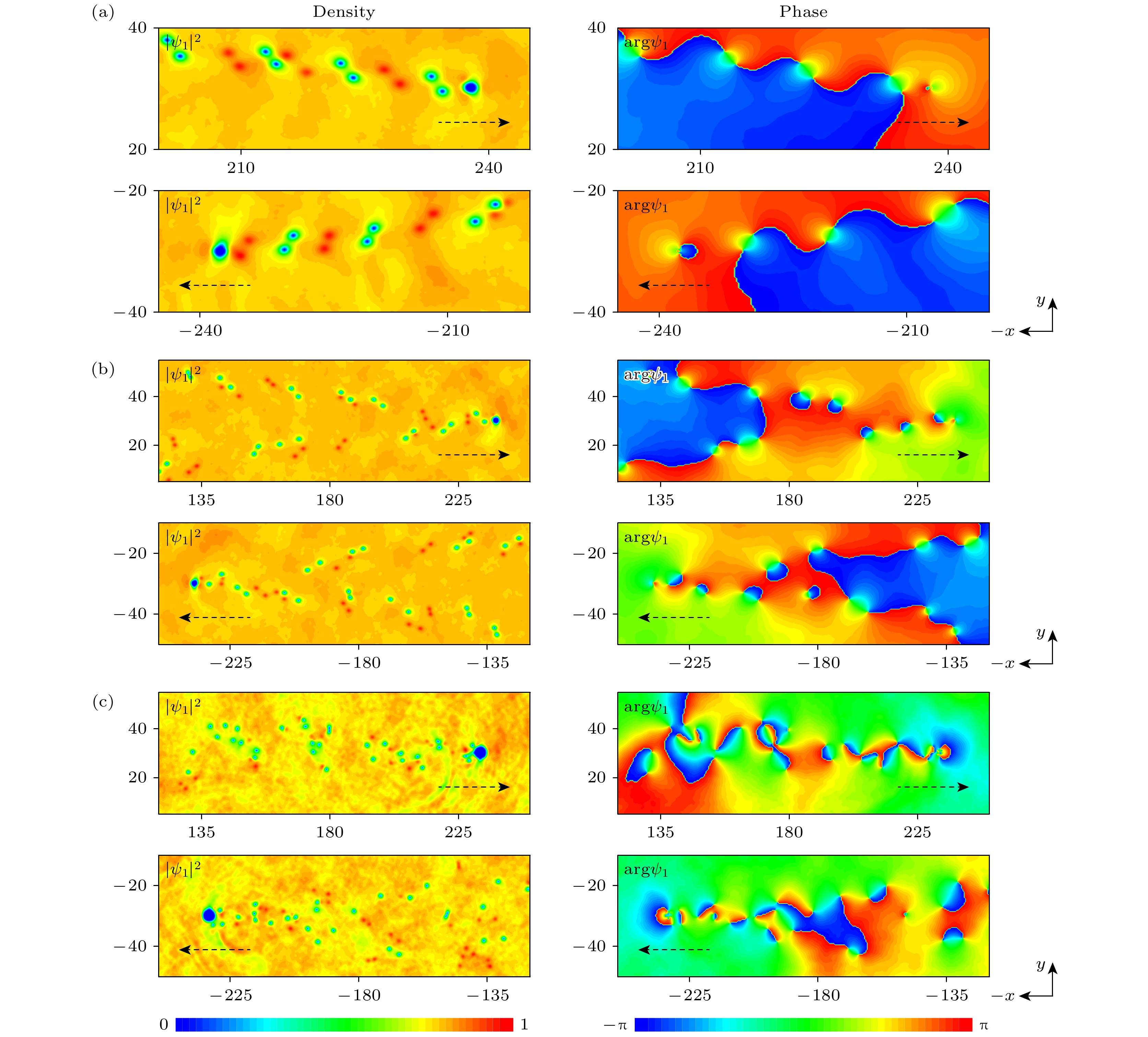
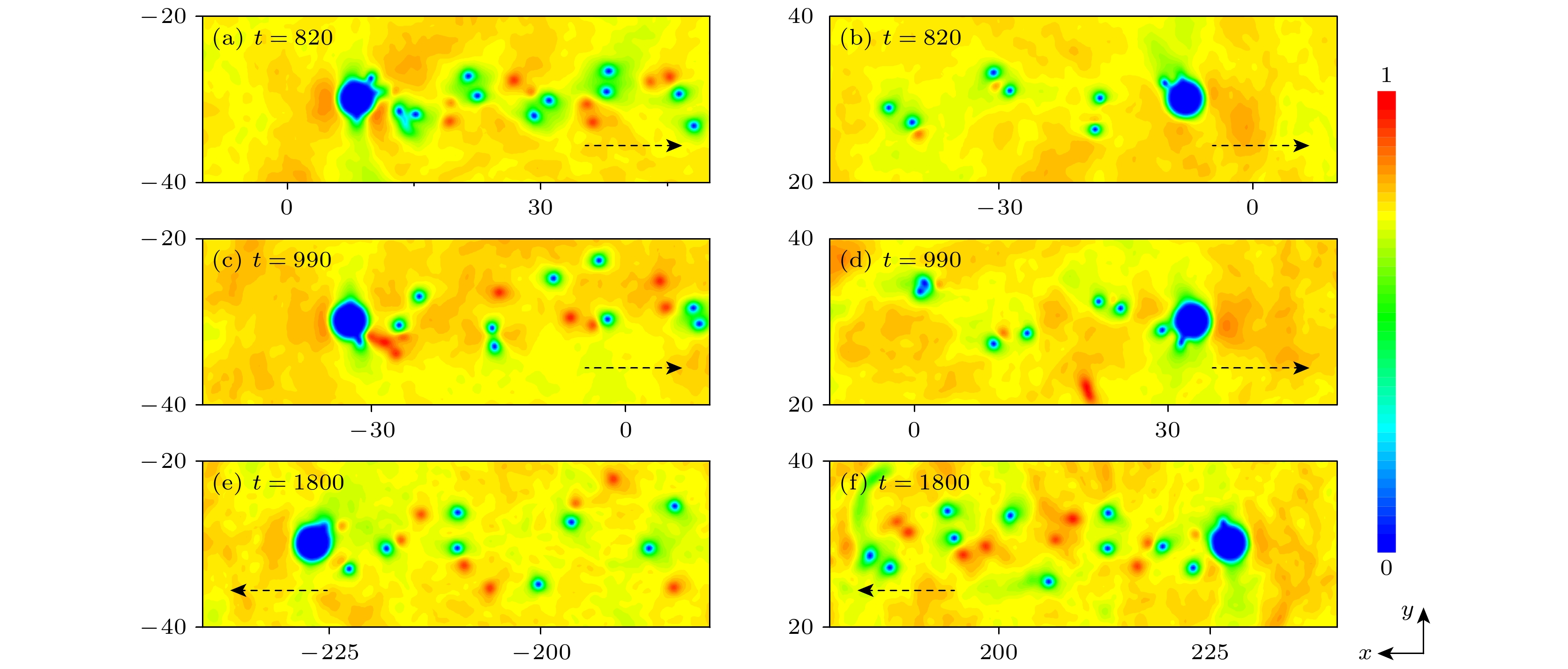
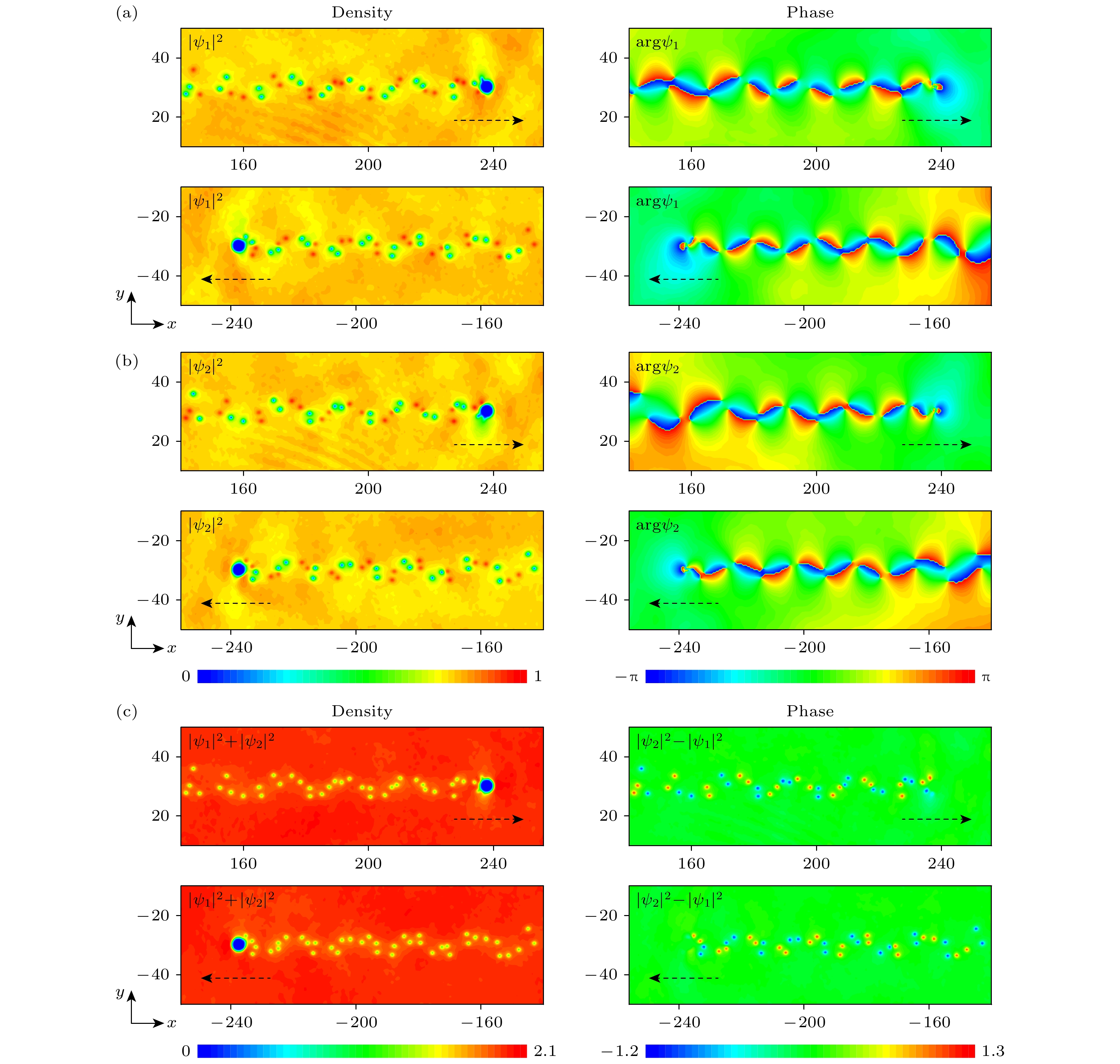
      为了研究障碍势后涡旋脱落的模式, 高斯障碍势$ V_{\rm R} $从初始位置$ (x_{0 {\mathrm{r}}}, y_{0 {\mathrm{r}}}) $沿－x方向移动以及从$ (-x_{0 {\mathrm{r}}}, -y_{0 {\mathrm{r}}}) $沿x方向运动. 选取增益-损耗强度 $ \varGamma=0.04 $及$ V_{\rm R} $的不同宽度和速度, 研究障碍势后涡旋脱落的各种密度和相位分布. 图1所示为相混合态双组分BEC中障碍势后形成异步量子Kármán涡街的密度及相应的相位分布. 如图1(a),(b)所示, 组分1和组分2中都出现了交错排布的两列涡旋对, 本文将涡旋对的这种排布形式命名为“异步量子Kármán涡街”. 其脱落方式为: 组分1中涡旋对从障碍势右侧脱落时, 组分2中涡旋对从障碍势左侧脱落, 待下次脱落时, 组分1和组分2中脱落的涡旋对交换位置, 因此在尾迹中交错排布. 从相位分布中发现, 不管障碍势沿着x还是–x方向移动, 上层涡旋对都是顺时针循环, 环量为$ 2\pi\hbar/(mD^2) $, 对应无量纲量为$ 2\pi $. 下层涡旋对都是逆时针循环, 环量为$ -2\pi\hbar/(mD^2) $[39], 相应的无量纲量是$ -2\pi $, $ D $代表涡旋对中两点涡之间的距离. 双组分中, 两列涡旋对之间的平均距离$ b\approx13.70 $, 且同一列中两个涡旋对之间的平均距离$ l\approx79.68 $, 所以$ b/l\approx0.17 $. 该比值小于经典流体中Kármán涡街稳定性条件$ b/l\approx0.28 $[7,40]. 从图1(c)可以看出, 系统中存在相对混乱的量子化涡旋, 但从单个组分来看, 尾迹模式仍然是量子Kármán 涡街. 相应地, 一个组分中产生了量子Kármán涡街, 在另一个组分的同一位置出现了涡旋密度峰构成的量子Kármán涡街, 将这样的复合结构称为半量子Kármán涡街. 形成这种现象的原因是组分1中的原子填充组分2中涡旋的中心位置, 但这个位置没有被填满, 所以这种复合结构也被称为无核涡街[41].

      图2给出了斜向漂移涡旋偶极子、V字型涡旋对和无规则量子湍流的密度和相位分布. 当障碍势的宽度较小且移动速度超过临界速度时[42], 障碍势后的尾迹更容易形成涡旋-反涡旋对, 即为涡旋偶极子, 如图2(a)所示. 可以注意到障碍势后脱落出涡旋偶极子, 且并未沿着障碍势的运动方向移动, 而是依次在组分1和组分2中斜向漂移排布, 我们将这种排布形式称为“斜向漂移涡旋偶极子”. 由于PT对称势的虚部破坏系统的局部对称性, 在其周围存在粒子的增益和损耗, 导致涡旋对向上或向下漂移. 如图2(b)所示, 当障碍势的移动速度增大时, 从障碍势脱落的涡旋对分布为V字型涡旋对. 因为形成的双列涡旋对不稳定, 受到扰动后将沿着斜向上和斜向下漂移, 最终形成V字型涡旋对. 从图2(a)和图2(b)的相位分布中观察到障碍势后脱落的涡旋对具有$ 2\pi\hbar/m $和$ -2\pi\hbar/m $的环量, 对应无量纲环量为$ \pm2\pi $. 当障碍势的宽度和速度较大时, 图2(c)给出了无规则量子湍流. 经长时间演化, 从障碍势脱落的点涡不稳定, 有的点涡组成涡旋对, 有的则形成涡旋簇, 有的依旧单独分布, 最终障碍势后的尾迹模式为无规则量子湍流. 我们发现组分1和组分2中障碍势后脱落的涡旋对移动不同步, 这可能是多分量情况中的普遍形式.

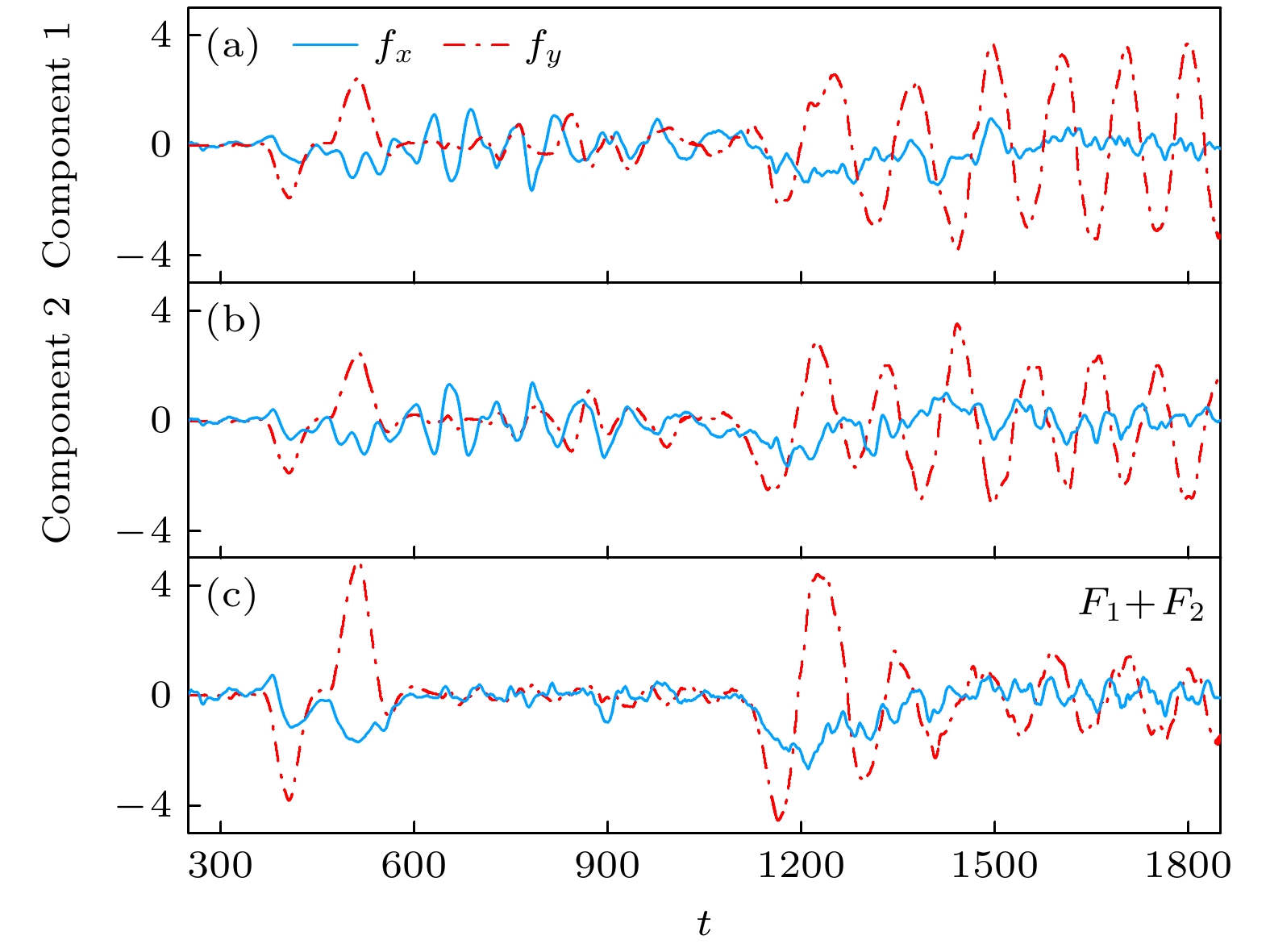
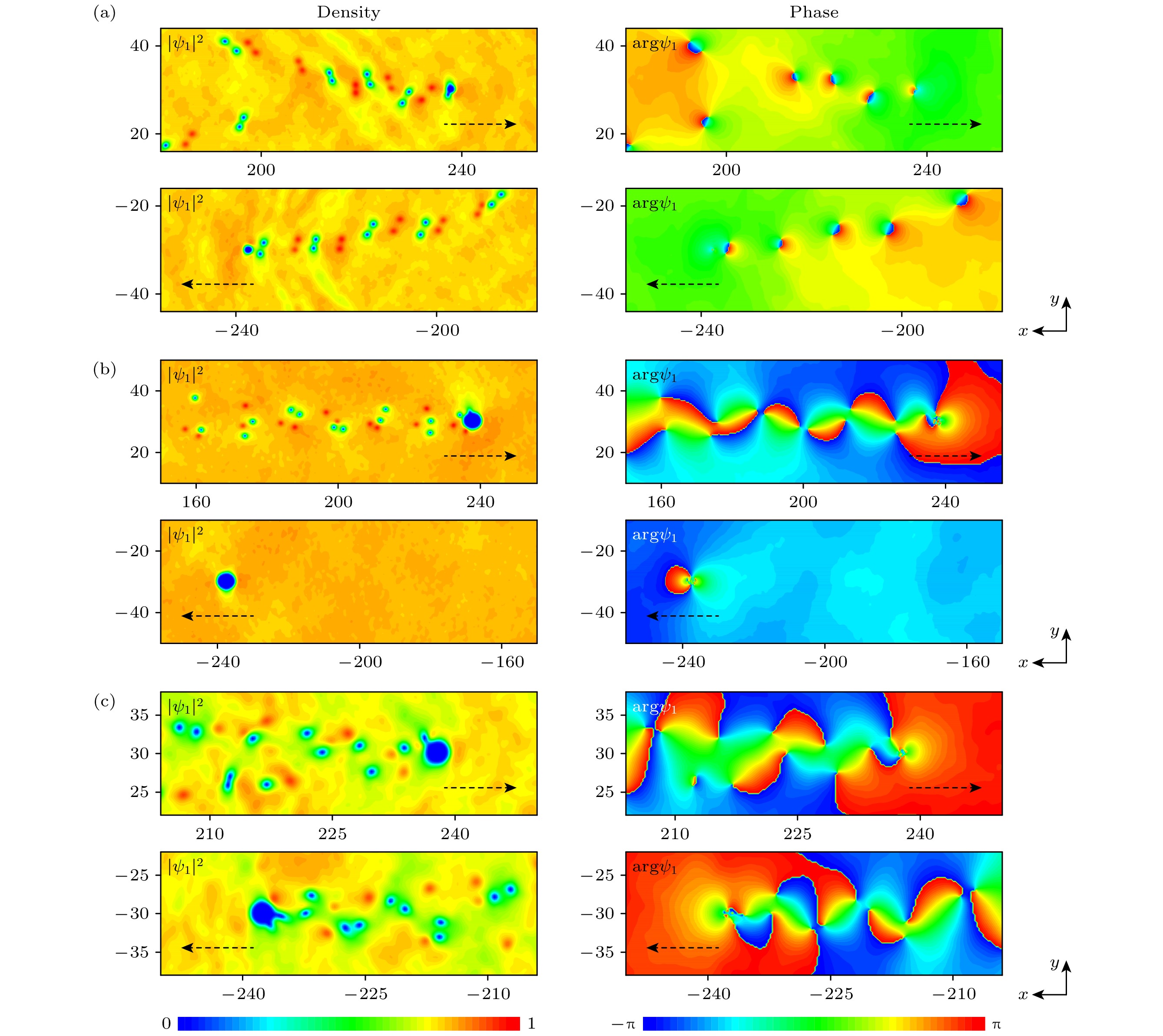
      图3给出了异步量子Kármán涡街形成过程中作用在移动障碍势上的拖拽力$ {f\mathit{\boldsymbol{}}}=(f_x, f_y)= {\mathrm{i}}{\partial_t}\displaystyle\int({\boldsymbol{\varPsi}}^\dagger\nabla{\boldsymbol{\varPsi}}){\mathrm{d}}x{\mathrm{d}}y $的演化过程. $ {\boldsymbol{\varPsi}}=(\psi_\uparrow, \psi_\downarrow)^{\rm T} $, 其中T表示转置. 图3(a)—(c)分别是组分1、组分2以及整个系统中脱落的涡旋对作用于障碍势上的拖拽力. 从图3可以发现, $ f_x $和$ f_y $在时间$ t\approx 365 $时开始振荡, 说明障碍势后涡旋对开始脱落并上下漂移. 这里, $ f_x $的振荡表示涡旋对的脱落频率, $ f_y $的振荡表示涡旋对向上或向下的运动频率. 当$ t\gtrsim1115 $时, $ f_y $周期性振荡, 且图3(a)中的谷值对应图3(b)中的峰值, 说明组分1和组分2中的涡旋对从障碍势后侧交替脱落, 随时间演化逐渐形成异步量子Kármán涡街.

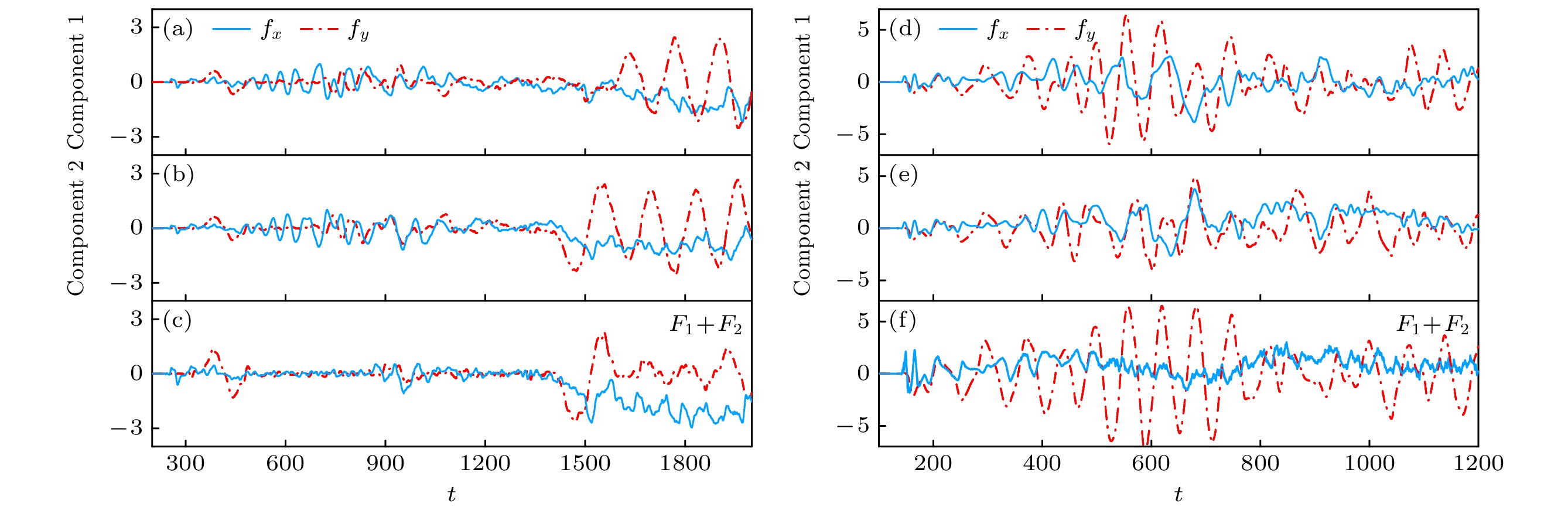
      该系统中还存在各种尾迹的组合模式. 图4给出了不同宽度和速度下移动障碍势后尾迹的几种典型组合模式. 由于组分1和组分2的结果类似, 这里只展示组分1的密度分布和相位分布. 图4(a)表示V字型涡旋对和斜向漂移涡旋偶极子的组合模式. 发现尾迹中涡旋对的中心不在同一直线, 且一排涡旋对之间的距离也不相等. 当宽度和速度达到$ d=2.3, \upsilon=0.43 $时, 障碍势沿着x方向移动产生的涡旋对构成异步量子Kármán涡街. 然而当障碍势沿着–x方向移动则形成稳定的层流, 如图4(b)所示. 当速度较大时, 障碍势后的尾迹为异步量子Kármán涡街和无规则量子湍流(图4(c)). 在具有PT对称势的相混合双组分BEC中出现组合模式可以这样理解: PT对势的虚部使其周围发生粒子的增益或损耗现象, 当障碍势经过该影响范围时, 粒子分布不均匀而导致涡旋对产生的数目不同以及运动轨迹也不一致, 甚至障碍势周围的速度无法达到产生涡旋对的临界速度, 使障碍势后侧无法脱落出涡旋对而形成无涡模式, 因此整个系统中产生的尾迹构成组合模式.

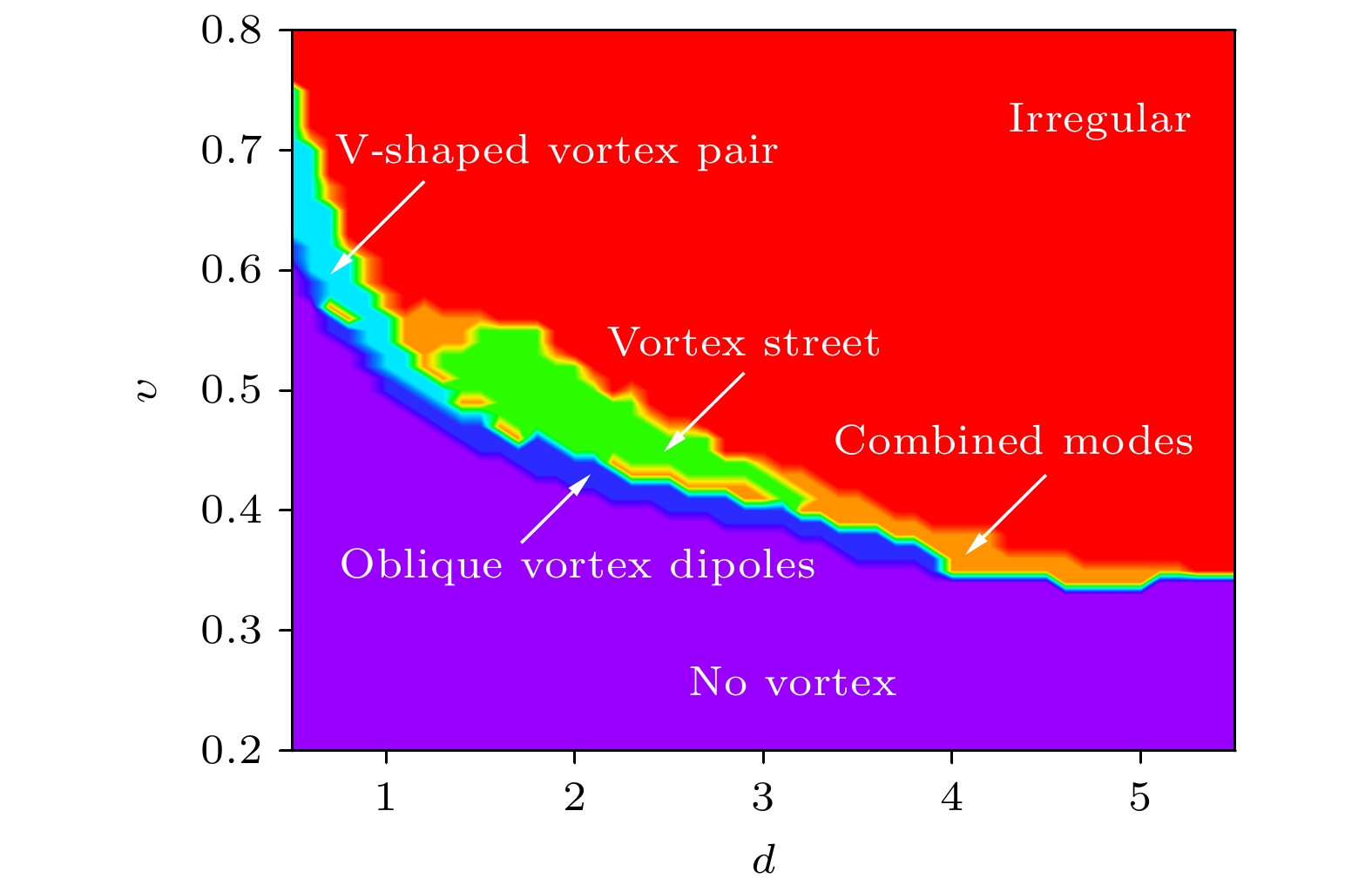
      图5反映了异步量子Kármán涡街分别与无涡和无规则量子湍流构成组合模式时产生的拖拽力随时间的演化过程. 图5(a)—(c)产生的拖拽力对应图4(b). 当$ t\lesssim255.8 $时, $ f_x $和$ f_y $约为零, 在此之前没有涡旋对产生. 当$ t\gtrsim1415.5 $时, $ f_y $周期性振荡, 而$ f_x $振荡却无明显的周期性. 说明障碍势后产生的涡旋对向上或向下漂移. 并且我们发现组分1中$ f_y $的谷值对应组分2中的峰值. 这一现象是由于组分1和组分2中的涡旋对同时从障碍势上下两侧脱落, 并形成异步量子Kármán涡街. 图5(d)—(f)给出了异步量子Kármán涡街和无规则量子湍流形成过程中产生的拖拽力(采用的参数与图4(d)一致). $ f_x $和$ f_y $从零开始振荡, 当$ t\gtrsim139.5 $时, $ f_y $的振荡具有一定的周期性且振幅在PT对称势虚部附近振幅较大, 意味着涡旋对在该附近向上或向下漂移更明显.

      改变障碍势不同宽度和速度进行数值计算, 得到了各种尾迹模式的参数区域. 如图6所示, 其中紫色、蓝色、浅蓝色、绿色、橙色和红色区域分别代表无涡、斜向漂移涡旋偶极子、V字型涡旋对、异步量子Kármán涡街、组合模式和无规则量子湍流. 其中, 异步量子Kármán涡街的参数范围为$ 1.2 < d < 3.3 $以及$ 0.41 < \upsilon < 0.56 $. 可以注意到组合模式的参数范围大部分分布在$ 0.8 < d < 1.6 $, $ 0.41 < \upsilon < 0.56 $和$ 3.2 < d < 5.2 $, $ 0.41 < \upsilon < 0.56 $两个区域, 也存在小部分区域零散分布. 当障碍势宽度$ d > 5.3 $时, 随着速度的增大, 尾迹模式从稳定的层流直接过渡到无规则量子湍流.

      为了进一步研究双组分BEC中PT对称势的虚部对异步量子Kármán涡街的影响. 图7给出了组分1中障碍势的宽度d = 1.9、速度$ \upsilon=0.48 $以及增益-损耗强度$ \varGamma=0.04 $时, 不同时间段的动力学演化过程. 如图7(a)和图7(b)所示, 当移动障碍势未进入虚部的影响范围时, 脱落的涡旋对规则分布并形成异步量子Kármán涡街. 但向左和向右运动的障碍势后脱的涡旋对的数目和距离并不相等. 从图7(c)和图7(d)发现, 当障碍势处于虚部的影响范围内时, 随着时间的演化其后脱落的部分涡旋对有演变成点涡的趋势. 并且障碍势后脱落的点涡使涡旋对的轨迹发生变化, 从而影响异步量子Kármán涡街的稳定性. 图7(e)和图7(f)是障碍势远离虚部时形成的尾迹. 发现一对涡旋中两点涡之间的距离明显增大. 最后, 组分1中依旧形成了Kármán涡街, 但从图7(e)中观察到组分2中障碍势后的尾迹形成V字型涡旋对. 这意味着PT对称势的虚部影响异步量子Kármán涡街的稳定性. 在演化的过程中会产生阵发性的异步量子Kármán涡街, 也会出现最初产生的异步量子Kármán涡街演化成V字型或其他尾迹模式的现象.

      通过研究, 本文提供了实验上观测相混合态双组分BEC中PT对称势下异步量子Kármán涡街的方案. 由$ ^{87}\rm Rb $原子组成的BEC系统, 其超精细态为$ |{f=1, m_f=-1}\rangle ， |{f=1, m_f=0}\rangle$[43,44]. 原子质量为$m\approx1.45\times {10^{-25}} $ kg. 两种超精细态的粒子数分别为$N \approx 2.62 \times {10^{5}} $. 一般凝聚体束缚在谐振子势中, 可通过组合磁四阱势和扁平状的光学偶极阱实现. 谐振子势的频率为$ ({\omega_x}, {\omega_y}, {\omega_z})\approx 2\pi\times(40, 56, 130) $Hz[43]. s波散射长度调节为$ a_{11} = a_{21} \approx 213 \mu_{\rm B} $[43], $ \mu_{\rm B} $为玻尔磁子, 可通过费什巴赫共振技术调节. 组内相互作用强度$ g_{11}\approx4.50\times {10^{-51}} $ J, $ g_{22}\approx4.05\times {10^{-51}} $ J, 组间相互作用强度$ g_{12} = g_{21} \approx 1.35 \times {10^{-51}}~\rm J$, 对应无量纲相互作用参数为$ g_{11}\approx1 $, $ g_{22}\approx0.9 $和$ g_{12}=g_{21}\approx0.3 $. 移动高斯障碍势, 即PT对称势的实部可通过固定在实验室框架内的两束排斥性激光束轴向穿透冷凝物产生[45]. 然后通过声光偏转器施加三角形波[22], 两束高斯激光束从初始位置$ (x_0, y_0)=(1.72, 0.25) $mm沿着–x方向移动以及从初始位置$ (-x_0, -y_0)= (-1.72, -0.25) $mm沿着x方向以速度$ \upsilon\approx0.099 $ mm/s移动. 激光功率控制其光圈的大小[46]. 当激光功率约为$ 2052 $ μW时, 障碍势的宽度$ d\approx 0.084 $ μm. 障碍势的峰值强度$ V_0\approx4.31\times{10^{-31}} $ J. 对于PT对称势的虚部, 其增益可以通过使用原子激光器将原子注入冷凝物来实现[47], 损耗则通过使用激光束将原子激发到激发态, 然后通过光子反冲将它们从凝聚物中喷射出来实现[48]. 增益-损耗强度为$ \varGamma\approx1.72\times{10^{-34}} $ J, 对应无量纲量为$ \varGamma\approx 0.04 $. 从而图1 所示的异步量子Kármán涡街可在实验中实现.

    4.   结　论

    • 本文研究了相混合态双组分BEC中PT对称势下障碍势后涡旋脱落的各种尾迹模式. 发现在组分1和组分2中脱落的涡旋对交错排布, 我们将这种排布形式命名为异步量子Kármán 涡街. 计算了两排涡旋对之间的距离b与一排涡旋对中两点涡之间的距离l之间的比值约为0.17, 该比值小于经典流体的稳定性条件0.28. 随着障碍势宽度和速度的变化也发现了其他的尾迹模式: 无涡、斜向漂移涡旋偶极子、V字型涡旋对、组合模式和无规则量子湍流. 同时计算了异步量子Kármán涡街产生时作用在障碍势上的拖拽力随时间的演化, 发现y方向上产生的拖拽力相比于x方向更有周期性. 本文同样分析了PT对称势的虚部对涡旋对和异步量子Kármán涡街稳定性的影响, 得到PT对称势的虚部会破坏涡街的稳定性. 最后, 为实现异步量子Kármán涡街提供了实验方案.

    参考文献 (48)

目录

/

返回文章
返回