首页
登录
注册
-
光谱成像仪因能同时获取观测目标的二维空间信息和一维光谱信息, 而在卫星遥感物质识别、分类和监测等领域具有重要价值[1–4]. 光谱辐射测量精度是光谱成像仪定量遥感能力的重要标志, 通过相对和绝对光谱辐射定标建立仪器测量数据与目标光谱辐射的对应关系, 是光谱成像仪研制过程中的必要环节.
星载光谱成像仪通常采用二维面阵探测器, 探测器各像元间响应不一致、光学系统不同视场角像面照度和不同波长透过效率不一致等会导致不同像元间光谱响应不一致, 进而使不同空间位置的相同目标测得的光谱曲线存在差异, 即“同物异谱”现象, 因此需要对成像光谱仪进行相对光谱响应的定标. 对于星载推扫式直接型光谱成像仪, 面阵探测器光谱维方向的不同像元对应不同谱段, 空间维一列像元对应相同谱段. 其相对光谱响应标定只需标定像面一列像元在某一波长处的响应差异, 通常可采用“单色仪+积分球”单色均匀光源实现一列像元间光谱响应不一致性的测量[5–7]. 而间接型光谱成像仪像面各像元接收到的是目标多谱段或全谱段辐射信号的叠加, 以干涉光谱成像仪为例, 其面阵探测器各像元对应的是目标全谱段辐射信号的叠加, 且各像元信号强度受到相位的余弦调制, 因此其相对光谱响应标定无法简单通过单色仪逐波长扫描的方法实现[8,9].
国内外学者对干涉光谱成像仪相对光谱响应标定进行了大量的研究工作. 但是, 在已有干涉成像光谱仪光谱辐射定标研究中, 多基于干涉光谱成像仪未一体化集成的前提下, 分多步对各像元的相对定标系数进行测量, 或者仅对面阵探测器空间维各行(而非整个面阵探测器)进行像元间光谱响应不一致性的校正. 例如, 相里斌等[10]在假定探测器各像元间的光谱辐射响应一致的前提下, 利用光谱辐射曲线已知的全色积分球实现了空间调制干涉光谱成像仪(spatially modulated imaging Fourier transform spectrometer, SMIFTS)平均光谱响应的测量. 赵葆常等[11]利用“行”平场方法实现了干涉光谱成像仪的平场. 利用均匀面光源作为平场光源, 在理想情况下空间方向各像元的干涉强度相同, 通过空间方向各像元间的响应差异即可实现标准光谱输入条件下像元间响应不一致性的修正. 崔燕[12]利用两步相对定标法实现了干涉光谱成像仪各像元点
$ (i, j) $ 相对定标系数$ C(i, j) $ 的测量. 先对探测器进行相对辐射定标得到高频相对定标系数$ {C}_{1}(i, j) $ , 再对干涉光谱成像仪全系统进行相对辐射定标得到低频相对定标系数$ {C}_{2}(i, j) $ , 两系数相乘即为最终相对定标系数. 以上方法多是基于准单色光源标定空间维像元间相对光谱响应不一致性, 未能实现间接型光谱成像仪全系统面阵探测器各像元间光谱响应函数的测量, 得到的相对光谱定标系数不具有普适性. 随着定量化遥感光谱辐射测量精度要求的不断提高, 探索一种能够全面标定干涉光谱成像仪全系统各像元光谱响应函数的方法, 对于提升光谱成像仪器的定量化测量精度具有重要价值.基于傅里叶变换光谱定标源的方法在探测器的相对光谱响应定标方面得到了广泛应用[13–15], 其通过对探测器接收到的时域干涉图进行傅里叶变换, 根据反演光谱的不一致性实现探测器相对光谱响应函数的测量, 具有光通量高、光谱分辨率可调、光谱范围宽等优点. 因此, 本文利用经过时间调制型傅里叶变换光谱仪余弦调制的宽谱光源作为定标源, 提出了一种适用于间接型光谱成像全系统(光学系统+面阵探测器)相对光谱响应函数测量方法, 能够一次性测量出面阵探测器各像元在不同波段处的相对光谱响应函数. 并以干涉光谱成像仪为例, 分析了相对光谱响应函数的测量和校正效果.
-
干涉型光谱成像仪属于间接型光谱成像仪的一种, 其不仅能获取景物目标的二维空间信息, 还能获得景物目标的一维光谱信息. 该仪器利用光的干涉原理将观测目标的光谱信息转换为干涉信息, 而干涉信息又与观测目标的光谱数据之间存在傅里叶变换关系. 因此, 通过对面阵探测器上的干涉信息进行逆傅里叶变换, 即可获取观测目标的光谱信息.
在理想情况下, 面阵探测器各像元的光谱响应一致, 不同空间位置的相同目标测得的光谱谱形和强度一样, 且与目标真实辐射光谱一致. 而在实际应用中, 光学元件的制造瑕疵、探测器的响应不一致、干涉仪膜系或胶合应力等因素均会导致系统焦平面不同像元间的光谱响应不一致, 影响复原光谱的谱形和强度, 进而影响目标的识别、分类和监测. 因此本节分析了像元间相对光谱响应不一致对复原光谱的影响, 并提出了对干涉光谱成像仪相对光谱响应标定的要求.
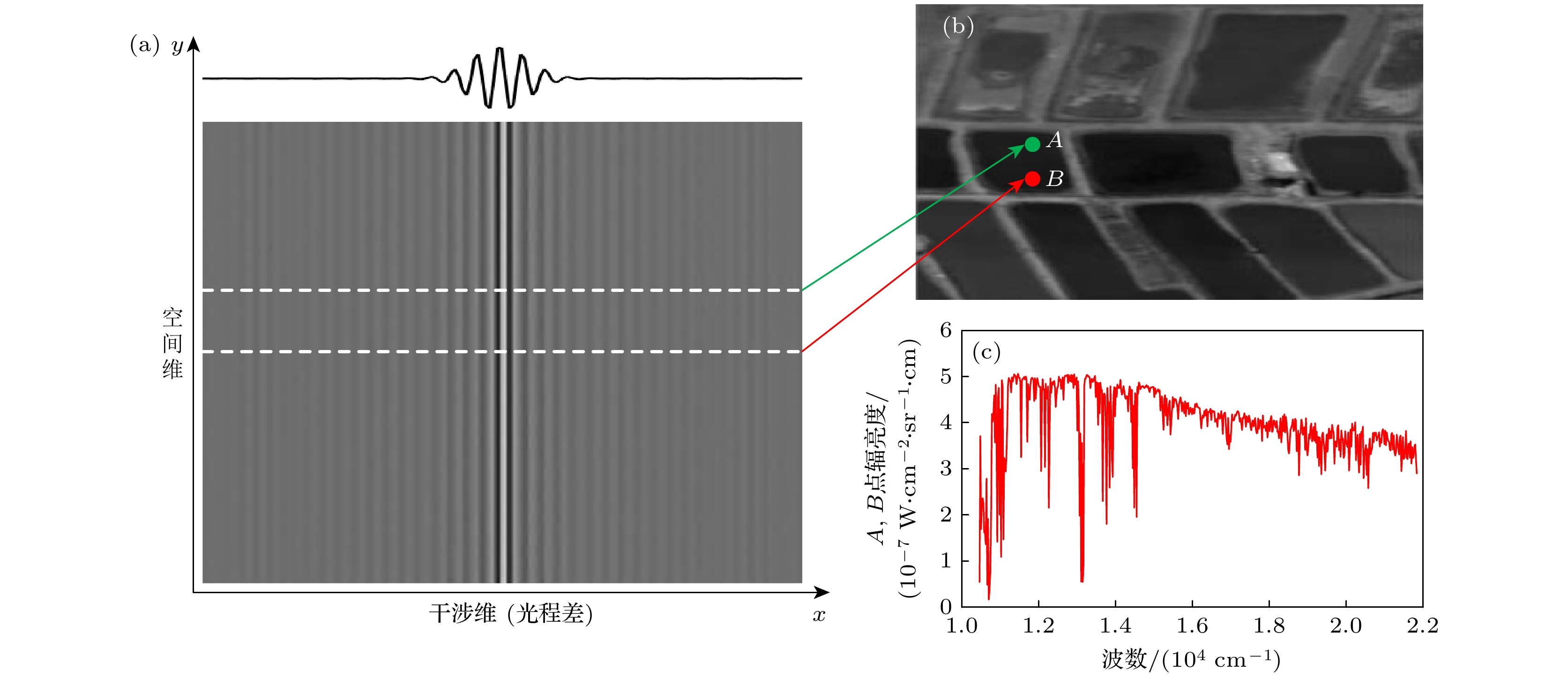
图1(a)所示为一列景物目标的干涉信息分布, x为干涉维序号, 对应景物目标点在不同光程调制下的干涉信息分布, y为空间维序号, 对应一列景物目标. 对每一行干涉信息进行逆傅里叶变换, 即可得到一列景物目标的光谱信息, 干涉信号
$ I\left(x, y\right) $ 可表示为[10,16]式中,
$ \sigma $ 为波数,$ B\left(\sigma \right) $ 为景物目标光谱分布,$ \varDelta (x,y) $ 为探测器上$ (x, y) $ 点对应的光程差,$ R\left(\sigma , x, y\right) $ 为相对光谱响应系数, 理想情况下$ R\left(\sigma , x, y\right)\equiv a $ (常数).如果探测器同一行内各像元的光谱响应一致, 仅不同行间的光谱响应不一致, 则
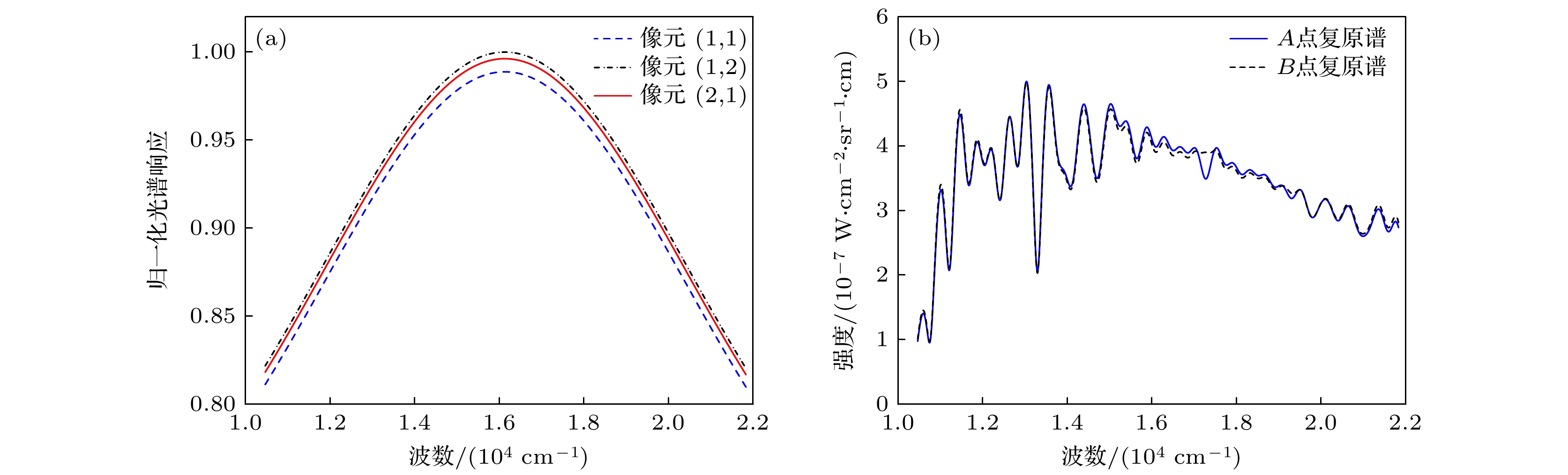
$ R(\sigma , x, y) $ 可简化为$ R(\sigma , y) $ . 此时, 各行干涉信号复原后的光谱分布为$ B(\sigma)R(\sigma, y) $ , 不同行复原光谱的谱形和幅值都可能会发生变化. 一般情况下, 无需对同一行的数据进行相对光谱响应标定, 只需对其进行绝对辐射定标.除不同行像元间光谱响应可能存在不一致外, 同一行像元间的光谱响应也会存在不一致[17]. 图2(a)为3个像元的光谱响应曲线, 表明不同像元的响应存在不一致性. 当景物目标点对应的一行像元存在光谱响应不一致时, 复原得到的光谱分布为目标点真实辐射光谱
$ B\left(\sigma \right) $ 与${\mathrm{FT}}\Big[\displaystyle\int R\left(\sigma , x, y\right) \times {\mathrm{c}}{\mathrm{o}}{\mathrm{s}}\left(2{\mathrm{\pi }}\sigma \Delta \left(x, y\right)\right){\mathrm{d}}\sigma \Big] $ 的乘积, 此时需要对每一行的数据进行相对光谱响应标定.假设图1(b)中两景物目标点A和B具有相同的辐射光谱分布, 如图1(c)所示. A和B点分别对应面阵探测器上不同行的像元, 通过给两行像元添加不同程度的光谱响应不一致性, 定性描述相对光谱响应不一致性对复原光谱的影响. 图2(b)展示了不同行光谱响应不一致对复原光谱的影响, 可以看出, 不同行间光谱响应不一致会使复原光谱出现不同程度的失真, 从而降低光谱测量的准确性和一致性.
为提高光谱反演精度, 需要对干涉光谱成像仪中每个探测器像元的光谱响应函数
$ R\left(\sigma , x, y\right) $ 进行标定, 以消除各种因素导致的像元间光谱响应的不一致. -
本文将干涉光谱成像仪像面的每个像元视为一个独立的接收单元, 利用时间调制型傅里叶变换光谱仪作为定标源, 在时间调制型傅里叶变换光谱仪进行光程差扫描的同时, 同步采集干涉光谱成像仪的干涉数据, 进而标定出干涉光谱成像仪全系统各像元的相对光谱响应函数
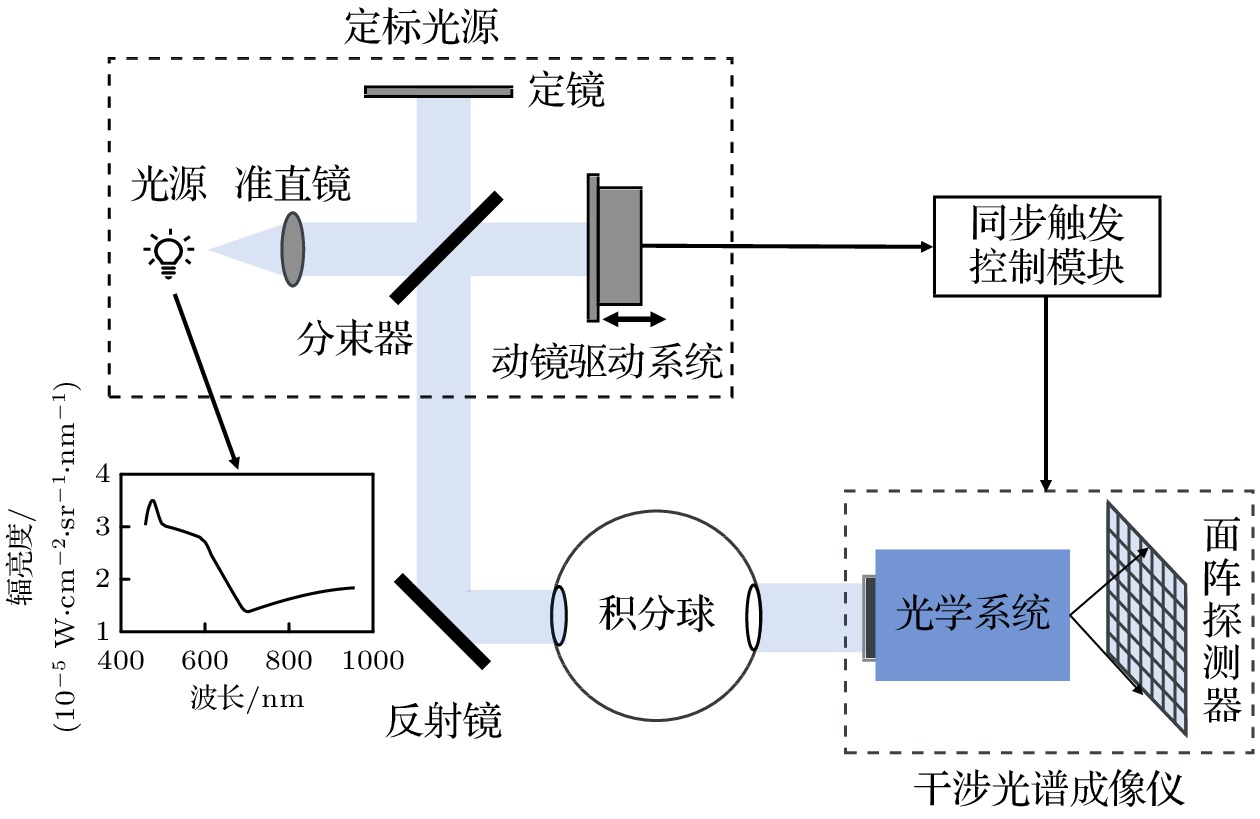
$ R\left(\sigma , x, y\right) $ .干涉光谱成像仪的相对光谱响应函数测试系统如图3所示, 主要由宽带复色光源、光学准直单元、时间调制型傅里叶变换光谱仪、积分球、待测干涉光谱成像仪及同步触发控制单元组成. 宽带复色光源经过时间调制型傅里叶变换光谱仪干涉调制后进入积分球, 经积分球匀光后形成全孔径全视场的均匀散射面光源, 而后进入干涉光谱成像仪并在像面产生干涉图. 时间调制型傅里叶变换光谱仪在不同的光程差调制状态下, 均可通过同步触发控制模块实现待测干涉光谱成像仪干涉数据的采集, 并在像面获得一幅干涉图.
积分球出口处光源特性
${B_{{\text{MI}}}}$ 可表示为式中,
$ \sigma $ 为入射光波数,$ {B}_{{\mathrm{S}}}\left(\sigma \right) $ 为宽带复色光源光谱分布,${\varDelta _{{\text{MI}}}}(t)$ 为t时刻时间调制型傅里叶变换光谱仪的光程差.干涉型光谱成像仪像面一行像元在不同时刻的干涉信号分布为
式中,
$ {\varDelta _{\text{S}}}\left( x \right) $ 为待测干涉光谱成像仪像面的光程差(以空间调制型干涉光谱成像仪为例),$ R\left(\sigma , x\right) $ 为相对光谱响应系数.依次提取干涉图序列中同一像元
$ {x}_{i} $ 处的光强, 组成时域离散干涉信号:对
$ {x}_{i} $ 像元处的时域干涉信号进行逆傅里叶变换, 得到$ {x}_{i} $ 像元对应的复原光谱:再提取一行像元在
$ {\sigma }_{j} $ 波数处的光谱幅值, 得到$ {\sigma }_{j} $ 波数处的空域信号:通过提取(6)式的基线得到信号的非调制项
$ {B}_{{\mathrm{S}}}\left({\sigma }_{j}\right)R\left({\sigma }_{j}, x\right) $ , 将非调制项除以宽带复色光源在$ {\sigma }_{j} $ 波数处的光谱幅值, 即可得到一行像元在$ {\sigma }_{j} $ 波数处的相对光谱响应系数$ R\left({\sigma }_{j}, x\right) $ . 依次提取一行像元在各个波数处的空域信号, 从而得到一行像元在目标全谱段处的相对光谱响应函数$ R\left(\sigma , x\right) $ .式中,
$ {I}_{{\mathrm{e}}{\mathrm{r}}{\mathrm{r}}{\mathrm{o}}{\mathrm{r}}}\left(x\right) $ 为待测干涉光谱成像仪存在光谱响应不一致时像面干涉信号的分布. 利用(7)式在频谱域对误差光谱和相对光谱响应函数倒数的傅里叶变换进行卷积[9]即可实现干涉光谱成像仪光谱响应不一致性的校正, 得到无误差光谱$ B\left(\sigma \right) $ . -
本节以干涉光谱成像仪为例, 利用数值分析方法示例说明了相对光谱响应函数的标定方法, 给出了标定流程和数据处理方法, 并将测量得到的相对光谱响应函数
$ R\left(\sigma , x\right) $ 用于光谱误差修正, 以验证本方法的有效性. -
干涉光谱成像仪仿真参数的选取如表1所列, 横向剪切干涉光谱成像仪[19]像面的光程差分布
$ {\varDelta _{\text{S}}}(x) $ 为$ {dx}/{f} $ . 其中, d为干涉光谱成像仪的剪切量, f为傅里叶变换成像物镜的焦距, x为探测器上各像元点距零光程差点的距离.对于相对光谱响应函数测试系统的定标源, 光源应选择具备稳定光谱辐射信号输出、且能够覆盖待测干涉光谱成像仪光谱范围的宽波段光源, 本文将氙灯和卤钨灯组合作为宽带复色光源, 仿真得到光源的辐射光谱分布如图3所示. 光程差采样间隔需满足Nyquist采样定理, 本文使光程差每隔150 nm采集一幅干涉图. 由(5)式可知, 时间调制型傅里叶变换光谱仪的光谱分辨率应满足瑞利判据, 且能够准确地分辨出每个像元复原光谱的谱形及其峰值和谷值, 因此, 选择动镜移动10000步, 当对干涉信号进行双边采样时, 对应的光谱分辨率为13.33 cm–1.
-
本节基于表1所列的仿真参数, 生成存在相对光谱响应不一致性的干涉图, 来示例说明相对光谱响应函数的测量及标定流程, 并验证本方法的有效性.
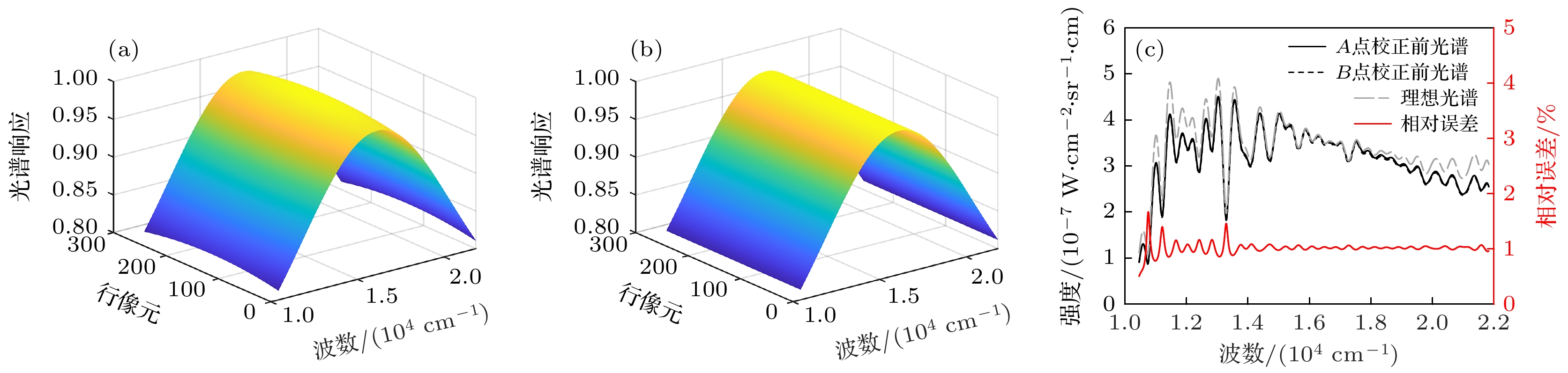
图1(c)为利用辐射传输软件模拟的大气谱线的光谱辐射分布, 假设探测器的光谱响应函数分布符合高斯分布, 并给不同像元添加1%的相对光谱响应不一致性偏差. 图4(a)和图4(b)分别为A和B点的相对光谱响应函数, 其中A点所对应的行像元间的光谱响应
$ R\left(\sigma , x, {y}_{A}\right){\mathrm{存}} $ 在1%的不一致, B点所对应的行像元间的光谱响应$ R\left(\sigma , {x, y}_{B}\right) $ 均与$ R\left(\sigma , 1, {y}_{A}\right) $ 相等. 基于(1)式生成A和B点所对应的干涉图, 对干涉图进行逆傅里叶变换得到图4(c)所示的A和B点的误差光谱. 定义光谱的相对误差$ {R}_{{\mathrm{E}}{\mathrm{r}}{\mathrm{r}}{\mathrm{o}}{\mathrm{r}}}\left(\sigma \right) $ 为式中,
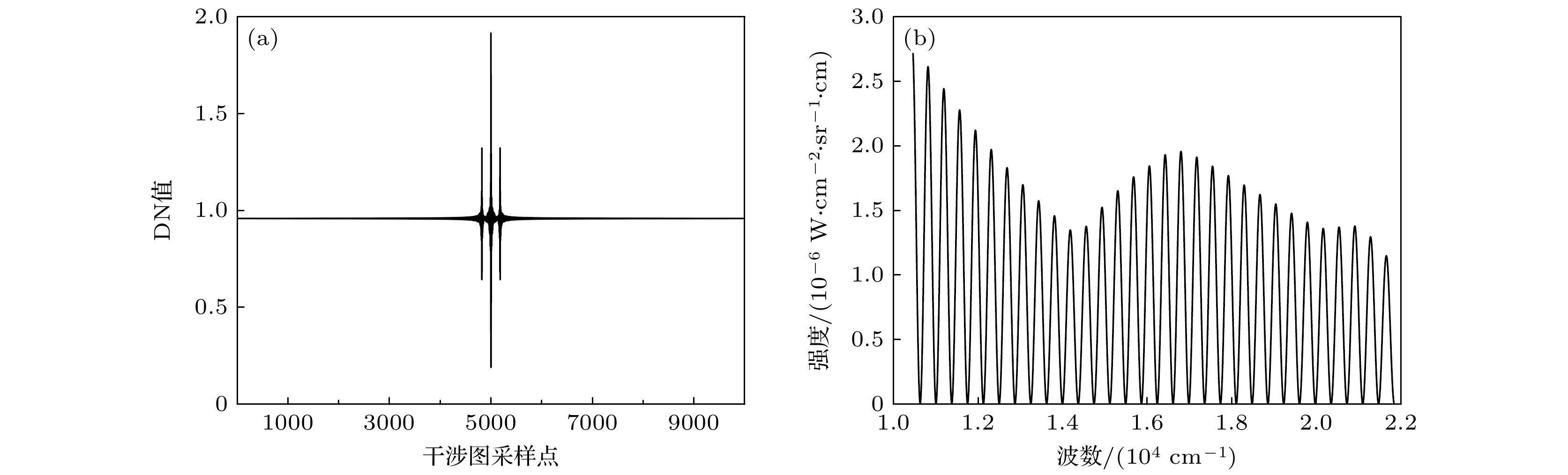
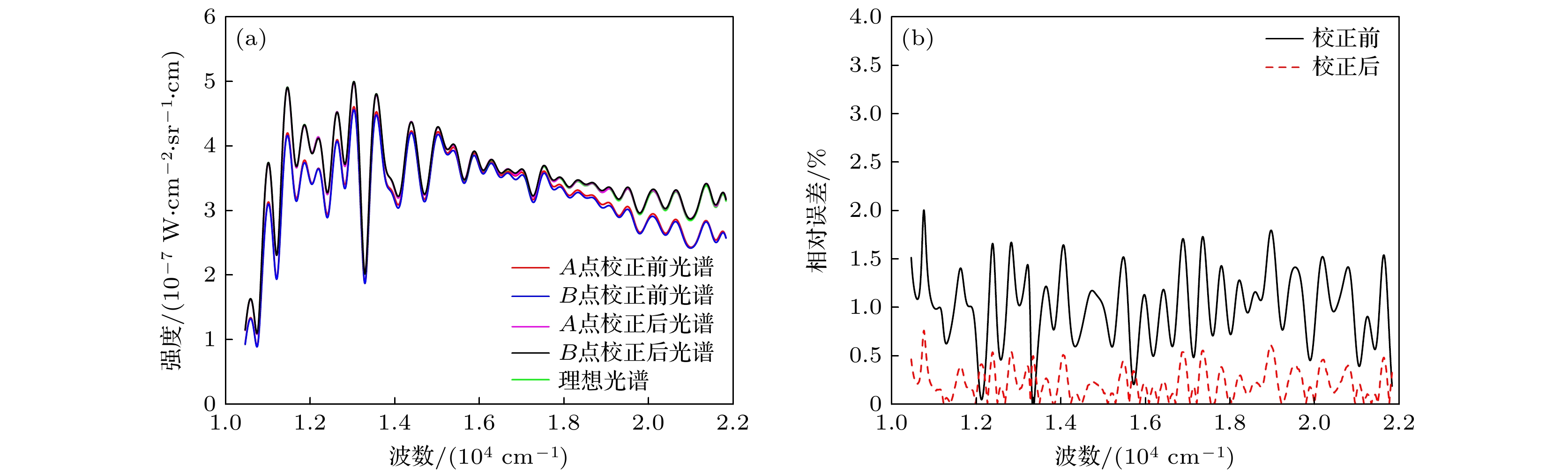
$ {S}_{A}\left(\sigma \right) $ 和$ {S}_{B}\left(\sigma \right) $ 分别为A和B点对应的复原光谱. 平均相对误差为所有波段处相对误差的平均值, 由仿真结果可知, A和B点对应的复原光谱的平均相对误差为1.02%. 为校正不同像元间相对光谱响应不一致性, 利用表1中相对光谱响应函数测试系统的仿真参数, 并基于图5所示的标定流程进行干涉光谱成像仪相对光谱响应函数的测量及标定.图6(a)为景物目标A点所对应行的第256个像元的时域干涉图
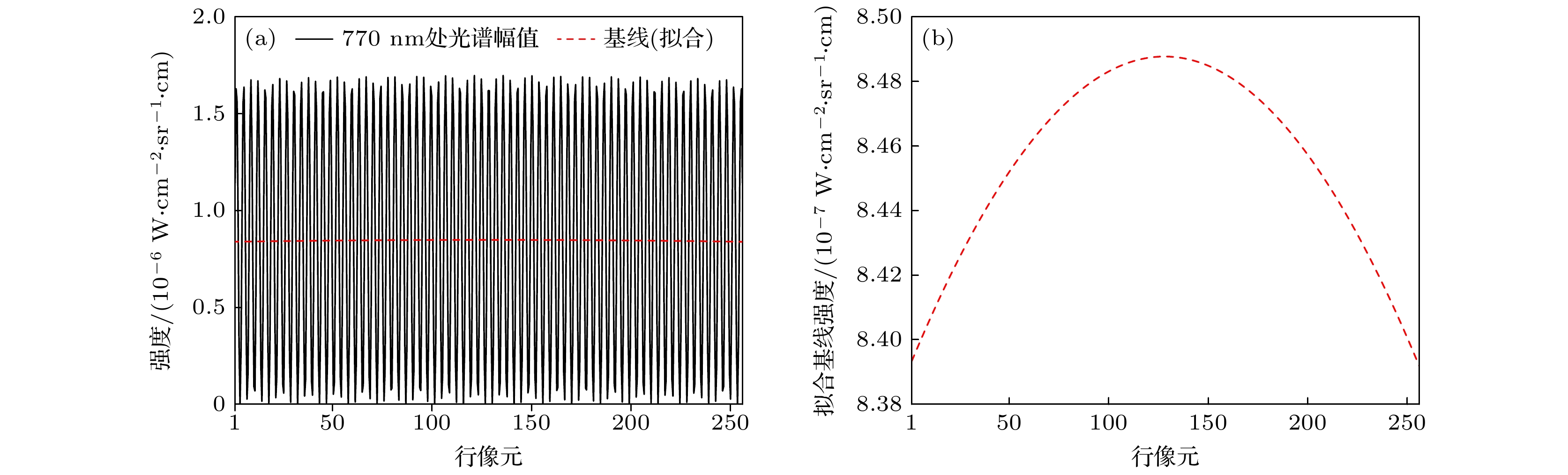
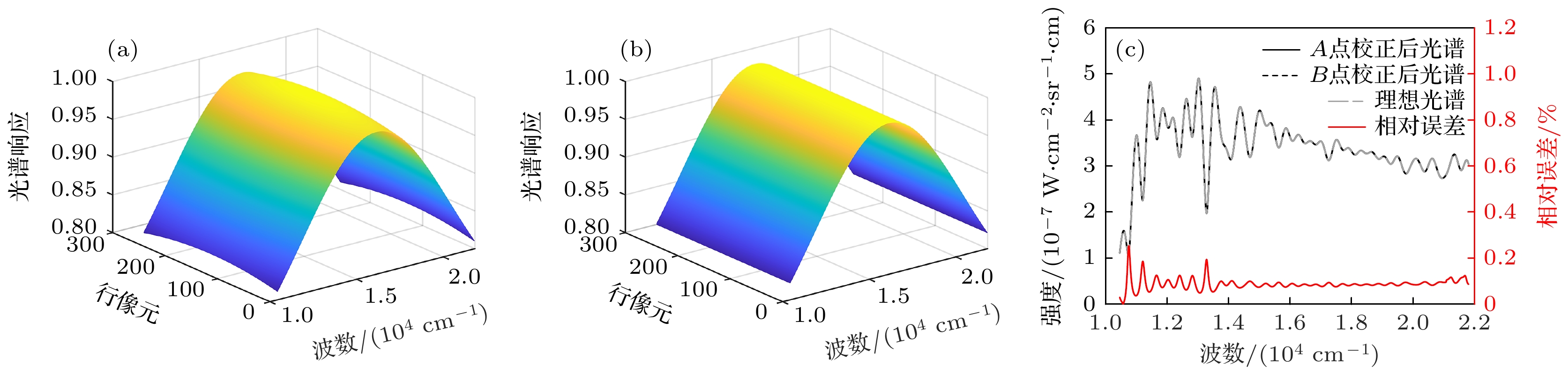
$ I\left(t, 256\right) $ , DN值表示干涉光谱成像仪在每个像素位置上测量的电磁波辐射强度. 采样点所对应的时间调制型傅里叶变换光谱仪的光程差为–0.075—0.075 cm. 图6(b)为复原得到的经过干涉光谱成像仪仪器函数调制的光谱, 不同像元经过仪器函数的调制效应不同. 图7所示为干涉光谱成像仪一行像元的复原光谱在770 nm处的光谱幅值所组成的空域信号及其非调制项拟合效果[20,21], 通过将非调制项除以宽带复色光源在该波长处的光谱幅值, 可以得到该波长处的相对光谱响应. 逐个波长进行拟合, 从而得到图8(a), (b)所示的相对光谱响应函数, 可以看出, 复原得到的相对光谱响应函数和图4给定的变化趋势基本一致.为评估测量得到的相对光谱响应曲面的准确性, 通过(7)式对干涉光谱成像系统的相对光谱响应不一致性进行校正. 相对光谱响应校正后的光谱和相对误差如图8(c)所示. 经过相对光谱响应不一致性的校正后, A和B点的平均相对误差由校正前的1.02%降至0.08%, 校正后的光谱与目标点的理想光谱高度重合. 这表明经过重构得到的相对光谱响应误差曲面能较好地匹配原始给定的相对光谱响应误差曲面. 但A和B点校正后的光谱仍然存在微小误差, 这是时间调制型傅里叶变换光谱仪最大步进光程差有限、非调制项的拟合结果有偏差、切趾函数的选择等原因导致的.
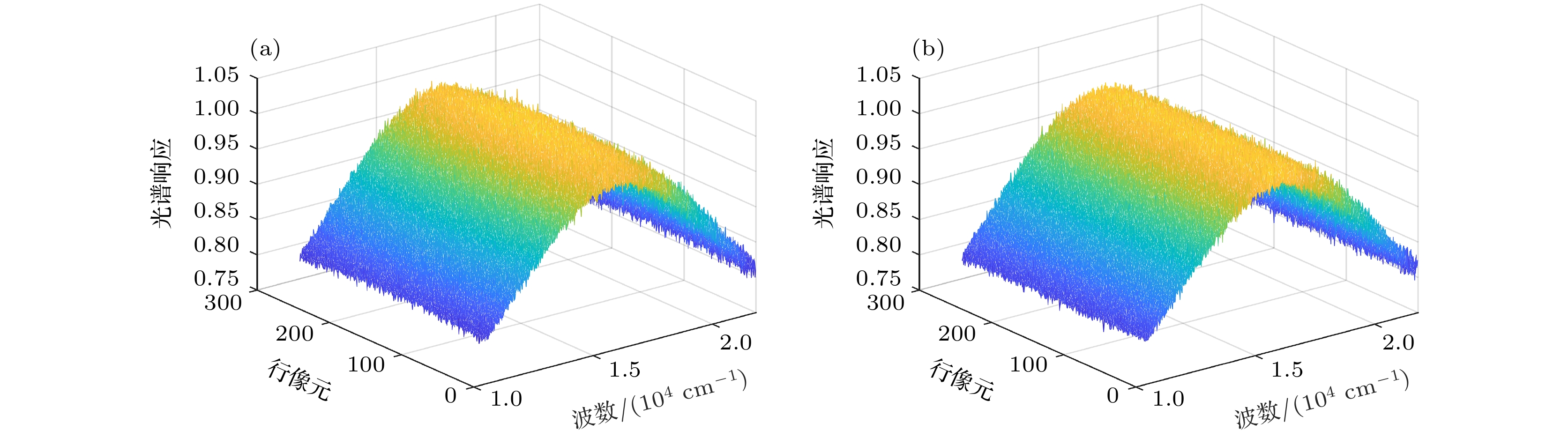
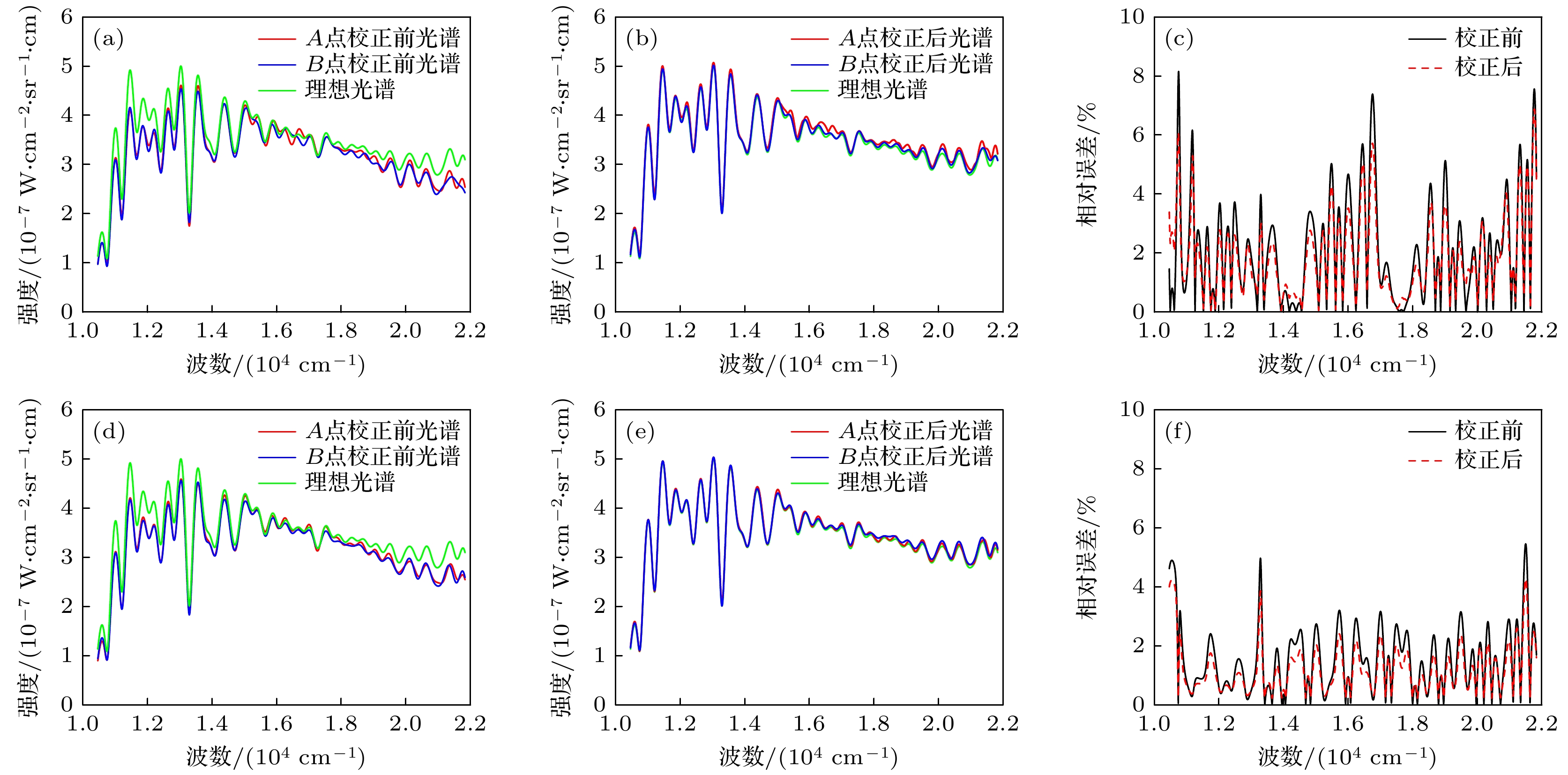
为进一步研究相对光谱响应函数测量和修正的有效性, 本节通过给原始干涉图添加不同程度的噪声, 仿真计算在不同信噪比下, 干涉光谱成像仪相对光谱响应函数的校正效果[22]. 图9给出了光谱信噪比(SNR)[17]为50时, A和B点对应行像元间的相对光谱响应函数的复原效果, 随机噪声的存在使复原得到的相对光谱响应函数出现小幅波动. 图10(a)—(c)分别是光谱信噪比为50时, A和B点校正前后的光谱及其相对误差. 经过相对光谱响应不一致性的校正后, A和 B点复原光谱的平均相对误差由2.09%降至1.86%, 但其相对于理想无噪声时的一致性较差. 这是因为系统噪声的存在会同时影响相对光谱响应函数
$ R\left(\sigma , x\right) $ 和景物的复原光谱$ {{\mathrm{F}}{\mathrm{T}}[I}_{{\mathrm{e}}{\mathrm{r}}{\mathrm{r}}{\mathrm{o}}{\mathrm{r}}}\left(x\right)] $ 的测量精度, 进而影响(7)式中校正后光谱$ B\left(\sigma \right) $ 的辐射测量精度. 图10(d)—(f)分别是光谱信噪比为100时, A和B点校正前后的光谱分布及其相对误差, 校正后A和B点复原光谱的平均相对误差由校正前的1.51%降至1.21%. 与光谱信噪比为50时相比, A和B点校正后光谱的一致性及其与目标点理想光谱的一致性均有所提高. 图11展示了系统信噪比为50时, 合并50帧干涉图后的仿真结果, 校正后A和B点复原光谱的平均相对误差由校正前的1.02%降至0.22%, 光谱的一致性得到显著提升, 且校正后的光谱更接近目标点的理想光谱. 因此, 在实际应用中可通过提高定标光源的亮度、延长曝光时间、合并多帧干涉图等手段提高光谱信噪比, 从而提升相对光谱响应函数的测量精度. -
本文基于间接型光谱成像仪的成像特点, 提出了一种以经过时间调制型傅里叶变换光谱仪余弦调制的宽谱光源为定标源的、系统级的相对光谱响应函数测量方法, 并建立了相应的数理模型, 该方法可准确测量出间接型光谱成像仪面阵探测器各像元在目标波段处的光谱响应差异. 通过对测量得到的相对光谱响应函数的倒数进行傅里叶变换, 并将其与误差光谱进行卷积, 即可消除像元间光谱响应的不一致性, 从而提升间接型光谱成像仪的光谱辐射测量精度. 为定性描述相对光谱响应函数的测量准确性, 本研究以干涉型光谱成像仪为例, 仿真分析了在理想无噪声和不同信噪比情况下相对光谱响应不一致性的校正效果. 结果表明采用本方法得到的相对光谱响应校正系数能够较好地修正像元间的响应不一致性, 提高了目标光谱测量的准确性和一致性, 验证了本文提出方法的有效性. 研究结果可为间接型光谱成像系统的相对光谱响应标定提供参考.
间接型光谱成像仪相对光谱响应函数标定方法
Calibration method of relative spectral response function of indirect imaging spectrometer
-
摘要: 间接型光谱成像仪通常采用面阵探测器作为光电转换器件, 探测器像元间光谱响应的不一致性会导致采集到的目标光谱失真, 所以标定和修正像元间光谱响应的不一致性是提升间接型光谱成像仪光谱辐射测量精度的重要手段. 本文以干涉光谱成像仪为例, 分析了系统像元间相对光谱响应不一致对目标光谱辐射测量准确性的影响, 提出了基于傅里叶变换调制定标源的间接型光谱成像仪全系统相对光谱响应函数测量方法, 并建立了相对光谱响应函数标定的数理模型. 仿真分析结果表明, 理想无噪声时, 像元间1%的相对光谱响应不一致性会对复原光谱造成1.02%的相对误差, 经过相对光谱响应校正后, 不同行复原光谱的相对误差降至0.08%. 最后, 仿真分析了相对光谱响应不一致性在不同光谱信噪比下的校正效果. 该方法可提高间接型光谱成像仪光谱测量的准确性和一致性.Abstract: In imaging spectrometers, area array detectors are usually used as photoelectric conversion devices, but the inconsistency of the spectral response among pixels can distort the collected target spectra. To improve the spectral radiometric accuracy of imaging spectrometers, calibrating and correcting the inconsistency of the spectral response among pixels is essential. The signal received by each pixel of area array detector of the indirect imaging spectrometer is usually the superposition of the target multi-spectral radiation signals or full-spectral radiation signals. Therefore, its relative spectral radiometric calibration requires measuring the spectral response of each pixel at different wavelengths on the array detector. Under the ideal conditions, the response values of each pixel in the area array detector are different, so the indirect imaging spectrometer cannot simply calibrate the relative spectral response (RSR) function between pixels by using the method of “monochromator + integrating sphere”. In this work, taking the interferometric imaging spectrometer for example, we analyze the influence of the inconsistency of the RSR among pixels on the target spectral radiation measurement accuracy, and propose a system-level RSR function measurement method for the indirect imaging spectrometer based on the Fourier transform modulation calibration source. In addition, we establish a mathematical model for calibrating the RSR function,and provide guidelines for selecting calibration system parameters such as light source, spectral resolution, and OPD sampling interval. The simulation results show that under the ideal noise-free condition, the 1% spectral response inconsistency among pixels results in a relative error of 1.02% to the recovered spectra. After RSR correction, the relative error of the recovered spectra of different rows decreases to 0.08%. Furthermore, in this work we simulate and analyse the influence of spectral signal-to-noise ratio on the calibration accuracy of the RSR function, and point out that increasing the brightness of the calibration light source, extending exposure time, and combining multi-frame interferograms can enhance RSR function calibration accuracy in practical applications. The research result can provide a theoretical basis for realizing the relative spectral radiometric calibration of indirect imaging spectrometer, which is of great significance in promoting quantitative spectral remote sensing.
-
-
图 2 像元间光谱响应不一致对复原光谱的影响 (a) 像元间的光谱响应曲线; (b) 不同行光谱响应不一致对复原光谱的影响
Figure 2. Effect of the spectral response inconsistency among pixels on the recovered spectrum: (a) Spectral response curves among pixels; (b) the effect of different spectral responses on the recovered spectrum.
图 3 干涉光谱成像仪相对光谱响应函数测试系统
Figure 3. Relative spectral response (RSR) function test system of interferometric imaging spectrometer.
图 4 理想无噪声情况下, 像元间光谱响应不一致对复原光谱的影响 (a) A点对应的相对光谱响应函数; (b) B 点对应的相对光谱响应函数; (c) A和B点误差光谱及其相对误差
Figure 4. Influence of the spectral response inconsistency among pixels on the recovered spectrum under ideal noise-free conditions: (a) RSR function corresponding to point A; (b) RSR function corresponding to point B; (c) error spectrum for points A and B and their relative error.
图 5 干涉光谱成像仪相对光谱响应函数测量及标定流程图
Figure 5. Flowchart of measurement and calibration of RSR function of interferometric imaging spectrometer.
图 6 理想无噪声情况下, 干涉光谱成像仪像面第256个像元的干涉图及复原光谱图(以目标点A点为例) (a)干涉图; (b)复原光谱
Figure 6. Under ideal noiseless condition, interferograms and recovered spectrum of the 256th pixel of the interferometric imaging spectrometer (take the point A for example): (a) Interferogram; (b) spectrum.
图 7 理想无噪声情况下,
$ {S}_{{\mathrm{p}}{\mathrm{e}}{\mathrm{c}}}\left(770\;{\mathrm{n}}{\mathrm{m}}, x\right) $ 及其基线拟合效果 (a)$ {S}_{{\mathrm{p}}{\mathrm{e}}{\mathrm{c}}}\left(770\;{\mathrm{n}}{\mathrm{m}}, x\right) $ ; (b) 基线拟合效果Figure 7. Under ideal noiseless condition,
$ {S}_{{\mathrm{p}}{\mathrm{e}}{\mathrm{c}}}\left(770\;{\mathrm{n}}{\mathrm{m}}, x\right) $ and its baseline fitting effect: (a)$ {S}_{{\mathrm{p}}{\mathrm{e}}{\mathrm{c}}}\left(770\;{\mathrm{n}}{\mathrm{m}}, x\right) $ ; (b) baseline fitting effect
图 8 理想无噪声情况下, 相对光谱响应函数的复原效果 (a) A点所对应的行像元间的相对光谱响应函数; (b) B点所对应的行像元间的相对光谱响应函数; (c) A和B点校正后的光谱及其相对误差
Figure 8. Restoration effect of the RSR function under ideal noise-free conditions: (a) RSR function among row pixels corresponding to point A; (b) RSR function among row pixels corresponding to point B; (c) corrected spectrum of points A and B and their relative error.
图 9 SNR = 50时, 相对光谱响应函数的复原效果 (a) A点; (b) B点
Figure 9. Restoration effect of RSR function when spectral SNR is 50: (a) Point A; (b) point B.
图 10 不同信噪比下, A和B点相对光谱响应的校正效果 (a) SNR = 50, 校正前光谱; (b) SNR = 50, 校正后光谱; (c) SNR = 50, 光谱的相对误差; (d) SNR = 100, 校正前光谱; (e) SNR = 100, 校正后光谱; (f) SNR = 100, 光谱的相对误差
Figure 10. Correction effect of RSR of points A and B at different SNR: (a) Uncorrected spectrum at SNR = 50; (b) corrected spectrum at SNR = 50; (c) relative error of spectrum at SNR = 50; (d) uncorrected spectrum at SNR = 100; (e) corrected spectrum at SNR = 100; (f) relative error of spectrum at SNR = 100.
图 11 SNR = 50, 合并50帧干涉图后A和B点相对光谱响应的校正效果 (a) 校正前后的光谱; (b)校正前后的相对误差
Figure 11. Correction effect of RSR of points A and B after combining 50 frames of interferograms at SNR = 50: (a) Spectra before and after correction; (b) relative error before and after correction.
表 1 干涉光谱成像仪相对光谱响应函数测试系统的仿真参数
Table 1. Simulation parameters of the RSR function measuring system for interferometric imaging spectrometer
参数 值 光谱范围/nm 458—956 剪切量 d/mm 0.68 焦距 f/mm 117 像元数 256×512 (光谱维2像元合并) 像元尺寸/μm 18 光源 氙灯 (458—700 nm)
卤钨灯 (700—956 nm)光程差采样间隔/nm 150 步数 10000 光谱分辨率/cm–1 13.33 光程差采样范围/cm –0.075—0.075 
下载: 导出CSV
-
[1] Luo H Y, Li Z W, Wu Y, Qiu Z W, Shi H L, Wang Q S, Xiong W 2023 Remote Sens. 15 1105 doi: 10.3390/rs15041105 [2] Lassalle G, Ferreira M P, La Rosa L E C, Scafutto R D P M, de Souza Filho C R 2023 ISPRS J. Photogramm. 195 298 doi: 10.1016/j.isprsjprs.2022.12.003 [3] 刘文龙, 刘学斌, 王爽, 严强强 2022 物理学报 71 094201 doi: 10.7498/aps.71.20211977 Liu W L, Liu X B, Wang S, Yan Q Q 2022 Acta Phys. Sin. 71 094201 doi: 10.7498/aps.71.20211977 [4] Calin M A, Calin A C, Nicolae D N 2021 Appl. Spectrosc. Rev. 56 289 doi: 10.1080/05704928.2020.1774381 [5] Jia J X, Wang Y M, Chen J S, Guo R, Shu R, Wang J Y 2020 Infrared Phys. Techn. 104 103115 doi: 10.1016/j.infrared.2019.103115 [6] 王建威, 李伟艳, 孙建颖, 李兵, 陈鑫雯, 谭政, 赵娜, 刘扬阳, 吕群波 2022 光谱学与光谱分析 42 2013 doi: 10.3964/j.issn.1000-0593(2022)07-2013-05 Wang J W, Li W Y, Sun J Y, Li B, Chen X W, Tan Z, Zhao N, Liu Y Y, Lü Q B 2022 Spectrosc. Spect. Anal. 42 2013 doi: 10.3964/j.issn.1000-0593(2022)07-2013-05 [7] 唐远河, 崔进, 郜海阳, 屈欧阳, 段晓东, 李存霞, 刘丽娜 2017 物理学报 66 130601 doi: 10.7498/aps.66.130601 Tang Y H, Cui J, Gao H Y, Qu O Y, Duan X D, Li C X, Liu L N 2017 Acta Phys. Sin. 66 130601 doi: 10.7498/aps.66.130601 [8] 李志伟, 熊 伟, 施海亮, 王先华, 叶函函, 韦秋叶, 乔延利 2014 红外 34 27 Li Z W, Xiong W, Shi H L, Wang X H, Ye H H, Wei Q Y, Qiao Y L 2014 Acta Opt. Sin. 34 27 [9] 王润昊, 孙影茹, 甘茵露, 吴兴江, 柯俊杰, 王新强, 甘永莹 2022 激光与光电子学进展 59 364 doi: 10.3788/LOP202259.1930002 Wang R H, Sun Y R, Gan Y L, Wu X J, Ke J J, Wang X Q, Gan Y Y 2022 Laser Optoelectronics Prog. 59 364 doi: 10.3788/LOP202259.1930002 [10] 相里斌, 计忠瑛, 黄旻, 王忠厚, 袁艳 2004 光学学报 33 850 Xiangli B, Ji Z Y, Huang M, Wang Z H, Yuan Y 2004 Acta Opt. Sin. 33 850 [11] Zhao B C, Yang J F, Xue B, Qiqo W D, Qiu Y H 2010 Acta Photon. Sin 39 769 [赵葆常, 杨建峰, 薛彬, 乔卫东, 邱跃洪 2010 光子学报 39 769]] doi: 10.3788/gzxb20103905.0769 Zhao B C, Yang J F, Xue B, Qiqo W D, Qiu Y H 2010 Acta Photon. Sin 39 769 doi: 10.3788/gzxb20103905.0769 [12] 崔燕 2009 博士学位论文(西安: 中国科学院研究生院西安光学精密机械研究所) Cui Y 2009 Ph. D. Dissertation (Xi’an: University of Chinese Academy of Sciences, Xi’an Institute of Optics and Precision Mechanics [13] Barrat C, Lepot T, Ramamonjisoa M, Fradcourt S 2016 Proc. SPIE 9987 307 doi: 10.1117/12.2242014 [14] Hedelius J K, Squire K J, Peterson J Q, Blagojević B, Gliese U B, Gorman E T, Moser D K, Rhodes Z, Sevilla P, Meister G 2022 Proc. SPIE 12232 283 doi: 10.1117/12.2631201 [15] Englert C R, Harlander J M, Marr K D, Harding B J, Makela J J, Fae T, Brown C M, Venkat Ratnam M, Vijaya Bhaskara Rao S, Immel T J 2023 Space Sci. Rev. 219 27 doi: 10.1007/s11214-023-00971-1 [16] 相里斌, 吕群波, 才啟胜, 方煜, 周锦松, 黄旻 2020 中国科学: 信息科学 50 1462 doi: 10.1360/SSI-2020-0150 Xiang L B, Lv Q B, Cai Q S, Fang Y, Zhou J S, Huang M 2020 Sci. Sin. Inf. 50 1462 doi: 10.1360/SSI-2020-0150 [17] 王爽 2014 博士学位论文(西安: 中国科学院研究生院西安光学精密机械研究所) Wang S 2014 Ph. D. Dissertation (Xi’an: University of Chinese Academy of Sciences, Xi’an Institute of Optics and Precision Mechanics [18] Wang F B, Zhou J S, Jing J J, Wu Q S, Cheng W 2015 Proc. SPIE 9811 114 doi: 10.1117/12.2205859 [19] 相里斌, 王忠厚, 刘学斌, 袁艳, 计忠瑛, 吕群波 2009 航天器工程 24 257 doi: 10.3969/j.issn.1673-8748.2009.06.008 Xiang L B, Wang Z H, Liu X B, Yuan Y, Ji Z Y, Lü Q B 2009 Spacecraft Engineering 24 257 doi: 10.3969/j.issn.1673-8748.2009.06.008 [20] 张亚飞 2023 博士学位论文(西安: 中国科学院西安光学精密机械研究所) Zhang Y F 2023 Ph. D. Dissertatio (Xi'an Institute of Optics and Precision Mechanics of CAS [21] 王昕, 康哲铭, 刘龙, 范贤光 2020 物理学报 68 200701 doi: 10.7498/aps.69.20200552 Wang X, Kang Z M, Liu L, Fan X G 2020 Acta Phys. Sin. 68 200701 doi: 10.7498/aps.69.20200552 [22] 孙晨, 冯玉涛, 傅頔, 张亚飞, 李娟 2020 物理学报 69 084201 doi: 10.7498/aps.69.20191179 Sun C, Feng Y T, Fu D, Zhang Y F, Li J 2020 Acta Phys. Sin. 69 084201 doi: 10.7498/aps.69.20191179 -
计量
- 文章访问数: 272
- HTML全文浏览数: 272
- PDF下载数: 4
- 施引文献: 0