首页
登录
注册
-
噪声广泛存在于各类工业设备和武器装备中, 吸声降噪是实现噪声控制的主要技术途径之一. 传统的吸声降噪措施主要依赖于吸声体的设计与运用[1]. 根据吸声机理不同, 传统的吸声体主要包括多孔吸声材料和共振吸声结构两大类[2]. 由于低频噪声的波长较长, 且具有较高的穿透能力, 而实际工程中对吸声体的安装空间、重量又有严苛约束, 传统的吸声体普遍难以实现对低频宽带噪声的高效吸收[3,4].
近年来, 声学超材料/超结构概念的提出与快速发展, 为解决低频噪声问题提供了新的思路[5]. 基于Helmholtz共振腔、微穿孔板、共振薄膜等共振式结构设计的吸声超材料/超结构得到了广泛关注[6]. Cai等[7]设计了一种基于卷曲空间的共面Helmholtz共振吸声超结构, 采用理论解析和实验测试两种方法对其吸声特性开展研究, 结果表明该结构能够在厚度17 mm条件下实现对400 Hz声波的近完美吸收(吸声系数接近为1), 其厚度仅为吸声峰频率对应波长的1/50. Wang等[8]设计了一种由入口为单个小孔的串联折叠通道构成的吸声超结构, 理论分析、数值计算、实验结果均表明该结构在厚度为22 mm时, 可实现252 Hz处近完美吸声. Wu等[9]基于微穿孔板和折叠通道设计了一种低频宽带复合吸声结构, 单通道结构在50 mm厚度条件下实现380 Hz处的低频近完美吸声, 相对吸声带宽达到73.7％, 通过并联的方式进一步设计了双通道结构, 将相对吸声带宽拓宽至82.2％. 进一步, 还设计了另一种微穿孔板复合折叠通道吸声结构[10], 理论研究结果表明, 在整体厚度60 mm时, 可实现200—500 Hz范围内平均吸声系数达到0.8的低频高效吸声; 在90 mm厚时, 可实现170—340 Hz频段内理论平均吸声系数达到0.85的优异吸声效果. Zhao等[11]提出了一种卷曲空腔与多孔材料复合吸声超结构, 可以在厚度30 mm条件下同时实现451 Hz处的近完美吸声和中高频段宽带高效吸声. Jin等[12]采用吸声逆向设计方法, 设计了一种穿孔鱼腹板与波纹夹心层复合超结构, 在厚度为36.4 mm条件下, 实现了567—758 Hz频段内最小吸声系数大于0.85, 平均吸声系数大于0.93的优异吸声效果. Liu等[13]设计了一种由多个非均匀截面的法布里-珀罗(Fabry-Pérot, FP)通道组成的吸声超结构, 可以灵活调节每个通道的阻抗特性. 研究结果表明, 当这种超结构含有27个元胞, 厚度为93 mm时, 在400—10000 Hz范围内平均吸声系数超过0.9, 在3000 Hz以上高频段也能高效吸收声波. Bai等[14]基于双端口非对称吸声器原理, 设计了一种尺寸渐变的声学超结构声衬, 建立了理论和仿真模型, 采用全模型理论计算和等效阻抗理论计算了流速对降噪效果的影响. 研究结果表明, 所设计的超结构声衬在厚度为2.5 cm时, 可以在252—692 Hz频带范围内实现3 dB以上的降噪效果. Liu等[15]基于Helmholtz共振器阻抗设计方法, 提出了一种改进的传递矩阵法, 研究了流动条件对具有无限阵列Helmholtz共振腔管道频带结构和声学性能的影响, 并采用数值计算方法验证了所提出模型的准确性, 分析了不同马赫数下声波能带结构和传递损失特性. 研究结果表明, 随着马赫数的提高, 带隙增大, 声波在管道内的声衰减减小, 共振频率向高频偏移.
为了更好地利用结构设计空间, 部分学者考虑将声入射通道嵌入到声学共振腔体内部, 构造了多种形式的内插管/内插缝型吸声超材料/超结构. Zhou等[16]将36个内插管Helmholtz共振腔并联, 构建了一种宽带吸声超材料, 在100 mm厚度条件下实现了320—6400 Hz范围内平均吸声系数达到0.93的高效吸声. Almeida等[17]提出了一种内插缝复合FP通道的吸声超结构(acoustic metasurfaces, AMS), 并与微穿缝板复合FP通道结构(acoustic metamaterials, AMM)进行对比, 结果表明, AMS结构在FP通道数更少的情况下, 单频结构的低频吸声性能仍然更优. 进一步, 他们将4通道与8通道单频结构进行耦合, 耦合后结构总厚度为21 mm, 分别在272 Hz与362 Hz处实现0.83的高效吸声与0.98的近完美吸声, 归一化带宽为50.6％. 需要指出的是, 他们所设计的双频复合吸声超结构虽然能够在低频处获得较高的吸声峰, 但其结构构造非常复杂, 总共由12个折曲通道组成, 不利于低成本制造与应用. Wu等[18]设计了一种内插缝与折叠通道复合形式的超结构声衬, 该声衬由13个不同内插缝与FP通道耦合而成, 总长520 mm, 厚度50 mm. 采用理论、仿真、实验3种方法, 研究了500—3000 Hz频段内, 不同流速、不同声压级工况下该声衬的声学性能. 结果表明, 无流工况下, 所设计声衬在700—2000 Hz频段内实现了吸声系数大于0.9的高效吸声, 明显优于传统的双自由度声衬.
综上所述, 以往研究已经充分表明, 共振式吸声超结构对中低频噪声有较好的吸收效果[19], 但是普遍还存在对500 Hz以下低频噪声的吸声带宽较窄的不足. 此外, 在实际工程应用中, 由于空间受限, 往往还需要在严苛厚度约束下实现低频宽带的吸声降噪[20], 如何突破薄层厚度与低频宽带吸声性能之间的矛盾, 依然是非常棘手的问题. 另外, 针对500 Hz以下低频段, 文献[17]开展了有关内插缝Helmholtz共振腔吸声结构的研究, 但仍存在吸声带宽较窄、腔体结构复杂的不足, 导致加工制造成本高昂的同时也容易产生加工误差, 影响实际效果和经济性[21]. 因此, 如何设计出适用于500 Hz以下低频宽带高效吸声, 且厚度薄、结构构造相对简单的吸声超结构, 依然是一项挑战性难题.
针对上述难题, 本文提出了一种基于内插缝Helmholtz共振腔的吸声超结构, 建立了理论解析与数值计算模型, 对结构的吸声性能与吸声机理进行深入分析, 随后开展优化设计, 并进行了实验验证. 研究表明, 所设计的典型吸声超结构在500 Hz以下低频宽带范围具有良好的吸声性能, 实验结果与理论解析及数值仿真结果吻合良好, 证明设计理论与方法切实有效可行.
-
本节对所提出的吸声超结构进行理论解析与数值仿真建模. 首先给出内插缝Helmholtz共振腔吸声超结构的构型, 然后采用矩形截面通道热黏性理论[22]和传递矩阵法(transfer matrix method, TMM)[23,24]获得结构表面声阻抗, 进而建立吸声系数求解模型. 另一方面, 采用Comsol Multiphsics有限元仿真软件建立了该吸声超结构的数值计算模型, 两种方法互为验证.
-
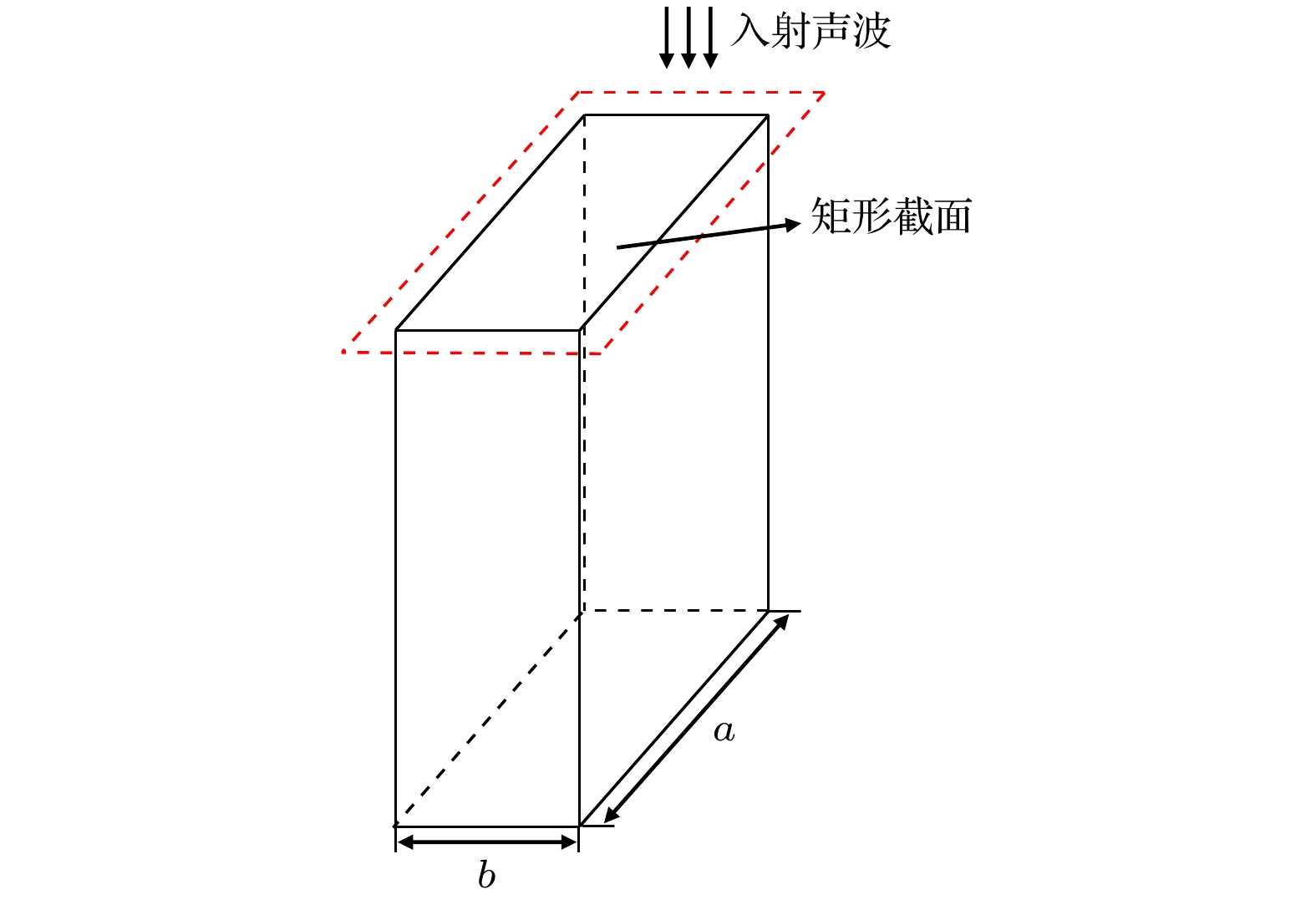
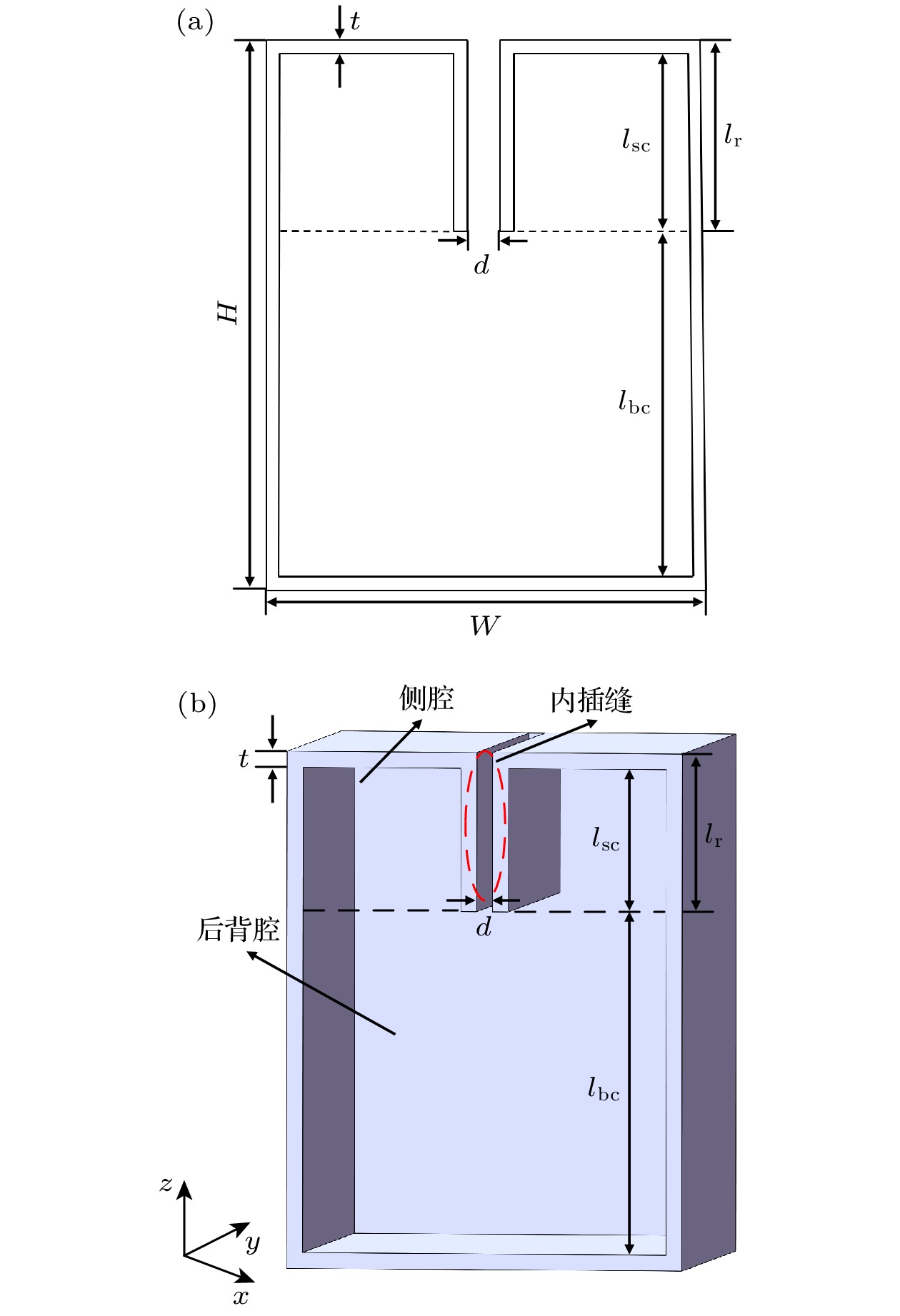
本文所提出的内插缝Helmholtz共振腔吸声超结构的单元胞结构如图1所示, 其由嵌入至空腔内部的长条形内插缝和空腔两部分组成. 图1标示了该单元胞结构的尺寸参数, 其中d和lr分别是内插缝的宽度和高度, H为总厚度, t为壁厚, lsc为内插缝旁侧腔部分的高度, lbc为后背腔高度. 内插缝中的空气介质代表共振结构的声质量, 空腔部分代表共振结构的声容. 入射声波沿z轴负方向垂直入射.
为了建立图1所示单元胞结构的吸声系数解析求解模型, 本文先采用矩形截面通道的热黏性理论计算内插缝部分的等效阻抗和等效波数, 然后采用传递矩阵法推导出结构表面声阻抗.
单元胞结构内插缝部分为一定高度的长条形矩形截面管道, 如图2所示. 根据Stinson[22]所提出的理论, 声波在矩形截面管道中传播时, 其等效密度和等效压缩系数可由下式求得[22]:
式中
其中, j为虚数单位, ω为角频率, a, b分别为垂直于声波传播方向截面的长和宽. P0, ρ0分别为空气的稳态压强和密度, c0为空气中声速. υ = μ/ρ0为空气运动黏度, 其中μ = 1.814×10–5 Pa·s为空气动力黏度;
$ \upsilon ' = \kappa/(\rho_0 \cdot C_v)$ ; κ = 0.0258为空气导热系数; γ = 1.4为空气比热容比; Cv = 718.1429 J/(kg·K)为空气定容比热容. 等效波数为[24]等效阻抗为[24]
内插缝部分传递矩阵为[24]
其中, Sr为垂直声波传播方向内插缝的横截面积, lre为内插缝的有效高度, 其值等于实际高度加上修正高度[25]:
气流流经管口时, 由于介质黏滞和声辐射的作用, 结构表面内插缝入口附近的空气流入内插缝内部, 从而使总的声质量增大, 端部修正如下[25,26]:
其中,
$\varphi $ 为内插缝横截面积Sr与前面板截面积St之比[27]:侧腔传递矩阵为[24]
其中, k0 = ω/c0为空腔中的波数, Z0 = ρ0c0为空气特性阻抗. lsc, Ssc分别为侧腔高度和横截面积. 后背腔传递矩阵为[24]
总传递矩阵为[24]
结构表面声压p0和体积速度u0与底部声压p1和体积速度u1之间的关系为[23]
所研究的吸声超结构底部为刚背衬边界条件, 因此有u1 = 0, 则p0 = T11p1, u0 = T21p1.
结构表面声阻抗为[28]
其中, Ra为结构表面声阻, Xa为结构表面声抗. xs = RaSt/Z0为归一化声阻, ys = XaSt/Z0为归一化声抗. 吸声系数为[27]
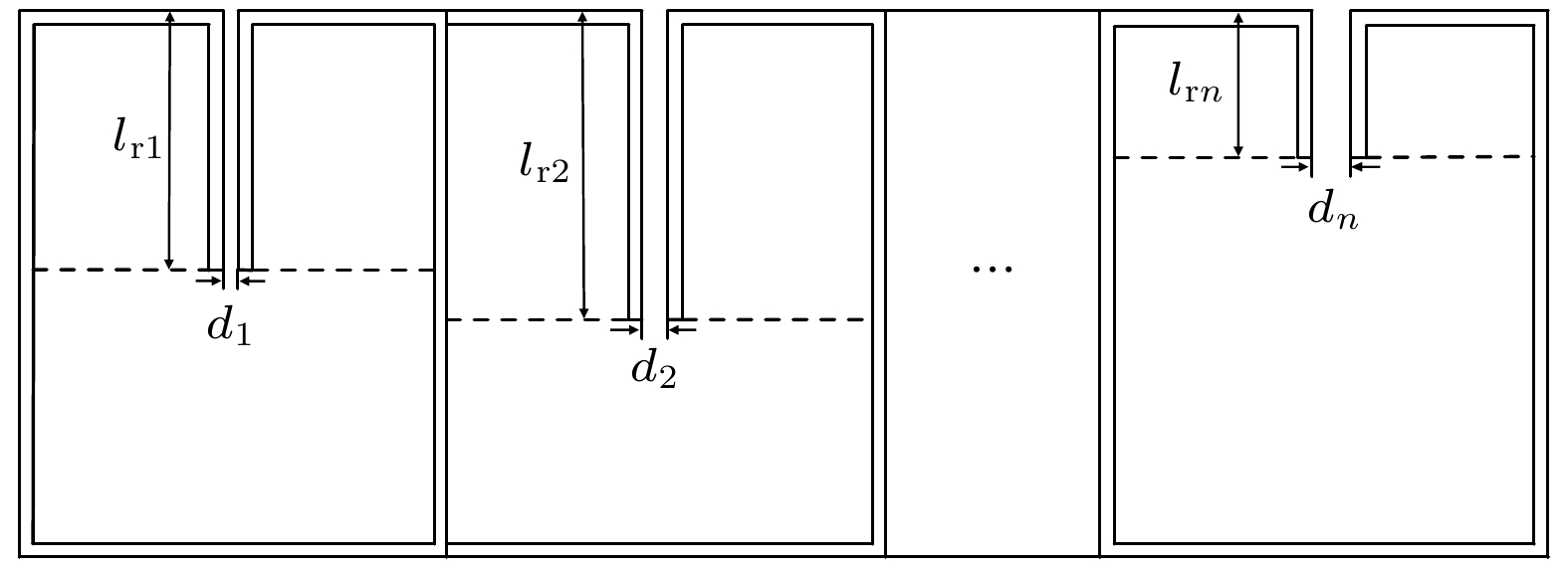
并联结构由不同内插缝宽和高度的单元胞沿x轴方向排列而成, 如图3所示. 并联后的整体表面声阻抗可由并联公式求得[29,30]
其中, Z1, Zn分别为第1个和第n个单元的表面阻抗, Zt为并联后吸声结构表面总阻抗.
-
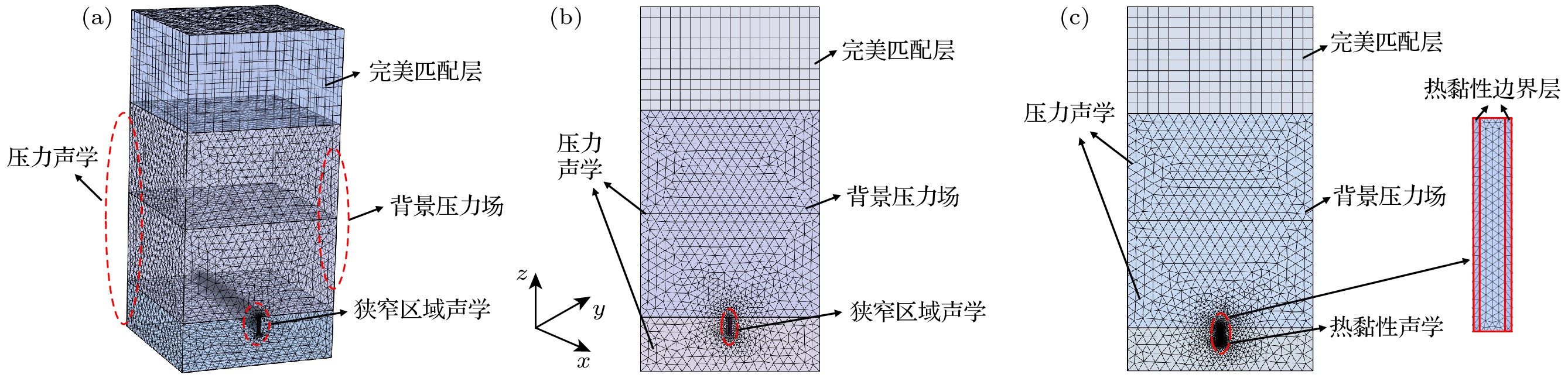
为了验证理论解析模型的有效性, 以及进一步研究内插缝Helmholtz共振吸声超结构的吸声机理, 本文采用多物理场仿真软件COMSOL Multiphsics建立有限元模型, 应用软件内置的压力声学模块和热黏性声学模块建立多物理场仿真分析模型[31,32], 仿真模型如图4所示.
结构内部采用压力声学进行计算, 结构上方区域定义为背景压力场. 入射声压定义为幅值为1 Pa的平面波, 沿z轴负方向垂直入射. 背景压力场的末端区域设置为完美匹配层, 用来模拟无限边界条件和无反射边界条件, 其他壁面设置为硬边界条件. 内插缝部分有两种定义方式来模拟声波的热黏性作用. 一种将内插缝部分直接定义为狭窄区域声学进行计算, 如图4(a), (b)所示. 另一种方法将内插缝热黏性边界层区域定义为热黏性声学, 内插缝其他部分依然定义为压力声学, 如图4(c)所示. 热黏性边界层厚度为[32]
-
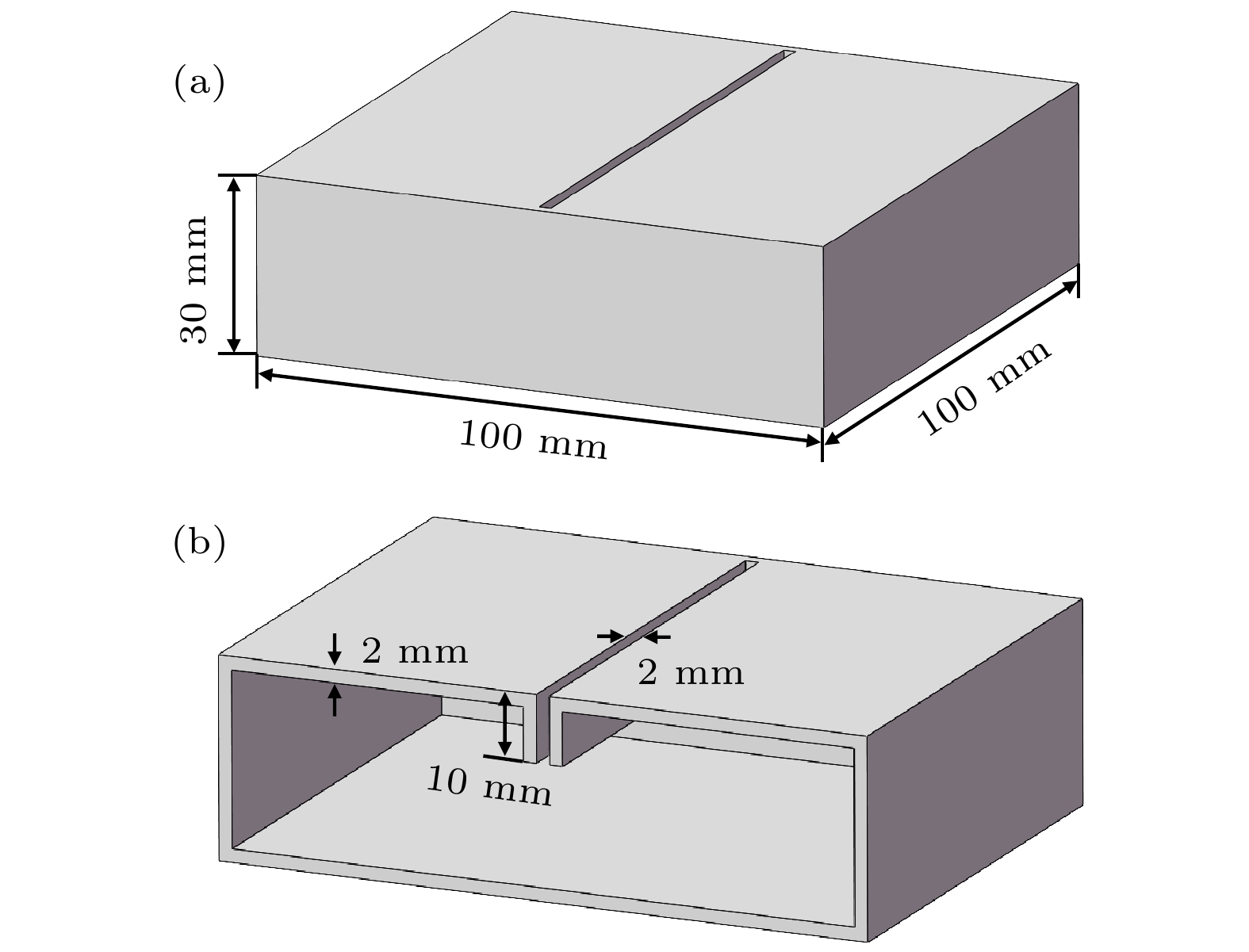
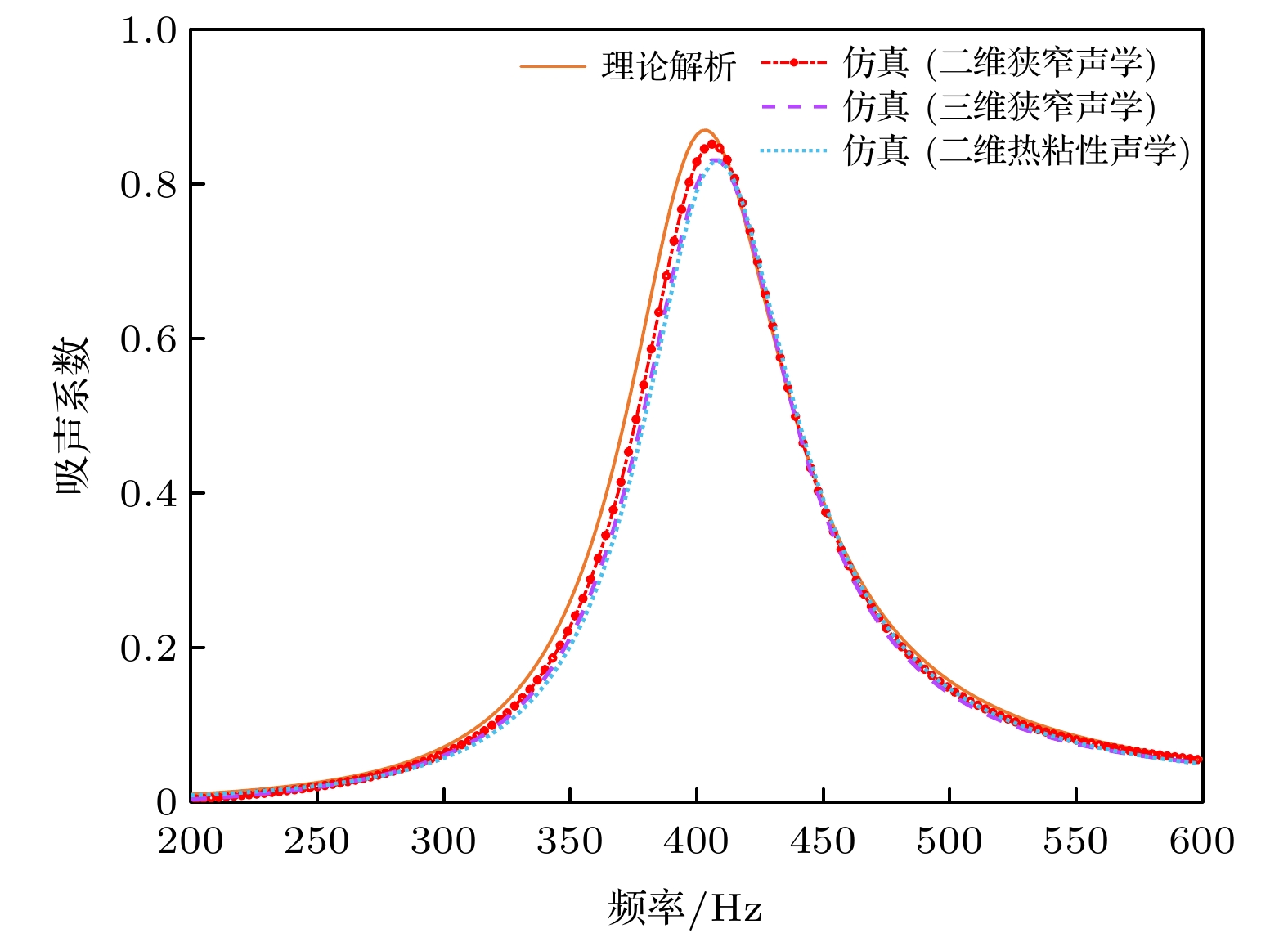
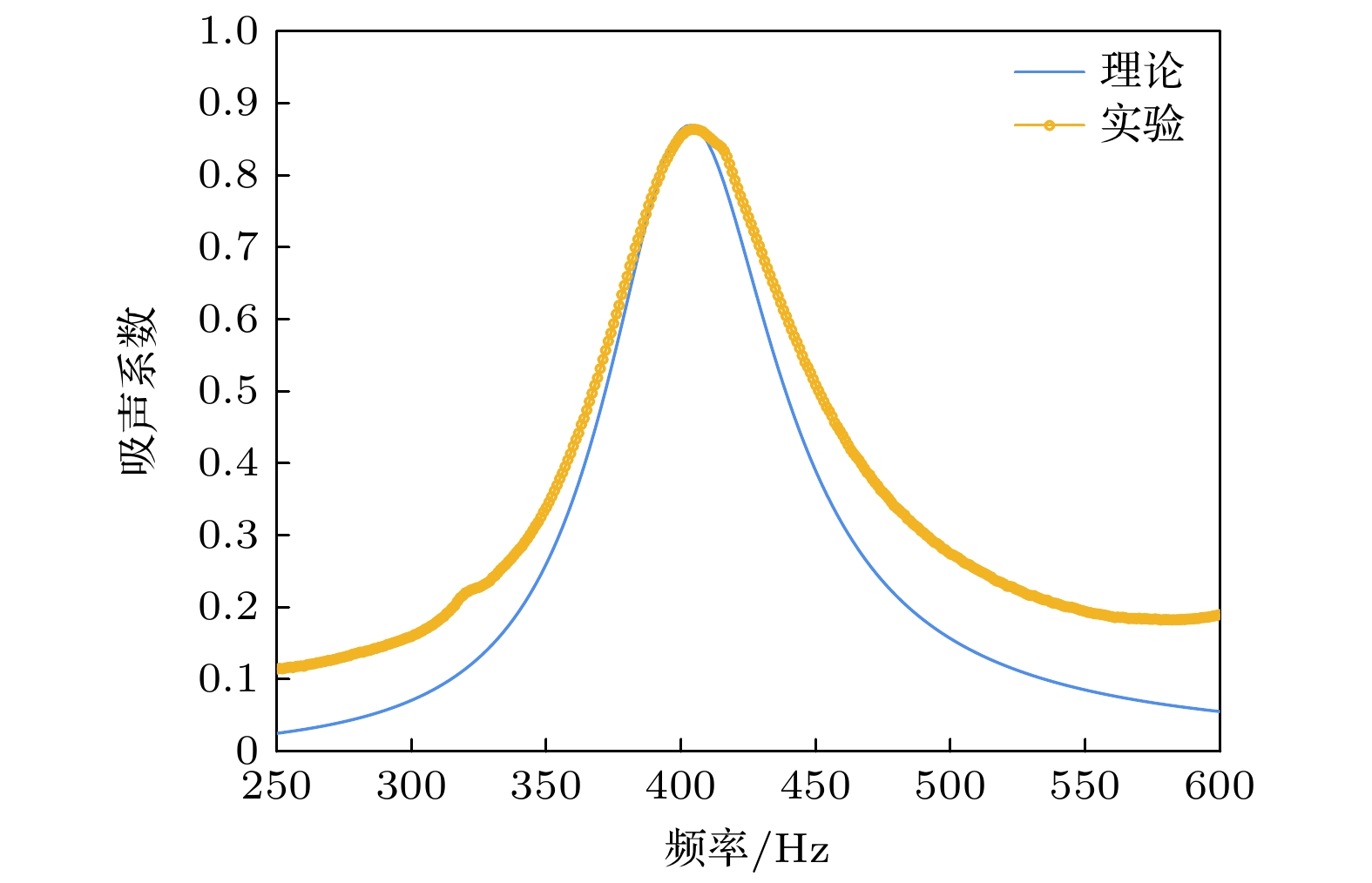
基于以上建立的理论模型与有限元模型, 本节对内插缝Helmholtz共振腔吸声超结构的吸声特性进行分析. 考虑的单元胞结构的参数如表1所示, 结构厚度为30 mm, 三维图如图5所示. 图6为吸声系数频响曲线. 结果表明, 理论解与数值解在误差范围内具有良好的一致性. 吸声曲线在404 Hz处出现吸声系数为0.88的高效吸声峰, 结构厚度与共振频率下波长比仅为1/28, 具有亚波长尺度下低频吸声特性. 采用二维狭窄声学、三维狭窄声学、二维热黏性声学计算, 三者结果基本符合, 为缩短计算时间, 提高计算效率, 后文采取二维模型进行计算. 采用热黏性声学计算是为了便于下一节分析吸声机理. 产生误差的主要原因为理论解析考虑了一定壁厚, 导致背腔的体积与仿真建模体积略有差异.
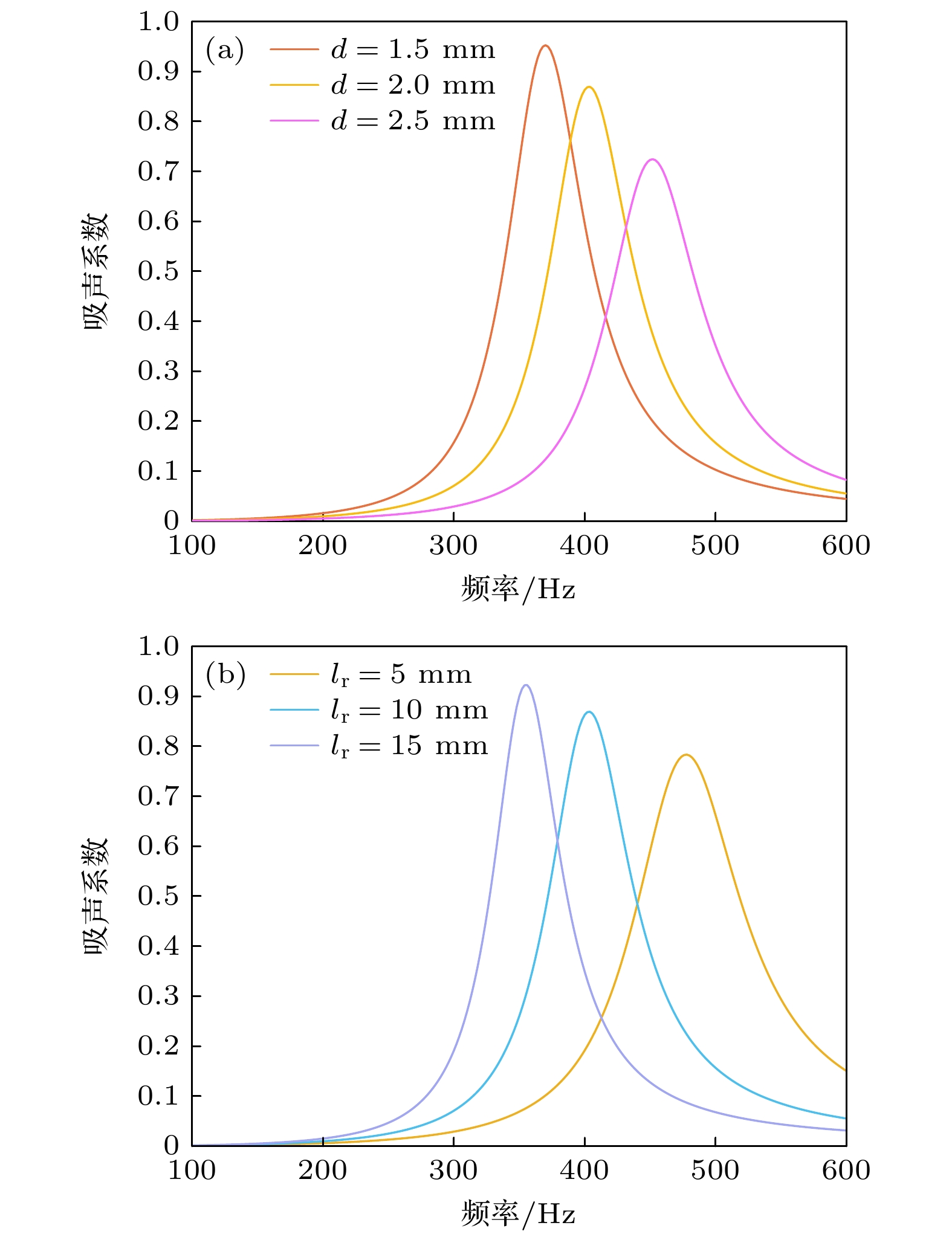
图7给出了单元胞内插缝Helmholtz共振腔在厚度为30 mm时, 吸声系数曲线随内插缝宽度和高度的变化. 可以看出, 在不改变结构整体厚度的情况下, 减小缝宽和增大缝高均可以降低吸声频率, 提高吸声效果. 此外, 内插缝宽度对吸声系数的影响较大, 内插缝宽度变化仅0.5 mm, 但吸声峰频率和峰值均有较大的变化.
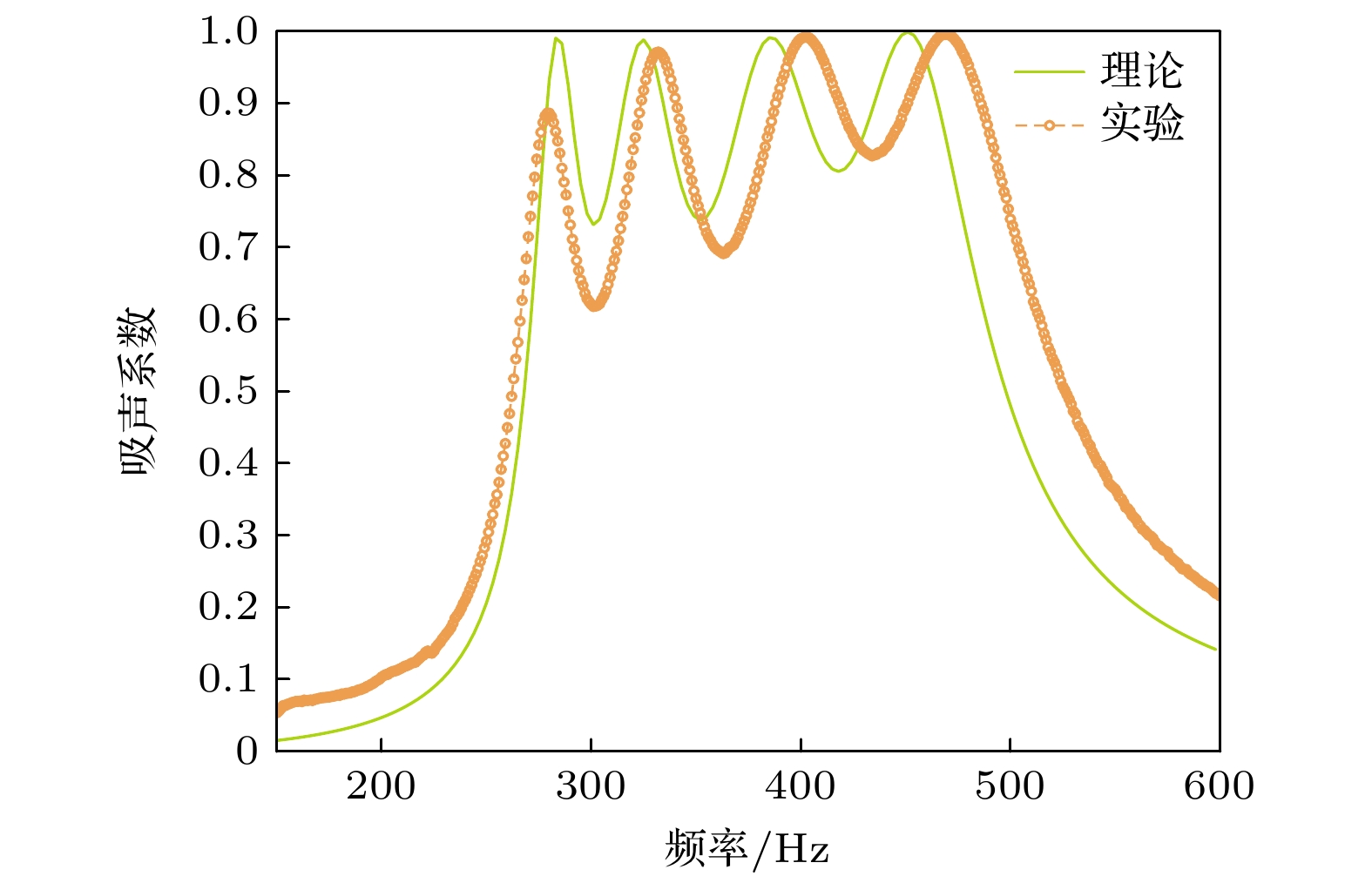
为进一步提高结构的低频吸声特性, 在总体厚度H = 50 mm约束下对内插缝Helmholtz共振腔结构进行解耦并联设计. 本节针对500 Hz以下频段, 设计了2种并联内插缝Helmholtz共振吸声结构, 分别为双元胞并联和四元胞并联结构, 如图8所示, 具体结构参数如表2和表3所示. 采用Matlab, Comsol Multiphsics对吸声系数进行理论解析与数值计算, 频响曲线如图9所示, 其中虚线为每个元胞未并联时的吸声曲线. 可以看出并联后吸声峰值有所提高, 带宽拓宽. 理论解与数值解在误差允许范围内符合良好, 进一步验证了理论与有限元方法的准确性. 双元胞结构在257 Hz与294 Hz处实现近完美吸声, 在275 Hz处出现吸声谷, 四元胞结构在262, 298, 352, 400 Hz处出现4个完美吸声峰, 这些吸声峰频率分别与各元胞的共振频率相对应. 元胞耦合后峰值频率有所偏移, 峰值相较于单元胞时有所增大, 有效吸声带宽拓宽. 当多元胞并联时, 非共振元胞会产生附加声抗在共振元胞上, 因此并联后元胞的共振频率较未并联时发生偏移. 当附加声抗为负时, 频率向高频移动. 反之, 向低频移动.
对比上述单元胞结构和多元胞结构的吸声系数计算结果可以看出, 与单元胞结构相比, 多元胞结构的理论解析与数值计算的吸声系数误差有所增大, 原因主要有以下两点. 一方面, 在理论解析模型中, 忽略了元胞侧壁的厚度尺寸, 但在有限元仿真模型中, 考虑了元胞侧壁的厚度尺寸, 并将其建模为刚性壁面, 因此导致理论解析模型与仿真模型的声波入射面表面积之间存在差异, 即仿真模型入射面积大于解析模型入射面积. 且随着并联元胞数量的增多, 引入的侧壁面越多, 导致这种差异越大, 两者计算得到的吸声系数差异越大. 另一方面, 实际吸声超结构的相邻元胞入口附近的声场存在耦合效应, 会使得峰值频率有所偏移, 而且元胞之间的距离越近, 耦合越强烈. 这种耦合效应在仿真模型中可以得到充分考虑, 但解析模型中没有考虑这种耦合效应, 因此解析模型计算得到的多元胞并联结构的吸声系数一定程度上形成了误差累积, 最终导致与仿真模型结果差异增大.
-
为揭示内插缝Helmholtz共振腔吸声超结构产生低频吸声峰的原因及调控规律, 本节将从简化等效模型、归一化声阻抗、复平面反射系数、声压云图与质点速度场4个方面进行分析.
根据已有研究, Helmholtz共振腔结构在低频范围可以近似简化等效为由等效声质量和等效声容构成的单自由度声学共振系统[27], 等效声质量和声容可分别近似表述为[27]
其中, V 代表后背腔体积.
结构表面声抗可以表示为[27]
当结构共振时, 声抗等于零, 即Xa=0, 由此可得共振频率为[27]
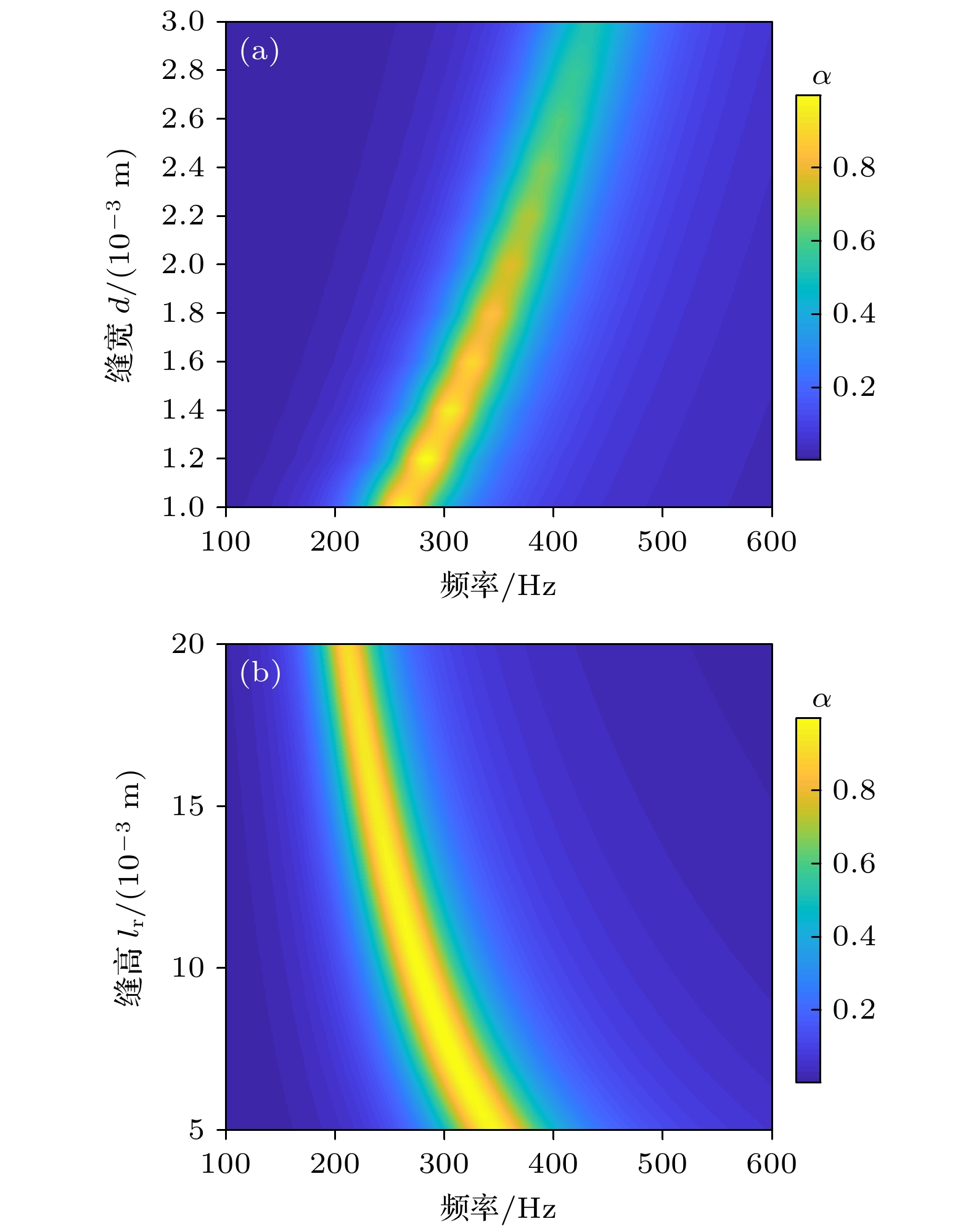
为了研究内插缝主要结构参数对吸声系数的影响规律, 绘制了吸声频谱随缝宽和缝高的变化, 如图10所示. 颜色从蓝到黄表示吸声系数从0到1. 可以看出减小缝宽和增大缝高均可以降低吸声频率, 提高吸声效果. 由(19)式可知, 缝宽减小, 内插缝横截面积Sr减小, 在缝高不变的情况下, 声质量Ma增大. 由 (22) 式可知, 声质量增大, 共振频率减小, 吸声峰向低频移动. 当缝宽不变时, 增大缝高lr亦会使声质量Ma增大, 共振频率减小. 即当后背腔体积V基本不变时, 内插缝宽度减小、高度增大时, 等效质量在增大, 因此固有频率减小, 峰值向低频移动. 但当缝宽增大到一定值后, 由于声波与壁面之间的黏滞作用减弱, 将不再出现完美吸声.
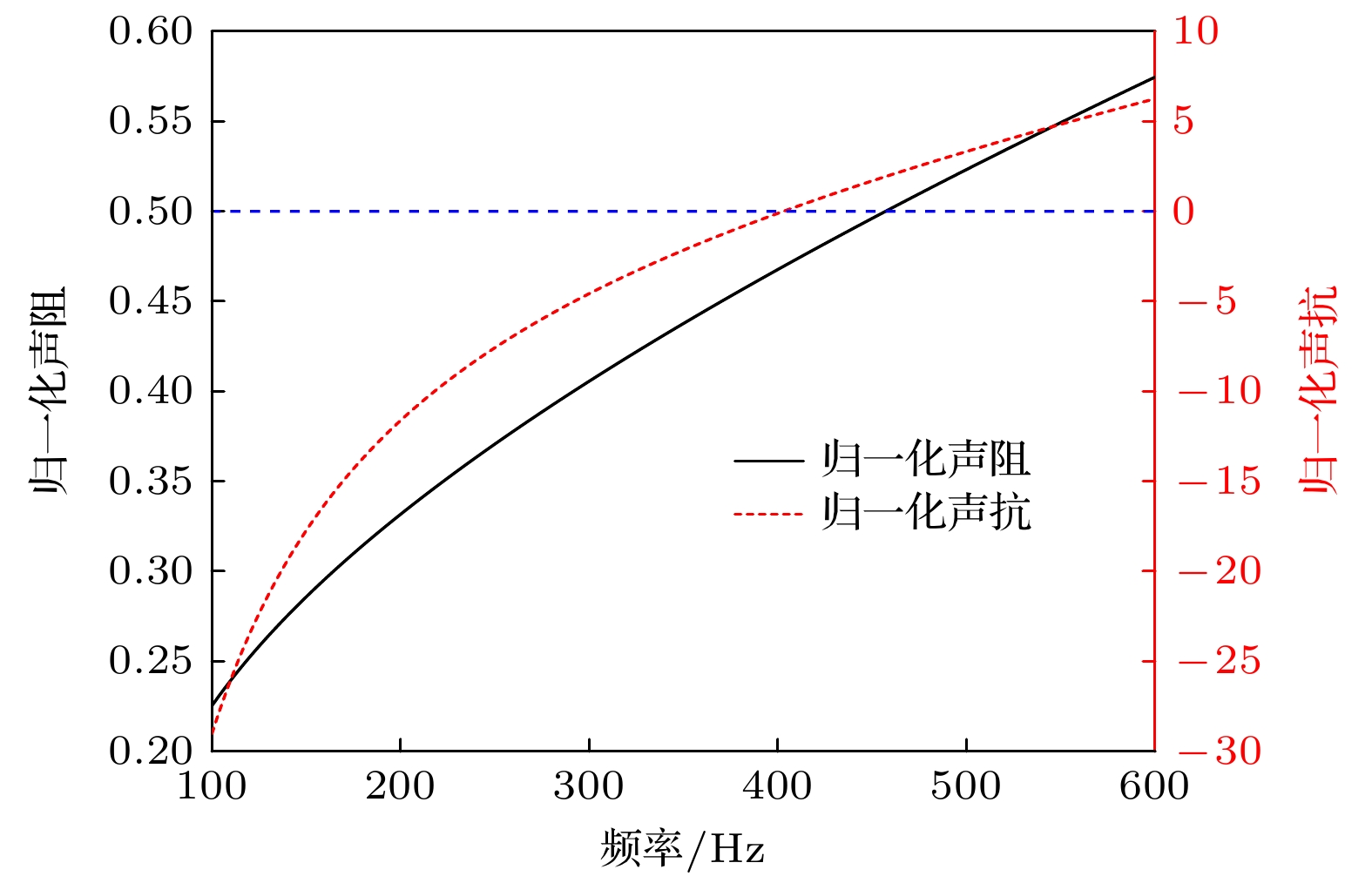
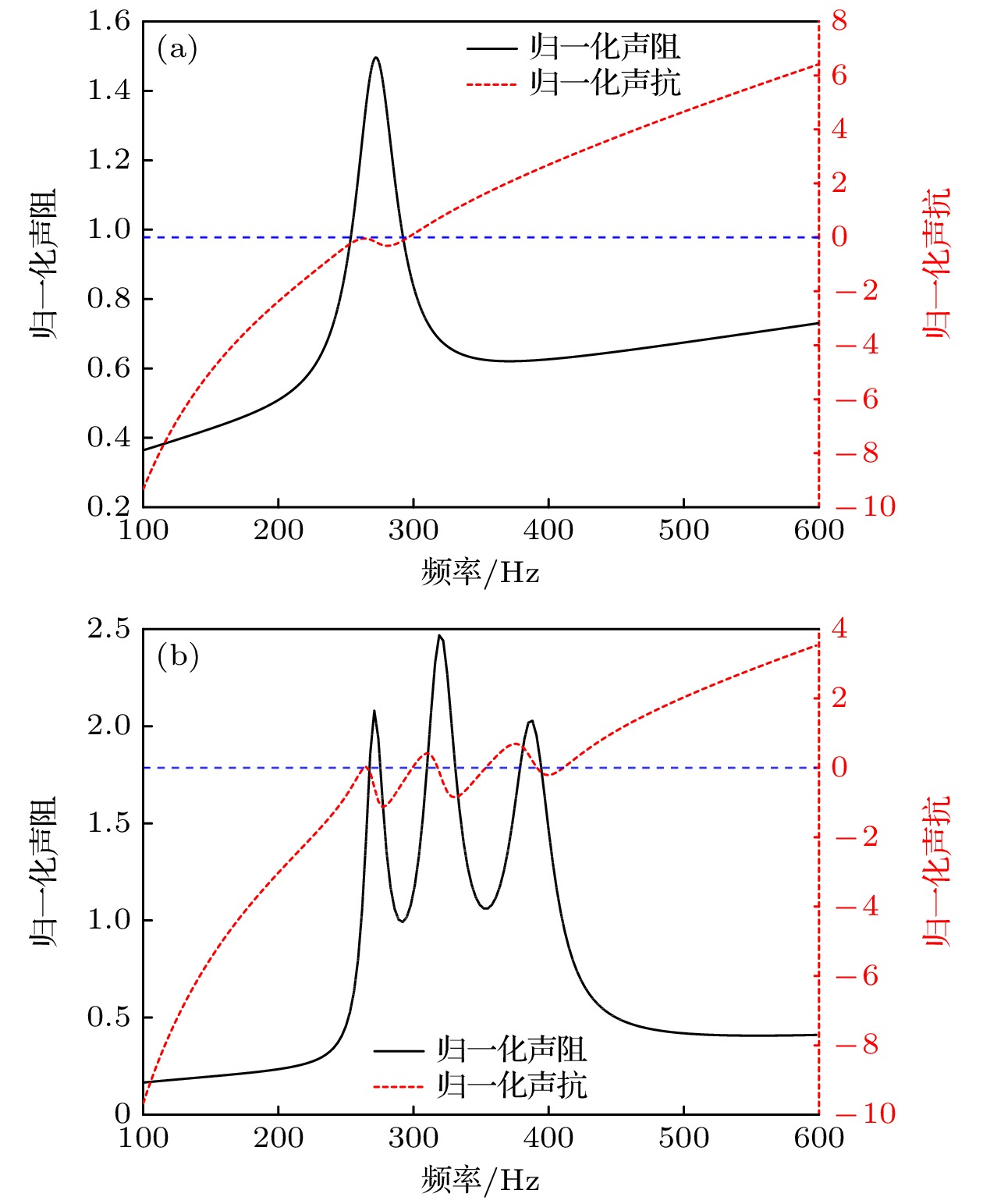
其次, 提取表面归一化声阻抗进行分析. 内插缝单元胞结构表面归一化声阻抗如图11所示, 黑线和红线分别对应声阻抗的实部和虚部. 可以看出, 归一化声抗ys在404 Hz处等于零, 表明结构在此频率下发生共振, 表现在频响曲线上为吸声曲线出现吸声峰. 若此时归一化声阻xs等于1, 表明与空气阻抗完全匹配, 实现对声波的完美吸收. 根据图11, 结构处于共振状态时, 归一化声阻略小于1, 这与吸声峰值为0.88相对应.
图12为双元胞与四元胞结构表面声阻抗, 在每个峰值处, 归一化声抗都过零点, 即ys = 0, 结构发生共振, 消耗声波能量. 此时双元胞并联结构归一化声阻xs分别为1.08, 0.93. 四元胞并联结构归一化声阻xs分别为1.1, 1.1, 1.06, 1, 基本满足与空气介质阻抗匹配条件, 因此吸声系数可以接近100％. 双元胞并联结构归一化带宽(指吸声系数大于0.5的带宽与中心频率的比值)达到44.8％, 总厚度为最大共振频率下对应波长的1/23. 四元胞并联结构归一化带宽达到60.6％, 总厚度为最大共振频率下对应波长的1/17, 结构具有良好的低频吸声性能和亚波长特性, 为连续带宽的行成奠定了基础.
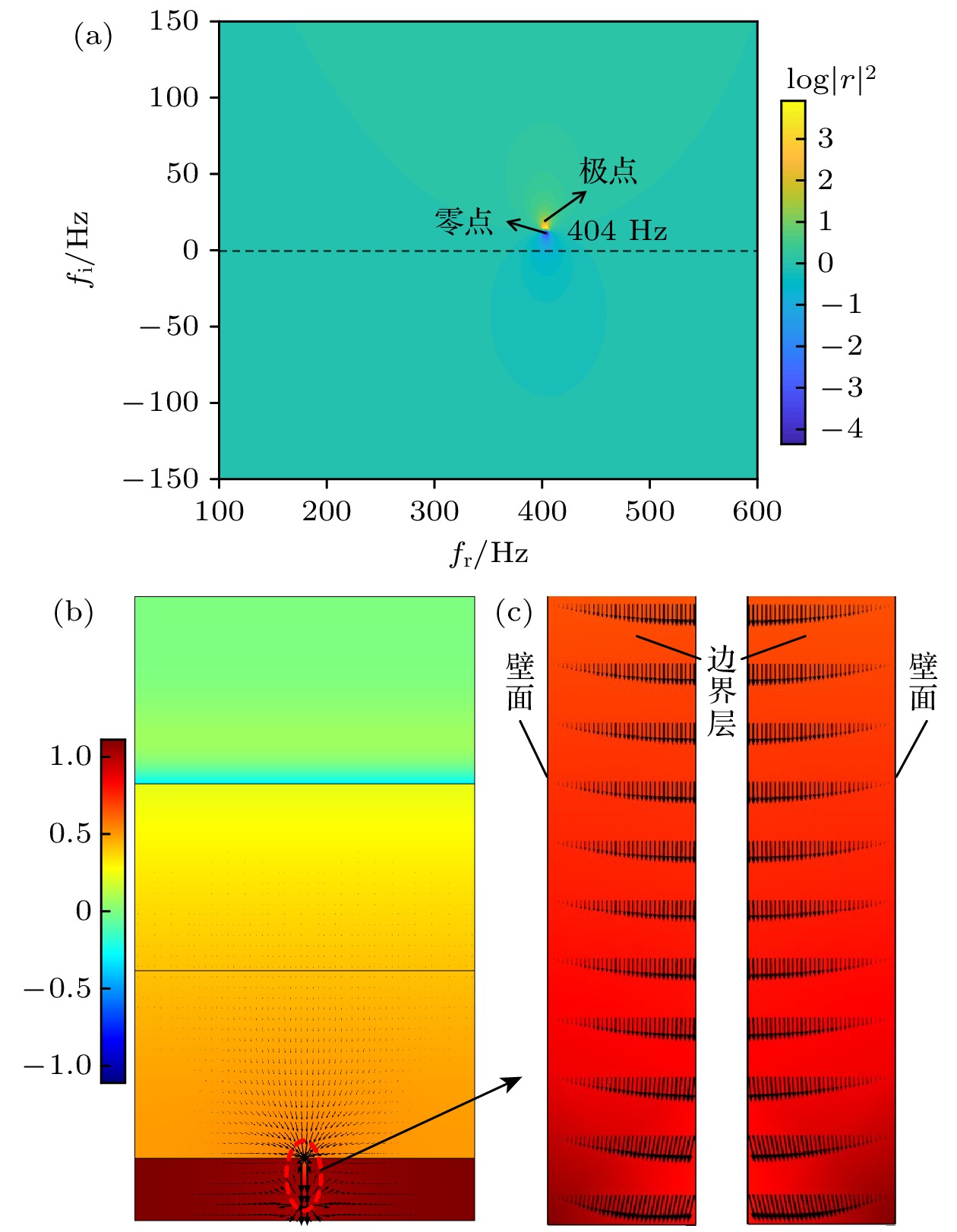
采用复平面上反射系数进一步揭示声波被完美吸收的机理. 反射系数在复平面上存在一对共轭的零点和极点, 零极点的实部与结构的共振频率相同. 已有研究表明, 极点虚部反映了在共振频率处反射系数相位变化的快慢[33]. 结构中热黏性损耗越大, 在复平面上反射系数的零点越接近实轴. 若零点刚好落在实轴上, 则表示在此频率下可以完全吸收声波. 图13(a)为单元胞结构复平面反射系数, fr和fi分别代表复频率实部和虚部. 可以看出, 零点与极点频率与吸声峰值频率对应. 由于单元胞结构在404 Hz共振频率处吸声系数为0.88, 而未能实现100％的完全吸收, 表现在复平面反射系数上为零点未能完全落在实轴上. 图13(b)为共振频率处, y-z平面声压云图与空气质点速度分布. 颜色由蓝变红表征声压逐渐增大. 黑色箭头大小表示空气介质速度值, 方向表示介质振动方向. 可以看出, 结构共振时, 从内插缝壁面到边界层边界处, 空气质点振速从零逐渐增大到最大值. 由于内插缝壁面速度为零, 较大的速度梯度产生了黏性摩擦, 导致声波耗散. 因此声波耗散主要发生在内插缝壁面至边界层范围内.
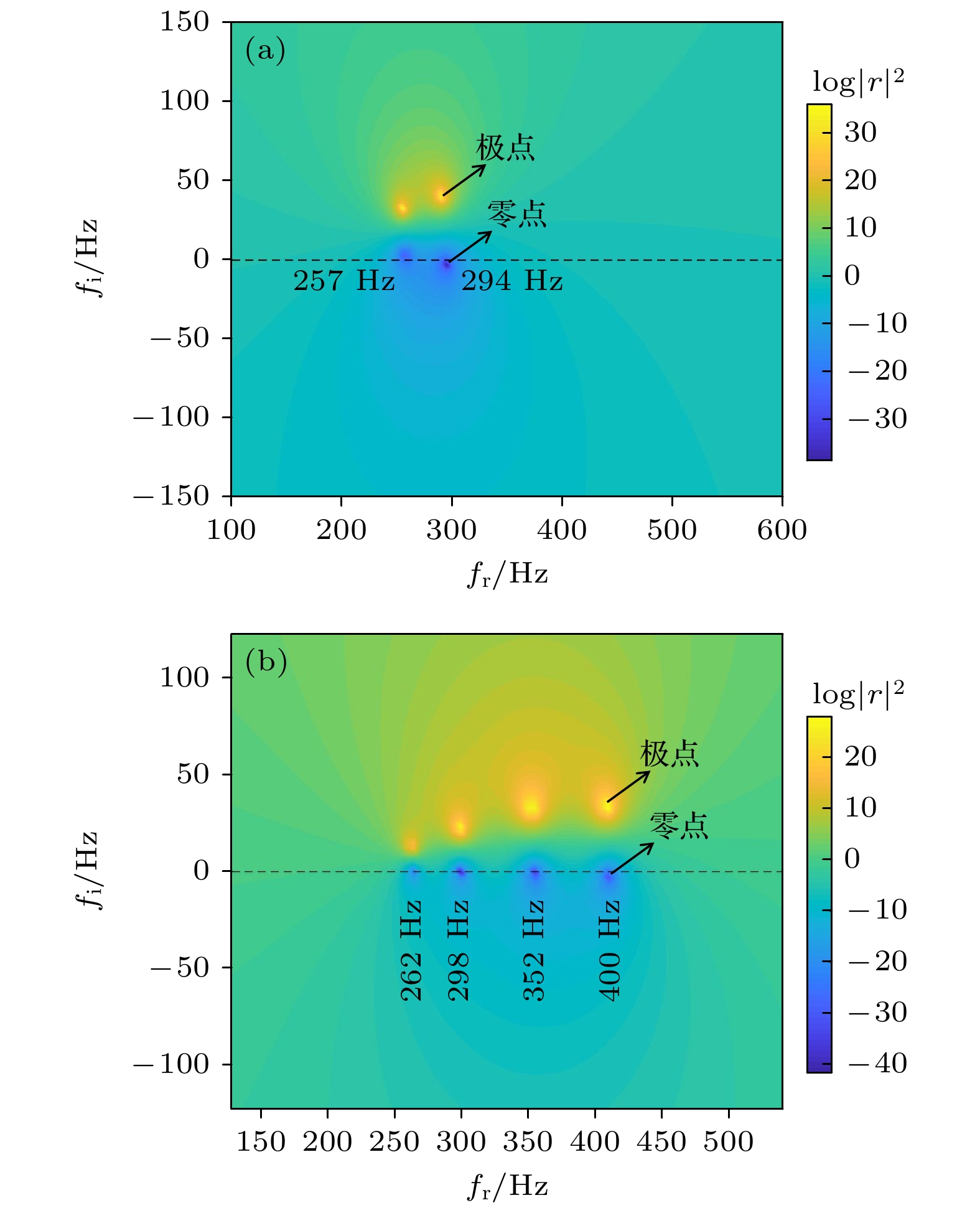
图14分别给出了双元胞和四元胞并联Helmholtz共振腔吸声超结构的反射系数在复平面上的分布. 可以看出, 反射系数零点和极点的实部均与共振频率一致, 且零点刚好落在实轴上. 说明结构内部与声波之间的黏滞损耗刚好达到临界耦合状态, 因此能完美吸收声波.
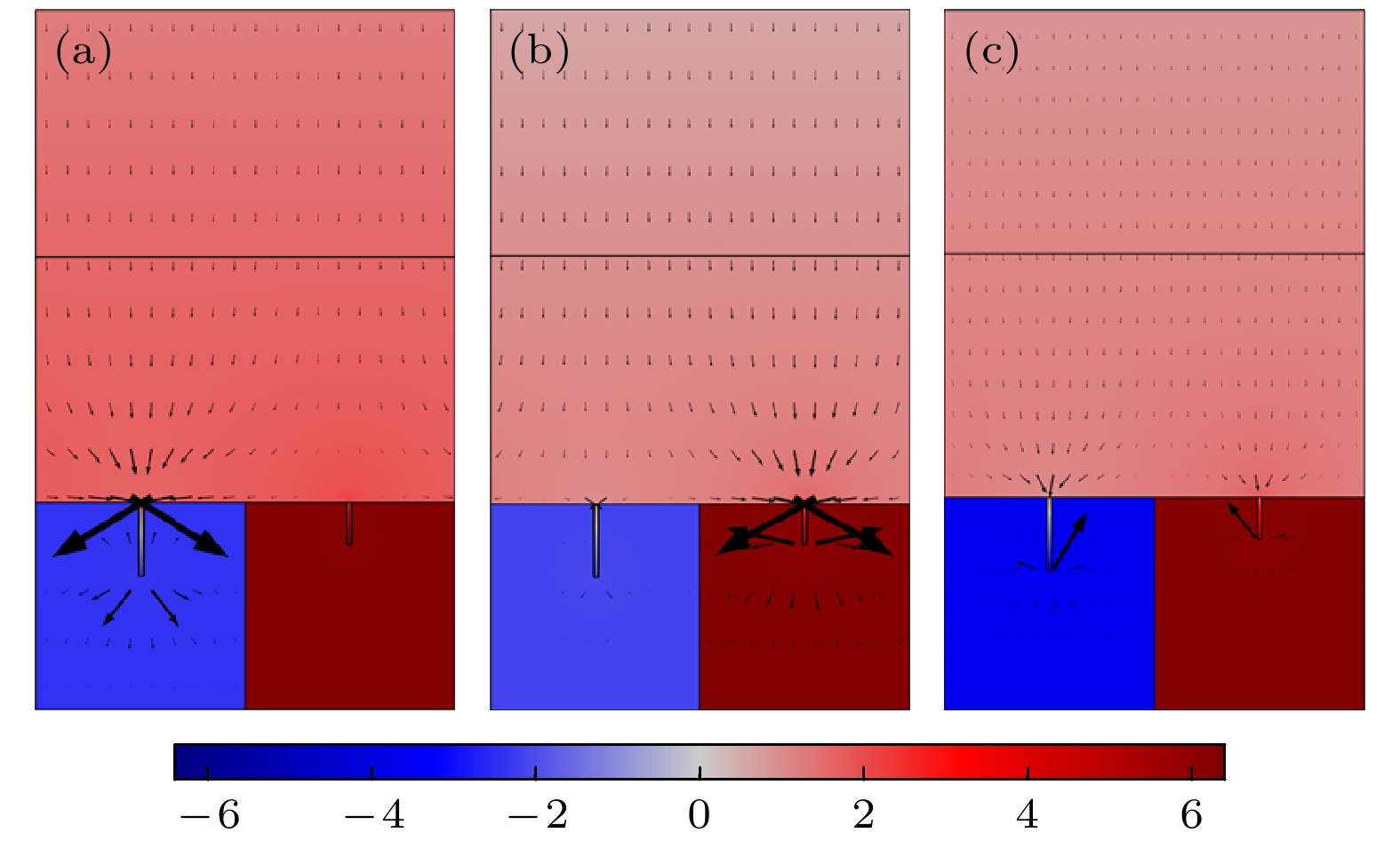
图15为双元胞并联吸声结构声压及空气粒子速度场分布, 在257 Hz和294 Hz两个峰值频率处, 元胞1和元胞2的内插缝内部空气质点振速最大, 结构内部质点振动与入射声场同相位, 声压幅值在空腔内部达到最大值. 图15(c)可以看出, 双元胞结构在275 Hz频率处于反共振状态, 这种反共振状态破坏了结构与入射声场介质的阻抗匹配条件, 部分空气质点振动相位与入射声波相反, 吸声曲线形成谷值. 不同单元在各自共振频率处发生共振形成吸声峰, 峰值频率的改变是由两个元胞之间耦合引起的.
-
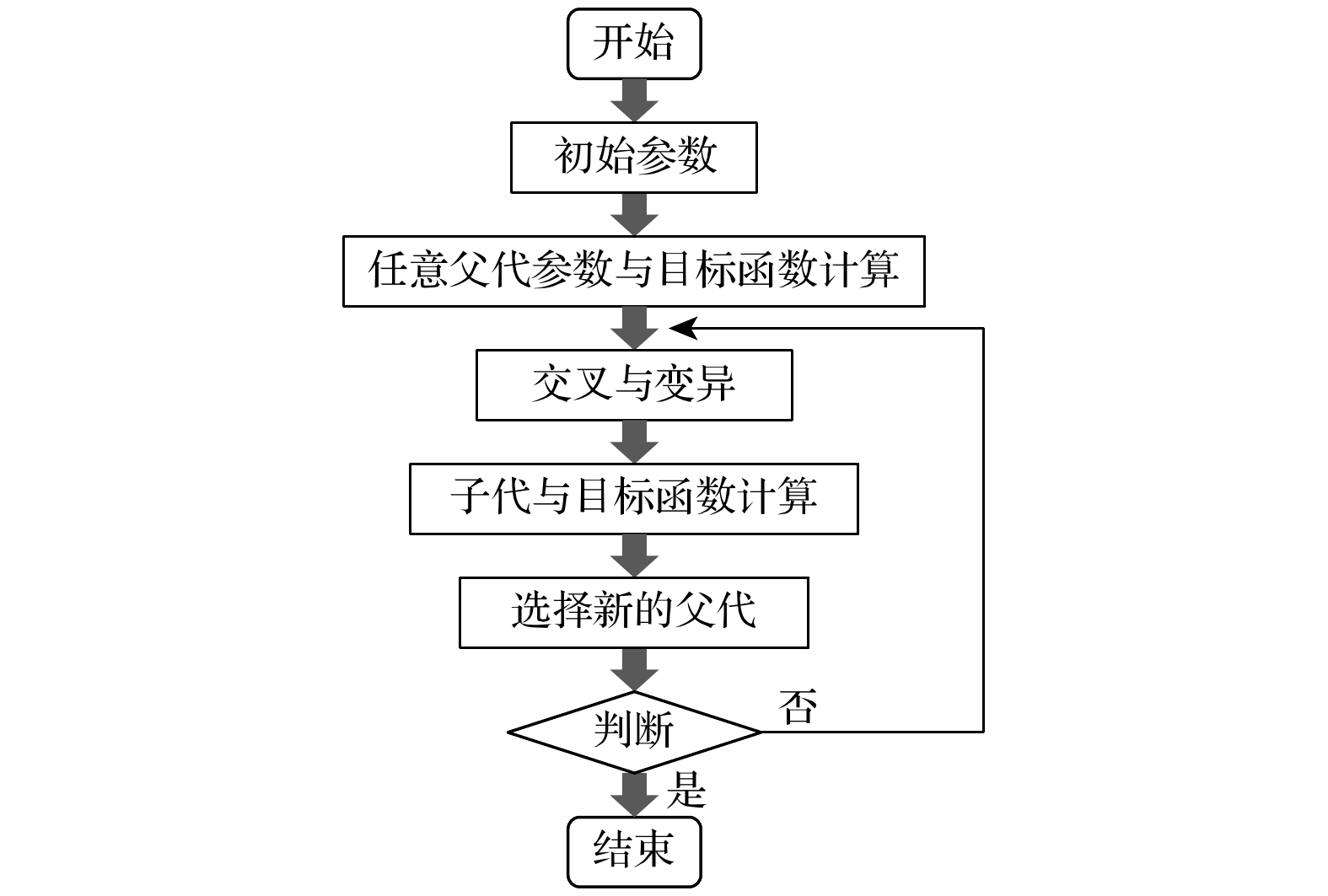
由于单个峰值带宽有限, 采用多个具有不同峰值的单元, 将其依次排列耦合, 最终形成连续的高效吸声频带是实现宽带吸声的有效方法之一. 为实现500 Hz以下低频段多目标频率高效吸声, 进一步拓宽带宽并提高低频吸声性能, 本节采用差分进化优化算法[34], 在总厚度90 mm的约束下, 对8元胞并联耦合结构开展参数优化设计, 最大限度拓宽吸声带宽, 流程图如图16所示. 每个元胞x方向宽度与y方向长度分别为25 mm, 200 mm. 各元胞沿x轴方向排列并联, 并联后结构总长度和总宽度均为200 mm.
考虑到热黏性效果与实际加工情况, 内插缝宽度优化区间为1—3 mm, 高度优化区间为5— 85 mm. 为了兼顾低频吸声与宽带特性, 目标函数定义为吸声系数的平均值与最小值之和, 可表示为
其中, α(f, hri)为与变量有关的频变吸声系数, f为频率, Nf为频率点数, 目标频段为150—400 Hz, 频率间隔为2 Hz. 此外, 本文中使用的变异缩放因子W0、交叉率Pc、种群数目Np和最大进化代数I0分别为0.8, 0.9, 40和1000. 对于子代种群中第i个个体的第j个变量, 当随机数小于交叉率时, 选择变异后个体变量; 否则, 选择父代个体中变量. 交叉策略的符号表达式如下:
从父代和子代中, 选择Np个目标函数值最大的个体, 作为新的父代, 选择具有最大目标函数的个体, 作为全局最优个体. 当全局最优个体的目标函数大于限定值或者循环次数大于最大进化代数时, 终止程序并输出全局最优个体.
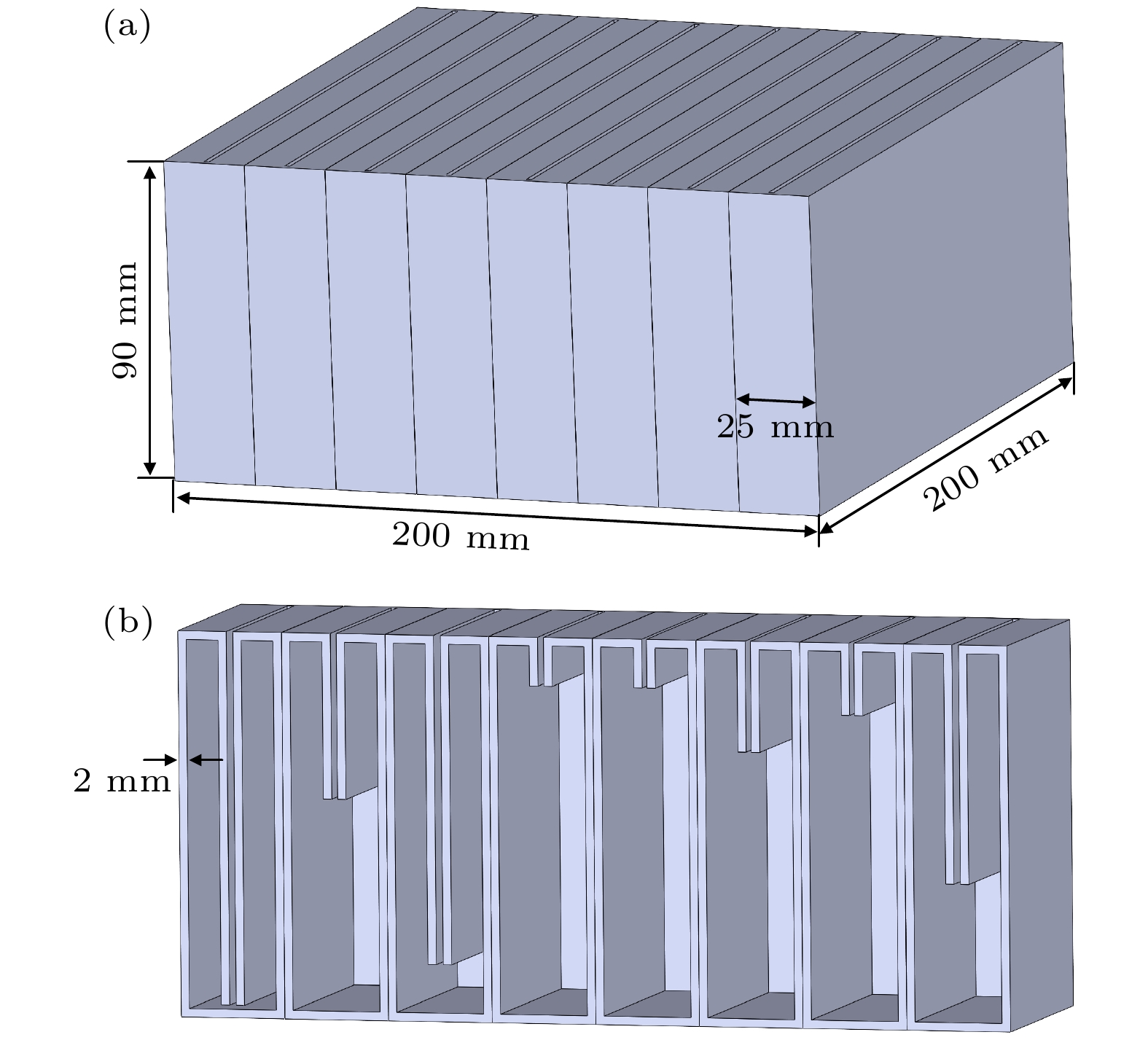
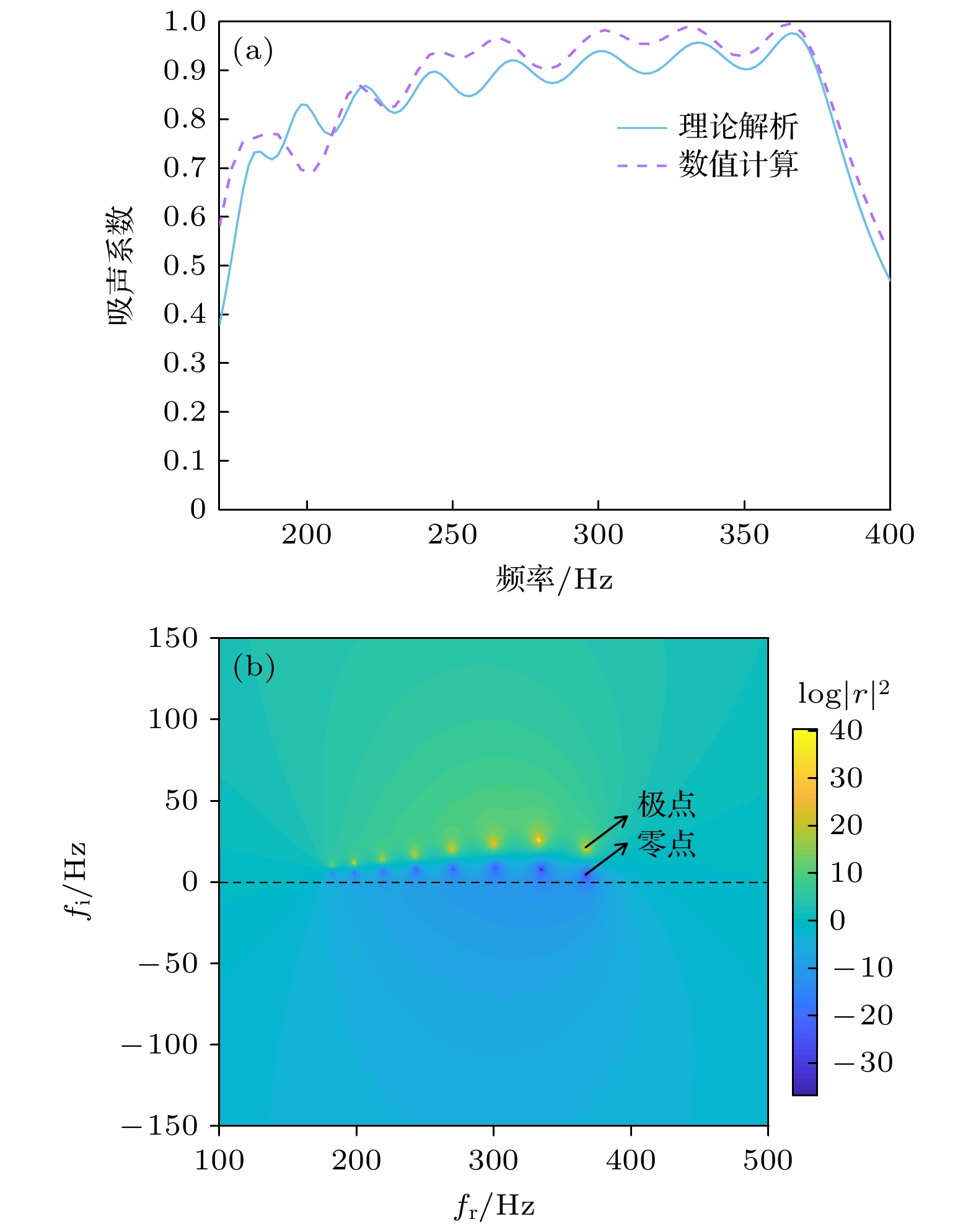
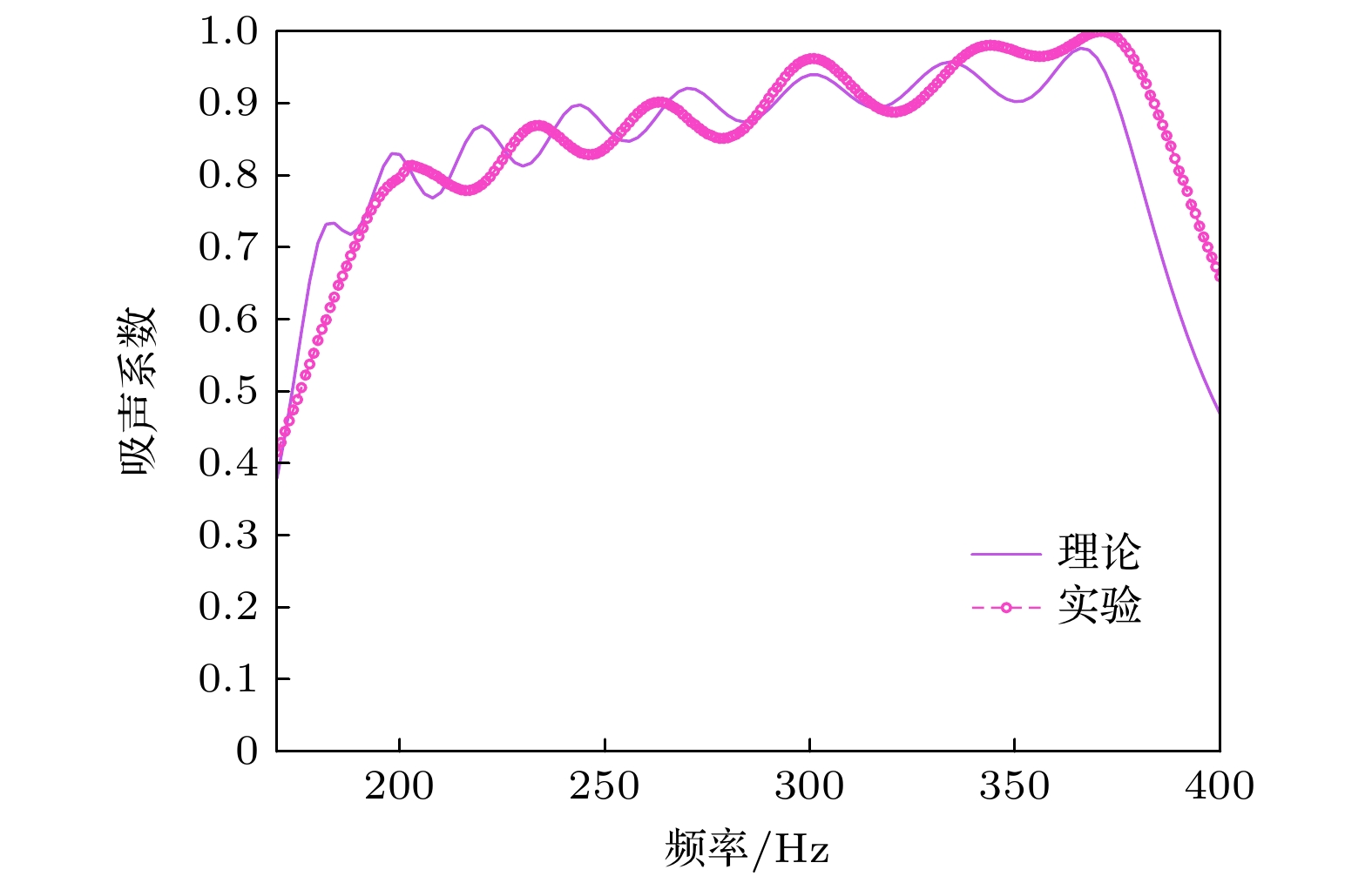
内插缝参数优化结果如表4所示, 三维如图17所示. 吸声系数和复平面零极点分布如图18所示. 吸声曲线在170—380 Hz频段内出现多个吸声峰, 平均吸声系数达到0.86, 归一化带宽达到78％, 峰值频率分别为182, 198, 220, 244, 270, 300, 334, 366 Hz, 复平面零极点数与峰值数相同, 频率与峰值频率一一对应, 且零点距离实轴较近, 这表明共振频率处吸声峰值较高. 在500 Hz以下低频段具有良好的吸声性能和宽带特性. 峰值数、通道数和归一化带宽, 在相同频段均优于Almeida等[17]提出的内插缝复合FP通道吸声超结构. 其次, 本文提出的内插缝Helmholtz共振腔多元胞并联耦合吸声超结构针对的是500 Hz以下低频段吸声降噪问题, 这与Wu等[18]所提出的内插缝复合折曲通道超结构声衬有所不同, 他们关注的降噪频段是500—3000 Hz. 此外, 本文所提出的内插缝Helmholtz共振腔吸声超结构还具有结构构型简单、易于低成本批量化加工制造等优点.
-
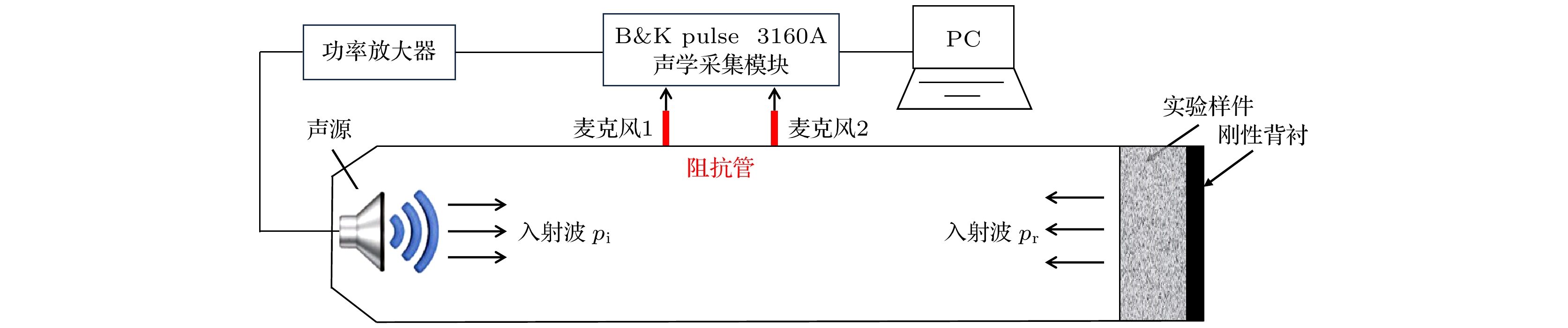
为验证所设计吸声超结构理论解析及数值计算方法的准确性, 制备实验样件, 开展吸声测试. 图19为实验测试系统示意图. 声学采集模块为B&K 3160A, 采用双传声器法测量样件的吸声系数. 4个实验样件的参数如表1—表4所示, 其厚度分别为30, 50, 50, 90 mm. 样件1—3在边长为100 mm的阻抗管中开展吸声测试实验, 样件4在边长为200 mm的阻抗管中进行. 图20为实验测试系统实物图, 图21为各样件实物照片. 样件1, 4采用树脂材料通过3D打印制备而成, 样件2, 3采用的是尼龙材料. 本文为方便单个样件的加工制造, 采用3D打印技术. 在实际应用中, 可以采用更低成本的批量化制造工艺, 例如拉挤成型工艺. 首先, 可采用拉挤成型工艺加工很长的等截面样件, 然后根据y方向尺寸进行批量化等间距切割, 实现腔体和内插缝集成结构的一体化批量化加工制造.
实验测试结果如图22—图25所示, 实测吸声系数与理论值总体变化趋势一致, 符合良好, 从实验的角度验证了理论方法的准确性. 对于单频内插缝Helmholtz共振结构, 理论共振频率和实验测得的共振频率均为404 Hz, 理论吸声峰值为0.88, 实验峰值为0.86, 相对误差约为1.2％. 其他并联结构理论与实测吸声峰频率和幅值相对误差均在5％以内. 实验结果与理论解析结果存在偏差的主要原因有以下两点. 一方面, 低频峰值主要是由整个结构中的低频共振元胞在其自身共振频率处发生共振产生的. 由(20)式—(23)式可知, 低频共振元胞的缝高值较大, 一般是所有并联元胞中缝高最大的. 样件采用的是3D打印制造, 由于内插缝缝宽较小, 在样件加工过程中, 内插缝部分容易产生加工误差, 尤其是缝高较高的低频元胞. 因此图23、图24中低频元胞对应峰值的实验结果比理论值小. 另一方面, 实际吸声超结构的相邻元胞入口附近的声场存在耦合效应, 会使得峰值频率有所偏移, 详见3.1节分析内容. 元胞之间的距离越近, 耦合越强烈. 理论解析模型中没有考虑这种耦合效应, 但在实际实验过程中, 这种耦合效应能够得到一定程度的体现, 导致理论解析与实验测得的吸声特性曲线有一定差异. 随着并联元胞数量的增多, 元胞间距减小, 耦合效应增强, 在一定程度上形成了误差累计, 最终导致理论结果与实验结果差异增大.
-
本文提出了一种内插缝Helmholtz共振腔吸声超结构, 建立理论解析与数值计算模型, 对其吸声性能和吸声机理进行深入分析, 并在此基础上进一步优化设计了低频宽带多元胞并联耦合结构, 最后开展了实验验证.
1)基于传递矩阵法和有限元数值计算方法, 建立了吸声系数理论解析与数值计算模型, 理论结果与数值结果符合良好. 设计的典型元胞及其并联结构均在小厚度条件下实现了目标频率的近完美吸声.
2)从简化等效模型参数、归一化声阻抗、复平面零极点分布、声压云图与质点速度场分布4个方面, 对内插缝Helmholtz共振腔吸声超结构的低频吸声机理进行阐释, 研究发现其吸声机理主要是内插缝壁面导致的声波热黏滞损耗.
3)采用差分进化优化算法, 开展了宽带优化设计. 设计了500 Hz以下具有多个完美吸声峰的并联耦合吸声超结构, 在厚度90 mm条件下, 实现了170—380 Hz范围内平均吸声系数达0.86, 归一化带宽达到78％的优异吸声效果.
4)制备了实验样件开展吸声测试, 实验结果与理论解析结果在关心频带范围内基本符合, 完成了理论解析、数值计算、实验3种方法的相互验证.
内插缝Helmholtz共振腔吸声超结构的机理分析与优化设计
Mechanism analysis and optimal design of sound-absorbing metastructure constructed by slit-embedded Helmholtz resonators
-
摘要: 低频噪声一直是噪声控制领域比较棘手的问题, 近年来吸声超结构的蓬勃发展为低频噪声控制提供了新理念. 本文提出了一种内插缝Helmholtz共振腔吸声超结构, 建立了其吸声特性计算的理论解析方法, 并与数值计算方法对比, 验证了解析方法的有效性. 随后, 从吸声曲线、简化等效模型、归一化声阻抗、声压云图与质点速度分布等多角度对吸声特性及吸声机理进行了深入分析. 进一步, 采用差分优化算法开展了多元胞并联耦合宽带优化设计, 优化后典型超结构实现了90 mm厚度下在170—380 Hz低频段内平均吸声系数达到0.86的优异吸声效果. 最后, 制备了若干样件, 开展吸声测试, 实验结果与理论结果符合良好, 验证了解析建模与优化设计方法的准确性. 本文提出的内插缝Helmholtz共振腔吸声超结构具有结构简单、低频吸声性能好, 且易于加工制造等特点, 在低频噪声控制领域具有广阔的应用前景.
-
关键词:
- 吸声超结构 /
- Helmholtz共鸣器 /
- 内插缝 /
- 低频吸声
Abstract:Low-frequency noise has always been a thorny problem in the field of noise control. In recent years, the development of sound-absorbing metastructures has provided new ideas for controlling low-frequency noise. In this work, we propose a low-frequency sound-absorbing metastructure constructed by Helmholtz resonators with embedded slit. Analytical and numerical models are established to analyze the sound absorption performance and mechanism of the proposed sound-absorbing metastructure, and optimization design is conducted to achieve low-frequency wideband absorption performance. The analytical modeling method and the performance of the proposed sound-absorbing metastructure are also experimentally verified. The main conclusions are summarized as follows. 1) By using transfer matrix method and finite element method, analytical and numerical models for calculating sound absorption coefficient are established. It is shown that analytical predictions are in good agreement with numerical calculations. It is demonstrated that a typical design of a 30-mm-thick single-cell metastructure can achieve a sound absorption coefficient of 0.88 at 404 Hz. Typical designs of two-cell parallel structure and the four-cell parallel structure (both with a thickness of 50 mm) can achieve two and four nearly perfect low-frequency sound absorption peaks in a frequency band of 200–400 Hz, respectively. 2) The low-frequency sound absorption mechanisms of the proposed metastructures are explained from four aspects: simplified equivalent model parameters, normalized acoustic impedance, complex-plane zero/pole distribution, and sound pressure cloud image and particle velocity field distribution. It is demonstrated that the main sound absorption mechanism is related to the thermal viscous loss of sound waves, caused by the inner wall of embedded slit. 3) The design for broadband low-frequency absorption performance is optimized by using differential evolution optimization algorithm. An optimized parallel-multi-cell coupled metastructure with multiple perfect sound absorption peaks below 500 Hz is realized. For a thickness of 90 mm, the sound absorption coefficient curve of an optimized metastructure exhibits 8 almost perfect sound absorption peaks and an average sound absorption coefficient of 0.86 in a frequency range of 170－380 Hz. 4) Experimental samples are fabricated to test sound absorption. Experimental results are basically consistent with the analytical predictions. The results from analytical model, numerical calculations and experimental measurements are mutually verified. In summary, the sound-absorbing metastructures with a thickness of sub-wavelength, proposed in this work, exhibit outstanding sound absorption performance at low frequencies. We demonstrate that they are suitable for low frequency broadband sound absorption below 500 Hz. Owing to their thin thickness and relatively simple construction, they have broad application prospects in practical noise control engineering. -
Key words:
- sound-absorbing metastructure /
- Helmholtz resonator /
- embedded slit /
- low frequency absorption .
-
-
图 1 内插缝Helmholtz共振吸声结构单元胞示意图
Figure 1. Schematic of single slit-embedded Helmholtz resonator.
图 2 矩形截面管道声传播示意图
Figure 2. Diagram of sound propagation in a rectangular section pipe.
图 4 有限元模型 (a) 三维狭窄声学模型; (b) 二维狭窄声学模型; (c) 二维热黏性声学模型
Figure 4. Finite element model: (a) Three-dimensional simulation model of narrow acoustic; (b) two-dimensional simulation model of narrow acoustic; (c) two-dimensional simulation model of thermoviscous acoustic.
图 7 吸声系数曲线 (a) 随缝宽的变化; (b) 随缝高的变化
Figure 7. Sound absorption coefficient curve: (a) Vary with width of slit; (b) vary with height of slit.
图 8 双元胞与四元胞并联示意图
Figure 8. Three-dimensional diagram of two cells and four cells in parallel.
图 9 吸声系数曲线 (a) 双元胞并联结构; (b) 四元胞并联结构
Figure 9. Sound absorption coefficient curve: (a) Two cells in parallel; (b) four cells in parallel.
图 10 吸声频谱 (a) 随缝宽的变化; (b) 随缝高的变化
Figure 10. Absorption spectrum: (a) Vary with width of slit; (b) vary with height of slit.
图 12 归一化声阻抗曲线 (a) 双元胞并联结构; (b) 四元胞并联结构
Figure 12. Normalized acoustic impedance curve: (a) Two cells in parallel; (b) four cells in parallel.
图 13 单元胞复平面反射系数与声压速度场分布
Figure 13. Zero-pole distribution of single cell on complex plane and distribution of sound pressure and velocity field.
图 14 反射系数在复平面的分布 (a) 双元胞结构; (b) 四元胞结构
Figure 14. Distribution of reflection coefficient log|r|2: (a) Two cells in parallel; (b) four cells in parallel.
图 15 声压及速度场分布 (a) 257 Hz; (b) 294 Hz; (c) 275 Hz
Figure 15. Sound pressure and velocity field distribution: (a) 257 Hz; (b) 294 Hz; (c) 275 Hz.
图 17 八元胞并联三维图(厚度90 mm)
Figure 17. Three-dimensional diagram of eight cells in parallel (thickness 90 mm).
图 18 吸声系数曲线及复平面零极点分布
Figure 18. Sound absorption coefficient curve and distribution of reflection coefficient log|r|2.
图 22 单元胞结构理论解析与实验测试吸声系数(样件1, 厚30 mm)
Figure 22. Comparison of theoretical and experimental sound absorption coefficient of single cell (Sample 1, thickness 30 mm).
图 25 多元胞并联理论解析与实验测试吸声系数(样件4, 厚90 mm)
Figure 25. Comparison of theoretical and experimental sound absorption coefficient of multiple cells in parallel (Sample 4, thickness 90 mm).
图 23 双元胞并联结构理论解析与实验测试吸声系数(样件2, 厚50 mm)
Figure 23. Comparison of theoretical and experimental sound absorption coefficient of two cells in parallel (Sample 2, thickness 50 mm).
图 24 四元胞并联结构理论解析与实验测试吸声系数(样件3, 厚50 mm)
Figure 24. Comparison of theoretical and experimental sound absorption coefficient of four cells in parallel (Sample 3, thickness 50 mm).
表 1 单个内插缝Helmholtz共振腔结构参数
Table 1. Structural parameters of single slit-embedded Helmholtz resonator.
长L/mm 宽D/mm 高H/mm 缝宽d/mm 缝高lr/mm 100 100 30 2 10 
下载: 导出CSV
表 2 双元胞并联结构参数
Table 2. Structural parameters of two cells in parallel.
长L/mm 宽D/mm 高H/mm 缝宽d1/mm 缝高lr1/mm 缝宽d2/mm 缝高lr2/mm 50 50 50 1.2 17.3 1.1 9.8
下载: 导出CSV
表 3 四元胞并联结构参数
Table 3. Structural parameters of four cells in parallel.
长L/mm 宽D/mm 高H/mm 缝宽d1/mm 缝高lr1/mm 缝宽d2/mm 缝高lr2/mm 缝宽d3/mm 缝高lr3/mm 缝宽d4/mm 缝高lr4/mm 50 50 50 2.7 42.3 1.7 17.9 1.3 8 1.3 4.7
下载: 导出CSV
表 4 多元胞并联结构参数
Table 4. Structural parameters of multivariate cells in parallel.
元胞 1 2 3 4 5 6 7 8 缝宽d/mm 1.5 1.4 1.7 1.4 1.1 1.2 1.1 1.5 缝高lr/mm 84 35.1 70.6 10.6 10.3 23.5 15.3 50.6
下载: 导出CSV
-
[1] Champoux Y, Allard J F 1991 J. Appl. Phys. 70 1975 doi: 10.1063/1.349482 [2] Panneton R 2007 J. Acoust. Soc. Am. 122 217 doi: 10.1121/1.2800895 [3] Trompette N, Barbry J, Sgard F, Nelisse H 2009 J. Acoust. Soc. Am. 125 31 doi: 10.1121/1.3003084 [4] Climente A, Torrent D, Sánchez-Dehesa J 2012 Appl. Phys. Lett. 100 144103 doi: 10.1063/1.3701611 [5] Ma G C, Sheng P 2016 Sci. Adv. 2 1501595 doi: 10.1126/sciadv.1501595 [6] 肖勇, 王洋, 赵宏刚, 郁殿龙, 温激鸿 2023 机械工程学报 59 277 doi: 10.3901/JME.2023.19.277 Xiao Y, Wang Y, Zhao H G, Yu D L, Wen J H 2023 J. Mech. Eng. 59 277 doi: 10.3901/JME.2023.19.277 [7] Cai X B, Guo Q Q, Hu G K, Yang J 2014 Appl. Phys. Lett. 105 121901 doi: 10.1063/1.4895617 [8] Wang Y, Zhao H G, Yang H B, Zhong J, Zhao D, Lu Z L, Wen J H 2018 J. Appl. Phys. 123 185109 doi: 10.1063/1.5026022 [9] Wu F, Xiao Y, Yu D, Zhao H, Wang Y, Wen J 2019 Appl. Phys. Lett. 114 151901 doi: 10.1063/1.5090355 [10] 吴飞, 黄威, 陈文渊, 肖勇, 郁殿龙, 温激鸿 2020 物理学报 69 134303 doi: 10.7498/aps.69.20200368 Wu F, Huang W, Chen W Y, Xiao Y, Yu D L, Wen J H 2020 Acta Phys. Sin. 69 134303 doi: 10.7498/aps.69.20200368 [11] Zhao H G, Wang Y, Yu D L, Yang H B, Zhong J, Wu F, Wen J H 2020 Compos. Struct. 239 111978 doi: 10.1016/j.compstruct.2020.111978 [12] Jin Y B, Yang Y L, Wen Z H, He L S, Cang Y, Yang B, Djafari-Rouhani B, Li Y, Li Y 2022 Int. J. Mech. Sci. 226 107396 doi: 10.1016/j.ijmecsci.2022.107396 [13] Liu C R, Yang Z R, Liu X L, Wu J H, Ma F Y 2023 APL Mater. 11 101122 doi: 10.1063/5.0174013 [14] 白宇, 张振方, 杨海滨, 蔡力, 郁殿龙 2023 物理学报 72 054301 doi: 10.7498/aps.72.20222011 Bai Y, Zhang Z F, Yang H B, Cai L, Yu D L 2023 Acta Phys. Sin. 72 054301 doi: 10.7498/aps.72.20222011 [15] Liu J W, Yu D L, Yang H B, Shen H J, Wen J H 2020 Chin. Phys. Lett. 37 34301 doi: 10.1088/0256-307X/37/3/034301 [16] Zhou Z L, Huang S B, Li D T, Zhu J, Li Y 2022 Natl. Sci. Rev. 9 171 doi: 10.1093/nsr/nwab171 [17] Almeida G D N, Vergara E F, Barbosa L R, Lenzi A, Birch R S 2021 Appl. Acoust. 183 108312 doi: 10.1016/j.apacoust.2021.108312 [18] Wu F, Ju Z G, Hu M, Zhang X, Li D, Liu K L 2023 J. Phys. D: Appl. Phys. 56 45401 doi: 10.1088/1361-6463/aca164 [19] Ma G C, Yang M, Xiao S W, Yang Z Y, Sheng P 2014 Nat. Mater. 13 873 doi: 10.1038/nmat3994 [20] Ge H, Yang M, Ma C, Lu M H, Chen Y F, Fang N, Sheng P 2018 Natl. Sci. Rev. 5 159 doi: 10.1093/nsr/nwx154 [21] Cummer S A, Christensen J, Alù A 2016 Nat. Rev. Mater. 1 16001 doi: 10.1038/natrevmats.2016.1 [22] Stinson M R 1991 J. Acoust. Soc. Am. 89 550 doi: 10.1121/1.400379 [23] Verdière K, Panneton R, Elkoun S D, Dupont T, Leclaire P 2013 J. Acoust. Soc. Am. 134 4648 doi: 10.1121/1.4824839 [24] Guo J W, Zhang X, Fang Y, Jiang Z Y 2021 Compos. Struct. 260 113538 doi: 10.1016/j.compstruct.2020.113538 [25] Tam C K W, Ju H, Jones M G, Watson W R, Parrott T L 2005 J. Sound Vib. 284 947 doi: 10.1016/j.jsv.2004.07.013 [26] Zieliński T G, Chevillotte F, Deckers E 2019 Appl. Acoust. 146 261 doi: 10.1016/j.apacoust.2018.11.026 [27] 杜功焕, 朱哲民, 龚秀芬 2012 声学基础(南京: 南京大学出版社)第159页 Du G H, Zhu Z M, Gong X F 2012 Acoustics Foundation (Nanjing: Nanjing University Press) p159 [28] Romero-García V, Theocharis G, Richoux O, Merkel A, Tournat V, Pagneux V 2016 Sci. Rep. 6 19519 doi: 10.1038/srep19519 [29] Lee F C, Chen W H 2001 J. Sound Vib. 248 621 doi: 10.1006/jsvi.2001.3825 [30] Liu J, Herrin D W 2010 Appl. Acoust. 71 120 doi: 10.1016/j.apacoust.2009.07.016 [31] Ruiz H, Claeys C C, Deckers E, Desmet W 2016 Mech. Syst. Signal Pr. 70 904 [32] Romero-García V, Sánchez-Pérez J V, Garcia-Raffi L M 2011 J. Appl. Phys. 110 14904 doi: 10.1063/1.3599886 [33] Qamoshi K, Rasuli R 2016 Appl. Phys. A 122 788 doi: 10.1007/s00339-016-0332-0 [34] Storn R, Price K 1997 J. Global Optim. 11 341 doi: 10.1023/A:1008202821328 -
计量
- 文章访问数: 314
- HTML全文浏览数: 314
- PDF下载数: 5
- 施引文献: 0