高级搜索

雷暴电场对LHAASO观测面宇宙线次级光子的影响

,  , 

downloadPDF

上一篇

下一篇

阿西克古, 周勋秀, 张云峰. 雷暴电场对LHAASO观测面宇宙线次级光子的影响[J]. 物理学报, 2024, 73(12): 129201-1. doi: 10.7498/aps.73.20240341
引用本文: 阿西克古, 周勋秀, 张云峰. 雷暴电场对LHAASO观测面宇宙线次级光子的影响[J]. 物理学报, 2024, 73(12): 129201-1. doi: 10.7498/aps.73.20240341
shu
Axikegu, Xun-Xiu Zhou, Yun-Feng Zhang. Effects of thunderstorms electric field on secondary photons of cosmic ray at large high altitude air shower observatory[J]. Acta Physica Sinica, 2024, 73(12): 129201-1. doi: 10.7498/aps.73.20240341
Citation: Axikegu, Xun-Xiu Zhou, Yun-Feng Zhang. Effects of thunderstorms electric field on secondary photons of cosmic ray at large high altitude air shower observatory[J]. Acta Physica Sinica, 2024, 73(12): 129201-1. doi: 10.7498/aps.73.20240341
shu

雷暴电场对LHAASO观测面宇宙线次级光子的影响

  • 1.

    攀枝花学院电气信息工程学院, 攀枝花　617000

  • 2.

    西南交通大学物理科学与技术学院, 成都　610031

  • 3.

    成都师范学院物理与工程技术学院, 成都　611130

    • 通讯作者: E-mail: axkg@my.swjtu.edu.cn.; 

  • 中图分类号: 92.60.Pw, 92.60.Ta, 52.80.Mg

Effects of thunderstorms electric field on secondary photons of cosmic ray at large high altitude air shower observatory

  • 1.

    School of Electrical and Information Engineering, Panzhihua University, Panzhihua 617000, China

  • 2.

    School of Physical Science and Technology, Southwest Jiaotong University, Chengdu 610031, China

  • 3.

    School of Physics and Engineering Technology, Chengdu Normal College, Chengdu 611130, China

    • Corresponding author: E-mail: axkg@my.swjtu.edu.cn.; 

  • MSC: 92.60.Pw, 92.60.Ta, 52.80.Mg

  • 摘要: LHAASO实验利用到达探测器的宇宙线次级粒子来获取原初宇宙线信息, 而次级粒子中成分最多的是光子. 雷暴期间, 大气电场会影响次级带电粒子, 进而改变地面光子信息. 本文利用Monte Carlo方法, 模拟研究了近地雷暴电场对LHAASO观测面次级光子的影响. 模拟中使用了一个厚度均匀、方向垂直于地面的电场模型. 结果表明, 雷暴电场中光子的数目和能量变化显著, 且依赖于电场强度. 当电场为–1000 V/cm时, 光子数目增加23%, 能谱变软, 当能量小于2 MeV时, 数目增加超过29%. 当电场为–1700 V/cm时, 光子数目呈指数增长, 达到279%, 能谱相较于–1000 V/cm变得更软, 当能量小于2 MeV时, 数目增加超过361%, 符合相对论电子逃逸雪崩机理. 这些变化主要源于电子被大气电场加速, 数目增加(–1000 V/cm中增加65%, –17000 V/cm中增加992%), 能谱变软. 同时, 高能自由电子通过轫致辐射产生光子, 导致光子的数目和能量也发生变化, 且变化趋势与电子的一致. 本模拟结果有助于理解雷暴期间LHAASO实验数据变化特点, 并为大气电场加速宇宙线次级带电粒子的物理机制提供信息.
    Abstract: Large high altitude air shower observatory (LHAASO) is a complex of extensive air shower (EAS) detector arrays, located on the Mt. Haizi (29°21' N, 100°08' E) at an altitude of 4410 m a. s. l., Daocheng, Sichuan Province, China. The information about primary cosmic rays can be obtained by using data from secondary particles measured at LHAASO, with photons make up the majority among these secondary particles. During thunderstorms, the atmospheric electric field can affect secondary charged particles (mainly positrons and electrons), thus changing the information of photons on the ground. In this work, Monte Carlo simulations are performed to investigate the effects of near-ground thunderstorm electric fields on cosmic ray secondary photons at LHAASO. A simple model with a vertical and uniform atmospheric electric field in a layer of atmosphere is used in our simulations. During thunderstorms, the number and energy of photons are found to significantly change and strongly depend on the electric field strength. In a field of –1000 V/cm (below the threshold of the relativistic runaway electron avalanche (RREA) process), the number of photons is increased by 23%. Also, the spectrum of photons softens, and the increased number of photons with energy less than 2 MeV exceeds 29%. In an electric field of –1700 V/cm (above the threshold of the RREA process), the number of photons experiences exponential growth, with an increase of 279%. The spectrum of photons becomes softer than that at –1000 V/cm, and the increased number with energy less than 2 MeV is more than 361%. It is consistent with the theory of RREA. For these phenomena of photons at LHAASO, the main factor is that the number of positrons and electrons are increased due to the acceleration of negative electric field on electrons, with increase of 65% in –1000 V/cm and 992% in –1700 V/cm, and the spectrum of positrons and electrons soften. Newborn free positrons/electrons may undergo bremsstrahlung and deposit part of their energy into photons, causing the change of number and energy of photons to follow roughly the same pattern as positrons and electrons. The simulation results can provide the information for understanding the variations of the data detected by LHAASO during thunderstorms and the acceleration mechanisms of secondary charged particles caused by an atmospheric electric field.
  • 加载中

  • 图 1  不加电场时光子和电子的数目(a)和比值(b)随大气深度的变化

    Figure 1.  The number of photons and electrons/positrons (a) and their ratios (b) as a function of atmospheric depth in absence of a field.

    下载: 全尺寸图片 幻灯片

    图 2  在–1700 V/cm的电场中, 电子和光子的数目随大气深度的变化(电场面积: 524—599 g/cm2)

    Figure 2.  The number of electrons/positrons and photons as a function of atmospheric depth in a field of –1700 V/cm (electric field area: 524–599 g/cm2).

    下载: 全尺寸图片 幻灯片

    图 3  在–1700 V/cm的电场中, 电子和光子的数目变化百分比随大气深度的变化(电场面积: 524—599 g/cm2)

    Figure 3.  Percent change of electrons/positrons and photons as a function of atmospheric depth in a field of –1700 V/cm (electric field area: 524–599 g/cm2).

    下载: 全尺寸图片 幻灯片

    图 4  在–1000 V/cm的电场中, 电子和光子的数目随大气深度的变化(电场面积: 524—599 g/cm2)

    Figure 4.  The number of electrons/positrons and photons as a function of atmospheric depth in a field of –1000 V/cm (electric field area: 524–599 g/cm2).

    下载: 全尺寸图片 幻灯片

    图 5  在–1000 V/cm的电场中, 电子和光子数目的变化(a)及变化百分比(b)随大气深度的变化(电场面积: 524—599 g/cm2)

    Figure 5.  Change (a) and percent change (b) of electrons/positrons and photons number as a function of atmospheric depth in a field of –1000 V/cm (electric field area: 524–599 g/cm2).

    下载: 全尺寸图片 幻灯片

    图 6  (a)不加电场时电子和光子数目随能量的变化; (b)归一化后的结果

    Figure 6.  The number (a) and normalized number (b) of electrons/positrons and photons as a function of energy in absence of a field.

    下载: 全尺寸图片 幻灯片

    图 7  (a)不同电场中电子和光子数目随能量的分布; (b) –1700 V/cm的电场中, 能量低于m的新增电子和光子数目与新增总电子和总光子数目之比随能量的变化

    Figure 7.  (a) The number of electrons/positrons and photons as a function of energy in absence of a field and in a field of –1700 V/cm; (b) the ratios of increasing number with energy less than m to total number as a function of energy in a field of –1700 V/cm.

    下载: 全尺寸图片 幻灯片

    图 8  在–1700 V/cm的电场中, 电子和光子的数目变化百分比随能量的变化

    Figure 8.  Percent change of electrons/positrons and photons as a function of energy in a field of –1700 V/cm.

    下载: 全尺寸图片 幻灯片

    图 9  不同电场中电子和光子数目随能量的分布

    Figure 9.  The number of electrons/positrons and photons as a function of energy in absence of a field and in a field of –1000 V/cm.

    下载: 全尺寸图片 幻灯片

    图 10  在–1000 V/cm电场中, 电子和光子数目变化百分比随能量的变化

    Figure 10.  Percent change of electrons/positrons and photons as a function of energy in a field of –1000 V/cm.

    下载: 全尺寸图片 幻灯片

    图 11  在–1000 V/cm电场中, 电子和光子数目积分变化百分比随能量的变化

    Figure 11.  Integral percent change of electrons/positrons and photons as a function of energy in a field of –1000 V/cm.

    下载: 全尺寸图片 幻灯片
  • [1] Qie X S, Yuan S F, Chen Z X, et al. 2021 Sci. China Earth Sci. 64 10 doi: 10.1007/s11430-020-9656-8
    [2] 刘冬霞, 郄秀书, 王志超, 吴学珂, 潘伦湘 2013 物理学报 62 219201 doi: 10.7498/aps.62.219201 Liu D X, Qie X S, Wang Z C, Wu X K, Pan L X 2013 Acta Phys. Sin. 62 219201 doi: 10.7498/aps.62.219201
    [3] 周勋秀, 王新建, 黄代绘, 贾焕玉, 吴超勇 2015 物理学报 64 149202 doi: 10.7498/aps.64.149202 Zhou X X, Wang X J, Huang D H, Jia H Y, Wu C Y 2015 Acta Phys. Sin. 64 149202 doi: 10.7498/aps.64.149202
    [4] Tsuchiya H, Enoto T, Torii T, et al. 2009 Phys. Rev. Lett. 102 255003 doi: 10.1103/PhysRevLett.102.255003
    [5] Hariharan B, Chandra A, Dugad S R, et al. 2019 Phys. Rev. Lett. 122 105101 doi: 10.1103/PhysRevLett.122.105101
    [6] Wilson C T R 1924 Proc. Phys. Soc. London 37 32D doi: 10.1088/1478-7814/37/1/314
    [7] Gurevich A V, Milikh G M 1992 Phys. Lett. A 165 463 doi: 10.1016/0375-9601(92)90348-P
    [8] Dwyer J R 2003 Res. Lett. 30 2055 doi: 10.1029/2003GL017781
    [9] Symbalisty E M D, Roussel-Dupre R A, Yukhimuk V A 1998 IEEE Trans. Plasma Sci. 26 1575 doi: 10.1109/27.736065
    [10] Alexeenko V V, Chernyaev A B, Chudakov A E, et a1. 1985 Proceeding of 19th International Cosmic Ray Conference. (La Jolla. USA: International Union of Pure and Applied Physics) pp352−355
    [11] Alexeenko V V, Khaerdinov N S, Lidvansky A S, Petkov V B 2002 Phys. Lett. A 301 299 doi: 10.1016/S0375-9601(02)00981-7
    [12] Bartoli B, Bernardini P, Bi X J, et al. 2018 Phys. Rev. D 97 042001 doi: 10.1103/PhysRevD.97.042001
    [13] Xu B, Bie Y G, Zhou D 2012 Chin. J. Space Sci. 32 501 (in Chinses) [徐斌, 别业广, 邹丹 2012 空间科学学报 32 501] doi: 10.11728/cjss2012.04.501 Xu B, Bie Y G, Zhou D 2012 Chin. J. Space Sci. 32 501 (in Chinses) doi: 10.11728/cjss2012.04.501
    [14] Chilingarian A, Mailyan B, Vanyan L 2012 Atmos. Res. 114-115 1 doi: 10.1016/j.atmosres.2012.05.008
    [15] Lindy N C, Benton E R, Beasley W H, et al. 2018 J. Atmos. Solar-Terr. Phys. 179 435 doi: 10.1016/j.jastp.2018.10.003
    [16] Yan R R, Huang D H, Zhao B, Axi K G, Zhou X X 2020 Chin. Astron. Astr. 44 146 doi: 10.1016/j.chinastron.2020.05.002
    [17] He H H, Zhang Y 2003 HEPNP 27 1106 (in Chinses) [何会海, 张勇 2003 高能物理与核物理 27 1106] doi: 10.3321/j.issn:0254-3052.2003.12.012 He H H, Zhang Y 2003 HEPNP 27 1106 (in Chinses) doi: 10.3321/j.issn:0254-3052.2003.12.012
    [18] Axikegu, Bartoli B, Bernardini P, et al. 2022 Phys. Rev. D 106 022008 doi: 10.1103/PhysRevD.106.022008
    [19] Grieder P K F 2010 Extensive Air Showers (Berlin: Springer
    [20] Fishman G F, Bhat P N, Mallozzi R, et al. 1994 Science 264 1313 doi: 10.1126/science.264.5163.1313
    [21] Smith D M, Lopez L I, Lin R P, et al. 2005 Science 307 1085 doi: 10.1126/science.1107466
    [22] Briggs M S, Fishman G J, Connaughton V, et al. 2010 J. Geophys. Res. 115 A07323 doi: 10.1029/2009JA015242
    [23] Tavani M, Marisaldi M, Labanti C, et al. 2011 Phys. Rev. Lett. 106 018501 doi: 10.1103/PhysRevLett.106.018501
    [24] Neubert T, Østgaard N, Reglero V, et al. 2020 Science 367 183 doi: 10.1126/science.aax3872
    [25] Yoshida S, Morimoto T, Ushio T, et al. 2008 Geophys. Res. Lett. 35 L10804 doi: 10.1029/2007GL032438
    [26] Abbasi R U, Abu-Zayyad T, Allen M, et al. 2018 J. Geophys. Res. Atmos. 123 6864 doi: 10.1029/2017JD027931
    [27] Wada Y, Enoto T, Nakazawa K, et al. 2019 Phys. Rev. Lett. 123 061103 doi: 10.1103/PhysRevLett.123.061103
    [28] Köhn C, Diniz G, Harakeh M N 2017 J. Geophys. Res. Atmos. 122 1365 doi: 10.1002/2016JD025445
    [29] McCarthy M P, Parks G K 1985 Geophys. Res. Lett. 12 393 doi: 10.1029/GL012i006p00393
    [30] Eack K B, Beasley W H, David R W, et al. 1996 J. Geophys. Res. 101 29637 doi: 10.1029/96JD01705
    [31] Chilingarian A, Daryan A, Arakelyan A K, et al. 2021 Phys. Rev. D 82 043009 doi: 10.1103/PhysRevD.82.043009
    [32] Torii T, Sugita T, Tanabe S, et al. 2009 Geophys. Res. Lett. 36 L13804 doi: 10.1029/2008GL037105
    [33] Torii T, Takeishi M, Hosono T 2002 J. Geophys. Res. 107 4324 doi: 10.1029/2001JD000938
    [34] Tsuchiya H, Enoto T, Yamada S, et al. 2007 Phys. Rev. Lett. 99 165002 doi: 10.1103/PhysRevLett.99.165002
    [35] Aharonian F, An Q, Axikegu, et al. 2023 Chin. Phys. C 47 015001 doi: 10.1088/1674-1137/ac9371
    [36] Cao Z, Aharonian F, An Q, et al. 2021 Science 373 425 doi: 10.1126/science.abg5137
    [37] Ma X H, Bi Y J, Chao Z, et al. 2022 Chin. Phys. C 46 030001 doi: 10.1088/1674-1137/ac3fa6
    [38] 陈松战, 赵静, 刘烨, 等 2017 核电子学与探测技术 37 1101 doi: 10.3969/j.issn.0258-0934.2017.11.009 Chen S Z, Zhan J, Liu Y, et al. 2017 Nucl. Electron. Detect. Technol. 37 1101 doi: 10.3969/j.issn.0258-0934.2017.11.009
    [39] Aharonian F, An Q, Axikegu, et al. 2021 Chin. Phys. C 45 085002 doi: 10.1088/1674-1137/ac041b
    [40] Heck D, Knapp J, Capdevielle J N, et al. 1998 CORSIKA: A Monte Carlo Code to Simulate Extensive Air Showers Wissenschaftliche Berichte, FZKA-6019
    [41] 周勋秀, 王新建, 黄代绘, 贾焕玉 2016 空间科学学报 36 49 doi: 10.11728/cjss2016.01.049 Zhou X X, Wang X J, Huang D H, Jia H Y 2016 Chin. J. Space Sci. 36 49 doi: 10.11728/cjss2016.01.049
    [42] NOAA national centers for environmental information, Magnetic Field Calculators: IGRF model 562 (1590-2024) https://www.ngdc.noaa.gov/geomag/calculators/magcalc.shtml#igrfwmm
    [43] Marshall T C, Stolzenburg M, Maggio C R, et al. 2005 Geophys. Res. Lett. 32 L03813 doi: 10.1029/2004GL021802
    [44] Chilingarian A, Hovsepyan G, Soghomonyan S, Zazyan M, Zelenyy M 2018 Phys. Rev. D 98 082001 doi: 10.1103/PhysRevD.98.082001
    [45] Axi K G, Zhou X X, Huang Z C, et al. 2022 Astrophys. Space Sci. 367 30 doi: 10.1007/s10509-022-04056-3
    [46] Chum J, Langer R, Baše J, et al. 2020 Earth Planets Space 72 28 doi: 10.1186/s40623-020-01155-9
    [47] Michimoto K J 1993 Atmos. Electr. 13 33 doi: 10.1541/jae.13.33
    [48] Dorman L I, Dorman I V, Iucci N, et al. 2003 J. Geophys. Res. 108 1181 doi: 10.1029/2002JA009533
    [49] Bethe H A 1930 Annalen Phys. 5 325 doi: 10.1142/9789812795755_0003
    [50] Buitink S, Huege T, Falcke H, Heck D, Kuijpers J 2010 Astropart. Phys. 33 1 doi: 10.1016/j.astropartphys.2009.10.006
  • 加载中
图( 11)
计量
  • 文章访问数:  182
  • HTML全文浏览数:  182
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-03-09
  • 刊出日期:  2024-06-20

雷暴电场对LHAASO观测面宇宙线次级光子的影响

    通讯作者: E-mail: axkg@my.swjtu.edu.cn.; 
  • 1. 攀枝花学院电气信息工程学院, 攀枝花　617000
  • 2. 西南交通大学物理科学与技术学院, 成都　610031
  • 3. 成都师范学院物理与工程技术学院, 成都　611130
  • 收稿日期:  2024-03-09

摘要: LHAASO实验利用到达探测器的宇宙线次级粒子来获取原初宇宙线信息, 而次级粒子中成分最多的是光子. 雷暴期间, 大气电场会影响次级带电粒子, 进而改变地面光子信息. 本文利用Monte Carlo方法, 模拟研究了近地雷暴电场对LHAASO观测面次级光子的影响. 模拟中使用了一个厚度均匀、方向垂直于地面的电场模型. 结果表明, 雷暴电场中光子的数目和能量变化显著, 且依赖于电场强度. 当电场为–1000 V/cm时, 光子数目增加23%, 能谱变软, 当能量小于2 MeV时, 数目增加超过29%. 当电场为–1700 V/cm时, 光子数目呈指数增长, 达到279%, 能谱相较于–1000 V/cm变得更软, 当能量小于2 MeV时, 数目增加超过361%, 符合相对论电子逃逸雪崩机理. 这些变化主要源于电子被大气电场加速, 数目增加(–1000 V/cm中增加65%, –17000 V/cm中增加992%), 能谱变软. 同时, 高能自由电子通过轫致辐射产生光子, 导致光子的数目和能量也发生变化, 且变化趋势与电子的一致. 本模拟结果有助于理解雷暴期间LHAASO实验数据变化特点, 并为大气电场加速宇宙线次级带电粒子的物理机制提供信息.

English Abstract

    全文HTML

    1.   引　言

    • 雷暴是一种局地对流性天气, 常伴随着闪电、冰雹、强风、暴雨等灾害性天气现象[1, 2], 持续时间长达几个小时[3]. 雷暴期间, 大气电场强度可以达到1000 V/cm[4]或更高[5], 如此强的电场对宇宙线次级带电粒子的影响是不可忽略的. Wilson[6]于1924年首次提出“逃逸电子”的概念, 认为雷暴云中的强电场可以把宇宙线次级粒子中质量很小的电子加速到很高的能量. 1992年, Gurevich和Milikh[7]提出了相对论逃逸电子雪崩机理(relativistic runaway electron avalanche, RREA), 认为能量约1 MeV 的宇宙线次级电子在雷暴电场中被加速, 当获得足够高的能量时, 会使空气分子电离产生新的自由电子, 新产生的自由电子又被雷暴电场加速, 如此往复, 从而引发雪崩效应, 使电子数目呈指数增长. Dwyer[8]和Symbalisty等[9]对引发RREA机制所需的逃逸阈值电场(ERB)进行了深入研究, 发现ERB跟海拔有关, 其表达式为

      其中Z是海拔高度(km); Eth-RB是海平面处的逃逸阈值电场, 约为2800 V/cm. 由(1)式可知, 当海拔Z = 4400 m时, 逃逸阈值电场ERB ≈ 1660 V/cm. 这意味着在高海拔地区必须有一个足够强的电场, 才能保障雪崩效应的发生.

      Alexeenko等通过分析Baksan中微子观测站实验数据, 于1985年首次发现雷暴期间地面宇宙线强度变化与大气电场有关[10], 并于2002给出宇宙线次级粒子中软成分电子的强度在电场中增加或下降[11]. Bartoli等[12]和徐斌等[13]通过分析ARGO-YBJ实验(只记录电磁粒子)单粒子模式下的雷暴事例, 发现地面宇宙线计数率在正电场中增加, 在负电场中下降, 变化幅度与大气电场强度和多重数有关. Chilingarian等[14]利用ASEC实验数据, 研究了雷暴期间地面宇宙线突然增强事件(thunderstorm ground event, TGE)的能谱分布, 发现雷暴期间电子的能谱变软. Lindy等[15]和Yan等[16]通过Monte Carlo模拟得出电场对不同能段电子的影响不同, 低能段电子数目增加明显, 而高能段则增加不明显.

      ARGO-YBJ探测器[17]只对带电粒子敏感, 雷暴期间大气电场直接作用于次级带电粒子(主要是电子), 使其到达探测面时的能量、数目、位置等信息发生改变, 从而影响探测器的触发率. Axikegu等[18]通过分析ARGO-YBJ实验Shower模式下的20个雷暴事例, 得到雷暴期间Shower事例率出现百分之几的变化, 且依赖于电场的强度、极性以及原初天顶角. 通过模拟研究, 发现这些现象是由大气电场对电子的加速/减速和偏转效应导致的. 文献[19]研究表明, 光子可以通过轫致辐射、电子对湮灭、切伦科夫辐射、自发辐射等方式产生. 雷暴期间, 宇宙线次级带电粒子(主要是正、负电子)受大气电场的加速/减速作用, 其数目、能量等信息会发生改变, 从而影响观测面上次级光子的信息.

      1994年, Fishman等[20]利用BATSE卫星实验首次观测到来自地球大气层、持续时间为几十至几百微秒的γ射线爆(thunderstorm ground flash, TGF). 他们发现这些TGF的能谱都比较硬, 能量可延伸至几十兆电子伏特(MeV). 这一特征与 由MeV量级电子产生的轫致辐射光谱一致, 于是他们推测TGF是由上层雷暴云中闪电先导尖端 放电引起的现象. 之后又有多个卫星实验相继称 探测到了来自地球大气层、且与闪电关联密切的 TGF[21-25]. 近些年来, 科学家们利用地面宇宙线实验观测到了云地间闪电放电过程中产生的γ射线爆, 称之为下行TGF[26-28]. 它们与普通的TGF相似, 持续时间极短, 为亚毫秒量级, 并伴有闪电. 有趣的是, 一些地面实验还观测到与雷暴云有关, 但持续时间为秒或分的γ射线辐射[29-34]. 显然, 这样的辐射不可能是由闪电引起, 反而更像是强雷暴电场造成的. 根据Gurevich的理论推算, 高能电子被强雷暴电场持续加速后会发生相对论逃逸电子雪崩, 进而引发X射线爆发[7]. 那么, 导致地面实验探测到雷暴期间γ射线持续增强的物理机制到底是什么? 雷暴云中产生的轫致辐射光子能否被高山实验探测到呢?

      高海拔宇宙线观测站LHAASO实验[35, 36]位于四川省稻城县海子山, 海拔约4410 m, 由WFCTA, KM2A和WCDA 这3个子阵列组成. 其中, WFCTA只能在晴朗且无月光的夜晚进行探测, KM2A中的MD只记录缪子信息[37]. 而对于KM2A中的ED[38], 当次级光子穿过铅锑板时, 会被转化为正、负电子对, 这些转化来的电子和大气簇射中原有的电子在穿过闪烁体时产生大量荧光, 并被PMT收集. 同样, 次级光子进入WDCA水池后也产生正、负电子对, 并与大气簇射中原有的电子一起转化为切伦科夫光被水中的PMT接收, 从而实现对电磁粒子的探测[39]. 可见, WCDA和KM2A中的ED对电子和光子都敏感, 然而它们却难以区分探测信号类型, 因此无法直接利用LHAASO实验观测数据来研究雷暴电场对宇宙线次级光子的影响. 为此, 本文采用Monte Carlo方法, 利用国际通用的模拟广延大气簇射软件包CORSIKA(cosmic ray simulations for kascade)[40], 模拟研究近地雷暴电场对LHAASO观测站宇宙线次级光子强度和能量的影响.

    2.   模拟参数设置

    • 本文使用的模拟广延大气簇射软件包是CORSIKA7.7410, 高能(>80 GeV)强相互作用模型采用QGSJETII-04, 低能(<80 GeV)相互作用模型为GHEISHA. 描述电子行为的是电磁级联EGS4中的子程序ELECTR, 模拟时, 在子程序中加入电场模型[41]. 研究表明, 原初宇宙线主要成分是质子, 其次是α粒子, 以及少量的电子、γ射线等. 本文以质子为例进行模拟研究, 选取的原初 能量范围为100 GeV—1 PeV(能谱指数为–2.7), 天顶角范围为0°—60°. 考虑到电场的加速作用, 模拟中电子和光子的截断能量为模拟程序所能追踪的最小能量, 即50 keV. 根据LHAASO观测站的海拔高度和经纬度(29.35°N, 100.13°E), 计算得到该站址地磁场水平分量Bx = 34.6 μT和垂直分量Bz = 35.9 μT [42].

      模拟中, 取雷暴电场的典型厚度, 1000 m[7,43,44], 在海拔4400—5400 m (对应的大气深度599—524 g/cm2)的空间范围内添加均匀且垂直于地面的大气电场. 与实际观测相比, 保持电场值不变可能会带来一定的偏差, 但这样可以更好地理解电场效应[12,45]. 由(1)式可知, 当海拔Z = 5400 m时, 逃逸阈值电场ERB ≈ 1470 V/cm. 为了研究不同强度的雷暴电场对地面宇宙线实验观测的影响, 模拟中选取两种典型的雷暴电场强度, 即–1000 V/cm(低于逃逸阈值电场)和–1700 V/cm(高于逃逸阈值电场), 本文以雷暴云电场方向指向地面为正方向.

    3.   模拟结果与讨论

    • 雷暴期间, 大气电场直接作用于宇宙线次级带电粒子(主要是正、负电子), 使其数目、能量等信息发生变化[18,35]. 由于带电粒子可以通过轫致辐射等方式产生光子, 因而雷暴电场对宇宙线次级光子也有一个间接的影响. 为此, 本文模拟研究了雷暴电场对宇宙线次级光子的影响. 为了更好理解雷暴期间光子数目和能量的变化, 本文还分析了雷暴电场对次级负电子和正电子(下文简称次级电子)的影响.

      • 3.1.   雷暴电场对光子强度的影响

      3.1.1.   不加电场时的模拟结果.

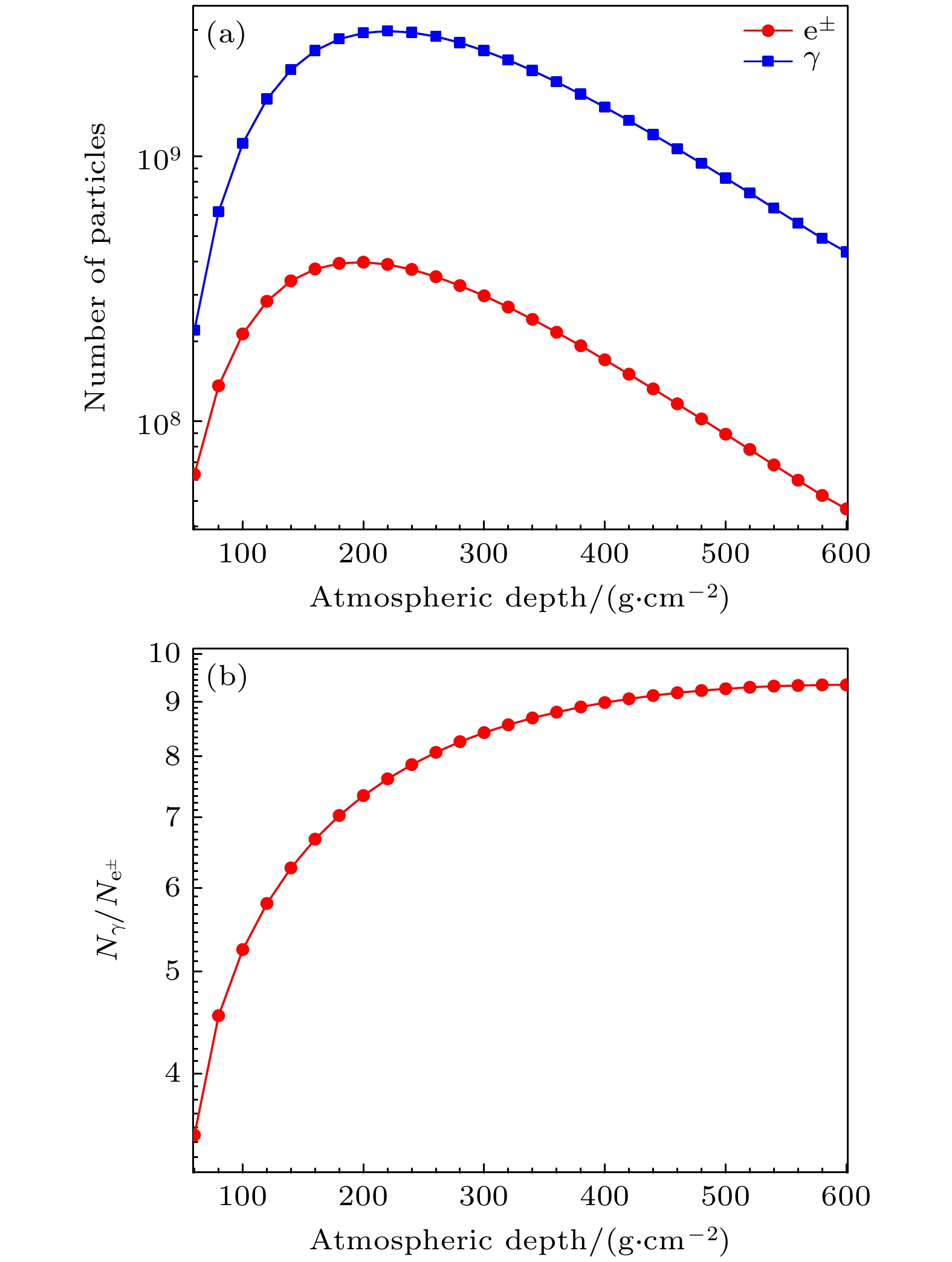
    • 图1(a)是原初能量为100 GeV—1 PeV的质子在大气簇射中产生的次级电子和光子数目随大气深度的变化. 可以看出, 在大气簇射过程中, 电子和光子的数目随大气深度的变化规律一致, 但它们的数目却相差甚远, 光子的数目远远超过电子的数目. 图1(b)展示了次级电子和光子数目的比值随大气深度的变化. 可以看出其比值随大气深度的增大而增大, 当大气深度超过500 g/cm2之后, 比值几乎不再增大, 保持在9.3左右. 可见, 对于地面宇宙线实验而言, 探测到的宇宙线次级粒子主要是光子, 因此, 研究雷暴期间光子的数目变化对把握LHAASO实验数据质量及后期的物理分析尤为重要.

      • 3.1.2.   电场强度为1700 V/cm(大于逃逸阈值电场)的模拟结果

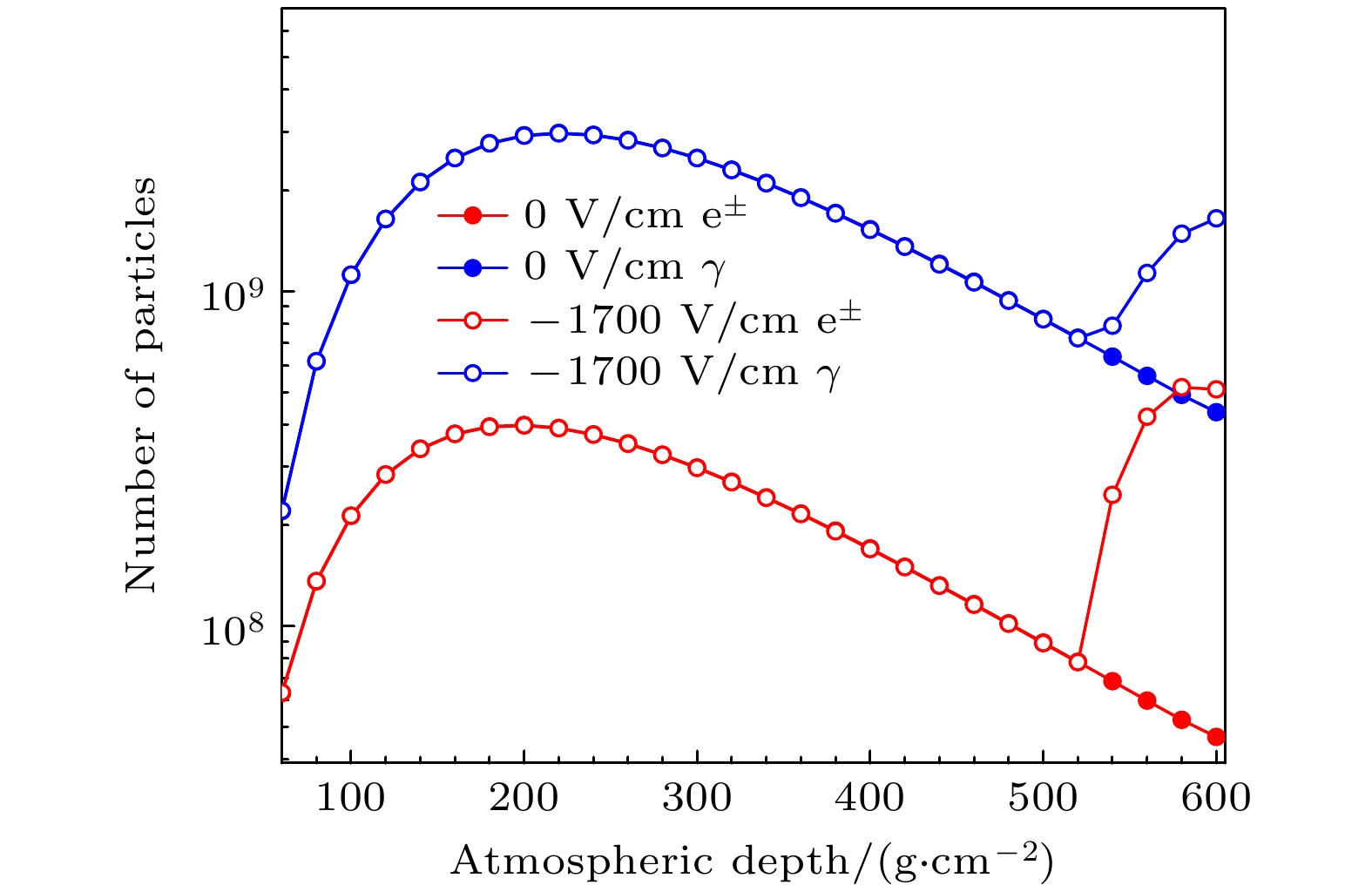
    • 图2展示了在–1700 V/cm的电场中电子和光子的数目随大气深度的变化(为了比较, 图中包含了不加电场时的模拟结果). 可以看到, 电子和光子在进入电场后, 数目呈指数增长. 当大气深度达到600 g/cm2时, 电子的数目为5.1×108, 光子的数目为1.7×109. 通过计算发现, 此时电子和光子的数目分别是不加电场时的10.9倍和3.8倍.

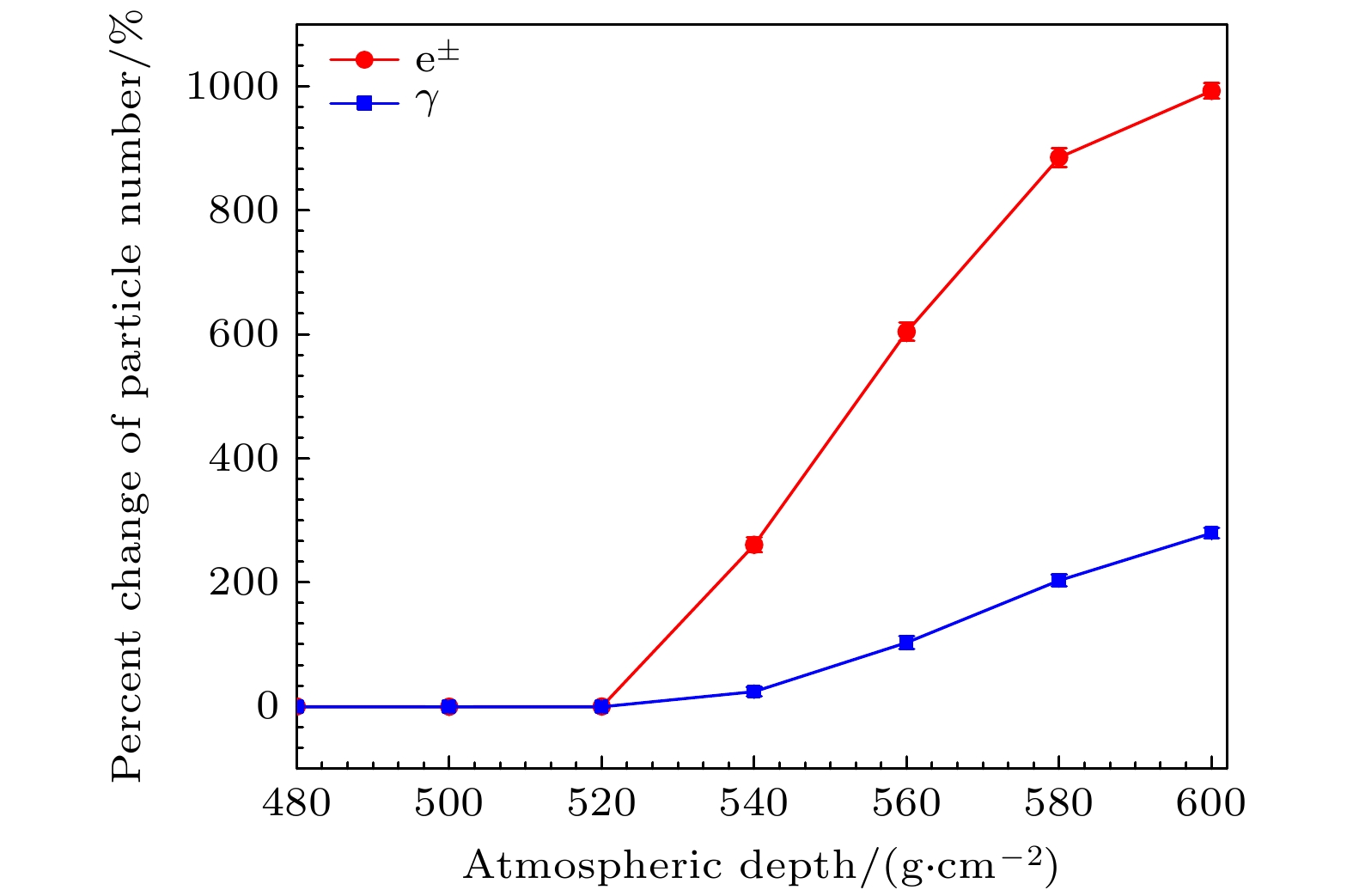
      为了清楚看到次级粒子在电场中的变化情况, 本文计算了电子和光子的数目变化百分比, 其表达式为

      式中, N和N0分别是加电场和不加电场时的次级粒子数目, 结果如图3所示. 从图3可以看到, 在–1700 V/cm的电场中, 电子和光子的数目变化非常显著, 且规律一致, 均随着大气深度的增大而增大. 当大气深度约为600 g/cm2时, 电子和光子的数目增加幅度分别达到992%和279%.

      在电场为–1700 V/cm(高于逃逸阈值电场)的区域内, 宇宙线次级电子被加速获得能量后会与空气分子碰撞, 电离出高能自由电子, 这些电子又被电场加速, 从而引发雪崩效应, 电子数目呈指数增长. 与此同时, 新产生的高能自由电子会通过轫致辐射产生能量较低的光子, 这些光子如果能量足够高, 反过来也会产生电子, 其表达式为: γ + (Z, A) → e± + (Z, A), 如此往复, 形成类似于广延大气簇射的电子-光子簇射, 使得光子数目也呈指数增加, 且变化规律与电子高度一致, 符合RREA机理[7]和Dwyer理论[8].

      • 3.1.3.   电场强度为1000 V/cm(小于逃逸阈值电场)的模拟结果

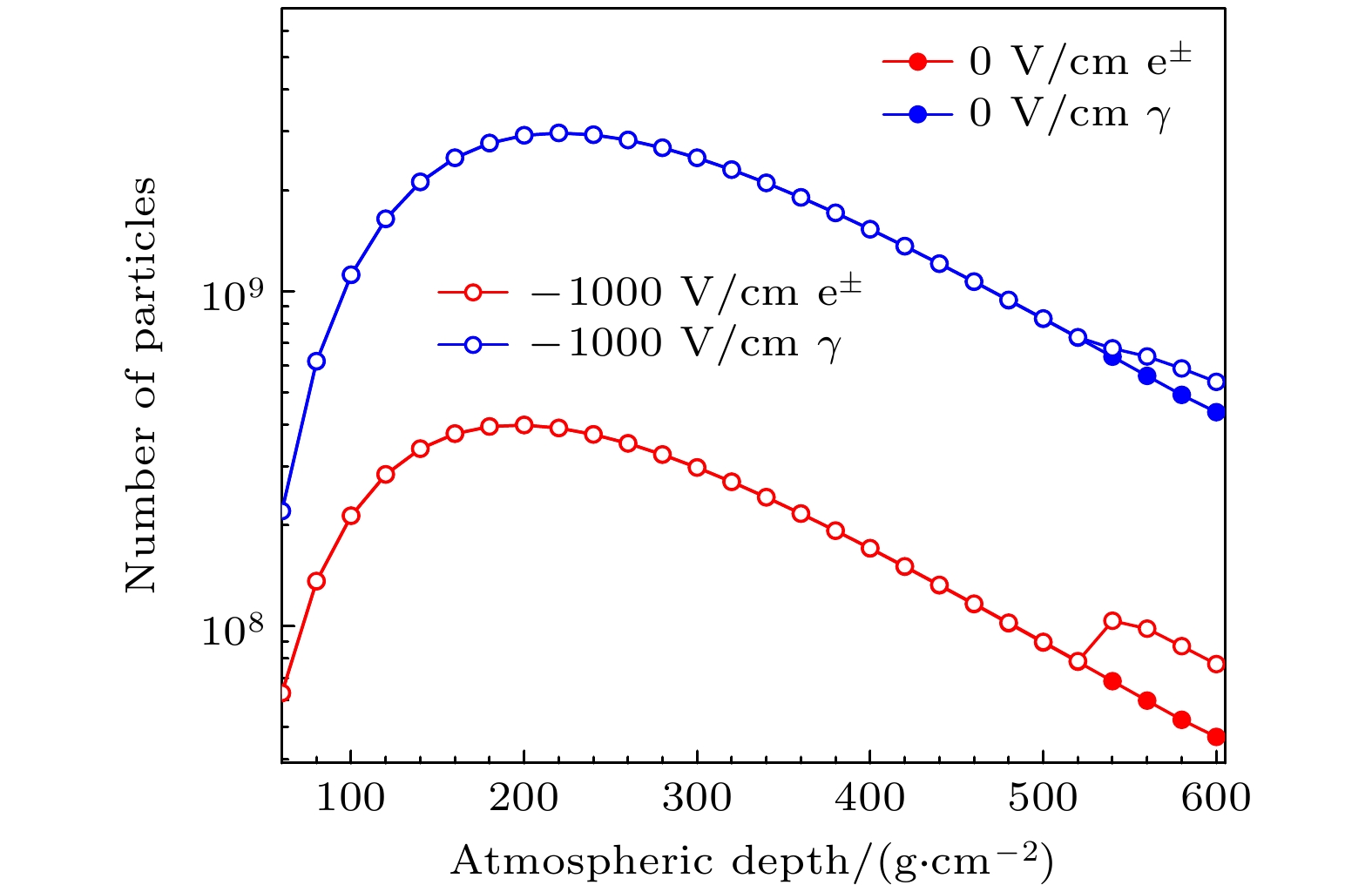
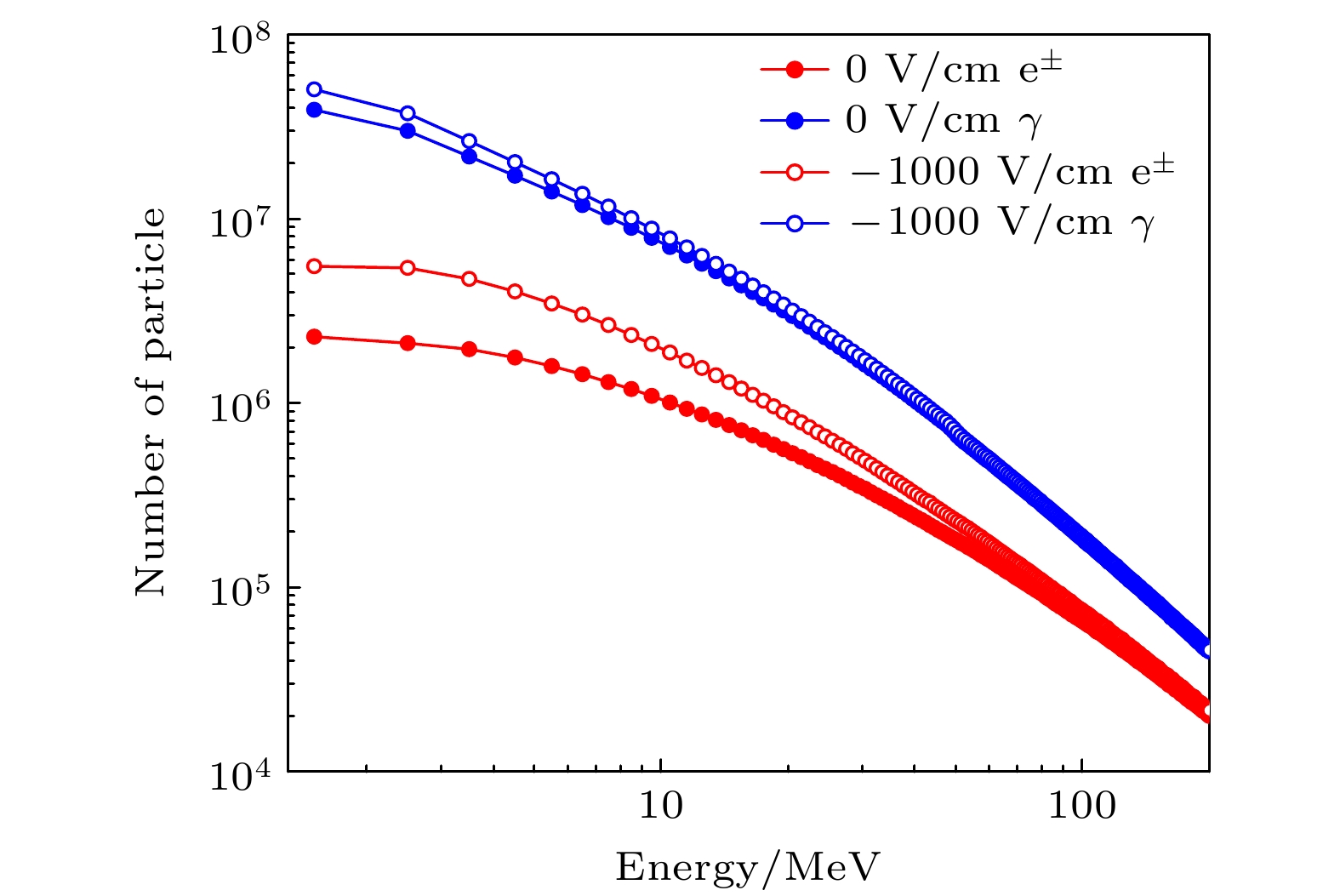
    • 观测表明[4, 46-48], 雷暴期间电场强度最大通常在800—1300 V/cm之间. 因此本文取电场–1000 V/cm进行模拟研究, 图4是在–1000 V/cm的电场中电子和光子的数目随大气深度的变化. 可以看出, 电子和光子进入电场(对应大气深度为524 g/cm2)后, 数目均增加.

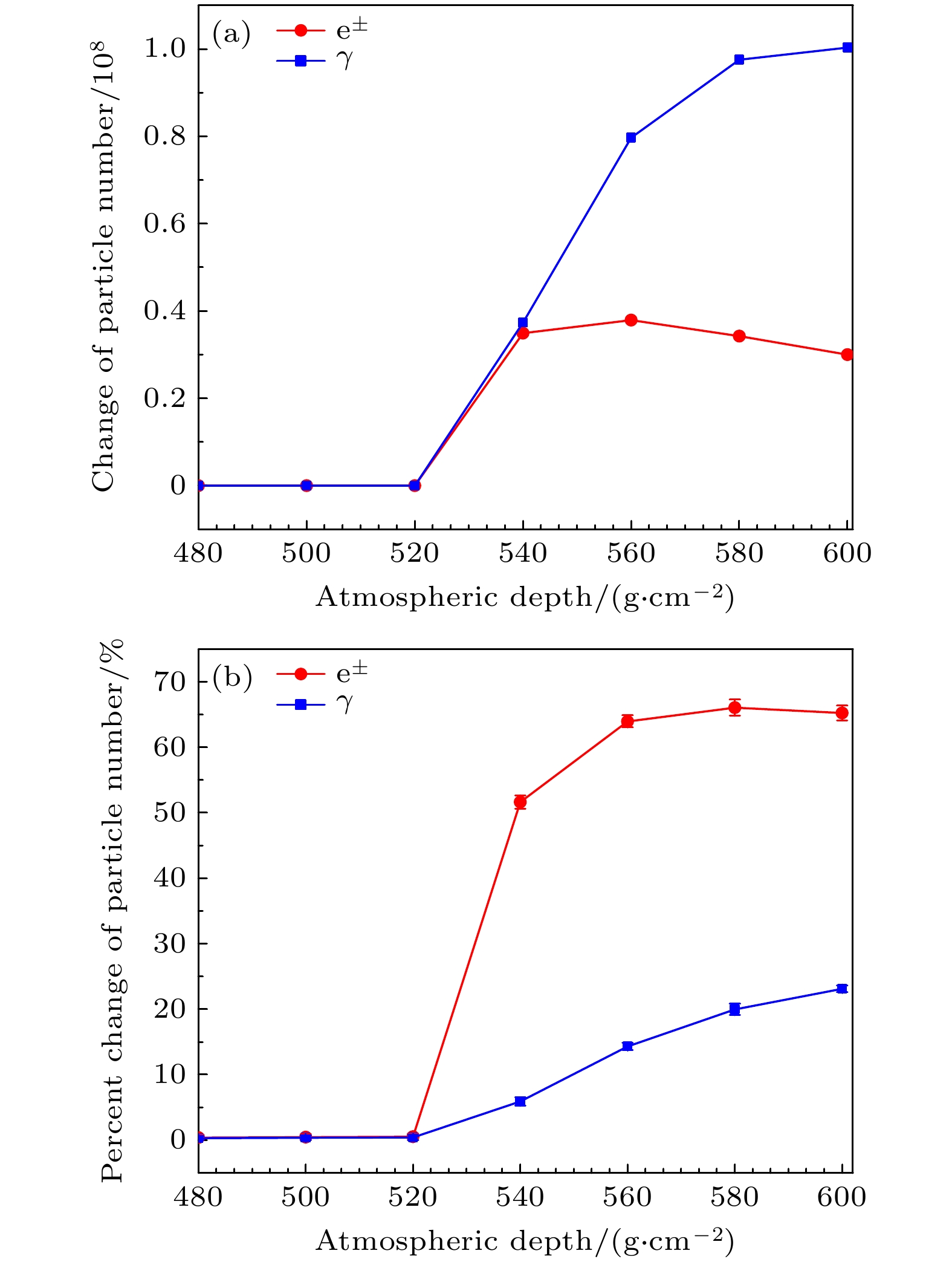
      图5(a)展示了在–1000 V/cm的电场中, 电子和光子的数目变化百分比随大气深度的变化. 可以看到, 当电子和光子进入电场区域后, 数目快速增加, 特别是光子, 当大气深度达到600 g/cm2时, 新增光子数目(3.0×107)是新增电子数目(1.0×108)的3.3倍. 图5(b)是电子和光子数目变化百分比的结果, 可以得到电场中电子和光子数目都增加. 对于电子, 其数目增加幅度随着大气深度快速增大, 在大气深度~580 g/cm2时达到最大(66%), 之后略有下降, 当大气深度达到600 g/cm2时, 电子数目增加65%; 而对于光子, 其数目增加幅度随着大气深度持续增加, 当大气深度达到600 g/cm2时, 增加幅度为23%.

      从图4和图5可以得到, 电场中电子和光子的数目都出现了增加, 且变化规律一致. 主要原因是在电场为–1000 V/cm(低于逃逸阈值电场)的区域内, 负电子被加速获得能量, 寿命延长, 使得它们在大气中的传播路径变得更长, 提高了电子产生轫致辐射光子的概率, 从而导致电场中光子的数目发生变化, 且变化趋势与电子的高度一致.

      • 3.2.   雷暴电场对光子能量的影响

    • 地面宇宙线实验中, 探测器对次级粒子的响应效率依赖于其能量, 一般情况下, 能量越高, 响应效率也越高. 因此, 研究雷暴期间LHAASO观测面宇宙线次级光子的能量变化对理解实验观测结果有重要意义.

      • 3.2.1.   不加电场的模拟结果

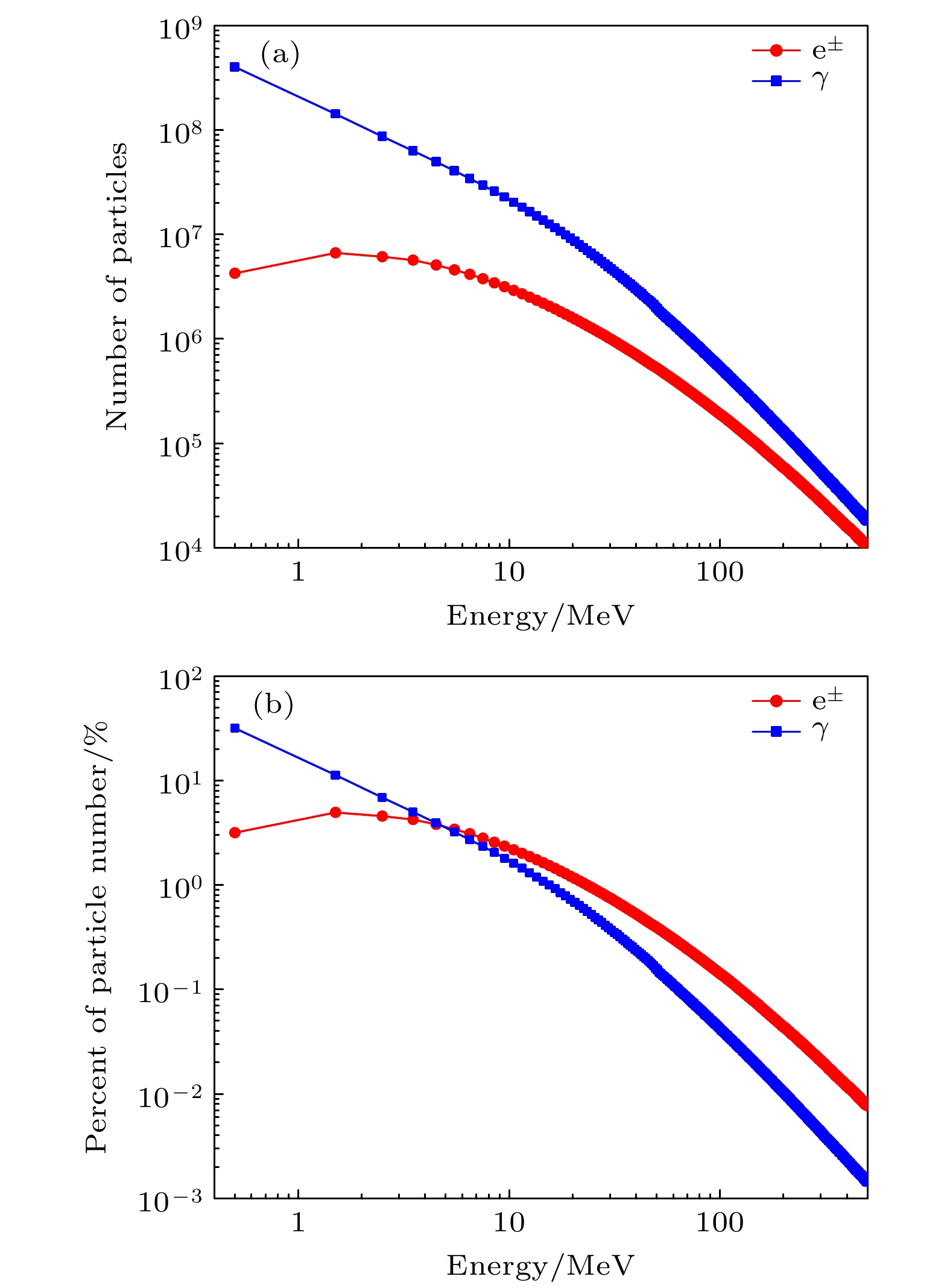
    • 图6(a)展示了原初能量为100 GeV—1 PeV的质子在大气簇射中产生的次级电子和光子在LHAASO观测面上的能量分布. 可以看出, 光子的数目比电子的多, 特别是当能量低于4 MeV时, 光子数目超过电子数目一个量级. 为了更好比较电子和光子的能量分布情况, 对图6(a)进行归一化处理, 其表达式为

      式中, 将能量划分为n个bin (1 bin = 1 MeV), Ni指第i个bin对应的粒子数, N0是总粒子数, 结果如图6(b)所示. 可以看出, 光子的能谱比电子的软, 数目主要分布在低能段.

      • 3.2.2.   电场强度为1700 V/cm(大于逃逸阈值电场)的模拟结果

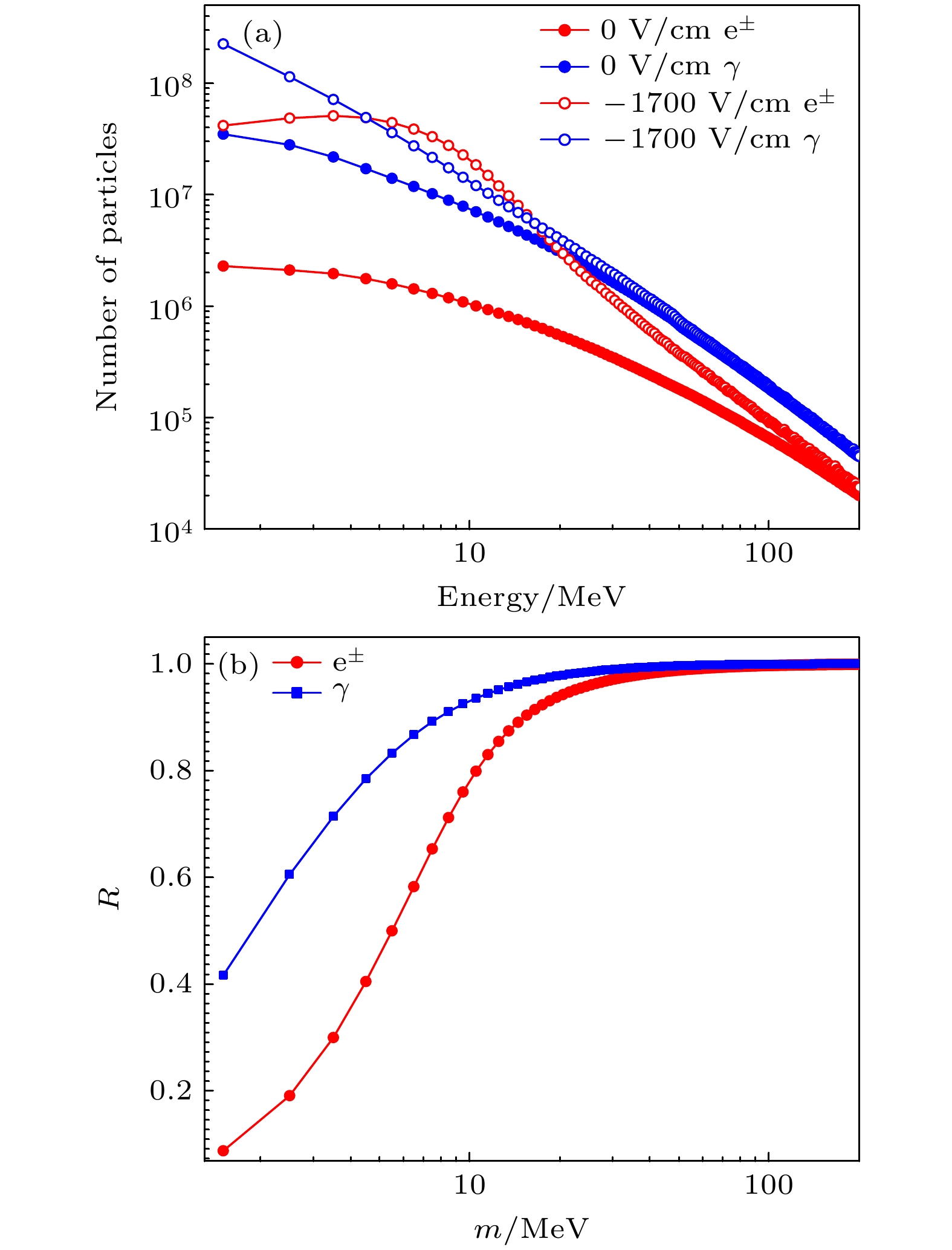
    • 图7(a)是在–1700 V/cm的电场中, 电子和光子数目随能量的分布(为了比较, 图中包含了不加电场时的模拟结果). 可以看出, 电场中电子和光子的能谱变软, 低能段粒子数目显著增加. 为了清楚地看到新增粒子分布情况, 本文将次级粒子能量划分为n个bin (1 bin = 1 MeV), 计算能量小于m (m = 1, 2, ···, n)时新增粒子数目之和与新增总粒子数目之比(R), 其表达式为

      式中, N是新增总粒子数目, Ni是第i个bin对应的新增粒子数目. 由(4)式得到R随m的分布, 如图7(b)所示. 可以发现, 能量小于20 MeV的新增光子数目占97.9%, 新增电子数目占94.3%; 而能量小于100 MeV的新增光子数目和电子数目占比均超过了99.7%. 可见, 雷暴期间新增光子和电子的数目几乎分布在几十个MeV以内.

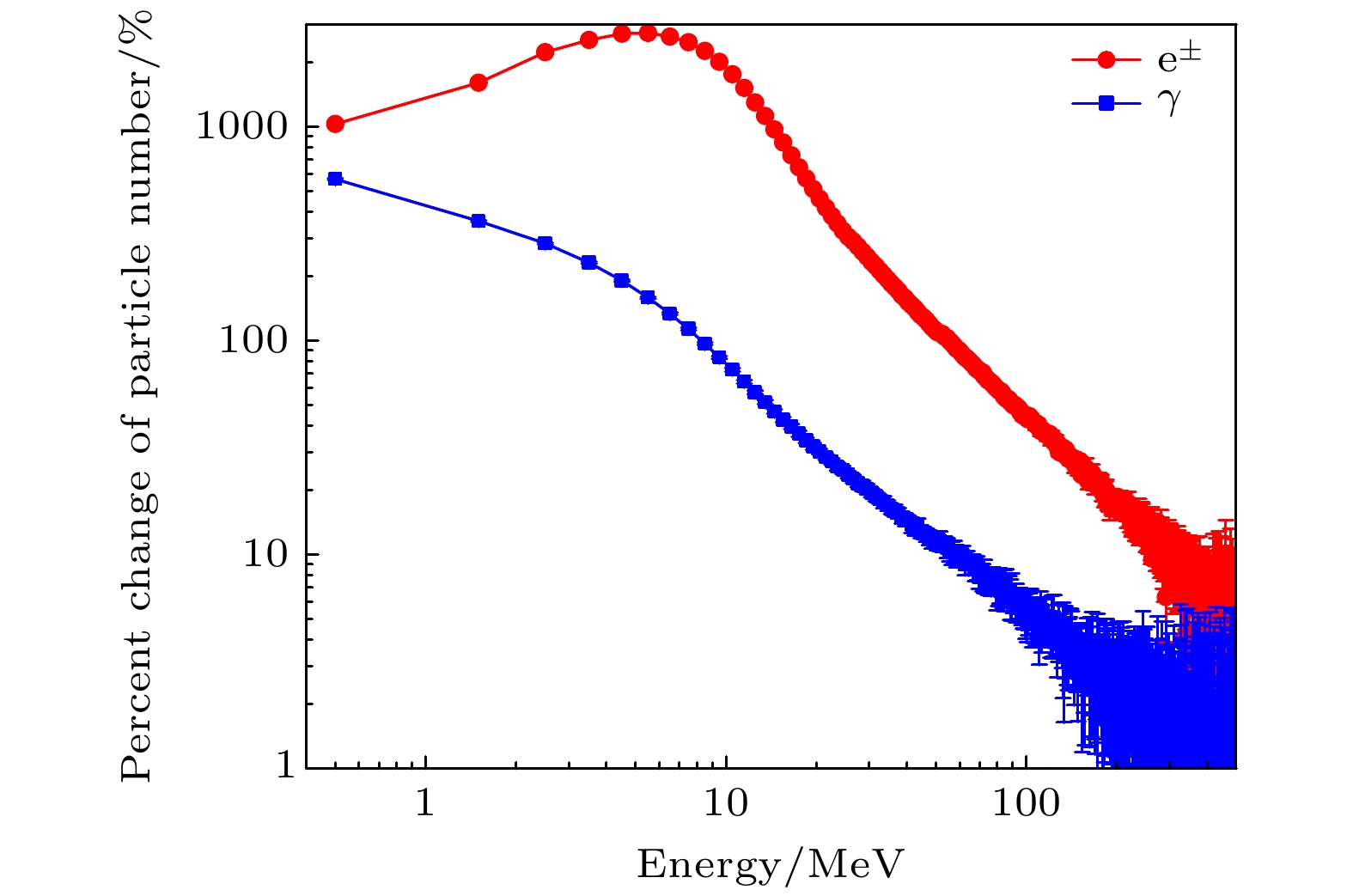
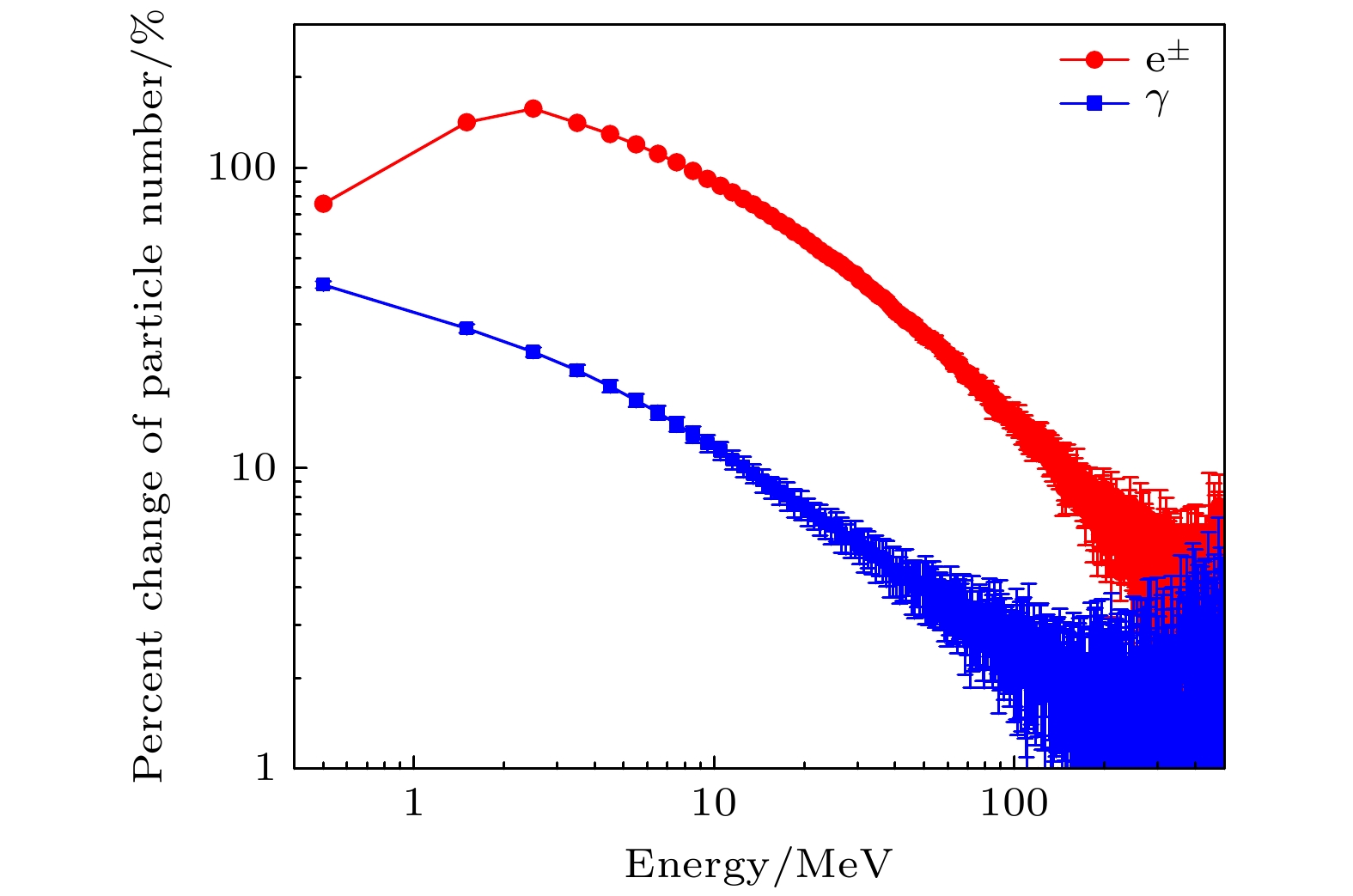
      图8是在–1700 V/cm的电场中, 电子和光子的数目变化百分比随能量的分布. 由图8可知, 当能量小于~30 MeV时, 电子和光子数目增加分别超过250%和20%. 然而, 对于更高能量区域的电子和光子, 数目增加相对较少.

      根据Bethe[49]理论, 当电子在电场中运动时会受到阻力作用, 其大小与电子的能量有关, 当能量大于1.4 MeV时, 受到的阻力随着能量的增大而增大. Buitink等[50]发现电子在电场中的平衡能量(即电子在电场中可被加速的最大能量)与电场强度和大气深度有关. 根据平衡能量公式, 当电场强度为1700 V/cm、大气深度为524 g/cm2时, 电子的平衡能量是100 MeV. 这意味着在强度为1700 V/cm的电场中, 当电子能量低于100 MeV时, 电子会被电场加速. 从图8可以看出, 能量低于几十MeV时发生相对论逃逸电子雪崩, 电子数目呈指数增加, 最大出现在5—6 MeV, 增加幅度达到2733%. 同时, 这些新产生的高能自由电子通过轫致辐射产生能量较低的光子, 使得光子数目在更低能量区域也呈指数增大, 且增加幅度依赖于能量. 能量越小, 增大幅度越大, 当能量低小于2 MeV时, 增大幅度超过361%, 符合RREA机理[7]. 然而, 当能量大于~30 MeV时, 电子数目增加幅度减小, 对应的轫致辐射光子亦如此, 不符合RREA机理, 反而与低于逃逸阈值电场中的情况极为相似. 主要原因是新增加的高能光子是由穿过雷暴电场的高能电子轫致辐射导致的. 然而, 由于高能电子在空气中因辐射而损失的能量很大, 致使高能电子无法引发RREA.

      • 3.2.3.   电场强度为1000 V/cm(低于逃逸阈值电场)的模拟结果

    • 图9是在–1000 V/cm的电场中, 电子和光子数目随能量的分布. 从图9可以看出, 电场中电子和光子数目都出现增加, 特别是在低能段. 统计得到, 当能量低于10 MeV时, 电子数目增加2.4×107, 占总新增电子数目的82.3%, 光子数目增加3.9×107, 占总新增光子数目的92.6%. 当能量达到100 MeV时, 电子数目增加2.9×107, 占总新增电子数目的98.3%, 光子数目增加4.2×107, 占总新增光子数目的99.4%.

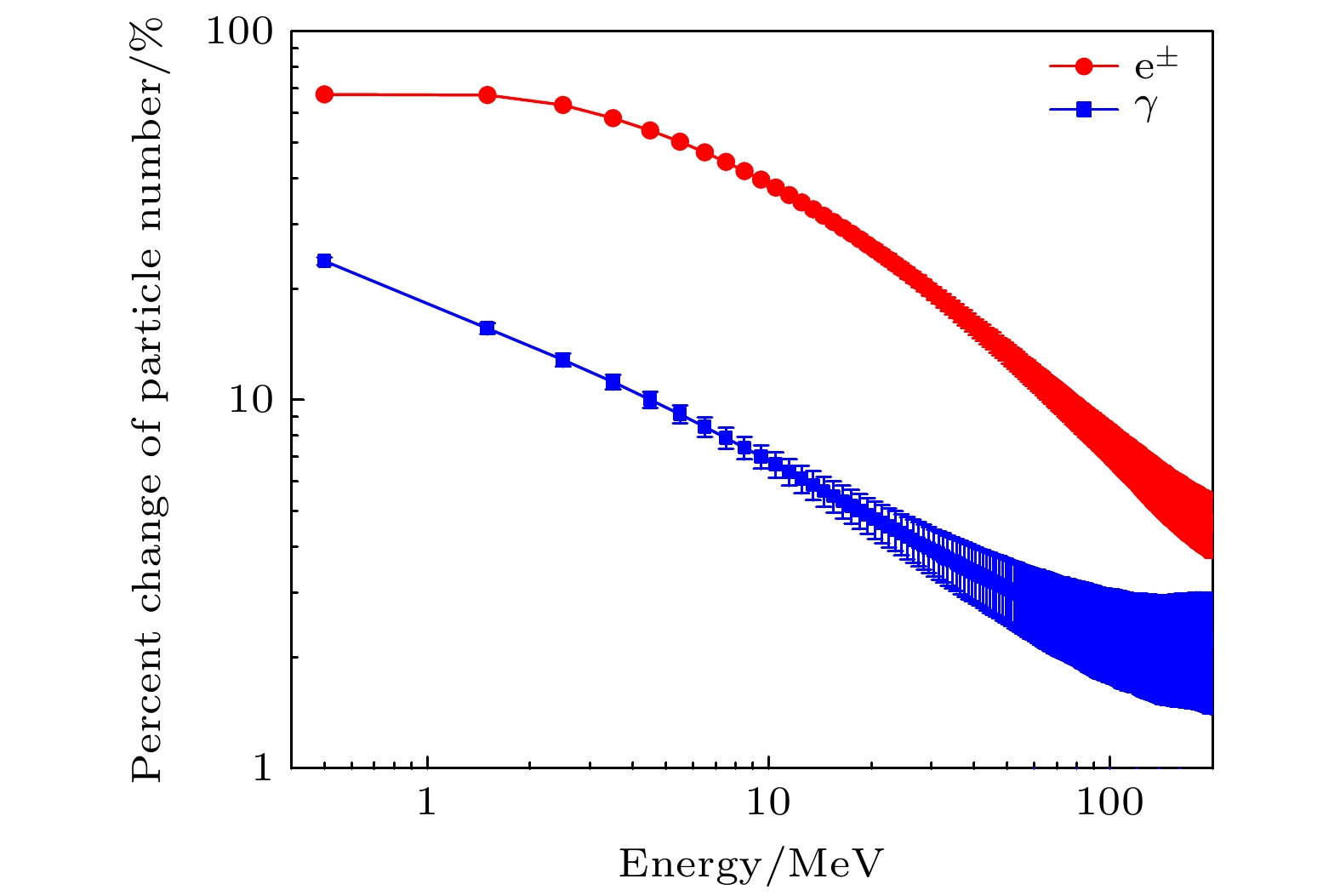
      图10展示了在–1000 V/cm的电场中, 电子和光子数目变化百分比随能量的分布. 从图10可以看出, 电场中电子和光子的数目变化对能量的依赖性很强. 电子数目增加幅度最大出现在2—3 MeV范围内, 约为157%; 而光子数目增加幅度则随能量的减小持续增大, 当能量低于2 MeV时, 增加幅度超过29%. 相比于低能粒子, 电场对高能区域的粒子影响要小得多, 当能量大于100 MeV时, 电子和光子的数目增加幅度分别低于14%和2%.

      为了研究雷暴电场对不同阈能探测器的影响, 本文对图10进行积分, 结果如图11所示. 可以看到, 能量越大, 次级粒子数目变化幅度越小. 当能量大于2 MeV时, 电子和光子的数目增加幅度分别小于63%和13%; 而当能量大于10 MeV时, 增加幅度分别低于38%和7%.

      从图7—图11可以看出, 宇宙线次级粒子在LHAASO观测面上的数目变化与电场强度和粒子能量密切相关. 当电场强度为1000 V/cm(低于逃逸阈值电场)时, 能量越低, 电子和光子数目增加越多; 而当电场强度增至1700 V/cm(大于逃逸阈值电场)时, 在低能量区域会发生相对论逃逸电子雪崩, 导致电子和光子数目急剧增加, 其增幅甚至可以达到1000 V/cm时的10倍以上.

    4.   结　论

    • 本文通过Monte Carlo方法, 利用CORSIKA7.7410软件包模拟研究了近地雷暴电场对LHAASO观测面宇宙线次级光子的影响. 为了深入理解次级光子的变化, 本文还结合雷暴期间电子数目和能量的变化进行了分析, 得到以下结论:

      1) 当电场为–1000 V/cm (小于逃逸阈值电场)时, 电子和光子数目随大气深度的增加而增加. 当簇射到达LHAASO观测面时, 电子和光子的数目增加幅度分别为65%和23%.

      2) 当电场为–1700 V/cm (大于逃逸阈值电场)时, 光子数目随大气深度的增加趋势与电子的一致, 呈指数增长. 在簇射到达LHAASO观测面时, 电子和光子的数目增加幅度分别达到992%和279%, 符合RREA机理[7]和Dwyer理论[8].

      3) 电场中电子和光子的能谱均变软, 变化幅度依赖于电场强度. 在–1000 V/cm的电场中, 电子数目增加幅度最大出现在2—3 MeV, 达到157%; 光子则表现为能量越小, 数目增加幅度越大, 当能量小于2 MeV时, 增加幅度超过29%. 同样的规律也出现在–1700 V/cm的电场中, 但变化幅度更大, 特别是在低能段, 发生相对论逃逸电子雪崩, 电子和光子数目呈现指数增长. 当电子能量为5—6 MeV时, 其数目增加幅度达到最大值, 增长了2733%; 而光子能量小于2 MeV时, 增加幅度超过361%, 规律与实验观测一致[14].

      4) 造成光子数目和能量在雷暴期间出现变化的主要原因是宇宙线次级电子进入电场区域后, 被大气电场加速获得能量, 并与空气分子碰撞电离出电子, 这些新产生的自由电子通过轫致辐射释放出光子, 导致光子数目和能谱的变化趋势与电子的一致.

      本文的模拟结果有助于理解雷暴期间宇宙线实验数据中电子和光子的相对贡献. 此外, 也为通过实验数据反演雷暴云特征提供了信息.

    参考文献 (50)

目录

/

返回文章
返回