近年来, 数值仿真已发展成为气体放电不可或缺的研究手段, 常用的模拟方法包括: 直接动理学(direct kinetic, DK)、粒子模拟(particle-in-cell, PIC)、流体模拟(fluid model)、混合模拟(hybrid model)等. 直接动理学方法直接求解玻尔兹曼方程, 相对PIC方法噪声很小, 具有较高的精度, 然而由于计算量的限制, 目前主要应用于一维模型^[1,2]. 粒子模拟方法引入了“宏粒子”的概念, 基于麦克斯韦方程(电磁)或泊松方程(静电)计算带电粒子之间的电(磁)场分布, 采用牛顿-洛伦兹运动方程来求解“宏粒子”的运动规律, 使用蒙特卡罗碰撞(Monte Carlo collision, MCC)处理粒子间的碰撞过程(伪碰撞). 粒子模拟存在计算量大、计算时间较长, 且难以处理等离子体复杂的化学反应过程等缺点, 常用于低气压、短间隙条件下放电的精细物理研究^[3-8]. 基于矩分析方法, 可将粒子(电子、离子等)的玻尔兹曼方程转变为描述放电宏观量的流体方程. 流体模拟方法将等离子体中的带电粒子进行流体处理, 一般包括粒子连续性方程、动量和能量守恒方程、以及描述电(磁)场分布的泊松(场)方程, 可以自洽求解得到放电过程中粒子密度、电流、电压等宏观参量^[9-11]. 然而, 流体模型的求解需对电子的能量分布函数进行合理假设, 会对仿真结果的准确性产生一定影响, 通常适用于高气压、大间隙(高$pd$值)放电过程的模拟. 混合模拟方法在流体模型的基础上兼顾了粒子的动理学过程, 例如对放电快电子进行蒙特卡罗模拟, 对离子和慢电子则采用流体方法, 可以更准确得到电子能量分布函数信息^[12-16]. 在高气压条件下, 当非局域动理学效应不显著时, 粒子的碰撞与输运过程通常满足局域场(或局域能量)近似, 可采用流体模型对放电物理过程进行合理描述.

目前, 流体模型已广泛应用于电晕放电^[17-19]、汤森放电^[20]、辉光放电^[15,21]、介质阻挡放电^[22-24]、流注放电^[25-28]、等离子体射流^[29,30]等多种放电形式的模拟研究. 由于其基本方程本身的通用性, 人们基于流体模型研究不同放电模式之间的过渡或转换特性. 例如, Kolobov等^[31,32]采用二维流体模型研究了汤森放电向辉光放电的过渡过程, 模拟得到了电流密度增加条件下, 汤森放电通道横向收缩, 向亚正常辉光、正常辉光状态的转变过程, 并基于放电伏安特性(current-voltage characteristic, CVC)曲线证明了放电的“回滞效应(hysteresis effect)”. 基于氩气放电的流体模型, Maric等^[21]仿真得到了包含汤森放电、亚正常辉光、正常辉光、反常辉光区的CVC曲线, 对反常辉光区的放电过程进行了详细研究, 确定了重粒子(氩离子$\text{Ar}^+$、快速中性粒子$\text{Ar}^\text{f}$)的电离和激发过程对放电维持起主要作用. Eliseev等^[33]建立了大气压下氩气微放电的一维流体模型, 在该模型中考虑了阴极与等离子体之间的传热过程, 得到了辉光放电到电弧放电过渡的CVC曲线, 但在该模型中重粒子反应系数是与温度无关的常数, 这与实际物理过程并不符. 基于氩气的二维流体模型, 本研究组^[34-38]仿真研究了电极表面突起结构/悬浮金属棒对微间隙击穿特性的影响, 得到了包含盖革-米勒放电、汤森放电、亚正常辉光、正常辉光、反常辉光等放电区域的较为完整的CVC曲线. 由于仅考虑了氩气的弹性碰撞、电离、激发等反应, 在阴极表面只考虑了二次电子发射过程, 且假设阴极温度为定值, 模型中未包含阴极热电子发射、等离子体与阴极的热传导等过程, 放电的CVC曲线未包含电弧放电区. Baeva等^[39-41]在流体模型的基础上考虑了阴极热电子发射过程、阴极与等离子体之间的热传递过程, 称之为“统一流体模型”, 并自洽求解了大气压下氩气微放电等离子体经历亚正常辉光、正常辉光、反常辉光及电弧放电的转换过程. Saifutdinov^[42-44]建立了氩气和氮气的统一流体模型, 得到了包含辉光放电和电弧放电的CVC曲线, 分析了电极长度对反常辉光放电的影响、阴极表面斑点的形状变化以及气体温度和阴极表面的不同加热机制. 然而, Baeva和Saifutdinov等的研究主要针对辉光放电区和电弧放电区, 没有包含盖革-米勒放电区和汤森放电区. 目前, 鲜有报道基于流体模型仿真得到完整(即包含盖革-米勒放电区、汤森放电区、亚正常辉光放电区、正常辉光放电区、反常辉光放电区、电弧放电区等各放电模式)的CVC曲线.

本文基于统一流体模型研究氩气微放电的等离子体特性. 数值模型包括电极区域内带电粒子的质量守恒方程(连续性方程)、能量守恒方程、调节放电电流密度的外电路方程、泊松方程, 考虑了阴极电子发射(二次电子、热电子发射)以及阴极与等离子体的热传导方程. 基于该模型, 仿真得到了包含盖革-米勒放电区(Geiger-Müller discharge regime, GM)、汤森放电区(Townsend discharge regime, TD)、亚正常辉光放电区(subnormal glow discharge regime, SG)、正常辉光放电区(normal glow dischagre regime, NG)、反常辉光放电区(abnormal glow discharge regime, AG)、电弧放电区(arc discharge regime, Arc)等各放电模式的完整CVC曲线, 对比分析了不同气压条件下($50$, $500\;\text{Torr} \;(1\; {\mathrm{Torr}}\; ≈\; 133.322 \;{\mathrm{Pa}}) $)放电典型参量的分布特性. 结果表明, 汤森放电区空间中电场分布几乎均匀, 空间电荷效应可忽略不计; 辉光放电区出现明显的阴极位降区和等离子体区, 空间电荷效应显著, 仿真结果与理论相符. 特别地, 反常辉光放电区由于粒子密度梯度增大, 出现电场反转现象. 电流密度进一步增大, 进入由热电子发射和热电离主导的电弧放电区, 此时带电粒子密度量级为$10^{22} \;\text{m}^{-3}$. 在气压为$500\;\text{Torr}$时, 气体温度峰值为$11850\;\text{K}$, 此时由于热传导作用, 阴极表面温度被加热至将近$4000\;\text{K}$.

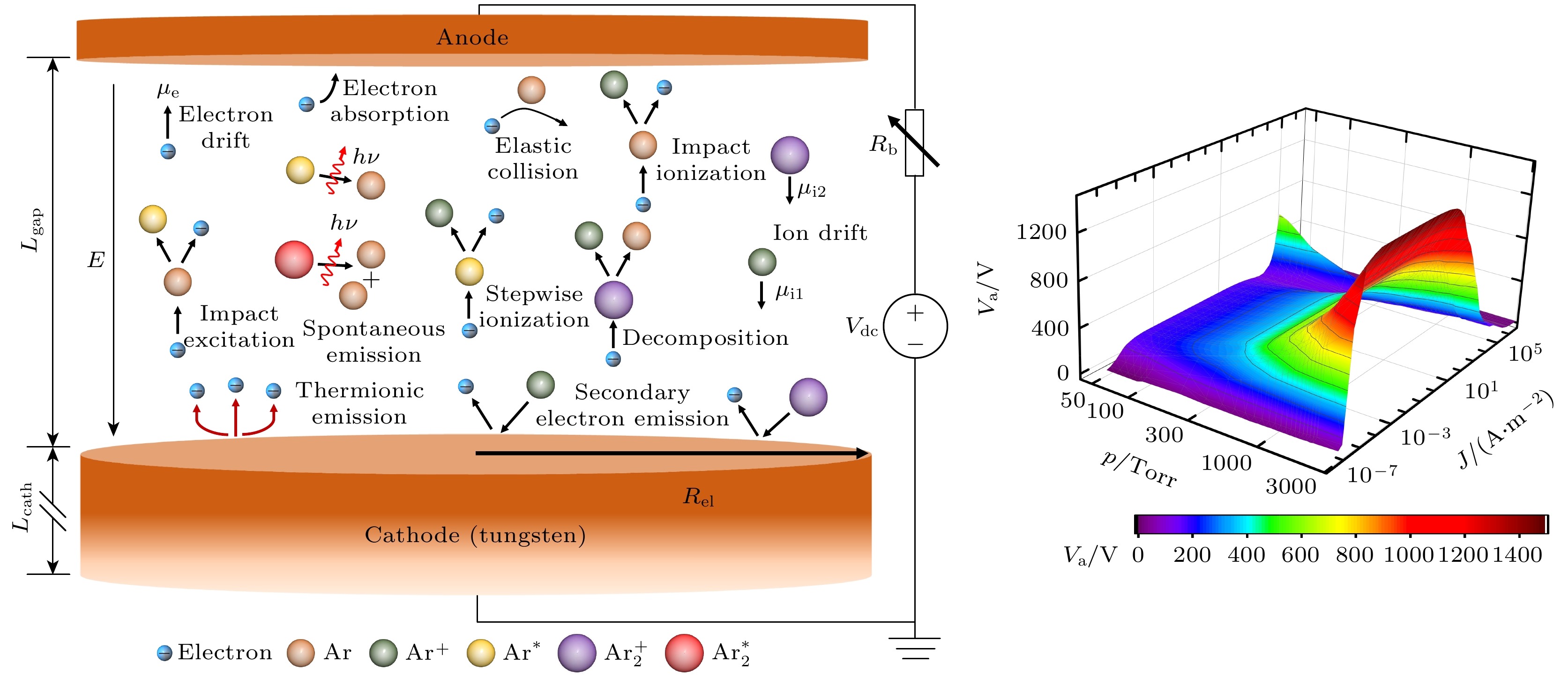
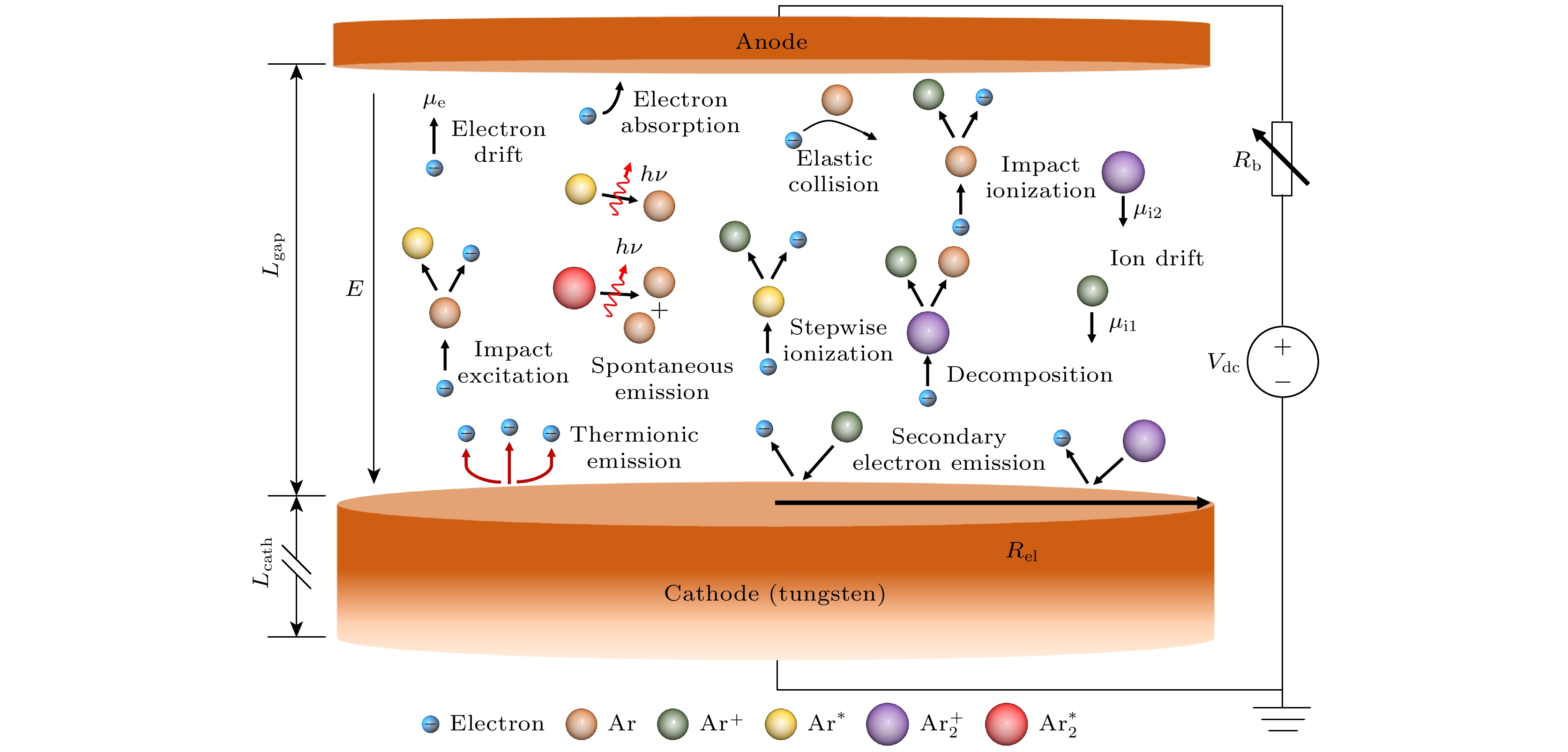
本文的统一流体模型考虑了气隙中粒子的输运与碰撞、电极表面发射(二次电子、热电子发射)及等离子体与阴极的热传导过程, 放电结构如图1所示. 其中, 电极间距为$L_\text{gap} = 400\;{\text{μm}}$, 电极半径为$R_\text{el} = 2\; {\text{mm}}$, 考虑电极间距远小于电极半径, 认为放电参数沿径向分布均匀, 因此将模型简化为沿轴向放电的一维模型. 定义阴极表面位置为$x_{\text{c}} = 0 \;{\text{μm}}$, 阳极表面位置为$x_\text{a} = 400 \;{\text{μm}}$. 考虑阴极导体(材料为钨)的热传导过程, 阴极长度设置为$L_\text{cath} = 20 \;{\text{mm}}$. 外电路由直流电源$V_\text{dc}$和限流电阻$R_\text{b}$组成, 通过调节电源电压或者镇流电阻可以改变回路中放电电流的大小, 使电极间放电处于不同的模式.

流体模型包含粒子的输运与碰撞两类基本过程. 其中输运过程包括: 1)带电粒子在电场作用下的定向迁移过程; 2)带电粒子空间分布不均匀, 存在密度梯度而引起的扩散过程. 碰撞过程包括弹性碰撞、非弹性碰撞等, 造成粒子的产生和消失(特别地, 高气压条件下还存在准分子原子的形成过程^[45]). 此外, 模型包含了激发、辐射、表面发射(二次电子、热电子发射)等过程. 本文考虑氩气为工作气体, 主要粒子有: 电子(e)、基态氩原子(Ar)、氩离子($\text{Ar}^+$)、分子离子($\text{Ar}_2^+$)^[46]、受激氩原子($\text{Ar}^*$)和氩二聚体($\text{Ar}_2^*$). 在碰撞过程中主要考虑了弹性碰撞(e + Ar $\rightarrow $ e + Ar)、氩原子的激发(e + Ar$\rightarrow $ e + $\text{Ar}^*$)和退激发(e + $\text{Ar}^*$ $\rightarrow $ e + Ar)、直接电离(e + Ar $\rightarrow $ 2e + $\text{Ar}^+$)和逐步电离(e + $\text{Ar}^*$ $\rightarrow $ 2e + $\text{Ar}^+$)、分子离子及二聚体的形成(e +$\text{Ar}_2^*$$\rightarrow 2{\mathrm{e}} + \text{Ar}_2^+$, $2{\mathrm{Ar}} + \text{Ar}^*$$\rightarrow {\mathrm{Ar}} + {\text{Ar}_2}$)与损失(${\mathrm{e}} + \text{Ar}_2^+$$\rightarrow $$\text{Ar}^*+{\mathrm{Ar}}$, 2$\text{Ar}_2^*$$\rightarrow $${\mathrm{e }}+ 2{\mathrm{Ar }}+\text{Ar}_2^+$)、辐射跃迁($\text{Ar}^*\rightarrow {\mathrm{Ar }}+ $$h\nu$, $\text{Ar}_2^*\rightarrow 2{\mathrm{Ar}} +$$h\nu$)、复合反应($2{\mathrm{Ar}} + \text{Ar}^+$$\rightarrow {\mathrm{Ar}} + $$\text{Ar}_2^+$)等过程, 如图1所示. 仿真过程中涉及到的等离子体化学反应及其反应系数如表1所列, 其中$T_\text{e}$表示电子温度, 单位为eV; $T_\text{g}$表示气体温度, 单位为K; $R_\text{g} = 8.314\; \text{J}/(\text{mol}\cdot \text{K})$为气体常数; $h = 6.62607015 \times 10^{-34} \;\text{J}\cdot\text{s}$为普朗克常数; $\Delta E$为对应反应过程的能量变化^[41].

流体模型需求解电子及重粒子的质量守恒(连续性)方程、动量守恒方程、能量守恒方程. 基于动量守恒方程的矩分析得到粒子通量的“漂移-扩散近似(drift-diffusion approximation)”表达式, 并通过泊松方程自洽求解电场(静电模型). 此外, 本文中的统一流体模型还包含了阴极与等离子体之间的能量传递过程, 耦合了热传导方程. 接下来对上述控制方程进行具体描述.

电子质量守恒(连续性)方程的表达式为

式中, $n_\text{e}$是电子密度; ${\boldsymbol{\varGamma}}_\text{e}$是电子的通量, 由“漂移-扩散近似”可知

其中, $\mu_\text{e}$和$D_\text{e}$是电子的迁移率和扩散系数. (1)式中$S_\text{e}= \displaystyle\sum\nolimits_{j = 1}^N R^\text{G}_j- \displaystyle\sum\nolimits_{j = 1}^M R^\text{L}_j$为碰撞引起的电子密度变化的源项, 取决于N个电子生成反应与M个电子消耗反应贡献的差值^[56]. 在本模型中, 电子数目的平衡由直接电离(R4)、逐级电离(R5, R6)、潘宁(Penning)电离(R11, R13)、复合反应(R8, R10)等过程决定, 因此有

其中, $n_k$(k为粒子种类, $k=\text{e},\; \text{Ar}, \;\text{Ar}^+, \; \text{Ar}_2^+,\; \text{Ar}^*, \text{Ar}_2^*$)为相应物种的浓度, $K_j$为第j个反应的速率系数. 对于重粒子反应, 通常使用速率常数或与气体温度相关的表达式, 如表1所列; 对于电子碰撞反应, $K_j$由电子能量ε、碰撞截面$\sigma_j(\varepsilon)$和电子能量分布函数(electron energy distribution function, EEDF)$f_0(\varepsilon)$的积分决定^[57], 其表达式为

其中, ${e} \;=\; 1.60217733 \times 10^{-19}\;\text{C}$为元电荷量, $m_\text{e} = 9.10956 \times 10^{-31}\;\text{kg}$为电子质量. 通常, 在流体模型中假设$f_0(\varepsilon)$为麦克斯韦分布.

电子能量守恒方程表达式为

式中, $n_{\varepsilon}$是电子能流密度, ${n_{\varepsilon }}={n_\text{e}}\bar{\varepsilon}$, $\bar{\varepsilon }=(3/2){T_\text{e}}$是电子的平均能量; ${\boldsymbol{E}}$为电场; $e{\boldsymbol{E}}\cdot{\boldsymbol{\varGamma}}_\text{e}$表示电子在电场中由于焦耳加热(Joule heating)带来的能量增益. ${\boldsymbol{\varGamma}}_{{\varepsilon}}$是电子能量的通量, 同样由“漂移-扩散近似”可知

其中, $\mu_\varepsilon$, $D_\varepsilon$是电子能量的迁移率和扩散系数; $\mu_\varepsilon$, $D_\varepsilon$与$\mu_\text{e}$, $D_\text{e}$的关系将在下文(2.3.3小节)中给出.

接下来分别说明(5)式右侧三项的含义和计算方法. 第1项$S_\varepsilon$表示非弹性碰撞导致的电子能量的增益或损失, 计算式为$S_\varepsilon= \displaystyle\sum\nolimits_{j}\Delta E_{\text{inel}, j}{R_{\text{inel}, j}}$, $\Delta{E_{\text{inel}, j}}$和$R_{\text{inel}, j}$为非弹性碰撞反应的能量变化及其相应的反应速率, 其中$\Delta{E_{{\text{inel}}, j}}= \displaystyle\sum\nolimits_{j}H_{\text{inel}, j}^{\text{P}}- \displaystyle\sum\nolimits_{j}H_{\text{inel}, j}^{\text{R}}$, 即反应的能量变化可以通过生成物与反应物焓值的差得到(见表1第5列). 第2项${Q}_\text{h}$为电子与原子弹性碰撞引起的能量变化^[42], 计算式为

其中, $m_\text{g}$是气体原子(Ar)的质量($m_\text{g} \gg m_\text{e}$), $\nu_\text{el}$是电子与气体原子弹性碰撞的频率. (5)式第3项${Q}_\text{rad,ff}$为等离子体中体积辐射造成的能量损失, 代表电子的轫致辐射(Bremsstrahlung radiation), 是由库仑碰撞引起的高速电子骤然减速时产生的辐射(又称“刹车辐射”或“制动辐射”), 其计算式为^[58]

这里$Q_\text{rad, ff}$取决于无量纲电子密度$\hat{n}_\text{e}=n_\text{e}/n_0$和无量纲原子密度$\hat{n}_\text{A}=n_\text{Ar}/n_0$(其中$n_0 = 10^{20} \;\text{m}^{-3}$), 由电子和原子之间的辐射($53.759\hat{n}_\text{e}^{1.25}{{\hat{n}}_\text{A}}$)、电子和离子之间的辐射($910\hat{n}_\text{e}^{2}$)两部分组成. 需要注意的是, 由于轫致辐射导致的能量损失并不会被系统中的重粒子所吸收, 而是直接“逃离”了系统, 所以重粒子能量守恒方程中没有该项的贡献^[59].

在(1)式和(5)式中, 对于电子的通量和电子能量的通量, 可由“漂移-扩散近似”得到, 即对玻尔兹曼方程进行一阶矩计算得到动量守恒方程, 忽略黏性力和惯性项, 只考虑静电场和各向同性的压强场, 并假设粒子满足理想气体状态方程, 得到通量的通用表达式

(9)式中通量由电场作用下的漂移项和密度梯度引起的扩散项组成. 其中, $\text{sgn}({q_k})$是识别粒子种类及其所带电荷量的函数:

对于电子, $\text{sgn}({q_k})=-1$, 由此得到(2)式和(6)式电子的通量和电子能量的通量表达式.

迁移率和扩散系数的计算式为

其中, $k_\text{B} = 1.380649 \times 10^{-23} \;\text{J}/\text{K}$是玻尔兹曼常数, ${\nu_\text{e}}$是动量转移频率, ${\nu_\text{e}}={{R_\text{e}}}/{{n_\text{e}}}$, ${R_\text{e}}= \displaystyle\sum\nolimits_{j}{{n_\text{e}}{n_j}{K_j}}$代表电子碰撞过程的总反应速率, $n_j$和$K_j$分别是第j个反应的目标物质的数密度和速率系数. 关于(11)式中$\mu_{\varepsilon }$与$\mu_\text{e}$、$D_{\varepsilon }$与$D_\text{e}$的“5/3”系数关系的推导见附录A. 迁移率和扩散系数可以由电子温度联系起来, 即爱因斯坦关系式:

对于中性粒子而言, 其输运过程不受电场影响, 即$\text{sgn}({q_k}) = 0$; 输运通量仅由密度梯度决定, 即${{\boldsymbol{\varGamma}}_\text{n}}=-{{D}_\text{n}}\nabla {{n}_\text{n}}$.

重粒子(背景气体)的输运方程为

式中, 气体密度$\rho_\text{g}$由理想气体状态方程得到; $m_k$为第k种物质的质量; ${Y_{k}}$为第k种物质的质量分数, 有$\displaystyle \sum\nolimits_k Y_k = 1$; ${{\boldsymbol{\varGamma}}_{k}}$为第k种物质的通量, 其表达式为

其中, M为混合物的平均摩尔质量, 由物质的质量分数和分子质量表示, $\dfrac{1}{M}= \displaystyle\sum\nolimits_k ({Y_k}/{M_k})$. (14)式说明物质k的通量不仅与自身密度梯度有关, 也与其他粒子的分布状态有关. $z_k$为第k种粒子的电荷量, 迁移率通过爱因斯坦关系式$\mu_k= {e D_k}/{k_\text{B} T_k}$得到. 物质k在混合物中的扩散系数定义为

式中, $x_k=({Y_k}/{M_k}) M$; 根据气体动力学理论^[60]二元扩散系数$D_{k j}$的表达式为

其中, $T_\text{g}$是气体的温度, $p_\text{g}$为气压, σ是兰纳-琼斯势(Lennard-Jones)势的特征长度, 单位是埃(Å), $\varOmega_{\mathrm{D}}$是物种k和j相互作用的碰撞积分, 可表示为^[61]

这里, 输运截面$Q_{k j}^{(l)}$描述了物种k和物种j之间的相互作用, $\gamma^2$为约化能量, $m_{k j}$为约化质量, 这三个变量的表达式分别为

其中, b和$\chi_{k j}$分别为瞄准距离和碰撞偏角, $\varepsilon_{k j}= \dfrac{1}{2}m_{k j}g^2$是由组分碰撞时相对速度g定义的初始动能, 上标l代表碰撞积分的类型, s代表碰撞积分的阶数, $\chi_{k j}$是碰撞参数b、动能$\varepsilon$和粒子间相互作用势$V(r)$的函数, r为相互作用粒子间的距离^[62]. 为方便计算, $\varOmega_{\mathrm{D}}$也可由下式拟合得到^[63,64]:

其中, A, B, C, D, E, F, G与H为拟合系数, $T^*= k_{\text{B}} {T_\text{g}}/{\varepsilon_{k j}}$为折合温度, $\; \varepsilon_{k j}=\left(\varepsilon_k \varepsilon_j\right)^{1 / 2}$为约化势阱深度, $\;\delta= {\mu_\text{d}^2}/{2 \varepsilon \sigma^3}$为描述粒子极性的无量纲参数, $\mu_\text{d}$为粒子的偶极矩, 单位为德拜(Debye), 德拜长度为$\lambda_{\text{De}}=\left(\varepsilon_0 T_{\text{e}} / e n_{\text{e}}\right)^{1 / 2}$, $\; \delta_{k j}=\left(\delta_k \delta_j\right)^{1 / 2}$.

重粒子(背景气体)的能量守恒方程为^[43]

其中, k种混合物质的比热容$C_\text{p, g}= {\displaystyle\sum\nolimits_k x_k C_{\text{p}, k}}\Big/ {\displaystyle\sum\nolimits_k x_k M_k}$, 第k种物质的热力学性质参数(摩尔热容$C_{\text{p}, k}$, 摩尔焓$h_k$, 摩尔熵$s_k$)来源于文献[65, 66].

(20)式左边第2项计算表达式为

其中, $\kappa_\text{T} = 0.5\left[\displaystyle\sum\nolimits_k x_k \kappa_k+\left({x_k}/{\kappa_k}\right)^{-1}\right]$为混合物的导热系数, $\kappa_\text{T} \nabla T_k$为热量通量, $ \displaystyle\sum\nolimits_{k}{h_{k}}{\boldsymbol{\varGamma}}_{k}$代表每一种粒子由于扩散产生的焓通量.

(20)式的右边代表在该反应体系中重粒子(即气体)的4种加热机制. 右边第1项${Q}_\text{h}$是电子与重粒子弹性碰撞引起重粒子的能量增益, 参见(7)式. 第2项$Q_\text{i}^\text{J}$是电场对离子做功而产生的热量, 即离子的焦耳加热, 在数值上$Q_\text{i}^\text{J}= {\boldsymbol{E}}\cdot \displaystyle \sum\nolimits_{j}{q_{\text{i}, j}}{{\boldsymbol{\varGamma}}_{\text{i}, j}}$. 本文中有两种正离子($\text{Ar}^+, \text{Ar}_2^+$), 且带电量大小均与电子相同, 故$Q_\text{i}^\text{J}=e{\boldsymbol{E}}\cdot ({{{\boldsymbol{\varGamma}} }_{\text{Ar}^+}}+ {{{\boldsymbol{\varGamma}} }_{\text{Ar}_{2}^{+}}})$. 第3项${Q_\text{quen}}= \displaystyle\sum\nolimits_{j}{\Delta{E_{\text{quen}, j}}{R_{\text{quen}, j}}}$表示激发态氩原子在淬灭过程中的能量源项, $\Delta{E_{\text{quen}, j}}$为第j个淬灭反应的能量变化(数值见表1). 第4项${Q_\text{rec}}= \displaystyle\sum\nolimits_j {\Delta{E_{\text{rec}, j}}{R_{\text{rec}, j}}}$为复合反应引起的能量增益, $\Delta{E_{\text{rec}, j}}$为第j个复合反应的能量变化(数值见表1).

描述空间中电场和电势分布的泊松方程为

其中, $\phi $为空间中的电势, ${\rho_\text{q}}=e({n_{\text{Ar}^+}}+{{n}_{\text{Ar}_2^{+}}}- {n_\text{e}})+\sigma_{\text{s}} \delta_{\text{s}}$为电荷密度, $\sigma_{\text{s}} \delta_{\text{s}}$代表边界(如介质表面)上的电荷密度^[67], 当$\delta_{\text{s}} = 0$时, 则为经典的泊松方程, ${\varepsilon_0}$为介电常数.

描述阴极附近传热过程的表达式为

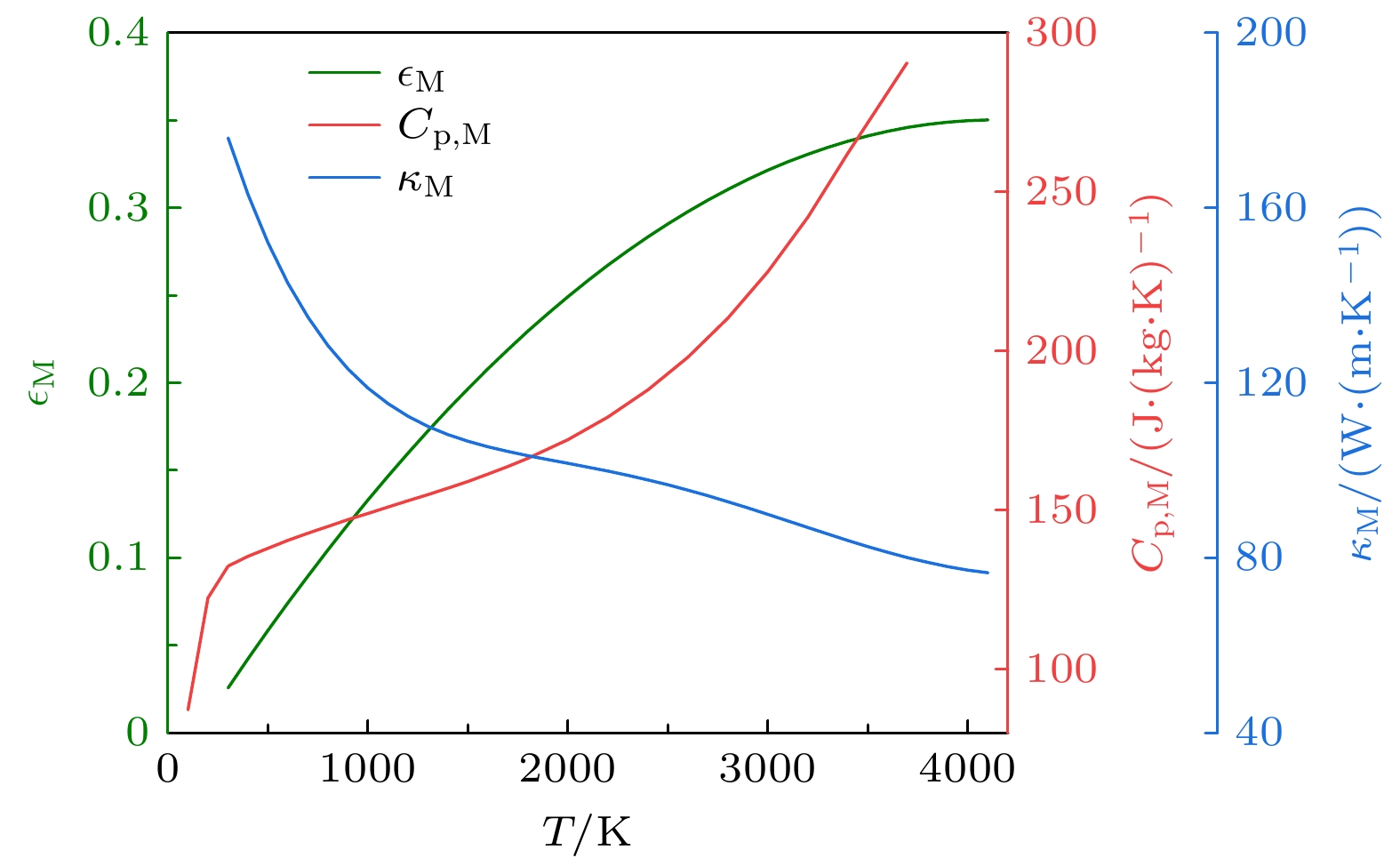
其中, $\rho_\text{M}$, $C_\text{p,M}$, $\kappa_\text{M}$分别为阴极金属材料(纯钨)的密度、比热容、热导率, $\rho_\text{M} = 19.35\;\text{g}/\text{cm}^3$; $C_\text{p,M}$, $\kappa_\text{M}$以及下文(2.4.5小节)中的发射率$ \epsilon_\text{M}$均为温度的函数^[68,69]. 如图2所示, $ \epsilon_\text{M}$和$C_\text{p,M}$与温度呈正相关随着温度的升高单调递增, $\kappa_\text{M}$的值随着温度的升高而减小.

外电路的控制方程为

该方程将外电路参数(电源电压$V_\text{dc}$、镇流电阻$R_\text{b}$、电路电流$I_\text{dis}$)与电极表面电流密度${\boldsymbol{J}}_\text{total}$、阳极电势$V_\text{a}$联系起来, 等离子体中的放电电流密度与电子通量、离子通量有关, 即${\boldsymbol{J}}_\text{total} = e{{{\boldsymbol{\varGamma}} }_\text{e}}- \displaystyle\sum\nolimits_{j}({q_{\text{i}, j}}{{{{\boldsymbol{\varGamma}} }_{\text{i}, j}}})$. 本文中, 考虑两种正离子, 且带电量大小与电子相同, 故有${\boldsymbol{J}}_\text{total}=e({{{\boldsymbol{\varGamma}} }_\text{e}}-{{{\boldsymbol{\varGamma}} }_{\text{Ar}^+}}- {{{\boldsymbol{\varGamma}} }_{\text{Ar}_2^+}})$.

为求解上述控制方程需在模型中设置相应的边界条件, 包括参与放电的各种粒子在边界处的通量, 以及在边界处发生的能量传递过程, 下面分别进行详细描述.

1)阴极边界. 考虑阴极处可能存在热运动过程、二次电子发射、热电子发射等过程, 故电子通量在阴极处的边界条件由下式描述:

这里, ${\boldsymbol{n}}$为单位法向量, 在指向电极表面时取值为1. ${v_\text{e,th}}=\sqrt{{8{k_\text{B}}{T_\text{e}}}/({\pi {m_\text{e}}}})$为电子热运动的平均速度. $\gamma_\text{se}$为阴极表面的二次电子发射系数, 取$\gamma_\text{se} = 0.096$^[33,70], $\gamma_\text{se}{\boldsymbol{\varGamma}} _{\text{i}, j}$表示第j种离子在阴极引起的二次发射电子的通量(在本模型中有$\text{Ar}^+$和$\text{Ar}_2^+$两种离子). ${{\boldsymbol{\varGamma}} }_\text{e,em}$是由热辐射过程从阴极发射的电子通量, 热发射电流密度为${{\boldsymbol{J}}_\text{e,em}}=-e{{{\boldsymbol{\varGamma}} }_\text{e,em}}$, 其计算表达式由理查森-肖特基(Richardson-Schottky)方程^[71]给出:

其中, $T_\text{c}$为阴极温度(单位为$\text{K}$); $A_\text{R}$为理查森常数, ${A_\text{R}} = {\lambda_\text{R}}{A_0}$, $A_0 = {4\pi {m_\text{e}}k_\text{B}^{2}e}/{{h^{3}}} = 1.2 \times {{10}^{6}}\;{\rm A}/ ({\rm m^2{\cdot}\text{\rm K}^2})$, ${\lambda _\text{R}}$为与材料有关的系数(对于金属钨, ${\lambda_\text{R}} = 0.5$), 因此${{A}_\text{R}} = 0.6 \times {{10}^{6}}\;\text{A}/({{\text{m}}^{\text{2}}}{\cdot} {{\text{K}}^{\text{2}}})$^[72]; $W_\text{f}$是阴极材料的功函数, 对于钨而言$W_\text{f} = 4.32\;\text{eV};\Delta W_\text{S} = e\sqrt{eE/(4\pi {{\varepsilon }_{0}}})$为考虑外电场作用的肖特基修正项.

2)阳极边界. 与阴极相比, 在阳极一般不存在二次电子发射过程和热发射过程^[73], 认为电子通量仅包含热运动项, 即

离子通量在阴极和阳极处表达式相同, 包括热运动项和由电场引起的漂移项^[32]:

其中, $v_\text{i,th}$是离子热运动的平均速度; $\alpha_\text{s}$的值取决于电场的方向,

激发态粒子的通量表达式在阴极和阳极处相同, 且由于激发态粒子为电中性, 其输运不受电场影响, 所以其通量表达式仅包含热运动项:

其中, $n_\text{exc}$是激发态粒子的密度, $v_\text{exc,th}$是其热运动平均速度, 在本文中激发态粒子包括$\text{Ar}^*$和$\text{Ar}_2^*$.

1)阴极边界. 电子能量在阴极处的边界条件以热平衡形式表示:

其中, $2{k_\text{B}}{T_\text{e}}$为沿正方向穿过某个平面时电子的平均动能, 推导过程见附录B; ${\varepsilon }_{\text{se}, {j}}=e({{E}_{\text{i}, j}}-2 W)$为由于离子撞击阴极表面发射出来的二次电子的平均能量, ${E}_{\text{i}, j}$是第j种离子的电离能; $\varepsilon_\text{e,em} = 2{k_\text{B}}{T_\text{c}}$为阴极热发射的电子的平均能量, $T_\text{c}$为阴极温度.

2)阳极边界. 在阳极一般不存在二次电子发射以及热发射过程, 所以电子在阳极的能量守恒方程(热平衡方程)只包括热运动项:

阴极热传导方程(23)在阴极与等离子体交界处的边界条件为^[43,44]

(33)式右边第1项${\boldsymbol{Q}}_\text{i}$描述了离子流到达阴极的能量流密度, 为阴极能量密度的增项:

其中, $T_\text{i}$是离子的温度(本文中$T_\text{i}=T_\text{g}$). 该项包含2部分: 1)离子穿过鞘层时在鞘层中获得的动能, 即$(3/2){k_\text{B}}T_\text{i}$; 2)离子的势能, 当离子运动到阴极表面时, 与阴极材料中的自由电子复合, 同时释放出电离能, 某些自由电子得到此电离能时, 这些电子可以克服阴极材料对它们的束缚能(即逸出功)而离开阴极, 该过程传递给阴极的能量为$({E_\text{i}}-W_\text{f})$.

第2项${\boldsymbol{Q}}_\text{g}$为阴极附近加热气体(等离子体)的热流密度, 见(21)式.

第3项${\boldsymbol{Q}}_\text{em}$为二次电子发射和热发射过程导致的阴极能量密度的损失, 其表达式为

其中, ${\boldsymbol{\varGamma}}_\text{e,em}$为热发射电流通量, $(W_\text{f}+2{k_\text{B}} T_\text{c})$表示在阴极表面由于热发射产生的电子所具有的能量, 该能量包含材料的逸出功(即势能)和电子穿过该阴极平面时的平均动能; ${{\boldsymbol{\varGamma}}_ \text{e,se}}= \displaystyle\sum\nolimits_{j}{\gamma_\text{se}{{{\boldsymbol{\varGamma}} }_{\text{i}, j}}}$为二次发射电子通量.

第4项${\boldsymbol{Q}}_\text{e}$为逆向电子能量密度(离开阴极的电子在电极间隙发生弹性碰撞, 碰撞后电子的运动方向会发生变化, 有可能由弹性散射返回阴极, 如果能量足以到达阴极表面将为阴极加热), 为阴极能量密度增项, 其表达式为

第5项${\boldsymbol{Q}}_\text{rad, B}$为考虑阴极黑体辐射释放出的能量, 为阴极能量损失项, 其表达式为

其中, $ \epsilon_\text{M} $为与阴极材料及温度有关的发射率(见图2)^[68,69], ${\sigma }_\text{SB} = 5.67 \times 10^{-8}\;\text{W}/(\text{m}^2\cdot\text{K}^4)$为斯蒂芬-玻尔兹曼(Stefan-Boltzmann)常数.

除此之外还需要设置回路中相应的电势和温度条件. 阳极处电势为$V_\text{a}$(由(24)式决定), 阴极接地, 其电势条件为$V_\text{c} = 0$. 阳极处温度设置为$T_\text{a} = 300\;\text{K}$, 阴极不与等离子体接触一侧的温度也设置为$T_{\text{c}, x=-20\;\text{mm}} = 300\;\text{K}$, 初始温度设置为$300\;\text{K}$, 其他计算域的温度变化由模型自洽求解.

本文基于COMSOL Multiphysics$ ^\circledR $ 软件^[74-76]对上述流体和传热方程进行数值求解. 电极间计算域由3000个网格单元组成, 单元大小比为10, 采用对称分布; 阴极体由200个网格单元组成, 单元大小比为200, 采用线性分布(远离阴极发射表面, 网格越稀疏). 本文对气压分别为$p_1 = 50 \;\text{Torr}$, $p_2 = 500 \;\text{Torr}$, 电极间距为$400\;{\text{μm}}$的微放电过程进行仿真研究. 为得到放电稳态时的参数, 仿真的物理时间为$100 \;\text{s}$.

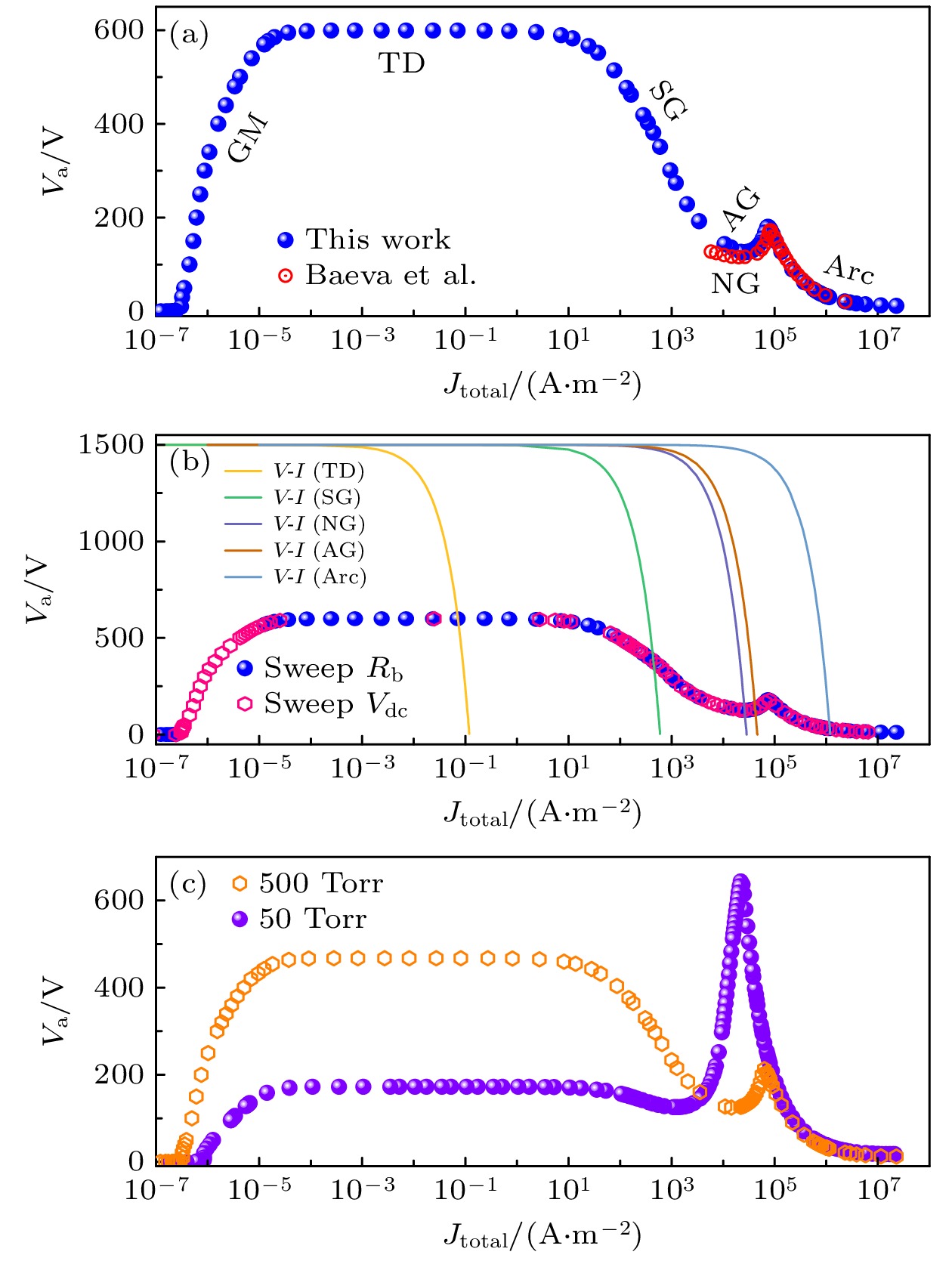
基于统一流体模型对高气压微放电过程进行数值模拟研究. 为验证统一流体模型的正确性, 首先与Baeva等^[39,40]的研究结果进行了对比. 设置电源电压$V_\text{dc} = 1500\;\text{V}$不变, 改变镇流电阻$R_\text{b}$的阻值, 得到不同阻值下放电稳态时的气隙电压($V_\text{a}$)与放电电流密度($J_\text{total}$)之间的关系, 即CVC曲线. 图3(a)中实心蓝点为本文中统一流体模型在$p_0 = 760 \;\text{Torr} \;(1 \;\text{atm})$时仿真计算得到的CVC曲线, 随着电流密度的增大, 放电模式从最初始的盖革-米勒放电区(Geiger-Müller discharge regime, GM)向汤森放电区(Townsend discharge regime, TD)、亚正常辉光放电区(subnormal glow discharge regime, SG)、正常辉光放电区(normal glow discharge regime, NG)、反常辉光放电区(abnormal glow discharge regime, AG)转变, 并最终过渡到电弧放电区(arc discharge regime, Arc)^[77,78], 涵盖了电流密度为$10^{-7}—10^{7}\;\text{A}/\text{m}^2$的大范围模拟结果, 完整包含了典型的放电模式. 该CVC曲线在正常辉光、反常辉光、电弧放电区与文献[39, 40]的结果一致, 验证了本文统一流体模型仿真结果的正确性. 在文献[39—41]的基础上, 本文中统一流体模型改进了重粒子(背景气体)的能量守恒方程((20)式), 完善考虑了背景气体加热机制, 在弹性碰撞和离子的焦耳加热项的基础上, 增加了淬灭反应和复合反应引起的能量变化项. 同时改进了阴极与等离子交界处的边界条件((33)式), 考虑了阴极表面更加完整的物理过程, 增加了阴极附近气体的热流密度项对阴极加热的贡献.

分别采用扫描电阻(固定电源电压$V_\text{dc}$不变, 改变镇流电阻$R_\text{b}$)、扫描电压(固定镇流电阻$R_\text{b}$不变, 改变电源电压$V_\text{dc}$)两种方式计算得到放电稳态时的CVC曲线, 两条曲线重合, 如图3(b)所示. 这一结果体现了CVC曲线是气体间隙的固有放电属性, 主要取决于放电基本过程, 上述两种计算方法在仿真结果上是等效的. 图3(b)中的五条$V{\text{-}}I$曲线为$V_\text{dc}$固定、$R_\text{b}$变化时外电路的特性曲线(由(24)式计算得出), 其与CVC曲线的交点决定了放电所处的模式或工作点, 依次为汤森放电区、亚正常辉光放电区、正常辉光放电区、反常辉光放电区及电弧放电区.

基于该统一流体模型, 计算了$V_\text{dc} = 1500\;\text{V}$时, $p_1 = 50 \;\text{Torr}$与$p_2 = 500 \;\text{Torr}$两个气压条件下的放电过程, 稳态时的CVC曲线如图3(c)所示. 两个气压条件下的CVC曲线整体趋势相似, 均包含完整的放电模式. 通过对比可以发现, 在汤森放电区, $50 \;\text{Torr}$时的放电电压小于$500 \;\text{Torr}$时的放电电压, 即$V_\text{a1} < V_\text{a2}$. 汤森放电区的放电电压对应气隙的击穿电压$V_\text{b}$. 根据帕邢(Paschen)定律^[79], 击穿电压是气压与间隙距离乘积($pd$)的函数, 为一条U形曲线. 本文研究条件下的$pd$值位于帕邢曲线的右半支, 当电极间距d保持不变时, 气压p升高时造成电子自由行程缩短, 电子能量积累效率低, 电离能力减弱, 因此需要更高的电压才能击穿气隙. $50 \;\text{Torr}$时的正常辉光放电电流密度小于$500 \;\text{Torr}$时的结果, 即$J_\text{total,n1} < J_\text{total,n2}$. 根据文献[80], 正常辉光放电中电极间隙的放电电流密度的估算式为

其中, $\varepsilon_0$为介电常数, $\mu_\text{i}$为离子的迁移率, $V_\text{C}$为阴极位降, $d_\text{C}$为阴极位降区的宽度. 正常辉光放电中阴极位降$V_\text{C}$与气压无关, 而阴极位降的宽度$d_\text{C}$与气压p成反比. 当气压升高时, 正常辉光放电的电流密度增大, 这也造成反常辉光放电区整体向右移动. 此外, $50 \;\text{Torr}$时反常辉光-电弧的转捩电压$V_\text{t1}$比$500 \;\text{Torr}$的转捩电压高, 即$V_\text{t1}>V_\text{t2}$. 当气压越高时放电气隙中的碰撞过程会越剧烈, 根据重粒子(背景气体)能量守恒方程((20)式)可知碰撞越剧烈, 气体温度越高, 气体温度的升高会引起气隙中热电离贡献的增大, 热电离贡献越大转捩电压就会越小.

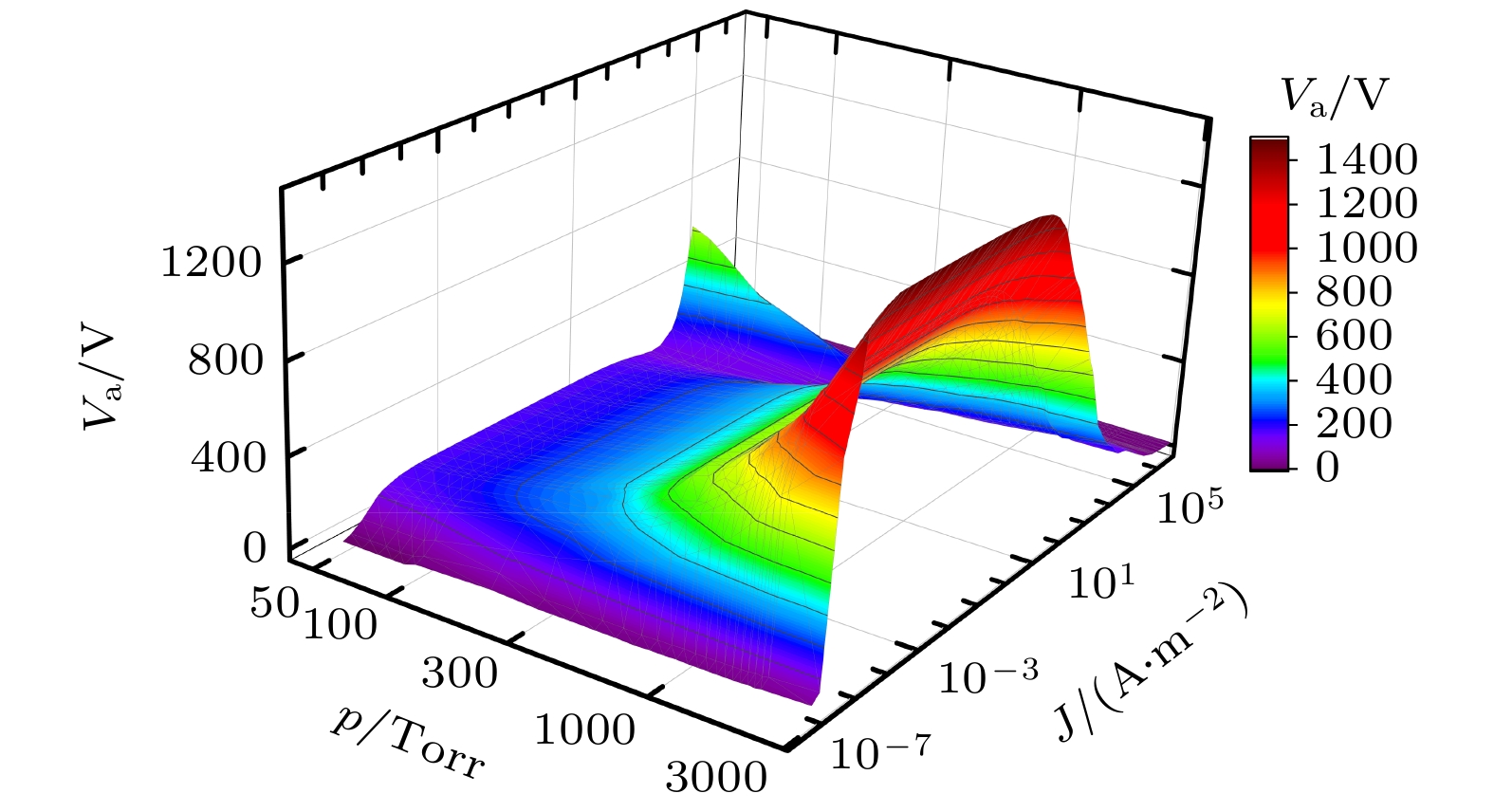
继续改变工作气压, 得到气压从$50\;\text{Torr}$到$3000\;\text{Torr}$变化时的CVC曲线, 如图4所示. 当气压高于$3000\;\text{Torr}$时, 外施电压$V_\text{dc} = 1500 \;\text{V}$不足以使间隙击穿, 需要提高电源电压才能得到完整的CVC曲线. 当气压低于$50\;\text{Torr}$时, 接近帕邢曲线的左半支, $pd$值较小, 流体模型不再适用. 图4中随着气压的升高, 汤森放电的放电电压逐渐升高, 正常辉光区的放电电流密度增加, 反常辉光-电弧转捩电压$V_\text{t}$则降低, 与图3(c)结果一致. 下面对$p_1 = 50 \;\text{Torr}$和$p_2 = 500 \;\text{Torr}$不同放电模式下的典型放电参量进行详细讨论.

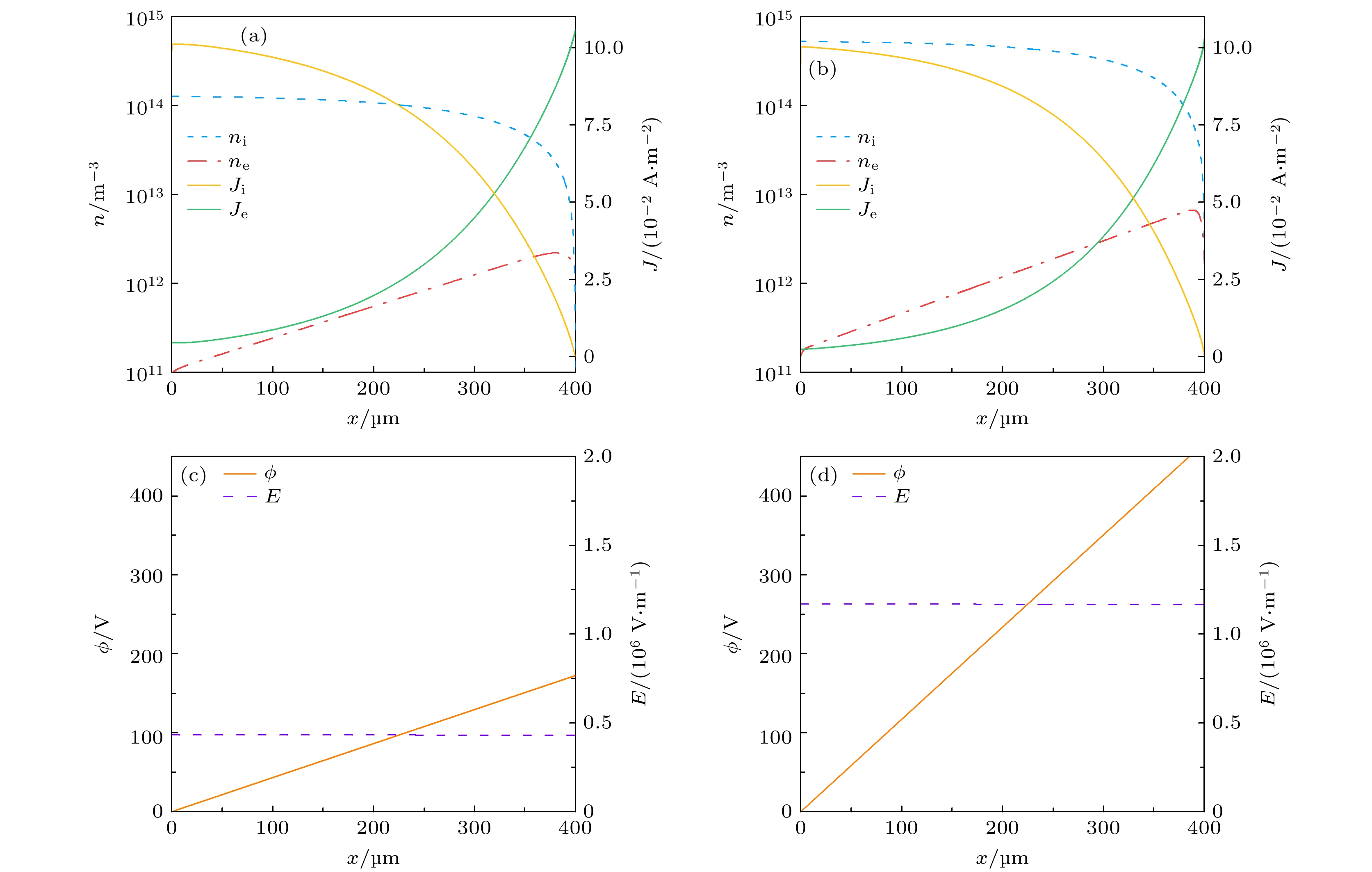
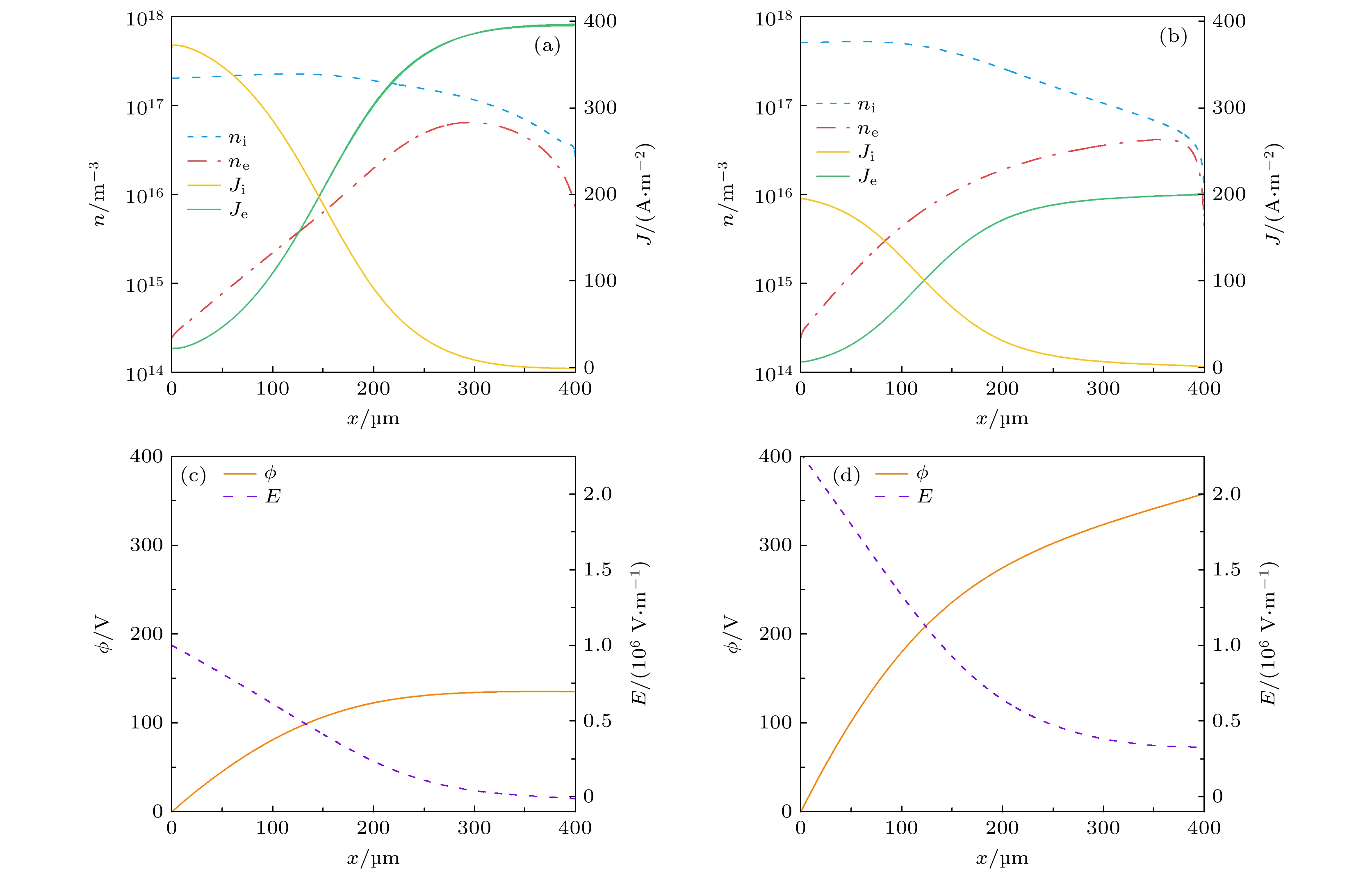
图5给出了汤森放电达到稳态时典型参数沿轴向的空间分布. 其中, 图5(a)和图5(b)分别展示了$50 \;\text{Torr}$和$500 \;\text{Torr}$气压条件下电子密度($n_\text{e}$)、离子密度($n_\text{i}=n_{\text{Ar}^+} + n_{\text{Ar2}^+}$)、电子电流密度($J_\text{e}$)、离子电流密度($J_\text{i}$)的空间分布. 通过不同气压条件下的对比可知, 气压越高, 电子平均自由程越小, 碰撞电离次数增加, 带电粒子密度增大. 电子密度从阴极到阳极逐渐增加, 与距离呈指数关系, 并且$500 \;\text{Torr}$时电子密度增长的斜率大于$50 \;\text{Torr}$的结果. 从汤森放电开始进入自持放电. 根据汤森理论^[81], 维持放电的主要过程为α过程(空间中电子崩的发展过程)和γ过程(阴极表面二次电子发射过程). 由α过程可知, 空间位置x处的电子密度$ n_\text{e}(x)$为

其中, ${n_0}$为由外界因素在阴极附近处的初始电子密度^[82,83], α为碰撞电离系数(可表示为电子密度对数值与距离变化关系的比例). 在均匀电场中α为常数, 其计算表达式为^[84]

其中, $x_1$和$x_2$为放电间隙中的位置坐标(此处取$x_1 = 100\;{\text{μm}}$, $x_2 = 300\;{\text{μm}}$); $n_\text{e1}$和$n_\text{e2}$分别为这两个位置处的电子密度($p_\text{1} = 50 \;\text{Torr}$时, $n_\text{e1} = 2.42 \times 10^{11}\; \text{m}^{-3}$, $n_\text{e2} = 1.25 \times 10^{12}\; \text{m}^{-3}$; $p_\text{2} = 500 \;\text{Torr}$时,$n_\text{e1} = 4.59 \times 10^{11}\; \text{m}^{-3}$, $n_\text{e2} = 3.01 \times 10^{12}\; \text{m}^{-3}$). 由(40)式得到$p_\text{1} = 50 \;\text{Torr}$, $p_\text{2} = 500 \;\text{Torr}$时的碰撞电离系数分别为$\alpha_1 = 8209.7 \;\text{m}^{-1}$, $\alpha_2 = 9402.8 \;\text{m}^{-1}$. 此外, α系数一般由电场大小、气压、气体种类决定^[80], 其表达式为

其中, A, B为与气体种类相关的参数, 对于氩气有$A = 10.2 \;\text{m}^{-1} \cdot\text{Pa}^{-1}$, $B = 176.3\; \text{V}/(\text{m}\cdot\text{Pa})$. (41)式的适用范围是$75\;\text{V}/(\text{m}{\cdot} \text{Pa}) < E/p < 450\;\text{V}/(\text{m}{\cdot} \text{Pa})$, 在该约化场强范围内, $p_\text{1} = 50 \;\text{Torr}$条件下求解得$\alpha_1 = 6481.5 \;\text{m}^{-1}$. $p_\text{2} = 500 \;\text{Torr}$时约化场强低于(41)式的适用范围, 根据文献[80]中结果插值估算得到$\alpha_2 = 7450 \;\text{m}^{-1}$. 值得一提的是, 由于(41)式仅考虑了最基本的电子碰撞原子的直接电离过程, 可能低估α系数. 本文模型中除了直接电离, 还考虑了逐级电离及二聚体的电离过程, 这些过程的存在导致有效电离系数的增加.

在阴极附近, 离子密度远大于电子密度, 由于二次电子发射过程, 在阴极表面有$e n_\text{e} v_\text{e} = \gamma_\text{se}q_\text{i} n_\text{i} v_\text{i}$(本文中$\gamma_\text{se} = 0.096\ll1$), 电场中电子的迁移速度远大于离子的迁移速度($v_\text{e}\gg v_\text{i}$), 因此在阴极处有$n_\text{i}\gg n_\text{e}$. 在放电空间中, 离子(电子)密度从阴极到阳极逐渐降低(增加), 正离子从阳极向阴极运动(电子运动方向与正离子相反). 放电总电流为$I(x)=e n_\text{e} v_\text{e}+q_\text{i} n_\text{i} v_\text{i}=e v_\text{e} {n_0}{\mathrm{e}}^{\alpha x} +q_\text{i} n_\text{i} v_\text{i}=I(x= d)= e v_\text{e} {n_0}{\mathrm{e}}^{\alpha d}$(阳极处离子电流为0). 根据电流连续性, 从阴极到阳极电子电流逐渐占主导, 离子电流占比减弱. 在汤森放电中, 整个放电间隙离子密度大于电子密度($n_\text{i}>n_\text{e}$). 在外电场(近似均匀)作用下, 以阳极附近为例, 根据电流连续性可知, 离子在阳极的通量为零, 且电子离子成对出现, 二者在阳极附近处密度接近; 由于电子的迁移速度大于离子的迁移速度(二者方向相反), 且电子雪崩发展与距离的指数成正比((39)式), 电子密度峰值在阳极附近, 而离子密度在阴极附近达到峰值.

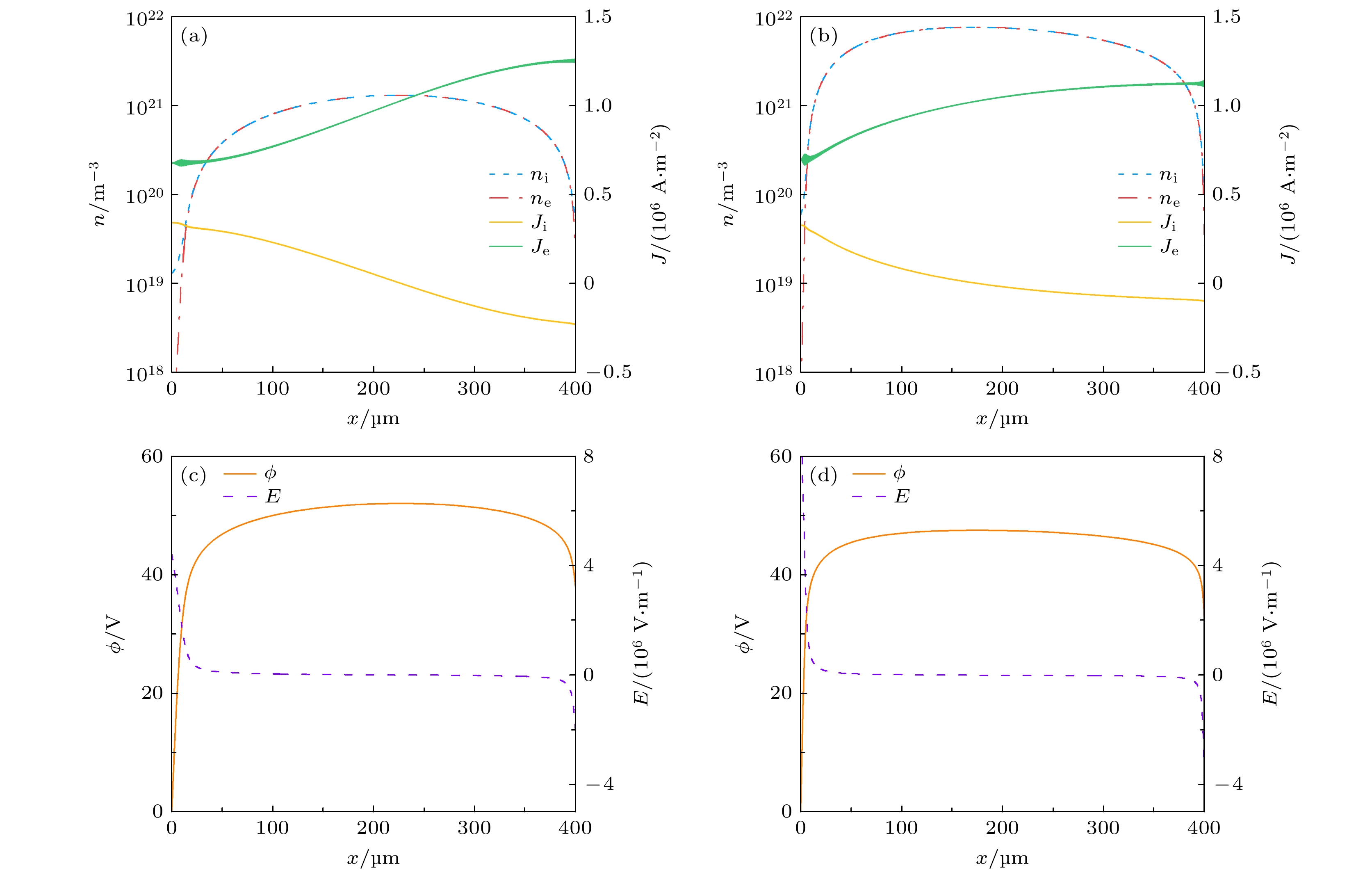
图5(c)和图5(d)分别为$ 50\;\text{Torr} $和$500 \;\text{Torr}$时电势(ϕ)和电场(E)的空间分布. 可以发现, 电势从阴极到阳极逐渐上升, 且斜率保持不变, 电场分布均匀. 尽管在阴极附近形成了净的正空间电荷, 但由于带电粒子密度绝对值较低($10^{14} \;\text{m}^{-3}$量级), 未导致明显的空间电场畸变, 尚未形成准中性等离子体区. 此外, $p_1 = 50 \;\text{Torr}$时的阳极电势$V_\text{a1} = 172.4 \;\text{V}$小于$p_2 =500 \;\text{Torr}$时的阳极电势$V_\text{a2}= 467.3 \;\text{V}$, 对应前文(图3(c))所述帕邢曲线右半支, 即击穿电压随气压的升高而上升^[79].

通过增加电压或放电电流, 碰撞电离与电荷输运将进一步发展, 放电将从经典的汤森放电区进入亚正常辉光放电区. 该区域的典型特点是放电具有负的伏安特性, 即气隙电压随着电流密度的增加而下降. 图6(a)与图6(b)分别给出了气压为50 Torr和500 Torr 时, 亚正常辉光放电区的电荷密度与电流密度分布. 其中, 带电粒子密度约为$10^{17} \;\text{m}^{-3}$量级, 明显高于汤森放电区. 此时, 放电间隙较为明显地呈现出阳极、阴极两个区域^[85], 整个放电间隙的离子密度仍总体大于电子密度, 表现为正空间电荷效应, 未形成电中性的等离子体区^[86], 离子密度峰值位置更靠近阴极, 电子密度峰值位置靠近阳极, 且与该处的离子密度更接近, 空间电荷对电场畸变的效应在阳极附近更加显著^[32]. 与汤森放电相比, 阴极附近依旧为离子电流密度占主导, 阳极附近电子电流密度占主导, 但电子、离子电流密度在阳极区分布变得平坦且二者的相交点向阴极移动. 图6(c)与图6(d)给出了气压为50和500 Torr 时电势与电场的空间分布, 可以看出在阳极附近均出现明显畸变. 阴极附近净空间电荷密度值较大导致电势在阴极区的斜率比阳极区的斜率更大, 阴极附近电场更强, 相应地, 主要的电位降出现在阴极区. 阳极附近由于空间电荷作用电场较小, 电势变化相对平缓. 通过对比, 两个气压条件下的放电参数分布特性相似, 但高气压下气隙电压明显更高, 阴极电场更强, 粒子数密度更高, 但电子电流密度幅值与低气压相比更低. 这是由于高气压下的约化场强偏低, 粒子的输运(漂移)速度更低所致. 值得一提的是, 恒流源一般较恒压源更容易稳定地维持亚正常辉光放电, 通过进一步增大放电电流, 将很快进入正常辉光放电区.

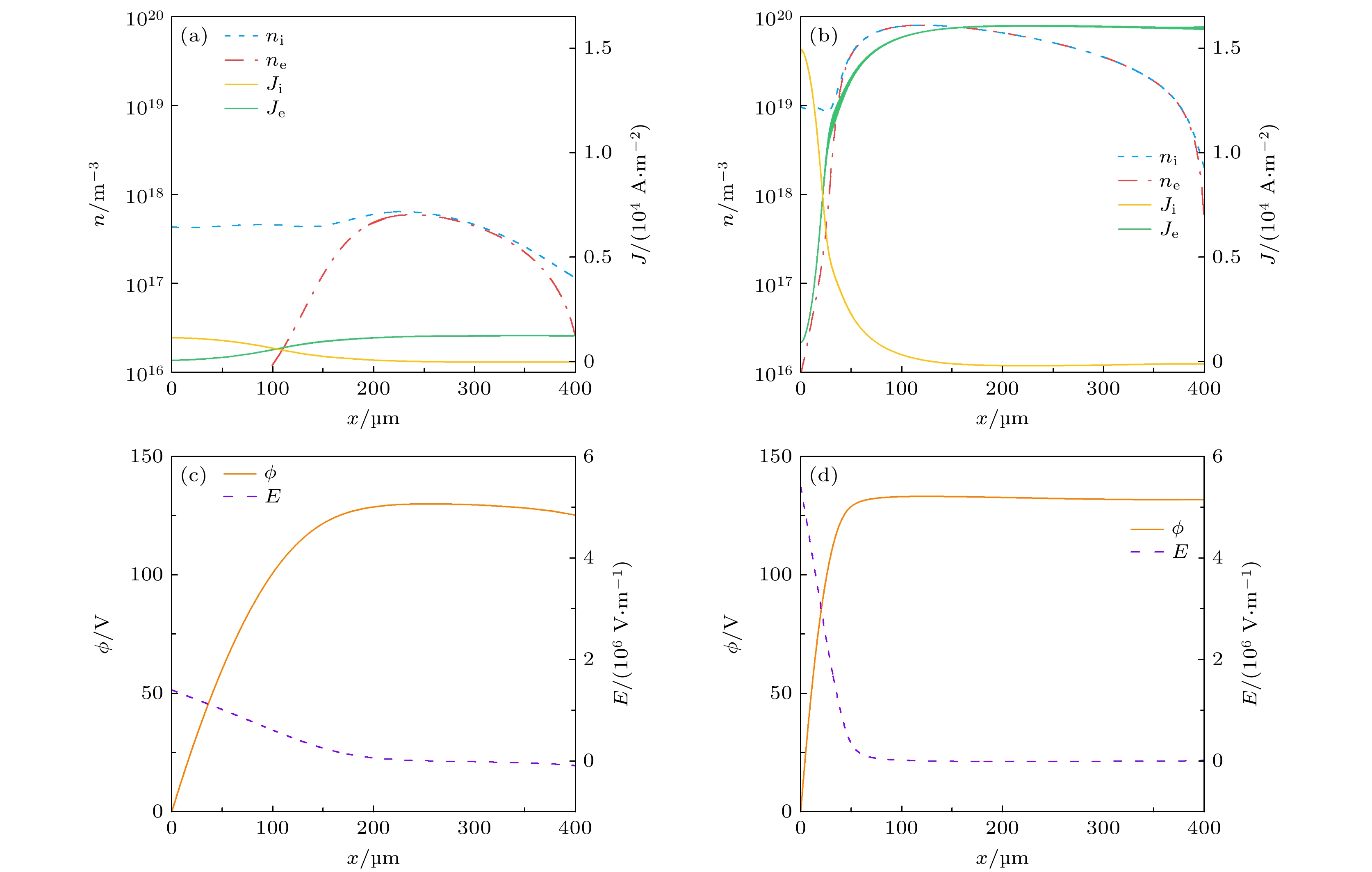
正常辉光是气体放电现象中一种重要形式, 其典型特征是放电发出柔和的光并充满放电空间, 放电通道在阴阳极之间呈明暗相间的光层分布, 从 阴极到阳极分别为阿斯顿(Aston)暗区、阴极辉光区、阴极暗区、负辉光区、法拉第(Faraday)暗区、正柱区、阳极暗区、阳极辉光区^[77,80]. 图7(a)和 图7(b)给出了正常辉光放电区带电粒子密度、电流密度的空间分布. 电极间隙出现等离子体区($n_\text{e} \approx n_\text{i}$). 与汤森放电区或亚正常辉光放电区相比, 正常辉光放电区空间电荷效应显著, 尤其在高气压条件下. $p_1 = 50 \;\text{Torr}$时等离子体区的长度$d_\text{PL1}$小于$p_2 = 500 \;\text{Torr}$时对应长度$d_\text{PL2}$, 即$d_\text{PL1} < d_\text{PL2}$. 这是由于正常辉光放电中的阴极位降区长度与气压呈负相关, 电极间距d增大或气压p升高时, $ d_\text{PL} $增加. 放电会根据参数自动调节主体区的长度$d_\text{PL}$来确保辉光工作点. 改变电极间隙距离d和气压p, 均会使鞘层长度发生改变, 通常低气压鞘层会占据更大的放电空间. 此外, 高气压下电子电流密度与离子电流密度的交点进一步靠向阴极, 在阴极区存在更显著空间电荷效应, 电子和离子电流密度在主体区幅值变化较小.

图7(c)和图7(d)为不同气压下正常辉光放电区的电势与场强的空间分布. 阴极区电势大幅升高, 随后变化平缓, 整个电极间电势差主要位于阴极区. 与之对应的是, 放电的强电场区也主要位于阴极附近, 最大电场位于阴极表面, 随着与阴极距离的增加, 电场接近线性下降, 主体区电场很小. 本文中仿真参数$p_1 = 50 \;\text{Torr}$时阴极位降$V_\text{C1} = 124.1 \;\text{V}$, $p_2 = 500 \;\text{Torr}$时$V_\text{C2} = 129.8 \;\text{V}$, 接下来对该结果的合理性进行分析. 根据文献[80], 正常辉光的阴极位降$V_\text{C}$可由下式估算:

根据(42)式可知, 正常辉光放电的阴极位降$V_\text{C}$主要取决于阴极二次电子发射系数$\gamma_\text{se}$、气体性质参数A和B. 本文条件下估算的阴极位降理论值为$V_\text{C} = 126.3 \;\text{V}$. 本文仿真模拟结果与理论估算值相近. 此外, 模拟得到的电势分布显示电极间电位略高于阳极的电位, 这一差值是典型的低气压短间隙辉光中的等离子体电位 (plasma potential), 详见Bogaerts等^[87,88]的研究描述.

辉光放电中阴极位降边界通常难以精确定义, 根据文献[89], 正常辉光放电阴极位降区边界(或鞘层边界)可由电场强度衰减至一定值(如电场最大值的14%)得到. 本文中, 确定$p_1 = 50 \;\text{Torr}$, $p_2 = 500 \;\text{Torr}$时阴极位降区的宽度分别为$d_\text{C1} = 160.3\;{\text{μm}}$,$d_\text{C2} = 35.1\;{\text{μm}}$. 一般地, 正常辉光放电可自动调节阴极区长度$d_\text{C}$, 使得放电工作点对应到帕邢曲线击穿电压的最小点(即Stoletov point^[90]). 当电极间隙总长度不变时, 若$d_\text{C1}>d_\text{C2}$, 则有$d_\text{PL1} < d_\text{PL2}$. 进一步观察发现, 阳极附近电场为负值, 即发生了电场(方向)反转(field reversal), 这与阳极附近存在负的电位差相对应. 将在反常辉光放电区对电场反转现象进行进一步讨论.

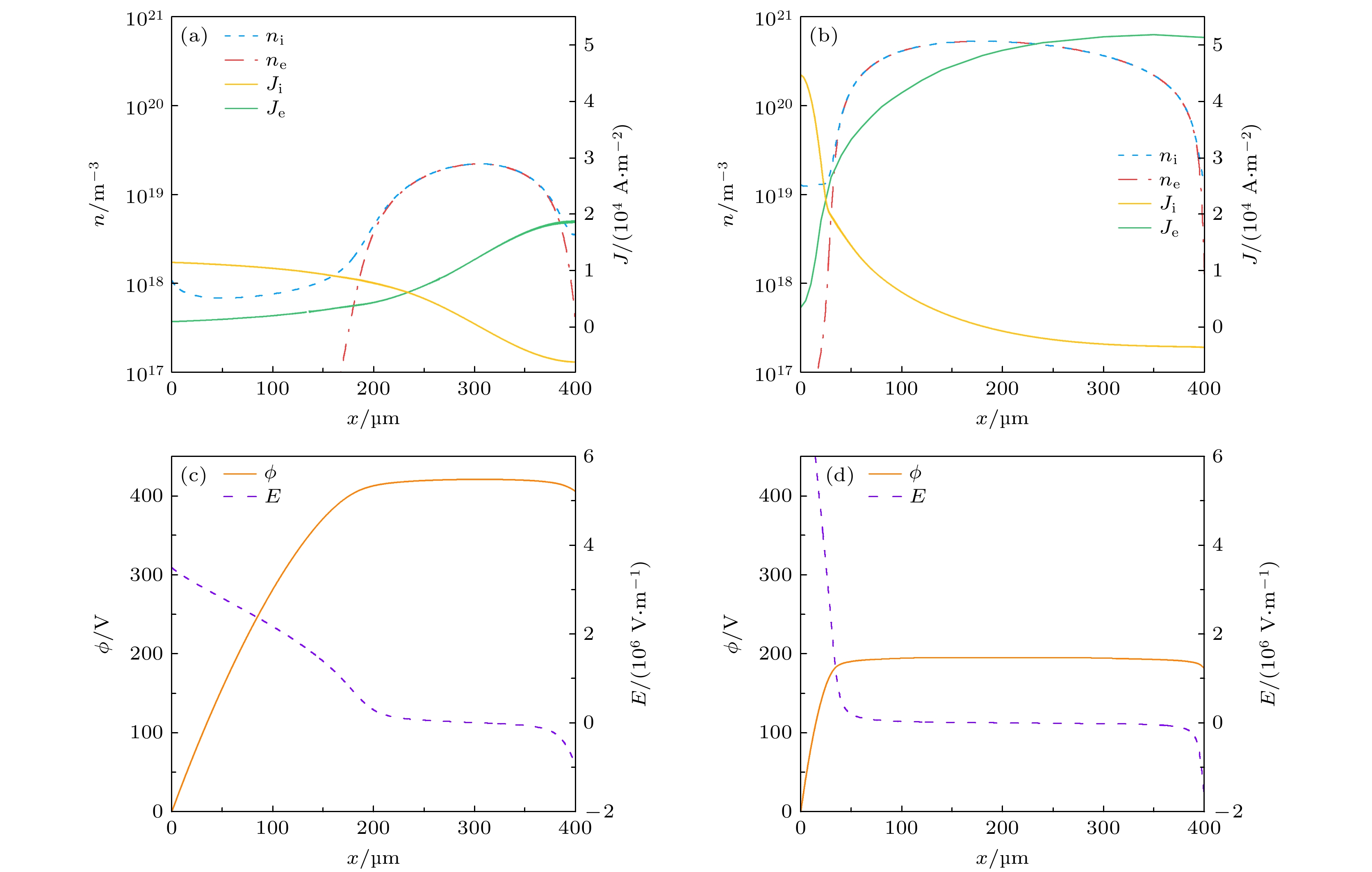
在正常辉光放电区, 电流尚未覆盖整个阴极表面, 随着放电电流增加, 阴极表面辉光面积成比例增加, 而电流密度则保持不变, 相应地, 阴极位降$V_\text{C}$近似为常量, 在CVC曲线上表现为接近水平线^[9]. 在阴极表面全部布满辉光之后, 随着放电电流的进一步增加, 电流密度与空间电荷密度成比例增长, 引起电场的进一步畸变, 放电进入反常辉光放电区. 这时阴极位降区的厚度$d_\text{C}$将进一步减小, 在给定气压和间距条件下, 随着电流的增加, 维持放电所需的气隙电压以及阴极位降$V_\text{C}$将迅速升高, 表现为正相关的反常辉光伏安特性曲线.

图8(a)和图8(b)展现了气压为$ 50\;\text{Torr} $和$500\;\text{Torr}$条件下反常辉光放电区带电粒子数密度和电流密度的空间分布. 此时, 放电带电粒子数密度增加至$10^{20} \;\text{m}^{-3}$量级, 空间电荷效应进一步加剧, 等离子区($n_\text{e} \approx n_\text{i}$)的宽度进一步扩展. 电子电流密度从阴极到阳极逐渐增加, 且在整个电极间隙为正值; 而离子电流密度从阴极到阳极逐渐减少, 在远离阴极位置处电流方向发生改变(由正值变为负值). 图8(c)和图8(d)为不同气压条件下电势与电场的空间分布. 与正常辉光放电类似, 电场在阴极区近似线性下降, 并在等离子区幅值较小、且变化不大, 但在阳极附近变为明显负值.

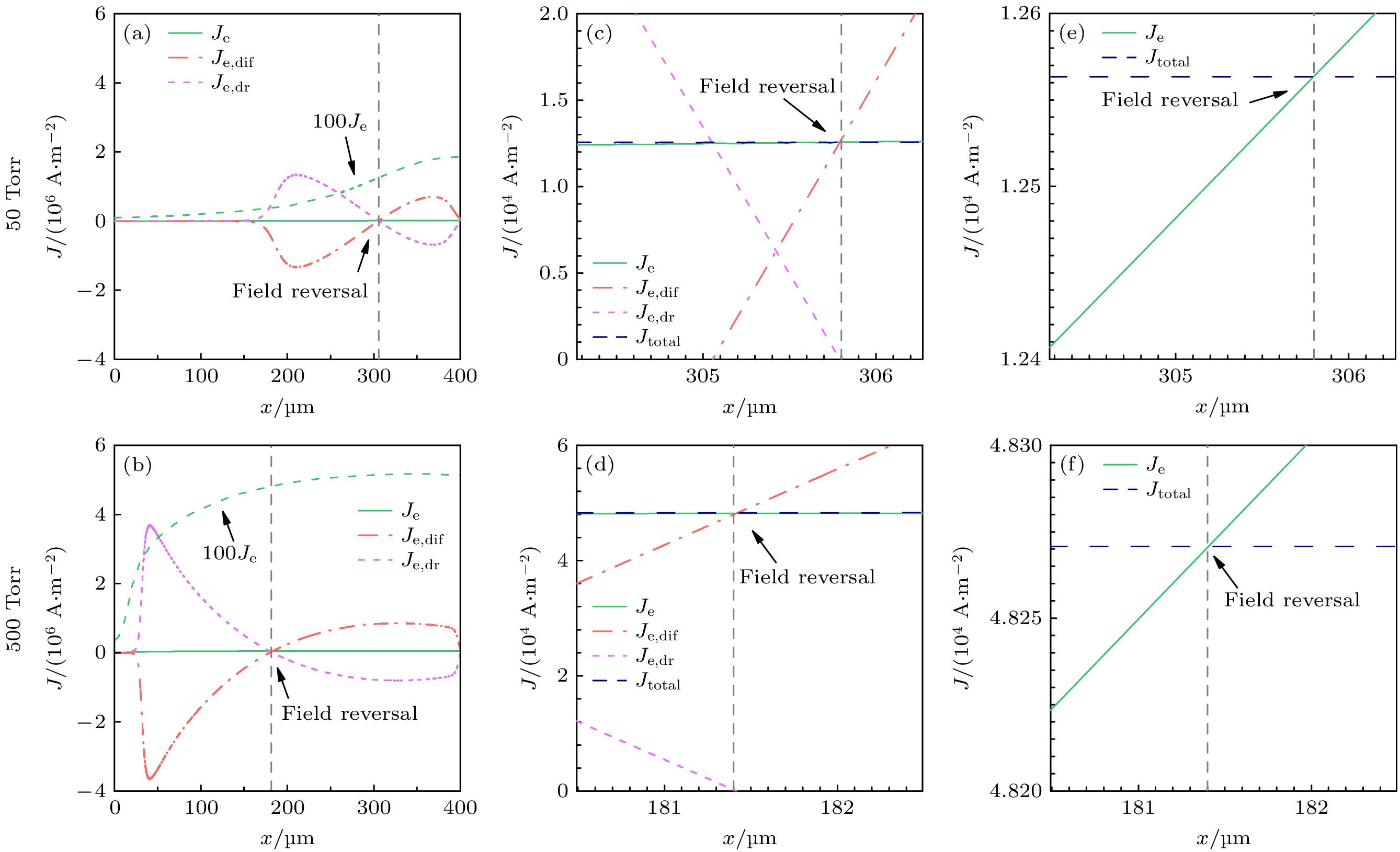
接下来对空间电场反转位置进行定量分析. 定义电场方向发生反转且幅值为零的位置坐标为$x_\text{r}$. 已有研究^[91,92]表明, 电场反转一般发生在短间隙辉光放电的负辉区, 非局域电离是导致放电空间发生电场反转的必要条件. 当气隙带电粒子密度梯度较大, 且慢电子扩散电流密度($J_\text{e, dif}$)超过总电流密度($J_\text{total}$)时, 会发生电场反转并延缓电子的扩散过程^[93], 使气隙中电流输运满足连续性定理. 图9为不同气压条件下放电总电流密度($J_\text{total}$)、电子电流密度($J_\text{e}$)、电子电流密度的扩散分量($J_\text{e, dif}$)和电子电流密度的漂移分量($J_\text{e, dr}$)的空间分布(注: 图9(a)和图9(b)中$J_\text{e}$幅值较小但不为零). 根据“漂移-扩散近似”, 电子电流密度可以由其扩散分量与漂移分量组成, 表达式分别为

从图9(a)和图9(b)可以看出, 在阴极附近$J_\text{e,dif} < 0$且数值上与$J_\text{e}$相近, 随后$J_\text{e,dif}$先降低后升高, 并由负值变为正值, 随后在某一点处有$J_\text{e,dif}=J_\text{e}$, 此处即为电场反转的位置; 在阳极附近有$J_\text{e,dif}>J_\text{e}$. 图9(c)和9(d)展现了不同气压下$x_\text{r}$附近的电流密度空间分布, 可以看出发生电场反转后, 电子扩散电流密度($J_\text{e,dif}$)在数值上超过了电子电流密度($J_\text{e}$), 此时在$x_\text{r}$处有电子漂移电流密度为零($J_\text{e,dr} = 0$). 离子电流密度在阴极附近占主导, 在放电间隙的其他区域数值较小, 可认为$J_\text{total}\approx J_\text{e}$. 特别地, 当发生电场反转时, 正离子在电场的作用下分别向阴极和阳极运动, 在$x_\text{r}$处离子的通量为零. 根据“漂移-扩散近似”, 离子电流密度为$J_\text{i}= J_\text{i,dif}+J_\text{i,dr}=e{D_\text{i}}\nabla {n_\text{i}}-e{\mu_\text{i}}{n_\text{i}}{\boldsymbol{E}}$. 在$x_\text{r}$处, 离子密度达到极值, 离子密度的梯度为零, 同时电场强度为零, 此处离子电流密度为零, 故总电流密度即等于电子电流密度($J_\text{total}= J_\text{e}$)^[94], 如图9(e)和图9(f)所示. 根据文献[95-98], 电场反转的位置与放电空间中离子密度最大值位置、电势极值位置对应. 表2列出了本模型中反常辉光放电区不同气压条件下计算得到的相关临界位置. 其中, $p_1 = 50 \;\text{Torr}$时电场反转的位置为$x_{\text{r}} = 305 \;\text{μm}$, $p_2 = 500 \;\text{Torr}$时$x_{\text{r}} = 183 \;\text{μm}$. 同时, 在$ 50\;\text{Torr} $和$500 \;\text{Torr}$两个气压条件下, 5个临界点位置几乎一致, 这与上述理论分析相符. 此外, Boeuf等^[94]基于高能电子的能量弛豫长度通过粒子法, 推导出了电场反转位置的计算式, 表明电场反转的位置$x_\text{r}$只与阴极鞘层长度$d_\text{C}$、间隙长度d和电离速率的衰变常数λ有关, 该结论与Maric等^[99]的实验结果相符合.

图8(c)和图8(d)中$p_1 = 50 \;\text{Torr}$时, 阴极位降区的宽度为$d_\text{C1} = 188.9\;{\text{μm}}$, 此时约化电流密度$J_\text{total,1}/p_1^2 = 4.96\;\text{A}/(\text{m}^2\cdot \text{Torr}^2)$, 约化阴极位降区长度$p_1 d_\text{C1} = 9.445 \times 10^{-3} \;\text{Torr}\cdot\text{m}$; 相应地, $p_2 = 500\;\text{Torr}$时, 阴极位降区宽度变为$d_\text{C2} = 33.1\;{\text{μm}}$, $J_\text{total,2}/p_2^2 = 0.1928\;\text{A}/(\text{m}^2\cdot \text{Torr}^2)$, $p_1 d_\text{C1} = 1.655 \times 10^{-2} \;\text{Torr}\cdot\text{m}$. 本文仿真结果也验证了$pd_\text{C}$与$J_\text{total}/p^2$成反比标度关系, 与文献[21, 100]中的实验结论一致.

随着放电电流密度的进一步增大, 气隙电压开始急剧下降, 放电从反常辉光放电区过渡到电弧放电区, CVC曲线具有负微分电阻特性(见图3中Arc区). 与辉光放电相比, 电弧放电具有低放电电压(可低至几伏)、高放电电流密度(可达$10^8 \;\text{A}/\text{m}^2$)的特点. 此时, 放电空间的电离机制以及阴极发射电子机制与辉光放电明显不同. 在电弧放电区, 放电由阴极表面的热发射过程和空间中的热电离过程主导, 而阴极表面的γ过程和空间中的α过程的影响相对变弱.

图10是对应电流密度为$10^6 \;\text{A}/\text{m}^2$时电弧放电区的放电参数分布. 图10(a)和图10(b)展示了在$ 50 \;\text{Torr} $和$500 \;\text{Torr}$气压条件下带电粒子数密度与电流密度分布. 在强烈的空间热电离作用下, 电子密度远高于辉光放电区, 达$10^{21}—10^{22} \;\text{m}^{-3}$量级. 放电空间较为明显地呈现出阴极区、等离子区和阳极区3个区域, 鞘层区大大缩短, 呈准中性的等离子区几乎占据了整个体区. 根据文献[101]对鞘层边缘的定义, 确定$({n_\text{i}-n_\text{e}})/{n_\text{i}} \approx 0.01$的位置为鞘层边缘. 本文仿真参数下, $p_1 = 50 \;\text{Torr}$, $p_2 = 500 \;\text{Torr}$对应的阴极鞘层厚度分别为$d_\text{cs1} = 23.8\;{\text{μm}}$, $d_\text{cs2} = 16.8\;{\text{μm}}$, 远小于辉光放电区的鞘层厚度. 此时, 电子电流密度从阴极到阳极逐渐升高; 离子电流密度从阴极到阳极逐渐降低, 在气隙中某一位置电流方向发生改变(由正值变为负值). 在整个放电气隙, 电子电流密度均大于离子电流密度, 二者不存在交点.

图10(c)和图10(d)为不同气压条件下电弧放电区电势和电场的空间分布. 电势在鞘层区几乎垂直增长/降低, 在主体区变化平缓. 与之对应, 电场在鞘层内剧烈下降, 阴极鞘层内为正, 在体区幅值较小. 与反常辉光放电类似, 电弧放电的电场在阳极区也为负值, 即出现了电场反转. 本文参数条件下, $p_1 = 50 \;\text{Torr}$与$p_2 = 500 \;\text{Torr}$对应的放电电压分别为$V_\text{a1} = 37.9\;\text{V}$, $V_\text{a2} = 32.5\;\text{V}$, 阴极位降分别为$V_\text{C1} = 51.7\;\text{V}$, $V_\text{C2} = 35.9\;\text{V}$, 均明显低于辉光放电区的情形. 在电弧放电区, 阴极受到大量高速正离子轰击被加热, 产生显著的热电子发射, 这种发射效率远高于正离子轰击阴极引起的二次电子发射. 这也类似于每个正离子碰撞阴极打出的电子平均数大大增加(即有效$\gamma_\text{se}$系数的大大增加), 根据(42)式可知$\gamma_\text{se}$越大, 阴极位降$V_\text{C}$越小.

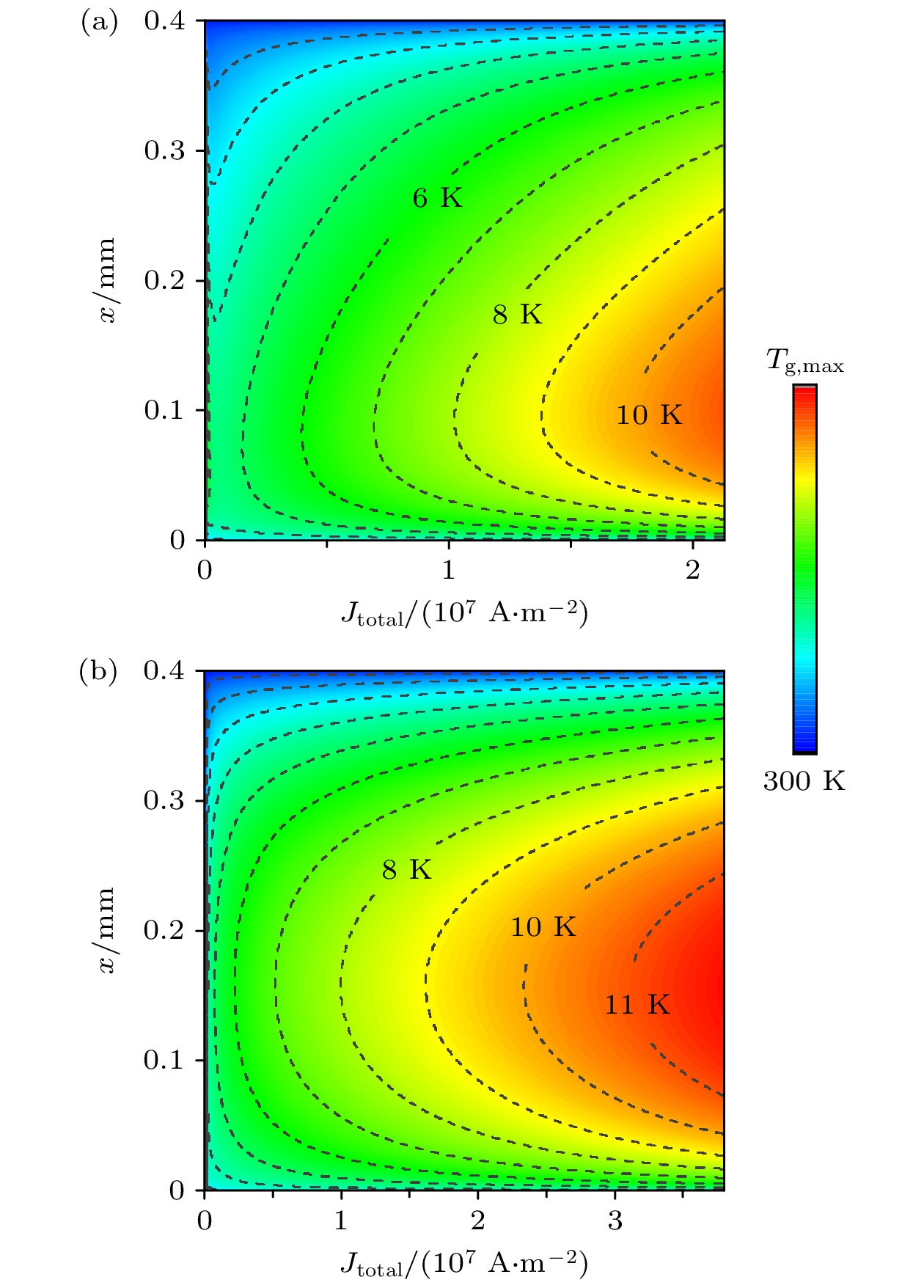
本文中, 气体温度的变化通过求解重粒子(背景气体)能量守恒方程(20)得到. (20)式中包含了背景气体被加热的4种机制, 包括: 电子与气体之间的弹性碰撞产生的能量增益、电场对离子做功产生的焦耳加热、激发态氩原子淬灭以及复合反应所引起的能量变化. 本文模型中阴极表面和气体的初始温度均为$300\; \text{K}$, 考虑放电过程中的气体加热、阴极热发射与热传导等过程, 随着放电电流密度的增加会出现明显的升温过程, 下面对温度的变化特性进行讨论. 图11(a)与图11(b)分别为$50 \;\text{Torr}$和$500 \;\text{Torr}$气压条件下气体温度的空间分布随放电电流密度的变化情况. 两种气压条件下, 间隙气体温度的分布特性类似, 气体温度随电流密度增加而升高. 相同电流密度条件下高气压对应的气体温度更高, $500 \;\text{Torr}$条件下, 气体温度峰值为$T_\text{g,max} = 11850 \;\text{K}$(对应最大电流密度工况).

总体而言, 气体温度从汤森放电区的$300 \;\text{K}$逐渐增加到电弧放电区的几千开, 但只有在电流密度大于$10^6 \;\text{A}/\text{m}^2$量级时, 气体温度才会在$300\; \text{K}$的基础上有显著提升并增大至$1000\;\text{K}$以上, 此时对应CVC曲线的电弧放电区. 这也说明只有进入热发射和热电离主导的电弧放电区, 气体加热效果才最为显著. 在某一电流密度下, 气体温度从阴极开始逐渐升高, 到达单一峰值后开始下降, 在阳极处为$300\;\text{K}$. 阴极受到离子轰击、气体传热等过程的影响在$300\;\text{K}$的基础上有所升高, 而阳极温度保持为$300\;\text{K}$, 气体温度峰值位置更靠近阴极侧.

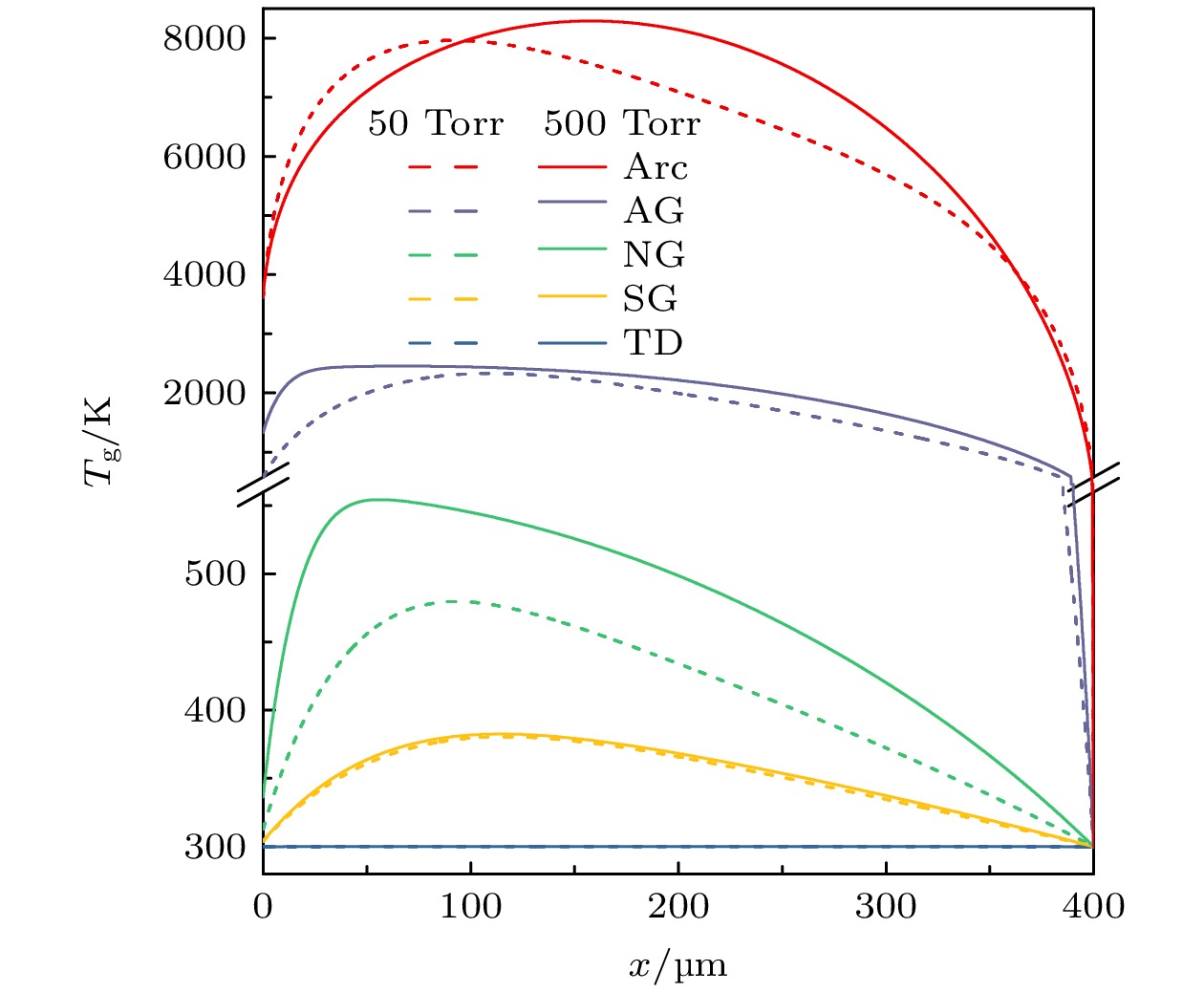
图12展现了$50 \;\text{Torr}$和$500 \;\text{Torr}$两个气压条件下典型放电模式间隙气体温度的空间分布. 在汤森放电区, 两个气压下气隙温度保持$300\; \text{K}$不变, 说明此时气体加热作用可以忽略不计. 在亚正常辉光放电区, 两个气压下气体温度分布基本重合, $p_{1} = 50 \;\text{Torr}$时在$116.6\;{\text{μm}}$处出现最高温度$380.6\;\text{K}$, $p_{2} = 500 \;\text{Torr}$时在$114.6\;{\text{μm}}$处出现最高温度$382.5\;\text{K}$. 在正常辉光放电区, 气体温度上升到$500\;\text{K}$左右, 两个气压下的温度差别变得显著. $p_{1} = 50 \;\text{Torr}$时在$93.2\;{\text{μm}}$处达到最高温度$479.9\;\text{K}$, $p_{2} = 500 \;\text{Torr}$时在$56.2\;{\text{μm}}$处达到最高温度为$554.4\;\text{K}$. 随着放电电流密度的增大, 在反常辉光放电区气体温度超过$2000\;\text{K}$, $p_{1} = 50 \;\text{Torr}$时最高温度为$2330.3\;\text{K}$(对应 $109.4\;{\text{μm}}$处), $p_{2} = 500 \;\text{Torr}$时最高温度为$2453.7\;\text{K}$ (对应$66.7\;{\text{μm}}$处). 在电弧放电区, 热发射成为阴极主要的发射机制, 热电离成为空间中产生电子的主导过程, 气体温度被加热到$8000\;\text{K}$的量级. $p_{1} = 50 \;\text{Torr}$时, 气体最高温度达$7962.1\;\text{K}$ (对应$92.1\;{\text{μm}}$处), $p_{2} = 500 \;\text{Torr}$时, 气体最高温度略高, 达$8288.9\;\text{K}$(对应$157.9\;{\text{μm}}$处). 图12表明随着放电电流密度的增加, 对气体的加热作用也越来越显著, 与图11中结果一致.

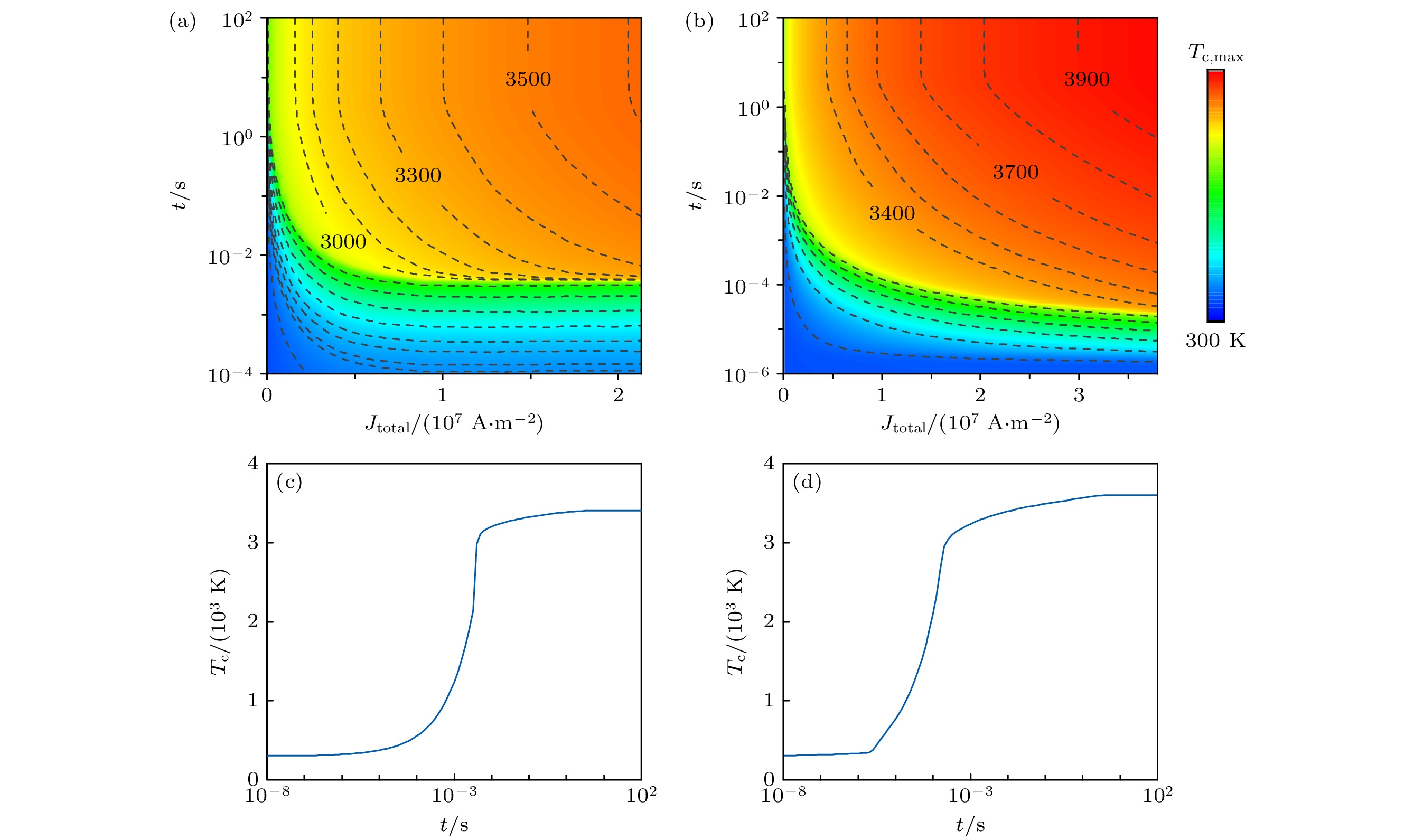
通过对比发现在电弧放电区,$50 \;\text{Torr}$气压条件下空间中温度最高点的位置比$500 \;\text{Torr}$气压下温度最高点更靠近阴极, 在其他放电模式中则更靠近阳极. 经研究发现在阴极附近气体温度的升高((20)式)主要通过离子的焦耳加热过程, 离子焦耳加热在数值上与电场的大小成正比关系. 在辉光放电放电区, $p_{1} = 50 \;\text{Torr}$时电场随位置变化的斜率比$p_{2} = 500 \;\text{Torr}$时更小, 因此$p_{1} = 50 \;\text{Torr}$时离子的焦耳加热随位置变化的斜率比$p_{2} = 500 \;\text{Torr}$时更小, 造成在低气压下温度最高点向阳极移动. 而在电弧放电区, 离子焦耳加热的变化率在阴极附近相近, 此时在放电间隙中$p_{2} = 500 \;\text{Torr}$时由弹性碰撞引起的加热比$p_{1} = 50 \;\text{Torr}$时更剧烈, 导致高气压下温度最高点位置向阳极移动.

阴极表面的温度通过求解由阴极与等离子热传导方程的边界条件((33)式)得到, 从(33)式可知阴极表面通过离子与电子的轰击、电极间气体的热传导作用被加热, 在二次电子发射、热发射、黑体辐射等过程中损失热量, 造成阴极表面温度的变化, 在放电达到稳态时阴极表面温度也达到稳态. 图13(a)和13(b)展现了在不同电流密度下阴极表面($x_\text{c} = 0\;{\text{μm}}$处)的温度随时间的演化过程. 两个气压条件下, 阴极表面温度的时间演化过程类似. 阴极表面温度随电流密度的增大而升高, 相同电流密度下高气压时对应的阴极表面温度更高, 在$500 \;\text{Torr}$气压条件下, 阴极表面温度峰值为$T_\text{c,max} = 3961 \;\text{K}$(对应最大电流密度工况). 总体而言, 阴极表面温度从汤森放电区的$300\;\text{K}$增至电弧放电区的几千开. 与图11相对应, 在电流密度大于$10^6 \;\text{A}/\text{m}^2$的电弧放电区, 阴极表面温度在$300\;\text{K}$的基础上有显著提升并增大至$1000\;\text{K}$以上. 图13(c)和图13(d)展示了电流密度为$1 \times 10^7 \;\text{A}/\text{m}^2$时阴极表面温度随时间的变化. $p_{1} = 50 \;\text{Torr}$气压条件下, 在$10^{-4} \;\text{s}$之前阴极温度保持$300\;\text{K}$几乎不变. 而$p_{2} = 500 \;\text{Torr}$气压条件下, 在$10^{-6} \;\text{s}$之前阴极温度几乎不变. 这说明气压越高粒子对阴极表面的传热效果越明显, 可以在更短的时间内引起阴极表面温度的变化, 但该过程对阴极表面的加热程度有限. $p_{1} = 50 \;\text{Torr}$气压条件下, 在$10^{-4}—10^{-2} \;\text{s}$之间等值线几乎水平且密集, 此时电流密度的变化对阴极表面的加热过程影响不大, 这是阴极表面温度显著增加的阶段, 从几百开增加至$3000\;\text{K}$以上. 在$ 10^{-2}— 10^{0} \;\text{s} $之间等值线斜率逐渐增大, 等值线逐渐稀疏, 此时温度缓慢提高. 这说明流体与固体之间的热传导过程需要一定的时间发展, 只有在电流密度足够大且时间足够长时, 等离子体对阴极的加热效果才会显著. 在$10^{0}—10^{2} \;\text{s}$之间的等值线竖直, 此时阴极温度达到最高值并保持稳态. $p_{2} = 500 \;\text{Torr}$气压条件下, 阴极表面温度的变化过程与之类似.

本文基于统一流体模型, 实现了广域参数条件下的放电数值仿真. 该模型包含放电等离子体的碰撞、辐射、输运等基本过程, 并耦合阴极电子发射(二次电子、热电子发射)、碰撞反应焓变、气体加热及阴极热传导方程. 对氩气的微间隙放电过程进行了数值仿真, 得到了包含盖革-米勒放电区、汤森放电区、亚正常辉光放电区、正常辉光放电区、反常辉光放电区、电弧放电区的典型伏安特性曲线, 放电电流密度范围为$10^{-7} —10^7 \;\text{A}/\text{m}^2$, 确定了各放电模式之间的过渡过程. 利用该模型, 模拟了气压分别为$ 50 \;\text{Torr} $和$500 \;\text{Torr}$、间距为$400 \;\text{μm}$的放电过程, 得到了典型放电模式下关键参数, 包括: 电子密度、离子密度、电流密度、电势、电场的空间分布特性. 模拟结果显示, 汤森放电区空间电场分布几乎均匀, 空间电荷效应可忽略; 在辉光放电区, 出现明显的阴极位降区和等离子体区, 空间电荷效应显著, 仿真结果与现有理论相符. 特别地, 对反常辉光放电区出现的电场反转现象进行了讨论, 证明了这一现象是由于粒子密度梯度的增大、电子扩散电流密度幅值超过总电流密度所致. 随着电流密度的进一步增大, 进入由热电子发射和热电离主导的电弧放电区, 电子密度量级为$10^{22} \;\text{m}^{-3}$. 在气压为500 Torr 条件下, 气体温度峰值为11850 K (高于50 Torr的情形); 由于热传导作用, 阴极电极表面温度被加热至将近4000 K. 该研究拓展了气体放电流体模型的应用, 实现了各放电模式的数值仿真. 后续工作考虑将该模型拓展至二维, 考虑更完备的电子发射模型(如热场发射), 更加完整地描述气体放电过程.

附录A详细给出正文中关于$\mu_{\varepsilon }$与$\mu_\text{e}$、$D_{\varepsilon }$与$D_\text{e}$的“5/3”比例关系的推导过程. 该推导分析等离子体中粒子的扩散现象(以电子扩散过程为例), 考虑粒子密度的空间非均匀性. 假设电子速度分布函数满足两项近似, 零阶项$f_0({\boldsymbol{r}}, v)$在空间上非均匀、在速度空间上各向同性; 一阶项表示电子实际分布函数$f({\boldsymbol{r}}, {\boldsymbol{v}})$与平衡态$f_0({\boldsymbol{r}}, v)$的轻微偏差, 满足

其中, $f_1({\boldsymbol{r}}, {\boldsymbol{v}})$是一阶小量, 有$\left|f_1\right| \ll f_0$.

考虑碰撞项的玻尔兹曼方程为

在稳态下, 采用碰撞项的弛豫模型(Krook)

其中, $\tau_\text{e}=\nu_{\mathrm{e}}^{-1}$为弛豫时间. 不考虑外力的作用, 可以将(稳态)玻尔兹曼方程简化为

即有

由(A5)式可以得到摄动分布函数

在扩散过程中, 由电子热运动引起的能量通量为

由于$f_0({\boldsymbol{r}}, v)$为各向同性, 故有 $\displaystyle\int_v v^2 {\boldsymbol{v}} f_0({\boldsymbol{r}}, v) \text{d}^3 v = 0$, 因此

将(A8)式转换为球坐标积分, 根据

可以得到

式中, $f_0({\boldsymbol{r}}, v)$由麦克斯韦分布函数给出

其中, $n_\text{e}$和$T_\text{e}$均为空间位置的函数. 假设电子动压保持不变, 即

根据(A12)式, 可以得到

即有

(A10)式中需要求解麦克斯韦分布的梯度, 即

(A15)式中右端第1项为

(A15)式中右端第2项为

将(A16)式与(A17)式相加, 提取公因式, 并利用(A14)式对${\nabla} n_\text{e}({\boldsymbol{r}})$进行变量替换, 整理可得

将(A18)式代入(A10)式可得

至此, (A19)式可改写成热传导形式, 即

其中, $\kappa_\text{e}$表示如下:

下面计算$\kappa_\text{e}$, 假设动量传递频率ν与v无关, 则(A21)式可以写成

分别计算(A22)式中的两个积分, 对于第1个积分式

其中, $v_{\text {th }}=(k_\text{B} T_\text{e} / m_\text{e})^{1 / 2}$为热速度(均方根速度). 令$a^2= {v^2}/({2 v_\text{th}^2})$, 代入(A23)式得

利用积分关系$\displaystyle\int_0^{\infty} \exp \left(-a^2\right) a^3 \text{d} a = 15\sqrt{\pi}/16$, (A24)式可整理为

考虑$p_\text{e}=n_\text{e} k_\text{B} T_\text{e}$, (A25)式可表示为

(A22)式中的第2个积分计算如下:

同样地, 基于$a^2={v^2}/({2 v_\text{th}^2})$进行变量替换, 利用$\displaystyle\int_0^{\infty} \exp \left(-a^2\right) a^8 \text{d} a = 105\sqrt{\pi}/32$, 代入(A27)式并考虑$p_\text{e}= n_\text{e} k_\text{B} T_\text{e}$, 整理后可得

将(A26)式、(A28)式代入(A22)式, 整理后可得

至此, 可以得到

根据“漂移-扩散”近似, 电子能量的扩散项表达式如下:

联立(A30)式、(A31)式, 可得

整理后得到

即有“$5/3$”系数关系:

将(A34)式代入爱因斯坦关系式, 可得

推导完毕.

正文中关于能流的边界条件设置, 认为沿正方向穿过某个平面时电子平均动能表达式为$W_\text{e} = 2{k_\text{B}}{T_\text{e}}$. 下面对该结论进行详细推导, 考虑在等离子体中的带电粒子满足麦克斯韦分布:

则带电粒子热运动的平均速度为

(B2)式为在$xyz$坐标下的表达式, 将其在球坐标下进行转换, 得到

其中, $v_{\text {th }}=(k_\text{B} T / m)^{1 / 2}$为热速度(均方根速度). 对(B3)式进行求解, 令$a^2={v^2}/({2 v_\text{th}^2})$, 代入(B3)式得

利用$\displaystyle \int_0^{\infty} \exp (-a^2) a^3 \text{d} a = 0.5$积分结果, 代入(B4)式有

这里得到了热运动的平均速度$\bar{v}=\left({8 k_\text{B} T}/{(\pi m)}\right)^{1 / 2}$.

下面求解沿$+z$方向的定向流${\boldsymbol{\varGamma}}_z$ (需要注意的是, 下述积分只在$v_z>0$的空间中进行), 根据$v_z=v\text{cos}\theta$, 在球坐标系下有

${\boldsymbol{\varGamma}}_z$是每秒内每平方米沿正方向穿过$z = 0$平面的粒子数. 下面计算$+z$方向的平均能流S_z,

同样利用$a^2={v^2}/({2 v_\text{th}^2})$进行变量替换, 根据积分结果$\displaystyle\int_0^{\infty} \exp \left(-a^2\right) a^5 \text{d} a = 1$, 代入(B7)式, 整理后可得

此时, 沿正方向穿过$z = 0$平面时粒子的平均动能为

特别地, 对电子而言有

推导完毕.