-
复杂网络为建模现实系统中个体间的复杂交互作用提供了有力的工具, 如社交网络[1,2]、基因网络[3,4]和交通网络[5,6]等. 通过分析网络的拓扑结构, 可以揭示网络的功能, 推断网络的演化过程等[7–10]. 然而这些研究都是建立在网络拓扑结构已知的情况下, 但是在通常情况下, 想要完全获取网络的拓扑结构是困难的, 这就需要发展一些重构方法完成从收集到的数据中推断出网络结构. 因此, 网络重构是研究网络拓扑结构的前提.
当已知网络中的动力学模型时, 可以用复杂网络上的动力学对个体间的相互作用和影响进行建模与刻画, 例如流行病在人群中的传播[11,12]、谣言在网络上的扩散[13,14]等, 同时个体间的动力学关系也可以反映出网络的拓扑结构, 所以可以利用动力学过程在不同时刻的时间序列数据对网络进行重构, 关于这方面的研究已经取得许多成果[15–19]. 在以往已知动力学模型重构网络结构的方法中, 通常都是利用时间序列数据和动力学机理构造一系列线性方程组[7,17,19–25], 每个方程组的求解结果对应着每个节点的局部连接关系, 通过求解线性方程组从而重构网络结构. 当网络中的动力学模型未知时, 可以将贝叶斯推断应用于网络重构当中[26–28], 通过先验知识和观测数据构建有关网络结构的后验概率分布, 利用极大似然估计重构网络结构. 此外将深度学习应用于网络重构当中可以使用自动微分的方法[29,30]对网络进行重构, 通过将网络结构参数化后建立关于观测数据与网络结构之间关系的损失函数, 之后利用观测数据对损失函数进行迭代, 从而获得有关网络结构的最优参数, 同时还可以用迁移学习的方法[31], 利用源域中的网络结构知识来重构目标域中的网络结构.
然而这些方法中基于线性化问题进行网络重构会面临阈值截断问题. 例如在线性方程组的求解结果中, 真实存在连接和不存在连接的求解结果存在明显的区别, 所以在求解单个线性方程组后, 可以直接从求解结果的直方图分布中分辨单个节点与其他节点的连接关系, 单个线性方程组求解结果的直方图分布中往往存在一个很明显的间断, 在这个间断区域内取一个阈值进行截断用于判断节点间的连接关系, 这种方法被称为为阈值截断方法(threshold truncation method, TTM), 该方法被广泛应在用网络结构的推断中[20–23]. 但这个截断方法存在着两个缺点: 1)如果真实存在连接的求解结果和不存在连接的求解结果混合在一起, 则会导致对应的直方图分布中的间隔不能反映真实的连边情况, 最终使得重构出的网络与真实结构差异巨大; 2)在真实网络结构未知的情况下, 虽然可以通过截断方法重构出每个节点的局部结构, 但是无法衡量每个节点的可重构性.
为了解决上述问题, 本文提出了一种基于高斯混合模型的无向网络重构方法. 首先, 根据求解一系列线性方程组得到的求解结果, 基于高斯混合模型[32]对每个方程组的求解结果进行聚类, 利用聚类结果的概率刻画节点间存在连接的可能性. 然后, 根据每个节点与其他节点存在连接的概率值, 基于信息熵定义一个可重构指标, 衡量每个节点的可重构性. 最后, 将提出的方法用于无向网络中, 筛选出可重构性高的节点并将这些节点与其他节点存在连接的概率作为训练集, 利用无向网络的对称特征来推断剩余节点与其他节点存在连接的概率. 通过在合成数据集和真实数据集上与现有的重构方法做比较, 结果表明本文的重构方法可以更有效地重构出网络的结构.
-
考虑一个拥有N个节点的无向网络
$ {G\left(V, E\right)} $ , 其中V表示节点集合, E表示边集合. 本文主要关注网络上的易感-感染-易感(SIS)动力学模型, 并使用基于平均场近似的最大似然估计(mean-field based maximum likelihood estimation, MM)[21]方法在这个动力学过程上构造线性方程组. SIS模型是流行病中常用的一种模型, 个体的状态在易感态和感染态中转化. MM方法是一个在动力学过程上构造线性方程组的理论框架, 这个框架适用于很多动力学模型. 下面将描述网络上的SIS动力学模型和使用MM方法在SIS动力学模型上构造线性方程组的过程.在SIS模型中, 每个节点有两个状态: 易感态和感染态. 令向量
$ {\boldsymbol{{s}}}^{i} $ 表示节点i在所有时间段的状态, 如果在t时刻节点i处于感染态,$ {s_{t}^{i}=1} $ , 反之,$ {s_{t}^{i}=0} $ . 假设节点i被感染的概率和恢复的概率分别为$ \lambda^i $ 和$ \mu^i $ , 则节点i受邻居感染从易感状变为感染状的概率为[33]其中,
$ m^i $ 表示节点i邻居中感染状态的节点个数. 令向量$ {\boldsymbol{A}}^{i} $ 表示节点i与其他节点的连接关系, 当节点i与节点j相邻时,$ {A_{j}^{i}=1} $ , 否则$ {A_{j}^{i}=0} $ , 所以在第t时刻节点i邻居中处于感染态的节点个数为$ {m_{t}^{i}}= \displaystyle\sum\nolimits_{j\not=i}{s_{t}^{j}}{A_{j}^{i}} $ , 则在t时刻节点i受邻居感染从易感状态变为感染状态的概率为接下来, 使用MM方法在SIS动力学模型上构造线性方程组. 在上述的SIS动力学模型中, 由节点i当前时刻的状态可以知道下一个时刻状态的条件概率, 所以节点i在所有时间段状态的联合概率函数可以表示为
式中, 第一个乘积项表示在
$ {s_{t}^{i}=0} $ 的情况下$ {s_{t+1}^{i}=0} $ 或$ {s_{t+1}^{i}=1} $ 的条件概率, 第二个乘积项表示在$ {s_{t}^{i}=1} $ 的情况下$ {s_{t+1}^{i}=0} $ 或$ {s_{t+1}^{i}=1} $ 的条件概率.因为在SIS模型中, 节点恢复过程与邻居无关, 所以节点从感染状恢复到易感态的过程和网络重构没有关系, 故可以省略(3)式后面的项, 并取对数则可以得到如下的似然函数:
然后求解相关参数
$ \lambda^i $ , 似然函数(4)对被感染率$ \lambda^i $ 求偏导后有:令
$ {\dfrac{\partial L\left({\boldsymbol{A}^{i}}, \lambda^i\right)} {\partial \lambda^i}=0} $ 有:之后应用平均场理论[34]可以得到以下近似:
其中
$ k^i $ 表示节点i的邻居个数,$ {\theta_{t}^{i}= \displaystyle\sum\nolimits_{j \not = i}s_{t}^{j}} $ 表示在t时刻除节点i以外, 其他节点被激活的个数. 令$ {{\left(1-\lambda^i\right)}^{\sum\limits_{j\not=i}{s_{t}^{j}}{A_{j}^{i}}}} {=\left(1-\lambda^i\right)^{\tfrac{k^i}{N-1}\theta_{t}^{i}}=\left(\gamma^i\right)^{\theta_{t}^{i}}} $ , 其中$ {{\gamma^i}= (1-\lambda^i)^{\tfrac{k^i}{N-1}}} $ , 则(6)式可以表示为通过数值解法可以得到
$ {{\gamma^i}={\tilde{\gamma}^i}} $ . 最后对似然函数(4)关于$ {{A_{l}^i}} $ 求偏导有:令
$ {\dfrac{\partial L\left({\boldsymbol{A}^{i}}, \lambda^i\right)}{\partial {A_{l}^i}}=0} $ 有:可以看出(10)式的指数项
$ {{\displaystyle\sum\nolimits_{j \not = i}s_{t}^{j}A_{j}^{i}}} $ 中的$ {A_{j}^{i}} $ 无法方便地求解. 为此考虑形如$ {\dfrac{a^x}{1-a^x}} $ 的式子, 当$ {x \to x_0} $ 时, 该式子根据泰勒展开为令
$ {x=\displaystyle\sum\nolimits_{j\not=i}{s_{t}^{j}}{A_{j}^{i}}} $ ,$ {a=1-\lambda^i} $ . 根据(7)式, 可以令$ {x_{0}\;=\;\dfrac{k^i}{N-1}\theta_{t}^{i}} $ (此时$ {x\approx x_{0}} $ ), 则$ a^{x_0}= (\tilde{\gamma}^i)^{\theta_{t}^{i}} $ . 令$ {f_{t}^{i}=} {\dfrac{(\tilde{\gamma}^i)^{\theta_{t}^{i}}}{1-(\tilde{\gamma}^i)^{\theta_{t}^{i}}}-\dfrac{(\tilde{\gamma}^i)^{\theta_{t}^{i}}}{{[1-(\tilde{\gamma}^i)^{\theta_{t}^{i}}]}^2}\theta_{t}^{i}\ln\tilde{\gamma}^i} ,~ g_{t}^{i}= \dfrac{\left(\tilde{\gamma}^i\right)^{{\theta}_{t}^{i}}}{[1-(\tilde{\gamma}^i)^{{\theta}_{t}^{i}}]^2} $ , 代入(10)式可得:因为除
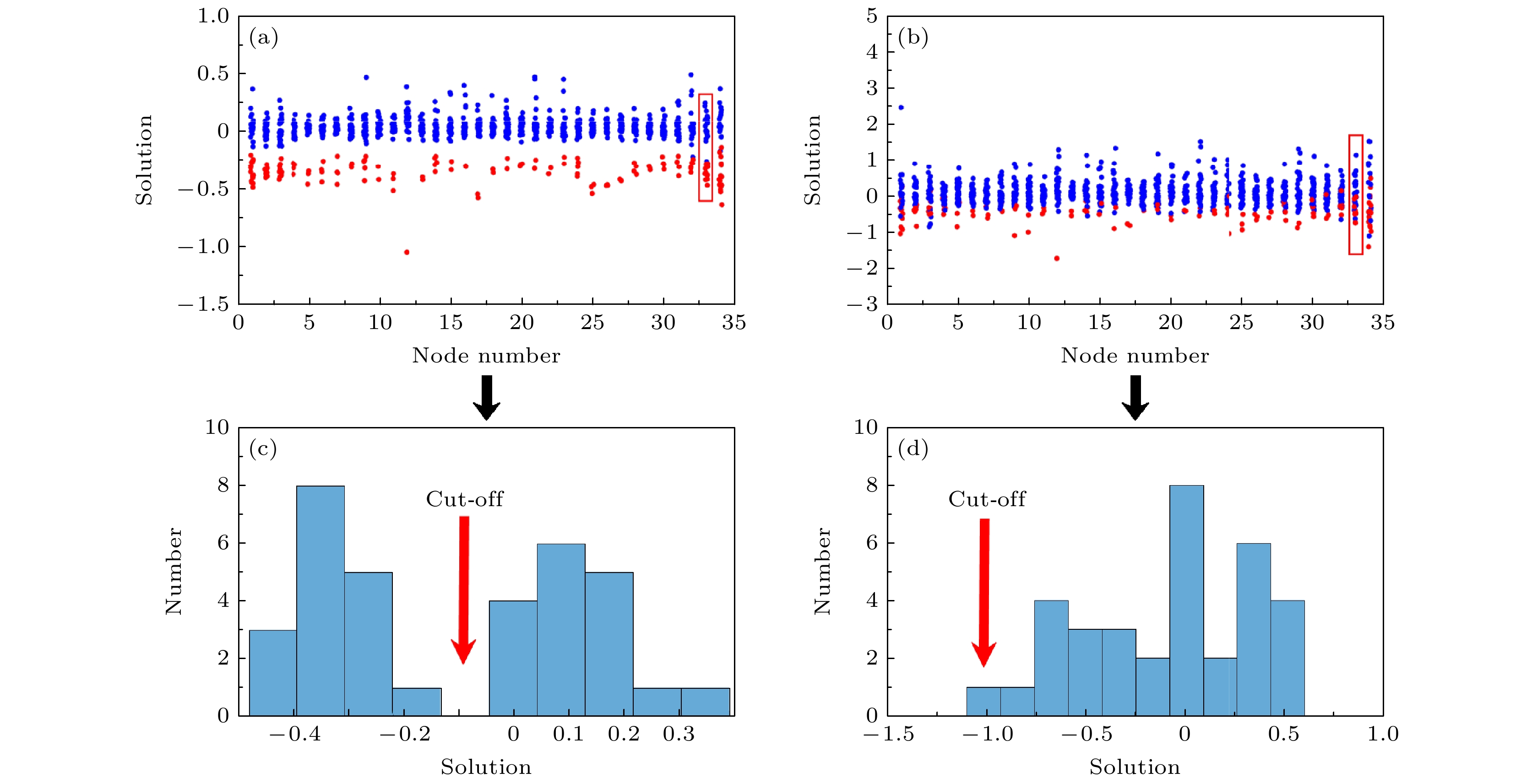
$ {\ln\left(1-\lambda^i\right)A_{j}^{i}} $ 外其他量都是已知的, 所以这是一个关于变量$ \ln\left(1-\lambda^i\right){\boldsymbol{A}^{i}} $ 的线性方程组. 其中, 虽然$ \lambda^i $ 是未知的, 但$ {\ln\left(1-\lambda^i\right)} $ 是一个常数, 因此可以通过求解$ \ln\left(1-\lambda^i\right){\boldsymbol{A}^{i}} $ 来得到关于节点i的局部结构.通过上述方法构造的一系列线性方程组的求解结果如图1所示. 在时间序列长度足够时, 线性方程组的求解结果中真实存在连接和不存在连接的求解结果存在明显的区别(如图1(a)所示), 所以在求解单个线性方程组后, 可以直接从求解结果的直方图分布中分辨单个节点与其他节点的连接关系(如图1(c)所示). 当时间序列长度不足时, 真实存在连接的求解结果和不存在连接的求解结果会混合在一起(如图1(b)所示), 则会导致对应的直方图分布中的间隔不能反映真实的连边情况(如图1(d)所示). 本文只介绍SIS模型通过MM构造线性方程组所遇到的问题, 然而其他方法构造的线性方程组也存在同样的问题, 无法通过简单的截断分辨求解结果对应的连接关系.
-
构造出关于每个节点的线性方程组之后, 每个方程组的求解结果都和一个节点与其他节点的连接关系有关, 但是通过求解结果并不能直接分辨出一个节点与其他节点的连接关系, 所以要重构出网络结构还需要一种有效的方法分辨求解结果代表的是存在连接还是不存在. 因此, 本文提出了一种基于高斯混合模型的无向网络重构方法(undirected network reconstruction based on Gaussian mixture model, UNRGMM), 将求解结果的分辨问题转化成聚类问题, 并基于高斯混合模型进行求解. 下面将详细介绍方法步骤.
对于构造的线性方程组(12), 求解后可以得到关于节点i与其他节点连接关系的求解结果, 这里用向量
$ {{\boldsymbol{{B}}^{i}}=\left(B_{j}^{i}\right)\in \mathbb{R}^{\left(N-1\right) \times 1}} $ 表示, 即$ B_{j}^{i}= A_{j}^{i}\ln\left(1-{\lambda}^i\right) $ . 因为$ {A_{j}^{i}} $ 的真实值为0或者1, 所以$ {{\boldsymbol{{B}}^{i}}} $ 中的值会集中在0和$ {\ln(1-\lambda^i)} $ 附近. 因此, 可以假设$ {B_{j}^{i}} $ 服从高斯混合分布, 即:其中,
$ {\phi\left(x|\mu_{k}, \sigma^{2}_{k}\right)} $ 为均值为$ {\mu_{k}} $ 方差为$ {\sigma^{2}_{k}} $ 的高斯分布,$ {{\boldsymbol{\theta}}=\left[\mu_{1}, \mu_{2}, \sigma^{2}_{1}, \sigma^{2}_{2}, \alpha_{1}, \alpha_{2}\right]^{{\mathrm{T}}}} $ ,$ {\alpha_{1}+\alpha_{2}=1} $ . 假设$ {{\boldsymbol{{B}}^{i}}} $ 中每个值都是独立分布的, 所以对数似然为对于高斯混合模型, 可以利用EM算法对模型参数进行迭代优化, 迭代公式定义为
其中,
$ {\gamma_{jk}^{i}} $ 可以表示i与j不存在连接的概率$ (k= 1) $ 和存在连接的概率$ {\left(k=2\right)} $ . 反复计算公式(15)—(18)直至收敛, 最终可以得到节点i与节点j之间存在连接的概率$ {\gamma_{j2}^{i}} $ . 初始时刻, 初始化均值$ {\mu_{1}} $ 设置为0,$ {\mu_{2}} $ 的值通过对$ {{\boldsymbol{{B}}^{i}}} $ 做柱状图获取, 即取柱状图最小值点与$ {{\boldsymbol{{B}}^{i}}} $ 中最小值的均值. 标准差$ {\sigma_{1}} $ 和$ {\sigma_{2}} $ 统一设置为$ {{\boldsymbol{{B}}^{i}}} $ 中值的标准差的1/2,$ {\alpha_{1}} $ 和$ {\alpha_{2}} $ 分别设置为0.8和0.2.在得到
$ {{\boldsymbol{{B}}^{i}}} $ 中每个值表示存在的连接概率后, 可以根据这些概率衡量节点i的可重构性. 例如, 当得到的概率全部接近0或者1, 则认为可重构性很高, 反之, 如果得到的概率全部在$ {0.5} $ 附近, 则很难判断这些值是表示存在连接还是表示不存在连接. 因为$ {\gamma_{j1}^{i}+\gamma_{j2}^{i}=1} $ , 所以基于信息熵定义一个可重构指标来衡量节点的可重构性, 节点i的重构性指标定义为$ {H(i)} $ 越小则节点i可重构性越高, 当$ {H(i)=0} $ 时, 表明对于任意节点j可以得到$ \gamma_{j2}^{i}=0 $ 或$ \gamma_{j2}^{i}=1. $ 由(19)式可以判断出哪些节点的可重构性高, 哪些节点可重构性低, 下面将方法用于无向网络中, 利用节点的可重构性高低和无向网络的对称特征重构出网络的结构.
步骤一: 首先利用每个节点与其他节点存在连接的概率
$ {\gamma_{j2}^{i}} $ 计算其可重构性指标$ {H(i)} $ , 然后设置阈值α把所有节点分为可重构性高的节点与可重构性低的节点两个部分:$ {\boldsymbol{V_{<\alpha}}}=\{v_{1}, v_{2}, \cdots, v_{k}\} $ 与$ {{\boldsymbol{V_{>\alpha}}} = \left\{v_{k+1}, v_{k+2}, \cdots, v_{N}\right\}} $ , 最后对于可重构性高的节点, 将它们与其他节点的连接概率$ {\gamma_{j2}^{i}\left(i \in {{\boldsymbol{V_{<\alpha}}}}, j \in 1, \cdots, N \right) } $ 作为最终结果, 并根据$ {\gamma_{j2}^{i}\left(i \in {{\boldsymbol{V_{<\alpha}}}}\right)} $ 重新计算可重构性低的节点与其他节点存在连接的概率更新$ {\gamma_{j2}^{i}\left(i \in {{\boldsymbol{V_{>\alpha}}}}\right)} $ .步骤二: 通过阈值分类得到可重构性高的节点与其他节点的连接概率, 接下来将重构出这部分节点的局部结构, 同时利用无向网络的对称特征推断可重构性低的节点的部分连接关系. 为此, 定义新的邻接矩阵
$ {\boldsymbol{\tilde{A}}} $ , 定义网络中不存在自环, 所以当节点$ {i=j} $ 时,$ {\tilde{A}_{j}^{i}} $ 的值为0, 当$ {i \not= j} $ 时, 元素$ {\tilde{A}_{j}^{i}} $ 的取值由节点i和节点j的可重构性和存在连接的概率$ {\gamma_{j2}^{i}} $ 和$ {\gamma_{i2}^{j}} $ 决定. 当节点i属于可重构性高的节点且可重构性比节点j要高时,$ {\tilde{A}_{j}^{i}} $ 的值取决于$ {\gamma_{j2}^{i}} $ ; 当节点j属于可重构性高的节点且可重构性比节点i要高时,$ {\tilde{A}_{j}^{i}} $ 的值取决于$ {\gamma_{i2}^{j}} $ ; 当节点i和节点j都属于可重构性低的节点时,$ {\tilde{A}_{j}^{i}} $ 的值为–1, 公式定义如下:其中,
$ [\cdot] $ 表示四舍五入取整. 得到的邻接矩阵$ {\boldsymbol{\tilde{A}}} $ 中非–1值表示重构出的部分网络结构.步骤三: 接下来需要重构出任意两个可重构性低的节点之间的连接关系, 即邻接矩阵
$ {\boldsymbol{\tilde{A}}} $ 中–1位置的元素. 对此, 可以利用可重构性低的节点中已经重构出的连接关系作为训练集推断未重构的连接关系. 首先, 对于任意一个可重构性低的节点$ {i \in {\boldsymbol{V_{>\alpha}}}} $ , 由(20)式可以知道向量$ {\boldsymbol{\tilde{A}}^{i}}=[\tilde{A}_{1}^{i}, \cdots, \tilde{A}_{i-1}^{i}, \tilde{A}_{i+1}^{i}, \tilde{A}_{N}^{i}]^{{\mathrm{T}}} $ 中哪些值为0, 1和–1. 定义$ {\boldsymbol{\beta}}_{{1}} $ 表示$ {\tilde{A}_{j}^{i}} $ 为0对应$ {B_{j}^{i}} $ 的集合; 定义$ {\boldsymbol{\beta}}_{{2}} $ 表示$ {\tilde{A}_{j}^{i}} $ 为1对应$ {B_{j}^{i}} $ 的集合. 通过贝叶斯分类器, 利用最大化后验概率准则, 即可得到$ {i \not= j} $ 时$ {B_{j}^{i}} $ 所属不存在连接或存在连接的概率为其中,
$ {w_{1}} $ ,$ {w_{2}} $ 分别代表$ {\tilde{A}_{j}^{i}=0} $ ,$ {\tilde{A}_{j}^{i}=1} $ .$ {P\left(w_{k}\right)} $ ,$ {\mu_{k}} $ ,$ {\sigma^{2}_{k}} $ 可由已知结果训练得到, 即$ P\left(w_{k}\right)\;= {\left|{\boldsymbol{\beta}_{k}}\right|}/({\left|{\boldsymbol{\beta}}_{{1}}\right|+\left|{\boldsymbol{\beta}}_{{2}}\right|}) $ ,$ {\mu_{k}} $ 和$ {\sigma^{2}_{k}} $ 分别为$ {{\boldsymbol{\beta}_{k}}} $ 中元素的均值和方差. 若求得$ {P\left(w_{1}|B_{j}^{i}\right)<P\left(w_{2}|B_{j}^{i}\right)} $ 则节点j是节点$ {{i}} $ 的邻居, 令$ {\tilde{A}_{j}^{i}=1} $ , 反之则$ {\tilde{A}_{j}^{i}=0} $ , 最终得到的邻接矩阵$ {\boldsymbol{\tilde{A}}} $ 作为网络重构结果. -
在合成网络和几个真实网络上测试了本文提出的方法UNRGMM和TTM的重构效果. 对于合成网络, 考虑了3种广泛使用的网络模型, 即Erd
$ {\ddot{o}} $ s-R$ {\acute{e}} $ nyi(ER)随机网络[35]、Watts-Strogatz (WS)小世界网络[36]和Barab$ {\acute{a}} $ si-Albert (BA)无标度网络[37]. 此外, 还考虑4个真实网络[21], 包括Karate网络、Dolphins网络、Football网络和Polbook网络, 这些真实网络的基本结构特征如表1所示. 为了评估这两种方法的重构效果, 本文采用了两个标准指标:$ {F_1} $ 和准确率($ {\mathrm{Accuracy }}$ )来测量网络重构效果. 它们的定义如下:其中p为精确率, 指预测出正确的边在所有预测边中所占的比例, r为召回率指预测出正确的边在所有真实边中所占的比例,
$ {\boldsymbol{A}} $ 为真实网络的邻接矩阵,$ {\boldsymbol{\tilde{A}}} $ 为重构出网络的邻接矩阵. 这两个指标分别从模型分类数据和网络结构数据两个方面来评估重构效果的好坏.首先, 我们在BA网络中分析公式(19)中定义的重构性指标
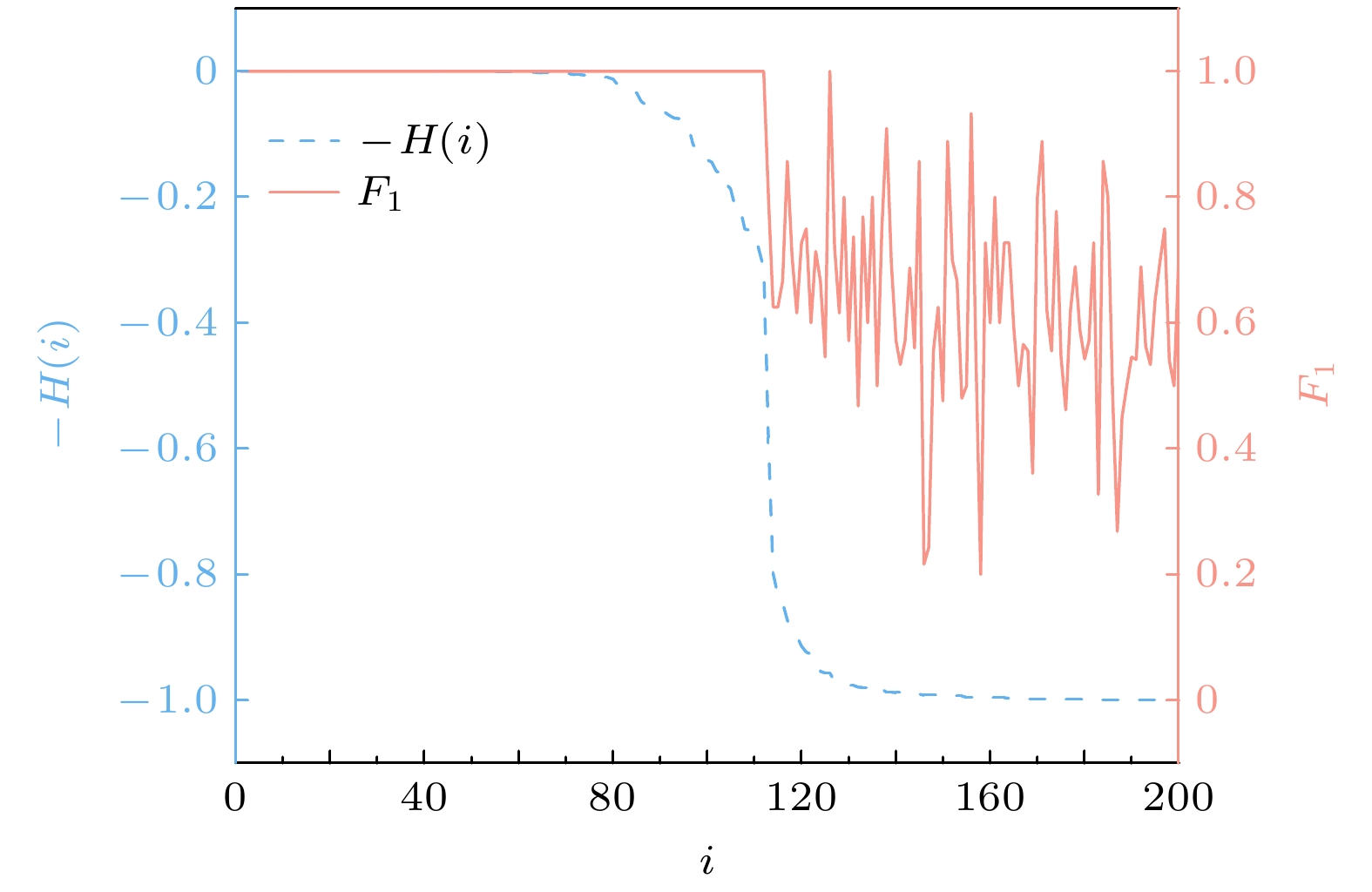
$ {H(i)} $ 与节点i重构效果之间的关系, 其中, 网络大小$ {N=200} $ , 平均度$ {\langle k\rangle =6} $ , 结果如图2所示. 可以看出当$ {-H(i)} $ 接近于0时, 节点的重构效果接近完全重构, 当$ {-H(i)} $ 降低时, 虽然存在个别节点拥有较高的重构效果, 但节点总体的重构效果也呈现降低趋势, 说明当$ {H(i)} $ 与节点的重构效果呈负相关, 低的$ {H(i)} $ 对应的节点重构效果好, 高的$ {H(i)} $ 对应的节点重构效果普遍较低. 因此可以将$ {H(i)} $ 用于衡量节点的重构效果,$ {H(i)} $ 越接近于0则节点i可重构性越高, 在无向网络中, 可以利用$ {H(i)} $ 接近于0的节点帮助$ {H(i)} $ 高的节点进行重构.其次, 在3种合成网络: ER网络、WS网络和BA网络上比较UNRGMM和TTM的重构效果, 如图3所示. 3个合成网络大小都是
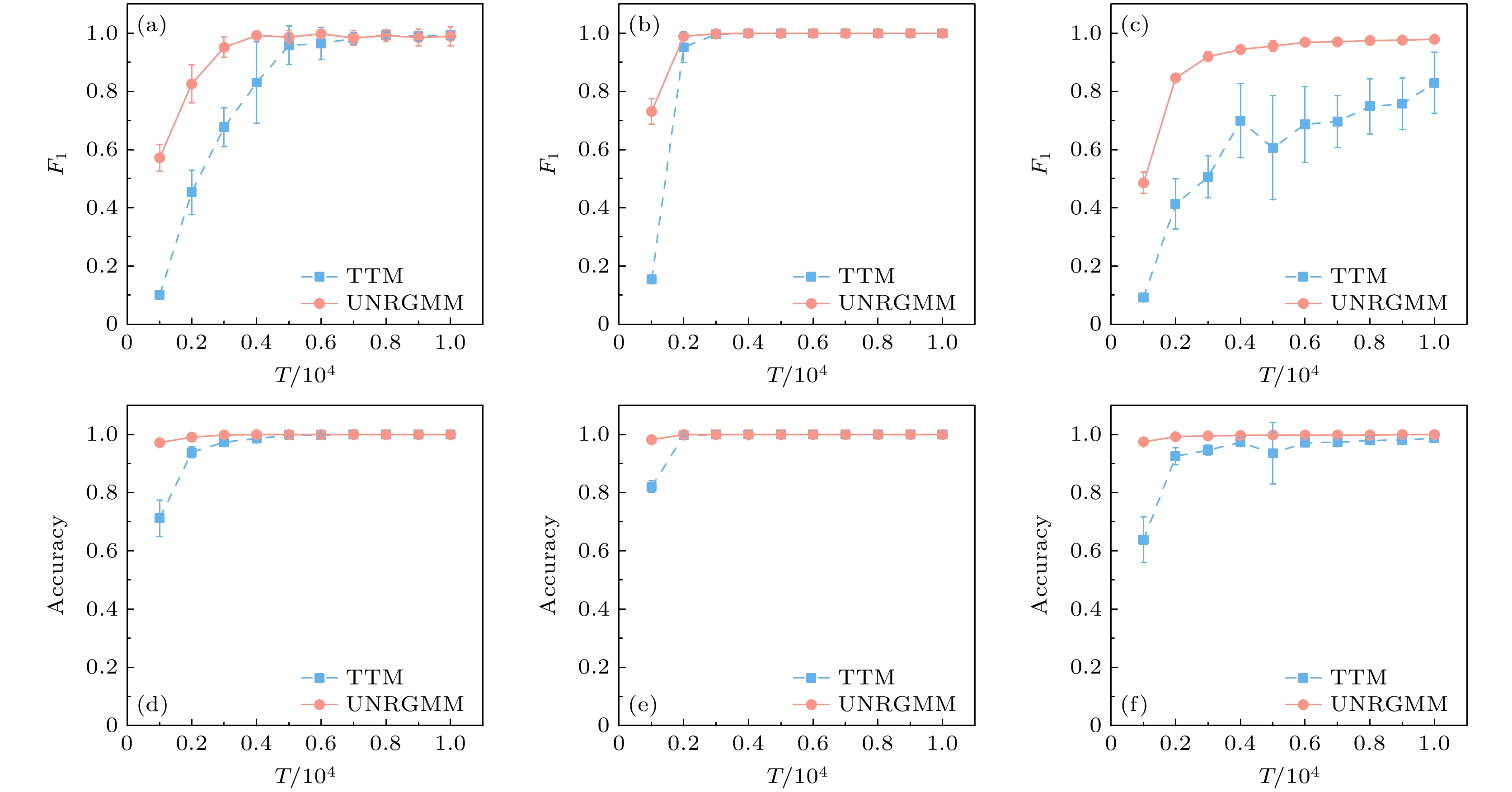
$ N= 200 $ , 平均度$ {\langle k\rangle =6} $ , 所有结果均为10次平均. ER网络上的比较结果展示在图3(a),(d)中, 可以看出在时间序列长度较低时, UNRGMM的重构效果优于TTM, 并且在时间序列长度$ {T=4000} $ 时UNRGMM就接近完全重构, 而TTM要在$ T= 5000 $ 时才接近完全重构. WS网络上的比较结果如图3(b),(e)所示, 可以看出UNRGMM和TTM的重构效果在WS网络上都能取得很好的效果, 在时间序列长度$ {T=3000} $ 时都接近完全重构, 但在时间序列长度低于$ {3000} $ 时, UNRGMM的重构效果要优于TTM, 这说明UNRGMM比TTM更适用于时间序列长度较少的情况. BA网络上的比较结果展示在图3(c),(f)中, 可以看出在BA网络中, UNRGMM的重构效果在所有时间段上都要优于TTM. 总体来看, UNRGMM的重构效果在3种合成网络上是要优于TTM, 特别是在BA网络中, 存在一些超大度节点不易重构, UNRGMM仍然能很好地重构出这些节点的结构, 而TTM的重构效果受到这些大度节点的影响导致重构效果变差.然后在4个真实网络上比较UNRGMM和TTM的重构效果, 结果列在表2中. 在表2中展现了每个真实网络在时间序列长度
$ {T=3000} $ 的情况下UNRGMM和TTM的重构结果比较, 在4个真实网络中UNRGMM的重构效果都好于TTM, 而后两个真实网络中无论是$ {F_1} $ 还是$ {\mathrm{Accuracy}} $ 指标, UNRGMM对比TTM都有很大程度的提升, 这是因为后两个真实网络节点数量和边数与前两个真实网络相比都更多, 这导致了TTM的重构效果变差, 而UNRGMM在节点数量和边数较多的网络中也能有较好的重构效果.随后对算法的鲁棒性进行分析, 在3种合成网络: ER网络、WS网络和BA网络生成的时间序列中加入噪声进行扰动, 3个合成网络大小都是
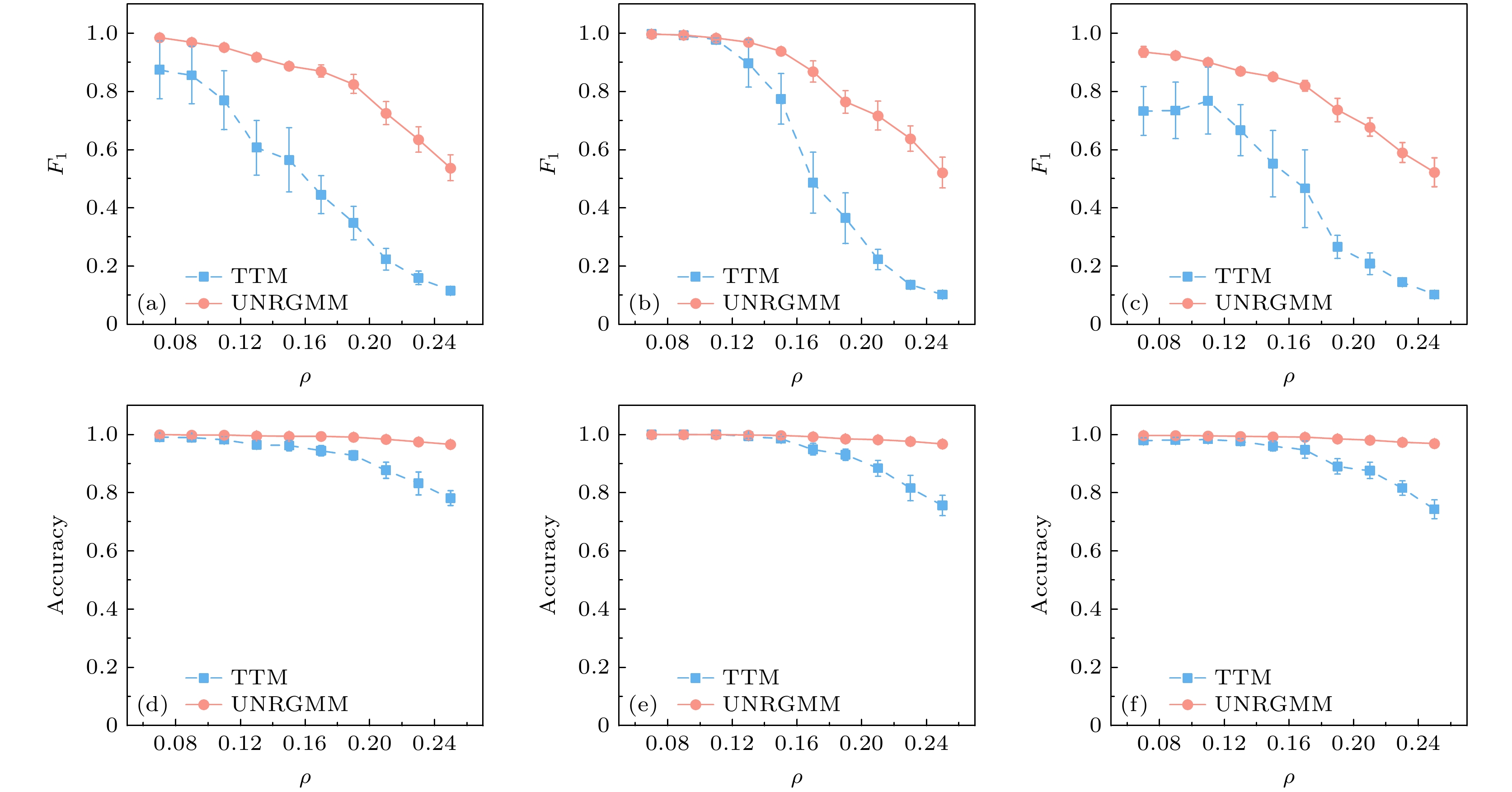
$ {N=200} $ , 平均度$ {\langle k\rangle =6} $ , 时间序列长度$ {T=5000} $ , 所有实验10次取平均. 从时间序列中随机选取$ {\rho \times N \times T} $ 个位置对其进行反转, 之后使用TTM和UNRGMM对该时间序列构建的线性方程组求解结果进行重构, 实验结果如图4所示, ER网 络上的比较结果展示在图4(a),(d)中, WS网络上的比较结果展示在图4(b),(e)中, BA网络上的比较结果展示在图4(c),(f)中. 从$ {F_1} $ 指标来看, 在3种网络中, 加入了20%的噪音后, TTM的重构效果变得非常低, 而UNRGMM的重构效果仍能达到0.7以上的重构效果, 加入了25%的噪音后, TTM基本上已经失去了重构效果, 但UNRGMM还能达到0.5以上的重构效果, 从$ {\mathrm{Accuracy}} $ 指标来看, UNRGMM能保持重构效果不受影响, 而TTM受到噪声影响下降明显. 总的来说, UNRGMM在这3种网络中都具有很好的鲁棒性且优于TTM.接下来, 比较不同平均度的网络对UNRGMM与TTM重构效果的影响, 如图5所示. 在3种合成网络: ER网络、WS网络和BA网络上分析不同平均度下UNRGMM与TTM的重构效果变化, 其中每个合成网络的大小都为
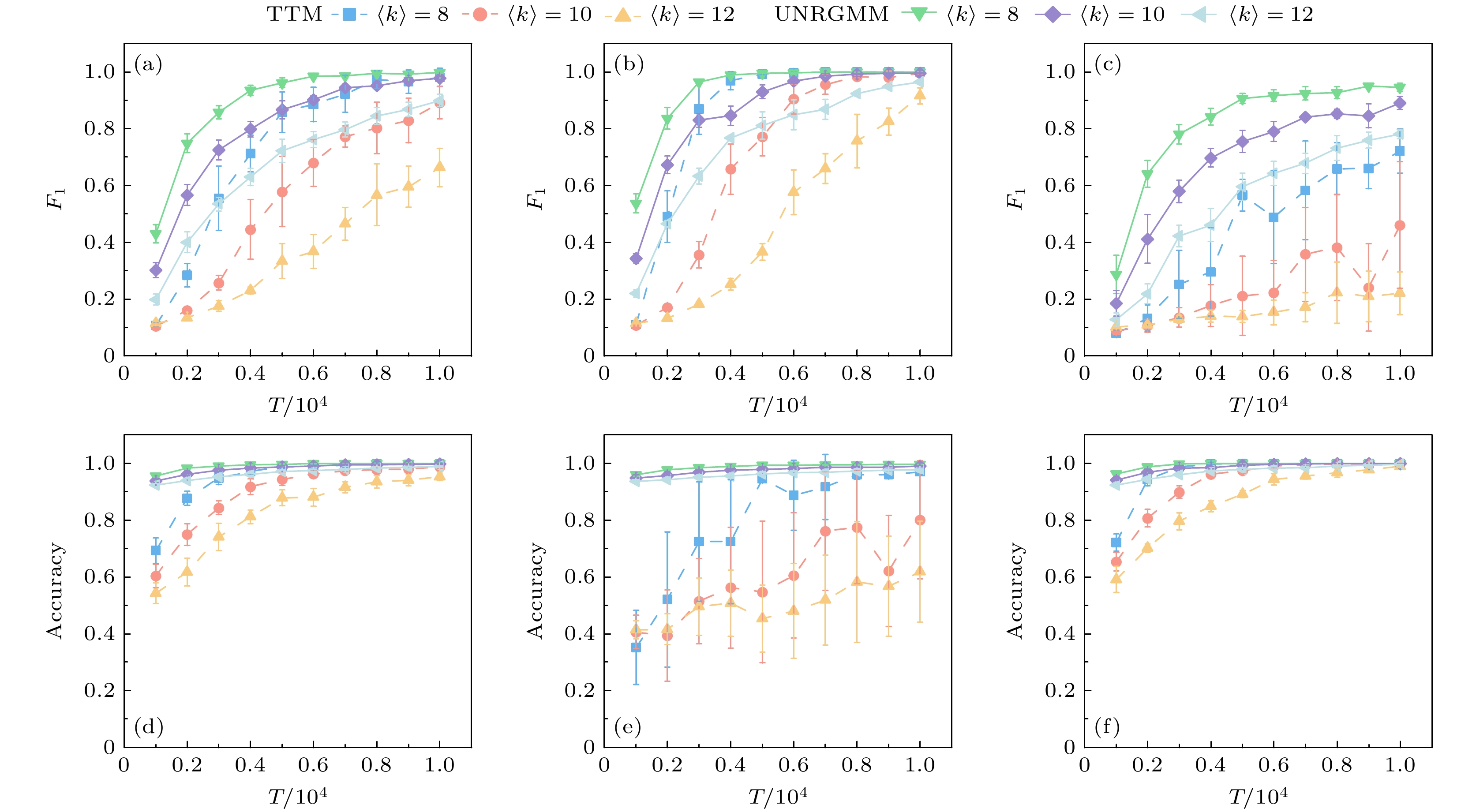
$ {N=200} $ , 所有结果均为10次平均. 图5(a),(d)比较了UNRGMM与TTM在ER网络上不同平均度下的重构效果, 在ER网络中, UNRGMM与TTM的重构效果 随着$ {\langle k\rangle} $ 的值增高而降低, 这是因为随着$ {\langle k\rangle} $ 的 增加导致需要预测出更多的连边. 与TTM相比, UNRGMM受到$ {\langle k\rangle} $ 的影响较低, 虽然重构效果降低但仍保持较高的重构效果, 而TTM受到$ {\langle k\rangle} $ 的影响, 重构效果下降非常快. 图5(b),(e)比较了UNRGMM与TTM在WS网络上不同平均度下的重构效果, 与在ER网络中相似, UNRGMM与TTM的重构效果随着$ {\langle k\rangle} $ 的值增高而降低, 且TTM受到$ {\langle k\rangle} $ 的影响大于UNRGMM. 图5(c),(f)比较了UNRGMM与TTM在BA网络上不同平均度下的重构效果, 在BA网络中, 当$ {\langle k\rangle=12} $ 时, TTM已经无法有效地重构出网络结构, 而UNRGMM虽然受到$ {\langle k\rangle} $ 的影响, 但随着时间序列长度的增加仍能有效重构出网络结构. 总的来说, UNRGMM受到$ {\langle k\rangle} $ 的影响小于TTM, 并且重构效果始终优于TTM.最后, 为了验证该方法的普适性和优越性, 在网络大小
$ {N=200} $ , 平均度$ {\langle k\rangle =6} $ 的BA网络上使用3种动力学模型: Ising动力学, Game动力学和Majority动力学来比较UNRGMM和TTM的重构效果, 所有结果均为10次平均, 如图6所示. 在图6(a),(d)中展示了Ising动力学使用本文介绍的MM方法构造线性方程组[10]后UNRGMM和TTM的重构效果, 可以看出UNRGMM具有很好的重构效果, 并且优于TTM, 说明在不同动力学的情况下, UNRGMM仍能保持很好的重构效果. 在图6(b),(e)及图6(c),(f)中分别展示了Game动力学和Majority动力学在使用文献[38]中的方法构造线性方程组后UNRGMM和TTM的重构效果, 可以看出, 使用了其他的方法构造线性方程组后UNRGMM依然保持很好的重构效果并且优于TTM, 说明UNRGMM具有普适性和优越性. -
网络重构问题一直都是复杂网络研究中重要的科学问题, 而以往的重构方法研究中大多将研究重点放在如何有效地构建线性方程组, 通过求解线性方程组来推断网络的结构, 从而忽略了在求解结果与网络结构中建立一个有效且科学的关系. 本文提出了一种基于高斯混合模型的无向网络重构方法, 建立了从求解结果到网络结构间的关系映射. 利用高斯混合模型将节点间连接关系的推断问题转化为求解结果的一个聚类问题, 并且提供了一个在真实网络结构未知的情况下衡量每个节点可重构性的指标. 将本文方法用于无向网络中, 还可以利用无向网络的对称特征提高重构的效果. 通过在合成数据和真实数据上采用不同动力学模型和不同构造线性方程组的方法进行实验, 与以往的截断重构方法的重构效果对比证明了本文方法的优势. 但是, 该方法主要适用于线性化重构结果的截断, 还有一些例如统计推断的方法, 在预测连边概率后同样面临着截断问题, 这类问题如何解决将是我们下一步的研究内容.
基于高斯混合模型的无向网络重构
Gaussian mixture model based reconstruction of undirected networks
-
摘要: 从数据中推断网络的结构作为复杂网络中一个重要科学问题已得到广泛关注. 现有的网络重构方法大多将网络重构问题转化为一系列线性方程组的求解问题, 然后通过某种截断方法对每个方程组的解进行截断, 从而确定每个节点的局部结构. 然而现有的截断方法大多存在着精度不足的问题, 且少有方法衡量每个方程组解的可截断性, 即节点的可重构性. 为了解决这些问题, 本文提出了一种基于高斯混合模型的无向网络重构方法. 该方法首先将节点间连接关系的推断问题转化为一个聚类问题, 然后利用高斯混合模型进行求解, 得到每个节点与其他节点的连接概率, 并根据概率定义一个基于信息熵的可重构指标, 从而在真实网络结构未知的情况下衡量每个节点的可重构性. 将该方法用于无向网络中, 可以利用无向网络的对称特征, 将可重构性高的节点作为训练集指导可重构性低的节点进行结构推断, 从而更好地重构出无向网络. 最后, 通过在合成数据和真实数据上与现有的截断方法进行比较, 证明了该方法可以更有效地重构出网络结构.Abstract: The reconstruction of network structure from data represents a significant scientific challenge in the field of complex networks, which has attracted considerable attention from the research community. The most of existing network reconstruction methods transform the problem into a series of linear equation systems, to solve the equations. Subsequently, truncation methods are used to determine the local structure of each node by truncating the solution of each equation system. However, truncation methods frequently exhibit inadequate accuracy, and lack methods of evaluating the truncatability of solutions to each system of equations, that is to say, the reconstructability of nodes. In order to address these issues, in this work an undirected network reconstruction method is proposed based on a Gaussian mixture model. In this method, a Gaussian mixture model is first used to cluster the solution results obtainedby solving a series of linear equations, and then the probabilities of the clustering results are utilized to depict the likelihood of connections between nodes. Subsequently, an index of reconstructibility is defined based on information entropy, thus the probability of connections between each node and other nodes can be used to measure the reconstructibility of each node. The proposed method is ultimately applied to undirected networks. Nodes identified with high reconstructibility are used as a training set to guide the structural inference of nodes with lower reconstrucibility, thus enhancing the reconstruction of the undirected network. The symmetrical properties of the undirected network are then employed to infer the connection probabilities of the remaining nodes with other nodes. The experiments on both synthetic and real data are conducted and a variety of methods are used for constructing linear equations and diverse dynamical models. Compared with the results from a previous truncated reconstruction method, the reconstruction outcomes are evaluated. The experimental results show that the method proposed in this work outperforms existing truncation reconstruction methods in terms of reconstruction performance, thus confirming the universality and effectiveness of the proposed method.
-
Key words:
- network reconstruction /
- Gaussian mixture model /
- reconstructability /
- undirected networks .
-

-
图 1 网络重构结果 (a)和(b)分别为求解两组一系列线性方程组的求解结果, 红色点表示存在连接关系的求解结果, 蓝色点表示不存在连接关系的求解结果; (c)为(a)中红色方框内节点求解结果的直方图分布; (d)为(b)中红色方框内节点求解结果的直方图分布. (a)和(b)中的横坐标表示网络中节点编号, 纵坐标表示线性方程组的求解结果, (c)和(d)中的横坐标表示线性方程组的求解结果, 纵坐标表示分布的数量
Figure 1. Network reconstruction results: (a) and (b) represent two different solution results for solving a series of linear equation systems, respectively, with red dots indicating solutions with connectivity and blue dots indicating solutions without connectivity; (c) represents histogram distribution of the solution result for the node within the red box in panel (a); (d) represents histogram distribution of the solution result for the node within the red box in panel (b). The horizontal axes in panels (a) and (b) represent the node number in the network, the vertical axes represent the solution results of the linear equation system, the horizontal axes in panels (c) and (d) represent the solution results of the linear equation system, and the vertical axes represent the number of distributions.
图 2
$ {H(i)} $ 与节点重构效果的关系 横坐标表示节点编号, 左纵坐标表示节点的可重构性指标负值$ {-H(i)} $ , 右纵坐标表示重构效果F1Figure 2. The relationship between
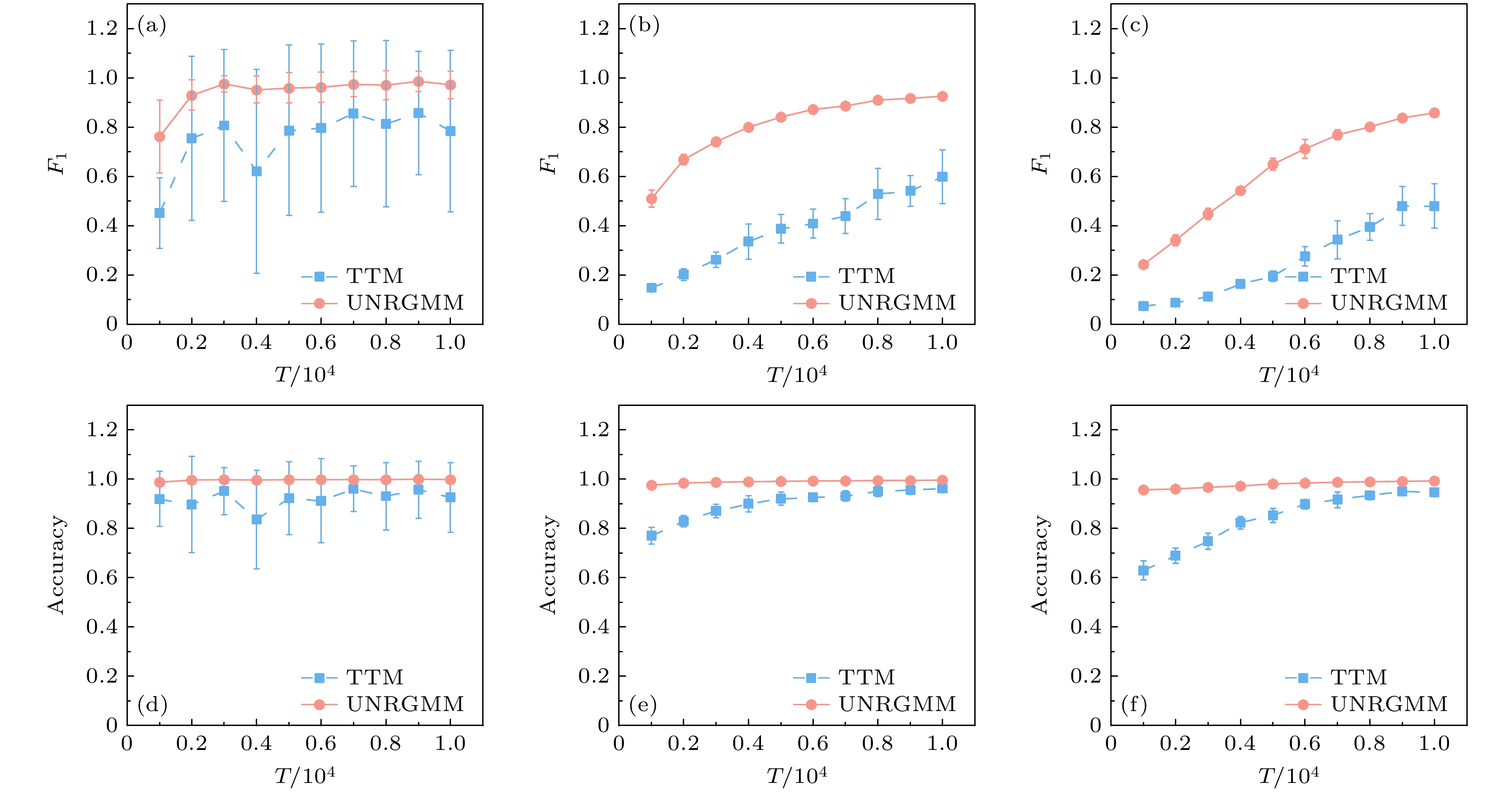
$ {H(i)} $ and node reconstruction effect: The horizontal axis represents the node number, the left vertical axis represents the negative value of node’s reconfigurability index$ {-H(i)} $ , and the right vertical axis represents the reconstruction effect F1图 3 UNRGMM与TTM在合成网络中的重构效果比较 (a)和(d)为ER网络上的重构效果; (b)和(e)为WS网络上的重构效果; (c)和(f)为BA网络上的重构效果. 误差棒表示10次独立实验的标准差
Figure 3. Comparison of reconstruction effects between UNRGMM and TTM in synthetic networks: (a) and (d) represent the reconstruction effect on the ER network; (b) and (e) represent the reconstruction effect on the WS network; (c) and (f) represent the reconstruction effect on the BA network. The error bar represents standard deviation over ten independent trials.
图 4 UNRGMM与TTM在噪声干扰下的重构效果 (a)和(d)为ER网络上的重构效果; (b)和(e)为WS网络上的重构效果; (c)和(f)为BA网络上的重构效果. 误差棒表示10次独立实验的标准差
Figure 4. The reconstruction effect of UNRGMM and TTM under noise interference: (a) and (d) represent the reconstruction effect on the ER network; (b) and (e) represent the reconstruction effect on the WS network; (c) and (f) represent the reconstruction effect on the BA network. The error bar represents standard deviation over ten independent trials.
图 5 UNRGMM与TTM在不同平均度的合成网络中的重构效果 (a)和(d)为ER网络上的重构效果; (b)和(e)为WS网络上的重构效果; (c)和(f)为BA网络上的重构效果. 误差棒表示10次独立实验的标准差
Figure 5. The reconstruction effect of UNRGMM and TTM in synthetic networks with different average degrees: (a) and (d) represent the reconstruction effect on the ER network; (b) and (e) represent the reconstruction effect on the WS network; (c) and (f) represent the reconstruction effect on the BA network. The error bar represents standard deviation over ten independent trials.
图 6 UNRGMM与TTM在不同动力学下的重构效果 (a)和(d)为Ising动力学的重构效果; (b)和(e)为Game动力学的重构效果; (c)和(f)为Majority动力学的重构效果. 误差棒表示10次独立实验的标准差
Figure 6. The reconstruction effect of UNRGMM and TTM under different dynamics: (a) and (d) represent the reconstruction effect for Ising dynamics; (b) and (e) represent the reconstruction effect for Game dynamics; (c) and (f) represent the reconstruction effect for Majority dynamics. The error bar represents standard deviation over ten independent trials.
表 1 真实网络结构特征N和E分别是节点和连边数量;
${\langle k\rangle}$ 表示平均度; C和r分别是聚类系数和分类系数; H是异质性程度, 定义为${H= {\langle k^2\rangle}/{{\langle k\rangle}^{2}}}$ Table 1. Real networks structure characteristics. N and E are the number of nodes and edges, respectively;
${\langle k\rangle}$ indicates the average degree; C and r are clustering coefficients and classification coefficients, respectively; H is the degree heterogeneity, defined as${H= {\langle k^2\rangle}/{{\langle k\rangle}^{2}}}$ .真实网络 N E $ {\langle k\rangle} $ 

C r H Karate 34 78 4.588 0.59 –0.476 1.693 Dolphins 62 159 5.129 0.29 –0.071 1.326 Football 115 613 10.661 0.4 0.162 1.007 Polbooks 105 441 8.40 0.49 –0.128 1.421 表 2 UNRGMM与TTM在真实网络中的重构结果比较
Table 2. Comparison of reconstruction results between UNRGMM and TTM on real networks.
真实网络 TTM UNRGMM F1 Accuracy F1 Accuracy Karate 0.723 0.889 0.989 0.997 Dolphins 0.776 0.951 0.970 0.995 Football 0.484 0.874 0.774 0.963 Polbooks 0.571 0.896 0.838 0.978 -
[1] Li X, Sun L, Ling M J, Peng Y 2023 Neurocomputing 549 126441 doi: 10.1016/j.neucom.2023.126441 [2] 张彦超, 刘云, 张海峰, 程辉, 熊菲 2011 物理学报 60 050501 doi: 10.7498/aps.60.050501 Zhang Y C, Liu Y, Zhang H F, Cheng H, Xiong F 2011 Acta Phys. Sin. 60 050501 doi: 10.7498/aps.60.050501 [3] Gardner T S, Di Bernardo D, Lorenz D, Collins J J 2003 Science 301 102 doi: 10.1126/science.1081900 [4] Geier F, Timmer J, Fleck C 2007 BMC Syst. Biol. 1 1 doi: 10.1186/1752-0509-1-1 [5] Gao C, Fan Y, Jiang S H, Deng Y, Liu J M, Li X H 2021 IEEE Trans. Intell. Transp. Syst. 23 6509 doi: 10.1109/TITS.2021.3058185 [6] Zhou Y M, Li S P, Kundu T, Bai X W, Qin W 2021 IEEE Trans. Network Sci. Eng. 8 2249 doi: 10.1109/TNSE.2021.3085818 [7] 张海峰, 王文旭 2020 物理学报 69 088906 doi: 10.7498/aps.69.20200001 Zhang H F, Wang W X 2020 Acta Phys. Sin. 69 088906 doi: 10.7498/aps.69.20200001 [8] Wang J Y, Zhang Y J, Xu C, Li J Z, Sun J C, Xie J R, Feng L, Zhou T S, Hu Y Q 2024 Nat. Commun. 15 2849 doi: 10.1038/s41467-024-47248-x [9] 康玲, 项冰冰, 翟素兰, 鲍中奎, 张海峰 2018 物理学报 67 198901 doi: 10.7498/aps.67.20181000 Kang L, Xiang B B, Zhai S L, Bao Z K, Zhang H F 2018 Acta Phys. Sin. 67 198901 doi: 10.7498/aps.67.20181000 [10] Xiang B B, Bao Z K, Ma C, Zhang X Y, Chen H S, Zhang H F 2018 Chaos: An Interdisciplinary Journal of Nonlinear Science 28 013122 doi: 10.1063/1.4990734 [11] Zhao J, Cheong K H 2024 IEEE Trans. Syst. Man Cybern. Part A Syst. Humans 54 6 doi: 10.1109/TSMC.2024.3349537 [12] Guo Q T, Jiang X, Lei Y J, Li M, Ma Y F, Zheng Z M 2015 Phys. Rev. E 91 012822 doi: 10.1103/PhysRevE.91.012822 [13] Li D D, Qian W Q, Sun X X, Han D, Sun M 2023 Appl. Math. Comput. 458 128233 [14] Lv X J, Fan D M, Li Q, Wang J L, Zhou L 2023 Physica A 627 129131 doi: 10.1016/j.physa.2023.129131 [15] 徐翔, 朱承, 朱先强 2021 物理学报 70 088901 doi: 10.7498/aps.70.20201756 Xu X, Zhu C, Zhu X Q 2021 Acta Phys. Sin. 70 088901 doi: 10.7498/aps.70.20201756 [16] Wang H, Ma C, Chen H S, Lai Y C, Zhang H F 2022 Nat. Commun. 13 3043 doi: 10.1038/s41467-022-30706-9 [17] Ma C, Wang H, Zhang H F 2023 Europhys. Lett. 144 21002 doi: 10.1209/0295-5075/ad07b2 [18] 杨浦, 郑志刚 2012 物理学报 61 120508 doi: 10.7498/aps.61.120508 Yang P, Zheng Z G 2012 Acta Phys. Sin. 61 120508 doi: 10.7498/aps.61.120508 [19] Ma C, Chen H S, Li X, Lai Y C, Zhang H F 2020 SIAM J. Appl. Dyn. Syst. 19 124 doi: 10.1137/19M1254040 [20] Shen Z S, Wang W X, Fan Y, Di Z R, Lai Y C 2014 Nat. Commun. 5 4323 doi: 10.1038/ncomms5323 [21] Liu Q M, Ma C, Xiang B B, Chen H S, Zhang H F 2019 IEEE Trans. Syst. Man Cybern. Part A Syst. Humans 51 4639 doi: 10.1109/TSMC.2019.2945363 [22] Zhang A B, Fan Y, Di Z R, Zeng A 2023 Chaos, Solitons Fractals 173 113712 doi: 10.1016/j.chaos.2023.113712 [23] Wang W X, Lai Y C, Grebogi C, Ye J P 2011 Phys. Rev. X 1 021021 [24] Li G J, Li N, Liu S H, Wu X Q 2019 Chaos: An Interdisciplinary Journal of Nonlinear Science 29 053117 doi: 10.1063/1.5093270 [25] Mei G F, Wu X Q, Wang Y F, Hu M, Lu J A, Chen G R 2017 IEEE Trans. Cybern. 48 754 doi: 10.1109/TCYB.2017.2655511 [26] Pandey P K, Adhikari B 2017 IEEE Trans. Knowl. Data Eng. 29 2072 doi: 10.1109/TKDE.2017.2725264 [27] Pandey P K, Adhikari B, Mazumdar M, Ganguly N 2020 IEEE Trans. Knowl. Data Eng. 34 3377 doi: 10.1109/TKDE.2020.3024779 [28] Ma C, Chen H S, Lai Y C, Zhang H F 2018 Phys. Rev. E 97 022301 [29] Zhang Z, Zhao Y, Liu J, Wang S, Tao R, Xin R, Zhang J 2019 Appl. Network Sci. 4 1 doi: 10.1007/s41109-018-0108-x [30] Xu X, Zhu X Q, Zhu C 2023 Complex Intell. Syst. 9 3131 doi: 10.1007/s40747-022-00893-5 [31] Mignone P, Pio G, D’ Elia D, Ceci M 2020 Bioinformatics 36 1553 doi: 10.1093/bioinformatics/btz781 [32] Reynolds D A 2009 Encyclopedia of Biometrics 741 659 [33] Wang Y, Chakrabarti D, Wang C X, Faloutsos C 2003 In 22nd International Symposium on Reliable Distributed Systems Florence, Italy, October 6–8, 2003 pp25–34 [34] Perotti J I, Tessone C J, Clauset A, Caldarelli G 2018 arXiv: 1806.07005 (Physics and Society [35] Erds P, Rényi A 1960 Publ. Math. Inst. Hungar. Acad. Sci. 5 17 [36] Watts D J, Strogatz S H 1998 Nature 393 440 doi: 10.1038/30918 [37] Barabási A L, Albert R 1999 Science 286 509 doi: 10.1126/science.286.5439.509 [38] Li J W, Shen Z S, Wang W X, Grebogi C, Lai Y C 2017 Phys. Rev. E 95 032303 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: