高级搜索

少电子离子束缚态电子g因子精密测量

downloadPDF

上一篇

下一篇

屠秉晟. 少电子离子束缚态电子g因子精密测量[J]. 物理学报, 2024, 73(20): 203103-1. doi: 10.7498/aps.73.20240683
引用本文: 屠秉晟. 少电子离子束缚态电子g因子精密测量[J]. 物理学报, 2024, 73(20): 203103-1. doi: 10.7498/aps.73.20240683
shu
Bing-Sheng Tu. Precise measurements of electron g factors in bound states of few-electron ions[J]. Acta Physica Sinica, 2024, 73(20): 203103-1. doi: 10.7498/aps.73.20240683
Citation: Bing-Sheng Tu. Precise measurements of electron g factors in bound states of few-electron ions[J]. Acta Physica Sinica, 2024, 73(20): 203103-1. doi: 10.7498/aps.73.20240683
shu

少电子离子束缚态电子g因子精密测量

  • 复旦大学现代物理研究所, 核物理与离子束应用教育部重点实验室, 上海EBIT实验室, 上海　200433

    • 通讯作者: bingshengtu@fudan.edu.cn

  • 中图分类号: 31.30.js, 32.10.Dk, 37.10.Ty

Precise measurements of electron g factors in bound states of few-electron ions

  • Shanghai EBIT Lab, Key Laboratory of Nuclear Physics and Ion-Beam Application (MOE), Institute of Modern Physics, Fudan University, Shanghai 200433, China

    • Corresponding author: bingshengtu@fudan.edu.cn

  • MSC: 31.30.js, 32.10.Dk, 37.10.Ty

  • 摘要: 少电子离子束缚态电子g因子的精密测量是借助原子分子体系研究束缚态量子电动力学(QED)理论的有效途径. 特别是在高电荷态重核体系中, 原子核与内壳层电子之间极强的电磁相互作用为研究极端电磁场环境下的QED效应提供了独一无二的条件. 通过精确测量束缚态电子g因子, 还可以分析核效应、测定核结构参数、确定基本物理常数等. 少电子离子束缚态电子g因子的研究已经成为精密谱学方向的前沿课题. 潘宁离子阱(借助稳态电磁场囚禁离子的系统)是进行g因子测量的有效实验装置之一. 本综述将对基于潘宁离子阱开展少电子离子束缚态电子g因子的实验研究进行全面回顾, 介绍基本实验原理与测量方法, 重点论述该领域在近几年中的重要实验成果, 并对未来发展进行简要展望.
    Abstract: The electron g factor is an important fundamental structural parameter in atomic physics, as it reveals various mechanisms of interactions between electrons and external fields. Precise measurements of g factors of bound electrons in simple atomic and molecular systems provide an effective method for investigating the bound-state quantum electrodynamics (QED) theory. Especially in highly-charged heavy ions (HCIs), the strong electromagnetic interactions between the nuclei and inner-shell electrons provide unique opportunities to test QED under extremely strong fields. Accurate measurements of the g factors of the bound-state electrons are also important for determining nuclear effects, nuclear parameters and fundamental constants. The research on g factors of the bound-state electrons has become a frontier topic in fundamental physics. A Penning trap, which uses steady-state electromagnetic fields to confine charged particles, is utilized to precisely measure the g factor. This paper presents a comprehensive review of the experiments on g factors for few-electron simple systems in Penning traps, including experimental principles, experimental setups, measurement methods, and a summary of important research findings. The physical concept of the electron g factor and its historical research background are introduced. The electron g factor is considered as an effective probe to study higher-order QED effects. Through high-precision measurements of the free electron g factor, discrepancies between the fine-structure constants and other experimental results in atomic physics are identified. Notably, the g factor of the 1s electron in HCIs deviates significantly from the value for free electrons as the atomic number increases. Experimental principles, including the principle of the Penning trap and the principle of measuring the bound-state electron g factors are discussed. A double-trap experiment setup and related precision measurement techniques are also introduced.This paper reviews several milestone experiments including (1) the stringent test of bound-state QED by precise measurement of bound-state electron g factor of a 118Sn49+ ion, (2) measurement of the g factors of lithium-like and boron-like ions and their applications, and (3) measurement of the g-factor isotope shift by using an advanced two-ion balance technique in the Penning trap, providing an insight into the QED effects in nuclear recoil. Finally, this paper summarizes the challenges currently faced in measuring the g factors of bound-state electrons in few-electron ion systems and provides the prospects for the future developments of this field.
  • 加载中

  • 图 1  自由电子g因子最低阶QED修正的费曼图描述, 直线代表自由传播的电子, 三角形表示电磁场而曲线表示电子与电磁场作用中的虚光子　(a)自能效应; (b)真空极化效应

    Figure 1.  Feynman diagrams of the first-order QED corrections of the free electron g-factor, the straight line represents the electron, curved lines as the photons and the triangle as the magnetic field: (a) The self-energy term; (b) the vacuum-polarization term.

    下载: 全尺寸图片 幻灯片

    图 2  类氢离子1s电子g因子与平均电场强度随原子序数Z的依赖关系

    Figure 2.  g factor of 1s electron and the mean electromagnetic field as a function of atomic number Z.

    下载: 全尺寸图片 幻灯片

    图 3  类氢离子基态g因子的高阶QED贡献与原子核效应随原子序数的依赖关系, 数据(图片)来自文献[11]

    Figure 3.  Relative contributions of the g factors of H-like ions as a function of atomic number Z, from Ref. [11].

    下载: 全尺寸图片 幻灯片

    图 4  潘宁离子阱剖面结构图, 离子运动与镜像电流测量原理示意图(图中部分素材由马克斯普朗克核物理研究所提供)

    Figure 4.  Cut model of Penning traps with illustration of ion motion and image current detection system (some of the materials in the image are provided by the Max-Planck-Institute for Nuclear Physics).

    下载: 全尺寸图片 幻灯片

    图 5  12C5+离子拉莫频率共振谱, 数据(图片)来自文献[16]

    Figure 5.  Larmor resonance of 12C5+ bound-state electron, from Ref. [16].

    下载: 全尺寸图片 幻灯片

    图 6  双阱实验装置剖面示意图, 图片来自文献[18]

    Figure 6.  Cut model of double penning trap system in Mainz, from Ref. [18].

    下载: 全尺寸图片 幻灯片

    图 7  基于双阱实验装置的g因子测量共振谱, 图片来自文献[18]

    Figure 7.  g-factor resonance spectrum from double Penning trap system in Mainz, from Ref. [18].

    下载: 全尺寸图片 幻灯片

    图 8  ALPHATRAP实验系统示意图, 高电荷态重离子由Heidelberg EBIT中产生, 离子束团引出后经过电荷态筛选、偏转、减速、聚焦后被潘宁阱俘获, 手动低温阀可以用来隔离室温束线与低温离子阱的真空环境, 保证离子阱内部真空度优于10–17 torr, 图片来自文献[13]

    Figure 8.  Schematic diagram of the ALPHATRAP experiment, the highly charged ions are produced in the Heidelberg EBIT, the ions are extracted, with charge-state selection, and injected into the Penning trap, the cryogenic valve can be closed to isolate the trap vacuum from the beamline, resulting in a vacuum better than 10–17 torr, from Ref. [13].

    下载: 全尺寸图片 幻灯片

    图 9  类锂离子基态g因子的高阶QED贡献, 电子-电子关联效应、Screened QED效应、原子核效应随原子序数的依赖关系, 数据(图片)来自文献[10]

    Figure 9.  Relative contributions (QED corrections, interelectronic interaction and screened QED) of the g factors of Li-like ions as a function of atomic number Z, from Ref. [10].

    下载: 全尺寸图片 幻灯片

    表 1  类氢12C5+, 16O7+, 20Ne9+, 28Si13+和118Sn49+基态g因子计算与实验数据表

    Table 1.  Experimental and theoretical g factors of 12C5+, 16O7+, 20Ne9+, 28Si13+和118Sn49+.

    12C5+ 16O7+ 20Ne9+ 28Si13+ 118Sn49+
    gDirac 1.99872135439(1) 1.99772600306(2) 1.99644517090 1.9930235716 1.90807920530
    Free QED 0.00231930437(1) 0.00231930437(1) 0.00231930435 0.00231930437(1) 0.00231930435
    BS-QED 0.00000084340(3) 0.00000159438(11) 0.00000265069(12) 0.0000058558(17) 0.000148098(298)
    FNS 0.00000000041 0.00000000155(1) 0.000 00000476(1) 0.000000 205 0.000014489(24)
    NR 0.00000008762 0.00000011697 0.00000014641 0.0000002051(1) 0.000000726
    Hadronic — — — — –0.000000002
    gtheo 2.00104159018(3) 2.00004702128(11) 1.99876727711(12) 1.995348958 0(17) 1.910561821(299)
    gexp 2.0010415964(45) 2.0000470254(46) 1.99876727699(19) 1.99534895910(81) 1.910562058962(914)
    注: gDirac 代表Dirac方程计算的g因子值, Free QED代表自由(电子)QED效应贡献, BS-QED代表束缚态(电子)QED效应贡献, FNS代表核尺寸效应贡献, NR代表核反冲效应贡献, Hadronic代表强子效应贡献. 12C5+, 16O7+, 28Si13数据来自于文献[10], 20Ne9+的数据来自于文献[12], 118Sn49+的数据来自于文献[13].
    下载: 导出CSV

    表 2  28Si11+, 40Ca17+和40Ar13+基态g因子计算与实验数据表

    Table 2.  Theoretical and experimental g factors of 28Si11+, 40Ca17+ and 40Ar13+.

    28Si11+ 40Ca17+ 40Ar13
    gDirac 1.9982547533 1.9964260253 0.66377545
    QED 0.0023202857 (17) 0.0023216601(17) –0.0007682(4)
    e-e int. 0.000314 8098 (22) 0.0004542910 (24) 0.0006500(2)
    FNS + NR 0.0000000436 0.0000000662 –0.0000091(2)
    gtheo 2.000889 8924 (28) 1.9992020426 (29) 0.6636482 (5)
    gexp 2.00088988845 (14) 1.9992020405 (11) 0.66364845532(93)
    注: QED代表经过屏蔽势修正后的束缚态QED效应, e-e int.代表电子-电子关联效应贡献; 28Si11+与40Ca17+数据来自于文献[23], 40Ar13数据来自于文献[24].
    下载: 导出CSV

    表 3  20Ne9+和22Ne9+基态g因子差以及相关核效应贡献的计算值, 数据来自文献[28]

    Table 3.  Contributions of the g-factor difference of 20Ne9+ and 22Ne9+ as well as the experimental result, from Ref. [28]

    效应贡献 $ {{\Delta }}g=g\left({}_{}{}^{20}{{\mathrm{N}}{\mathrm{e}}}_{}^{9+}\right)-g\left({}_{}{}^{22}{{\mathrm{N}}{\mathrm{e}}}_{}^{9+}\right) $
    ($ \times {10}^{-9} $)
    FNS 0.166(11)
    Recoil, non-QED 13.2827
    Recoil, QED 0.0435
    Recoil, (α/π)(me/M) –0.0103
    Recoil, (me/M)2 –0.0077
    Nuclear polarization 0.0001(3)
    Δg total theory 13.474(11)
    Δg experiment 13.47524(53)stat(99)sys
    下载: 导出CSV
  • [1] Landé A 1921 Z. Für Phys. 5 231
    [2] Kusch P, Foley H M 1947 Phys. Rev. 72 1256
    [3] Kinoshita T 1990 Advanced Series on Directions in HighEnergy Physics (Singapore: World Scientific) pp218-321
    [4] Schwinger J 1948 Phys. Rev. 73 416 doi: 10.1103/PhysRev.73.416
    [5] Laporta S, Remiddi E 1996 Phys. Lett. B 379 283 doi: 10.1016/0370-2693(96)00439-X
    [6] Aoyama T, Hayakawa M, Kinoshita T, Nio M 2012 Phys. Rev. Lett. 109 111807 doi: 10.1103/PhysRevLett.109.111807
    [7] Fan X, Myers T G, Sukra B A D, Gabrielse G 2023 Phys. Rev. Lett. 130 071801 doi: 10.1103/PhysRevLett.130.071801
    [8] Shabaev V M, Glazov D A, Plunien G, Volotka A V 2015 J. Phys. Chem. Ref. Data 44 031205 doi: 10.1063/1.4921299
    [9] Breit G 1928 Nature 122 649
    [10] Werth G, Sturm S, Blaum K 2018 Adv. At. Mol. Opt. Phys. 67 257
    [11] Sturm S, Arapoglou I, Egl A, Höcker M, Kraemer S, Sailer T, Tu B, Weigel A, Wolf R, López-Urrutia J C, Blaum K 2019 Eur. Phys. J. Spec. Top. 227 1425 doi: 10.1140/epjst/e2018-800225-2
    [12] Heiße F, Door M, Sailer T, Filianin P, Herkenhoff J, König C M, Kromer K, Lange D, Morgner J, Rischka A, Schweiger C, Tu B, Novikov Y N, Eliseev S, Sturm S, Blaum K 2023 Phys. Rev. Lett. 131 253002 doi: 10.1103/PhysRevLett.131.253002
    [13] Morgner J, Tu B, König C M, Sailer T, Heiße F, Bekker H, Sikora B, Lyu C, Yerokhin V A, Harman Z, Crespo López-Urrutia J R, Keitel C H, Sturm S, Blaum K 2023 Nature 622 53 doi: 10.1038/s41586-023-06453-2
    [14] Brown L S, Gabrielse G 1986 Rev. Mod. Phys. 58 233 doi: 10.1103/RevModPhys.58.233
    [15] Tu B, Si R, Shen Y, Wang J, Wei B, Chen C, Yao K, Zou Y 2023 Phys. Rev. Res. 5 043014 doi: 10.1103/PhysRevResearch.5.043014
    [16] Hermanspahn N, Häffner H, Kluge H J, Quint W, Stahl S, Verdú J, Werth G 2000 Phys. Rev. Lett. 84 427 doi: 10.1103/PhysRevLett.84.427
    [17] Sturm S, Wagner A, Schabinger B, Blaum K 2011 Phys. Rev. Lett. 107 143003 doi: 10.1103/PhysRevLett.107.143003
    [18] Häffner H, Beier T, Hermanspahn N, Kluge H J, Quint W, Stahl S, Verdú J, Werth G 2000 Phys. Rev. Lett. 85 5308 doi: 10.1103/PhysRevLett.85.5308
    [19] Verdú J, Djekić S, Stahl S, Valenzuela T, Vogel M, Werth G, Beier T, Kluge H J, Quint W 2004 Phys. Rev. Lett. 92 093002 doi: 10.1103/PhysRevLett.92.093002
    [20] Sturm S, Wagner A, Schabinger B, Zatorski J, Harman Z, Quint W, Werth G, Keitel C H, Blaum K 2011 Phys. Rev. Lett. 107 023002 doi: 10.1103/PhysRevLett.107.023002
    [21] Martínez A J G, López-Urrutia J R C, Fischer D, Orts R S, Ullrich J 2007 J. Phys. Conf. Ser. 72 012001 doi: 10.1088/1742-6596/72/1/012001
    [22] Zinenko D V, Glazov D A, Kosheleva V P, Volotka A V, Fritzsche S 2023 Phys. Rev. A 107 032815 doi: 10.1103/PhysRevA.107.032815
    [23] Kosheleva V P, Volotka A V, Glazov D A, Zinenko D V, Fritzsche S 2022 Phys. Rev. Lett. 128 103001 doi: 10.1103/PhysRevLett.128.103001
    [24] Arapoglou I, Egl A, Höcker M, Sailer T, Tu B, Weigel A, Wolf R, Cakir H, Yerokhin V A, Oreshkina N S, Agababaev V A, Volotka A V, Zinenko D V, Glazov D A, Harman Z, Keitel C H, Sturm S, Blaum K 2019 Phys. Rev. Lett. 122 253001 doi: 10.1103/PhysRevLett.122.253001
    [25] Shabaev V M, Glazov D A, Oreshkina N S, Volotka A V, Plunien G, Kluge H J, Quint W 2006 Phys. Rev. Lett. 96 253002 doi: 10.1103/PhysRevLett.96.253002
    [26] Yerokhin V A, Berseneva E, Harman Z, Tupitsyn I I, Keitel C H 2016 Phys. Rev. Lett. 116 100801 doi: 10.1103/PhysRevLett.116.100801
    [27] Köhler F, Blaum K, Block M, Chenmarev S, Eliseev S, Glazov D A, Goncharov M, Hou J, Kracke A, Nesterenko D A, Novikov Y N, Quint W, Minaya Ramirez E, Shabaev V M, Sturm S, Volotka A V, Werth G 2016 Nat. Commun. 7 10246 doi: 10.1038/ncomms10246
    [28] Sailer T, Debierre V, Harman Z, Heiße F, König C, Morgner J, Tu B, Volotka A V, Keitel C H, Blaum K, Sturm S 2022 Nature 606 479 doi: 10.1038/s41586-022-04807-w
    [29] Debierre V, Keitel C H, Harman Z 2020 Phys. Lett. B 807 135527 doi: 10.1016/j.physletb.2020.135527
    [30] Schneider A, Sikora B, Dickopf S, Müller M, Oreshkina N S, Rischka A, Valuev I A, Ulmer S, Walz J, Harman Z, Keitel C H, Mooser A, Blaum K 2022 Nature 606 878 doi: 10.1038/s41586-022-04761-7
    [31] Kaiser A, Dickopf S, Door M, Behr R, Beutel U, Eliseev S, Kaushik A, Kromer K, Müller M, Palafox L, Ulmer S, Mooser A, Blaum K 2024 Appl. Phys. Lett. 124 224002 doi: 10.1063/5.0206779
    [32] Devlin J A, Wursten E, Harrington J A, Higuchi T, Blessing P E, Borchert M J, Erlewein S, Hansen J J, Morgner J, Bohman M A, Mooser A H, Smorra C, Wiesinger M, Blaum K, Matsuda Y, Ospelkaus C, Quint W, Walz J, Yamazaki Y, Ulmer S 2019 Phys. Rev. Appl. 12 , 044012 DOI: 10.1103/PhysRevApplied.12.044012
    [33] Ketter J, Eronen T, Höcker M, Streubel S, Blaum K 2014 Int. J. Mass Spectrom. 358 1 doi: 10.1016/j.ijms.2013.10.005
    [34] Tu B, Hahne F, Arapoglou I, Egl A, Heiße F, Höcker M, König C, Morgner J, Sailer T, Weigel A, Wolf R, Sturm S 2021 Adv. Quantum Technol. 4 2100029 doi: 10.1002/qute.202100029
    [35] Bohman M, Grunhofer V, Smorra C, Wiesinger M, Will C, Borchert M J, Devlin J A, Erlewein S, Fleck M, Gavranovic S, Harrington J, Latacz B, Mooser A, Popper D, Wursten E, Blaum K, Matsuda Y, Ospelkaus C, Quint W, Walz J, Ulmer S, BASE Collaboration 2021 Nature 596 514 doi: 10.1038/s41586-021-03784-w
    [36] Will C, Wiesinger M, Micke P, Yildiz H, Driscoll T, Kommu S, Abbass F, Arndt B P, Bauer B B, Erlewein S, Fleck M, Jäger J I, Latacz B M, Mooser A, Schweitzer D, Umbrazunas G, Wursten E, Blaum K, Devlin J A, Ospelkaus C, Quint W, Soter A, Walz J, Smorra C, Ulmer S 2024 Phys. Rev. Lett. 133 023002 doi: 10.1103/PhysRevLett.133.023002
  • 加载中
图( 9) 表( 3)
计量
  • 文章访问数:  292
  • HTML全文浏览数:  292
  • PDF下载数:  2
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-05-14
  • 刊出日期:  2024-10-20

少电子离子束缚态电子g因子精密测量

    通讯作者: bingshengtu@fudan.edu.cn
  • 复旦大学现代物理研究所, 核物理与离子束应用教育部重点实验室, 上海EBIT实验室, 上海　200433
  • 收稿日期:  2024-05-14

摘要: 少电子离子束缚态电子g因子的精密测量是借助原子分子体系研究束缚态量子电动力学(QED)理论的有效途径. 特别是在高电荷态重核体系中, 原子核与内壳层电子之间极强的电磁相互作用为研究极端电磁场环境下的QED效应提供了独一无二的条件. 通过精确测量束缚态电子g因子, 还可以分析核效应、测定核结构参数、确定基本物理常数等. 少电子离子束缚态电子g因子的研究已经成为精密谱学方向的前沿课题. 潘宁离子阱(借助稳态电磁场囚禁离子的系统)是进行g因子测量的有效实验装置之一. 本综述将对基于潘宁离子阱开展少电子离子束缚态电子g因子的实验研究进行全面回顾, 介绍基本实验原理与测量方法, 重点论述该领域在近几年中的重要实验成果, 并对未来发展进行简要展望.

English Abstract

    全文HTML

    1.   引　言

      1.1.   自由电子g因子

    • 在原子物理中, 朗德g因子是联系原子磁矩与总角动量的无量纲参数. 由Landé[1]于1921年提出, 用来解释反常塞曼效应. 随后, 在1925年Uhlenbeck和Goudsmit提出了自旋的概念, 认为电子自身具有像轨道角动量$ l $一样的内禀角动量$ s $, 而原子的总角动量$ J $就是$ l $与$ s $的矢量耦合. 由此, 原子能级在外磁场下的分裂可以表示为

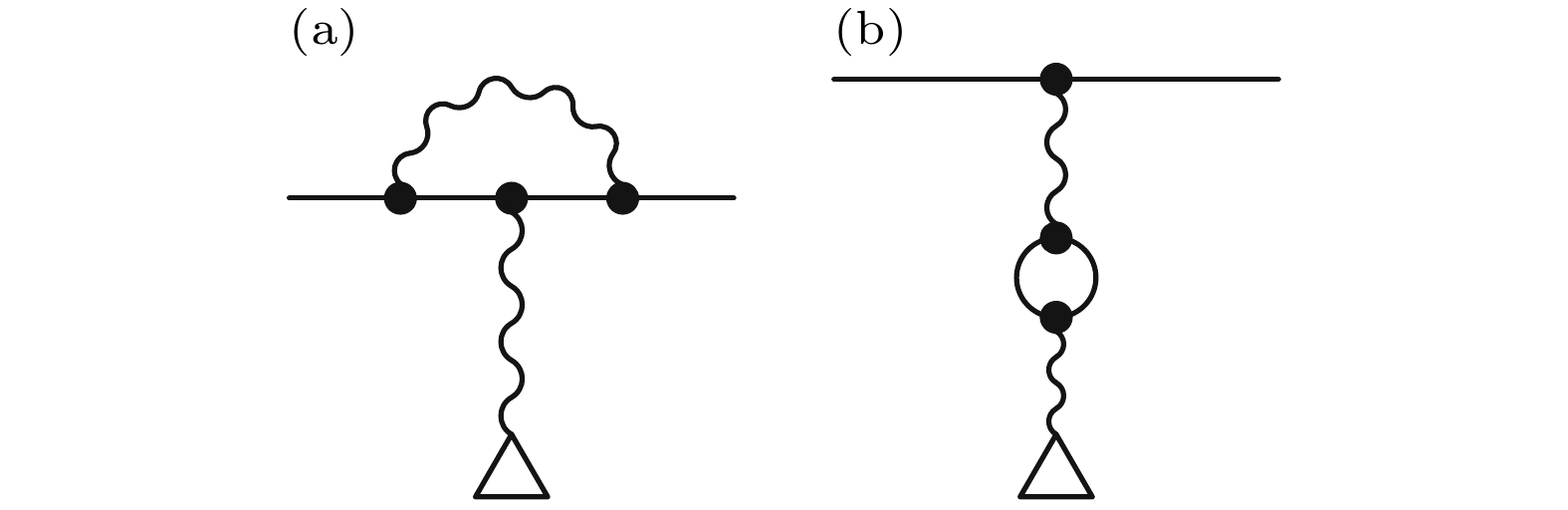
      其中, $ {\mu }_{{\mathrm{B}}}=\dfrac{{{e}}\hslash }{2{m}_{{\mathrm{e}}}} $称为玻尔磁子, $ {m}_{J} $为总角动量在磁场方向的投影值. Dirac在1928年提出了描述自由电子的相对论波动方程, 推导得到电子的自旋角动量等于$ {1}/{2}\hslash $, 并确定了朗德g因子等于2. 随着微波射频技术的发展, Kusch和Foley[2]精确测量了镓原子$ {}_{}{}^{2}{{\mathrm{P}}}_{3/2}^{} $与$ {}_{}{}^{2}{{\mathrm{P}}}_{1/2}^{} $能级g因子的比值, 发现结果偏离了Dirac方程的预言值. 这一实验同著名的兰姆位移都表明电子与真空电磁场之间的相互作用会影响原子能级, 从而促使了量子电动力学(QED)的诞生.

      在QED理论框架下, 最低阶的修正(first order corrections)可由费曼图描述(见图1). 由此引起自由电子g因子的偏离值(或称为反常g因子)常用$ {a}_{{\mathrm{e}}}\equiv {1}/{2}(g-2) $表示, 并以$ \left(\alpha /\pi \right) $的展开式表达为[3]

      其中$ \alpha $为精细结构常数. 式中前3项系数可以通过严格解析计算得到[4,5], 而$ {C}_{8} $和$ {C}_{10} $系数分别包含891以及12672个费曼图描述的相互作用过程, 目前仅能通过数值方法进行计算[6]. 此外, 反常g因子中还包含强子效应、弱电效应等, 其中强子真空极化项(hadronic vacuum-polarization)的贡献已经超过五阶QED效应. 理论上精确计算这些效应对确定自由电子g因子至关重要[6]. 实验上, Fan等[7]借助潘宁离子阱装置囚禁单个电子, 对反常g因子进行了高精度的实验测量, 最新实验结果显示g因子的测量精度已经达到0.13 ppt (‌ppt表示10–12). 结合QED理论计算结果, 在0.1 ppb (‌ppb表示10–9)精度下给出了精细结构常数$ \alpha $的参考值, 该值与(Rb, Cs)原子干涉仪实验结果存在明显偏差, 成为了目前这一领域的未解之谜.

      • 1.2.   束缚态电子g因子

    • 当电子被束缚在原子体系内, 整个原子的磁矩是通过电子的自旋轨道耦合效应体现的, 这时电子g因子的表达式可以表示为

      其中, 大写的角动量表示多电子体系的耦合角动量. 对于如碱金属体系, 基态$ {}_{}{}^{2}{{\mathrm{S}}}_{1/2}^{} $的g因子为2, 而类硼离子体系基态$ {}_{}{}^{2}{{\mathrm{P}}}_{1/2}^{} $的g因子为2/3. 在QED框架下(3)式的计算并不严格正确, 束缚态电子与电磁场的相互作用, 即束缚态QED效应, 使得g因子偏离该式计算的结果. 同样采用费曼图可以描述束缚态电子与电磁场相互作用, (类似于图1)在理论上需要考虑自能项和真空极化项的贡献[8]. 最低阶的相对论修正是由Breit[9]计算得到, 他给出类氢离子的1s电子g因子的表达式为

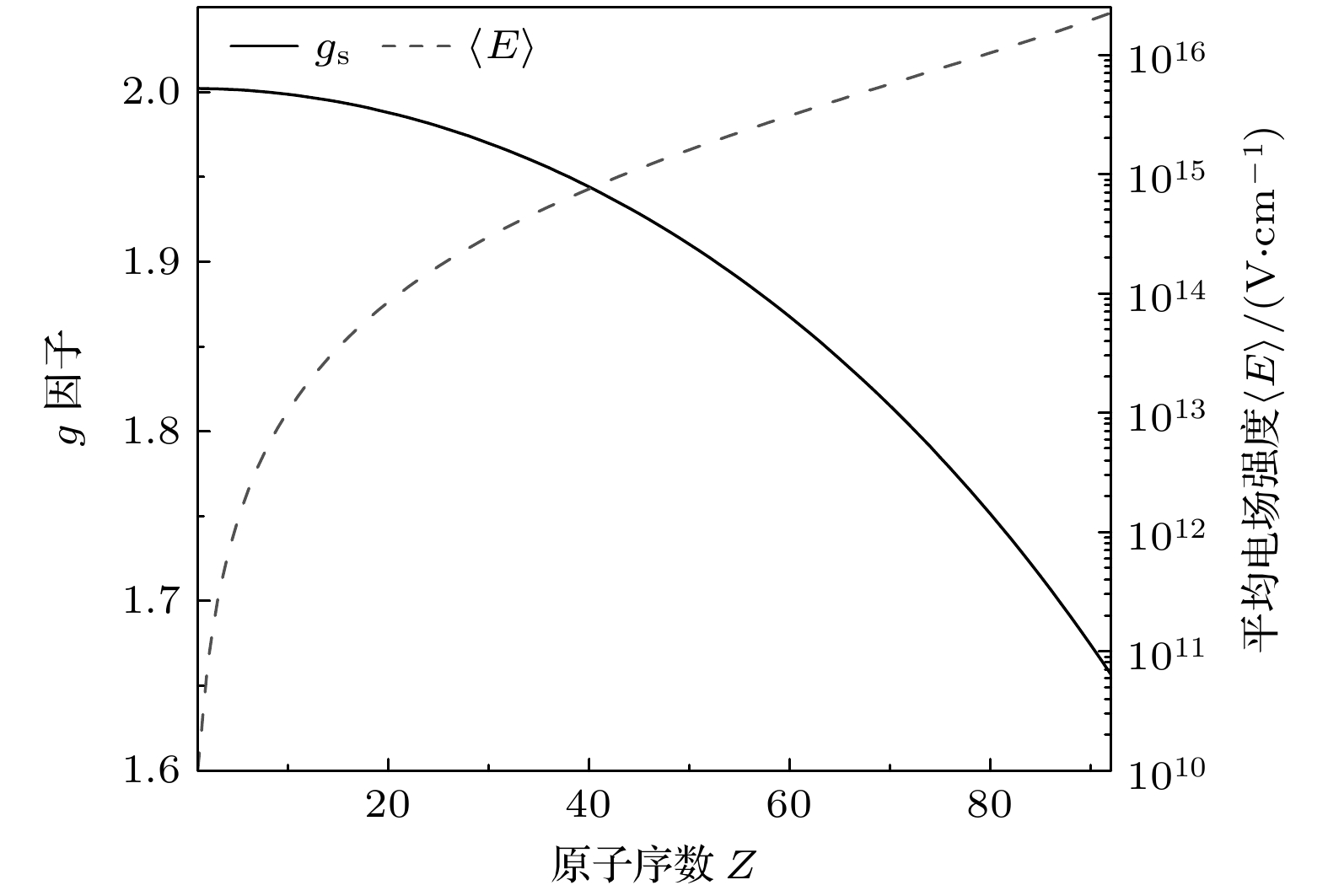
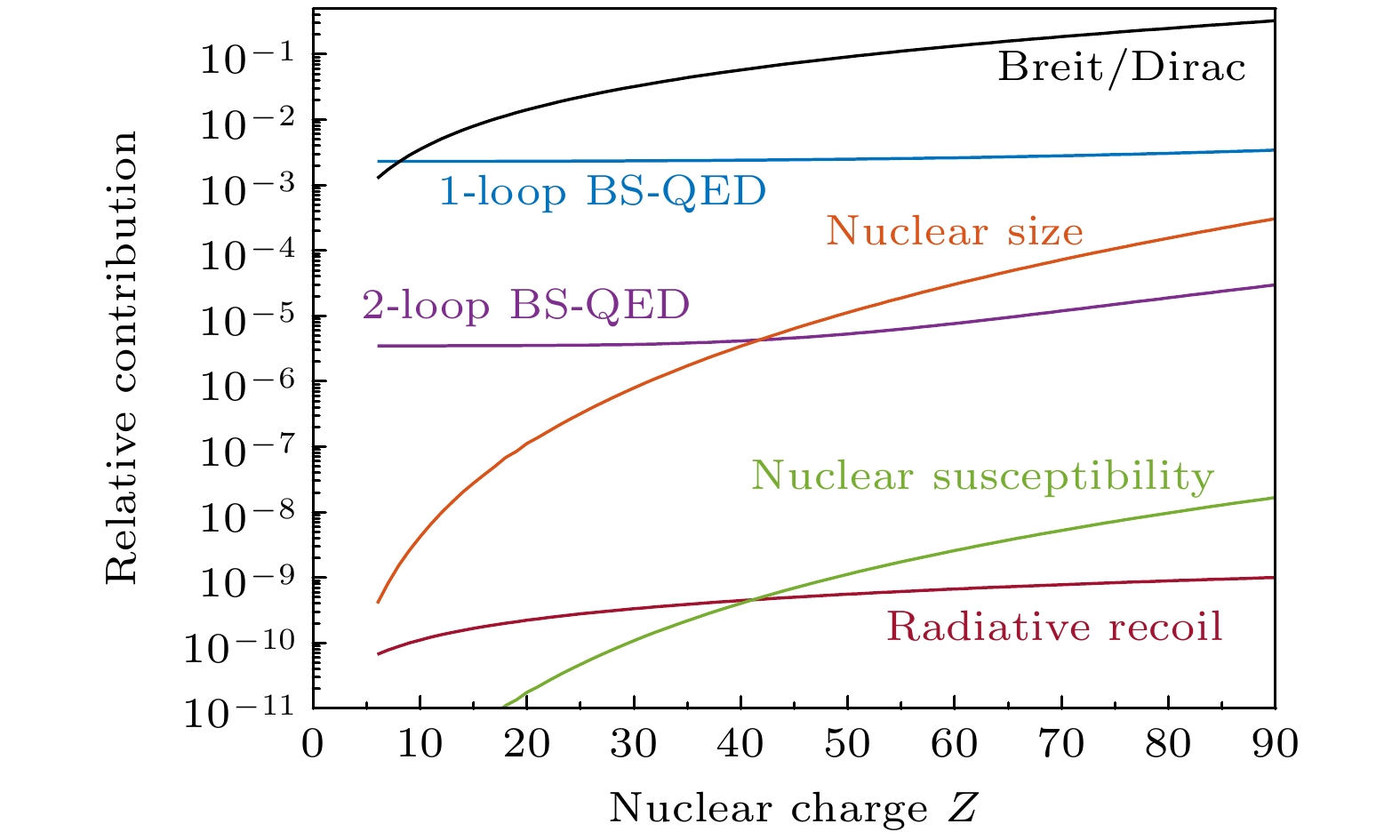
      从(4)式可以发现, 束缚态电子g因子依赖$ Z\alpha $的指数变化. 对于$ {{\mathrm{U}}}^{91+} $而言$ Z\alpha \sim 0.67 $, 远大于轻核元素. 如图2所示, U91+离子的1s电子感受到的平均库仑电场强度约1016 V/cm, 已经远超过实验室强激光所能产生的极端电磁场强度. 根据计算, 它的g因子相比自由电子偏小17%. 此外, 如图3所示, 高阶QED效应(1-loop QED和2-loop QED)以及原子核效应包括有限核尺寸效应(finite nuclear size, FNS)、核反冲效应(nuclear recoil, NR)以及核磁化效应(nuclear susceptibility, NS)等都随着原子序数的增长呈现指数增大趋势. 通过束缚态电子g因子的研究将有助于理解电子与原子核之间的复杂相互作用过程, 检验在强电磁场环境下QED理论的准确性, 认识目前理论的适用范围以及探索可能存在的新物理[10,11].

      实验上, 德国美因茨大学与马克斯普朗克核物理研究所的课题组先后对类氢12C5+, 16O7+, 20Ne9+, 28Si13+和118Sn49+离子的基态(1s)电子g因子进行了实验测量. 表1总结了g因子的实验结果以及QED效应与核效应项的理论值. 类氢12C5+离子基态电子g因子中束缚态QED效应(1-loop QED和2-loop QED)贡献为0.00000084340(3), 而118Sn49+离子1s电子g因子中束缚态QED效应贡献为0.000148098(298), 两相比较下重核中的束缚态QED效应显著增大了175倍. 目前, 电子g因子的实验测量精度已经优于10–10水平, 成功观测2-loop QED效应并检验了理论计算的准确性, 在重元素中还有望观察到3-loop QED的贡献. 相比之下, 束缚态电子g因子的理论计算精度随着原子序数Z的增大而逐渐降低. 主要原因是理论上无法对高阶QED效应中涉及的费曼图描述的所有相互作用进行完全计算, 那些未能完全计算的高阶QED效应也随$ Z\alpha $呈指数增大, 因此他们所带来的误差在重元素中也相应放大.

      • 1.3.   科学意义

    • 电子g因子是原子物理中一个非常重要的基本结构参数, 它隐含了电子与外场相互作用的各种机理. 通过对电子g因子的精确测量, 可以窥探相互作用中的一些(微弱的)高阶效应, 加深对复杂作用机制的理解, 并有机会寻找到现有理论的缺陷和不足, 成为发现新物理的探针.

      本文将着重于回顾少电子离子体系束缚态电子g因子精密谱学的实验研究, 包括实验装置、测量方法与重要研究成果等.

      引言介绍电子g因子的物理概念以及它的研究历史与背景, 分别通过自由电子g因子与束缚态电子g因子的研究阐明了电子g因子是研究高阶QED效应、原子核效应等的有效途径. 通过对自由电子g因子高精度的实验测量, 得出了精细结构常数与其他原子物理实验结果不符合. 发现随着原子序数增长, 重元素1s电子g因子明显偏离自由电子g因子值的现象.

      实验原理部分介绍潘宁离子阱的工作原理, 少电子离子束缚态电子g因子的测量原理, 双阱实验方法和相关精密测量技术的发展.

      重要研究成果主要介绍以下几个内容. 1) ALPHATRAP课题组在类氢重离子1s电子g因子测量-融合了高能电子束离子阱(EBIT)与精密潘宁离子阱, 拓展了少电子离子束缚态电子g因子的研究体系, 成功测量了118Sn49+离子基态(1s)电子g因子, 检验QED理论在强电磁场环境下的适用性. 2)从单电子体系的研究过渡到多电子体系(类锂与类硼体系)g因子精密测量-多电子离子体系中的电子g因子还反映了电子-电子关联效应与电子屏蔽QED效应. 通过对基态电子g因子的测量可以检验各种原子结构理论对电子-电子关联效应计算的正确性. 此外, 通过测量同一元素的类氢、类锂和类硼离子的电子g因子, 并计算类氢与类锂(或类硼)电子g因子的权重差值, 可以消除原子核尺寸效应的影响, 从而在更高精度下检验QED理论, 提供了一种精细结构常数测量的新方法. 3)通过测量两个同位素离子的电子g因子偏移量来确定原子核效应及其结构参数的方法.

      最后, 本文将对目前少电子离子体系束缚态电子g因子精密测量研究中所面临的挑战进行总结, 并针对这些困难提出解决思路, 对该领域未来的发展方向进行展望.

    2.   实验原理

    • 潘宁离子阱(简称潘宁阱)是一个通过囚禁离子开展精密测量的实验系统. 潘宁阱中通常存在一个高达几个特斯拉的匀强磁场来约束离子, 在这个静磁场下带电量为q, 质量为m的离子的回旋运动频率可以表示为

      如果这个离子具有磁矩(来自电子的运动), 那它会绕着磁场做拉莫进动, 进动频率可以表示为

      结合上述两式消除磁场B, 可以得到g因子的表达式为

      在质量与电荷参数已知的情况下(往往来源于原子质量数据库和CODATA数据库), 只要通过测量离子的回旋运动频率$ {\omega }_{{\mathrm{c}}} $与拉莫进动频率$ {\omega }_{{\mathrm{L}}} $就可以得到g因子值.

      • 2.1.   潘宁阱原理

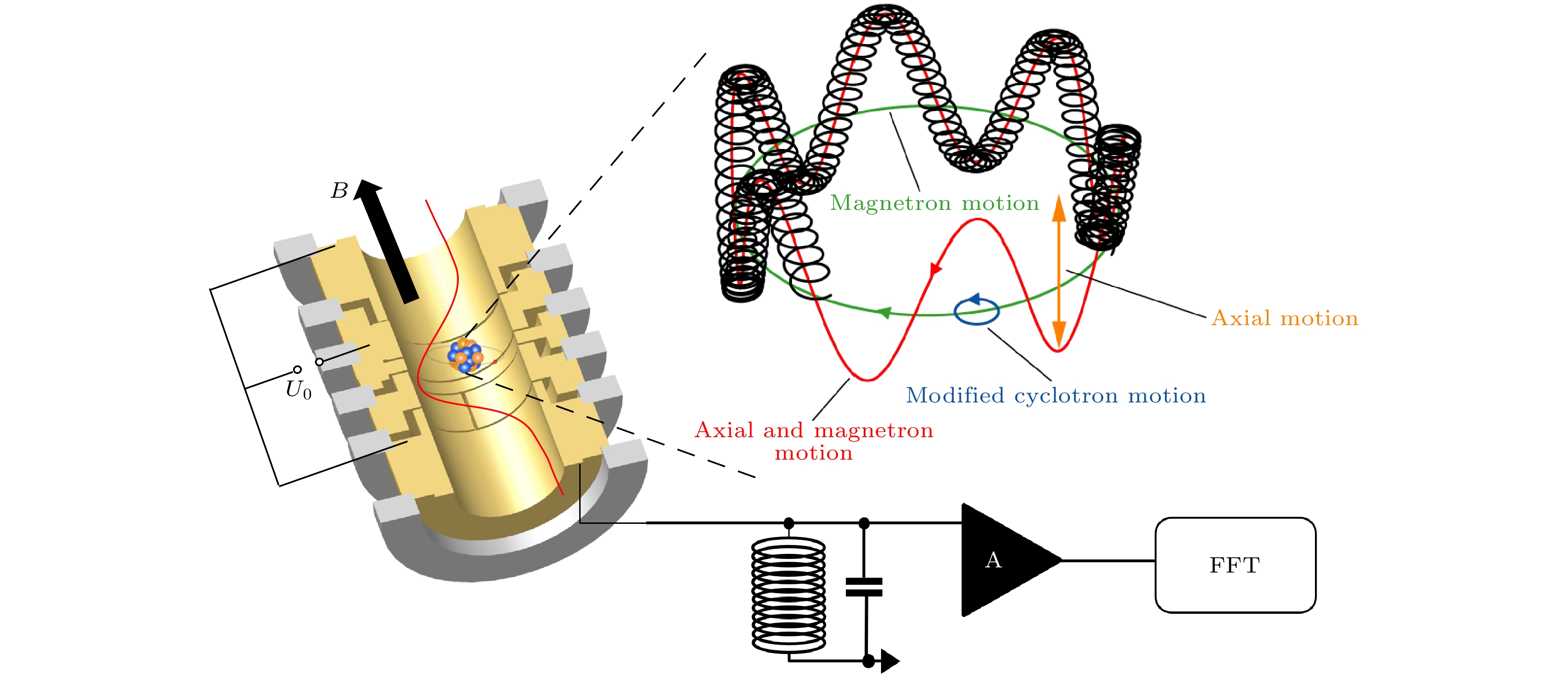
    • 潘宁阱是g因子测量的核心实验装置, 它通过轴向的匀强磁场和四极静电势组合成的电磁场实现对带电粒子的全空间约束. 匀强磁场由超导螺线管线圈产生, 而四极静电势通常由双曲面电极或多组环状电极产生(如图4). 带电粒子在潘宁阱中具有3个本征运动模式, 如图4所示, 分别为修正回旋运动(modified cyclotron motion)、磁控运动(magnetron motion)以及轴向的简谐振荡(axial oscillation), 3种运动的频率分别由$ {\omega }_{+} $, $ {\omega }_{-} $与$ {\omega }_{z} $表示, 并满足关系$ {\omega }_{c}\approx {\omega }_{+}\gg {\omega }_{z}\gg {\omega }_{-} $. 根据不变性原理[14]:

      通过测量3个本证运动频率, 就可以计算自由回旋运动频率值.

      潘宁阱实验往往只要求测量单个离子, 这样可以最大程度减小系统性误差. 同时, 对单个离子进行长时间的重复性测量, 就需要采用“非破坏性”的测量方法, 即镜像电流法. 如图4所示, 离子在潘宁阱中的谐振运动会在电极表面诱导出一个镜像电流, 这个镜像电流的频率与离子的振动频率一致. 单离子诱导的镜像电流大约在fA量级, 通过一个超导线圈绕制的谐振器可以将这个电流信号共振放大成电压信号, 再经过放大器、频谱分析仪(FFT)就可以得到离子的频率信号. 离子的轴向谐振运动正是采用这种方式直接读出, 而径向运动频率, 往往是通过边带耦合至轴向运动后, 再由镜像电流法读出[11,15].

      • 2.2.   g因子测量原理

    • 潘宁阱中g因子测量的原理运用了连续斯特恩-盖拉赫效应(continuous Stern-Gerlach effect), 它指出原子磁矩在梯度磁场下会感受到作用力. 如果尝试在潘宁阱的主磁场上叠加一个二阶磁场梯度项, 使得新磁场表示为

      那么原子磁矩在轴向上会额外受到一个二阶磁场势产生的力:

      因此, 离子的轴向运动频率就会根据磁矩在磁场方向的投影值产生偏移:

      对于类氢离子而言, 1s电子自旋产生的磁矩在磁场方向投影值为$ {\pm{1}/{2}g\mu }_{{\mathrm{B}}} $, 相应的能级分裂可以表示为

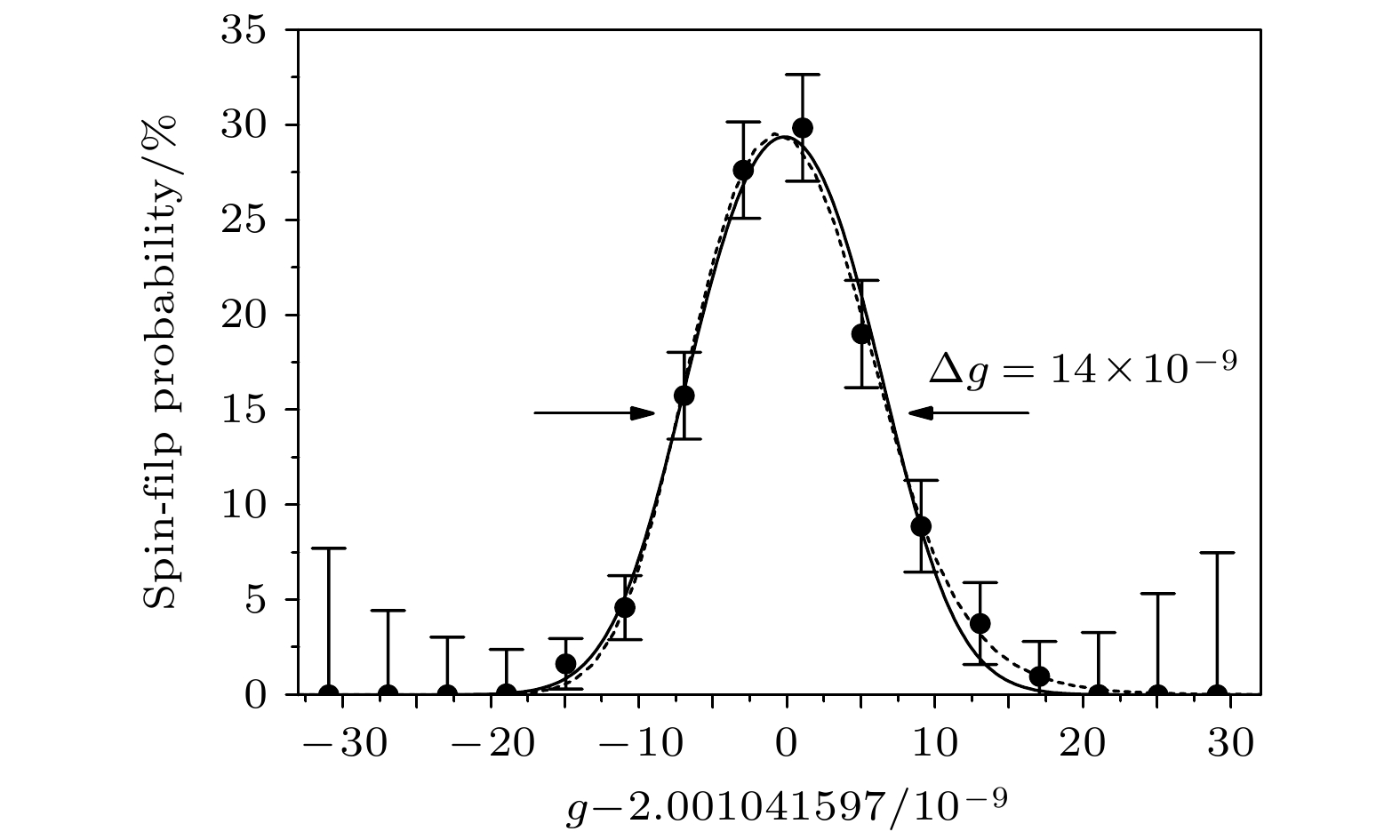
      在3.8 T磁场强度下, 12C5+ 离子的1s电子的拉莫频率$ {\omega }_{{\mathrm{L}}} \approx 2{\mathrm{\pi }}\times 104{\mathrm{G}}{\mathrm{H}}{\mathrm{z}} $.

      借助射频微波可以诱导电子在两个分裂能级间跃迁, 即自旋翻转态之间跃迁. 一旦电子自旋态出现翻转, 根据连续斯特恩-盖拉赫效应, 离子的轴向运动频率就会发生偏移. 基于此可以判断射频微波频率与拉莫频率是否形成共振, 当射频微波频率与拉莫频率共振时, 电子翻转概率(spin-flip probability)达到最大. 通过扫描射频微波频率并测量12C5+离子1s电子的自旋翻转情况, 就可以获得拉莫频率共振谱, 如图5所示. 共振谱表现出明显的非对称线型, 这主要是由于离子轴向谐振运动与磁场梯度项的耦合造成的.

      • 2.3.   双阱实验方法与测量技术

    • 如图5的实验结果中, 非对称线型会对拉莫进动频率的测量带来显著误差. 为了解决这一问题, 双阱实验方法就此诞生. 如图6所示, 潘宁阱核心区由两个离子阱组成, 分别为精密测量阱(precision trap)与分析阱(analysis trap). 精密测量阱安装在磁场最均匀的区域(即B2 = 0), 使得离子回旋运动频率与拉莫进动频率的测量足够准确. 分析阱的中心电极使用铁磁性材料, 在强磁场下会产生一个二阶磁场梯度. 基于连续斯特恩-盖拉赫效应就可以在分析阱中探测电子自旋的取向, 即磁矩在磁场轴的投影方向.

      实验开始时, 让离子储存在分析阱中, 通过微波激发和轴向频率测量, 根据(11)式确定电子的自旋取向. 随后, 将离子传输至精密测量阱中, 测量离子的回旋运动频率$ {\omega }_{{\mathrm{c}}} $. 同一时间在电子拉莫频率$ {\omega }_{{\mathrm{L}}} $附近扫描入射微波$ {\omega }_{{\mathrm{r}}{\mathrm{f}}} $. 最后, 再将离子传输回分析阱中, 再次测定电子的自旋取向. 如果在分析阱中前后两次测量的电子自旋态发生了翻转, 这就表明在精密测量阱中微波激发频率$ {\omega }_{{\mathrm{r}}{\mathrm{f}}} $与电子拉莫频率$ {\omega }_{{\mathrm{L}}} $形成共振, 反之则不形成共振. 在多次测量之后, 可以根据电子自旋态翻转的概率与扫描频率$ {\omega }_{{\mathrm{r}}{\mathrm{f}}} $和回旋运动频率$ {\omega }_{{\mathrm{c}}} $的比值作图并根据(7)式转化成g因子的共振谱(见图7). 该共振谱表现为对称的高斯型, 且半高全宽远小于图5中非对称拉莫频谱的共振峰. 基于双阱实验技术, g因子的测量精度可以达到10–9. 随后, 美因茨大学的课题组成员发展了相位测量法(PnA)、电子学反馈冷却技术等, 成功将g因子的测量误差降低至10–10以下[12,17], 也是目前对于单离子g因子测量的最高精度.

    3.   少电子离子束缚态电子g因子精密谱实验

      3.1.   类氢重离子体系电子g因子精密测量

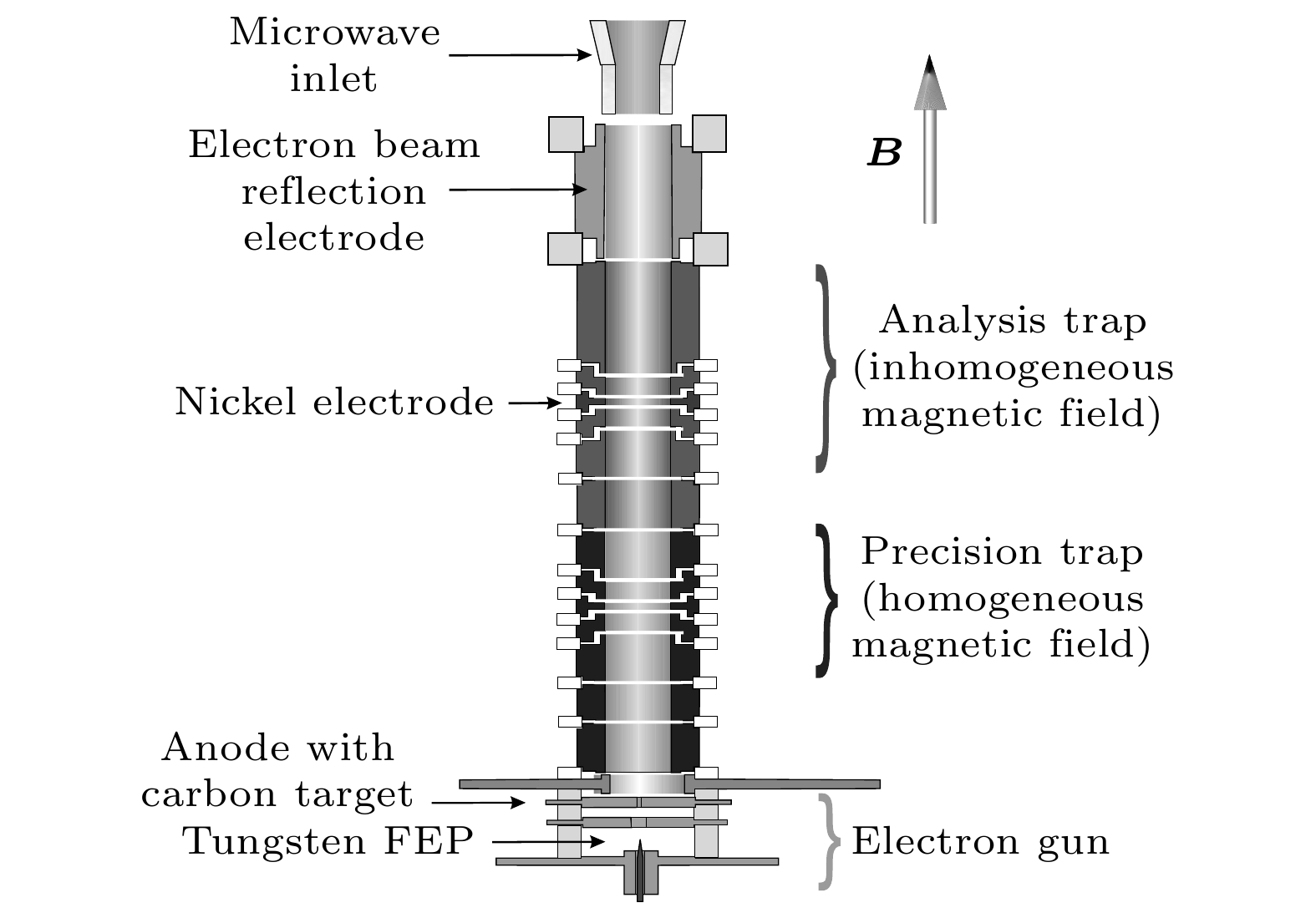
    • 美因茨大学的课题组先后在潘宁阱中对类氢12C5+[18], 16O7+[19]和28Si13+ [20]基态g因子进行了精确测量. 实验中, 他们采用内部小型电子束离子源(mini-EBIT)产生类氢离子. 结构如图6所示, 由场发射阴极发射的电子束轰击到靶电极, 将靶电极上的原子溅射出来. 脱离靶的原子通过和电子束的连续碰撞产生高电荷态离子. 由于mini-EBIT内部结构尺寸仅在毫米级别, 限制了施加在阴极和阳极间的电势差, 因此它无法产生高能电子束电离重核元素的最内壳层电子, 如铅离子1s电子的结合能约为100 keV远高于mini-EBIT中的电子束能量(数个keV). 为此, 马克斯普朗克核物理研究所的ALPHATRAP课题组利用了高能电子束离子阱(Heidelberg EBIT)[21]产生类氢重离子, 随后将离子团引出并注入至潘宁阱, 制备成单个离子开展了类氢重离子体系电子g因子精密测量.

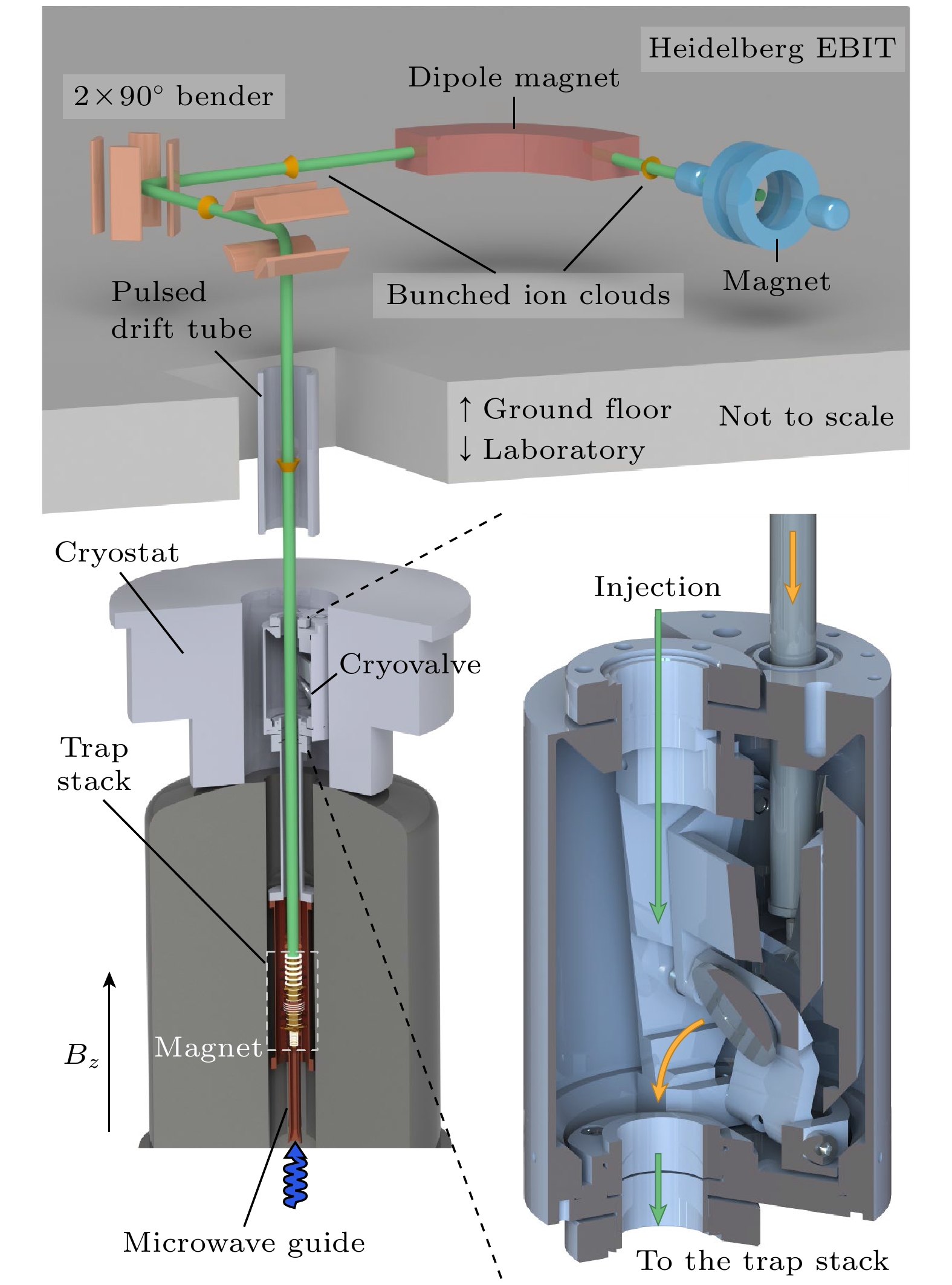
      ALPHATRAP实验系统如图8所示[13], 高能电子束离子阱是由电子枪、漂移管、收集器以及一组超导赫姆霍兹线圈组成. 电子束由电子枪出射, 经过漂移管上的电压加速与超导线圈形成的强磁场压缩后, 在漂移管中心电子束能量可达100 keV以上, 密度高于1011个/cm3. 当高能量与高密度的电子束与注入的原子碰撞之后, 原子的外层电子在数秒内被快速电离, 形成高电荷态离子. 引出的离子团定向动能大约在$ 8\;{\mathrm{k}}{\mathrm{V}}\times q $, 经过偏转磁铁筛选出正确的电荷态后, 再借助脉冲漂移管可以有效地将离子团减速到$ 100\;{\mathrm{V}}\times q $, 最后利用聚焦透镜将离子团导向至潘宁阱中被捕获. 被捕获的离子团可能有数十至数百个离子, 也可能包含(荷质比十分相近)不同种类的离子. 离子温度大约在数个eV, 对应几万摄氏度. 利用电子学阻尼冷却与离子纯化技术[11]可以将离子提纯, 最终制备成单个低温离子(温度约6 K).

      基于这套实验系统, Morgner等[13]精确测量了类氢118Sn49+离子基态电子g因子为1.910562058962(73)stat(42)sys(910)ext, 相对误差在$ 5\times {10}^{-10} $水平. 该结果与目前理论计算值1.910561821(299)在1个标准偏差内吻合, 观测到2-loop QED的贡献, 检验了束缚态QED理论在类氢Sn(Z=50)离子体系(平均库仑势场为1015 V/cm)中的准确性. 实验的主要误差来自于现有的原子核质量参数的误差, 这一误差有望通过潘宁阱质量测量来减小, 使得实验测量精度可以达到10–11. 基于该实验精度有望可以观测到3-loop QED效应, 但是受限于目前理论计算精度(2-loop QED效应的理论误差远大于3-loop QED的贡献), 这个高阶效应尚无法检验.

      • 3.2.   类锂与类硼离子体系电子g因子精密测量

    • 类锂与类硼离子也是典型的少电子体系, 他们都只有一个价电子, 分别是2s和2p1/2. 然而, 理论上计算基态g因子值要比类氢离子复杂且困难的多. 主要体现在内壳层的电子会产生一个屏蔽势, 这个屏蔽势不但与价电子产生直接相互作用引入修正(称为interelectronic-interaction或电子-电子关联效应)[22], 还可以对单电子QED效应产生电子屏蔽修正(screened QED效应)[23]. 以类锂离子体系为例, g因子各部分的贡献随原子序数的依赖关系如图9所示, 电子-电子关联效应已经超过1-loop QED效应的贡献, 而屏蔽势引入的QED效应的修正也十分显著, 超越了2-loop QED效应的贡献.

      实验上, 美因茨大学和马克斯普朗克核物理研究所的课题组对28Si11+, 40Ca17+和40Ar13+基态电子g因子进行了精密测量, 结果列于表2[23]. 实验误差与类氢离子体系g因子测量在相当水平, 但理论计算精度(特别是对类硼离子体系)远落后于类氢离子, 这种困难正是由于内壳层电子屏蔽势对g因子计算带来的影响. 反过来, 由于实验精度很高, 因此通过类锂与类硼体系实验与理论计算的对比, 可以有效检验不同屏蔽势理论模型在g因子计算中的适用性.

      • 3.3.   精细结构常数的确定

    • 由gDirac的表达式(4)可知, 通过精确测量g因子值可以反推精细结构常数$ \alpha $. 对于类氢离子体系而言, $ \alpha $的误差由下式决定[25]:

      (13)式表明在不考虑实验和理论g因子误差的情况下, 测量重核元素的电子g因子反推得到的$ \alpha $值更准确. 目前, 实验g因子测量精度已经接近10–11水平, 如果束缚态QED效应可以严格求解从而使得理论计算精度达到同等水平, 那么通过U91+离子基态g因子可以将$ \alpha $值测定到$ {10}^{-10} $精度以下. 然而, 根据图3所示, 即使认为束缚态QED贡献可以完全严格计算, 但由于在重元素中核体积效应十分显著, 而核体积效应的误差主要来自于核参数如电荷半径的数据误差. 因此, 通过类氢重离子确定精细结构常数将会受限于核参数的误差.

      为了有效减小核效应影响, 更精确的确定精细结构常数, Shabaev等[25]和Yerokhin等[26]先后提出了通过测量类氢离子的电子g因子与同一元素的类锂或类硼离子的电子g因子的权重差值来确定$ \alpha $值. g因子权重差值可以表示为

      其中$ \xi = {\Delta {g}_{{\mathrm{N}}{\mathrm{S}}}^{{\mathrm{L}}{\mathrm{i}}\left({\mathrm{B}}\right)\text-{\mathrm{l}}{\mathrm{i}}{\mathrm{k}}{\mathrm{e}}}}\big/{\Delta {g}_{{\mathrm{N}}{\mathrm{S}}}^{{\mathrm{H}}\text-{\mathrm{l}}{\mathrm{i}}{\mathrm{k}}{\mathrm{e}}}} $, 为类锂(或类硼)g因子中的核效应贡献与类氢g因子核体积效应(FNS)贡献的比值, 这个比值可以通过理论准确计算. 如此一来, 在差值$ {g}' $中受限于核结构参数确定$ \alpha $值的最大误差项(核体积效应)就可以完全消除. ALPHATRAP课题组已经针对类锂与类硼118Sn离子的基态g因子进行了测量, 在理论计算的支持下将会在这一研究课题上继续推进.

      • 3.4.   核参数与核效应测量

    • 对于两个同位素而言, 譬如类锂体系40Ca17+和48Ca17+, 电子g因子的各项效应中电子-电子关联、束缚态电子的QED效应都是相同的. 两个同位素g因子的偏差仅体现在核效应上, 如核尺寸效应与核反冲效应. Köhler等[27]通过分别测量40Ca17+和48Ca17+的基态g因子并作差值, 提取了核反冲效应对2s电子g因子的贡献. 随后, Sailer等[28]借助双离子耦合技术, 即将20Ne9+离子与其同位素22Ne9+离子囚禁在同一个磁控运动轨道上, 这样两个离子在相同的磁场环境下做同步拉莫进动. 由于同位素位移效应使得两个离子的g因子并不完全相等, 因此两者的拉莫进动频率之间存在一个偏差, 这个差值最终体现在同步拉莫进动的相位差会随时间呈现振荡图像. 实验中, 利用同步Ramsay微波激发方法准确观测到了这个相位振荡, 进而测量了20Ne9+与22Ne9+离子基态电子g因子的同位素偏移量. 表3给出了g因子同位素偏移的理论与实验结果. 实验测量的相对精度达到$ 5.6\times {10}^{-13} $超过单离子g因子测量精度两个数量级, 而理论计算的相对精度在$ 8.2\times {10}^{-12} $. 通过超高精度的g因子同位素偏移测量, 首次检验了QED效应在核反冲中的贡献(表3中Recoil QED = 0.0435). 由于核尺寸效应的误差较大, 更高阶的核反冲修正效应尚无法得到检验. 核尺寸效应计算是以核电荷半径为输入参数, 对于20Ne和22Ne核而言, 他们的核电荷半径差参考值为$ \delta \langle {r}^{2}{ \rangle }^{1/2}=0.0530\left(34\right) $. 如果利用实验测量的g因子同位素偏移作为基准, 可以反推核电荷半径差值为$ \delta \langle {r}^{2}{ \rangle }^{1/2}=0.0533\left(4\right) $, 新的数据比参考值更加准确. 此外, 通过g因子同位素偏移的精确测量, 还可以检验第5作用力(fifth-force)模型并为新物理出现确定观测边界[28,29].

      对于有核自旋的少电子离子体系而言, 如3He+离子(I = 1/2), 基态1s能级在外场下分裂成4条能级, 分别对应$ \left|1\rangle\right.:({m}_{j}=1/2, {m}_{I}=1/2) $, $ \left|2\rangle\right.: ({m}_{j}=1/2, {m}_{I}=-1/2) $, $ \left|3\rangle\right.:({m}_{j}=-1/2, {m}_{I}=1/2) $与$ \left|4\rangle\right.:({m}_{j}=-1/2, {m}_{I}=-1/2) $. 他们各自的能量可以表示为[30]

      其中, $ {E}_{{\mathrm{H}}{\mathrm{F}}{\mathrm{S}}} $为无外场下的超精细分裂. 实验上采用类似电子g因子的测量方法, 对$ \left|1\rangle\right.\leftrightarrow \left|2\rangle\right. $, $ \left|1\rangle\right.\leftrightarrow \left|3\rangle\right. $, $ \left|2\rangle\right.\leftrightarrow \left|4\rangle\right. $与$ \left|3\rangle\right.\leftrightarrow \left|4\rangle\right. $四个能级间距进行了测量, 提取了电子g因子$ {g}_{{\mathrm{e}}}=-2.00217741579{\left(34\right)}_{{\mathrm{s}}{\mathrm{t}}{\mathrm{a}}{\mathrm{t}}}{\left(30\right)}_{{\mathrm{s}}{\mathrm{y}}{\mathrm{s}}} $、核子g因子$ {g}_{I}=-4.2552506997{\left(30\right)}_{{\mathrm{s}}{\mathrm{t}}{\mathrm{a}}{\mathrm{t}}}{\left(17\right)}_{{\mathrm{s}}{\mathrm{y}}{\mathrm{s}}}{\left(1\right)}_{{\mathrm{t}}{\mathrm{h}}{\mathrm{e}}{\mathrm{o}}} $、超精细分裂系数$ {E}_{{\mathrm{H}}{\mathrm{F}}{\mathrm{S}}}=-8665 649865.77{\left(26\right)}_{{\mathrm{s}}{\mathrm{t}}{\mathrm{a}}{\mathrm{t}}}{\left(1\right)}_{{\mathrm{s}}{\mathrm{y}}{\mathrm{s}}} $ 这3个原子结构参数. 计算得到核磁矩$ {\mu }_{{}_{}{}^{3}{\mathrm{H}}{\mathrm{e}}}= -16.217050033\left(14\right) $ MHz/T, 比之前的数据精度提高一个数量级, 由$ {E}_{{\mathrm{H}}{\mathrm{F}}{\mathrm{S}}} $还可以计算3He的Zemach半径为 rz = 2.608(24) fm, 相比于电子散射方法得到的数据rz = 2.528(16) fm显示出一定偏差.

    4.   总结与展望

    • 基于潘宁离子阱实验技术的少电子离子基态电子g因子精密测量发展至今已有20余年, 推动了原子分子光物理精密测量.

      发展微波测量技术、双阱实验方法、相位灵敏的测量方法、离子冷却技术等, 电子g因子的实验测量精度逐步提高至$ 5\times {10}^{-11} $(40Ca17+[27]). 采用双离子耦合技术与同步Ramsay微波激发方法测量了同位素g因子偏移值, 实验精度达到$ 5.6\times {10}^{-13} $, 超过单离子的电子g因子测量精度100倍[28], 精确检验了少电子离子体系中的QED效应、核效应等. 借助外部高电荷态离子源, 如高能电子束离子阱, 促使研究体系从轻核元素逐渐过渡至重核元素, 通过对118Sn49+ 基态电子g因子的实验测量, 发现它与自由电子g因子的偏离值显著增大, 检验了束缚态QED理论在1015 V/cm库仑势场中的适用性[13]. 从类氢离子体系逐步过渡到研究类锂体系与类硼离子体系, 通过对2s, 2p电子g因子的测量, 可以精确观测电子-电子关联效应、电子屏蔽QED效应等, 检验原子结构的理论. 从核自旋为0的体系过渡到研究非0核自旋离子体系, 借助测量多个电子分裂能级, 不但可以精确获得电子g因子值, 还可以确定核子g因子、核电磁半径与超精细分裂系数等重要原子结构参数.

      在测量技术上针对单离子的电子g因子测量精度已经逼近测量极限, 提高测量精度至ppt水平需要进一步控制系统性偏差. 目前, 主要的系统性偏差来自于电磁场不稳定性与非均匀性引入的测量不确定性. 提高电磁场的稳定性主要依赖于技术进步, 譬如研发更高稳定性的电压源[31]或者对外磁场扰动做进一步屏蔽[32]. 电磁场非均匀性引入的系统性误差是与离子热运动幅度紧密相关的[33], 要减小该误差可以进一步降低离子的温度, Tu等[34]首先开展了激光冷却与协同冷却的理论研究, 随后, Bohman等[35]和Will等[36]成功将质子温度冷却到100mK量级.

      随着ALPHATRAP课题组成功融合了高能电子束离子阱与精密潘宁阱——从EBIT中引出类氢118Sn49+离子并注入潘宁阱中进行基态电子g因子的精密测量, 原理上可以测量自然界中任意元素类氢离子的电子g因子值. 但实际上还需考虑的, 其一, 类氢离子极容易和背景气体发生电荷交换降低它的电荷态. ALPHATRAP实验系统通过测量类氢118Sn49+离子的稳定囚禁时间, 估算了类氢208Pb81+(Z=82)离子可以稳定囚禁约1个月, 证明了在现有实验系统中开展高精度g因子实验的可行性. 其二, 类氢208Pb81+的电离能约100 keV, 要在EBIT中产生足够数量的离子要求电子束能量达到250 keV, 目前的HD-EBIT是无法做到的. 相关课题组成员正在建设更大型的电子束离子阱Hyper-EBIT, 可以产生更大流强、更高能量的电子束.

      利用同一元素类氢与类锂(或类硼)离子体系的电子g因子权重差值提取精细结构常数值, 是一种全新的测量精细结构常数的方法. 但更高精度的测量要求重核电子g因子的实验和理论精度均达到10–11. 潘宁离子阱系统已经证明了实验上的可行性. 理论上距离10–11的精度目标还存在不小差距, 主要原因在于高阶QED效应随原子序数Z增大而显著增强, 基于“从头算”的理论方法尚无法将2-loop QED项完整计算, 或者说完整计算需要的时间和计算资源非常大. 这一方面还有待理论学家进一步优化理论方法和计算手段.

      感谢刘佳林在本论文修改工作中做出的贡献.

    参考文献 (36)

目录

/

返回文章
返回