首页
登录
注册
下载:
-
活性粒子是具有自驱动能力的个体, 它们通过消耗自身或周围环境的能量来实现自我驱动[1,2]. 由于活性粒子具有热平衡物质所没有的新颖性质, 近几年在物理、生物及化学等领域, 尤其在微纳米科学和生命科学方面活性粒子的应用备受关注[3–9], 如精子、大肠杆菌等生物粒子以及一些人造活性粒子等[10–15]. 依据运动方式的不同, 活性粒子大致可分为自驱动粒子(粒子具有自驱动速度, 没有自转角速度)、活性手征粒子(粒子具有自驱动速度, 也有自转角速度)和极性活性手征粒子(粒子具有自驱动速度和自转角速度, 而且粒子取向遵循一定的规则)[16–18]. 活性粒子因其可产生自我驱动的非平衡动力学性质被广泛研究, 其中定向输运和相分离已成为当前微观粒子输运研究中一个重要课题[19–24]. 在由大量活性手征粒子组成的系统中活性粒子分离有多种方式, 如利用非对称障碍物进行分离[25–28 ]、引入反馈机制进行分离机制[29]、采用不同类粒子相混合进行分离等[30,31], 这些分离方式主要是针对混合在一起两种不同手征的活性粒子进行分离.
Weber等[32]研究了具有不同扩散系数的被动粒子组成的二元混合系统中粒子的相分离现象, 由于粒子间的相互碰撞作用, 尤其是扩散系数不同的两种粒子的相互作用, 扩散系数较小的粒子逐渐聚集到一起形成团簇, 而扩散系数较大的粒子分散在团簇周围形成相对稀疏的类气相[23]. 在此基础上, Kumari等[33]通过引入周期势场, 进一步优化了上述混合系统中具有不同扩散系数被动粒子的分离, 扩散系数小的粒子会聚集到势场极小值附近, 产生更好的分离效果. 然而不同扩散系数对活性手征粒子分离的影响尚未被研究, 本文的研究点聚焦于此. 本文将详细分析在不同扩散系数活性手征粒子组成的二元混合系统中相对扩散系数、活性粒子的自驱动速度、自转角速度以及粒子填充率对系统中粒子分离效果的影响.
-
同文献[32, 33]一样, 一个由N个活性手征粒子组成的二元混合平面系统, 系统是边长为L的正方形格子, 且系统满足周期性边界条件. 在系统中Nhot = N/2个“热”粒子的平动扩散系数DTH较大, 而另外Ncold = N/2个“冷”粒子的平动扩散系数DTL则较小. 引入相对平动扩散系数D = DTL/DTH, 它反映了两种粒子平动扩散系数的相对大小, 为了便于后续的分析本文令DTH = 1. 在过阻尼条件下活性手征粒子满足如下的朗之万动力学方程:
其中, xi, yi, θi分别是粒子的横坐标、纵坐标和角坐标, i = 1, 2, ···, N. v0是粒子的自驱动速度, μ是迁移率. DT和Dθ分别为平动扩散系数和转动扩散系数, ξi是均值为零的高斯白噪声, 满足
$ \langle {\xi _i^\alpha \xi _j^\beta \left( {{t'}} \right)} \rangle = {\delta _{ij}}{\delta _{\alpha \beta }}\delta \left( {t - {t'}} \right) $ , α, β = x, y, θ. ω是粒子的自转角速度, ω > 0表示粒子逆时针转动, ω < 0表示顺时针转动, 当ω = 0时粒子成为没有手征性的自驱动粒子.粒子间的相互作用采用短程的弹性简谐力, 当rij < 2a时Fij = –k(rij – 2a)r0, 其中rij = |ri – rj|, r0 = (ri – rj)/rij是rij的单位矢量, a是粒子的半径, k是弹性系数, 而当rij ≥ 2a时Fij = 0.
引入时间尺度1/(μk)和长度尺度a对方程(1)—(3)进行无量纲化, 无量纲化后的朗之万动力学方程为
其中
$ {\hat x_i} = x_i/a $ ,$ {\hat y_i} = y_i/a$ ,$ \hat t = \mu kt$ ,$ {\hat y_0} = v_0/(\mu ka) $ ,$ \hat \omega $ = ω/(μk),$ {\hat D_{\text{T}}} $ = DT/(μk),$ {\hat D_\theta } $ = Dθ/(μk). 在后续的讨论分析中, 文中均采用无量纲量, 为了便于书写省略各参量上面的“帽子”. 本文采用Runge-Kutta二阶随机算法对(4)式—(6)式进行数值模拟. 在模拟计算中, 粒子初始位置和初始方向分别在正方形格子(即初始时刻“冷”“热”粒子均匀随机分布在方形格子中)和[0, 2π]范围内均匀随机分布, 模拟计算的时间步长为dt = 10–3, 总时间为104. 为了减小误差提高精度, 计算结果均采用计算20次后的统计平均值, 其他参数L = 40, a = 1, μ = 1, k = 100, N = 300, DTH = 1. -
在研究分析粒子分离时, 最大团簇粒子数比是一个可以反应粒子分离效果的重要参数. 因在系统中主要形成的是“冷”粒子团簇, 所以关注重点是“冷”粒子的聚集情况, 则对于“冷”粒子其最大团簇粒子数占比P =
$\langle $ nmax$\rangle $ ×100/Ncold, 其中nmax是“冷”粒子形成的最大团簇中“冷”粒子数. 相对于被动粒子(自驱动速度v0 = 0, 自转角速度ω = 0), 活性手征粒子的自驱动速度v0和自转角速度ω均不为零, 这两个参量必然会对系统中活性粒子的分离效果产生重要影响. 另外, 粒子填充率反映了系统中粒子总面积占方形格子面积的比例, 即系统中所有粒子占的面积与二维平面系统面积之比Ф = Nπa2/L2. 相对平动扩散系数D = DTL/DTH对分离效果的影响也不容忽略. 另外, 为了更好地解释“冷” 粒子的聚集, 引入“冷”粒子有效扩散系数DeffL[29,34]:其中Δri(t)≡ri(t) – ri(0), i = 1, 2, ···, Ncold.
-
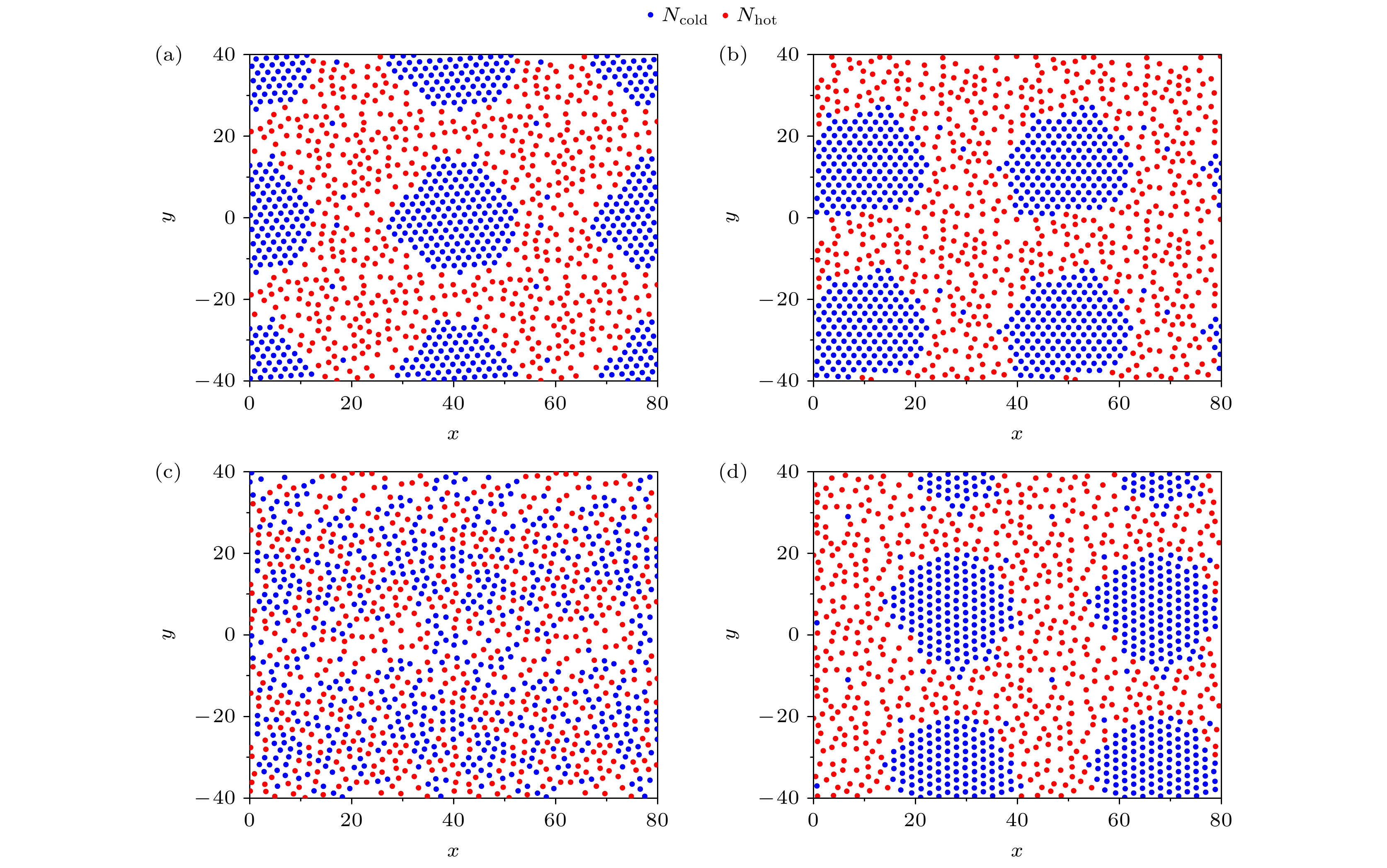
对于存在不同平动扩散系数DTL和DTH的“冷”(蓝色)“热”(红色)粒子组成的被动粒子系统, 由于粒子间的相互作用和“冷 粒子相对于“热”粒子较小的扩散行为, “冷”粒子会被“热”粒子逐渐包围而聚集形成团簇, 达到分离效果, 如图1(a)所示. 图1(b), (c)显示的是在自驱动粒子(即自转角速度ω = 0, 自驱动速度v0≠0)组成的系统中, “冷”“热”粒子的分离情况. 不同之处是图1(b))中v0 = 0.1比较小, 而图1(c))中v0 = 1则比较大, 由图1(b), (c)可以看到, 粒子的聚集效果完全不同. 图1(b)显示当系统中粒子的v0较小时, v0对“冷”粒子形成团簇的影响很小, 可以近似忽略. “冷”粒子运动缓慢“热”粒子运动活跃, 由于粒子间的相互作用“冷”粒子逐渐被“热”粒子包围而聚集, 情况类似图1(a)中显示的被动粒子. 在图1(c)显示的系统中粒子的v0较大, “冷”粒子的扩散行为加强, v0对“冷”粒子团簇形成的作用不可忽视. 由于v0较大“热”粒子并不能通过粒子间的相互作用而使“冷”粒子聚集, 较大的自驱动速度使“冷”粒子可冲破“热”粒子的束缚, 此时“冷”粒子不会形成团簇而出现相分离现象. 图1(d)显示的是由活性手征粒子(即ω≠0, v0≠0)组成的系统, 其中v0 = 1, ω = 10. 由图1(c), (d)可以看到, 当v0均为1的情况下, 在由自驱动粒子组成的系统(图1(c))与由活性手征粒子组成的系统(图1(d))中粒子的聚集效果完全不同, ω具有重要作用. 活性手征粒子运动时的重要物理量是回转半径R = v0/ω, 其大小近似反映了粒子活动范围. 对于活性手征粒子系统, v0 = 1较大但是由于ω = 10的存在, 这使得粒子的回转半径R = 0.1, 即粒子的扩散减弱, 活动范围较小. 此时”冷“粒子会逐渐聚到一起形成团簇而产生相分离.
-
在本文建立的活性手征粒子二元混合系统中, “冷”粒子能否逐渐聚集形成团簇而达到分离主要由3个量决定, 分别是粒子回转半径R (由v0和ω决定)、相对扩散系数D和粒子间的相互作用, 后文将详细对这些量进行讨论.
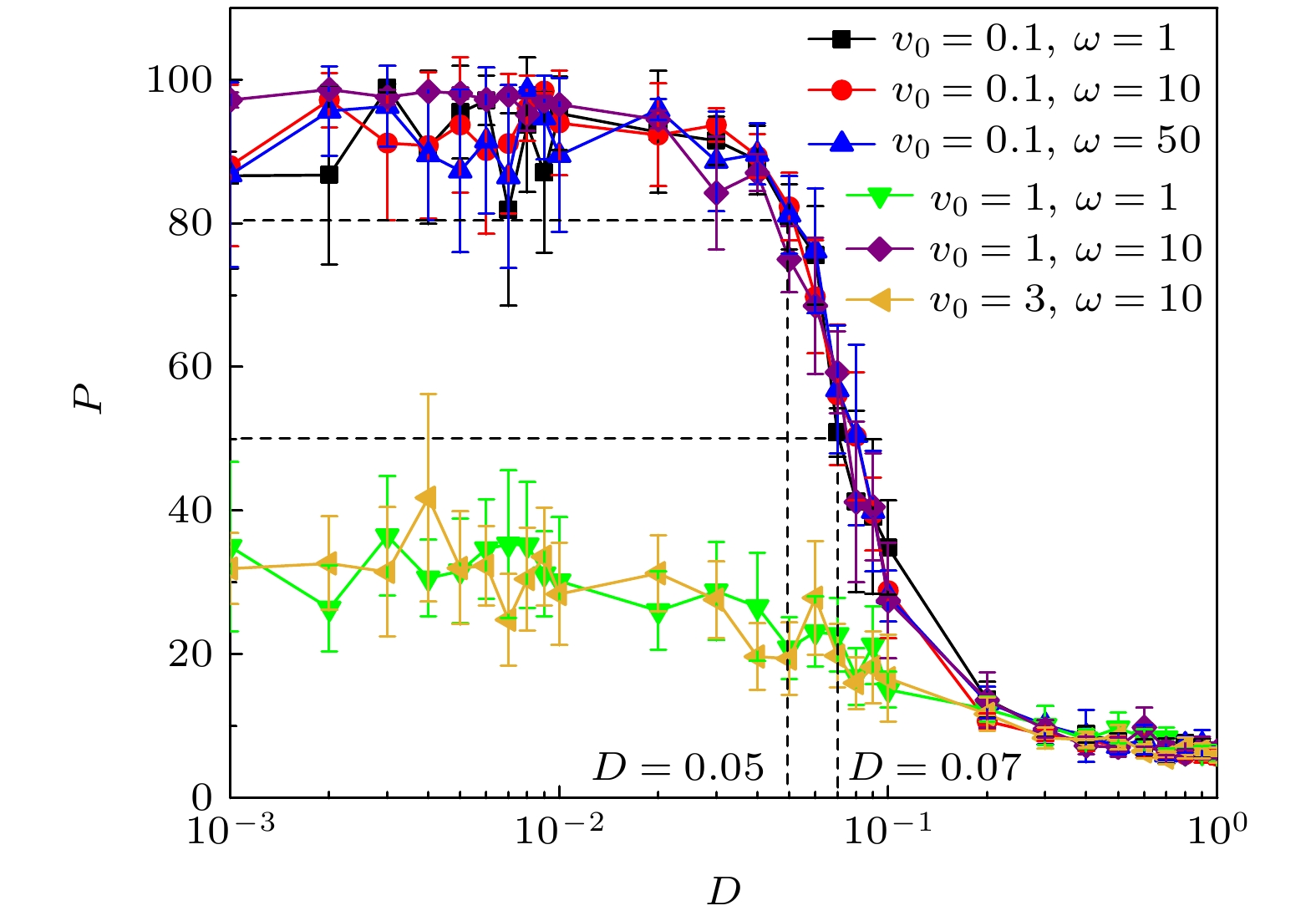
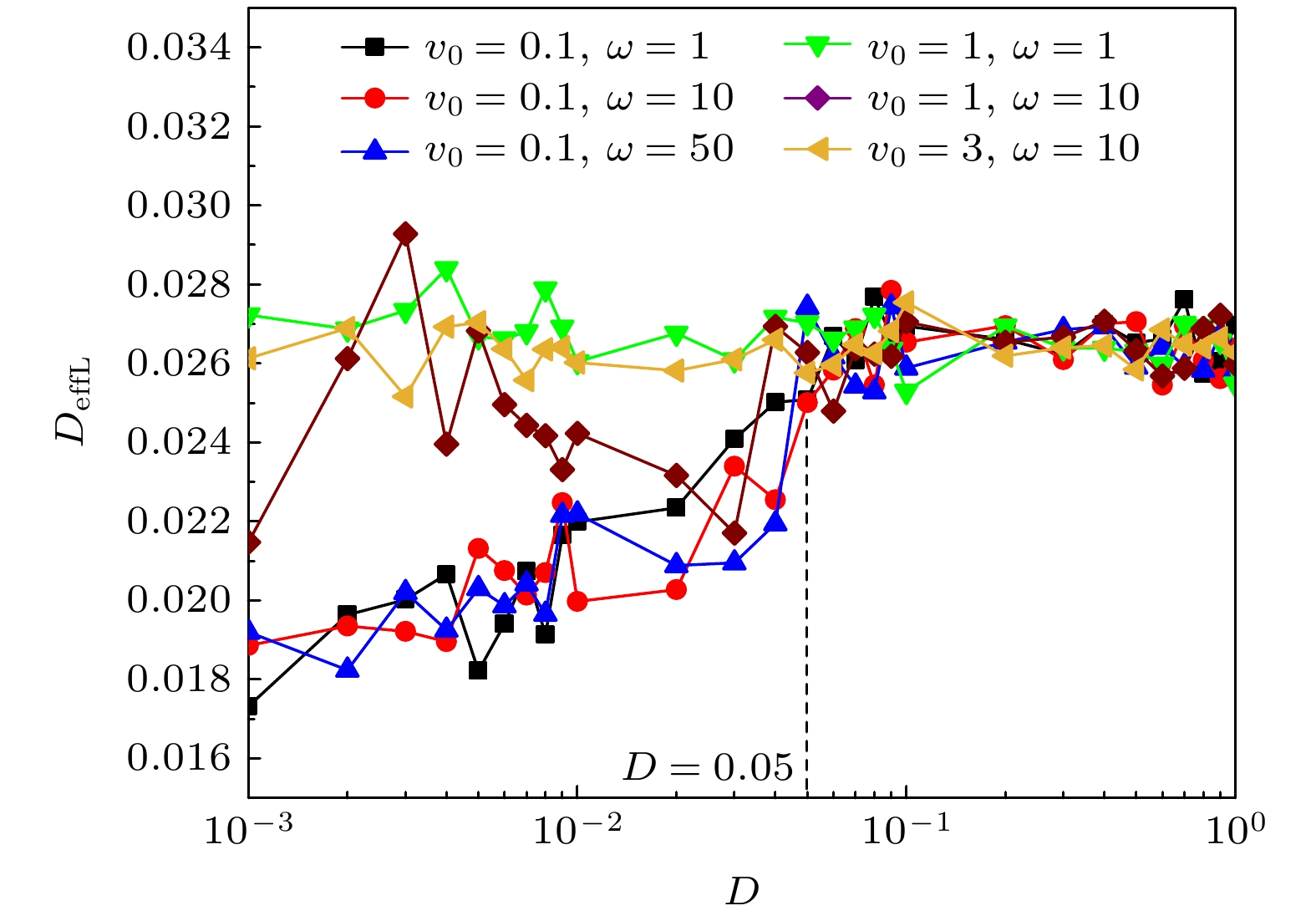
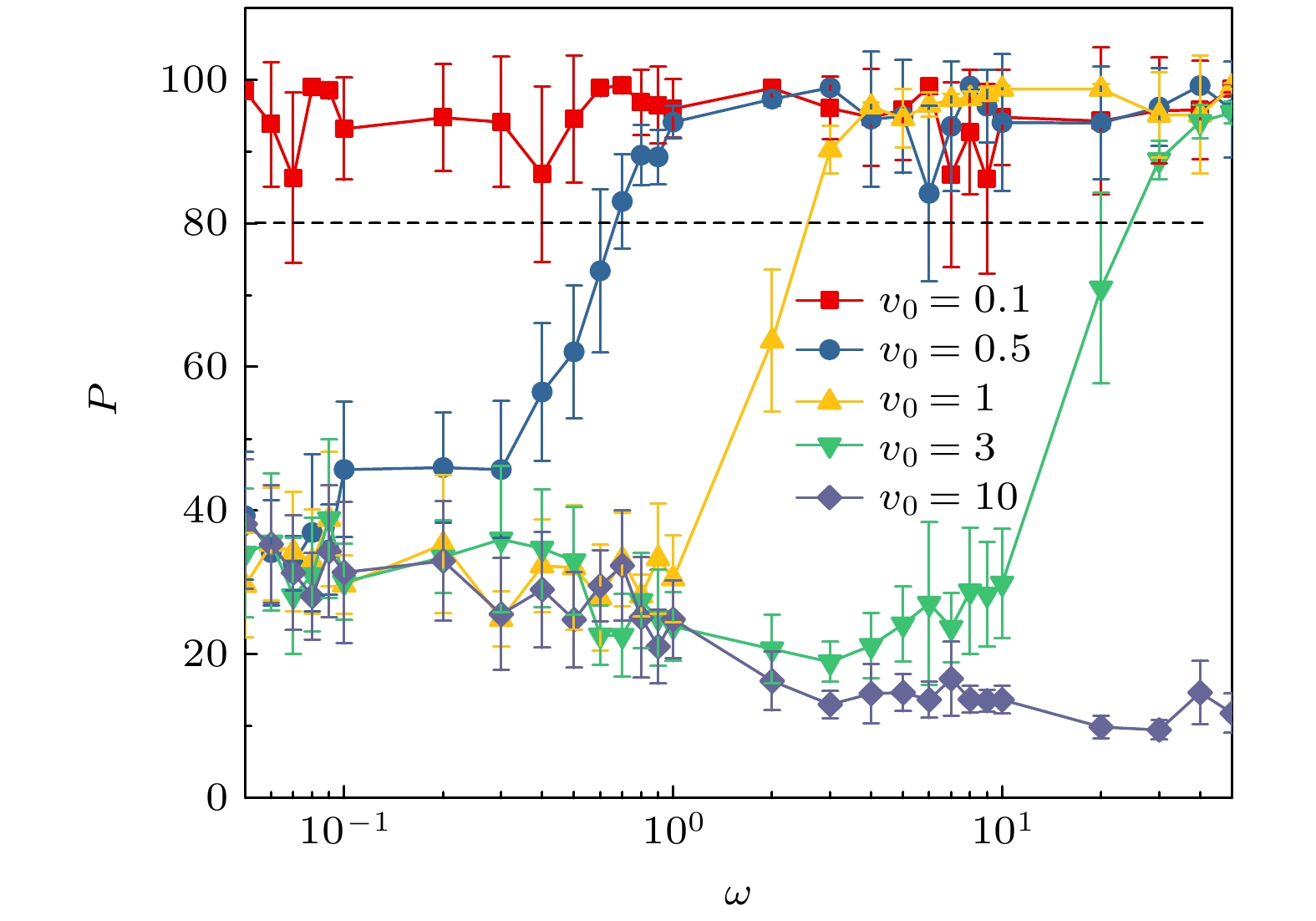
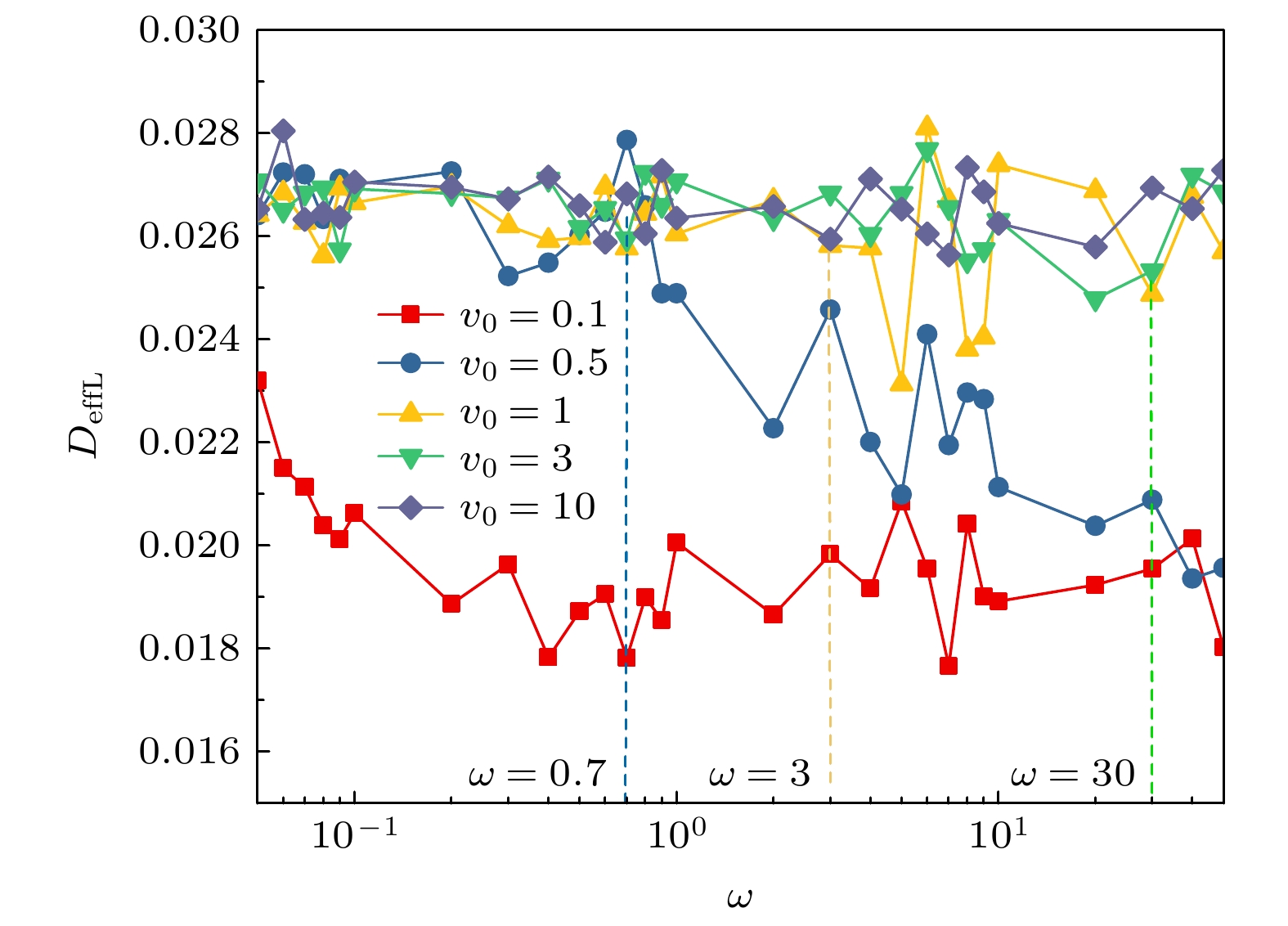
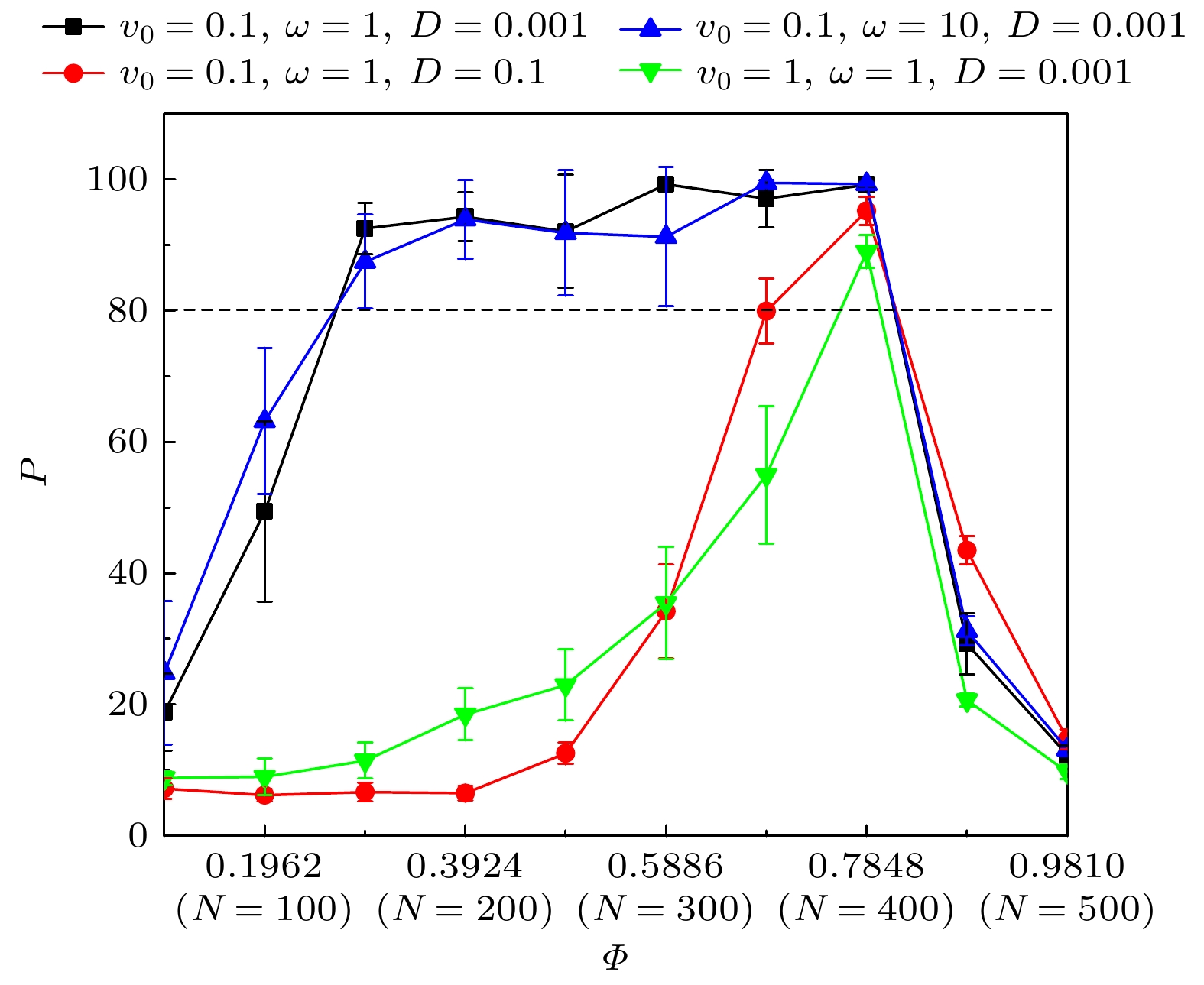
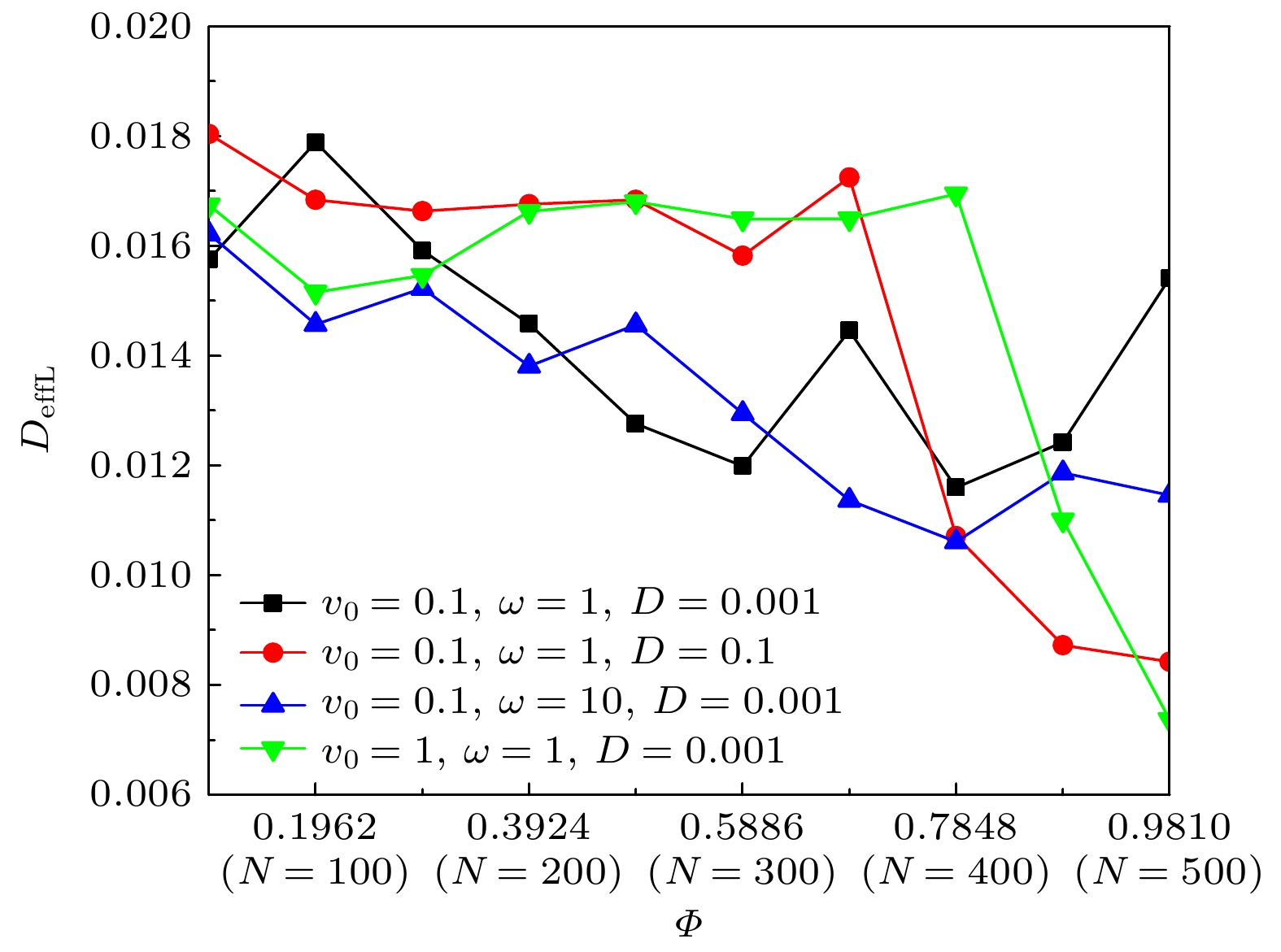
图2和图3分别是不同的v0和ω时“冷”粒子的最大团簇粒子数占比P和有效扩散系数DeffL随相对扩散系数D的变化曲线, 两图中曲线两两相互对应. 对于图2中的6条曲线, 总体上当D增大过程中P逐渐减小, 而图3中的6条曲线DeffL值逐渐增大. 这说明在D较小时, “冷”粒子的扩散较弱有利于粒子的分离, 而大的D使“冷”粒子的扩散行为增强, 粒子不会出现相分离现象. 对于(v0, ω)分别等于(0.1, 1), (0.1, 10), (0.1, 50)这3条曲线, 即回旋半径R分别为0.1, 0.01, 0.002, 由图2和 图3可以看到, 当D很小(0.001—0.05区间范围)时, P均大于80而DeffL值在0.018附近相对较小. 此时“冷”粒子的扩散行为较弱, 可很好地聚集而产生大的团簇. 小的扩散和小的回旋半径R意味着“冷”粒子在很小范围内原地转动, 并伴有不断无规则小波动, 同时扩散较大的“热”粒子通过碰撞使得“冷”粒子逐渐聚集而形成大的团簇. “冷”粒子的小范围活动, 对于其形成大的团簇很重要. 随着D的增大(0.005—0.07区间范围), P很快从80减小到50, DeffL增大到0.027. 这时“冷”粒子虽然仍有小的回转半径R, 但是D的增大使得部分“冷”粒子扩散增强突破了周围“热”粒子的束缚, 系统很难形成较大的“冷”粒子团簇. 随着D的进一步增大(0.07—1区间范围), P从50进一步减小到10, 而DeffL仍然保持在较大的0.027, “冷”粒子大的无规则扩散运动更容易挣脱“热”粒子的束缚, 不会形成大团簇. 对于(v0, ω)分别等于(3, 10)和(1, 1)这两条曲线即回转半径R分别等于0.3, 1, 由图2和图3可以看到, 不管D很大还是很小, P都很小, 而DeffL却很大(如图2 中P < 30, 图3中 DeffL = 0.027), 这表明此时“冷”粒子的扩散行为较强, 在方形格子系统中“冷”粒子形成的团簇粒子数都很小. 粒子回转半径R的增大使得粒子(不管“冷”粒子还是“热”粒子)的活动范围较大, 不再是小范围“原地踏步”, 尤其是当D较大时在大回转和扩散二者的双重作用下, “冷”粒子不会聚集到一起形成大团簇.
另外, 当(v0, ω) = (1, 10)时, 图3中DeffL值与图2中的P值对应不太理想, 曲线被D = 0.05分为两段, 如图中虚线所示. 当D > 0.05时, DeffL = 0.027数值较大, 这和其他5条曲线相同. 当D < 0.05时DeffL值波动较大, 与其他曲线中DeffL相对稳定的逐渐增大不同, 这是因为在ω和D相同的情况下(可与v0 = 0.1, ω = 10曲线进行对比), 大的v0引起粒子间的碰撞增多扩散较大, 但是由于粒子具有较大的ω, 这时“冷”粒子仍是可以聚集形成大的团簇, 如图2所示. 类似较大的v0引起DeffL明显波动的情况在图5和图7中也存在, 此时系统中的“冷”“热”粒子仍可出现相分离现象.
-
由3.2节可知, 回转半径R对“冷”粒子形成大的团簇具有重要的影响, 而决定R的是粒子自驱动速度v0和自转角速度ω.
图4和图5分别为不同的ω和D时“冷”粒子的最大团簇粒子数占比P和有效扩散系数DeffL随v0变化曲线, 两图曲线同样两两相互对应. 可看到两图中4条曲线变化趋势大致相同, 当v0逐渐增大时, P逐渐变小, 而DeffL却逐渐增大, 逐渐增大的v0使“冷”粒子的扩散行为增强, 阻碍系统进入分离态, 相反逐渐减小的v0则有利于系统进入分离态.
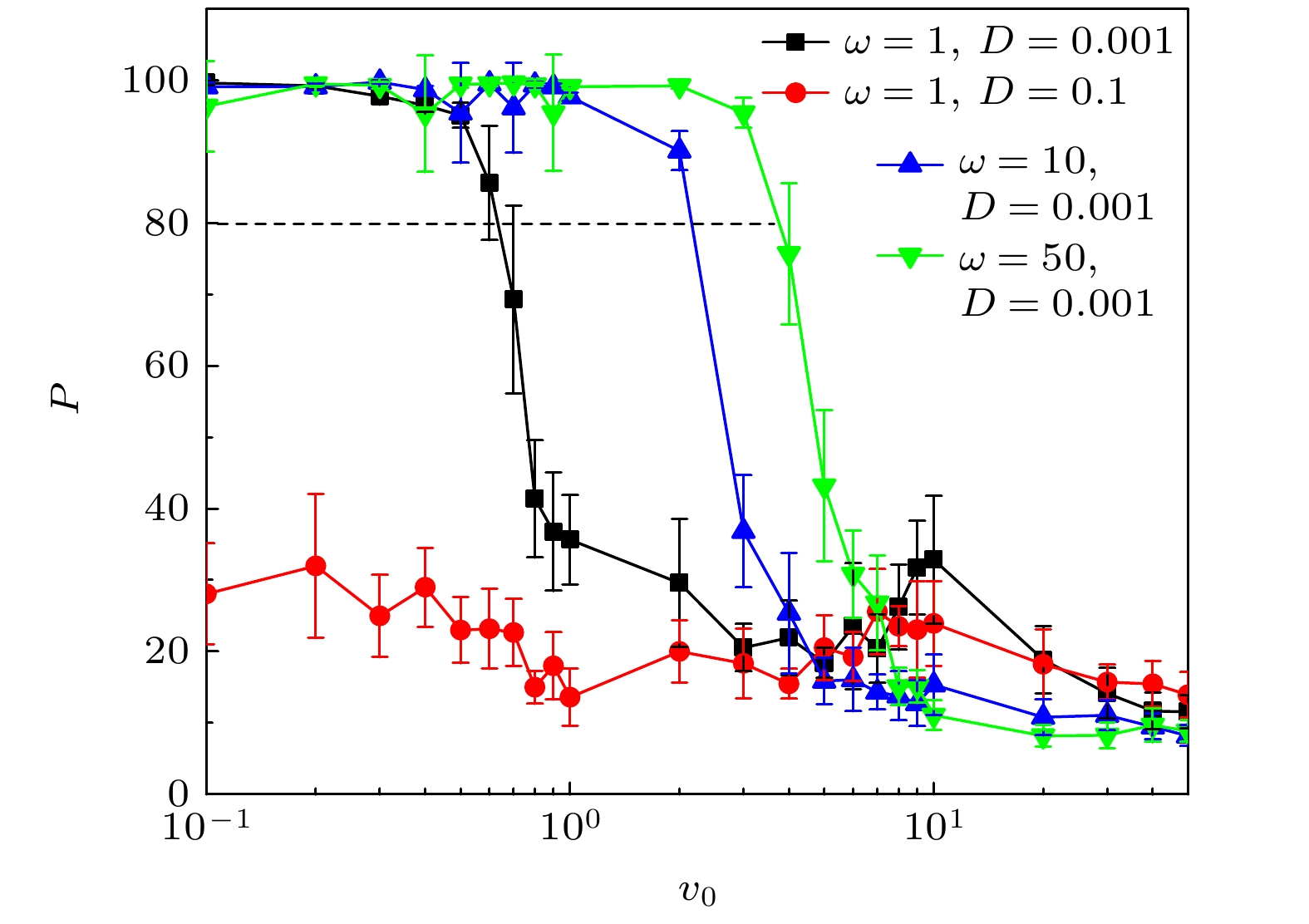
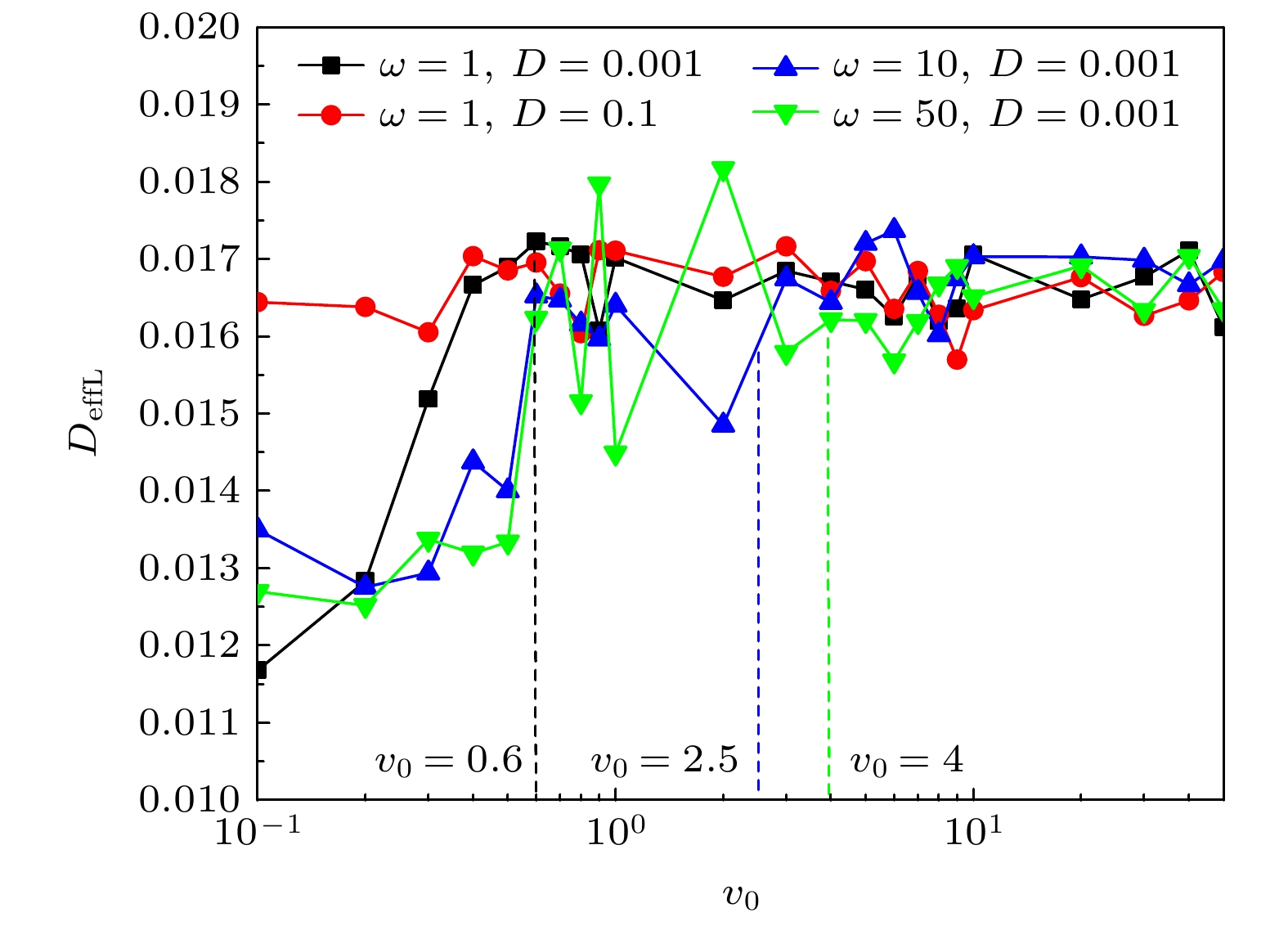
从图4和图5可以看出, 4条曲线仍存在不同, 当D = 0.001, ω分别等于1, 10, 50时, v0较小时P均大于80, 即系统中“冷”粒子基本都会聚集到一个大的团簇, 此时DeffL都很小, 说明“冷”粒子的扩散行为很弱便于聚集. 3条曲线的区别在于随着v0的增大, P先快速减小时的值不同. 对于ω = 1的曲线, P从v0 = 0.6开始快速减小, 对于ω = 10和50的两条曲线P分别从v0 = 2.5和4开始快速减小. 从图5可以看到, 3条曲线的DeffL分别在v0 = 0.6, 2.5和4时已变得比较大, “冷”粒子的扩散逐渐增强. 3条曲线对应的回转半径R分别是Rω = 1 = 0.6, Rω = 10 = 0.25和Rω = 50 = 0.08(图5中虚线). 这说明在D相同的情况下, 随着ω的增大“冷”粒子形成最大团簇而达到分离所需的最大v0也在增大, 而最大回转半径R减小, v0与ω的增大是不同步的, v0的相对增大率小于ω的相对增大率. 究其动力学原因在于, 假设随着ω的增大, v0也同步增大, 即它们增大时回转半径R不变, 这意味着在相同时间内v0或ω较大的粒子运动路程长, 必然会和其他粒子产生更多的碰撞, 扩散就会增大, 这导致“冷”粒子的汇聚程度变小分离效果减弱, 与图5中DeffL曲线显示的“冷”粒子扩散情况相一致. 所以v0相比于ω要进行缓慢增大以减小回转半径R, 以此来抵消增多的碰撞作用, 确保“冷”粒子可形成大团簇. 这是手征粒子具有的特征与粒子间碰撞作用相互竞争的结果.
当ω = 1, D = 0.001, 0.1时, 当v0很小(如0.1—0.6区间)时D = 0.001曲线的P远大于D = 0.1曲线的, 而DeffL小于D = 0.1曲线的. 在R和D都很小时“冷”粒子的扩散行为较弱, 易于形成大的团簇, 相反D很大“冷”粒子的扩散行为增强, 很难聚集形成大团簇. 当v0很大(如0.6—50区间)时两曲线几乎重叠在一起, P都很小而DeffL很大. 相对于很大的v0, D对“冷”粒子形成团簇的影响很小, 这时“冷”粒子的扩散行为较强, 系统很难形成大团簇产生相分离.
-
图6和图7所示分别为不同v0时“冷”粒子最大团簇粒子数占比P和有效扩散系数DeffL随ω的变化曲线, 其中D = 0.001很小. 由两图可以看到, 在ω∈[0.05, 50]区间内v0 = 0.1曲线的P较大且均大于80, 而DeffL却都很小, 数值在0.018附近. “冷”粒子因具有较小的v0(R也很小)和较小的D, 其扩散行为较弱, 只在很小的区域内“原地”运动. 再加上“热”粒子的“驱赶”, 这种情况下系统中“冷”粒子可以形成大团簇达到相分离. 对于v0 = 10的曲线P都小于30, 而对应的DeffL却很大, 数值都在0.027附近, “冷”粒子扩散能力较强. “冷”粒子此时具有较大的v0(R也很大), 即活动范围很大, 可突破“热”粒子的束缚. 此时系统不会出现相分离现象, 对应的P值很小.
当v0分别等于0.5, 1和3时, 随着ω的增大, P从30左右增大到80以上(图6), 而DeffL从0.027逐渐减小到0.018(图7). 这说明随着ω增大, “冷”粒子的扩散行为越来越弱, 系统从不可分离态逐渐进入可分离态. 此外, 图6和图7中的这3条曲线(v0 = 0.5, 1和3)具有显著的不同, P达到80以上时所对应的ω是不同的. 对于这3条曲线, ω分别大于0.7, 3和30时P达到80以上(如图7中的虚线所示), “冷”粒子的DeffL从较大的0.027开始减小, 扩散行为逐渐减弱. 此时粒子回转半径
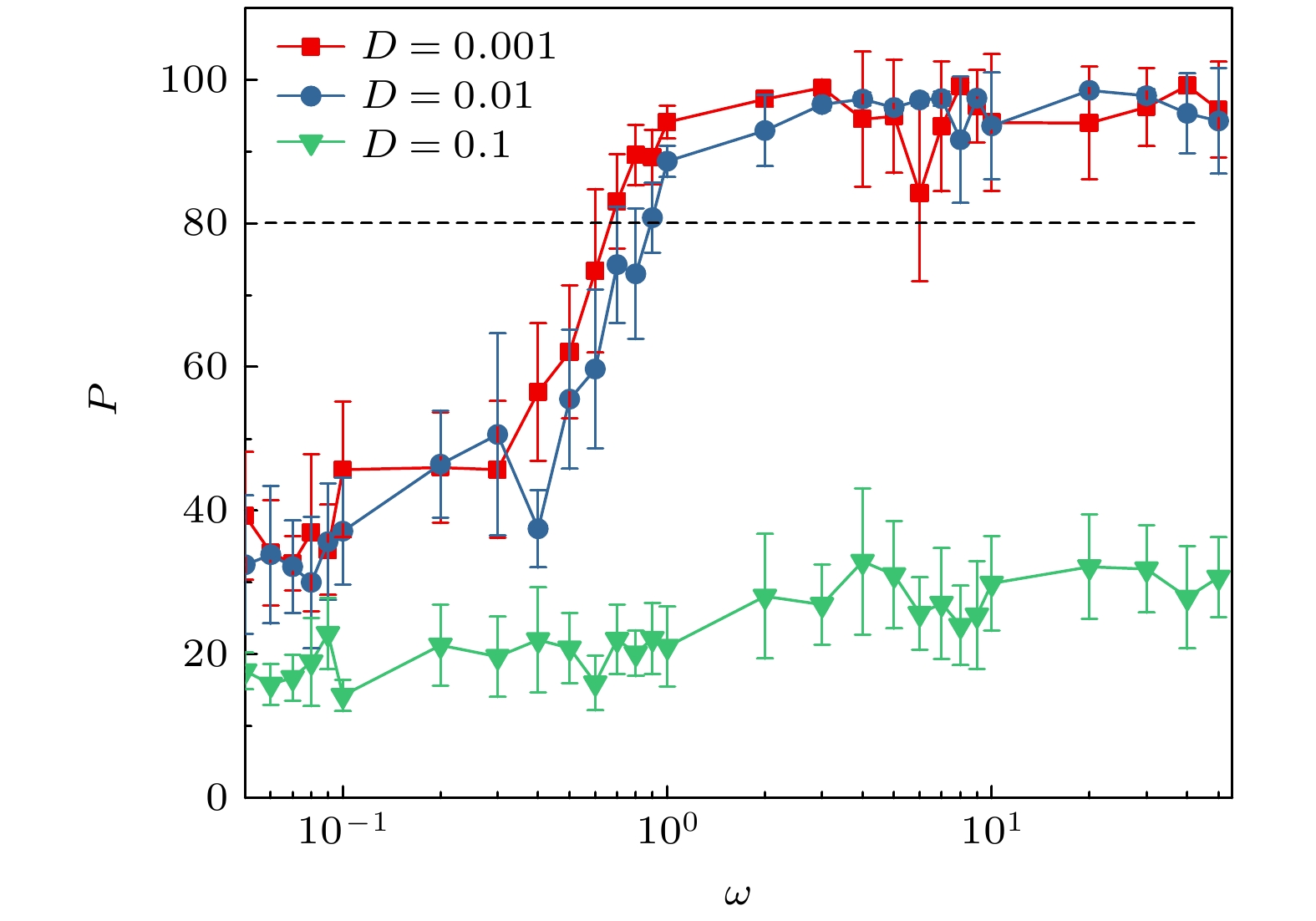
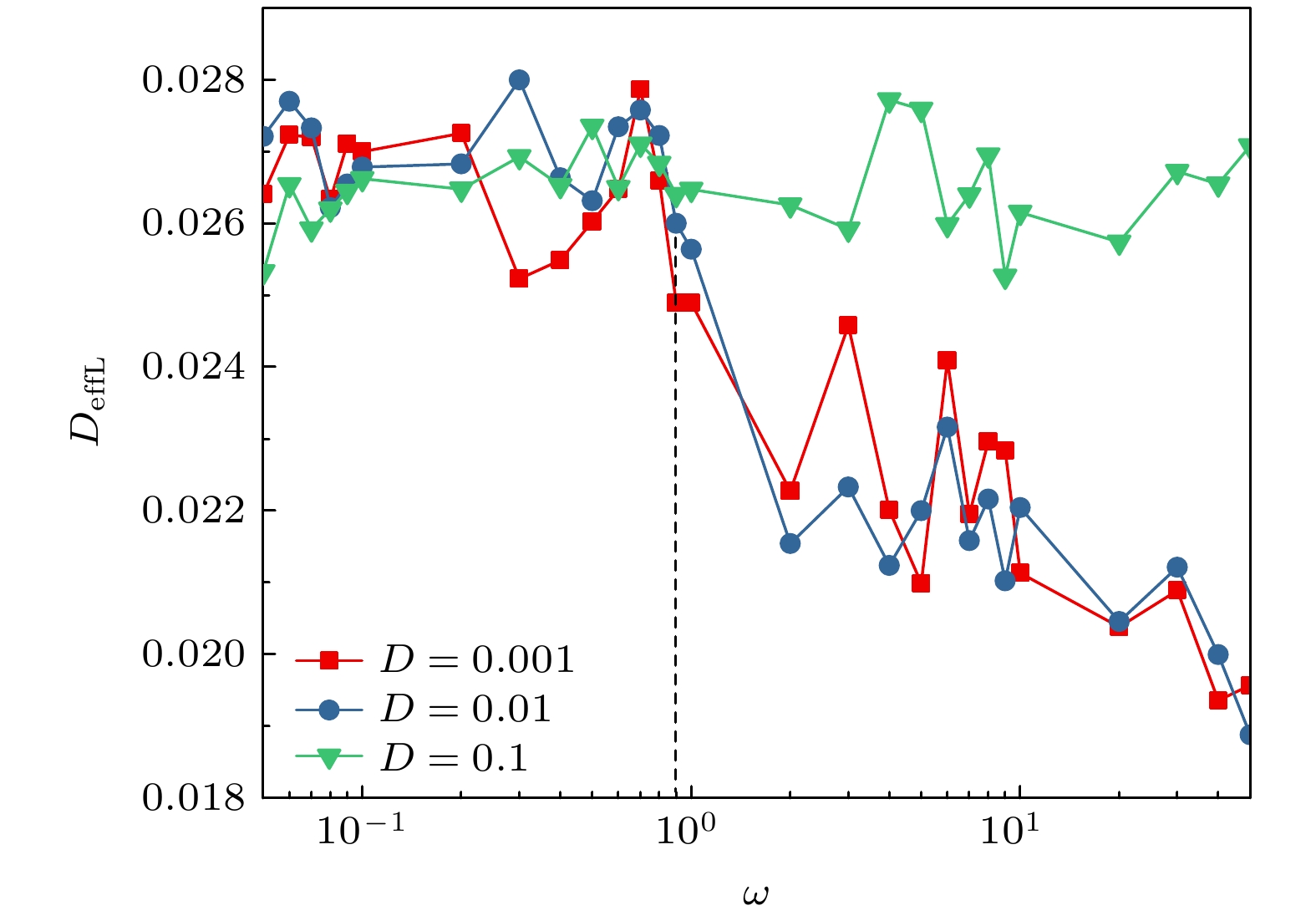
$R_{v_0 = 0.5 }\approx 0.71 $ ,$R_{v_0 = 1 }\approx 0.33 $ 和$R_{v_0 = 3}\approx 0.1 $ , 这说明D相同情况下当v0增大时, “冷”粒子形成最大团簇而达到分离所需的最小ω也在增大, 但是最大回转半径R减小, 二者的增大不同步, ω的相对增大率大于v0的相对增大率. 图7中v0 = 1, 3时, DeffL的变化趋势与v0 = 0.5明显不同, DeffL分别从ω = 3和30开始出现明显波动, 但是由于粒子具有较大的ω, 这时“冷”粒子仍形成大的团簇, 如图6所示P都可大于80.图8和图9所示分别为不同相对扩散系数D下“冷”粒子的最大团簇粒子数占比P和有效扩散系数DeffL随ω的变化曲线, 其中v0 = 0.5. D = 0.001, 0.01时, 随着ω的增大, P值从30左右逐渐增大到80以上, DeffL从0.027减小到0.018. 虚线P = 80将曲线分为两段, 对应的分界点处ω = 0.9. 这说明当ω较大时“冷”粒子的扩散较弱, 更易于形成大团簇而产生相分离, 另外ω越大也意味着粒子的回转半径R越小, 粒子的活动范围相对也越小. D = 0.001曲线的P值比D = 0.01曲线略大一些, 而DeffL值比D = 0.01曲线小一些. 这是由于D值的增大会使冷粒子的扩散行为加强, 不利于“热”粒子对“冷”粒子的束缚, “冷”粒子难以形成大的团簇. 对于D = 0.1曲线, 由于D值较大所以在ω∈(0.05, 50)整个横坐标范围内P都很小而 DeffL很大, “冷”粒子扩散行为较强, 不能形成大团簇.
-
粒子填充率Ф对系统分离效果会产生重要的作用, 因为方形格子系统中粒子数影响粒子间的相互碰撞频率, 碰撞是“冷”粒子逐渐聚集形成大团簇的重要因素. 不同v0, ω和D时“冷”粒子的最大团簇粒子数占比P随Ф的变化曲线如图10所示. 图11所示为“冷”粒子的有效扩散系数DeffL随Ф的变化曲线, 图10和图11中的曲线相互对应. 由图10看到, 随着Ф的增大, P值呈先增大后减小的非单调变化, 即每条曲线都存在使P最大的最优Ф值, 并且最优Ф值的区间宽度不同. 对于(v0, ω, D)分别等于(0.1, 1, 0.001)和(0.1, 10, 0.001)这两条曲线, 根据上文对图4的分析知道当N = 300时, P很大即系统中“冷”粒子可以形成大团簇, 而相同条件下Ф很小(如N < 150)时, “冷”粒子并不能形成大团簇. 原因是由于“热”粒子很少, 虽然“冷”粒子的v0和D都很小, 但是少量的“热”粒子对“冷”粒子的碰撞束缚作用不足以使“冷”粒子聚集形成大团簇, “冷”粒子的扩散行为较强, 如图11所示. 当Ф很大(如N > 400)时“冷”粒子同样不能形成大团簇, 因为此时方形格子系统几乎快被粒子占满, “冷”粒子只能在自身位置附近进行微小振动, 图11显示此时“冷”粒子扩散行为较弱, 它们不会聚集到一起形成大的团簇.
当(v0, ω, D)分别等于(0.1, 1, 0.1)和(1, 1, 0.001)时, 最优Ф值宽度变窄, 只有在N = 400附近P值可达到最大, 这是因为D或v0的增大都会增加“冷”粒子的扩散, 粒子的运动范围增大, 这可从图11中DeffL较大看出. 此时系统要使“冷”粒子聚集而形成大团簇就需要增大“热”粒子的束缚作用, 从粒子数角度分析这意味着需要增加系统中的粒子数, 即要求相对大的Ф, 这样最优Ф值宽度变窄. 当然如果D或v0足够大, 系统不会存在最优Ф使系统出现“冷”“热”粒子相分离的现象.
-
本文通过建立活性手征粒子不同扩散系数的二元混模型研究了粒子相对扩散系数D、自驱动速度v0、自转角速度ω和粒子填充率Ф (即粒子数N)对系统中“冷”粒子聚集形成大团簇效果的影响. 首先, D反映了系统中“冷”“热”粒子相对扩散的剧烈程度, 较小的D有利于系统粒子的分离, 而较大的D则会增大“冷”粒子的扩散减弱相分离效果. 其次, 在ω和D不变时, 减小v0可减小R值减弱粒子的扩散, 系统中粒子的分离效果加强. 随着粒子ω的增大, “冷”粒子可形成最大团簇而达到分离时所需要的最大v0也增大, 对应的粒子最大回转半径R却减小. 在v0和D不变时, 增大ω也会减弱粒子的扩散, 使分离效果加强. 当v0越大时“冷”粒子形成最大团簇所需的最小ω也越大, 同样最大回转半径R也越小. v0和ω的增大(或减小)不是同步的, v0的相对变化率小于ω的相对变化率. 这是活性手征粒子所具有的特征与粒子间碰撞作用相互竞争的结果. 另外, 随着Ф的增大, “冷”粒子最大团簇粒子数占比P呈先增大后减小的非单调变化, 每条曲线都存在一定的最优Ф值区间宽度. 相对扩散系数D和自驱动速度v0的增大, 会使曲线的最优Ф值区间宽度变窄并向右偏移.
在本文建立的活性手征粒子二元混合模型中, 二元是指系统中平动扩散系数分别为DTL和DTH的两类“冷”“热”粒子, 分离是指对“冷”粒子与“热”粒子的区分, 并没有对粒子的自转角速度ω的转动方向做限制. 如果系统中同时存在ω>0(逆时针)和ω<0(顺时针)两种粒子, 本文所建立的模型并不能分离这两种粒子, 这方面的研究将在后续工作中进行.
具有不同扩散系数的活性手征粒子分离
Separation of active chiral particles with different diffusion coefficients
-
摘要: 近几年对活性粒子的研究已成为很多领域研究者关注的重要课题之一, 其中关于活性手征粒子的相分离问题具有重要的理论和实际意义. 本文通过朗之万动力学研究了具有不同扩散系数的活性手征粒子组成的二元混合系统中粒子的相分离. 较小的相对扩散系数有利于“冷”粒子形成大的团簇而分离, 较大的相对扩散系数则会减弱分离效果. 由于粒子特征(自驱动速度、自转角速度)和相对扩散系数对粒子间碰撞作用的影响, 系统要使“冷”“热”粒子达到相分离, 自驱动速度和自转角速度的增大(或减小)不能同步, 自驱动速度的相对变化率要小于自转角速度的相对变化率. 通过分析“冷”粒子有效扩散系数的变化, 系统相分离现象得到了很好的解释. 有效扩散系数较小意味着“冷”粒子会聚集形成较大的团簇, 系统可出现相分离现象, 而当有效扩散系数较大时“冷”粒子的扩散较强, 不会形成大的团簇产生相分离. 另外, 随着粒子填充率的增大“冷”粒子最大团簇粒子数占比曲线进行先增大后减小的非单调变化, 每条曲线存在一段最优粒子填充率宽度. 相对扩散系数和自驱动速度的增大, 会使曲线的最优填充率宽度变窄并向右偏移.Abstract: In recent years, the study of active particles has become one of the important topics concerned by researchers in many fields, among which the phase separation of active chiral particles has important theoretical and practical significance. In this paper, the phase separation of binary mixed systems composed of active chiral particles with different diffusion coefficients is studied by Langevin dynamics. A smaller relative diffusion coefficient is conducive to the formation of large clusters and the separation of “cold” particles, while a larger relative diffusion coefficient will weaken the separation effect. Due to the influence of particle characteristics (self-driven velocity, self-rotational angular velocity) and relative diffusion coefficient on the collision between particles, if one wants the “cold” and “hot” particles to reach phase separation, increasing (or reducing) the self-driven velocity and self-rotational angular velocity cannot be synchronous, and the relative rate of change of self-driven velocity is smaller than that of the self-rotational angular velocity. By analyzing the changes of the effective diffusion coefficient of “cold” particles, the phenomenon of phase separation in the system can be better explained. A smaller effective diffusion coefficient means that the “cold” particles will aggregate into larger clusters, and the system may exhibit phase separation. However, when the effective diffusion coefficient is larger, the diffusion of “cold” particles is stronger and the “cold” particles will not form large clusters, which means that the system cannot aggregate into phase separation. In addition, with the filling rate of particle increasing, the proportion curve of the number of cold particles in maximum cold particle cluster undergoes a non-monotonic change, specifically, it first increases and then decreases. Each curve has an optimal filling rate but its width is different .With the increase of the relative diffusion coefficient and self-driven velocity, the width of the optimal filling rate of the proportion curve will become narrower and shift toward the right.
-
Key words:
- active particles /
- chirality /
- Langevin equation /
- diffusion coefficient .
-
-
图 1 三种不同系统中粒子的相分离(Ncold = Nhot = N/2 = 150, D = DTL/DTH = 0.001) (a)被动粒子系统(v0 = 0, ω = 0); (b)自驱动粒子系统(v0 = 0.1, ω = 0); (c)自驱动粒子系统(v0 = 1, ω = 0); (d)活性手征粒子系统(v0 = 1, ω = 10)
Figure 1. Phase separation of particles in three different systems (Ncold = Nhot = N/2 = 150, D = DTL/DTH = 0.001): (a) The system of passive particles (v0 = 0, ω = 0); (b) the system of self-driven particles (v0 = 0.1, ω = 0); (c) the system of self-driven particles (v0 = 1, ω = 0); (d) the system of active chiral particles (v0 = 1, ω = 10).
图 2 不同的v0和ω时“冷”粒子最大团簇粒子数占比P随相对扩散系数D的变化曲线
Figure 2. The proportion P of “cold” particle in the largest cluster as a function of the relative diffusion coefficient D for different values of v0 and ω.
图 3 不同的v0和ω时“冷”粒子的有效扩散系数DeffL随相对扩散系数D的变化曲线
Figure 3. The effective diffusion coefficient DeffL of “cold” particle as a function of the relative diffusion coefficient D for different values of v0 and ω.
图 4 不同ω和D时“冷”粒子的最大团簇粒子数占比P随自驱动速度的v0变化
Figure 4. The proportion P of “cold” particle in the largest cluster as a function of the self-driven velocity v0 for different values of ω and D .
图 5 不同ω和D时“冷”粒子的有效扩散系数DeffL随自驱动速度的v0变化
Figure 5. The effective diffusion coefficient DeffL of “cold” particle as a function of the self-driven velocity v0 for different value of ω and D .
图 6 不同v0时“冷”粒子的最大团簇粒子数占比P随自转角速度ω的变化(D = 0.001)
Figure 6. The proportion P of “cold” particle in the largest cluster as a function of the self-rotational angular velocity ω for different values of v0 with D = 0.001.
图 7 不同v0时“冷”粒子的有效扩散系数DeffL随自旋角频率ω的变化(D = 0.001)
Figure 7. The effective diffusion coefficient DeffL of “cold” particle as a function of the self-rotational angular velocity ω for different values of v0 with D = 0.001.
图 8 不同D时“冷”粒子的最大团簇粒子数占比P随自转角速度ω的变化(v0 = 0.5)
Figure 8. The proportion P of “cold” particle in the largest cluster as a function of the self-rotational angular velocity ω for different values of D with v0 = 0.5.
图 9 不同D时“冷”粒子的有效扩散系数DeffL随自旋角频率ω的变化(v0 = 0.5)
Figure 9. The effective diffusion coefficient DeffL of “cold” particle as a function of the self-rotational angular velocity ω for different values of D with v0 = 0.5.
图 10 不同v0, ω和D时“冷”粒子的最大团簇粒子数占比P随粒子填充率Φ变化曲线
Figure 10. The proportion P of “cold” particle in the largest cluster as a function of the filling rate of particle for different values of v0, ω and D.
-
[1] Ramaswamy S 2010 Ann. Rev. Condens. Matt. Phys. 1 323 doi: 10.1146/annurev-conmatphys-070909-104101 [2] Howse J S, Ebbens S J 2010 Soft Matter 6 726 doi: 10.1039/b918598d [3] Lobaskin V, Romenskyy M 2013 Phys. Rev. E 87 052135 doi: DOI:https://doi.org/10.1103/PhysRevE.87.052135 [4] Edwards A M, Phillips R A, Watkins N W, Freeman M P, Murphy E J, Afanasyev V, Buldyrev S V, da Luz M G, Raposo E P, Stanley H E, Viswanathan G M 2007 Nature 449 1044 doi: 10.1038/nature06199 [5] Brambilla M, Ferrante E, Birattari M, Dorigo M 2013 Swarm Intelligence 7 1 doi: 10.1007/s11721-012-0075-2 [6] Helbing D 2001 Rev. Mod. Phys. 73 1067 doi: 10.1103/RevModPhys.73.1067 [7] Marchetti M C, Joanny J F, Ramaswamy S, Liverpool T B, Prost J, Rao M, Simha R A 2013 Rev. Mod. Phys. 85 1143 doi: 10.1103/RevModPhys.85.1143 [8] Wang J, Gao W 2012 ACS Nano 6 5745 doi: 10.1021/nn3028997 [9] Chen C, Liu S, Shi X Q, Chaté H, Wu Y 2017 Nature 542 210 doi: 10.1038/nature20817 [10] Berg H C 2003 Biochem 72 19 [11] Berg H C 2004 Ecoli in Motion (New York: Springer Press) pp39–47 [12] Nishiguchi D, Sano M 2015 Phys. Rev. E 92 052309 [13] Ma X, Hahn K, Sanchez S 2015 J. Am. Chem. Soc. 137 4976 doi: 10.1021/jacs.5b02700 [14] Li J, Singh V V, Sattayasamitsathit S, Orozco J, Kaufmann K, Dong R, Gao W, Jurado-Sanchez B, Fedorak Y, Wang J 2014 ACS Nano 8 11118 doi: 10.1021/nn505029k [15] Abdelmohsen L K, Peng F, Tu Y, Wilson D A 2014 J. Mater. Chem. B 2 2395 doi: 10.1039/C3TB21451F [16] Vlope G, Gigan S, Volpe G 2014 Am. J. Phys. 82 659 doi: 10.1119/1.4870398 [17] Bechinger C, Di Leonardo R, Löwen H, Reichhardt C, Volpe G, Volpe G 2016 Rev. Mod. Phys. 88 045006 doi: 10.1103/RevModPhys.88.045006 [18] Ai B Q, Shao Z G, Zhong W R 2018 soft matter 14 4388 doi: 10.1039/C8SM00444G [19] 张何朋, 施夏清, 杨明成 2022 物理 51 217 doi: DOI:10.7693/wl20220401 Zhang H P, Shi X Q, Yang M C 2022 Physics 51 217 doi: DOI:10.7693/wl20220401 [20] Cates M E, Tailleur J 2015 Annu. Rev. Condens. Matter Phys. 6 219 doi: 10.1146/annurev-conmatphys-031214-014710 [21] Fily Y, Marchetti M C 2012 Phys. Rev. Lett. 108 235702 doi: 10.1103/PhysRevLett.108.235702 [22] Redner G S, Hagan M F, Baskaran A 2013 Biophys. J. 104 640a doi: 10.1103/PhysRevLett.110.055701 [23] Speck T, Bialké J, Menzel A M, Löwen H 2014 Phys. Rev. Lett. 112 218304 doi: 10.1103/PhysRevLett.112.218304 [24] 夏益祺, 谌庄琳, 郭永坤 2019 物理学报 68 161101 doi: 10.7498/aps.68.20190425 Xia Y Q, Shen Z L, Guo Y K 2019 Acta Phys. Sin. 68 161101 doi: 10.7498/aps.68.20190425 [25] Kaiser A, Popowa K, Wensink H H, Lowen H 2013 Phys. Rev. E 88 022311 doi: DOI:https://doi.org/10.1103/PhysRevE.88.022311 [26] Wan M B, Reichhardt C O, Nussinov Z, Reichhardt C 2008 Phys. Rev. Lett. 101 018102 doi: 10.1103/PhysRevLett.101.018102 [27] Ahuja S 2011 Chiral Separation Methods for Pharmaceutical and Biotechnological Products (Hoboken: John Wiley and Sons Press) p131 [28] Wu J C, Dong T W, Jiang G W, An M, Ai B Q 2020 J. Chem. Phys. 152 034901 doi: 10.1063/1.5141040 [29] 廖晶晶, 蔺福军 2020 物理学报 69 220501 doi: 10.7498/aps.69.20200505 Liao J J, Lin F J 2020 Acta Phys. Sin. 69 220501 doi: 10.7498/aps.69.20200505 [30] Kümmel F P, Shabestari P, Lozano C, Volpe G, Bechinger C 2015 Soft Matter 11 6187 doi: 10.1039/C5SM00827A [31] Zhu W J, Li T C, Zhong W R, Ai B Q 2020 J. Chem. Phys. 152 1849031 [32] Weber S N, Weber C A, Frey E 2016 Phys. Rev. Lett. 116 058301 doi: 10.1103/PhysRevLett.116.058301 [33] Kumari S, Nunes A S, Araújo N A, Telo da Gama M M 2017 J. Chem. Phys. 147 174702 doi: 10.1063/1.4992797 [34] Ai B Q 2017 Phys. Rev. E 96 012131 doi: 10.1103/PhysRevE.96.012131 -
计量
- 文章访问数: 215
- HTML全文浏览数: 215
- PDF下载数: 4
- 施引文献: 0