水下爆炸对舰船的毁伤效应主要取决于爆炸产生的冲击波和气泡的载荷特性. 其中, 气泡运动持续时间较长, 产生的脉动压力和低频滞后流可以对舰船造成总体破坏. Rayleigh^[1]于20世纪初期对流体中空腔的塌缩现象进行了数学描述, 为水中空化泡的动力学行为提供了初步的研究方法. 随着对气泡可导致舰船结构严重损伤认识的深入, 人们开展了大量爆炸气泡的运动规律、载荷特性及其与水中结构的耦合作用等研究工作. Cole^[2]采用实验数据与理论推导相结合的方法, 较为系统地对水下爆炸的物理现象和规律进行了论述, 给出的气泡理论模型和相关实验数据沿用至今; 而Plesset^[3]则在Rayleigh工作的基础上, 推导出了经典的Rayleigh-Plesset(RP)方程, 用于描述无限大不可压缩流场中球形气泡的自由运动, 为水下爆炸气泡动力学研究奠定了基础. 由于RP方程对流体不可压缩的假设, 忽略了波辐射引起的气泡能量损失, 因此, 后续的气泡动力学研究在此基础上进行了不同程度的修正. 其中, Gilmore^[4]考虑了流体黏性和表面张力的影响; Keller^[5] 通过引入波动理论, Prosperetti和Lezzi^[6,7]通过引入微扰理论, 分别建立了近流场、远流场作用的可压缩模型, 考虑了压力波辐射的能量损失; Best^[8]考虑了气泡迁移及其导致的压力变化效应; Geers和Hunter^[9]建立了自由/重力场、可压缩流体中的单气泡运动模型, 给出任意位置的流场参数. 与此同时, 以美国为代表的海军强国通过对实船爆炸考核的方式开展了大量的气泡毁伤研究, 积累了丰富的实验数据^[2]. 我国对水中气泡的研究始于20世纪80年代, 目前颇具代表性的为哈尔滨工程大学的研究工作. 哈尔滨工程大学船舶工程学院的张阿漫、姚熊亮等在气泡的动力学理论、气泡与弹性结构及多气泡之间的耦合作用等方面进行了较为详细的研究工作^[10–15], 并于2023年建立了统一理论(Unified Theory)的方程构架 ^[16], 可将多种气泡运动的修正因素纳入其中, 还通过多种理论与计算方法初步建立了可用于水下爆炸及毁伤效应模拟的工业软件FSLAB^[17]. 西安近代化学研究所的段超伟等^[18]从气泡脉动的载荷特性出发, 对其动力学理论、实验、数值模拟等进行研究总结, 提出应综合考虑气泡内部和水中环境因素的气泡动力学模型. 总而言之, 气泡及其在水下复杂环境中的动态演化规律与多种因素相关, 至今还没有较为精准的物理模型可以描述, 但是, 目前对于气泡在水下相对简单环境中的运动规律已经有了较为深入的理论认识和实验数据.

以上对水下爆炸气泡的研究多采用了常规的化爆技术途径. 但是, 对于温度更高、热辐射更强的水下爆炸而言, 气泡的形成、初始状态、内部成分等均与化爆气泡有所不同. 例如, 核爆会在瞬间释放大量能量, 其爆心处的能量密度(初始温度、压强)远高于化爆, 爆炸产生的强辐射会将爆心周围的水介质汽化, 这可能是水下核爆气泡产生的主要原因. Thomsen与Ruhl^[19]通过相关研究明确指出, 核爆气泡内部的大量蒸气产物会导致气泡能量更加快速地耗散到水中, 从而消弱气泡的脉动行为, 并随爆深的增加而越为显著. 因此, 现有化爆气泡的理论模型是否也能用于对更高能量密度爆炸气泡运动规律的描述, 目前尚无定论.

鉴于以上原因, 研究人员试图通过水下电爆炸丝和激光聚焦的技术途径开展气泡的相关研究, 它们与化爆的最大区别在于, 爆心的能量密度可以更高, 气泡的主要成分为可冷凝蒸气. 从20世纪60年代开始, 以美国海军放射防御实验室为主的国外研究机构利用水下电爆炸丝的技术开展了水下爆炸的相关研究工作. Kriebel与Bechtel^[20]利用高速相机和压电传感器等给出了水面附近不同水深丝爆产生的气泡、冲击波、波浪以及水柱等物理图像和数据, 对观察到的特征现象及相互关联性进行了研究, 还对其与化爆的异同之处进行了对比和分析; Buntzen^[21]和Hege^[22]假设水下电爆丝为黑体辐射, 通过对丝爆发射光谱强度分布的测量, 初步给出了爆心区域的温度, 以及热辐射能在丝爆总能量中的占比关系. 21世纪后, 鉴于水下电爆炸丝及其产生的冲击波在纳米材料、油气勘探等领域的潜在应用前景, 国内外相关科研人员开展了大量的水下电爆炸实验研究^[23–26]. 其中, Antonov等^[27]采用特殊构型的金属丝阵负载在水中实现了TPa量级的高能量密度极端环境. 但是, 目前几乎所有工作的研究重点都集中在丝爆过程的物理规律以及如何获得更强的冲击波, 而鲜有对气泡的研究报道. 水下激光聚焦气泡的优点为气泡内部较透明, 有利于对气泡塌缩时刻产生的射流进行诊断. 但是, 由于实验中的总沉积能量较少导致气泡尺寸较小, 使得显性物理现象和规律不易观测, 同时高功率激光器等实验设备运行较为复杂, 因此利用水下激光聚焦的方式开展水下气泡的相关研究较少. 1975年, Lauterborn与Bolle^[28]通过激光聚焦气泡实验给出了气泡在收缩末期及近刚性界面位置的泡壁运动轨迹; 宗思光等^[29]在2011年曾利用激光聚焦击穿不同特性的液体, 对液体的黏性系数与冲击波、气泡脉动及其压力波强度的关联性进行了研究; Jia等^[30]对水中激光聚焦产生气泡的初始演化过程也进行了一定研究. 综上所述, 根据已有的相关研究结果可见, 利用电爆炸的技术途径开展水下气泡研究具有以下特点: 一是通过对驱动电流和金属丝负载等参数调控, 可以在水中获得较高的能量密度沉积; 二是气泡产生的机理和成分不同于化爆, 导致其演化规律有所不同; 三是实验设备相对简单, 诊断测试易于开展.

本文介绍了开展水下电爆炸气泡实验研究的初步进展. 第2节对实验进行了介绍, 包括放电装置、测试仪器及诊断布局, 给出了实验相关的设置参数; 第3节对获取的典型实验数据进行了分析, 包括实验重复性、铜丝电爆炸过程及爆心能量密度、气泡的产生和演化过程, 并通过现有的动力学模型与实验数据的比较对气泡的运动和能量特性进行了分析, 明确了后续研究的主要物理问题; 最后对实验及得到的初步结论进行了总结.

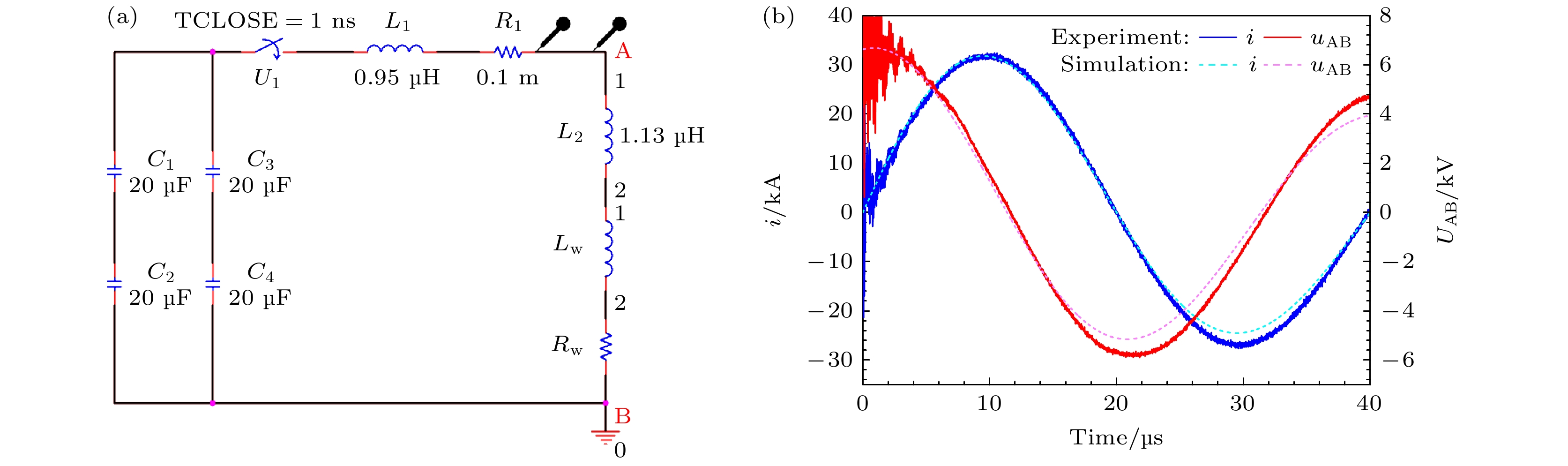
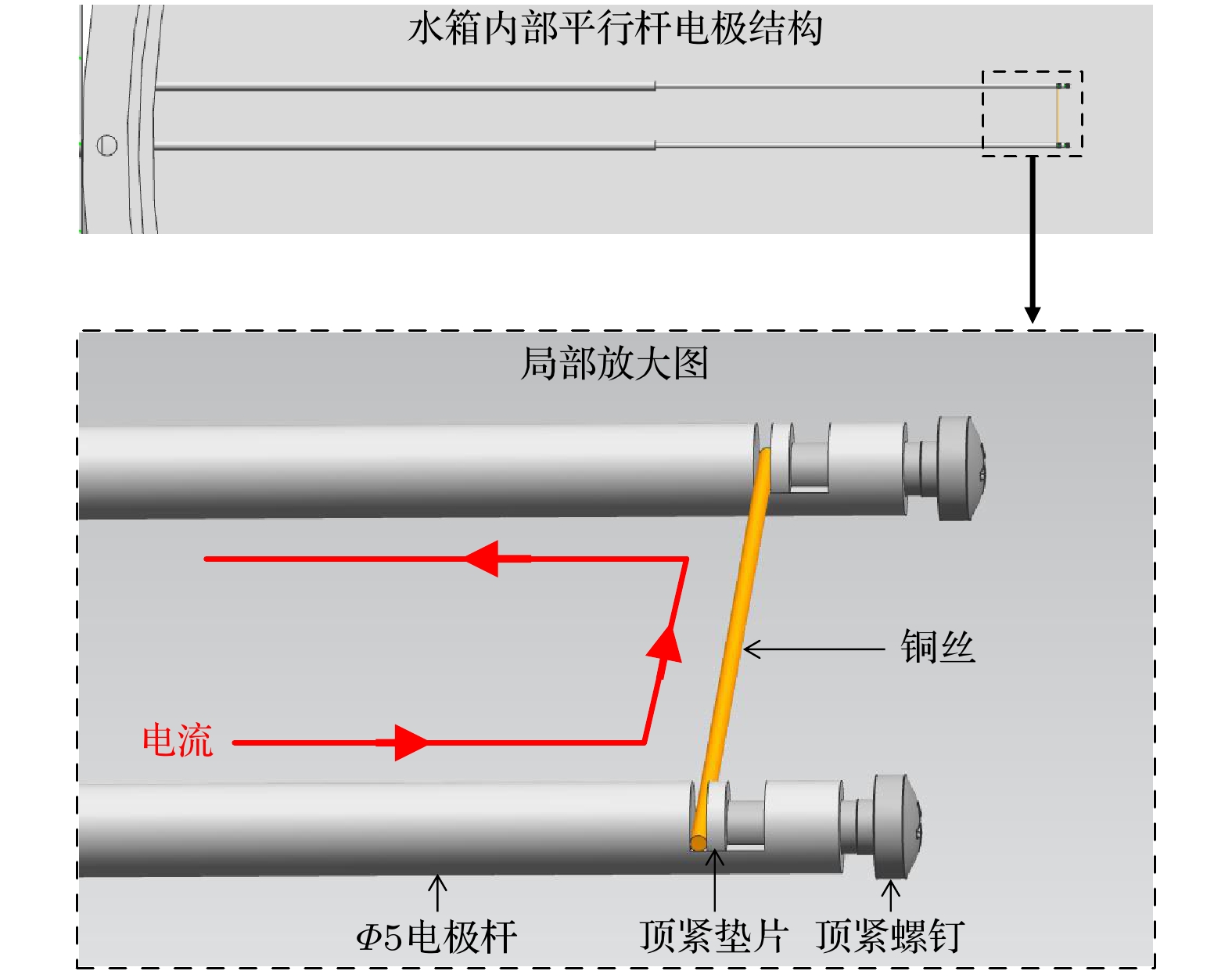
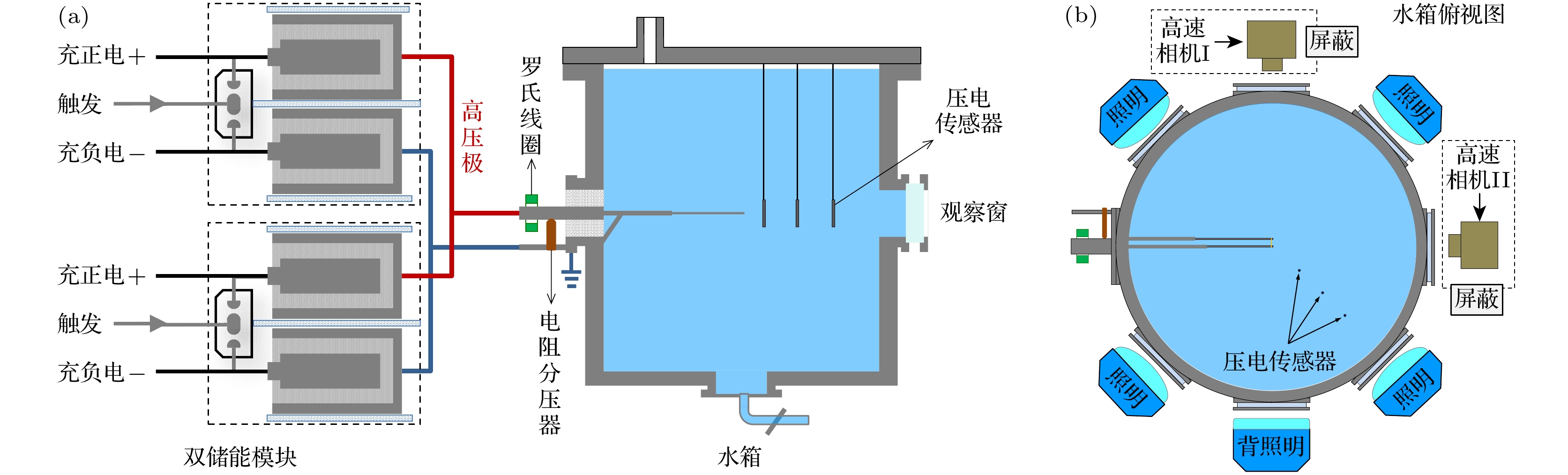
水下电爆炸丝实验装置主要由2个并联的储能-放电模块和爆炸水箱组成, 如图1(a)所示. 每个储能-放电模块由2台20 μF的电容器和1个气体轨道开关串联构成, 电容器采用正、负充电方式. 充电后的模块通过气体开关被触发后产生上升前沿(0—100%)约10 μs、峰值大于100 kA的脉冲电流. 水箱为圆筒形, 内部直径和高度均为1.8 m, 侧面设有用于图像拍摄和补光的玻璃窗口. 为了减弱电极结构对气泡自由运动的影响, 水箱内部采用了2根直径5 mm的平行圆杆状电极结构设计, 电极间隙50 mm, 如图1(b)所示. 负载则采用直径0.9 mm、长度50 mm的单根纯铜丝, 通过紧顶螺钉连接并固定于电极杆末端之间(水箱中心位置). 实验时, 水箱几乎注满去离子水, 水阻大于10 MΩ·cm, 水面上的空气压强为常压.

为了准确获得金属丝上的能量沉积, 必须先对装置各部分的电参数进行确认. 装置的总电容$ C = ({{{C_1} + {C_2}}})/{2} + ({{{C_3} + {C_4}}})/{2} = 20 $ μF; 在水箱入口位置(电阻分压器测点)对电极短路, 通过测量短路放电电流的周期T₁, 计算出水箱外部的回路电感$ {L_{1}} = {{T_1^2}}/({{4{\pi ^2}C}}) $; 采用金属棒代替铜丝, 使用相同的方法计算出装置的总电感L, 则水箱内部的结构电感L₂ = L – L₁ – L_stick (L_stick为短路金属棒电感). 在此基础上, 使用PSpice软件模拟短路放电, 通过对各部分的电参数进行微调并与实测电流比对, 最终确定了装置的等效电路, 如图2(a)所示. 结果显示, 水箱外部和内部回路的结构电感分别为L₁ = 0.95 μH和L₂ = 1.13 μH, 而装置总放电回路中的电阻几乎可以忽略不计. 短路放电的电流和电压实测波形与软件模拟结果比较如图2(b)所示. 图2(b)中, 蓝色和红色实线分别表示实测电流、电压波形, 浅蓝色和粉色虚线分别表示电流、电压波形的模拟结果. 可以看出, 电流、电压波形在相位和初始峰值上吻合较好, 在后续幅值上略有差异. 导致此现象的主要原因可能是短路金属棒与电极的连接处存在接触电阻, 电流流过后导致接触电阻阻值减小, 故后续的实测电流幅值偏大.

实验中, 忽略铜丝电离膨胀引起的电感变化, 铜丝上的功率P_W和沉积能量E_w可通过以下公式计算获得

式中, u_W为铜丝上的电阻电压; u_AB为水箱入口处的电压, 通过电阻分压器测量获得; i为铜丝上的电流, 采用罗氏线圈测量获得; L₂为水箱内部结构电感; L_w为铜丝的电感, l为铜丝长度; d为铜丝直径.

电阻分压器和标准罗氏线圈的布局见图1(a). 其中, 电阻分压器的阻值为2.1 kΩ, 并联于放电回路的水箱入口处(等效电路图中的A, B两端), 经标定对于数十kV的脉冲电压其分压比例为1∶970, 不确定度约为±2%; 罗氏线圈采用标准产品, 可测脉冲电流的最大峰值和最快上升前沿时间分别为500 kA和400 ns, 满足实验中峰值100—200 kA、上升前沿约10 μs的脉冲电流测量需求, 线圈的灵敏度0.001 V/A, 实验中实测电流噪声的最大信号为40 mV, 因此对应电流的测量精度为±4 kA. 另外, 考虑所用示波器精度、电缆衰减以及电感参数误差等其他因素, 最终计算得到的沉积功率和能量的不确定度不超过±10%.

实验中, 使用2台高速数字相机拍摄气泡的演化图像, 布局见图1(b). 其中, 相机I的拍摄视角位于铜丝轴向方向, 对气泡脉动全过程进行拍摄, 帧频为10000 frames/s, 曝光时间设定为2—10 μs, 满足气泡脉动过程(数十毫秒)的时间分辨需求. 相机II的拍摄视角垂直于铜丝轴向方向, 主要对气泡的产生过程进行拍摄, 帧频为110000 frames/s, 曝光时间设定为1—2 μs, 基本满足气泡产生初期演化过程(百微秒量级)的时间分辨要求, 但是对于铜丝电离阶段的演化过程(数十微秒), 其时间分辨略有不足. 另外, 相机II还采用了中性滤光片对爆炸初期产生的强光进行衰减. 两台相机拍摄的气泡图像的尺寸通过爆心区域(相机聚焦平面)已知尺寸的电极结构作为参考标准给出, 图像的读取误差约为3个像素, 对应精度0.6 mm. 为了防止相机在实验过程中受到装置放电产生的空间电磁场干扰, 对相机采取了电磁屏蔽和光电隔离措施.

实验采用了3支压电传感器来测量爆炸产生的冲击波. 传感器布置于爆心的同一方向, 高度与爆心相同, 见图1(b). 为了避免传感器被损坏以及信号受到放电干扰, 3支传感器距爆心的距离分别设置为250 mm, 450 mm和650 mm. 冲击波信号通过同轴电缆输入至信号适调仪, 经适调仪放大后输出至示波器并被记录. 传感器的最大量程34.5 MPa, 时间响应为1.5 μs, 经过标定后的灵敏度约为0.15 V/MPa. 实验中获取信号的最大噪声约30 mV, 对应的测量精度为±0.2 MPa.

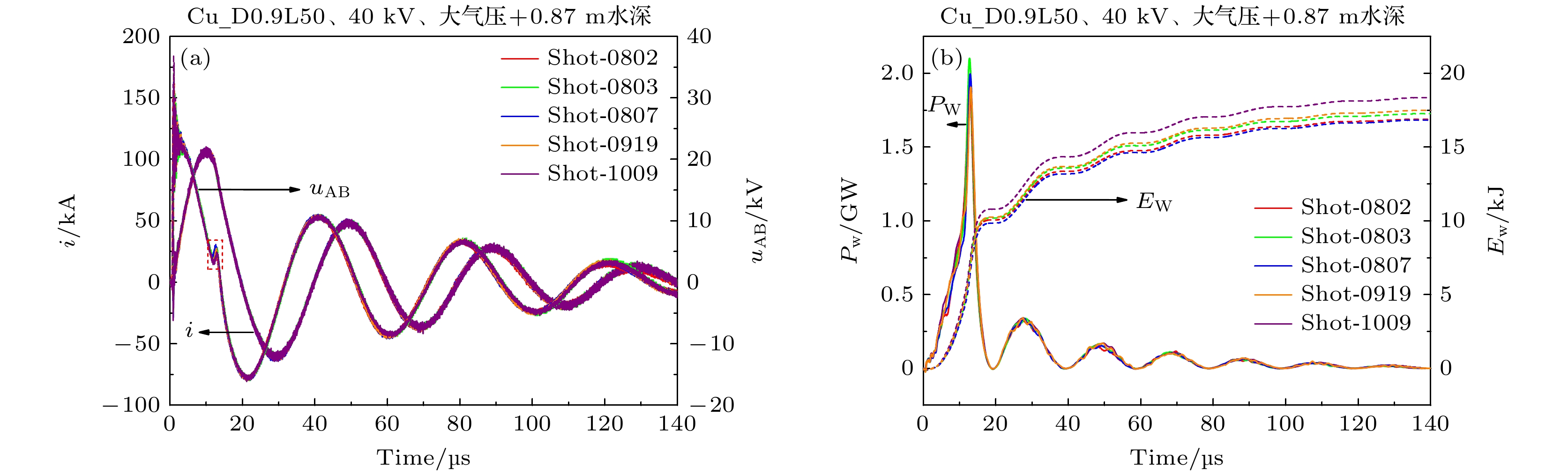
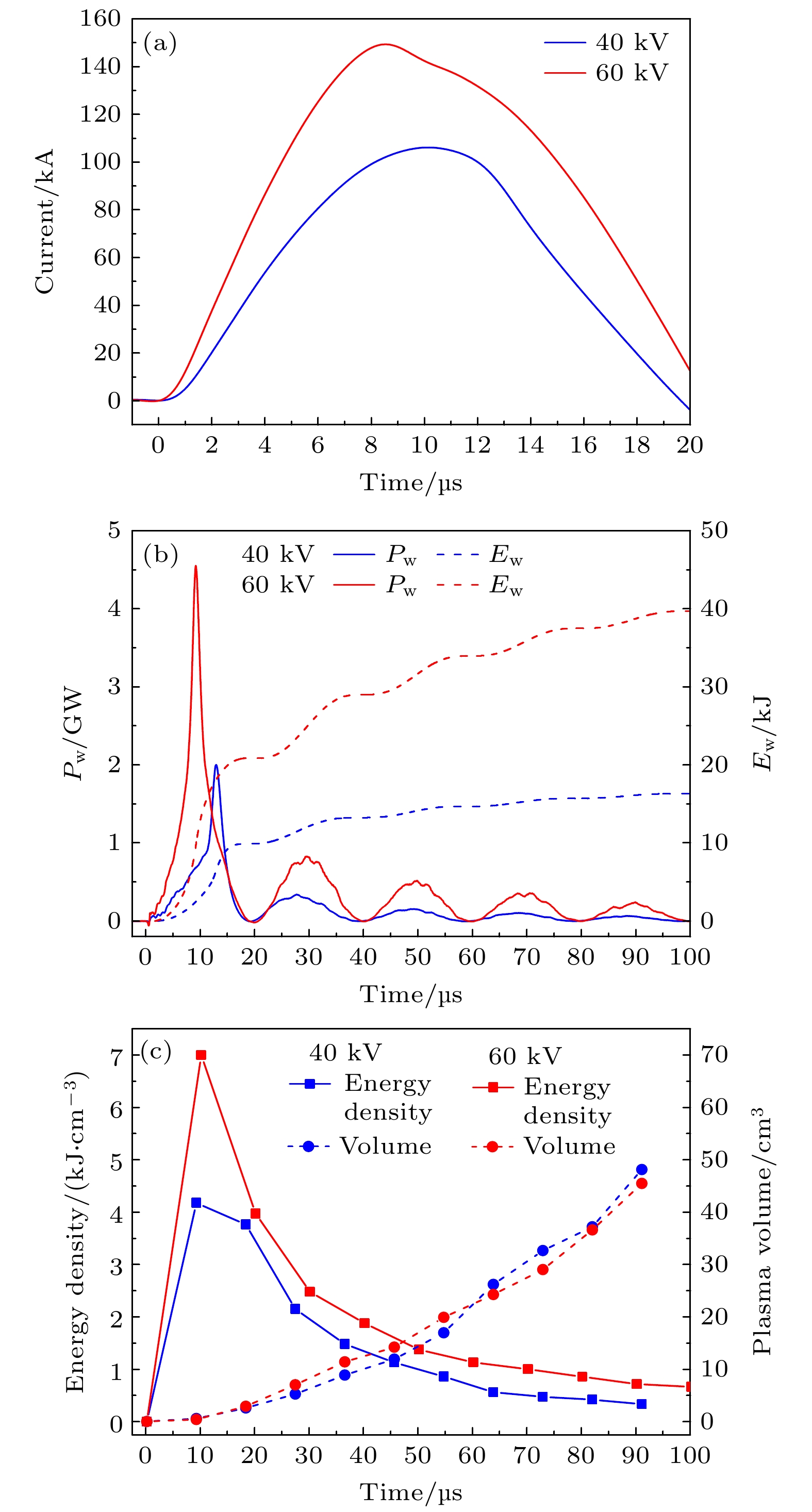
图3(a)给出了充电40 kV时不同发次实验的实测电流、电压波形(充电60 kV实验结果与其类似). 从图3(a)可以看出, 电压波形总体重复性较好, 但是在金属丝被电离阶段, 即电压发生突变附近(图中红色方框内), 电压波形略有差异. 分析认为, 这是由于铜丝在装配过程中的差异所导致. 铜丝两端与电极杆通过紧顶螺钉的连接方式固定, 如图4所示, 而人工装配的差异可导致连接位置的接触电阻有所不同. 另外, 紧顶在电极杆内部的部分铜丝可能参与了爆炸, 但参与份额无法控制, 即实际爆炸丝的长度有所不同, 这会导致铜丝的电离过程以及电离期间的电阻差异. 以上两个原因共同导致了分配在铜丝上的电压略有不同.

实验中电流波形的重复性较好, 这是因为, 虽然铜丝在每发实验中的电阻存在差异, 但与总放电回路相比, 这个误差就显得很小. 所以只要保证每发实验中充电电压值的精度, 就可以保证回路中电流的一致性.

铜丝上的电压差异最终会导致铜丝上沉积功率和能量的差异, 如图3(b)所示. 从图3(b)可以看出, 当铜丝上的沉积功率约为2 GW时, 其差异范围为±0.1 GW; 沉积能量约为17.5 kJ时, 其差异范围为±0.8 kJ. 另外, 铜丝在电离过程中的电阻差异还会导致铜丝在电离时间上略有差异(约±0.2 μs). 根据实验经验, 后续通过优化金属丝与电极杆之间的连接方式设计, 可以基本上消除由于人工装配带来的差异, 进一步提高实验的重复性, 并对爆炸能量进行精确控制.

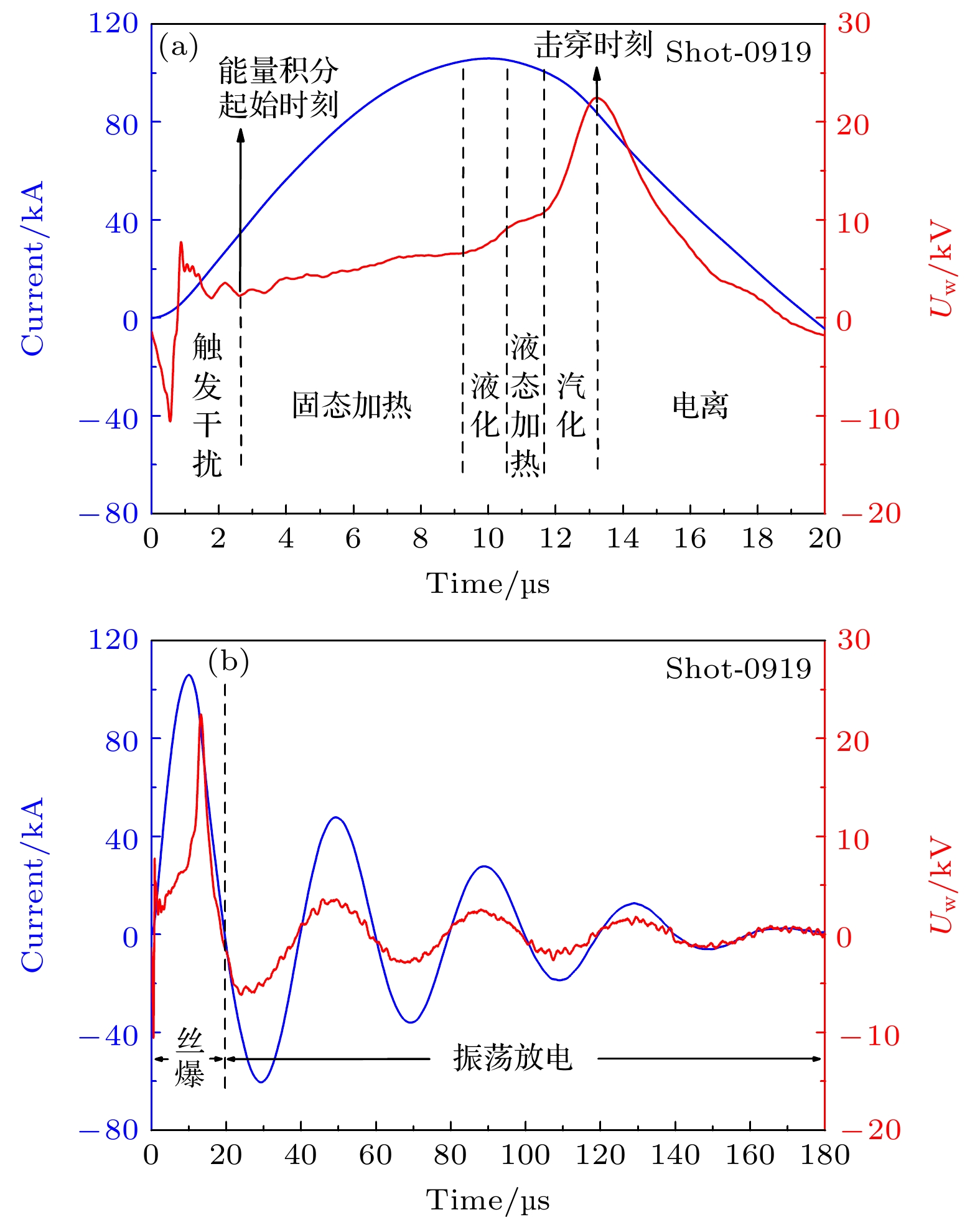
实验中, 铜丝电爆炸的典型电压和电流波形如图5所示. 图5中, 蓝色实线为丝上电流波形, 红色实线为丝上的电阻电压波形, 图5(a)和图5(b)对应同一发次实验中不同的放电阶段. 从图5(a)可以看出, 当电流流过铜丝时, 铜丝经过了固态 加热、液化(电阻率变化导致电压斜率变化)、液态加热(电阻率变化减缓导致电压斜率变缓)和汽 化(电阻率急剧变大导致电压急剧上升)的相变过程. 在此过程中, 铜丝上的电阻逐渐变大, 电阻电压随之增加. 铜丝在电流峰值到达后不久被击穿 电离, 此时的电阻电压达到最大值. 在此之后, 由于铜丝被电离为等离子体, 导致其阻值急剧下降, 电阻电压随之下降. 由于电极之间的最大电压远小于水的击穿电压^[31], 因此不存在除去丝爆区域之外的其他水中放电通道(根据Oreshkin等^[32]的 研究结果, 丝等离子体表面约几微米的水介质可能被电离并形成微弱的放电通道), 也就是说, 沉积 于水中的能量均集中在爆心区域. 从图5(b)可以看出, 电流在装置放电回路中振荡直至消耗殆尽, 总持续时间约为180 μs, 而气泡从产生到其脉动行为的持续时间通常为数十毫秒. 因此, 在放电中后期由于电流振荡而导致铜丝等离子体上的累计能量沉积理论上对气泡能有所贡献, 应当计入爆炸总能量.

根据(1)式—(4)式可计算出铜丝上的沉积功率和能量, 通过相机II拍摄的图像可获得等离子体的外形尺寸并计算得到其体积, 进而可获得等离子体的能量密度. 图6分别给出了不同充电条件下铜丝上的电流、功率、沉积能量以及等离子体体积和能量密度的典型实验结果. 从图6可以看出, 铜丝上的电流上升速率越快, 其功率和沉积能量就越高, 而铜丝在膨胀初始阶段的体积差别不大, 因此其能量密度也越高. 目前实验在充电60 kV时获得的水中沉积能量密度达到了7 kJ/cm³, 与TNT(6.95 kJ/cm³)相当. 计划在后续实验中, 通过提升电流上升速率(提高功率)、采用高原子序数材料的金属丝(提高电阻率和比热容)以及增加水箱内部压力(抑制等离子体膨胀)等方法, 可进一步提升爆心的能量密度.

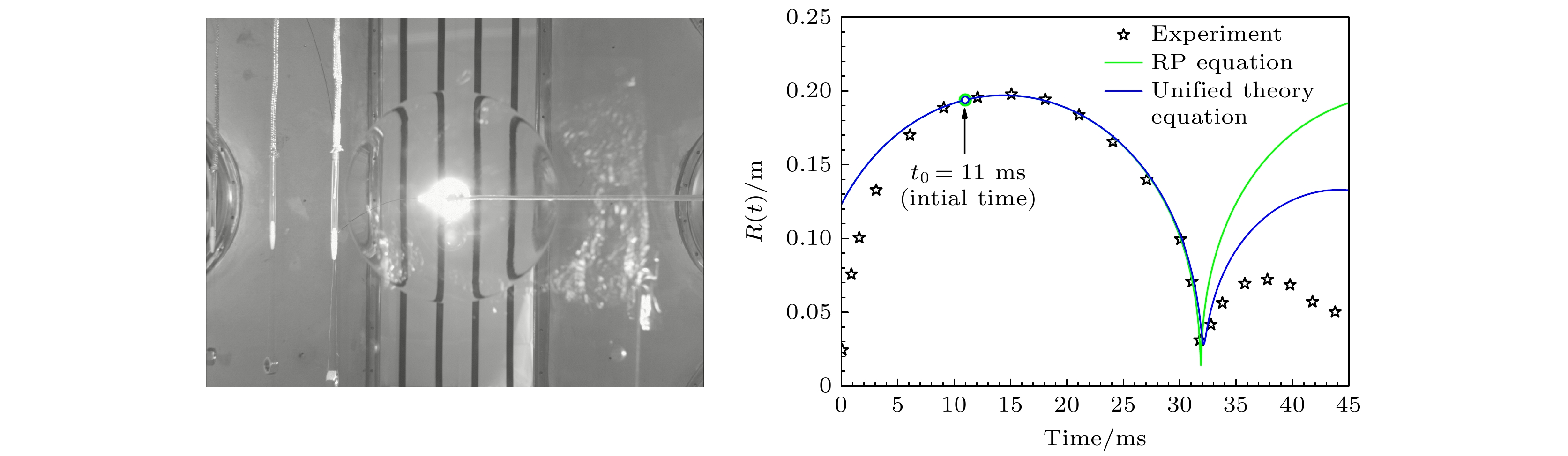
实验中拍摄的气泡在产生阶段的典型演化过程图像如图7所示. 从图7可以看出, 铜丝在初期被电离的过程中快速膨胀, 产生冲击波并向外传播(见18.2 μs时刻图像); 之后等离子体继续膨胀并逐渐形成了气泡的初始形态. 由于爆炸丝的外形尺寸, 导致气泡在膨胀初期为圆柱形, 并在向外膨胀的过程中逐渐演变为球形(与Zhang等^[33]报道中装药外形对气泡初始膨胀影响的结论相似). 实验图像显示从铜丝演变为球形气泡的持续时间约1 ms, 理论上此持续时间会随铜丝长度的减小而减少. 当气泡膨胀到约600 μs时, 其表面开始出现明显的亮度较暗的薄层结构, 这应该是气泡表面的水被汽化所导致, 此现象与Kolacek等^[34]给出的描述一致.

众所周知, 水下爆炸气泡的动力学行为机制总体上可以描述为: 爆炸产生高温气体形成气泡, 由于气泡内部的压强大于周围的水压, 导致气泡加速向外膨胀并推水做功, 使水具有了一定的动能和势能, 同时, 气泡内部的压强随气泡体积的增大而迅速减少. 当气泡的内部压强小于周围水压时, 气泡将在惯性作用下继续做减速膨胀运动, 直至膨胀到最大状态; 此时, 由于周围水压大于气泡内压, 气泡在周围水压的作用下开始做收缩运动, 内部压强逐渐增加, 并于内压大于周围水压时在惯性作用下继续收缩, 直至气泡体积再一次达到最小值、内部压强达到最大值. 在此之后, 气泡按照以上规律周而复始地做膨胀收缩运动, 并在浮力的作用下做垂直向上迁移, 直至浮出水面或能量耗尽. 气泡在运动过程中的能量耗散主要包含两部分: 气泡推水运动导致的波动能量耗散和气泡对周围水介质的热能耗散. 对于水下电爆丝气泡, 在爆炸初期, 由于丝等离子体的高温特性, 在热耗散中可能会包含一定份额的热辐射能量.

图8给出实验中相机I拍摄到的气泡前二次脉动过程的典型演化图像. 根据目前对丝爆过程的理论研究, 铜丝在电离初期急剧向外膨胀, 首先会在水中产生冲击波并以声速向外传播, 此后等离子体继续膨胀并演变为气泡, 如图8中第一幅图所示. 从图8可以看到, 气泡在第一次膨胀过程中, 内部出现了中心区域较亮、边缘区域较暗的现象, 这说明气泡内部存在温度或压强的阶梯分布; 气泡第1次脉动周期为34.6 ms, 第二次脉动周期约10 ms; 在气泡第一次脉动的收缩阶段, 由于上、下压差导致气泡底部收缩较快, 最终形成了类半球形的结构; 另外, 气泡在脉动过程中具有明显的上浮现象. 总体来说, 实验中观测到气泡的总脉动次数不超过4次, 明显少于化爆气泡, 这说明电爆丝气泡在运动过程中的能量耗散更快. 实验还观测到, 气泡在多次脉动后直接消失在水中, 无明显浮出水面的现象, 这说明气泡内部的成分主要以可冷凝 蒸气为主, 即铜蒸气和水蒸气的混合汽体, 除此之外, 还应该存在少量的电解气体. 从图8还可以看出, 气泡在第一次收缩结束时, 内部的铜等离子体冷却后形成的金属颗粒喷射到气泡外部, 并在后续过程中随气泡一起运动, 对气泡形成遮挡, 导致在此之后无法清晰地分辩气泡的边界位置. 个别图像中出现的大量亮斑现象应该是观察窗玻璃受到水压导致其透光性有所变化.

下面尝试利用现有的经典RP气泡动力学方程和气泡运动统一理论方程对实验数据进行分析. RP方程给出了单球形气泡在无限大不可压缩静流场中的运动规律:

统一理论方程则将RP方程、Keller-Miksis等方程纳入了它的物理模型构架内, 不但考虑了流体的可压缩性, 还考虑了气泡的浮力效应, 其方程形式如下:

方程(5)—(7)均假设气泡内的气体为理想气体, 也就是说, RP方程不考虑气泡的能量损耗, 而统一理论方程只考虑了流体波动的能量耗散. 方程中, R为随时间变化的气泡半径; v表示气泡质心的垂直移动速度; ρ为水的密度, 取值1000 kg/m³; C为水中声速, 取值1500 m/s; g为重力加速度, 取值9.8 N/kg; C_a为质量附加系数, 取值为1; C_d为阻力系数, 取值为0.5; P_∞为气泡中心的环境压强, 在本实验中即为爆心处静水压, 取值为1.095×10⁵ Pa (对应0.87 m水深+1个大气压); P_b为气泡壁外表面压强, 当气泡半径较大时, 可忽略气泡表面水的张力和黏性应力, 此时P_b≈P_g(气泡内部压强, 假设气泡内部压强均布), 对于理想气体, $ {P}_{\text{g}}={P}_{0}({R}_{0}^{3\gamma }/{R}^{3\gamma })\text{ }+{P}_{\text{V}} $, 其中P₀为气泡内部初始压强, R₀为气泡初始半径, P_V为常温下的饱和水蒸气压力, 取值2338 Pa, γ为气泡内部气体的绝热指数; H为气泡表面的焓差, 此时可简化为$ ({P_{\text{b}}} - {P_\infty })/\rho $. 对于求解二阶偏微分方程(5), 必须给出其初始条件, 即R₀和$ {\dot R_0} $, 以及γ和P₀; 对于求解方程(6)和方程(7), 还需给出气泡质心的初始速度v₀.

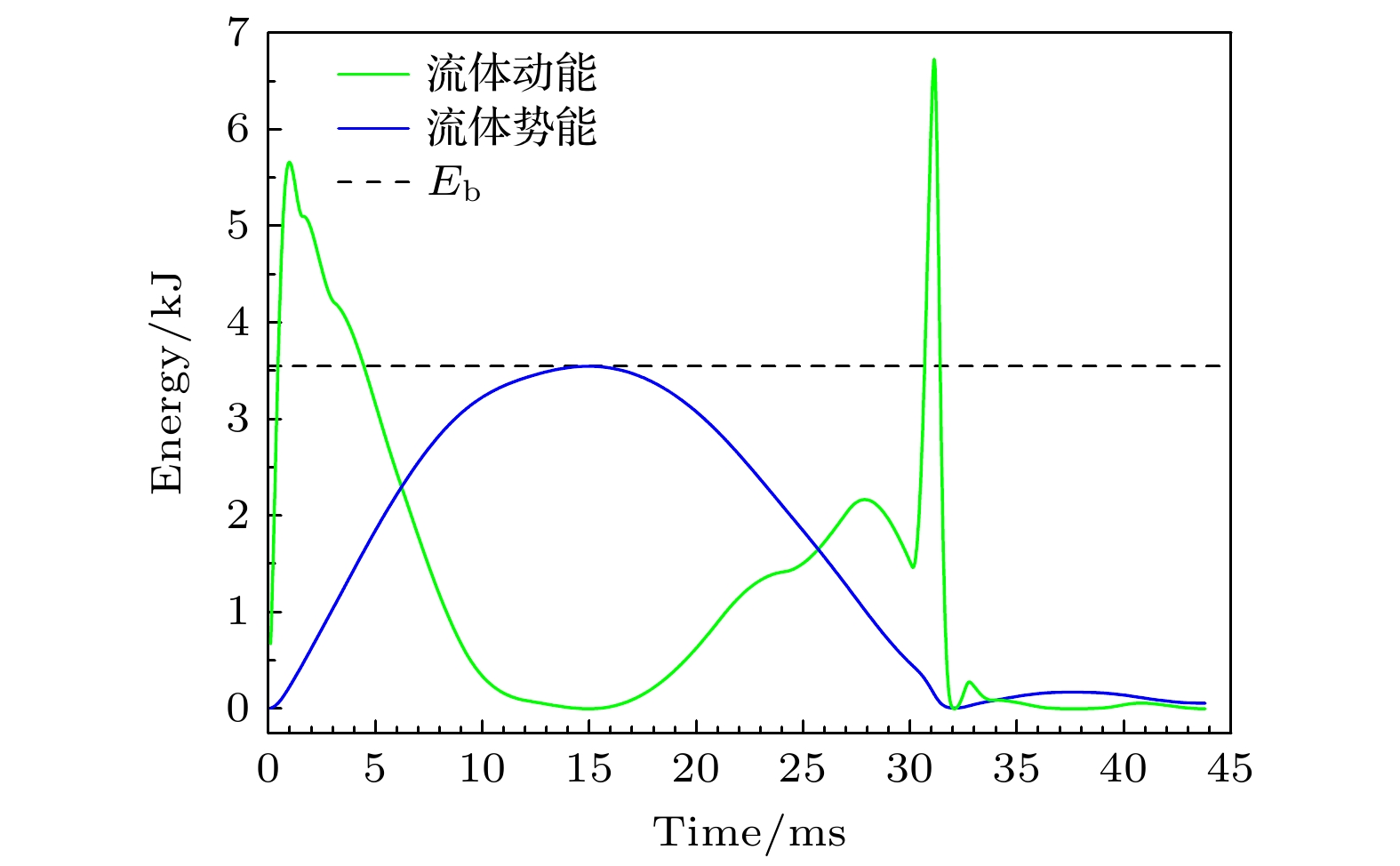
实验获取了气泡的运动全过程图像, 因此可以得到任意时刻的R, $ \dot R $和v₀. 由于气泡的内部压强与其内能相关, 因此, 可以通过气泡的能量守恒来计算P₀. 我们知道, 气泡的总能量E_b表达式可以通过对RP方程积分得到(忽略铜丝体积):

式中, V = 4πR³/3表示气泡的体积, 等式右边第一项可视为气泡对流体做功导致的流体动能, 第二项视为流体具有的势能, 第三项则代表气泡的内能. 当气泡膨胀到最大半径R_m时, 此时流体动能为零, 气泡内能较小可以忽略(内能与$ {R^{3(\gamma - 1)}} $成反比), 因此气泡的总能量约等于此时流体具有的势能, 即$ {E_{\text{b}}} \approx 4\pi R_{\text{m}}^3{P_\infty }/3 $. 由于R_m可以通过实验测量获得, 因此, 通过(8)式可以给出气泡在任意半径R(t)时的内部压力P_g(t). 在计算过程中我们发现, 对于所有实验发次, 气泡在第一次膨胀过程中的大部分时间里, 周围流体的动能与势能之和大于气泡总能量. 图9给出了充电40 kV实验中, 气泡周围流体的动能(绿色实线)、势能(蓝色实线)、以及气泡总能量(3547 J, 黑色虚线). 由图9可以看出, 在4.5 ms之前, 流体的动能大于气泡总能量; 在约10 ms之前, 流体动能与势能之和大于气泡总能量, 并在约1 ms时达到最大值5895 J. 这说明, 在气泡的第一次膨胀过程中, 约有近40%的能量通过热耗散的途径传输给了水介质, 使其升温或汽化.

分析认为, 在气泡第一次膨胀后期, 气泡内部压强较小导致温度降低, 此时气泡内部气体可视为理想绝热气体, 对水介质的热量传递可以忽略. 因此, 可以借鉴Wang^[35]在确定气泡初始条件时采用的反向积分法, 取10 ms后的某一时刻作为方程的初始条件, 对方程进行求解, 然后将求解获得的气泡轨迹在时间轴上向后平移对应的时间长度, 即可得到忽略了热能损失情况下的气泡运动轨迹. 目前实验获得的爆心最大能量密度与TNT化爆相当, 此状态下γ的取值范围与常规压强下相当, 暂取γ = 4/3.

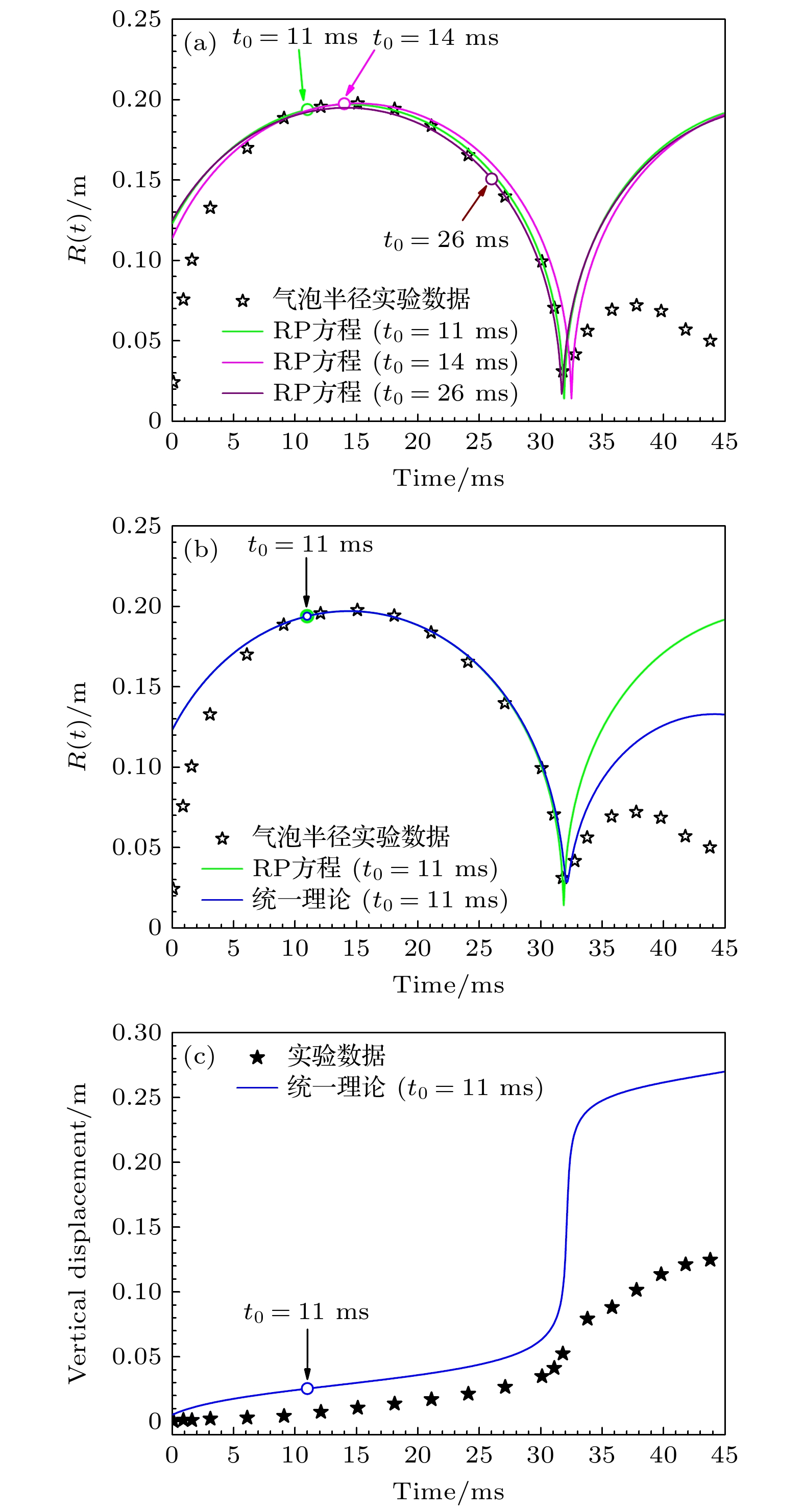
按照以上方法计算得到的理论模拟结果与实验数据如图10所示. 图10(a)给出了采用RP方程、选取3个不同时刻的初始条件求解得到的气泡膨胀半径. 可以看出, 这3条轨迹相互之间差别不大, 说明在选取不同t₀时刻的时间段内, 气泡内部气体可视为理想气体, 几乎没有热损耗, 也间接证明了这种确定初始条件方法的可行性. 图10(b)给出了相同初始条件下, 两种理论模型的计算结果及其与实验数据的比较. 可以看出: 首先, 在气泡第一次脉动周期内, 两种模型基本吻合, 这说明没有考虑能量损耗的RP方程在对气泡第一次脉动轨迹进行模拟时, 与考虑了流体波动能量耗散的统一理论方程几乎没有区别, 即气泡的波动能量损耗主要为第二次膨胀时产生的脉动压力波损耗; 在第一次脉动结束时, 统一理论得到的气泡最小半径略大于RP方程, 似乎更接近实验结果, 通过对计算过程分析, 这是因为统一理论考虑了气泡的浮力效应所导致. 其次, 在首次脉动周期内, 从大约9 ms开始到脉动结束, 两种理论模型都与实验数据符合较好, 说明在这个阶段, 气泡内部气体可视为理想气体, 几乎无能量损耗; 在9 ms之前, 气泡半径的模拟结果明显与实验数据不符, 这是因为我们在计算气泡总能量时, 没有计入气泡在膨胀初期的热损耗, 导致气泡内部压强及泡壁速度的计算结果偏小, 而半径偏大. 最后, 对于第二次脉动周期, RP方程由于没有考虑能量损耗, 因此计算得到的第二次膨胀最大半径R_m2 = R_m, 而统一理论考虑了气泡能量的波动损耗, 因此R_m2 < R_m, 但与实验数据比较仍然偏大, 这说明气泡在第二次膨胀阶段依然有较为明显的热能损耗. 图10(c)给出了气泡质心在垂直方向上浮位移的实验数据和统一理论的计算结果. 分析认为, 在第一个脉动周期内, 模拟结果略大于实验数据, 是因为在9 ms之前气泡半径的模拟结果较大, 因此产生的浮力和上浮距离较大; 在第二个脉动周期内, 模拟结果大于实验数据, 也是因为模型未考虑热耗散导致其半径的模拟结果偏大. 由此可知, 假设可以获得气泡在0 ms时刻附近的内部压强并选取为初始条件, 那么在第一次脉动周期内, 气泡半径的模拟结果与实验数据的对比变化趋势将与图10(b)中给出的第二次脉动周期内的变化趋势具有相似性.

以上两种理论模型中与气泡内能关联的表述项为气泡的内部压强, 其表述关系式均以理想气体为前提, 没有考虑气泡内能的热耗散. 通过对实验数据的模拟和分析发现, 气泡在第一和第二次膨胀前期, 均有相当部分的热能耗散, 因此, 开展气泡在膨胀初期的热能耗散机理和水介质相变研究, 并将此因素纳入方程中, 是下一步的工作方向. 另外, 在计算过程中, 绝热指数γ的取值目前也存在疑议. 对于单原子气体和水蒸气, γ一般对应取值为5/3和4/3, 并随温度和压强变化. 图10中显示, 当γ取值为4/3时, 气泡半径在膨胀后期和收缩阶段的模拟结果和实验数据较为吻合, 说明此时气泡内部温度不高, 遵循理想气体特性并且内部的主要成分应该为水蒸气, 而在膨胀初期, 由于铜丝的电离, 气泡内部可能含有相当成分的铜蒸气. 目前还无法对气泡在脉动过程中内部成分的变化及其占比和温度进行诊断, 因此, 对γ的取值还需后续开展研究和分析.

本文介绍了采用电爆炸丝的技术途径开展水下爆炸气泡研究的初步实验研究进展. 实验结果显示, 目前通过电爆丝的技术途径在水中获得的沉积能量密度与TNT相当; 气泡由金属等离子体膨胀演化产生, 总脉动次数不超过4次, 并在能量耗尽后直接溃灭于水中, 说明气泡内部的主要成分为可冷凝气体. 通过对气泡的能量和动力学分析发现, 在脉动周期的膨胀阶段, 气泡在推水做功的同时, 相当一部分内能通过热传导或热辐射耗散到水介质中使水产生相变, 导致现有理论模型对此阶段气泡半径的模拟结果与实验数据具有一定差异. 实验结果说明了水下电爆炸技术可以作为水下爆炸气泡研究的有效实验手段之一, 初步明确了电爆炸气泡与化爆气泡在物理特征上的差异性, 并为后续需要研究的物理问题及研究工作指明了方向. 本文中对气泡能量的分析结果对开展较高温度爆炸气泡、激光聚焦气泡等具有明显热耗散特征的气泡动力学研究具有一定的借鉴作用.

对于下一步的研究工作, 首先计划通过对脉冲功率水中加载技术的研究进一步提高水中的沉积能量密度和爆心温度. 在此基础上, 开展高能量密度气泡的特征规律及其与化爆气泡的差异研究. 同时, 还需要提升对实验条件和参数的控制, 获取可信度较高的实验数据, 为物理规律的分析提供支撑.