首页
登录
注册
-
将功率超声波应用到液态合金凝固过程中能够有效地细化晶粒, 从而提升金属材料的力学性 能[1–4]. 当前, 不同学者已经提出了多种理论阐明超声对于晶粒细化的作用机制[5,6], 其中一种是超声空化效应可以诱导枝晶晶粒碎断, 即气泡稳态/瞬态空化产生的力足够碎断枝晶. 近年来, 通过开展透明有机合金[7,8]或金属材料[9,10]的原位观测实验, 捕捉到了超声场中气泡运动过程及其对树枝晶的破碎过程. 例如, Shu 等[8]利用高速摄像发现超声场中空化气泡破裂产生的作用力可以导致琥珀腈枝晶分枝的根部断裂. Priyadarshi 等[9]采用原位高速观测技术, 发现 Al3Zr 金属间化合物的破碎主要源于气泡溃灭产生的冲击波.
由于超声场中液态金属凝固过程具有高度的瞬态和动态性, 很难准确获得熔体中的声场和流场信息, 更难捕捉到气泡空化细节以及气泡与晶粒间的相互作用. 因此, 研究者采用数值模拟方法研究了空化效应及其对生长晶粒的作用机制[11–19]. 早期学者们[12–14]发现了超声波频率、振幅、液体黏度和表面张力与气泡温度、压强及气泡半径的相关性. 近年来, 吴学由和梁金福[15]研究了气泡初始平移速度和驻波声场分布对气泡的脉动、平移、形变、非球形振动和稳定性的影响. Wang 等[16]的模拟结果表明气泡间二次 Bjerknes 力随声压幅值的升高而增大, 随液体黏度、表面张力和密度的增大而降低. Cao 等[17]分析了材料的声阻抗对气泡溃灭产生的射流和冲击波的促进或抑制作用. Shan等[18]基于格子玻尔兹曼方法, 研究发现固体壁的几何特征会影响其对溃灭气泡的阻滞作用, 使气泡溃灭过程更加多样. 以上研究主要集中在超声场中气泡的径向振动、平移和形变、气泡与气泡间的相互作用以及不同壁面处气泡的运动规律, 鲜有研究聚焦于气泡对枝晶的碎断作用. Zhang 等[19]用循环力代替气泡稳态振荡产生的周期性脉冲力作用于枝晶二次分枝根部, 发现应力足以引发二次分枝的变形及断裂. 然而, 该模型只关注了稳态空化对枝晶的碎断作用, 未考虑枝晶对气泡径向脉动的影响. 综上所述, 已有的数值模拟和实验研究均忽略了枝晶与气泡间的耦合作用, 导致超声场中气泡空化与枝晶的相互作用机制尚不明确.
本文以丁二腈(SCN)-2%水(H2O, 摩尔分数 2%)透明有机溶液为研究对象, 采用有限元方法模拟了超声作用下液体中单个气泡稳态/瞬态空化过程. 在此基础上, 建立超声场中气泡与枝晶相互作用模型, 分析了驱动声压、枝晶形貌、气泡与枝晶距离对振荡气泡和枝晶应力分布特征的影响, 从而揭示超声作用下气泡与枝晶的相互作用机制.
-
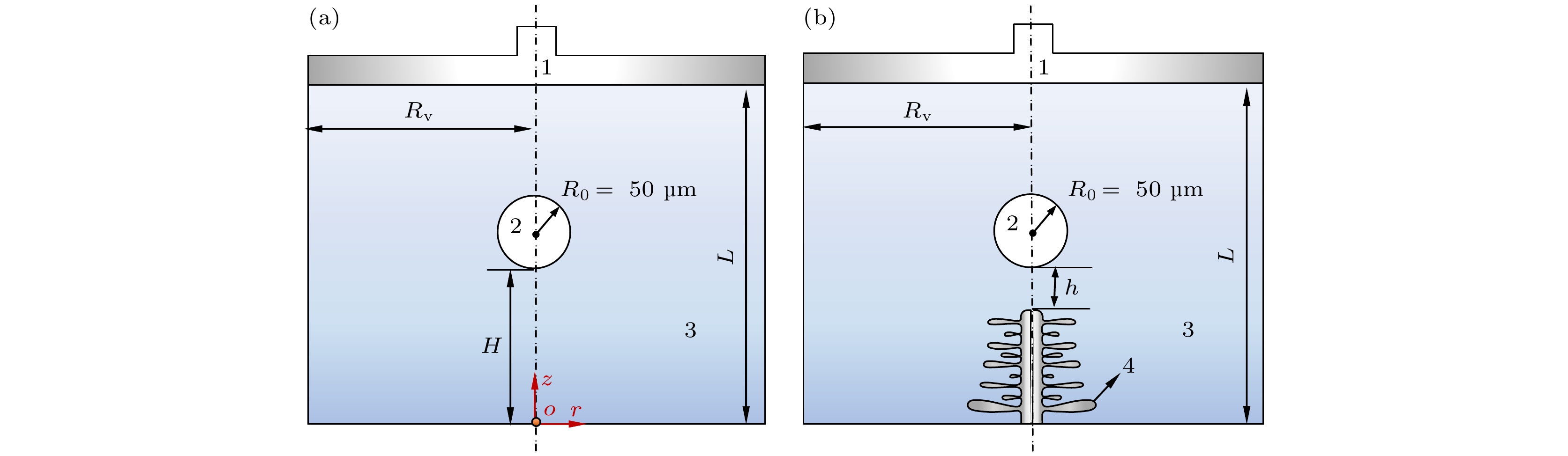
采用二维轴对称模型模拟超声作用下液体中单个气泡的振荡生长及溃灭过程. 如图1(a)所示, 将初始半径 R0 为 50 μm的气泡置于半径 Rv 为 0.9 mm、高度 L 为1.4 mm的计算区域轴线上, 空化气泡的下边缘与计算区域底部的距离为 H, 该区域内充满 SCN-2%H2O 溶液. 假设该溶液为均匀且不可压缩的牛顿流体, 液体中的流速和压强可通过 Navier-Stokes 方程计算得到[20]:
其中
${\boldsymbol u} $ 是速度, p 是压强,${\boldsymbol I} $ 是单位张量, ρl 是液体密度, μl 是黏度.假设气泡内的气体在无扩散条件下服从多方定律[21]:
其中Pg是微气泡内的气体压强, Vb是气泡的瞬时体积, γ是气体的多变指数. 由于振荡过程中气泡并非稳定球形, 定义Rb为气泡等效半径. 初始条件下, Rb = R0, 且气泡内的压强与液相中的保持平衡.
超声作用下气泡与枝晶相互作用的几何模型如图1(b)所示, 单个 SCN 树枝晶位于气泡正下方, 二者距离为 h. 在方程(1)—方程(4)的基础上, 假设 SCN 树枝晶为均匀各向同性线弹性材料, 满足固体力学方程[22]:
式中ρs 为树枝晶密度;
${{\boldsymbol{d}}_{\rm s}} $ 为枝晶分枝位移向量;${\boldsymbol{\sigma}} $ 为应力张量, 满足各向同性线弹性本构方程[22],其中 λ 和 μ 为 Lamè 系数, 与弹性模量E 和泊松比 ν 有关, 即
$ \lambda = \nu E/\left(1+\nu \right)\left(1-2\nu \right) $ ,$ \mu = E/2(1+ \nu ) $ ;$T_{\rm r}({\boldsymbol{\varepsilon }}) $ 为体积应变. 应变张量${\boldsymbol{\varepsilon }} $ 满足以下方程[22]:通过在计算区域顶部施加正弦压力导入超声, 其边界条件为
式中P0表示环境压力; Pa为声压幅值; 角频率ω = 2πf, 其中f为超声频率, t为时间. 超声场中气泡溃灭所需的空化阈值可以表示为
其中σg为表面张力. 计算区域的侧壁以及底部都采用无滑移边界条件
${\boldsymbol u}=0 $ .气泡和 SCN-2%H2O 溶液界面处的压强满足[23]:
在气泡下方加入枝晶, 在流体-枝晶界面上, 枝晶壁的应力为
式中,
$ {\boldsymbol{n}} $ 和$ {\boldsymbol{\tau }}$ 分别为流体-枝晶界面法向和切向的单位矢量. 此外, 流体-枝晶界面还必须满足速度连续性和压力连续性条件:式中,
${{\boldsymbol{d}}_{\text{s}}} $ 为枝晶分枝位移向量,${\boldsymbol{\sigma }} $ 是枝晶所受的应力. 枝晶底端固定在计算区域下侧边界处, 其约束条件为${{\boldsymbol{d}}_{\text{s}}}=0 $ . 计算中所用到的物理量数值如表1 所列. 本模型将超声场中气泡振荡与溃灭模型和枝晶的固体力学结合, 考虑了气泡-溶液、溶液-枝晶两个相互作用边界, 涉及了气-液-固三相以及声场、流场和应力场的多物理场耦合, 从而可以系统研究枝晶上的应力分布和气泡的动态运动. -
利用单轴超声凝固原位观测实验装置[17]记录了 20 kHz超声作用下 SCN-2%H2O 溶液中的气泡运动和枝晶生长过程. 实验过程中, 玻璃样品盒装满 SCN-2%H2O 溶液并且由上下两部分组成. 其中, 上端玻璃盒尺寸为 25 mm×25 mm×14 mm用于容纳变幅杆并引入超声, 而下端 12.5 mm×1 mm×45 mm的玻璃盒用于观测枝晶生长及气泡振荡. 当超声换能器开始作用时, 打开光源(Cossim LG-系列光纤冷光源), 通过高速摄像机(Photron Fastcam SA-Z)捕捉凝固过程中枝晶与空化泡之间的动态相互作用. 图像采集速率为 40000 fps, 分辨率为 1024 pixel×512 pixel.
-
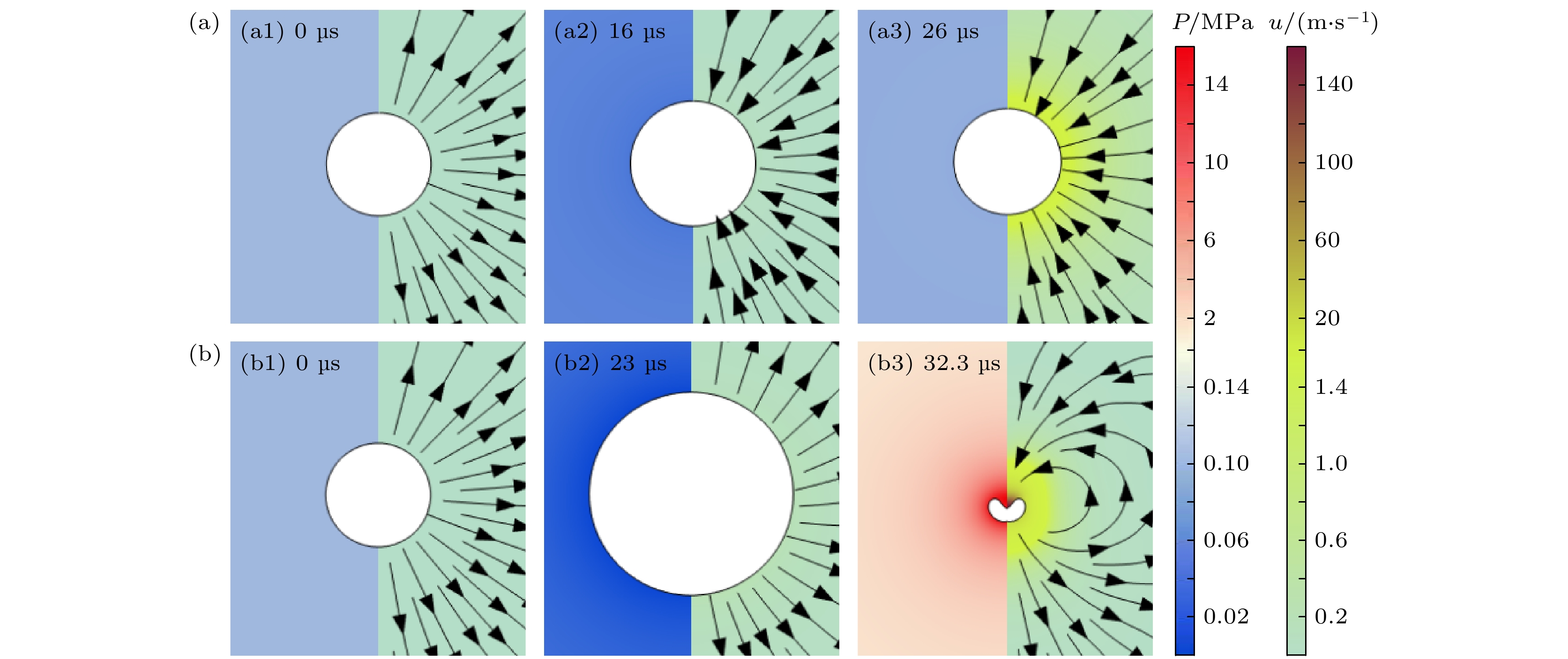
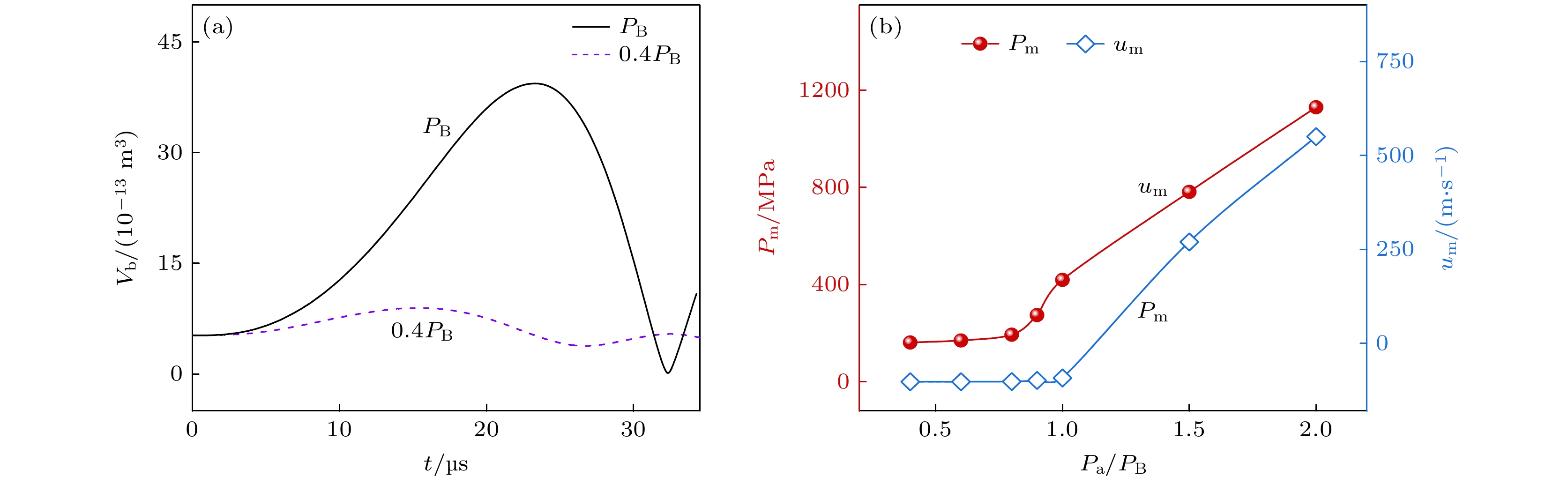
不同超声振幅作用下气泡振荡及溃灭过程如图2 所示, 其中气泡左右两边的云图分别表示液体中压强和流速, 黑色箭头为液体流动方向. 当驱动声压Pa为0.4PB时, 气泡始终保持球形, 以体积振荡模式发生稳态空化. 当驱动声压达到空化阈值时, 气泡先膨胀后快速溃灭分裂成两部分, 发生分裂振荡. 由黑色箭头方向可知液体在气泡膨胀时远离气泡, 收缩时流向气泡. 图3 展示了不同声压条件下气泡体积的变化规律及溶液中最大压强和流速. 当气泡体积振荡时, 其最大和最小体积分别为 8.95×10–13 m3和 3.32×10–13 m3, 最大压强为 2 个大气压, 最大流速可以达到 2.43 m/s. 气泡分裂振荡时, 在初始阶段(0—23 μs), 气泡保持球形膨胀, 最大体积可以达到 3.935×10–12 m3(图3(a)), 为气泡初始体积的 7.5 倍. 随后气泡迅速收缩, 在 31.17 μs发生凹陷, 并快速分裂为两部分, 同时产生16 MPa瞬时声强和 160 m/s射流(图3(b)), 远高于稳态空化条件. 因此, 相较于低驱动声压下气泡的体积振荡, 气泡在高驱动声压作用下可以形成分裂振荡, 能够在分裂瞬间产生极高的压强和流速. 不同驱动声压下液体中的最大压强及最大流速如图3(b)所示. 当驱动声压Pa < PB时, 气泡振荡获得的最大压强(Pm)和最大流速(um)随Pa缓慢增大. 当Pa达到PB 并持续升高时, 气泡转为瞬态空化, Pm和um迅速增大, 在Pa = 2PB时可分别达到 1000 MPa和 628 m/s. 这种高压和超高流速的极端环境将对其中的物理化学过程产生重要影响.
-
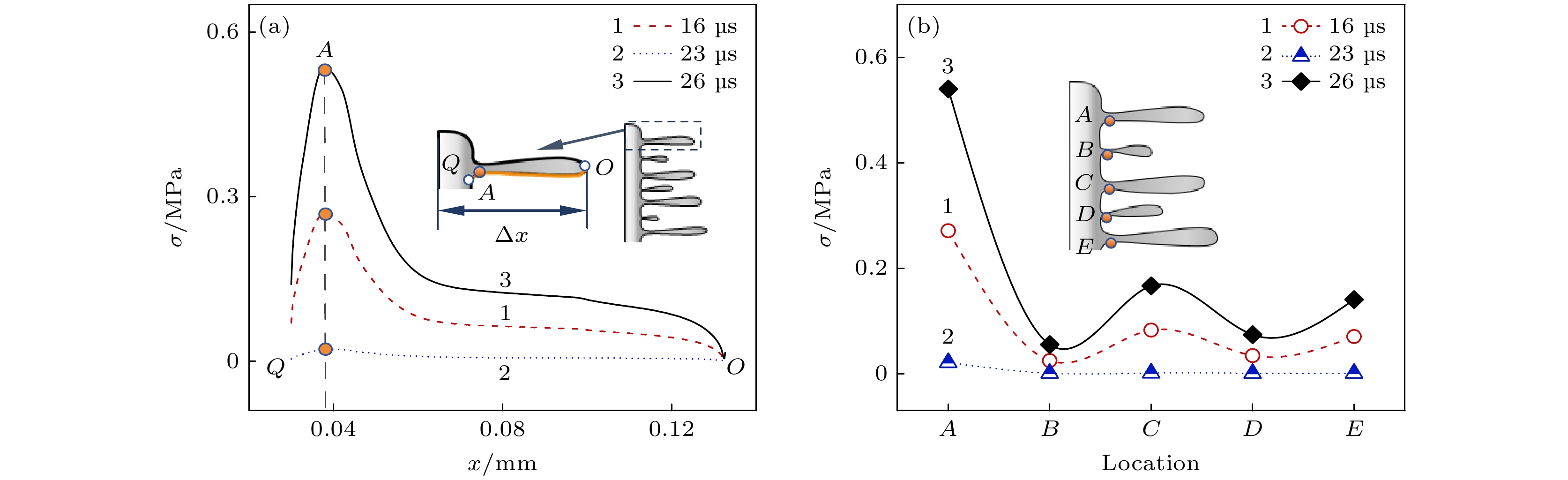
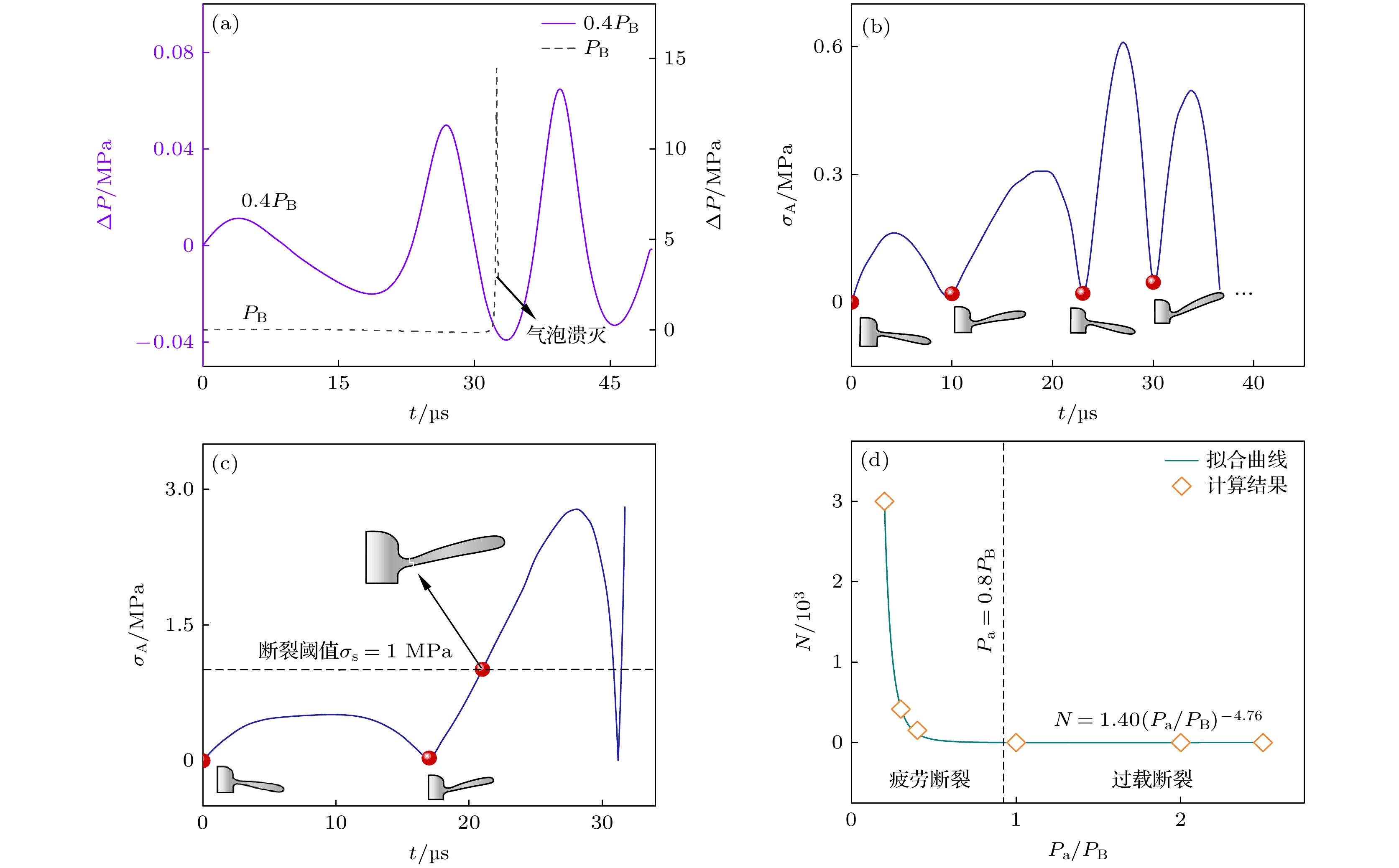
在气泡正下方h = 0.2 mm处放置一个SCN树枝晶, 通过耦合求解气泡状态方程((10)式)和流体状态方程((1), (2)式)获得气泡振荡在流体域中产生的压强和流场分布, 然后计算出分枝与液体接触表面的应力, 将其作为载荷代入固体力学方程以计算分枝上的应力分布, 从而构建气-液-固三相耦合的多物理场模型, 研究超声场中气泡与枝晶的相互作用规律. 图4(a)为0.4PB驱动声压下 SCN 树枝晶二次分枝表面的应力分布随时间的变化规律. 从图4(a)可以看出, 气泡振荡导致应力主要集中于二次分枝根部A点附近, 26 μs时可达到0.53 MPa. 在枝晶主干以及二次分枝尖端应力较小, 仅为0.003 MPa. 进一步比较了不同位置处的二次分枝根部的应力演化规律, 如图4(b)所示. 不同时刻二次分枝根部 A 点受力都大于其他分枝根部, 因此, 该处应力应该最先达到并超过其屈服强度(约 1 MPa[27])而发生断裂. 由此可见, 气泡空化产生的射流和瞬态高压导致应力集中在枝晶的二次分枝根部, 使其更易成为疲劳断裂点.
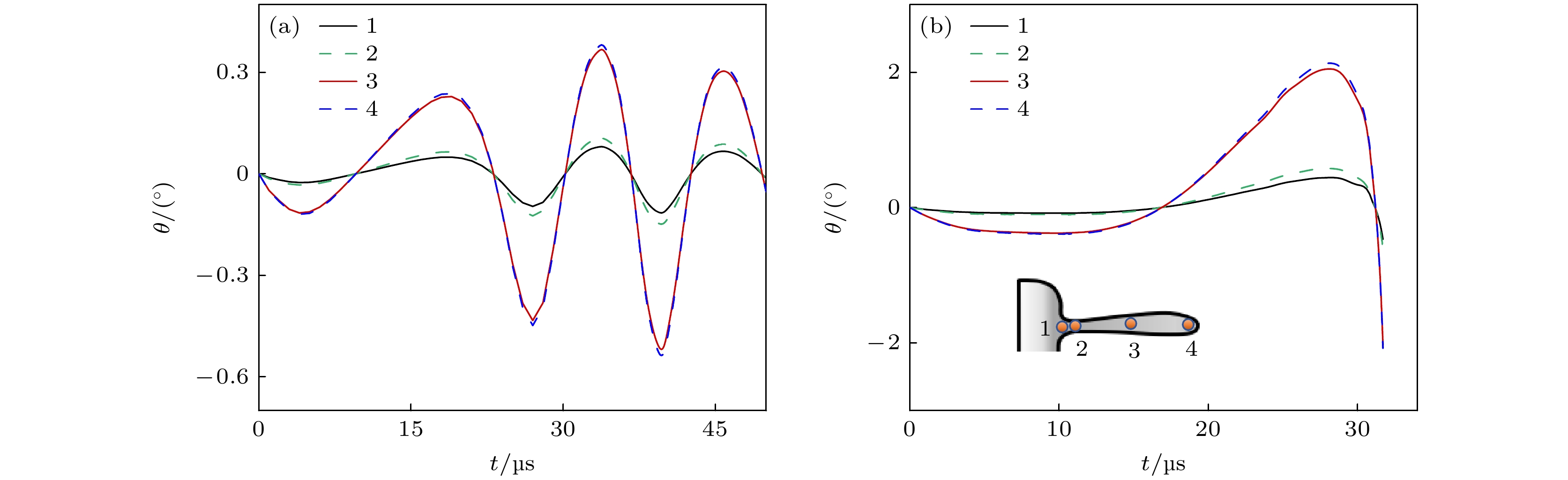
图5 定量分析了枝晶顶部第一个二次分枝不同位置的偏转角度θ随时间的变化规律. 从图5(a)中可知 0.4PB振幅下二次分枝根部偏转角的范围在 –0.1°—0.1°之间, 二次分枝中部和尖端处偏转角度成倍增大, 其范围增大到 –0.5°—0.4°之间. 在PB驱动声压下也存在相同规律, 二次分枝中部和尖端处先向下偏转 0.4°后向上偏转 2°, 是根部偏转角度的4倍(如图5(b)). 由此可知, 在空化产生的压强和流动的作用下, 分枝根部的偏转角度远低于分枝臂, 表明在外部应力作用下枝晶根部难以发生较大形变, 使得二次分枝上的应力集中在根部, 导致根部断裂的发生.
以枝晶顶部第一个二次分枝为研究对象, 分析了其在不同驱动声压下的断裂机制, 如图6 所示. 当驱动声压为 0.4PB 小于空化阈值时, 枝晶二次分枝根部所受应力随着气泡内部与外部压强差进行周期性变化, 二次分枝也在周期性应力作用下不断上下弯折. 结合图6(a)和图6(b)可知 0—9 μs液体中最大压强小于气泡内压强, 即压差 ΔP > 0, 二次分枝向下弯折, 其根部应力变化趋势与 ΔP 相同, 都是先增大后减小. 9—23 μs时压差 ΔP < 0, 二次分枝向上弯折, 其根部应力随压差增大而升高, 降低而减小. 23 μs时气泡内外压强的相对大小再次翻转, 同时枝晶弯折方向也随之改变. 根据超声场的周期性变化, 气泡外部与内部的压差不断正负交替, 二次分枝也不断上下弯折. 稳态空化条件下, 气泡壁面压力及二次分枝根部压力随时间的变化具有良好的周期性规律, 其变化周期与驱动声压一致. Wang等[27]计算出气泡壁面施加在枝晶上的周期性压力, 将其幅值作为应力疲劳曲线(S-N曲线)中循环载荷的压力幅值. 本文也通过此方法将二次分枝根部所受的一个周期内的压力幅值作为循环载荷的压力幅值引入疲劳模型, 并代入 S-N 疲劳曲线[27], 可以计算出二次分枝在经历 153 个弯折周期后达到断裂阈值σs = 1 MPa而发生疲劳断裂. 由此可以看出, 在超声气泡稳态振荡产生的循环压力作用下, 二次分枝以与超声气泡相同的频率上下弯曲, 使得分枝根部产生疲劳应力, 从而引起分枝断裂. 图6(c)展示了Pa达到PB时A点应力随时间的变化规律, 发现二次分枝仅经历一次上下弯折, 在 21 μs时根部受力就达到σs而发生过载断裂. 进一步计算了不同驱动声压下的二次分枝疲劳断裂周期, 如图6(d)所示. 随着Pa的增加, 二次分枝断裂所需的弯折周期数快速下降, Pa = 0.4PB 处下降速度开始趋于平缓. 当Pa增至0.8PB时, 二次分枝从疲劳断裂变为过载断裂. 通过数值拟合可知, 二次分枝发生断裂所需的疲劳周期数N与Pa/PB的关系符合如下幂函数关系:
-
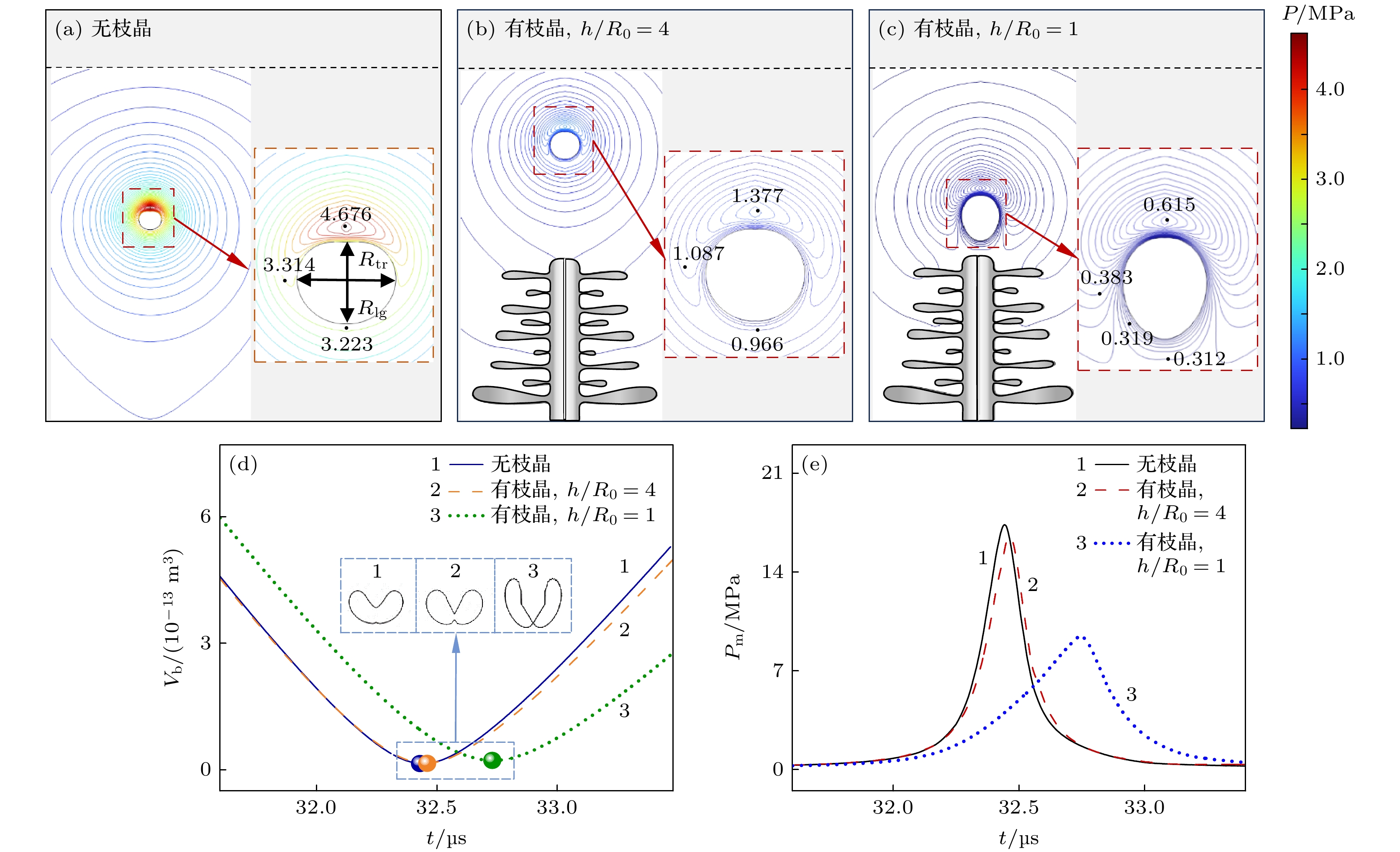
图7 进一步研究了当超声声压幅值 Pa = PB, 改变气泡下缘与枝晶顶部距离 h, 气泡与枝晶的相互作用过程与机理. 图7(a)—(c)是气泡顶部开始凹陷时刻气泡周围压强等值线的分布图. 当气泡下方无枝晶, 即可认为气泡与枝晶距离无限大时, 气泡凹陷呈椭球状, 横向半径Rtr大于纵向半径Rlg, 辐射压强达到 3.314—4.676 MPa, 且最大值出现在气泡正上方. 当气泡与枝晶距离为4R0时, 气泡凹陷呈近似球状, 在邻近流体中辐射的压强降低至 0.966—1.377 MPa. 当气泡与枝晶距离减小至R0, 气泡呈椭球状, 但此时纵向半径大于横向半径, 向周围流体中辐射的压强进一步降低. 由此可见, 随着气泡与枝晶距离的减小, 气泡溃灭时的形态发生“椭球状(Rtr > Rlg)到球状再到椭球状(Rlg < Rtr)”的转变, 辐射出的瞬态压强显著降低, 但压强最大值始终位于气泡正上方. 溃灭过程中气泡体积和流体中最大压强的定量分析结果如图7(d)和图7(e)所示. 不同间距下气泡均从正上方发生溃灭, 这是因为正上方流体中的压强远大于其他区域, 导致该区域最容易凹陷. 随着气泡与枝晶距离的减小, 气泡压缩到最小体积的时间由 8.32 μs增至 8.81 μs, 流体中的最大压强由16.9 MPa降低至 9.4 MPa, 且达到峰值的时间延后 0.3 μs.
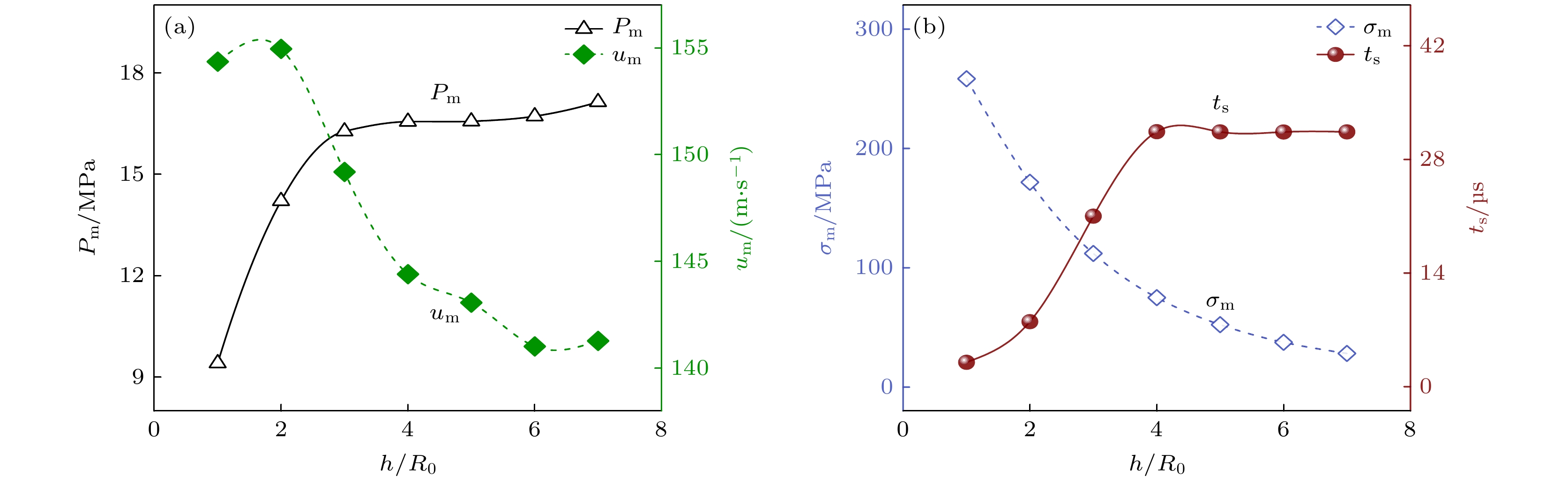
图8 统计了气泡动力学特性和 SCN 枝晶二次分枝受力断裂随距离 h 的变化规律. 图8(a) 展示了气泡溃灭在流体中产生的最大压强和流速与距离 h 的相关性. 当气泡与枝晶间距由 R0 增加至 3R0 时, 气泡溃灭产生的最大压强从9.41 MPa线性增大至 16.27 MPa. 气泡与枝晶间的距离进一步增大, 最大压强升高速率变缓, 当距离 h 达到 7R0 时, 气泡溃灭产生的最大压强为 17.14 MPa, 与无枝晶条件下气泡溃灭产生的一致, 此时枝晶对气泡的影响基本忽略不计. 而当 h 处于 2R0 和 4R0 之间时, 枝晶的靠近使得气泡溃灭产生的最大流速从144 m/s增加至155 m/s. 当h高于4R0或低于2R0时, h的变化对气泡运动过程的影响逐渐减弱. 由图8(b)可知, 随着气泡与枝晶距离的增加, 气泡空化对二次分枝根部的作用效果被削弱, 根部所受应力下降. 二次分枝断裂时间随h的增加先快速线性增加, 后趋于平缓保持在 31.39 μs. 基于以上研究, 发现枝晶壁面的阻滞作用使得靠近的气泡被拉长, 气泡发生溃灭的时间延迟, 在邻近流体中辐射的压强降低流速增大. 但距离的减小降低了压力与流速传播过程中的损失, 枝晶界面被施加更大的载荷, 枝晶内部产生更大应力, 使枝晶断裂时间缩短.
-
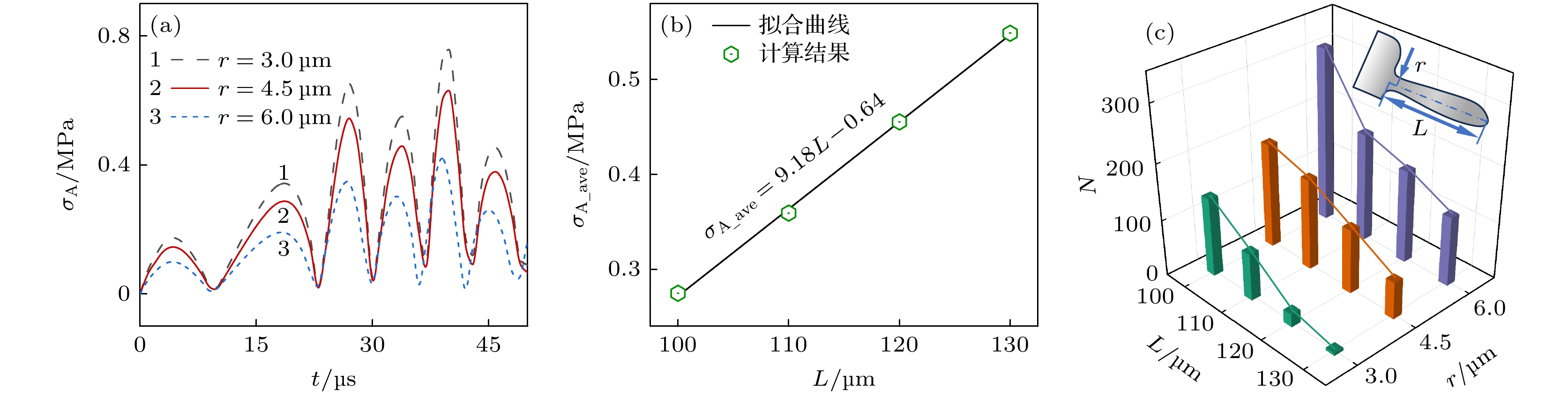
以枝晶顶部离气泡最近的二次分枝为研究对象, 固定h = 4R0且Pa = 0.4PB, 研究了二次分枝根部半径及长度对断裂周期的作用规律, 如图9所示. 当二次分枝长度L为 100 μm时, 其根部A点所受应力随其半径 r 的减小而增大(图9(a)). 当二次分枝根部半径r为 3 μm, A点在一个振动周期内所受的平均应力随L的增大线性增加(图9(b)). 同时考虑r和L对分枝断裂的影响, 如图9(c)所示, 发现当 r 很小而L很大时, 即使Pa = 0.4PB气泡仅发生体积振荡并无法产生高压及射流时, 二次分枝仍会过载断裂. 与此同时, 对比了二次分枝长度L及根部半径r对二次分枝断裂周期的调控效果, 发现L变化对断裂弯折周期数的影响是r的二倍. 所以, 当二次分枝较长或半径较小时极易引起碎断.
-
超声作用下无限液体中单个球形气泡的半径变化可通过 Keller-Miksis (K-M)方程[26]获得:
式中cl 为液体中的声速, Pv 为气泡的蒸汽压. 气泡内部压强 Pg 可通过求解以下微分方程获得[28]:
其中,
${k_{\text{g}}}$ 代表气体导热率,${T_{\text{g}}}$ 为气泡内部温度, 上标$ \dot R $ 和$ \ddot R $ 分别代表物理量对时间的一阶导数和二阶导数. 气泡表面的温度梯度可近似表示为$ {\mathrm{d}}{T}_{\text{g}}/{\mathrm{d}}r{|}_{r=R}=(T-{T}_{0})/\delta $ , 其中T0 为液体温度; δ 表示热边界厚度[26],这里, κ 代表气体热扩散系数. 通过热力学第一定律计算可以得到气泡内部温度[26]:
式中, Cv 为气体热容; Vb 代表气泡体积; 假定气泡始终保持球形振荡, lth 为热扩散尺度,
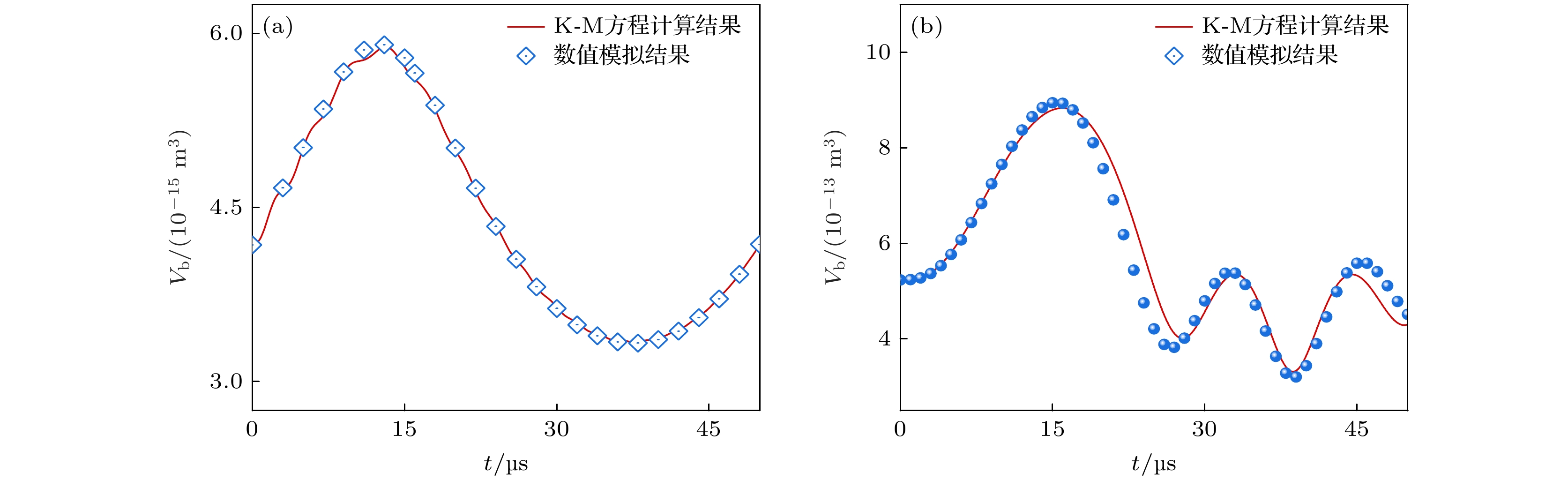
为验证本文中构建的有限元模型的准确性, 将其与K-M 方程计算结果进行对比, 相关计算参数如表1 所列. 以初始半径 R0 为10 和 50 μm的气泡为例, 分别采用有限元方法和 K-M 方程计算了其在 0.4PB 驱动声压下的体积演化, 如图10 所示. 有限元模拟结果与 K-M 方程解析解基本一致, 这说明本文构建的有限元模型能够准确预测气泡的运动过程, 并且将其与固体力学模型结合能够表征气泡与枝晶的相互作用.
-
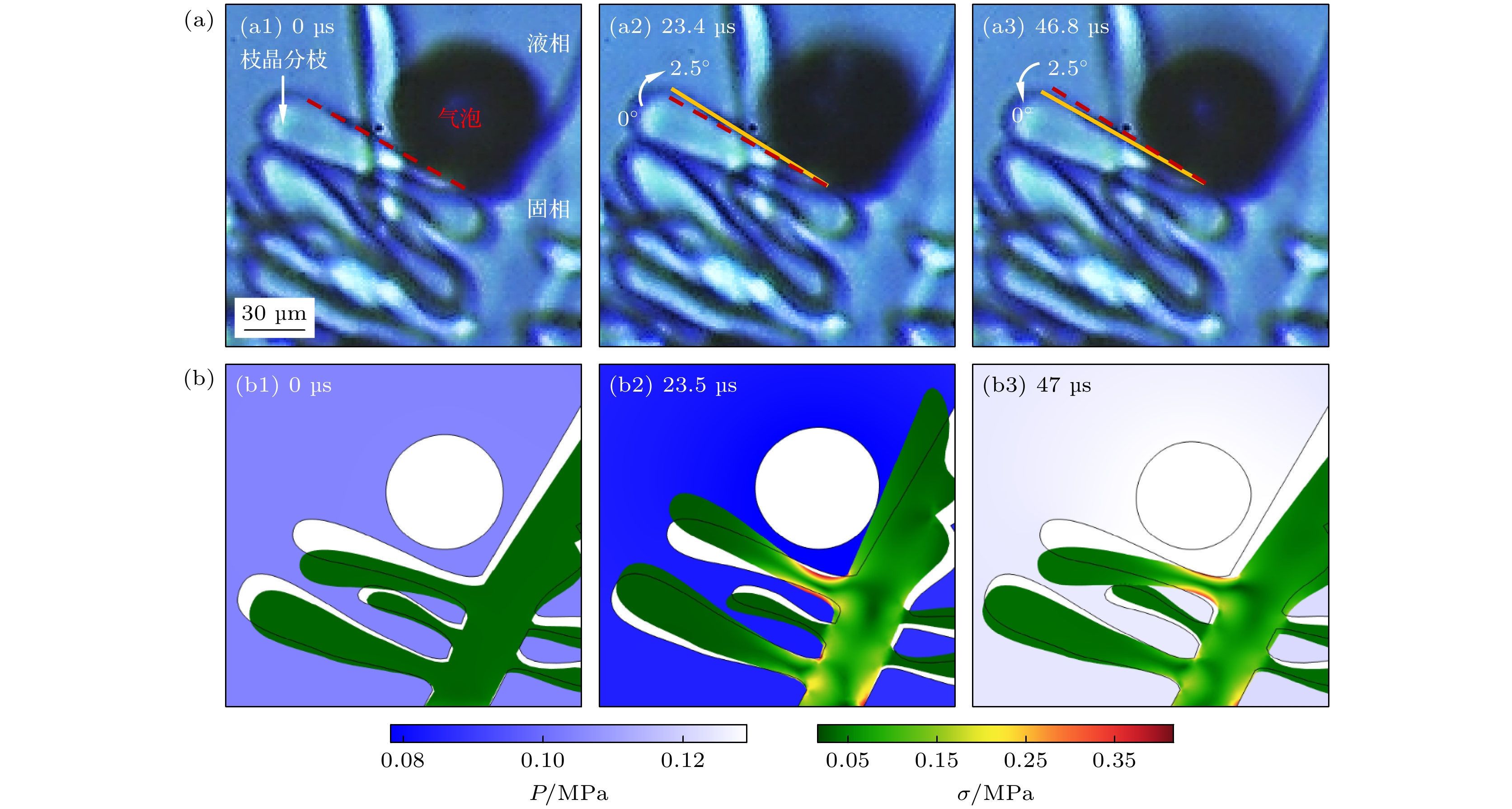
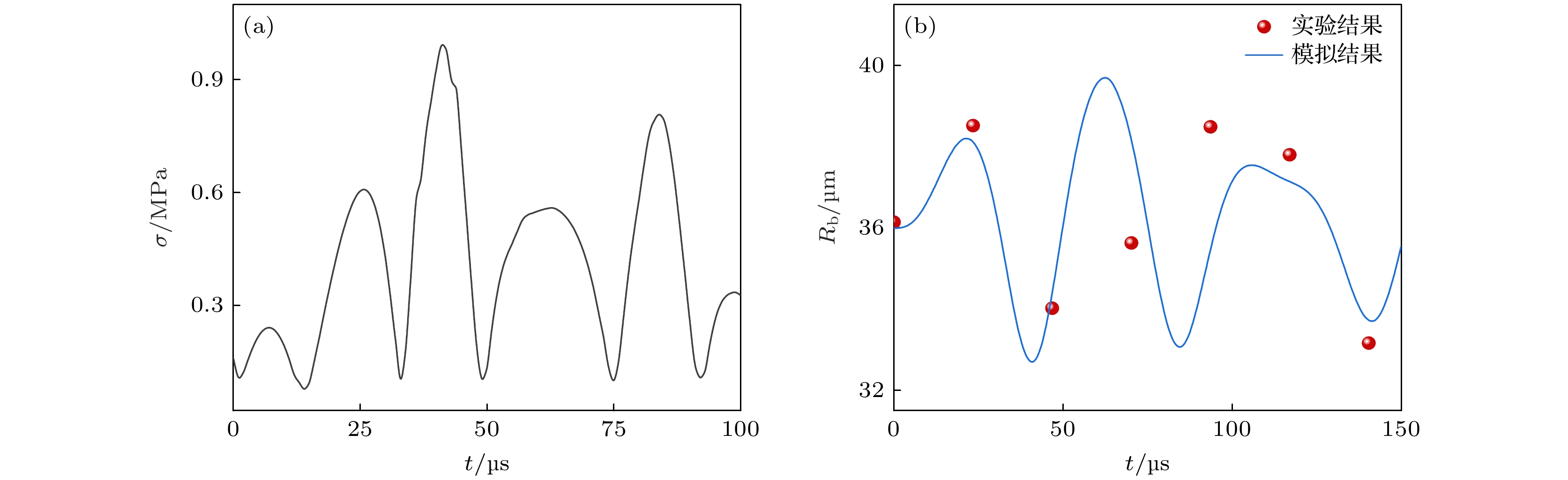
为了验证气泡与枝晶间动态相互作用模型的可行性, 将模拟与实验结果进行了对比(如图11 和 图12 所示). 实时观测结果如图11(a)所示, 可以发现初始状态下半径为 36.1 μm的气泡位于枝晶主干和二次分枝的夹角处, 部分气泡壁与主干和分枝相互接触. 黄色实线为分枝上边界当前时刻位置, 红色虚线为位置参考线, 并定义两条线间的夹角θ为二次分枝的弯曲角度. 23.4 μs时气泡半径约 38.8 μm, 气泡下方的二次分枝向上偏折约 2.5°, 由于枝晶的影响气泡形貌从球形向三角形偏离. 在 46.8 μs气泡半径约 33.5 μm且形貌恢复为近球形, 二次分枝向下偏折约 2.5°后恢复初始状态. 模拟结果中二次分枝以与超声气泡相同的频率上下弯曲, 在 0 和 47 μs时枝晶向下偏转, 23.5 μs时分枝向上偏转(图11(b)). 模拟与实验获得的二次分枝偏折状态及气泡的变化规律完全相符. 进一步数值模拟了气泡下方的枝晶二次分枝根部的应力分布, 如图12(a)所示. 应力在多个周期内始终低于断裂阈值, 因此其断裂模式主要为疲劳断裂. 在图12(b)中比较了实验和数值计算过程中多个周期内气泡半径随时间的变化规律. 存在枝晶的条件下, 数值模拟的气泡振荡规律仍与实时观测结果基本相符, 证明了本文构建的模型能够准确预测超声场中气泡与枝晶的相互作用过程. 然而, 数值模拟的气泡半径与实验测定的仍存在一定的数值误差, 主要由于以下两个因素导致: 一是实验中气泡的半径是通过多次测量拍摄结果并取平均值获得, 测量统计过程中存在偏差; 二是模拟过程中气泡初始半径以及施加超声振幅无法精确获得, 同时为了防止计算过程中网格畸变, 模型中气泡无法像实验一样完全接触枝晶.
-
以透明 SCN-2%H2O 溶液为研究对象, 通过构建有限元模型, 系统研究了超声作用下液体中气泡的径向脉动的运动规律及其与附近枝晶的相互作用, 并与实验结果对比, 主要得到以下结论:
1) 随着超声场驱动声压增大至空化阈值, 气泡由体积振荡转变为分裂振荡, 并在分裂瞬间产生高达16 MPa的压强和 160 m/s的射流.
2) 气泡体积振荡时, 枝晶二次分枝周期性上下弯折, 最大应力位于二次分枝根部, 达到屈服强度导致疲劳断裂. 而气泡分裂振荡时, 瞬态的高压和射流促使二次分枝在一个弯折周期内达到屈服强度并过载断裂. 二次分枝弯折周期与驱动声压符合幂函数关系.
3) 随着气泡与枝晶距离减小, 气泡收缩时纵向半径逐渐高于横向半径, 气泡溃灭产生的最大压强减小, 最大流速逐渐升高. 增加二次分枝臂长度或者减小根部半径均能够降低其疲劳断裂周期数, 从而引发枝晶碎断.
4) 数值模拟的气泡振荡及其对枝晶的动态偏转与实验结果基本一致, 表明本文构建的有限元模型能够准确预测气泡与枝晶的相互作用过程.
超声场中气泡运动规律及其与枝晶相互作用机制
Motion law of cavitation bubbles in ultrasonic field and mechanism of their interaction with dendrites
-
摘要:
采用有限元模拟和高速摄影实验研究了液体中单个气泡在超声作用下的振荡及溃灭规律, 并揭示了气泡空化与邻近枝晶间的相互作用机制. 结果表明, 增大驱动声压促使气泡振荡模式由体积振荡转变为分裂振荡, 从而显著地提升液体中的瞬态压强和流动速度. 当气泡下方存在一个枝晶时, 随着驱动声压的增加, 二次分枝的断裂模式发生从高周疲劳断裂向低周疲劳断裂再到过载断裂的转变, 且断裂周期呈幂函数下降趋势. 气泡距离枝晶越近, 压缩状态下气泡的纵向半径逐渐大于横向半径, 且压缩时间增加, 最小气泡体积降低. 另外, 气泡与枝晶距离的减小导致气泡溃灭产生的最大压强显著降低, 而最大流速呈现先增大后降低的趋势. 若二次分枝的根部半径减小或长度增加, 二次分枝疲劳断裂周期数显著减小, 从而更容易诱发枝晶碎断. 理论计算的气泡膨胀收缩和二次分枝断裂过程与实验结果基本一致, 表明本文构建的模型能够准确预测超声场中的气泡运动及其与枝晶相互作用过程.
Abstract:Ultrasound treatment (UST) has been demonstrated to be an effective approach to refining the microstructures of metallic alloys during solidification. The cavitation-induced fragmentation is considered as the major mechanism for grain refinement in the recent study, but the interaction between dynamic bubble motion and dendrite behaviour has been rarely investigated previously. In this work, the dynamic behaviour of cavitation bubbles and their interactions with succinonitrile (SCN)-2% (mole fraction) water organic transparent alloy are systematically investigated by high-speed digital image technique and numerical simulation. It is found that increasing the driving pressure transforms the bubble oscillation mode from volume oscillation to splitting oscillation, which significantly enhances the transient pressure and flow strength in the liquid. When a dendrite exists below the bubble, the fracture mode of the secondary branch undergoes a transition from high peripheral fatigue fracture to low peripheral fatigue fracture and to overload fracture with the increase of the driving acoustic pressure, and the fracture period is shortened in the form of a power function trend. The closer the bubble is to the dendrite, the longeritudinal radius of the bubble is gradually larger than the transverse radius during compression, and with the bubble shrink time increasing, the minimum bubble volume decreases. In addition, the decrease in distance between bubbles and dendrites leads to a significant reduction in the maximum pressure generated by bubble collapse, while the maximum flow rate shows a trend of first increasing and then decreasing. When the root radius of the secondary branch decreases or its length increases, the number of fatigue fracture cycles of the secondary branch decreases significantly. The calculated bubble expansion and contraction and secondary dendrite rupture processes are basically consistent with the experimental results, which indicates that the model constructed in this work can accurately predict the bubble motion and its interaction with dendrite in ultrasonic field.
-
Key words:
- power ultrasound /
- bubble dynamics /
- dendrite fragmentation /
- finite element simulation .
-
-
图 1 超声场中气泡振荡和溃灭模型的几何示意 (a) 单个气泡运动模型; (b) 气泡与枝晶间相互作用模型; 1, 变幅杆; 2, 气泡; 3, SCN-H2O溶液; 4, SCN枝晶
Figure 1. Geometrical schematic of the bubble oscillation and collapse model within the ultrasonic field: (a) Model of single bubble motion; (b) model of bubble-dendrite interaction; 1, horn; 2, bubble; 3, SCN-H2O solution; 4, SCN dendrite.
图 2 不同声压振幅条件下的气泡形貌和声场及流场分布 (a) Pa = 0.4PB; (b) Pa = PB
Figure 2. Bubble morphology and distributions of acoustic field and flow field with different ultrasonic amplitudes: (a) Pa = 0.4PB; (b) Pa = PB.
图 3 气泡动力学与超声振幅的相关性 (a) 气泡体积随时间的变化; (b) 最大声压及最大声流与声压振幅 Pa 的关系
Figure 3. Correlation between bubble dynamics and ultrasonic amplitude: (a) Bubble volume versus time; (b) maximum sound pressure and maximum sound flow versus sound pressure amplitude Pa.
图 4 声压幅值 0.4PB 时气泡振荡过程中二次分枝上应力分布 (a)二次分枝下表面应力分布; (b) 不同高度二次分枝根部应力
Figure 4. Stress distribution on the secondary branch during bubble oscillation at a sound pressure amplitude of 0.4PB: (a) Stress distribution on the lower surface of the secondary branch; (b) stress on the secondary branch root at different heights.
图 5 不同声压条件下二次分枝偏转角度随时间变化 (a) Pa = 0.4PB; (b) Pa = PB
Figure 5. Changes of the deflection angle of the secondary branch with time under different sound pressures: (a) Pa = 0.4PB; (b) Pa = PB.
图 6 不同声压条件下二次分枝断裂机制 (a) 0.4PB 和 PB 振幅下气泡内外压差; (b) 0.4PB 驱动声压下A点应力随时间的变化; (c) PB 驱动声压下 A 点应力随时间的变化; (d) 分枝断裂所需弯折周期随声压幅值 Pa 的变化
Figure 6. Mechanism of secondary branch breakage under different sound pressures: (a) Pressure difference between inside and outside the bubble at 0.4PB and PB; (b) variation of stress at point A with time at the ultrasonic amplitude of 0.4PB; (c) variation of stress at point A with time at the ultrasonic amplitude of PB; (d) variation of fragmentation cycle number with sound pressure amplitude Pa.
图 7 声压振幅 PB 条件下气泡体积及最大压强与枝晶距离的相关性 (a)—(c) 气泡顶部开始凹陷时刻的压强分布图; (d) 气泡体积随时间变化, 其中插图为气泡体积最小时的形貌; (e) 流体中最大压强随时间的变化规律
Figure 7. Correlation of bubble volume and maximum pressure with the distance of dendrites under acoustic pressure amplitude PB: (a)–(c) Pressure distributions at the moment when the top of the bubble starts to dimple; (d) variation of bubble volume with time, where the sugfigure shows the morphology of the bubble with the smallest volume; (e) evolution of the maximum pressure in the fluid with time.
图 8 Pa = PB 条件下间距h对气泡溃灭和二次分支断裂的作用规律 (a) 气泡溃灭在流体中产生的最大压强和流速; (b) 二次分枝上最大应力及其断裂所需时间的变化规律
Figure 8. Effect of distance h on the bubble collapse and secondary branch fragmentatio Pa = PB: (a) Maximum pressure and flow rate in the fluid produced by bubble collapse; (b) variation of the maximum stress on the secondary branch and fragmentation cycle number.
图 9 声压幅值 0.4PB 作用下二次分枝根部A点应力和断裂周期与其根部半径 r 和长度 L 的关系 (a) L = 100 μm 时A点应力随时间变化; (b) r = 3 μm时A点一个周期内的平均应力与 L 的相关性; (c) 断裂周期与 r 和 L 的关系
Figure 9. Relationship of the stress at point A and fragmentation cycle number to root radius r and length L of the secondary branch at Pa = 0.4PB: (a) Stress versus time for L = 100 μm; (b) correlation of the average stress over a cycle with L for r = 3 μm; (c) fragmentation cycle number versus r and L.
图 10 数值模拟与 K-M 方程计算的气泡体积随时间的变化 (a) R0 = 10 μm; (b) R0 = 50 μm
Figure 10. Comparison of the numerical results and K-M equation for volume oscillation: (a) R0 = 10 μm; (b) R0 = 50 μm.
图 11 超声作用下气泡与枝晶动态相互作用的实验观测和数值模拟对比 (a) 实验观测; (b) 数值模拟
Figure 11. Comparison of dynamic interaction between bubbles and dendrites by experimental observations and numerical simulation under ultrasound: (a) Experimental observations; (b) numerical simulation.
图 12 二次分枝根部应力和气泡形貌与时间的相关性 (a) 根部应力变化的模拟结果; (b) 气泡半径变化的实验验证
Figure 12. Correlation of secondary branch root stress and bubble morphology with time: (a) Simulation results of root stress variation; (b) experimental validation of bubble radius variation.
表 1 声场和流场计算所用物理量数值
Table 1. Values of physical parameters used in sound and flow field calculations.
下载: 导出CSV
-
[1] He L, Wu M, Li L, Hao H 2006 Appl. Phys. Lett. 89 131504 doi: 10.1063/1.2357857 [2] Huang H, Qin L, Tang H B, Shu D, Yan W T, Sun B D, Mi J W 2021 Ultrason. Sonochem. 80 105832 doi: 10.1016/j.ultsonch.2021.105832 [3] Wei X, Li X L, Zhang L Q, Lü Q G 2022 Int. J. Heat Mass Transfer 192 122914 doi: 10.1016/j.ijheatmasstransfer.2022.122914 [4] Wu W, Wang D, Zhai W, Wang J, Wei B 2023 J. Appl. Phys. 133 115102 doi: 10.1063/5.0135344 [5] Sander J R G, Zeiger B W, Suslick K S 2014 Ultrason. Sonochem. 21 1908 doi: 10.1016/j.ultsonch.2014.02.005 [6] Cui B, Chen K, Yang Y, Lü Y, Zhang F, Liu S 2024 Mater. Chem. Phys. 318 129297 doi: 10.1016/j.matchemphys.2024.129297 [7] Wang S, Kang J, Zhang X, Guo Z 2018 Ultrasonics 83 26 doi: 10.1016/j.ultras.2017.08.004 [8] Shu D, Sun B D, Mi J W, Grant P S 2012 Metall. Mater. Trans. A 43 3755 doi: 10.1007/s11661-012-1188-3 [9] Priyadarshi A, Khavari M, Subroto T, Conte M, Prentice P, Pericleous K, Eskin D, Durodola J, Tzanakis I J E 2021 Ultrason. Sonochem. 70 105260 doi: 10.1016/j.ultsonch.2020.105260 [10] Wang B, Tan D Y, Lee T L, Khong J C, Wang F, Eskin D, Connolley T, Fezzaa K, Mi J W 2018 Acta Mater. 144 505 doi: 10.1016/j.actamat.2017.10.067 [11] 马艳, 林书玉, 徐洁 2018 物 理学报 67 034301 doi: 10.7498/aps.67.20171573 Ma Y, Lin S Y, Xu J 2018 Acta Phys. Sin. 67 034301 doi: 10.7498/aps.67.20171573 [12] Qu W X, Xie Y H, Shen Y, Han J, Zhu T 2017 Math. Model. Eng. Probl. 4 173 doi: 10.18280/mmep.040406 [13] Lind S J, Phillips T N 2012 Theor. Comput. Fluid Dyn. 26 245 doi: 10.1007/s00162-011-0227-9 [14] Samiei E, Shams M, Ebrahimi R 2011 Eur. J. Mech. B. Fluids 30 41 doi: 10.1016/j.euromechflu.2010.09.002 [15] 吴学由, 梁金福 2021 物 理学 报 70 184301 doi: 10.7498/aps.70.20210513 Wu X Y, Liang J F 2021 Acta Phys. Sin. 70 184301 doi: 10.7498/aps.70.20210513 [16] Wang X J, Ning Z, Lü M, Yao J S, Sun C H 2022 J. Phys. Soc. Jpn 91 014401 doi: 10.7566/JPSJ.91.014401 [17] Cao S, Wang G, Coutier-Delgosha O, Wang K 2021 J. Fluid Mech. 907 A17 doi: 10.1017/jfm.2020.810 [18] Shan M L, Yang Y, Kan X F, Yin C, Han Q B 2024 Chin. Phys. B 33 064701 doi: 10.1088/1674-1056/ad3343 [19] 张颖, 吴文华, 王建元, 翟薇 2022 物理学报 71 244303 doi: 10.7498/aps.71.20221101 Zhang Y, Wu W H, Wang J Y, Zhai W 2022 Acta Phys. Sin. 71 244303 doi: 10.7498/aps.71.20221101 [20] Hosseinkhah N, Chen H, Matula T J, Burns P N, Hynynen K 2013 J. Acoust. Soc. Am. 134 1875 doi: 10.1121/1.4817843 [21] Delale C F, Pasinlioğlu Ş 2023 Phys. Fluids 35 023330 doi: 10.1063/5.0131921 [22] Zakerzadeh R, Zunino P 2018 Meccanica 54 101 doi: 10.1007/s11012-018-00932-x [23] 秦对, 邹青钦, 李章勇, 王伟, 万明习, 冯怡 2021 物理学报 70 154701 doi: 10.7498/aps.70.20210194 Qian D, Zhou Q Q, Li Z Y, Wang W, Wan M X, Feng Y 2021 Acta Phys. Sin. 70 154701 doi: 10.7498/aps.70.20210194 [24] Wang S, Guo Z P, Zhang X P, Zhang A, Kang J W 2019 Ultrason. Sonochem. 51 160 doi: 10.1016/j.ultsonch.2018.10.031 [25] Murakami K, Yamakawa Y, Zhao J, Johnsen E, Ando K 2021 J. Fluid Mech. 924 A38 doi: 10.1017/jfm.2021.644 [26] Chen X S, Bayanheshig, Jiao Q B, Tan X, Wang W 2021 Int. J. Heat Mass Transfer 171 121074 doi: 10.1016/j.ijheatmasstransfer.2021.121074 [27] Wang S, Kang J, Guo Z P, Lee T L, Mi J W 2018 Acta Mater. 165 388 doi: 10.1016/j.actamat.2018.11.053 [28] Wu W H, Wang J Y, Zhai W, Wei B B 2023 Metall. Mater. Trans. B 54 1845 doi: 10.1007/s11663-023-02799-0 -
计量
- 文章访问数: 555
- HTML全文浏览数: 555
- PDF下载数: 8
- 施引文献: 0