高级搜索

Ti-2.5Al-2Zr-1Fe在慢应变速率下的氢脆行为与机理研究

,  ,  ,  ,  ,  ,  ,  ,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

赵有鹏, 刘晓勇, 刘辉, 房坤, 王佳, 罗先甫, 徐宁, 孙绪鲁, 刘煜, 高宇昊, 吴泽鹏, 李雪峰, 张欣耀. Ti-2.5Al-2Zr-1Fe在慢应变速率下的氢脆行为与机理研究[J]. 物理学报, 2024, 73(21): 216103-1. doi: 10.7498/aps.73.20240896
引用本文: 赵有鹏, 刘晓勇, 刘辉, 房坤, 王佳, 罗先甫, 徐宁, 孙绪鲁, 刘煜, 高宇昊, 吴泽鹏, 李雪峰, 张欣耀. Ti-2.5Al-2Zr-1Fe在慢应变速率下的氢脆行为与机理研究[J]. 物理学报, 2024, 73(21): 216103-1. doi: 10.7498/aps.73.20240896
shu
You-Peng Zhao, Xiao-Yong Liu, Hui Liu, Kun Fang, Jia Wang, Xian-Fu Luo, Ning Xu, Xu-Lu Sun, Yu Liu, Yu-Hao Gao, Ze-Peng Wu, Xue-Feng Li, Xin-Yao Zhang. Study of hydrogen embrittlement behavior and mechanism of Ti-2.5Al-2Zr-1Fe by slow strain rate method[J]. Acta Physica Sinica, 2024, 73(21): 216103-1. doi: 10.7498/aps.73.20240896
Citation: You-Peng Zhao, Xiao-Yong Liu, Hui Liu, Kun Fang, Jia Wang, Xian-Fu Luo, Ning Xu, Xu-Lu Sun, Yu Liu, Yu-Hao Gao, Ze-Peng Wu, Xue-Feng Li, Xin-Yao Zhang. Study of hydrogen embrittlement behavior and mechanism of Ti-2.5Al-2Zr-1Fe by slow strain rate method[J]. Acta Physica Sinica, 2024, 73(21): 216103-1. doi: 10.7498/aps.73.20240896
shu

Ti-2.5Al-2Zr-1Fe在慢应变速率下的氢脆行为与机理研究

  • 洛阳船舶材料研究所, 海洋腐蚀与防护全国重点实验室, 洛阳　471023

    • 作者简介: 赵有鹏: pyz99912@163.com .
    通讯作者: E-mail: liuxiaoyongsjtu@163.com.; 

  • 中图分类号: 61.82.Bg, 88.30.Nn, 71.70.Fk, 62.20.M-

Study of hydrogen embrittlement behavior and mechanism of Ti-2.5Al-2Zr-1Fe by slow strain rate method

  • National Key Laboratory of Marine Corrosion and Protection, Luoyang Ship Material Research Institute, Luoyang 471023, China

    • Corresponding author: E-mail: liuxiaoyongsjtu@163.com.; 

  • MSC: 61.82.Bg, 88.30.Nn, 71.70.Fk, 62.20.M-

  • 摘要: 通过慢拉伸、恒位移等加载方法, 评估了含氢Ti-2.5A1-2Zr-1Fe合金的力学性能衰减行为及氢脆敏感性的变化. 利用扫描电子显微镜对断口微观形貌特征进行了分析, 并采用二次离子质谱仪对氢的宏观分布进行了表征, 揭示了断口脆性区域与氢宏观分布之间的内在联系. 此外, 结合位错载氢运动模型及扩散方程, 探讨了氢的扩散机制以及慢应变速率对氢扩散过程产生的影响. 为了进一步探索氢化物的存在性, 利用透射电子显微镜对表面高氢浓度层和裂纹尖端及其附近物相进行了表征分析, 最终未发现氢化物相的析出, 综合上述实验数据和微观物相结构分析, 对Ti-2.5Al-2Zr-1Fe合金的氢脆机制进行了探讨, 认为该合金的氢脆机制由HEDE机制主导.
    Abstract: The Ti-2.5Al-2Zr-1Fe used as hull structural material, is susceptible to hydrogen embrittlement induced by corrosion and hydrogen evolution in marine environments. Considering the long-term service of ships, the hydrogen embrittlement behavior under slow strain rate is crucial for evaluating the alloy’s service performance and ensuring long-term ship structural safety. In order to investigate the hydrogen embrittlement mechanism of Ti-2.5Al-2Zr-1Fe alloy under slow strain rate conditions, this study combines slow tension and constant displacement loading techniques to systematically evaluate the attenuation of mechanical properties and the dynamic changes in hydrogen embrittlement sensitivity of hydrogen-containing Ti-2.5Al-2Zr-1Fe alloy. Employing scanning electron microscopy (SEM), we thoroughly analyze the microstructural features of fracture surfaces. Meanwhile, the close correlation between the brittle zone at the fracture site and the macroscopic distribution of hydrogen atoms is elucidated by using secondary ion mass spectrometry (SIMS). Additionally, theoretical analysis based on diffusion equations reveals a notable increase in hydrogen diffusion distance within the Ti-2.5Al-2Zr-1Fe alloy as hydrogen charging time increases. Further, using the dislocation-hydrogen interaction model, we derive a critical strain rate threshold $ {\varepsilon _0} = {{\left( {30RT} \right)} {/ } {\left( {\rho DE} \right)}} $ for dislocation-mediated hydrogen transport in titanium alloys. When the externally applied strain rate ε falls below this threshold, dislocations efficiently capture and transport hydrogen atoms, enhancing hydrogen diffusion depth and significantly augmenting the alloy’s hydrogen embrittlement sensitivity, thereby accelerating material embrittlement. The Vickers-hardness (HV) test further elucidates the dual nature of hydrogen’s influence on titanium alloy properties: although moderate hydrogen content slightly enhances surface hardness, exceeding a specific threshold leads to a major negative influence on plasticity, far exceeding the benefits of surface hardening, resulting in a substantial decline in overall mechanical performance. To comprehensively decipher the hydrogen embrittlement mechanism of Ti-2.5Al-2Zr-1Fe alloy, transmission electron microscopy (TEM) is employed to analyze the phase composition in regions of high hydrogen concentration, crack tips, and their vicinities. The analysis results indicate that no direct precipitation of hydrides is observed; instead, hydrogen atoms preferentially accumulate in the β-phase, prompting microcrack propagation along β-phase boundaries. According to the aforementioned experimental data and microstructural analysis, we propose that the hydrogen embrittlement mechanism in Ti-2.5Al-2Zr-1Fe alloy is primarily governed by the HEDE mechanism. Furthermore, when the strain rate falls below ε0, it synergizes with the dislocation-mediated hydrogen transport mechanism, vastly expanding the influence scope of the HEDE mechanism and exacerbating the alloy’s hydrogen embrittlement sensitivity.
  • 加载中

  • 图 1  Ti-2.5Al-2Zr-1Fe微观组织图

    Figure 1.  Microstructures of the Ti-2.5Al-2Zr-1Fe plate used in this work.

    下载: 全尺寸图片 幻灯片

    图 2  圆棒拉伸试样尺寸（单位为 mm）

    Figure 2.  Dimensions of tensile specimen used in this work (unit: mm).

    下载: 全尺寸图片 幻灯片

    图 3  WOL试样尺寸图(单位为 mm)

    Figure 3.  Dimensions of WOL sample used in this work (unit: mm).

    下载: 全尺寸图片 幻灯片

    图 4  聚焦离子束(FIB)制取TEM试样过程示意图

    Figure 4.  Process of preparing TEM samples by focused ion beam (FIB) used in this work.

    下载: 全尺寸图片 幻灯片

    图 5  取测氢试样的取样示意图

    Figure 5.  Schematic diagram of the sampling of H content test

    下载: 全尺寸图片 幻灯片

    图 6  不同充氢时间下的拉伸曲线　(a) 常规拉伸; (b) 慢应变拉伸

    Figure 6.  Tensile stress-strain curves of the differently charged samples: (a) Conventional tensile test; (b) slow strain tensile test

    下载: 全尺寸图片 幻灯片

    图 7  两种应变速率下性能变化　(a) 断面收缩率; (b) 延伸率; (c) 抗拉强度

    Figure 7.  Variation curves of mechanical properties of samples at different strain rates: (a) Reduction of area; (b) percentage elongation; (c) tensile strength.

    下载: 全尺寸图片 幻灯片

    图 8  两种应变速率下的氢脆敏感性变化

    Figure 8.  Variation curves of hydrogen embrittlement sensitivity at different strain rates.

    下载: 全尺寸图片 幻灯片

    图 9  常规拉伸试样断口的宏观和微观形貌图　(a), (b), (c) 0 h常规拉伸试样; (d), (e), (f) 8 h常规拉伸试样

    Figure 9.  Macroscopic and microscopic morphology of fracture surface in the conventional tensile test: (a), (b), (c) The 0 h conventional tensile sample; (d), (e), (f) the 8 h conventional tensile sample.

    下载: 全尺寸图片 幻灯片

    图 10  慢拉伸试样断口的宏观和微观形貌图　(a), (b), (c) 0 h慢拉伸试样; (d), (e), (f) 8 h慢拉伸试样

    Figure 10.  Macroscopic and microscopic morphology of fracture surface in the slow tensile test: (a), (b), (c) The 0 h slow tensile sample; (d), (e), (f) the 8 h slow tensile sample.

    下载: 全尺寸图片 幻灯片

    图 11  不同充氢时间下试样断口的宏观形貌图　(a)—(d) 24—264 h的常规拉伸试样; (e)—(h) 24—264 h的慢拉伸试样

    Figure 11.  Macroscopic morphology of the fracture surface of the differently charged samples: (a)–(d) The conventional tensile samples are 24–264 h; (e)–(h) the slow tensile samples are 24–264 h.

    下载: 全尺寸图片 幻灯片

    图 12  试样表面硬度随充氢时间的变化

    Figure 12.  Variation of surface hardness of specimen with charging time.

    下载: 全尺寸图片 幻灯片

    图 13  二次离子质谱分析结果　(a)氘的分布; (b)铝的分布

    Figure 13.  The SIMS analysis results of Ti-2.5A1-2Zr-1Fe alloy: (a) Distribution of deuterium; (b) distribution of aluminum.

    下载: 全尺寸图片 幻灯片

    图 14  不同温度下氢分布情况

    Figure 14.  Distribution of hydrogen at different temperatures.

    下载: 全尺寸图片 幻灯片

    图 15  充氢48 h WOL试样的断口宏观形貌

    Figure 15.  Macro-morphology of fracture surface of WOL sample in constant displacement experiment after pre-cracking after 48 hours of charging.

    下载: 全尺寸图片 幻灯片

    图 16  (a) 充氢48 h WOL试样断口TEM形貌; (b) A区域的SAED图样; (c) B区域的SAED图样

    Figure 16.  (a) The TEM morphology of fracture surface of WOL sample charged with hydrogen for 48 h; (b) the SAED pattern in area A; (c) the SAED pattern in area B.

    下载: 全尺寸图片 幻灯片

    图 17  Ti-2.5Al-2Zr-1Fe合金不同充氢时间下氢扩散深度理论值

    Figure 17.  Theoretical values of hydrogen diffusion depth of Ti-2.5A1-2Zr-1Fe alloy at different charging time.

    下载: 全尺寸图片 幻灯片

    图 18  载氢位错与相界交互行为及其机制示意图

    Figure 18.  Schematic Diagram of the interaction behavior and mechanism between hydrogen-loaded dislocations and phase boundaries.

    下载: 全尺寸图片 幻灯片

    表 1  二次离子质谱测试参数

    Table 1.  Parameters of SIMS testing.

    入射能量/keV 入射角/(°) 电流强度/pA 扫描面积/m2 极性及质量范围/amu
    30 45 1.142 500×500 负离子模式 0—227
    下载: 导出CSV
  • [1] 杨锐, 马英杰, 雷家峰, 胡青苗, 黄森森 2021 金属学报 57 1455 doi: 10.11900/0412.1961.2021.00353 Yang R, Ma Y J, Lei J F, Hu Q M, Huang S S 2021 Acta Metall. Sin. 57 1455 doi: 10.11900/0412.1961.2021.00353
    [2] 何燕, 周刚, 刘艳侠, 王皞, 徐东生, 杨锐 2018 物理学报 67 050203 doi: 10.7498/aps.67.20171670 He Y, Zhou G, Liu Y X, Wang H, Xu D S, Yang R 2018 Acta. Phys. Sin. 67 050203 doi: 10.7498/aps.67.20171670
    [3] 吴明宇, 弭光宝, 李培杰 2024 物理学报 73 086103 doi: 10.7498/aps.73.20240003 Wu M Y, Mi G B, Li P J 2024 Acta. Phys. Sin. 73 086103 doi: 10.7498/aps.73.20240003
    [4] 丁智松, 高巍, 魏敬鹏, 金耀华, 赵晨, 杨巍 2022 物理学报 71 028102 doi: 10.7498/aps.71.20210835 Ding Z S, Gao W, Wei J P, Jin Y H, Zhao C, Yang W 2022 Acta. Phys. Sin. 71 028102 doi: 10.7498/aps.71.20210835
    [5] Robertson I M, Sofronis P, Nagao A 2015 Metall. Mater. Trans. A 46 2323 doi: 10.1007/s11661-015-2836-1
    [6] Venezuela J, Zhou Q J, Liu Q L 2018 Mater. Today Commun. 17 1 doi: 10.1016/j.mtcomm.2018.07.011
    [7] Olden V, Thaulow C, Johnsen R 2008 Mater. Des. 29 1934 doi: 10.1016/j.matdes.2008.04.026
    [8] Lynch S P 2007 NACE International Corrosion Conference Nashville, Tennessee, March, 2007 p07493
    [9] Wang X, Zhu R T, Li C Y, Wang X, Huang P F 2020 Rare Met. Mater. Eng. 49 3769
    [10] Zhang S Q, Wan J F, Zhao Q Y 2020 Corros. Sci 164 108345 doi: 10.1016/j.corsci.2019.108345
    [11] Xu Y L, Li L T 2021 Mater. Res. Express 8 046531 doi: 10.1088/2053-1591/abf8e7
    [12] 汪洋, 吴冰, 宿彦京, 邢焰, 王向轲, 高鸿, 李岩 2020 有色金属工程 10 33 doi: 10.3969/j.issn.2095-1744.2020.05.007 Wang Y, Wu B, Su Y J, Xing Y, Wang X K, Gao H, Li Y 2020 Nonferrous Met. Eng. 10 33 doi: 10.3969/j.issn.2095-1744.2020.05.007
    [13] Sun Z G, Hou H L 2008 J. Alloys Compd. 476 550 doi: 10.1016/j.jallcom.2008.09.054
    [14] Liu X Y, Wang J, Gao L Q 2021 J. Alloys Compd. 862 158669 doi: 10.1016/j.jallcom.2021.158669
    [15] Tien J, Thompson A W, Bernstein I M 1976 Metall. Trans. A 7 821 doi: 10.1007/BF02644079
    [16] 吴明宇, 弭光宝, 李培杰, 黄旭 2023 物理学报 72 166102 doi: 10.7498/aps.72.20230396 Wu M Y, Mi G B, Li P J, Huang X 2023 Acta Phys. Sin. 72 166102 doi: 10.7498/aps.72.20230396
    [17] 周伟, 姚泽坤, 谭立军, 郭鸿镇, 张建伟, 梁晓波 2011 稀有金属材料与工程 40 1230 Zhou W, Yao Z K, Tan L J, Guo H Z, Zhang J W, Liang X B 2011 Rare Met. Mater. Eng. 40 1230
    [18] 赵晓丽, 张永健, 邵成伟, 惠卫军, 董瀚 2018 金属学报 54 1031 doi: 10.11900/0412.1961.2017.00435 Zhao X L, Zhang Y J, Shao C W, Hui W J, Dong H 2018 Acta Metall. Sin. 54 1031 doi: 10.11900/0412.1961.2017.00435
    [19] 张滨, 郑华, 刘实, 王隆保 2005 原子能科学技术 39 522 doi: 10.3969/j.issn.1000-6931.2005.06.011 Zhang B, Zheng H, Liu S, Wang L B 2005 At. Energy Sci. Technol. 39 522 doi: 10.3969/j.issn.1000-6931.2005.06.011
    [20] Chen C Q, Li S X, Lu K 2003 Acta Mater. 51 931 doi: 10.1016/S1359-6454(02)00495-0
    [21] 王艳飞, 巩建鸣, 蒋文春, 姜勇, 唐建群 2011 金属学报 47 594 Wang Y F, Gong J M, Jiang W C, Jiang Y, Tang J Q 2011 Acta Metall. Sin. 47 594
    [22] 刘战伟 2009 桂林电子科技大学学报 29 108 doi: 10.3969/j.issn.1673-808X.2009.02.008 Liu Z W 2009 J. Guilin Univ. Electron. Technol. 29 108 doi: 10.3969/j.issn.1673-808X.2009.02.008
    [23] 孙志杰, 王洋 2020 材料开发与应用 35 94 Sun Z J, Wang Y 2020 Dev. Appl. Mater. 35 94
    [24] 刘晓镇, 韩恩厚, 宋影伟 2023 中国有色金属学报 33 307 doi: 10.11817/j.ysxb.1004.0609.2021-42682 Liu X Z, Han E H, Song Y W 2023 Chin. J. Nonferrous Met. 33 307 doi: 10.11817/j.ysxb.1004.0609.2021-42682
    [25] 王秀英, 孙力玲, 刘日平, 姚玉书, 张君, 王文魁 2004 物理学报 53 3845 doi: 10.3321/j.issn:1000-3290.2004.11.041 Wang X Y, Sun L L, Liu R P, Yao Y S, Zhang J, Wang W K 2004 Acta Phys. Sin. 53 3845 doi: 10.3321/j.issn:1000-3290.2004.11.041
    [26] 孙永伟, 陈继志, 刘军 2015 金属学报 51 1315 Sun Y W, Chen J Z, Liu J 2015 Acta Metall. Sin. 51 1315
    [27] 李洪佳, 孙光爱, 龚建, 陈波, 王虹, 李建, 庞蓓蓓, 张莹, 彭述明 2014 物理学报 63 236101 doi: 10.7498/aps.63.236101 Li H J, Sun G A, Gong J, Chen B, Wang H, Li J, Pang B B, Zhang Y, Peng S M 2014 Acta Phys. Sin. 63 236101 doi: 10.7498/aps.63.236101
    [28] Kan B, Wu W J, Yang Z X, Li J X 2020 Mater. Sci. Eng. A 775 138963 doi: 10.1016/j.msea.2020.138963
    [29] Wang M Q, Akiyama E, Tsuzaki K 2007 Corros. Sci. 49 4081 doi: 10.1016/j.corsci.2007.03.038
    [30] 王贞, 刘静, 张施琦, 黄峰 2022 中国腐蚀与防护学报 42 106 doi: 10.11902/1005.4537.2020.259 Wang Z, Liu J, Zhang S Q, Huang F 2022 J. Chin. Soc. Corros. Prot. 42 106 doi: 10.11902/1005.4537.2020.259
  • 加载中
图( 18) 表( 1)
计量
  • 文章访问数:  209
  • HTML全文浏览数:  209
  • PDF下载数:  3
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-06-28
  • 刊出日期:  2024-11-05

Ti-2.5Al-2Zr-1Fe在慢应变速率下的氢脆行为与机理研究

    通讯作者: E-mail: liuxiaoyongsjtu@163.com.; 
    作者简介: 赵有鹏: pyz99912@163.com
  • 洛阳船舶材料研究所, 海洋腐蚀与防护全国重点实验室, 洛阳　471023
  • 收稿日期:  2024-06-28

摘要: 通过慢拉伸、恒位移等加载方法, 评估了含氢Ti-2.5A1-2Zr-1Fe合金的力学性能衰减行为及氢脆敏感性的变化. 利用扫描电子显微镜对断口微观形貌特征进行了分析, 并采用二次离子质谱仪对氢的宏观分布进行了表征, 揭示了断口脆性区域与氢宏观分布之间的内在联系. 此外, 结合位错载氢运动模型及扩散方程, 探讨了氢的扩散机制以及慢应变速率对氢扩散过程产生的影响. 为了进一步探索氢化物的存在性, 利用透射电子显微镜对表面高氢浓度层和裂纹尖端及其附近物相进行了表征分析, 最终未发现氢化物相的析出, 综合上述实验数据和微观物相结构分析, 对Ti-2.5Al-2Zr-1Fe合金的氢脆机制进行了探讨, 认为该合金的氢脆机制由HEDE机制主导.

English Abstract

    全文HTML

    1.   引　言

    • 钛合金具有比强度高、耐腐蚀以及生物相容性好等特点, 被广泛应用于航空、航天、船舶、兵器、化工以及医疗等领域[1–4]. 然而, 钛与氢具有较高的亲和力, 在钛合金的加工、酸洗、焊接以及析氢环境服役过程中可能发生吸氢导致氢含量升高, 氢含量达到一定阈值会引发材料塑性显著降低, 进而造成氢致开裂事故的发生[5,6].

      因而, 自上世纪起, 国内外研究者对合金中的氢脆现象进行了广泛深入的探究, 提出了多种致脆机理, 包括弱键理论[7](HEDE)、氢诱导位错发射理论[8](AIDE)、应力诱导氢化物滞后开裂理论[9]以及氢致局部塑性增强理论[10](HELP)等. 目前, 这些理论虽未对所有材料中的氢脆现象形成统一的解释, 但研究者普遍认为氢脆的发生需要一定的孕育时间, 原因在于氢在材料中的扩散、聚集直至引发开裂是一个依赖于持久应力作用、浓度梯度等因素的缓慢过程. 因此, 近年来针对α钛与α+β钛合金的慢应变速率或恒载荷等长周期试验下的氢脆行为与机理研究得到了广泛关注. 例如, Xu和Li[11]在对Ti-6321合金的慢拉伸性能研究中发现, 当氢含量较低(65 μg/g)时, 氢的引入促进了位错的运动和孪晶的形核, 这种影响使得材料在局部区域 展现出更高的塑性, 但同时也增加了氢脆的风险. Ti-6Al-4V的慢拉伸实验研究表明[12], 材料塑性随氢含量升高而降低, 这是因为氢在钛合金中的扩散速率较低, 导致其会在钛合金表面区域聚集, 进而产生氢化物, 造成裂纹萌生、扩展, 引发氢致开裂. 与上述研究不同的是, 冲击等实验在研究α钛与α+β钛合金性能时, 由于实验周期过短, 其研究结果主要局限于反映氢对现有物相产生影响进而促进其裂纹的萌生与扩展行为, 未能深入地探讨位错等缺陷与氢化物形成过程对钛合金的氢致开裂行为产生的内在影响. 以对Ti-6Al-4V氢脆研究为例, 其冲击韧性的降低[13]归因于马氏体相与β相的减少, 进而促进了材料中裂纹的萌生与扩展, 研究中并未观察到氢化物的形成, 这可能与冲击实验周期过短密切相关. 此外, 在Ti-2.5Al-2Zr-1Fe合金的冲击实验[14]中同样未观察到氢化物的析出, 其氢致脆机理主要源于氢在β相中的选择性溶解, 削弱了原子间的键合力, 从而导致材料在冲击载荷下出现显著的塑性损失. 以上研究表明, 慢拉伸等长周期试验能够更好地反映出氢对晶体内部位错行为与物相变化的影响, 从而推测出氢在材料内部扩散、聚集直至引发开裂的过程, 与实际服役环境中氢脆现象更为契合. 相比之下, 冲击等短周期实验由于其时间限制, 没有足够的孕育期, 对氢在材料内部聚集、致脆的内在影响难以反映, 这种局限性使得短周期实验在揭示氢脆机制方面存在一定的不足. 另外, 在钛合金实际服役中, 氢的分布往往是不均匀的, 但目前的研究主要聚焦于氢含量与钛合金力学性能的关系, 而针对氢分布状态对氢脆行为及其内在机制的影响尚缺乏详尽与深入的探索. 由于氢的分布状态对氢脆敏感性具有显著影响, 因此, 对于慢应变速率下氢的分布变化导致的氢脆行为及机理研究尤为重要.

      为了进一步探究钛合金氢脆的滞后性及长期影响, 本研究采用了一系列实验手段. 选定Ti-2.5Al-2Zr-1Fe合金为研究对象, 该合金作为我国自主研发的船用中高强度钛合金, 广泛应用于船体结构等关键领域, 其在海洋环境中服役时, 不可避免地会面临腐蚀析氢等诱发氢脆的敏感条件. 前期的研究已揭示, 在充氢条件下, 该合金的冲击韧性出现显著的下降[14]. 然而, 鉴于船舶的长周期服役特性, 慢应变速率下的氢脆行为更能真实反映合金在服役过程中的表现, 对于提升船舶结构的长期安全可靠性具有更为深远的意义. 因此, 本研究重点集中于探讨Ti-2.5Al-2Zr-1Fe合金在慢应变速率条件下的氢脆机制. 通过在不同应变速率下进行拉伸试验, 对比分析了不同氢含量对钛合金力学性能的影响规律; 利用扫描电子显微镜(scanning electron microscope, SEM)观察了在不同拉伸速率下氢含量的变化对钛合金致脆行为的影响规律及其断口特征; 通过维氏硬度测量(Vickers-hardness, HV), 评估了氢宏观分布对表面硬度的影响; 采用位错载氢运动模型[15]分析了氢在不同应变速率下的致脆行为差异; 采用二次离子质谱(secondary ion mass spectrometry, SIMS)表征了氢的宏观分布, 并通过氢分布与慢拉伸及常规拉伸断口形貌分布的关联性分析了氢在材料中分布对致脆行为的影响, 借助透射电子显微镜(transmission electron microscope, TEM)观察了氢在Ti-2.5Al-2Zr-1Fe合金中的存在形式并分析了其致脆机制. 在上述试验研究的基础上, 我们深入讨论了氢在Ti-2.5Al-2Zr-1Fe合金材料中的分布、存在形式以及其在材料中聚集、孕育和致脆的内在机制. 本研究旨在为深入理解钛合金氢脆的滞后性以及制定有效的防控措施提供理论依据.

    2.   实验材料与方法

      2.1.   实验材料

    • 实验选用10 mm厚Ti-2.5Al-2Zr-1Fe轧制板材, 其沿厚度、轧制方向的三维微观组织如图1所示. Ti-2.5Al-2Zr-1Fe合金由α, β相两个基本物相组成, 它们的晶体结构分别为HCP与BCC[1], α相占比约95.9%, β相占比约4.1%, 并且β相沿α相界周围分布[14].

      • 2.2.   充氢实验方法

    • 由电源提供稳定的直流电流, 采用电化学方法进行充氢, 试样作阴极, 碳棒作阳极, 电流密度为10 mA/cm2, 电解质为5% (质量分数)的稀硫酸溶液.

      • 2.3.   常规拉伸实验与慢拉伸实验

    • 常规拉伸性能测试参照GBT 228.1-2010《金属材料拉伸试验第1部分: 室温试验方法》进行, 所需的试样尺寸如图2所示.

      采用INSTRON 5928型电子万能材料试验机对充氢后试样进行常规拉伸试验, 试验过程中弹性阶段与屈服阶段的应变速率均为0.00025 m/s, 拉伸阶段的应变速率为0.0067 m/s. 由于氢含量检测需要在试样拉断后进行, 这可能导致氢的逸出, 造成实验误差, 因此我们选用充氢时间作为衡量氢含量变化的参数.

      慢拉伸试验参照GB/T 15970.7-2017《金属和合金的腐蚀应力腐蚀试验第7部分: 慢应变速率试验》进行. 为便于与常规拉伸试验进行直观对比, 选取与常规拉伸试验相同尺寸的试样, 如图2所示. 慢拉伸速率为6.4×10–9 m/s, 将试样安装在MFDL-100慢拉伸应力腐蚀试验机上, 空气温度范围(25±2) ℃, 湿度范围30%—50%.

      • 2.4.   预裂纹恒位移加载试验

    • 预裂纹恒位移加载试验采用楔形张开加载(wedge opening load, WOL)试样, 尺寸如图3所示, 实验前先在MTS370-250 kN电液伺服疲劳试验机上预制裂纹, 试样预制裂纹参数为: 最后阶段最大应力强度因子Kfmax = 22.0 MPa·m1/2, 试验频率f = 8 Hz, 试验波形为正弦波, 循环次数N = 10000—13000次. 随后充氢96 h, 借助装在试样一个臂上的加载螺栓, 顶住另一个臂上的垫块进行恒位移加载, 通过COD规测量裂纹嘴张开位移, 用柔度法计算裂纹尖端K值, 最终加载K值为0.75KIC.

      试验环境为空气, 试验温度(25±2) ℃ , 试验时间30 d, 到期后将试样卸载, 清洗后将试样拉开, 用扫描电子显微镜观察试样断口形貌和脆性区裂纹扩展情况, 用透射电子显微镜观察试样微观形貌, 进一步分析钛合金脆性裂纹区域氢的存在形式.

      • 2.5.   TEM制样与物相组织标定

    • 采用透射电子显微镜(TEM)对2.4节中预裂纹恒位移加载试验后的WOL试样裂尖处进行观察, 随后对裂尖周围物相进行衍射标定以确认该物相的种类. 由于传统的电解双喷制样方法使用的HClO4会引入氢化物[14], 干扰实验结果, 因此选用了聚焦离子束技术(focus ion beam, FIB)制备TEM的观察试样来降低物相标定结果的误差[16]. 具体实验方法: 首先, 在SEM监控下找到裂尖区域, 并在该区域上沉积一层Pt薄膜作为切割区域的标记, 如图4(a)和图4(b); 随后采用Ga离子源轰击标记区域的四周, 直到溅射出足以让机械臂取出目标区域试样的空间, 如图4(c); 将纳米机械臂贴于待切区域边缘, 向该区域沉积一层Pt使机械手和待拾取的样品连接起来, 如图4(d); 翻转样品台使样品侧面正对离子源, 进行离子束切割, 直至薄片状样品从基体上分离出来; 移动纳米机械手将拾取的样品黏接在微型样品托上, 再喷一层Pt, 使样品和样品托连接起来, 如图4(e); 对样品进行减薄处理, 直至厚度小于100 nm, 以满足观察需要, 对样品进行离子束清洗、抛光, 以提升TEM观察的质量, 最终得到的样品见图4(f).

      • 2.6.   氢随扩散深度的分布情况测试

    • 为测定氢随扩散深度的浓度分布情况, 本研究沿垂直于试样的板厚方向, 即厚度方向, 连续取样, 将规格为120 mm×50 mm×10 mm的板材充氢96 h后, 沿厚度方向取一系列大小相同的试样, 此处试样的大小为2 mm×2 mm×2 mm, 沿板厚方向的取样方法如图5所示, 在10 mm厚的试样上由上表面至下表面每下降1 mm取一个测氢试样. 随后将样品通过ONH836气体分析仪进行氢含量测定, 得到氢在材料厚度方向, 从上表面至下表面不同位置氢浓度分布情况.

      为消除酸洗、磨抛等处理过程中可能引入的氢对实验结果的干扰, 依照2.2节中充氢方法, 采用D2O (H2O质量分数≤0.01%)与D2SO4 (D质量分数≥99.5%)配置的5%(质量分数)氘代硫酸溶液充当电解质, 对试样进行48 h的充氢处理, 随后在室温下静置30 d后, 对D进行二次离子质谱表征(SIMS), 与式样制备过程中引入的H进行区分, 并获取充氢过程中氢在钛合金中的分布情况. 二次离子质谱的样品尺寸为10 mm×10 mm×6 mm. 使用ION-TOF GmbH二次离子质谱仪(SIMS)沿厚度方向由表面至心部对充氘试样进行表征, 观察氘在试样中的分布情况. 实验中, 使用Bi+作为离子源具体参数如表1所列.

    3.   实验结果

      3.1.   不同应变速率对充氢Ti-2.5Al-2Zr-1Fe合金拉伸性能的影响

    • 为探究氢含量与应变速率对钛合金拉伸性能的影响, 设计了针对不同充氢时间下钛合金的常规拉伸实验与慢拉伸实验. 图6(a)为充氢0—264 h试样的常规拉伸曲线, 图6(b)为充氢0—264 h试样的慢拉伸曲线, 为直观地探究随氢含量升高Ti-2.5Al-2Zr-1Fe合金的性能的变化, 将延伸率、断面收缩率及抗拉强度等重要力学性能指标随充氢时间变化的曲线绘制在图7中.

      由图7(a)和图7(b) 可见, Ti-2.5Al-2Zr-1Fe合金随充氢时间的延长, 断面收缩率与延伸率整体都呈下降趋势. 由图7(c)可见, 常规拉伸和慢拉伸试样强度随充氢时间的变化趋势一致, 均为先升后降, 但常规拉伸强度高于慢拉伸. 这是因为钛合金等温变形过程中, 当应变速率增加时, 其显微组织会变得更加细化, 这会促使常规拉伸强度较慢拉伸有所提升[17].

      充氢时间在0—8 h区间内, 常规拉伸试样的断面收缩率、延伸率的变化尚不明显, 而慢拉伸试样的断面收缩率与延伸率数值均发生了大幅度降低, 此时慢拉伸试样已经产生了较为严重的塑性损失, 说明当氢含量较低时, 慢应变速率下的钛合金对氢更敏感. 充氢时间在8—48 h区间内, 慢拉伸试样的断面收缩率与延伸率的降低幅度逐渐减小, 而常规拉伸试样在充氢8 h后断面收缩率与延伸率迅速降低, 说明在这个氢含量区间内, 常规拉伸下的钛合金试样开始显现出对氢的敏感性. 充氢时间在48—264 h区间内, 慢拉伸试样与常规拉伸试样断面收缩率与延伸率的变化趋于稳定, 并且二者较为接近, 说明在充氢时间大于48 h后, 影响钛合金的氢脆敏感性的主导因素不再是应变速率.

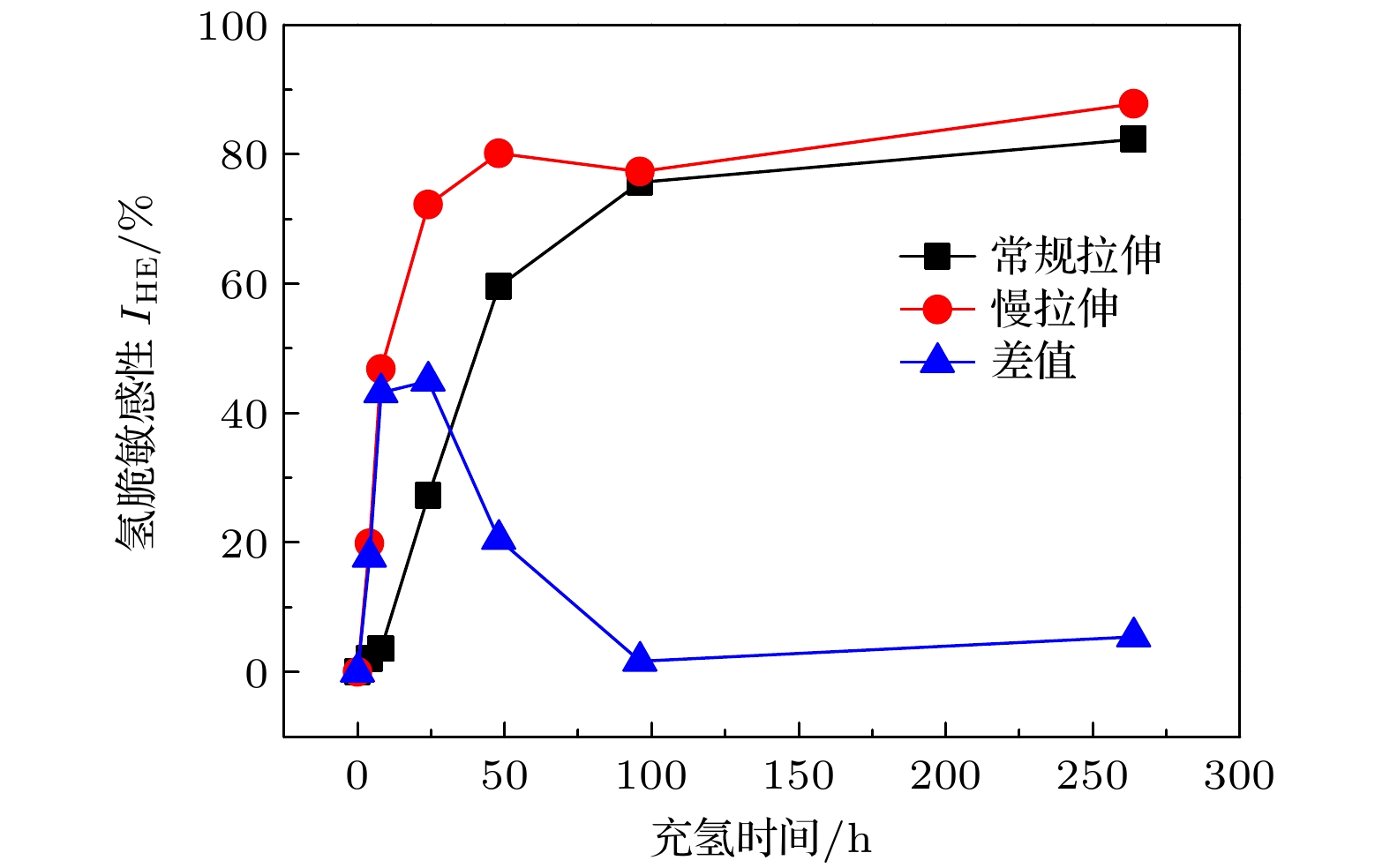
      由上述分析可以初步判断, 氢含量较低时, 钛合金对氢的敏感性受应变速率的控制. 为探求其具体变化, 采用了氢脆敏感性(充氢时塑性指标下降的相对量)来评估[18]:

      式中, IHE是氢脆敏感性, 其值越大说明材料氢脆越敏感; Z是不同充氢时间下材料延伸率; Z0是未充氢状态下材料的延伸率. 通过计算得出了两种应变速率下试样氢脆敏感性IHE随氢含量变化的曲线, 如图8所示. 充氢时间在0—8 h区间内, 慢拉伸试样的IHE值升高了20%, 而常规拉伸试样在该区间内尚未表现出明显的氢脆敏感性. 当充氢时间达到8 h时, 慢拉伸试样的IHE值已经达到46.8%, 而此时常规拉伸的IHE值仍在0附近. 并且在充氢时间8—48 h内常规拉伸试样的IHE值增幅始终低于慢拉伸, 这说明当氢含量较低时, 慢应变速率下的钛合金对氢更加敏感. 当充氢时间达48 h, 常规拉伸与慢拉伸试样的氢脆敏感性都逐渐趋于最大值, 二者的氢含量较高且相近, 分别为900 μg/g和920 μg/g. 这说明当氢含量较高时, 钛合金的氢脆敏感性主导因素逐渐由应变速率转变为氢含量的变化.

      • 3.2.   不同应变速率下预充氢试样断口的微观形貌

    • 为研究氢含量与应变速率对钛合金拉伸性能的影响, 对常规拉伸与慢拉伸试样断口进行了SEM分析. 图9为未充氢试样与充氢8 h试样的常规拉伸断口形貌图. 由图9(a)—(c)可见, 未充氢试样的常规拉伸断口形貌以韧窝为主, 呈现出良好的韧性. 由图9(d)—(f)可见, 充氢8 h试样的断口边缘出现了宽度为0.6—0.7 mm的环状脆性区, 脆性区内可见少量沿轧制方向的二次裂纹, 断口中心区域仍以韧窝为主, 我们推测这是由于氢聚集于表面区域产生脆化的结果.

      图10为未充氢试样与充氢8 h试样的慢拉伸断口形貌图. 由图10(a)—(c)可见, 未充氢试样的慢拉伸断口形貌以韧窝为主, 这与常规拉伸试样断口形貌基本一致. 图10(d)—(f)是充氢8 h慢拉伸试样断口形貌图, 实验结束后试样的断口边缘同样出现了环状脆性区, 但宽度大于常规拉伸试样, 约为1.3—1.4 mm, 尽管充氢8 h的慢拉伸试样氢含量较低, 仅为56 μg/g, 但在试样断口边缘环状脆性区内仍可见较多二次裂纹, 且二次裂纹尺寸较大. 由于脆性区宽度往往与氢扩散深度有关, 因此我们可以初步推测, 在慢应变速率下试样的氢扩散深度更大, 进而产生更高的氢脆敏感性.

      图11为充氢24—264 h试样在两种拉伸速率下的断口形貌图, 慢拉伸试样断口和常规拉伸试样断口均出现了贯穿心部的二次裂纹, 并且这种贯穿心部的二次裂纹区面积随充氢时间的延长而增大, 两种拉伸速率下的试样都发生了明显的塑性损失, 且二者塑性损失程度逐渐接近. 当氢含量升高至一定阈值后, 影响试样氢脆敏感性的主导因素不再是应变速率, 而是氢含量的变化.

      • 3.3.   氢含量对表面硬度的影响

    • 在3.1节中发现常规拉伸和慢拉伸试样都出现了抗拉强度小幅度升高后又迅速降低的现象, 其峰值分别在充氢时间24 h与8 h出现, 推测这是由于钛合金吸氢量较低时, 氢聚集于表面区域所产生的表面硬化的结果. 为验证此推论, 对试样表面进行了维氏硬度(HV)的测量, 如图12所示, 我们发现, 试样的表面硬度先在充氢时间0—48 h区间内小幅度增加, 当充氢时间超过48 h后开始迅速下降, 并逐渐趋于平稳状态. 这也初步印证了我们的推测, 即当氢含量较低时, 氢聚集于表面区域产生了表面硬化现象.

      • 3.4.   氢扩散分布的表征

    • 由于充氢后氢聚集于材料表面区域, 将充氘48 h试样静置了30 d, 使其中的氘有足够的时间扩散并达到平衡状态. 随后将静置后的试样进行二次离子质谱分析(SIMS), 以探究氢在钛合金试样中的扩散机制及分布情况. 图13为试样中氘和铝元素分布情况的二次离子质谱表征结果. 可以发现材料中的Al的宏观层面上基本呈均匀分布, 说明对该材料的SIMS表征时的信号强度是稳定的, 而氘在合金中从表面到心部方向信号强度逐渐降低, 这表明氢浓度在钛合金中的宏观分布是不均匀的, 而是随氢扩散距离的增加逐渐递减. 此外, 该试样在充氘48 h后又静置了30 d, 这表明钛合金吸氢结束后长时间静置依旧不能使氢扩散均匀. 另外, 有报道认为充氢会导致氢在表面富集产生氢化物[19], 一方面阻止氢继续进入, 一方面也造成了氢浓度分布不均. 为此进行了对Ti-2.5Al-2Zr-1Fe合金表面高氢层的TEM表征, 以确定是否形成氢化物层, 具体见3.5节.

      另一方面, 为探究温度对氢在材料中扩散分布的影响, 首先对2.6节的试样充氢96 h, 随后, 分别对充氢试样进行24 h的常温静置与24 h的400 ℃的保温处理, 最后, 按照2.6节的测氢方法检测了试样在不同深度的氢含量分布, 并据此绘制了氢浓度沿厚度方向由上至下不同位点的宏观分布, 见图14. 经过400 ℃保温处理的试样, 其氢浓度分布相较于室温试样更为均匀. 这初步表明, 随着温度的升高, 氢在材料中的扩散速率得以提升, 从而导致了氢分布的均匀化.

      • 3.5.   预裂纹恒位移加载试验结果

    • 由于慢拉伸实验的周期较短, 通常仅为7—10 d, 且应力集中主要出现在颈缩阶段, 而预裂纹恒位移实验不仅能够提供更长时间的准静态载荷, 还能在裂尖产生足够的应力集中来诱导氢的扩散、聚集, 因此对充氢48 h的WOL试样进行了为期30 d的预裂纹恒位移实验, 并对试验后的断口进行了透射电子显微镜观察(TEM)与选区衍射分析(SAED)来研究氢在Ti-2.5Al-2Zr-1Fe合金中的存在形式及其在应力集中处的致脆机理. 图15为WOL试样的断口形貌. 可以看出, 试样裂纹扩展线呈弧形, 由二次裂纹尺寸推测弧形中间凸出部位的脆性远高于边缘区. 造成这种现象一方面是由于试样裂纹尖端外表面所受应力状态和试样断口内部所受应力状态不同[20], 裂纹尖端中部受三向应力, 应力比边缘大, 导致裂纹尖端中部裂纹扩展较边缘快, 呈现出弧形的断口形貌. 另一方面, 在三向应力作用下, 氢原子会沿晶界扩散进入裂纹尖端区引起氢脆[21], 而本实验周期较长, 氢有足够的时间扩散至三向应力集中处大量聚集, 因此断口中心区域脆性更高, 裂纹扩展更深, 使断口应力腐蚀形貌呈弧形.

      为进一步探究氢致脆的机理, 选择在脆性区的微裂纹附近通过FIB制取TEM试样, 图16(a)是裂纹尖端的TEM形貌图, 可见裂纹主要沿α相界周围的β相扩展. 图16(b)为裂纹尖端附近晶粒A和B处的选区电子衍射图, 对衍射花样进行标定, 确定物相分别为α与β相, 并未发现氢化物, 这也进一步证明了本实验的充氢浓度下未产生氢化物.

    4.   分析与讨论

      4.1.   氢扩散深度与充氢时间的关系

    • 由3.2节中不同充氢时间下常规拉伸与慢拉伸试样脆性区面积的变化, 可以发现随充氢时间的延长, 常规拉伸与慢拉伸试样的脆性区都呈由边缘向心部的扩张趋势, 进而导致Ti-2.5Al-2Zr-1Fe合金试样氢脆敏感性的升高, 这可能与氢由材料边缘至心部的扩散深度有关. 为了深入探究此现象产生的具体机制, 我们计算了不同充氢时间下氢扩散的理论深度值变化, 并结合断口实际脆性区面积得出不同充氢时间下氢扩散深度值, 分析充氢时间与氢扩散深度的关系. 氢扩散深度理论值的计算公式为

      式中, 室温下钛合金氢扩散系数D = 3.31×10–8 cm2/s[22]; x为氢扩散深度, 单位mm; t为氢扩散时间, 单位s. 通过计算得到了8—264 h预充氢时间下的氢扩散深度的理论值分别为x8 = 0.436 mm, x24 = 0.755 mm, x48 = 1.068 mm, x96 = 1.510 mm, x264 = 2.505 mm, 并绘制出了对应的氢扩散深度随充氢时间的变化关系图, 如图17所示. 随充氢时间的延长, 氢扩散的深度逐渐增大, 这与在3.2节中观察到的脆性区形貌变化趋势基本一致. 这也印证了我们的推论, 即随充氢时间的延长, Ti-2.5Al-2Zr-1Fe合金中氢扩散深度增大, 进而导致材料氢脆敏感性的增大.

      • 4.2.   氢在Ti-2.5Al-2Zr-1Fe合金的浓度分布及扩散机制

    • 由3.2节中不同充氢时间下常规拉伸与慢拉伸试样脆性区形貌的变化, 我们发现试样边缘二次裂纹数目比心部多, 这可能是由于钛合金吸氢后, 即使经过长时间的扩散, 氢依旧无法均匀分布, 而是始终呈现扩散浓度随扩散距离的增大而递减的分布情况. 而在3.4节中对充氢48 h静置30 d试样的SIMS表征也发现了氘信号强度由试样边缘区到心部逐渐降低. 针对该现象的发生, 我们有两种推论, 第1种是由于充氢时, 氢主要聚集于试样表层区域, 导致表层区氢浓度过高从而析出氢化物[23], 导致可扩散的氢越来越少, 因此随扩散深度的增加氢浓度逐渐降低, 但在3.5节中通过对充氢48 h的WOL试样进行TEM表征后发现试样中并未析出氢化物, 因此可以排除这种推论. 第2种推论是随着氢扩散过程的进行, 试样表面区域的氢浓度逐渐降低, 浓度梯度作为氢扩散的驱动力逐渐减弱, 而氢与钛的亲和力强[24], 从而形成了阻碍氢扩散的能量势垒, 这种能量势垒与浓度梯度形成了动态平衡状态, 导致随氢扩散距离的增加, 氢的扩散速率逐渐降低, 当氢扩散至一定深度后, 氢的扩散速率显著降低, 几乎可以忽略不计, 最终呈现氢浓度随扩散深度增加而递减的分布情况. 若要实现氢的均匀分布, 则需要极长的时间来达成这一状态.

      为验证第2种推论, 可以根据菲克第一定律进行分析:

      式中, J为扩散通量; D为扩散系数; dρ/dx为浓度梯度. 在钛合金内部, 充氢时, 边缘区氢浓度远大于材料心部, 这便形成了氢的浓度梯度, 而浓度梯度就是氢扩散的驱动力. 由(3)式可以发现, 随着氢扩散过程的进行, 浓度梯度逐渐减弱, 进而导致扩散通量J降低.

      而扩散系数D计算公式如下[25]:

      式中, D为扩散系数, D0为与温度无关的前置系数, Q为扩散激活能, kB为玻尔兹曼常数, T为温度. 由(4)式可见, 扩散系数D的大小与温度有关, 若要证明第2种推论的准确性, 其关键在于证明扩散能量势垒的存在, 当扩散驱动力增加时, 氢是否可以克服能量势垒继续扩散, 进而增加扩散通量, 侧面证明第2种推论的准确性. 因此可以采用升高温度的方法, 温度升高时, 一方面, 扩散系数D会增大, 根据菲克第一定律, 扩散通量进而增大; 另一方面, 温度升高时, 氢的热激活能也会增大, 进而增大氢的扩散驱动力, 当增大到一定程度时, 氢会克服一部分扩散势垒, 在原来的基础上进一步扩散, 最终导致氢的扩散通量增加, 浓度分布更加均匀. 而3.4节中分别对充氢96 h后室温静置试样与充氢96 h后400 ℃的热处理试样进行不同深度的氢含量变化情况检测. 结果显示, 充氢结束后随温度的升高, 氢随扩散深度的浓度分布更加均匀, 相较于室温静置试样, 即使在较短的时间内, 400 ℃保温试样中的氢进行进一步的扩散. 这表明了氢在Ti-2.5Al-2Zr-1Fe合金中扩散势垒的存在, 进而验证了第2种推论的准确性.

      • 4.3.   应变速率对Ti-2.5Al-2Zr-1Fe合金的氢脆敏感性的影响

    • 基于3.1节的研究结果, 观察到在充氢时间较短的阶段(0—48 h), 慢拉伸试样的氢脆敏感性明显高于常规拉伸试样. 随后, 在3.1节发现当试样中充氢时间较低时(0—24 h), 相较于常规拉伸试样, 慢拉伸试样的脆性区更大, 即氢的扩散深度更大. 因此, 我们推测当钛合金氢含量较低时, 应变速率对合金中氢的扩散深度有一定影响, 进而影响材料的氢脆敏感性. 研究表明 [26,27], 材料产生塑性变形时产生的缺陷通常以位错为主, 而位错核心是强陷阱, 它能吸引并捕获氢, 导致氢与位错产生结合作用.

      Tien等[15]也提出位错载氢运动理论, 认为位错作为氢陷阱会对氢的产生束缚作用, 因此当位错移动时会携带氢随着位错一起运动, 而位错载氢运动也会导致氢扩散实际距离增大[28]. 当材料中可动位错的运动速率VC小于位错载氢运动临界速率VH时, 位错会携带氢共同运动, VH的公式如下:

      式中, D为有效氢扩散系数, R为气体常数, T为实验温度, $\boldsymbol b $为Burgers矢量, E为位错与氢原子的结合能.

      材料在拉伸过程中, 应变速率ε与可动位错运动速率VC的关系为[29]

      式中, ρ为可动位错密度. 将(5)式和(6)式进行整理, 可以得出可动位错的运动速率VC与位错载氢运动临界速率VH的关系式为

      在常温下, ρ, D, E, R, T均为定值, 而当可动位错的运动速率VC低于位错载氢运动临界速率VH的关系式时, 即VH/VC > 1, 可以得出钛合金位错载氢运动的应变速率范围及临界值ε0为

      对于氢含量较低的钛合金试样, 应变速率ε低于位错载氢运动的应变速率临界值ε0时, 位错会捕获并携带氢共同运动. 当载氢位错运动至相界处时会遭遇阻碍, 这导致原本被位错捕获的氢原子得以释放, 进而在相界附近引发一系列复杂的交互行为, 如图18所示. 由于材料边缘区域与心部之间始终维持着氢的浓度梯度, 这为氢原子自发向心部扩散提供了不竭动力. 因此, 氢原子自发地向相界聚集并穿越相界, 深入材料心部. 在慢拉伸实验的长周期持久应力作用下, 材料经历长时间的塑性形变过程, 这一过程不仅赋予氢原子充足的时间在相界进行自扩散, 还促使材料内部持续生成向心部迁移的位错. 当氢穿越相界后, 新产生的位错再次捕获并携带穿越相界的氢原子, 共同向材料心部迁移, 致使钛合金试样在慢应变速率下的氢扩散距离较常规拉伸速率的更大, 进而导致该应变速率的氢脆敏感性较常规拉伸速率更高. 而我们在3.1节中得到的常规拉伸与慢拉伸试样氢脆敏感性随充氢时间的变化规律, 与3.2节中脆性区的变化也印证了该理论模型的准确性, 也就是说慢拉伸速率与常规拉伸速率的值满足6.4×10–9 m/s < ε0 < 6.7×10–3 m/s, 即在慢拉伸实验中发生了位错载氢运动, 导致慢拉伸实验中氢扩散深度更大, 进而导致氢脆敏感性更高, 这与DP780[30]与Q960E[28]的氢脆敏感性研究是相契合的.

      而当氢含量较高, 即充氢时间较大时(48—264 h), Ti-2.5Al-2Zr-1Fe合金中氢在边缘区域与心部之间的浓度梯度也会随之显著加剧, 这会给氢由边缘区向心部的自扩散行为提供更强的驱动力. 在此情况下, 氢的扩散速度加快, 甚至超过了位错运动的速度, 使得氢的扩散不再完全依赖于位错作为载体进行迁移的机制, 而是氢的自扩散机制逐渐占据主导地位, 推动大量氢原子向材料心部聚集. 随着氢自扩散过程的持续进行, 大量氢原子在材料相界处积聚, 这种积聚效应显著削弱了相界的强度, 进而导致材料氢脆现象的发生. 因此, 在氢含量较高的条件下, 慢拉伸试样与常规拉伸试样氢脆敏感性逐渐接近并趋于同一水平, 这主要归因于二者在该环境下的氢脆机制趋于一致. 这表明在高氢含量环境下, 氢的自扩散成为其对材料产生性能的衰减作用主导因素.

      • 4.4.   少量氢对钛合金性能的影响

    • 图7(c)展示了常规拉伸和慢拉伸试样的强度随充氢时间的变化. 可以看出, 常规拉伸和慢拉伸试样强度随充氢时间的变化曲线近乎平行. 这表明在两种拉伸速率下, 试样强度的变化趋势基本一致, 随着氢含量的增加, 试样在常规拉伸和慢拉伸实验中的抗拉强度都呈先升后降的趋势, 当充氢时间为0—8 h区间内, 慢拉伸拉伸试样的抗拉强度由初始值718 MPa提升至峰值738 MPa, 增幅为3%, 随后迅速下降; 当充氢时间在0—24 h区间内, 常规拉伸试样的抗拉强度由初始值777 MPa提升至峰值819 MPa, 增幅约为5%, 充氢时间超过24 h后迅速降低. 我们初步推断这是由于少量的氢在钛合金表面区域产生了表面硬化的作用, 从而使钛合金的抗拉强度有了小幅度升高. 但当钛合金氢含量超过一定阈值时, 氢对材料塑性的弱化开始占主导作用, 导致材料强度显著降低. 为验证这一推论, 我们在3.3节中探究了试样表面硬度随充氢时间的变化(图12). 由图12可见, 试样的充氢时间在0—48 h范围内, 表面硬度随充氢时间的增加而产生小幅度的上升, 当充氢时间大于48 h后, 表面硬度开始下降, 并逐渐趋于平稳. 该结果印证了少量的氢会造成钛合金材料表面硬化进而提升材料抗拉强度的推论, 而当氢含量超过一定阈值时, 氢对材料的塑性造成的影响作用将显著高于表面强化作用, 造成材料强度的降低.

      • 4.5.   Ti-2.5Al-2Zr-1Fe合金的氢脆机理

    • 目前提出的主要氢脆机制有: 应力诱导氢化物滞后开裂理论[9]、氢增强局部塑性(HELP)[10]、吸附诱导位错发射(AIDE)[8]和弱键理论(HEDE)[7].

      首先, 应排除应力诱导氢化物滞后开裂理论, 因为已经在3.5节中对充氢48 h后静置30 d的WOL试样进行了TEM分析, 最终未发现氢化物相的析出, 因此可以说明氢即使长时间在Ti-2.5Al-2Zr-1Fe合金中通过三向应力诱导作用下聚集, 也不会造成氢化物的析出. 根据应力诱导氢化物理论[9], 氢会向三向应力最大处扩散聚集, 引起局部氢浓度饱和, 生成非稳态氢化物, 当应力释放后该氢化物会发生可逆转变恢复固溶态. 由于该过程的直观性观测难以完成, 因此, 只能通过侧面证据来证明在本研究中该过程的存在性. 在3.5节预裂纹应力腐蚀实验中, 氢会在三向应力诱导作用下聚集于预制裂纹中心处, 而合金的塑性会随着氢含量升高产生量变到质变的突变. 原因在于, 氢含量较低时, 三向应力诱导氢聚集后, 应力集中处的氢浓度急剧增加, 当氢浓度增加到一定程度时会析出氢化物, 此时材料会产生明显的韧脆转变, 塑韧性指标出现台阶式下降. 而我们的实验结果表明, 材料的拉伸和慢拉伸性能均未出现明显的突变台阶. 综上所述, 本研究中钛合金试样所产生的氢脆现象并非源于应力诱导氢化物滞后开裂机制.

      其次, HELP机制是基于溶质氢通过增加位错的迁移率从而导致材料局部塑性降低的概念, 这种机制下断口形貌的主要特征形态为滑移带断裂, 主要以滑移痕迹、小平面和撕裂脊等特征为主. 然而, 本研究中的常规拉伸与慢拉伸实验中的所有断口形貌均并未观察到这些特征. 有研究表明[8], HELP的主要作用为促进裂纹的萌生过程, 并不是裂纹的扩展过程, 而在3.5节中预裂纹应力腐蚀实验表明, 氢主要对裂纹的扩展过程起到了显著的促进作用, 并未直接导致新裂纹的产生. 这也进一步证实本实验中钛合金试样的氢脆并非由HELP机制引发.

      再次, AIDE理论认为表面吸附的氢将会影响氢吸附层以下几个原子层的金属键合力, 从而促进位错的发射[8]. 从3.5节TEM结果发现, 裂纹主要在β相周围扩展, 这意味着相较于α相, 氢对β相的弱化作用更为显著. 从两相的晶体结构来看, α相为HCP结构, β相为BCC结构[1], 因此, α相的滑移系比β相少. 考虑到AIDE对位错发射的促进作用, 氢对β相的弱化作用应显著强于对α相的弱化作用, 这与我们实验中观察到的裂纹扩展倾向性相吻合. 但AIDE机制主要是在合金处于液态腐蚀介质中时, 表面发生析氢反应, 对裂纹面或裂纹尖端产生弱化效应, 而本研究均针对钛合金试样中的内部氢进行研究, 在对材料充氢处理后将试样置于干燥空气中进行试验, 并未引入腐蚀介质, 因此, 不能证明AIDE机制为Ti-2.5Al-2Zr-1Fe合金试样氢脆的主导机制.

      本研究认为弱键理论(HEDE)是Ti-2.5Al-2Zr-1Fe合金产生氢脆现象的主导机理. 原因在于, HEDE机制认为溶解在材料中的氢会显著地降低金属原子间的键合力, 导致材料强度、塑性降低[7]. Liu等[14]针对Ti-2.5Al-2Zr-1Fe合金充氢试样的SIMS研究显示氢主要分布于α相界周围的β相中, 因此可以说明氢更容易在β相聚集. 通过3.5节中TEM表征也直观地观察到裂纹沿β相扩展, 这表明氢主要在β相发生选择性溶解, 并造成该处的Ti—Ti键发生弱化, 最终导致材料产生塑性损失, 这与HEDE机制相吻合. 此外, 我们在4.3节中的研究发现, 在Ti-2.5Al-2Zr-1Fe合金中应变速率低于特定阈值的情况下, 位错会通过捕获并携带氢共同运动, 这一过程加速了氢的扩散, 进而提高了钛合金对氢的敏感性. 然而, 这一过程还会与HEDE机制产生耦合作用, 扩大HEDE氢脆机制的影响范围, 进而加剧Ti-2.5Al-2Zr-1Fe合金的脆化.

    5.   结　论

    • 1)本研究通过计算氢在Ti-2.5Al-2Zr-1Fe合金中随充氢时间增长的理论扩散深度, 并结合试样断口脆性区随充氢时间的扩张情况, 得出: 随着充氢时间的延长, 氢在Ti-2.5Al-2Zr-1Fe合金中的扩散距离显著增加. 这种扩散行为的加剧导致了脆性区不断向材料的内部(心部)扩展, 从而显著提高了材料的氢脆敏感性.

      2)慢应变速率下, Ti-2.5Al-2Zr-1Fe合金中的氢向应力集中处扩散聚集, 但该区域氢浓度并未达到足以诱发氢化物析出的阈值. 因此, 氢更倾向于在β相中积聚, 进而导致微裂纹沿β相扩展, 这与HEDE机制相吻合, 进一步分析表明, 氢在合金中的扩散过程主要受限于钛与氢之间强亲和力所构建的扩散势垒, 而非氢化物的直接作用. 此扩散势垒与合金内部的氢浓度梯度构成了一种动态平衡状态, 显著地减缓了氢的扩散速率.

      3)基于对位错载氢模型推演得出, 钛合金位错载氢运动的应变速率临界值$ {\varepsilon _0} = {{\left( {30 RT} \right)} {/ } {\left( {\rho DE} \right)}} $, 当应变速率低于ε0时, 位错会捕获并携带氢共同运动, 导致氢扩散深度增加, 氢脆敏感性提高, 并与HEDE氢脆机制发生耦合作用, 进一步扩大HEDE氢脆机制的影响范围, 并加剧该合金的脆化现象.

      4)氢对钛合金性能具有双重影响: 少量氢能增强钛合金的表面硬度, 从而提升其强度; 但氢含量超过某阈值时, 会显著地降低材料的塑性, 这一负面效应远超其表面硬化带来的益处.

    参考文献 (30)

目录

/

返回文章
返回