高级搜索

面向半导体工艺的平面线圈感性耦合氩等离子体源的三维流体模拟研究

,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

赵明亮, 邢思雨, 唐雯, 张钰如, 高飞, 王友年. 面向半导体工艺的平面线圈感性耦合氩等离子体源的三维流体模拟研究[J]. 物理学报, 2024, 73(21): 215201-1. doi: 10.7498/aps.73.20240952
引用本文: 赵明亮, 邢思雨, 唐雯, 张钰如, 高飞, 王友年. 面向半导体工艺的平面线圈感性耦合氩等离子体源的三维流体模拟研究[J]. 物理学报, 2024, 73(21): 215201-1. doi: 10.7498/aps.73.20240952
shu
Ming-Liang Zhao, Si-Yu Xing, Wen Tang, Yu-Ru Zhang, Fei Gao, You-Nian Wang. Three-dimensional fluid simulation of a planar coil inductively coupled argon plasma source for semiconductor processes[J]. Acta Physica Sinica, 2024, 73(21): 215201-1. doi: 10.7498/aps.73.20240952
Citation: Ming-Liang Zhao, Si-Yu Xing, Wen Tang, Yu-Ru Zhang, Fei Gao, You-Nian Wang. Three-dimensional fluid simulation of a planar coil inductively coupled argon plasma source for semiconductor processes[J]. Acta Physica Sinica, 2024, 73(21): 215201-1. doi: 10.7498/aps.73.20240952
shu

面向半导体工艺的平面线圈感性耦合氩等离子体源的三维流体模拟研究

  • 大连理工大学物理学院, 三束材料改性教育部重点实验室, 大连　116024

    • 作者简介: 赵明亮: mlzhao@dlut.edu.cn .
    通讯作者: E-mail: fgao@dlut.edu.cn.; 

  • 中图分类号: 52.50.Qt, 52.65.-y

Three-dimensional fluid simulation of a planar coil inductively coupled argon plasma source for semiconductor processes

  • Key Laboratory of Materials Modification by Laser, Ion, and Electron Beams (Ministry of Education), School of Physics, Dalian University of Technology, Dalian 116024, China

    • Corresponding author: E-mail: fgao@dlut.edu.cn.; 

  • MSC: 52.50.Qt, 52.65.-y

  • 摘要: 针对平面线圈感性耦合氩气放电, 本文基于自主开发的三维等离子体流体力学程序, 数值模拟了线圈结构以及放电气压对等离子体空间分布的影响. 研究表明, 由于线圈在环向上具有不对称性, 电子密度也具有明显的环向不均匀性. 随着气压的增大, 这种环向不均匀性逐渐增强. 通过减小线圈的开口, 可以提高等离子体的环向均匀性. 此外, 针对双线圈驱动放电, 还研究了内外双线圈电流幅值之比对于等离子体均匀性的影响. 结果表明, 通过改变内外线圈电流幅值的比值, 有利于提高等离子体的径向均匀性.
    Abstract: In this paper, the effect of the coil structure, as well as the gas pressure, on the spatial distribution of an inductively coupled argon plasma is numerically investigated based on our developed three-dimensional fluid model. The model is based on a modified ambipolar diffusion model, in which the electron density is solved under the quasi-neutral condition, the ion density and neutral particle density are obtained by solving continuity equations, and the ion flux is achieved by solving the full momentum balance equation. In addition, the inductive electric field is governed by the Maxwell equations, which are solved in the frequency domain. The results show that the electron density is nonuniform along the azimuthal direction due to the asymmetry of the coil structure, and the uniformity becomes better as gas pressure decreases. Besides, the plasma azimuthal uniformity can also be improved by reducing the opening of the coil. As the coil radius increases, the plasma density decreases, while the radial uniformity of the plasma improves, and the azimuthal uniformity deteriorates. In addition, the influence of the current amplitude ratio between the inner coil and outer coil on the plasma uniformity in dual-coil discharge is also investigated. It is found that the plasma radial uniformity becomes better by reducing the inter-to-outer coil current amplitude ratio. The results obtained in this work demonstrate that the plasma uniformity can be improved by optimizing the coil structure and adjusting the discharge parameters, which is of significant importance in etching and deposition processes.
  • 加载中

  • 图 1  计算区域示意图

    Figure 1.  Schematic diagram of the calculation region.

    下载: 全尺寸图片 幻灯片

    图 2  网格划分示意图

    Figure 2.  Schematic diagram of the grid.

    下载: 全尺寸图片 幻灯片

    图 3  (a)单线圈腔室结构示意图; (b)单组线圈

    Figure 3.  Schematic diagram of (a) the single-coil chamber structure and (b) the single coil.

    下载: 全尺寸图片 幻灯片

    图 4  (a)电子密度、(b)电子温度、(c)感应电场幅值以及(d)感性沉积功率密度的三维空间分布, 其中气压为2 Pa, 放电功率100 W

    Figure 4.  Three-dimensional spatial distribution of the (a) electron density, (b) electron temperature, (c) induced electric field amplitude, and (d) induced deposited power density. The gas pressure is 2 Pa, the discharge power is 100 W.

    下载: 全尺寸图片 幻灯片

    图 5  不同轴向位置的$r{\text{-}}\phi $平面上的电子密度的分布(气压分别为3 Pa和13 Pa, 功率为100 W) 　(a), (d) 介质窗下方8 cm; (b), (e) 介质窗下方5 cm; (c), (f) 介质窗下方2 cm

    Figure 5.  Distribution of electron density in the $r{\text{-}}\phi $ cross section for different axial positions: (a), (d) 8 cm below the quartz window; (b), (e) 5 cm below the quartz window; (c), (f) 2 cm below the quartz window. The gas pressure is 3 Pa and 13 Pa, the power is 100 W

    下载: 全尺寸图片 幻灯片

    图 6  基片台上方1 cm处的$r{\text{-}}\phi $平面的电子密度分布(气压为2 Pa)　(a) 200 W; (b) 300 W; (c) 400 W; (d) 500 W

    Figure 6.  Distribution of electron density in the $r{\text{-}}\phi $ plane which is 1 cm above the substrate: (a) 200 W; (b) 300 W; (c) 400 W; (d) 500 W. The gas pressure is 2 Pa.

    下载: 全尺寸图片 幻灯片

    图 7  不同线圈的开口弧度的单匝线圈　(a) ${\text{π}}/15$; (b) ${\text{π/}}5$; (c) ${\text{π/}}3$; (d) $7{\text{π/}}15$

    Figure 7.  Single circle coil with different opening sizes: (a) ${\text{π}}/15$; (b) ${\text{π/}}5$; (c) ${\text{π/}}3$; (d) $7{\text{π/}}15$.

    下载: 全尺寸图片 幻灯片

    图 8  气压为12 Pa, 功率为300 W时, 线圈开口的大小对于电子密度环向分布的影响　(a) ${\text{π}}/15$; (b) ${\text{π/}}5$; (c) ${\text{π/}}3$; (d) $7{\text{π/}}15$

    Figure 8.  Effect of the size of the coil opening on the azimuthal distribution of electron density: (a) ${\text{π}}/15$; (b) ${\text{π/}}5$; (c) ${\text{π/}}3$; (d) $7{\text{π/}}15$

    下载: 全尺寸图片 幻灯片

    图 9  气压为12 Pa, 功率为300 W时, (a), (b)不同$x$轴方向位置的$y{\text{-}}z$平面上的电子密度的分布, 线圈开口弧度分别为${\text{π}}/15$和$7{\text{π/}}15$; (c), (d)不同$y$轴方向位置的$x{\text{-}}z$平面上的电子密度的分布, 线圈开口弧度分别为${\text{π}}/15$和$7{\text{π/}}15$

    Figure 9.  (a), (b) Distributions of electron density in the $y{\text{-}}z$ plane at different x-direction positions with coil openings of ${\text{π}}/15$ and $7{\text{π/}}15$; (c), (d) the distributions of electron density in the $x{\text{-}}z$ plane at different y-direction positions with coil openings of ${\text{π}}/15$ and $7{\text{π/}}15$. The gas pressure is 12 Pa and the power is 300 W.

    下载: 全尺寸图片 幻灯片

    图 10  线圈半径对电子密度环向分布的影响　(a) 3 cm; (b) 9 cm; (c) 12 cm

    Figure 10.  Effect of coil radius on the azimuthal distribution of electron density: (a) 3 cm; (b) 9 cm; (c) 12 cm.

    下载: 全尺寸图片 幻灯片

    图 11  (a)双线圈腔室结构示意图; (b)内外双线圈

    Figure 11.  (a) Schematic diagram of the dual-coil chamber structure; (b) the internal and external dual coil.

    下载: 全尺寸图片 幻灯片

    图 12  不同的内外线圈的相对位置下, 电子密度在$r{\text{-}}\phi $平面上的分布(气压为12 Pa, 功率为300 W, 内外线圈电流幅值比为1∶1)　(a) case 1; (b) case 2; (c) case 3; (d) case 4

    Figure 12.  Distribution of electron density in the $r{\text{-}}\phi $ plane for different relative positions of the inner and outer coils: (a) case 1; (b) case 2; (c) case 3; (d) case 4. The pressure is 12 Pa, the power is 300 W, and the coil current ratio is 1∶1.

    下载: 全尺寸图片 幻灯片

    图 13  不同的内外线圈电流幅值比下, (a), (b)电子密度、(c), (d)电子温度、(e), (f)感性沉积功率密度和(g), (h)感应电场的幅值在$r{\text{-}}\phi $平面上的分布, 气压为12 Pa, 功率为300 W

    Figure 13.  Distribution of (a), (b) electron density, (c), (d) electron temperature, (e), (f) induced deposition power density and (g), (h) amplitude of induced electric field in the $r{\text{-}}\phi $ plane for different relative positions of the inner and outer coils. The pressure is 12 Pa and the power is 300 W.

    下载: 全尺寸图片 幻灯片

    表 1  氩等离子体中的碰撞反应及速率系数

    Table 1.  Collision reactions and rate coefficients in argon plasma.

    编号 反应表达式 反应系数/(m3·s–1) 文献
    1 ${\text{e + Ar}} \to {\text{e + Ar}}$ $ 2.336 \times {10^{ - 14}}T_{\text{e}}^{1.609}\exp \left[ {0.0618{{\left( {\ln {T_{\text{e}}}} \right)}^2} - 0.1171{{\left( {\ln {T_{\text{e}}}} \right)}^3}} \right] $ [1]
    2 ${\text{e + Ar}} \to {\text{e + A}}{{\text{r}}^*}$ $2.48 \times {10^{ - 14}}T_{\text{e}}^{0.33}\exp \left( { - 12.78/{T_{\text{e}}}} \right)$ [1]
    3 ${\text{e + Ar}} \to 2{\text{e + A}}{{\text{r}}^ + }$ $2.34 \times {10^{ - 14}}T_{\text{e}}^{0.59}\exp \left( { - 17.44/{T_{\text{e}}}} \right)$ [1]
    4 ${\text{e + A}}{{\text{r}}^*} \to 2{\text{e + A}}{{\text{r}}^ + }$ $2.05 \times {10^{ - 13}}\exp \left( { - 4.95/{T_{\text{e}}}} \right)$ [22]
    5 ${\text{e + A}}{{\text{r}}^*} \to {\text{e + Ar}}$ $2.0 \times {10^{ - 13}}$ [22]
    6 $ {\text{A}}{{\text{r}}^*}{\text{ + A}}{{\text{r}}^*}{\text{ }} \to {\text{Ar + A}}{{\text{r}}^ + }{\text{ + e}} $ $6.2 \times {10^{ - 16}}$ [22]
    注: 其中电子温度用电子伏(eV)为单位.
    下载: 导出CSV
  • [1] Lieberman M A, Lichtenberg A J 2005 Principles of Plasma Discharges and Materials Processing (New York: Wiley) pp350–351
    [2] 王友年, 宋远红, 张钰如 2024 射频等离子体物理基础(北京: 科学出版社) 第314页 Wang Y N, Song Y H, Zhang Y R 2024 Fundamentals of Radio-frequency Plasma Physics (Beijing: Science Press) p314
    [3] Rauf S, Kenney J, Collins K S 2009 J. Appl. Phys. 105 103301 doi: 10.1063/1.3126718
    [4] Kenney J, Rauf S, Collins K S 2009 J. Appl. Phys. 106 103302 doi: 10.1063/1.3259420
    [5] Agarwal A, Bera K, Kenney J, Likhanskii A, Rauf S 2017 J. Phys. D: Appl. Phys. 50 424001 doi: 10.1088/1361-6463/aa88f0
    [6] Ventzek P L, Sommerer T J, Hoekstra R J, Kushner M J 1993 Appl. Phys. Lett. 63 605 doi: 10.1063/1.109963
    [7] Thorsteinsson E, Gudmundsson J 2010 J. Phys. D: Appl. Phys. 43 115201 doi: 10.1088/0022-3727/43/11/115201
    [8] Thorsteinsson E, Gudmundsson J 2010 J. Phys. D: Appl. Phys. 43 115202 doi: 10.1088/0022-3727/43/11/115202
    [9] Hjartarson A, Thorsteinsson E, Gudmundsson J 2010 Plasma Sources Sci. Technol. 19 065008 doi: 10.1088/0963-0252/19/6/065008
    [10] Takao Y, Kusaba N, Eriguchi K, Ono K 2010 J. Appl. Phys. 108 093309 doi: 10.1063/1.3506536
    [11] Mattei S, Nishida K, Onai M, Lettry L, Tran M Q, Hatayama A 2017 J. Comput. Phys. 350 891 doi: 10.1016/j.jcp.2017.09.015
    [12] Kushner M J 2009 J. Phys. D: Appl. Phys. 42 194013 doi: 10.1088/0022-3727/42/19/194013
    [13] Sun X Y, Zhang Y R, Li X C, Wang Y N 2015 Phys. Plasmas 22 053508 doi: 10.1063/1.4921670
    [14] Wang Y H, Wei L, Zhang Y R, Wang Y N 2015 Chin. Phys. B 24 095203 doi: 10.1088/1674-1056/24/9/095203
    [15] Wu H M, Yu B W, Li M, Yang Y 2002 IEEE Trans. Plasma Sci. 25 1 doi: 10.1109/27.557479
    [16] Kushner M J, Collison W Z, Grapperhaus M J, Holland J P, Barnes M S 1996 J. Appl. Phys. 80 1337 doi: 10.1063/1.362932
    [17] Panagopoulos T, Kim D, Midha V, Economou D J 2002 J. Appl. Phys. 91 2687 doi: 10.1063/1.1448673
    [18] Brcka J 2016 Jpn. J. Appl. Phys. 55 07LD08 doi: 10.7567/JJAP.55.07LD08
    [19] 赵明亮, 张钰如, 高飞, 宋远红, 王友年 2023 力学学报 55 2891 doi: 10.6052/0459-1879-23-302 Zhao M L, Zhang Y R, Gao F, Song Y H, Wang Y N 2023 Chin. J. Theor. Appl. Mech. 55 2891 doi: 10.6052/0459-1879-23-302
    [20] De Bleecker K, Bogaerts A, Gijbels R, Goedheer W 2004 Phys. Rev. E 69 056409 doi: 10.1103/PhysRevE.69.056409
    [21] Ariskin D, Schweigert I, Alexandrov A, Bogaerts A, Peeters F M 2009 J. Appl. Phys. 105 063305 doi: 10.1063/1.3095760
    [22] Lee C, Lieberman M 1995 J. Vac. Sci. Technol. A 13 368 doi: 10.1116/1.579366
  • 加载中
图( 13) 表( 1)
计量
  • 文章访问数:  227
  • HTML全文浏览数:  227
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-07-09
  • 刊出日期:  2024-11-05

面向半导体工艺的平面线圈感性耦合氩等离子体源的三维流体模拟研究

    通讯作者: E-mail: fgao@dlut.edu.cn.; 
    作者简介: 赵明亮: mlzhao@dlut.edu.cn
  • 大连理工大学物理学院, 三束材料改性教育部重点实验室, 大连　116024
  • 收稿日期:  2024-07-09

摘要: 针对平面线圈感性耦合氩气放电, 本文基于自主开发的三维等离子体流体力学程序, 数值模拟了线圈结构以及放电气压对等离子体空间分布的影响. 研究表明, 由于线圈在环向上具有不对称性, 电子密度也具有明显的环向不均匀性. 随着气压的增大, 这种环向不均匀性逐渐增强. 通过减小线圈的开口, 可以提高等离子体的环向均匀性. 此外, 针对双线圈驱动放电, 还研究了内外双线圈电流幅值之比对于等离子体均匀性的影响. 结果表明, 通过改变内外线圈电流幅值的比值, 有利于提高等离子体的径向均匀性.

English Abstract

    全文HTML

    1.   引　言

    • 感性耦合等离子体源(inductively coupled plasma sources, ICPs)广泛应用于半导体芯片制造工艺中, 如刻蚀、沉积、离子注入等[1]. 与容性耦合等离子体源(capacitively coupled plasma sources, CCPs)相比, ICP具有诸多的优点, 例如ICP的放电气压低、等离子体密度高等[2].

      等离子体的均匀性是衡量半导体工业等离子体源的一个重要指标, 因为其直接影响刻蚀与沉积的均匀性, 从而影响芯片的生产质量. 因此, 如何提高等离子体的均匀性是等离子体源研究的一个热点课题. 目前, 研究和设计等离子体源的主要科学方法包括实验诊断和数值模拟. 一般来说, 实验诊断的成本较高, 而且由于工艺腔室的诊断窗口数量较少, 导致了实验诊断手段能够直接观测到的信息非常少. 与实验相比, 数值模拟技术同时具有时间优势和成本优势, 而且可以得到更多的腔室内部的等离子体信息, 例如各种粒子的密度、温度、等离子体的均匀性等. 因此, 国内外相关半导体设备公司非常重视数值模拟和仿真, 例如应用材料公司的Rauf等[3–5]开发了一系列程序, 用来对ICP和 CCP腔室的研发进行仿真.

      通常采用流体模型[6]、整体模型[7–9]和粒子模型[10,11]对等离子体源进行数值模拟. 流体模型由于其计算速度比粒子模型快, 同时模拟的维度要比整体模型高, 因此从各种模型中脱颖而出, 成为实际工艺等离子体源模拟的主要模型. 最为有名的流体仿真程序是Kushner[12]开发的HPEM. 其早期的工作主要是针对ICP进行二维流体模拟, 即假设ICP腔室完全是环向对称的, 因此可以在柱坐标下的r -z平面上进行模拟[13–15]. 经过这几十年的发展, 流体模型开始向三维模拟方向发展. 这是因为有一些效应必须采用三维模型才能进行研究, 例如线圈的结构引起的等离子体环向不均匀性. Kushner等[16]利用三维流体模型研究了线圈的形状和腔室结构对于等离子体参数均匀性的影响, 其结果表明, 合理地设计线圈的结构, 可以有效提高等离子体的均匀性. Panagopoulos等[17]基于三维有限元流体模型, 研究了ICP腔室的进气口、出气口、功率分布等对于粒子密度均匀性和刻蚀均匀性的影响, 放电气体为Cl2. 通过模拟发现, 当刻蚀过程是离子主导时, 沉积功率的分布是影响刻蚀均匀性的最重要因素. 使用对焦环可以显著降低环向的非均匀性. Brcka[18]基于COMSOL软件, 对大面积多线圈ICP源进行了三维流体模拟研究. 研究中对比了分布式平面多线圈ICP源和集成多线圈ICP源. 结果表明, 通过调节这两种结构ICP源的线圈电流、相位、频率, 可以调节等离子体的分布和化学反应. 然而, 该工作假设离子通量满足迁移扩散近似, 忽略了离子的惯性项, 当气压较低时, 结果存在一定的误差. 尽管以上提到了有关三维ICP模拟的工作, 然而, 与二维流体模拟相比, 三维 ICP源的模拟研究非常少, 而且仿真速度较慢. 目前的大多数三维ICP模拟都是基于COMSOL等商业软件, 而国外的三维流体学术代码获取受限, 因此为了对ICP源的三维效应进行模拟, 非常有必要自主开发三维流体快速模拟程序.

      本文基于自主开发的三维流体模拟程序[19], 对典型的圆柱形ICP工艺腔室进行了数值模拟, 研究了不同的气压、功率以及线圈结构对于等离子体均匀性的影响.

    2.   模型描述

    • 三维流体模型由两个模块组成, 即流体模块和电磁场模块. 电磁场模块负责求解射频线圈产生的感应电磁场, 以及等离子体的感性沉积功率密度. 流体模块负责求解各种粒子的输运过程. 下文分别对这两个模块进行描述.

      • 2.1.   电磁场模块

    • 根据法拉第感应定律, 线圈中的射频电流可以在等离子体中感应出感应电磁场, 等离子体中的电子在感应电场的作用下, 又可以产生感应电流. 感应电磁场满足麦克斯韦方程组:

      其中E为感应电场, B是感应磁场, ${\mu _0}$是真空磁导率, ${\mu _{\text{r}}}$是相对磁导率, ${\varepsilon _0}$是真空介电常数, ${\varepsilon _{\text{r}}}$是相对介电常数, ${{\boldsymbol{J}}_{{\text{coil}}}}$是线圈的电流密度. ${{\boldsymbol{J}}_{\text{p}}}$是等离子体电流密度, 其满足如下方程:

      式中$e$是单位电荷, ${n_{\text{e}}}$是电子密度, ${m_{\text{e}}}$是电子质量, ${\nu _{{\text{en}}}}$是电子与背景中性粒子的弹性碰撞频率. 假设电场和电流等物理量随时间的变化是简谐振荡的, 即对于任意的物理量$\boldsymbol A $, 有${\boldsymbol{A}}\left( {r, t} \right) = {\tilde{\boldsymbol A}}\left( r \right){{\text{e}}^{ - {\text{j}}\omega t}}$, 其中${\tilde{\boldsymbol A}}$为矢量$\boldsymbol A $的复幅值, $r$表示空间位置矢量, $\omega = 2{\text{π}}f$为放电的角频率, $f$为放电频率, j为虚数单位. 利用感应电场的散度为零, 并经过一系列的推导[19], 最终可以得到如下方程:

      其中${\sigma _{\text{p}}} = \dfrac{{{e^2}{n_{\text{e}}}}}{{{m_{\text{e}}}\left( {{\nu _{{\text{en}}}} - {\text{j}}\omega } \right)}}$为等离子体电导率. 一旦确定出感应电场和等离子体电流密度, 就可以得到射频电源沉积到等离子体中的感性沉积功率密度为

      可以看出, 感性沉积功率密度依赖于电子密度. 在确定电子的能量平衡方程时将用到${P_{{\text{ind}}}}$, 见下文介绍.

      需要说明在是, 本文主要关注H模式下的放电, 此时放电主要由线圈产生的感应电场维持, 因此没有考虑线圈的容性耦合. 在H模式下, 由于电子密度较高, 鞘层很薄, 线圈两端的电压对等离子体不起主导作用. 因此, 在H模式下, 忽略线圈的容性耦合是合理的. 然而, 当放电处于E模式时, 放电主要由线圈高压端产生的容性电场维持, 此时必须考虑线圈的容性耦合.

      • 2.2.   流体模块

    • 在等离子体流体力学模型中, 将电子和离子看作一个双流体, 它们分别由密度、流速和温度等物理量来描述. 离子的连续性方程为

      其中, ${n_{\text{i}}}$是离子的密度, ${{\boldsymbol{u}}_{\text{i}}}$是离子的定向速度, ${S_{\text{i}}}$是离子的源项.

      离子的定向速度通过离子的动量方程得到:

      其中, ${m_{\text{i}}}$是离子的质量; ${q_{\text{i}}}$是离子的电荷量; ${{\boldsymbol{E}}_{\text{s}}}$为空间电荷分离产生的静电场; ${T_{\text{i}}}$是离子的温度, 本工作假设离子的温度恒定, 为室温330 K; ${k_{\text{B}}}$是玻尔兹曼常数; ${{\boldsymbol{M}}_{\text{i}}}$是离子在碰撞过程中导致的动量转移.

      对于半导体工艺中采用的ICP源, 通常运行在H模式下, 其密度较高(${10^{17}}—{10^{18}}{\text{ }}{{\text{m}}^{ - 3}}$), 使得器壁处的鞘层很薄, 其厚度远远小于腔室的尺寸, 因此可以忽略鞘层对于放电的影响. 这样, 可以假设等离子体满足准电中性条件, 即:

      因此可以得到电子的密度${n_{\text{e}}}$. 另一方面, 由于电子的质量很轻, 其通量满足迁移扩散近似:

      其中${\mu _{\text{e}}} = \dfrac{e}{{{m_{\text{e}}}{\nu _{{\text{en}}}}}}$是电子的迁移率, ${D_{\text{e}}} = \dfrac{{{k_{\text{B}}}{T_{\text{e}}}}}{{{m_{\text{e}}}{\nu _{{\text{en}}}}}}$是电子的扩散系数.

      在ICP中, 电场可以分为两类, 第1类是由线圈产生的感应电场, 感应电场通过求解麦克斯韦方程组得到. 第2类是由电荷分离产生的静电场${{\boldsymbol{E}}_{\text{s}}}$, 本文通过令正电荷通量等于负电荷通量来确定${{\boldsymbol{E}}_{\text{s}}}$[19], 即离子通量${n_{\text{i}}}{{\boldsymbol{u}}_{\text{i}}}$等于电子通量${\varGamma _{\text{e}}}$, 由此得到:

      这种方法避免了求解耗时的泊松方程, 因此可以极大地提高程序的计算效率.

      电子的温度${T_{\text{e}}}$由如下能量守恒方程确定:

      式中, ${{\boldsymbol{Q}}_{\text{e}}}$是电子的能流矢量,

      其中${K_{\text{e}}} = {5}/{2}{k_{\text{B}}}{n_{\text{e}}}{D_{\text{e}}}$是电子的热传导系数; ${S_{{\text{energy}}}}$表示电子在碰撞过程中损失的能量.

      此外, 还要考虑激发态(或亚稳态)粒子的扩散过程, 其由如下连续性方程描述:

      其中, ${n_{\text{n}}}$是中性粒子的密度; ${S_{\text{n}}}$是中性粒子的源项; ${\varGamma _{\text{n}}}$是中性粒子的扩散通量, 其形式为${\varGamma _{\text{n}}} = - {D_{\text{n}}}\nabla {n_{\text{n}}}$, ${D_{\text{n}}}$是中性粒子的扩散系数[20,21].

      • 2.3.   计算区域与边界条件

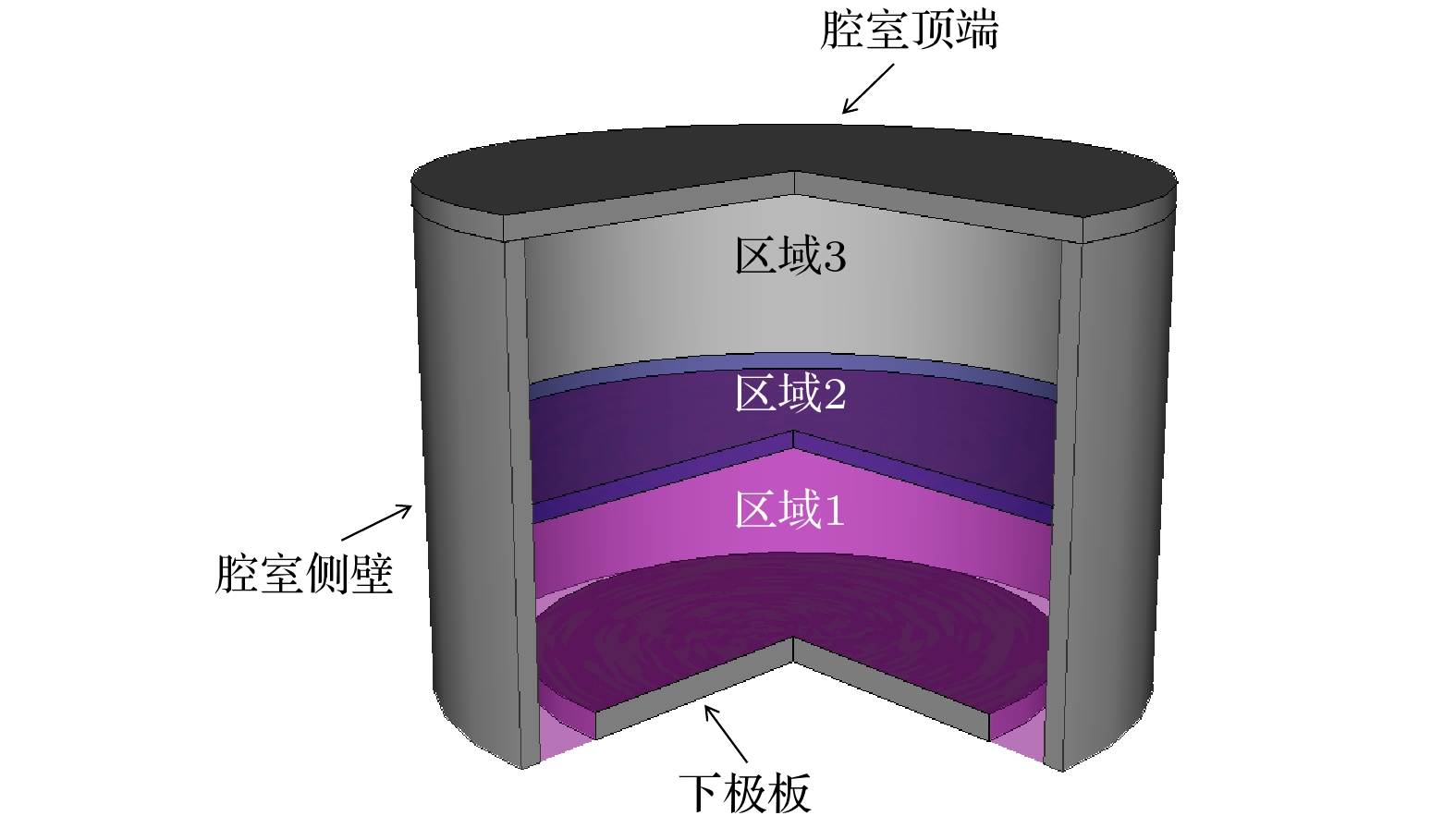
    • 图1为计算区域的示意图. 模拟中将ICP腔室划分为3个区域. 电磁模块的计算区域包括区域1、区域2和区域3. 流体模块的计算区域为区域1, 即等离子体区域. 当数值求解以上方程时, 需要给定合适的边界条件. 对于离子, 在腔室的器壁处以及介质窗下方, 离子的密度连续, 即$\nabla {n_{\text{i}}} \cdot {{\boldsymbol{e}}_{\text{n}}} = 0$, 离子的速度为玻姆速度${u_{\text{B}}} = {\left( {{{{k_{\text{B}}}{T_{\text{e}}}} {/ } {{m_{\text{i}}}}}} \right)^{1/2}}$, 且方向指向侧壁或介质窗; 在腔室器壁处以及介质窗下方, 电子的热通量满足${{\boldsymbol{Q}}_{\text{e}}} = 2{k_{\text{B}}}{T_{\text{e}}}{{\boldsymbol{\varGamma }}_{\text{e}}}$; 中性粒子的通量满足${\varGamma _{\text{n}}} = \dfrac{1}{4}{n_{\text{n}}}\sqrt {\dfrac{{8{k_{\text{B}}}{T_{\text{n}}}}}{{{\text{π}}{m_{\text{n}}}}}} $, 且方向指向边界, 其中${T_{\text{n}}} = 330{\text{ K}}$是中性粒子的温度, ${m_{\text{n}}}$是中性粒子的质量. 感应电场在腔室侧壁处、下极板以及腔室顶端满足理想导体边界条件, 即切向电场为零.

      • 2.4.   碰撞过程

    • 本文采用的放电气体为氩气, 模拟过程中一共考虑6种反应, 分别为电子与基态原子的弹性碰撞、激发碰撞和电离碰撞(编号1, 2, 3), 电子与亚稳态原子的电离碰撞和退激发碰撞(编号4和5), 以及亚稳态原子之间的电离碰撞(编号6), 如表1所列.

      • 2.5.   数值方法

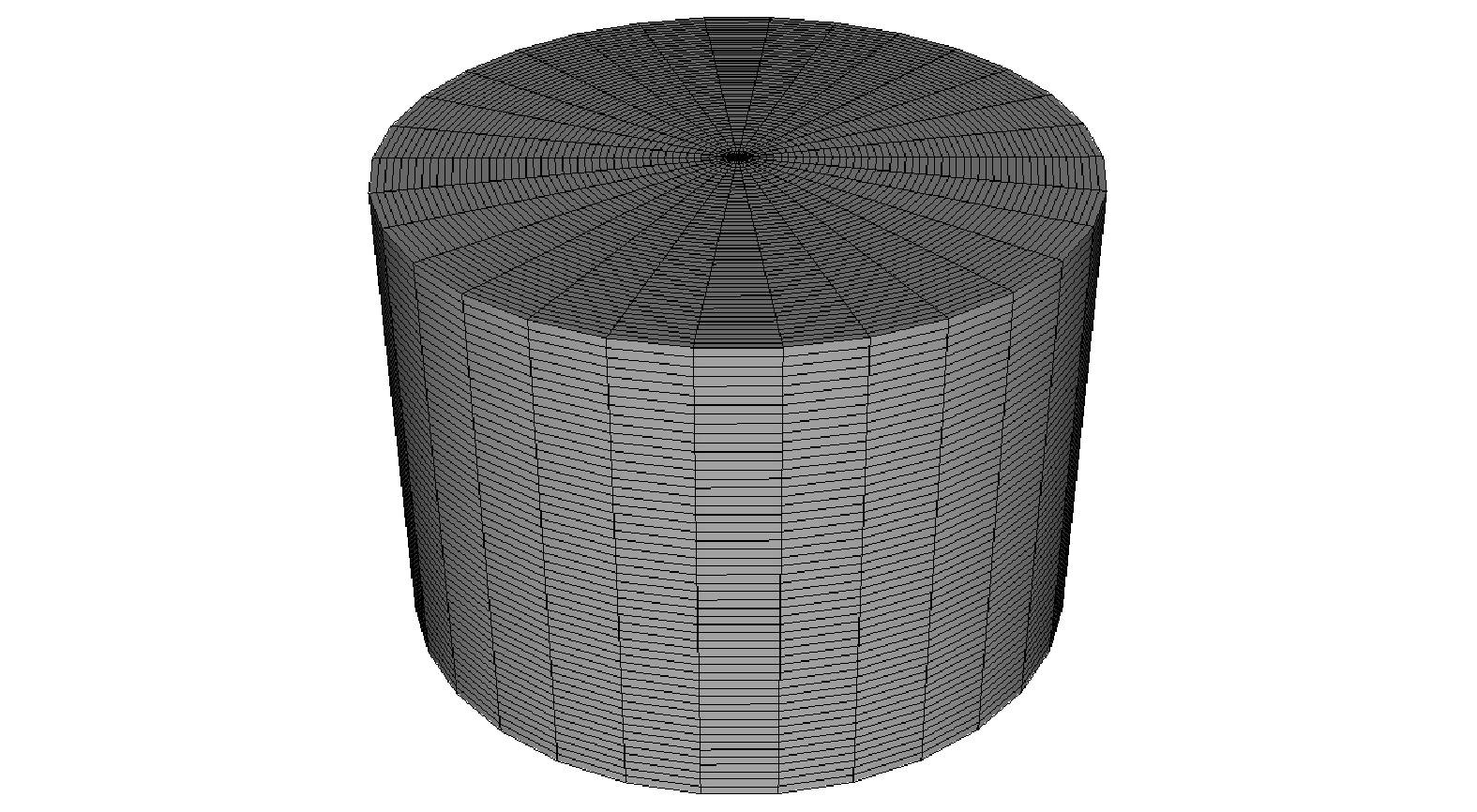
    • 在数值模拟中使用的离散网格如图2所示, 并将电磁场方程和等离子体流体方程在柱坐标系下进行离散, 且均采用有限差分法进行数值求解. 由于在电磁场模型中采用频域有限差分方法求解, 因此每个射频周期只需要求解一次电磁场. 此外, 电子能量方程在时间上采用隐式方法进行求解, 离子连续性方程和离子动量方程在时间上采用显式方法进行求解. 对于离子动量方程中的电场力项, 使用迎风格式进行离散, 而其他项均采用中心差分进行离散.

    3.   结果与讨论

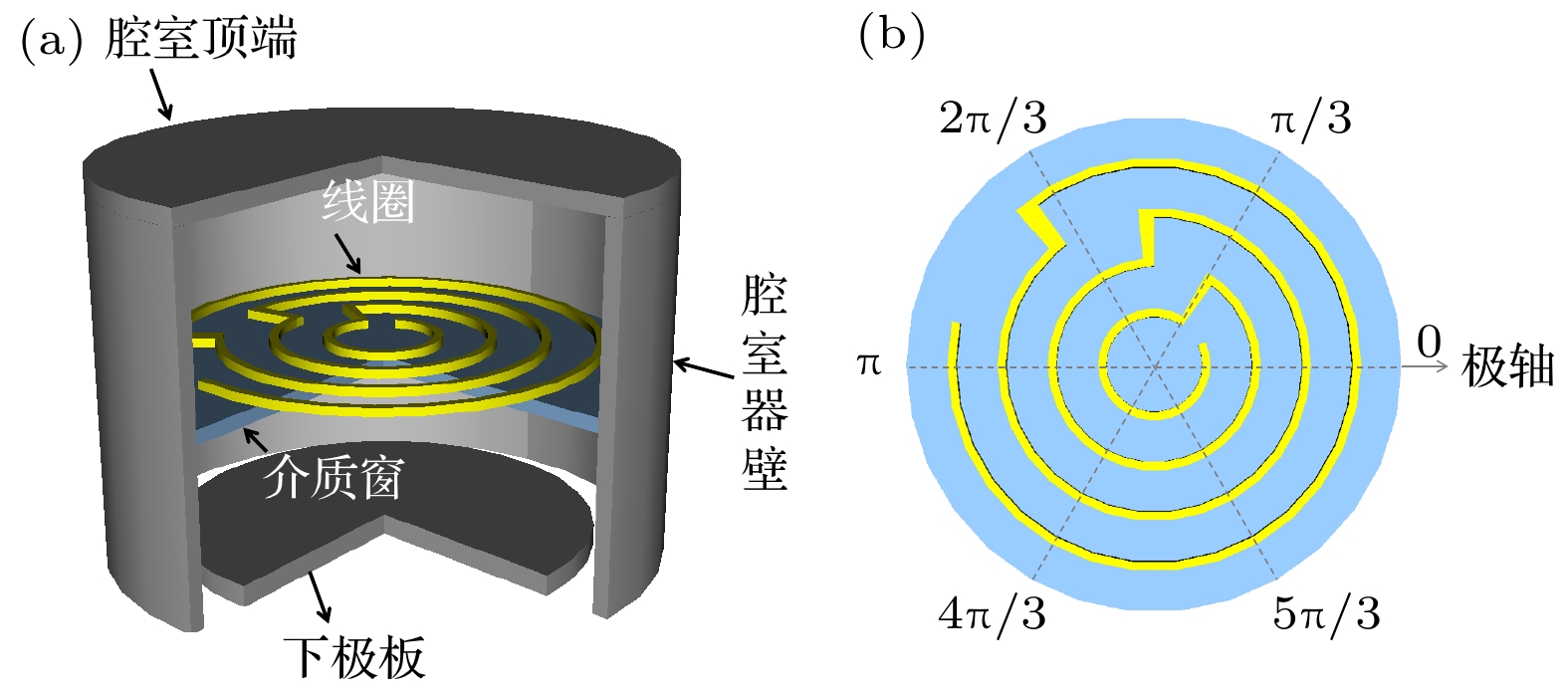
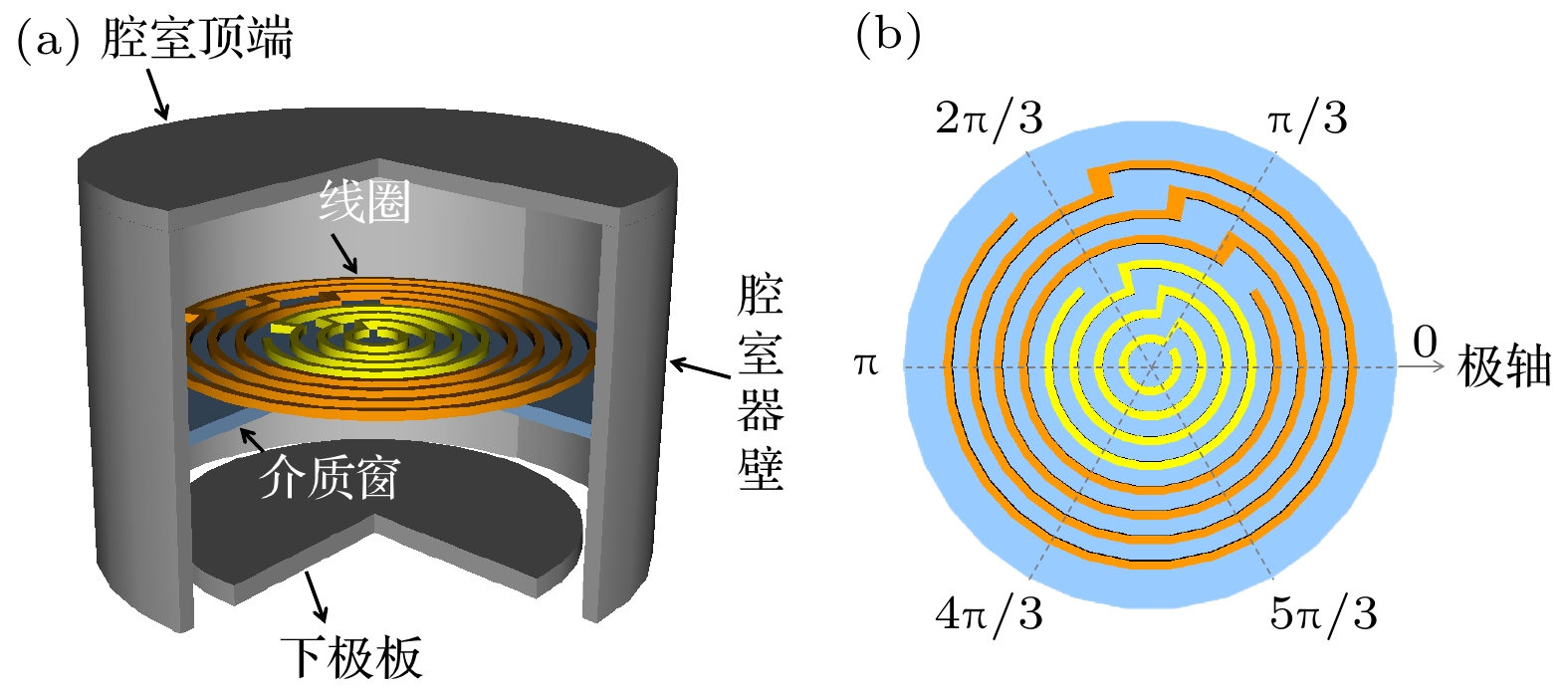
    • 放电腔室结构为圆柱形, 如图3(a)所示, 其中腔室的半径为15 cm, 等离子体区的高度为10 cm, 介质窗的厚度为1.2 cm, 屏蔽罩的高度为10 cm, 基片台的高度为1.2 cm. 射频线圈放置在介质窗上方. 线圈中的射频电流为13.56 MHz. 图3(b)所示为单组线圈的结构示意图, 单组线圈的半径以及开口大小均可以改变.

      • 3.1.   单组线圈对于等离子体均匀性的影响

      3.1.1.   等离子体参数的三维空间分布

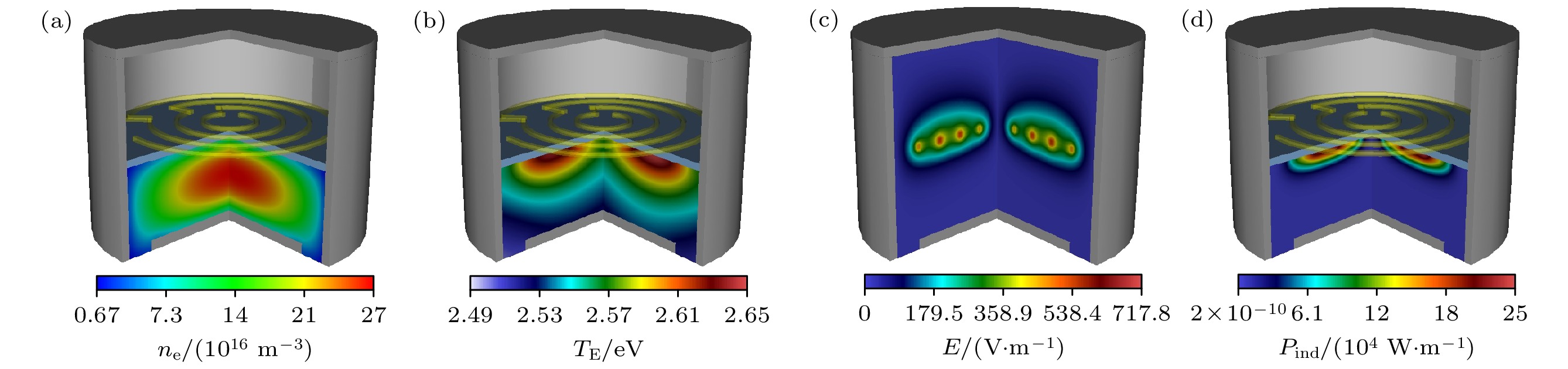
    • 图4给出了单线圈驱动放电的电子密度、电子温度、感应电场幅值和感性沉积功率密度的三维空间分布, 其中放电气压为2 Pa, 功率为100 W. 在Intel(R) Xeon(R) Silver 4114 CPU @ 2.20 GHz型号的计算机上, 运行 1000个射频周期只需要2 h左右. 从图4可以看到, 电子密度的最大值位于腔室中心处, 这是由电子的迁移和扩散过程所致. 电子温度的最大值位于介质窗的下方, 这是因为电子主要在位于介质窗下方的趋肤层内吸收能量, 因此此处的电子能量最大. 感应电场在线圈的周围最大, 在等离子体内部, 感应电场几乎为0, 这是因为等离子体对感应电场有屏蔽作用. 从感性沉积功率密度的分布可以明显看出趋肤层.

      • 3.1.2.   气压的影响

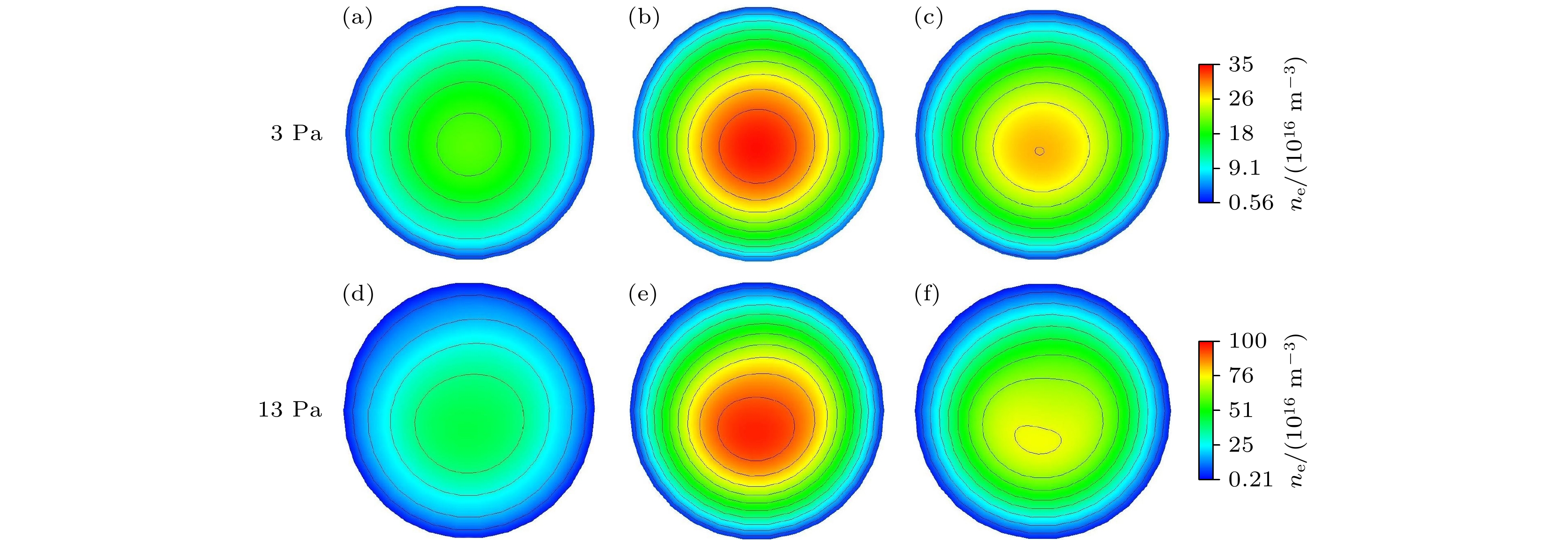
    • 图5为不同气压(3 Pa和13 Pa)、不同轴向位置的$r {\text{-}} \phi $平面上的电子密度的分布, 其中功率为100 W. 当气压为3 Pa时, 可以看到在介质窗下方2 cm处, 电子密度的分布微弱的偏离圆心, 这是由于线圈的环向非对称结构导致的. 即使在介质窗下方8 cm处, 电子密度的分布仍然存在微弱的偏心. 当气压为13 Pa时, 电子密度偏离圆心更加显著. 这是因为随着气压的增大, 电子与背景中性粒子的弹性碰撞频率增大, 电子的迁移率和扩散系数减小, 电子密度的局域性增强, 因此均匀性变差. 同时可以注意到, 随着距离介质窗越来越远, 电子密度的环向非均匀性得到明显的改善. 这是因为在远离介质窗的位置, 线圈对于等离子体的影响减弱, 线圈产生的电场主要分布在趋肤层内.

      • 3.1.3.   功率的影响

    • 图6所示为不同放电功率下, 基片台上方1 cm处$r\text{-}\phi $平面上的电子密度分布, 其中放电气压为 2 Pa. 从图6可以看出, 当功率从200 W增加到500 W时, 电子密度明显增大, 而放电功率对于电子密度的分布没有明显的影响, 电子密度呈现出中间区域高、边缘低的分布.

      • 3.1.4.   线圈开口的影响

    • 通过上文的分析可知, 当气压较高时, 线圈的形状会对等离子体的均匀性产生显著的影响, 下面进一步研究线圈形状的作用. 为了方便说明问题, 这里以单匝线圈为例.

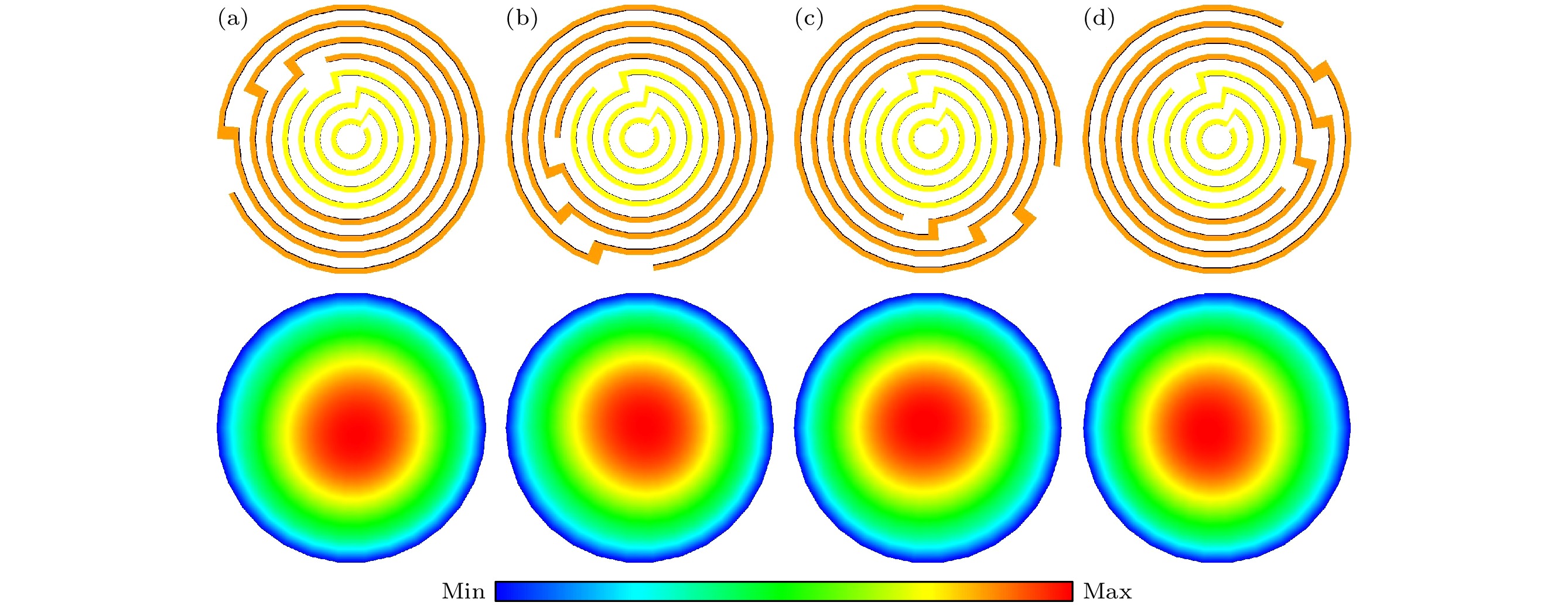
      首先研究线圈的开口对于等离子体均匀性的影响. 图7 所示为4种不同开口大小的线圈, 其中线圈的半径为6 cm, 图7(a)—(d)中线圈的开口弧度分别为${\text{π}}/15$, ${\text{π/}}5$, ${\text{π/}}3$, $7{\text{π/}}15$. 图8为不同线圈开口大小的情况下, 介质窗下方5 cm处的$r\text{-}\phi $平面内的电子密度分布. 其中气压为12 Pa, 功率为300 W. 当线圈的开口较小时, 电子密度的环向均匀性较好, 随着线圈的开口越来越大, 电子密度的分布逐渐偏离圆心, 即电子密度的环向均匀性明显变差. 这是因为线圈开口处感应电场和感性沉积功率密度明显低于其他位置, 导致开口对应位置处的电子密度最低, 破坏了环向的对称性.

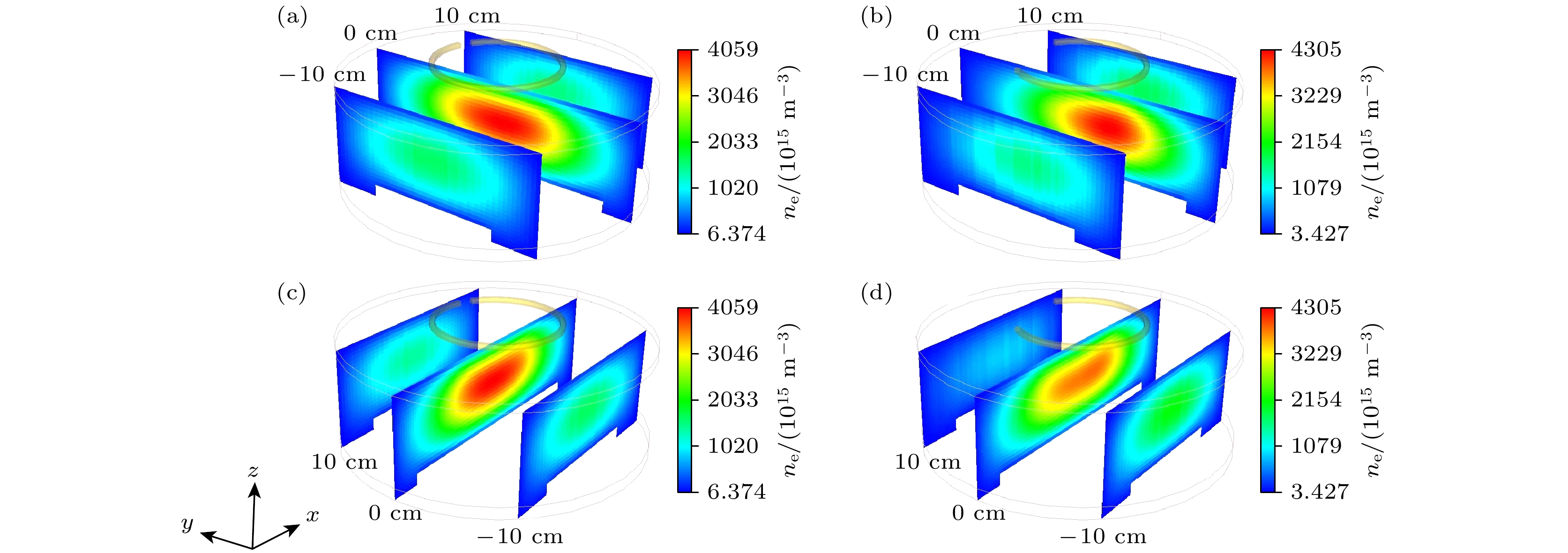
      图9(a), (b)为不同$x$向位置的$y{\text{-}}z$平面上的电子密度的分布, 线圈开口弧度分别为${\text{π}}/15$和$7{\text{π/}}15$. 其中放电气压为12 Pa, 功率为300 W. 可以看到, 当线圈的开口为${\text{π}}/15$时, $y{\text{-}}z$平面上的电子密度分布比较均匀, 而当线圈的开口为$7{\text{π/}}15$时, 电子密度的分布明显向$y$轴的负方向偏移. 这是因为线圈的开口主要在$y$轴的正方向, 此处感应电场和电离率低于$y$轴的负方向, 电子密度也在$y$轴的正方向较高. 图9(c), (d)为不同$y$方向位置的$x{\text{-}}z$平面上的电子密度的分布, 线圈开口弧度分别为${\text{π}}/15$和$7{\text{π/}}15$. 可以看到, 在两种线圈开口下, $x{\text{-}} z$平面上的电子密度分布都很均匀. 这是因为线圈的开口主要沿$y$轴方向, 并没有破坏$x$方向的对称性. 综上所述, 较大的线圈开口会明显破坏等离子体的均匀性, 减小线圈开口的大小有助于提高等离子体的均匀性. 然而需要指出的是, 线圈的开口太小也会带来负面的效应. 在实验上, 由于线圈的一端接地, 另一端接功率源, 因此两端之间存在明显的电压降, 若线圈两端距离太近, 会使得线圈两端间的静电场过强, 进而导致E模式过强, 甚至发生打火. 所以在实际的线圈设计中, 应该保持平衡, 从而确定最佳的开口大小.

      • 3.1.5.   线圈半径的影响

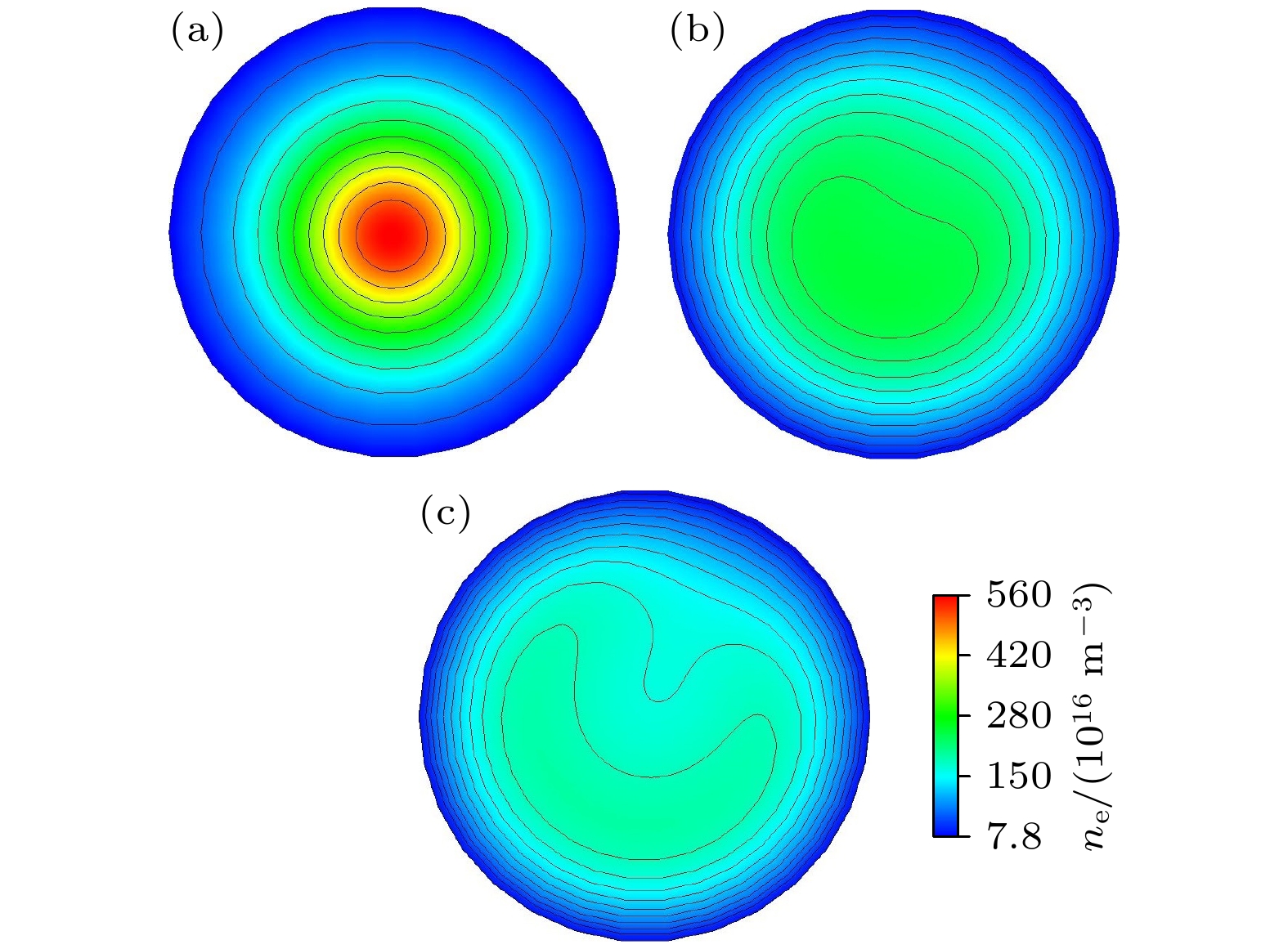
    • 除了线圈开口大小的影响, 线圈半径也会对等离子体的分布产生影响. 图10 给出了不同半径的单匝线圈放电情况下, 在介质窗下方 5 cm 处的$r\text{-}\phi $平面内电子密度的空间分布, 其中气压为 12 Pa, 功率为 300 W, 线圈的开口弧度为${\text{π}}/15$, 线圈的半径分别为 3 cm, 9 cm 和 12 cm. 可以看到, 随着半径的增大, 等离子体的密度有所下降, 等离子体的径向均匀性变好, 然而环向均匀性变差.

      • 3.2.   内外双线圈对于等离子体均匀性的影响

    • 上文研究了单组线圈放电对于等离子体均匀性的影响, 然而单组线圈的可调节参数有限. 下面采用一种更复杂的线圈结构, 即图11所示的内外双线圈. 这种线圈具有更多的可调节参数, 例如内外线圈的相对位置以及内外线圈的电流幅值之比均可调节.

      • 3.2.1.   内外线圈相对位置的影响

    • 图12为不同的内外线圈相对位置下, 介质窗下方1 cm处的$r\text{-}\phi $平面上的电子密度的分布. 其中气压为12 Pa, 放电功率为300 W. 一共考虑了4种相对位置, 即case 1—case 4. 固定内部线圈的位置, 旋转外部线圈的位置. 内外线圈的电流幅值比固定为 1∶1. 可以看到随着外部线圈的旋转, 电子密度的分布也发生了明显的旋转. 虽然改变内外线圈的相对位置可以明显改变电子密度的分布, 然而电子密度仍然存在明显的环向不均匀性, 即内外线圈的相对位置对等离子体的环向均匀性没有明显的调制作用.

      • 3.2.2.   内外线圈电流幅值比的影响

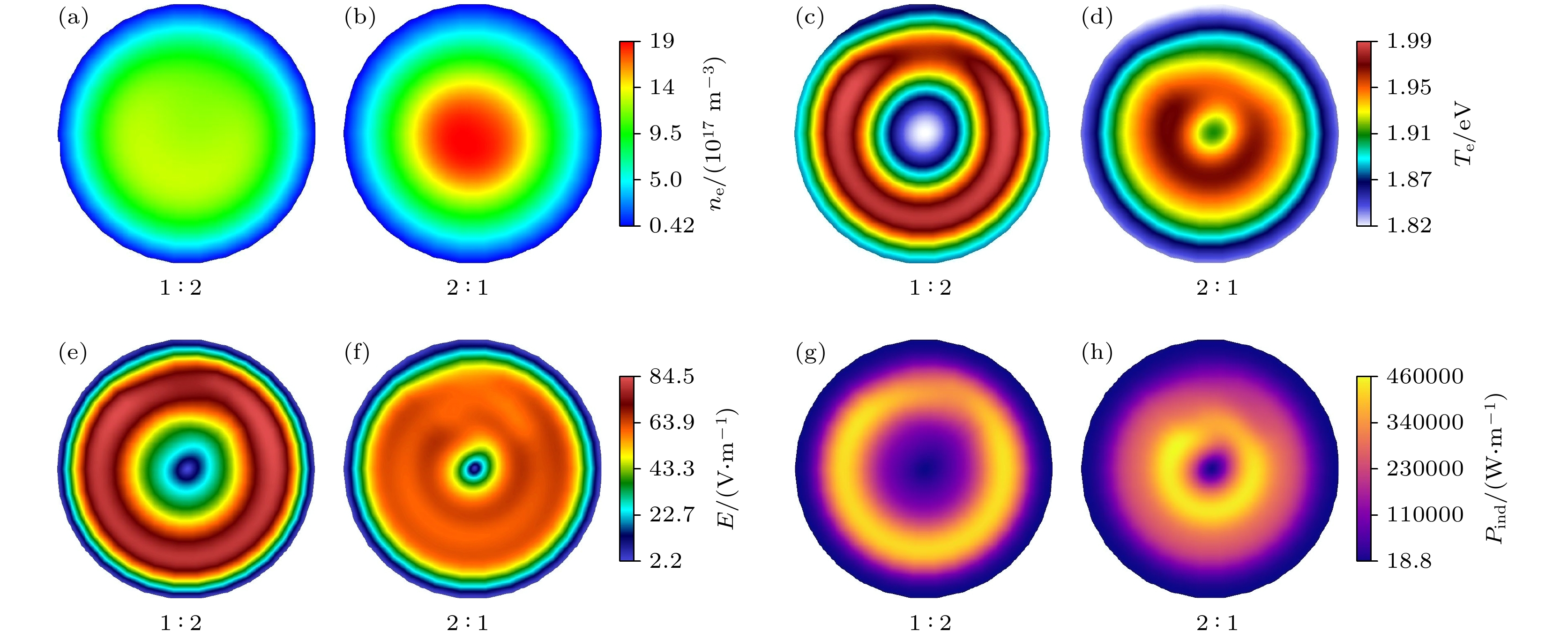
    • 最后, 研究不同的内外线圈电流幅值比对于等离子体参数的影响. 图13为电子密度、电子温度、感性沉积功率密度以及感应电场的幅值在介质窗下方1 cm处的$r\text{-}\phi $平面上的分布. 其中气压为12 Pa, 功率为300 W, 内外线圈的电流比分别为1∶2和2∶1. 从图13(a)—(d)可以看到, 当内外线圈电流的幅值比为1∶2时, 电子密度的分布较为分散, 径向均匀性较好; 电子温度在外侧一圈的值较大, 径向中心的电子温度较低. 而当内外线圈电流的幅值比为2∶1时, 电子密度的分布更加局域在中心, 即中心处与边缘处的电子密度相差较大, 电子密度的径向均匀性较差. 内侧一圈的电子温度较高. 不同电流幅值比下, 电子密度和电子温度的分布可以通过感应电场以及感性沉积功率密度的分布进行解释.

      图13(e), (f)所示为不同电流幅值比下的感应电场幅值的分布. 当电流幅值比为 1∶2 时, 由于外侧线圈的电流较大, 因此产生的感应电场大于内侧线圈产生的电场, 感应电场整体上呈现出外侧大、内侧小的趋势. 同时由于感性沉积功率密度正比于感应电场幅值的平方, 因此此时的感性沉积功率密度也呈现出外侧大、内侧小的分布, 如图13(g)所示. 当电流幅值比为 2∶1 时, 内侧线圈的电流较大, 此时内侧线圈产生的感应电场较大, 感性沉积功率密度也呈现出内侧大、外侧小的分布, 如图13(h)所示. 总体来说, 电流幅值比为 2∶1 时, 等离子体的径向均匀性更好. 因此, 通过调节内外线圈的电流幅值比可以有效调节等离子体的径向均匀性.

    4.   结　论

    • 本文针对感性耦合放电, 建立了一种改进的等离子体双极扩散模型, 并自主开发了三维流体模拟程序, 研究了真实工艺腔室几何结构下气压、功率和线圈的形状对于等离子体均匀性的影响. 研究表明, 随着功率的增大, 等离子体的密度明显增大, 但是功率对于等离子体的环向均匀性影响不大. 随着气压的升高, 等离子体的环向均匀性变差, 随着距离介质窗越来越远, 这种环向的非均匀性得到改善. 减小线圈的开口大小有利于提高等离子体的均匀性. 通过对内外双线圈放电进行研究, 可以发现, 内外双线圈的相对位置对于等离子体的环向均匀性影响不大. 调节内外双线圈的电流幅值比, 可以有效地调节等离子体的径向均匀性. 当内外线圈的电流幅值比为1∶2时, 等离子体的径向均匀性更好. 在未来的研究中, 我们将考虑等离子体与背景气体的流场、热场的耦合, 并对复杂工艺气体(如碳氟气体)放电进行三维模拟. 另外, 当放电处在E模式时, 在双线圈放电中两线圈相邻处, 可能会有较强的电场, 会对放电的径向均匀性产生一定的影响. 在以后的工作中, 将把容性耦合考虑到模型中, 进一步完善模型的功能.

    参考文献 (22)

目录

/

返回文章
返回