-
在神经科学领域, 神经元的离子通道阻塞与噪声对其放电特性具有重要影响[1,2]. 离子通道作为神经元细胞膜上的关键蛋白结构, 调控离子流的进出, 从而影响神经元的兴奋性和传导能力[3], 进一步影响神经元能量传递的效率[4,5]. 阻塞这些通道或改变它们的噪声特性, 可以显著改变神经元的放电模式[1], 从而影响神经网络的整体功能. 这些离子通道固有的特性不仅决定了神经元动作电位的激发模式, 也是理解信息传递机制的关键.
离子通道的固有特性对神经元放电特性的影响已经被广泛认可, 具体的实验研究也进一步证实了离子通道阻塞在调控神经元动作电位中的关键作用. 例如, Narahashi和Moore[6]通过生理实验证明了河豚毒素(tetrodotoxin, TTX)和四乙胺(tetraethylammonium, TEA)对钠离子(Na+)和钾离子(K+)通道的阻塞作用. 王荣等[7]对Hodgkin-Huxley (HH)神经元研究了离子通道阻塞对神经放电行为的影响, 发现Na+通道阻塞会抑制神经元兴奋而K+通道阻塞可逆转神经元兴奋性, Zhou等[2]继续研究发现离子通道阻塞与周期性信号刺激的HH神经元放电稳定性之间的复杂关系. 刘少宝等[8]在网络尺度上揭示了离子通道阻塞会导致螺旋波的形成. 同时, 周期性放电、簇放电[9]以及混沌放电等现象[10]及其动力学形成过程也被深入研究[11], 并且有研究发现离子通道阻塞可以在HH神经元组成的神经网络中增强和优化spike的相干与同步, 进一步说明离子通道阻塞在一定程度上可以影响信号的传输[12].
神经元动作电位的特性还与噪声等因素密切相关, 大量研究揭示了输入噪声引起的随机共振现象及其生物物理机制[13]. 神经元内离子通道的固有噪声对动作电位发放的影响也受到广泛关注. 生理研究表明, 神经元对多次相同输入往往会表现出不同的动作电位[14,15], 相关学者已经证实通道噪声会显著改变神经元的动力学行为, 例如产生自发的动作电位[16,17]、影响脉冲时间精度等[18,19]. 因此, Faisal等[14]提出一种神经元固有通道噪声理论, 区别于输入信号噪声与突触噪声, 以表征神经元离子通道固有的随机性. 生理实验发现, 通道噪声在影响前海马皮层神经元的动力学过程中发挥了关键作用[20], 同时也会显著影响星状神经元射频模式的变化以及带来阈下振荡[21]. 在模型仿真领域, 马尔科夫[22,23]、蒙特卡罗[24,25]等随机模拟方法被广泛应用到神经元通道噪声的模拟中, 然而往往伴随复杂的计算. Fox和Lu[26]通过耦合离子通道之间电压依赖的开闭概率, 结合Fokker-Planck随机方程, 修正了随机HH神经元模型, 简化其模型复杂度的同时提升了随机模拟的准确性. Goldwyn等[27,28]分析对比了HH神经元输入电流噪声、Subunit噪声、 Conductance噪声和马尔科夫链4种噪声模型, 其中马尔科夫过程最贴近实际神经元随机发放的状态, Conductance噪声与马尔科夫过程的差异最小. 文献[29–31]采用随机微分方程替代蒙特卡罗, 基于改进的Langevin-like方法[29,30]进行近似, 准确地再现了精确微观模拟在各种条件下的统计特性[31].
为了更详细地探索神经元非线性动力学的内在机理, 引入了分岔分析[32]这一动力学分析工具, Guckenheimer和Labouriau[33]针对HH神经元进行了复杂的分岔分析, 发现随参数h的变化, 动作电位表现出局限于参数空间区域的多种形式, 引起了人们对神经元进行动力学分岔分析的关注, 黎丽等[34]发现了兴奋性自突触在亚临界Hopf分岔附近压制神经元电活动的反常作用, Guo等[35]建立了一个由FHN和HR神经元组成的记忆电阻耦合的异质神经网络, 以时滞为控制参数从理论上推导了在稳定点附近存在Hopf分岔的条件, 将分岔分析应用于异质神经网络. 在应用方面, Xie等[36]通过设计滤波反馈控制器控制HH神经元Hopf分岔的产生, 以期望达到治疗癫痫[37]、帕金森[38,39]等疾病的效果. 分岔分析和神经元通道噪声研究不仅加深了我们对神经元动作电位变化的理解, 也对神经性疾病如癫痫的治疗策略提供了新的见解, 展示了理论研究在临床应用中的重要性.
迄今为止, 关于神经元通道阻塞与通道噪声的研究主要集中于单室神经元模型. 然而, 随着计算科学和生物技术的不断进步, 神经元仿真模型已经取得了显著的发展. Ward和Rhodes[40]结合HH神经元模型与树突结构, 在形态学上构建了多室神经元模型, 成功捕捉到LIF神经元模型无法生成的动作电位. 此外, 多室神经元模型在树突隔室中实现了神经形态硬件上的异或逻辑求解[41,42], 引发了科学界对其广泛关注. 因此, 分析多室神经元模型离子通道阻塞和噪声对其放电特性的影响, 揭示其动力学过程的内在机理具有重要的意义与价值. 海马体, 尤其是其CA3区域, 因其循环链接的复杂网络结构而被认为是空间导航和情景记忆的关键区域[43], 同时该区域的神经元也显示出易发生癫痫活动的特性[44,45]. 在此背景下, CA3区域椎体细胞的放电模式得到了深入研究, 以期揭示其在神经网络中的功能. Pinsky和Rinzel[46]于1994年提出了PR (Pinsky-Rinzel)神经元两室模型, 该模型作为海马体CA3区最小的多室神经元模型, 已被广泛应用于研究锐波纹波振荡[47]、速率编码和时间编码[48,49], 以及树突形态对放电模式的影响[50]等多个方面. 2024年, Zhang 等[51]简化双室PR神经元模型并应用于脉冲神经网络(SNN)以实现优秀的时间分类能力, 该网络具有较快的收敛速度以及低能耗的特点, 在SNN领域取得重大突破. 因此, 针对双室PR神经元进行深入的机理分析具有重要意义. Hahn和Durand[52]在2001年采用分岔分析研究了神经元放电特性随钾浓度变化的转变, 但未提供详尽的分析方法. Atherton等[53]通过采用连续函数改写原始的PR神经元方程, 解决了非连续性的问题, 并采用数值延拓的方法执行全系统分岔和快慢动力学分析, 从而揭示了钙离子和树突电压相位差如何影响爆发和稳定尖峰状态之间的不规则尖峰活动. 改进的PR神经元模型不仅再现了原始模型的放电方式, 精确描述了海马体CA3区的特性, 还因其便于分岔分析, 成为研究通道噪声动力学的理想对象.
多室神经元的精细结构能够同时捕捉时空特性, 具有丰富的响应和内在机理, 其在记忆、决策等生理活动上具有特殊意义. 尽管以往的研究已为多室神经元模型的动力学分岔分析奠定了坚实的基础, 但当前研究在分析多室神经元模型时, 往往忽视了通道噪声的影响; 同时, 关于神经元通道阻塞的研究也主要限于单室HH神经元, 而以PR神经元为代表的多室模型通过引入树突室, 考虑了电位沿树突和轴突的传递特性[54], 能够更加精确地模拟神经元的复杂形态和电传导特性, 更符合神经元互连的结构属性. 同时, 多室神经元中特有的钙离子(Ca2+)浓度会影响神经递质释放的概率, 对多节律性放电具有关键作用[55]. 因此, 本研究基于改进的PR 神经元模型[53], 通过引入离子通道阻塞与噪声并特别引入Ca2+通道阻塞, 旨在扩展对神经元动力学过程的理解. 通过Hopf分岔、双参数分岔分析、频率特性和变异系数(coefficient of variation, CV)等指标的研究, 本文深入探讨了不同离子通道阻塞对PR神经元放电特性的影响. 此外, 通过分别构建PR神经元Subunit噪声模型和Conductance噪声模型, 结合峰峰间隔分析(inter-spike interval, ISI)研究其响应特性, 并使用低于阈值的刺激研究其是否存在随机共振现象. 本研究分析了不同通道噪声过程对多室神经元放电特性的影响, 探讨了这些噪声过程在改善多室神经元放电性能中的差异. 这些发现不仅丰富了我们对多室神经元在通道阻塞影响下动作电位模拟的理解, 还拓展了通道噪声在调控神经元电生理活动中作用的认识, 为未来研究神经系统中复杂的信息编码方式提供了新的视角和工具.
-
本模型基于平滑的PR神经元模型[53], 结合HH神经元模型中的Na+, K+通道阻塞, 并针对多室神经元中Ca2+离子对节律性放电的关键作用, 特别引入了Ca2+通道阻塞机制, 构建带离子通道阻塞的PR神经元模型, 从而模拟PR神经元模型中Ca2+通道的特性, 以探索不同程度的离子通道阻塞如何影响神经元的频率特性以及在Hopf分岔附近的放电行为, 具体表述如(1)式所示:
其中,
${V_{\text{s}}}$ 为胞体室膜电位,${V_{\text{d}}}$ 为树突室膜电位,${C_{\text{m}}}$ 为细胞膜电容,$ {I_{{\text{Leak}}}} $ 为漏电流,$ {I_{{\text{Na}}}} $ 为胞体室瞬态钠电流,$ {I_{{{\text{K}}_{{\text{DR}}}}}} $ 为延迟整流钾电流,$ {I_{{\text{Ca}}}} $ 为持续钙电流,$ {I_{{{\text{K}}_{{\text{Ca}}}}}} $ 为钙激活的钾电流,$ {I_{{{\text{K}}_{{\text{AHP}}}}}} $ 为超极化后的钾电流,$ {I_{{\text{DS}}}} $ 和$ {I_{{\text{SD}}}} $ 分别为胞体室和树突室耦合的电流,$ {I_{{\text{Sapp}}}} $ 和$ {I_{{\text{Dapp}}}} $ 分别为胞体室和树突室输入的电流, p 为胞体室影响的电压占比整个神经元模型比例. 在本研究中, p = 0.5, 即PR神经元中胞体室和树突室各占一半.$ {g_{{\text{Na}}}} $ ,$ {g_{{{\text{K}}_{{\text{DR}}}}}} $ ,$ {g_{{\text{Ca}}}} $ ,$ {g_{{{\text{K}}_{{\text{Ca}}}}}} $ ,$ {g_{{{\text{K}}_{{\text{AHP}}}}}} $ ,$ {g_{\text{C}}} $ 和$ {g_{\text{L}}} $ 为最大电导参数,$ {V_{{\text{Na}}}} $ ,$ {V_{\text{K}}} $ ,$ {V_{{\text{Ca}}}} $ ,$ {V_{\text{L}}} $ 分别是钠、钾、钙和漏电流的反转电位, m, h, n, s, q, c是取决于驱动电流的电压激活和失活门控参数,$ \chi ({\text{Ca}}) $ 为钙的饱和参数,$ {x_{{\text{Na}}}} $ ,$ {x_{\text{K}}} $ 和$ {x_{{\text{Ca}}}} $ 分别是Na+, K+, Ca2+通道参数的阻塞系数, 输入采用恒定电流刺激, 模型参数的取值见表1. -
Subunit噪声指在单个离子通道的亚单位水平上, 由于亚单位的随机活动(如蛋白门控的随机开闭)而导致的随机噪声, 侧重于微观层面. 因此, 考虑到上述离子通道噪声的特性, 门控变量服从方程[27]:
其中, Na+通道和K+通道总数分别为
$ {N_{{\text{Na}}}} = {\rho _{{\text{Na}}}} \cdot S $ ,$ {N_{\text{K}}} = {\rho _{\text{K}}} \cdot S $ , S为神经元膜面积大小,$ {\rho _{{\text{Na}}}} $ 和$ {\rho _{\text{K}}} $ 分别表示Na+和K+通道每平方微米上的通道数量, 称为膜密度, 分别为$ {\rho _{{\text{Na}}}} = 60 {\text{ μ}}{{\text{m}}^{{ - }}}^{2} $ ,$ {\rho _{\text{K}}} = 18 {\text{ μ}}{\text{m}}^{-2} $ . 将表征离子通道数量的$ {N_{{\text{Na}}}} $ 和$ {N_{\text{K}}} $ 置于通道噪声模型的分母上, 以实现神经元通道噪声随离子通道数量增加而下降的效果. -
Conductance噪声来源于多种离子通道的随机开闭引起的整体膜电位变化, 表现为膜电导的宏观波动. 本模型基于PR神经元胞体室的电导模型, 电流平衡方程为[28]
该模型为确定性神经元模型, 包含漏电流、Na+电流、K+电流及树突和胞体输入电流. 以Na+电流为例,
$ {I_{{\text{Na}}}} = {g_{{\text{Na}}}}m_\infty ^2 h\left( {{V_{\text{s}}} - {V_{{\text{Na}}}}} \right) $ , 其简化形式为$ {I_{{\text{Na}}}} = {g_{{\text{Na}}}}(t)\left( {{V_{\text{s}}} - {V_{{\text{Na}}}}} \right) $ , 由于神经元存在大量的离子通道,$ {g_{{\text{Na}}}}(t) $ 等参数在大量的研究中被认为是确定性值[56]. 然而, 从微观角度,$ {g_{{\text{Na}}}}(t) $ 等参数随时间具有随机性, 存在不确定性. 因此, 本节从微观视角, 针对PR模型引入单个离子通道的随机开闭, 并将其拓展到N个通道组成的离子通道群, 从而分析对神经元模型中平衡电流的影响[31].首先, 推理得到Na+, K+, Ca2+通道的转移概率矩阵A, 即跃迁矩阵(详见附录A). 如(4)式和(5)式所示:
再通过计算其非零特征根绝对值和的倒数来确定模型中的时间常数
${\tau _0}$ , 稳态方差$\sigma _n^2$ 通过附录A中的计算以及PR神经元离子通道本身固有的开关数量确定, 最终得到PR神经元Conductance噪声模型的$\sigma _n^2$ 和${\tau _0}$ 见表2和表3. -
实验部分利用Xppauto软件中Cvode求解器对神经元动作电位进行数值模拟, 神经元动作电位仿真的时间步长为0.01 ms. 同时用到该软件中的Auto功能对模型进行单参数分岔和双参数分岔分析, 最后, 本文用ISI和CV指标对神经元放电特性进行分析, 并使用信噪比(signal to interference plus noise ratio, SNR)和信息熵(entropy, H)分别研究PR神经元中的随机共振现象和编码能力. 其中ISI公式为
式中,
$ {t_i} $ 和$ {t_{i + 1}} $ 分别代表第i和i+1次动作电位的发生时间. CV公式如下:其中, ISI的平均值和ISI平方的平均值分别为
$ \langle T\rangle = \displaystyle\frac{1}{n}\sum\nolimits _{i=1}^{n}\left({t}_{i}-{t}_{i-1}\right), $ $ \langle {T}^{2}\rangle =\displaystyle\frac{1}{n}\sum\nolimits _{i=1}^{n} ({t}_{i}- {t}_{i-1})^{2} $ . 变异系数CV表征神经元放电的稳定性, CV值越小说明放电越规律. 信噪比的公式如下:信噪比是用来衡量信号强度相对于背景噪声强度的一个重要指标, 其单位是dB, 随机共振是指在适度的噪声水平下, 系统的输出信噪比反而会达到一个峰值, 这意味着噪声在一定条件下可以增强系统对信号的响应.
$ {P_{{\text{signal}}}} $ 表示信号功率,$ {P_{{\text{noise}}}} $ 代表噪声功率. 信息熵的公式如下:其中, X是神经元的脉冲序列, 由一系列脉冲
$ {x_i} $ 组成,$ P({x}_{i}) $ 是序列中第$ i $ 种放电模式出现的概率, n是总的放电模式数量. 信息熵越高, 代表信号中所含信息越丰富, 但是相对地, 其信号的随机性更强. -
平滑PR 神经元模型输入电流阈值为0.3 mA, 即刚好能产生动作电位, 当输入电流为5 mA时具有较为稳定的动作电位, 因此, 本节的实验使用0.3 mA和5 mA的输入电流, 分析PR神经元在不同阻塞程度和输入电流下的动作电位时间序列, 如图1和图2所示.
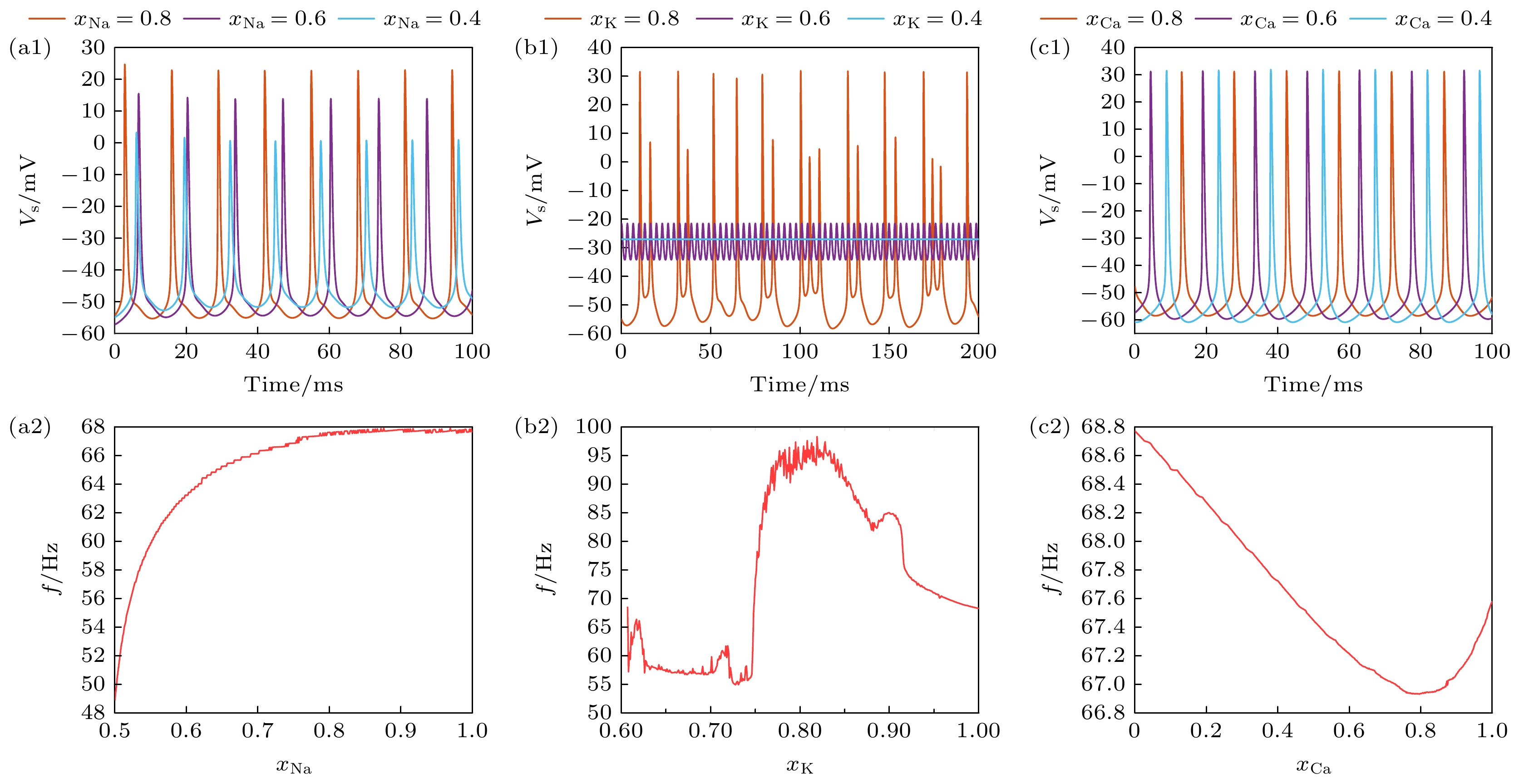
当Na+通道阻塞程度(
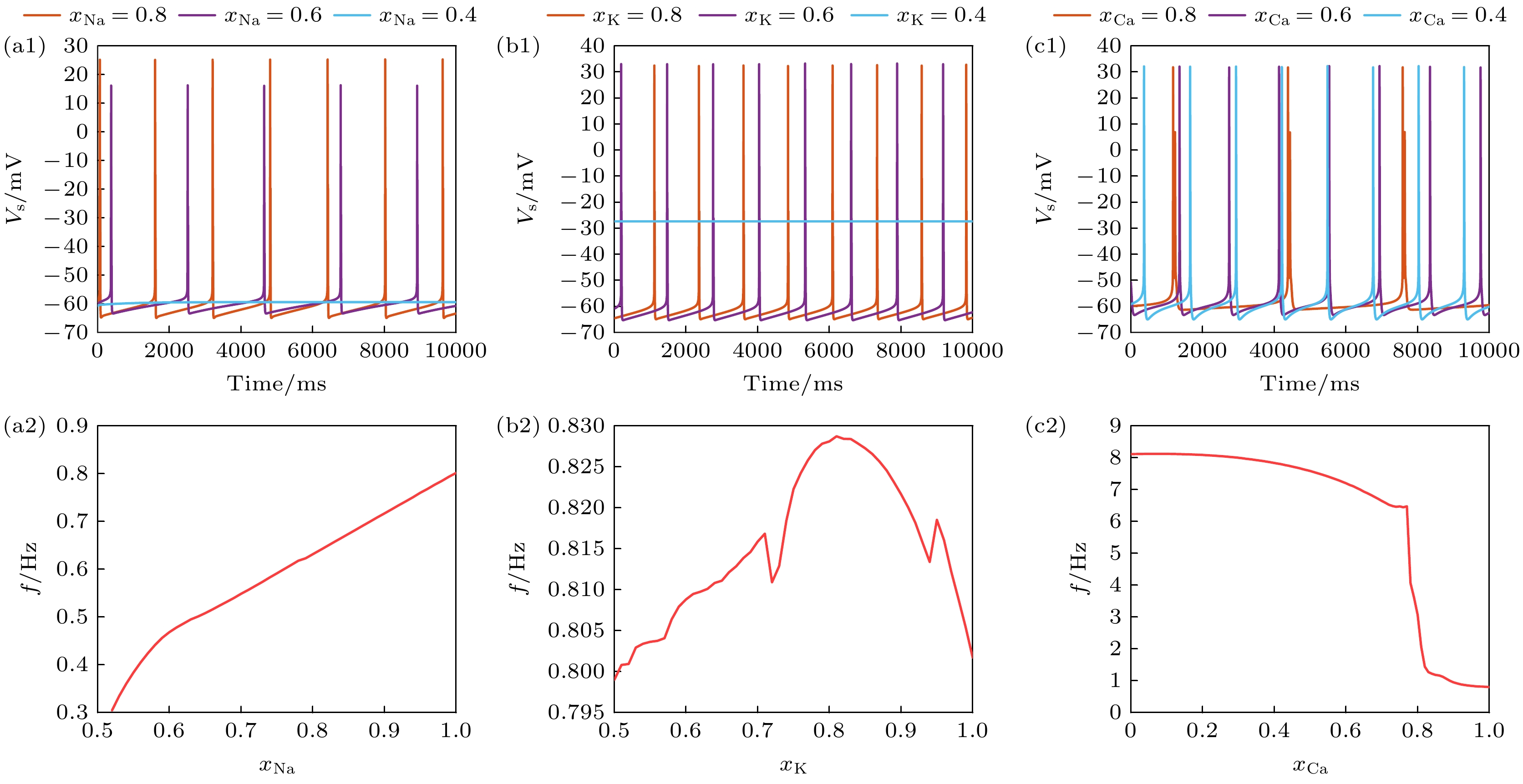
$ {x_{{\text{Na}}}} = 1 $ 表示无阻塞)分别在0.8, 0.6和0.4时, 在10000 ms内神经元动作电位尖峰个数分别为7, 5, 0, 表明随着Na+通道阻塞程度的增加, 动作电位发放频率逐渐减小, 且当阻塞程度达到一定数值时神经元会进入静息状态如图1(a1)所示. 在分析PR神经元频率特性与Na+通道阻塞的关系后可以发现, 钠离子阻塞会抑制PR神经元放电, 如图1(a2)所示. 相对地, 针对K+通道的分析揭示了其阻塞程度增加, 放电频率先增后减的趋势, 如图1(b1), (b2)所示. 而Ca2+通道阻塞则会导致放电频率先显著增大后趋近于稳定值, 整体呈现倒S形, 如图1(c1), (c2)所示. 为了证明上述离子通道阻塞对PR神经元放电特性影响的普遍性, 我们还选取了$ {I_{{\text{Sapp}}}} = 5 {\text{ mA}} $ 的输入电流进行分析, 如图2所示.图2展示了在
$ {I_{{\text{Sapp}}}} = 5 {\text{ mA}} $ 的输入电流下, PR神经元模型中各离子通道的阻塞程度对动作电位发放状态的影响, 以探索其与$ {I_{{\text{Sapp}}}} = 0.3 {\text{ mA}} $ 时的差异. 实验结果显示, 在高电流输入下, Na+通道阻塞抑制放电的特性没有变化, 但随着Na+通道阻塞程度增加, 其频率下降的速度变快, 如图2(a1), (a2)所示; K+通道适度阻塞促进放电的特性仍然存在, 但当K+通道阻塞过大时, 放电频率新表现出振荡特性, 如图2(b1), (b2)所示; Ca2+通道阻塞整体促进放电的特性没有发生变化, 但是相比于低电流输入刺激时, 其频率的变化显得更有规律, 表现出与K+通道阻塞相反的特性, 即适度的Ca2+通道阻塞抑制放电, 但最终促进放电, 如图2(c1), (c2)所示. 这些发现强调了输入电流强度在离子通道阻塞对神经元动作电位调控中的重要作用.进一步分析发现, 当K+, Na+通道阻塞到一定程度时, 神经元会进入不同的静息电位; Na+通道完全阻塞时, 胞体室的动作电位稳定在–60 mV. K+通道阻塞时, 胞体室动作电位分别稳定在–26 mV, 而Ca2+通道阻塞只会调节神经元放电特性, 并不会改变其放电状态. 这些结果符合离子通道阻塞导致的内部离子流动变化的预期, 揭示了K+, Na+通道开放程度在神经元动作电位发放过程中的关键调控作用.
-
为了更加深刻地探索PR神经元离子通道阻塞对神经元放电特性的影响, 本研究采用
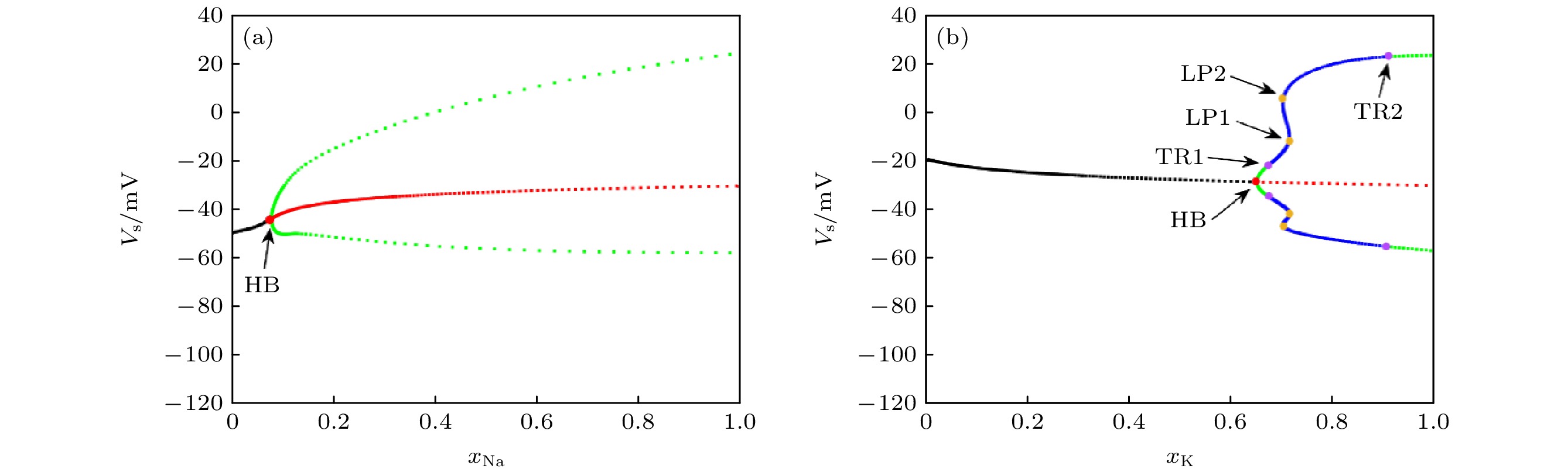
$ {I_{{\text{Sapp}}}} = 5 {\text{ mA}} $ 的输入电流进行离子通道阻塞分岔分析, 初始步长为0.1, 得到如图3所示的PR神经元动作电位关于离子通道阻塞的分岔图.由于Ca2+通道阻塞不会导致PR神经元动作电位状态的变化, 因此不适宜用于分岔分析. 图3中红色点表示Hopf分岔节点, 其左边代表神经元处于稳定状态(静息状态), 右边表示周期振荡状态, K+通道阻塞的各个分岔节点在图3(a)中标出, 而Na+通道阻塞的分岔相比K+通道更加单一如图3(b)所示, 其Hopf分岔节点在
$ {x_{{\text{Na}}}} = 0.0798 $ 处. 结合表4, 可以具体分析K+通道分岔的具体节点: 在Hopf分岔节点$ {x_{\text{K}}} = 0.6507 $ 处, PR神经元动作电位发放状态从稳定的静息态转向周期发放状态. 在节点处进行Hopf分岔分析, 其中紫色节点表示环面分岔点1和2 (TR1和TR2), 黄色节点分别表示极限点分岔1和2 (LP1和LP2).通过上述实验可以得到详细的动力学分析过程, 在TR1处, 神经元的动作电位由稳定的周期解(限环)过渡到拟周期状态(环面), 动作电位不再是由单一周期构成, 而是多周期叠加. 在LP1处, 系统稳定性的根本性变化, 在LP2处动作电位处于拟周期或混沌状态, 无明显的放电周期, 在TR2处动作电位从拟周期态成功转变为周期性发放状态. 这些结果揭示了PR神经元在不同K+ 离子通道阻塞程度下动作电位发放模式的关键变化, 增强了我们对其动力学行为的理解. 为了进一步探索
$ {x_{\text{K}}} $ ,$ {x_{{\text{Na}}}} $ 的Hopf分岔节点与输入电流的变化, 将在后续的研究中引入双参数分岔分析. -
为了详细分析离子通道阻塞程度和输入电流对平滑PR神经元动作电位频率的影响, 本节采用ISI和CV指标, 展示了频率与通道阻塞程度及输入电流三者的关系. 具体实验在输入电流
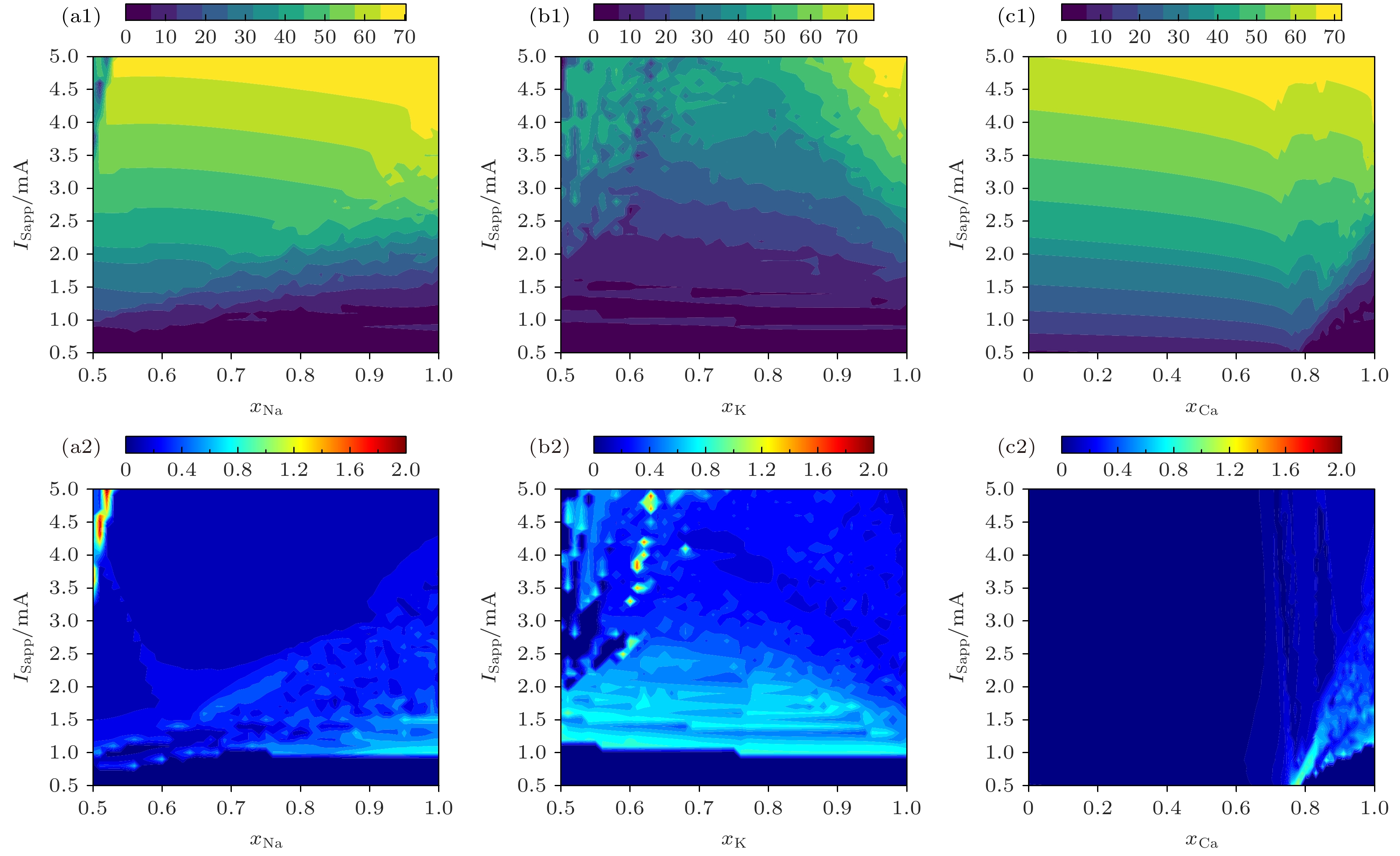
$ {I_{{\text{Sapp}}}} $ 为0.3 mA和5 mA的条件下进行, 以深入理解PR神经元频率特性的变化规律, 相关结果如图4所示. 在较低的$ {I_{{\text{Sapp}}}} $ 下, Na+和K+通道阻塞对动作电位发放频率的影响有限; 随着$ {I_{{\text{Sapp}}}} $ 的增大, 通道阻塞对放电频率的影响显著增强; 与此相反, Ca2+通道阻塞在低$ {I_{{\text{Sapp}}}} $ 下显著影响放电频率, 而在高$ {I_{{\text{Sapp}}}} $ 下影响减弱.随着
$ {I_{{\text{Sapp}}}} $ 增大, 适度的K+通道阻塞继续促进动作电位发放, 但最大发放频率对应的K+阻塞程度也随$ {I_{{\text{Sapp}}}} $ 提高. Na+通道阻塞对发放频率的抑制作用保持不变, 在中低程度阻塞下发放频率缓慢下降, 而在高程度阻塞时迅速下降, 且这一转折点随$ {I_{{\text{Sapp}}}} $ 增大而提高. 针对Ca2+通道, 存在一个与$ {I_{{\text{Sapp}}}} $ 无关的临界阻塞值(约0.78), 高于此值时放电频率表现混沌, 低于此值时放电频率稳定, 如图4(c1)所示.最后, 对比图4(a2), (b2), (c2), 发现Na+, K+通道在高阻塞时CV值较高, 放电更加混沌; 而Ca2+通道则相反, 显示出较高的放电规律性. 从
$ {I_{{\text{Sapp}}}} $ 角度看, Na+, K+和Ca2+通道在低$ {I_{{\text{Sapp}}}} $ 时均表现出更混沌的放电特性 -
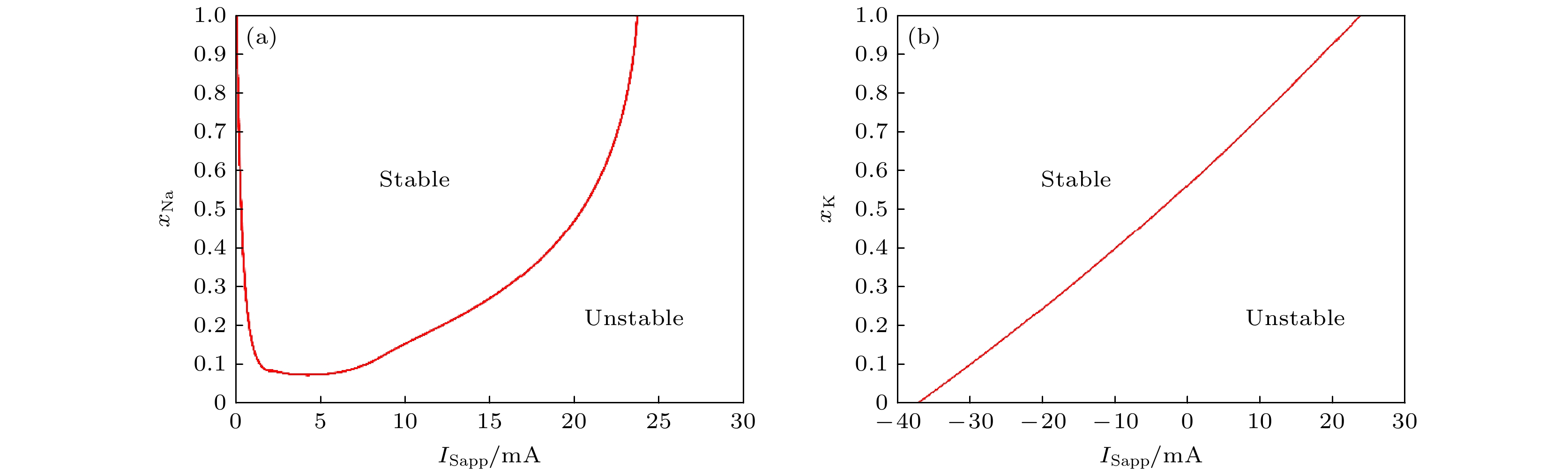
由于K+和Na+通道阻塞的Hopf分岔节点会随输入电流产生变化, 为揭示其变化规律, 本研究采用
$ {I_{{\text{Sapp}}}} $ 和$ {x_{\text{K}}} $ ,$ {x_{{\text{Na}}}} $ 组合进行双参数分岔分析, 结果如图5所示. 通过分析图5(a), (b), 我们确认了PR神经元在输入电流低于0.3 mA或高于23.7 mA时维持静息状态, 这与Atherton等[53]的研究结果相符. 此外, K+通道的Hopf分岔节点随输入电流呈近似线性递增的趋势, 表明随电流增大, 神经元对K+通道开放度的依赖性增强, 从而需要更高的通道开放度以触发动作电位. 相反, Na+通道Hopf分岔节点的变化可近似为线性下降和指数上升两阶段, 反映了其复杂的内在机理.在输入电流为0.3 mA时, 有效的动作电位需要K+通道开放系数为0.57, 而Na+通道需完全开放. 当电流增大到1.3 mA时, K+通道的开放度线性增大以支持连续放电, 而Na+通道迅速下降至0.1. 进一步增大电流至3.6 mA时, Na+通道的开放度需求降至最低点0.075, 显示出动态调整的复杂性. 当输入电流达到23.7 mA时, 两种离子通道均需完全开放才能激发动作电位, 这一点强调了在极端电流条件下, 神经元放电依赖于高度精确的离子通道控制. 这些发现为神经元如何在不同电生理环境下调整其电活动提供了深刻的洞见, 有助于理解神经系统在复杂条件下的适应性调节.
-
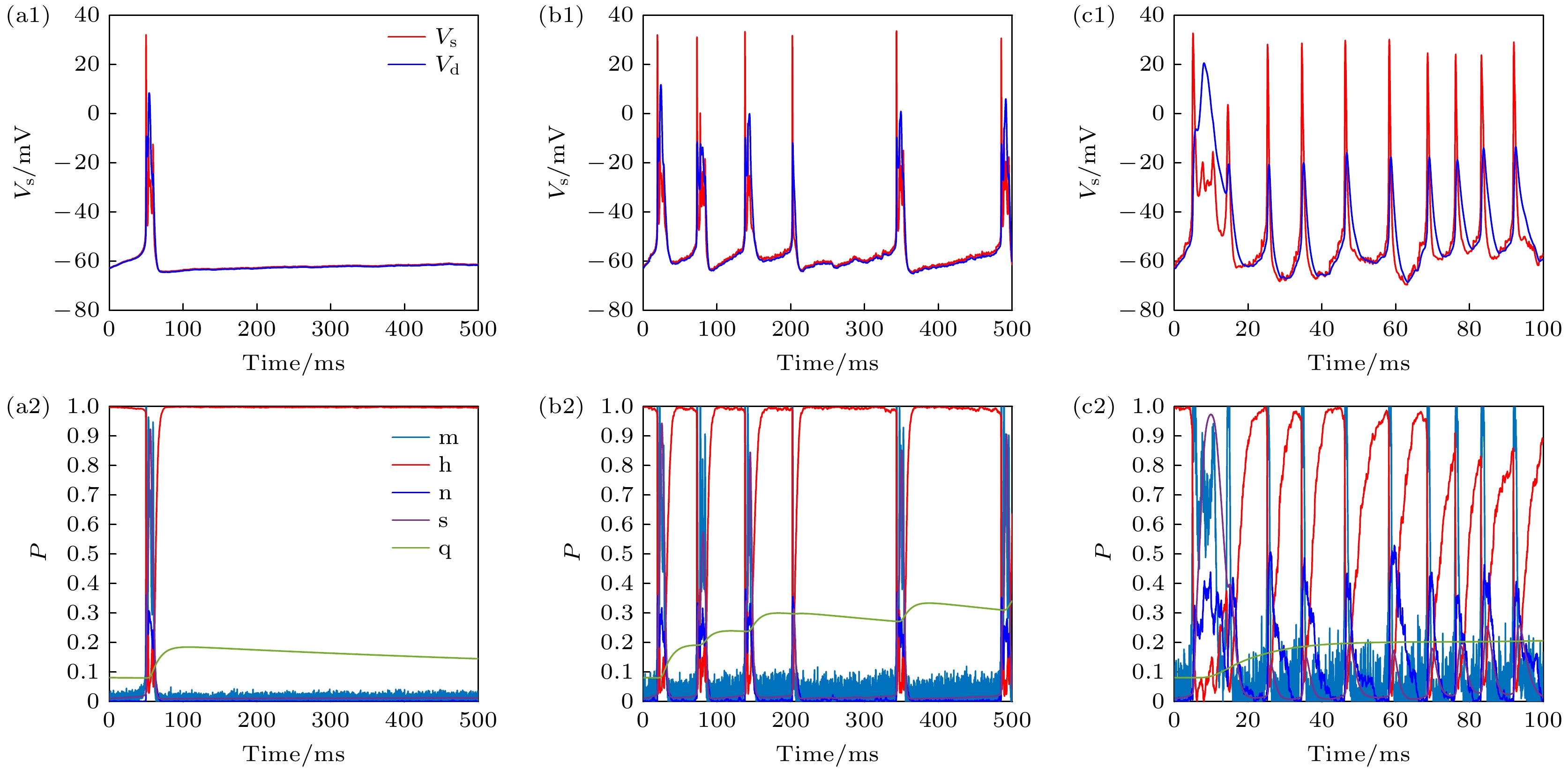
本小节先使用0.3 mA的最小驱动电流刺激不同膜面积的PR神经元以观察其随机共振现象. 通过改变PR神经元Subunit噪声模型的膜面积, 研究了离子通道数量对动作电位发放的影响. 由图6可知, 随着通道噪声增加, 神经元对微弱刺激的反应敏感性增强, 表现出随机共振现象. 这一结果表明, 通道噪声的存在显著促进了PR神经元在低输入电流下的动作电位发放, 揭示了噪声在神经元动态行为中的功能性角色.
分析图6不仅可以观察到通道噪声引起的随机共振现象, 同时发现随着通道噪声的增强, 神经元随机波动也增强, 脉冲放电变得不稳定、不平滑, 如图6(a1), (b1), (c1)所示. 为了进一步分析其内在机理, 我们研究了PR神经元Subunit噪声模型各个离子通道开关概率的变化以解释其动作电位变化的过程. 图6(a2), (b2), (c2)中的m代表Na+通道激活变量, 表示Na+通道打开概率; h代表Na+通道失活变量, 表示Na+通道关闭概率; n表示K+通道激活变量, 表示K+通道打开概率, s表示Ca2+通道激活变量, 表示和Ca2+通道打开概率; q表示慢K+电流激活变量, 与Ca2+激活后的超极化电流有关. 通过分析神经元放电的底层离子通道的开闭变化, 可以发现随着通道噪声的增加, 其m, h, n的随机性和波动增加, 而s和q虽然会发生变化, 但没有影响其平滑的变化过程. 因此, 在Subunit噪声模型中, 虽然各个离子通道都会影响其动作电位的随机性, 但m, h, n对动作电位的影响仍然是主要的, 而s和q不会影响动作电位的波动, 主要调控其放电节律.
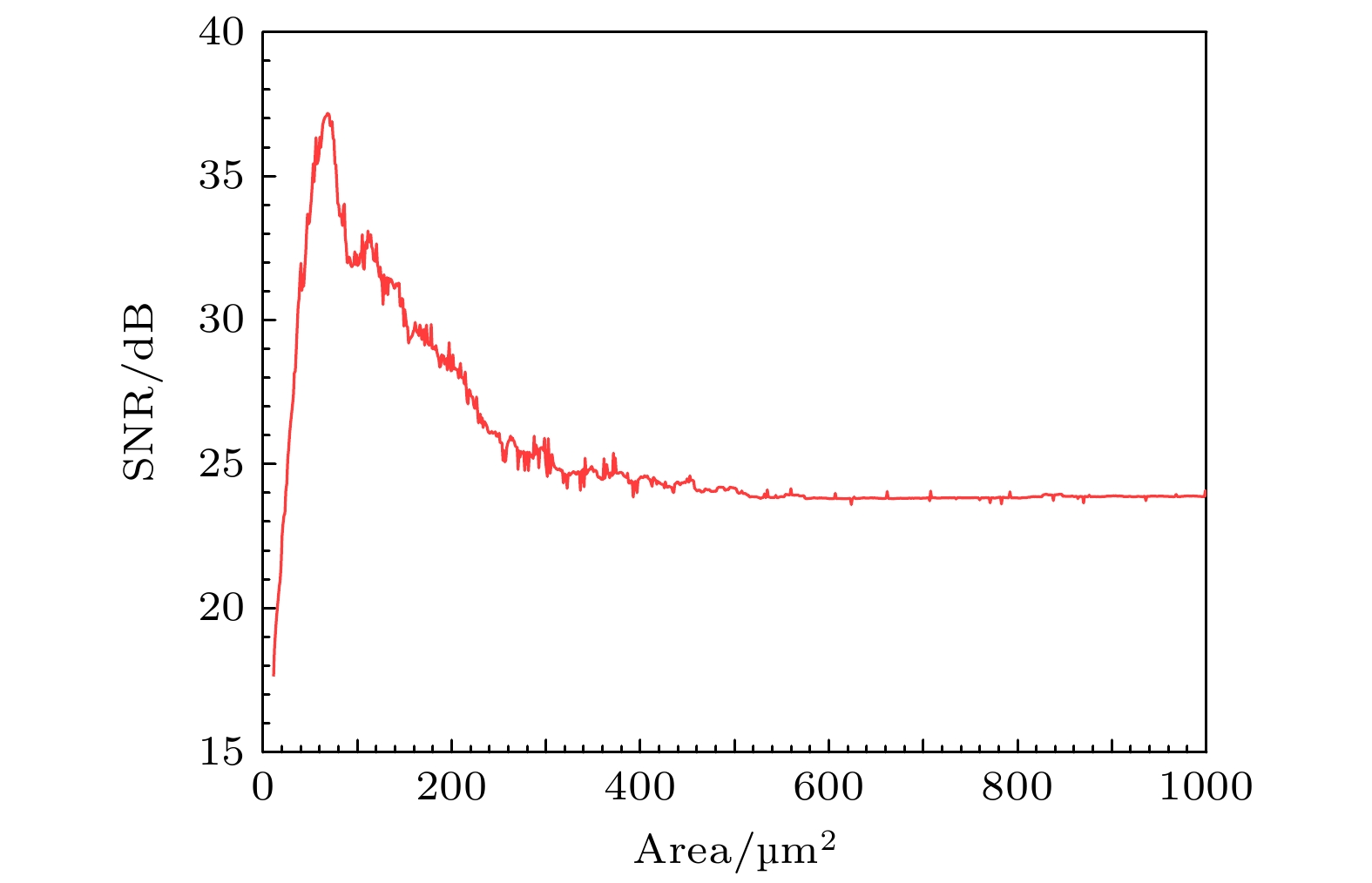
为了进一步研究PR神经元Subunit噪声模型的随机共振现象, 本节引入SNR进行分析, 具体如(8)式所示. 实验使用0.25 mA的次阈电流输入进行刺激, 仿真时间和仿真步长分别为30000 ms和0.01 ms, 对神经元输出的时序脉冲信号进行 傅里叶变换, 并进行功率谱的计算, 最终计算其在不同膜面积下的信噪比, 结果如图7所示.
图7中的SNR值随膜面积的增大先上升后下降, 存在一个明显的峰值. 当膜面积上升到72.18 μm2时, 其对应的SNR值也上升到最高值37.47 dB, 随后, 随着神经元膜面积的增大, 信噪比缓慢下降并最终趋于稳定, 这一现象较好地诠释了PR神经元Subunit噪声模型中的随机共振现象.
-
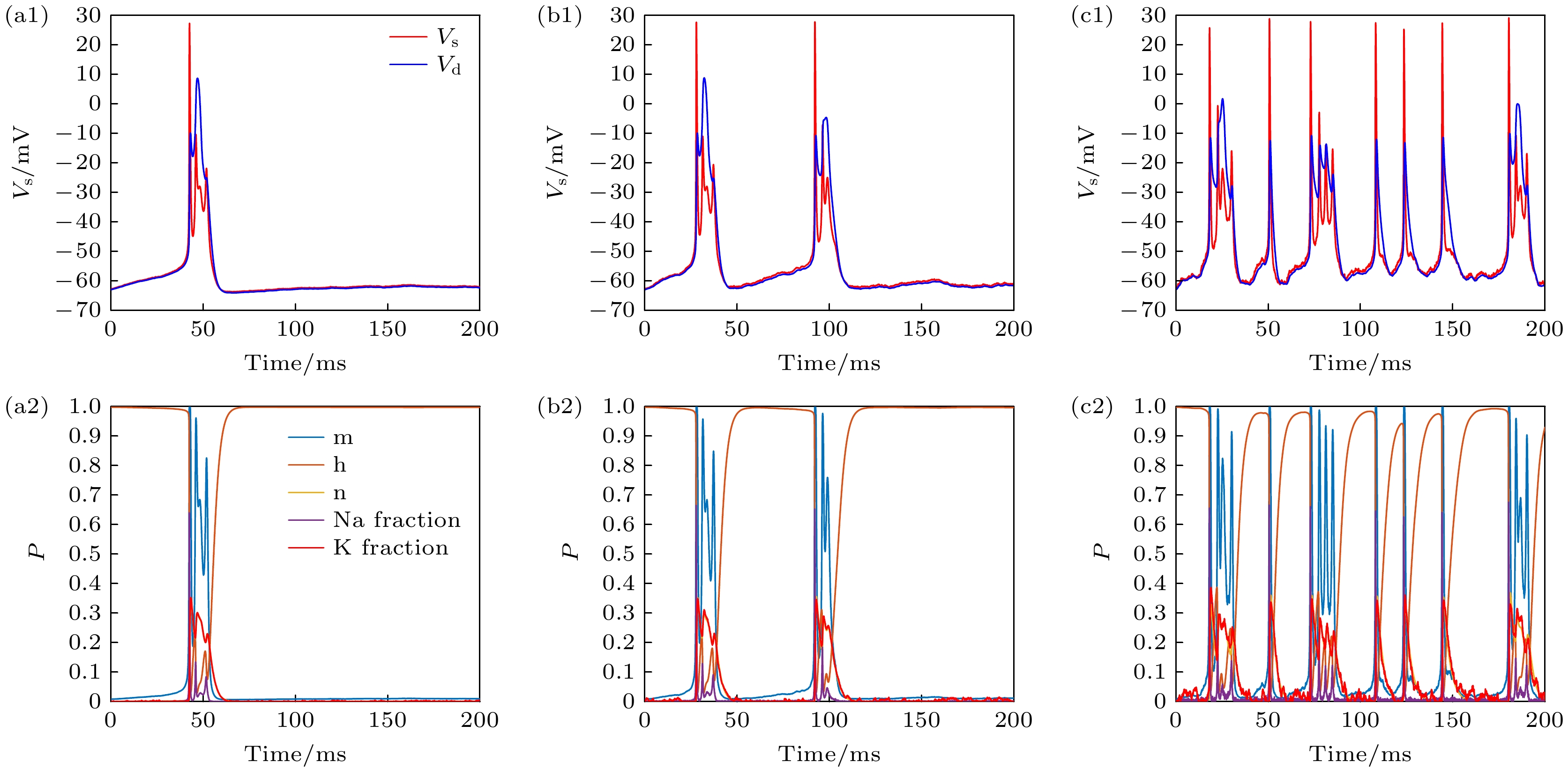
同样地, 针对电压钳位电导诱导的PR神经元Conductance通道噪声模型的分析. 首先以输入电流为0.3 mA作为神经元动作电位的刺激, 得到图8所示的动作电位序列和各个离子通道参数的变化.
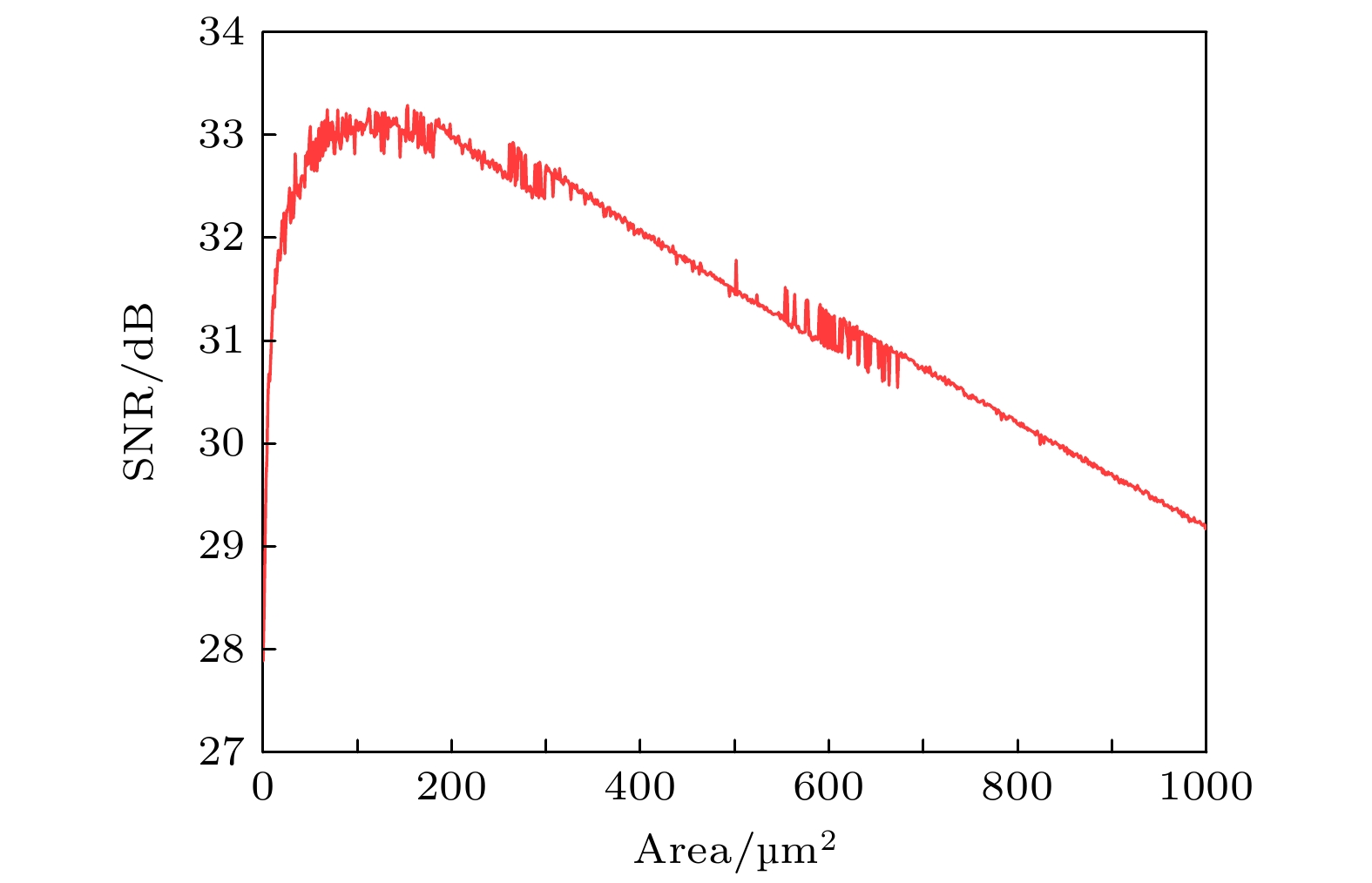
分析图8发现, 针对低输入刺激, 适当的噪声有助于神经元动作电位的发放, 这一现象与Subunit模型的结果一致, 说明Conductance通道噪声模型也具有随机共振特性. 但对比离子通道参数的波动幅度, 发现Conductance噪声模型具有更加稳定的特点. 为了更加深入地探究Conductance噪声模型的随机共振现象, 同样采用信噪比进行和Subunit噪声模型相同的实验, 其实验结果如图9所示.
图9中的信噪比同样存在一个明显的峰值. 当膜面积上升到151.21
${\text{ μ}}{{\text{m}}^2}$ 时, 其对应的SNR值也上升到最高值33.29 dB, 随后随着神经元膜面积的增大, SNR缓慢下降, 这一现象同样诠释了 PR神经元Conductance噪声模型中的随机共振现象.上述实验揭示了两个噪声模型都存在的随机共振现象, 然而却没有对比两个模型之间的差异, 为了深入分析Subunit和Conductance噪声模型在放电特性和编码能力上的差异, 后续使用ISI分布和信息熵进行深入对比研究.
-
为了更加形象地展示Subunit和Conductance噪声模型对PR神经元放电特性的影响, 我们选取
$ {I_{{\text{Sapp}}}} = 5 {\text{ mA}} $ 的输入电流和膜面积为1, 10, 100的3种不同情况进行刺激, 以期望涵盖低、高输入刺激和不同的噪声等级, 并以栅格图的形式进行展示, 结果如图10所示.对比Subunit和Conductance噪声模型可以发现, 跨同样的膜面积, Conductance噪声模型从更稳定的放电到达了更不稳定的放电, 说明其放电序列受膜面积的影响更加强烈. 为了更深入地分析两种噪声模型对神经元编码特性和放电模式的影响, 我们使用5 mA的输入电流, 并使用ISI分布进行研究, 其结果如图10所示.
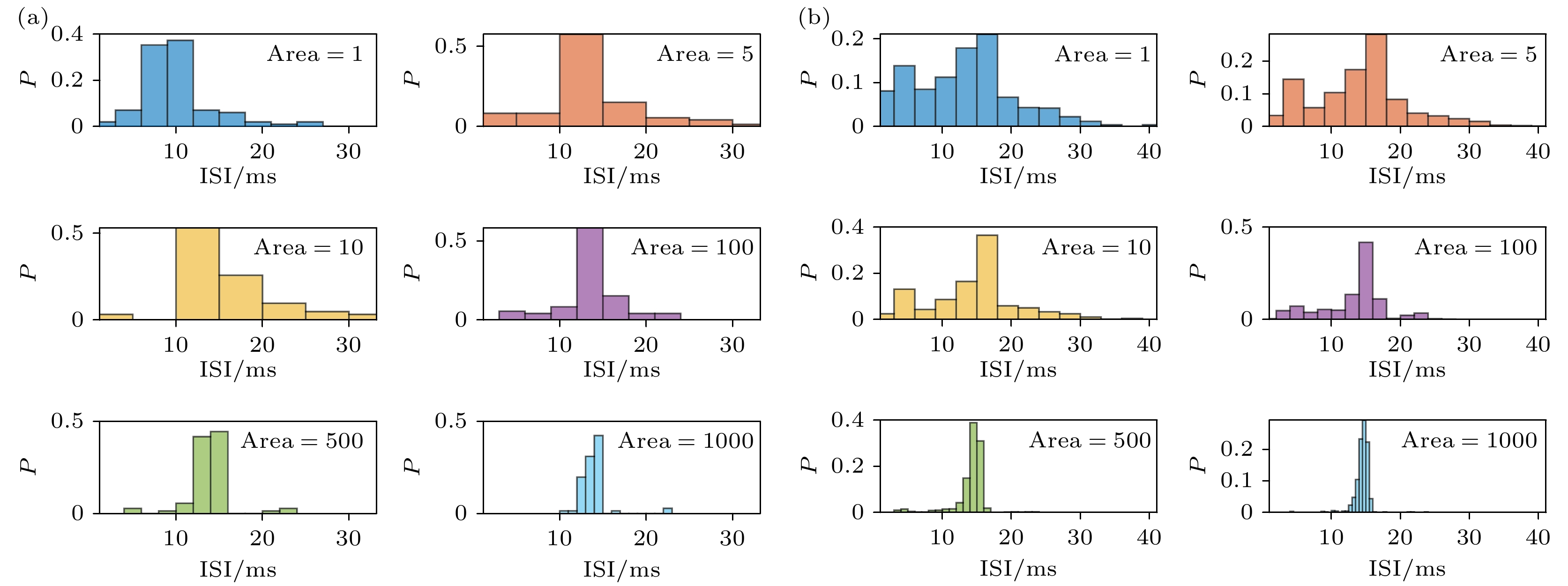
通过图11可以发现, 随着通道噪声的变小, 无论哪种通道噪声模型, 其ISI分布都会逐渐趋于集中, 并且集中在15 ms左右. 同时发现, 同样是将膜面积从1增大到1000 μm2, Conductance噪声模型会将更不集中的信号变得更加集中, 这暗示着Conductance噪声模型更强的编码能力, 为了进一步分析这两个噪声模型的编码能力, 引入信息熵进行定量分析, 计算了不同膜面积下的信息熵, 最后并估算了单位膜面积能表征的信息熵水平, 其结果见表5.
通过对比Conductance噪声模型和Subunit噪声模型在不同膜面积以及单位面积下的信息熵, 我们发现Conductance噪声模型的信息熵远高于Subunit噪声模型, 因此可以得到Conductance模型的动作电位携带更多的信息, 具有更强的编码能力, 但是相对地, Conductance噪声模型拥有更高的信息熵, 说明其稳定性较差. 尽管两种模型在处理噪声的方式上存在差异, 但它们对动作电位的影响具有较高的一致性. 这种一致性突显了两种模型在模拟神经元放电行为时的可靠性.
-
本文深入探讨了离子通道阻塞对多室神经元放电特性的影响, 利用放电频率等指标, 揭示了K+, Na+, Ca2+通道的具体作用. 研究结果表明, 适度的K+通道阻塞能够促进神经元的放电活动, 而Na+通道的阻塞则抑制放电, 与HH模型的表现一致. Ca2+通道的阻塞对动作电位的频率影响复杂, 但总体促进放电并表现出节律性的特点. 此外, 随着输入电流的增大, Na+和K+通道阻塞对放电频率的影响更为显著, 而Ca2+通道阻塞的影响则在低输入电流下更为明显.
同时, 利用单参数和双参数分岔分析, 本文进一步分析了离子通道阻塞的影响. 通过双参数Hopf分岔分析, 发现K+离子阻塞导致其Hopf分岔点随电流呈近似线性增加的特点, 表明高电流下K+通道的开放更为关键. Na+通道的阻塞显示出复杂的Hopf分岔行为, 呈现非单调的变化.
在噪声模型的构建中, 本文借鉴了HH通道噪声模型, 构建PR神经元的Conductance噪声模型, 结合信息熵和信噪比研究其编码能力与随机共振的特点, 并与Subunit模型进行对比. 结果显示, 上述两个噪声模型均展示了随机共振现象. 此外, 通过ISI分布和信息熵分析, 发现不同噪声模型对放电特性的影响各异, 但Conductance模型对膜面积更敏感, 显示出更强的编码能力.
综上所述, 本研究不仅揭示了离子通道阻塞对神经元放电特性的细致影响, 而且通过引入单参数和双参数分岔分析, 提供了更深入的理解. 钙离子通道的复杂作用进一步丰富了我们对神经系统功能多样性的理解, 凸显了钙离子在神经活动中的独特角色. 同时, 所开发的噪声模型及其分析不仅为神经元放电特性提供了新的理解工具, 也为神经网络尺度上的研究提供了理论基础, 具有重要的生物意义和广泛的应用前景.
-
针对Conductance噪声模型概率转移矩阵的推导, 为了便于分析, 本模型引入Johnston和Wu[57]关于通道噪声的假设: 1)所有离子通道在统计学意义上是独立的; 2)为了简化计算, 所有离子通道最大电导为g1; 3)离子通道数量N较大且已知; 4)单通道动力学由马尔科夫过程描述, 其转移概率仅取决于当前状态和门控变量, 而不取决于先前的历史; 5)与通道动力学相比, 门控变量变化缓慢, 具有时间常数
${\tau _i}$ .基于上述假设, 可以得到:
$ {g_{{\text{Na}}}}(t) = {\bar g_{{\text{Na}}}}{n_0}(t) $ ,$ {\bar g_{{\text{Na}}}} = {g_1}N $ , 其中g1是离子通道的最大电导, N是离子通道数量,$ {n_0}(t) $ 是非平稳随机变量, 表示离子通道群处于开放状态的比例, 其瞬时值根据二项概率分布函数确定, 完全由$ {p_0}(t) $ 决定,$ {p_0}(t) $ 是单个离子通道处于开放状态的概率. 若$N{p_0}(t)(1 - {p_0}(t)) \gg 1$ , 则中心极限定理成立,$ {n_0}(t) $ 的二项分布可以用高斯近似, 在随机过程理论中,$ {n_0}(t) $ 又叫扩散过程, 生成一个Ornstein-Uhlenbeck过程而不是采用离散动力学形式的蒙特卡罗模拟[31], 从而达到有效且精确的计算模拟效果. 其均值和稳态方差分别为$ {\bar n_0}(t) $ 和$\sigma _n^2$ , 并伴随时间常数${\tau _0}$ , 计算过程如(A1)式和(A2)式所示:其中,
$\xi (t)$ 是一个${{\varDelta - {\mathrm{correlated}}}}$ 零均值高斯过程, 重点在于$\sigma _n^2$ 和${\tau _0}$ 的计算, 其中$\sigma _n^2$ 通过扩散矩阵D和跃迁矩阵A计算;${\tau _0}$ 的取值是跃迁矩阵A非零特征根绝对值和的倒数, 根据Fox和Lu[26]提出的关于离子通道转移矩阵和扩散矩阵的计算, 这些参数都是从电压函数表示的速率常数$ \alpha $ 和$ \beta $ 导出的, 在本文中我们进行推广并应用到PR神经元模型.首先, 用
$ {w_n}\left( {p', p} \right) $ 表示钾离子通道中, 在很小的$ {{\Delta }}t $ 时间内, K+通道开启-关闭的可能性如(A3)式所示:同理, 可以推导出Na+通道开启-关闭的转移概率, 由于Na+通道的特殊性, 使用
$ {w_m}\left( {p', p} \right) $ 和$ {w_h}\left( {p', p} \right) $ 联合表示, 如(A4)式和(A5)式所示:同时, 考虑到PR神经元模型的特殊性, Ca2+通道在神经元动作电位的发放中发挥了显著作用. 因此, 采用上述方式模拟Ca2+通道的转移概率, 用
$ {w_{{\text{Ca}}}}\left( {p', p} \right) $ 表示, 如(A6)式所示:然后, 引入全局耦合的概念, 该概念表明一个通道的转移概率可以影响其他通道, 通过上述
$ w\left( {p', p} \right) $ 公式计算通道开闭矩阵, 即称为转移矩阵A. 其计算公式如(A7)式—(A9)式所示:由于Na+通道中存在两个m激活通道和一个h失活通道, 因此这3个通道存在00, 10, 20, 01, 11, 21共6种状态, 其转移矩阵A中的参数计算公式如(A10)式—(A14)式所示:
(A7)式—(A14)式中, 涉及的x和y的计算形式如(A15)式所示:
利用上述推导过程, 即可计算跃迁矩阵中各个元素的数值.
通道阻塞与噪声对多室神经元响应状态影响的内在机理
Intrinsic mechanism of influence of channel blocking and noise on response state of multicompartmental neurons
-
摘要:
多室神经元的精细结构能够同时捕捉时空特性, 具有丰富的响应和内在机理. 本研究基于Pinsky-Rinzel两室神经元模型, 提出多室神经元通道阻塞与噪声对神经元响应状态影响的分析方法. 首先, 钙离子(Ca2+)浓度影响神经递质释放的概率, 对多室神经元的节律性放电具有关键作用, 因此特别引入Ca2+通道阻塞, 构建带离子通道阻塞的多室神经元模型. 其次推导跃迁矩阵等核心参数构建Pinsky-Rinzel神经元Conductance噪声模型, 并与Subunit噪声模型对比. 最终, 通过单参数Hopf分岔解释各个离子通道阻塞下的动力学过程; 双参数分岔显示钾离子(K+)的Hopf节点随输入电流呈近似线性递增关系, 而钠离子(Na+)则近似为线性下降和指数上升两阶段; 通过变异系数等指标发现K+适度阻塞促进放电, Na+阻塞抑制放电, Ca2+阻塞总体上促进放电的特性. 另外, 在低于阈值信号刺激时, 两种噪声模型均产生随机共振, Conductance模型表现出更强的编码能力. 本研究揭示了离子通道阻塞与噪声在神经信号传递中的复杂机制, 为研究神经信息编码提供新的视角和工具.
-
关键词:
- Pinsky-Rinzel神经元 /
- 通道噪声 /
- 通道阻塞 /
- Hopf分岔分析
Abstract:The fine structure of multi-compartment neurons can simultaneously capture both temporal and spatial characteristics, offering rich responses and intrinsic mechanisms. However, current studies of the effects of channel blockage and noise on neuronal response states are mainly limited to single-compartment neurons. This study introduces an analytical method to explore theintrinsic mechanism of channel blockage and noise effects on the response states of multi-compartment neurons, by using the smooth Pinsky-Rinzel two-compartment neuron model as a case study. Potassium, sodium, and calcium ion channel blockage coefficient are separately introduced to develop a smooth Pinsky-Rinzel neuron model with ion channel blockage. Methods such as single-parameter bifurcation analysis, double-parameter bifurcation analysis, coefficient of variation, and frequency characteristics analysis are utilized to examine the effects of various ion channel blockages on neuronal response states. Additionally, smooth Pinsky-Rinzel neuron Subunit noise model and conductance noise model are constructed to investigate their response characteristics by using interspike interval analysis and coefficient of variation indicators. Subthreshold stimulation is used to explore the presence of stochastic resonance phenomena. Single-parameter bifurcation analysis of the ion channel blockage model elucidates the dynamic processes of two torus bifurcations and limit point bifurcations in Pinsky-Rinzel neuron firing under potassium ion blocking. Double-parameter bifurcation analysis reveals a nearly linear increase in the Hopf bifurcation node of potassium ions with input current, whereas sodium ions exhibit a two-stage pattern of linear decline followed by exponential rise. The analysis of average firing frequency and coefficient of variation indicates that the moderate potassium channel blockage promotes firing, sodium channel blockage inhibits firing, and calcium channel blockage shows the complex characteristics but mainly promotes firing. Subthreshold stimulation of the channel noise model demonstrates the stochastic resonance phenomena in both models, accompanied by more intense chaotic firing, highlighting the positive role of noise in neural signal transmission. The interspike interval and coefficient of variation indicators show consistent variation levels for both noise models, with the conductance model displaying greater sensitivity to membrane area and stronger encoding capabilities. This study analyzes the general frequency characteristics of potassium and sodium ions in a multi-compartment neuron model through ion channel blocking model, providing special insights into the unique role of calcium ions. Further, the study explores stochastic resonance by using ion channel noise model, supporting the theory of noise-enhanced signal processing and offering new perspectives and tools for future studying complex information encoding in neural systems. By constructing an ion channel blockage model, the effects of potassium and sodium ions on the frequency characteristics of multi-compartment neurons are analyzed and the special influences of calcium ions are revealed. Using the ion channel noise model, the stochastic resonance is investigated, supporting the theory that the noise enhances signal processing. This research offers a new perspective and tool for studying the complex information encoding in neural systems.
-
Key words:
- Pinsky-Rinzel neuron /
- channel noise /
- channel blocking /
- Hopf bifurcation analysis .
-

-
图 1 在
$ {I_{{\text{Sapp}}}} = 0.3 {\text{ mA}} $ 时, 不同离子通道阻塞程度下PR神经元动作电位序列与放电频率 (a1) Na+通道阻塞下的动作电位序列; (a2)频率随Na+通道阻塞的变化; (b1) K+通道阻塞下PR神经元动作电位序列; (b2) 频率随K+通道阻塞的变化; (c1) Ca2+通道阻塞下PR神经元动作电位序列; (c2) 频率随Ca2+通道阻塞的变化, (a1), (b1), (c1)中红色实线代表阻塞系数为0.8, 绿色实线代表阻塞系数为0.6, 蓝色实线代表阻塞系数为0.4Figure 1. Action potential sequence and discharge frequency of PR neurons under different degree of ion channel obstruction, when
$ {I_{{\text{Sapp}}}} = 0.3 {\text{ mA}} $ : (a1) Sequence of action potentials induced by obstruction of Na+ ion channels; (a2) variation in frequency with obstruction of Na+ ion channels; (b1) action potential sequence of PR neurons blocked by K+ ion channels; (b2) variation in frequency with obstruction of K+ ion channels; Action potential sequence of PR neurons under obstruction of (c1) Ca2+ ion channels; (c2) variation in frequency with obstruction of Ca2+ ion channels. In (a1), (b1) and (c1), the red solid line represents the blocking coefficient of 0.8, the green solid line represents the blocking coefficient of 0.6, and the blue solid line represents the blocking coefficient of 0.4.图 2
$ {I_{{\text{Sapp}}}} = 5 {\text{ mA}} $ 时, 不同离子通道阻塞程度下PR神经元动作电位序列与放电频率 (a1) Na+通道阻塞下的动作电位序列; (a2)频率随Na+通道阻塞的变化; (b1) K+通道阻塞下PR神经元动作电位序列; (b2) 频率随K+通道阻塞的变化; (c1) Ca2+通道阻塞下PR神经元动作电位序列; (c2) 频率随Ca2+通道阻塞的变化Figure 2. Action potential sequence and discharge frequency of PR neurons under different degree of ion channel obstruction, when
$ {I_{{\text{Sapp}}}} = 5 {\text{ mA}} $ : (a1) Sequence of action potentials induced by obstruction of Na+ ion channels; (a2) variation in frequency with obstruction of Na+ ion channels; (b1) action potential sequence of PR neurons blocked by K+ ion channels; (b2) variation in frequency with obstruction of K+ ion channels; (c1) action potential sequence of PR neurons under obstruction of Ca2+ ion channels; (c2) variation in frequency with obstruction of Ca2+ ion channels.图 3
$ {I_{{\text{Sapp}}}} = 3 {\text{ mA}} $ 时, K+, Na+通道阻塞的分岔分析 (a) K+通道阻塞下的分岔分析结果; (b) Na+通道阻塞下的分岔分析结果, 图中HB表示Hopf分岔(Hopf bifurcation)节点, 表示系统中一个稳定的固定点变为不稳定的固定点, 同时在该点附近产生一个稳定的极限环; TR表示环面分岔(torus bifurcation), 系统中一个稳定的极限环进一步发生变化, 形成一个准周期轨道; LP表示极限点分岔(limit point bifurcation), 也称为鞍结分岔(fold bifurcation), 表示一个稳定和一个不稳定的点, 随着参数变化而碰撞并消失; 图中黑色表示稳定状态, 红色表示不稳定状态, 绿色代表周期状态, 蓝色代表非周期状态Figure 3. Bifurcation analysis of K+, Na+ ion channel obstruction when
$ {I_{{\text{Sapp}}}} = 3 {\text{ mA}} $ : (a) Results of a bifurcation analysis based on K+ ion channel obstruction; (b) results of a bifurcation analysis in the sense of Na+ ion channel obstruction. In the diagram, HB represents a Hopf bifurcation node, which indicates that a stable fixed point in the system becomes an unstable fixed point, while a stable limit cycle emerges near this point; TR represents a Torus bifurcation, where a stable limit cycle in the system undergoes further changes, leading to the formation of a quasi-periodic orbit; LP represents a limit point bifurcation, also known as a fold bifurcation, indicating a collision and disappearance of a stable and an unstable point as the parameter changes. In the diagram, black represents stable states, red represents unstable states, green represents periodic states, and blue represents non-periodic states.图 4 PR神经元频率特性与输入电流、离子通道阻塞的关系 (a1) 频率与Na+通道阻塞、输入电流的关系; (a2) CV与Na+通道阻塞的关系; (b1)频率与K+通道阻塞、输入电流的关系; (b2) CV与K+通道阻塞的关系; (c1)频率与Ca2+通道阻塞、输入电流的关系; (c2) CV与Ca2+通道阻塞的关系
Figure 4. Relationship between frequency characteristics of PR neurons and input current and ion channel blocking: (a1) Relationship of frequency with Na+ ion channel obstruction and input current; (a2) relationship between CV and obstruction of Na+ ion channels; (b1) relationship of frequency with K+ ion channel obstruction and input current; (b2) relationship between CV and obstruction of K+ ion channels; (c1) relationship between frequency and Ca2+ ion channel obstruction and input current; (c2) relationship between CV and obstruction of Ca2+ ion channels.
图 5 PR神经元双参数分岔分析结果 (a) PR神经元与Na+通道阻塞、输入电流的双参数分岔分析; (b) PR神经元与K+通道阻塞、输入电流的双参数分岔分析
Figure 5. Results of two-parameter bifurcation analysis of neurons: (a) Two-parameter bifurcation analysis of PR neuron and Na+ ion channel obstruction and input current; (b) two-parameter bifurcation analysis of PR neuron and K+ ion channel obstruction and input current
图 6 PR神经元Subunit噪声模型不同膜面积下的动作电位序列和离子通道参数变化 (a1) Area = 100, 低离子通道噪声水平下的动作电位; (a2) Area = 100, 低离子通道噪声水平下各个离子通道参数的变化; (b1) Area = 10, 中离子通道噪声水平下的动作电位; (b2) Area = 10, 中离子通道噪声水平下各个离子通道参数的变化; (c1) Area = 1, 高离子通道噪声水平下的动作电位; (c2) Area = 1, 高离子通道噪声水平下各个离子通道参数的变化
Figure 6. Changes of action potential sequence and ion channel parameters under different membrane area of neuron Subunit noise model: (a1) Area = 100, action potential at low ion channel noise level; (a2) Area = 100, change of parameters of each ion channel at low ion channel noise level; (b1) Area = 10, action potential at medium ion channel noise level; (b2) Area = 10, change of parameters of each ion channel at medium ion channel noise level; (c1) Area = 1, action potential at high ion channel noise level; (c2) Area = 1, change of parameters of each ion channel at high ion channel noise level.
图 8 PR神经元Conductance噪声模型不同膜面积下的动作电位序列和离子通道参数变化 (a1) Area = 10, 低离子通道噪声水平下的动作电位; (a2) Area = 10, 低离子通道噪声水平下各个离子通道参数的变化; (b1) Area = 1, 中离子通道噪声水平下的动作电位; (b2) Area = 1, 中离子通道噪声水平下各个离子通道参数的变化; (c1) Area = 0.1, 高离子通道噪声水平下的动作电位; (c2) Area = 0.1, 高离子通道噪声水平下各个离子通道参数的变化
Figure 8. Changes of action potential sequence and ion channel parameters under different membrane area of neuron Conductance noise model: (a1) Area = 10, action potential at low ion channel noise level; (a2) Area = 10, parameters of each ion channel at low ion channel noise level; (b1) Area = 1, action potential at medium ion channel noise level; (b2) Area = 1, parameters of each ion channel at medium ion channel noise level; (c1) Area = 0.1, action potential at high ion channel noise level; (c2) Area = 0.1, parameters of each ion channel at high ion channel noise level.
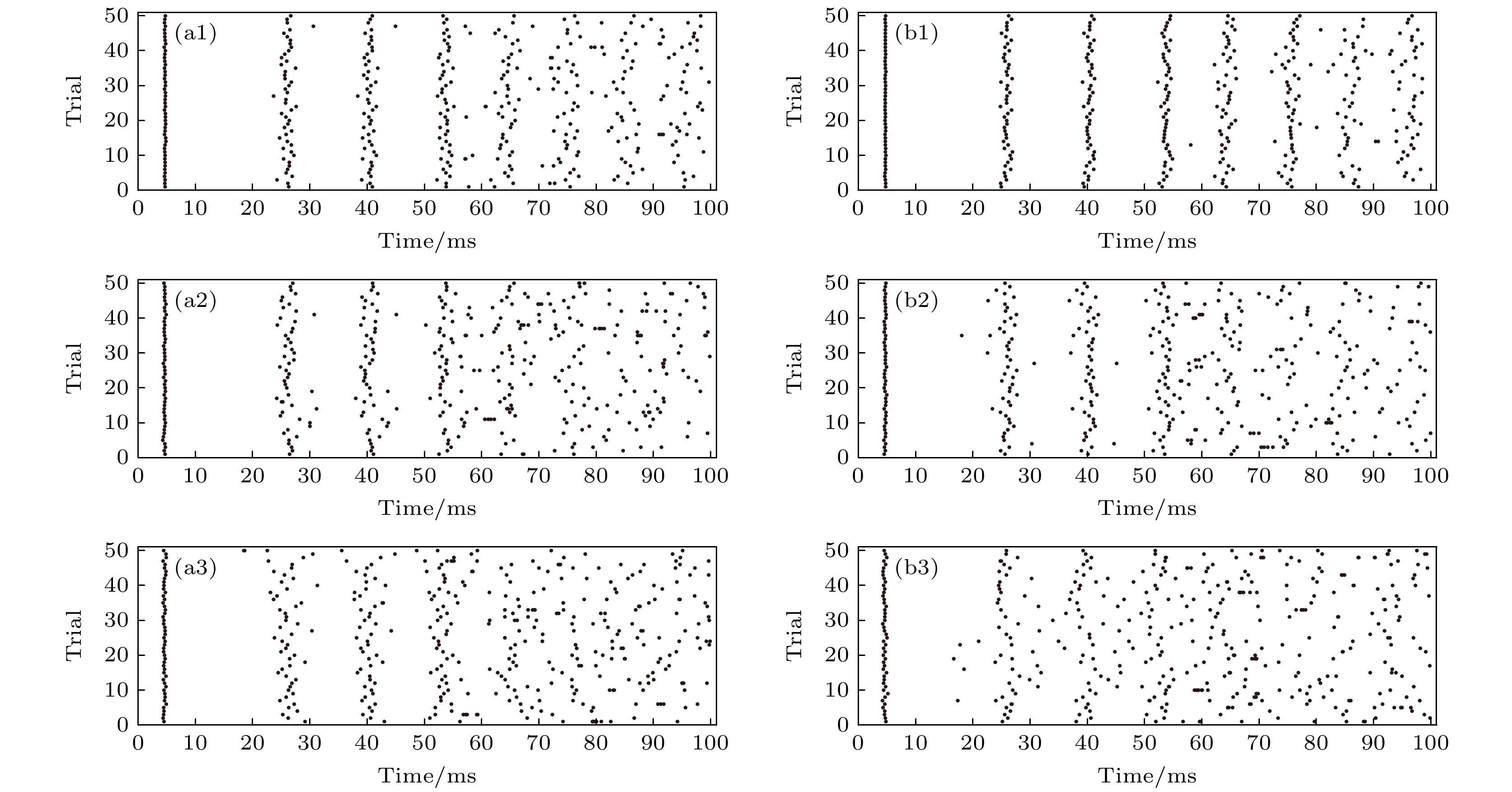
图 10 PR神经元Subunit和Conductance噪声模型在不同膜面积下的动作电位序列栅格图 (a1) Area = 100, 低噪声水平下Subunit噪声引导的栅格图; (a2) Area = 10, 中噪声水平下Subunit噪声的栅格图; (a3) Area = 1, 高噪声水平下Subunit噪声引导的栅格图; (b1) Area = 100, 低噪声水平下Conductance噪声引导的栅格图; (b2) Area = 10, 中噪声水平下Conductance噪声引导的栅格图; (b3) Area = 1, 高噪声水平下Conductance噪声引导的栅格图; 图中横坐标代表时间, 纵坐标代表实验次数, 在本实验中我们进行了50次放电
Figure 10. Raster plots of action potential sequences for PR neuron Subunits and Conductance noise model at different membrane areas: (a1) Raster plot driven by Subunit noise with Area = 100, under low noise level; (a2) raster plot driven by Subunit noise with Area = 10, under medium noise level; (a3) raster plot driven by Subunit noise with Area = 1, under high noise level; (b1) raster plot driven by Conductance noise with Area = 100, under low noise level; (b2) raster plot driven by Conductance noise with Area = 10, under medium noise level; (b3) raster plot driven by Conductance noise with Area = 1, under high noise level. In the figure, the horizontal coordinate represents the time, and the vertical coordinate represents the number of experiments. In this experiment, we carried out 50 discharges.
图 11 PR神经元不同噪声模型和不同噪声程度下的ISI分布, 横坐标代表相邻脉冲之间的间隔(ISI), 纵坐标P表示ISI值落在横坐标对应值上的概率 (a) Subunit噪声模型; (b) Conductance噪声模型
Figure 11. The ISI distribution of PR neurons under different noise models and different noise levels, the horizontal axis represents the interval between adjacent spikes (ISI), and the vertical axis represents the probability of the ISI values falling within the corresponding bins on the horizontal axis, denoted as P: (a) Subunit noise model; (b) Conductance noise model.
表 1 PR神经元模型中参数取值
Table 1. Parameter value in PR neuron model.
参数 取值 参数 取值 ${C_{\text{m}}}$ /(μF·cm–2)3 $ {g_{\text{L}}} $ /(μF·cm–2)0.1 $ {g_{{\text{Na}}}} $ /(μF·cm–2)30 $ {g_{\text{C}}} $ /(μF·cm–2)2.1 $ {g_{{\text{KDR}}}} $ /(μF·cm–2)15 $ {V_{{\text{Na}}}} $ /mV60 $ {g_{{\text{KCa}}}} $ /(μF·cm–2)15 $ {V_{\text{K}}} $ /mV–75 $ {g_{{\text{KAHP}}}} $ /(μF·cm–2)0.8 $ {V_{{\text{Ca}}}} $ /mV80 $ {g_{{\text{Ca}}}} $ /(μF·cm–2)10 $ {V_{\text{L}}} $ /mV–60 表 2 PR神经元本征噪声模型中系数取值
Table 2. Coefficient value of PR neuron intrinsic noise model.
系数 钠 钾 钙 $\sigma _1^2$ $\dfrac{1}{N}{m^4}h(1 - h)$ $\dfrac{1}{N}n(1 - n)$ $\dfrac{2}{N}{s^3}(1 - s)$ $\sigma _2^2$ $\dfrac{2}{N}{m^3}{h^2}(1 - m)$ — $\dfrac{1}{N}{s^2}{(1 - s)^2}$ $\sigma _3^2$ $\dfrac{1}{N}{m^2}{h^2}{(1 - m)^2}$ — — $\sigma _4^2$ $\dfrac{2}{N}{m^3}h(1 - m)(1 - h)$ — — $\sigma _5^2$ $\dfrac{1}{N}{m^2}h{(1 - m)^2}(1 - h)$ — — 表 3 PR神经元本征噪声模型中时间常数取值
Table 3. Value of time constant in the intrinsic noise model of PR neuron.
系数 钠 钾 钙 系数 钠 钾 钙 ${\tau _1}$ ${\tau _h}$ ${\tau _n}$ ${\tau _s}$ ${\tau _4}$ $\dfrac{{{\tau _m}{\tau _h}}}{{{\tau _m} + {\tau _h}}}$ — — ${\tau _2}$ ${\tau _m}$ — $ {{{\tau _s}}}/{2}$ ${\tau _5}$ $\dfrac{{{\tau _m}{\tau _h}}}{{{\tau _m} + 2{\tau _h}}}$ — — ${\tau _3}$ ${{{\tau _m}}}/{2}$ — — — — — — 表 4 钾离子通道分岔分析的节点
Table 4. Nodes of bifurcation analysis of potassium ion channels.
节点名称 HB TR1 LP1 LP2 TR2 $ {x_{\text{K}}} $ 的值0.6507 0.6745 0.7146 0.7021 0.9104 表 5 PR神经元两种噪声模型下的信息熵
Table 5. Information entropy of PR neurons under two different noise models.
噪声模型 膜面积/μm2 单位面积 1 10 100 500 1000 Subunit(信息熵)/bits 2.39 2.17 2.06 1.81 1.66 1.87 Conductance(信息熵)/bits 3.31 3.18 3.16 3.12 2.96 3.13 -
[1] Xu Y, Jia Y, Ge M Y, Lu L L, Yang L J, Zhan X 2018 Neurocomputing 283 196 doi: 10.1016/j.neucom.2017.12.036 [2] Zhou X Y, Xu Y, Wang G W, Jia Y 2020 Cogn. Neurodyn. 14 569 doi: 10.1007/s11571-020-09593-7 [3] Zhu J L, Qiu H, Guo W L 2023 Biophys. J. 122 496 doi: 10.1016/j.bpj.2022.12.037 [4] Yan H R, Yan J Q, Yu L C, Shao Y F 2024 Chin. Phys. B 33 058801 doi: 10.1088/1674-1056/ad21f5 [5] 吴静, 潘春宇 2022 物理学报 71 048701 doi: 10.7498/aps.70.20211626 Wu J, Pan C Y 2022 Acta Phys. Sin. 71 048701 doi: 10.7498/aps.70.20211626 [6] Narahashi T, Moore J W 1968 J. Gen. Physiol. 51 93 doi: 10.1085/jgp.51.5.93 [7] 王荣, 吴莹, 刘少宝 2013 物理学报 62 220504 doi: 10.7498/aps.62.220504 Wang R, Wu Y, Liu S B 2013 Acta Phys. Sin. 62 220504 doi: 10.7498/aps.62.220504 [8] 刘少宝, 吴莹, 郝忠文, 李银军, 贾宁 2012 物理学报 61 020503 doi: 10.7498/aps.61.020503 Liu S B, Wu Y, Hao Z W, Li Y J, Jia N 2012 Acta Phys. Sin. 61 020503 doi: 10.7498/aps.61.020503 [9] Adair R K 2003 Proc. Natl. Acad. Sci. USA 100 12099 doi: 10.1073/pnas.2034447100 [10] Xiao F L, Fu Z Y, Jia Y, Yang L J 2023 Chaos Soliton. Fract. 166 112969 doi: 10.1016/j.chaos.2022.112969 [11] 梁艳美, 陆博, 古华光 2022 物理学报 71 230502 doi: 10.7498/aps.71.20221416 Liang Y M, Lu B, Gu H G 2022 Acta Phys. Sin. 71 230502 doi: 10.7498/aps.71.20221416 [12] Gong Y B, Hao Y H, Lin X, Wang L, Ma X G 2011 BioSystems 106 76 doi: 10.1016/j.biosystems.2011.07.001 [13] Longtin A 1993 J. Stat. Phys. 70 309 doi: 10.1007/BF01053970 [14] Faisal A A, Selen L P J, Wolpert D M 2008 Nat. Rev. Neurosci. 9 292 doi: 10.1038/nrn2258 [15] Ermentrout G B, Galán R F, Urban N N 2008 Trends Neurosci. 31 428 doi: 10.1016/j.tins.2008.06.002 [16] Chow C C, White J A 1996 Biophys. J. 71 3013 doi: 10.1016/S0006-3495(96)79494-8 [17] Mahapatra C, Samuilik I 2024 Mathematics 12 1149 doi: 10.3390/math12081149 [18] van Rossum M C W, O’Brien B J, Smith R G 2003 J. Neurophysiol. 89 2406. doi: 10.1152/jn.01106.2002 [19] Chen Y, Yu L C, Qin S M 2008 Phys. Rev. E 78 051909 doi: 10.1103/PhysRevE.78.051909 [20] Stacey W C, Durand D M 2001 J. Neurophysiol. 86 1104 doi: 10.1152/jn.2001.86.3.1104 [21] Lu L, Jia Y, Kirunda J B, Xu Y, Ge M Y, Pei Q M, Yang L J 2019 Nonlinear Dyn. 95 1673 doi: 10.1007/s11071-018-4652-9 [22] Sengupta B, Laughlin S B, Niven J E 2010 Phys. Rev. E 81 011918 doi: 10.1103/PhysRevE.81.011918 [23] Maisel B, Lindenberg K 2017 Phys. Rev. E 95 022414 doi: 10.1103/PhysRevE.95.022414 [24] Anderson D F, Ermentrout B, Thomas P J 2015 J. Comput. Neurosci. 38 67 doi: 10.1007/s10827-014-0528-2 [25] Kilinc D, Demir A 2017 IEEE Trans. Biomed. Circuits Syst. 11 958 doi: 10.1109/TBCAS.2017.2679039 [26] Fox R F, Lu Y 1994 Phys. Rev. E 49 3421 doi: 10.1103/PhysRevE.49.3421 [27] Goldwyn J H, Shea-Brown E 2011 PloS Comput. Biol. 7 e1002247 doi: 10.1371/journal.pcbi.1002247 [28] Goldwyn J H, Imennov N S, Famulare M, Shea-Brown E 2011 Phys. Rev. E 83 041908 doi: 10.1103/PhysRevE.83.041908 [29] Huang Y D, Rüdiger S, Shuai J W 2015 Phys. Biol. 12 061001 doi: 10.1088/1478-3975/12/6/061001 [30] Cox D R 2017 The Theory of Stochastic Processes (New York: Routledge) pp1–408 [31] Linaro D, Storace M, Giugliano M 2011 PloS Comput. Biol. 7 e1001102 doi: 10.1371/journal.pcbi.1001102 [32] Tuckerman L S, Barkley D 2000 Bifurcation Analysis for Timesteppers (New York: Springer) pp453–466 [33] Guckenheimer J, Labouriau J S 1993 Bull. Math. Biol. 55 937 doi: 10.1007/BF02460693 [34] 黎丽, 赵志国, 古华光 2022 物理学报 71 050504 doi: 10.7498/aps.71.20211829 Li L, Zhao Z G, Gu H G 2022 Acta Phys. Sin. 71 050504 doi: 10.7498/aps.71.20211829 [35] Guo Z H, Li Z J, Wang M J, Ma M L 2023 Chin. Phys. B 32 038701 doi: 10.1088/1674-1056/aca601 [36] Xie Y, Chen L N, Kang Y M, Aihara K 2008 Phys. Rev. E 77 061921 doi: 10.1103/PhysRevE.77.061921 [37] Erhardt A H, Mardal K A, Schreiner J E 2020 J. Comput. Neurosci. 48 229 doi: 10.1007/s10827-020-00746-5 [38] Hu B, Xu M B, Zhu L Y, Lin J H, Wang Z Z, Wang D J, Zhang D M 2022 J. Theor. Biol. 536 110979 doi: 10.1016/j.jtbi.2021.110979 [39] Wang Z Z, Hu B, Zhu L Y, Lin J H, Xu M B, Wang D J 2022 Commun. Nonlinear Sci. Numer. Simul. 114 106614 doi: 10.1016/j.cnsns.2022.106614 [40] Ward M, Rhodes O 2022 Front. Neurosci. 16 881598 doi: 10.3389/fnins.2022.881598 [41] Stöckel A, Eliasmith C 2022 Neuromorph. Comput. Eng. 2 024011 doi: 10.1088/2634-4386/ac724c [42] Nomura M, Chen T Q, Tang C, Todo Y, Sun R, Li B, Tang Z 2024 Electronics 13 1367 doi: 10.3390/electronics13071367 [43] Kühn S, Gallinat J 2014 Hum. Brain Mapp. 35 1129 doi: 10.1002/hbm.22239 [44] Biagini G, D’Arcangelo G, Baldelli E, D’Antuono M, Tancredi V, Avoli M 2005 Neuromol. Med. 7 325 doi: 10.1385/NMM:7:4:325 [45] Sendrowski K, Sobaniec W 2013 Pharmacol. Rep. 65 555 doi: 10.1016/S1734-1140(13)71033-8 [46] Pinsky P F, Rinzel J 1994 J. Comput. Neurosci. 1 39 doi: 10.1007/BF00962717 [47] Taxidis J, Coombes S, Mason R, Owen M R 2012 Hippocampus 22 995 doi: 10.1002/hipo.20930 [48] Kamondi A, Acsády L, Wang X J, Buzsáki G 1998 Hippocampus 8 244 doi: 10.1002/(SICI)1098-1063(1998)8:3<244::AID-HIPO7>3.0.CO;2-J [49] Booth V, Bose A 2001 J. Neurophysiol. 85 2432 doi: 10.1152/jn.2001.85.6.2432 [50] Mainen Z F, Sejnowski T J 1996 Nature 382 363 doi: 10.1038/382363a0 [51] Zhang S M, Yang Q, Ma C X, Wu J B, Li H Z, Tan K C 2024 Proceedings of the AAAI Conference on Artificial Intelligence Vancouver, Canada, February 20–27, 2024 p16838 [52] Hahn P J, Durand D M 2001 J. Comput. Neurosci. 11 5 doi: 10.1023/A:1011250329341 [53] Atherton L A, Prince L Y, Tsaneva A K 2016 J. Comput. Neurosci. 41 91 doi: 10.1007/s10827-016-0606-8 [54] Harnett M T, Makara J K, Spruston N, Kath W L, Magee J C 2012 Nature 491 599 doi: 10.1038/nature11554 [55] Clarke S G, Scarnati M S, Paradiso K G 2016 J. Neurosci. 36 11559 doi: 10.1523/JNEUROSCI.0066-16.2016 [56] Koudriavtsev A B, Jameson R F, Linert W 2001 The Law of Mass Action (Berlin: Springer Science & Business Media) pp1–441 [57] Johnston D, Wu S M S 1994 Foundations of Cellular Neurophysiology (Cambridge, MA: MIT Press) pp1–710 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: