-
地球辐射带是指地球空间中被地磁场捕获的高能粒子聚集区域, 其高能粒子通量受太阳和地磁活动影响而处于高度动态变化中, 其中波粒相互作用是导致辐射带电子损失的重要机制之一[1–8]. 辐射带中的高能粒子会对穿越其中的航天器和宇航员造成不可逆转的伤害, 通过人工手段减少辐射带高能电子通量是近年来的研究热点, 深入理解辐射带波粒相互作用对于研究人工影响辐射带技术具有重要科学意义[9–11]. 不同于磁层中自然激发的等离子体波动, 人工台站甚低频波是由人类活动产生的, 并能对地球辐射带的动态变化产生影响, 同时也为研究近地空间波粒相互作用提供了很好的机会[12–16].
地基台站发射的用于与潜艇通信的甚低频(VLF)信号在沿着地球-低电离层波导传播的过程中, 部分电磁波能量穿越电离层并进入内磁层. 这些人工台站VLF信号在内磁层中以哨声模传播并与电子发生回旋共振, 引起内辐射带中几十至几百keV电子投掷角扩散并沉降至大气中, 进而导致内辐射带电子损失[17–22]. 磁层中的人工台站VLF信号主要分布于夜侧, 因为日侧电离层密度增大, 对波动的吸收更强. 在低轨卫星观测数据中, 泄漏进入磁层中的台站信号主要集中在台站附近, 呈现近圆形分布, 并从信号穿透位置沿着磁力线传播至共轭半球. 磁层中台站信号的强度和辐射范围与台站发射功率呈正相关[23,24]. 基于范阿伦卫星波动数据的统计分析显示, 源自位于澳大利亚的NWC台站(21.82°S, 114.17°E, 发射功率为1 MW)的信号在内磁层中L < 2的区域相对较强, 对内辐射带数百keV电子的动态变化有较大影响[25–30].
Sauvaud等[31]分析DEMETER卫星电子通量数据发现, NWC台站信号会导致L = 1.4—1.7处漂移损失锥中100—600 keV电子通量增强, 增强的电子通量呈现能量与L-shell的依赖性, 满足电子与NWC台站信号发生一阶回旋共振时能量与L的对应关系, 并根据这一特征将其命名为“条缕状”能谱. 这些被台站信号散射的电子会向东漂移至南大西洋异常(SAA)区, 在内辐射带中形成一条新的电子沉降带. Gamble等[32]分析了NWC台站发射时间与卫星观测“条缕状”能谱之间的联系, 发现NWC台站以东观测到的“条缕状”能谱与NWC台站信号密切相关, 表明NWC台站信号可以导致内辐射带数百keV电子沉降. Li等[33]基于DEMETER卫星观测的内带准捕获电子的统计工作也印证了这一结论, 并发现卫星观测到的增强的电子通量能级范围以及通量大小会随着经度增加而增大.
之前的大多数研究都是通过理论分析一阶回旋共振关系来证明台站信号与增强的准捕获电子通量之间的关系[21,31,34]. Selesnick等[35]通过考虑了电子径向扩散、波动散射和电子漂移的随机模型, 模拟得到了与卫星观测基本吻合的“条缕状”能谱, 但未揭示被台站信号散射的电子沿经度的分布规律. Liu等[36]基于Drift-Diffusion-Source模型, 模拟了2009年3月19日NWC台站分别位于日侧和夜侧时L = 1.7处200 keV电子通量沿经度的分布. 当假设波幅为15 pT时, 模拟结果与DEMETER卫星观测基本吻合, 表明NWC台站位于夜侧时, 卫星在L = 1.7处观测的准捕获电子的主要来源是被台站信号散射的捕获电子, 可以推测当天L = 1.7处台站信号幅值约为15 pT. 从Liu等[36]的模拟结果可以发现, 台站信号散射导致的准捕获电子通量呈现沿经度增加的趋势, 但该工作没有模拟和评估除L = 1.7以外其他L处NWC台站信号对电子的散射效应.
本文将基于准线性理论计算内辐射带中台站信号引起的电子弹跳平均投掷角扩散系数, 然后通过Drift-Diffusion-Source模型模拟台站信号散射内辐射带电子形成“条缕状”能谱的过程, 并与卫星观测对比进行分析, 明晰内辐射带电子从被台站信号散射到漂移进入南大西洋异常区沉降的完整变化过程. 本文第2节将介绍使用的卫星数据以及“条缕状”能谱观测结果, 第3节介绍Drift-Diffusion-Source模型和波动参数的选取, 第4节将展示数值模拟结果, 第5节总结主要结论.
-
DEMETER卫星是由法国国家空间研究中心(CNES)于2004年6月底发射的太阳同步极轨卫星, 主要用于研究由地震和火山喷发等自然现象或人类活动导致的电离层扰动现象[37]. 卫星轨道高度约为710 km, 提供约10:30 LT (local time)和约22:30 LT的观测. 卫星上搭载的粒子探测器(IDP)可以测量70 keV—2.34 MeV能量范围的电子通量, 探测的电子局地投掷角约为90°. 卫星有巡查和详查两种工作模式, 这两种工作模式下测量的能量分辨率分别为17.8 keV和8.9 keV[38].
由于真实的地球磁场不是偶极子场, 地磁强度在经度分布上有强弱差异, 其中SAA区地磁场强度最小. 电子在地磁场中沿磁力线做弹跳运动时保持第一绝热不变量守恒, 即μ = p2sin2α/(2m0B) = Const, 其中p是电子动量, m0是电子的静止质量, B是磁场强度, α为电子投掷角(电子运动方向与背景磁力线的夹角), 电子沿磁力线弹跳过程中投掷角随纬度增加逐渐增大,当电子投掷角α = 90°时电子到达弹跳折返点即磁镜点. 电子漂移至磁场较弱的区域时, 由于μ保持不变即磁镜点处磁场强度不变, 磁镜点高度会下降至更低的高度, 在SAA区域会降至最低. 当电子磁镜点高度下降至100 km高度时, 认为电子将与大气分子碰撞发生沉降, 这时电子的赤道投掷角(电子在磁赤道处的投掷角)大小被称为弹跳损失锥(BLC). 由于地磁场随经度的强弱变化, 不同经度处的BLC大小也不相同, 其中最大的BLC被称为漂移损失锥(DLC). 据此辐射带中的电子分为三种类型: 沉降电子、准捕获电子、捕获电子[39,40]. 沉降电子是指赤道投掷角小于局地BLC的电子, 其将在一个弹跳周期内沉降在大气中; 准捕获电子是指赤道投掷角大于局地BLC但是小于DLC的电子, 可以存在数个弹跳周期, 直至漂移至某一区域后因赤道投掷角小于局地BLC而沉降, 准捕获电子会在一个漂移周期内损失; 捕获电子是赤道投掷角大于DLC被地磁场稳定捕获的电子. 捕获电子在无扰动的情况下生命周期很长, 而在有波动与电子发生共振引起电子投掷角扩散时, 会使得电子的赤道投掷角减小至DLC内, 导致电子发生损失. DEMETER卫星由于其低轨道高度的特性, 可以观测到这三种不同类型的电子: 在SAA区域观测到的为捕获电子, 在SAA区域共轭的北半球观测到的为沉降电子, 在其他区域观测到的为准捕获电子[41–43], 为研究台站信号散射电子的过程提供了很好的观测机会.
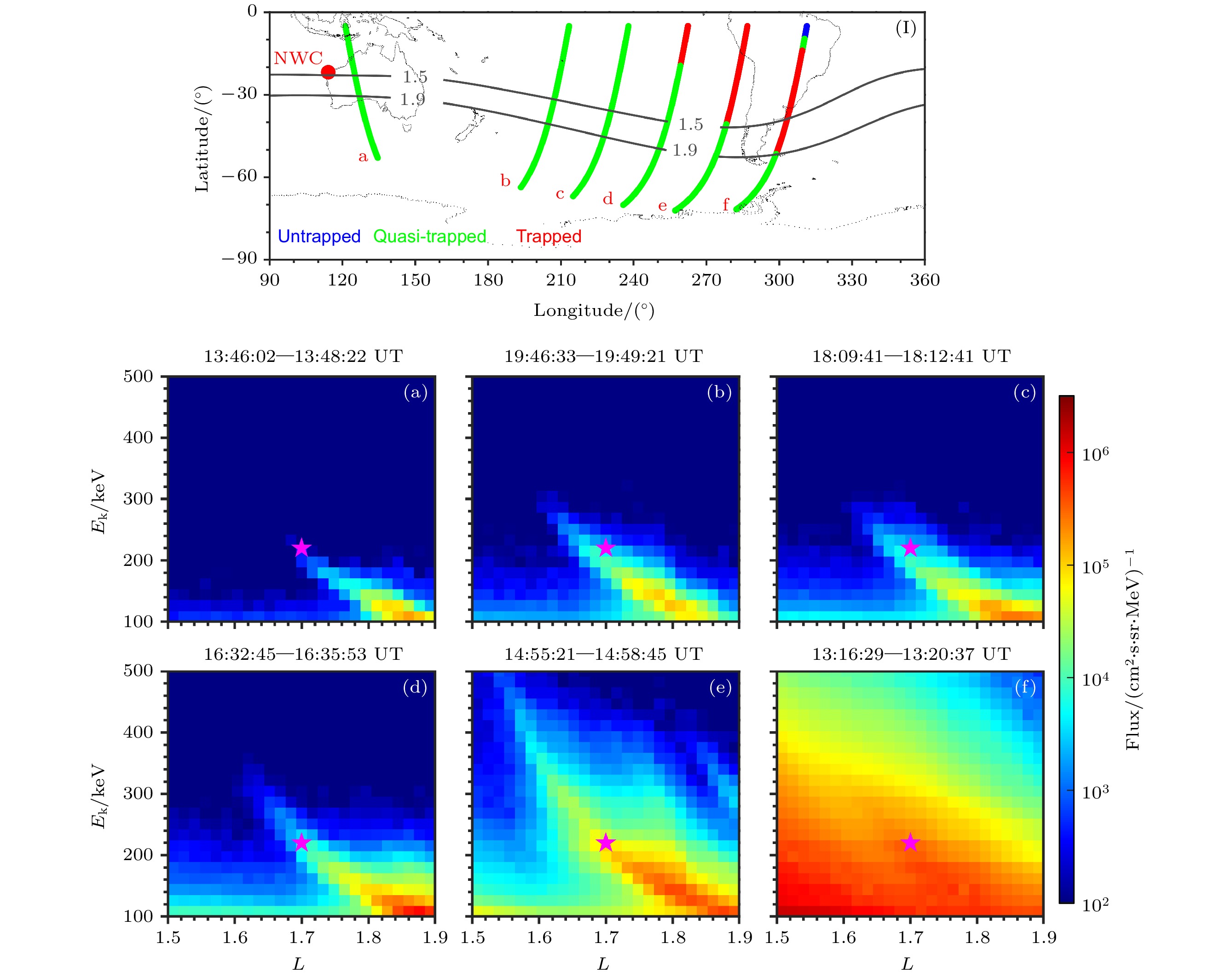
图1(I)展示的是2009年3月19日NWC台站位于夜侧时, DEMETER卫星轨道在地理经纬度地图上的路径, 轨道的颜色表示基于IGRF磁场模型计算得到的卫星测量的电子类型[42]. 蓝色表示沉降电子, 绿色表示准捕获电子, 红色表示捕获电子. 红色圆点标识的是NWC台站的位置, 黑色的实线表示L = 1.5和L = 1.9的等值线. 红色字母a—f表示卫星轨道沿经度的分布次序, 其中轨道a测量位置在NWC台站附近, 测量的主要是准捕获电子, 而轨道f位于SAA区域, 测量的主要是捕获电子.
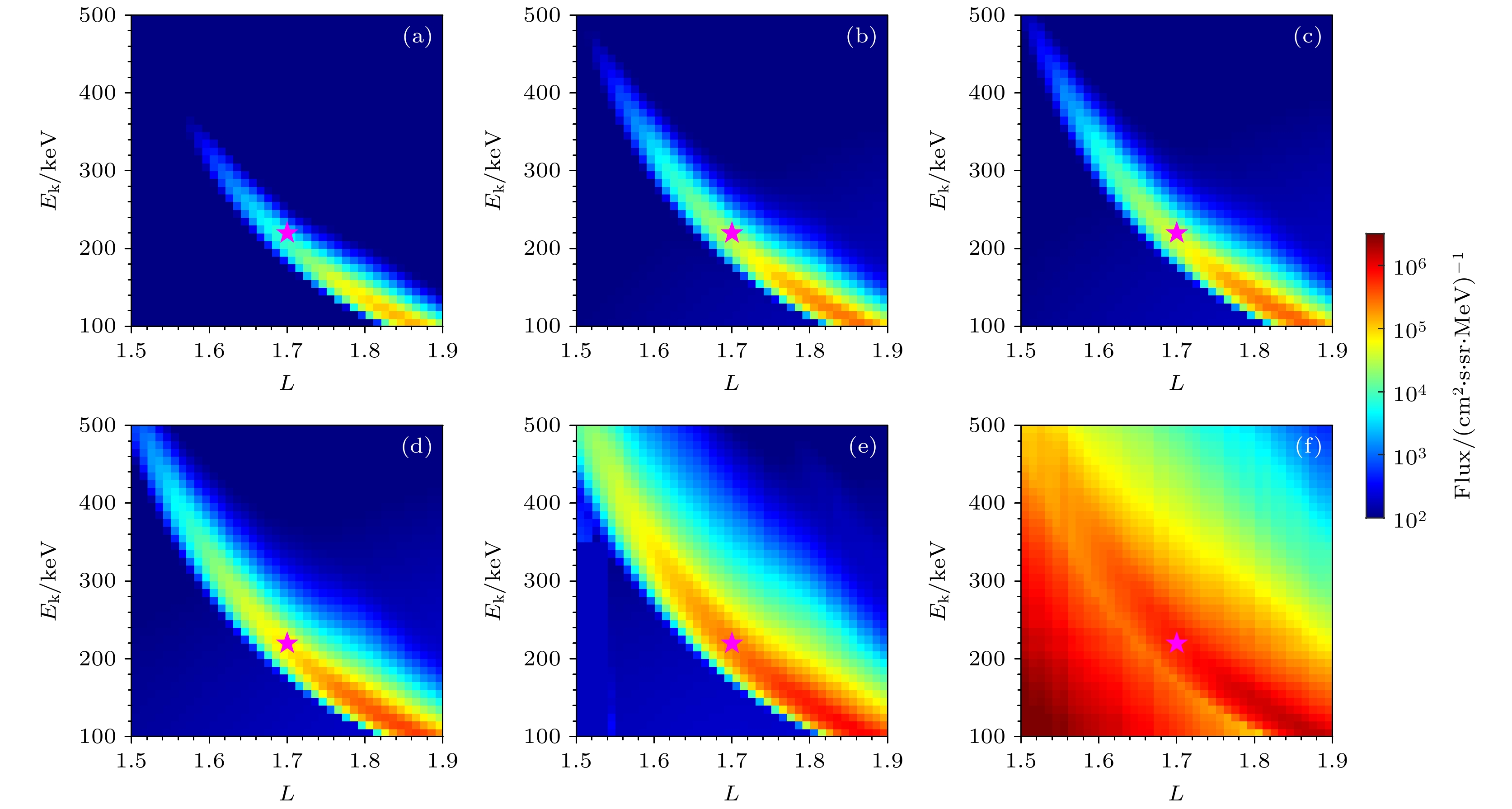
图1(a)—(f)分别对应着图1(I)中轨道a—f在L = 1.5—1.9处观测到的L-Ek能谱. 横坐标是L值, 纵坐标是能量(Ek), 颜色表示的是电子通量的大小. 各个能谱相应的观测时间标在子图的顶部. 能谱中电子通量增强部分呈现出随着L增加能量减小的特征, 这是NWC台站信号与捕获电子发生回旋共振, 将捕获电子散射进漂移损失锥导致准捕获电子通量增强所致, 称为“条缕状”能谱[31]. 图中品红色五角星表示L = 1.7, Ek = 220 keV的位置, 满足电子与传播角为60°的台站信号在赤道处的一阶回旋共振关系[41]. 由于DEMETER卫星只能提供卫星高度处观测的磁场信息和密度信息, 计算回旋共振关系时采用了IGRF磁场模型和Ozhogin等[44]的等离子体层密度模型得到赤道处背景磁场和密度值. 从图1中可以看到, 在不同轨道观测的“条缕状”能谱中, 五角星都位于“条缕状”结构的中心位置. 对比不同轨道观测的“条缕状”能谱, 可以看出不同经度处观测的“条缕状”能谱通量大小以及能级范围会有所不同, 其中在台站附近观测最弱且能级范围最小(轨道a). 随着卫星观测位置靠近SAA区域, “条缕状”结构的电子能级范围逐渐增大, 通量逐渐增强. 文章后续章节中将对多个轨道观测的“条缕状”能谱进行模拟, 并分析“条缕状”能谱随经度变化呈现差异性的原因. 同时值得注意的是, 轨道f测量的是捕获电子, 但在能谱中也存在“条缕状”结构, 本文将在后文中对这一现象成因进行分析.
-
使用Full Diffusion Code计算准线性理论下NWC台站信号导致的电子弹跳平均投掷角扩散系数, 以量化台站信号对电子的散射效应[45,46]. 首先需要确定台站信号的径向分布模型, 一般认为台站信号与电子在赤道附近发生相互作用, 而DEMETER卫星无法观测到相应的赤道处的波动. 于是选用Xiang等[30]使用范阿伦双星6年观测数据统计的冬季夜侧的NWC台站信号的径向分布模型进行计算. 因为对于>12 kHz电磁波动, 范阿伦卫星只提供单分量的电场功率谱数据, 无法确定磁层中的NWC台站信号传播角的大小. 前人的统计研究认为在L > 1.7的区域, 台站信号主要以导管波传播(传播方向与地磁场磁力线夹角较小), 而L < 1.7台站信号主要以非导管波传播(传播角较大)[23,25]. 而基于DEMETER、范阿伦波动数据和射线追踪方法, Zhang等[47]表明台站信号主要是以非导管波传播. Gu等[48]通过对比范阿伦卫星观测的俄罗斯Alpha台站(11.9 kHz)坡印廷矢量与射线追踪结果, 也得出台站信号在磁层中主要以非导管方式传播的结论.
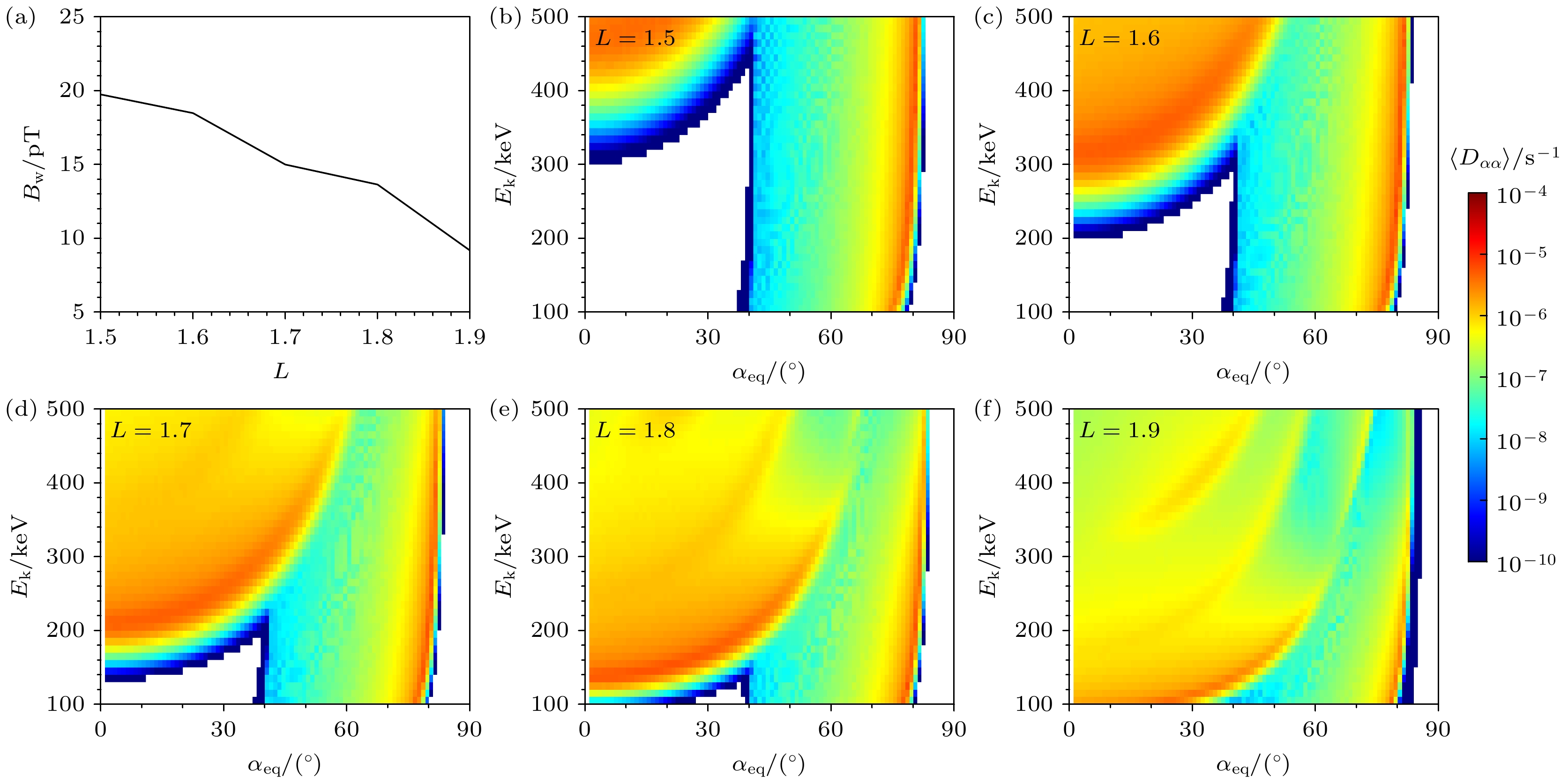
Ma等[26]通过射线追踪得到北半球发射的20 kHz左右台站信号传播至L < 2赤道处时, 波动传播角大小为50°—70°. 据此, 本文计算投掷角扩散系数时, 假设赤道附近台站信号的波传播角分布模型为θmin = 30°, θmax = 80°, θm = 60°, θd = 20°[13], 采用偶极子磁场模型和Ozhogin等[44]的等离子体层密度模型, 纬度范围取0º—25°[25]. 因为内辐射带中L-shell相同时, 由偶极子磁场模型和IGRF磁场模型得到的赤道附近磁场强度近乎一致, 计算卫星电子类型时以及后文使用模型模拟时使用IGRF磁场模型, 是因为不同经度处局地的弹跳损失锥大小会发生变化, 故此处为了计算方便, 采用偶极子磁场模型. 将Xiang等[30]中统计的冬季夜侧NWC台站信号电场功率谱密度转换成相应的磁场强度, 用于计算台站信号导致的投掷角弹跳平均扩散系数[46,49]. 由于全球统计平均后的波幅会低估这一天的台站信号强度, 故我们假设L = 1.7处的波幅为15 pT[36], 将上述基于Xiang等[30]统计结果计算得到的NWC台站信号的径向分布, 按照L = 1.7处放大到15 pT的比例整体进行放大, 得到的结果如图2(a)所示.
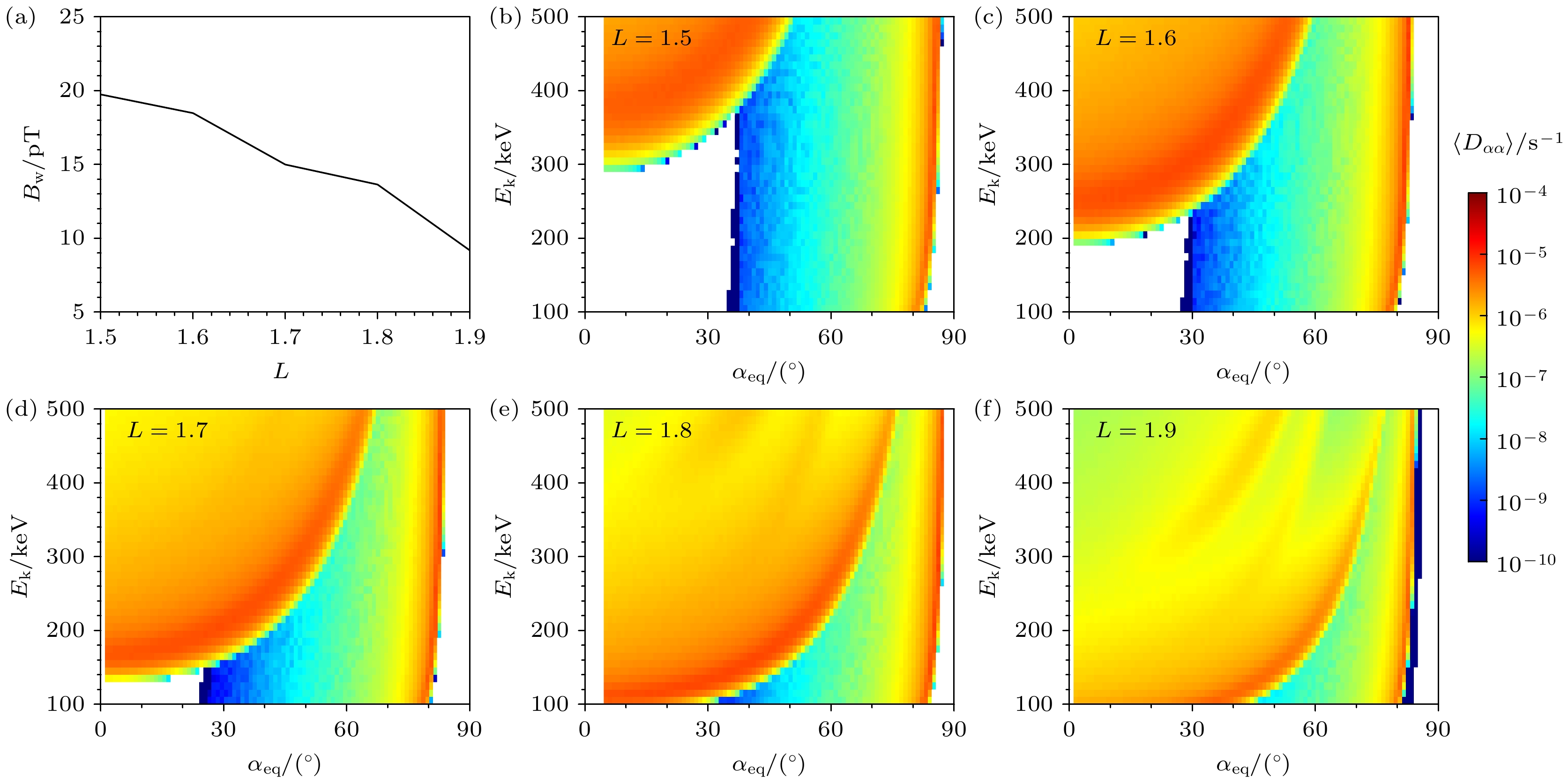
基于上述假设, 计算得到的部分扩散系数如图2(b)—(f)所示. 图2(b)—(f)中横坐标为电子的赤道投掷角, 纵坐标为电子能量, 颜色表示电子弹跳平均投掷角扩散系数的大小. 可以看到在L = 1.6处(图2(c)), 电子弹跳平均投掷角扩散系数分为两部分: 较低投掷角>200 keV部分为回旋共振导致的投掷角扩散系数, 较高投掷角部分则是由朗道共振导致的投掷角扩散系数. 回旋共振部分投掷角扩散系数的峰值集中在约300 keV, 随着投掷角的增大, 扩散系数峰值对应的能量也在增加, 扩散系数峰值约为10–5.5 s–1. 随着L值增加, 扩散系数峰值对应的能量减小, 同时由于波幅的减小, 扩散系数的值也在减小. 在L = 1.9处, 扩散系数峰值约为10–6 s–1. 其中图2(e)与图2(f)中存在多条扩散系数的峰值纹路, 从下至上分别对应着1阶、–1阶、2阶回旋共振.
-
Xiang等[50]提出了一种新的模型用以模拟内辐射带电子通量, 称为Drift-Diffusion-Source模型. 该模型考虑了辐射带中多种物理机制共同作用下, 电子通量的演化过程. 模型包含了电子在更接近真实磁场的IGRF磁场模型中的漂移过程、由库仑碰撞和波粒相互作用导致电子的扩散过程, 以及宇宙射线反照中子衰变(CRAND)过程. CRAND是指源自超新星爆发的高能宇宙线与地球上层大气相互作用生成反照中子, 反照中子又衰变生成质子、电子和反中微子的过程. CRAND是平静时期内辐射带内缘的高能电子的主要来源机制[42,51,52]. 基于该模型, Xiang等[53]发现平静时期槽区电子通量是CRAND过程和波动散射达到动态平衡的结果, 表明平静时期CRAND过程生成电子通量的贡献不容忽视. 模型方程如下式所示:
其中J是电子通量; wd是弹跳平均的漂移频率;
$\phi $ 是地磁经度; αeq是电子赤道投掷角;${G_0}\left( {{\alpha _{{\text{eq}}}}} \right) = \dfrac{{v{\tau _{\text{b}}}}}{2}$ , τb是弹跳周期, v是电子速度. Se是指CRAND过程生成电子速率, 表达式如下:其中
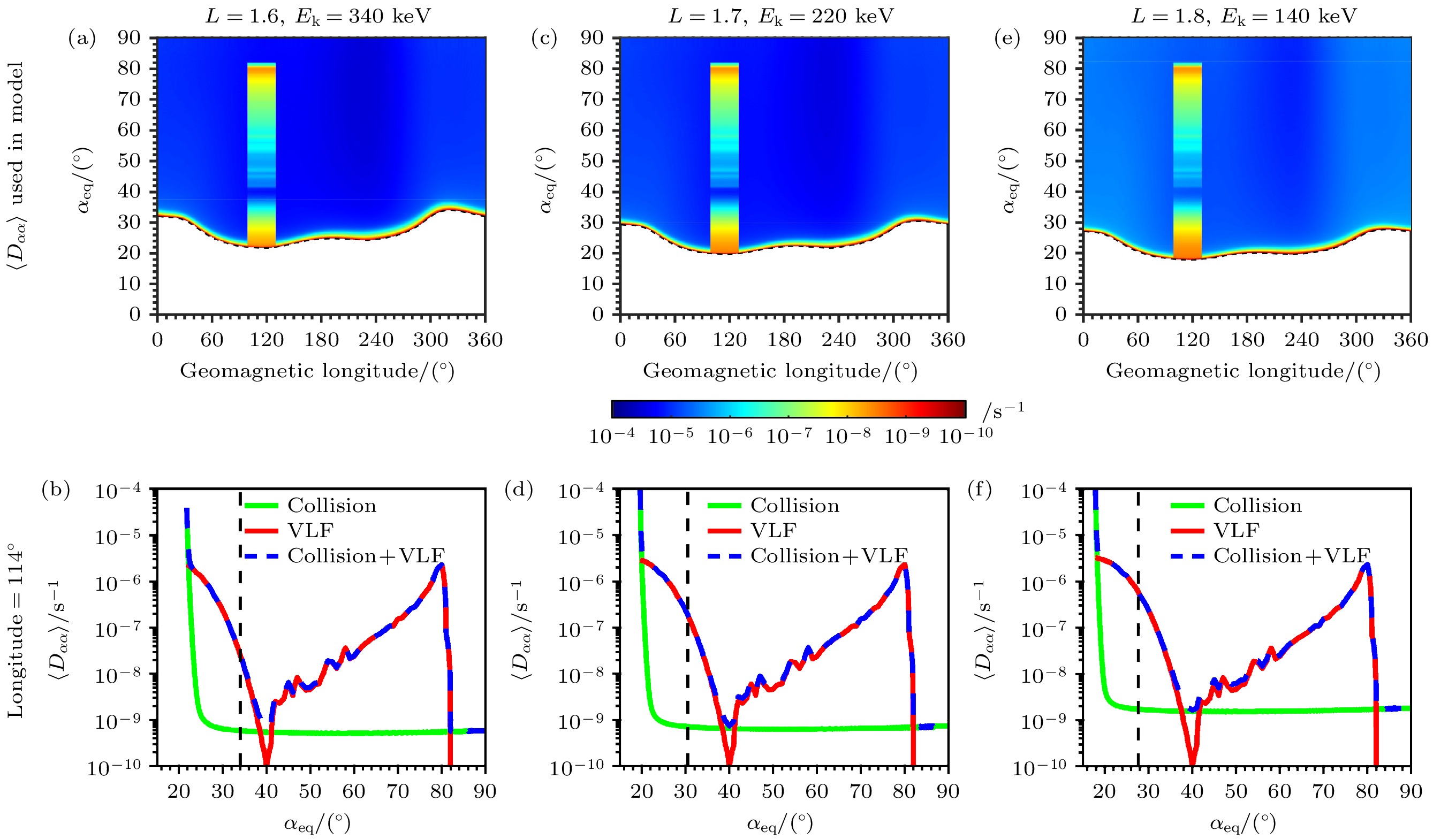
${q_0}$ = 1.0×10–13 cm–3 s–1 ster–1 [52];$\varphi \left( E \right)$ 是中子β衰变能谱[54]. 相较于传统的考虑偶极子场的模型, Drift-Diffusion-Source模型可以更直观地展示电子通量在漂移过程中的动态变化, 尤其是准捕获电子通量的变化.图3的第一行是针对不同L处不同能级的电子, 模型采用的投掷角扩散系数, 横坐标为地磁经度, 纵坐标表示赤道投掷角, 颜色表示扩散系数的大小. 黑色虚线表示使用IGRF磁场模型计算的局地弹跳损失锥(BLC), 最大值即为漂移损失锥(DLC). 从左至右分别对应的是L = 1.6处340 keV, L = 1.7处220 keV, L = 1.8处140 keV电子的投掷角扩散系数, L与电子能级满足在赤道处与传播角为60°台站信号的一阶回旋共振关系. 图3的第二行展示了第一行图中经度114°处, 不同机制导致扩散系数大小随投掷角的分布, 绿色实线表示库伦碰撞导致的投掷角扩散系数, 红色的实线是VLF波动导致的投掷角扩散系数, 蓝色的虚线是二者之和, 黑色虚线表示相应L处DLC的大小.
以图3(a)为例, 扩散系数分为两个部分: 一部分是经度[99°, 129°]处投掷角扩散系数较大的区域, 即NWC台站经度±15°的范围, 表示的是VLF台站信号散射作用范围, 扩散系数的大小对应的是台站信号在L = 1.6处引起的340 keV电子投掷角扩散系数; 另一部分是台站信号影响范围外电子与大气分子发生库仑碰撞引起的电子投掷角扩散系数[55], 可以看出库仑碰撞导致的投掷角扩散系数在BLC边缘处的值很大, 随着投掷角增加扩散系数急剧减小. 由图3(b)可以看到VLF台站信号导致的扩散系数最大约为3×10–6 s–1, 随着投掷角的增加而减小. 在高投掷角处较大的扩散系数是朗道共振导致的. BLC边缘处碰撞导致的投掷角扩散系数远大于台站信号散射引起的电子投掷角扩散系数, 而在其他投掷角处, 台站信号导致的投掷角扩散系数更大. 对比不同L处的电子投掷角扩散系数, 可以看到局地BLC附近扩散系数值相近, 且随着L的增加局地BLC减小, 但不同L的DLC处扩散系数值不同.
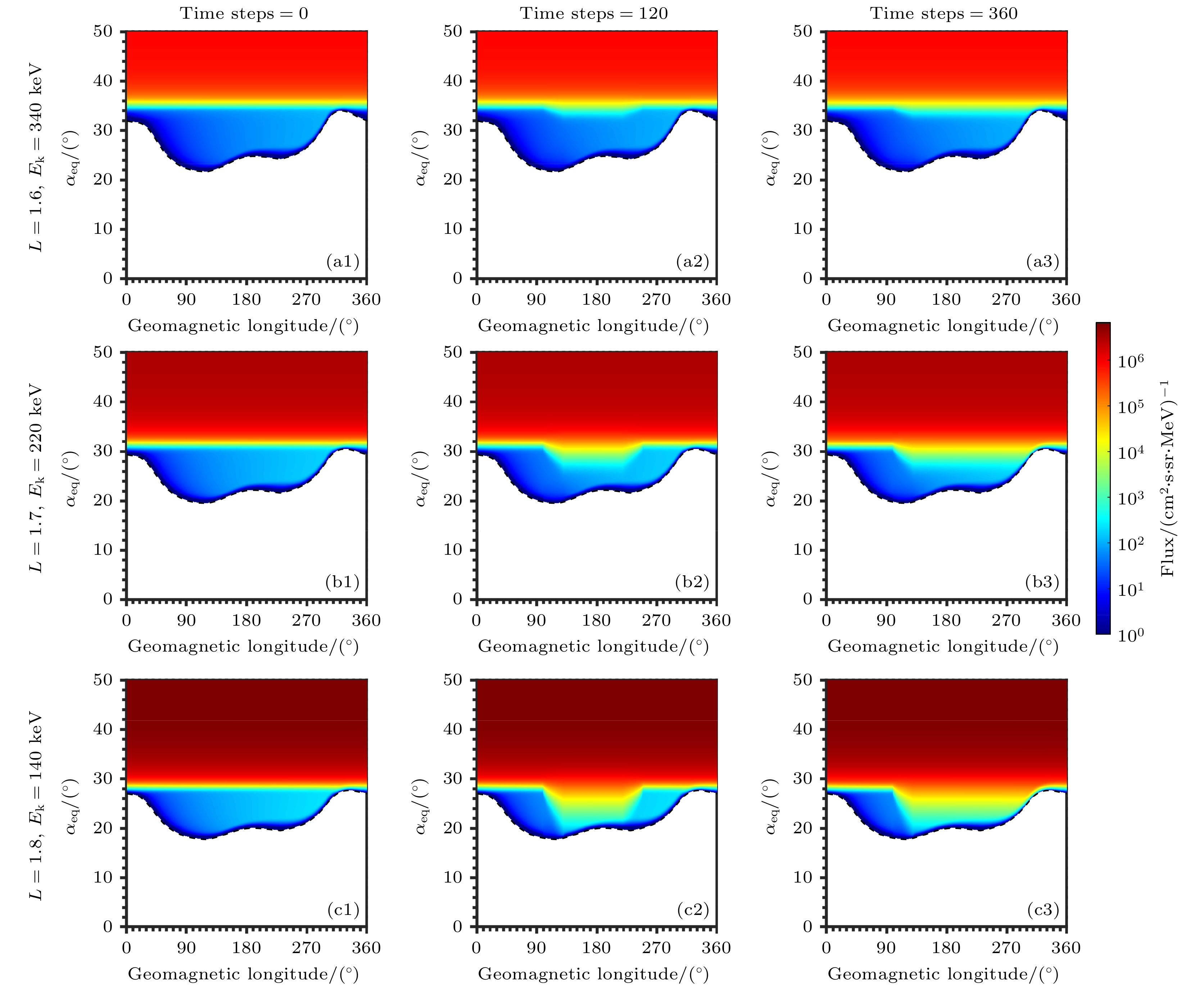
图4展示了模型模拟电子通量演化过程. 从上至下每一行分别为不同模拟步长时L = 1.6处340 keV, L = 1.7处220 keV, L = 1.8处140 keV电子通量随经度和赤道投掷角的分布, 颜色表示电子通量的大小. 从左至右每一列模拟步长分别为0, 120, 360. 模型模拟的1步长表示电子在经度上漂移1°需要的时间(L = 1.6处340 keV电子漂移经度1°约为16.8 s, L = 1.7处220 keV电子漂移经度1°约为23 s, L = 1.8处140 keV电子漂移经度1°约为32.5 s).
首先看L = 1.6处, 340 keV电子通量模拟结果(图4(a1)—(a3)). 图4(a1)即为模拟的初始条件. 图4(a1)中赤道投掷角大于DLC的为捕获电子, 赤道投掷角大于BLC小于DLC的为准捕获电子. 显然捕获电子通量较大, 而准捕获电子通量较小. 在无台站信号散射时, 准捕获电子通量主要来源于CRAND, 且准捕获电子的通量随着电子向东漂移逐渐累积, 直至漂移到SAA区域时损失到大气中. BLC内的通量置零, 表示粒子弹跳到100 km高度处时会损失在大气中. 由于低轨卫星只能提供单个赤道投掷角对应的电子通量, 而模拟需要电子通量的全投掷角分布, 于是首先假设捕获电子通量的投掷角分布符合f = f0 sinαeq, 其中f0是指赤道投掷角为90°的电子通量. 在考虑长时间CRAND和大气碰撞模拟得到较为稳定的电子投掷角分布后, 按照卫星观测捕获电子赤道投掷角处对应的通量与卫星观测的比值, 将电子通量的投掷角分布整体放大, 得到捕获电子通量的投掷角初始分布[53]. 初始分布中(图4(a1))所有经度上捕获电子通量分布是一样的, 而准捕获电子通量分布通过一个漂移周期内CRAND生成电子通量得到. 图4(a2)是模型模拟了120个时间步长后的电子通量分布, 可以看到在经过台站信号作用的区域后(经度范围99°—129°), 准捕获电子通量增加. 由于投掷角扩散系数不够强, 准捕获电子通量并未被扩散到较低的赤道投掷角处. 值得注意的是, 台站信号只存在于经度[99°, 129°]范围, 在图4(a3)中可以看到被台站信号散射的电子, 会持续向东漂移直至损失在SAA区域.
对比不同L处的电子散射过程, 可以看到台站信号对L = 1.8处140 keV电子的散射更强, 电子被扩散到更低的投掷角. 从图3中可知三种情况下, BLC附近的台站信号扩散系数是相近的, 图4中电子被扩散的程度各不相同: 台站信号对L = 1.6处340 keV电子扩散最弱, 对L = 1.8处140 keV电子扩散最强. 导致这种现象的原因有两个: 一是电子的初始通量大小不同, L = 1.6处340 keV电子初始通量最小, 而L = 1.8处140 keV电子初始通量最大; 二是不同情况下DLC处扩散系数大小不同, 对比图3中右列中DLC附近扩散系数的大小, 可以看出L = 1.6处340 keV电子的扩散系数在DLC附近最小, L = 1.8处140 keV电子的扩散系数在DLC附近最大.
在下一节中, 将通过模型模拟台站信号对不同L、不同能量电子的散射效应, 提取卫星观测经度和投掷角对应的模拟值得到模拟的能谱[36,50,52], 并对不同经度处的能谱进行比较分析.
-
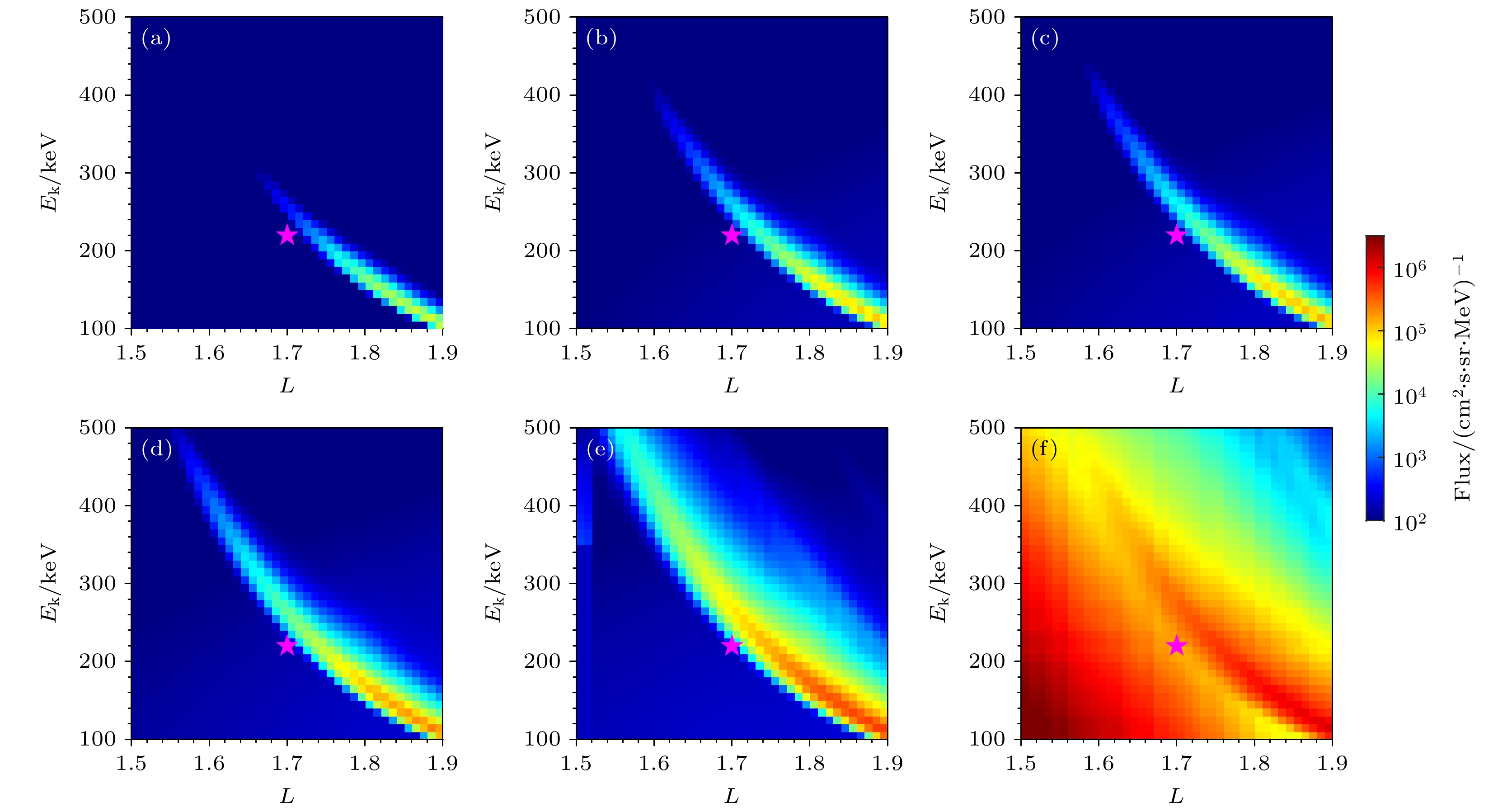
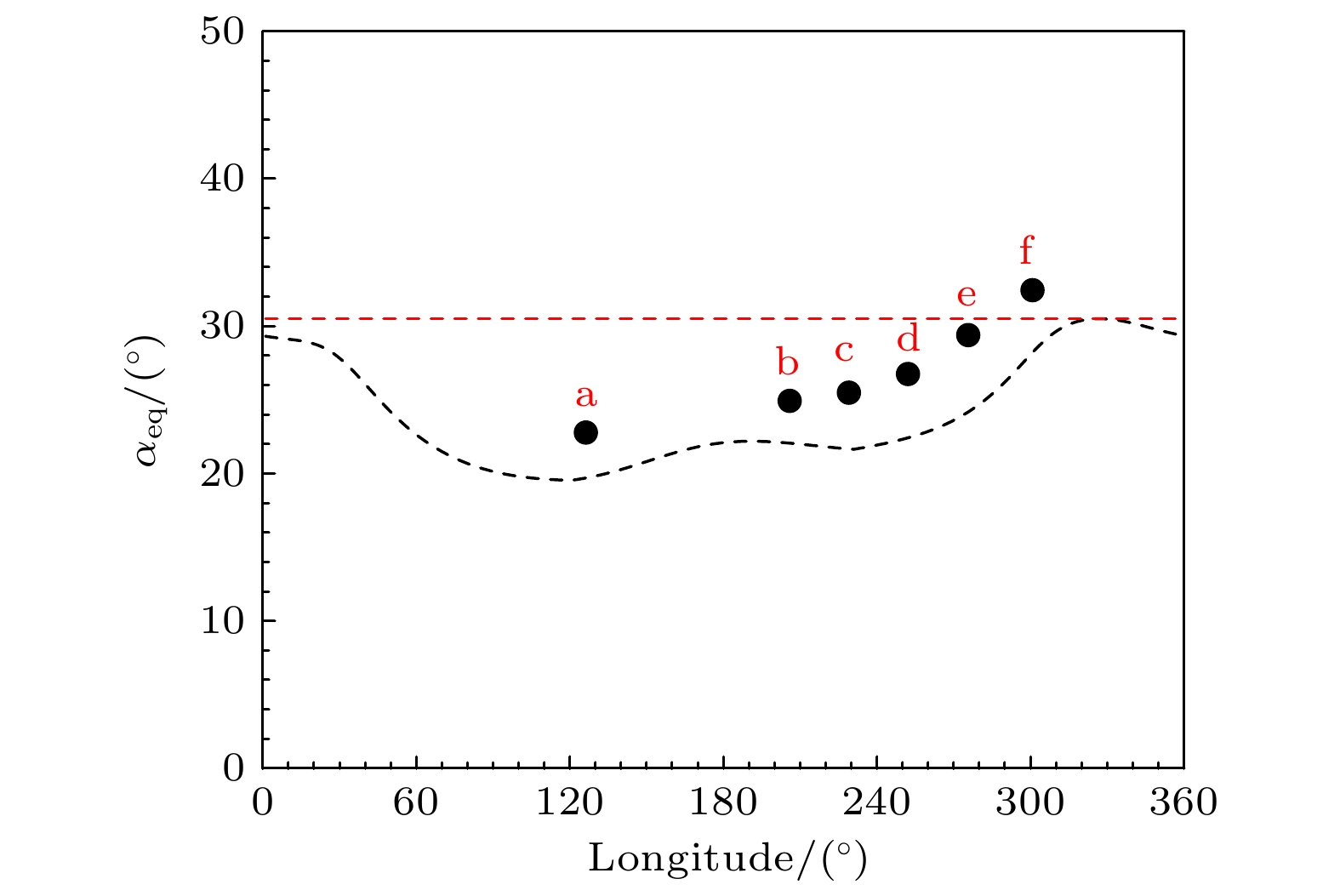
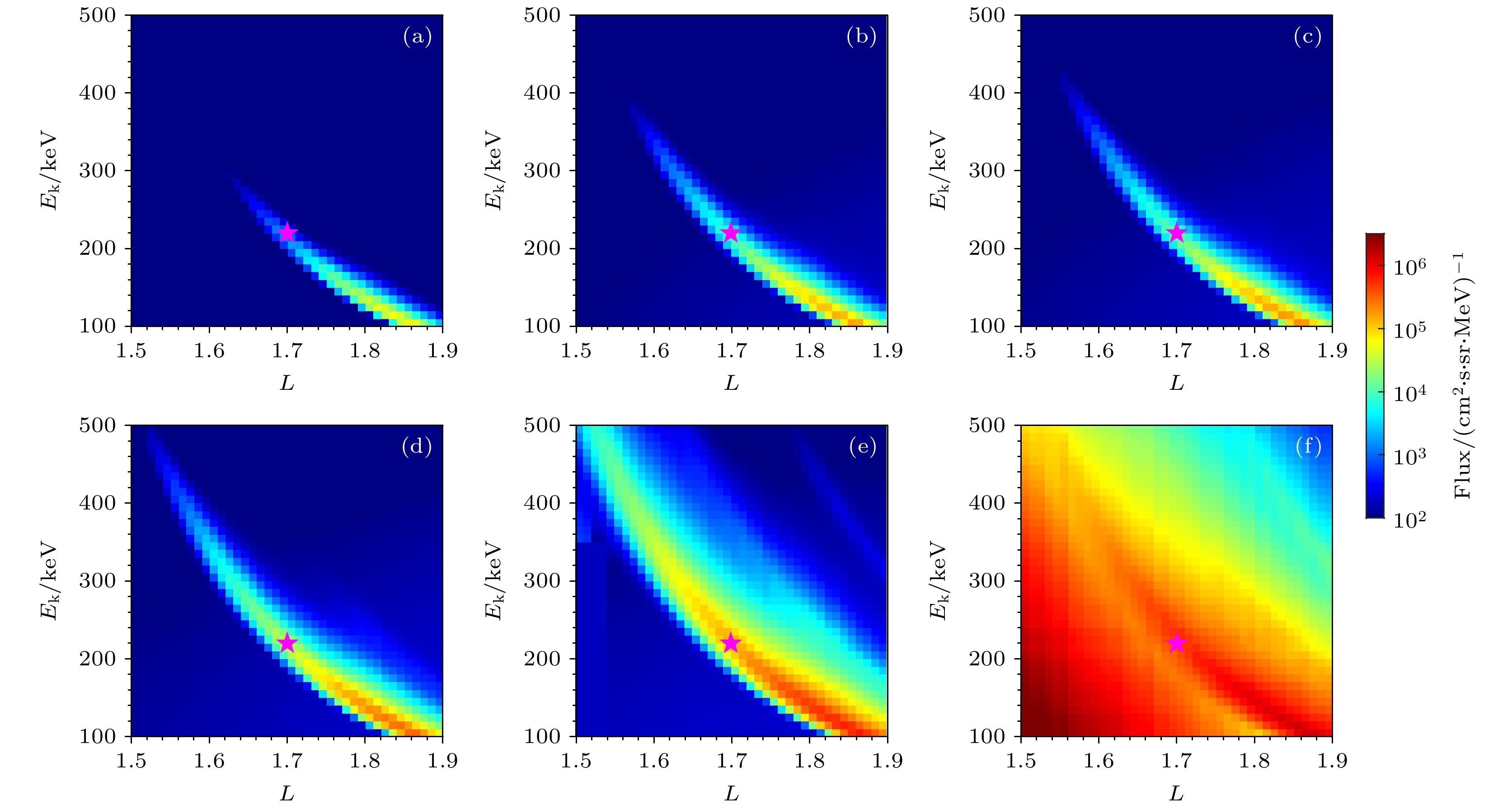
依照第3节中描述的方法, 模拟的多个轨道观测的“条缕状”能谱如图5所示. 图5(a)—(f)模拟结果与图1(a)—(f)的卫星观测能谱一一对应, 品红色的五角星标示出L = 1.7, Ek = 220 keV位置, 与图1中相同. 对比图5和图1, 可以看出模拟结果基本复现了观测的“条缕状”能谱特征: 散射电子能级随着L的增加而减小, 且随着卫星观测轨道与SAA区域距离减小, “条缕状”结构的能级范围逐渐增加、通量逐渐增强. 导致这一特征的原因是在不同经度处, 卫星观测的电子赤道投掷角发生了变化. 图6展示了L = 1.7处卫星在不同经度观测的电子赤道投掷角大小, 次序与图1中展示的观测轨道一一对应. 黑色虚线表示使用IGRF磁场模型计算的局地弹跳损失锥(BLC), 红色虚线表示最大局地弹跳损失锥, 即漂移损失锥(DLC). 可以看出卫星轨道接近SAA区域的过程中, 卫星观测的电子赤道投掷角的大小逐渐接近DLC. 结合图4可以看出, 台站信号不能将电子散射至较小的赤道投掷角时, 卫星在台站附近无法观测到相应增强的准捕获电子通量. 而靠近SAA区域, 卫星观测的赤道投掷角增大, 便能观测到被台站信号散射进DLC的准捕获电子.
值得注意的是轨道a—e观测的电子赤道投掷角在DLC内, 为准捕获电子, 而轨道f观测的电子赤道投掷角大于DLC, 为捕获电子. 之所以捕获电子中可以观测到“条缕状”能谱, 是因为碰撞导致了DLC附近电子通量减小(如图4第1列所示), 而轨道f观测电子投掷角在DLC外边缘, 台站信号将较高投掷角电子扩散至较低的投掷角后, 使得DLC附近电子通量增加, 故在捕获电子通量中也能观测到“条缕状”结构.
由于图5中品红色五角星位于模拟“条缕状”结构的下方, 表明目前采用的波动模型散射电子能级高于实际观测值. 如果改变计算参数减小电子的共振能量, 将可以使模拟结果与观测更加吻合. 根据回旋共振公式, 电子共振能量与波动传播角、频率、背景密度等参数相关[41], 而台站信号在磁层中是频率范围固定的窄带信号, 故在后文中只讨论传播角和背景密度对模拟结果的影响.
-
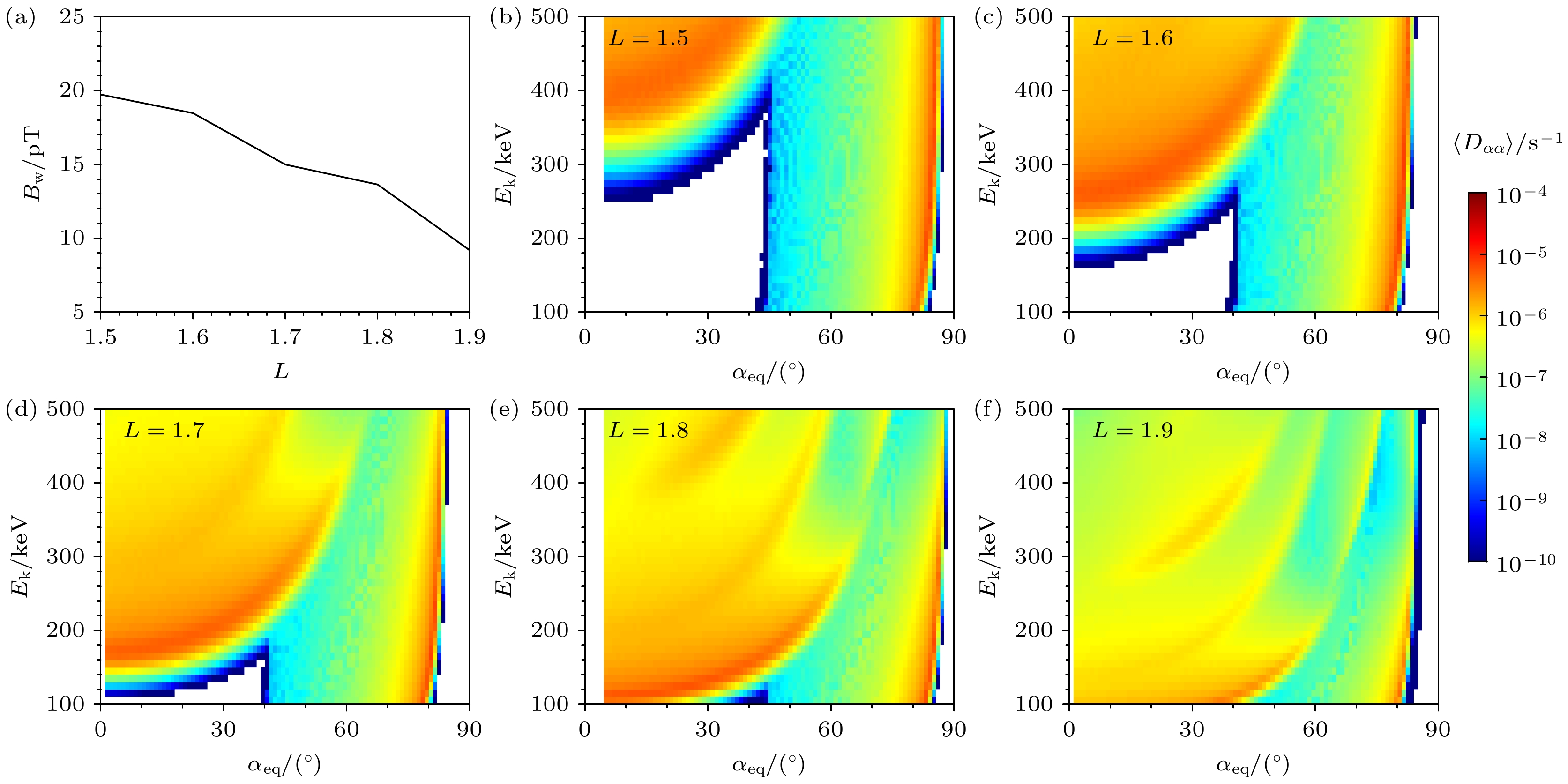
首先分析波动传播角对模拟结果的影响, 保持其他参数不变. 因为波传播角减小时, 电子共振能量也会减小[41], 故本节减小波动模型的中心传播角进行模拟. 图7为中心传播角为40°时计算得到的电子弹跳平均投掷角扩散系数, 格式同图3. 传播角模型相应更改为θmin = 0°, θmax = 80°, θm = 40°, θd = 20°[13], 其他参数设置相同. 对比图3和图7可以看出, 当台站信号波幅相同时, 中心传播角减小, 不仅能导致共振能量减小, 计算的波动扩散系数也会增大. 图8展示了当波动中心传播角为40°时模拟的结果, 品红色五角星位置与图1中一致. 从图8可以看到当波动中心传播角为40°时, 模拟结果中品红色五角星位置位于“条缕状”结构中心位置, 但模拟的“条缕状”结构的能量范围和通量与观测相比偏大. 比如图1(a)的观测能谱中“条缕状”结构的尖端位置在L = 1.68处240 keV, 而图8(a)的模拟能谱中“条缕状”结构的尖端位置在L = 1.58处360 keV. 比较图5和图8可以看出, 相同L处波动中心传播角为40°时模拟的“条缕状”结构能量范围和通量更大.
-
接着分析背景密度对模拟结果的影响, 保持其他参数不变. 背景密度增加会导致电子共振能量减小[56], 于是增大Ozhogin等[44]的密度模型值进行模拟. 图9为将背景密度扩大1.3倍后计算得到的电子弹跳平均投掷角扩散系数. 对比图3和图9可以看出, 背景密度增加后, 相同的L处计算的扩散系数的最小共振能量减小. 图10为将背景模型密度扩大1.3倍时的模拟结果. 从图10可以看到密度增大为模型值的1.3倍时, 模拟结果中品红色五角星位于“条缕状”结构的中心, 与观测值基本一致. 对比图5和图10可以看出, 密度的改变不会导致模拟的“条缕状”结构的长度发生很明显的改变, 但密度增大后, 低能级处电子通量增加, 与观测值更为接近. 表明背景密度变大, 会导致台站信号对低能级电子扩散更强.
台站信号导致的电子能量扩散系数比投掷角扩散系数值小近2个数量级[26], 作用较小, 且本文模拟的是准捕获电子通量, 这些电子在一个漂移周期内就会损失在南大西洋异常区, 能量散射作用在这么短时间产生的效果十分微弱, 因此本文模拟中没有考虑. 由以上的模拟结果可以看出, 尽管模拟过程中各参数采取的是较为简单的模型假设, 但调整波动传播角或背景密度值后, 模拟能谱与卫星观测能谱十分接近, 不仅复现出了观测中“条缕状”能谱随经度分布的差异性, 也模拟出了捕获电子中的“条缕状”能谱, 表明目前采用的模型假设是合理的. 若要真实评估台站信号的散射效应, 还需要更确切台站信号传播角和背景密度等参数数据. 该研究表明准线性理论和Drift-Diffusion-Source模型适用于分析内辐射带中人工台站信号散射电子过程, 同时也可以基于该方法评估台站信号对内辐射带电子损失的贡献.
-
本文基于Drift-Diffusion-Source模型, 模拟了DEMETER卫星于2009年3月19日多个轨道观测到的NWC台站信号散射电子形成的“条缕状”能谱, 并进行了参数化分析, 模拟结果较好地复现了不同经度处观测的“条缕状”能谱的特征, 得到的主要结论如下:
1)低轨卫星观测的电子赤道投掷角会随经度发生变化, 导致卫星在不同经度处观测能谱中的“条缕状”结构的能级范围及通量大小存在差异;
2)库仑碰撞会导致漂移损失锥附近电子通量减小, 台站信号的扩散作用使得损失锥附近电子通量增加, 导致捕获电子中也能观测到“条缕状”能谱;
3)对于2009年3月19日这天的卫星观测, 假设传播角为60°时, 模拟“条缕状”能谱的能级高于观测值, 但将传播角更改为40°或将背景密度扩大为模型值的1.3倍时, 模拟结果与观测更为接近.
本文的研究结果表明Drift-Diffusion-Source模型可以直观清晰地复现内辐射带电子通量的动态变化过程, 揭示准捕获电子通量随经度的分布特征. 结合低轨卫星观测数据, 可系统研究辐射带中的波粒相互作用过程. 通过定量分析台站信号对电子的散射效应和“条缕状”能谱的形成过程, 可以加深对近地空间波粒相互作用的理解, 为发展人工影响辐射带技术提供重要依据.
NWC人工甚低频台站信号产生“条缕状”准捕获电子能谱的模拟研究
Simulation study on “Wisp” electron spectra generated by NWC very low frequency transmitter signals
-
摘要: 遍布全球的人工甚低频台站发射的信号主要用于对潜通信, 在夜间, 这些信号可以泄漏进磁层与内辐射带中几十至几百keV电子发生回旋共振, 从而导致电子沉降. 这一过程是导致内辐射带电子损失的重要原因, 也是磁层-电离层耦合过程中能量和物质输运的重要环节. 被台站信号散射的电子呈现出能量随L增加而减小的“条缕状”能谱结构, 与台站信号和电子的一阶回旋共振能量曲线相符. 低轨卫星可以对“条缕状”能谱结构进行清晰地观测, 为研究近地空间波粒相互作用提供了重要契机. 本文基于Drift-Diffusion-Source模型, 复现了DEMETER卫星于2009年3月19日多个轨道测量的NWC台站信号导致的“条缕状”能谱, 量化了NWC台站信号对辐射带电子的散射作用, 明晰了NWC台站信号的幅度和传播角, 揭示了内辐射带电子漂移过程中的动态变化规律, 为开发人工影响辐射带技术提供了重要理论参考.Abstract: Very low frequency (VLF) signals emitted by worldwide spread ground-based man-made transmitters mainly propagate in Earth-ionospheric waveguides and are used for submarine communication. A portion of these signals penetrate the ionosphere and leak into the magnetosphere when the ionospheric electron density decreases on the nightside due to the attenuated sunlight. The VLF transmitter signals in the magnetosphere can scatter electrons with energy of several hundred keV in the inner radiation belt into the drift loss cone through cyclotron resonance. This is an important loss mechanism for electrons in the inner radiation belt and plays an important role in transferring energy and mass from magnetosphere to ionosphere. Electrons scattered by transmitter signals exhibit a “wisp” characteristic in L-Ek spectrum, satisfying the first-order cyclotron resonance relationship between the electrons and the transmitter signals. The “wisp” spectrum can be clearly observed by low earth orbit satellites, presenting opportunities to study wave-particle interactions in near-Earth space. In this study, using the Drift-Diffusion-Source model, we reproduce the “wisp” spectrum formed by scattering effects of NWC transmitter signals observed by DEMETER satellite on March 19, 2009. Our simulation results suggest that the equatorial pitch angle of electrons, observed by DEMETER, varies with the longitude, resulting in distinctions in the observed “wisp” spectrum along different longitudes. Specifically, as the satellite approaches South Atlantic Anomaly (SAA) region, both the energy range and flux level of the observed “wisp” spectrum gradually increase. When the previously studied wave normal angle model (with a central wave normal angle of 60°) and the background electron density model are used, the energy range of the simulated “wisp” spectra is higher than the observed value. Adjusting the central wave normal angle to 40° or increasing the background density by a factor of 1.3, the simulated results accord well with the observations. Our results elucidate the scattering effect of NWC transmitter signals on electrons in the radiation belt, and emphasize the importance of analyzing the formation of “wisp” spectrum for understanding wave-particle interactions in near-earth space. Additionally, the Drift-Diffusion-Source model can be used to study wave-particle interactions in the inner radiation belt, helping to develop radiation belt remediation technology.
-

-
图 1 (I) 2009年3月19日NWC台站位于夜侧时, DEMETER卫星轨道在地理经纬度地图上的投影, 轨道的颜色表示卫星测量电子的类型. 蓝色表示沉降电子, 绿色表示准捕获电子, 红色表示捕获电子. 红色圆点标示出NWC台站的位置, 黑色实线表示L = 1.5和L = 1.9的等值线. 红色字母表示卫星轨道沿经度的分布次序; (a)—(f) (I)中轨道a—f在L = 1.5—1.9处观测到的L-Ek能谱, 颜色表示通量的大小. 能谱中增强的电子通量源自被台站信号散射的捕获电子, 称为“条缕状”能谱. 品红色五角星表示L = 1.7, Ek = 220 keV, 满足电子与传播角为60°的台站信号在赤道处的一阶回旋共振关系
Figure 1. (I) Trajectories of the DEMETER satellite on geographic map when the NWC station was at the nightside on 19 March 2009. The trajectories are color-coded by the electron type. Blue, red, and green represent untrapped, quasi-trapped, and trapped electrons, respectively. The red dot marks the location of the NWC station, and the solid black lines indicate the contours of L = 1.5 and L = 1.9, respectively. The red letters indicate the order of satellite orbits along longitude; (a)–(f) the electron spectra on L-Ek plane observed by DEMETER in orbits a – f shown in (I), respectively. The enhanced electron fluxes in the spectrum source from trapped electrons scattered by the transmitter signals, which is called “wisp” spectrum. The magenta stars indicate L = 1.7, Ek = 220 keV, satisfying the first-order equatorial cyclotron resonance relationship between the electron and the transmitter signal with wave normal angle of 60°.
图 2 (a) 计算使用的NWC台站信号幅值随L的变化; (b)—(f)中心传播角为60°的台站信号在L = 1.5–1.9引起的电子弹跳平均投掷角扩散系数
$\langle D_{\alpha\alpha} \rangle $ , 横轴为电子的赤道投掷角αeq, 纵轴为电子能量Ek, 颜色表示$\langle D_{\alpha\alpha} \rangle $ 的大小Figure 2. (a) The amplitudes of the NWC transmitter signals used for calculation; (b)–(f) the color-coded bounce-averaged pitch angle diffusion coefficients
$\langle D_{\alpha\alpha} \rangle $ as a function of equatorial pitch angle αeq and electron kinetic energy Ek induced by NWC transmitter signals with 60° central wave normal angle at L = 1.5–1.9, respectively.图 3 (第一行)模型中采用的电子的弹跳平均投掷角扩散系数
$\langle D_{\alpha\alpha} \rangle $ , 从左至右分别为L = 1.6处340 keV电子、L = 1.7处220 keV电子、L = 1.8处140 keV电子的$\langle D_{\alpha\alpha} \rangle $ , 横坐标表示地磁经度, 纵坐标表示赤道投掷角, 颜色表示扩散系数的大小, 黑色虚线表示使用IGRF磁场模型计算的局地弹跳损失锥大小, VLF台站信号作用经度范围为[99°, 129°]; (第二行)经度114°处, 不同机制导致的扩散系数随投掷角的变化, 黑色虚线表示相应L处的漂移损失锥的大小Figure 3. (The first line) The color-coded
$\langle D_{\alpha\alpha} \rangle $ as a function of αeq and geomagnetic longitude used in the model, from left to right, is respectively 340 keV at L = 1.6, 220 keV at L = 1.7 and 140 keV at L = 1.8. The black dashed lines represent the local bounce loss cone calculated based on IGRF model, and the longitude range of VLF transmitter signal is [99°, 129°]. (The second line)$\langle D_{\alpha\alpha} \rangle $ as a function of αeq at longitude = 114°. The black dash lines represent the drift loss cone at the corresponding L.图 4 (从上至下)每一行分别为模型模拟L = 1.6处340 keV, L = 1.7处220 keV, L = 1.8处140 keV电子漂移过程中, 通量随经度和赤道投掷角的分布, 颜色表示电子通量的大小. (从左至右)每一列分别为模型模拟步长为0, 120, 360时的结果, 1步长表示电子漂移经度1°所需的时间, L = 1.6处340 keV电子漂移经度1°约为16.8 s, L = 1.7处220 keV电子漂移经度1°约为23 s, L = 1.8处140 keV电子漂移经度1°约为32.5 s
Figure 4. (From top to bottom) Each row is the color-coded simulated electron fluxes as function of longitude and αeq during the drift process. (From left to right) Each column represents simulated time step is 0, 120 and 360 respectively. 1 step represents the time required for electron drift 1° longitude. 1 step for 340 keV electron at L = 1.6 is about 16.8 s, for 220 keV electron at L = 1.7 is about 23 s, and for 140 keV electron at L = 1.8 is about 32.5 s.
图 5 假设台站信号中心传播角为60°时, 模拟得到的L-Ek能谱, 颜色表示电子通量的大小, 与图1(a)—(f)的卫星观测能谱一一对应
Figure 5. Simulated L-Ek spectra assuming the central wave normal angle of the NWC transmitter signal is 60°, which correspond one to one with Figure 1(a)-(f).
图 6 卫星不同轨道在L = 1.7处观测的电子赤道投掷角, 黑色虚线表示使用IGRF磁场模型计算的局地弹跳损失锥大小, 红色虚线表示漂移损失锥大小
Figure 6. The αeq of electrons observed in different orbits of the satellite at L = 1.7, the black dashed line represents the local bounce loss cone calculated using the IGRF magnetic field model, and the red dashed line represents the drift loss cone.
图 7 (a) 计算使用的NWC台站信号幅值; (b)—(f)中心传播角为40°的台站信号在L = 1.5–1.9引起的电子弹跳平均投掷角扩散系数
$\langle D_{\alpha\alpha} \rangle $ , 横轴为电子的赤道投掷角αeq, 纵轴为电子能量Ek, 颜色表示$\langle D_{\alpha\alpha} \rangle $ 的大小Figure 7. (a) The amplitude of the NWC transmitter signals used for calculation; (b)–(f) the color-coded bounce-averaged pitch angle diffusion coefficients
$\langle D_{\alpha\alpha} \rangle $ ; as a function of equatorial pitch angle αeq and electron kinetic energy Ek induced by NWC transmitter signals with 40° central wave normal angle at L = 1.5–1.9, respectively.图 9 (a) 计算使用的NWC台站信号幅值; (b)—(f)背景密度扩大1.3倍之后, 中心传播角为60°的台站信号在L = 1.5—1.9引起的电子弹跳平均投掷角扩散系数
$\langle D_{\alpha\alpha} \rangle $ , 横轴为电子的赤道投掷角αeq, 纵轴为电子能量Ek, 颜色表示$\langle D_{\alpha\alpha} \rangle $ 的大小Figure 9. (a) The amplitude of the NWC transmitter signals used for calculation; (b)–(f) the color-coded bounce-averaged pitch angle diffusion coefficients
$\langle D_{\alpha\alpha} \rangle $ as a function of equatorial pitch angle αeq and electron kinetic energy Ek induced by NWC transmitter signals with 60° central wave normal angle at L = 1.5–1.9, respectively, when the background density is enlarged by a factor of 1.3 -
[1] Baker D N, Kanekal S G, Hoxie V C, Henderson M G, Li X, Spence H E, Elkington S R, Friedel R H W, Goldstein J, Hudson M K, Reeves G D, Thorne R M, Kletzing C A, Claudepierre S G 2013 Science 340 186 doi: 10.1126/science.1233518 [2] Dong J, Xiang Z, Ni B, Liu Y 2023 J. Geophys. Res. Space Phys. 128 e2023JA031869 doi: 10.1029/2023JA031869 [3] Guo D, Xiang Z, Ni B, Cao X, Fu S, Zhou R, Gu X, Yi J, Guo Y, Jiao L 2021 Geophys. Res. Lett. 48 e2021GL095714 doi: 10.1029/2021GL095714 [4] Guo D, Xiang Z, Ni B, Jin T, Zhou R, Yi J, Liu Y, Dong J 2023 J. Geophys. Res. Space Phys. 128 e2023JA031407 doi: 10.1029/2023JA031407 [5] Tang C L, Xie X J, Ni B, Su Z P, Reeves G D, Zhang J C, Baker D N, Spence H E, Funsten H O, Blake J B, Wygant J R, Dai G Y 2018 J. Geophys. Res. Space Phys. 123 4895 doi: 10.1029/2017JA025142 [6] Yang X, Ni B, Yu J, Zhang Y, Zhang X, Sun Y 2017 J. Geophys. Res. Space Phys. 122 6255 doi: 10.1002/2016JA023204 [7] Zhu Q, Cao X, Gu X, Ni B, Xiang Z, Fu S, Summers D, Hua M, Lou Y, Ma X, Guo Y, Guo D, Zhang W 2021 J. Geophys. Res. Space Phys. 126 e2020JA029057 doi: 10.1029/2020JA029057 [8] 曹兴, 陆鹏, 朱琪, 马新, 倪彬彬 2023 地球物理学报 66 1796 doi: 10.6038/cjg2022Q0669 Cao X, Lu P, Zhu Q, Ma X, Ni B B 2023 Chin. J. Geophys. 66 1796 doi: 10.6038/cjg2022Q0669 [9] Carlsten B E, Colestock P L, Cunningham G S, Delzanno G L, Dors E E, Holloway M A, Jeffery C A, Lewellen J W, Marksteiner Q R, Nguyen D C, Reeves G D, Shipman K A 2019 IEEE Trans. Plasma Sci. 47 2045 doi: 10.1109/TPS.2019.2910829 [10] Golkowski M, Harid V, Hosseini P 2019 Front. Astron. Space Sci. 6 2 doi: 10.3389/fspas.2019.00002 [11] Johnston W R, Ginet G P, Starks M J, McCollough J P, Sanchez J C, Song P, Galkin I A, Inan U S, Lauben D S, Tu J, Reinisch B W, Linscott I R, Roche K, Stelmash S, Allgeier S, Lambour R, Schoenberg J, Gillespie W, Farrell W M, Xapsos M A, Roddy P A, Lindstrom C D, Pedinotti G F, Huston S L, Albert J M, Sinclair A J, Davis L D, Carilli J A, Cooke D L, Parker C W 2023 J. Geophys. Res. Space Phys. 128 e2022JA030771 doi: 10.1029/2022JA030771 [12] Claudepierre S G, Ma Q, Bortnik J, O'Brien T P, Fennell J F, Blake J B 2020 Geophys. Res. Lett. 47 e2019GL086056 doi: 10.1029/2019GL086056 [13] Hua M, Li W, Ni B, Ma, Q., Green, A., Shen, X., Claudepierre S G, Bortnik J, Gu X, Fu S, Xiang Z, Reeves G D 2020 Nat. Commun. 11 4847 doi: 10.1038/s41467-020-18545-y [14] Hua M, Bortnik J, Ma Q, Bernhardt P A 2022 Geophys. Res. Lett. 49 e2022GL099258 doi: 10.1029/2022GL099258 [15] Ni B, Hua M, Gu X, Fu S, Xiang Z, Cao X, Ma X 2022 Sci. China, Ser. D Earth Sci. 65 391 doi: 10.1007/s11430-021-9850-7 [16] Ni B, Summers D, Xiang Z, Dou, X, Tsurutani B T, Meredith N P, Dong J, Chen L, Reeves G D, Liu X, Tao X, Gu X, Ma X, Yi J, Fu S, Xu W 2023 J. Geophys. Res. Space Physics 128 e2023JA031325 doi: 10.1029/2023JA031325 [17] Abel B, Thorne R M 1998 J. Geophys. Res. 103 2385 doi: 10.1029/97JA02919 [18] Albert J M, Starks M J, Selesnick R S, Ling A G, O'Malley S, Quinn R A 2020 J. Geophys. Res. Space Phys. 125 e2019JA027030 doi: 10.1029/2019JA027030 [19] Graf K L, Inan U S, Piddyachiy D, Kulkarni P, Parrot M, Sauvaud J A 2009 J. Geophys. Res. Space Phys. 114 A07205 [20] Imhof W L, Reagan J B, Voss H D, Gaines E E, Datlowe D W, Mobilia J, Helliwell R A, Inan U S, Katsufrakis J, Joiner R G 1983 Geophys. Res. Lett. 10 361 doi: 10.1029/GL010i004p00361 [21] Koons H C, Edgar B C, Vampola A L 1981 J. Geophys. Res. Space Phys. 86 640 doi: 10.1029/JA086iA02p00640 [22] Li L Y, Wang Z Y, Yu J, Cao J B 2021 J. Geophys. Res. Space Phys. 126 e2020JA028879 doi: 10.1029/2020JA028879 [23] Clilverd M A, Rodger C J, Gamble R, Meredith N P, Parrot M, Berthelier J J, Thomson N R 2008 J. Geophys. Res. Space Phys. 113 A04211 [24] 王亚璐, 项正, 泽仁志玛, 倪彬彬, 刘阳希子, 张学民, 欧阳新艳, 吴迎燕, 申旭辉 2023 地球物理学报 66 4451 doi: 10.6038/cjg2023R0421 Wang Y L, Xiang Z, Zeren Z M, Ni B B, Liu Y X Z, Zhang X M, Ouyang X Y, Wu Y Y, Shen X H 2023 Chin. J. Geophys. 66 4451 doi: 10.6038/cjg2023R0421 [25] Ma Q, Mourenas D, Li W, Artemyev A, Thorne R M 2017 Geophys. Res. Lett. 44 6483 doi: 10.1002/2017GL073885 [26] Ma Q, Gu W, Claudepierre S G, Li W, Bortnik J, Hua M, Shen X C 2022 J. Geophys. Res. Space Phys. 127 e2022JA030349 doi: 10.1029/2022JA030349 [27] Meredith N P, Horne R B, Clilverd M A, Ross J P J 2019 J. Geophys. Res. Space Phys. 124 5246 doi: 10.1029/2019JA026715 [28] Ross J P J, Meredith N P, Glauert S A, Horne R B, Clilverd M A 2019 J. Geophys. Res. Space Phys. 124 5260 doi: 10.1029/2019JA026716 [29] Wang Y L, Zhang X M, Shen X H 2018 Earth Planet. Phys. 2 538 doi: 10.26464/epp2018052 [30] 项正, 林显浩, 陈薇, 王勇, 陆鹏, 龚文颖, 马文琛, 花漫, 刘阳希子 2021 地球物理学报 64 3860 doi: 10.6038/cjg2021P0131 Xiang Z, Lin X H, Chen W, Wang Y, Lu P, Gong W Y, Ma W C, Hua M, Liu Y X Z 2021 Chin. J. Geophys. 64 3860 doi: 10.6038/cjg2021P0131 [31] Sauvaud J-A, Maggiolo R, Jacquey C, Parrot M, Berthelier J-J, Gamble R J, Rodger C J 2008 Geophys. Res. Lett. 35 L09101 [32] Gamble R J, Rodger C J, Clilverd M A, Sauvaud J-A, Thomson N R, Stewart S L, McCormick R J, Parrot M, Berthelier J-J 2008 J. Geophys. Res. Space Phys. 113 A10211 [33] Li X, Ma Y, Wang P, Wang H, Lu H, Zhang X, Huang J, Shi F, Yu X, Xu Y, Meng X, Wang H, Zhao X, Parrot M 2012 J. Geophys. Res. Space Phys. 117 A04201 [34] Vampola A L, Kuck G A 1978 J. Geophys. Res. Space Phys. 83 2543 doi: 10.1029/JA083iA06p02543 [35] Selesnick R S, Albert J M, Starks M J 2013 J. Geophys. Res. Space Phys. 118 628 doi: 10.1002/jgra.50095 [36] Liu Y, Xiang Z, Ni B, Li X, Zhang K, Fu S, Gu X, Liu J, Cao X 2022 Geophys. Res. Lett. 49 e2021GL097443 doi: 10.1029/2021GL097443 [37] Parrot M 2006 Planet. Space Sci. 54 411 doi: 10.1016/j.pss.2005.10.012 [38] Sauvaud J A, Moreau T, Maggiolo R, Treilhou J P, Jacquey C, Cros A, Coutelier J, Rouzaud J, Penou E, Gangloff M 2006 Planet. Space Sci. 54 502 doi: 10.1016/j.pss.2005.10.019 [39] Li X, Schiller Q, Blum L, Califf S, Zhao H, Tu W, Turner D L, Gerhardt D, Palo S, Kanekal S, Baker D N, Fennell J, Blake J B, Looper M, Reeves G D, Spence H 2013 J. Geophys. Res. Space Phys. 118 6489 doi: 10.1002/2013JA019342 [40] Tu W, Selesnick R, Li X, Looper M 2010 J. Geophys. Res. Space Phys. 115 A07210 [41] Hu J, Xiang Z, Ma X, Liu Y, Dong J, Guo D, Ni B 2024 Space Weather 22 e2023SW003827 doi: 10.1029/2023SW003827 [42] Zhang K, Li X, Xiang Z, Khoo L Y, Zhao H, Looper M D, Schiller Q, Temerin M A, Sauvaud J A 2020 J. Geophys. Res. Space Phys. 125 e2020JA028086 doi: 10.1029/2020JA028086 [43] 胡立凡, 项正, 顾旭东, 倪彬彬, 张效信, 郭建广, 张贤国, 朱昌波, 郭德宇, 付松, 刘阳希子, 董俊虎, 赵怡雯 2023 地球物理学报 66 2252 doi: 10.6038/cjg2022Q0613 Hu L F, Xiang Z, Gu X D, Ni B B, Zhang X X, Guo J G, Zhang X G, Zhu C B, Guo D Y, Fu S, Liu Y X Z, Dong J H, Zhao Y W 2023 Chin. J. Geophys. 66 2252 doi: 10.6038/cjg2022Q0613 [44] Ozhogin P, Tu J, Song P, Reinisch B W 2012 J. Geophys. Res. Space Phys. 117 A06225 [45] Ni B, Thorne R M, Shprits Y Y, Bortnik J 2008 Geophys. Res. Lett. 35 L11106 [46] Ni B, Thorne R M, Meredith N P, Shprits Y Y, Horne R B 2011 J. Geophys. Res. Space Phys. 116 A10207 [47] Zhang Z, Chen L, Li X, Xia Z, Heelis R A, Horne R B 2018 J. Geophys. Res. Space Phys. 123 5528 doi: 10.1029/2018JA025637 [48] Gu W, Chen L, Xia Z, Horne R B 2021 Geophys. Res. Lett. 48 e2021GL093987 doi: 10.1029/2021GL093987 [49] Liu Y X Z, Xiang Z, Guo J G, Gu X D, Fu S, Zhou R X, Hua M, Zhu Q, Yi J, Ni B B 2021 Acta Phys. Sin. 70 149401 [刘阳希子, 项正, 郭建广, 顾旭东, 付松, 周若贤, 花漫, 朱琪, 易娟, 倪彬彬 2021 物理学报 70 149401] doi: 10.7498/aps.70.20202029 Liu Y X Z, Xiang Z, Guo J G, Gu X D, Fu S, Zhou R X, Hua M, Zhu Q, Yi J, Ni B B 2021 Acta Phys. Sin. 70 149401 doi: 10.7498/aps.70.20202029 [50] Xiang Z, Li X, Temerin M A, Ni B, Zhao H, Zhang K, Khoo L Y 2020 a J. Geophys. Res. Space Phys. 125 e2019JA027678 doi: 10.1029/2019JA027678 [51] Li X, Selesnick R, Schiller Q, Zhang K, Zhao H, Baker D N, Temerin M A 2017 Nature 552 382 doi: 10.1038/nature24642 [52] Xiang Z, Li X, Selesnick R, Temerin M A, Ni B, Zhao H, Zhang K, Khoo L Y 2019 Geophys. Res. Lett. 46 1919 doi: 10.1029/2018GL081730 [53] Xiang Z, Li X, Ni B, Temerin M A, Zhao H, Zhang K, Khoo L Y 2020 b J. Geophys. Res. Space Phys. 125 e2020JA028042 doi: 10.1029/2020JA028042 [54] Selesnick R S 2015 J. Geophys. Res. Space Phys. 120 2912 doi: 10.1002/2014JA020963 [55] Selesnick R S 2012 J. Geophys. Res. Space Phys. 117 A08218 [56] Reidy J A, Horne R B, Glauert S A, Clilverd M A, Meredith N P, Rodger C J, Ross J P, Wong J 2024 J. Geophys. Res. Space Phys. 129 e2023JA031641 doi: 10.1029/2023JA031641 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: