首页
登录
注册
下载:
-
塑料闪烁体通常具有时间响应快、发光产额高、机械性能优良等优点, 在MeV能段脉冲中子辐射场诊断中具有广泛的应用[1]. 中子在塑料闪烁体中的作用过程较为复杂, 在低能段(<2 MeV)主要通过中子同质子(氢核)发生n-p作用, 反冲质子在闪烁体中沉积能量引起发光. 随着中子能量升高, n-p弹性散射之外的中子能量沉积(比如n-C弹性散射、中子吸收等)不能忽略, 随着所产生带电粒子能量的升高, 其在体积有限塑料闪烁体中逃逸的可能就越高, 并且电子、质子等粒子在塑料闪烁体中的光产额随能量非线性变化[2], 所以中子闪烁探测器的能量响应曲线并不平坦. 在中子能谱测量等应用中, 必须对塑料闪烁体的中子能谱响应进行测量[3,4].
塑料闪烁体中子能谱响应通常通过测量(准)单能中子入射到闪烁体上的脉冲幅度谱[5]或探测器输出电流[3–6]获得, 或者测量质子能谱响应[7]. 受限于中子源, 这种方法只能测量有限几个能点[8–11], 或是使用模拟计算结果[12], 给探测器数据分析带来一定的困扰. 尤其是对近百MeV高能中子的能量响应, 可用实验结果很少[13–15], 并且不同的模拟计算程序结果差异较大[15]. 2018年中国散裂中子源(China Spallation Neutron Source, CSNS)建 成[16], 其白光中子束线(white neutron source, WNS)能以25 Hz的频率提供能谱连续的中子脉冲, 中子脉宽42 ns, 能谱范围0.3 eV—200 MeV[17], 为闪烁探测器中子能谱响应测量提供了更加便利的条件. 本文基于散裂中子源白光中子束线, 测量了不同厚度ST401塑料闪烁体的中子能谱响应曲线, 并对实验结果进行分析讨论.
-
闪烁体中子能谱响应S(En)(
$ S({E_{\text{n}}}) = {{{\varPsi _{{E_{\text{n}}}}}}}/{{{I_{{E_{\text{n}}}}}}}$ )一般指闪烁体光输出随入射中子能量的变化情况, 可由下式定义:式中
$ {\varPsi _{{E_{\text{n}}}}} $ 表示能量为En的一个或多个中子进入闪烁体时, 闪烁体产生的光子数,$ {I_{{E_{\text{n}}}}} $ 表示进入探测系统的中子数量.对具体的闪烁体-光电探测系统, 其中子能谱响应SD(En)定义如下:
式中,
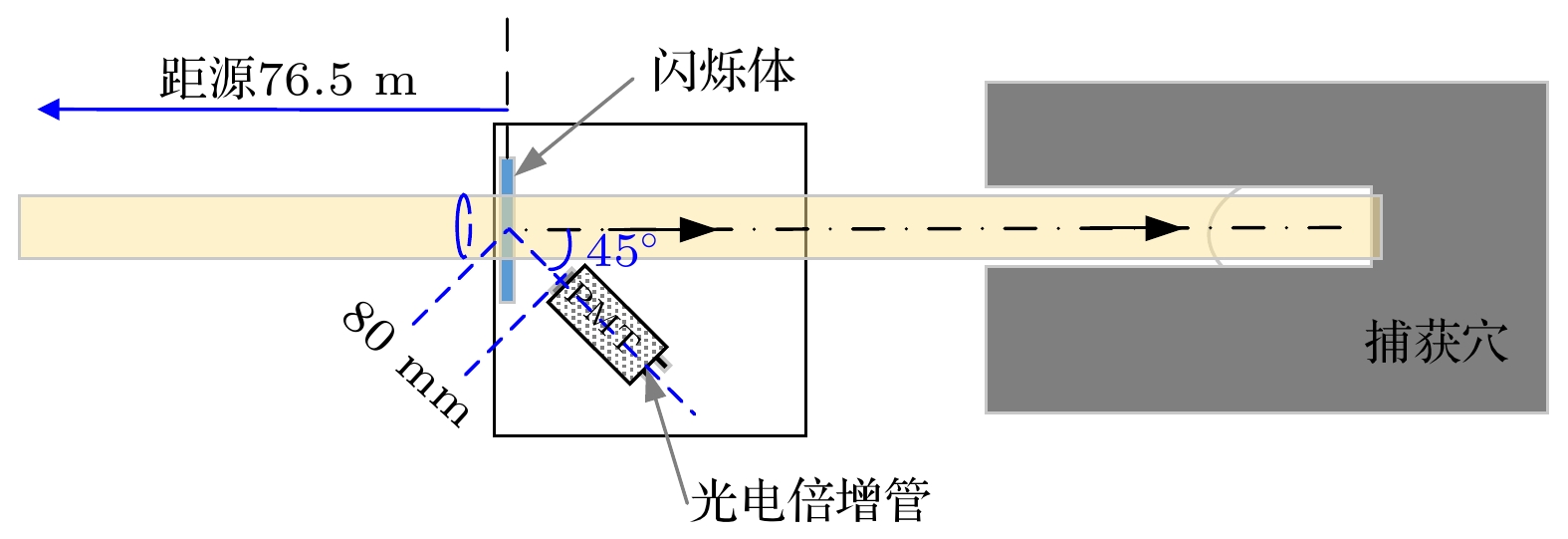
$ {Q_{{E_{\text{n}}}}} $ 表示能量为En的一个或多个中子进入探测系统时, 探测系统的输出电荷, ηC表示探测系统的光子收集效率, SD(λ)表示探测系统对闪烁体输出光子的平均灵敏度, 是闪烁体发光波长λ的函数. 对同一探测系统, 相同类型的闪烁体, ηC和SD(λ)均为常数, 所以探测器中子能谱响应曲线的分布与变化趋势和闪烁体相同, 可以使用探测器的中子能谱响应曲线表征闪烁体的中子能谱响应.在散裂中子源白光束线上开展了闪烁体中子能谱响应测量实验, 布局如图1所示. 中子经约76.5 m真空管道到达闪烁体, 避开中子束流放置光电倍增管(photomultiplier tube, PMT, 南京北方夜视集团生产, N2021)以降低中子直照产生的干扰, 使用LeCroy8108示波器记录PMT输出的脉冲信号.
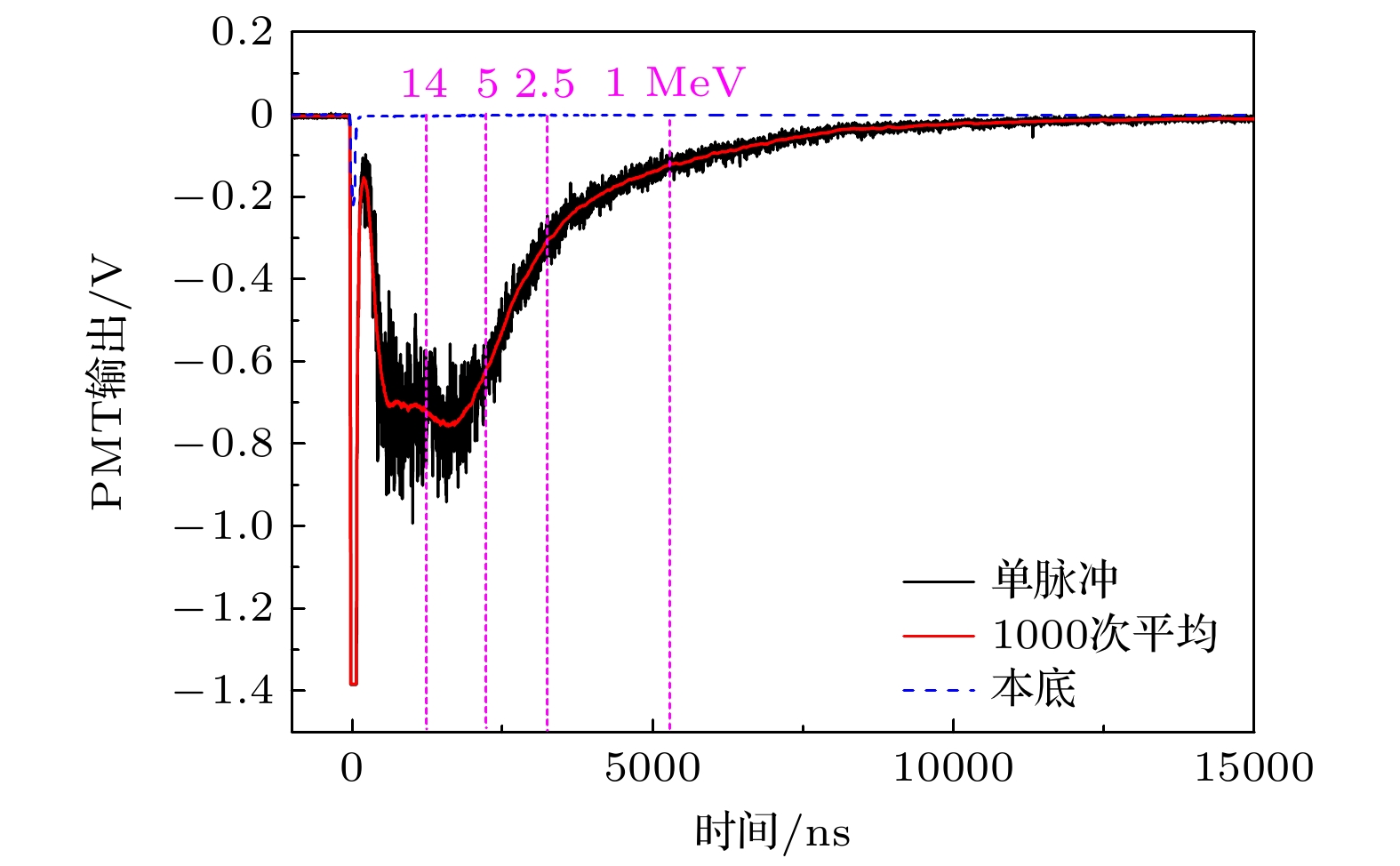
实验中, 记录的典型波形(厚度5 mm ST401)如图2所示, 高能质子打靶产生中子脉冲的同时, 伴随产生一个伽马脉冲, 根据中子到达闪烁体时刻与伽马峰的时间差判断该时刻中子的能量, 图中零时刻为波形的伽马峰值时刻. 为了保证中子波形有足够的垂直分辨率, 使伽马脉冲冲出示波器量程(但仍处于PMT线性范围内). 从图2波形可以看出, 经过1000次平均之后, 得到了信噪比较高的闪烁体输出波形. 图中本底信号为遮挡闪烁体发光后的PMT输出波形, 本底波形上只观测到幅值约200 mV的伽马散射峰, 说明在此布局下散射中子的影响噪声可以忽略.
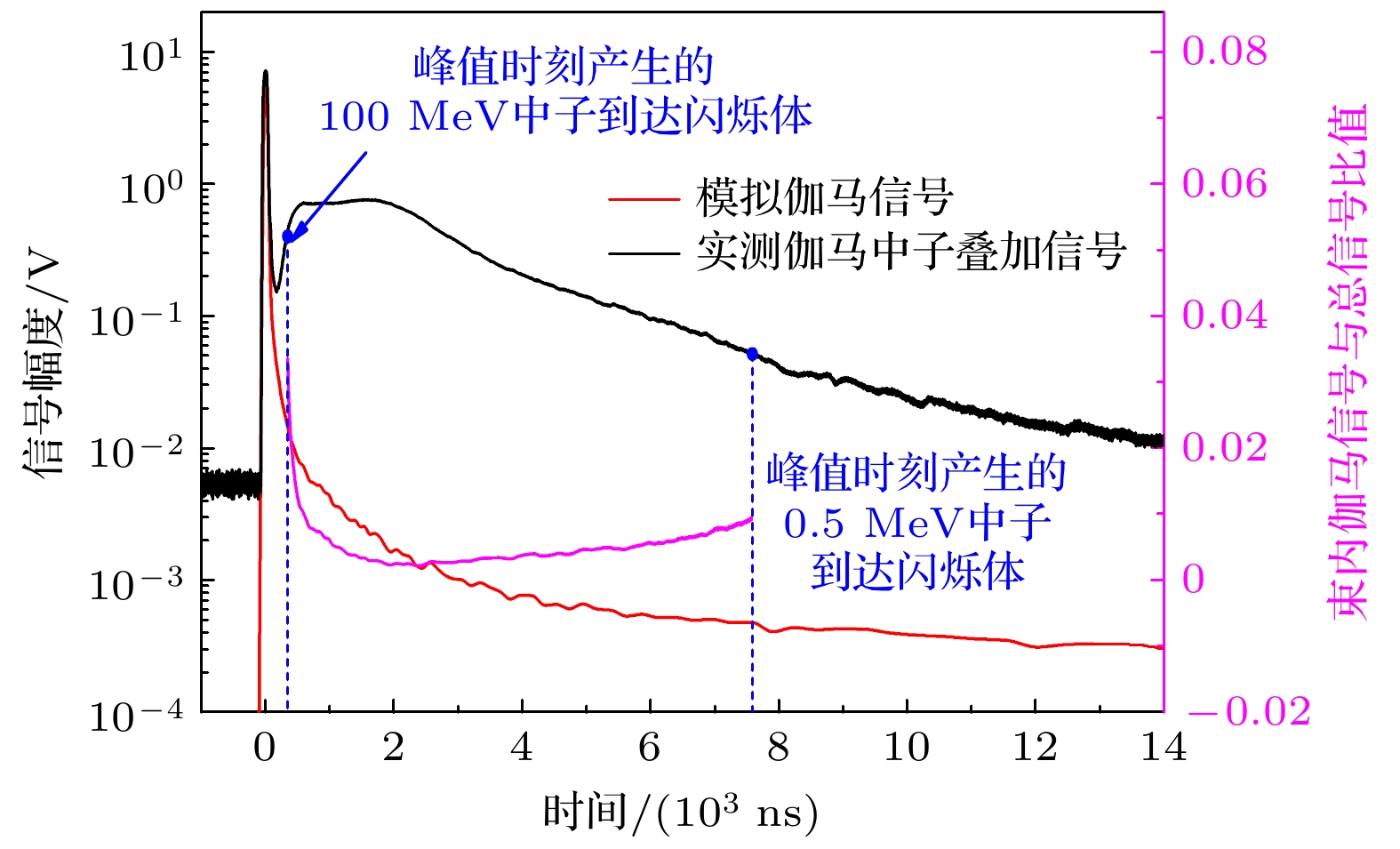
100 MeV和0.5 MeV中子到达闪烁体的时刻分别为伽马峰后342 ns和7569.7 ns, 相对MeV中子, 近百MeV的高能中子强度相对较低, 可能受到伽马闪信号、束内伽马等的干扰. 下文分析这些因素对中子能谱响应测量的影响.
-
根据文献[18]的研究结果, 伽马峰后342 ns(此时伽马峰值产生的100 MeV中子到达闪烁体), 束内伽马较伽马flash峰值下降超过3个量级. 使用文献[18]图3(b)中的模拟数据评估束内伽马在5 mm厚ST401塑料闪烁体上产生的信号, 如图3中红色实线所示. 图3中粉色实线为本文关注能段(0.5—100 MeV)模拟束内伽马信号与实测信号的比值, 在伽马峰后342 ns (100 MeV中子), 束内伽马产生信号的占比最高, 占总信号约3%; 随后伽马占比迅速降低, 在峰后2136 ns (5.4 MeV中子)占比最低, 仅占0.24%; 之后缓慢上升, 直至7570 ns (0.5 MeV中子), 束内伽马信号占比仍低于1%. 所以束内伽马对低于100 MeV中子能谱响应标定的影响可以忽略.
-
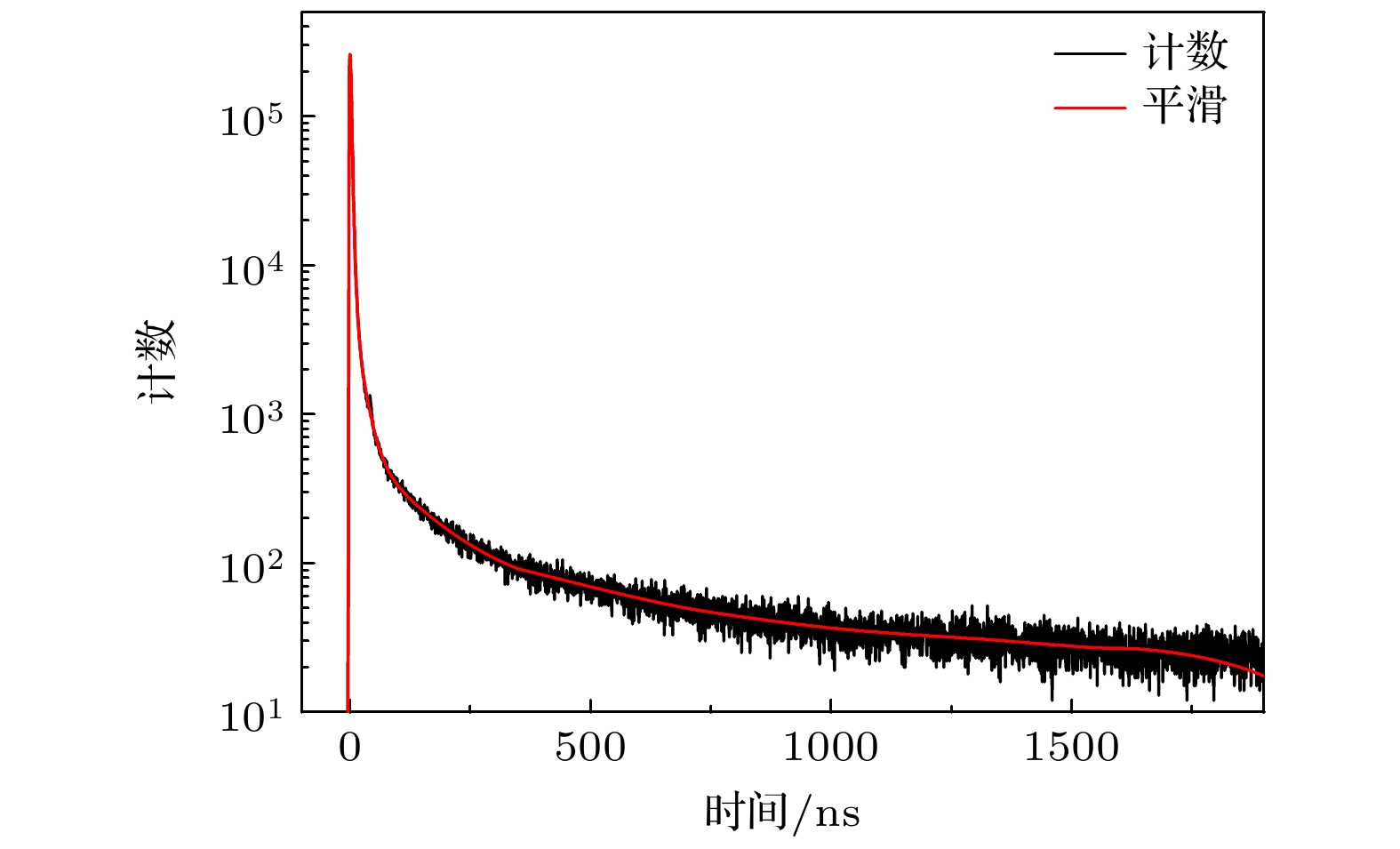
使用单光子计数法[19]测量本次实验所用ST401塑料闪烁体(d = 5 mm)的发光慢成分(137Cs源激发), 测量结果如图4所示. 峰后343 ns塑料闪烁体慢成分已降低至峰值的0.03% (峰值计数), 影响可以忽略.
-
中子源脉宽约42 ns, 也就是说同一时刻到达闪烁体的中子有一定的能量分布, 下面分析中子源脉宽对能谱响应测量的影响.
假设中子源的时间谱为f(t), 峰值时刻为T0, 能谱为g(E), 中子脉冲时间谱和能谱相互独立. 那么T1时刻, 到达距离源L闪烁体的中子能谱h(E)可以写为
式中, ttof是指中子飞行L所需的时间, 考虑相对论效应的中子飞行时间公式可以写为
式中L单位是m, E的单位是MeV, 等号右边括号中第2项为相对论效应修正项, 对低能中子可以忽略不计.
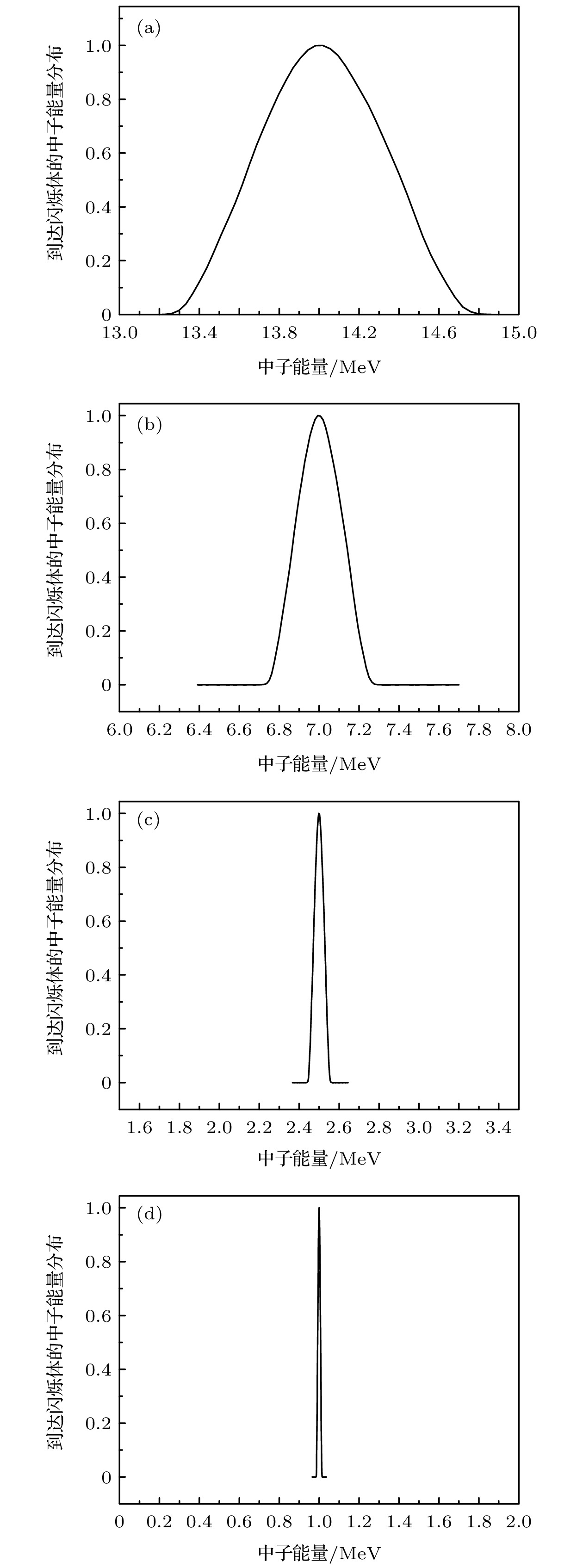
使用伽马波形代替中子时间谱, 计算得出伽马峰后1268.7 ns (14 MeV), 1890.4 ns (7 MeV), 3326.2 ns (2.5 MeV)和5404.3 ns (1 MeV)这4个时刻到达闪烁体的中子能谱(归一化)情况. 如图5所示. 从图5可以看出, 能量越高, 同一时刻到达闪烁体的中子能量分布就越宽: 1268.7 ns时刻到达闪烁体的中子能量为(14±0.7) MeV; 而5404.3 ns时刻到达闪烁体的中子能量为(1±0.01) MeV.
对能量较低(≤1 MeV)的中子, 闪烁体处中子能量宽度≤1%, 对能谱测量的影响可以忽略. 对能量较高中子, 同一时刻到达闪烁体的中子能量分布范围较宽(约5%@14 MeV, 约2.8%@7 MeV, 约2%@2.5 MeV), 但由于塑料闪烁体在较高能中子的能谱响应曲线较为平缓[15], 而且, 中子源在较高能段上也不存在特征峰等突变[17], 综合考虑闪烁体处的中子能量宽度影响较小, 在不确定度中加以考虑即可.
忽略中子源时间宽度, (2)式可以写为
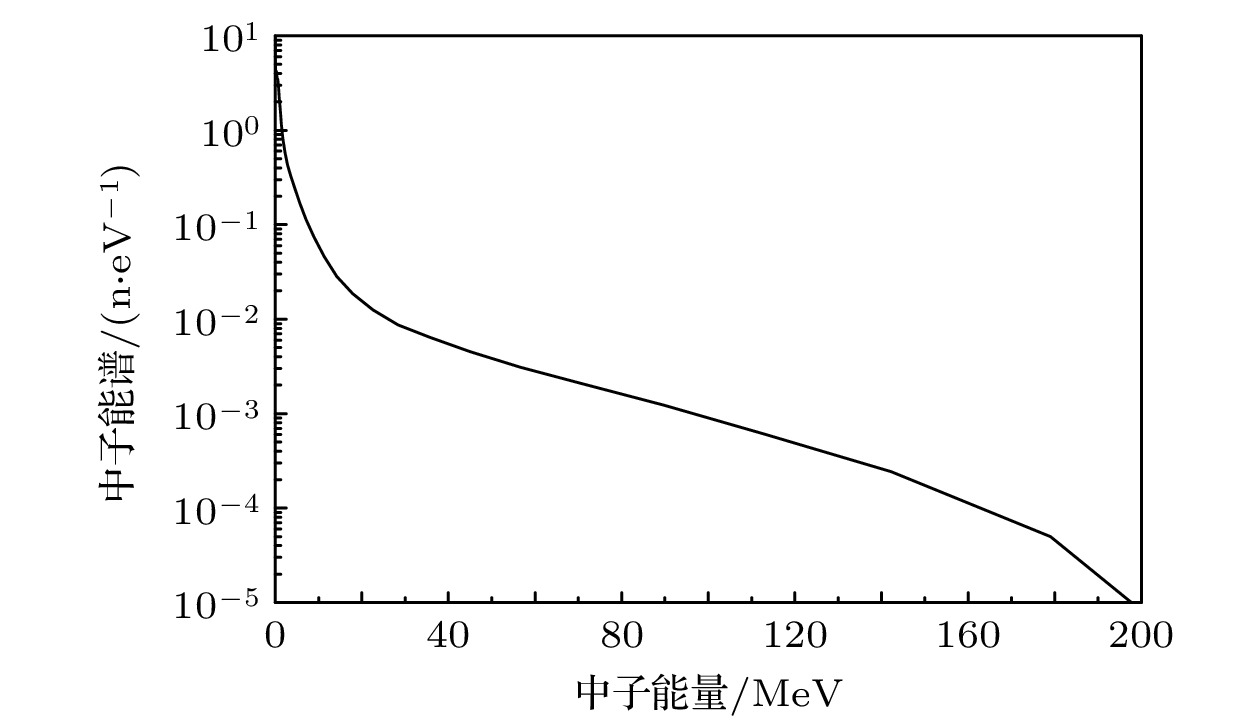
式中, IPMT指白光中子源一个脉冲在测量系统上产生的电流信号,
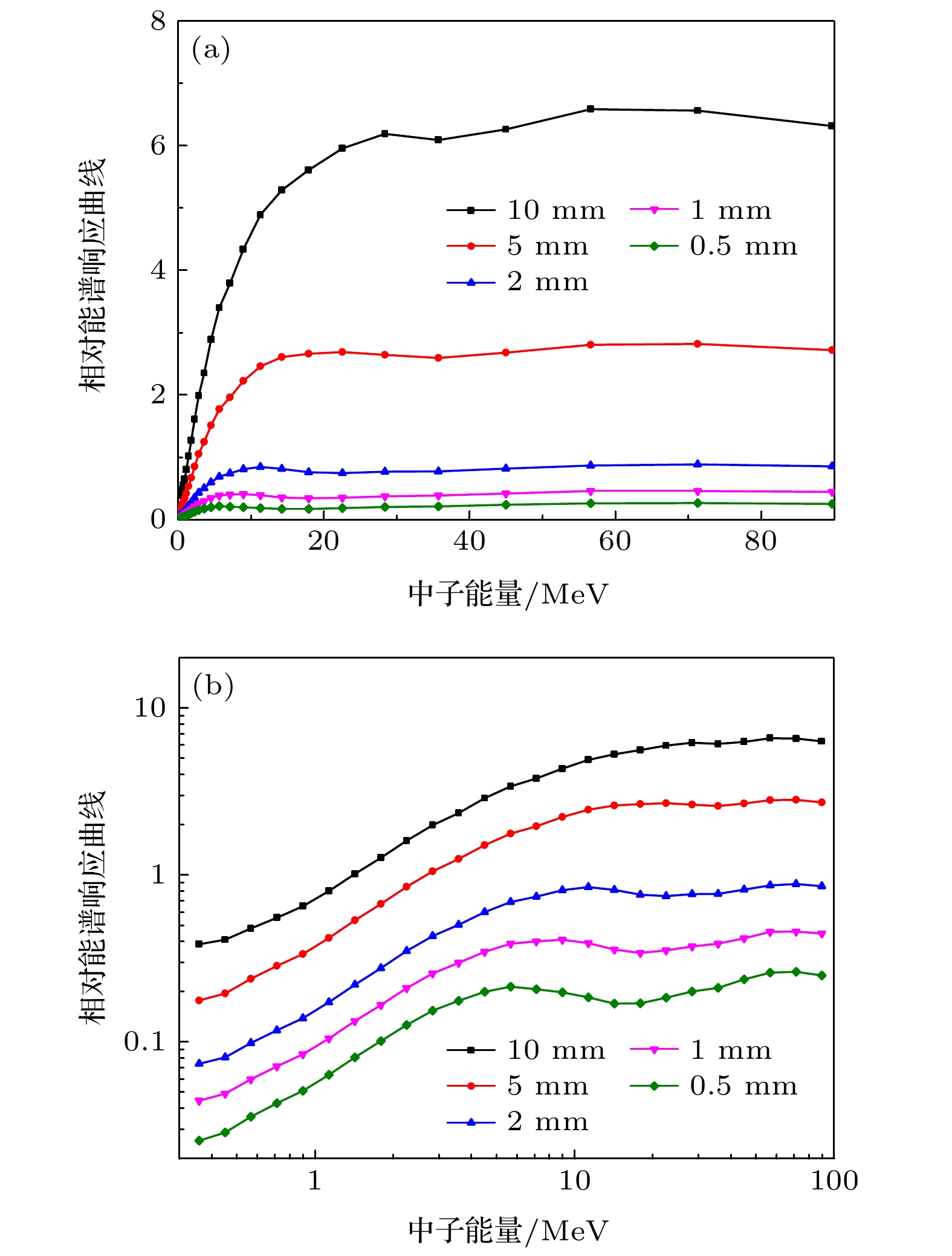
$ {\varPhi _{{E_i} - {E_{i + 1}}}} $ 表示能量处于Ei和Ei+1之间的中子数, 由中子源能谱Φ(E)给出. 塑料闪烁体能谱响应范围(0.5—200 MeV)内中子源能谱Φ(E)如图6所示[17].使用上述方法测量了直径250 mm, 厚度分别为0.5, 1, 2, 5, 10 mm共5种不同ST401塑料闪烁体的中子能谱响应, 测量过程中, 保持实验布局不变, 以保证闪烁体-PMT光耦合效率不变, 5种不同厚度塑料闪烁体相对能谱响应如图7所示. 从图中能够看出, 中子能量低于2 MeV时, 闪烁体中子能谱响应近似线性; 随着中子能量升高, 能量响应偏离线性, 闪烁体越薄, 偏离能量越低. 偏离线性后, 不同厚度闪烁体的能谱响应曲线出现先下降、后上升的趋势, 整体趋于平坦.
-
ST401是一种典型的三元塑料闪烁体, 它使用聚苯乙烯作基质, 对联三苯作第一闪烁物质, POPOP作移波剂[20]. 从元素成分上, 主要由C, H 两种元素构成, H原子和C原子数密度分别为约0.052410 atoms/(barn·cm)和约0.047346 atoms/(barn·cm) [21].
影响粒子-闪烁体作用发光效率的因素主要包括粒子在闪烁体中的能量沉积和沉积能量的光转换效率. 中子与ST401的作用主要包括以下过程.
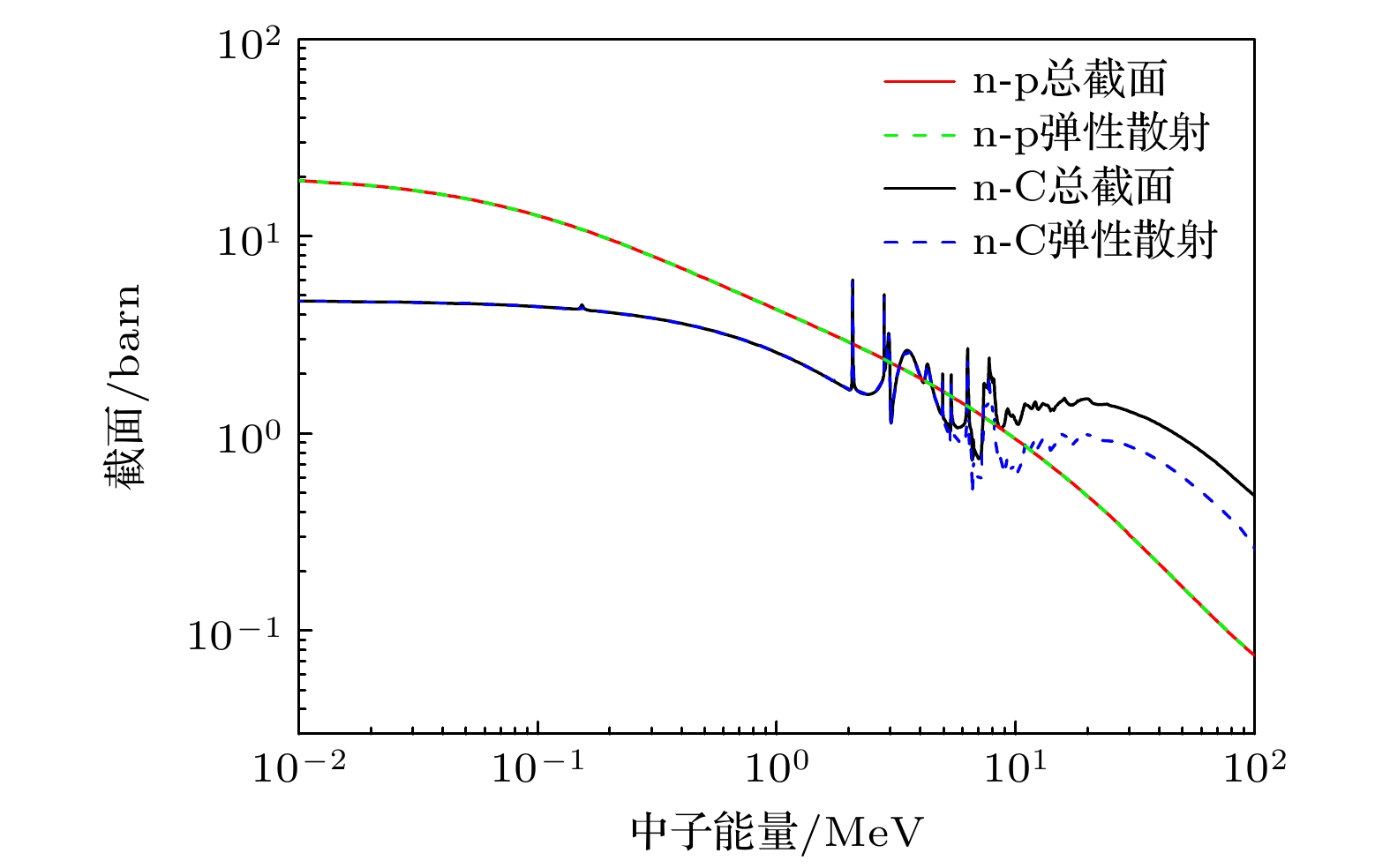
1)中子和质子(H核)、C核的弹性散射, 或者中子被C 原子俘获释放产生Be, B, C 等带电离子或者电子, 在闪烁体中产生能量沉积. 能量沉积物理过程主要由闪烁体中C, H元素比例和各作用过程截面决定, 截面数据如图8所示[21]. 从截面数据可以看出, 当中子能量低于2 MeV时, 中子与氢核弹性散射产生的质子占主导地位. 但随着能量升高, n-C截面相对n-p截面逐渐不可忽略.
2)产生的质子、离子或电子在闪烁体中沉积能量, 引起发光, 发光强度可通过(6)式—(11)式(光响应函数)描述[22]:
式中, L(Ex)表示种类x粒子在闪烁体中产生的发光, Ex表示x粒子在闪烁体中的沉积能量.
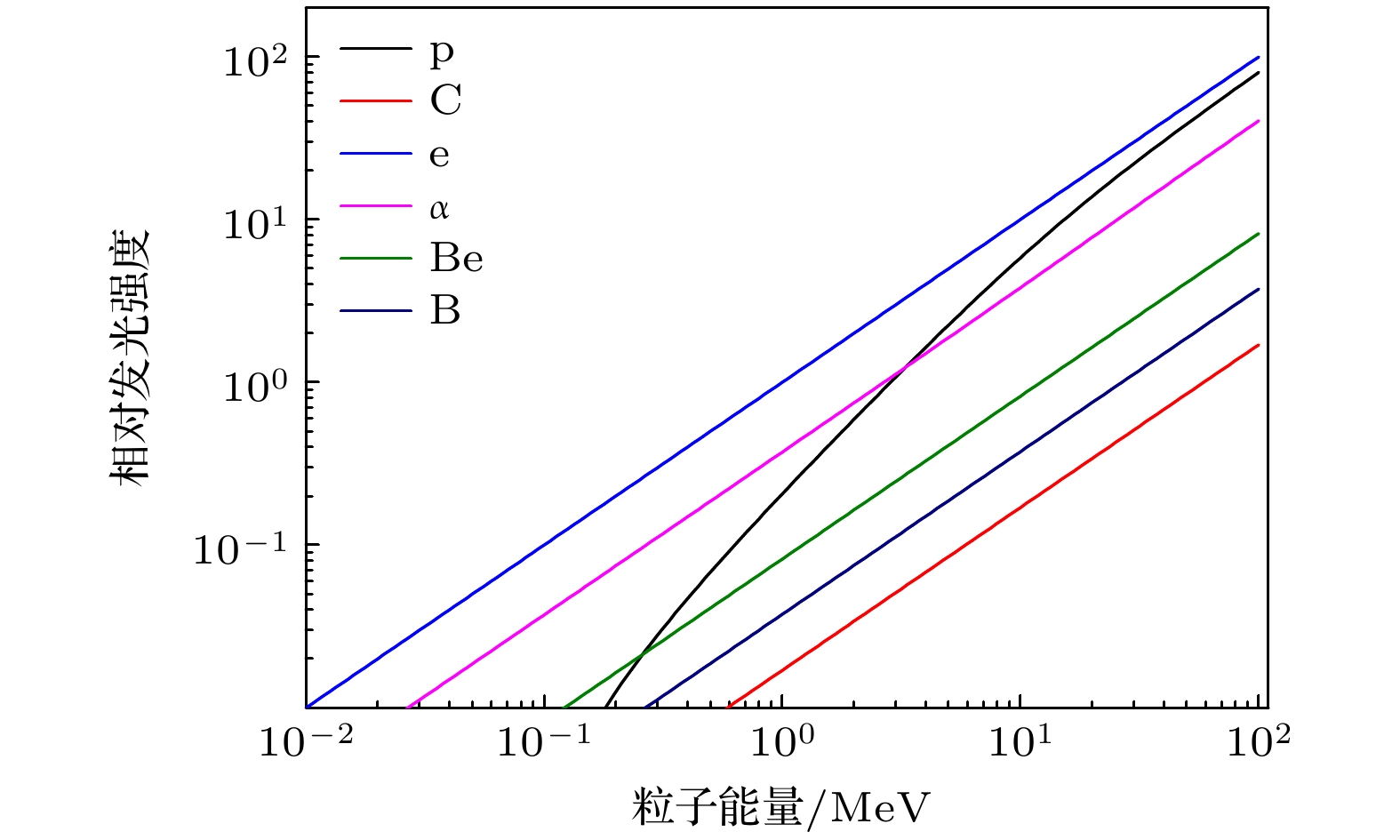
光响应函数曲线如图9所示. 比较各条曲线可以看出, 目前关注的几类粒子在塑料闪烁体中的光响应函数近似线性, 质子的光响应函数偏离线性最明显. 相同能量的不同粒子在塑料闪烁体中的发光效率差距较大, 总的趋势是带电粒子越重, 发光效率越低, 相同能量的电子发光效率是C核的约60倍. 所以虽然在中子能量高于2 MeV时, n-C作用截面就已经开始不能忽略, 但考虑到n-C主要产物为C, α, Be, B等原子核, 它们在闪烁体中的发光函数要明显低于相同能量的电子和质子, 所以较多研究人员认为中子能量大于8—10 MeV时, n-C作用产生的发光不可忽略[22].
-
根据3.1节的分析, 若闪烁体体积足够大, 入射闪烁体的中子能量全沉积, 塑烁的中子能谱响应曲线近似直线, 但实测中子能谱响应曲线近似对数函数, 这主要由于中子能量不能全部沉积在闪烁体中造成. 对厚度有限的塑料闪烁体, 中子射入闪烁体后, 产生的散射中子和带电粒子都可能从闪烁体中逃逸, 只有部分能量能够沉积进而产生发光——此为所谓的边界效应. 边界效应使闪烁体发光强度-中子能量曲线偏离线性, 接近对数曲线.
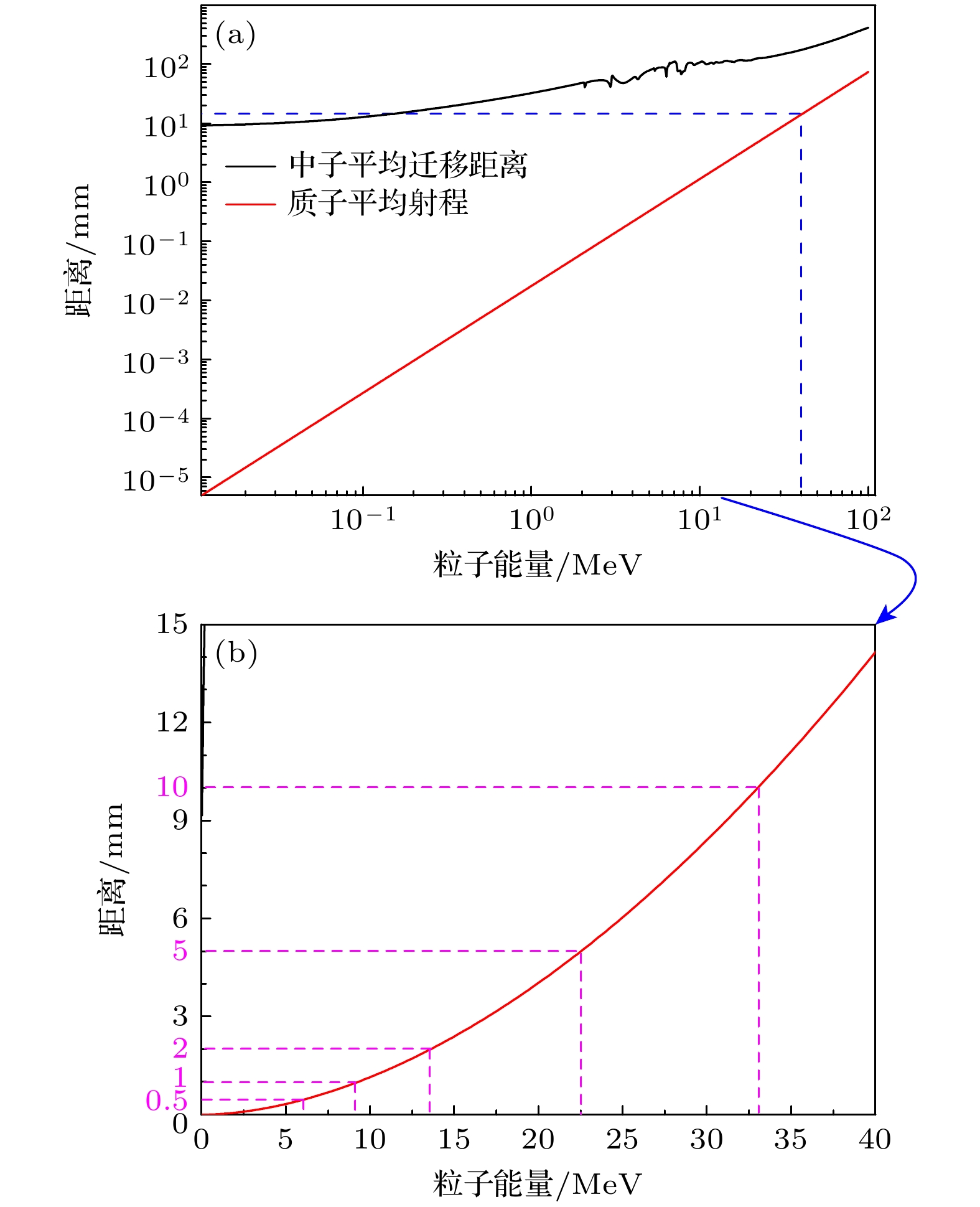
本文所介绍闪烁体为Φ250 mm的圆柱形平板, 中子入射方向垂直于圆柱面. 相对于中子束斑尺寸(Φ60 mm), 闪烁体平面方向尺寸足够大, 高能粒子主要从垂直于入射方向的圆柱面逃逸. 不同能量中子在闪烁体中的平均自由程λs、迁移长度λt和不同能量质子在塑料闪烁体中的射程R[15]分别可由下式评估:
式中, n为闪烁体的核密度, 单位为barn–1·cm–1; σs为有效散射截面, 单位为barn; A为闪烁体质量数, 对塑料闪烁体其值约为5.95; Ep为质子能量, 单位为 MeV; 平均自由程、迁移长度和射程R的单位均为mm, ρscin为闪烁体的密度, 单位为g/cm3. 从(12)式和(13)式可以看出, 在塑料闪烁体中中子迁移长度是其平均自由程的约1.13倍. 中子迁移长度、质子射程同中子/质子的能量关系如图10所示. 在MeV能段, 中子在塑料闪烁体中的迁移距离大于本文研究的闪烁体厚度, 质子的平均射程为mm量级, 所以对本文所研究的塑料闪烁体, 闪烁体光输出强度迅速偏离线性的主要是由质子从闪烁体中逃逸造成.
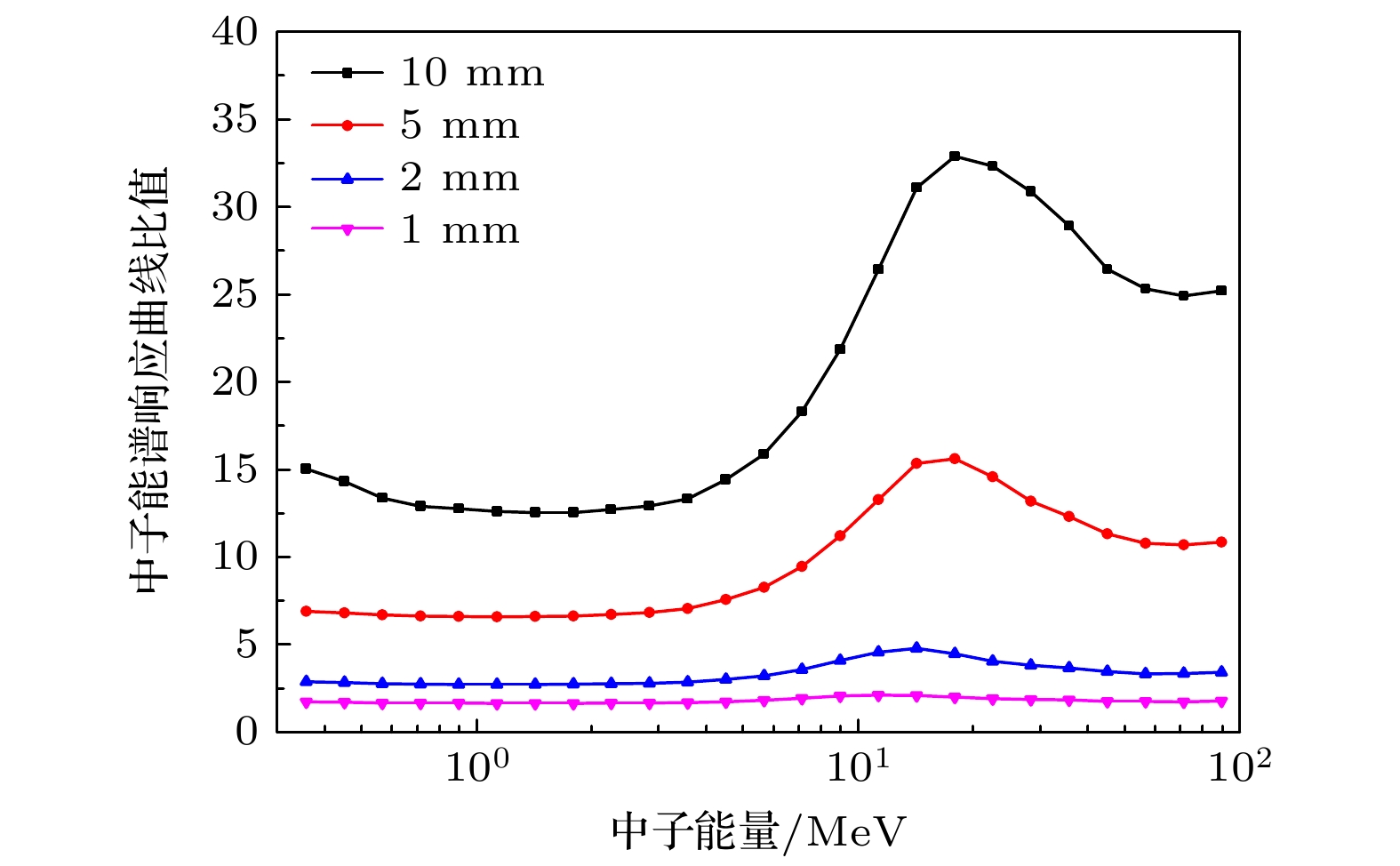
边界效应使不同厚度塑料闪烁体的灵敏度比值随中子能量的变化曲线不再是常数. 画出10, 5, 2和1 mm塑料闪烁体能谱响应曲线与0.5 mm的比值, 如图11所示. 能量较低时, 散射质子能量低, 平均自由程短, 只有靠近闪烁体边界处产生的部分质子可能逃逸, 所以在低能段不同厚度塑料闪烁体中子灵敏度比值近似为常数: 中子能量<3 MeV时, 10, 5, 2和1 mm与0.5 mm塑料闪烁体灵敏度的比值约为12.8, 6.6, 2.7和1.6; 随着中子能量升高, 薄闪烁体中逃逸的质子比例开始高于厚闪烁体, 所以这一比值曲线开始上升; 随着中子能量的进一步升高, 从厚闪烁体中逃逸的质子比例也开始升高, 厚、薄塑料闪烁体灵敏度比值下降, 形成了一个峰值. 当最高能量散射质子的平均自由程超过厚闪烁体厚度约2倍后, 厚、薄闪烁体灵敏度比值趋向定值, 此时, 10, 5, 2和1 mm与0.5 mm塑料闪烁体灵敏度的比值约为24.9, 10.7, 3.3和1.7.
-
利用中国散裂中子源白光中子束线, 测量了不同厚度塑料闪烁体ST401中子能谱响应曲线, 并对测量影响因素和曲线形成的物理机理进行简单分析. 测量和分析结果表明, 在0.5—100 MeV能量区间, 厚度为数mm的塑料闪烁体, 能谱响应曲线形状接近对数曲线. 并且受边界效应影响, 不同厚度塑料闪烁体的灵敏度比值随中子能量的变化曲线不是常数. 本文介绍的测量结果可为脉冲中子探测系统和图像诊断系统灵敏度设计[23]、脉冲中子能谱解谱[24]等工作提供参考.
不同厚度ST401中子能谱响应测量与分析
Measurement and analysis of neutron spectrum responses of ST401 scintillators with different thickness
-
摘要: 在MeV能段脉冲中子测量中, 塑料闪烁体是应用最为广泛的一种材料, 其中子能谱响应是脉冲中子能谱测量所需的关键数据. 基于中国散裂中子源白光中子束线, 使用飞行时间法测量了0.5—10 mm共5种不同厚度塑料闪烁体ST401对0.5—100 MeV能段的中子能谱响应曲线, 分析了束内伽马、伽马闪产生的闪烁体慢成分和中子源脉宽对中子能谱响应的影响. 受有限体积闪烁体边界效应影响, 不同厚度中子能谱响应曲线形状接近对数曲线, 质子逃逸是闪烁体能谱响应曲线偏离线性的主要原因, 闪烁体越厚, 偏离线性的中子能量越高.Abstract: In the measurement of pulsed neutrons in the MeV energy range, plastic scintillators are one of the most widely used materials, and their neutron energy spectrum responses are key data of pulsed neutron energy spectrum measurement. The neutron energy spectrum responses of ST401 plastic scintillators with 5 different thickness values ranging from 0.5 to 10 mm in an energy range from 0.5 MeV to 100 MeV are measured by using the time-of-flight (TOF) method on the white neutron source (WNS) beamline of the China Spallation Neutron Source (CSNS). The effects of in-beam gamma rays, the gamma flash produced slow component of scintillator, and the pulse width of the neutron source on the measurement of neutron spectrum response are analyzed. Owing to the boundary effect of the finite volume of the scintillator, the neutron energy spectrum response curves of ST401 with different thickness values present approximately logarithmic shape, and proton escape is the main reason for the deviation of the curve from linearity. The thicker the scintillator, the higher the neutron energy deviates from linearity.
-
Key words:
- plastic scintillators /
- neutron energy spectrum response /
- boundary effect .
-
-
图 1 闪烁体中子能谱响应测量布局示意图
Figure 1. Sketch of measuring the neutron spectrum response of a scintillator on WNS of CSNS.
图 3 束内伽马对塑料闪烁体中子能谱响应测量的影响
Figure 3. Influence of in-beam gamma on plastic scintillators’ neutron spectrum response measurements.
图 5 伽马峰后不同时刻到达闪烁体处中子能谱 (a)伽马峰后1268.7 ns; (b) 伽马峰后1890.4 ns; (c) 伽马峰后3326.2 ns; (d) 伽马峰后5404.3 ns
Figure 5. The neutron spectrum at the scintillator at different time intervals after the γ flash peak: (a) 1268.7 ns; (b) 1890.4 ns; (c) 3326.2 ns; (d) 5404.3 ns.
图 7 不同厚度塑料ST401中子能谱响应 (a) 线性坐标; (b) 对数坐标
Figure 7. The neutron spectrum responses of ST401 scintillators with different thicknesses: (a) Linear coordinates; (b) logarithmic coordinates.
图 8 中子能量0.01—100 MeV的n-p和n-C作用截面曲线
Figure 8. n-p and n-C cross sections from 0.01 to 100 MeV.
图 9 塑料闪烁体对不同种类粒子的光响应函数
Figure 9. Light response function of plastic scintillators to different particles.
图 10 0.01—100 MeV质子(中子)在塑料闪烁体中的平均射程(迁移长度) (a) 对数坐标; (b) (a)图中蓝色虚线方框内曲线在线性坐标下的放大展示
Figure 10. The average range (migration length) of 0.01–100 MeV protons (neutrons) in plastic scintillators: (a) Range and migration length in logarithmic coordinates; (b) enlargement of the curves in the blue square in (a).
-
[1] 刘兆庆 1994 脉冲辐射场诊断技术 (北京: 科学出版社)第12页 Liu Z Q, 1994 Pulse Radiation Field Diagnostic Technology (Beijing: Science Press) p12 [2] 易义成, 宋朝晖, 管兴胤, 韩和同, 卢毅, 郝帅 2023 现代应用物理 14 10202 doi: 10.12061/j.issn.2095-6223.2023.010202 Yi Y C, Song Z H, Guan X Y, Han H T, Lu Y, Hao S 2023 Mod. Appl. Phys. 14 10202 doi: 10.12061/j.issn.2095-6223.2023.010202 [3] 杨洪琼, 彭太平, 杨建伦, 唐正元, 杨高照, 李林波, 胡孟春, 王振通, 张建华, 李忠宝, 王立宗 2004 核电子学与探测技术 24 640 Yang H Q, Peng T P, Yang J L, Tang Z Y, Yang G Z, Li L B, Hu M C, Wang Z T, Zhang J H, Li Z B, Wang L Z 2004, Nucl. Electron. & Detect. Technol. 24 640 [4] 姚志明, 段宝军, 宋顾周, 严维鹏, 马继明, 韩长材, 宋岩 2017 物理学报 66 062401 doi: 10.7498/aps.66.062401 Yao Z M, Duan B J, Song G Z, Yan W P, Ma J M, Han C C, Song Y 2017 Acta Phys. Sin. 66 062401 doi: 10.7498/aps.66.062401 [5] Verbinski V V, Burrus W R, Love T A, Zobel W, Hill N W, Textor R 1968 Nucl. Instrum. Methods 65 8 doi: 10.1016/0029-554X(68)90003-7 [6] 张国光, 欧阳晓平, 张建福, 王志强, 张忠兵, 马彦良, 张显鹏, 陈军, 张小东, 潘洪波, 骆海龙, 刘毅娜 2006 物理学报 55 2165 doi: 10.7498/aps.55.2165 Zhang G G, Ouyang X P, Zhang J F, Wang Z Q, Zhang Z B, Ma Y L, Zhang X P, Chen J, Zhang X D, Pan H B, Luo H L, Liu Y N 2006 Acta Phys. Sin. 55 2165 doi: 10.7498/aps.55.2165 [7] Madey R, Waterman F M, Baldwin A R, Knudson J N, Carlson J D, Rapaport J 1978 Nucl. Instrum. Methods 151 445 doi: 10.1016/0029-554X(78)90154-4 [8] 张传飞, 彭太平, 罗小兵, 李如荣, 张建华, 夏宜君, 杨志华, 林理彬 2002 四川大学学报(自然科学版) 39 487 Zhang C F, Peng T P, Luo X B, Li R R, Zhang J H, Xia Y J, Yang Z H, Lin L B 2002 J. Sichuan Univ. (Nat. Sci. Ed. ) 39 487 [9] 彭太平, 罗小兵, 张传飞, 李如荣, 张建华, 夏宜君, 杨志华 2002 原子核物理评论 19 357 doi: 10.11804/NuclPhysRev.19.03.357 Peng T P, Luo X B, Zhang C F, Li R R, Zhang J H, Xia Y J, Yang Z H 2002 Nucl. Phys. Rev. 19 357 doi: 10.11804/NuclPhysRev.19.03.357 [10] 罗小兵, 张传飞, 彭太平, 李如荣, 张建华, 夏宜军, 杨志华 2004 核电子学与探测技术 24 186 Luo X B, Zhang C F, Peng T P, Li R R, Zhang J H, Xia Y J, Yang Z H 2004 Nucl. Electron. & Detect. Technol. 24 186 [11] 宋顾周, 谢红卫, 王奎禄, 朱宏权 2008 核电子学与探测技术 28 845 doi: 10.3969/j.issn.0258-0934.2008.04.042 Song G Z, Xie H W, Wang K L, Zhu H Q 2008 Nucl. Electron. Detect. Technol. 28 845 doi: 10.3969/j.issn.0258-0934.2008.04.042 [12] 杨建伦, 彭先觉, 杨洪琼, 杨高照, 王立宗, 钟耀华 2004 核电子学与探测技术 24 346 doi: 10.3969/j.issn.0258-0934.2004.04.005 Yang J L, Peng X J, Yang H Q, Yang G Z, Wang L Z, Zhong Y H 2004 Nucl. Electron. Detect. Technol. 24 346 doi: 10.3969/j.issn.0258-0934.2004.04.005 [13] Edelstein R M, Russ J S, Thatcher R C, Elfield M, Miller E L, Reay N W, Stanton N R, Abolins M A, Lin M T, Edwards K W, Gill D R 1972 Nucl. Instrum. Methods 100 355 doi: 10.1016/0029-554X(72)90706-9 [14] Betti G, Guerra A D, Giazotto A, Giorgi M A, Stefanini A, Botterill D R, Braben D W, Clarke D, Norton P R 1976 Nucl. Instrum. Methods 135 129 [15] Cecil R A, Anderson B D, Madey R 1979 Nucl. Instrum. Methods 161 439 doi: 10.1016/0029-554X(79)90417-8 [16] Wei J, Chen H S, Chen Y W, et al. 2009 Nucl. Instrum. Meth. A 600 10 doi: 10.1016/j.nima.2008.11.017 [17] Chen Y H, Luan G Y, Bao J, et al. 2019 Eur. Phys. J. A 55 145 doi: 10.1140/epja/i2019-12861-8 [18] 任杰, 阮锡超, 陈永浩 等 2020 物理学报 69 172901 doi: 10.7498/aps.69.20200718 Ren J, Ruan X C, Chen Y H, et al. 2020 Acta Phys. Sin. 69 172901 doi: 10.7498/aps.69.20200718 [19] 袁秀丽, 姚岁劳, 王丹妮, 阎珍德, 唐兆荣, 蒋李君, 高兴兵, 殷生华, 贾景光, 张志雄, 林德雨2024 GB/T13181-2024(北京: 中国标准出版社) Yuan X L, Yao S L, Wang D N, Yan Z D, Tang Z R, Jiang L J, Gao X B, Yin S H, Jia J G, Zhang Z X, Lin D Y 2024 GB/T13181-2024 (Beijing: China Standard Press [20] 汲长松 1990 核辐射探测器及其实验技术手册 (北京: 原子能出版社) Ji C S 1990 Handbook of Nuclear Radiation Detectors & Their Experiment Techniques (Beijing: Atomic Energy Press [21] http://physics.nist.gov/PhysRefData/XrayMassCoef/tab2.html/ [2024-8-30] [22] Gohil M, Banerjee K, Bhattacharya S, Bhattacharya C, Kundu S, Rana T K , Mukherjee G, Meena J K, Pandey R, Pai H, Ghosh T K, Dey A, Mukhopadhyay S, Pandit D, Pal S, Banerjee S R, Bandhopadhyay T 2012 Nucl. Instrum. Meth. A 664 304 [23] 杨洋, 党同强, 王志刚, 王明煌, 杨战国, 常博, 宋勇, 周涛 2024 现代应用物理 15 10201 doi: 10.12061/j.issn.2095-6223.2024.010201 Yang Y, Dang T Q, Wang Z G, Wang M H, Yang Z G, Chang B, Song Y, Zhou T 2024 Mod. Appl. Phys. 15 10201 doi: 10.12061/j.issn.2095-6223.2024.010201 [24] 秋妍妍, 谭志新, 易晗, 贺永宁, 赵小龙, 樊瑞睿 2023 现代应用物理 14 30203 Qiu Y Y, Tan Z X, Yi H, He Y N, Zhao X L, Fan R R 2023 Mod. Appl. Phys. 14 30203 -
计量
- 文章访问数: 190
- HTML全文浏览数: 190
- PDF下载数: 4
- 施引文献: 0