-
1998年, Bender和 Boettcher[1]首先发现了一类具有实本征谱的非厄米哈密顿量, 即满足宇称-时间反演(parity-time reversal, PT)对称性的非厄米哈密顿量. 具有PT对称系统的非厄米哈密顿量可以具有全实能谱(exact)[1,2], 这为揭示开放系统中的奇异行为和非厄米物理[3–5]的应用前景提供了一个极好的平台. 人们已经在各种物理环境中观察到了PT对称现象, 包括波导和光纤阵列[6,7]、光子电路和晶格[8,9]、微环状谐振器[10,11]等. 相比于固体体系, 原子介质由于其良好的量子效应和能级的可操控性成为研究PT对称的理想选择[12–14], 另外, 研究者们利用原子的特性和先进光学技术控制有效(实和虚)势[15–18], 开展了非厄米物理的研究. PT对称中从未破缺相到破缺相的相变点称为破缺点(EP), 到目前为止, PT对称体系和其中的EPs[19]具有许多有趣的性质和潜在的应用[20–27], 引起了极大的关注.
一个非厄米系统在各个维度中都满足PT对称条件时, 称为PT对称系统. 在最近的理论工作中, 研究发现一个方向反射不变的多维势[例如,
$V^*(x, y) = V(-x, y) $ 或$V^*(x, y) = V(x,- y) $ ]满足PT对称, 称为部分PT对称, 同时展现全实光谱[28–30], 并显示从未破缺相到破缺相的相变. 部分PT对称性的研究, 可以在不施加严格PT对称条件的情况下, 提供一种实现全实光谱的方法, 极大地扩展了一维以外全实谱非厄米系统的研究范围[31], 促进了高维非厄米系统的发展.本文主要在原子介质中研究部分PT对称. 利用铯原子Λ型三能级系统实现了部分PT对称的实验观察. 一束探测光和一束耦合光作用于铯原子蒸气池中, 耦合光覆盖整个探测光, 而泵浦光仅覆盖探测光的右半部分, 导致在探测光区域中出现增益和损耗的区域, 这样构建了一个二维的部分PT对称光学势. 因为泵浦光的光斑仅在x方向覆盖探测光光斑的一半, 因而称之为部分PT对称. 实验中通过改变耦合光和探测光的腰斑比, 观察到部分PT对称系统中由未破缺相向破缺相的转变, 此外通过测量探测光束强度分布的不对称度, 实现了部分PT对称中破缺点的测量, 理论计算与实验测量符合得很好.
-
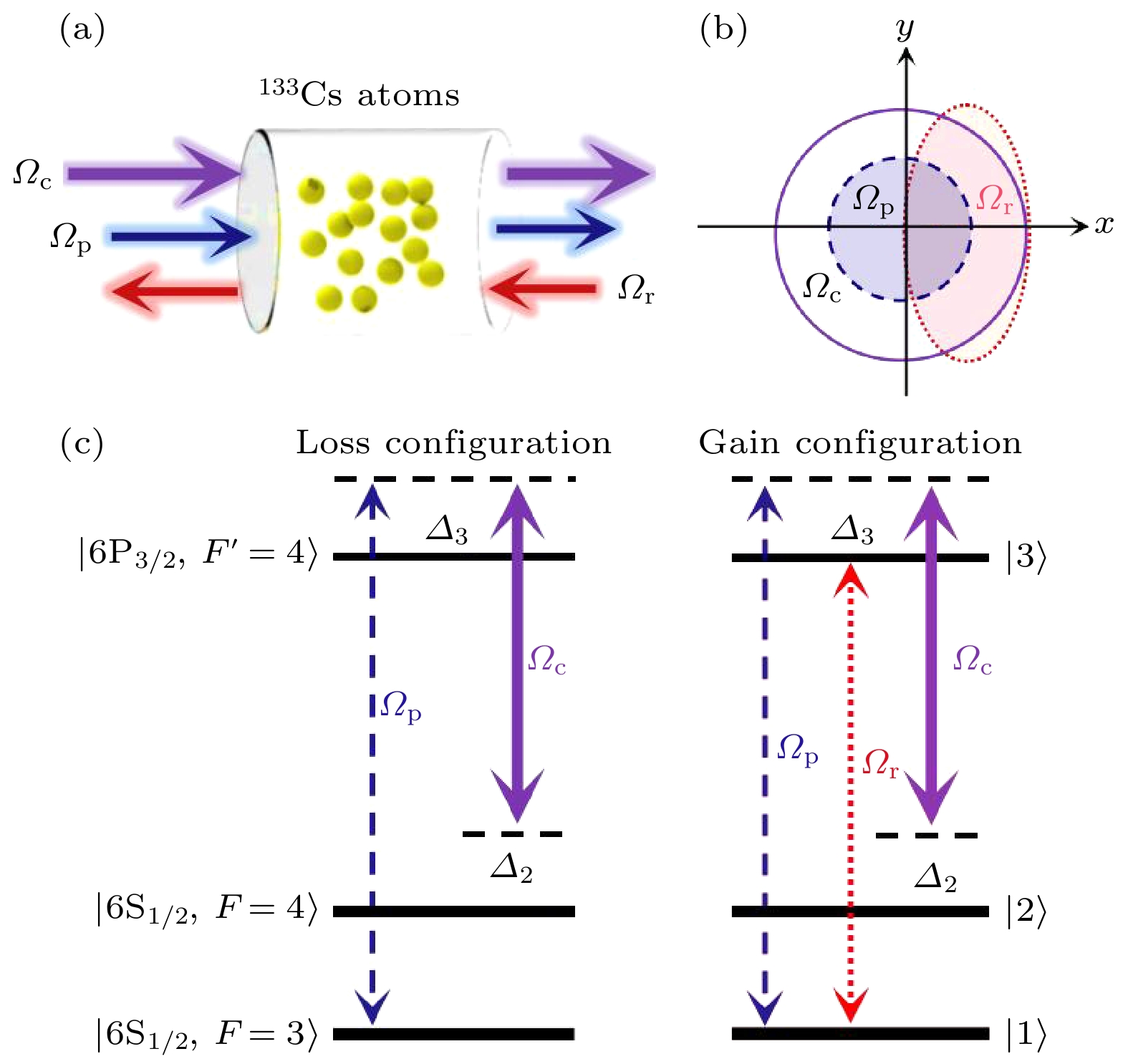
部分PT对称系统的实验装置如图1(a)所示, 852 nm的探测光Ωp (ωp = 110 μm)和耦合光Ωc均为圆形高斯腰斑, 相互重叠且同向入射作用于长度L = 2 cm, 直径Φ = 25 mm的圆柱形石英玻璃铯原子样品中. 泵浦光Ωr与探测光和耦合光反向传播, 且泵浦光斑设置为椭圆形高斯光斑, 其高斯束腰半径分别为短轴ωr1 = 200 μm和长轴ωr2 = 700 μm, 如图1(b)所示, 在实验中我们调整泵浦光使之覆盖探测光的右半边区域, 从而构建一个二维的光学势. 实验中采用铯原子Λ型三能级结构如图1(c)所示, 3束激光由两台半导体激光器 (852 nm, DLpro, 线宽 100 kHz) 提供, 探测光的频率由偏振光谱稳频技术锁定在
$ \left| {6{{\mathrm{S}}_{1/2}}, F = 3} \right\rangle \to \left| {6{{\mathrm{P}}_{3/2}}, F' = 4} \right\rangle $ 的共振跃迁线上, 并通过双通的AOM正偏频482 MHz及单通的AOM正偏频125 MHz, 实现探测光频率正偏频607 MHz(设置探测光的正偏频大于多普勒展宽, 以避免多普勒背景对信号的影响); 耦合光的频率作用于$| 6{{\mathrm{S}}_{1/2}}, F = 4 \rangle \to \left| {6{{\mathrm{P}}_{3/2}}, F' = 4} \right\rangle $ 的跃迁, 使用F-P超稳腔锁定到满足Λ型三能级原子的双光子拉曼吸收的频率, 构成部分PT对称的损耗通道, 如图1(c)左半边所示. 为了构造增益通道, 施加了泵浦光使其共振作用于$ \left| {6{{\mathrm{S}}_{1/2}}, F = 3} \right\rangle \to \left| {6{{\mathrm{P}}_{3/2}}, F' = 4} \right\rangle $ 的跃迁. 泵浦光的作用是改变两个基态能级的布居, 从而调控Λ型三能级系统的吸收, 在一定条件下形成原子系统的增益通道, 如图1(c)右半边所示. 从原子气室出射的探测光经半透半反镜后分为两束, 一束进入光电探测器PD (PDA36A2), 用来测量探测光的吸收/增益信号, 另一束进入CCD(MTV-1881EX)用来检测探测光的光斑分布. -
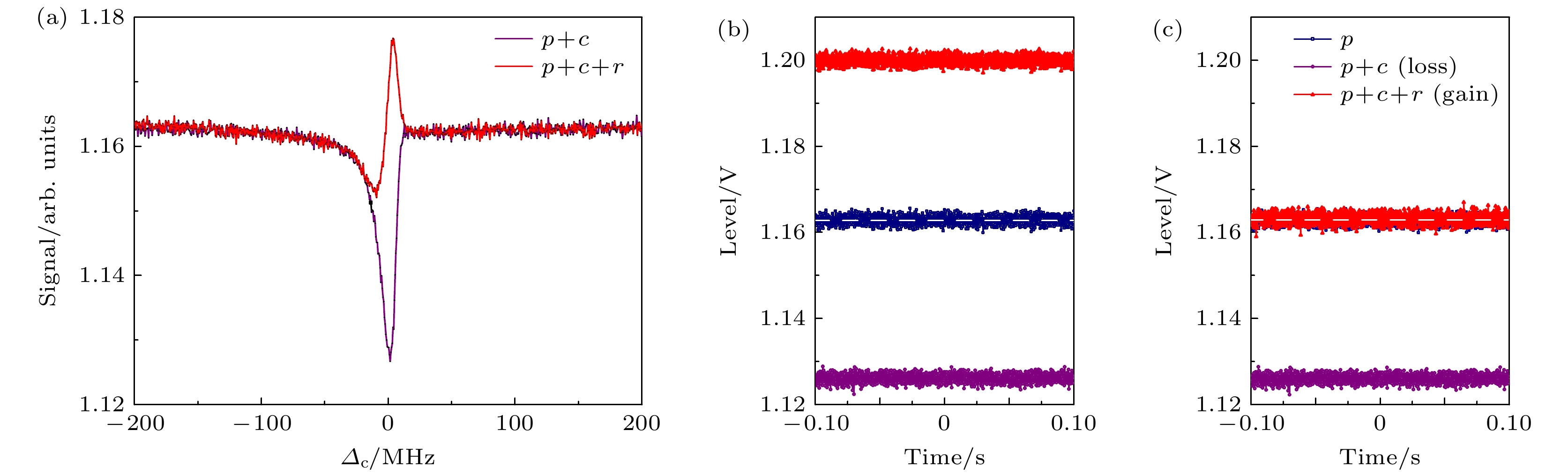
实验中首先固定探测光的激光频率, 扫描耦合光的激光频率观察部分PT对称系统的增益与损耗光谱. 当泵浦光不存在时, 由探测光和耦合光拉曼跃迁形成的损耗光谱如图2(a)中p+c (紫色曲线)所示; 当泵浦光存在时, 系统对探测光的吸收减小, 如图2(a)中p+r+c (红色曲线)所示. 为获得部分PT对称系统的平衡条件, 首先令实验中泵浦光的光斑全部覆盖探测光, 此时3束激光的频率锁定且满足Δ3 = 607 MHz的条件, 同时对3束激光的功率也实现稳定, 利用PD测量只有探测光时的信号p (藏青色点线)、耦合光与探测光形成三能级拉曼跃迁形成的吸收信号p+c (紫色点线)以及3束光同时作用形成p+c+r的增益信号 (红色点线), 可以看到增益信号和损耗信号对称的分布在只有探测光存在时电平信号的两侧, 如图2(b)所示, 此时泵浦光与探测光完全重合. 然后移动泵浦光使之与探测光的光斑的一半重合, 参见图1(b), 对应的电平信号如图2(c)所示, p+c+r对应的电平信号(红色点线)与只有p(藏青色点线)时的信号重合. 我们定义损耗与增益间隔分别为
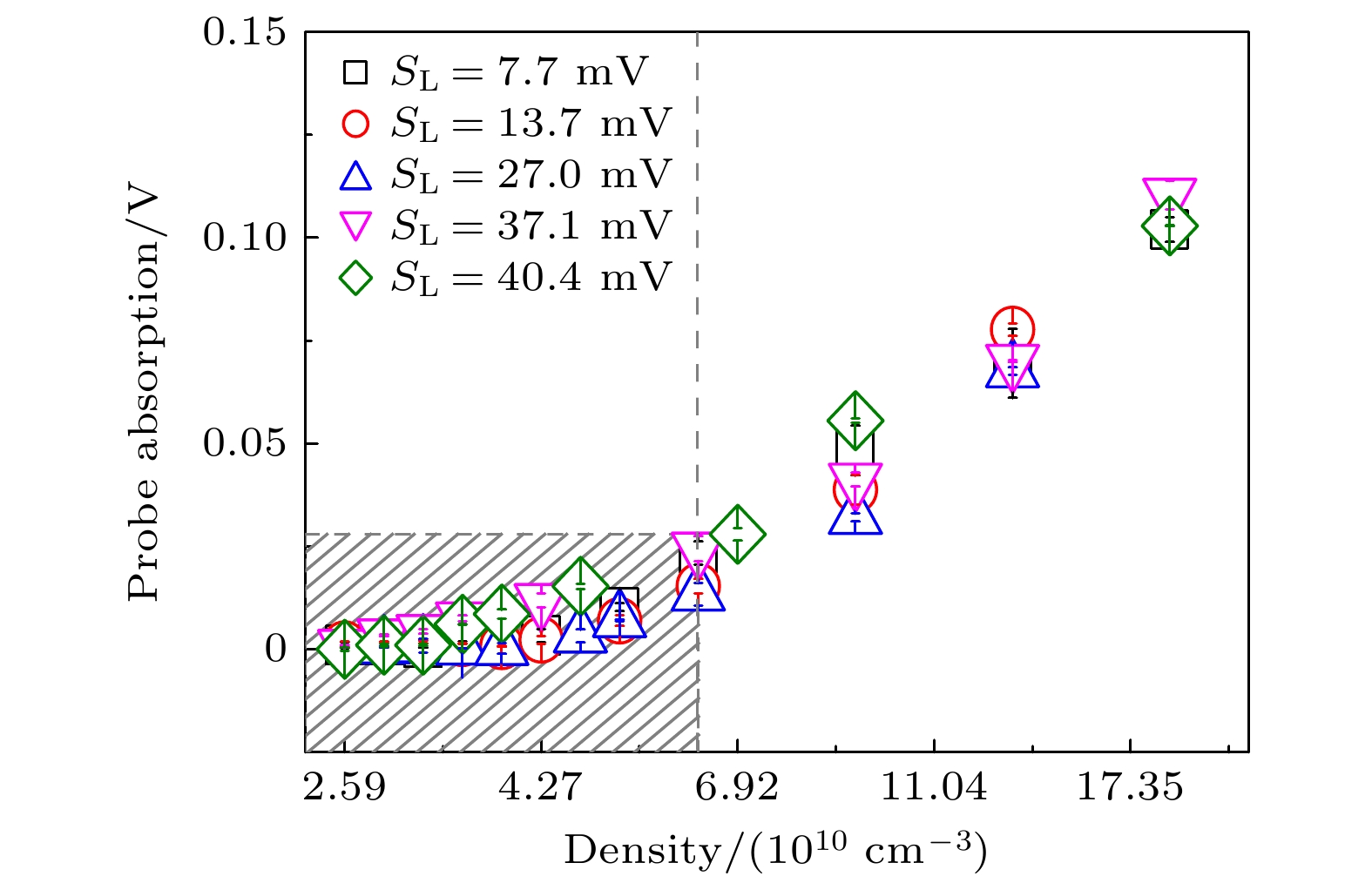
$S_{\rm L} = p - (p+c) $ 和$S_{\rm GL} = (p+c+r) - p$ . 当增益和损耗相等, 即SGL = 0时, 部分PT对称系统处于平衡状态, 以下的实验条件都处于平衡状态.为了寻找部分PT对称相变点的位置, 在实验中首先研究了系统初始增益间隔SL = 7.7 mV时, 探测光吸收信号随原子密度的依赖关系如图3所示. 可以看到当铯原子密度小于
$ \rho \lt 6.29 \times {10^{10}}\; {\text{c}}{{\text{m}}^{{{ - 3}}}} $ 时${S_{{\text{GL}}}} \approx 0$ , 表示系统工作在部分PT对称区域, 如图3中灰色区域所示; 当原子密度$\rho \gt 6.29 \times {10^{10}}\; {\text{c}}{{\text{m}}^{{{ - 3}}}}$ 时,${S_{{\text{GL}}}} \gt 0$ 表示系统的平衡条件被破坏, 系统处于部分PT对称破坏区域, 即非部分PT对称区域. 为了进一步研究增益间隔SGL与原子密度的关系, 我们改变初始损耗间隔SL = 7.7 mV(黑色方块)、13.7 mV(红色圆圈)、27.0 mV(蓝色正三角形)、37.1 mV(玫红色倒三角形)和40.4 mV(绿色菱形), 实验中测量了不同原子密度时的SGL(两次实验测量结果的平均值), 如图3所示. 由图可知, 初始损耗间隔SL的大小对部分PT对称没有影响, 但随着原子密度的增加系统进入非部分PT对称区域.实验中选取初始损耗间隔为SL = 13.7 mV, 且系统满足平衡条件, 研究系统的PT对称和相变过程. 除了上述通过测量探测光的光强外, 还可以利用CCD观察探测光的分布情况来研究部分PT对称特性. 下面主要介绍通过光斑分布的测量研究部分PT对称. 当系统处于部分PT对称时, 探测光光斑分布呈现均匀分布; 而当系统处于PT对称破缺时, 探测光光斑呈非均匀分布. 在理论上, 由微扰理论求解Maxwell-Bloch方程可知该系统可以通过改变耦合光与探测光的腰斑比σ可以获得部分PT对称破缺的条件.
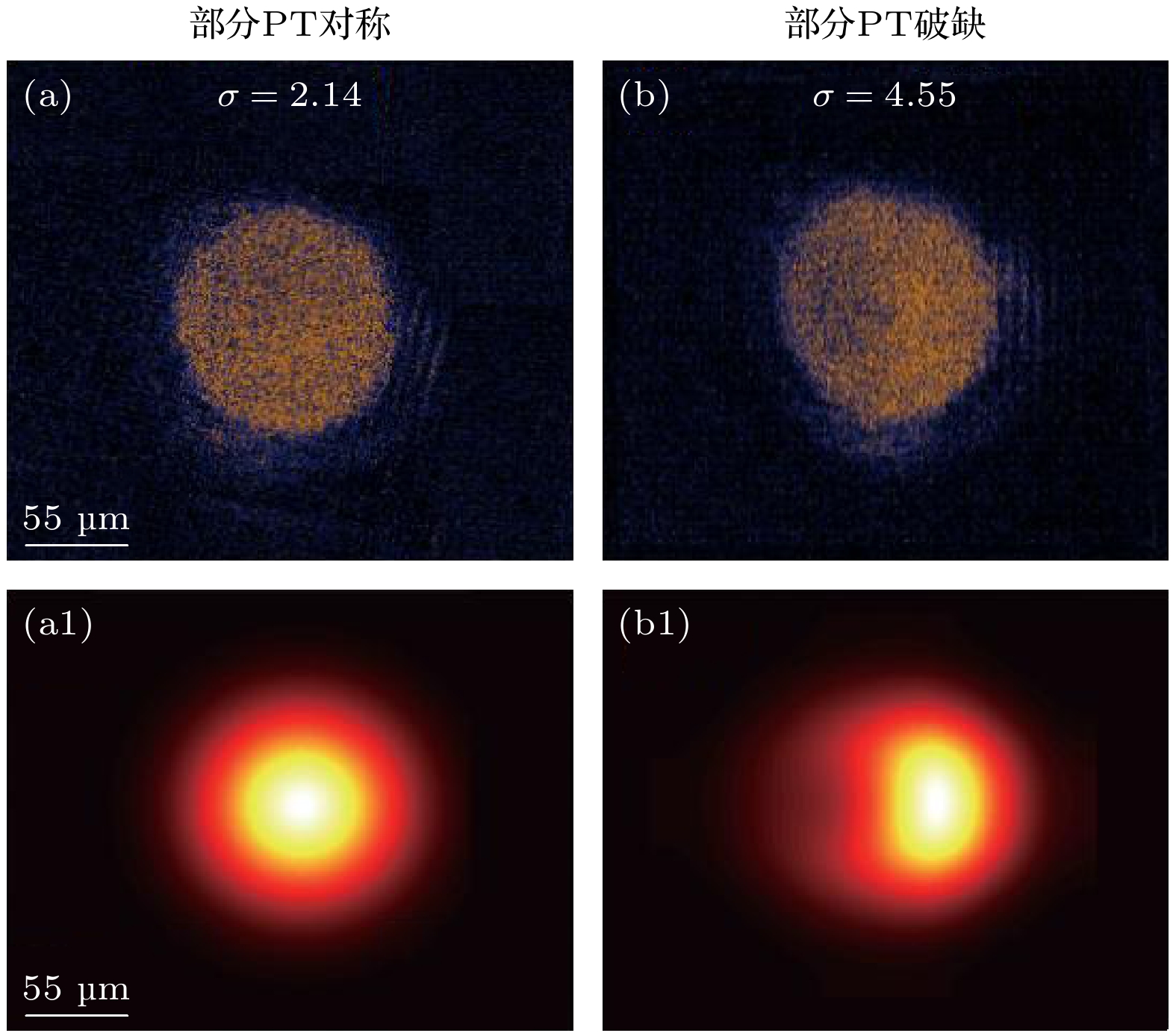
在实验中为了观察部分PT对称的相变过程以及相变(EP)点的位置, 在实验中固定探测光 的腰斑ωp = 110 μm不变, 改变耦合光腰斑ωc 的大小, 从而改变耦合光与探测光的腰斑比σ = ωc /ωp, 对部分PT对称的EP点进行研究[32], 在实验中通过探测光的光斑空间分布进行研究. 研究表明, 当耦合光与探测光的腰斑比
$ \sigma = 2.14 $ 时, 探测光的光斑为均匀分布系统处于部分PT对称区域, 如图4(a)所示; 当耦合光与探测光的腰斑比$ \sigma = 4.55 $ 时, 探测光光斑分布呈现不均匀的分布, 左半边暗的区域表示系统的吸收, 右半边亮的区域表示系统的增益, 此时系统处于PT破缺的状态, 如图4(b)所示, 图4(a1), (b1)为对应的理论模拟, 可以看到理论模拟与实验结果符合得很好.在部分PT对称系统处于平衡的条件下, 为了进一步研究系统中部分PT对称与破缺过程, 我们定义不对称度Dasym来描述探测光强分布:
其中, Ip, right 和Ip, left分别表示探测光的光斑右半部分和左半部分对应的平均强度.
当探测光光斑的不对称度
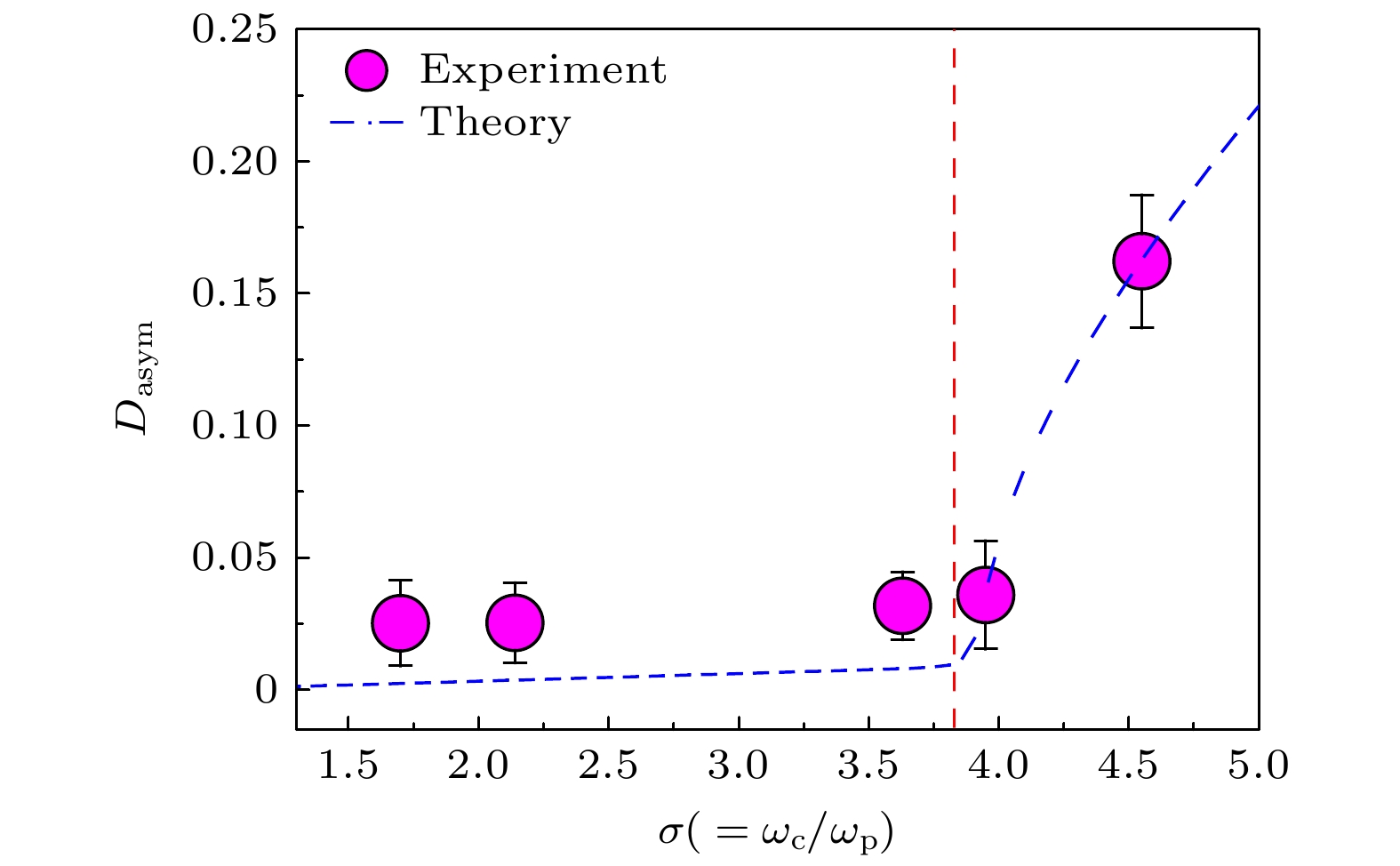
${D_{{\text{asym}}}} = 0$ 时, 表示系统处于部分PT对称状态; 当$0 \lt {D_{{\text{asym}}}} \lt 1$ 时表示系统处于部分PT对称破缺状态. 为了进一步研究部分PT对称与破缺的相变过程, 实验中固定铯原子密度$\rho = 3.87 \times {10^{10}}\; {\text{c}}{{\text{m}}^{{{ - 3}}}}$ , 研究探测光的光斑不对称度Dasym与耦合光与探测光腰斑比σ的依赖关系如图5所示, 当耦合光与探测光的腰斑比$\sigma \lt 3.8$ (红色虚线左边)时, 探测光强度分布的不对称度Dasym接近于0, 此时系统处于部分PT对称区域; 而当耦合光与探测光的腰斑比$\sigma \gt 3.8$ 时(红色虚线右边), 探测光强度分布的不对称度Dasym快速增大, 表明系统进入部分PT对称破缺的区域. 图5中的蓝色虚线表示理论计算的结果, 与实验测量结果的平均值相吻合, 误差棒为5次测量的标准偏差. 由此可以判定, 该系统的破缺(EP)点为腰斑比$\sigma = {\sigma _{\rm cr}} \approx 3.8$ , 此研究对于原子系统的部分PT对称及相变过程具有重要的意义, 可利用本系统实现部分PT对称相变点的精密测量. -
本工作在室温铯原子蒸气池中构建了由基态
$\left| {6{{\mathrm{S}}_{1/2}}, F = 3} \right\rangle $ ,$\left| {6{{\mathrm{S}}_{1/2}}, F = 4} \right\rangle $ 和第一激发态$| 6{{\mathrm{P}}_{3/2}}, F' = 4 \rangle $ 形成的Λ型三能级系统, 首次构建了含有增益与损耗的铯原子体系, 观察到了部分PT对称. 在部分PT对称系统的平衡条件下, 通过改变耦合光和探测光的腰斑比σ, 观察到部分PT对称系统中从对称向破缺相的转变. 此外我们通过测量探测光强度分布的不对称度Dasym, 精确地测量了部分PT对称的破缺点$\sigma = {\sigma _{\rm cr}} \approx 3.8$ , 理论计算与实验测量值符合得很好. 此工作为非厄米光学系统中多维激光束的控制奠定了基础, 可利用本系统实现部分PT对称相变点的精密测量, 同时对激光束不同部位的光放大器和衰减器的设计具有潜在的应用价值.
铯原子系统中部分PT对称的研究
Investigation of partial parity-time symmetry in cesium atomic system
-
摘要: 本文主要研究铯原子Λ型三能级原子的部分PT对称和相变, 利用铯原子基态$\left| {6{{\mathrm{S}}_{1/2}}, F = 3} \right\rangle $、$| 6{{\mathrm{S}}_{1/2}}, $$ F = 4 \rangle $和激发态$\left| {6{{\mathrm{P}}_{3/2}}, F' = 4} \right\rangle $组成Λ型三能级原子系统, 由失谐Δ3 = 607 MHz的探测光与耦合光形成双光子拉曼吸收, 构成损耗通道. 增加了共振作用于能级$\left| {6{{\mathrm{S}}_{1/2}}, F = 3} \right\rangle $与$\left| {6{{\mathrm{P}}_{3/2}}, F' = 4} \right\rangle $跃迁的泵浦光改变两个基态能级的布居, 从而使Λ型三能级系统的吸收减小, 在一定条件下形成原子系统的增益通道, 从而构成部分PT对称的原子系统. 实验中通过改变耦合光和探测光的腰斑比σ, 观察到部分PT对称系统中由对称向破缺相的转变. 此外研究了探测光束强度分布的不对称程度Dasym, 精确地测量了部分PT对称的破缺点, 理论计算与实验测量结果相符. 本文所报道的部分PT对称性及其相变的结果, 为主动操纵非厄米系统中的多维激光束开辟了一条途径, 并在设计激光不同部分的光放大和衰减光学器件方面具有潜在的应用价值.Abstract:
Parity-time (PT) in atomic systems is of great significance for exploring exotic phenomena in non-Hermitian physics and non-Hermitian systems. It has been found that if PT symmetry is satisfied only in a certain spatial direction, then the Hamiltonian of the system still has a spectrum with eigenvalues of real numbers, which is called partial PT symmetry. In this paper, we use a Λ-type three-level atomic system, which is composed of two ground states $\left| {6{{\mathrm{S}}_{1/2}}, F = 3} \right\rangle $,$\left| {6{{\mathrm{P}}_{3/2}}, F' = 4} \right\rangle $and an excited state $\left| {6{{\mathrm{P}}_{3/2}}, F' = 4} \right\rangle $of cesium atom, to investigate the partial PT symmetry. A probe laser with the detuning of Δ3 = 607 MHz and a coupling laser satisfy the condition of two-photon Raman absorption of cesium atom, forming a loss channel. In order to construct the gain channel, we add the repumping laser that resonates during the transition of $\left| {6{{\mathrm{S}}_{1/2}}, F = 3} \right\rangle $to $\left| {6{{\mathrm{P}}_{3/2}}, F' = 4} \right\rangle $, changing the population of the two ground state energy levels, thus reducing the absorption of the Λ level system and forming the gain channel of the atomic system under certain conditions. In order to obtain the equilibrium condition of the partial PT-symmetric system, firstly, the light spot of the repumping laser in the experiment is covered by the probe laser, and then the repumping laser is moved to overlap with half of the probe laser of the detection light. When the gain and loss are balanced, the partial PT-symmetric system is in equilibrium. By changing the beam-waist ratio σ of the coupling laser to the probe laser, the transition from symmetry to broken phase is observed in partial PT-symmetric systems. By measuring the asymmetry of the detection-beam intensity distribution Dasym, we can accurately determine the partial PT symmetry breaking point, and the breaking point is located at $\sigma = {\sigma _{{\mathrm{cr}}}} \approx 3.8$. The theoretical calculations are in good agreement with the experimental measurements. The results of partial PT symmetry and its phase transition, reported in this study, open up a way to actively manipulate multidimensional laser beams in non-Hermitian systems and have potential applications in the design of optical devices for laser amplification and attenuation in different parts of the laser. -
Key words:
- partial PT symmetry /
- gain and loss /
- PT symmetry broken .
-

-
图 1 (a) 实验装置示意图. (b)铯原子气室中探测光、耦合光和泵浦光横截面. 探测光和耦合光为圆形高斯光斑, 泵浦光设计为椭圆形高斯光斑, 与探测光和耦合光的一半重合, 形成二维部分PT对称的损耗和增益通道. (c)铯原子基态和激发态三能级构成部分PT系统中损耗(左)与增益通道(右)的能级示意图, Ωp, Ωc和 Ωr为Rabi频率, Δ2和Δ3分别为激光束的频率失谐
Figure 1. (a) Sketch of the experimental setup. (b) The probe and coupling laser are circular Gaussian, and the repumping laser is designed as elliptical Gaussian, the coupling laser covers the whole probe beam, whereas the repumping laser covers the right-half region of the probe beam, which creates a 2D partially PT-symmetric potential for the probe laser. (c) Energy level diagram of loss and gain channels in the three-level component PT system of cesium atoms, the left and right panels show the loss and gain configurations, respectively; Ωp, Ωc and Ωr are Rabi frequencies and Δ2 and Δ3 are frequency detuning of laser beam.
图 2 (a) Λ型三能级原子系统中的损耗p + c (紫色)与增益p + c + r (红色)的光谱; (b)测量增益和损耗对应的PD 信号, p代表频率远离失谐的情况; p + c对应探测光与耦合光共同作用的结果; p + c + r对应的是3束光同时存在的情况. 此时泵浦光与探测光的光斑完全重叠; (c) 部分PT系统处于平衡位置时探测光增益和损耗分别对应的电平信号, 移动泵浦光的光斑与探测光光斑的一半重合, 此时对应的信号p + c + r与p 完全重合
Figure 2. (a) Spectra of loss p + c (purple) and gain p + c + r (red) in a Λ-type three-level atomic system; (b) the measurements of PD signals for the gain and loss of the probe laser, the signal p corresponds to that the probe laser with the frequency far detuning from the resonance; p + c corresponds to that the probe laser propagates in the atoms driven only by the coupling laser; p + c + r corresponds to that the probe laser propagates in the atoms driven by both coupling and repumping lasers, repumping laser is fully overlapped with the probe beam, which the signals p + c + r and p + c are located symmetrically about the signal p; (c) the repumping laser is then moved to behalf overlapped with the probe beam, in which the signal p + c + r coincides with the signal p.
图 3 实验测量初始损耗间隔分别为SL = 7.7, 13.7, 27.0, 37.1和40.4 mV时, 增益SGL与原子密度ρ的关系, 灰色虚线左边代表的是部分PT对称区域, 右边是部分PT对称破坏区域, 误差棒是两次测量的标准偏差
Figure 3. (a) Relationship between the gain SGL and the atomic density when the initial loss interval is SL = 7.7, 13.7, 27.0, 37.1 and 40.4 mV, respectively, the gray dotted line on the left represents a partial PT symmetry region, and on the right is a non-partial PT-symmetry region, error bars denote standard error of two measurements.
图 4 (a) 耦合光与探测光的腰斑比
$ \sigma = 2.14 $ , 系统处于部分PT对称区域时对应的探测光的光斑是均匀分布, 对应的理论模拟结果(a1); (b) 耦合光与探测光的腰斑比$ \sigma = $ $ 4.55 $ 时, 探测光光斑分布呈现不均匀的分布, 且左半边暗右半边亮, 此时系统处于PT破缺, 对应的理论模拟(b1)Figure 4. (a) Measured result for
$ \sigma = 2.14 $ of the probe intensity distribution, which is uniform, and the numerical results corresponding to panel (a1). (b) Measured result for$\sigma = 4.55$ of the partial PT symmetry broken, and the numerical results corresponding to panel (b1).图 5 探测光的光斑不对称度Dasym与耦合光和探测光的腰斑比σ的依赖关系, 可以看到部分PT破缺点的位置是σ = σcr ≈ 3.8, 玫红色圆圈是实验测量结果, 蓝色虚线是理论计算结果, 红色虚线左边代表的是部分PT对称区域, 右边是部分PT对称破缺区域, 误差棒是5次测量的标准偏差
Figure 5. Experimental measurements (magenta circle) and calculations (blue line) of Dasym as a function of beam-waist ratio σ, where the EP locates at σ = σcr ≈ 3.8, the red dotted line represents the partial PT symmetry region on the left and the partial PT symmetry broken region on the right, error bars denote standard error of five measurements.
-
[1] Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243 doi: 10.1103/PhysRevLett.80.5243 [2] Bender C M 2005 Contemp. Phys. 46 277 doi: 10.1080/00107500072632 [3] Klaiman S, Cederbaum L S 2008 Phys. Rev. A 78 062113 doi: 10.1103/PhysRevA.78.062113 [4] El-Ganainy R, Makris K G, Khajavikhan M, Musslimani Z H, Rotter S Christodoulides D N 2018 Nat. Phys. 14 11 doi: 10.1038/nphys4323 [5] Ashida Y, Gong Z, Ueda M 2020 Adv. Phys. 69 249 doi: 10.1080/00018732.2021.1876991 [6] Konotop V V, Shchesnovich V S, Zezyulin D A 2012 Phys. Lett. A 376 2750 doi: 10.1016/j.physleta.2012.07.027 [7] Szameit A, Rechtsman M C, Bahat-Treidel O, Segev M 2011 Phys. Rev. A 84 021806(R doi: 10.1103/PhysRevA.84.021806 [8] Feng L, Ayache M, Huang J, Xu Y L, Lu M H, Chen Y F, Fainman Y, Scherer A 2011 Science 333 729 doi: 10.1126/science.1206038 [9] Regensburger A, Bersch C, Miri M, Onishchukov G, Christodoulides D N, Peschel U 2012 Nat. Phys. 488 167 doi: 10.1038/nature11298 [10] Peng B, Özdemir S K, Lei F, Monifi F, Gianfreda M, Long G L, Fan S, Nori F, Bender C M, Yang L 2014 Nat. Phys. 10 394 doi: 10.1038/nphys2927 [11] Wen J M, Jiang X, Jiang L, Xiao M 2018 J. Phys. B: At. Mol. Opt. Phys. 51 222001 doi: 10.1088/1361-6455/aae42f [12] Hang C, Huang G X, Konotop V V 2013 Phys. Rev. Lett. 110 083604 doi: 10.1103/PhysRevLett.110.083604 [13] Peng P, Cao W C, Shen C, Qu W Z, Wen J M, Jiang L, Xiao Y H 2016 Nat. Phys. 12 1139 doi: 10.1038/nphys3842 [14] Jiang Y, Mei Y F, Zuo Y, Zhai Y H, Li J S, Wen J M, Du S W 2019 Phys. Rev. Lett. 123 193604 doi: 10.1103/PhysRevLett.123.193604 [15] Zhang Z Y, Zhang Y Q, Sheng J T, Yang L, Miri M A, Christodoulides D N, He B, Zhang Y P, Xiao M 2016 Phys. Rev. Lett. 117 123601 doi: 10.1103/PhysRevLett.117.123601 [16] Zhang Z Y, Feng Y, Ning S H, Malpuech G, Solnyshkov D D, Xu Z F, Zhang Y P, Xiao M 2022 Photonics Res. 10 958 doi: 10.1364/PRJ.447404 [17] Feng Y, Liu Z Z, Liu F, Yu J W, Liang S, Li F, Zhang Y P, Xiao M, Zhang Z Y 2023 Phys. Rev. Lett. 131 013802 doi: 10.1103/PhysRevLett.131.013802 [18] Zhang Z Y, Liang S, Septembre I, Yu J W, Huang Y P, Liu M C, Zhang Y P, Xiao M, Malpuech G, Solnyshkov D 2024 Phys. Rev. Lett. 132 263801 doi: 10.1103/PhysRevLett.132.263801 [19] Miri M A, Alù A 2019 Science 363 7709 doi: 10.1126/science.aar7709 [20] Chong Y D, Ge L, Stone A D 2011 Phys. Rev. Lett. 106 093902 doi: 10.1103/PhysRevLett.106.093902 [21] Xiao L, Zhan X, Bian Z H, Wang K K, Zhang X, Wang X P, Li J, Mochizuki K, Kim D, Kawakami N, Yi W, Obuse H, Sanders B C, Xue P 2017 Nat. Phys. 13 1117 doi: 10.1038/nphys4204 [22] Zhang J, Peng B, Özdemir S K, Pichler K, Krimer D O, Zhao G M, Nori F, Liu Y X, Rotter S, Yang L 2018 Nat. Photonics 12 479 doi: 10.1038/s41566-018-0213-5 [23] Shui T, Yang W X, Liu S P, Li L, Zhu Z H 2018 Phys. Rev. A 97 033819 doi: 10.1103/PhysRevA.97.033819 [24] Li J M, Harter A K, Liu J, de Melo L, Joglekar Y N, Luo L 2019 Nat. Commun. 10 855 doi: 10.1038/s41467-019-08596-1 [25] Xiao L, Deng T S, Wang K K, Zhu G Y, Wang Z, Yi W, Xue P 2020 Nat. Phys. 16 761 doi: 10.1038/s41567-020-0836-6 [26] Xiao L, Deng T S, Wang K K, Wang Z, Yi W, Xue P 2021 Phys. Rev. Lett. 126 230402 doi: 10.1103/PhysRevLett.126.230402 [27] 唐原江, 梁超, 刘永椿 2022 物理学报 71 171101 doi: 10.7498/aps.71.20221323 Tang Y J, Liang C, Liu Y C 2022 Acta Phys. Sin. 71 171101 doi: 10.7498/aps.71.20221323 [28] Yang J 2014 Opt. Lett. 39 1133 doi: 10.1364/OL.39.001133 [29] Kartashov Y V, Konotop V V, Torner L 2015 Phys. Rev. Lett. 115 193902 doi: 10.1103/PhysRevLett.115.193902 [30] Wang H, Huang J, Ren X, Weng Y, Mihalache D, He Y 2018 Rom. J. Phys. 63 205 [31] Ge L, Stone A D 2014 Phys. Rev. X 4 031011 doi: 10.1103/PhysRevX.4.03101 [32] Xue Y M, Hang C, He Y H, Bai Z Y, Jiao Y C, Huang G X, Zhao J M, Jia S T 2022 Phys. Rev. A 105 053516 doi: 10.1103/PhysRevA.105.053516 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: