-
Rydberg态是指将原子最外层电子激发至主量子数很大的轨道上的状态, 即电子被放置在一个距离核很远的轨道上, 这类电子被激发到高能级激发态的原子被称为Rydberg原子. Rydberg原子具有轨道半径大、运动轨道周期长、束缚能低、寿命长等特点, 这些特性使其成为原子分子光物理领域的重要研究对象, 在量子计算、量子通信和量子传感等领域得到新的应用[1–3], 是量子信息系统实现的重要途径. Rydberg原子间的相互作用导致Rydberg阻塞效应[4,5], 在这种情况下距离Rydberg原子一定范围内的其他原子的激发会受到抑制, 使得阻塞区域内仅存在单原子激发, 实现特定量子态的量子存储[6,7].
传统Rydberg原子的制备常采用的是单光子激发[8]或多光子激发方法[9], 通过对激光的控制, 能够实现光子的选择性吸收将电子激发到特定的Rydberg态. 通常将原子从基态激发至高激发态需要较大的能量, 以碱金属为例, 单光子激发所需的光子频率在紫外波段, 多光子激发则通常使用红外和可见光波段的能量. 碱金属原子最外层轨道只有一个电子, 可以看作由带正电的原子实和价电子组成的类氢结构, 使其在Rydberg态的制备中具有重要应用. 而随着强场物理的不断发展, 伴随着电场力和库仑势共同作用下产生的各种物理现象[10–12], 强激光场下的Rydberg态激发(Rydberg states excitation, RSE)成为了制备Rydberg原子的一种新方法. 相较于传统的通过共振激发Rydberg态原子的制备方式, 强激光与原子分子作用产生的Rydberg波包可以同时包含多个相干的Rydberg态, 且制备方式简单, 产生的Rydberg态具有很好的相干性. 尽管强场Rydberg态激发具有多方面的优点, 目前对其产生机制却没有一个确切的结论, 因此强场Rydberg态激发中内含的物理过程一直以来备受人们关注[13].
目前有关强场Rydberg态激发存在两种可能的机制, 分别为受挫电离(frustrated tunneling ionization, FTI)和多光子共振激发. 1987 年, Freeman等[14]发现能级移动导致阈上电离过程中的共振增强. 1992年, De Boer和Muller[15]基于多光子电离的理论提出了多光子共振激发机制, 认为激发态产率受到因激光强度变化导致的能级移动影响. 2006年, Wang等[16]数值求解含时薛定谔方程(time-dependent Schrödinger equation, TDSE), 提出了阈上电离的再捕获机制, 即在强场电离的过程结束时有部分电子被再捕获到激发态. 2008 年, Nubbemeyer等[17]实验测量了强激光场下中性激发态氦原子的产率, 发现强激光场下Rydberg态的产额随着椭偏度的增大而急剧降低, 提出了受挫电离的机制, 即在强激光场的作用下, 基态上的电子通过被扭曲的库仑势而发生隧穿, 当其返回离子实附近时并不回到基态, 而是被母离子俘获到高的Rydberg态, 称为受挫的隧穿电离.
由于强激光诱导束缚态之间的动态共振和不同电离时刻产生的电子波包干扰, Rydberg态激发对驱动激光的强度[18–20]、波长[21]、脉冲持续时间[22,23]和载波包络相位[24,25]存在明显的依赖关系. 随着激光整型技术的发展, 通过特定的激光场可以优化Rydberg态的产率, 例如双色激光场[26,27]、三色激光场[28]、半周期对激光场[29]和π相位阶跃[30]可以实现对特定Rydberg态的选择性激发. 近年来, 在理论上发现激光脉冲包络能够对激发和电离过程产生影响, 这为电子动力学的相干调控提供了新的途径[31,32]. 在实验上也证明了可以通过光栅对压缩器的非线性啁啾来实现对激光时域包络的控制[33]. 然而, 激光脉冲包络如何影响Rydberg态激发, 以及是否可以使用不对称激光包络来控制Rydberg态激发, 目前还尚未有定论.
本文采用经典轨迹蒙特卡罗(classical trajectory Monte Carlo, CTMC)和数值求解含时薛定谔方程方法, 从理论上研究了强激光场中Rydberg态产生的激光包络效应, 计算了不同不对称包络 参数下的Rydberg态布居. 基于定量再散射理论(quantitative rescattering, QRS), 阐明了布居数随不对称参数的变化以及再捕获率与激光脉冲包络线的关系, 并给出再捕获率的解析公式.
-
本文分别使用CTMC方法[23]和Qprop软件包求解TDSE方法[34], 计算强度为
$ 1\times 10^{14}\; {\mathrm{W/cm}}^2 $ 、波长为800 nm的强激光场作用下氢原子的Rydberg态占比. 选择激光脉冲在z方向极化, 形式为$ F(t)=F_{0}f(t)\cos(\omega t+\phi) $ . 这里$ F_{0} $ 为峰值电场振幅,$ \omega $ 为激光角频率,$ \phi $ 为激光的载波包络相位;$ f(t) $ 由如下激光包络线给出:其中
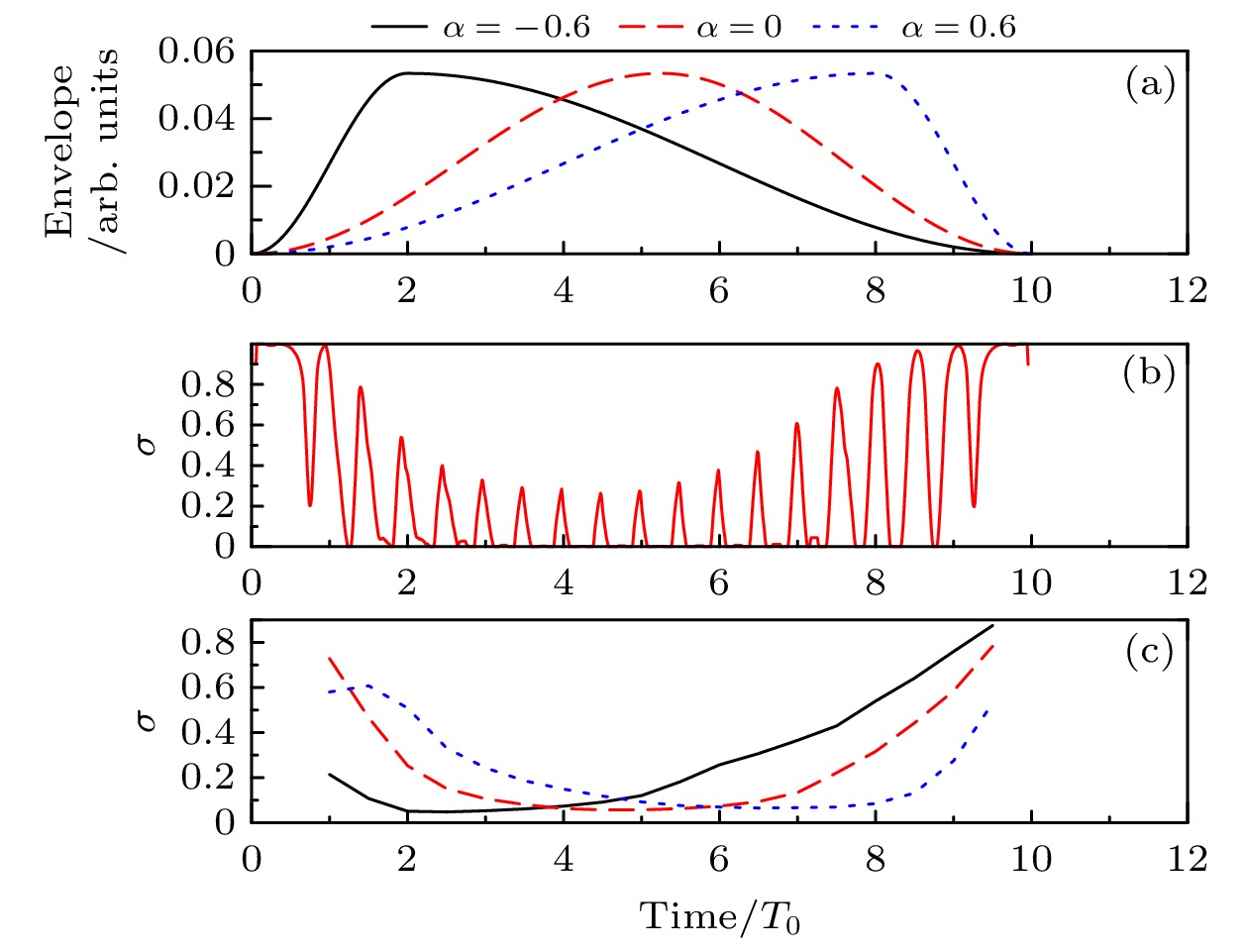
$ \tau=nT_0 $ 为脉冲总持续时间,$ \tau\mathrm{_{\mathrm{l}}} $ 为上升沿的宽度,$ \tau-\tau\mathrm{_l} $ 为下降沿的宽度,$ T_0 $ 为激光周期; n为总周期数, 计算中分别取10, 15, 20. 为了描述激光包络的形状, 定义不对称参数用来描述上升沿与整个脉冲的时间宽度之比. 负α值对应上升沿短于半脉冲的情况, 正α值对应上升沿长于半脉冲的情况. 不同α和相同脉冲持续时间
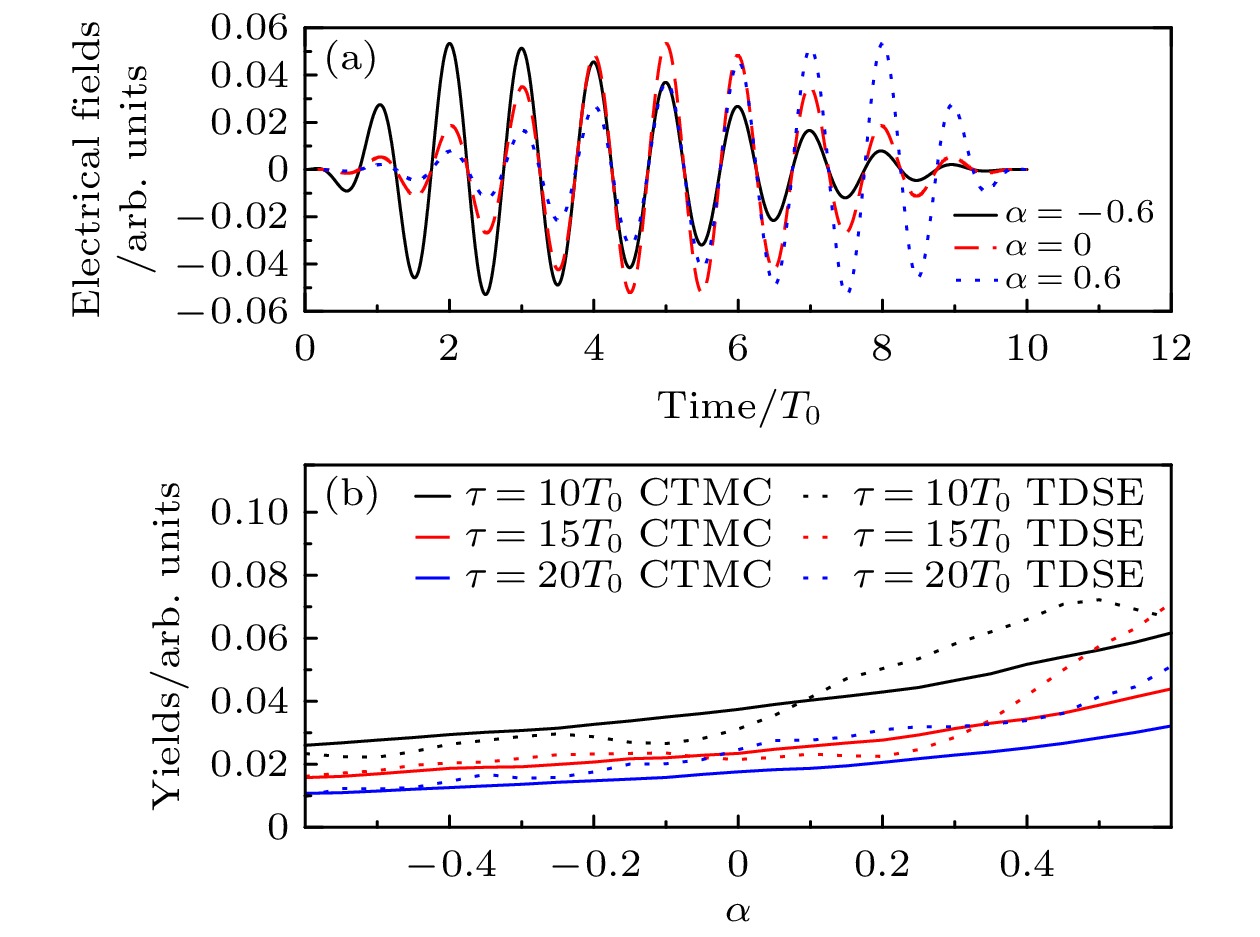
$ \tau=10 T_0 $ 的电场如图1(a)所示. 黑色实线、红色虚线和蓝色点线分别为$ \alpha=-0.6, 0, 0.6 $ 时, 对应$ \tau=10 T_0 $ 时上升沿持续时间$ \tau_{\mathrm{l}}=2 T_0, 5 T_0, 8 T_0 $ .$ \alpha=\pm0.6 $ 的激光脉冲电场关于$ t=\tau/2 $ 对称.在CTMC计算中, 假设电子在每一个瞬间都沿着激光偏振方向隧穿出来, 根据ADK (Ammosov-Delone-Krainov)隧穿理论的初始动量分布和电离率[35,36],
$ t_0 $ 时刻电子隧穿速率为其中
$ \kappa=\sqrt{2 I_{\mathrm{p}}} $ ,$ I_{\mathrm{p}} $ 为原子电离势. 在每个激光参数下, 计算10亿个电子轨迹, 轨迹的初始纵向动量(沿瞬时激光偏振方向)为零, 初始横向动量(垂直于瞬时激光偏振方向)呈概率分布:每个电子轨迹的权重为
电离时刻和初始横向动量分别在参数空间
$ [0, \tau] $ 和$ [0, 3\sigma_{\perp}] $ 两个坐标中进行均匀随机采样, 其中$ \sigma_{\perp}=\sqrt{F(t_0)/\kappa} $ 是$ p_{\perp}^{\mathrm{i}} $ 高斯分布的宽度. 初始动量设为$ p_x^{\mathrm{i}} = p_\perp^{\mathrm{i}}\cos(\alpha) $ ,$ p_y^{\mathrm{i}} = p_\perp^{\mathrm{i}}\sin(\alpha) $ , 其中α是$ p_{\perp}^{\mathrm{i}} $ 与x轴之间的夹角, 且在$ [0, 2\pi) $ 之间均匀随机采样[24,37].通过求解激光场和库仑势共同作用下的牛顿方程, 能够得到激光脉冲末端电子的位置
$\boldsymbol r $ 和 动量$\boldsymbol q $ . 为了确定电子被重新捕获时的激发态, 我们计算了经典主量子数$ n_{\mathrm{c}} = 1/\sqrt{2 |E_{\mathrm{f}}|} $ , 其中$ E_{\mathrm{f}}= -1/r+q^2/2<0 $ 为束缚电子的总能量. 量子数根据以下准则判定[38,39]:通过对末态能量
$ E_{\mathrm{f}}=-1/r+q^2/2<0 $ 的轨迹求和来计算Rydberg态的总量: -
图1(b)中黑、红、蓝线分别表示
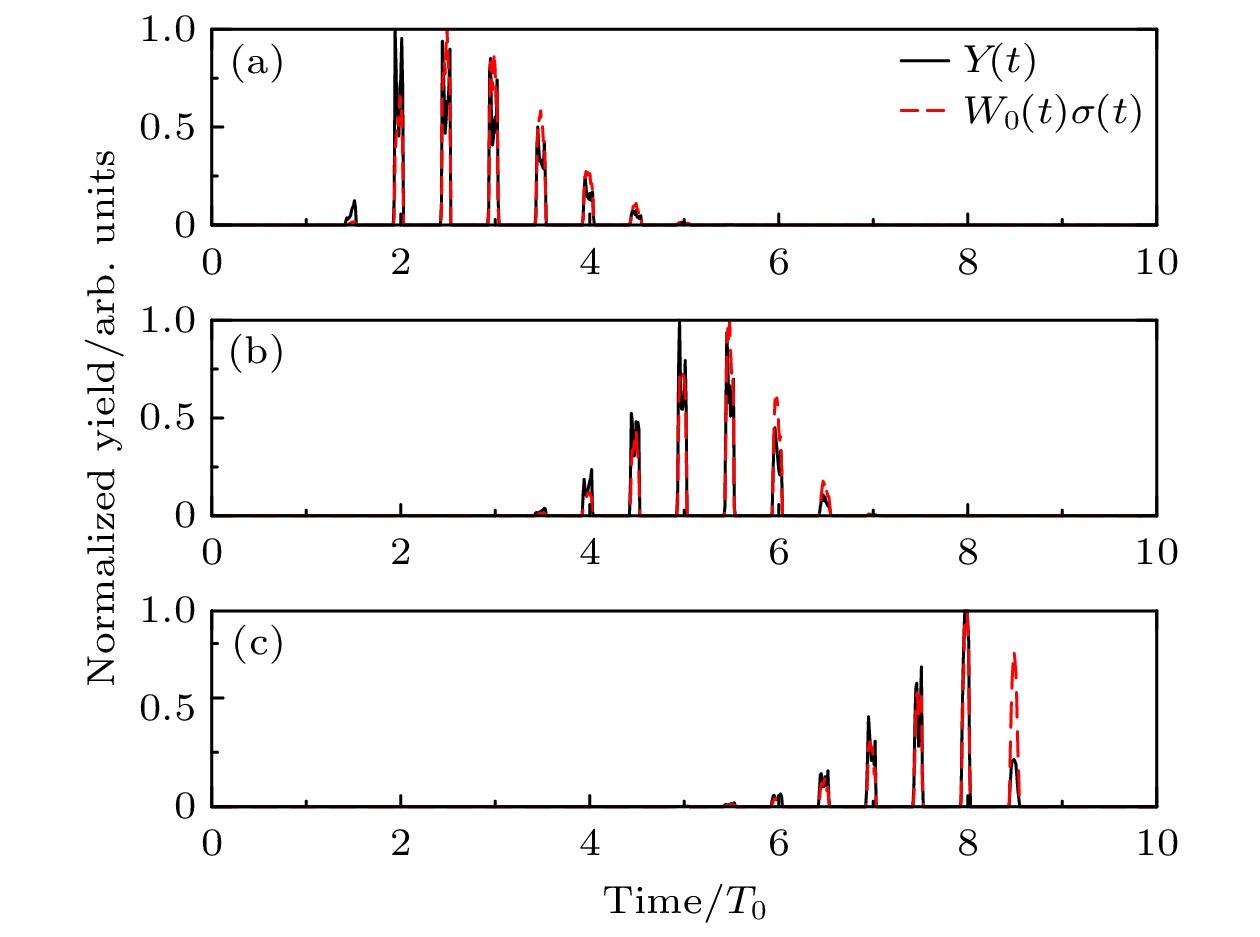
$ \tau=10 T_0, ~ 15 T_0, 20 T_0 $ 下不同α的Rydberg态的总产额. 实线和点线分别表示使用CTMC和TDSE的计算结果. 当α从–0.6增至0.6时, Rydberg态的产率约增大1倍, 表明在上升沿较长的激光脉冲中更有可能产生Rydberg态. 为了研究激光场波形对激发动力学的影响, 我们比较了$ \alpha=0, \pm0.6 $ 激光脉冲下随时间变化的Rydberg态布居. 如图2所示, Rydberg态主要是由电子在每个半周期的场峰附近隧穿产生的[24,40], 可以称之为“载波效应”. 当$ \alpha=-0.6, 0 $ 和0.6时, Rydberg态布居主要来自于$ t\in[2 T_0, 4 T_0], [4 T_0, 6 T_0] $ 和$ [6 T_0, 8 T_0] $ 处的电子隧穿. 主导周期随着包络线的不对称性而变化, 这可称为“包络效应”.将定量再散射理论[41]推广到强激光激发, 在强场中重新捕获到Rydberg轨道的电子产率由
确定, 其中
$ W_0 (t) $ 和$ \sigma(t) $ 为t时刻隧穿电子的电离率和再捕获率. 当$ \alpha=0, \pm0.6 $ 时, 归一化Rydberg态布居与$ W_0(t)\sigma(t) $ 的时间依赖性吻合, 验证了定量再散射理论理论在强激光激发过程中的适用性. 再捕获率通过$ \sigma(t)=N_{\mathrm{r}}(t)/N(t) $ 计算, 其中$ N(t) $ 和$ N_{\mathrm{r}}(t) $ 分别是在时间t隧穿的所有电子和再捕获电子的数量. 由于原子的能级因交流斯塔克效应会发生强烈的变化[25,42,43], 很难确定隧穿电子进入特定Rydberg轨道的再捕获时间, 因此将电子的再捕获率$ \sigma(t) $ 定义为隧穿时间的函数.由于电离率
$ W_0(t) $ 只与电场有关, 所以激光包络不对称的Rydberg态单调变化可归因于随时间变化的再捕获速率$ \sigma(t) $ . 对比图3(b)、图3(a)和图1(a)所示的再捕获率$ \sigma(t) $ 、激光包络线和$ \alpha=0 $ 时的激光场, 再捕获率与激光包络线呈负相关, 与各半周期内电场幅值呈正相关. 如图3(c)所示, 在每个半周期内对$ \alpha=-0.6, 0 $ 和$ 0.6 $ 的再捕获率进行积分, 以消除载波效应. 对于不同的不对称参数, 再捕获率与包络线呈普适的负相关关系, 使得再捕获率在隧穿电离的主导周期内达到最小.基于半经典模型的隧穿电子再捕获条件[24,40], 可估算得到每半周期内隧穿坐标(隧穿时间和垂直动量)相空间的再捕获截面:
其中
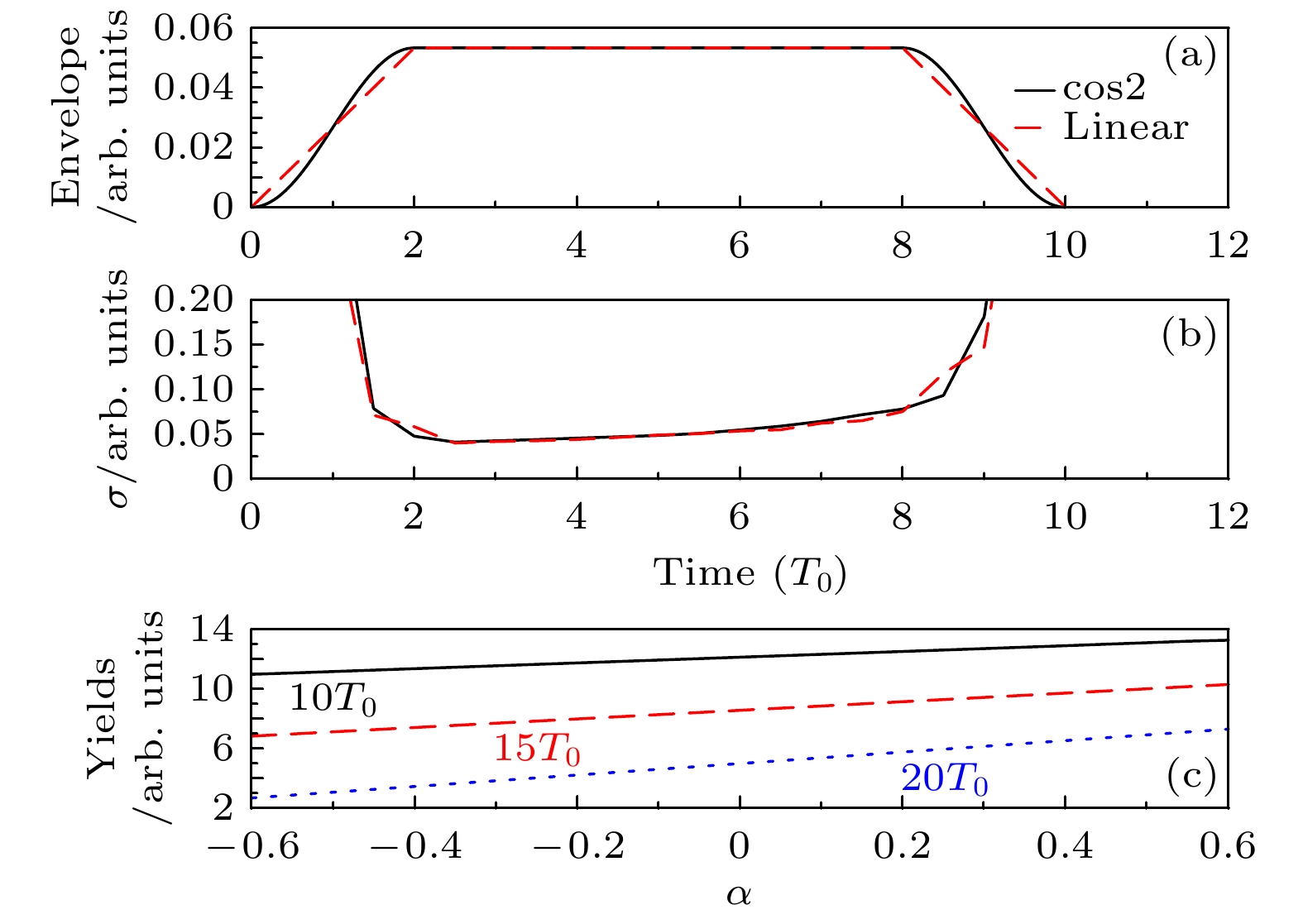
$ t_> \approx - \dfrac{\lambda}{\omega} - \dfrac{1}{F} ({4}/{\tau})^{1/3} $ 和$ t_< \approx -\lambda/\omega $ 分别为半周期内最小和最大隧穿时间,$ v_{{\mathrm{max}}} \approx \dfrac{\left({4}/{\tau}\right)^{1/3}}{1-2{F}/{(2 I_{\mathrm{p}})^2}} $ 为再捕获电子的最大隧穿动量, F 为峰值电场. 对于 CTMC计算中使用的激光参数, 有$ F\ll2 I_{\mathrm{p}} $ 和$ \varSigma ^*\propto \omega/(F\tau^{2/3}) $ , 对应于$ \sigma(t) $ 和$ f(t) $ 之间的负相关关系.为了研究包络上随时间变化的再捕获率的不对称性, 比较了具有余弦平方边缘和线性边缘的梯形激光包络中Rydberg态的产生, 如图4(a)所示. 在图4(b)中包络线的平台范围(
$ t\in[2 T_0, 8 T_0] $ )内, 平均再捕获率随着时间的延长而增大. 这种增大是由于当残余激光相互作用时间超过特定标准时, 隧穿电子的轨迹从再捕获转变为弹性散射, 这使得Rydberg态的布居对于激光脉冲持续时间非常敏感[22]. Rydberg态产额随上升沿持续时间增大正是由于包络峰值之后的激光作用时间缩短导致的再捕获率逐渐增大.结合再捕获率的包络效应和载波效应, Rydberg态的产率随时间的变化近似为
再捕获率的激光包络项和载波项分别近似为
$ ({t - \tau + c})/{f(t)} $ 和$ \cos(\omega t+\phi) $ . 如图4(c)所示, 利用(10)式计算Rydberg态总体对不对称参数α的依赖性, 随着α的增大与图1(b)中利用CTMC和TDSE计算的总体一致. -
Rydberg原子由于高激发态形成很大的电偶极矩, 拥有范围和强度远大于一般基态原子的相互作用, 是理想的量子物理研究平台. 近年来强场激发为相干多位Rydberg态的产生提供了可行方案. 本文采用CTMC和TDSE方法对不对称激光包络进行了计算, 发现随着不对称参数的线性增大, Rydberg态的占比增大. 基于定量再散射理论, 计算出的再捕获率的时间依赖性与激光包络和残余激光相互作用时间呈负相关, 称为包络效应. 结合载波效应, 提出了计算Rydberg态布居的解析公式. 本文研究结果为利用激光包络控制增强Rydberg态的产生打开了大门, 利用激光包络影响Rydberg态产生的新机理, 为强场激发原子分子的超快动力学提供了新的调控手段, 也为基于Rydberg原子的超快量子信息技术提供了新的方案.
强场激发Rydberg态的激光包络调控
Laser envelope control of strong field excited Rydberg states
-
摘要: 强激光相干激发为Rydberg态的产生和调控提供了新的手段. 本文主要研究不对称包络强激光场中Rydberg态产生的动力学过程, 发现Rydberg态的产率随激光包络上升沿的持续时间延长而增加. 利用电离率与随时间变化的再捕获率的乘积计算Rydberg态的布居, 将定量再散射理论推广到强场激发过程中. 通过分析Rydberg态的产生窗口, 得到了再捕获率的解析公式, 发现再捕获率与包络形状呈负相关, 并随剩余相互作用时间的延长而减小. 利用激光包络影响Rydberg态产生的新机理, 为强场激发原子分子的超快动力学提供了新的调控手段, 也为基于Rydberg原子的超快量子信息技术提供了新的方案.Abstract: Rydberg atoms are important building blocks for quantum technologies, and because of their unique tunable quantum properties, they possess new applications in quantum computing, quantum communication, and quantum sensing. Besides the widely-used few-photon resonant excitation for the specific Rydberg state, multiple Rydberg states can be populated coherently and efficiently through the frustrated tunneling ionization or the Coulomb potential recapture effect in a strong laser field. The excitation of Rydberg states in a strong field provides an opportunity for realizing the ultrafast quantum control on Rydberg atom and bridging the gap between strong field physics and quantum information technology. Using the classical trajectory Monte Carlo method and Qprop package to solve time-dependent Schrödinger equation, we calculate the population of Rydberg states. Our results show that the population increases with the increase of parameter of the asymmetric laser envelope. Based on the quantitative rescattering theory, the calculated time-dependent recapture rate is negatively related to the laser envelope and the residual laser interaction time, which is termed the envelope effect. Combined with the carrier-wave effect, an analytic formula can be used to calculate the Rydberg state population: $ Y(t) \propto $$ W_0\left(t\right) \dfrac{t-\tau+c}{f\left(t\right)} \cos \left(\omega t+\phi\right) . $ This result opens the way to enhancing the generation of Rydberg states by using the laser envelope control, which is beneficial to the future quantum technology based on the Rydberg states generated in the strong laser field.
-
Key words:
- Rydberg states /
- strong field excitation /
- ultrafast dynamics .
-

-
图 1 Rydberg态产额随激光脉冲参数的变化 (a)具有相同脉冲持续时间
$ \tau=10 T_0 $ 和不同不对称参数α的激光电场, 其中黑色实线、红色虚线、蓝色点线分别对应$ \alpha= $ $ -0.6, ~0, ~0.6 $ ; (b)在不同激光脉冲持续时间下, Rydberg态的产率随不对称参数的变化而变化, 黑、红、蓝线分别对应$ \tau= $ $ 10T_0,~ 15T_0, ~20T_0 $ , 实线和点线分别为CTMC和TDSE计算的Rydberg态激发的产率, 当α从–0.6增至0.6时, Rydberg态的产率约增大1倍, 表明在上升沿较长的激光脉冲中更有可能产生Rydberg态Figure 1. Rydberg state yield variation with laser pulse parameters. (a) Laser electric fields with the same pulse duration
$ \tau=10 T_0 $ and different asymmetric parameters α. Black solid line, red dashed line and blue dotted line are for$ \alpha=-0.6,~ 0, ~0.6 $ respectively. (b) The yields of Rydberg states change with the asymmetric parameter under different laser pulse duration. Black, red and blue lines are for$ \tau=10 T_0, 15 T_0, 20 T_0 $ , while solid line and dotted line are for RSE yields calculated using CTMC and TDSE respectively. The yields of the Rydberg states approximately double when α increases from –0.6 to 0.6, indicating the Rydberg states are more possible to be generated in the laser pulse with longer rising edge.图 2 Rydberg态的时间依赖性, 在相同脉冲持续时间
$ \tau= $ $ 10 T_0 $ 下, 不对称参数(a)—(c)$ \alpha=-0.6, 0, 0.6 $ 时的$ Y(t) $ (黑色实线)和$ W_0(t)\sigma(t) $ (红色虚线), Rydberg态主要是由电子在每个半周期的场峰附近隧穿产生的, 称为“载波效应”, 对于不同的α, 主导周期随包络线的不对称性而变化, 这可称为“包络效应”Figure 2. Time dependence of the Rydberg states yields. (a)−(c) The time dependence of the Rydberg states yields Y(t) (black solid line) and
$ W_0(t)\sigma(t) $ (red dashed line) with the same pulse duration$ \tau=10 T_0 $ and the asymmetric parameters$ \alpha=-0.6, 0, 0.6 $ . The Rydberg states are mainly generated from electrons tunneling near the field peak of each half-cycle termed as “carrier-wave effect”. For different α, the dominating cycles change with the asymmetry of the envelope, which can be termed as “envelope effect”.图 3 不对称包络下的时间依赖性 (a)不同不对称参数下的激光脉冲包络线; (b)激光包络对称
$ \alpha=0 $ 时再捕获率的时间依赖性; (c)不同不对称参数下每半周期平均总再捕获率的时间依赖性; 在(a)和(c)中, 黑色实线、红色虚线和蓝色点线分别表示$ \alpha=-0.6,~ 0, ~0.6 $ , 对于不同的不对称参数, 再捕获率与包络线均呈现负相关关系, 使得再捕获率在隧穿电离的主导周期内达到最小Figure 3. Time dependence of the recapture rate with asymmetric laser pulse envelopes: (a) Laser pulse envelopes with different asymmetric parameters; (b) the time dependence of the recapture rate with symmetric laser envelope
$ \alpha=0 $ ; (c) the time dependence of the total recapture rate averaged in every half-cycle with different asymmetric parameters; black solid line, red dashed line and blue dotted line are for$ \alpha=-0.6,~ 0, ~0.6 $ respectively in (a) and (c), the negative relation between recapture rate and the envelope is universal for different asymmetric parameters, making the recapture rate attain minimization in the dominating cycles of tunneling ionization.图 4 梯形激光脉冲包络线下的时间依赖性 (a)具有余弦平方和线性边缘的梯形激光脉冲包络; (b)梯形激光脉冲包络每半周期总再捕获率的时间依赖性, 当残余激光相互作用时间超过特定标准时, 电子轨迹从再捕获转变为弹性散射; (c)在与图1相同的激光参数下, 利用(10)式得到的Rydberg态的产率, 其中随α的增大与利用CTMC和TDSE计算得到的布居吻合得很好
Figure 4. Time dependence of the recapture rate with trapezoidal laser pulse envelopes: (a) Trapezoidal laser pulse envelopes with cosine square and linear edges; (b) the time dependence of the total recapture rate in every half-cycle with trapezoidal laser pulse envelopes, the increase can be due to the change of the electron’s trajectory from recapture to elastic recollision when the residual laser interaction time exceed a specific criterion; (c) the yield of the Rydberg states using Eq. (10) under the same laser parameters with Fig. 1, where the increase with α agrees well with the calculated population using CTMC and TDSE.
-
[1] Saffman M, Walker T G, Mølmer K 2010 Rev. Mod. Phys. 82 2313 doi: 10.1103/RevModPhys.82.2313 [2] Jing M Y, Hu Y, Ma J, Zhang H, Zhang L J, Xiao L T, Jia S T 2020 Nat. Phys. 16 911 doi: 10.1038/s41567-020-0918-5 [3] Adams C S, Pritchard J D, Shaffer J P 2020 J. Phys. B: At. Mol. Opt. Phys. 53 012002 doi: 10.1088/1361-6455/ab52ef [4] Urban E, Johnson T A, Henage T, Isenhower L, Yavuz D D, Walker T G, Saffman M 2009 Nat. Phys. 5 110 doi: 10.1038/nphys1178 [5] Pan L, Zhai H 2022 Phys. Rev. Res. 4 L032037 doi: 10.1103/PhysRevResearch.4.L032037 [6] Jaksch D, Cirac J I, Zoller P, Rolston S L, Côté R, Lukin M D 2000 Phys. Rev. Lett. 85 2208 doi: 10.1103/PhysRevLett.85.2208 [7] Baur S, Tiarks D, Rempe G, Dürr S 2014 Phys. Rev. Lett. 112 073901 doi: 10.1103/PhysRevLett.112.073901 [8] Vassen W, Cohen-Tannoudji C, Leduc M, et al. 2012 Rev. Mod. Phys. 84 175 doi: 10.1103/RevModPhys.84.175 [9] Saffman M, Walker T G 2002 Phys. Rev. A 66 065403 doi: 10.1103/PhysRevA.66.065403 [10] Corkum P B 1993 Phys. Rev. Lett. 71 1994 doi: 10.1103/PhysRevLett.71.1994 [11] Schafer K J, Yang B, DiMauro L F, Kulander K C 1993 Phys. Rev. Lett. 70 1599 doi: 10.1103/PhysRevLett.70.1599 [12] Becker W, Liu X J, Ho P J, Eberly J H 2012 Rev. Mod. Phys 84 1011 doi: 10.1103/RevModPhys.84.1011 [13] 沈星晨, 刘洋, 陈淇, 吕航, 徐海峰 2022 物理学报 71 233202 doi: 10.7498/aps.71.20221258 Shen X C, Liu Y, Chen Q, Lü H, Xu H F 2022 Acta Phys. Sin. 71 233202 doi: 10.7498/aps.71.20221258 [14] Freeman R R, Bucksbaum P H, Milchberg H, Darack S, Schumacher D, Geusic M E 1987 Phys. Rev. Lett. 59 1092 doi: 10.1103/PhysRevLett.59.1092 [15] De Boer M P, Muller H G 1992 Phys. Rev. Lett. 68 2747 doi: 10.1103/PhysRevLett.68.2747 [16] Wang B B, Li X F, Fu P M, Chen J, Liu J 2006 Chin. Phys. Lett. 23 2729 doi: 10.1088/0256-307X/23/10/029 [17] Nubbemeyer T, Gorling K, Saenz A, Eichmann U, Sandner W 2008 Phys. Rev. Lett. 101 233001 doi: 10.1103/PhysRevLett.101.233001 [18] Eichmann U, Saenz A, Eilzer S, Nubbemeyer T, Sandner W 2013 Phys. Rev. Lett. 110 203002 doi: 10.1103/PhysRevLett.110.203002 [19] Li Q G, Tong X M, Morishita T, Wei H, Lin C D 2014 Phys. Rev. A 89 023421 doi: 10.1103/PhysRevA.89.023421 [20] Ortmann L, Hofmann C, Landsman A S 2018 Phys. Rev. A 98 033415 doi: 10.1103/PhysRevA.98.033415 [21] Liu M Q, Xu S P, Hu S L, Becker W, Quan W, Liu X J, Chen J 2021 Optica 8 765 doi: 10.1364/OPTICA.418636 [22] Ortmann L, Hofmann C, Ivanov I A, Landsman A S 2021 Phys. Rev. A 103 063112 doi: 10.1103/PhysRevA.103.063112 [23] Zhao J, Liu J L, Wang X W, Zhao Z X 2024 Chin. Phys. Lett. 41 013201 doi: 10.1088/0256-307X/41/1/013201 [24] Liu J L, Zhao J, Huang Y D, Wang X W, Zhao Z X 2020 Phys. Rev. A 102 023109 doi: 10.1103/PhysRevA.102.023109 [25] Chetty D, Glover R D, Tong X M, deHarak B A, Xu H, Haram N, Bartschat K, Palmer A J, Luiten A N, Light P S, Litvinyuk I V, Sang R T 2022 Phys. Rev. Lett. 128 173201 doi: 10.1103/PhysRevLett.128.173201 [26] Larimian S, Lemell C, Stummer V, et al. 2017 Phys. Rev. A 96 021403 doi: 10.1103/PhysRevA.96.021403 [27] Venzke J, Gebre Y, Becker A, Jaroń-Becker A 2020 Phys. Rev. A 101 053425 doi: 10.1103/PhysRevA.101.053425 [28] Solanpää J, Räsänen E 2018 Phys. Rev. A 98 053422 doi: 10.1103/PhysRevA.98.053422 [29] Zhang B, Chen W B, Zhao Z X 2014 Phys. Rev. A 90 023409 doi: 10.1103/PhysRevA.90.023409 [30] Zhao X Y, Wang C C, Hu S L, Li W D, Chen J, Hao X L 2019 Chin. Phys. B 28 083202 doi: 10.1088/1674-1056/28/8/083202 [31] Toyota K, Saalmann U, Rost J M 2015 New J. Phys. 17 073005 doi: 10.1088/1367-2630/17/7/073005 [32] Ning Q C, Saalmann U, Rost J M 2018 Phys. Rev. Lett. 120 033203 doi: 10.1103/PhysRevLett.120.033203 [33] Leemans W P, Catravas P, Esarey E, Geddes C, Toth C, Trines R, Schroeder C B, Shadwick B A, Van-Tilborg J, Faure J 2002 Phys. Rev. Lett. 89 174802 doi: 10.1103/PhysRevLett.89.174802 [34] Tulsky V, Bauer D 2020 Comput. Phys. Commun. 251 107098 doi: 10.1016/j.cpc.2019.107098 [35] Ammosov M V, Delone N B, Krainov V P 1986 J. Exp. Theor. Phys. 64 1191 doi: 10.1117/12.938695 [36] Delone N B, Krainov V P 1991 J. Opt. Soc. Am. B 8 1207 doi: 10.1364/JOSAB.8.001207 [37] Liu J L, Chen W B, Zhang B, Zhao J, Wu J H, Yuan J M, Zhao Z X 2014 Phys. Rev. A 90 063420 doi: 10.1103/PhysRevA.90.063420 [38] Becker R L, MacKellar A D 1984 J. Phys. B:At. Mol. Opt. Phys. 17 3923 doi: 10.1088/0022-3700/17/19/015 [39] Emmanouilidou A, Lazarou C, Staudte A, Eichmann U 2012 Phys. Rev. A 85 011402 doi: 10.1103/PhysRevA.85.011402 [40] Shvetsov-Shilovski N I, Goreslavski S P, Popruzhenko S V, Becker W 2009 Laser Phys. 19 1550 doi: 10.1134/S1054660X09150377 [41] Le A T, Lucchese R R, Tonzani S, Morishita T, Lin C D 2009 Phys. Rev. A 80 013401 doi: 10.1103/PhysRevA.80.013401 [42] Chetty D, Glover R D, deHarak B A, et al. 2020 Phys. Rev. A 101 053402 doi: 10.1103/PhysRevA.101.053402 [43] Bengs U, Patchkovskii S, Ivanov M, Zhavoronkov N 2022 Phys. Rev. Res. 4 023135 doi: 10.1103/PhysRevResearch.4.023135 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: