-
近年来, 核实验学家利用“冷熔合反应”和“热熔合反应”合成了Z = 107—118号元素以及一系列同位素[1–8]. 目前, 实验上合成的最重原子核是294Og[6–8]. 元素周期表的第七周期已经被填满, 合成119, 120号元素成为核物理领域的下一个目标. 核实验学家已经利用热熔合反应对合成119, 120号元素开展了探索工作[9,10]. 另外, 研究者们也发展了一系列的理论模型对合成Z = 119, 120新核素的截面进行系统研究[11–14]. 但由于靶材料的选择范围有限, 合成119, 120号元素仍然面临很多挑战. 人工合成的超重核往往不稳定, 会发生α衰变或者自发裂变. 其中, α衰变已经发展成为鉴别新元素或新核素的有力工具之一. 实验上通过探测超重核α衰变链的半衰期来识别是否产生新核素[15–19]. 研究超重核的α衰变半衰期除了能够鉴别新核素外, 还可以从中提取一些核结构信息. 因此, 理论研究Z = 119, 120超重核的α衰变性质也是研究者们非常关注的课题之一.
20世纪20年代, Gamow[20], Gurney和Condon[21]的研究均将α衰变现象成功地解释为量子隧穿效应. 之后, 基于量子隧穿效应, 研究者们发展了很多理论模型用于α衰变半衰期的研究[22–31], 比如双中心壳模型[24]、结团模型[25]和液滴模型[26–28]等. 此外, 还发展了一系列的经验公式用于计算超重核的α衰变半衰期[32–40]. 这些模型和经验公式不同程度地再现了超重核α衰变半衰期的实验数据. 1989年, Malik和Gupts [22]通过在相互作用势中加入亲和势用于研究结团放射的半衰期. 之后, 该模型被广泛地用于α衰变、单质子和双子发射半衰期的研究[41–47]. 研究者们将该模型称为UFM[44–47]或者库仑亲和势模型(Coulomb and proximity potential model, CPPM)[48–50]. 由于超重核一般具有四极形变或者更高阶形变, 较大的形变可能影响裂变位垒的高度, 从而影响原子核的半衰期. 因此, 利用UFM模型研究超重核的α衰变半衰期时有必要考虑原子核的形变效应. 另一方面, 相关研究表明预形成因子对α衰变半衰期的计算有着重要影响, 并且在模型中引入解析的预形成因子表达式有助于提高模型的计算精度[51–59]. 因此, 本文的研究动机之一就是在UFM模型[44–47]中考虑原子核的四极形变, 研究形变效应对超重核α衰变半衰期的影响. 接着, 在考虑形变的UFM模型中引入预形成因子的解析表达式, 以期提高模型的计算 精度.
近些年来, 相关研究预言N = 178是超重核区新的中子幻数[60–62], 并且N = 178附近超重核的合成、结构和衰变性质的研究引起了人们的广泛关注[63–68]. Brewer和其合作者曾尝试利用48Ca束流轰击249–251Cf靶核来合成超重核296Og[63]. Bao等[64]利用双核模型对合成296Og的可能性进行了理论分析. 还有研究者讨论了N = 178超重核的α衰变和结团放射等[65–68]. 因此, 将改进后的UFM模型推广至Z = 118—120超重核α衰变性质的研究具有重要的科学意义, 这是本文的第2个研究动机.
-
基于量子隧穿的α衰变过程, 其半衰期可由(1)式给出:
式中,
$ \lambda = {\nu _0}P $ 为α衰变常数, 其中$ {\nu _0} $ 和$ P $ 分别为α粒子碰撞位垒的频率和穿透位垒的概率. 一般$ {\nu _0} $ 可由经典方法计算得到:式中,
$ {R_{\text{p}}} $ ,$ {E_{\text{α }}} $ 和$ {M_{\text{α }}} $ 分别为母核的电荷半径、α粒子的动能和质量. 穿透概率$ P $ 通常可利用WKB近似方法得到:式中,
$ \mu = {A_{\text{d}}}{A_{\text{α }}}/({A_{\text{d}}} + {A_{\text{α }}}) $ 表示发射粒子和子核的约化质量,$ {R_{{\text{in}}}} $ 和$ {R_{{\text{out}}}} $ 分别为穿透位垒的入射点和出射点, 由$ V({R_{{\text{in}}}}) = V({R_{{\text{out}}}}) = {Q_{\text{α }}} $ 给出.$ V(r) $ 为体系的核-核相互作用势, 包含库仑势、离心势和亲和势:其中, 离心势
$ {V_{\text{l}}}(r) = l(l + 1){\hbar ^2}/(2\mu {r^2}) $ . 在之前的研究中[44–47], 核-核相互作用势使用的是球形的库仑势和1977年Blocki等[69]提出的亲和势. 除了1977年版本的亲和势外, 研究者们还提出了很多其他形式的亲和势, 比如Bass版本的亲和势[70–72], 参数化的Woods-Saxon势[73,74]等. 由于重核和超重核一般都具有轴对称形变性质. 为了在核势中引入原子核的四极形变, 本文的库仑势$ {V_{\text{C}}}(r) $ 和亲和势$ {V_{\text{P}}}(r) $ 分别采用形变的库仑势和形变的Woods-Saxon势, 其表达式分别为[75](5)式中
$ {\overline R _{{\text{P(d)}}}} $ 表示具有四极形变的母核或者子核的电荷半径,$ \beta _{2}^{{\text{p(d)}}} $ 表示母核或子核的四极形变参数,$ {P_2}(\cos \theta ) $ 为勒让德多项式. (6)式中$ {V_0} $ 和$ a $ 分别表示Woods-Saxon势阱的深度和弥散参数, 其值分别取为80 MeV和0.68 fm. 本文中α粒子的电荷半径取为1.6755 fm, 当不考虑原子核的四极形变时, 母核和子核的球形电荷半径可采用以下形式[40]:考虑原子核的四极形变后, 母核和子核的电荷半径可定义为
由于本文只考虑原子核的四极形变效应, 因此, 这里
$ \lambda $ 的取值为2. 这里需要注意的是考虑原子核的四极形变后, 利用(2)式计算碰撞频率时母核的电荷半径也要使用形变的电荷半径. 从(8)式可以看到, 将原子核的四极形变取为0时, 即不考虑原子核的四极形变, 形变的电荷半径可退化为球形的电荷半径, 从而使(5)式和(6)式中形变的核-核相互作用势退化成球形的核-核相互作用势. 为了观察原子核的形变是否会影响α衰变半衰期, 本文将不包含原子核四极形变的版本称为UFM, 而考虑原子核四极形变的版本称为IMUFM1.为了在IMUFM1版本中引入预形成因子, 衰变常数可改写成
$ \lambda = {\nu _0}P{S_{\text{α }}} $ . 其中预形成因子$ {S_{\text{α }}} $ 对数形式的解析表达式可采用以下形式[51–53]:其中,
$ {Z_{{\text{c1}}}} $ 和$ {Z_{{\text{c2}}}} $ 表示与母核质子数相邻的两个质子幻数, 即$ {Z_{{\text{c1}}}} \leqslant Z \leqslant {Z_{{\text{c2}}}} $ . 同样,$ {N_{{\text{c1}}}} $ 和$ {N_{{\text{c2}}}} $ 表示与母核中子数相邻的两个中子幻数, 即$ {N_{{\text{c1}}}} \leqslant N \leqslant {N_{{\text{c2}}}} $ . 由于本文的研究对象为重核和超重核区, 因此, (9)式可进一步写成以下形式:其中, 系数
$ a $ ,$ b $ ,$ c $ 和$ d $ 可通过拟合$ Z \geqslant 92 $ 重核和超重核的α衰变半衰期的实验数据得到. 由于偶-偶原子核的特殊性, 在拟合参数时将数据集分为偶-偶数据集和其他(包含偶-奇, 奇-偶和奇-奇)数据集, 其值列于表1. 这里将包含预形成因子$ {S_{\text{α }}} $ 的版本称为IMUFM2. -
首先利用UFM, IMUFM1和IMUFM2三个版本分别计算了
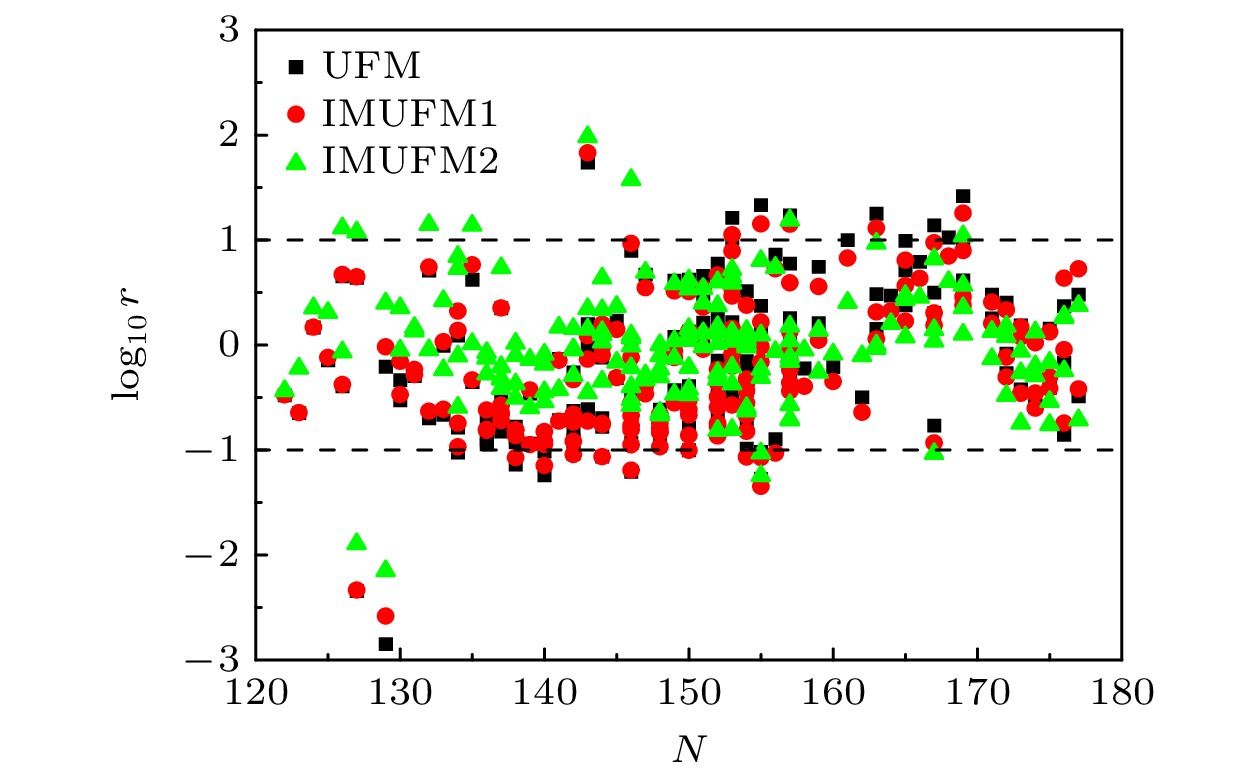
$ Z \geqslant 92 $ 重核和超重核的α衰变半衰期. 为了直观地观察计算结果与实验数据之间的差异, 分别计算了实验值与3种模型的理论值之间的比率($ r = T_{{\text{1/2}}}^{{\text{Expt}}{.}}/T_{{\text{1/2}}}^{{\text{Cal}}{.}} $ ). 一般情况下, 如果$ {\log _{10}}r $ ($ {\log _{10}}r = {\log _{10}}T_{{\text{1/2}}}^{{\text{Expt}}{.}} - {\log _{10}}T_{{\text{1/2}}}^{{\text{Cal}}{.}} $ )值落在–1和1之间, 则认为理论计算与实验数据符合较好. 其中$ T_{{\text{1/2}}}^{{\text{Expt}}{.}} $ 和$ T_{{\text{1/2}}}^{{\text{Cal}}{.}} $ 分别表示α衰变的实验半衰期和理论半衰期. 在计算中α粒子带走的最小轨道角动量l根据自旋宇称选择定则来确定. α衰变能$ {Q_{\text{α }}} $ 取自AME2020质量表[76],$ T_{{\text{1/2}}}^{{\text{Expt}}{.}} $ 和原子核的自旋宇称取自NUBASE2020质量表[77]. 图1所示为UFM, IMUFM1和IMUFM2三个版本的$ {\log _{10}}r $ 值随中子数N的变化. 从图1可以看到, 绝大部分的$ {\log _{10}}r $ 值均落在–1到1之间, 说明即便不考虑原 子核的四极形变和预形成因子, UFM模型也能 较好地再现重核和超重核的α衰变半衰期的实验数据. 比较UFM, IMUFM1和IMUFM2的计算结果, 发现UFM和IMUFM1的计算结果比较接近, 而IMUFM2的计算结果更加接近于0, 这表明IMUFM2的精度有了明显的提高.为了进一步定量研究模型精度, 利用(11)式和(12)式计算了理论值与实验值之间的平均偏差和标准偏差:
其中,
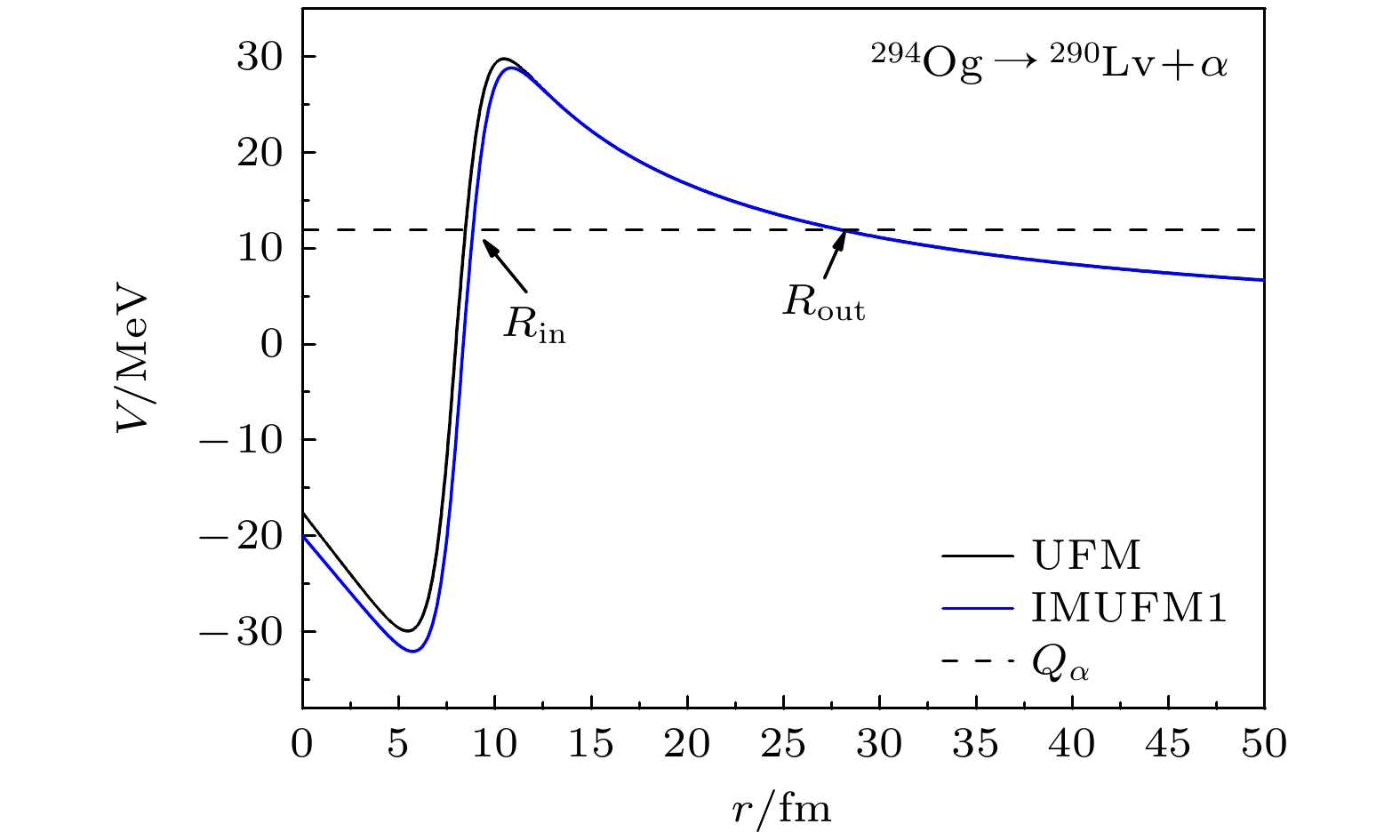
$ n $ 表示发生α衰变的事件总数. 利用UFM, IMUFM1和IMUFM2计算的$ \overline \sigma $ 和$ \sqrt {\overline {{\sigma ^2}} } $ 值分别列在表2中. 通过观察表2总体数据的$ \overline \sigma $ 值, 发现考虑原子核的形变效应后,$ \overline \sigma $ 值从0.5760减小到0.5619, 而考虑预形成因子后$ \overline \sigma $ 值会进一步减小到0.3816. 说明在模型中考虑原子核的形变效应有利于提高模型的精度, 如果引入α粒子预形成因子会使模型的精度进一步提高32.09%. 为了解释原子核的形变效应对半衰期的影响, 图2展示了294Og发生α衰变过程的核-核相互作用势. 图2中黑色实线对应的是未考虑原子核形变效应的情况, 蓝色实线为考虑原子核的形变效应的情况, 从中可以看到原子核的形变效应会使穿透位垒降低, 进而影响穿透概率. 同时, 从图2也可以看到, 原子核的形变效应对核-核相互作用势的影响是微弱的, 这也解释了表2中IMUFM1的精度仅仅比UFM的精度提高了2.45%.为了检验模型的可靠性以及能否将改进后的模型推广至研究
$ Z = 118—120 $ 超重核的α衰变性质, 表3比较了$ Z \geqslant 110 $ 超重原子核α衰变半衰期的实验值和利用UFM, IMUFM1和IMUFM2三个版本计算的理论值. 从表3可以看到, 在一定误差范围内, 3个版本可以不同程度地再现实验数据. 对于表3中大多数的超重核, IMUFM1和IMUFM2的预言能力优于UFM, 并且利用IMUFM2计算的理论值更接近于实验数据. 因此, 在考虑原子核形变效应的基础之上, 引入预形成因子是必要的.我们知道α衰变半衰期对Qα 值的依赖非常敏感. 然而, 大部分超重核的α衰变能是未知的. 所以, 研究者们通常利用原子核的质量来获取Qα 值, 即
$ {Q_{\text{α }}} = {M_{\text{p}}} - {M_{\text{d}}} - {M_{\text{α }}} $ , 其中$ {M_{{{{\mathrm{p, d}}, \alpha }}}} $ 表示母核或者子核或者α粒子的质量过剩. 因此, 可靠的质量模型对于精确预言超重核的α衰变半衰期非常关键. 截止到目前, 人们已经发展了多种核质量模型[78–85], 而且这些质量模型能够不同程度地再现重核和超重核的Qα 值的实验数据[86]. 本文利用FRDM2012[79], WS4[80]和KTUY[81]三种质量模型分别提取了$ Z = 118—120 $ 同位素链的Qα 值. 由于IMUFM2是在IMUFM1的基础上改进的, 并且IMUFM2的总体精度较高, 所以表4仅列出了IMUFM2的预言结果. 目前, 实验上仅测量了294Og的Qα值和对数半衰期, 其值分别为11.87 MeV和–3.155 s. 从表4可以看到, 利用FRDM2012, WS4和KTUY三种质量模型提取的Qα 值分别为12.365, 12.198和11.165 MeV, 对应的α衰变半衰期分别为–4.382, –4.017和–1.571 s. 由于利用WS4质量模型提取的Qα 值更接近于实验值, 导致该质量模型预言的α衰变半衰期与实验数据更符合. 另外, 不同的质量模型预言的Qα 值会存在差异, 进而导致预言的半衰期出现数量级的差别.除了α衰变, 自发裂变(spontaneous fission, SF)是超重核另外一种重要衰变模式. 超重核的 稳定性往往取决于这两种衰变模式的竞争. 由于自发裂变具有更加复杂的物理机制, 所以准确地描述自发裂变的物理过程就变得异常困难. 1955年, Swiatecki[87]考虑原子核自发裂变的随机性以及壳层结构对半衰期的影响等物理因素, 通过拟合自发裂变半衰期的实验数据提出一个经验公式. 之后, 研究者们在此基础上提出了很多改进的版本[88–90]. 为了讨论
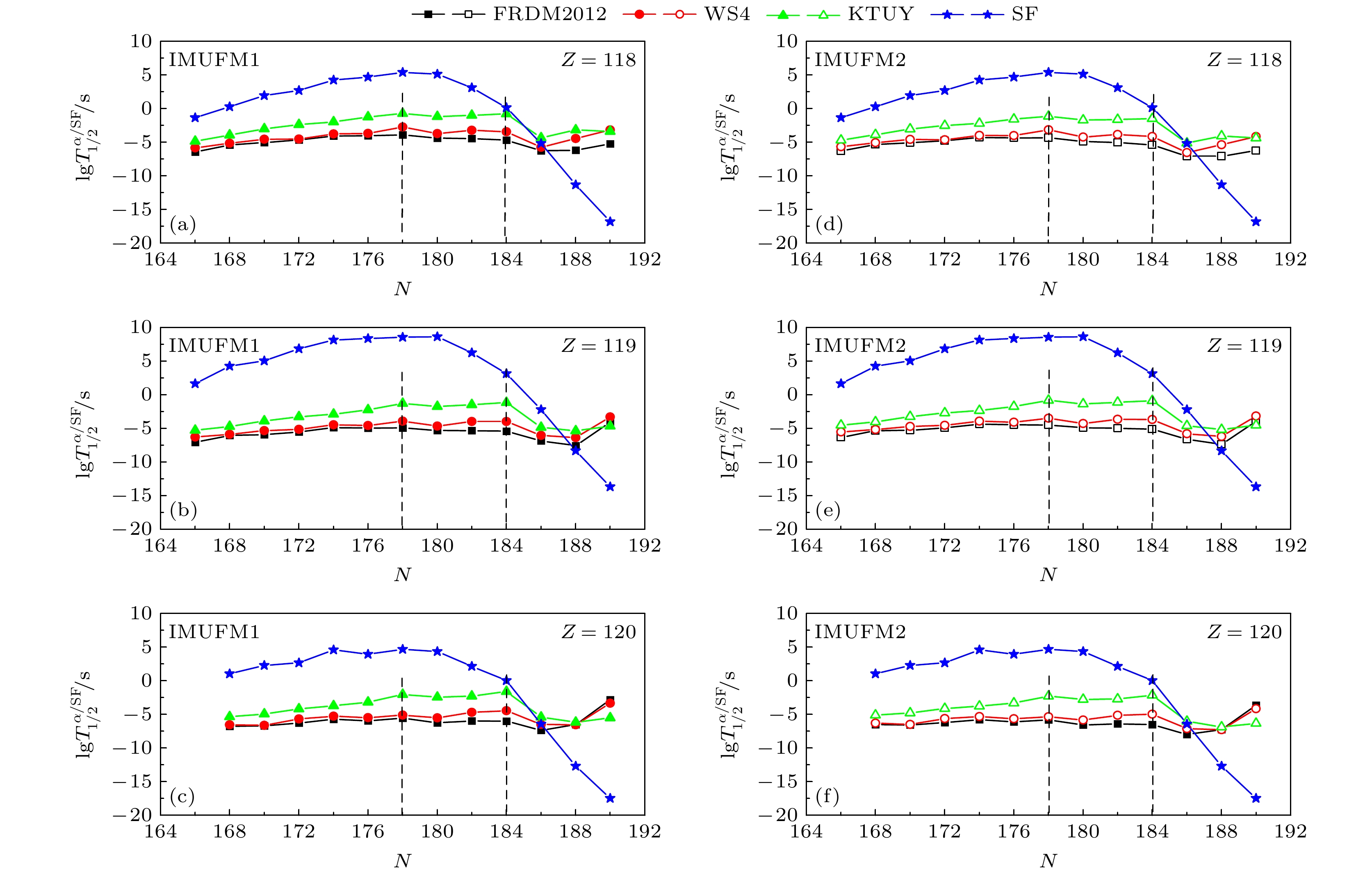
$ Z = 118—120 $ 同位素链上原子核的α衰变与自发裂变的竞争, 本文利用考虑同位旋效应和壳修正的Swiatecki经验公式[90]来计算相应原子核的自发裂变半衰期, 其公式为式中,
$ {\log _{10}}(T_{{\text{1/2}}}^{{\text{yr}}}) $ 表示以年为单位的自发裂变对数半衰期,$ I = (N - Z)/A $ 表示母核的同位旋效应,$ {E_{{\text{sh}}}} $ 为壳修正项,$ {h_{\text{i}}} $ 表示未配对核子的阻碍效应. 通过拟合Th到Fl同位素链自发裂变半衰期的实验数据, 可得到(13)式中的系数$ {c_1} $ ,$ {c_2} $ ,$ {c_3} $ ,$ {c_4} $ 和$ {h_{\text{i}}} $ 的值分别为 1174.353, –47.667和0.471和3.379 [90]. 图3将$ Z = 118—120 $ 同位素链的自发裂变半衰 期和利用IMUFM1和IMUFM2预言的α衰变半衰期分别画在一个坐标系中. 其中, 图3(a)—(c)为IMUFM1预言的结果, 图3(d)—(f)为IMUFM2预言的结果. 另外, 图3使用不同颜色的图标对FRDM2012, WS4和KTUY三种质量模型进行区分. 从图3可以看到, 利用FRDM2012和WS4两种质量模型预言的α衰变半衰期非常接近, 而利用KTUY质量模型预言的半衰期比另外两种质量模型的结果大1个数量级左右. 虽然3种质量模型预言的半衰期有所差别, 但随同位素链的演化趋势是一致的, 并且在N = 178和N = 184处出现了转折点. 特别是WS4质量模型预言的N = 178处的幻数效应更加明显. 因此, 研究N = 178附近超重核的稳定性有助于为将来实验上鉴别新核素提供理论参考. 除了从图3中获取核结构信息外, 通过比较自发裂变和α衰变半衰期的大小, 发现Z = 118和120同位素链在N = 186时两种衰变模式出现了重合. 而119同位素链在N = 188时才出现自发裂变半衰期低于α衰变半衰期. 总之, 这3条同位素链在N = 186附近出现了衰变模式的改变, 并且, N<186核区的超重核均以α衰变为主.为了讨论N = 178超重核的稳定性, 表5讨论了296Og, 297119和298120 α衰变链的衰变模式. 其中, 原子核自发裂变半衰期利用(13)式计算得到. 将利用FRDM2012, WS4和KTUY 3种质量模型提取的Qα值分别输入到IMUFM1和IMUFM2, 得到相应的α衰变半衰期. 通过比较自发裂变和α衰变半衰期的大小, 预言了这3条α衰变链的主要衰变模式. 3种质量模型预言的衰变模式和从文献[77]中得到的实验衰变模式分别列在表5的最后4列, 其中, 括号中的衰变模式表示IMUFM2的预言结果. 对于WS4和KTUY两种质量模型, 利用IMUFM1和IMUFM2预言的衰变模式与实验结果完全一致. 而FRDM2012质量模型预言的288Fl, 285Nh和286Fl的衰变模式是自发裂变, 与实验结果相反. 然而观察288Fl结果, 虽然IMUFM1的预言结果与实验结果相反, 但利用IMUFM2的计算结果与实验一致, 这也再次说明引入预形成因子的必要性. 以上关于超重核α衰变半衰期和衰变模式的研究可以为将来实验上鉴别新核素提供理论参考.
-
本文通过考虑原子核的形变效应和引入α粒子预形成因子的解析表达式, 对UFM模型进行改进. 利用改进后的模型系统地计算了Z = 118—120同位素链的α衰变半衰期, 主要得到以下结论.
1) 考虑原子核的形变效应后, IMUFM1的精度比UFM提高了2.45%. 引入预形成因子的解析表达式后, IMUFM2的精度会进一步提高32.09%, 表明预形成因子对α衰变半衰期的影响比形变效应的影响更大. 另外, 通过比较
$ Z \geqslant 110 $ 超重核α衰变半衰期的实验值与理论值, 验证了将IMUFM2推广至超重核的α衰变研究是合理的.2) 将从FRDM2012, WS4和KTUY 3种核质量模型提取的Z = 118—120同位素链的Qα 值分别输入到IMUFM1和IMUFM2中, 得到了这3条同位素链的α衰变半衰期. 通过观察半衰期随同位素链的演化, 发现3种质量模型预言的半衰期演化趋势一致, 在N = 178和N = 184处会出现转折点, 但KTUY质量模型预言的半衰期会比另外两种质量模型预言的结果大1个数量级左右. 通过比较3条同位素链α衰变和自发裂变半衰期的大小, 发现N<186质量核区的超重核均以α衰变为主. 理论预言的Z = 118—120超重核的α衰变半衰期可以为将来实验上鉴别新核素提供理论依据.
3) 通过讨论296Og, 297119和298120 3条α衰变链自发裂变与α衰变之间的竞争, 发现相比于FRDM2012质量模型, WS4和KTUY质量模型能更好地再现N = 178 α衰变链上超重核的衰变模式. 在FRDM2012质量模型下, 通过比较利用IMUFM1和IMUFM2预言的288Fl衰变模式, 发现IMUFM2理论预言与实验结果更符合, 再次说明在模型中引入α粒子预形成因子是必要的.
Z = 118—120超重核α衰变性质的研究
Research on α decay properties of superheavy nuclei with Z = 118–120
-
摘要: 本文通过考虑原子核的形变效应和引入α粒子预形成因子的解析表达式对统一裂变模型(unified fission model, UFM)进行改进. 通过考虑原子核形变效应得到了改进的UFM (improved UFM-1, IMUFM1), 在IMUFM1基础上引入α粒子预形成因子的解析表达式得到了进一步改进的UFM (improved UFM-2, IMUFM2). 利用UFM, IMUFM1和IMUFM2三个版本分别对$ Z \geqslant 92 $重核和超重核的α衰变半衰期进行了系统地计算. 通过计算理论值和实验值之间的平均偏差和标准偏差, 发现IMUFM1的精度比UFM的精度仅提高了2.45%, 而IMUFM2的精度却提高了32.09%. 接着, 通过有限力程小液滴模型(finite-range Droplet model-2012, FRDM2012), Weizsäcker-Skyrme-4 (WS4)和Koura-Tachibana-Uno-Yamada (KTUY) 3种质量模型分别提取了Z = 118—120同位素链的α衰变能, 并利用IMUFM1和IMUFM2计算了相应的α衰变半衰期. 通过观察半衰期随同位素链的演化, 发现不同质量模型预言的演化趋势是一致的, 而且在N = 178和N = 184处会出现转折点, 但不同的质量模型预言的α衰变半衰期会出现数量级的差异. 另外, 通过讨论α衰变和自发裂变之间的竞争, 发现N<186质量核区的超重核以α衰变为主. 最后, 结合上述3种核质量模型, 利用IMUFM1和IMUFM2讨论了296Og, 297119和298120 α衰变链的衰变模式, 发现WS4和KTUY两种质量模型的预言结果与实验结果一致. 尽管FRDM2012质量模型预言的288Fl, 285Nh 和 286Fl的衰变模式与实验结果有所差别, 但对于288Fl, IMUFM2的预言结果比IMUFM1更符合实验测量结果, 再次验证了IMUFM2的合理性和可靠性. 上述研究结果可为将来实验鉴别新核素提供理论依据.Abstract: An unified fission model (UFM) has been improved by considering the nuclear deformation effect and introducing an analytical expression of preformation factor. The improved version of the UFM by taking into consideration the nuclear deformation effect is named IMUFM1. Based on the IMUFM1, the further improved version is termed IMUFM2, which incorporates an analytical expression of the preformation factor. Within the UFM, the IMUFM1 and the IMUFM2, the α decay half-lives of heavy and superheavy nuclei with $ Z \geqslant 92 $are systematically calculated. The calculated standard deviation between the calculation results and the experimental data shows that the accuracy of the IMUFM1 is improved by 2.45% compared with that of the UFM. The accuracy of the IMUFM2 will be further improved by 32.09% compared with that of the IMUFM1, which implies that the nuclear deformation effect and the preformation factor are both important in prediction. Then, the α decay half-lives of Z = 118–120 isotopes are predicted from the IMUFM1 and the IMUFM2 by inputting the α decay energy values that are extracted from the sinite-range droplet model (FRDM), the Weizsäcker-Skyrme-4 (WS4) model and the Koura-Tachibaba-Uno-Yamads (KTUY) formula, respectively. The observed evolution of the α decay half-lives indicates that the evolution trends obtained from the above-mentioned three mass models are consistent with each other and the shell effects occur at N = 178 and 184, but their orders of magnitude, obtained from different mass models, are different from each other. Meanwhile, the comparison of half-lives between α decay and spontaneous fission shows that the dominant decay modes of the superheavy nuclei with N < 186 are α decay. Finally, the decay modes of 296Og, 297119 and 298120 α decay chains are predicted within the IMUFM1 and the IMUFM2 by using these three mass models, showing that the predictions from the WS4 mass model and KTUY mass model are more consistent with the experimental measurements. Form the FRDM2012 mass model, the predictions of 288Fl, 285Nh and 286Fl within the IMUFM1 mass model are not consistent with the experimental measurements, however, the prediction of 288Fl from the IMUFM2 is good agreement with the experimental measurement, which once again verifies the rationality and reliability of the IMUFM2. This study may be helpful for identifying new nuclide in future experiments.
-
Key words:
- superheavy nuclei /
- unified fission model /
- α decay /
- spontaneous fission .
-

-
偶-偶 其他 系数 126 < N < 152 N > 152 126 < N < 152 N > 152 a –0.3583 0 5.2940 0 b 0.0298 –0.0099 0.0388 –0.0606 c 0.0022 0.0382 8.7843×10–4 0.0214 d 0.0017 0.0102 –0.0241 0.0042 表 2
$ Z \geqslant 92 $ 重核和超重核α衰变半衰期的理论值与实验值之间的平均偏差$ \overline \sigma $ 和标准偏差$ \sqrt {\overline {{\sigma ^2}} } $ Table 2. The average deviation
$ \overline \sigma $ and the standard deviation$ \sqrt {\overline {{\sigma ^2}} } $ between the calculated ones and the experimental data of the heavy and superheavy nuclei with$ Z \geqslant 92 $ .模型 $ \overline \sigma $ $ \sqrt {\overline {{\sigma ^2}} } $ 总值(n = 178) 偶-偶(n = 56) 其他(n = 122) 总值(n = 178) 偶-偶(n = 56) 其他(n = 122) UFM 0.5760 0.6617 0.5367 0.7066 0.7292 0.6960 IMUFM1 0.5619 0.6822 0.5067 0.6855 0.7434 0.6572 IMUFM2 0.3816 0.2232 0.4544 0.5320 0.3390 0.6002 表 3
$ Z \geqslant 110 $ 超重核α衰变半衰期的实验值与理论值, 其中Qα值取自于文献[76], 实验半衰期和原子核的自旋宇称取自文献[77]Table 3. The experimental and calculated α decay half-lives of superheavy nuclei with
$ Z \geqslant 110 $ . Here the Qα values taken from Ref. [76], and the experimental α decay half-lives and the nuclear spin parity taken from Ref. [77], respectively.母核 子核 Qα/MeV $ J_i^{\text{π}} $ $ J_j^{\text{π}} $ l $ {\log _{10}}T_{{\text{1/2}}}^{{\text{Expt}}{.}}{\text{/s}} $ $ {\log _{10}}T_{{\text{1/2}}}^{{\text{Cal}}{.}}{\text{/s}} $ UFM IMUFM1 IMUFM2 267Ds 263Hs 11.78 3/2+# 3/2+# 0 –5.00 –4.956 –4.764 –4.295 269Ds 265Hs 11.51 — 3/2+# 0 –3.638 –4.384 –4.194 –3.777 270Ds 266Hs 11.117 0+ 0+ 0 –3.688 –3.479 –3.340 –3.602 273Ds 269Hs 11.37 — 9/2+# 0 –3.620 –4.105 –3.934 –3.620 272Rg 268Mt 11.197 — — 0 –2.377 –3.377 –3.205 –2.783 278Rg 274Mt 10.85 — — 0 –2.097 –2.596 –2.403 –2.134 279Rg 275Mt 10.53 — — 0 –0.77 –1.794 –1.616 –1.373 280Rg 276Mt 10.149 — — 0 0.633 –0.786 –0.623 –0.405 277Cn 273Ds 11.62 — — 0 –3.102 –4.095 –3.910 –3.534 281Cn 277Ds 10.43 — — 0 –0.745 –1.212 –1.121 –0.847 282Nh 278Rg 10.78 — — 0 –0.854 –1.800 –1.753 –1.422 284Nh 280Rg 10.28 — — 0 –0.013 –0.492 –0.422 –0.142 285Nh 281Rg 10.01 — — 0 0.663 0.258 0.328 0.581 286Nh 282Rg 9.79 — — 0 1.079 0.891 0.911 1.139 285Fl 281Cn 10.56 — — 0 –0.678 –0.932 –0.883 –0.547 286Fl 282Cn 10.36 0+ 0+ 0 –0.657 –0.390 –0.351 –0.836 287Fl 283Cn 10.17 0+ — 0 –0.292 0.130 0.168 0.453 288Fl 284Cn 10.076 0+ 0+ 0 –0.185 0.386 0.272 –0.309 289Fl 285Cn 9.95 — — 0 0.322 0.731 0.627 0.860 287Mc 283Nh 10.76 — — 0 –1.222 –1.140 –1.107 –0.741 288Mc 284Nh 10.65 — — 0 –0.752 –0.861 –0.828 –0.487 289Mc 285Nh 10.49 — — 0 –0.387 –0.442 –0.408 –0.093 290Mc 286Nh 10.41 — — 0 –0.076 –0.232 –0.200 0.090 290Lv 286Fl 11 0+ 0+ 0 –2.046 –1.458 –1.444 –1.846 291Lv 287Fl 10.89 — — 0 –1.585 –1.186 –1.172 –0.826 292Lv 288Fl 10.791 0+ 0+ 0 –1.796 –0.940 –1.052 –1.551 293Lv 289Fl 10.68 — — 0 –1.155 –0.667 –0.737 –0.442 293Ts 289Mc 11.32 — — 0 –1.602 –1.973 –2.238 –1.861 294Ts 290Mc 11.18 — — 0 –1.155 –1.636 –1.881 –1.530 294Og 290Lv 11.87 0+ 0+ 0 –3.155 –2.985 –3.110 –3.430 表 4 利用IMUFM2预言的Z = 118—120同位素链α衰变半衰期, Qα值分别取自FRDM2012[79], WS4[80]和KTUY[81]质量模型
Table 4. The predicted α decay half-lives of superheavy nuclei with Z = 118–120 isotopes within the IMUFM2 by inputting the Qα values that extracted from FRDM2012[79], WS4[80], and KTUY[81] mass tables, respectively.
母核 FRDM2012 WS4 KTUY Qα/MeV $ {\log _{10}}T_{{\text{1/2}}}^{{\text{Cal}}{.}}{\text{/s}} $ Qα/MeV $ {\log _{10}}T_{{\text{1/2}}}^{{\text{Cal}}{.}}{\text{/s}} $ Qα/MeV $ {\log _{10}}T_{{\text{1/2}}}^{{\text{Cal}}{.}}{\text{/s}} $ 282Og 13.115 –5.234 13.494 –5.960 12.935 –4.877 284Og 13.565 –6.311 13.227 –5.673 12.745 –4.711 286Og 13.045 –5.346 12.915 –5.087 12.335 –3.873 288Og 12.855 –5.081 12.616 –4.591 11.905 –3.035 290Og 12.665 –4.786 12.601 –4.653 11.645 –2.523 292Og 12.385 –4.301 12.240 –3.987 11.465 –2.194 294Og 12.365 –4.382 12.198 –4.017 11.165 –1.571 296Og 12.275 –4.335 11.752 –3.151 10.945 –1.148 298Og 12.485 –4.901 12.182 –4.243 11.115 –1.705 300Og 12.505 –5.062 11.956 –3.852 11.035 –1.617 302Og 12.615 –5.407 12.041 –4.168 10.945 –1.504 304Og 13.395 –7.080 13.122 –6.557 12.435 –5.146 285119 14.055 –6.359 13.612 –5.553 13.085 –4.451 287119 13.365 –5.366 13.278 –5.195 12.705 –4.041 289119 13.465 –5.311 13.157 –4.716 12.455 –3.268 291119 13.235 –4.941 13.048 –4.573 12.165 –2.705 293119 12.915 –4.362 12.715 –3.949 11.985 –2.355 295119 12.935 –4.477 12.758 –4.113 11.705 –1.774 297119 12.895 –4.501 12.424 –3.512 11.285 –0.853 299119 13.075 –4.929 12.764 –4.298 11.475 –1.389 301119 13.075 –5.012 12.426 –3.664 11.345 –1.150 303119 13.105 –5.141 12.416 –3.707 11.215 –0.887 305119 13.855 –6.639 13.424 –5.828 12.815 –4.628 288120 13.845 –6.523 13.725 –6.303 13.105 –5.110 290120 13.745 –6.571 13.700 –6.488 12.835 –4.796 292120 13.775 –6.215 13.467 –5.634 12.715 –4.125 294120 13.485 –5.788 13.242 –5.315 12.495 –3.774 296120 13.585 –6.103 13.343 –5.640 12.225 –3.306 298120 13.235 –5.804 13.007 –5.345 11.625 –2.280 300120 13.695 –6.572 13.319 –5.854 11.885 –2.784 302120 13.545 –6.421 12.890 –5.125 11.795 –2.704 304120 13.545 –6.529 12.763 –4.970 11.515 –2.135 306120 14.275 –7.977 13.787 –7.108 13.225 –6.028 表 5 296Og, 297119和298120 α衰变链的衰变模式, 其中Qα值分别取自FRDM2012[79], WS4[80]和 KTUY[81]质量表
Table 5. Decay modes of 296Og, 297119 and 298120 α decay chains, here the Qα values taken from FRDM2012[79], WS4[80] , and KTUY[81] mass tables, respectively.
母核 $ {\log _{10}}T_{{\text{1/2}}}^{{\text{Cal}}{.}}{\text{/s}} $ FRDM2012 $ {\log _{10}}T_{{\text{1/2}}}^{{\text{Cal}}{.}}{\text{/s}} $ WS4 $ {\log _{10}}T_{{\text{1/2}}}^{{\text{Cal}}{.}}{\text{/s}} $ KTUY $ {\log _{10}}T_{{\text{1/2}}}^{{\text{Cal}}{.}}{\text{/s}} $ 衰变模式 SF Qα/MeV IMUFM1 IMUFM2 Qα/MeV IMUFM1 IMUFM2 Qα/MeV IMUFM1 IMUFM2 FRDM2012 WS4 KTUY Expt. 296Og 5.39 12.275 –3.919 –4.335 11.752 –2.735 –3.151 10.945 –0.732 –1.148 α(α) α(α) α(α) — 292Lv 5.34 10.815 –1.115 –1.614 11.127 –1.911 –2.410 10.335 0.195 –0.304 α(α) α(α) α(α) α 288Fl 3.02 9.165 3.100 2.519 9.645 1.561 0.980 9.465 2.123 1.542 SF(α) α(α) α(α) α 284Cn –2.15 8.955 3.281 2.617 9.544 1.375 0.712 9.225 2.385 1.721 SF(SF) SF(SF) SF(SF) SF 297119 8.53 12.895 –4.940 –4.501 12.424 –3.951 –3.512 11.285 –1.291 –0.853 α(α) α(α) α(α) — 293Ts 8.28 11.395 –2.396 –2.019 11.622 –2.963 –2.586 10.725 –0.708 –0.331 α(α) α(α) α(α) α 289Mc 7.12 10.085 0.731 1.046 10.296 0.129 0.444 10.005 0.966 1.281 α(α) α(α) α(α) α 285Nh 3.04 9.125 3.075 3.328 9.810 0.917 1.171 9.555 1.693 1.946 SF(SF) α(α) α(α) α 281Rg –1.89 9.215 2.128 2.320 9.758 0.455 0.647 9.785 0.374 0.566 SF(SF) SF(SF) SF(SF) SF 298120 4.68 13.235 –5.567 –5.804 13.007 –5.108 –5.345 11.625 –2.043 –2.280 α(α) α(α) α(α) — 294Og 4.67 12.365 –4.062 –4.382 12.198 –3.698 –4.017 11.165 –1.252 –1.571 α(α) α(α) α(α) α 290Lv 3.71 11.065 –1.610 –2.011 11.084 –1.657 –2.059 10.575 –0.323 –0.725 α(α) α(α) α(α) α 286Fl 1.54 9.465 2.30 1.815 9.970 0.756 0.272 9.725 1.489 1.004 SF(SF) α(α) α(α) α 282Cn –3.78 9.425 1.788 1.221 10.140 –0.331 –0.898 10.135 –0.317 –0.884 SF(SF) SF(SF) SF(SF) SF -
[1] Hofmann S, Munzenberg G 2000 Rev. Mod. Phys. 72 733 doi: 10.1103/RevModPhys.72.733 [2] Morita K, Morimoto K, Kaji D, Akiyama T, Goto S, Haba H, Ideguchi E, Katori K, Koura H, Kudo H, Ohnishi T, Ozawa A, Suda T, Sueki K, Tokanai F, Yamaguchi T, Yoneda A, Yoshida A 2004 J. Phys. Soc. Jpn. 73 2593 doi: 10.1143/JPSJ.73.2593 [3] Morita K, Morimoto K, Kaji D, Haba H, Ozeki K, Kudou Y, Sumita T, Wakabayashi Y, Yoneda A, Tanaka K, Yamaki S, Sakai R, Akiyama T, Goto S, Hasebe H, Huang M, Huang T, Ideguchi E, Kasamatsu Y, Katori Y, Kariya Y, Kikunaga H, Koura H, Kudo H, Mashiko A, Mayama K, Mitsuoka S, Moriya T, Murakami M, Murayama H, Namai S, Ozawa A, Sato N, Sueki K, Takeyama M, Tokanai F, Yamaguchi T, Yoshida A 2012 Rev. Mod. Phys. 81 103201 [4] Oganessian Y T, Abdullin F S, Bailey P D, Benker D E, Bennett M E, Dmitriev S N, Ezold J G, Hamilton J H, Henderson R A, Itkis M G, Lobanov Y V, Mezentsev A N, Moody K J, Nelson S L, Polyakov A N, Porter C E, Ramayya A V, Riley F D, Roberto J B, Ryabinin M A, Rykaczewski K P, Sagaidak R N, Shaughnessy D A, Shirokovsky I V, Stoyer M A, Subbotin V G, Sudowe R, Sukhov A M, Tsyganov Yu S, Utyonkov V K, Voinov A A, Vostokin G K, Wilk P A 2010 Phys. Rev. Lett. 104 142502 doi: 10.1103/PhysRevLett.104.142502 [5] 周善贵 2017 原子核物理评论 34 318 doi: 10.11804/NuclPhysRev.34.03.318 Zhou S G 2017 Nucl. Phys. Rev. 34 318 doi: 10.11804/NuclPhysRev.34.03.318 [6] Oganessian Y T, Utyonkov V K, Lobanov Y V, Abdullin F S, Polyakov A N, Sagaidak R N, Shirokovsky I V, Tsyganov Yu S, Voinov A A, Gulbekian G G, Bogomolov S L, Gikal B N, Mezentsev A N, Iliev S, Subbotin V G, Sukhov A M, Subotic K, Zagrebaev V I, Vostokin G K, Itkis M G, Moody K J, Patin J B, Shaughnessy D A, Stoyer M A, Stoyer N J, Wilk P A, Kenneally J M, Landrum J H, Wild J F, Lougheed R W 2006 Phys. Rev. C 74 044602 doi: 10.1103/PhysRevC.74.044602 [7] Oganessian Y T, Utyonkov V K 2015 Nucl. Phys. A 944 62 doi: 10.1016/j.nuclphysa.2015.07.003 [8] Oganessian Y T, Sobiczewski A, Ter-akopian G M 2017 Phys. Scr. 92 023003 doi: 10.1088/1402-4896/aa53c1 [9] Oganessian Y T, Utyonkov V K, Lobanov Y V, Abdullin F S, Polyakov A N, Sagaidak R N, Shirokovsky I V, Tsyganov Yu S, Voinov A A, Mezentsev A N, Subbotin V G, Sukhov A M, Subotic K, Zagrebaev V I, Dmitriev S N, Henderson R A, Moody K J, Kenneally J M, Landrum J H, Shaughnessy D A, Stoyer M A, Stoyer N J, Wilk P A 2009 Phys. Rev. C 79 024603 doi: 10.1103/PhysRevC.79.024603 [10] Kozulin E M, Knyazheva G N, Itkis I M, Itkis M G, Bogachev A A, Krupa L, Loktev T A, Smirnov S V, Zagrebaev V I, Äystö J, Trzaska W H, Rubchenya V A, Vardaci E, Stefanini A M, Cinausero M, Corradi L, Fioretto E, Mason P, Prete G F, Silvestri R, Beghini S, Montagnoli G, Scarlassara F, Hanappe F, Khlebnikov S V, Kliman J, Brondi A, Di Nitto A, Moro R, Gelli N, Szilner S 2010 Phys. Lett. B 686 227 doi: 10.1016/j.physletb.2010.02.041 [11] Wang N, Zhao E G, Scheid W, Zhou S G 2012 Phys. Rev. C 85 041601 doi: 10.1103/PhysRevC.85.041601 [12] Li J X, Zhang H F 2022 Phys. Rev. C 106 034613 doi: 10.1103/PhysRevC.106.034613 [13] Li F, Zhu L, Wu Z H, Sun J, Guo C C 2018 Phys. Rev. C 98 014618 doi: 10.1103/PhysRevC.98.014618 [14] Zhang M H, Zhang Y H, Zou Y, Wang C, Zhu L, Zhang F S 2024 Phys. Rev. C 109 014622 doi: 10.1103/PhysRevC.109.014622 [15] Varga K, Lovas R G, Liotta R J 1992 Phys. Rev. Lett. 69 37. [16] Wauters J, Bijnens N, Denooven P, Huyse M, Hwang H Y, Reusen G, von Schwarzenberg J, Van Duppen P, Kirchner R, Roeckl E 1994 Phys. Rev. Lett. 72 1329 doi: 10.1103/PhysRevLett.72.1329 [17] Andeyev A N, Huyse M, Van Duppen P, et al. 2000 Nature 405 430 doi: 10.1038/35013012 [18] Khuyagbaatar J, Yakushev A, Dullmann C E, Ackermann D, Andersson L L, Asai M, Block M, Boll R A, Brand H, Cox D M, Dasgupta M, Derkx X, Di Nitto A, Eberhardt K, Even J, Evers M, Fahlander C, Forsberg U, Gates J M, Gharibyan N, Golubev P, Gregorich K E, Hamilton J H, Hartmann W, Herzberg R D, Heßberger F P, Hinde D J, Hoffmann J, Hollinger R, Hübner A, Jäger E, Kindler B, Kratz J V, Krier J, Kurz N, Laatiaoui M, Lahiri S, Lang R, Lommel B, Maiti M, Miernik K, Minami S, Mistry A, Mokry C, Nitsche H, Omtvedt J P, Pang G K, Papadakis P, Renisch D, Roberto J, Rudolph D, Runke J, Rykaczewski K P, Sarmiento L G, Schädel M, Schausten B, Semchenkov A, Shaughnessy D A, Steinegger P, Steiner J, Tereshatov E E, Thörle-Pospiech P, Tinschert K, Torres De Heidenreich T, Trautmann N, Türler A, Uusitalo J, Ward D E, Wegrzecki M, Wiehl N, Van Cleve S M, Yakusheva V 2014 Phys. Rev. Lett. 112 172501 doi: 10.1103/PhysRevLett.112.172501 [19] Oganessian Y T, Utyonkov V K, Shumeiko M V, Abdullin F S, Adamian G G, Dmitriev S N, Ibadullayev D, Itkis M G, Kovrizhnykh N D, Kuznetsov D A, Petrushkin O V, Podshibiakin A V, Polyakov A N, Popeko A G, Rogov I S, Sagaidak R N, Schlattauer L, Shubin V D, Solovyev D I, Tsyganov Y S, Voinov A A, Subbotin V G, Bublikova N S, Voronyuk M G, Sabelnikov A V, Bodrov A Y, Aksenov N V, Khalkin A V, Gan Z G, Zhang Z Y, Huang M H, Yang H B 2024 Phys. Rev. C 109 054307 [20] Gamow G 1928 Z. Phys. 51 204 doi: 10.1007/BF01343196 [21] Gurney R W, Condon E U 1928 Nature 122 439 doi: 10.1038/122439a0 [22] Malik S S, Gupts R K 1989 Phys. Rev. C 39 1992. doi: 10.1103/PhysRevC.39.1992 [23] Buck B, Merchant A C, Perez S M 1993 At. Data Nucl. Data Tables 54 53 doi: 10.1006/adnd.1993.1009 [24] Mirea M 1996 Phys. Rev. C 54 302 doi: 10.1103/PhysRevC.54.302 [25] 任中洲, 许昌 2006 原子核物理评论 23 369 Ren Z Z, Xu C 2006 Nucl. Phys. Rev. 23 369 [26] Royer G 2000 J. Phys. G. Nucl. Part. Phys. 26 1149 doi: 10.1088/0954-3899/26/8/305 [27] Zhang H F, Royer G, Wang Y J, Dong J M, Zuo W, Li J Q 2009 Phys. Rev. C 80 057301 doi: 10.1103/PhysRevC.80.057301 [28] 张海飞, 包小军, 王佳眉, 黄银, 李君清, 张鸿飞 2013 原子核物理评论 30 241 doi: 10.11804/NuclPhysRev.30.03.241 Zhang H F, Bao X J, Wang J M, Huang Y, Li J Q, Zhang H F 2013 Nucl. Phys. Rev. 30 241 doi: 10.11804/NuclPhysRev.30.03.241 [29] Zou Y T, Pan X, Liu H M, Wu X J, He B, Li X H 2021 Phys. Scr. 96 075301 doi: 10.1088/1402-4896/abf795 [30] 张凯林, 韩胜贤, 岳生俊, 刘作业, 胡碧涛 2024 物理学报 73 062101 doi: 10.7498/aps.73.20231627 Zhang K L, Han S X, Yue S J, Liu Z Y, Hu B T 2024 Acta. Phys. Sin. 73 062101 doi: 10.7498/aps.73.20231627 [31] 王艳召, 崔建坡, 刘军, 苏学斗 2017 原子能科学技术 51 1544 doi: 10.7538/yzk.2016.youxian.0825 Wang Y Z, Cui J P, Liu J, Su X D 2017 At. Energy Sci. Tech. 51 1544 doi: 10.7538/yzk.2016.youxian.0825 [32] Sobiczewski A, Patyk Z, Cwiok S 1989 Phys. Lett. B 224 279 [33] Luo S, Qi L J, Zhang D M, He B, Chu P C, Li X H 2023 Eur. Phys. J A 59 125 doi: 1.https://doi.org/10.1140/epja/s10050-023-01040-5 [34] Poenaru D N, Nagame Y, Gherghescu R A, Greiner W 2002 Phys. Rev. C 66 049902 doi: 10.1103/PhysRevC.66.049902 [35] Poenaru D N, Gherghescu R A, Carjan N 2007 Eur. Lett. 77 62001 doi: 10.1209/0295-5075/77/62001 [36] Shin E, Lim Y, Hyun C H, Oh Y 2016 Phys. Rev. C 94 024320 doi: 10.1103/PhysRevC.94.024320 [37] Qian Y B, Ren Z Z 2012 Phys. Rev. C 85 027306 doi: 10.1103/PhysRevC.85.027306 [38] Sahu B, Paira R, Rath B 2013 Nucl. Phys. A 908 40 doi: 10.1016/j.nuclphysa.2013.04.002 [39] Akrawy D T, Ahmed A H 2019 Phys. Rev. C 100 044618 doi: 10.1103/PhysRevC.100.044618 [40] Xing F Z, Qi H, Cui J P, Gao Y H, Wang Y Z, Gu J Z, Yong G C 2022 Nucl. Phys. A 1028 122528 doi: 10.1016/j.nuclphysa.2022.122528 [41] Balasubramaniam M, Gupta Raj K 1999 Phys. Rev. C 60 064316 doi: 10.1103/PhysRevC.60.064316 [42] Santhosh K P, Biju R K 2009 J. Phys. G. Nucl. Part. Phys. 36 015107 doi: 10.1088/0954-3899/36/1/015107 [43] Balasubramaniam M, Arunachaiam N 2005 Phys. Rev. C 71 014603 doi: 10.1103/PhysRevC.71.014603 [44] Dong J M, Zhang H F, Zuo W, Li J Q 2010 Chin. Phys. C 34 182 doi: 10.1088/1674-1137/34/2/005 [45] Dong J M, Zhang H F, Li J Q, Scheid W 2009 Eur. Phys. J. A 41 197 doi: 10.1140/epja/i2009-10819-1 [46] Zhu T B, Hu B T, Zhang H F, Dong J M, Li Q J 2011 Commun. Theor. Phys. 55 307 doi: 10.1088/0253-6102/55/2/20 [47] Xing F Z, Cui J P, Wang Y Z, Gu J Z 2021 Chin. Phys. C 45 124105 doi: 10.1088/1674-1137/ac2425 [48] Santhosh K P 2022 Phys. Rev. C 106 054604 doi: 10.1103/PhysRevC.106.054604 [49] Zhu D X, Liu H M, Xu Y Y, Zou Y T, Wu X J, Chu P C, Li X H 2022 Chin. Phys. C 46 044106 doi: 10.1088/1674-1137/ac45ef [50] Zhu D X, Li M, Xu Y Y, Wu X J, He B, Li X H 2022 Phys. Scr. 97 095304 doi: 10.1088/1402-4896/ac8585 [51] Zhang H F, Royer G 2008 Phys. Rev. C 77 054318 doi: 10.1103/PhysRevC.77.054318 [52] Cui J P, Gao Y H, Wang Y Z, Gu J Z 2020 Phys. Rev. C 101 014301 doi: 10.1103/PhysRevC.101.014301 [53] Zhang S, Zhang Y L, Cui J P, Wang Y Z 2017 Phys. Rev. C 95 014311 doi: 10.1103/PhysRevC.95.014311 [54] Santhosh K P, Jose T A 2021 Phys. Rev. C 104 064604 doi: 10.1103/PhysRevC.104.064604 [55] 邢凤竹, 崔建坡, 王艳召, 顾建中 2022 物理学报 71 062301 doi: 10.7498/aps.71.20211839 Xing F Z, Cui J P, Wang Y Z, Gu J Z 2022 Acta. Phys. Sin. 71 062301 doi: 10.7498/aps.71.20211839 [56] Wang Y Z, Xing F Z, Cui J P, Gao Y H, Gu J Z 2023 Chin. Phys. C 47 084101 doi: 10.1088/1674-1137/acd680 [57] Qi L J, Zhang D M, Luo S, Zhang G Q, Chu P C, Wu X J, Li X H 2023 Phys. Rev. C 108 014325 doi: 10.1103/PhysRevC.108.014325 [58] Chandran Megha, Santhosh K P 2023 Phys. Rev. C 107 024614 doi: 10.1103/PhysRevC.107.024614 [59] Wang Y Z, Xing F Z, Zhang W H, Cui J Z, Gu J P 2024 Phys. Rev. C 110 064305 doi: 10.1103/PhysRevC.110.064305 [60] Nakada H, Sugiura K 2014 Prog. Theor. Exp. Phys. 2014 033D02 [61] Thakur S, Kumar S, Kumar R 2013 Braz. J. Phys. 43 152 doi: 10.1007/s13538-013-0127-0 [62] Mo Q H, Liu M, Wang N 2014 Phys. Rev. C 90 024320 doi: 10.1103/PhysRevC.90.024320 [63] Brewer N T, Utyonkov V K, Rykaczewski K P, Oganessian Y T, Abdullin F S, Boll R A, Dean D J, Dmitriev S N, Ezold J G, Felker L K, Grzywacz R K, Itkis M G, Kovrizhnykh N D, McInturff D C, Miernik K, Owen G D, Polyakov A N, Popeko A G, Roberto J B, Sabel'nikov A V, Sagaidak R N, Shirokovsky I V, Shumeiko M V, Sims N J, Smith E H, Subbotin V G, Sukhov A M, Svirikhin A I, Tsyganov Y S, Van Cleve S M, Voinov A A, Vostokin G K, White C S, Hamilton J H, Stoyer M A 2018 Phys. Rev. C 98 024317 doi: 10.1103/PhysRevC.98.024317 [64] Bao X J 2019 Phys. Rev. C 100 011601(R [65] Sobiczewski A 2016 Phys. Rev. C 94 051302(R [66] Mohr P 2017 Phys. Rev. C 95 011302(R [67] Santhosh K P, Jost T A, Deepak N K 2021 Phys. Rev. C 103 064612 doi: 10.1103/PhysRevC.103.064612 [68] Nithya C, Santhosh K P 2023 Phys. Rev. C 108 014606 doi: 10.1103/PhysRevC.108.014606 [69] Blocki J, Randruo J, Swiatecki W J, Tsang C F 1977 Ann. Phys. 105 427 doi: 10.1016/0003-4916(77)90249-4 [70] Bass R 1973 Phys. Lett. B 47 139 doi: 10.1016/0370-2693(73)90590-X [71] Bass R 1974 Nucl. Phys. A 231 45 doi: 10.1016/0375-9474(74)90292-9 [72] Bass R 1977 Phys. Rev. Lett. 39 265 [73] Reisdorf W 1994 J. Phys. G: Nucl. Part. Phys. 20 1297 doi: 10.1088/0954-3899/20/9/004 [74] Winther A 1995 Nucl. Phys. A 594 203 doi: 10.1016/0375-9474(95)00374-A [75] Wong C Y 1973 Phys. Rev. Lett. 31 766 doi: 10.1103/PhysRevLett.31.766 [76] Wang M, Huang J W, Kondev F G, Audi G, Naimi S 2021 Chin. Phys. C 45 030003 doi: 10.1088/1674-1137/abddaf [77] Kondev F G, Wang M, Huang J W, Naimi S, Audi G 2021 Chin. Phys. C 45 030001 doi: 10.1088/1674-1137/abddae [78] Möller P, Nix J R, Myers W D, Swiatecki W J 1995 At. Data Nucl. Data Tables 59 185 doi: 10.1006/adnd.1995.1002 [79] Möller P, Sierk A J, Ichikawa T, Sagawa H 2016 At. Data Nucl. Data Tables 109–110 1 doi: 10.1016/j.adt.2015.10.002 [80] Wang N, Liu M, Wu X Z, Meng J 2014 Phys. Lett. B 734 215 doi: 10.1016/j.physletb.2014.05.049 [81] Koura H, Tachibana T, Uno M, Yamada M 2005 Prog. Theor. Phys. 113 305 doi: 10.1143/PTP.113.305 [82] Kirson M W 2008 Nuclear Phys. A 798 29 doi: 10.1016/j.nuclphysa.2007.10.011 [83] Bhagwat A 2014 Phys. Rev. C 90 064306 doi: 10.1103/PhysRevC.90.064306 [84] Goriely S 2015 Nucl. Phys. A 933 68 doi: 10.1016/j.nuclphysa.2014.09.045 [85] Zhang K Y, Cheoun M K, Choi Y B, Pooi S C, Dong J M, Dong Z H, Du X K, Geng L S, Ha E, He X T, Heo C, Ho M C, In E J, Kim S, Kim Y, Lee C H, Lee J, Li H X, Li Z P, Luo T P, Meng J, Mun M H, Niu Z M, Pan C, Papakonstantinou P, Shang X L, Shen C W, Shen G F, Sun W, Sun X X, Tam C K, Wang C, Wang X Z, Wong S H, Wu J W, Wu X H, Xia X W, Yan Y J, Yeung R W Y, Yiu T C, Zhang S Q, Zhang W, Zhang X Y, Zhao Q, Zhou S G 2022 At. Data Nucl. Data Tables 144 101488 doi: 10.1016/j.adt.2022.101488 [86] Wang Y Z, Wang S J, Hou Z Y, Gu J Z 2015 Phys. Rev. C 92 064301 doi: 10.1103/PhysRevC.92.064301 [87] Swiatecki W J 1955 Phys. Rev. J. 100 937 doi: 10.1103/PhysRev.100.937 [88] Xu C, Ren Z Z 2005 Phys. Rev. C 71 014309 doi: 10.1103/PhysRevC.71.014309 [89] Ren Z Z, Xu C 2005 Nucl. Phys. A 759 64 doi: 10.1016/j.nuclphysa.2005.04.019 [90] Bao X J, Guo S Q, Zhang H F 2015 J. Phys. G. Nucl. Part. Phys. 42 085101 doi: 10.1088/0954-3899/42/8/085101 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: