-
拓扑绝缘体作为近年来迅速发展的研究领域, 其核心概念在于由拓扑不变量预测的拓扑态[1-5]. 在传统框架下, 受到保护的拓扑态在边界处聚集, 而体态则在整个系统中扩展[3]. 然而, 非厄米项的引入可能会颠覆这种局域化行为[6-35]. 具体地, 非厄米性会促使大量体本征态聚集在体系边界处, 被称为非厄米趋肤效应[36-53]. 有趣的是, 拓扑边缘态在边界处却可能会去局域化[54-56].
准无序是凝聚态物理学中的另一个核心概念, 它通常引起安德森局域化, 即波函数可以局域在系统的任意位置, 而不仅仅是在边界处. 现有研究表明, 非厄米性与准无序的结合能催生一系列新颖的物理现象[57-80]. 例如, 文献[62]表明零能模式仅位于链的一端. 局域化转变可以与PT对称性紧密相 关[63]. 为了精确衡量系统的局域化特性, 研究者们引入了逆参与率和归一化参与率等概念[81,82]. 然而, 以往的研究通常将系统视为整体进行分析研究. 我们发现通过将系统严格划分为不同部分(体态与边缘态), 可以揭示更多有趣的局域化现象.
本文构造了一个非厄米准周期项位于非对角位置的Su-Schrieffer-Heeger (SSH)模型, 分别探索体态和边缘态的局域化性质. 体态将经历二次局域化转变, 同时边缘态经历出现-消失-再出现的转变. 此外, 在局域化转变点处, 归一化参与率的导数出现了明显的突变. 本文的工作为理解系统局域化现象提供了新的视角.
-
考虑一个广义的SSH模型, 其哈密顿量为
这里,
$ t_{1} $ 和$ t_{2} $ 分别代表原胞内部和原胞间的跃迁幅度; 符号[·]表示取整; γ为非厄米参数;$ \beta = ({\sqrt5 - 1})/{2} $ 表征准周期;$ W_{1} $ 和$ W_{2} $ 是准周期强度. 准周期项出现在哈密顿量的非对角位置, 这确保系统具有子晶格对称性:$ {\boldsymbol{C}}H{\boldsymbol{C}}^{-1} = -H $ , 其中$ {\boldsymbol{C}} = {\mathrm{diag}}(1, -1, 1, -1, \cdots, 1, -1) $ . 因此, 该系统的拓扑性质可以由缠绕数和零模来刻画. 实空间的拓扑数定义为[83-85]其中X代表位置坐标;
$ Q = \displaystyle\sum\nolimits_{n}(|\varPsi^{(n)R}\rangle \langle\varPsi^{(n)L}|- {\boldsymbol{C}}|\varPsi^{(n)R}\rangle \langle\varPsi^{(n)L}|{\boldsymbol{C}}^{-1}) $ ,$ |\varPsi^{(n)R}\rangle $ 和$ |\varPsi^{(n)L}\rangle $ 分别由$ H|\varPsi^{(n)R}\rangle = E_{n}|\varPsi^{(n)R}\rangle $ 和$ H^{\dagger}|\varPsi^{(n)L}\rangle = E_{n}^{*}|\varPsi^{(n)L}\rangle $ 得到; 链长$ L = 2 N $ 被分为三部分, 长度分别为l,$ L' $ 和l, 即$ 2 l+L' = L $ ,${\mathrm{ Tr}}' $ 代表仅仅对中间长度为$ L' $ 的链求迹, 为了使得μ为整数, L和l的取值都必须足够大.在系统尺寸较大时, 波函数的局域化性质可以由逆参与率 (IPR) 和归一化参与率 (NPR) 描述[81,82,86,87]. 系统含有非厄米项将导致
$ \big||\varPsi^{(n)R}\rangle \big| \neq \big||\varPsi^{(n)L}\rangle\big| $ . 因此, 波函数的局域化性质应当由下式描述:和
本文工作的核心为独立地探索体态与边缘态的局域化性质, 因此可以定义如下表达式:
其中S表示链的长度. 在拓扑非平庸区域,
$ S = L-2 $ , 其中2代表零能边缘态的数目, 而体态数目为$ L-2 $ . 在拓扑平庸区域, 则有$ S = L $ . 与IPR和NPR类似,${\rm{IPR}} ^{{\mathrm{Bulk}}} $ 和${\rm{NPR}} ^{{\mathrm{Bulk}}} $ 也是用来分析系统波函数的局域化性质的. 定量地说,${\rm{IPR}} ^{{\mathrm{Bulk}}} = 0 $ $ (\neq0) $ 和${\rm{NPR}} ^{{\mathrm{Bulk}}}\neq0 $ $ ( = 0) $ 表明了体态的扩展(局域)性质. 从定义可以看出,${\rm{IPR}} ^{{\mathrm{Bulk}}} $ 和${\rm{NPR}} ^{{\mathrm{Bulk}}} $ 的结果可能会受到系统尺寸的影响. 因此, 为了避免有限尺寸效应, 这里尽可能选择大系统尺寸. 另外,${\rm{IPR}} ^{{\mathrm{Bulk}}} $ 和${\rm{NPR}} ^{{\mathrm{Bulk}}} $ 均不为零时代表着体态为共存态, 即一些本征态是扩展的, 同时一些本征态是局域的. 为了方便讨论, 将${\rm{IPR}} ^{{\mathrm{Bulk}}} $ 和${\rm{NPR}} ^{{\mathrm{Bulk}}} $ 分别简记为${\rm{IPR}} ^{{\mathrm{B}}} $ 和${\rm{NPR}} ^{{\mathrm{B}}} $ .同时, 绝对值最小的能量值对应的波函数的局域化性质可以由
${\rm{IPR}} ^{{\mathrm{Edge}}} $ 和${\rm{NPR}} ^{{\mathrm{Edge}}} $ (简记为${\rm{IPR}} ^{0} $ 和${\rm{NPR}} ^{0} $ ) 描述: -
基于上面的讨论, 本节分别探索体态和边缘态的局域化性质和拓扑特性.
-
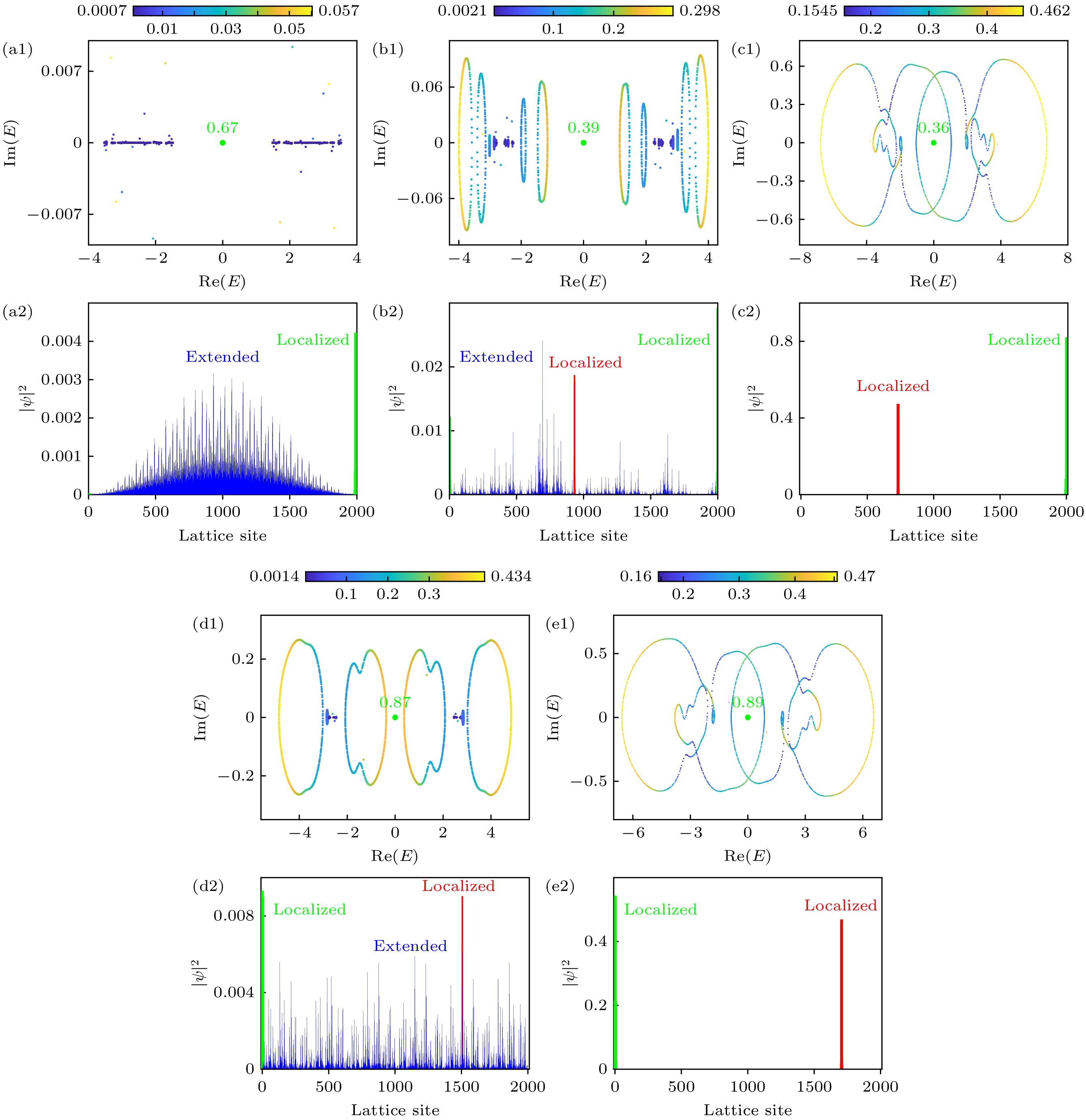
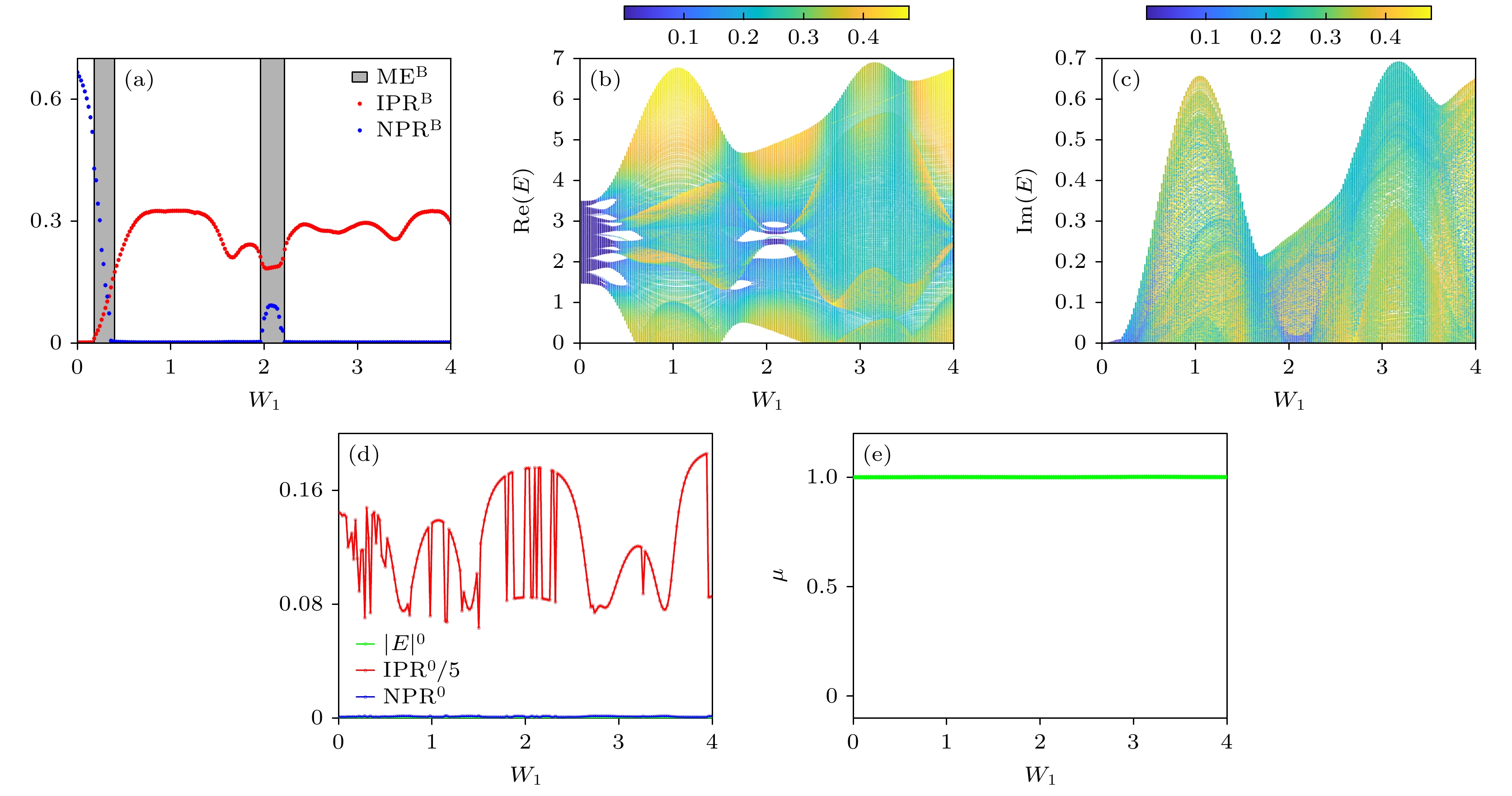
图1(a)清晰展示了体态的
${\rm{IPR}} ^{{\mathrm{B}}} $ (红色星号组成的曲线)和${\rm{NPR}} ^{{\mathrm{B}}} $ (蓝色星号组成的曲线)的演变.${\rm{IPR}} ^{{\mathrm{B}}} $ 和${\rm{NPR}} ^{{\mathrm{B}}} $ 在灰色区域内同时非零, 表明局域态和扩展态在体中共存. 根据文献[81, 82]的标记方法, 我们将此区域称为ME$ ^{{\mathrm{B}}} $ . 图1(b)和图1(c)展示了${\rm{IPR}} ^{|\varPsi^{n}\rangle} $ 标记的体能谱, 其中${\rm{IPR}} ^{|\varPsi^{n}\rangle} $ 的值直接反映了对应体本征态的局域化程度. 注意到子晶格对称性对系统的限制:${\rm{IPR}} ^{|\varPsi^{n}\rangle} $ =${\rm{IPR}} ^{{\boldsymbol{C}}|\varPsi^{n}\rangle} $ 和${\rm{NPR}} ^{|\varPsi^{n}\rangle} $ =${\rm{NPR}} ^{{\boldsymbol{C}}|\varPsi^{n}\rangle} $ , 我们只需关注复平面上半部分的能谱. 图1(b)通过颜色渐变揭示了体态的演变规律: 当$ 0 < W_{1} < 0.18 $ 时, 体态均为扩展态. 在$ 0.18 < W_{1} < 0.38 $ 时, 能谱的附着色逐渐过渡到青色, 这意味着越来越多的扩展态转变为局域态, 同时也说明了在该区域内体态为扩展与局域共存. 直到$ W_{1} = 0.38 $ , 体态全转变为局域态. 尤为值得注意的是, 当$ 1.96 < W_{1} < 2.22 $ 时, 部分局域态会再次转变为扩展态, 也就说体态再一次扩展与局域共存. 然而随着$ W_{1} $ 进一步增大到$ W_{1} > 2.22 $ , 所有体态最终再次全部转变为局域态. 有趣的是, 第二次呈现扩展状态的本征态数目很少, 这也可以用体能谱的虚部反映 (图1(c)). 这些分析表明准无序会诱导体态经历扩展-共存-局域-共存-局域的转变. 图1(d)探索了边缘态的局域化性质, 其中零模在整个参数范围内始终存在, 即系统处于拓扑非平庸的状态(图1(e)). 从另外一个角度分析,${\rm{IPR}} ^{0}\neq0 $ 和${\rm{NPR}} ^{0} = 0 $ 始终成立, 这同样意味着对应的本征态是局域的. 值得注意的是,${\rm{IPR}} ^{0} $ 的振荡行为揭示了即使每个零模都在边界处局域, 但局域化程度却大相径庭, 且与准无序强度并非正相关.接下来, 图2详细展示了体态和边缘态的局域化行为. 图2(a1)—(e1)给出了体能量值和对应的
${\rm{IPR}} ^{n} $ , 其中绿点特指零能模式$ |E|^{0} $ , 相关数字为${\rm{IPR}} ^{0} $ 的值. 为了直观地呈现系统的各种局域化现象, 图2(a2)—(e2)给出了波函数(包括体和边缘) 的空间分布. 当$ W_{1} = 0.15 $ 时, 图2(a1)和图2(a2)显示${\rm{IPR}} ^{{\mathrm{B}}} $ 的值很小, 表明此时的本征态是扩展态. 当准无序增加到$ W_{1} = 0.35 $ 时, 图2(b1)和图2(b2)表明${\rm{IPR}} ^{{\mathrm{B}}} $ 的范围从零到有限值, 反映出体态为扩展态与局域态共存. 当准无序强度增大到$ W_{1} = 1 $ 时, 图2(c1)和图2(c2)表明${\rm{IPR}} ^{{\mathrm{B}}} $ 为有限值, 那么这时体态全部为局域态. 再进一步, 图2(d1)和图2(d2)表明当$ W_{1} = 2.02 $ 时, 体态会再一次成为共存态. 最后, 当$ W_{1} = 3.8 $ 时, 图2(e1)和图2(e2)表明所有的体态再一次转变为局域态.正如以上讨论, 准无序会导致体态经历扩展-共存-局域-共存-局域的转变. 也就是说, 通过改变准无序强度, 可以诱导体态出现二次局域的现象. 接下来考虑非厄米项对局域化性质的影响.
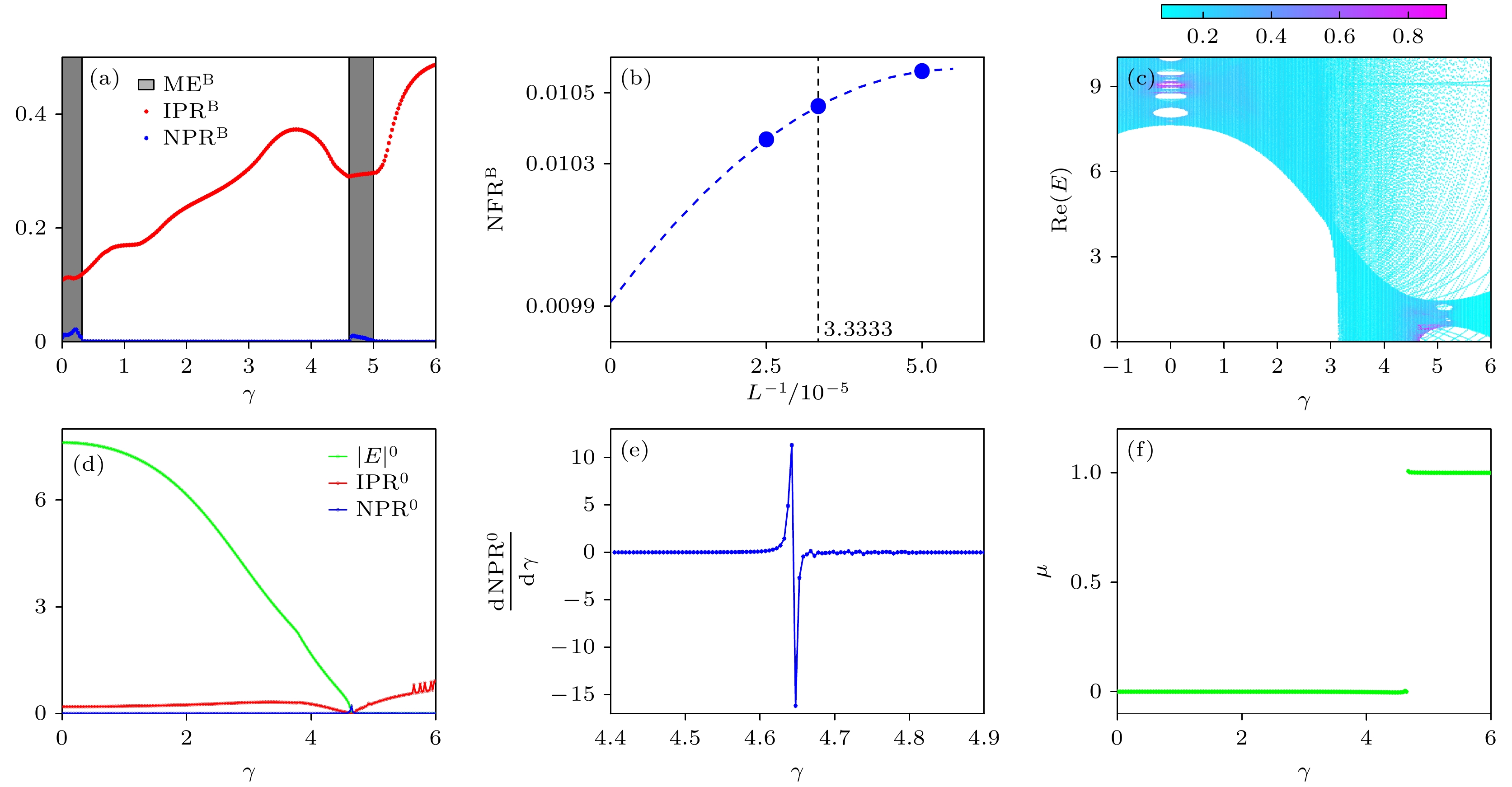
图3(a)展示了
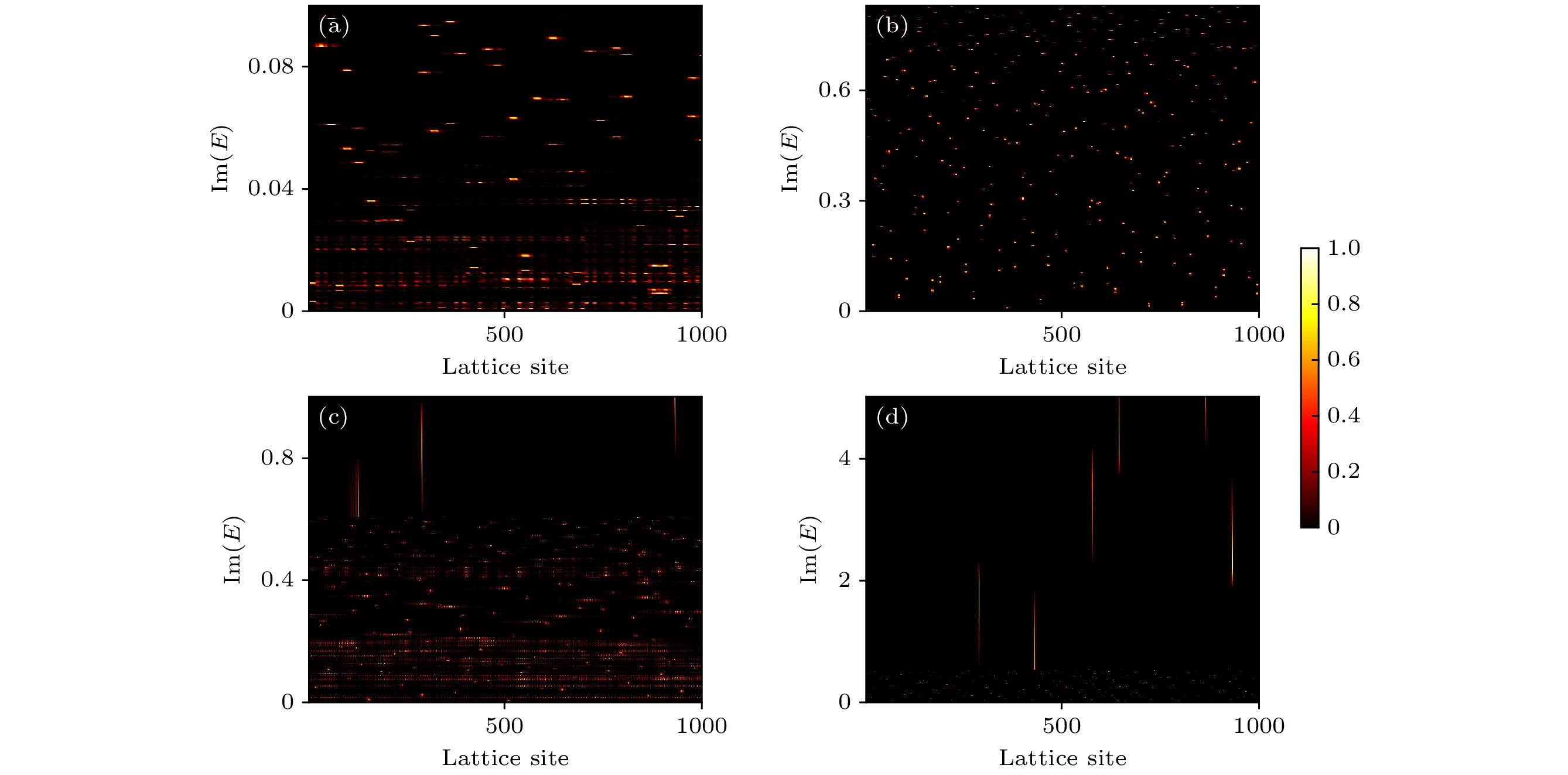
${\rm{IPR}} ^{{\mathrm{B}}} $ 和${\rm{NPR}} ^{{\mathrm{B}}} $ 随γ的变化趋势. 显然, 存在两个${\rm{NPR}} ^{{\mathrm{B}}} $ 不为零的区域, 即通过改变非厄米参数, 体态呈现两个临界区间($ \gamma\in $ [0, 0.32], [4.61, 5]). 注意到在第二个临界区域中${\rm{NPR}} ^{{\mathrm{B}}} $ 的值很小, 为排除有限尺寸效应, 图3(b)给出了$ L = 20000 $ ,$ 30000 $ 和$ 40000 $ 时${\rm{NPR}} ^{{\mathrm{B}}} $ 在$ \gamma = 4.66946 $ 的值. 显然,${\rm{NPR}} ^{{\mathrm{B}}} $ 在热力学极限下确实不为零. 本征态的局域化转变行为也可以通过它的分形维度η进行阐明, 其定义为$ \eta^{|\varPsi^{n}\rangle} = -\dfrac{{\mathrm{log}}({\mathrm{IPR}}^{|\varPsi^{n}\rangle})}{{\mathrm{log}}(L)} $ [86,88]. 从图3(c)可以看到, 紫色和青色相互交织, 即$ \gamma\in[0, 0.32] $ 时$ \eta\approx 0 $ 和$ \eta\approx 1 $ 同时出现, 说明体态是局域和扩展共存. 此外, 能谱的附着色表明当$ 0.32 < \gamma < 4.61 $ 时$ \eta \approx 0 $ , 即所有体态都是局域化的. 令人惊讶的是, 当γ增加到$ 4.61 < \gamma < 5 $ 区域时, 一些扩展的体态再次出现, 表明体再次进入共存状态. 最终, 所有的体态都转化为局域态. 即非厄米效应将导致体态经历共存-局域-共存-局域的转变. 另外, 图3(d)给出了绝对值最小的能量值对应的波函数的局域化现象. 显然, 无论系统是处于拓扑平庸还是非平庸, 波函数都是局域的, 唯一的例外出现在局域化转变点处, 或者说在拓扑相变点处. 可以看出${\rm{NPR}} ^{0} $ 在相变点附近的变化范围很小. 为了更清晰地确定该变化, 图3(e)给出了系统尺寸$ L = 12000 $ 时${\rm{NPR}} ^{0} $ 的导数, 可以发现在上述相变点处存在一个明显的突变. 此外, 图3(f)展示了系统的缠绕数, 其拓扑相变点和图3(d)能谱的变化一致.为了直观展现非厄米诱导的各种局域化现象, 图4给出了与所有体本征值相对应的归一化本征态. 图4(a)显示当
$ \gamma = 0.2 $ 时, 部分体态在开链中扩展, 而另一些本征态则在某些位置局域. 进一步观察图4(b), 可以发现随着γ的增大, 原先扩展的体态逐渐转变为局域态. 当非厄米值继续增加时, 一些局域态再次回到图4(c)中的扩展态. 然而, 如图4(d)所示, 随着非厄米值的进一步增大, 这些扩展的本征态最终将永远转化为局域态. 因此, 非厄米参数也会导致体态出现二次局域现象. -
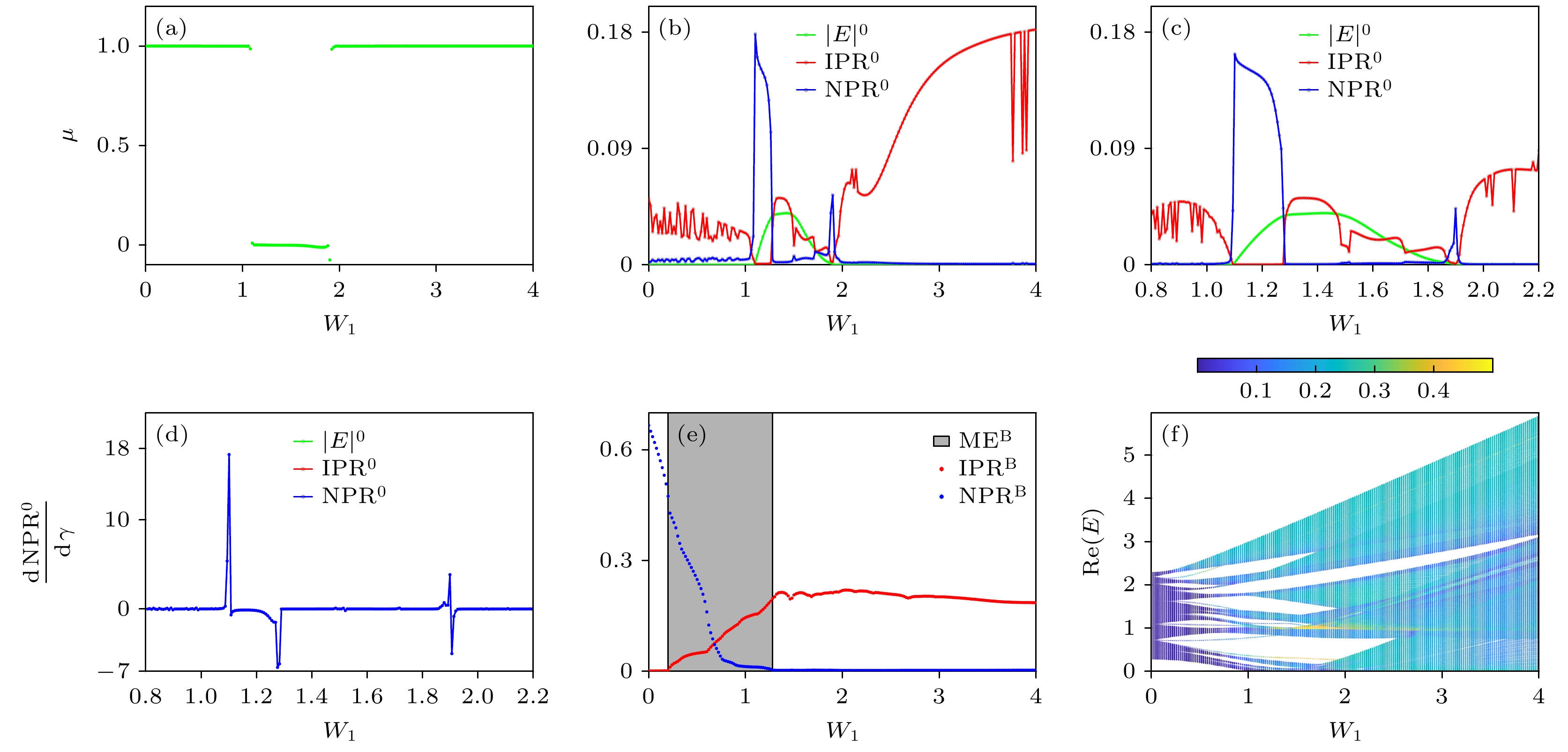
为了准确地探索边缘态的局域化特性, 图5(a)给出系统的相图并讨论边缘的局域化性质. 图5(b)及图5(c)中以
$ W_{1} $ 为自变量展示了${\rm{IPR}} ^{0} $ 和${\rm{NPR}} ^{0} $ 的变化趋势. 当$ W_{1} = 0 $ 时,${\rm{IPR}} ^{0}\neq0 $ 和${\rm{NPR}} ^{0} = 0 $ 意味对应的态是局域的[3]. 进一步, 如图5(c) 所示, 在$ W_{1} = 1.09 $ 处,${\rm{IPR}} ^{0} $ 骤降至零而${\rm{NPR}} ^{0} $ 跃升至非零值, 这一突变标志着本征态发生了剧烈的局域化转变. 同时, 拓扑零能模式在$ W_{1} = 1.09 $ 处消失, 即在该点发生了拓扑相变. 出乎意料的是, 即使在$ 1.09 < W_{1} < 1.905 $ 的拓扑平庸区域中, 本征态在$ W_{1} = 1.276 $ 附近也会经历从${\rm{IPR}} ^{0} = 0 $ 和${\rm{NPR}} ^{0}\neq0 $ 到${\rm{IPR}} ^{0}\neq0 $ 和${\rm{NPR}} ^{0} = 0 $ 的局域化转变, 即从扩展态转变到局域态. 另外, 当准无序强度在$ W_{1} = 1.905 $ 附近时,${\rm{NPR}} ^{0} $ 会经历零-非零-零的变化过程, 同时${\rm{IPR}} ^{0} $ 经历非零-零-非零的波动, 表明此时本征态发生了局域化转变. 同时, 绝对值最小的能量值再次变为零, 意味着在$ W_{1} = 1.905 $ 处系统发生了拓扑相变.图5(d)清晰地展示出在局域化转变点,
${\rm{NPR}} ^{0} $ 从零转变到非零, 反之亦然. 注意到当$ W_{1}\in[0, 4] $ 时,$ \max[{\mathrm{NPR}}^{0}]\approx0.17 $ , 即${\rm{NPR}} ^{0} $ 的变化幅度较小. 为了更精确地描述转变点, 图5(f)给出了数值计算的${\rm{NPR}} ^{0} $ 对$ W_{1} $ 的导数. 对比图5(d)和图5(c)可以发现, 在局域化转变处,$ \dfrac{{\mathrm{dNPR}}^{0}}{{\mathrm{dW }}{1}} $ 呈现出非常尖锐的峰值, 其形态与δ函数相似. 这提供了一个更加明确的指标来识别并定位局域化转变点.对于体态, 图5(e)清晰地描绘了
${\rm{IPR}} ^{{\mathrm{B}}} $ (红色星号构成的曲线)和${\rm{NPR}} ^{{\mathrm{B}}} $ (蓝色星号构成的曲线)的演变过程. 显然,${\rm{IPR}} ^{{\mathrm{B}}} $ 和${\rm{NPR}} ^{{\mathrm{B}}} $ 在$ 0.2 < W_{1} < 1.28 $ 范围内同时非零, 这明确指出局域态和扩展态在体中共存. 此外, 图5(f)展示了${\rm{IPR}} ^{|\varPsi^{n}\rangle} $ 标记的体能谱. 当$ W_{1} = 0 $ 时, 系统退化为具有非平庸拓扑相的SSH系统(如图5(a)所示$ \mu = 1 $ ), 体态呈现为扩展态[3]. 在准无序大小达到$ W_{1} = 0.2 $ 之前, 体态一直保持为扩展态. 但是当$ W_{1} $ 从0.2增加到1.28时, 可以观察到越来越多的扩展态转变为局域态, 这再次印证了扩展态与局域态可以在体态共存. 最终当$ W_{1} > 1.28 $ 时, 附着在能谱的深蓝色完全消失, 标志着所有的体态都转变为局域态. -
基于准周期非厄米系统, 对体态和边缘态的局域化性质进行了详尽的分析. 结果表明, 体态可以具有二次局域化现象, 即准无序诱导的扩展-共存-局域-共存-局域转变, 或非厄米诱导的共存-局域-共存-局域转变. 随着准无序强度的增加, 拓扑边缘态会消失并重新出现, 并且拓扑相变点与边缘状态的局域化转变点相对应. 此外, 归一化参与率的导数也在这些转变点出现了明显的不连续变化.
虽然本文仅以(1)式中的简单哈密顿量为例, 但分析过程(拓扑不变量的定义, 体态和边缘态的单独讨论)和结果可以自然地推广到具有子晶格对称框架下的其他系统. 此外, 许多实验方案和技术已经被提出用于产生非厄米和准无序[89-94], 因此我们的系统可以在一些人工系统中得以实现. 本文采用的方法有助于加深对系统局域化行为的理解.
非厄米准周期系统中的二次局域体态和局域-扩展的边缘态
Reentrant localized bulk and localized-extended edge in quasiperiodic non-Hermitian systems
-
摘要: 局域化是物理学中一个基础且极具潜力的研究领域. 基于广义Su-Schrieffer-Heeger模型, 本文针对其非厄米项以准周期、非对角形式出现的特点, 提出了一种新的分析框架, 旨在分别探讨体态与边缘态的局域化特性. 对于体态, 它可以经历由准无序诱导的扩展-共存-局域-共存-局域的转变, 或者是由非厄米特性引起的共存-局域-共存-局域的转变. 同时边缘态可以被破坏和恢复, 且其拓扑相变与局域化转变完全同步. 最后, 发现在局域化转变点处归一化参与率的导数展现出明显的不连续性. 本文的结果不仅展示了体态和边缘态局域化性质的多样性, 而且为局域化研究开辟了一个新的研究视角.Abstract:
The localization is one of the active and fundamental research areas in topology physics. In this field, a comprehensive understanding of how wave functions distribute within a system is crucial. This work delves into this topic by proposing a novel systematic method based on a generalized Su-Schrieffer-Heeger (SSH) model. This model incorporates a quasiperiodic non-Hermitian term that appears at an off-diagonal position, adding a layer of complexity to the traditional SSH framework. By utilizing this model, we analyze the localization behaviors of both bulk state and edge state. For the bulk states, the analysis reveals a fascinating transition sequence. Specifically, the bulk states can undergo an extended-coexisting-localized-coexisting-localized transition, which is induced by the introduction of quasidisorder. This transition is not arbitrary but is rather conformed by the inverse participation ratio (IPR), a metric that quantifies the degree of localization of a wave function. As quasidisorder increases, the bulk states initially remain extended, but gradually, some states begin to be localized. A coexistence region appears where both extended and localized states are present. Further increase in quasidisorder leads to a complete localization of all bulk states. However, remarkably, within a certain range of quasidisorder strengths, the localized states can once again transition back to an extended state, creating another coexistence region. This complex behavior demonstrates the rich and diverse localization properties of the bulk states in non-Hermitian quasiperiodic systems. In addition to the IPR, other metrics such as the normalized participation ratio (NPR) and the fractal dimension of the eigenstates also play important roles in characterizing the localization behavior. These metrics provide a more in-depth understanding of the transition process and help to confirm the existence of the coexistence regions. Overall, we comprehensively analyze the localization behaviors of bulk and edge states in non-Hermitian quasiperiodic systems based on a generalized SSH model. The proposed systematic method present new insights into the complex interplay between quasidisorder, non-Hermiticity, and localization properties in topological physics. -
Key words:
- non-Hermitian /
- quasidisorder /
- reentrant-localized /
- topological phase transition .
-

-
图 1 (a)
${\rm{IPR}} ^{{\mathrm{B}}} $ (红)和${\rm{NPR}} ^{{\mathrm{B}}} $ (蓝)随$ W_{1} $ 的变化, 灰色区域代表共存状态; (b), (c)体能谱的实部和虚部, 附着色代表本征态 的${\rm{IPR}} ^{|\varPsi^{n}\rangle} $ 值; (d)拓扑零能$ |E|^{0} $ 与对应的$ {\text{IPR}^{0}}/{5} $ 和${\rm{NPR}} ^{0} $ ; (e)拓扑不变量. 参数为$ t_{1} = 1 $ ,$ t_{2} = 2.5 $ ,$ \gamma = 0.2 $ ,$ L = 2000 $ 和$ W_{2} = -2\cos(3 W_{1})+2 $ Figure 1. (a)
${\rm{IPR}} ^{{\mathrm{B}}} $ (red) and${\rm{NPR}} ^{{\mathrm{B}}} $ (blue) versus$ W_{1} $ , the shaded regions stand for coexisting regimes; (b), (c) real and imaginary parts of bulk energy spectrum, where the dressed colors stand for different values of${\rm{IPR}} ^{|\varPsi^{n}\rangle} $ for each bulk eigenstates; (d) topological edge modes$ |E|^{0} $ , accompanied by the corresponding$ {\text{IPR}^{0}}/{5} $ and${\rm{NPR}} ^{0} $ ; (e) topological invariant as a function of$ W_{1} $ . Common parameters are$ t_{1} = 1 $ ,$ t_{2} = 2.5 $ ,$ \gamma = 0.2 $ ,$ L = 2000 $ and$ W_{2} = -2\cos(3 W_{1})+2 $ .图 2 (a1)—(e1)复平面能谱及其
${\rm{IPR}} ^{|\varPsi^{n}\rangle} $ ; (a2)—(e2)蓝色和红色曲线代表一些体态的局域性质, 绿色条代表边缘态的局域性质. 为了显示清楚, 这些物理量已按比例缩放. (a1), (a2)$ W_{1} = 0.15 $ , 所有体态均为扩展态; (b1), (b2)$ W_{1} = 0.35 $ , 一些态仍为扩展态, 但一些态转为局域态; (c1), (c2)$ W_{1} = 1 $ , 所有的体态均转变为局域态; (d1), (d2)$ W_{1} = 2.02 $ , 部分已经局域的本征态会再转变为扩展态; (e1), (e2)$ W_{1} = 3.8 $ , 所有的体态再次全部转变为局域态. 其他参数和图1取值一致Figure 2. (a1)–(e1) Energy spectrum on the complex plane with corresponding
${\rm{IPR}} ^{|\varPsi^{n}\rangle} $ ; (a2)–(e2) both the blue and red lines stand for the localized properties of some bulk eigenstates, and the zero-energy state is shown as the green bar. For a better visibility, the values have been scaled proportionally. (a1), (a2)$ W_{1} = 0.15 $ , all bulk eigenstates are extended; (b1), (b2)$ W_{1} = 0.35 $ , some eigenstates are still extended while some are localized; (c1), (c2)$ W_{1} = 1 $ , all bulk eigenstates are transformed into localized; (d1), (d2)$ W_{1} = 2.02 $ , some already localized states will change into extended; (e1)–(e2)$ W_{1} = 3.8 $ , all bulk eigenstates are transformed into localized again. Other parameters are the same as the ones in Fig. 1.图 3 (a)
$ L = 12000 $ , 随着γ变化的${\rm{IPR}} ^{{\mathrm{B}}} $ (红)和${\rm{NPR}} ^{{\mathrm{B}}} $ (蓝), 两个灰色区域代表共存状态; (b)$ \gamma = 4.66946 $ ,${\rm{NPR}} ^{{\mathrm{B}}} $ 的有限尺寸效应分析, 系统尺寸分别为$ L = 20000 $ ,$ 30000 $ 和$ 40000 $ ; (c)体能谱实部, 不同附着色代表$ \eta^{|\varPsi^{n}\rangle} $ 的不同取值,$ L = 6000 $ ; (d)$ |E|^{0} $ 与对应的${\rm{IPR}} ^{0} $ 和${\rm{NPR}} ^{0} $ 随着γ的变化趋势,$ L = 2000 $ ; (e)系统尺寸$ L = 12000 $ 时${\rm{NPR}} ^{0} $ 对γ的导数; (f)拓扑不变量随参数γ的变化趋势,$ L = 2000 $ . 其他参数为$ t_{1} = 9 $ ,$ t_{2} = 1 $ ,$ W_{1} = 0.0039 $ 和$ W_{2} = 1.563 $ Figure 3. (a)
$ L = 12000 $ ,${\rm{IPR}} ^{{\mathrm{B}}} $ (red) and${\rm{NPR}} ^{{\mathrm{B}}} $ (blue) evolving with γ, the two shaded regions stand for intermediate regimes; (b) finite size scaling analysis of${\rm{NPR}} ^{{\mathrm{B}}} $ at$ \gamma = 4.66946 $ for$ L = 20000 $ ,$ 30000 $ and$ 40000 $ , respectively; (c) real parts of bulk energy spectrum for$ L = 6000 $ , where different colors stand for different values of$ \eta^{|\varPsi^{n}\rangle} $ ; (d) evolution of$ |E|^{0} $ versus γ associated with${\rm{IPR}} ^{0} $ and${\rm{NPR}} ^{0} $ ,$ L = 2000 $ ; (e) derivative of${\rm{NPR}} ^{0} $ with respect to γ for$ L = 12000 $ ; (f) topological invariant versus parameter γ for$ L = 2000 $ . Common parameters are$ t_{1} = 9 $ ,$ t_{2} = 1 $ ,$ W_{1} = 0.0039 $ and$ W_{2} = 1.563 $ .图 4 所有归一化体态的空间分布. 为了表示清楚, 系统尺寸取
$ L = 1000 $ , 并适当缩减能量值范围 (a)$ \gamma = 0.2 $ , 扩展态与局域态一起出现; (b)$ \gamma = 1 $ , 所有扩展态均转变为局域态; (c)$ \gamma = 4.66946 $ , 一些局域态会转回扩展态; (d)$ \gamma = 5.5 $ , 所有态再次变为局域态. 其他参数和图3 一致Figure 4. Spatial distributions of normalized bulk eigenstates with the change of eigenvalues. For enhanced visibility, the system size is
$ L = 1000 $ , and the values of the energies have been cut down appropriately: (a)$ \gamma = 0.2 $ , the extended and localized eigenstates appearing together; (b)$ \gamma = 1 $ , all extended eigenstates being transformed into the localized; (c)$ \gamma = 4.66946 $ , some localized eigenstates turning to the extended; (d)$ \gamma = 5.5 $ , all extended eigenstates being transformed into the localized once again. Other parameters are the same as the ones in Fig. 3.图 5 (a)拓扑不变量随
$ W_{1} $ 的变化趋势; (b)$ |E|^{0} $ 与对应的${\rm{IPR}} ^{0} $ 和${\rm{NPR}} ^{0} $ 随$ W_{1} $ 的演化; (c) 图(b)其中一部分的详细信息; (d)${\rm{NPR}} ^{0} $ 的导数, 显然其中存在一些不连续的点; (e)以$ W_{1} $ 为自变量的${\rm{IPR}} ^{{\mathrm{B}}} $ (红)和${\rm{NPR}} ^{{\mathrm{B}}} $ (蓝), 阴影区域表示扩展态和局域态共存; (f)体能谱的实部, 附着在其上的不同颜色代表不同的${\rm{IPR}} ^{|\varPsi^{n}\rangle} $ 值. 图(a), (b), (e) 和(f)$ L = 2000 $ , 图(c)和(d)$ L = 10000 $ , 其他参数为$ t_{1} = 1 $ ,$ t_{2} = 1.3 $ ,$ \gamma = 0.05 $ 和$ W_{2} = W_{1} $ Figure 5. (a) Topological invariant versus
$ W_{1} $ ; (b) evolution of$ |E|^{0} $ via$ W_{1} $ , associated with${\rm{IPR}} ^{0} $ and${\rm{NPR}} ^{0} $ ; (c) detailed information on the localization of the eigenstates with the lowest energy; (d) derivative of${\rm{NPR}} ^{0} $ , where there exist some discontinuity points; (e)${\rm{IPR}} ^{{\mathrm{B}}} $ (red) and${\rm{NPR}} ^{{\mathrm{B}}} $ (blue) being plotted as a function of$ W_{1} $ . The shaded region indicates the coexisting regime, with extended and localized eigenstates being coexistence; (f) real part of bulk energy spectrum, where different colors stand for different values of${\rm{IPR}} ^{|\varPsi^{n}\rangle} $ . For panels (a), (b), (e) and (f)$ L = 2000 $ , and for panels (c) and (d)$ L = 10000 $ . Same parameters are$ t_{1} = 1 $ ,$ t_{2} = 1.3 $ ,$ \gamma = 0.05 $ and$ W_{2} = W_{1} $ . -
[1] Bansil A, Lin H, Das T 2016 Rev. Mod. Phys. 88 021004 doi: 10.1103/RevModPhys.88.021004 [2] Chiu C K, Teo J C Y, Schnyder A P, Ryu S 2016 Rev. Mod. Phys. 88 035005 doi: 10.1103/RevModPhys.88.035005 [3] Asbóth J, Oroszlány L, Pályi A 2016 A Short Course on Topological Insulators 919 2 doi: 10.1007/978-3-319-25607-8 [4] Bernevig B A, Hughes T L 2013 Topological Insulators and Topological Superconductors (Princeton: Princeton University Press [5] Shen S Q 2012 Topological Insulators Dirac Equation in Condensed Matters (Vol. 174) (Berlin: Springer doi: 10.1007/978-3-642-32858-9 [6] Yokomizo K, Murakami S 2020 Phys. Rev. Research 2 043045 doi: 10.1103/PhysRevResearch.2.043045 [7] Martinez Alvarez V M, Barrios Vargas J E, Foa Torres L E F 2018 Phys. Rev. B 97 121401 doi: 10.1103/PhysRevB.97.121401 [8] Wu H, Wang B Q, An J H 2021 Phys. Rev. B 103 L041115 doi: 10.1103/PhysRevB.103.L041115 [9] He P, Huang Z H 2020 Phys. Rev. A 102 062201 doi: 10.1103/PhysRevA.102.062201 [10] Torres L E F F 2019 J. Phys.: Mater. 3 014002 doi: 10.1088/2515-7639/ab4092 [11] Esaki K, Sato M, Hasebe K, Kohmoto M 2011 Phys. Rev. B 84 205128 doi: 10.1103/PhysRevB.84.205128 [12] Hu Y C, Hughes T L 2011 Phys. Rev. B 84 153101 doi: 10.1103/PhysRevB.84.153101 [13] Zhu B, Lü R, Chen S 2014 Phys. Rev. A 89 062102 doi: 10.1103/PhysRevA.89.062102 [14] Malzard S, Poli C, Schomerus H 2015 Phys. Rev. Lett. 115 200402 doi: 10.1103/PhysRevLett.115.200402 [15] Xu Y, Wang S T, Duan L M 2017 Phys. Rev. Lett. 118 045701 doi: 10.1103/PhysRevLett.118.045701 [16] Zhan X, Xiao L, Bian Z, Wang K, Qiu X, Sanders B C, Yi W, Xue P 2017 Phys. Rev. Lett. 119 130501 doi: 10.1103/PhysRevLett.119.130501 [17] Zeuner J M, Rechtsman M C, Plotnik Y, Lumer Y, Nolte S, Rudner M S, Segev M, Szameit A 2015 Phys. Rev. Lett. 115 040402 doi: 10.1103/PhysRevLett.115.040402 [18] Rufangura P, Folland T G, Agrawal A, Caldwell J D, Iacopi F 2020 J. Phys.: Mater. 3 032005 doi: 10.1088/2515-7639/ab9d10 [19] Jin L, Song Z 2019 Phys. Rev. B 99 081103 doi: 10.1103/PhysRevB.99.081103 [20] Borgnia D S, Kruchkov A J, Slager R J 2020 Phys. Rev. Lett. 124 056802 doi: 10.1103/PhysRevLett.124.056802 [21] Takata K, Notomi M 2018 Phys. Rev. Lett. 121 213902 doi: 10.1103/PhysRevLett.121.213902 [22] Chen Y, Zhai H 2018 Phys. Rev. B 98 245130 doi: 10.1103/PhysRevB.98.245130 [23] Lang L J, Wang Y, Wang H, Chong Y D 2018 Phys. Rev. B 98 094307 doi: 10.1103/PhysRevB.98.094307 [24] Harari G, Bandres M A, Lumer Y, Rechtsman M C, Chong Y D, Khajavikhan M, Christodoulides D N, Segev M 2018 Science 359 eaar4003 doi: 10.1126/science.aar4003 [25] Xiao L, Deng T, Wang K, Zhu G, Wang Z, Yi W, Xue P 2020 Nat. Phys. 16 761 doi: 10.1038/s41567-020-0836-6 [26] Zhou H, Peng C, Yoon Y, Hsu C W, Nelson K A, Fu L, Joannopoulos J D, Soljačić M, Zhen B 2018 Science 359 1009 doi: 10.1126/science.aap9859 [27] Deng T S, Yi W 2019 Phys. Rev. B 100 035102 doi: 10.1103/PhysRevB.100.035102 [28] Ezawa M 2019 Phys. Rev. B 99 201411 doi: 10.1103/PhysRevB.99.201411 [29] Kawabata K, Higashikawa S, Gong Z, Ashida Y, Ueda M 2019 Nat. Commun. 10 297 doi: 10.1038/s41467-018-08254-y [30] Kawabata K, Ashida Y, Katsura H, Ueda M 2018 Phys. Rev. B 98 085116 doi: 10.1103/PhysRevB.98.085116 [31] Cai J Q, Yang Q Y, Xue Z Y, Gong M, Guo G C, Hu Y 2019 arXiv:1812.02610 [cond-mat.mes-hall] [32] Lee C H, Li L, Gong J 2019 Phys. Rev. Lett. 123 016805 doi: 10.1103/PhysRevLett.123.016805 [33] Yoshida T, Kudo K, Hatsugai Y A 2019 Sci. Rep. 9 16895 doi: 10.1038/s41598-019-53253-8 [34] Luitz D J, Piazza F 2019 Phys. Rev. Research 1 033051 doi: 10.1103/PhysRevResearch.1.033051 [35] Rosenthal E I, Ehrlich N K, Rudner M S, Higginbotham A P, Lehnert K W 2018 Phys. Rev. B 97 220301 doi: 10.1103/PhysRevB.97.220301 [36] Lee T E 2016 Phys. Rev. Lett. 116 133903 doi: 10.1103/PhysRevLett.116.133903 [37] Kunst F K, Edvardsson E, Budich J C, Bergholtz E J 2018 Phys. Rev. Lett. 121 026808 doi: 10.1103/PhysRevLett.121.026808 [38] Xiong Y 2018 J. Phys. Commun. 2 035043 doi: 10.1088/2399-6528/aab64a [39] Yao S, Wang Z 2018 Phys. Rev. Lett. 121 086803 doi: 10.1103/PhysRevLett.121.086803 [40] Yokomizo K, Murakami S 2019 Phys. Rev. Lett. 123 066404 doi: 10.1103/PhysRevLett.123.066404 [41] Zhang K, Yang Z, Fang C 2020 Phys. Rev. Lett. 125 126402 doi: 10.1103/PhysRevLett.125.126402 [42] Yang Z, Zhang K, Fang C, Hu J 2020 Phys. Rev. Lett. 125 226402 doi: 10.1103/PhysRevLett.125.226402 [43] Li L, Lee C H, Mu S, Gong J 2020 Nat. Commun. 11 1 doi: 10.1038/s41467-020-18917-4 [44] Guo G F, Bao X X, Tan L 2021 New J. Phys. 23 123007 doi: 10.1088/1367-2630/ac38ce [45] Bao X X, Guo G F, Tan L 2021 J. Phys. Condens. Matter 33 465403 doi: 10.1088/1361-648X/ac2040 [46] Gong Z, Ashida Y, Kawabata K, Takasan K, Higashikawa S, Ueda M 2018 Phys. Rev. X 8 031079 doi: 10.1103/PhysRevX.8.031079 [47] Ghatak A, Das T 2019 J. Phys. Condens. Matter 31 263001 doi: 10.1088/1361-648X/ab11b3 [48] Shen H, Zhen B, Fu L 2018 Phys. Rev. Lett. 120 146402 doi: 10.1103/PhysRevLett.120.146402 [49] Leykam D, Bliokh K Y, Huang C, Chong Y D, Nori F 2017 Phys. Rev. Lett. 118 040401 doi: 10.1103/PhysRevLett.118.040401 [50] Denner M M, Skurativska A, Schindler F, Fischer M H, Thomale R, Bzdušek T, Neupert T 2021 Nat. Commun. 12 5681 doi: 10.1038/s41467-021-25947-z [51] Yin C, Jiang H, Li L, Lü R, Chen S 2018 Phys. Rev. A 97 052115 doi: 10.1103/PhysRevA.97.052115 [52] Kawabata K, Shiozaki K, Ueda M, Sato M 2019 Phys. Rev. X 9 041015 doi: 10.1103/PhysRevX.9.041015 [53] Okuma N, Kawabata K, Shiozaki K, Sato M 2020 Phys. Rev. Lett. 124 086801 doi: 10.1103/PhysRevLett.124.086801 [54] Zhang X, Gong J 2020 Phys. Rev. B 101 045415 doi: 10.1103/PhysRevB.101.045415 [55] Longhi S 2018 Annalen der Physik 530 1800023 doi: 10.1002/andp.201800023 [56] Zhu W, Teo W X, Li L, Gong J 2021 Phys. Rev. B 103 195414 doi: 10.1103/PhysRevB.103.195414 [57] Chen C, Qi L, Xing Y, Cui W X, Zhang S, Wang H F 2021 New J. Phys. 23 123008 doi: 10.1088/1367-2630/ac38cc [58] Jiang X P, Qiao Y, Cao J P 2021 Chin. Phys. B 30 097202 doi: 10.1088/1674-1056/ac11e5 [59] Wang B X, Zhao C Y 2021 Phys. Rev. A 103 013727 doi: 10.1103/PhysRevA.103.013727 [60] Tang L Z, Zhang G Q, Zhang L F, Zhang D W 2021 Phys. Rev. A 103 033325 doi: 10.1103/PhysRevA.103.033325 [61] Agarwal K S, Joglekar Y N 2021 Phys. Rev. A 104 022218 doi: 10.1103/PhysRevA.104.022218 [62] Zeng Q B, Yang Y B, Xu Y 2020 Phys. Rev. B 101 020201 doi: 10.1103/PhysRevB.101.020201 [63] Liu Y, Wang Y, Liu X J, Zhou Q, Chen S 2021 Phys. Rev. B 103 014203 doi: 10.1103/PhysRevB.103.014203 [64] Liu T, Guo H, Pu Y, Longhi S 2020 Phys. Rev. B 102 024205 doi: 10.1103/PhysRevB.102.024205 [65] Zhai L J, Yin S, Huang G Y 2020 Phys. Rev. B 102 064206 doi: 10.1103/PhysRevB.102.064206 [66] Cai X 2021 Phys. Rev. B 103 014201 doi: 10.1103/PhysRevB.103.014201 [67] Longhi S 2021 Phys. Rev. B 103 054203 doi: 10.1103/PhysRevB.103.054203 [68] Zhang C, Sheng L, Xing D 2021 Phys. Rev. B 103 224207 doi: 10.1103/PhysRevB.103.224207 [69] Zhai L J, Huang G Y, Yin S 2021 Phys. Rev. B 104 014202 doi: 10.1103/PhysRevB.104.014202 [70] Wang Z H, Xu F, Li L, Xu D H, Wang B 2021 Phys. Rev. B 104 174501 doi: 10.1103/PhysRevB.104.174501 [71] Zhao X M, Guo C X, Kou S P, Zhuang L, Liu W M 2021 Phys. Rev. B 104 205131 doi: 10.1103/PhysRevB.104.205131 [72] Longhi S 2019 Phys. Rev. Lett. 122 237601 doi: 10.1103/PhysRevLett.122.237601 [73] Zhou L 2021 Phys. Rev. Research 3 033184 doi: 10.1103/PhysRevResearch.3.033184 [74] Jiang H, Lang L J, Yang C, Zhu S L, Chen S 2019 Phys. Rev. B 100 054301 doi: 10.1103/PhysRevB.100.054301 [75] Hou J, Wu Y J, Zhang C 2021 Phys. Rev. A 103 033305 doi: 10.1103/PhysRevA.103.033305 [76] Zhang D W, Chen Y L, Zhang G Q, Lang L J, Li Z, Zhu S L 2020 Phys. Rev. B 101 235150 doi: 10.1103/PhysRevB.101.235150 [77] Wu C, Fan J, Chen G, Jia S 2021 New J. Phys. 23 123048 doi: 10.1088/1367-2630/ac430b [78] Zuo Z W, Kang D 2022 Phys. Rev. A 106 013305 doi: 10.1103/PhysRevA.106.013305 [79] 吴瑾, 陆展鹏, 徐志浩, 郭利平 2022 物理学报 71 113702 doi: 10.7498/aps.71.20212246 Wu J, Lu Z P, Xu Z H, Guo L P 2022 Acta Phys. Sin. 71 113702 doi: 10.7498/aps.71.20212246 [80] Roy S, Chattopadhyay S, Mishra T, Basu S 2022 Phys. Rev. B 105 214203 doi: 10.1103/PhysRevB.105.214203 [81] Li X, Li X P, Das Sarma S 2017 Phys. Rev. B 96 085119 doi: 10.1103/PhysRevB.96.085119 [82] Li X, Das Sarma S 2020 Phys. Rev. B 101 064203 doi: 10.1103/PhysRevB.101.064203 [83] Song F, Yao S, Wang Z 2019 Phys. Rev. Lett. 123 246801 doi: 10.1103/PhysRevLett.123.246801 [84] Zhang D W, Tang L Z, Lang L J, Yan H, Zhu S L 2020 Science China Physics, Mechanics & Astronomy 63 267062 doi: 10.1007/s11433-020-1521-9 [85] Luo X W, Zhang C W 2023 Appl. Phys. Lett. 123 081111 doi: 10.1063/5.0153523 [86] Evers F, Mirlin A D 2008 Rev. Mod. Phys. 80 1355 doi: 10.1103/RevModPhys.80.1355 [87] Roy S, Khaymovich I M, Das A, Moessner R 2018 SciPost Phys. 4 025 doi: 10.21468/SciPostPhys.4.5.025 [88] Longhi S, Gatti D, Della Valle G 2015 Phys. Rev. B 92 094204 doi: 10.1103/PhysRevB.92.094204 [89] Weidemann S, Kremer M, Helbig T, Hofmann T, Stegmaier A, Greiter M, Thomale R, Szameit A 2020 Science 368 311 doi: 10.1126/science.aaz8727 [90] Wang K, Dutt A, Yang K Y, Wojcik C C, Vučković J, Fan S 2021 Science 371 1240 doi: 10.1126/science.abf6568 [91] Helbig T, Hofmann T, Imhof S, Abdelghany M, Kiessling T, Molenkamp L W, Lee C H, Szameit A, Greiter M, Greiter M, Thomale R 2020 Nat. Phys. 16 747 doi: 10.1038/s41567-020-0922-9 [92] Ghatak A, Brandenbourger M, van Wezel J, Coulais C 2020 Proc. Natl. Acad. Sci. U.S.A. 117 29561 doi: 10.1073/pnas.2010580117 [93] Liu T, He J J, Yoshida T, Xiang Z L, Nori F 2020 Phys. Rev. B 102 235151 doi: 10.1103/PhysRevB.102.235151 [94] Brouwer P W, Silvestrov P G, Beenakker C W J 1997 Phys. Rev. B 56 R4333 doi: 10.1103/PhysRevB.56.R4333 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: