高级搜索

基于Shockley-Queisser模型的异质结太阳电池极限效率计算

,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

祝曾伟, 张美荣, 乔宝蓉, 陈佳, 杨慧永, 周大勇. 基于Shockley-Queisser模型的异质结太阳电池极限效率计算[J]. 物理学报, 2025, 74(3): 038801-1. doi: 10.7498/aps.74.20240941
引用本文: 祝曾伟, 张美荣, 乔宝蓉, 陈佳, 杨慧永, 周大勇. 基于Shockley-Queisser模型的异质结太阳电池极限效率计算[J]. 物理学报, 2025, 74(3): 038801-1. doi: 10.7498/aps.74.20240941
shu
Zengwei ZHU, Meirong ZHANG, Baorong QIAO, Jia CHEN, Huiyong YANG, Dayong ZHOU. Shockley-Queisser theory based calculation of efficiency limit of heterojunction solar cells[J]. Acta Physica Sinica, 2025, 74(3): 038801-1. doi: 10.7498/aps.74.20240941
Citation: Zengwei ZHU, Meirong ZHANG, Baorong QIAO, Jia CHEN, Huiyong YANG, Dayong ZHOU. Shockley-Queisser theory based calculation of efficiency limit of heterojunction solar cells[J]. Acta Physica Sinica, 2025, 74(3): 038801-1. doi: 10.7498/aps.74.20240941
shu

基于Shockley-Queisser模型的异质结太阳电池极限效率计算

  • 材料科学姑苏实验室, 苏州　215123

    • 作者简介: 祝曾伟: zengwei_zhu@163.com .
    通讯作者: E-mail: zhoudayong2021@gusulab.ac.cn.

  • 中图分类号: 88.40.H-, 88.40.-j, 73.40.-c, 78.20.-e

Shockley-Queisser theory based calculation of efficiency limit of heterojunction solar cells

  • Gusu Laboratory of Materials, Suzhou 215123, China

    • Corresponding author: E-mail: zhoudayong2021@gusulab.ac.cn.

  • MSC: 88.40.H-, 88.40.-j, 73.40.-c, 78.20.-e

  • 摘要: Shockley-Queisser (S-Q)模型定义的理想太阳能电池是光伏器件分析的一个重要里程碑. 异质结太阳电池是光伏热门研究领域之一. 本文基于光伏电池S-Q模型基础, 针对异质结太阳电池空间势垒区能带不连续对光生载流子的输运存在的阻碍作用, 修订S-Q模型中的假设, 引入空间势垒区有限迁移率假设, 推导异质结太阳电池光电转换方程, 计算光电转换效率. 5780 K黑体辐射、电池温度300 K条件下计算结果表明最高转换效率约为31%; 异质结太阳能电池的开路电压可以超过窄带隙半导体的带隙限制; 高迁移率、低串阻条件下, 降低宽带隙半导体的光子吸收数目、增加窄带隙半导体光子吸收数目, 异质结太阳电池存在效率损失.
    Abstract: The ideal solar cell defined by the Shockley-Queisser (S-Q) theory is an important milestone in the analysis of photovoltaic devices based on some assumptions. One or more of the above assumptions are gradually avoided, and even exceed or approach the S-Q efficiency limit, so the development and improvement of S-Q theory is necessary. Heterojunction solar cells are one of the hot research fields in photovoltaics. In order to address the hindering effect of energy band discontinuity in the spatial barrier region of heterojunction solar cells on the transport of photogenerated carriers, the assumptions of S-Q theory based on the original S-Q theory of photovoltaic cells are revised in this work. The carrier mobility in the barrier region is assumed to be finite, and the infinite mobility in the S-Q model is abandoned. But the mobility in the N-type and the P-type neutral region are still infinite. The lumped relationship between carrier mobility and resistance in the barrier region is derived. Therefore, the physical process of charge transport is described in detail in this paper based on the continuity equation for semiconductors by considering the effect of absorption coefficients to prevent the quasi-Fermi level from crossing the conduction or valence band. Thus, the revised S-Q theoretical limit model of heterojunction solar cell is constructed. The diode equivalent circuit diagram is deduced and the photovoltaic conversion efficiency is evaluated eventually. The loss effects of charge transmission and band gap mismatch on the performance of heterojunction solar cells are analyzed in detail. The calculation results under the condition of 5780 K blackbody radiation and 300 K cell temperature with N-type wide bandgap (EH) and P-type narrow bandgap (EL) materials show that the highest conversion efficiency is about 31% with a hole resistance of 0.01 Ω·cm2 and electronic resistance of 0.01 Ω·cm2. The calculations show that the electronic resistance has a more negative and complicated effect on solar cell performance than hole resistance. When Re and Rh are small, the best conversion efficiency is in a range between 1.22 eV and 1.32 eV of the narrow bandgap. Increasing Re can increase the open circuit voltage of solar cells, but there are losses in efficiency and fill factor of solar cells. When Re is large enough, for example, Re = 1000 Ω·cm2, the open circuit voltage of solar cells is not limited by EL and can exceed the bandgap limit of the narrow bandgap material. Increasing Rh will also reduce efficiency, but the effect is not so great as Re. The change of absorption coefficient can cause the photogenerated current of L and H branches to change, and the radiation recombination losses of both branches can be regulated.
  • 加载中

  • 图 1  (a)异质结结构图; (b)异质结等效电路图; (c)适当电压、无限迁移率能带分布; (d)大电压、无限/有限迁移率能带分布; 这里Re为对电子的电阻(Ω·cm2), Rh为对空穴的电阻(Ω·cm2), DL, DH为窄带隙、宽带隙材料等效二极管, JL和JH为窄带隙、宽带隙材料产生的光生电流

    Figure 1.  (a) Heterojunction structure diagram; (b) heterojunction equivalent circuit diagram; (c) infinite mobility band distribution under appropriate voltage; (d) infinite/finite mobility band distribution under high voltage. Re is the resistance to electrons (Ω·cm2), and Rh is the resistance to holes (Ω·cm2). DL and DH are equivalent diodes made of narrow bandgap and wide bandgap materials. JL and JH are photocurrent generated by narrow bandgap and wide bandgap materials, respectively.

    下载: 全尺寸图片 幻灯片

    图 2  有限迁移率条件下能带图

    Figure 2.  Energy band diagram under limited mobility conditions.

    下载: 全尺寸图片 幻灯片

    图 3  Eff分布图(α = 1, Rh = 0.01 Ω·cm2, Re = 0.01 Ω·cm2, EH = 1.52—3.12 eV , EL = 0.52—1.42 eV)

    Figure 3.  Eff profile (α = 1, Rh = 0.01 Ω·cm2, Re = 0.01 Ω·cm2, EH = 1.52—3.12 eV , EL = 0.52—1.42 eV).

    下载: 全尺寸图片 幻灯片

    图 4  I-V曲线(α = 1, EL = 0.82 eV, EH = 0.92, 1.52, 2.82 eV, Rh = 0.01 Ω·cm2, Re = 0.1, 1, 10, 1000 Ω·cm2)

    Figure 4.  I-V curves (α = 1, EL = 0.82 eV, EH = 0.92, 1.52, 2.82 eV, Rh = 0.01 Ω·cm2, Re = 0.1, 1, 10, 1000 Ω·cm2).

    下载: 全尺寸图片 幻灯片

    图 5  Eff分布图(α = 1, Rh = 0.01 Ω·cm2, Re = 1 Ω·cm2, EH = 1.52—3.12 eV, EL = 0.52—1.42 eV)

    Figure 5.  Eff profile (α = 1, Rh = 0.01 Ω·cm2, Re = 1 Ω·cm2, EH = 1.52–3.12 eV, EL = 0.52–1.42 eV).

    下载: 全尺寸图片 幻灯片

    图 6  (a) Eff -EH曲线(Rh = 0.01 Ω·cm2, EL = 0.52 eV); (b) Voc -EH曲线(Rh = 0.01 Ω·cm2, EL = 0.52 eV); (c) Eff -EL曲线(Rh = 0.01 Ω·cm2, EH = 1.52 eV); (d) Jsc -EL曲线(Rh = 0.01 Ω·cm2, EH = 1.52 eV)

    Figure 6.  (a) Eff -EH curves (Rh = 0.01 Ω·cm2, EL = 0.52 eV); (b) Voc -EH curves (Rh = 0.01 Ω·cm2, EL = 0.52 eV); (c) Eff -EL curves (Rh = 0.01 Ω·cm2, EH = 1.52 eV); (d) Jsc -EL curves (Rh = 0.01 Ω·cm2, EH = 1.52 eV).

    下载: 全尺寸图片 幻灯片

    图 7  Eff分布图(α = 1, Rh = 0.01 Ω·cm2, Re = 10 Ω·cm2, EH = 1.52—3.12 eV, EL = 0.52—1.42 eV)

    Figure 7.  Eff profile (α = 1, Rh = 0.01Ω·cm2, Re = 10 Ω·cm2, EH = 1.52–3.12 eV, EL = 0.52–1.42 eV).

    下载: 全尺寸图片 幻灯片

    图 8  Eff -Re曲线

    Figure 8.  Eff -Re curves.

    下载: 全尺寸图片 幻灯片

    图 9  (a) Eff -EH曲线(EL = 1.12 eV, Re = 0.01 Ω·cm2); (b) Eff -Rh曲线

    Figure 9.  (a) Eff -EH curves (EL = 1.12 eV, Re = 0.01 Ω·cm2); (b) Eff -Rh curves.

    下载: 全尺寸图片 幻灯片

    图 10  Eff -α曲线(EL = 1.12 eV)

    Figure 10.  Eff -α curves (EL = 1.12 eV).

    下载: 全尺寸图片 幻灯片
    下载: 全尺寸图片 幻灯片
  • [1] 沈文忠, 李正平 2014 硅基异质结太阳电池物理与器件(北京: 科学出版社) 第28页 Shen W Z, Li Z P 2014 Physics and Devices of Silicon Heterojunction Solar Cells (Beijing: Science Press) p28
    [2] Li Y, Ru X N, Yang M, et al. 2024 Nature 626 105 doi: 10.1038/s41586-023-06948-y
    [3] Wang M H, Shi Y 2024 Sci. China Chem. 67 1117 doi: 10.1007/s11426-023-1899-y
    [4] Wang T Y, Deng W Q, Cao J P, Yan F 2023 Adv. Energy Mater. 13 2201436 doi: 10.1002/aenm.202201436
    [5] 张美荣, 祝曾伟, 杨晓琴, 于同旭, 郁骁琦, 卢荻, 李顺峰, 周大勇, 杨辉 2023 物理学报 72 058801 doi: 10.7498/aps.72.20222019 Zhang M R, Zhu Z W, Yang X Q, Yu T X, Yu X Q, Lu D, Li S F, Zhou D Y, Yang H 2023 Acta Phys. Sin. 72 058801 doi: 10.7498/aps.72.20222019
    [6] 王傲 2021 博士学位论文(南京: 南京理工大学) Wang A 2021 Ph. D. Dissertation (Nanjing: Nanjing University of Science and Technology
    [7] Li T H, Wang C, Hu C Z, Zhang N, Xiong Q, Zhang Z L, Li F, Zhang Y Y, Wu J H, Gao P 2024 Small Sci. 4 2300218 doi: 10.1002/smsc.202300218
    [8] Zhao Y F, Procel P, Han C, et al. 2023 Sol. Energy Mater. Sol. Cells 258 112413 doi: 10.1016/j.solmat.2023.112413
    [9] Long W, Yin S, Peng F G, Yang M, Fang L, Ru X N, Qu M H, Lin H F, Xu X X 2021 Sol. Energy Mater. Sol. Cells 231 111291 doi: 10.1016/j.solmat.2021.111291
    [10] Jiang K, Zhang H H, Zhang L P, Meng F Y, Gao Y F, Yu X R, Zhao D M, Li R, Huang H W, Hao Z D, Liu Z X, Liu W Z 2023 Sci. China Mater. 66 4891 doi: 10.1007/s40843-023-2610-y
    [11] Shockley W, Queisser H J 1961 J. Appl. Phys. 32 510 doi: 10.1063/1.1736034
    [12] Ahmad F, Lakhtakia A, Monk P B 2020 Appl. Phys. Lett. 117 033901 doi: 10.1063/5.0017916
    [13] Guillemoles J F, Kirchartz T, Cahen D, Rau U 2019 Nat. Photonics 13 501 doi: 10.1038/s41566-019-0479-2
    [14] Guillemoles J F, Kirchartz T, Cahen D, Rau U 2021 Nat. Photonics 15 165 doi: 10.1038/s41566-021-00775-1
    [15] Markvart T 2021 Nat. Photonics 15 163 doi: 10.1038/s41566-021-00772-4
    [16] Marti A 2019 IEEE J. Photovolt. 9 1590 doi: 10.1109/JPHOTOV.2019.2932626
    [17] 熊超, 陈磊, 袁洪春, 姚若河 2013 太阳能学报 34 746 Xiong C, Chen L, Yuan H C, Yao R H 2013 Acta Energ. Sol. Sin. 34 746
    [18] Anderson R L 1962 Solid-State Electron. 5 341 doi: 10.1016/0038-1101(62)90115-6
    [19] Qian C, Bai Y, Ye H R, Chen Y, Ye L, Zhang C, Ma Z, Chen T, Fan H L, Huang Y L, Liu W Z, Yu J S, Yu J 2024 Sol. Energy 274 112585 doi: 10.1016/j.solener.2024.112585
    [20] 刘恩科, 朱秉升, 罗晋生 2008 半导体物理学(第7版) (北京: 电子工业出版社) 第148页 Liu E K, Zhu B S, Luo J S 2008 The Physics of Semiconductors (7th Ed.) (Beijing: Publishing House of Electronics Industry) p148
  • 加载中
图( 11)
计量
  • 文章访问数:  189
  • HTML全文浏览数:  189
  • PDF下载数:  2
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-07-08
  • 刊出日期:  2025-02-05

基于Shockley-Queisser模型的异质结太阳电池极限效率计算

    通讯作者: E-mail: zhoudayong2021@gusulab.ac.cn.
    作者简介: 祝曾伟: zengwei_zhu@163.com
  • 材料科学姑苏实验室, 苏州　215123
  • 收稿日期:  2024-07-08

摘要: Shockley-Queisser (S-Q)模型定义的理想太阳能电池是光伏器件分析的一个重要里程碑. 异质结太阳电池是光伏热门研究领域之一. 本文基于光伏电池S-Q模型基础, 针对异质结太阳电池空间势垒区能带不连续对光生载流子的输运存在的阻碍作用, 修订S-Q模型中的假设, 引入空间势垒区有限迁移率假设, 推导异质结太阳电池光电转换方程, 计算光电转换效率. 5780 K黑体辐射、电池温度300 K条件下计算结果表明最高转换效率约为31%; 异质结太阳能电池的开路电压可以超过窄带隙半导体的带隙限制; 高迁移率、低串阻条件下, 降低宽带隙半导体的光子吸收数目、增加窄带隙半导体光子吸收数目, 异质结太阳电池存在效率损失.

English Abstract

    全文HTML

    1.   引　言

    • 异质结太阳能电池由宽带隙和窄带隙半导体材料之间形成PN结组成[1]. 太阳光光子首先由宽带隙半导体材料吸收, 窄带隙半导体材料吸收剩余可吸收光子. 传统晶硅异质结太阳电池是光伏行业热门研究方向之一, 实验室最高转换效率已达27.1%, 也是目前晶硅太阳电池最高效率, 55 μm厚柔性晶硅异质结电池实验室转换效率达到26%[2]. 近十年, 新兴钙钛矿材料体系太阳电池取得了飞速发展, 实验室最高转换效率已突破26%[3], 其3层半导体材料的PIN电池结构, 异质宽带隙N/P型材料在本征层钙钛矿材料体内形成空间势垒区, 驱动光生载流子分离. 钙钛矿太阳电池通过不同的宽带隙N/P型传输层材料体系, 匹配不同能带需求, 提高电池转换效率[4,5]. 光伏电池能量转换过程中的损耗机理一直是研究难点和热点[6], 界面复合损失[7]、体复合损失[8]、传输电阻损失[9]、光学损耗[10]等都限制电池效率的提升, 但由于这些损耗可以降低甚至避免, 计算理论极限效率时不加以讨论. 1961年, Shockley和Queisser[11]通过使用细致平衡的基本热力学原理, 分析光伏电池能量转换极限, 即Shockley-Queisser (S-Q)极限, 是太阳能电池中最重要的理论基础之一. S-Q极限包括以下5个基本假设.

      P1: 光子能量Eopt＞Eg, 则光子被太阳电池吸收;

      P2: 太阳电池吸收一个Eopt > Eg的光子, 只产生一对电子(e)-空穴(h);

      P3: e-h对弛豫释放的能量对太阳电池温度(Tcell)无影响, 即Tcell保持不变;

      P4: e-h对辐射复合产生光子或形成电流被导出;

      P5: 完美理想接触, 无欧姆损失.

      S-Q理论是太阳电池最重要的理论基础之一, 随着新型高效光伏材料、新型光伏器件不断涌出, 上述某个或某些假设基本被规避, 降低了实际的能量损失, 取得了非常高的转换效率, 有些甚至超过或接近S-Q效率限制, 发展和改进S-Q理论是必要的. Ahmad等[12]计算预测了CIGS/CZTSSe双吸收体异质结太阳电池理论效率可到34.45%, 超过S-Q极限限制. 2019年Guillemoles等[13,14]和2021年Markvart[15]进一步讨论和分析S-Q模型, 并尝试通过引入品质因子进一步修正S-Q模型. 2019年, Martí[16]构建了基于S-Q模型的异质结电池理论极限模型, 分析了在46050倍极限聚光条件下异质结电池极限效率介于宽带隙和窄带隙半导体单带隙太阳电池极限效率之间. 2013年, 熊超等[17]基于细致平衡基本理论, 通过引入Anderson扩散模型[18]描述势垒区阻碍, 形成CdS/CdTe 异质结太阳电池的 I-V特性表达式以及最大光电转换效率的求法. 此外, 在硅基异质结电池或者钙钛矿电池结构中, 通常为了抑制前表面材料对光生载流子的寄生吸收造成额外非辐射复合损失, 会把前表面材料薄膜厚度减到数十纳米量级, 保证PN结电场驱动, 同时降低在该区域的光吸收, 调控宽带隙材料光学吸收也是电池中需要考虑的因素之一[9,19].

      在上述研究之上, 本文以N型宽带隙和P型窄带隙为例, 基于S-Q理论基本原理, 建立考虑吸收率影响的异质结太阳电池极限效率计算模型, 分析不同势垒区载流子迁移率限制、不同禁带宽度条件下, 异质结太阳电池效率分布.

    2.   理论模型

      2.1.   假设条件

    • S-Q模型中P4和P5假设载流子部分被辐射复合, 余下能被完全收集, 且在传输的过程中没有任何其他损失, 即载流子具有无限大的迁移率. 电子和空穴电流连续性方程[20]:

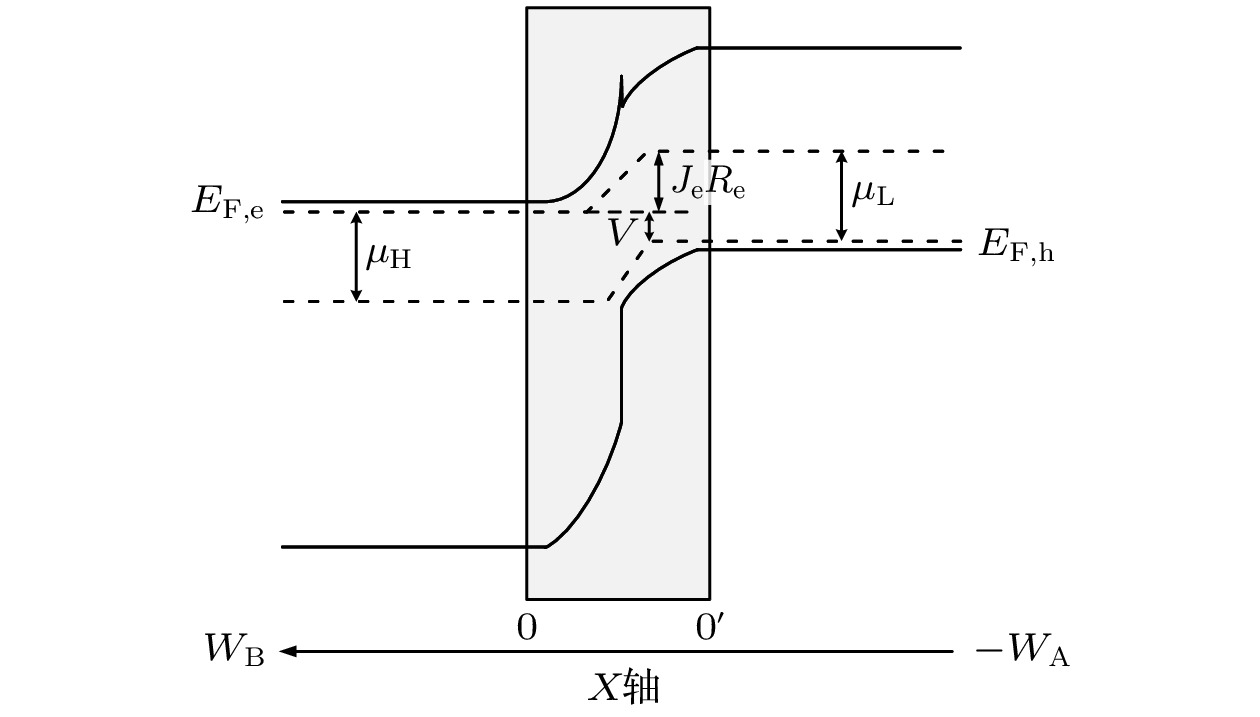
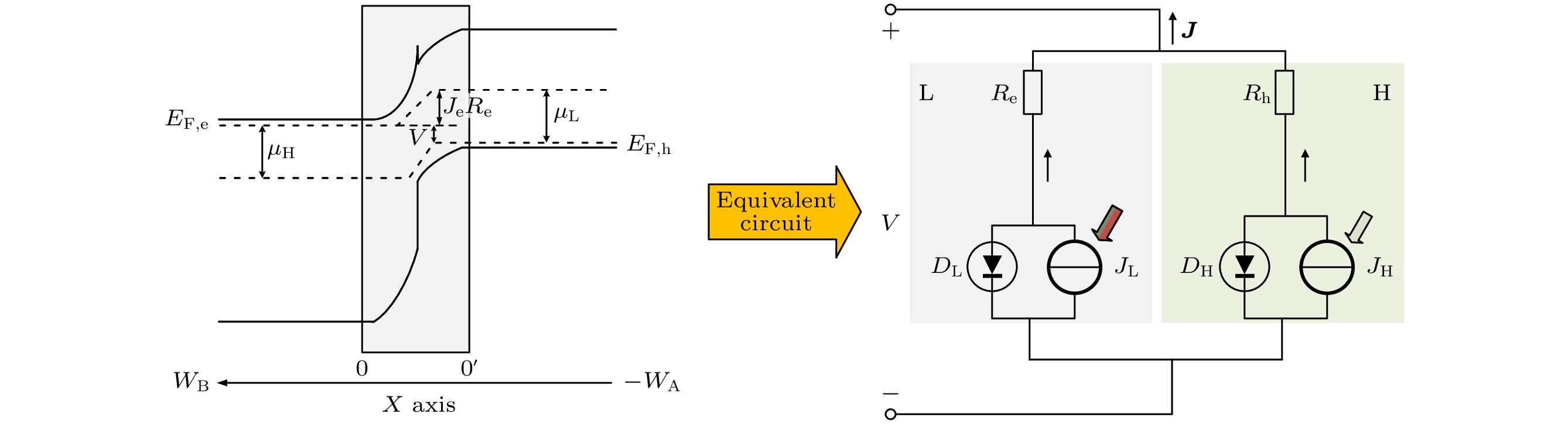
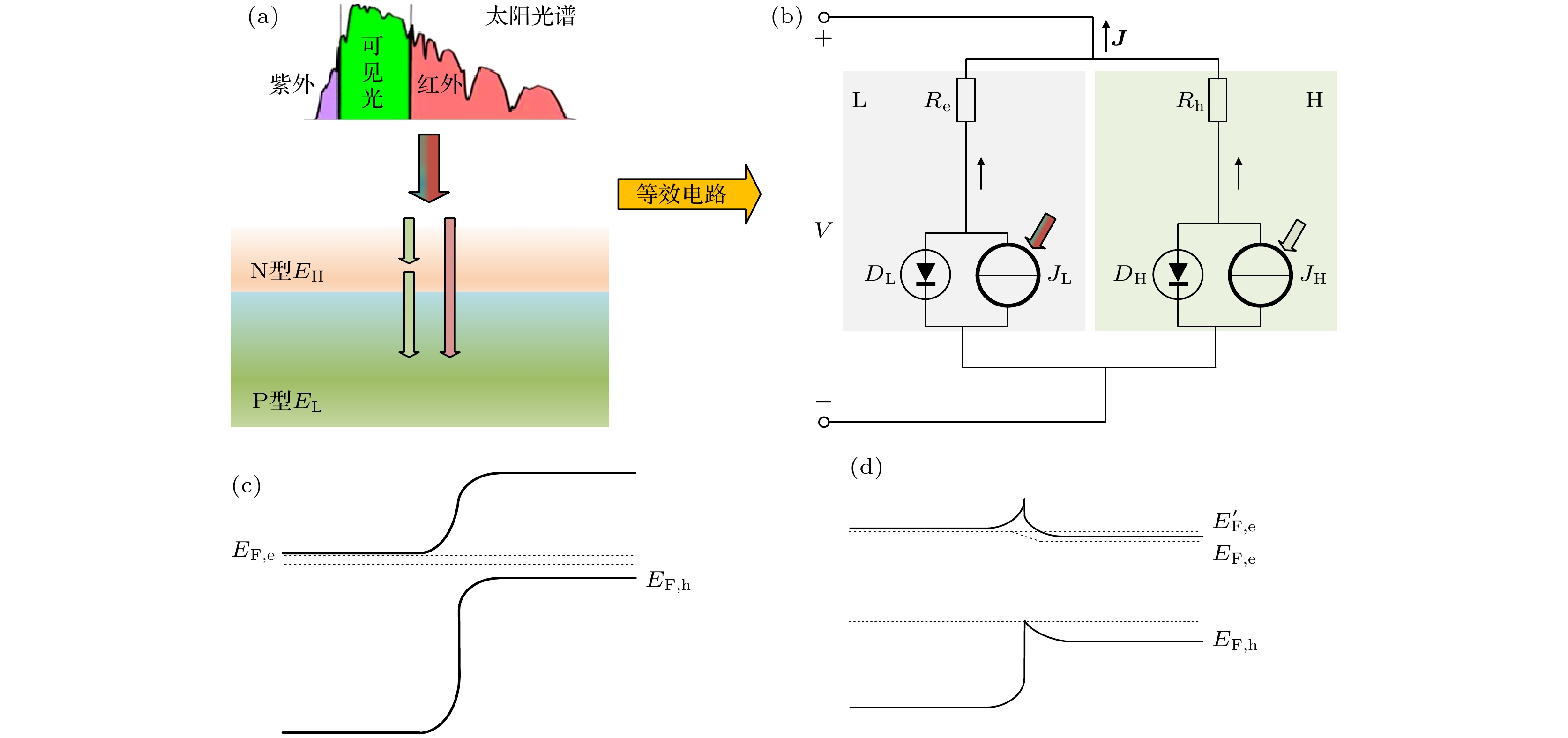
      其中, $ {\mu }_{{\mathrm{e}}/{\mathrm{h}}} $为电子/空穴迁移率; $ {J}_{{\mathrm{e}}/{\mathrm{h}}} $为电子/空穴电流密度; $ {E}_{{\mathrm{F}}, {\mathrm{e}}/{\mathrm{h}}} $为电子/空穴准费米能级; n, p为电子、空穴电荷密度. 所以, 当$ {\mu }_{{\mathrm{e}}/{\mathrm{h}}} $→∞时, $ \dfrac{{{\mathrm{d}}E}_{{\mathrm{F}}, {\mathrm{e}}/{\mathrm{h}}}}{{\mathrm{d}}x} $→0, 准费米能级保持水平.

      如图1(a)所示, 所构建的异质结太阳电池模型是由N型宽带隙半导体电池材料(禁带宽度为EH)和P型窄带隙半导体材料(禁带宽度为EL)构成, 太阳光由宽带隙一侧射入, 宽带隙材料吸收能量大于宽带隙禁带宽度的部分太阳光, 剩余波段范围内的太阳光由P型窄带隙半导体电池材料吸收. 图1(c)为异质结太阳电池在外加适当电压(V)条件下准费米能级分布保持水平, 图1(d)中$ {E'_{{\text{F, e}}}} $为 外加足够电压时S-Q模型中的电子准费米能级分布, 则在P型区域内, 电子准费米能级越过导带, 导致在P型侧准费米能级势能差($ {\mu _{\text{L}}} = {E_{{\text{F, e}}}} - {E_{{\text{F, h}}}} $)大于EL, 但μL接近EL时, 窄带隙半导体会有巨大的受激光子发射, 阻碍μL接近以及越过EL. 因此, 本文在S-Q模型基础之上, 如图2能带图所示, 假设在势垒区内载流子迁移率为有限值, 放弃S-Q模型中迁移率为无穷大值假设, N型和P型电中性区域迁移率仍为无穷大值, 形成的新费米能级分布如图1(d)中$ {E_{{\text{F, e}}}} $. 在上述假设基础之上, 本文忽略异质结电池界面处特征峰影响, 电子/空穴可以平稳、无损迁移过界面, 并且忽略N/P型材料相互光电辐射-吸收耦合影响、折射率都为1; 在势垒区, 不吸收光子, 不产生电流; 同时, 假定宽带隙材料对吸收波段范围内的光子, 吸收率(α)可在0—1内变化, 窄带隙材料吸收率为1, 其对吸收波段内的光子可以完全吸收, 其等效电路图如图1(b)所示.

      • 2.2.   理想计算模型

    • 根据黑体辐射公式, 温度为T的黑体, 辐射光子能量大于禁带宽度的光子流密度F表示为

      其中, $ \varOmega $为立体角, 单位rad; h为普朗克常数; c为光速; μ为黑体内电子和空穴之间的化学势差, 即为准费米能级电势差, 单位eV; $ {k}_{{\mathrm{B}}} $为玻尔兹曼常数; E1, E2为辐射光子能带区间下限、上限, 单位eV; y为光子能量, eV.

      如图2所示, 由于流经太阳能电池的总电流密度J是恒定的(即与x无关), 为方便起见, 选择在x = 0处进行计算:

      其中, Je是电子电流密度, 单位mA/cm2; Jh是空穴电流密度, 单位mA/cm2. 假设窄带隙材料背面完美反射, 则窄带隙材料背面无辐射输出, 假设在表界面$ -{W}_{{\mathrm{A}}} $处完美钝化, 因此Je (x =$ -{W}_{{\mathrm{A}}} $) = 0, Je计算如下:

      其中, r为电子-空穴对复合速率, 单位cm–3; g为电子-空穴对产生速率, 单位cm–3; $ {F}_{{\mathrm{e}}{\mathrm{m}}, {\mathrm{L}}} $表示窄禁带区域单位时间和单位面积发射的光子数; $ {F}_{{\mathrm{a}}{\mathrm{b}}{\mathrm{s}}, {\mathrm{L}}} $表示窄禁带区域单位时间和单位面积吸收的光子数; 在00' 势垒区范围内无电荷产生和复合, Je(x = 0) = Je(x = 0'); e为电子元电荷.

      其中Ts, Tc为太阳和环境温度, 单位K; Fabs,L/H,S/amb为宽/窄带隙材料从太阳/环境中单位时间和单位面积吸收的光子数; Fem,L,F为窄带隙材料前表面单位时间和单位面积发射的光子数. Jh计算式如下:

      其中, 假设在表界面$ {W}_{{\mathrm{B}}} $处完美钝化, 因此Jh(x = $ -{W}_{{\mathrm{B}}} $) = 0; $ {F}_{{\mathrm{e}}{\mathrm{m}}, {\mathrm{H}}} $表示宽禁带区域单位时间和单位面积发射的光子数; $ {F}_{{\mathrm{a}}{\mathrm{b}}{\mathrm{s}}, {\mathrm{H}}} $表示宽禁带区域单位时间和单位面积吸收的光子数; 势垒区无电荷产生和复合, Jh(0)= Jh(0').

      其中, (6)式和(8)式中μH, μL为宽带隙和窄带隙材料的准费米能级电势能差.

      根据连续性方程(1)和(2), 可得

      其中, R为电阻, 单位Ω·cm2. 至此本文推导了势垒区有限迁移率与电阻之间的物性关系, 考虑宽带隙材料吸收率的影响, 最终I -V方程为

      其中, 例如α = 1表示宽带隙半导体材料对波长范围内的光子全部吸收; α = 0.2表示宽带隙半导体材料对波长范围内的光子吸收20%, 剩余80%透过宽带隙半导体材料由窄带隙材料吸收.

    3.   结果与分析

    • 本节在第2节模型推导基础之上, 对(4)—(10)式迭代求解, 得到不同(α, EL, EH, Re, Rh)数据组的I-V曲线, 着重分析和研究(α, EL, EH, Re, Rh)对电池转换效率(Eff)、填充因子(FF)、开路电压(Voc)、短路电流(Jsc)电池电性能参数影响及其机理.

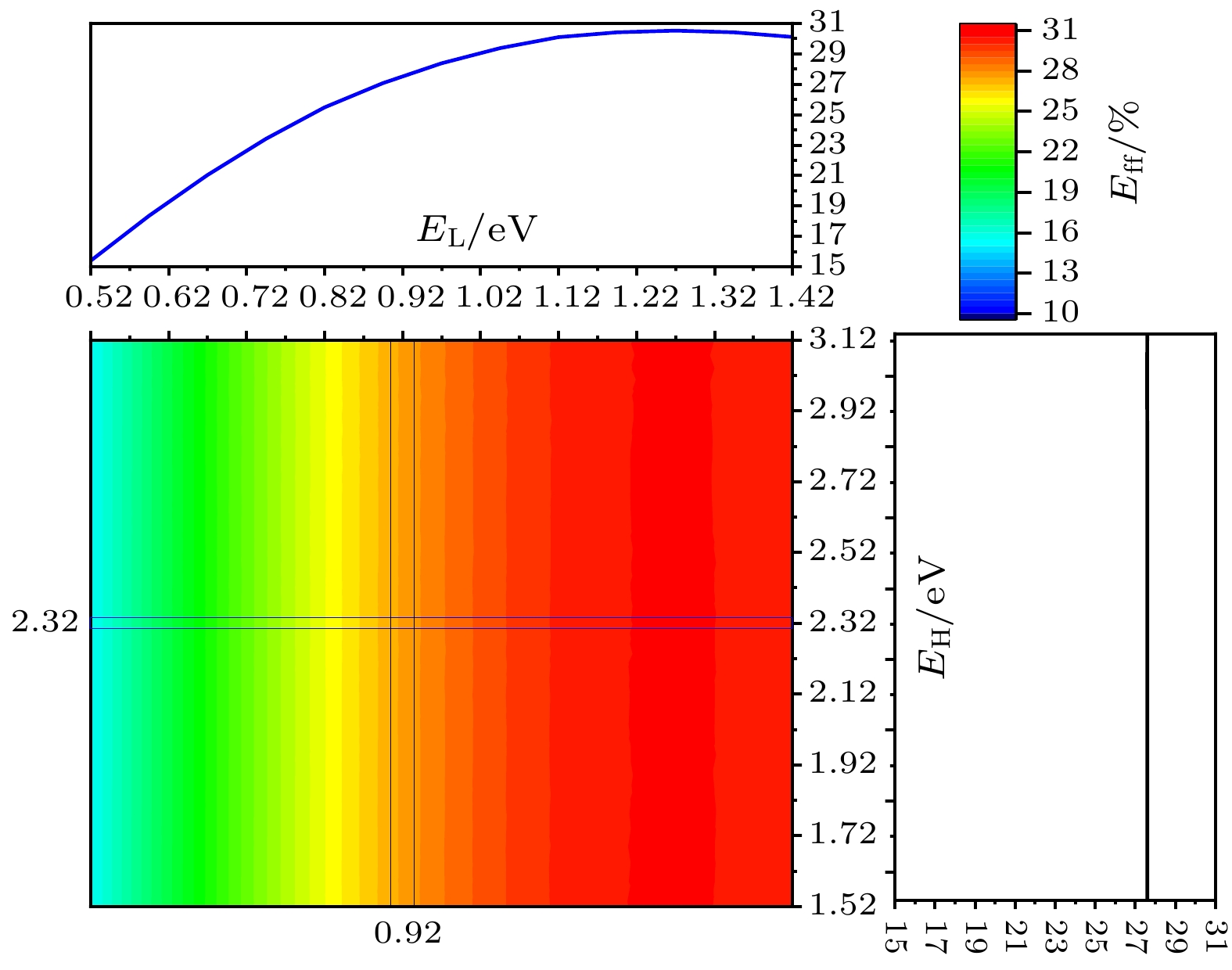
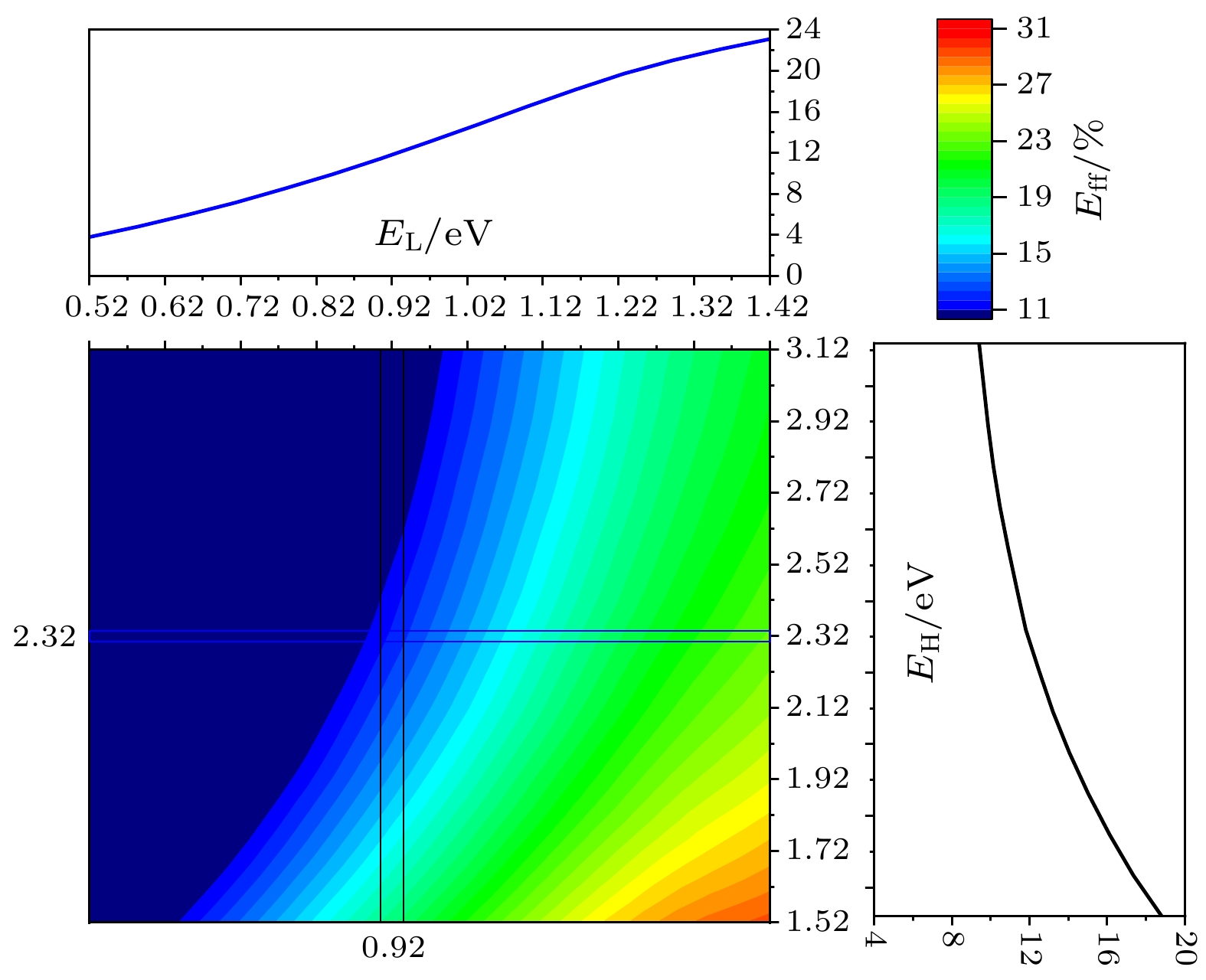
      当Re, Rh都取较小值时, 效率分布与同质结太阳电池相近, 如图3所示Eff等高线及剖面图, 从纵向上, 固定EL值, 随着EH增大, Eff保持不变, 如图中右侧剖面图所示; 从横向上, 固定EH值, 随着EL增大, Eff先增大后减小. 此时, 空间势垒区迁移率较大, 对载流子阻碍较小, 对电池电性能影响较小, DL, DH所受电压近似为外加电压, 即$ {\mu _{\text{L}}} = V + {J_{\text{e}}}{R_{\text{e}}} \approx V < {E_{\text{L}}} $, $ {\mu _{\text{H}}} = V + {J_{\text{h}}}{R_{\text{h}}} \approx V < {E_{\text{H}}} $, EL为主要限制条件, 计算结果表明EL在1.22—1.32 eV之间时候取得最优转换效率, 约为30.5%, 与EH取值无关. Re = 0.1 Ω·cm2, Rh = 0.1, 1 Ω·cm2时, 与图3中具有相似计算结果, 文中未展示具体结果.

      • 3.1.   支路L对电性能影响

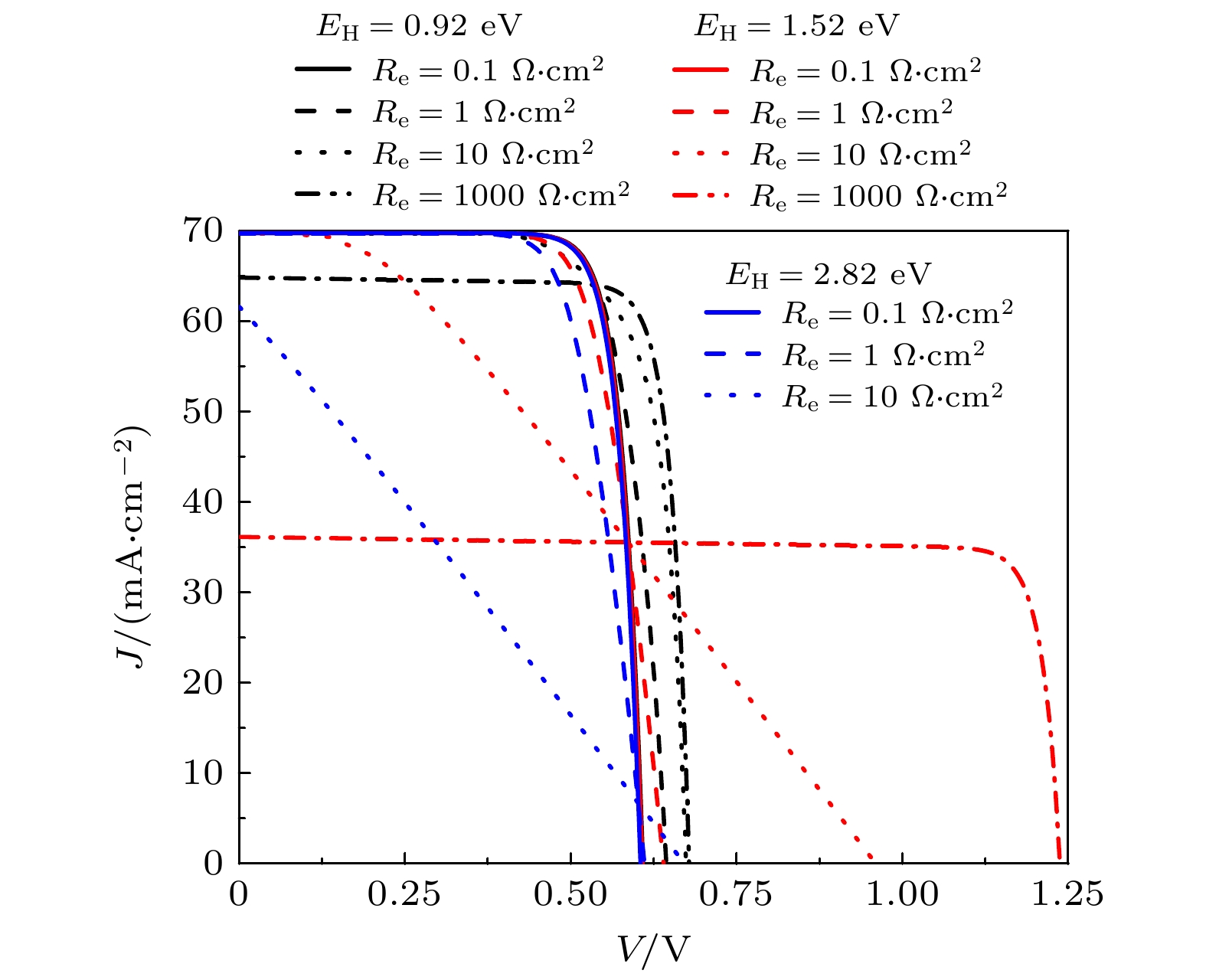
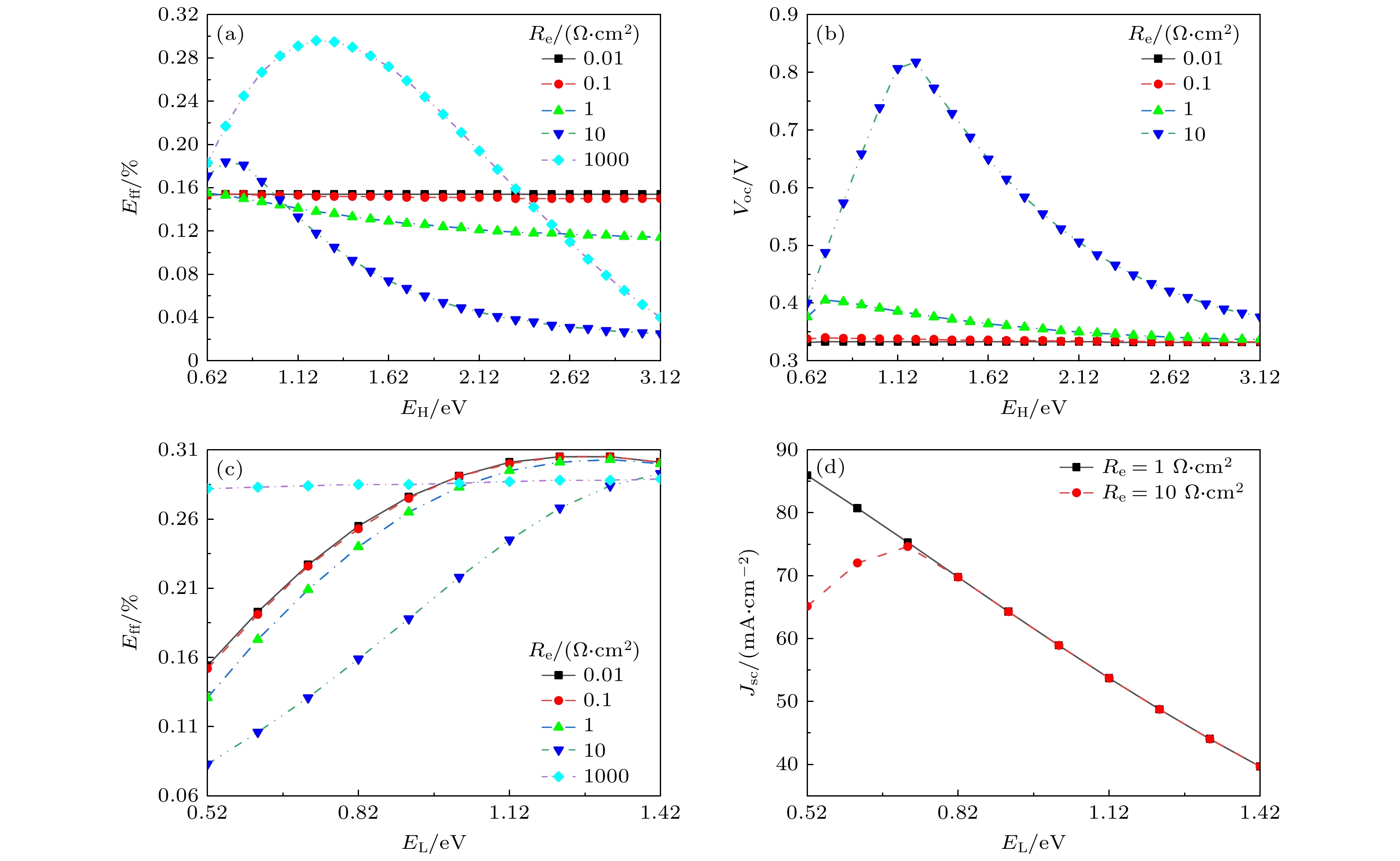
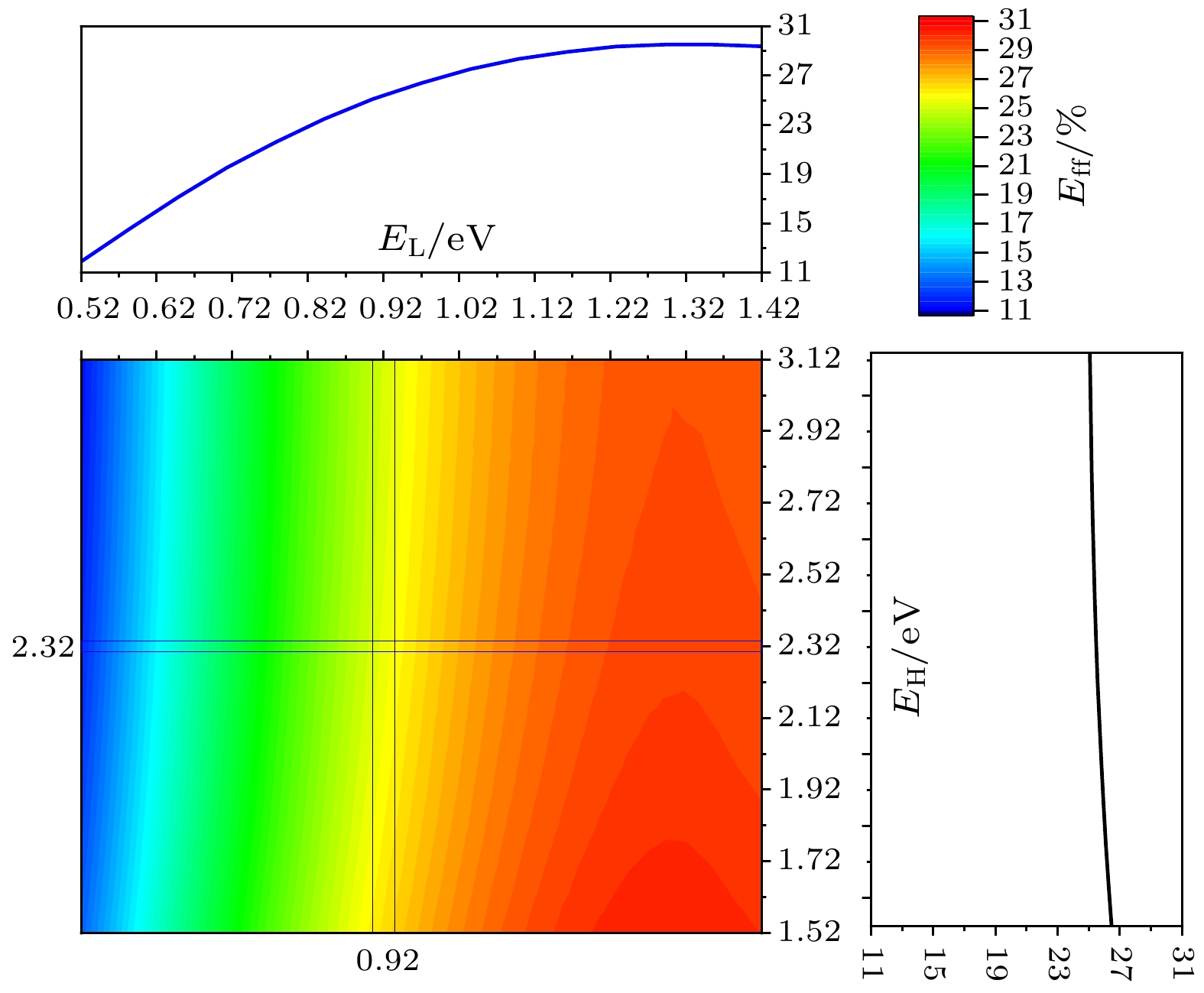
    • 本节在第2节基础之上着重分析图1(b)左侧支路L对电池电性能影响. 由图3可知, Re = 0.01 Ω·cm2, Rh = 0.01 Ω·cm2时, 可忽略Re和 Rh的影响, EL是限制电池电性能参数的主要因素, 与EH几乎无关. 图4所示为Re = 0.1, 1, 10, 1000 Ω·cm2时的太阳电池I-V曲线, 电池电性能受到EL, EH及Re的综合影响, 变化趋势更加复杂. 在给定EH和Re条件下, EL增大, 有利于提高太阳电池Voc, 但降低了太阳电池Jsc. 结合图1(b), L支路流过正向电流时, L支路中DL的电压为$ {\mu _{\text{L}}} = V + {J_{\text{e}}}{R_{\text{e}}} $, 随着Re逐渐增大, 此时不能忽略JeRe项对电性能的影响, Re增强了DL辐射复合电流; 继续增大外加电压V, L支路流过反向电流, 此时Re抑制了DL辐射复合电流, 其具体体现为Re = 0.1, 1, 10 Ω·cm2时Voc逐渐增大; Re取足够大时, 如Re = 1000 Ω·cm2, L支路视为断路, 只有H支路对外输出电能, 视为同质结太阳电池, 电池Voc不受EL限制影响. 随着EH增大, 不同EL和Re值的影响会有明显差异, 本文将在下述内容中针对典型Re值, 进一步阐述EL-EH组合导致的电性能变化趋势和机理.

      图5所示为Re = 1 Ω·cm2时 Eff关于EL, EH变化趋势图. 固定EL值, 随着EH增大, Eff下降, 如图5中右侧剖面图, 而图3中保持不变, EH逐渐增大, 窄带隙材料层吸收的光子数目增多, 光生电流变大, 但此时JeRe对μL增大作用增强, 复合损失增大, 导致电池转换效率下降. 但如图6(a), (b)所示, 当Re = 10, 1000 Ω·cm2时, EH从EL+0.1 eV增大, Eff和Voc均呈现先增大后减小趋势, 并且Re越大现象越明显. EL固定, 太阳电池Jsc最大值也即固定, 根据上述分析Re具有流过正向电流时增强准费米能级势能差、流过反向电流时削弱准费米能级势能差的作用, Re = 0.01, 0.1, 1 Ω·cm2时, 与图5右侧剖面图结果趋势一致, 但Re = 10, 1000 Ω·cm2时, EH增大, L支路中DL的辐射复合电流增大, 同时H支路DH的辐射复合电流降低, 且该阶段DH中降低的辐射复合起主要作用; 继续增大EH, DL中增大的辐射复合起主要作用, 所以其物理过程体现在电池性能上即为图6(a), (b)中电池Eff和Voc呈现先增大后减小的趋势. 固定EH值, 随着EL增大, Eff先提高后趋于稳定略下降, 如图5中上方剖面图, 与图3中趋势一致. 同样地, EL是限制Eff的主要因素, 起决定性作用. 另外, 根据计算结果, EL固定取值越大, Eff随EH增大而变化的幅度越小, 且Eff最大值提升明显, EL在1.22—1.42 eV之间Eff取得最大值; EH固定取值越大, Eff随EL增大而变化的幅度越大.

      图7所示为Re = 10 Ω·cm2时Eff关于EL, EH变化趋势图. 沿着EH轴增大, Eff下降趋势明显, 较图5中下降趋势更加明显; 沿着EL轴增大, Eff逐渐升高, 但较图3和图5电池的效率损失增大. 并且, Re = 10 Ω·cm2时的Eff值较Re = 0.01, 1 Ω·cm2时的Eff值明显下降. 但此时, EL依然起到决定性作用. 如图6(c), (d)所示典型电参变化曲线, 整体上与Re = 1 Ω·cm2时相比, Re = 10 Ω·cm2时电参数变化具有不一样变化趋势. Re = 1 Ω·cm2时, 随着EL增大, Jsc降低, 电池辐射复合损失降低, 所以Eff, Voc和FF都提升. 但Re = 10 Ω·cm2时, 如图6(c), (d)所示, Jsc先增大后减小, 其原因是流过DL的辐射复合电流为主导项, 根据计算数据, 即使当外加电压V = 0时μL也接近EL值, 辐射复合损失电流较大, 所以随着EL增大, EL与μL差值增大, 辐射复合损失降低, 所以Jsc增大; 继续增大EL, EL对Jsc的限制作用起主导作用, 所以Jsc下降.

      Re = 1000 Ω·cm2时, L支路接近断路, V在0—Voc范围内Je ≈ 0, 此时, 起限制性作用的为EH, 近似为同质结电池, 所以如图6(c)所示Re = 1000 Ω·cm2时Eff -EL变化曲线, EL对电池性能几乎没有影响, 同时此时Voc超过了EL的限制.

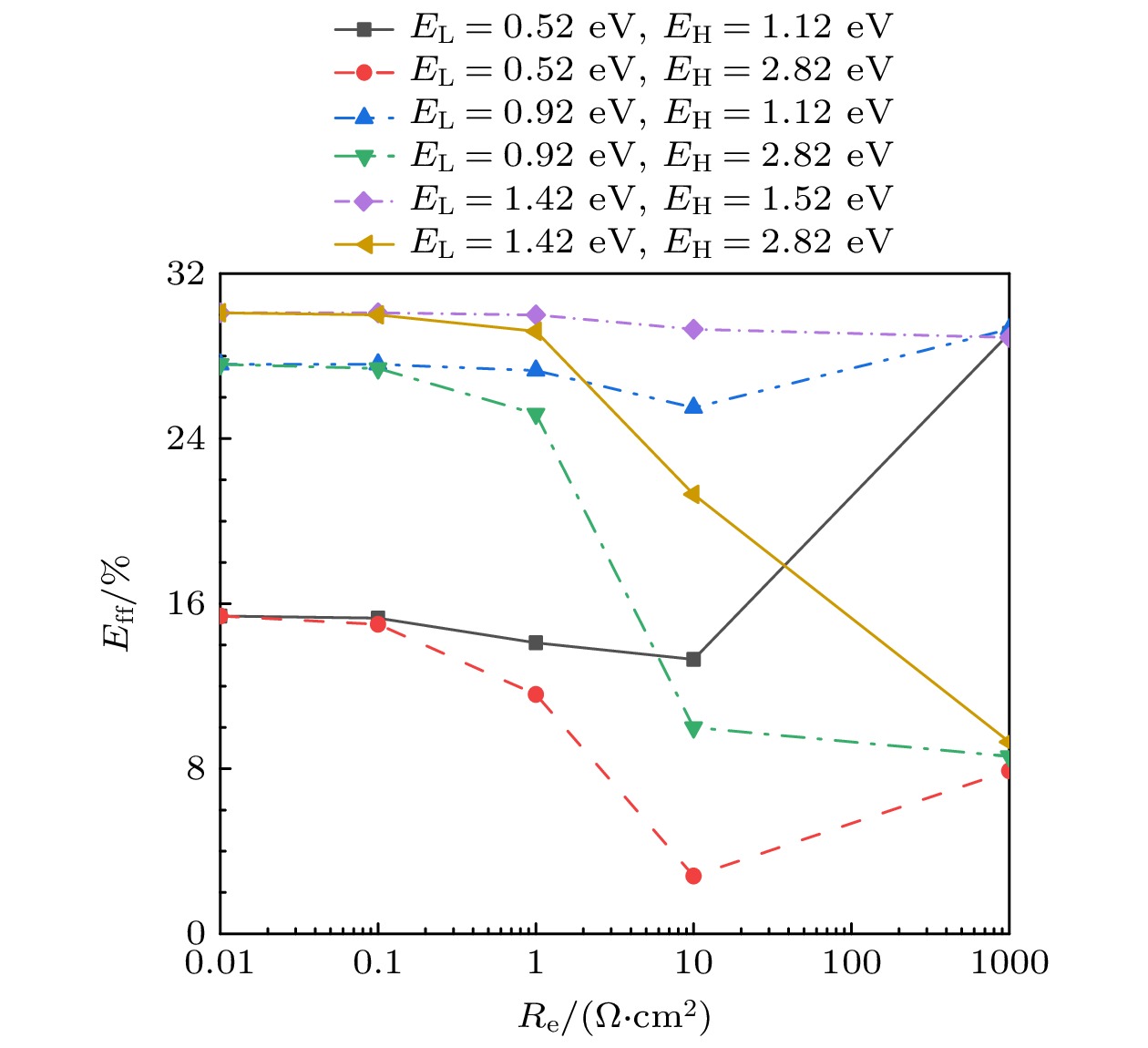
      图8为Eff关于Re的变化曲线. Re在0.01—10 Ω·cm2之间变化时, 电池Eff逐渐降低, 但EL越大、EH越小, 效率越大, 并且随Re变化导致的Eff衰减幅度越小, 如图8中当Re = 1000 Ω·cm2时转化效率反而得到提升, 此时L支路视作为断路状态, 电池接近为同质结, 提升了转换效率.

      • 3.2.   支路H对电性能影响

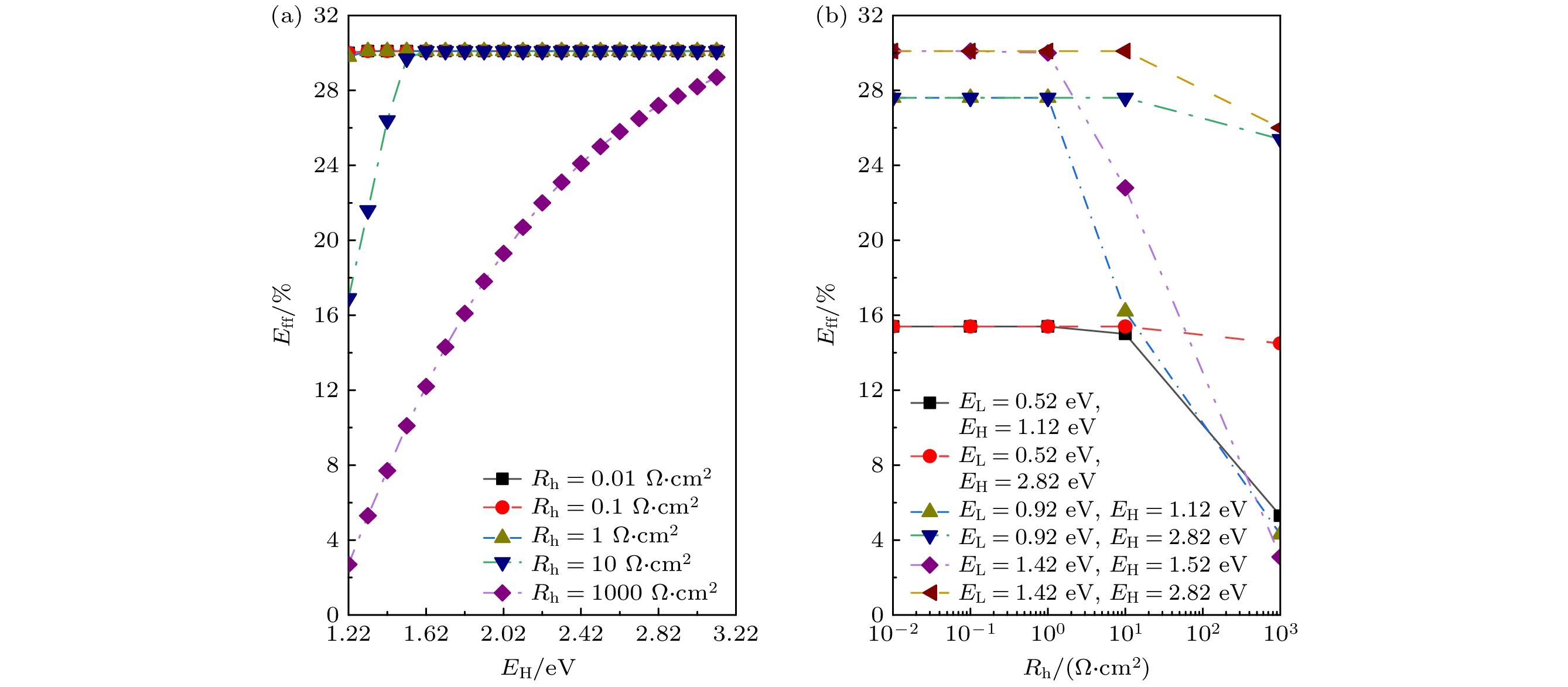
    • H支路主要受EH和Rh影响, 与L支路没有关系. 本小节在第2节基础之上着重分析图1(b)左侧支路H对电池电性能影响. 如图9(a)所示计算结果, 在Rh = 0.01, 0.1, 1 Ω·cm2时, Eff随着EH增大曲线几乎没有变化; Rh = 10 Ω·cm2时, 随着EH增大, Eff逐渐提升, 并在1.62 eV与Rh = 0.01, 0.1, 1 Ω·cm2的曲线重合; Rh = 1000 Ω·cm2时, Eff随着EH增大而增大, 向Rh = 0.01, 0.1, 1 Ω·cm2的曲线逐渐逼近. 结合3.1节分析, 因为EH较大, Rh = 0.01, 0.1, 1 Ω·cm2时造成的辐射复合可忽略, 所以3条曲线重合. 而当Rh = 10 Ω·cm2时, JhRh对μH起到增强作用, EH ≤ 1.52 eV时, 即使V = 0, μH = JhRh ≈ 0.3 V, 明显增强准费米能级势能差, 随着V增大, H支路不能忽略JhRh对费米能级裂分增强作用; 而EH > 1.52 eV时, JH降低, 相同外加电压V, EH与μH差值增大, 可以忽略辐射复合. 所以Eff逐渐增大, 同样Voc和FF具有相同变化趋势; 而Jsc随着EH增大保持不变, 这是因为在V = 0时, EH与μH = JhRh差值较大, 激发的辐射复合损失较小, 几乎可以忽略. 当Rh = 1000 Ω·cm2时, 可以认为H支路断路, L支路起主要限制作用, 随着EH增大, L支路光生电流增大, 电池Jsc增大, Voc增大, FF和Eff增大.

      • 3.3.   α对电性能影响

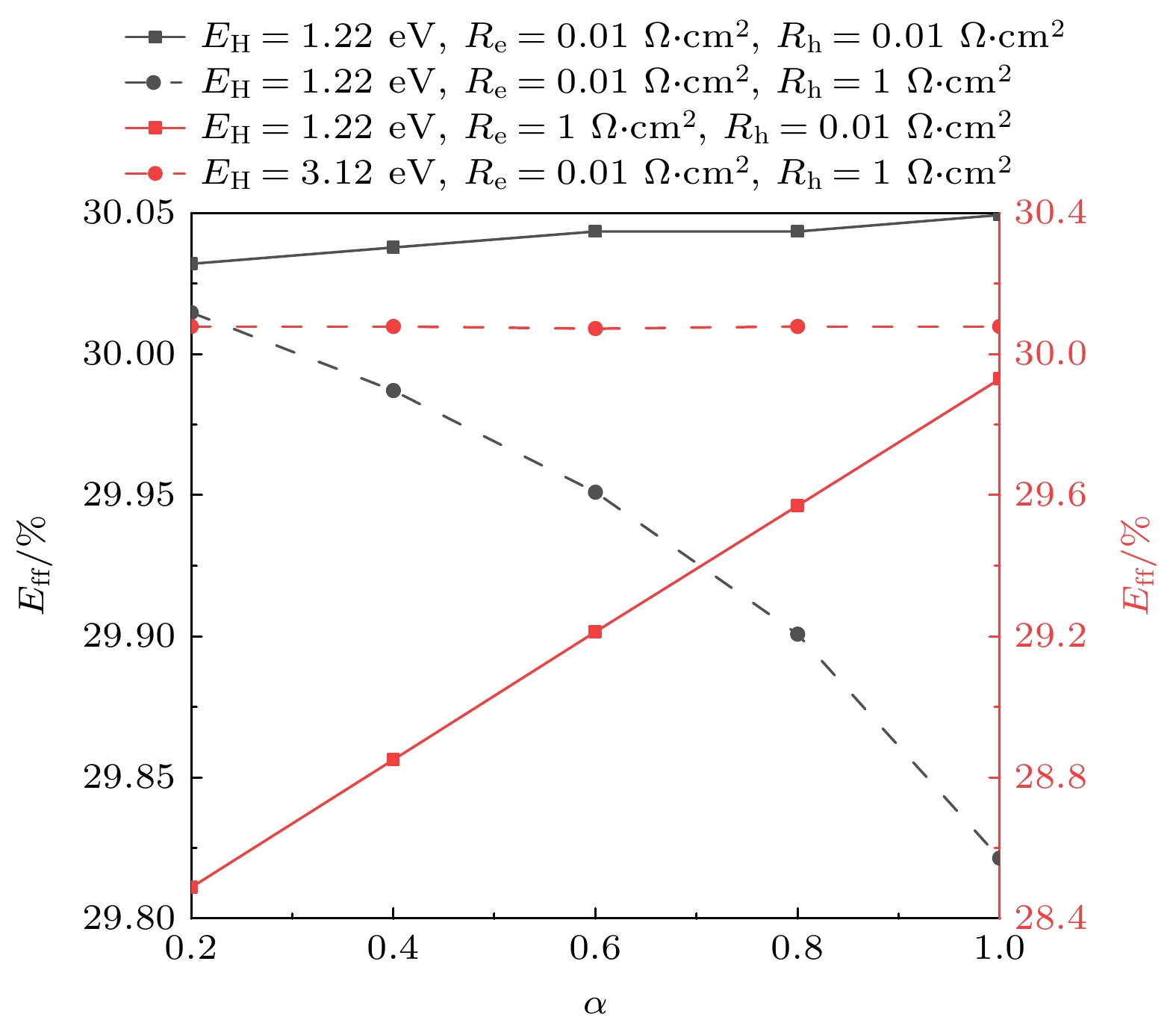
    • 本节将通过调整宽带隙材料吸收系数α, 分析顶层宽带隙材料吸收系数为0.2, 0.4, 0.6, 0.8, 1.0条件下Re取为0.01, 0.1, 1 Ω·cm2及Rh取为0.01, 0.1, 1 Ω·cm2时的异质结电池电参.

      α越小, 透射光子越多, JH越小, JL越大, 相当于H支路的光学带隙降低, 但电学带隙保持不变. 由3.1节和3.2节可知, Rh的影响小于Re的影响, α越小, L支路电流越大, Re增强准费米能级分裂作用, 导致L支路辐射复合损失增大, 必然导致Eff下降, 并且Re越大, 效率损失越严重, 如图10所示, Re = 1 Ω·cm2和α = 0.2时Eff最小. H支路上, α越小, JH降低, EH足够大时, 如EH = 3.12, α的影响可以忽略不计; EH接近EL时, H支路电流增大, Rh增强准费米能级分裂作用, 降低α可以降低辐射复合损失, 增大转换效率, 如图Rh = 1 Ω·cm2时的计算结果, 但在Rh较小时, 可以忽略H支路复合损失, 增大α可以降低L支路的辐射复合损失, 如图Rh = 0.01, 0.1 Ω·cm2时的计算结果.

    4.   结　论

    • 本文在光伏电池S-Q极限理论基础之上, 将势垒区无穷大迁移率假设改为有限迁移率假设, 进而推导出势垒区迁移率与电阻间的内在物理表达, 从而构建了异质结电池S-Q理论极限模型. 电池性能受到α, EL, EH, Re和 Rh多重影响, 趋势复杂, 本文以顶层N型宽带隙材料、底层P型窄带隙为例, 逐个分析了电子空穴迁移率(表现为电阻Re)和空穴迁移率(表现为电阻Rh)对不同EL, EH组合电池的影响.

      Re, Rh取较小值时, EL在1.22—1.32 eV之间取得最优转换效率. 增大Re可以提高太阳电池Voc, 但太阳电池Eff和FF存在损失, 当Re足够大时, 例如Re = 1000 Ω·cm2时, 太阳电池开路电压不受EL限制, 而由宽带隙材料带隙EH限制; 增大Rh同样降低了电池Eff和FF, 但其影响程度小于Re. 吸收系数的变化, 使得L和H支路光生电流发生变化, 进而可以对L或者H支路的辐射复合损失进行调控.

    参考文献 (20)

目录

/

返回文章
返回