-
最大割问题(MCP)[1]作为组合优化领域的一个经典问题, 在包括统计物理、图像处理等诸多领域有重要应用. 然而, 除了一些特殊情形, 最大割问题仍是一个非确定性多项式时间(NP)完全问题, 目前没有已知的高效经典算法可以在多项式时间内完成求解. 针对最大割问题常见的解决策略是采用近似优化算法去逼近最优解, 并通过逼近率来衡量算法的有效性. 现有研究普遍认为, 即使不要求精确得到最优解, 取得逼近率超过
$ 16/17 $ (近似为$ 0.9412 $ )的解仍是NP难问题[2]. 目前相对最有效的经典策略是Goemans-Williamson算法, 可实现约$ 0.878 $ 的逼近率, 但距理论上限仍有相当距离[3].另一方面, 以量子计算为代表的先进算力正在为许多经典难题提供新的解决方案, 并在诸多有重大价值的关键领域, 如新型材料、医药研发、信息安全、人工智能等方面展现了巨大的应用潜力. 然而, 受限于当前操控水平, 量子计算体系正处于所谓含噪的中等规模量子(NISQ)[4]时代, 其特点是缺乏量子纠错应对噪声的干扰, 计算规模有限, 适用于浅层低复杂度的量子算法线路的模拟. 为此, 如何在NISQ时代, 探索与之相适应的量子算法[5-8], 发挥量子计算的优势成为一个重大的挑战. 这其中, 量子近似优化算法(QAOA)[9]作为一种新兴的量子算法, 在组合优化问题上展现了巨大潜力, 引起了广泛的关注.
QAOA算法的基本思路是通过量子态的迭代演化逐渐逼近问题的最优解. 由于具备在多项式时间内找到近似全局最优解的潜力, QAOA在处理部分复杂的优化问题时尤有价值. 有鉴于此, 近年来借助QAOA算法解决最大割问题, 实现超经典算法的量子优势成为当前研究的热点. 然而, QAOA解决最大割问题面临的一个关键挑战是其使用的量子线路往往较深, 需要的双比特量子逻辑门个数也较多(如受控非门)[10-15]. 这使得其在缺乏量子纠错保护的NISQ设备上的实际运行效果大打折扣, 特别是随着量子线路深度的增加, 噪声累积问题变得尤为严重, 极大地限制了QAOA的性能表现[16-19].
近年来, 为了提升QAOA在NISQ体系中的实际性能, 研究人员开发了多种变体. 这些变体主要分为两大类. 第一类是通过将QAOA与特定结构相结合来增强性能. 例如, Chandarana等[20]提出的DC-QAOA在传统QAOA中加入了与问题相关的反绝热驱动项, 这一策略不仅加快了算法的收敛速度, 而且减少了所需的线路深度. 同样, Magann等[21]提出的FALQON+通过针对性的QAOA初始化过程, 有效改进了8—14个节点的非同构图上标准QAOA的初始化效果. 此外, Chalupnik等[22]通过增加一个多参数的问题无关层而提出的QAOA+, 实现了对多种问题的泛化能力, 尤其是在处理随机正则图上的最大割问题时显著提升了逼近率. Sun等[23]考虑到平移不变性对QAOA性能的影响, 从而在应用QAOA时, 使量子线路与待求解问题的对称性保持一致, 可以有效提升其效率和准确度.
第二类变体旨在优化QAOA的线路模型结构来提升低深度QAOA的逼近比. 例如, Wurtz和Love[24]提出的ST-QAOA利用经典近似解来构建特定问题的量子线路, 实现了与经典算法相当的性能, 并在低深度条件下超越了传统QAOA. Wang等[25]通过引入Quantum Dropout, 并选择性地精简部分量子线路来维持总损失函数不变, 在一些组合优化问题上提升了QAOA的性能表现. 此外, Herrman等[26]提出的MA-QAOA线路模型通过为问题哈密顿量和混合哈密顿量中的每个元素分配独立的参数, 提高了算法的灵活性和逼近率.
尽管现有研究在一定程度上提高了低深度QAOA的逼近率, 但在追求高逼近率的情况下, 线路的深度仍然是一个挑战. 本文面向最大割问题, 设计了一种浅层低复杂度的QAOA线路模型. 特别地, 与QAOA+在完整的QAOA层之后引入与X旋转门的形式引入问题无关层不同, 本文通过在最大割问题的QAOA目标哈密顿量中引入泡利Y旋转门, 改善了单层QAOA的逼近率. 在至多15个节点的最大割问题上验证了该线路. 结果显示, 与标准QAOA算法相比, 尽管增加了经典优化参数的数量, 但逼近率获得显著提升, 这意味着达到更接近最优解所需的层数和双比特量子逻辑门个数显著降低, 从而显著降低了量子噪声对量子线路的影响, 更适用于当前NISQ计算设备. 进一步地, 将这一方法与其他QAOA及其变体, 包括MA-QAOA和QAOA+进行了对比, 发现在全连接图、正则图和随机图的最大割问题上, 本文提出的方法在相似复杂度的情况下, 能够实现更高的逼近率.
-
最大割问题[1]是图论中的一个经典NP难问题, 其目标是求一种分割方法, 将一个图的节点分割成两个互不相交的子集, 以使得被切断的边数量最大. 具体来讲, 在一个无向图
$ G=(V, E) $ 中, V表示图G的节点集, E表示图G的边集. 那么该图上的割是指将图的节点集V分割成两个互不相交的集合$ (V1, V2) $ 的一种划分方式, 其中每个割对应一个边集合, 这些边的两个节点被划分在不同的节点集合中. 割的大小可定义为这个边集合的大小, 即被割开边的条数. 最大割问题即找到一个割开边数最多的分割方法.令
$ {{z}_{u}} $ 表示节点u ($ u\in V $ )所处的集合(集合0、集合1), 即$ {{z}_{u}}\in \left\{ 0, 1 \right\} $ . 当$ (u, v)\in E $ 时, 用$ {{p}_{(u, v)}} $ 的值表示边$ (u, v) $ 是否为被割边, 0代表不是被割边, 1代表是, 即$ {{p}_{(u, v)}}\in \left\{ 0, 1 \right\} $ , 则有这样, 一个割的被割边的条数C为
最大割问题的目标就是最大化C, 此时图G的节点划分就是问题的解.
-
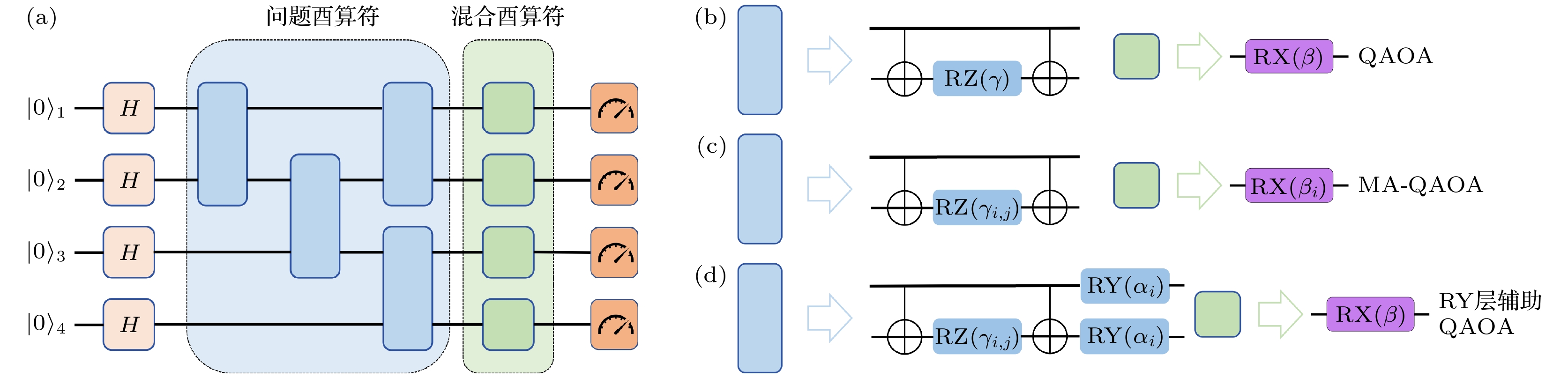
QAOA(量子近似优化算法)是一种受绝热量子计算启发的量子算法, 其核心思想是将经典优化问题映射到量子哈密顿量上, 并通过一系列参数化的酉变换优化量子态, 使得该量子态的期望值尽可能接近优化问题的最优解. 完整起见, 本文将其过程概述如下(详情可参见文献[9]). QAOA算法的量子演化线路由两个交替出现的酉算符组成: 问题酉算符和混合酉算符, 一个问题酉算符和一个混合酉算符对应QAOA的一层(层数一般用p表示, 单层则
$ p=1 $ ), 框图如图1所示. 其中, 问题酉算符一般定义为其中,
$ {{H}_{\mathrm{C}}} $ 表示问题哈密顿量; γ表示角度, 为问题酉算符的参数,$ \gamma \in \mathbb{R} $ . 混合酉算符定义为其中,
$ \beta \in[0, \pi] $ ,$ H_\mathrm{B} $ 是所有单比特泡利X算子的和, 也称为混合哈密顿量, 即若QAOA量子线路层数为p, 则对于任意整数
$ p>1 $ 和$ 2 p $ 个角度$ \gamma_1, \cdots, \gamma_p \equiv \mathit{\boldsymbol{\gamma}} $ 和$ \beta_1, \cdots, \beta_p \equiv \mathit{\boldsymbol{\beta}} $ , 可定义角度依赖的量子态为其中, γ和β的下标代表量子线路的层数,
$ \left| { s } \right\rangle $ 表示所有基态的均匀叠加态, 即通过经典优化器优化参数
$ \left( {{\mathit{\boldsymbol{\gamma}} }^{*}}, {{\mathit{\boldsymbol{\beta}} }^{*}} \right) $ , 使(6)式中量子态$ |\mathit{\boldsymbol{\gamma}}, \mathit{\boldsymbol{\beta}} \rangle $ 对应的$ {{H}_{\mathrm{C}}} $ 期望值$\langle {{C}}\rangle $ 尽可能接近优化问题的最优解, 即完成QAOA的求解, 如图1所示. -
最初提出的QAOA算法并非对于任何特定类别的优化问题都是最优的. 事实上, 越来越多的研究表明, 针对不同的问题, QAOA变体往往有更好的性能表现. 下面简单介绍两种常用的主流QAOA变体, 方便后续做对比.
1) 多角度QAOA
Herrman等[26]提出了多角度QAOA (MA-QAOA)来改进QAOA. MA-QAOA通过增加可变参数来提高逼近率, 量子线路结构如图1(c)所示. 该变体在量子线路的问题酉算符层和混合酉算符层增加了角度参数. 传统的QAOA可视为MA-QAOA的特例. Herrman等[26]的研究表明, 相同逼近率下, MA-QAOA与标准QAOA相比所需要的量子线路更浅.
2) QAOA+
Chalupnik等[22]提出了一种称为QAOA+的QAOA变体. 该变体在传统的
$ p=1 $ 的QAOA基础上, 增加了一个额外的多参数、问题无关的层. QAOA+可以在保持线路深度低于$ p=2 $ QAOA的情况下, 获得比$ p=1 $ QAOA更高的逼近率, 该量子线路图如图2所示. -
QAOA通常采用梯度下降法进行参数优化, 其参数量将随着QAOA层数的递增而显著增长. 同时, 伴随梯度下降时出现的指数级衰减现象, 整个线路的参数优化复杂度急剧上升, 这成为QAOA在实际应用中所面临的重要挑战. 另外, QAOA的层数增多也会给NISQ硬件平台带来巨大的实现压力. 这是因为NISQ硬件通常具有有限的相干时间和较高的双比特量子逻辑门错误率, 难以应对过多的线路层数. 因此, 如何在现有硬件条件下实现QAOA的有效利用就显得尤为关键. 这促使我们设计一种既能够充分利用NISQ体系的计算能力, 又能够避免由于层数过多带来的错误累积问题, 高效解决最大割问题的QAOA策略, 由于引入了绕Y轴的旋转操作, 我们称之为RY层辅助QAOA.
在标准的QAOA单层线路中, 通常在问题层后使用一层RX门(即泡利X旋转门)进行混合操作. 考虑到组合优化问题的特征, 每个问题层可以进一步细分为多个问题单元. 我们提出的RY层辅助QAOA, 将混合操作具体化到每个问题单元上. 具体来讲, 就是在问题酉算符层引入包含独立参数的RY门(即泡利Y旋转门), 如图1(d)所示. 在每个量子比特实现了任意的幺正操作, 从而扩大了希尔伯特探索空间, 显著提升了单层算法的性能. 以最大割问题为例, RY层辅助QAOA策略如下.
1) 制备初始量子态: 根据问题图的大小确定量子线路的量子比特个数n. 从n个
$|0\rangle $ 量子比特出发, 对每个量子比特进行H门操作可以得到系统初始量子态$|s\rangle $ , 其中$|s\rangle $ 如(7)式所示.2) 问题哈密顿量的构建: 将
$ z={(Z+I)}/{2}\; $ 代入(2)式中(I, Z分别为单位算子和泡利Z算子), 并省略式中单位算子, 可得到最大割问题目标函数对应的问题哈密顿量$ {{H}_{\mathrm{C}}} $ [9]:3) 构造RY层辅助QAOA量子线路: 根据问题哈密顿量构造QAOA问题层量子线路, 在问题层线路后面引入RY层. 这样, 问题层酉算符可以表示为
(10)式和(11)式是应用Trotter分解法(即
$ \mathrm{e}^{\hat{A}+\hat{B}} \approx \mathrm{e}^{\hat{A}} \mathrm{e}^{\hat{B}} $ )得到的, 式中E表示问题图边, 序号集合$ {\mathit{\boldsymbol{{t}_{k}}}}=\left( {{t}_{k, 1}}, {{t}_{k, 2}}, \cdots , {{t}_{k, 2 m}} \right) $ , k为QAOA线路中的层数, m是问题图边的数量, Y是泡利Y算子. 酉算子$ \mathop{\mathrm{e}}^{-\mathrm{i}{{\gamma }_{k}}{{Z}_{u}}{{Z}_{v}}} $ 可以由CNOT门和RZ门(即泡利Z旋转门)组合实现. 推导如下:因此,
$ U\left( {{H}_{\mathrm{C}}}, {{\gamma }_{k}}, {{t}_{k}} \right) $ 可以表示为对于混合酉算符,
$ {{H}_{\mathrm{B}}} $ 为生成元,$ {{\beta }_{k}} $ 为旋转角度参数, 将$ U\left({{H}_{\mathrm{B}}}, {{\beta }_{k}} \right) $ 的值代入, 可以得到其中, X是泡利X算子. 酉算子
$ \mathop{\mathrm{e}}^{-\mathrm{i}{{\beta }_{k}}{{X}_{{v}}}} $ 可以由RX门实现,$ U\left({{H}_{\mathrm{B}}}, {{\beta }_{k}} \right) $ 可以表示为4) 求解期望值: 初始量子态通过p层QAOA量子线路得到输出量子态:
通过对
$ \left| { \mathit{\boldsymbol{\gamma}} , \mathit{\boldsymbol{\beta}} , \mathit{\boldsymbol{t}} } \right\rangle $ 进行测量, 得到$ {{H}_{\mathrm{C}}} $ 在$ \left| { \mathit{\boldsymbol{\gamma}} , \mathit{\boldsymbol{\beta}} , \mathit{\boldsymbol{t}} } \right\rangle $ 上的期望值$ \langle C\rangle $ ,5) 参数优化: 优化量子线路中的参数, 使得
$ {{H}_{\mathrm{C}}} $ 在对$ \left| { \mathit{\boldsymbol{\gamma}} , \mathit{\boldsymbol{\beta}} , \mathit{\boldsymbol{t}} } \right\rangle $ 上的期望值尽可能大.6) 重复执行: 重复进行步骤4)和5), 直到结果收敛, 得到最佳参数
$ \left({{\mathit{\boldsymbol{\gamma}} }^{*}}, {{\mathit{\boldsymbol{\beta}} }^{*}}, {{\mathit{\boldsymbol{t}}}^{*}} \right) $ .7) 输出结果: 初始量子态通过RY层辅助QAOA后得到输出量子态, 经多次测量取最优解输出.
在最大割问题中, CNOT-RZ-CNOT门的数量与问题图边的数量有关. 每多一条边, 需要在每层量子线路中, 增加两个RY旋转门, 引入两个参数. 虽然增加的RY门会加深单层线路的深度, 增加参数优化的计算量, 但由于其会显著增加单层算法的学习和模拟性能而降低线路层数, 对整体量子线路而言, 深度反而会降低, 同时整个线路所实现的逼近率也会获得显著提升.
-
本文使用MindSpore Quantum [27]量子计算框架, 实现了标准QAOA及其主流变体MA-QAOA和QAOA+, 并与本文提出的RY层辅助QAOA进行了对比实验. 选取的最大割问题涵盖了多种图结构, 包括完全图、3-正则图、4-正则图, 以及边概率在0.3—0.5之间的随机图, 如图3所示. 完全图代表了节点之间密集连通的系统, 3-正则图和4-正则图则提供了更为统一的网络拓扑, 而随机图则模拟了较为不可预测的情况. 受经典计算机模拟能力所限, 与当前主流实验一样, 本文所用图的规模设定为从5节点到15节点不等, 考察不同图复杂情况下的算法性能. 并通过节点数不断上升变化的过程对比分析本文提出的量子线路与标准QAOA及其变体在随着问题复杂性而展现的可拓展性. 本文采用的进行参数优化的优化器为Adam, 学习率设为0.05, 迭代次数为200次.
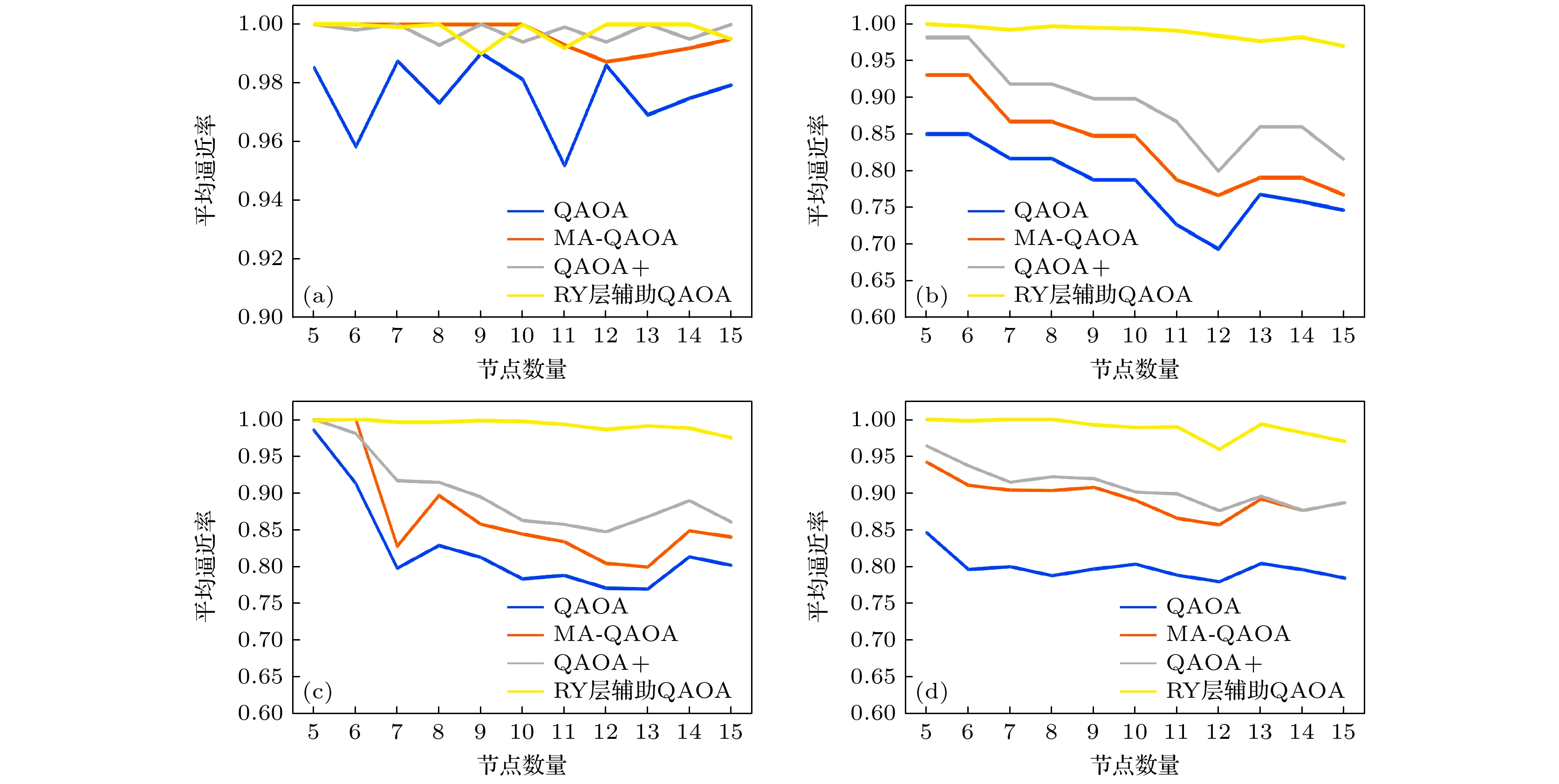
本节评估了本文所提出的QAOA新变体与标准QAOA及其现有的主流变体(均为单层)在不同图类型和规模下的平均逼近率. 对不同类型的问题图以及节点数量, 均采用50张图进行实验, 结果如图4所示.
由图4易见, 随着图规模的增加, 平均逼近率呈下降趋势. 同时, 上述量子优化策略对图的类型有很强的依赖关系. 下面对图的类型、图的规模对不同QAOA变体性能的影响进行详细分析.
首先看各QAOA变体在不同图类型下的性能, 如图4所示, 图的类型(完全图、正则图或随机图)显著影响了QAOA变体实现的逼近率. 在节点数小于10时, 所有变体在应用于完全图时展现出优秀的平均逼近率(0.98). 应用于正则图以及随机图时, 标准QAOA, MA-QAOA和QAOA+性能下降明显, QAOA的平均逼近率下降到了0.85以下, MA-QAOA和QAOA+的平均逼近率降到了0.9左右. 值得注意的是, 本文提出的RY层辅助QAOA性能受到的影响较小, 平均逼近率仍能保持在0.98以上. 随着节点数量的增加, 这种趋势变得更加明显. 在完全图中, 大多数变体在10—15个节点时能够保持相当高的性能, 平均逼近率超过0.98. 然而, 在具有10—15个节点的正则图和随机图中, 标准QAOA, MA-QAOA和QAOA+的性能显著下降, QAOA的平均逼近率在0.65—0.8之间, MA-QAOA的逼近率在0.75—0.9之间, QAOA+的逼近率在0.8—0.9之间. RY层辅助QAOA的逼近率虽然有所浮动, 但仍能保持在0.96以上. 可见, 本文的RY层辅助QAOA相比其他几种变体, 受不同图类型的影响最小, 鲁棒性最强.
从图的规模来看, 图4显示出, 随着正则图和随机图中图节点数量的增加, 平均逼近率有减少的趋势. 在完全图中, 平均逼近率减少的程度较小. 特别地, 随着图规模的增长, QAOA变体的平均逼近率显著降低. 值得注意的是, RY层辅助QAOA在图节点数量增加时表现出更强的稳健性. 例如, 对于MA-QAOA, 逼近率从5个节点的0.99 (4-正则图)和0.94 (随机图)下降到15个节点的0.84 (4-正则图)和0.88 (随机图). 同样, RY层辅助QAOA的逼近率从5个节点的0.997 (4-正则图)和0.995 (随机图)到15个节点时, 仍保持0.985 (4-正则图)和0.97 (随机图)的高逼近率.
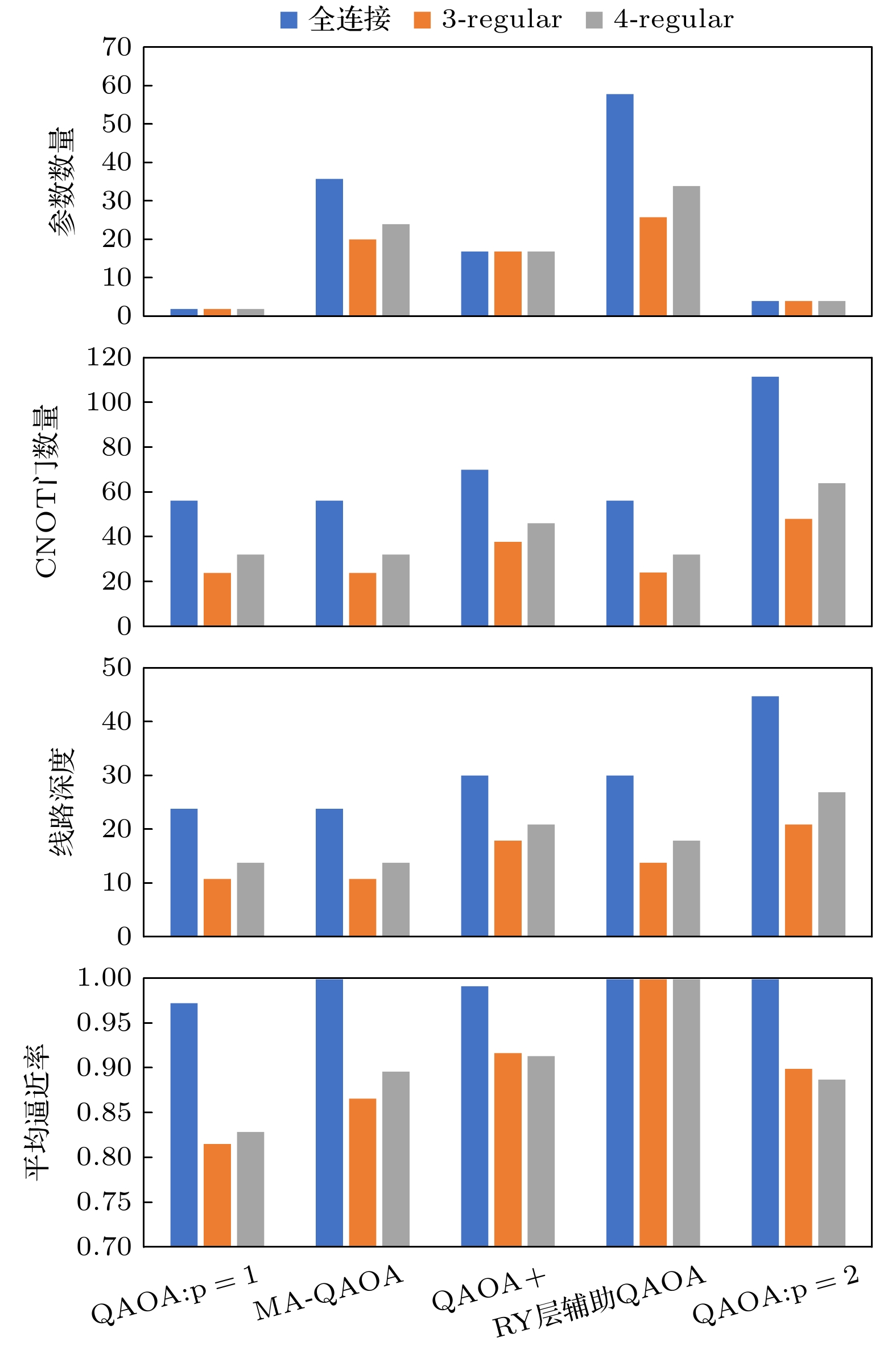
随后, 对比本文提出的RY层辅助QAOA与其标准版及目前已有的各主流变体在最大割问题上的资源消耗情况. 实验以8节点图为例, 结果如图5所示. 和标准单层QAOA量子线路相比, RY层辅助QAOA, MA-QAOA和QAOA+都通过添加额外参数来提高算法性能(QAOA+额外又添加了CNOT门, 又会增加错误产生风险). 而在性能方面, 对于正则图, RY层辅助QAOA的平均逼近率显著优于标准的QAOA及其主流变体MA-QAOA和QAOA+. 特别地, 对于边较少的3-正则图而言, RY层辅助QAOA通过少量的参数增加, 即获得了显著的性能增益, 在逼近率和资源使用方面取得了更好的均衡.
值得注意的是, 由于RY层辅助QAOA和QAOA+都添加了额外的门来提高性能, 所以在
$ p=1 $ 时它们的线路深度会大于$ p=1 $ 的标准QAOA, 但小于$ p=2 $ 的QAOA. 由图5可以看出,$ p=1 $ 的QAOA+平均逼近率略优于$ p=2 $ 的标准QAOA, 而$ p=1 $ 的RY层辅助QAOA的平均逼近率则明显优于$ p=2 $ 的标准QAOA. 所以,$ p=1 $ 的RY层辅助QAOA虽然单层线路深度相比$ p=1 $ 的标准QAOA深, 但后者想要获取相同的平均逼近率则需要更多的层数, 导致整体深度反而更高, 同时CNOT门数量也会大幅增多. 如表1所列, 在相同逼近率下, RY层辅助QAOA相比其他变体线路深度更低, CNOT门数量也更少, 也将更适应于实际含噪声的量子体系.为了进一步验证RY层辅助QAOA在NISQ情形下的鲁棒性, 在MindSpore Quantum量子 计算框架下添加了随机噪声, 并对双层QAOA与RY层辅助QAOA进行了比较实验. 其中噪声 参数的设置参照近年来IBM处理器的噪声参 数[28], 具体为: 双比特量子门发生错误概率
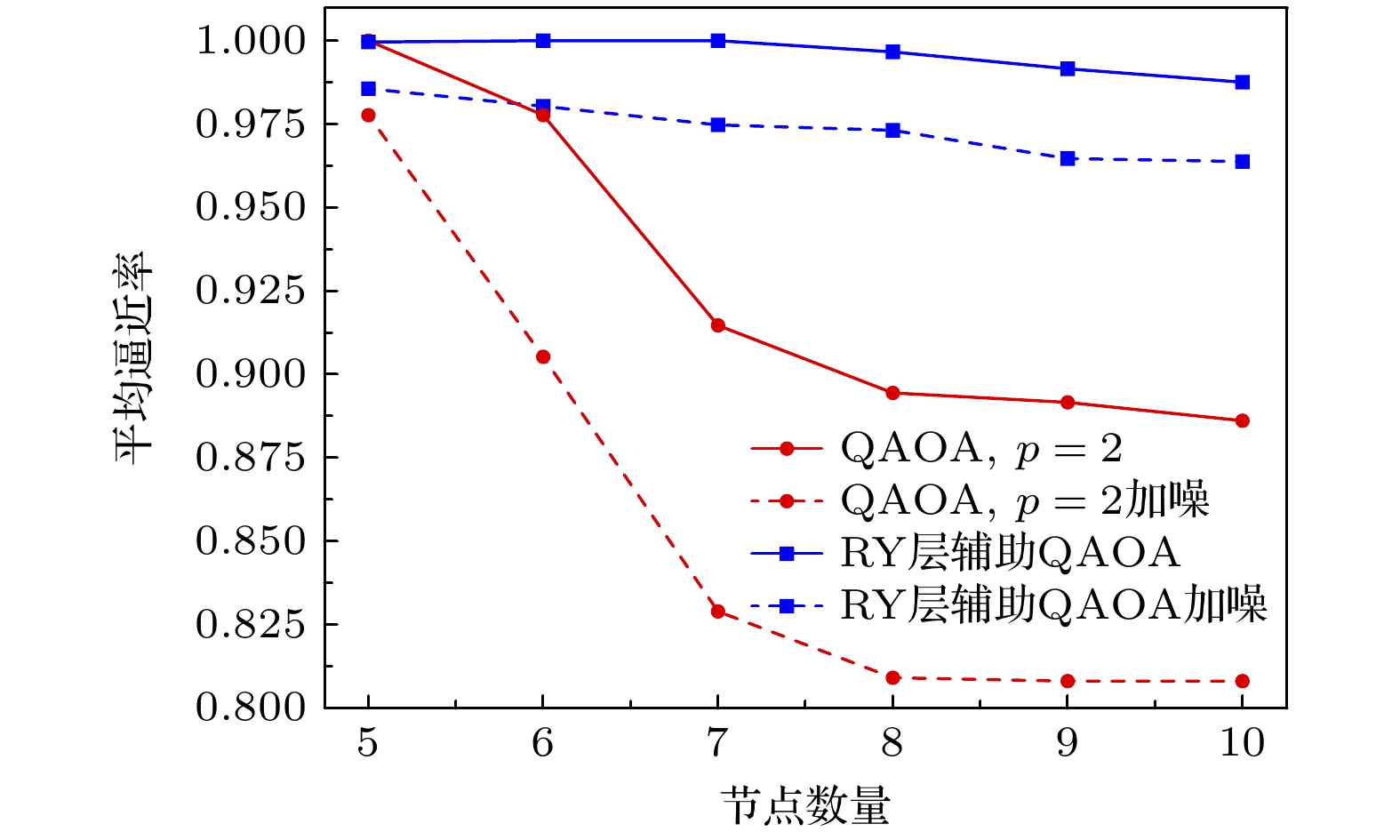
$ p= 2.848 \times 10^{-3} $ 的去极化噪声, 而单比特量子门上为$ p= 4.43\times 10^{-4} $ 的去极化噪声. 受篇幅所限, 这里给出5—10节点的4-正则图下, 两种网络模型的实验仿真结果, 具体如图6所示. 容易看到, 本文所提出的RY层辅助QAOA在噪声情况下具有更好的鲁棒性. 以图6中的7节点4-正则图为例, 双层标准的QAOA在7节点正则图上的平均逼近率由约0.91下降至约0.83, 降幅为0.08; 而RY层辅助QAOA的平均逼近率由约1下降至约0.975, 仅降低了0.025. -
本文通过在标准QAOA算法中针对最大割问题的目标哈密顿量线路中引入泡利Y旋转门, 提高了量子试探函数在单次迭代中的操控灵活性和希尔伯特空间的检索效率, 显著提升了QAOA在最大割问题上的性能表现. 在完全图、3-正则图、4-正则图和边概率在0.3—0.5之间的随机图等不同的问题图上, 基于MindSpore Quantum平台将本文提出的RY层辅助QAOA与标准的QAOA及其现有的主流变体MA-QAOA和QAOA+进行了对比实验. 结果表明, 本文提出的QAOA线路新变体RY层辅助QAOA在降低深度、减少CNOT双比特量子逻辑门数量的同时, 依然达到更优的逼近率, 具备更高可靠性的潜力.
面向最大割问题的量子近似优化算法设计
Design of quantum approximation optimization algorithm for the maximum cut problem
-
摘要: 量子近似优化算法(QAOA)作为含噪的中等规模量子(NISQ)计算时代的重要算法, 在最大割问题上展现了极大的优势和潜力. 然而由于缺乏量子纠错的支持, 在NISQ体系中计算的可靠性会随着算法的线路深度增加而急剧下降. 这样, 如何针对最大割问题设计高效的浅层低复杂度QAOA, 是当前NISQ时代展现量子计算优势所面临的一个重要挑战. 本文在标准QAOA算法解决最大割问题的目标哈密顿量线路中引入泡利Y旋转门, 通过提高量子试探函数在单次迭代中的操控灵活性和希尔伯特空间的检索效率, 显著提升了QAOA在最大割问题上的性能表现. 基于MindSpore Quantum平台的模拟实验表明, 与标准QAOA及当前其主流变体MA-QAOA和QAOA+等相比, 本文提出的QAOA新变体——RY层辅助QAOA在可降低线路深度、减少CNOT双比特量子逻辑门数量的同时, 依然可达到更优的逼近率, 具备更高可靠性的潜力.Abstract: The max-cut problem (MCP) is a classic problem in the field of combinatorial optimization and has important applications in various fields, including statistical physics and image processing. However, except for some special cases, the MCP still encounters a non-deterministic polynomial complete problem (an NP-complete problem), and there is currently no known efficient classical algorithm that can solve it in polynomial time. The quantum approximate optimization algorithm (QAOA), as a pivotal algorithm in the noisy intermediate-scale quantum (NISQ) computing era, has shown significant potential for solving the MCP. However, due to the lack of quantum error correction, the reliability of computations in NISQ systems sharply declines as the circuit depth of the algorithm increases. Therefore, designing an efficient, shallow-depth, and low-complexity QAOA for the MCP is a critical challenge in demonstrating the advantages of quantum computing in the NISQ era.In this paper, according to the standard QAOA algorithm, we introduce Pauli Y rotation gates into the target Hamiltonian circuit for the MCP. By enhancing the flexibility of quantum trial functions and improving the efficiency of Hilbert space exploration within a single iteration, we significantly improve the performance of QAOA on the MCP.We conduct extensive numerical simulations using the MindSpore quantum platform, and compare the proposed RY-layer-assisted QAOA with standard QAOA and its existing variants, including MA-QAOA and QAOA+. The experiments are performed on various graph types, including complete graphs, 3-regular graphs, 4-regular graphs, and random graphs with edge probabilities between 0.3 and 0.5. Our results show that the RY-layer-assisted QAOA achieves higher approximation ratios in all graph types, particularly in regular and random graphs, where traditional QAOA variants are difficult to implement. Moreover, the proposed method exhibits strong robustness as the graph size increases, and can maintain high performance even for larger graphs. Importantly, the RY-layer-assisted QAOA requires fewer CNOT gates and has a lower circuit depth than the standard QAOA and its variants, making it more suitable for NISQ devices with limited coherence times and high error rates.In conclusion, the RY-layer-assisted QAOA provides a promising approach for solving MCP in the NISQ era. By improving the approximation ratio while reducing circuit complexity, this method demonstrates significant potential for practical quantum computing applications, thus paving the way for developing more efficient and reliable quantum optimization algorithms.
-
Key words:
- quantum approximate optimization algorithm /
- max-cut /
- quantum computing /
- quantum circuit .
-

-
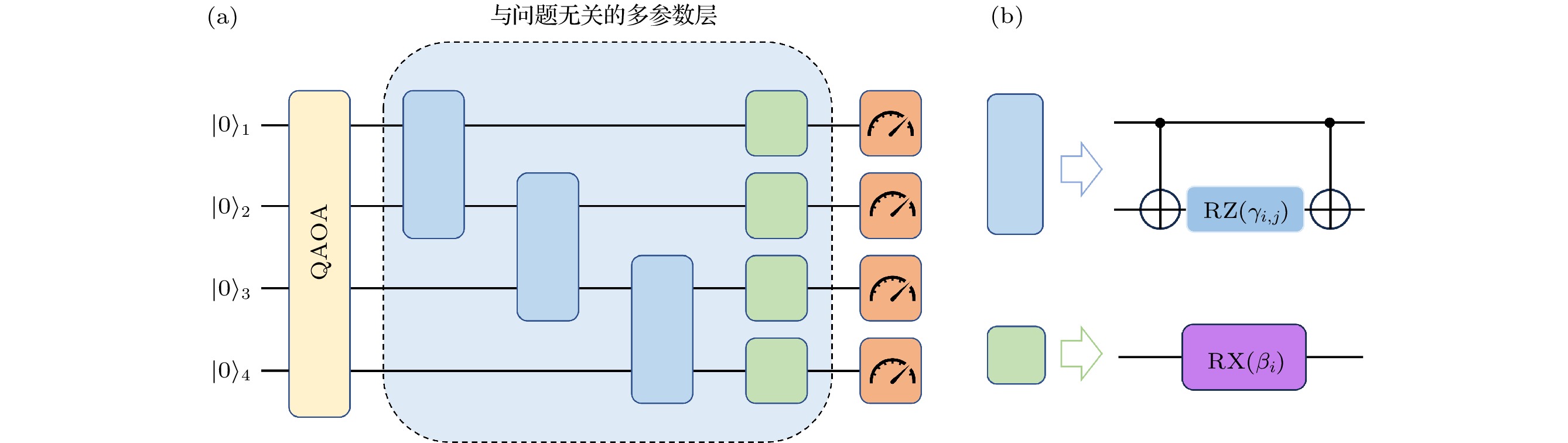
图 1 (a) 由问题酉算符和混合酉算符构成的单层QAOA量子线路框图; (b)标准QAOA的问题酉算符(蓝色)和混合酉算符(紫色)的分解; (c) MA-QAOA问题酉算符(蓝色)和混合酉算符(紫色)的分解; (d) RY层辅助QAOA问题酉算符(蓝色)和混合酉算符(紫色)的分解
Figure 1. (a) Single-layer QAOA quantum circuit diagram composed of problem and mixing operators; (b) decomposition of the problem operator (blue) and mixing operator (purple) in standard QAOA; (c) decomposition of the problem operator (blue) and mixing operator (purple) in MA-QAOA; (d) decomposition of the problem operator (blue) and mixing operator (purple) in RY-layer-assisted QAOA
图 4 单层QAOA, MA-QAOA, QAOA+和RY层辅助QAOA分别在四类图上的平均逼近率 (a)完全图; (b) 3-regular图; (c) 4-regular图; (d)随机图. 这里的问题图由NetworkX库随机生成
Figure 4. Average approximation ratios of single-layer QAOA, MA-QAOA, QAOA+, and RY-layer-assisted QAOA on the four types of graphs: (a) Complete graphs; (b) 3-regular graphs; (c) 4-regular graphs; (d) random graphs. The problem instances are randomly generated using the NetworkX library
表 1 100个8节点随机问题图上, 各变体达到0.9的逼近率需要的平均线路深度、参数数量及CNOT门数
Table 1. The average circuit depth, number of parameters, and number of CNOT gates required for each variant to achieve an approximation ratio of 0.9 on 100 random 8-node problem graphs.
变体 线路深度 参数数量 CNOT门数量 QAOA 61.09 7.54 104.96 MA-QAOA 31.76 84.61 53.73 QAOA+ 50.09 38.52 89.54 RY层辅助QAOA 21.92 29.84 27.84 -
[1] Adjiman C S, Schweiger C A, Floudas C A1998 Mixed-Integer Nonlinear Optimization in Process Synthesis // Du D Z, Pardalos P M Handbook of Combinatorial Optimization (Boston: Springer) pp1–12 [2] Håstad J 2001 JACM 48 798 doi: 10.1145/502090.502098 [3] Goemans M X, Williamson D P 1995 JACM 42 1115 doi: 10.1145/227683.227684 [4] Preskill J 2018 Quantum 2 79 doi: 10.22331/q-2018-08-06-79 [5] Cruz D, Fournier R, Gremion F, et al. 2019 Adv. Quantum Technol. 2 1900015 doi: 10.1002/qute.201900015 [6] Zhang J, Hegde S S, Suter D 2020 Phys. Rev. Lett. 125 030501 doi: 10.1103/PhysRevLett.125.030501 [7] Wernsdorfer W, Godfrin C, Balestro F 2019 Bulletin of the American Physical Society Boston, USA, pS36 [8] Borle A, Elfving V, Lomonaco S J 2021 SciPost Phys. Core 4 031 doi: 10.21468/SciPostPhysCore.4.4.031 [9] Farhi E, Goldstone J, Gutmann S 2014 arXiv: 1411.4028 [quant-ph] [10] Guerreschi G G, Matsuura A Y 2019 Sci. Rep. 9 6903 doi: 10.1038/s41598-019-43176-9 [11] Herrman R, Ostrowski J, Humble T S, Siopsis G 2021 Quantum Inf. Process. 20 1 doi: 10.1007/s11128-020-02935-8 [12] Wurtz J, Lykov D 2021 Phys. Rev. A 104 052419 doi: 10.1103/PhysRevA.104.052419 [13] Akshay V, Philathong H, Morales M E, Biamonte J D 2020 Phys. Rev. Lett. 124 090504 doi: 10.1103/PhysRevLett.124.090504 [14] Wurtz J, Love P 2021 Phys. Rev. A 103 042612 doi: 10.1103/PhysRevA.103.042612 [15] Farhi E, Gamarnik D, Gutmann S 2020 arXiv: 2005.08747 [quant-ph] [16] Xue C, Chen Z Y, Wu Y C, Guo G P 2021 Chin. Phys. Lett. 38 030302 doi: 10.1088/0256-307X/38/3/030302 [17] Wang S, Fontana E, Cerezo M, Sharma K, Sone A, Cincio L, Coles P J 2021 Nat. Commun. 12 6961 doi: 10.1038/s41467-021-27045-6 [18] Marshall J, Wudarski F, Hadfield S, Hogg T 2020 IOPSN 1 025208 doi: 10.1088/2633-1357/abb0d7 [19] Alam M, Ash-Saki A, Ghosh S 2019 arXiv: 1907.09631[quant-ph] [20] Chandarana P, Hegade N N, Paul K, Albarrán-Arriagada F, Solano E, Del Campo A, Chen X 2022 Phys. Rev. Res. 4 013141 doi: 10.1103/PhysRevResearch.4.013141 [21] Magann A B, Rudinger K M, Grace M D, Sarovar M 2022 Phys. Rev. Lett. 129 250502 doi: 10.1103/PhysRevLett.129.250502 [22] Chalupnik M, Melo H, Alexeev Y, Galda A 2022 2022 IEEE International Conference on Quantum Computing and Engineering (QCE) Broomfield, USA, Sept. 18–23, 2022 p97 [23] Sun Z H, Wang Y Y, Cui J, Fan H 2023 NJP 25 013015 doi: 10.1088/1367-2630/acb22c [24] Wurtz J, Love P J 2021 TQE 2 1 doi: 10.1109/TQE.2021.3122568 [25] Wang Z D, Zheng P L, Wu B, Zhang Y 2023 Phys. Rev. Research 5 023171 doi: 10.1103/PhysRevResearch.5.023171 [26] Herrman R, Lotshaw P C, Ostrowski J, Humble T S, Siopsis G 2022 Sci. Rep. 12 6781 doi: 10.1038/s41598-022-10555-8 [27] Xu X, Cui J, Cui Z, et al. 2024 arXiv: 2406.17248[quant-ph] [28] AbuGhanem M 2024 arXiv: 2410.00916[quant-ph] -


 首页
首页 登录
登录 注册
注册



 下载:
下载: