复杂网络系统中节点传播动力学的研究是当代网络科学和系统科学的前沿热点问题. 在现实世界中, 许多系统都可以抽象建模为复杂网络^[1]. 很多网络过程如扩散传播、故障级联、同步现象等, 都与网络中的一些特殊节点密切相关. 通过量化节点重要性, 能够发现网络中的核心集群、枢纽节点、瓶颈连接等拓扑特征, 进而预测和控制网络行为. 在应用领域, 节点重要性排序具有广泛的实践意义. 比如在社交网络营销中, 识别影响力节点有助于信息高效传播; 在防疫工作中, 及时控制超级传播节点对阻断疫情扩散至关重要; 在互联网络管理中, 保护关键节点可显著提高网络鲁棒性.

目前有许多方法用于评估节点在整个复杂网络中的传播性能. 其中典型的评价方法包括但不限于度中心性 (DC)^[2]、介数中心性 (BC)^[3]、特征向量中心性^[4]、接近中心性^[5] 以及k-shell分解法^[6]. 以上的评价方法都是基于网络基本的拓扑结构. 据研究者发现, k-shell方法在分解网络时, 其有效的划分能为节点的位置信息提供一个良好的参考指标. Kitsak等^[6]以及Bae和Kim^[7]认为高度中心性与高介数中心性的节点在某些情况下的传播能力有限, 但位于核中心的节点具有更高的影响力. 因此, 有许多研究者通过基于k-shell方法来对节点重要性评估方法做出改进. 例如Zeng和 Zhang^[8]提出了基于k-shell的混合度分解(mixed degree decomposition, MDD)方法, 该方法在k-shell方法^[6]剥离节点的过程上为剩余节点增加了消耗度的概念, 从而使节点重要性的评估更具有单调性; Liu等^[9] 提出了一种改进k-shell方法的方法, 即通过移除网络中的冗余链接来提高节点评价的准确性. 他们提到, 在真实网络中存在着核心类似的群体, 这些群体具有较大的k-shell值但传播效率较低. 至此, 他们通过定义每条边的扩散重要性度量来识别在传播过程中具有相对较低扩散重要性的边, 这些边往往导致形成局部密集连接的冗余链接. 通过过滤掉这些冗余链接并将k-shell方法应用于剩余网络, 从而得到一个更准确的评价指标.

有许多研究者通过现有的物理定律来模拟、衡量复杂网络中节点之间的相互作用力, 从而计算出节点在网络中的传播性能. Ma等^[10]提出的引力模型Gravity将节点的度作为节点的质量, 节点到节点之间的有效最短路径作为两者之间的距离. 由万有引力公式可得, 距离与两节点之间的引力成反比, 从而计算出各个节点的影响力. 由于仅以节点的度作为其质量比较单一, 并且由度中心性获得的影响力得分不具有辨识性, 单调性不足. Li等^[11] 提出了DKGM, 在引力模型Gravity的基础上, 将节点的k核值与度值用于衡量它的质量, 并在此基础上引入了阶段数这一概念: 通常情况下, 前面分解的节点较后面分解的节点更具有影响力. 除此之外, 还有研究将节点在网络中的全局信息纳入考量, 融入到引力模型中对网络的节点性能进行评估: Liu等^[12]提出了一个广义力学模型, 该模型引入了特征向量中心性, 将网络节点迭代而出的特征向量作为各节点在网络中的引力系数, 这样就将网络的全局信息与节点的局部信息结合在一起, 得到了一个广义的力学模型. Zhao等^[13]提出了一种基于随机游走的重力模型, 以改进传统重力模型中计算节点间最短路径导致的高时间复杂度问题: 利用随机游走代替最短路径计算, 将复杂度从$ O(|V|^2) $降低到$ O(|V| \times c\times l/r) $, 其中c是每个节点的行走次数, l是行走长度, r是每次行走获取的样本数. Yang和Xiao^[14]提出KSGC引力模型, 他们认为相较于网络核外部的节点, 核心节点对于外围节点所施加的引力效应与外围节点对核心节点的引力效应之间存在显著的非对称性. 对此, 他们在KSGC引力模型中引入了基于k-shell值差异的吸引力系数, 这一系数用来量化因位置不同所产生的引力差异. 这种方法不仅考虑了节点的直接连接度, 还考虑到了节点在网络整体架构中的嵌入程度, 从而提高了模型对于节点性能评估的分辨率和准确性.

近年来, 诸多学者在研究如何准确计算节点性能的过程中引入了混合度量策略, 旨在克服单一指标可能存在的局限性, 实现更优的节点排序效能. Yu等^[15]通过综合考量节点的聚类系数、一阶和二阶邻居数量的影响, 进而提出了节点传播熵(node propagation entropy, PE), 其能够准确地识别复杂网络中的关键节点. Jaoude^[16]提出了一种基于信息熵的自适应节点重要性评估方法(EBSAM). 此方法通过动态调整节点权重, 评估节点对网络稳定性的贡献, 有效解决了传统评估方法难以灵活应对复杂网络不同结构特征的问题. Hu等^[17]提出一种统一的多准则评价框架, 该框架包含了5个基于直观想法的规则, 通过这些规则和利用偏序关系的等价类来对节点的重要性进行排名. Chiranjeevi等^[18]提出一个名为ICDC (isolating and clustering distance centrality)的新指标, 通过结合节点的局部和全局拓扑信息, 纠正了一些现有中心性指标仅考虑连接性或聚类性而导致排名不平衡的缺点. Wang等^[19]表明引力模型结合k-shell值和节点度的混合度量能显示出最佳节点排序性能, 他们融合了k-shell值与度这两种中心性指标, 将目标节点的k-shell值作为其自身质量, 而邻居节点则以其度作为自身质量, 以这样的方法构建了混合引力模型. 阮逸润等^[20]将h指数^[21]、结构洞理论中的网络约束系数^[22]、k-shell^[6]数作为混合度量, 将这些指标纳入引力模型, 以此作为目标节点性能的衡量依据. 除此之外, 韩忠明等^[23]依托结构洞理论与关键节点排序文献, 精选网络约束系数^[22]、PageRank^[24]及聚类系数等7大经典指标, 以此为基础将ListNet排序学习模型^[25] 应用于复杂网络关键节点排序. 通过集成这7个度量标准来建立一套评估结构洞^[22]中关键节点的新排序方案.

在复杂网络研究中, 节点重要性的准确评估始终是研究的核心议题. 现有引力模型尝试结合节点的局部信息和全局拓扑特征, 但在平衡两者的作用方面仍存在显著不足, 主要表现在以下两个方面: 一是对节点在网络中位置的精细划分不够, 难以全面捕捉节点的全局影响力; 二是未能充分体现节点的局部结构特性, 导致关键节点识别的准确性受限. 此外, 传统模型往往忽略核心节点与外围节点之间引力效应的非对称性, 进一步削弱了模型对复杂网络的适用性和精准度.

为解决上述问题, 本文提出以下方法: 首先定义了引力修正因子NGCF (node gravity correction factor), 用于综合评估节点的全局影响力与局部结构特性. NGCF结合特征向量中心性(量化节点全局地位及其与高影响力邻居的关联)与网络约束 系数 (揭示节点在结构洞中的桥梁作用), 全面描述节点在网络中的地位和功能. 其次, 为解决传 统模型忽视核心节点与外围节点间非对称引力效应的问题, 提出非对称吸引因子AAF (asymmetric attraction tactor). 该因子通过量化核心节点对外围节点的强影响力及外围节点对核心节点的弱反馈, 提升了对网络引力场效应的刻画能力.

基于上述改进, 本文提出了BGIM及其扩展版本BGIM+, 在传统引力模型基础上融合信息熵、NGCF与AAF, 构建了更精确的引力场模型. 实验表明, 该方法在多个网络中表现优异, 为关键节点识别提供了新的视角与工具.

本文内容安排如下: 第2节简要回顾并归纳当前学术界关于节点重要性评估的经典方法与引力模型; 第3节详细阐述本研究提出方法的核心理念与设计思路; 第4节介绍实验用到的数据集; 第5节详述实验的模型选取、实验参数设置以及结果的评价标准; 第6节给出实验结果的展示和相关讨论; 第7节进行方法的复杂性分析; 第8节给出本文的结论.

对于给定的复杂网络G = (V, E ), 其中V表示网络中的顶点集, E表示网络中的连边集合. 一个网络中的连接关系通过邻接矩阵$ {\boldsymbol{A}} = (a_{ij})_{n × n} $确定, 其中, $ a_{ij} = 1 $表示i到j存在直接的连边; $ a_{ij} = 0 $表示i到j不存在连边. 在复杂网络分析中, 度中心性^[2]方法是通过节点的度来量化其在网络中的重要性. 具体公式如下:

该指标认为, 节点的度值越高, 其在网络中的影响力越大, 因为具有更多连接的节点更有可能成为信息流动的中心节点. 然而, 度中心化不一定能很好地反映一个网络的集中程度, 特别是在具有树状结构的网络中. 在这种网络中, 尽管存在一个明显的中心节点, 但由于外围节点也有一定的连接度, 因此度中心化值可能较低, 不能准确地反映出网络的集中程度^[26,27].

特征向量中心性(eigenvector centrality)^[4]是用于衡量节点在复杂网络中重要性的另一种重要指标. 它不仅考虑节点本身的连接数量, 还关注节点所连接节点的中心性. 其数学表达式为

其中, $ {\mathrm{EC}}(i) $是节点i的特征向量中心性, λ是特征值.

各个中心性评价方法各有优缺点, 度中心性计算简便直观, 易于理解, 特别适用于度分布集中且节点作用相对均匀的网络结构. 而特征向量中心性适合评估节点在整个网络中的综合影响力. 二者共同的局限性在于它们仅依赖局部或全局路径信息, 而未能完全捕捉到节点在多维度互动中的复杂作用.

信息熵(entropy)是信息论中的一个重要概念, 用于度量系统中不确定性或信息的平均量. 由香农(Shannon)于1948年提出, 其数学公式为

其中, $ H(X) $表示随机变量X的熵, $ p(x_i) $是事件$ x_i $发生的概率, n是事件的总数. 信息熵的值越大, 表示信息系统的不确定性越高, 反之, 表示系统的信息结构越有序, 确定性越强.

在网络传播过程中, 信息熵可以有效反映节点的“信息贡献度”. 如果一个节点与多个其他节点保持复杂且多样化的连接结构, 并且这些连接的权重分布较为均匀, 则该节点的信息熵较高. 这意味着节点在信息传播中的潜力较大, 能够在网络中发挥更为广泛的影响力. 它的计算方法为

其中$ j \in \varGamma(i) $是节点i的邻居集合, $ k_i $是节点的度.

与传统的度数指标主要衡量节点的直接连接数量不同, 信息熵能够更全面地反映网络中信息传播的复杂性. 例如, 尽管两个节点的度数可能相同, 但它们在网络中的信息传播能力可能存在显著差异. 信息熵提供了一种更为细致的衡量方式, 综合考虑了节点的连接模式、传播潜力以及连接的多样性.

传统的k-shell方法在分解网络时忽视了节点与其邻居节点的移除信息, 即节点的耗尽度 (exhausted degree). Zeng和Zhang^[8]提出了一种名为混合度分解的方法, 该方法通过记录节点的剩余度和耗尽度来计算节点的传播能力. MDD方法的具体流程如下.

1) 初始化每个节点的混合度: 对于网络中每个节点i, 初始化其混合度$ k_{\mathrm{m}}(i) $等于剩余度$ k_{\mathrm{r}}(i) $. 此时网络中没有节点被移除, 每个节点的剩余度等于其原始度数.

2) 移除混合度最小的一组节点: 对网络中所有节点的混合度$ k_{\mathrm{m}}(i) $进行排序, 去除当前网络中混合度最小的一组节点(记作M ), 并为节点分配最终得分. 随后, 更新移除节点的邻居节点的耗尽度.

3) 计算剩余节点的新混合度: 对于每个未被移除的节点i, 计算其新混合度$ k_{\mathrm{m}}(i) $, 公式为

其中, λ是一个可调参数, 用于平衡剩余度与耗尽度在决定节点混合度中的相对权重.

4) 重复移除和更新过程: 重复步骤2)和3), 每次移除混合度小于等于M的节点, 直至所有节点完成剥离.

k-shell方法虽然有效且计算效率较高, 但在特定情况下会因忽略节点的耗尽度导致低估了一些局部高聚类节点的实际影响力, 而MDD方法结合剩余度和耗尽度信息, 有效地消除了k-shell方法的局限性, 提高了节点重要性评估的精度.

结构洞理论是由社会学家Burt等^[22]在研究社会网络的竞争关系时提出的, 它揭示了网络中非冗余联系的缺失对网络成员获取信息和建立竞争优势的影响. 结构洞指的是网络中两个未直接相连的个体之间存在的空缺, 这种空缺形成了一个“结构洞”. 占有结构洞的节点因其特殊的位置能够接触到两个原本分离的网络部分, 从而具备信息传递的独特优势, 能够在社交网络、商业网络等环境中获取额外的信息和资源.

在复杂网络分析中, 结构洞节点的重要性体现在其能够充当中间人的角色, 通过连接不同的网络社群, 结构洞节点能够比其邻居节点掌握更多的非重叠信息和关系资源. Burt等^[22]通过引入网络约束系数(network constraint, NC)这一量化指标来衡量节点形成结构洞时所受到的约束程度. 其表达式为

其中, $ \mu_{ij} $表示节点j在节点i的所有邻居中的影响力占比, q表示节点i的直接邻居与节点j的直接邻居的共同交集. 当节点i和节点j存在连边时, $ z_{ij} = 1 $, 反之为0.

$ {\mathrm{NC}}_i $的大小反映了节点i在维持与邻居j的关系时受到的约束程度, 这与邻居数量、拓扑结构紧密度有关. 节点i的邻居越多, 或者与邻居间形成的闭合三角形越少, 则形成的结构洞越大. 即$ {\mathrm{NC}}_i $的值越小, 节点在网络中接触外界资源的能力更强; 相反, ${\mathrm{ NC}}_i $值大则意味着节点在网络中的位置相对封闭, 难以获得新资源, 传播能力受限.

Ma等^[10]介绍了一种基于引力模型的方法, 用于识别复杂网络中具有强大传播能力的节点. 该模型借鉴物理学中引力定律的思想: 节点在网络中的影响力可以类比于物理系统中天体与天体间的引力关系. 在该模型中, 每个节点的影响力由其自身度数和与其他节点间的最短距离共同决定, 具体计算公式如下:

这里$ ks(i) $代表节点i的k-shell值; $ \psi_i $表示节点i的邻居集合; $ d_{ij} $是节点i和节点j之间的最短距离; R表示截断半径; 而参数α是一个调整因子, 通常取值为2, 对应于引力随距离平方递减的规律. 这种表达方式体现了节点的影响力与它自身的度数以及它与其他节点间的距离有关, 即节点本身的质量越大, 与其他节点距离越近, 其在传播过程中的影响力就越大.

此外, Liu等^[12]通过为引力模型加入特征向量中心性这一度量来对网络中节点的重要性进行评估, 从而提出了一种用于评估复杂网络中节点重要性的广义力学模型(C_WG). 公式为

其中, $ e_i $为第i个节点归一化的特征向量中的第i个值, 该模型结合了节点在网络中的全局信息, 通过考虑节点的度数以及与其他节点的距离和权重来评估节点的影响力.

Yang和Xiao^[14]为引力模型提出引力系数这一概念, 他们认为位于网络中心部分的节点可能比位于外围的节点具有更大的吸引力, 即网络中节点对节点的引力作用会被它们自身所处的位置影响. 所以在基于引力模型的计算过程中, 他们考虑了节点的位置, 以k-shell值差异表示的节点之间的位置差异作为吸引力系数. 他们提出的模型公式如下:

其中$ C_{ij} $用于量化节点i对节点j因位置差异带来的引力差. 通过计算$ C_{ij} $, 可以有效地反映这种不对称性, 使得模型在评估节点重要性时, 能够同时考虑节点的层次结构以及位置特性.

Yang和Xiao^[14]提出的KSGC引力模型通过节点的k-shell值量化节点间的引力差. 然而, k-shell方法在每次迭代中仅根据节点的剩余度划分k-shell值, 无法有效区分同一壳层中位置优越或性能显著的节点, 限制了其在关键节点识别中的表现. 实际上, 节点的地理位置与网络结构的耦合关系对引力场模型至关重要. 理想的引力场模型应能准确捕捉节点间因位置差异而产生的相互作用力变化.

为克服上述局限性, 本文提出采用MDD法对节点进行细粒度分层. 与传统k-shell方法相比, MDD不仅能保留节点的全局拓扑特征, 还能够对节点位置进行更精确的划分, 从而提升引力模型对节点间引力效应的描述能力. 基于此改进, 引入非对称吸引因子(asymmetric attraction factor, AAF)来量化节点间的引力差异, 定义为

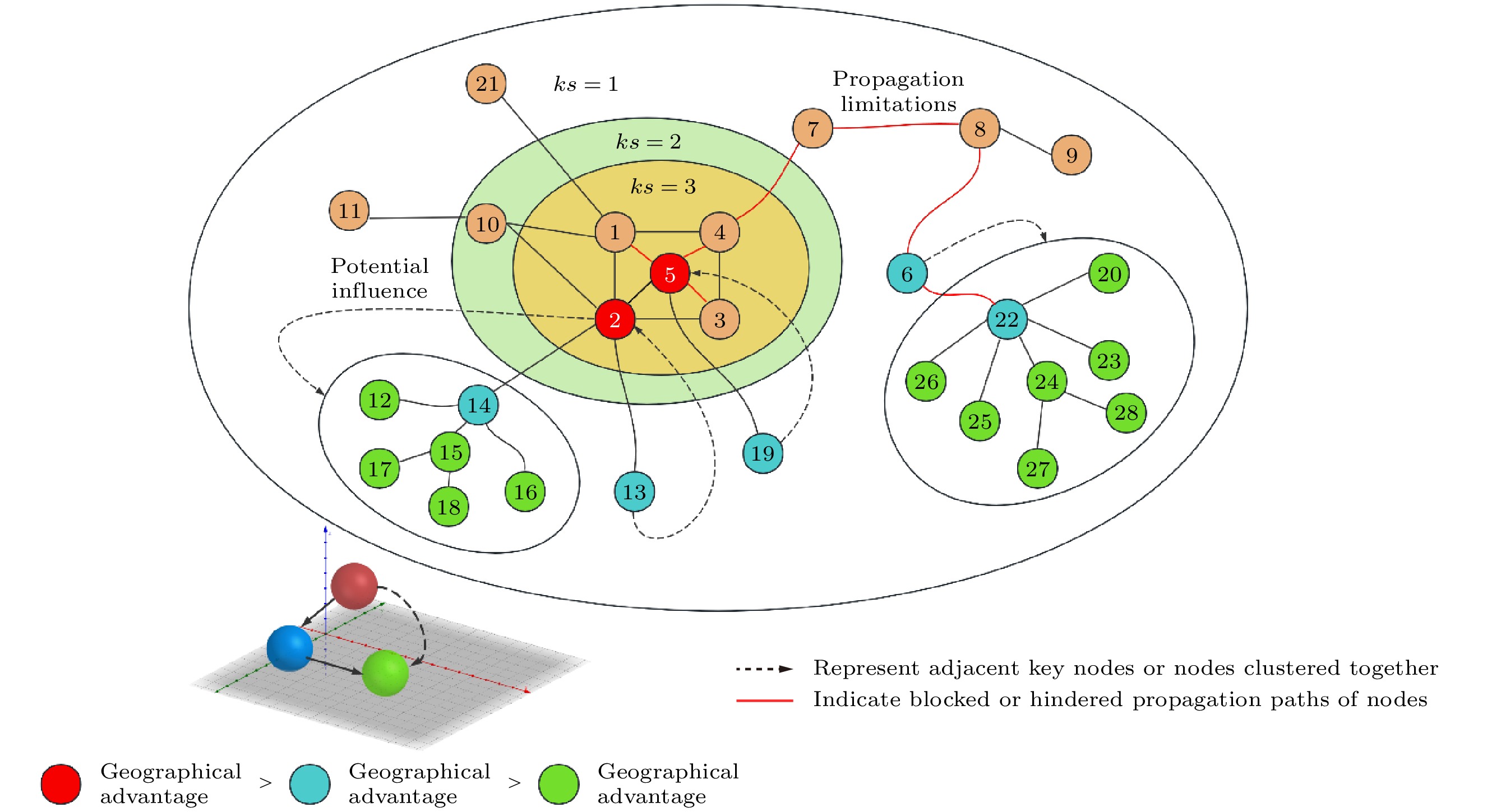
其中, $ {\mathrm{MDD}}(i) $表示节点i的混合度分解值. MDD方法通过记录节点的剩余度与消耗度, 能够有效区分具有相同k-shell值的节点, 并识别在局部网络中具有更高影响力的节点. 例如, 如图1所示, 节点14比节点12, 15, 16, 17, 18更靠近网络中心, 但它们的k-shell值均为1, 无法区分位置差异. 而通过MDD分层(λ设为0.7), 得到$ {\mathrm{MDD}}(14) = 4.7 $, $ {\mathrm{MDD}}(15) = 3.7 $, ${\mathrm{MDD}}(12) = {\mathrm{MDD}}(16) ={\mathrm{MDD}}(17) = {\mathrm{ MDD}}(18) = 1 $, 进一步细化了节点间的地位差异. 此外, 节点13与14的k-shell值同为1, 但节点14因处于局部高聚类结构中, 其$ {\mathrm{MDD }}$值高于节点13, 即$ {\mathrm{MDD}}(14) > {\mathrm{MDD}}(13) $. MDD算法能够更好地捕捉节点在网络中的实际位置, 特别是在局部高聚类的网络结构中. 将MDD融入引力模型, 通过计算节点间MDD值的差异, 更准确地反映节点间因位置差异而产生的相互作用力变化.

构造一个客观综合的引力场, 仅仅通过地理位置这一度量来评估节点是不够的, 因为这些方法难以全面反映节点在全局传播中的潜在影响力以及在局部结构中的独特作用. 为此, 本文进一步提出了节点引力修正因子NGCF (node gravity correction factor), 其公式如下:

其中, $ {\mathrm{EC}}(i) $为节点i的特征向量中心性值, 它衡量节点i在全局网络中的传播能力, 反映了节点通过层层关联在信息传播中所能达到的深度和广度, 突出了节点的整体影响力; $ {\mathrm{NC}}(i) $则表示节点i的网络约束系数, 它量化了节点i在局部结构中的受限程度, 也揭示了其是否充当了不同社区之间的桥梁角色. 通过将$ {\mathrm{EC}}(i) $和$ {\mathrm{NC}}(i) $的非线性关系纳入评估体系, $ {\mathrm{NGCF}}(i) $在全局与局部特性之间实现了动态平衡: 当节点的局部约束较小($ {\mathrm{NC}}(i) $低)时, 模型会放大节点的全局影响力权重, 从而更准确地反映结构洞节点的独特性; 当节点的局部约束较高($ {\mathrm{NC}}(i) $高)时, 模型则削弱节点的全局权重, 避免过度依赖全局中心性. 这种动态调节机制不仅提升了模型对局部特性的敏感性, 同时有效避免了对全局中心性的不合理依赖, 从而实现了全局与局部信息的平衡评估.

在引力模型中, 节点的度数通常用于衡量节点的重要性, 但这一单一指标未能充分考虑节点间连接的多样性及信息流动潜力. 为克服这一不足, 本文采用信息熵替代传统度数指标, 用以评估节点在网络中的传播效应. 信息熵能够从概率分布的角度反映节点的连接不确定性和信息丰富性, 高信息熵节点不仅在局部连接中具有关键作用, 还可能在全局范围内显著影响信息传播. 此外, 异质性网络中存在枢纽节点影响力被过度放大、桥梁节点在稀疏网络中重要性被忽视的问题. 为此, 本文引入全局归一化调整机制, 结合网络平均度$ \langle k \rangle $、节点对最大度值$ {\mathrm{max}}(k_i, k_j) $以及局部度分布偏差系数(LDDC), 以平衡网络的异质性, 增强模型在稀疏与密集网络中的稳定性. 基于此, 构建了双维系数熵权重引力模型(BGIM), 其公式如下:

其中, $ {\mathrm{BGIM}}(i) $表示节点i的重要性, $ {\mathrm{NGCF}}(i) $为节点i的引力修正因子, ${\mathrm{AAF}}_{ij} $为节点i与节点j因位置差异而产生的引力作用差的量化值, $ H(i) $和$ H(j) $分别表示节点i和节点j的信息熵, $ d_{ij} $为节点i与节点j之间的最短路径, R为引力作用的半径阈值. $ {\mathrm{LDDC}} $计算公式中, 分母表示节点在其领域内的平均度, 分子则为该节点在局部领域内的度分布标准差.

在该模型中, BGIM结合节点信息熵、NGCF和AAF, 引入了全局归一化机制, 有效缓解了高度异质性网络中节点重要性分布的不均衡问题. 模型综合考虑了节点的潜在影响力、局部邻域结构、网络中的地理位置特性以及节点间的相互引力差异, 构建了一个能够精准评估复杂网络节点性能的引力场模型. 最后, 再对方法进行扩展得到BGIM+, 定义为

其中$ 0 < \gamma < 1 $, 较小的γ值倾向于减轻高BGIM值影响力的邻居节点作用, 而较大的γ值则强化此类节点的影响力效应. 为兼顾广泛适用性并探索不同设置下的效果, 后续实验将参数γ设置在0.7—0.9的范围内, 以此为基准进行系列研究, 旨在全面理解参数变化对结果的影响.

为了验证所提方法的性能, 首先对本文提到的图1进行实验验证, 然后再选取8个网络在SIR模型上进行仿真研究. 这些网络包括: 爵士音乐人合作网络Jazz, 美国航空网络USAir, 欧洲大型 研究机构的电子邮件EEC网络, 社会电子邮件 Email网络, 政治博客圈网络PB, 以及互联网路由器层级拓扑网络Router, 社交圈网络Facebooks, 美国西部电力网络Power. 表1列出了这些网络的统计特征, 包括网络节点总数N、网络连边数E、节点间平均最短距离$ \langle d \rangle $、节点平均度$ \langle k \rangle $、网络集聚系数c、网络最大$ ks $值、信息传播阀值$ \beta_{{\mathrm{th}}} $以及信息传播率$ \beta_{\mathrm{c}} $. 从表1可以看到, 各个网络在节点数、连边数以及其他统计特征上都有显著差异. PB网络和Router网络展示了较大的节点和连边数, 表明网络结构复杂. 而Jazz和Email网络则在节点数、集聚系数和最大$ ks $值上都体现出了不同的特性, 这些网络的多样性为本文方法提供了丰富的测试环境, 有助于验证其在不同领域网络中的适用性和有效性.

为了评估节点在复杂网络中的传播能力, 本文采用了经典的SIR模型^[28,29]进行实验. SIR模型是一种广泛应用于疾病传播模拟的流行病学模型, 同时也常被用于研究信息扩散和病毒传播等问题. 该模型将网络中的节点划分为三种状态: 易感(susceptible, S)、感染(infected, I)和恢复(recovered, R). 实验中, SIR模型的具体设置如下: 首先, 在模型初始化阶段, 将节点集合I中的所有节点设置为感染状态(I), 其余节点均处于易感状态(S). 集合I中的节点即为我们评估的传播节点. 在状态转移规则中, 感染状态的节点以概率β感染其所有易感状态的邻居节点. 同时, 每个感染节点以概率μ恢复为恢复状态(R), 并且不再参与后续传播过程. 在传播过程中, 模型按照上述规则进行状态更新. 感染节点会尝试感染其所有的易感邻居节点, 被感染的节点在下一时间步转变为感染状态, 而原感染节点可能恢复为恢复状态. 整个传播过程持续进行, 直到网络中不再有新的感染节点, 即所有感染节点均转变为恢复状态.

在参数设置方面, 感染概率β是关键参数, 决定了感染节点在每个时间步尝试感染邻居节点的概率. 为了确保模拟结果的有效性, β的取值参考网络的流行病阈值$ \beta_{\mathrm{th}} $, 计算公式为$ \beta_{\mathrm{th}} = \langle k \rangle / \langle k^2 \rangle $, 其中$ \langle k \rangle $为网络的平均度, $ \langle k^2 \rangle $为网络的二阶平均度^[30]. 基于此设置, 实验能够有效观测到传播过程的动态特性. 恢复概率μ表示感染节点转变为恢复状态的概率. 为保证一般性, 本文在所有实验中统一设置$ \mu = 1.00 $, 即感染节点在一个时间步后必然恢复. 实验过程如下: 将集合$ I_0 $中的每个节点初始化为感染状态, 网络中其余节点初始化为易感状态. 执行SIR模型的传播过程, 并记录最终恢复状态节点的数量$ R(i) $, 将其作为节点i的传播性能指标. 为了确保实验结果的稳健性与可靠性, 本文采用了基于网络规模动态调整的实验重复策略. 具体而言, 对于节点数较少的小型网络($ N < 1000 $), 每个实验执行1000次传播模拟; 而对于节点数较多的大规模网络($ N \geqslant 1000 $), 实验次数适度减少至800次, 以在降低计算负担的同时保持结果的有效性. 通过多次模拟, 汇总每个节点的传播能力, 并取其平均值作为节点的传播效率指标, 用以反映其在网络传播过程中的影响力.

为了评估不同节点重要性测量方法与实际传播能力之间的相关性, 本文采用了Kendall Tau^[31]系数(Kendall’s Tau rank correlation coefficient). Kendall Tau系数是一种衡量两个变量之间相关性的非参数统计方法, 适用于评估两个排名列表之间的一致性. 给定两个排名列表X和Y, Kendall Tau系数τ的定义为

其中, N是排名列表中的元素总数; $ N_{\mathrm{c}} $是排名列表中成对一致的元素对数量, 即在两个排名列表中排名顺序相同的元素对; $ N_{\mathrm{d}} $是排名列表中成对不一致的元素对数量, 即在两个排名列表中排名顺序相反的元素对. 如果两个排名列表完全一致, $ \tau = 1 $; 如果完全不一致, $ \tau = -1 $; 对于完全独立的两个排名列表, $ \tau = 0 $.

为了评估不同中心性测量方法在区分节点重要性方面的效果, 实验采用了单调关系指标(monotonicity index), 记作$ M(R) $. 单调关系指标$ M(R) $用于衡量一种排名方法在多大程度上能够将节点性能区分开来, 是一个衡量排名方法精度的重要指标. 单调关系指标$ M(R) $的定义如下:

其中, N是网络中节点的总数, $ N_r $是具有相同中心性值的节点的数量, R是节点集合. 通过计算$ M(R) $, 可以判断中心性测量方法是否能够有效地区分网络中的所有节点. 若$ M(R) $ = 1, 则表示每个节点都被赋予了不同的中心性值, 排名方法具有完美的区分度; 若$ M(R) $ = 0, 则表示所有节点都具有相同的中心性值, 排名方法完全无法区分节点的重要性.

在小规模网络的实验与结果分析中, 我们对图1中的关键节点采用多种中心性指标进行了综合评估, 包括度中心性(DC)、接近中心性(CC)、介数中心性(BC)、混合度分解法(MDD)、Gravity和Gravity+方法、C_WG、KSGC方法, 以及本文提出的BGIM和BGIM+方法. 节点的具体评估排名见表2.

核心节点的比较表明, 节点5虽位于核心区域并属于最内层节点, 但其对外核层的连接性较弱, 限制了信息传播能力. 相比之下, 节点2虽接近核心, 但因与外核节点建立了更广泛的连接, 具有更强的传播潜力. 在局部聚类与传播效率方面, 节点22因周围存在高聚类结构表现出较强的局部连通性, 但其信息传播受限于邻域范围, 难以扩展至全网. 相反, 节点14在小团体内影响显著, 且接近网络核心, 有助于促进信息向外扩散.

在全局与局部信息融合方面, BGIM方法通过整合全局与局部信息, 提供了全面的评估视角. 例如, 在KSGC和C_WG方法中, 节点3的排名优于节点14, 但从全局与局部结构结合的视角看, 节点14因接近两个重要社团而更具传播优势. 此外, 对于节点的潜在传播性能, 节点6作为桥梁节点虽因网络约束其传播性能受限, 但连接了以节点22为核心的社群, 展现了重要的潜在传播能力. 而节点7虽靠近核心社群, 但传播距离的限制削弱了其连接其他社群的能力. 由此可见, 在评估节点性能时需综合考虑其潜在的传播影响.

以上分析得到了SIR, BGIM和BGIM+方法的验证(见表2), 进一步证明了BGIM与BGIM+ 构造的引力场空间在评估节点重要性方面的有效性和准确性. 总体来看, 不同中心性指标在节点重要性评估中各有侧重, 而BGIM与BGIM+方法通过综合考虑节点的全局位置、局部特征和传播潜力, 为识别具有广泛传播能力的节点提供了有力工具, 尤其在复杂网络环境下展现出显著优势.

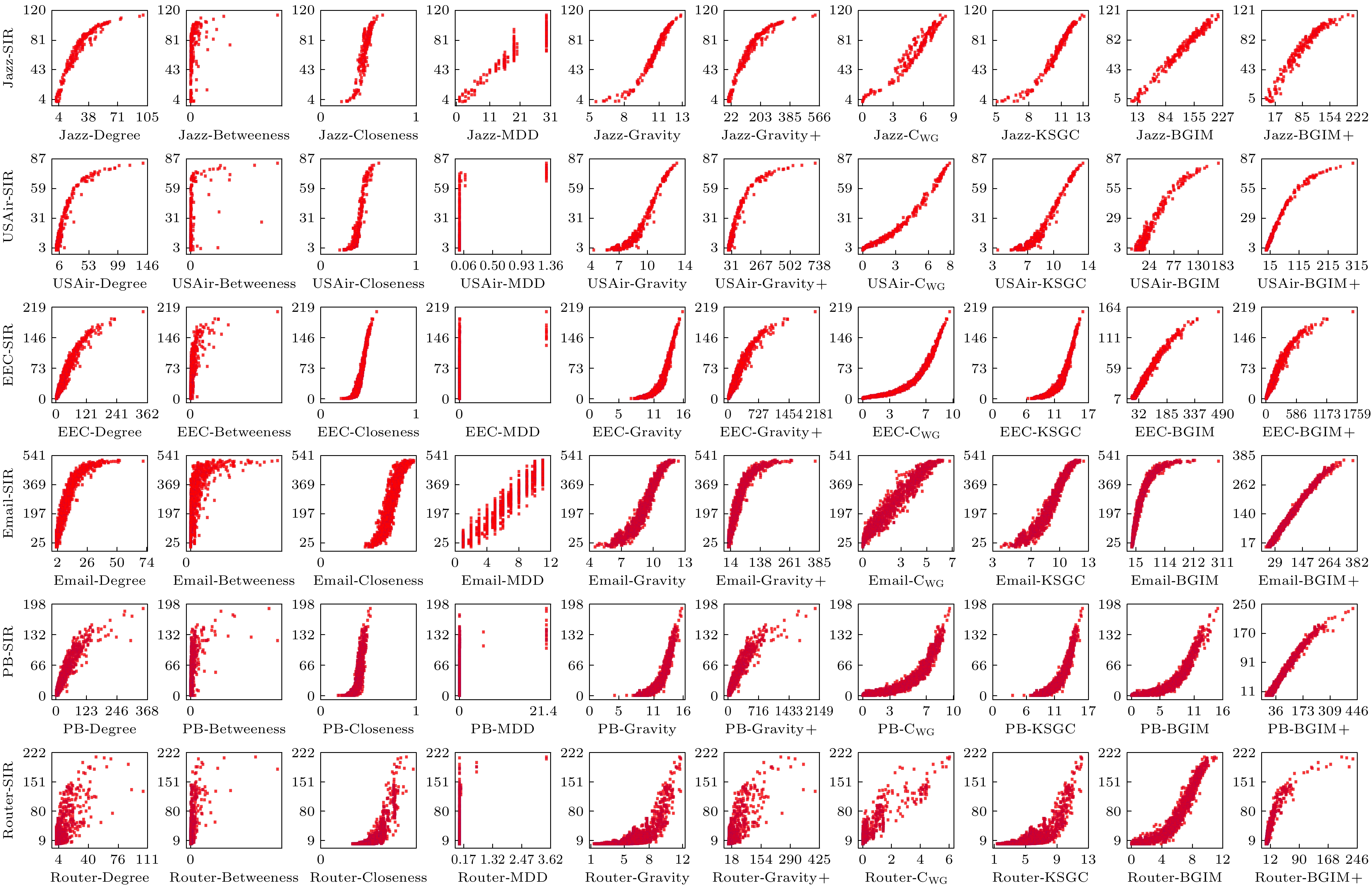
SIR模型通过模拟网络中节点在易感(susceptible)、感染(infected)和恢复(recovered)三种状态间的动态转化, 追踪信息在网络中的传播路径, 从而量化节点在传播过程中的影响力. 本实验采用Kendall相关系数度量各中心性评价方法与SIR模型模拟结果之间的相关性, 以检验不同方法在识别关键节点方面的有效性. 由实验结果(见图2)可知, Degree, Closeness及多种引力模型(如G, G+, C_WG, KSGC, BGIM和BGIM+)与SIR模型排名均呈现一定正相关. 然而, Betweenness和MDD的表现略显不足, 说明单纯依赖全局路径或局部度信息的评价方式在结构复杂的网络中存在明显局限.

整体而言, 在不同类型的网络中, BGIM和BGIM+节点重要性排序与SIR模型模拟结果更为贴近, 展示出较强的适用性和鲁棒性. 究其原因, 主要在于它们在节点评价中综合考虑了网络位置、信息熵与非对称引力因子, 从而能够更全面地刻画节点在传播过程中的影响力. 相比之下, 度中心性和接近中心性在部分网络中表现尚可, 但随着网络拓扑的复杂化, 这两种方法的区分度与稳定性明显下降. MDD虽然尝试融合局部和全局信息, 通过邻居节点度分布来提升评估精度, 然而在多样性强的网络中, 其识别精度并无显著提升. 对于引力模型中的各类变体, G模型主要依赖节点度值及拓扑距离来度量节点引力, 虽能在部分网络(如Jazz, Email)保持相对稳定的表现, 但在结构高度异质的网络(如Router)中, 因过度依赖节点度值, 难以有效识别核心节点. C_WG 则更倾向于凸显节点的全局特性, 尽管在PB网络中结果与BGIM接近, 但在其余网络中, 由于对全局中心性的偏重, 其效果仍略逊于BGIM. 相比之下, BGIM与BGIM+在规模较大、结构更为复杂的网络中表现尤其突出, 尤其当需要兼顾网络位置和传播潜力时, 其相关性明显高于KSGC. 究其根本, 这两种方法在设计上不仅考量了节点在网络中的全局地位, 还结合引力修正机制来调整节点在异质性网络中的影响力分布, 使关键节点的识别更具准确性与一致性.

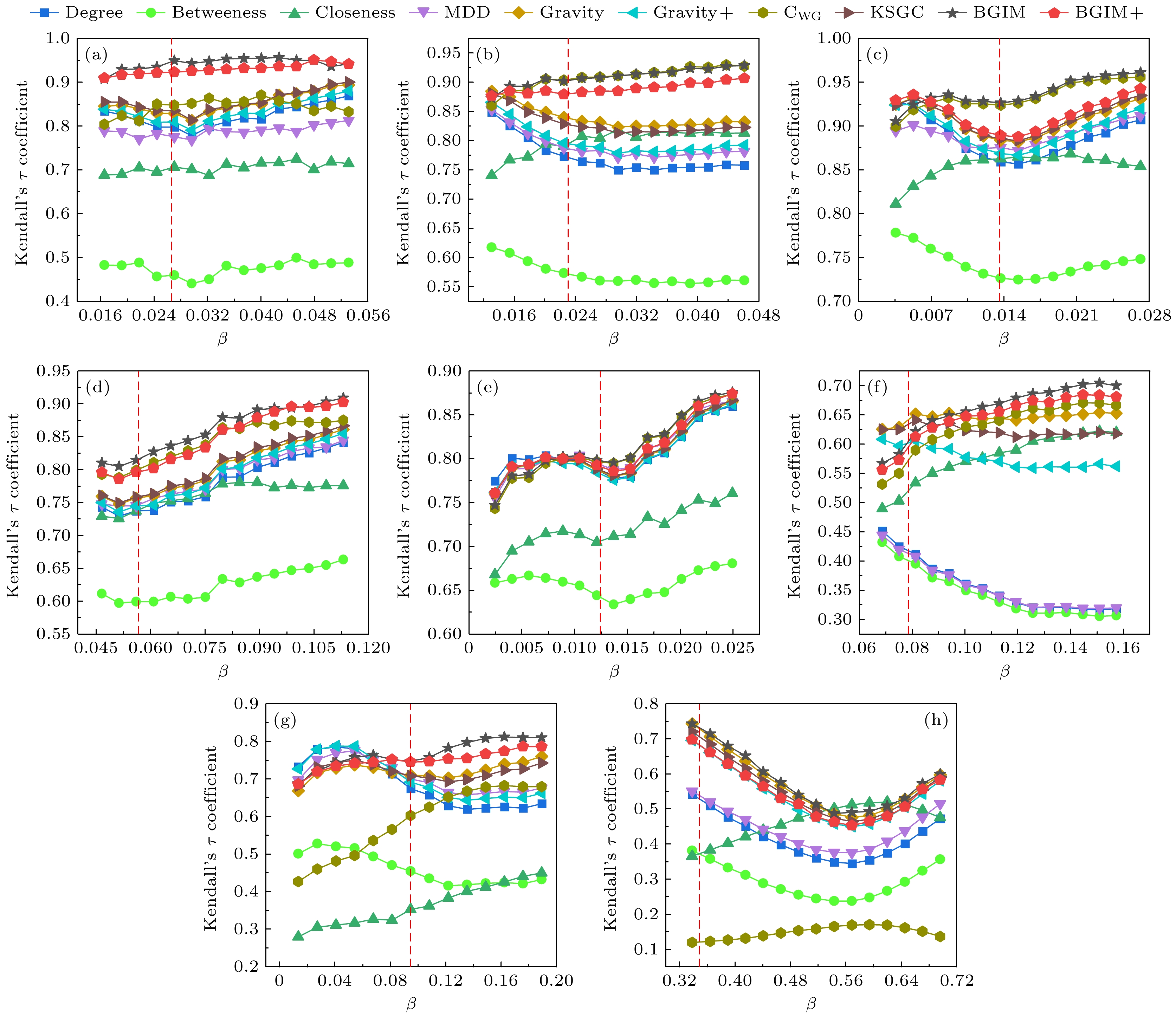
需要指出的是, 上述结果主要基于单一传播率进行比较, 只能反映单一时间片下的排名表现. 为提高评估的全面性与准确性, 我们将各网络的传播阈值用作衡量基准, 并设置传播区间为 [$ \beta_{\mathrm{th}}-\alpha $, $ \beta_{\mathrm{th}} \times 2 $](其中$ \alpha = 0.01 $), 以观察在阈值附近扰动时不同方法表现的变化情况. 当$ \beta_{\mathrm{th}}-\alpha < 0 $时, 将传播区间的下限置为0, 即 [0, $ \beta_{\mathrm{th}} \times 2 $]. 此外, 为进一步验证BGIM与BGIM+在多种网络结构下的适用性, 本实验及第6.3节引入了Facebook网络和Power网络进行更系统的对比评估. 通过不同传播率条件下的相关系数分析, 能够更细致地考察各方法与SIR排名在不同扩散环境下的契合度.

从图3的结果可见, 在大多数网络中, 当传播率超过传播阈值时, BGIM与BGIM+拥有更高的相关性, 说明它们在模拟真实扩散过程时对节点重要性的衡量更为精准. 虽然度中心性或基于度的引力方法(如Degree, Gravity, KSGC等)在低传播率下尚能发挥作用, 但当传播率逐步接近或超越阈值时, 这些方法开始出现性能下滑. 究其原因, 在低传播率下, 信息传播局限于局部节点间, 而当传播率升高, 信息传播范围扩展至全网, 需要对节点的全局地位进行更全面的刻画. 混合度量方法(C_WG, BGIM, BGIM+)则在不同传播率下均维持了较高的稳定性, 尤其是BGIM与BGIM+, 在节点数量较多、结构更复杂的网络中, 其排名更能与SIR的传播结果保持紧密衔接. 以EEC网络为例, 当传播率越过阈值后, BGIM+很快就能逼近BGIM的表现, 反映出其在全局范围内有效整合网络位置和传播潜力的能力. 值得注意的是, C_WG依赖特征向量中心性的全局优势, 易于赋予与高中心性节点相连的节点更多权重; BGIM则通过引入结构洞网络约束系数来限制特征向量中心性的过度放大, 使得对节点重要性的评估更加客观而全面, 特别在大规模网络中表现尤为突出. 由此可见, 在结构多样且规模庞大的网络中, 将节点的局部与全局特征结合起来进行综合评估, 对于准确识别关键节点至关重要.

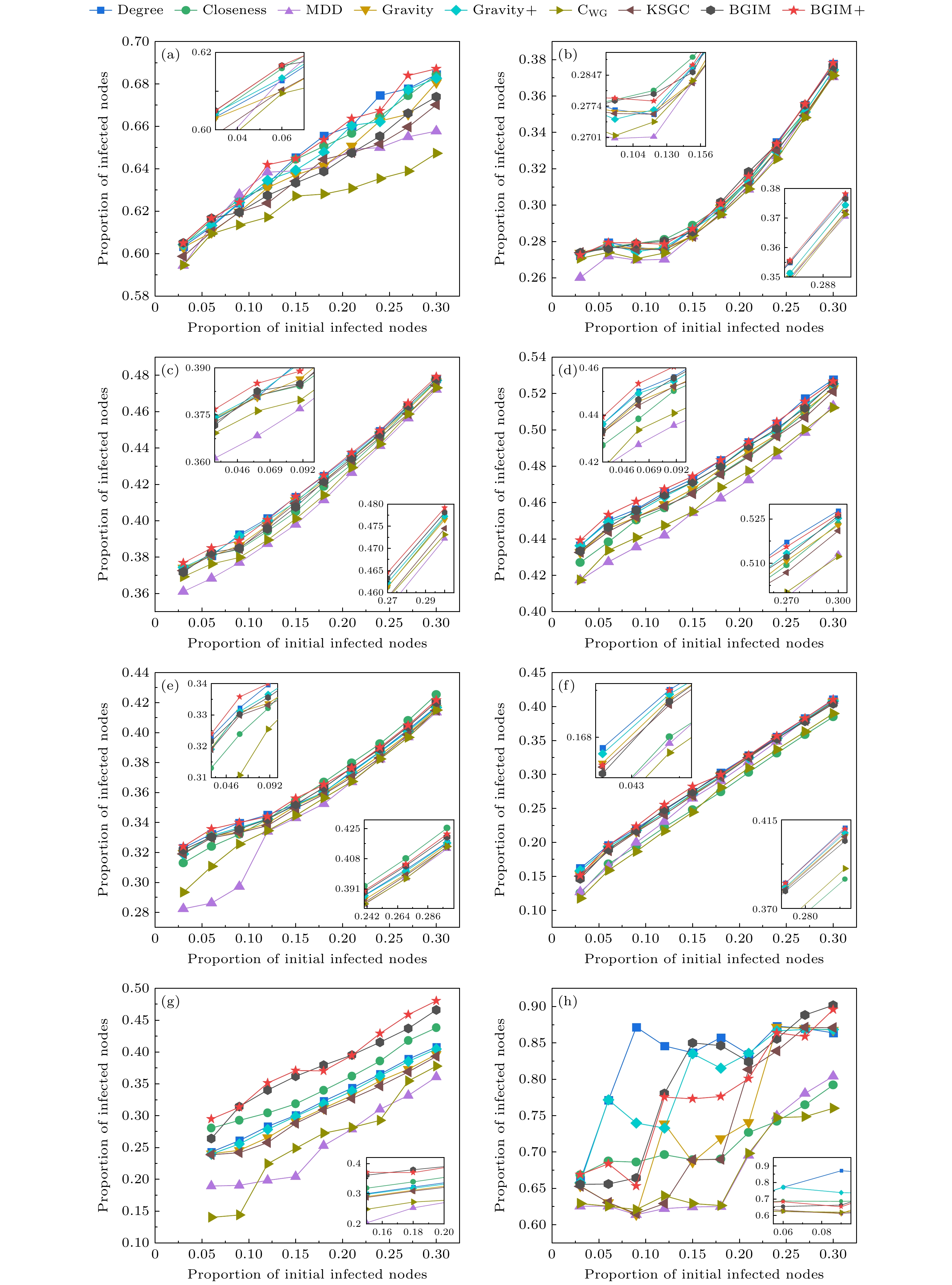
为了进一步评估BGIM与BGIM+在复杂网络环境下识别重要节点的性能, 将它们与现有方法得到的节点排名进行比较, 观察这些节点在相同条件下的传播能力. 实验结果如图4所示. 具体而言, 选取了各个中心性评价方法得到排名中的前3%至30%的节点, 并将这些节点作为初始感染节点在SIR模型上进行模拟传播. 为确保实验结果的普适性, SIR模型的参数设置如下: 传播率为传播阈值的两倍, 恢复率为1. 在时间节点t = 30时, 记录网络中受感染节点所占的百分比, 以此揭示各个方法在不同网络中的传播表现. 实验结果显示, Degree和Closeness方法在整个传播过程中均表现出色. 这是因为Degree方法选择的初始节点通常具有较多的邻居节点, 而Closeness方法选择的节点则具有较高的中心性, 能够迅速覆盖网络中的其他节点. 然而, 在Jazz网络和Router网络中, 尽管这些方法在传播初期表现出较高的感染率, 但随着传播的推进, 感染率增幅逐渐放缓. 该现象的根本原因在于, 这些方法主要关注节点的节点度数和距离. 在Router网络等环境中, 这些局部属性能够在早期引发快速传播, 但随着时间的推移, 在维持高效传播方面的能力逐渐显现出一定的局限性.

与此相反, 各个引力模型评价方法在初期的感染率较低, 因为在这一阶段网络中的关键节点数量较少, 其影响力尚未完全发挥. 在后期阶段, 这些方法的感染率持续上升, 特别是BGIM和BGIM+方法, 感染率达到较高水平并趋于稳定. 这是因为在选取节点的过程中, BGIM和BGIM+方法基于多种指标, 不仅关注节点的信息熵, 还考虑在网络中的地理位置和传播条件等因素. 在高初始感染节点比例的情况下, BGIM和BGIM+通过多指标评估, 逐步识别关键节点并实现跨社区传播, 在感染率提升和稳定性方面表现更优. 相比之下, 其他引力模型虽然在初期表现良好, 但在后期由于过度依赖局部或全局结构, 在复杂网络中无法持续维持高效传播.

在部分情况下, 例如在Router网络初始感染节点为0.03—0.05的阶段, BGIM与BGIM+方法表现并不优异. 这是因为Router网络具有密集的社区结构, 使得信息在局部区域内能够快速传播, 但在跨社区传播时速度会减慢. BGIM和BGIM+方法在这种网络结构中, 需要一定的时间来识别并利用关键节点以实现跨社区传播. 相较与传播初期, BGIM和BGIM+方法更侧重于在中后期阶段通过综合评价提高整体传播效率. 这使得它们在初期阶段的表现相对不如Degree和Closeness方法. 各中心性评价方法在不同网络中的表现有所差异, 但BGIM和BGIM+方法在多数网络中都展现了较强的识别和利用关键节点的能力.

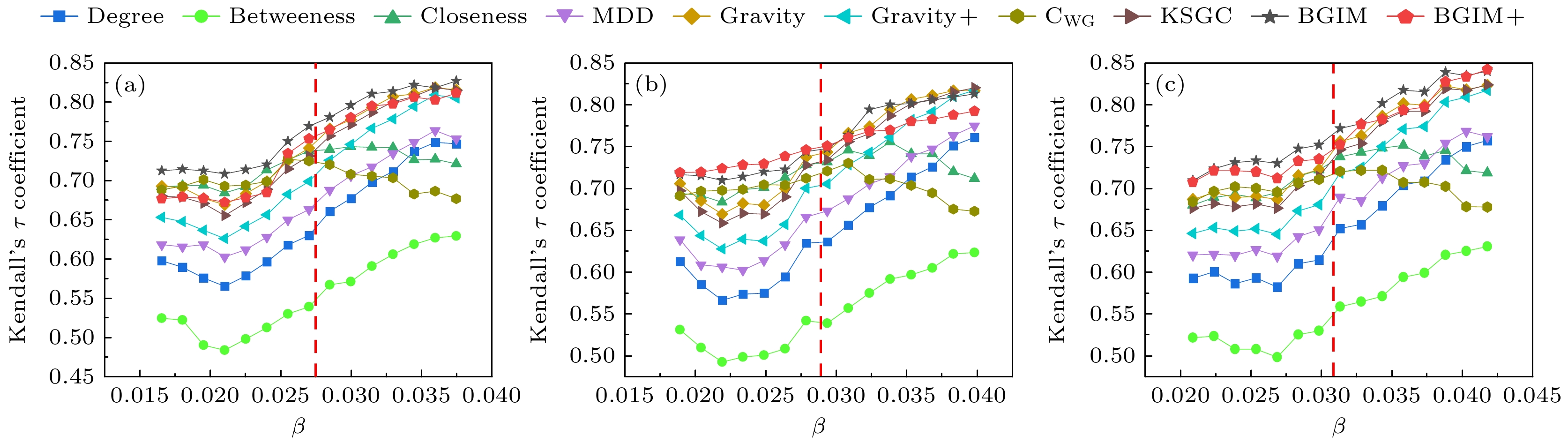
为了进一步验证所提评价方法的稳健性和可靠性, 本节采用Lancichinetti-Fortunato-Radicchi (LFR) 基准模型生成具有真实社区结构的人工合成网络进行实验. LFR模型因能够模拟复杂网络中的真实社区结构而广泛应用于网络科学研究. 具体参数设置如下: 节点数$ N = 2000 $, 度数分布的幂律指数$ \tau_1 \in [1.5, 1.8] $, 社区大小分布的幂律指数$ \tau_2 \in [1.2, 1.4] $, 混合参数$ \mu \in [0.1, 0.2] $(控制跨社区连接边的比例). 基于上述参数, 生成了平均度分别为$ \langle k \rangle = 5, 10, 15 $的网络, 用以代表不同密度的网络结构. 这些网络具备现实世界网络中多样化的社区结构特征, 可全面评估各中心性指标的可靠性和适用性. 通过调整平均度, 我们考察了中心性方法在不同连边密度网络中的表现, 从而验证其在各种复杂网络环境下的适用性. 在传播动力学模拟中, 同样采用SIR模型, 传播率β的取值区间为$ [\beta_{\mathrm{th}} - \alpha, \beta_{\mathrm{th}} \times 2] $(其中$ \alpha = 0.01 $), 确保传播率在阈值附近合理变化. 通过在上述传播率区间内的不同传播率下, 计算各中心性方法所得节点排序与SIR模型模拟结果之间的Kendall相关系数, 深入分析了各方法在关键节点识别方面的有效性和可靠性, 实验结果如图5所示. 实验表明, 由LFR模型生成的三种不同平均度网络对中心性评价方法进行了更加严格的验证. 一些算法在稀疏网络中表现优异, 但在稠密网络中表现不佳, 例如主要基于全局信息的Closeness和C_WG方法. 这是因为随着平均度的增加, 网络变得更加密集, 节点之间的路径长度缩短, 当传播率高于传播阈值时, 全局特征对传播过程的影响逐渐减小. 在稀疏网络($ \langle k \rangle = 5 $)中, 度中心性主要关注节点的局部连接, 无法有效反映节点在整体传播中的潜力. 而BGIM和BGIM+方法强调全局视角, 能够综合考虑节点在网络中的整体位置及潜在传播能力, 因此在这种条件下表现更优. 在中等密度网络($ \langle k \rangle = 10 $)来看, 网络连接强度介于稀疏与稠密之间, 社区特性较为明显, 跨社区传播的影响逐渐显现. BGIM和BGIM+方法中的引力修正因子动态调整了局部与全局信息的权重, 使其在跨社区传播过程中更具适应性, 表现优于其他方法. 进一步, 在稠密网络($\langle k \rangle = 15 $)中节点连接更密集, 路径长度显著缩短, 社区特性逐渐减弱, 节点的全局特性逐渐被平均化. 尽管全局特性的重要性减弱, 但BGIM和BGIM+方法通过结构洞约束系数对节点的重要性进行精细化评估, 能够识别在传播过程中具有长尾效应的关键节点, 从而在稠密网络中依然表现出较高的适应性和有效性. 总体来看, BGIM与BGIM+ 方法凭借引力修正因子, 通过结构洞网络约束系数与特征向量中心性非线性制约的关系, 在不同密度的网络中均能实现对局部信息与全局信息的有效平衡, 从而在各种网络环境下展现了较强的适用性和稳健性.

本节对各引力模型评价方法的单调性进行了量化分析, 旨在清晰地展示不同方法在节点排名区分度方面的表现. 在表3中, 单调性最优的数值用红色字体标出. 表3中结果表明C_WG与BGIM方法在所选网络中表现出更佳的单调性. 具体而言, 尽管BGIM在Email和Router网络中的区分度略逊于C_WG, 但在其余网络中, BGIM始终占据首位, 显示出其在多数情况下更优的节点排名区分能力.

BGIM的时间复杂度主要由三部分构成: MDD排序、引力修正因子的计算和双维引力模型的核心计算. MDD排序的时间复杂度为$ O(N \log N) $, 其中N为网络节点数. 由于每次迭代需遍历所有节点, 最坏情况下需要N次迭代, 故其时间复杂度为$ O(N^2 \log N) $. 引力修正因子的计算包括特征向量中心性和网络约束系数的求解. 特征向量中心性通过Lanczos迭代法计算, 复杂度为$ O(M) $, 其中M为邻接矩阵中非零元素个数; 网络约束系数需遍历每个节点及其邻居关系, 复杂度为$ O(N \cdot k^2) $, 其中k为平均度. 因此, 引力修正因子的整体计算复杂度为$ O(M + N \cdot k^2) $. 双维引力模型的核心计算涉及每个节点与其邻居或在距离阈值内的节点进行引力累加, 复杂度为$ O(N \langle k \rangle^{R}) $, 其中R为影响半径.

在空间复杂度方面, BGIM主要依赖于邻接矩阵和节点属性的存储. 邻接矩阵的存储需$ O(N^2) $空间; 每个节点还需存储多个属性, 如特征向量中心性、网络约束系数、k-shell值、MDD值、引力值及引力差异系数等. 总体而言, BGIM的空间复杂度为$ O(N^2) $.

综上所述, BGIM的总体时间复杂度主要由引力系数和累加项计算决定, 即$ O(N \langle k \rangle^{R}) $, 其中平均度$ \langle k \rangle $和影响半径R是关键因素. 在稀疏网络($ \langle k \rangle $较小)且R适当的情况下, 算法的计算效率较高. 为进一步优化计算效率, 可合理选择较小的R值以减少计算量; 同时, 利用稀疏矩阵存储和快速遍历优化计算过程; 此外, 通过并行或分布式计算, 将任务分解到多设备环境中以显著提升效率.

在复杂网络研究中, 如何有效评估节点的影响力是一个关键问题. 本文借鉴物理学中的引力场理论, 提出了将信息熵、引力修正因子和非对称吸引因子引入到引力模型的方法, 旨在更真实地模拟物理世界中的引力效应, 避免资源过度集中于少数高连接度节点, 从而综合评估网络节点的传播性能. 通过引入信息熵, 反映节点状态的不确定性和信息丰富程度. 引力修正因子和非对称吸引因子的引入, 模拟了物理引力中质量和距离对引力作用的影响, 使得节点之间的“引力”作用更加符合物理规律. 这样的设计使得节点既不会因为局部高密度聚集而获得过高的得分, 也不会因为作为“桥梁”节点而被低估其潜在影响力, 全面考虑了节点在网络拓扑中的实际地位. 在实验部分, 本文将所提方法与传统的中心性评估方法及其他引力模型进行了对比分析. 在8个真实世界的网络(Jazz, USAir, EEC, Email, PB, Router, Facebook, Power)和LFR生成的不同密度的合成网络上进行了实验, 结果表明, 本文提出的方法在识别节点重要性方面展现了明显的优势. 该方法不仅能够准确评估节点在网络中的影响力, 而且在不同类型和规模的网络中均表现出较高的稳健性和适用性.