近似三角形强冲击波界面反射形成卸载稀疏波的作用下, 在靠近自由面一定深度的靶板内部产生拉伸作用区域, 当拉伸应力足够高时, 将导致靶板材料产生拉伸损伤破坏/破碎, 一般将这一物理现象称之为微层裂. 靶板材料损伤/断裂以及破碎形成的颗粒尺寸(质量)分布以及颗粒速度的分布特征不仅直接影响惯性约束聚变(ICF)、内爆过程的汇聚压缩, 而且也直接关系到一些高速侵彻/爆轰加载下的毁伤效应和超高速碰撞下太空结构防护性能的有效评估. 前期的研究一般在飞片撞击方波加载层裂实验基础上, 对材料层裂损伤机理的认识不断深入, 相关学者基于经验或介观唯象物理给出了一些层裂损伤模型^[1–5], 但这也导致了这些模型的适用范围具有一定的局限性^[4,6], 如高温、高压、高应变率极端加载以及工程中复杂波形加载下损伤模型的适用性就有待商酌. 现阶段的研究分析表明: 缺乏材料内部微介观缺陷演化信息是制约损伤模型进一步完善和发展的关键因素之一^[7].

结构金属材料在高应变率下的塑性变形和破坏的机理是复杂的, 并受到微介观结构中的非均质性的影响, 包括晶界、界面的分布和预先存在的缺陷或杂质的密度等, 这些介观尺度非均质性的分布可以提供孔洞形核位置, 并耦合加载条件, 进一步影响损伤材料内部微孔洞/微裂纹的分布特征及其演化规律, 进而影响层断裂/破碎行为, 这就需要认真审视材料内部的成核过程. NAG模型中成核方程是基于实验金相观测结果和微观统计方法给出的^[1], 成核孔洞的数量随应力增大呈指数形式增长, 但实验统计的孔洞数也可能包含孔洞汇合的因素; Tonks等^[4]计算时采用了孔洞数随应力线性增加的简单处理方法; Molinari和Wright^[5]认为因材料内部微缺陷的类型不同导致的孔洞成核应力也不同, 并唯像地采用Weibull概率分布函数和Gaussian概率分布函数描述孔洞成核过程; Trumel等^[8]考虑了已有孔洞对成核的影响, 认为孔洞增长引起的孔洞周围的塑性变形区域对新孔洞成核有抑制作用, 进而采用损伤程度控制孔洞成核截止时刻; 而对于目前常用的Gurson层裂损伤模型^[2], 其成核计算采用的是平均处理方法(即损伤度的计算), 并没有涉及孔洞分布的介观信息. 上述给出的几种基于唯象分析、具有代表性孔洞成核计算方法, 或是只考虑部分影响成核的因素, 或是在应用过程中的解析推导不方便, 这就需要在分析孔洞成核过程中综合考虑不同因素的影响, 同时也最好明确孔洞成核开始以及孔洞成核截止的临界条件及其计算方法.

损伤演化的精确定量是理解材料破坏机理的关键, 也是发展和验证材料损伤破坏模型的必要条件. 在材料内部层裂损伤演化的整个过程中, 因孔洞成核、增长和汇合的存在, 孔洞的分布特征不断变化, 损伤增长在本质上也不是线性的^[9,10], 这就意味着需要在时间发展过程中正确捕捉损伤增长速度以及孔洞分布的变化情况. 目前的损伤模型尚不能完全合理地反映孔洞分布空间上的离散化与损伤增长连续性之间的相互关联, 且对损伤增长速率使用的是一阶近似, 这使得基于实验标定模型可调参数后, 虽然可以在一定加载范围内较好地模拟层裂实验^[11,12], 但针对极端加载情况则需要重新调整参数^[13]; 同时, 传统的回收样品金相观测或X射线扫描成像等实验手段可以提供样品中损伤的定量化信息, 但不能捕捉到孔洞成核和增长的时间演化信息, 且这些较低的应力、应变率下的变形机制可能不能反映在更极端的应力、应变率下的变形机制, 这在一定程度上限制了损伤模型有效性的验证和发展. 近年来随着实验技术的发展, Coakley等^[14]利用飞秒X射线自由电子脉冲对靶板进行原位探测, 并利用小角X射线散射监测孔洞分布的演化, 给出了材料内部损伤实时原位变化情况; MacNider等^[15]利用吸收对比成像技术在约1.6 μm空间分辨率下直接成像金属层裂损伤的时间演化过程, 并观察到孔洞分布和尺寸与时间和微观结构的依赖关系, 尽管这些实验数据信息还有待完善和深入挖掘, 但新的实验技术为进一步验证和发展动态损伤预测模型带来了可能. 现阶段一些相关学者基于实验、理论分析和数值模拟探讨强冲击下材料内部微介观缺陷(孔洞)分布特征变化与损伤发展之间的关联, 寻求构建精细化的损伤物理模型. 针对层裂损伤演化初期的特征, 本文讨论了层裂损伤早期发展过程中的孔洞分布特征的变化情况.

为了精细化描述延性金属层裂损伤孔洞微介观分布特征的演化规律, 在已有认识的基础上, 将损伤发展过程可以进一步划分为: 损伤发展早期的孔洞成核与增长、损伤发展中期孔洞增长以及损伤发展后期的孔洞增长与汇合3个典型阶段^[9]. 损伤发展的早期旧孔洞增长与新孔洞成核并存, 且新成核孔洞数量一方面随着应力的增长而增加, 另一方面随着旧孔洞数量的增加和孔洞尺寸的增长(即损伤的增长)而减少, 即新成核孔洞数量从零开始, 呈现先增加后减少, 最后归于零. 这个时期的损伤度很小, 可以采用无限介质中的孔洞增长方程描述孔洞增长过程, 同时, 损伤对应力的影响可以近似忽略, 且应力近似线性增长^[5]. 当应力达到材料的层裂强度时, 发生层裂损伤区域的材料完全塑性变形, 新孔洞的成核截止^[16,17].

通过对孔洞成核过程的唯象分析, 孔洞成核方程应该包括引起成核孔洞数增加的应力项和导致成核孔洞数减少的损伤度项, 而损伤的计算又包含孔洞数和孔洞大小的乘积, 不同因素纠缠在一起, 不利于损伤的解析推导过程. 考虑到损伤发展早期损伤与应力之间的相互影响很小, 可以唯象采用孔洞成核概率随应力增大先增大后减小的概率分布函数描述孔洞的成核过程, 借此代替损伤对孔洞成核的影响, 这一处理方法类似于Molinari和Wright^[5]所采用的方法, 但其物理涵义不同, 后面的解析解与分子动力学计算统计结果以及实验观测结果的对比也验证了此方法的适用性. 我们最终选用了三角函数形式的概率分布函数, 即

显然, $ \displaystyle\int_{{p_{{\text{c0}}}}}^{{p_{{\text{spall}}}}} {g\left( p \right){\text{d}}p = 1} $. 其中, $ p $为加载的拉伸应力($ {p_{{\text{c0}}}} \leqslant p \leqslant {p_{{\text{spall}}}} $), 对应时刻为$ t $; $ {p_{{\text{spall}}}} $为材料的层裂强度, 对应时刻为$ {t_{{\text{spall}}}} $; $ {p_{{\text{c0}}}} $为孔洞开始成核的成核临界应力, 对应时刻为$ {t_{{\text{c0}}}} $, 且有

这里, $ {Y_0} $和$ G $为材料的屈服强度和剪切模量. (1)式反映了孔洞成核概率随应力增长的变化情况: 当$ {p_{{\text{c0}}}} \leqslant p \leqslant \left( {{p_{{\text{c0}}}} + {p_{{\text{spall}}}}} \right)/2 $时, 孔洞成核数随应力的增长而增加; 当$ \left( {{p_{{\text{c0}}}} + {p_{{\text{spall}}}}} \right)/2 < p \leqslant {p_{{\text{spall}}}} $时, 孔洞成核数随应力的增长而减少, 这体现了已有孔洞增长对新成核孔洞的抑制作用.

而累计成核孔洞数占总孔洞数的份额$ f\left( N \right) $随应力增长的变化为

考虑到这一阶段应力近似线性增长, 又有:

此外, 在损伤早期发展阶段, 强加载下延性金属材料内部的孔洞基本上保持球形增长, 且可以采用孤立孔洞的增长方程描述孔洞的变化^[5], 即

式中, $ {p_{\text{c}}} $为半径$ a $孔洞成核时刻的成核应力. 则根据(1)式, 这部分孔洞的体积为

积分上式得到所有孔洞的体积为

式中,

根据损伤度$ \phi $的定义, 且考虑到损伤发展早期的损伤度很小, 则有

对(7)式采用多次分布积分, 然后再对损伤度进行二次微分求导(时间求导), 可以推导得出简单的损伤演化方程:

显然, 该损伤演化方程不仅反映了材料微细观结构的影响, 也反映了加载的率效应. 同时, 相对于Molinari和Wright^[5]基于孔洞成核Weibull概率分布函数或Gaussian概率分布函数数值求解损伤度值, 新的损伤演化解析方程更方便实际应用. 不过, (8)式给出的是层裂损伤早期的演化过程, 其后的损伤增长不仅需要考虑孔洞间的相互作用, 也需要耦合孔洞汇合对损伤增长的影响, 因而完整的损伤演化方程需要分阶段描述.

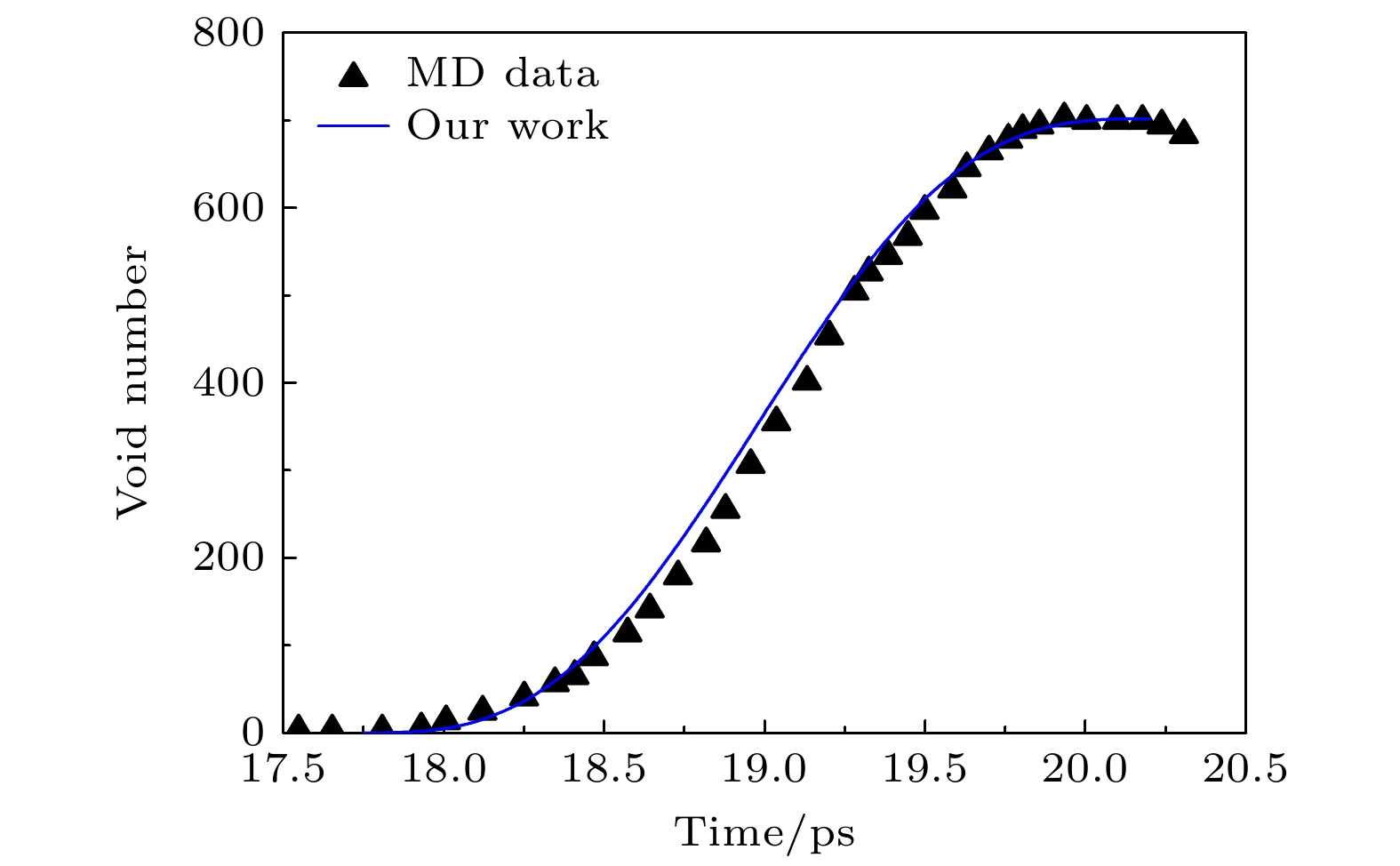
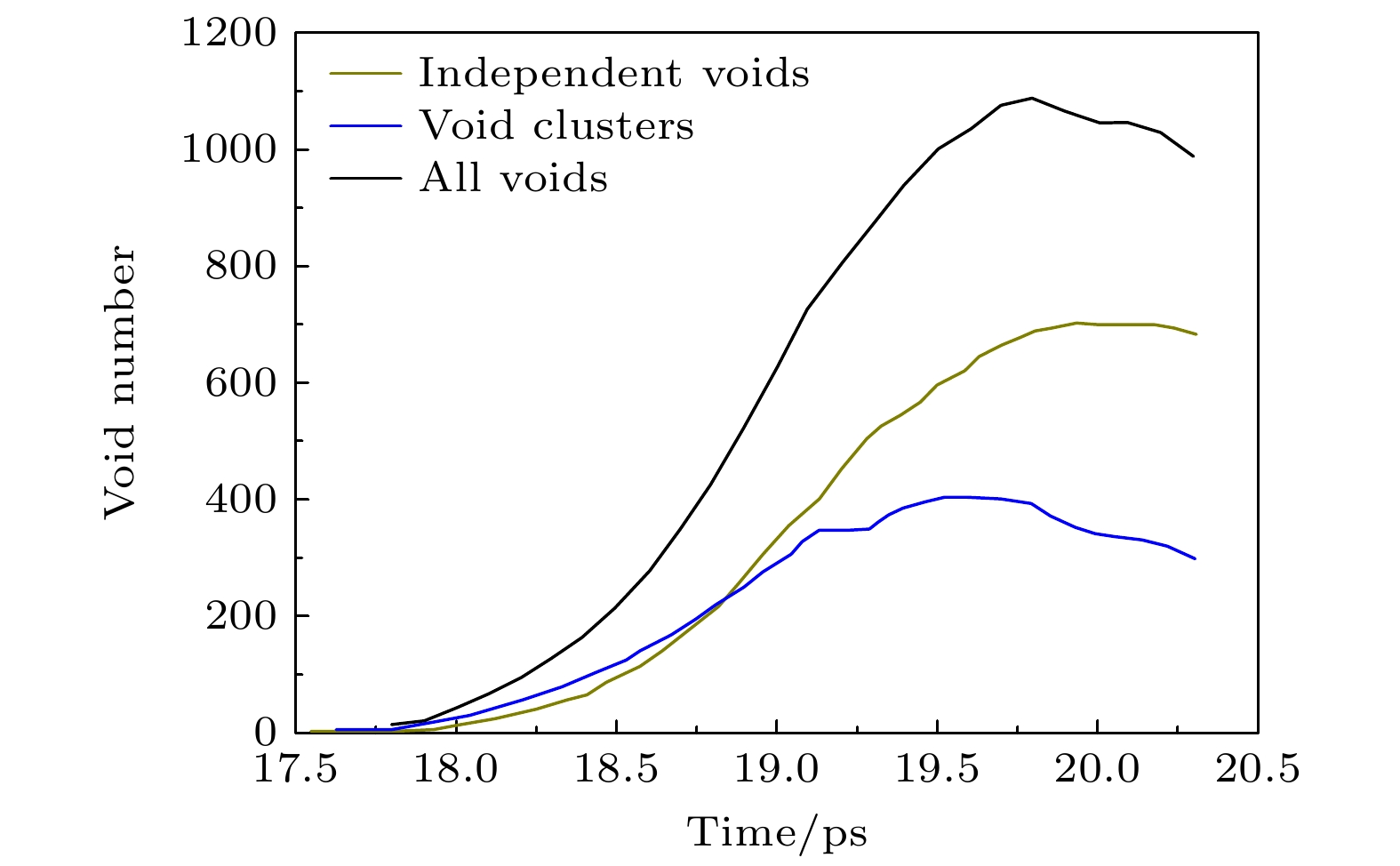
Rawat等^[10]采用分子动力学(MD)程序模拟了单晶铜在5×10⁹ s^–1拉伸应变率加载下的损伤破坏过程, 并统计了孤立孔洞数和孔洞簇数(void clusters)随时间的变化规律(见图1): 孔洞数开始增长阶段即为孔洞的成核过程, 当孔洞之间发生汇合时, 孔洞数减少. 基于(3)式, 则孔洞数随时间的变化规律可以表示为

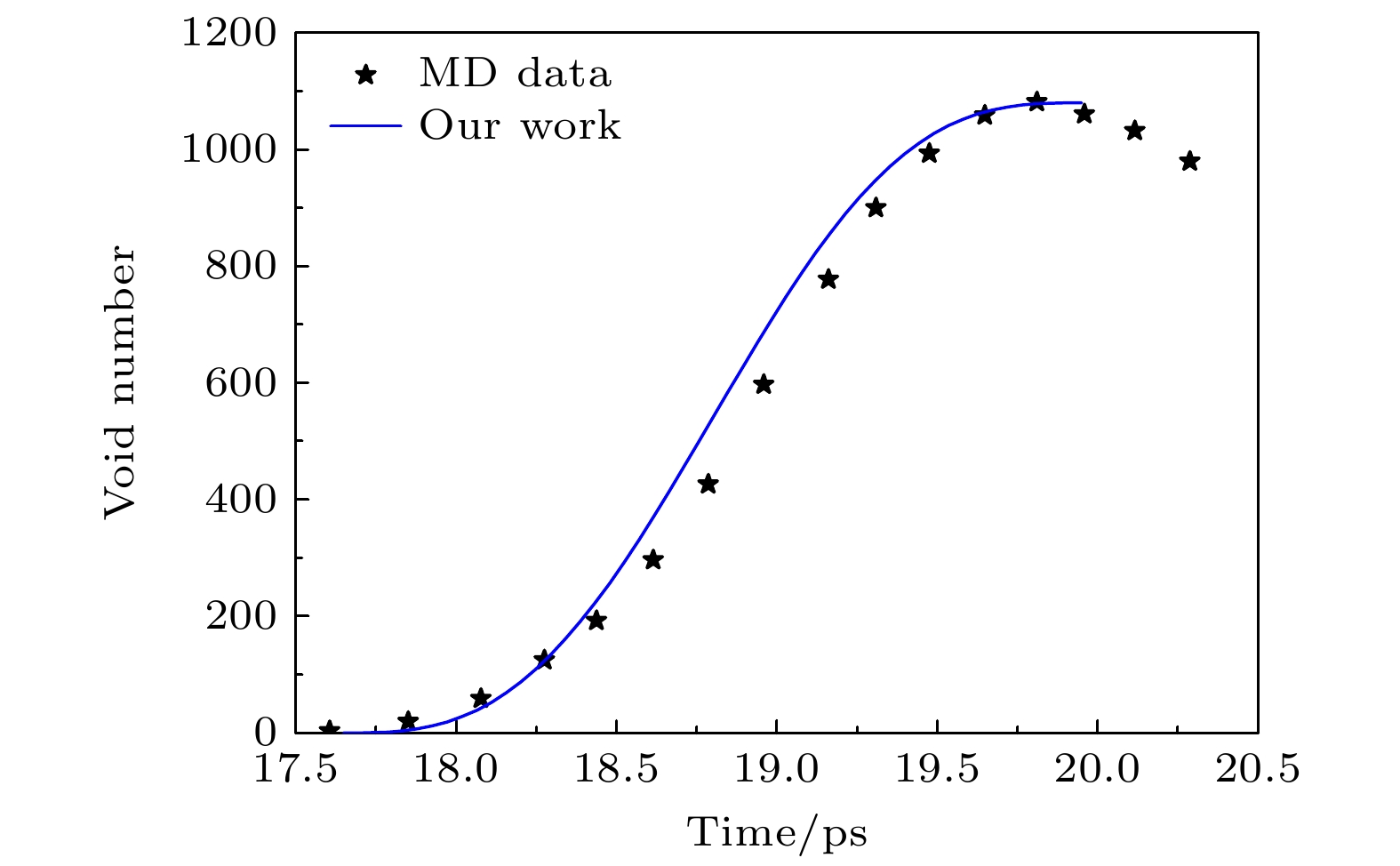
其中, $ {N_0} $为成核孔洞的总数, 即数值计算统计结果中孔洞数的最大值. 由图1可以读出孔洞开始出现的时刻即为孔洞最初成核时刻$ {t_{{\text{c0}}}} $; 孔洞数达到最多的时刻即为孔洞成核截止时刻$ {t_{{\text{spall}}}} $, $ {t_{{\text{c0}}}} \leqslant t \leqslant {t_{{\text{spall}}}} $这一时间段即为层裂损伤早期演化阶段(孔洞成核与增长阶段). 图2给出了孤立孔洞数随时间变化的分子动力学统计结果和(9)式解析计算结果的对比. 对于孔洞簇的定义, Rawat和Chaturvedi ^[18]认为较大的、非近似球形的空隙为孔洞簇, 其成因可能是因为相邻孔洞之间的汇合形成的, 不过, 我们认为其成因是因为孔洞增长引起局部的应力不均匀性导致孔洞增长的不均匀性(即使存在孔洞汇合现象, 其数量也是小量, 这个时期仍以孔洞成核和独立增长为主), 故此, 将孤立孔洞数和孔洞簇数的总数(即图1中的All voids)与(9)式解析计算结果进行对比(见图3), 从中可以看到, 图2和图3的解析计算结果与分子动力学统计结果均符合得很好, 因此我们倾向于这个时期的孔洞簇仍为孤立孔洞的一部分.

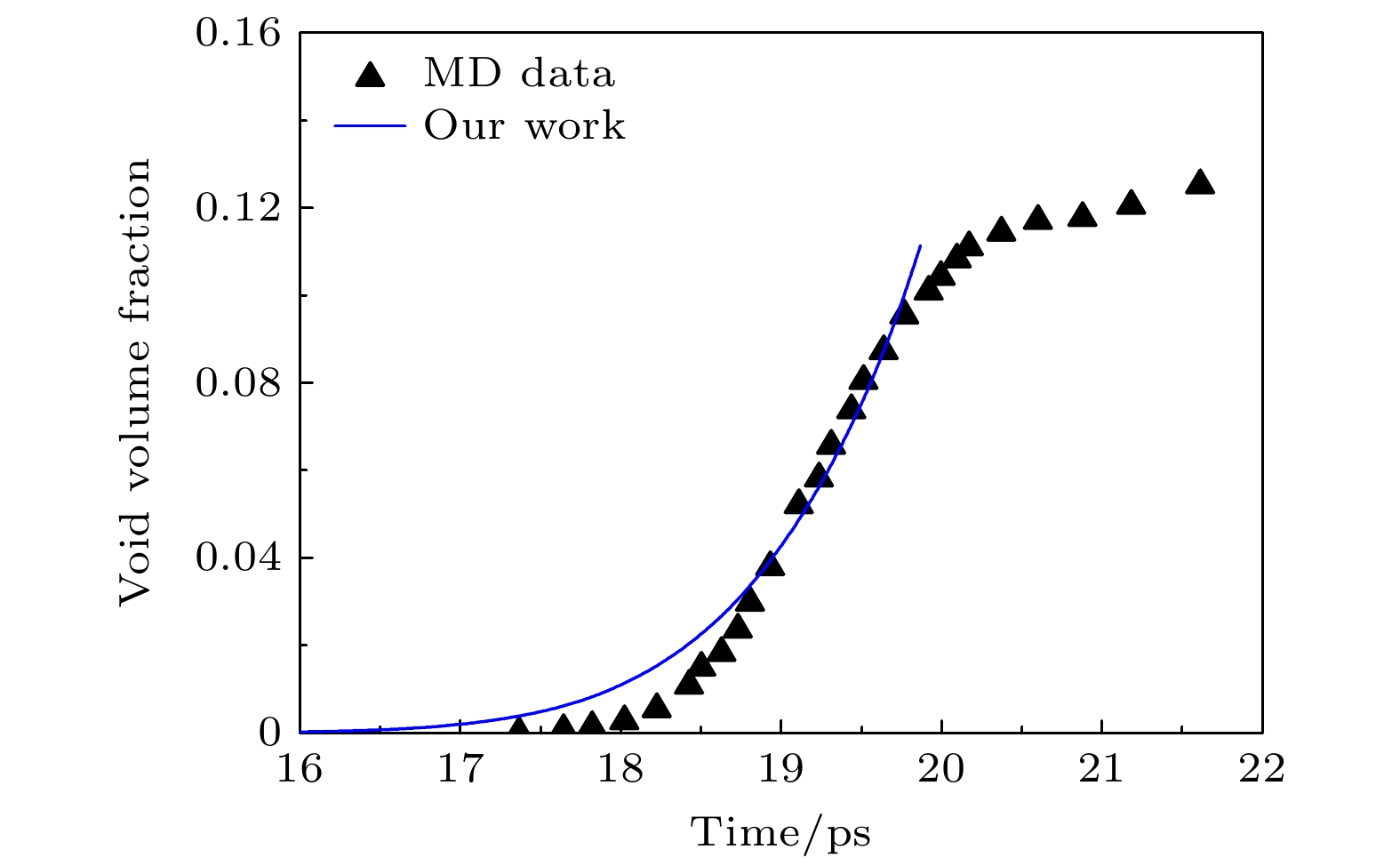
选取参数$ {N_0} = 1.7 \times {10^{24}} {{\text{ m}}^{{{ - 3}}}} $, 图4为(8)式损伤的解析计算结果与MD统计结果的比较, 层裂发展前期的损伤演化趋势二者定性符合较好, 验证了新的损伤演化方程的适用性; 在约19.7 ps时刻以后, 损伤对应力增长的抑制作用逐渐显现, 同时孔洞汇合也可能开始发生, 进而导致了其后二者的损伤发展趋势不同, 而这一时刻也正好对应图3中孔洞数达到最大的时刻, 也就是说, 精细化的损伤过程需要分段描述, 而19.7 ps时刻以后的损伤计算应该采用耦合孔洞汇合影响的损伤方程.

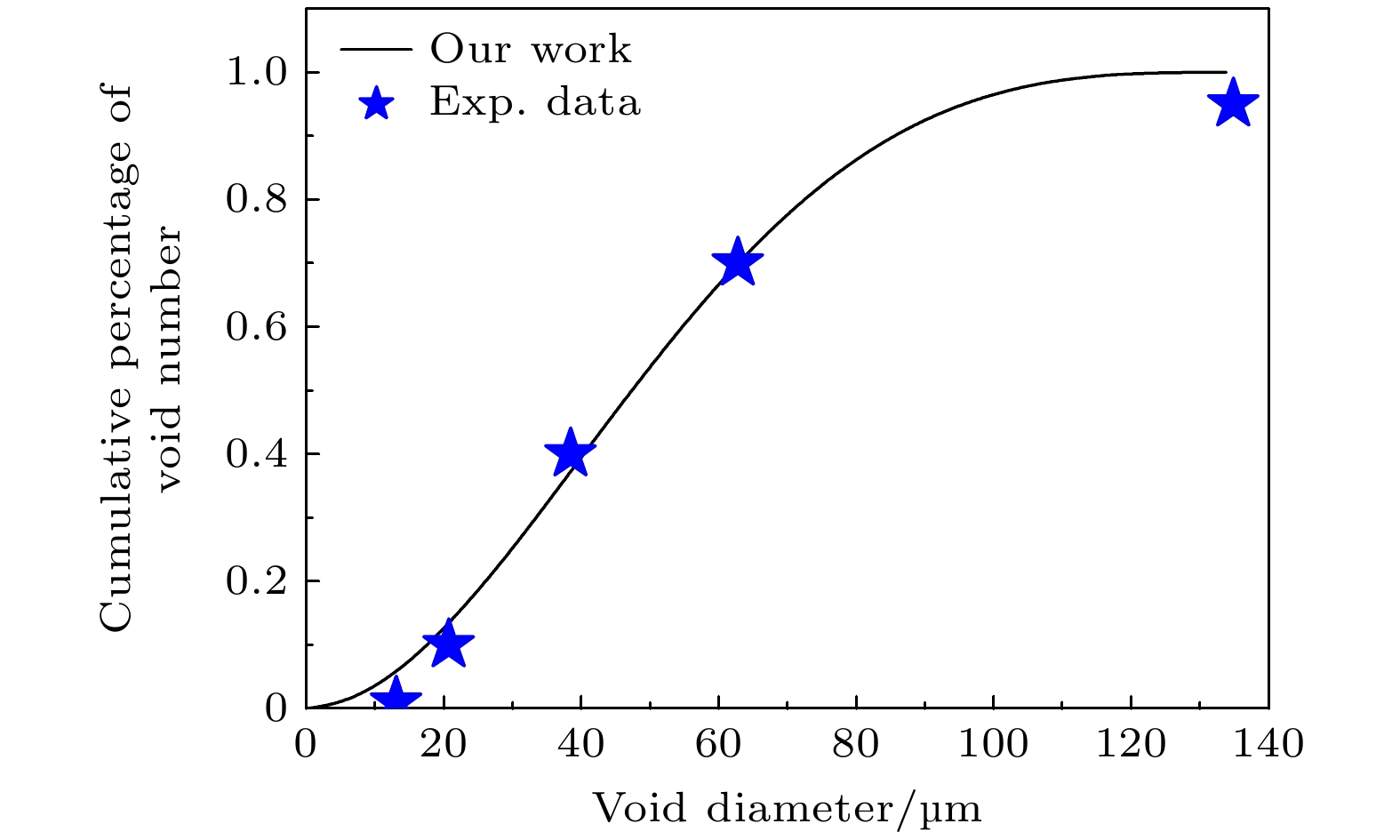
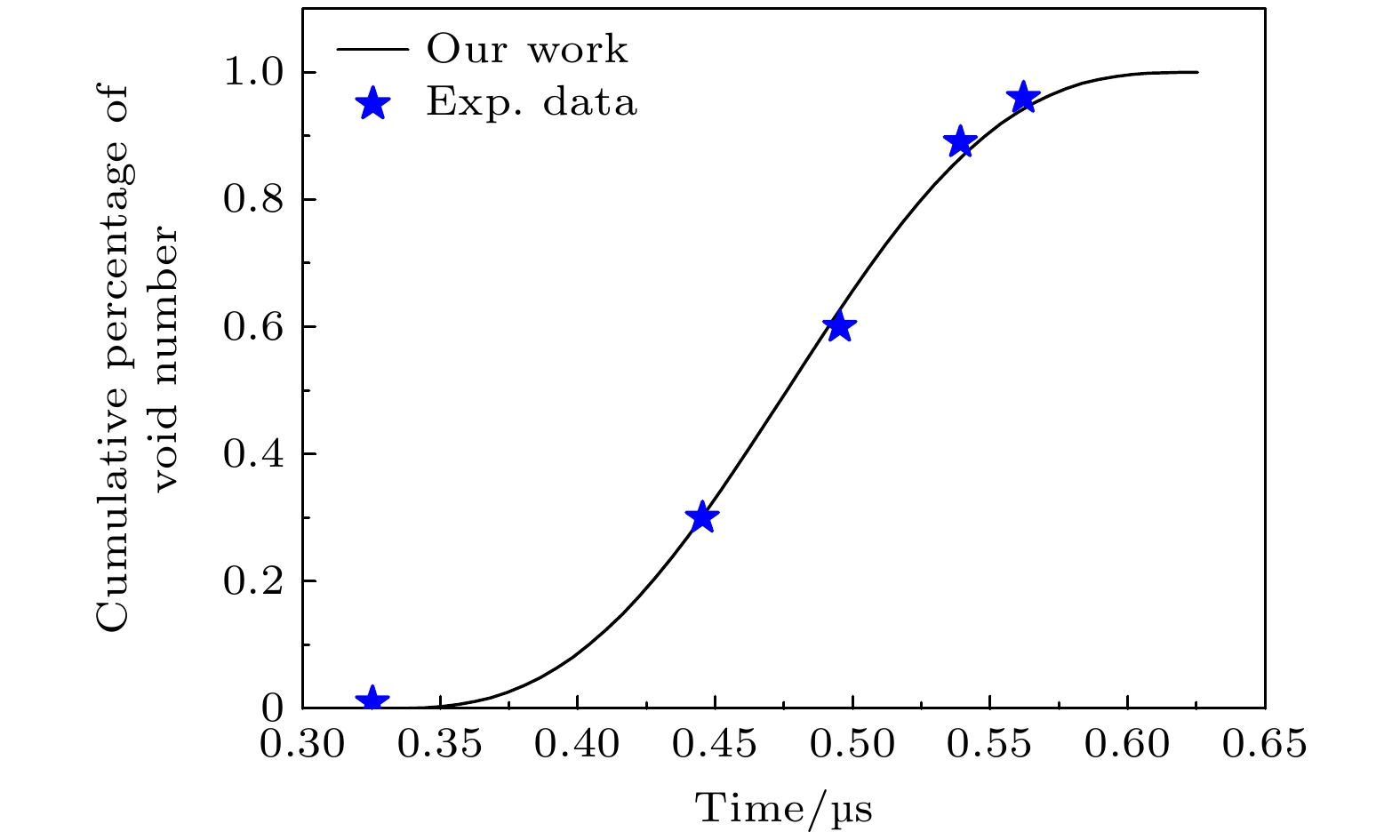
2000年, Rivas等^[19]针对商业纯钽、高纯钽和含预损伤高纯钽材料情况开展了较为完整的实验, 给出了3种材料层裂实验的自由面速度曲线、损伤分布结果, 并以用对数正态分布或对数正态分布和威布尔分布函数的线性组合来拟合孔洞分布情况. 虽然该初始层裂实验与本文分析的层裂损伤早期演化问题相同, 但实验给出的数据属于损伤发生后的终态数据, 这与我们分析的早期损伤演化过程不同, 需要对实验数据进行进一步整理. 为此, 针对高纯钽的初始层裂实验提取几个典型的实验点数据进行处理, 即提取的孔洞直径分别为13.077, 20.745, 38.435, 62.766和134.87 μm, 对应的小于该直径孔洞数占孔洞总数的百分比分别为1%, 10%, 40%, 70%, 95%, 并将其与理论模型的计算结果比较(注: 文献实验数据图中的横坐标采用的是复杂函数形式, 很难读取更多实验数据).

基于实验给出的自由面速度曲线, 计算得到材料的层裂强度$ {p_{{\text{spall}}}} = 7.23~\rm GPa $和加载应力率$ \dot p = \dot \varepsilon \cdot {\rho _0}C_0^2 = 1.156 \times {10^7} {\text{ GPa/s}} $($ {\rho _0} $, $ {C_0} $为材料的初始密度和体积声速, $ \dot \varepsilon $为加载应变率). 对于初始层裂实验, 我们可以近似认为当应力达到$ p = {p_{{\text{spall}}}} $(即$ t = {t_{{\text{spall}}}} $)时的孔洞大小就是实验最后观测到的孔洞大小, 即

显然, 最大孔洞半径为

且有

根据(1)式, 当前成核的孔洞数份额又可以写成:

将(12)式代入, 并注意:

则有

积分上式便得到孔洞总数份额随孔洞半径的变化关系:

最大孔洞半径$ {a_{\max }} $的确定有两种方法: 1)首先由公式$ {p_{{\text{c0}}}} = {2}/{3}{Y_0}\left[ {1 + \ln (2 G/{Y_0})} \right] $计算孔洞开始成核的成核临界应力为$ {p_{{\text{c0}}}} $, 再代入(11)式计算得到; 2)若实验中没有给出材料的基本力学参数, 则可以选取一组实验数据, 孔洞半径$ a $和小于该孔洞半径的所有孔洞所占份额$ f\left( a \right) $, 求解(15)式得到. 本文采用的是第2种方法, 在得到最大孔洞半径$ {a_{\max }} $后, 图5为(15)式的解析解计算结果(黑实线)和实验数据的对比, 二者符合得也较好.

图5给出的是与损伤演化终态实验结果的对比, 而我们更关心的是损伤早期发展过程中微孔洞分布特征的变化, 即孔洞数随时间的变化规律. 考虑到这个阶段应力是线性增加的, 即$ p = \dot pt $, 在得到孔洞开始成核的成核临界应力$ {p_{{\text{c0}}}} $以及层裂强度$ {p_{{\text{spall}}}} $后, 则有: $ {t_{{\text{c0}}}} = {p_{{\text{c0}}}}/\dot p $和$ {t_{{\text{spall}}}} = {p_{{\text{spall}}}}/\dot p $, 将此二值代入(3)式即可计算孔洞数随时间的变化规律. 同时, 在已知$ {t_{{\text{spall}}}} $和孔洞大小情况下, 根据(10)式则计算得到该孔洞的成核时刻. 不过, 这里需要注意的是, 上文给出的百分比为小于某一直径孔洞数占孔洞总数的百分比, 这些孔洞均为该直径孔洞成核时刻以后成核的孔洞, 而(3)式代表的是已经成核孔洞占总孔洞数的百分比, 二者是互补的, 即二者相加和为“1”. 图6为整理后的实验数据与(3)式解析解计算结果的对比, 二者符合得也很好.

层裂损伤发展早期涵盖了微观尺度的孔洞成核和介观尺度的孔洞增长过程, 且介观尺度的孔洞增长对微观尺度的孔洞成核又存在抑制作用, 不同因素纠缠在一起, 这为构建有效描述层裂损伤早期发展过程的物理方法带来了困难. 基于对层裂损伤发展早期孔洞成核过程的物理分析, 经过多次尝试, 我们最终选用三角函数形式表征孔洞成核过程的成核概率分布函数. 本文给出的孔洞成核概率分布函数不仅没有可调参数(其中的孔洞开始成核临界应力/时间和孔洞成核截止临界应力/时间两个参数属于层裂损伤模型参数, 且容易确定), 而且解析解计算的孔洞数随时间的变化过程与微观的分子动力学的计算统计结果和宏介观层裂实验结果符合均很好. 同时, 推导出的损伤演化方程计算的损伤早期发展过程与MD计算统计结果也定性(半定量)符合较好, 这也验证了新方法具有较好的适用性, 并在一定程度上可以反映层裂损伤早期微孔洞分布特征的变化规律. 当然, 为了描述层裂损伤演化的全过程, 还需要解析孔洞汇合对孔洞分布特征的影响以及孔洞汇合对损伤演化过程的影响, 将在接下来的工作中开展进一步的研究.