首页
登录
注册
下载:
-
中红外区域光谱对应分子振转能级的基频带跃迁, 其包含丰富的分子能级信息, 结合腔衰荡光谱技术(CRDS)等方法, 对中红外光谱进行精密测量可以用于验证基本物理定律、反演基本物理常数以及检测超低浓度气体. 特别地, 自20世纪90年代量子级联激光器(QCL)被发明以来[1], 中红外光谱技术得到极大的推动. 通过精确设计量子阱结构中的层厚度和材料组合, QCL可以在广泛的波长范围内实现激光发射, 涵盖范围包括从中红外到太赫兹波段. 此外QCL体积小, 可以实现较高的功率输出(>100 mW)和长时间的稳定运行. 由于以上优势, 基于QCL的中红外光谱测量给气体检测[2]、化学动力学[3]、医学成像[4]等领域中带来了巨大的发展潜力. 得益于近乎为零的线宽展宽因子(LBF), 理想情况下QCL输出激光的线宽接近肖洛-汤斯极限, 可达百Hz量级[4]. 但是因为在运行过程中存在温度起伏、机械振动、驱动电流噪声等技术噪声的影响[5], QCL自由运转时的频率噪声大, 其线宽一般在MHz量级, 这导致其获得的光谱分辨率低, 并且由于激光频率随温度和激光电流的变化会产生长期漂移, 因此无法实现精密光谱测量, 特别是对窄线宽非线性光谱(包括饱和吸收光谱以及多光子吸收光谱等)的测量.
为了抑制激光频率噪声, 可采用主动稳频技术, 例如饱和吸收稳频[6]、Pound-Drever-Hall (PDH)稳频[7–9] 、光学反馈锁定[10–12]、兰姆凹陷稳频[13]等. 2021年, 本课题组[14]利用光学反馈实现了QCL到超稳高精细度光学腔的锁定, 获得中红外超稳激光源, 将激光线宽压窄到Hz量级, 频率漂移小于20 kHz/12 h. 但是这类方法受限于光学谐振腔或饱和吸收介质的特性, 锁定范围较窄, 只适用于静态的频率稳定, 激光频率无法调谐, 因此同样无法实现精密光谱测量.
利用超稳激光源作为主激光器, 再结合光学锁相环(OPLL)和偏频锁定, 实现从激光到主激光的锁定, 可以压窄从激光线宽的同时, 通过改变偏频频率, 实现对从激光器频率的精准控制, 从而满足精密光谱测量的需求. 其中, 光学锁相环是一种利用电子反馈来实现两束激光的频率和相位锁定的闭环控制环路, 是保证从激光性能的重要因素. 1999年, Bordonalli等[15]结合光注入锁定和光学锁相环, 在零差OPLL系统中实现了总线宽为36 MHz的两台分布式反馈(DFB)半导体激光器低至0.006 rad2 (500 MHz带宽)的锁定相位误差方差和超过26 GHz的锁定范围. 2009年, Satyan等[16]展示了相干克隆的概念, 并利用光学锁相环实现了线宽4 MHz的半导体激光器与光纤激光器的锁定, 锁定后半导体激光器的线宽压窄到30 kHz. 2011年, Steed等[17]使用单片集成将激光器和光电二极管之间的光路延迟降低到20 ps以下, 将半导体激光器锁定到外部主激光器, 将激光线宽从1.1 MHz压窄到150 kHz. 2018年王建等[18]在光学锁相环反馈回路中加入可调超前移相功能电路, 将DFB半导体激光器线宽从2 MHz压窄到10 kHz. 2023年, Wang等[19]利用光学锁相环双路反馈控制外腔半导体激光器的电流与压电陶瓷(PZT), 实现了两路半导体激光器的频率和相位的长期锁定, 拍频信号的频谱宽度约为1 Hz, 残余相位误差为0.04 rad2. 然而, 以往光学锁相环系统中通常采用的光纤激光器和固体激光器等, 其固有激光频率噪声低, 激光线宽通常远小于1 MHz, 因此不需要设计宽带宽的伺服系统就可以实现较好的锁定效果. 然而, QCL频率噪声大, 通常其线宽大于5 MHz. 此外受到低噪声、大电流激光驱动的限制, QCL和驱动系统的调制带宽通常只有百kHz, 这大幅度增加了光学锁相环的设计难度. 尽管通过使用双环锁定[20]或边带锁定[21]可以来避免调制带宽小的影响, 但边带锁定系统较为复杂, 双环锁定由于QCL的结构限制也难以实现.
为了解决这个问题, 本文提出一种结合强光学反馈与光学锁相环结合的QCL偏频锁定系统, 同时实现对QCL激光线宽压窄以及频率的精准控制. 该技术首先使用强光学反馈抑制从激光频率的高频噪声, 从而提前压窄从QCL线宽[22], 减小了系统对光学锁相环带宽的需求. 然后使用光学锁相环实现从激光到一个窄线宽超稳主激光器的锁定, 并且通过结合相位超前电路抑制QCL在频率调制中180°相位反转的影响, 从而扩展光学锁相环的带宽. 本文首先分析了锁相环和强光学反馈的基本原理, 介绍并搭建了结合强光学反馈与光学锁相环的QCL偏频锁定系统, 然后分析了锁定后的性能, 最终利用获取的窄线宽可调的中红外激光器进行了腔衰荡光谱信号的测量.
-
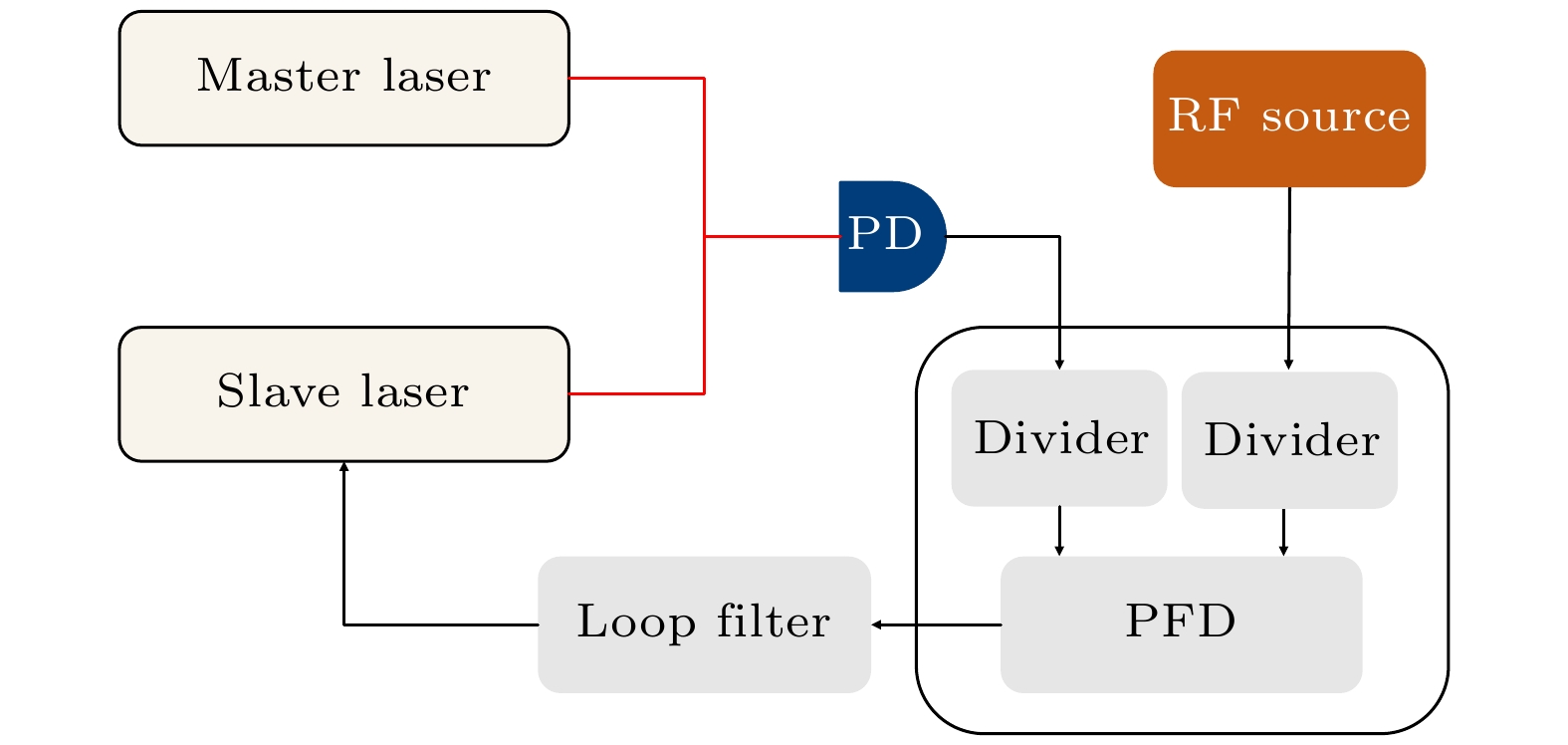
实验中所采用光学锁相环的基本原理如图1所示, 主要由主激光器(master laser)、从激光器(slave laser)、光电探测器(PD)、射频源(RF)、分频器(frequency divider)、鉴相器(PFD)和环路滤波器(loop filter, LF)构成. 主激光器和从激光器的光信号
$ {E_{\text{m}}}(t) $ 和$ {E_{\text{s}}}(t) $ 分别可以表示为式中,
$ {E_{\text{m}}} $ 和$ {E_{\text{s}}} $ 分别为主从两个激光的振幅,$ {\omega _{\text{m}}} $ 和$ {\omega _{\text{s}}} $ 分别为主从激光的频率,$ {\varphi _{\text{m}}} $ 和$ {\varphi _{\text{s}}} $ 分别为主从激光的初始相位. 两束激光拍频后由光电探测器将光信号转换成电信号, 输出的电压${U_{{\text{PD}}}}$ 可以表示为式中
${R_{{\text{PD}}}}$ 为光电探测器的等效电阻,$R'$ 为光电探测器的响应度. 射频源产生的信号${E_{{\text{RF}}}}(t)$ 可以表示为${E_{{\text{RF}}}}(t)$ 与经过光电探测器得到的信号${U_{{\text{PD}}}}$ 混频后, 滤去直流分量输出的信号可以表示为式中
${K_{{\text{PD}}}} = 2{R_{{\text{PD}}}}R'{E_{\text{m}}}{E_{\text{s}}}$ 为探测器的等效增益,${E_{{\text{RF}}}}$ 为射频信号的幅度,${K_{{\text{mix}}}}$ 为鉴相器的增益. 鉴相器输出的信号通过环路滤波器后输入到从激光器驱动, 从而控制其频率和相位. 输入到从激光器的电流可以表示为式中,
${K_{\text{s}}}$ 为从激光器驱动的电压电流转换系数, 单位为${\text{mA/V}}$ ;$ {f_{{\text{LP}}}}(t) $ 为环路滤波器的频率响应函数, 从激光器的相位被调制为式中,
${K_0}$ 为从激光器增益因子, 单位为${\text{rad/(mA}} \cdot {\text{s}})$ . 当环路锁定时:式中,
$ {\varphi _{{\text{e0}}}} $ 为相位稳态误差,$\sin \left( {{\phi _{{\text{e0}}}}} \right) = ( {\omega _{\text{m}}} + {\omega _{{\text{RF}}}} - {\omega _{\text{s}}} )/{K_{{\text{dc}}}}$ ,${\omega _{\text{s}}}$ 为从激光器自由运行的频率,${K_{{\text{dc}}}}$ 为直流增益, 由(7)式可知增大直流增益可以减小相位稳态误差, 当从激光器相位波动时光学锁相环重复以上过程实现闭环锁定. 通过该过程可以使从激光器的频率和相位与主激光器一致, 实现了相位锁定, 降低了从激光器的相位噪声. -
光学反馈是一种将部分输出光重新导回到激光器腔内的技术, 这一反馈光与激光器增益介质的相互作用能够显著影响激光的频谱特性. 为了量化反馈对线宽的影响, 我们基于速率方程的理论框架来描述QCL的载流子和光子的动态行为. 通过Lang-Kobayashi模型[23]对反馈光的相位和强度进行建模, 并分析了反馈引入的干涉对激光频谱的影响. 光学反馈下的QCL速率方程描述了不同激光态的载流子和光子数变化, 其中最关键的方程为电场相位(
$\phi $ )方程:其中,
$\alpha _{\text{H}}^{}$ 是线宽展宽因子,$m$ 为增益级数,${G_0}$ 是增益系数,$\Delta N$ 为布居数反转,${\tau _{\text{p}}}$ 是光子寿命,${F_\phi }(t)$ 为自发辐射噪声,${k_{\text{c}}}$ 是反馈耦合系数,${r_{{\text{ext}}}}$ 是反馈比例,$S$ 为光子数,${\tau _{{\text{ext}}}}$ 是外部腔延迟时间,${{\Delta }}\phi $ 是反馈光与腔内光场的相位差.光学反馈下的量子级联激光器(QCL)本征线宽可表示为[24]
其中,
$\beta $ 为自发辐射因子,${N_3}$ 为上能级,${\phi _0}$ 为反馈相位,$C = {k_{\text{c}}}{\tau _{{\text{ext}}}} \sqrt {{r_{{\text{ext}}}}(1 + \alpha _{\text{H}}^{2})} $ 为反馈强度系数,$\Delta {\omega _{\text{s}}}$ 为反馈引起的频移. 当$C >1 $ (${r_{{\text{ext}}}}$ > –27 dB)时, 激光器线宽对反馈相位${\phi _0}$ 依赖性逐渐降低, 光学反馈的强相干作用提高了腔内光子的有效寿命和系统的品质因数(Q值), 大大减弱了相位噪声的影响, 从而实现无相位控制的线宽压低. 这一机制为高精度激光应用提供了一种高效而稳定的解决方案. -
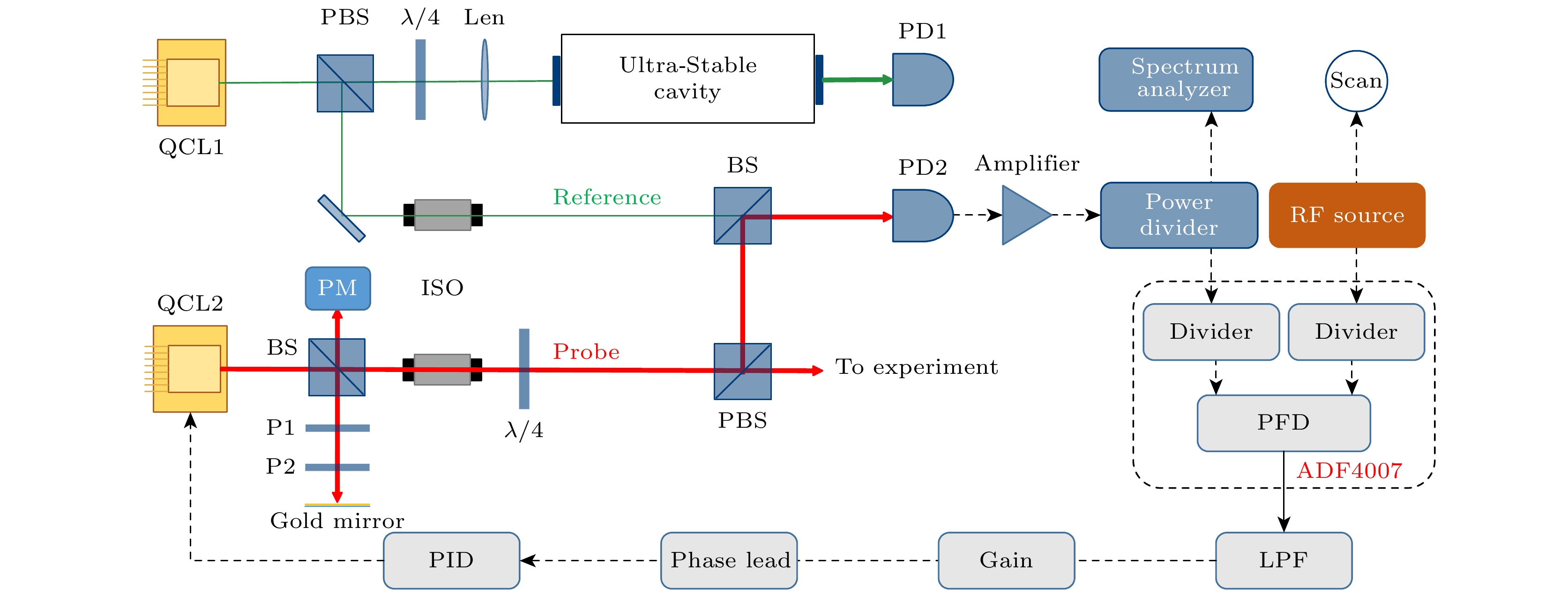
结合强光学反馈和光学锁相环的中红外激光频率锁定实验系统如图2所示, 实验所用从激光器为DFB-QCL (ADtech, ATO4527, HHL封装), 中心波长为4527 nm, 最大输出功率为19 dBm. 激光器由低噪声电流源驱动, 温度控制在20 ℃, 整个激光器被安装在自制的黄铜散热底座上, 底座由水冷循环散热. 出射后的激光经分束棱镜(BS)分成两束, 一束通过偏振片P1, P2, 再经过反射镜直接反射回激光器, 形成光学反馈, 通过旋转P1, P2来控制其反馈率大于–27 dB, 此时工作在强光学反馈机制下[24]. 在强光学反馈下, 对激光频率噪声抑制作用不受反馈距离(即反馈相位)的影响, 因此可以实现对激光波长的大范围连续调谐. 另一束光用于激光相位锁定, 经过光隔离器(ISO)、1/4波片(
$\lambda {\text{/4}}$ )、偏振分束棱镜(PBS)和分束棱镜(BS)后与主激光拍频入射到光电探测器PD2, 该束光在拍频前功率为4.7 dBm.作为参考光的主激光器利用光学反馈锁定到一个中红外超稳腔上, 通过锁定环内噪声评估, 激光器线宽被压窄到了1.1 Hz, 长期漂移小于20 kHz/12 h[14]. 主激光经PBS分束后依次通过ISO, BS后与从激光拍频入射到PD2, 该束激光在拍频前功率为1.7 dBm. 光电探测器将两束光的拍频信号转换成电信号送入功率放大器(amplifier), 将其功率放大到0 dBm后由1/9功分器(power divider)将其分成两路. 小信号送入频谱仪来监测拍频的频谱信息, 其中频谱分析仪的跨度设置为4 MHz, 分辨率带宽(RBW)设置为10 Hz; 大信号送入主要由ADF4007芯片构成的锁相环电路中, 同时由射频源产生的参考信号作为调节偏移频率, 被送入电路的另一个输入口.
光学锁相环主要基于锁相环芯片ADF4007, 该芯片由一个数字鉴频鉴相器(PFD), 一个精密电荷泵和一个分频/预分频器构成, 作用于拍频信号的分频器可以被设置为8, 16, 32, 64, 射频信号的分频器固定设置为2, 两路信号最高可实现32倍的频率差. 将拍频信号分频器设置为16, 分频后的信号与经过2分频的射频参考信号在进入锁相环芯片的PFD之前会被ADF4007转换成类似方波的阶跃信号, PFD比较这两个方波信号, 输出一个占空比反映两个信号之间的频率差和 相位差的方波信号, PFD的输出与电荷泵相连, 方波信号作用于电荷泵控制其通断, 产生反馈电流. 反馈电流通过低通滤波器后转化成电压形式的误差信号, 该误差信号经过放大器和相位超前电路后输入到PID控制器, 产生的校正信号送入激光驱动, 通过改变激光电流从而实现对从激光器频率的锁定.
-
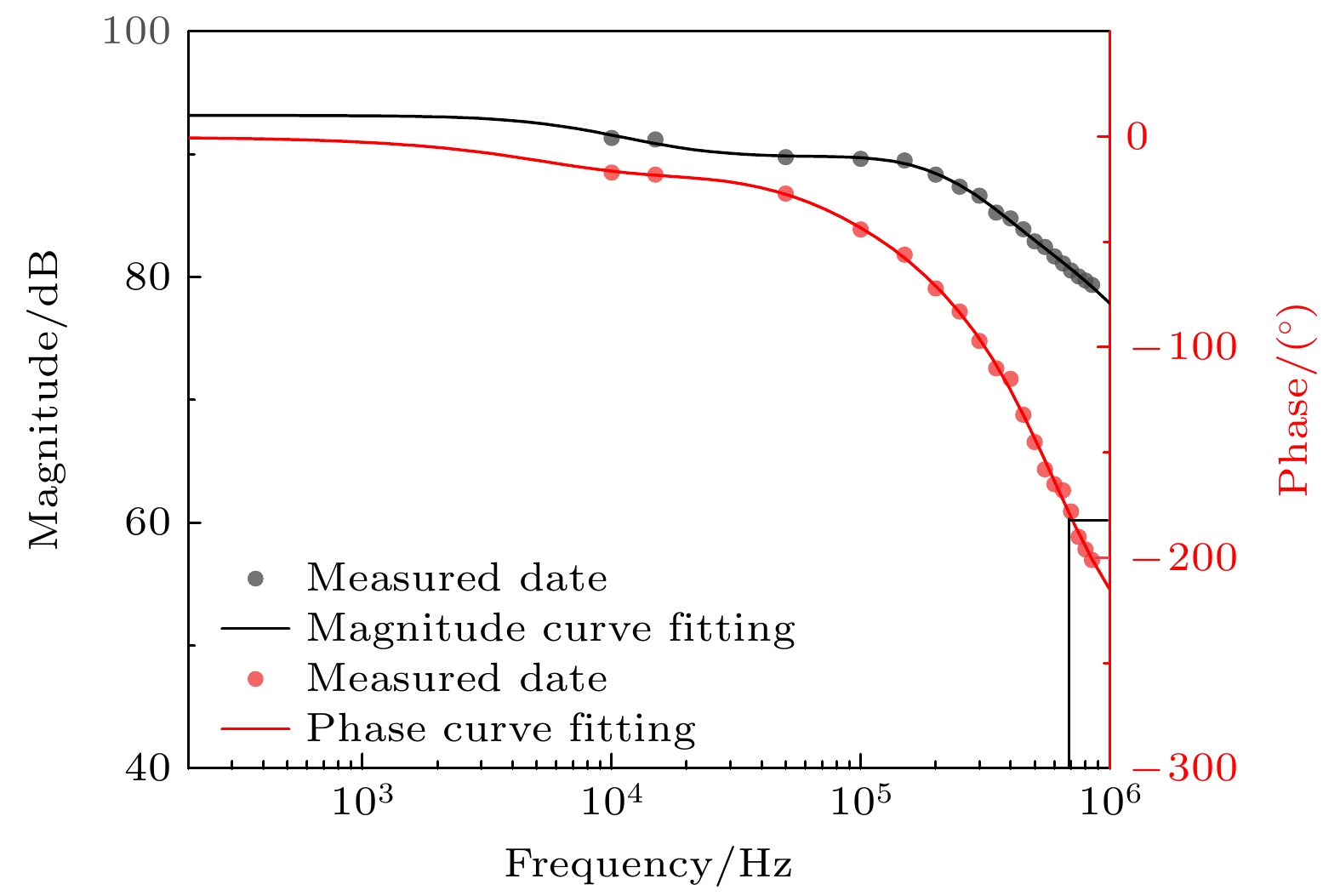
在光学锁相环中, 锁定带宽越宽, 锁定性能越好, 因此良好的锁定要求根据系统传递函数来设计锁相环中的PID系统. 因此, 我们首先测量了从激光器系统(包括激光器以及激光驱动)的频率响 应. 实验中, 利用氧化亚氮吸收线侧翼作为鉴频器, 首先将激光的中心频率固定在吸收线的侧翼, 使用相同幅度不同频率的正弦波调制激光器的电流, 并且记录穿过氧化亚氮吸收池光信号和调制信号的相位差和幅度比, 通过吸收线斜率和驱动器的转化系数将电压变化转化激光器的频率响应. 测得的结果如图3所示, 黑色曲线是激光器的幅频响应(对应左纵轴), 红色曲线是激光器的相频响应(对应右纵轴). 可以看到激光系统响应呈现类似低通滤波器特性, 在700 kHz出现了相位180°反转的现象, 该反转点的存在限制了从激光器调制的频率响应, 从而导致光学锁相环的带宽减小, 最终限制锁定 性能.
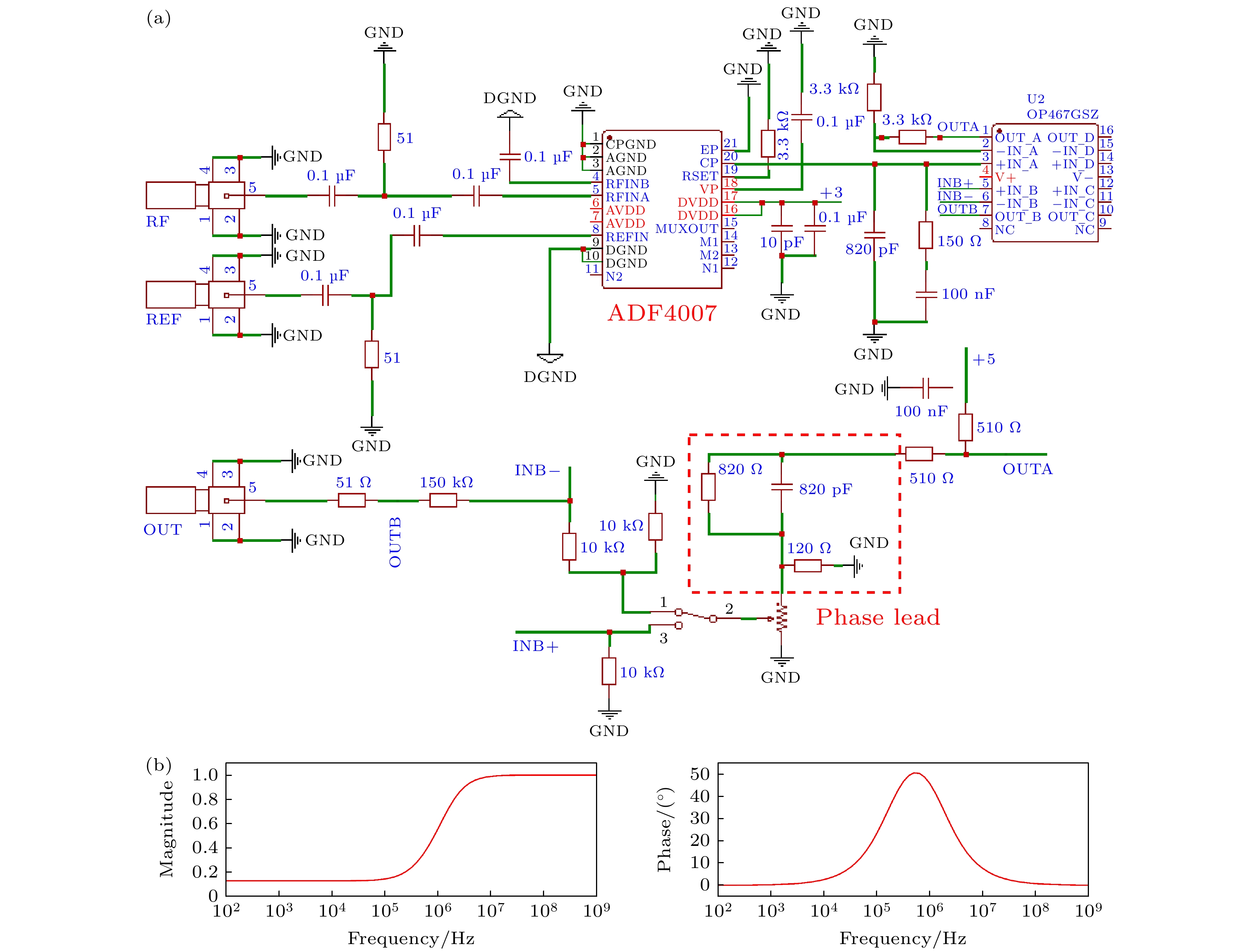
为了拓展锁定带宽, 在锁相环电路中引入了一个无源相位超前模块, 其电路原理如图4(a)中红框所示, 其波特(Bode)图如图4(b)所示, 该电路在频率10 kHz—100 MHz内驱动都可以补偿相位, 并且在700 kHz处补偿效果达到最佳, 超前达到了50°, 因此可以有效将光学锁相环的相位反转点后移, 增大了环路带宽.
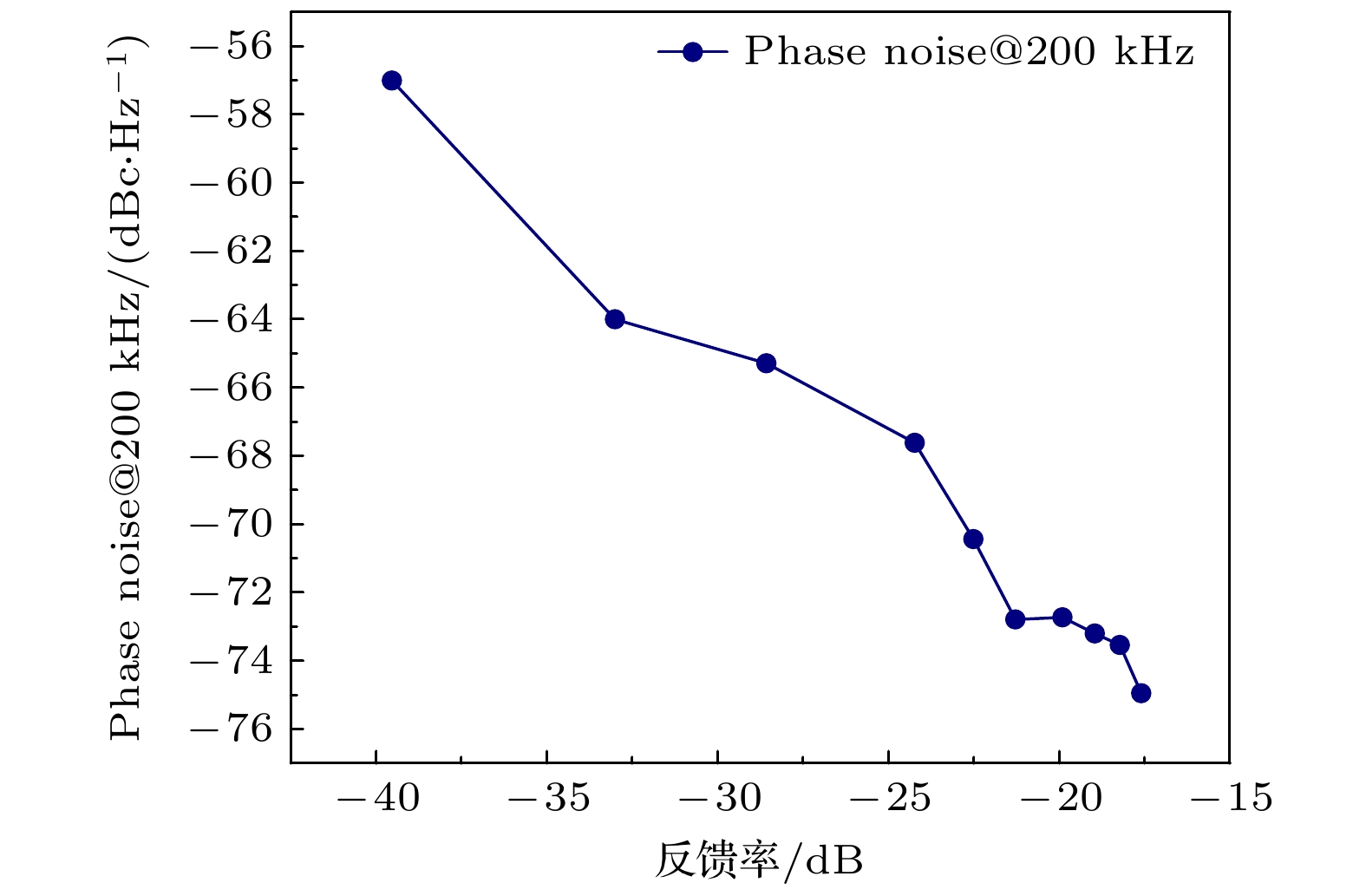
强光学反馈的反馈率是影响从激光器线宽压窄和锁相难度的重要因素之一. 合适的反馈率有助于更有效地压窄激光器线宽, 降低锁相难度. 通过固定偏振片P1 (图2), 旋转偏振片P2来调节反馈率, 不同反馈率下锁定后的拍频信号相位噪声(@200 kHz)如图5所示. 结果表明, 随着反馈率的增大, 强光学反馈对于噪声的抑制效果逐渐提高, 在不引起系统失调的范围内尽可能选择大反馈率, 通过估计实验中反馈率约为–20 dB.
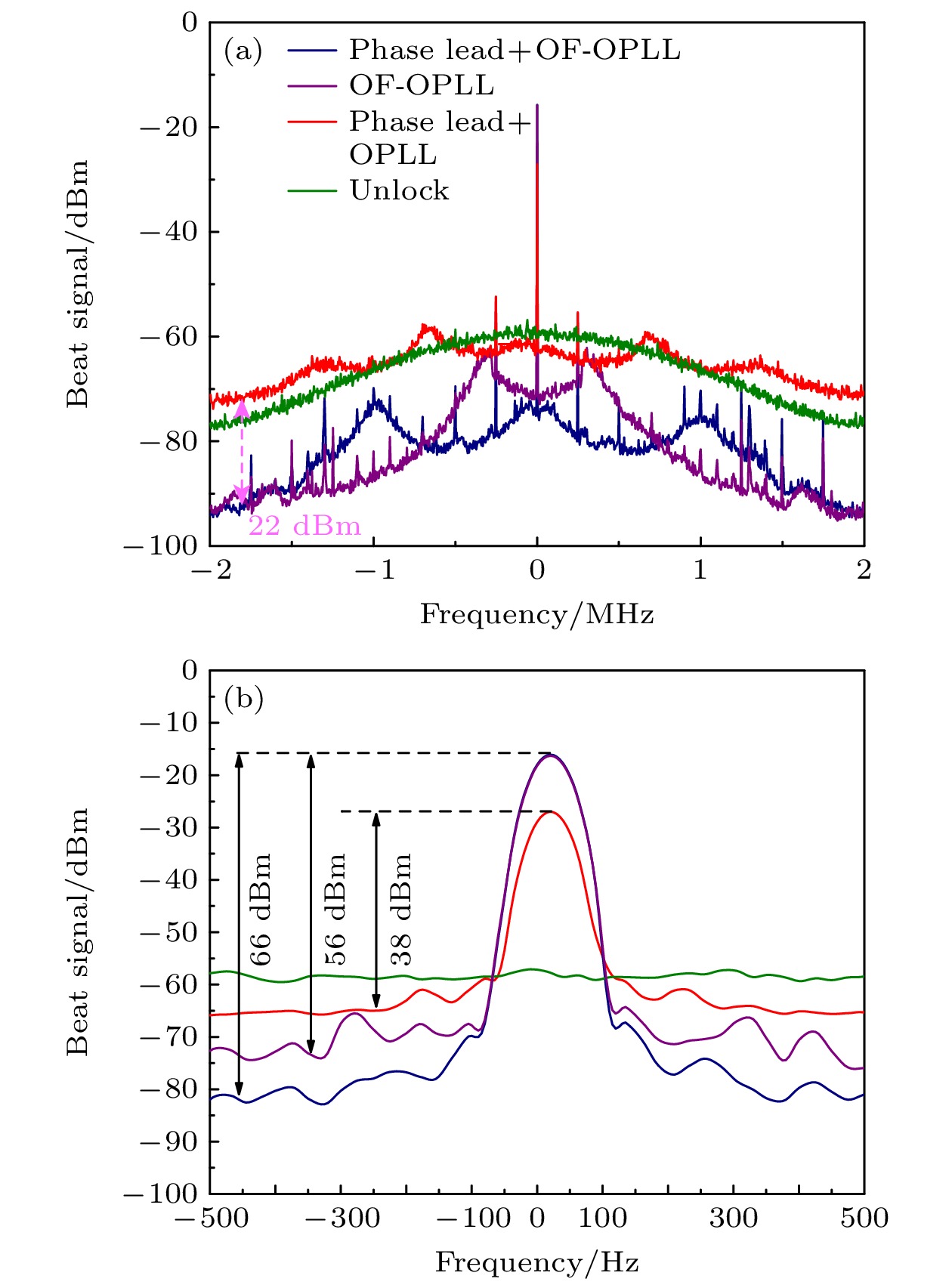
基于自行设计的光学锁相环系统, 实现了从激光器到主激光的锁定, 利用PD2获得的两个激光拍频信号的噪声功率谱如图6(a)所示, 图6(b)是放大中心部分的拍频细节图. 图中绿色曲线是只实现频率锁定、未进行相位锁定(只简单反馈控制从激光的中心频率)的拍频信号功率谱结果, 可以看到从激光的频率噪声覆盖0 Hz—2 MHz之间, 并且在2 MHz处其噪声谱幅度仅比中心0 Hz处低18 dBm. 红色曲线是使用OPLL锁定后的拍频信号功率谱, 由于相位锁定进一步抑制了激光频率噪声, 锁定后大部分功率集中在窄拍频中心处, 比仅单一频率锁定的结果提高了38 dBm; 紫色曲线是结合强光学反馈以及光学锁相环(OF-OPLL)的功率谱结果, 可以看到由于光学反馈的自注入锁定过程, 将低频到高频(2 MHz以上)的噪声都进行了抑制, 尤其是在高频处(2 MHz)噪声水平降低了22 dBm, 而在中心处的功率达到了56 dBm, 信号两侧出现的隆起表示了锁定带宽为300 kHz. 蓝色曲线是增加相位超前电路后的结果, 相位超前电路的加入, 使得系统的环路带宽被扩展到了1 MHz, 并且低频噪声被进一步降低, 在中心处的功率进一步提升, 达到了66 dBm.
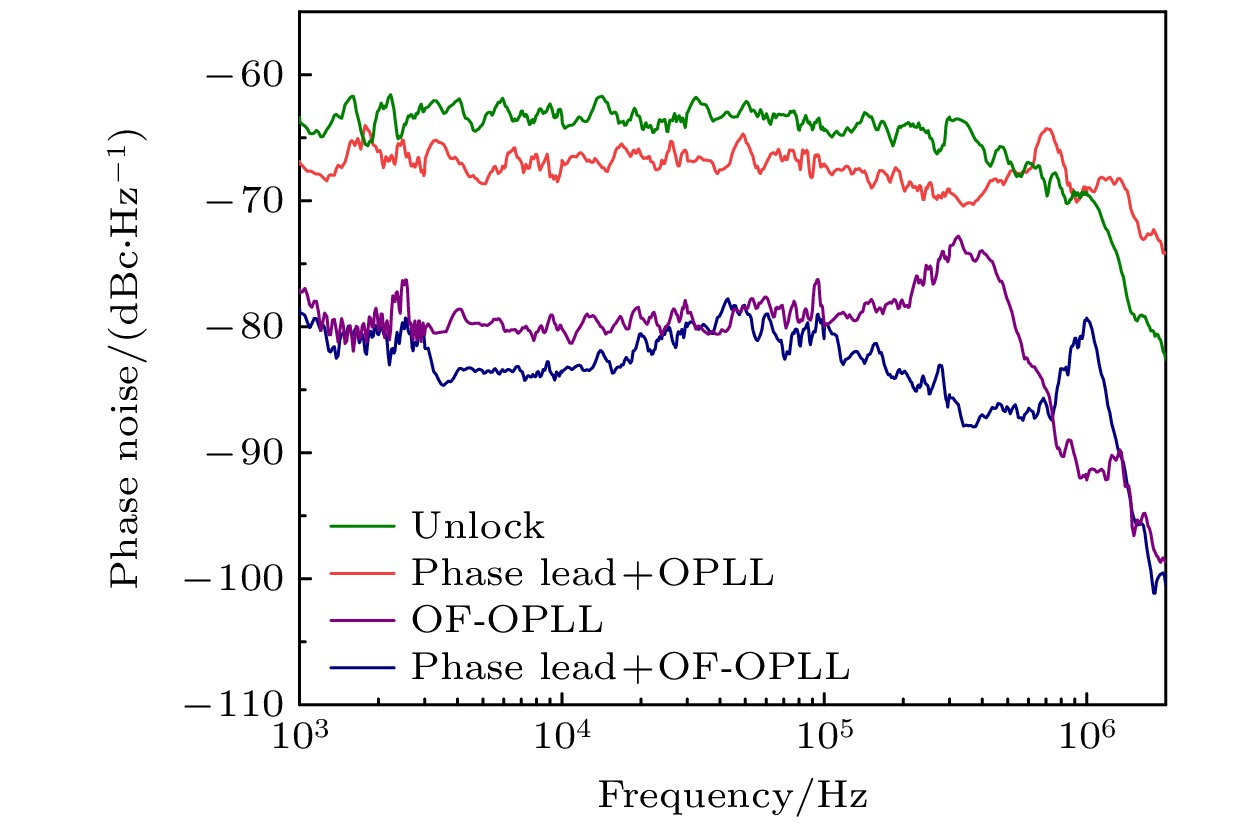
为进一步表征系统的锁定性能, 使用频谱分析仪测量了不同锁定方法下拍频信号的相位噪声, 得到的结果如图7所示. 从图7可以看出, 相比于单一频率锁定的结果(绿色曲线), 使用OPLL (红色曲线)的相位噪声降低了4 dBc/Hz@2 kHz, 达到了–67 dBc/Hz@2 kHz. 增加强光学反馈后(紫色曲线), 相位噪声被大幅度抑制, 在低频处降低了17 dBc/Hz@2 kHz, 此时相位噪声为–81 dBc/Hz@2 kHz; 在高频处, 强光学反馈对相位噪声的抑制效果更加明显, 在高频处降低了20 dBc/Hz@2 MHz, 达到了–101 dBc/Hz@2 MHz.
接着对锁定前后的激光器线宽进行评估. 实验中利用氧化亚氮吸收线作为鉴频器, 将未锁定的激光器频率控制在吸收线的侧翼某一位置, 通过测量穿过吸收池后光强抖动反演出激光频率噪声, 获得的频率噪声功率谱密度如图8中绿线所示. 利用β分离线方法[25], 得到自由运转下激光器的线宽是3.8 MHz. 为了评估锁定后的激光频率, 利用误差信号和频率误差之间的关系, 将锁定后的误差信号反演了频率噪声谱密度[26], 得到的锁定后主激光器和从激光器的频率噪声谱密度结果如图8中蓝色和红色曲线所示. 从图8可以看出, 锁定后从激光器的频率噪声在低频段和高频段都被大幅度抑制, 在100 Hz处抑制比达到79 dB, 在400 kHz处抑制比达36 dB. 同时从激光器的频率噪声特性在低频部分与主激光器保持一致, 但在50 kHz之后, 由于光学锁相环引入额外噪声导致从激光器的频率噪声略高于主激光器. 从图8中蓝色曲线可见, 当傅里叶电子频率在200—400 kHz时, 激光频率噪声谱密度表现为白噪声响应,
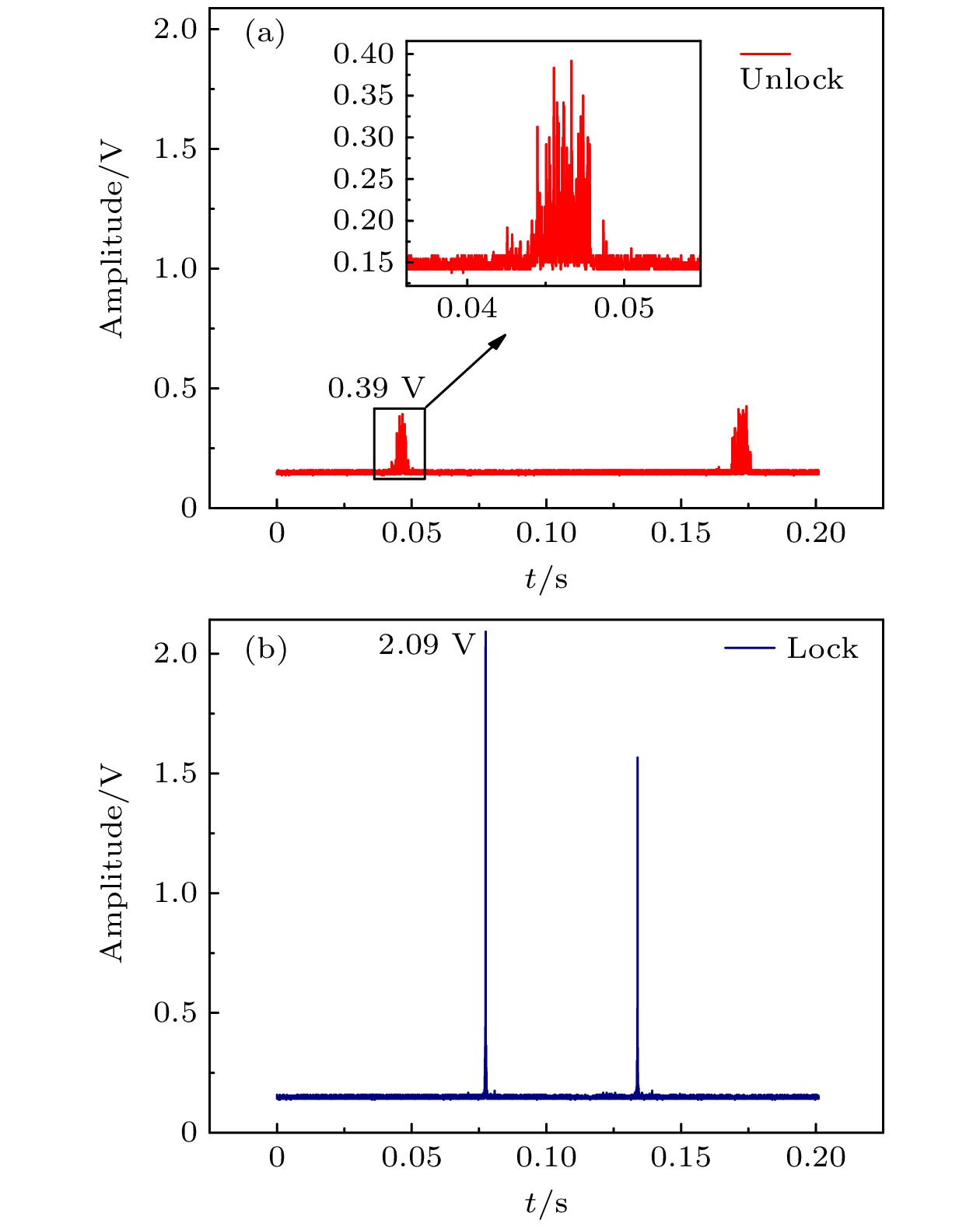
${S_{\mathrm{f}}}(\phi ) \approx 0.95$ Hz2/Hz, 根据激光频率功率谱密度及相位噪声${S_{\mathrm{f}}}(\phi )$ 与线宽$\Delta v$ 的公式$\Delta v = {\text{π}}{S_{\text{f}}}(\phi )$ 计算得出激光线宽${\text{π}}{S_{\text{f}}}(\phi ) = 3$ Hz[27]. 需要指出的是这种线宽评估方法会引入误差, 因为误差信号不仅反映了激光的频率噪声, 还受到了激光强度噪声以及电子噪声的影响.将锁定后的从激光作为光源进行CRDS测量. CRDS实验中使用一个精细度为10000的法布里-珀罗(FP)腔, 用一个频率为10 Hz的三角波扫描光学腔上的压电陶瓷, 从而调谐腔长, 测量获得的透射信号如图9所示. 图9(a)为锁定前获得的腔透射信号, 而图9(b)为光学锁相环锁定后得到的信号. 从图9可知, 由于自由运转下激光频率噪声大, 某一时刻只有少部分的激光频率成分与腔的本征模式重合、可以耦合进入光学腔, 因此腔模幅度低(大约0.39 V), 并且腔模杂乱. 而光学锁相环锁定后, 激光频率噪声被大幅度抑制, 更多的频率成分可以与腔模重合, 因此腔模幅度被提高了5倍以上, 可以达到2.09 V.
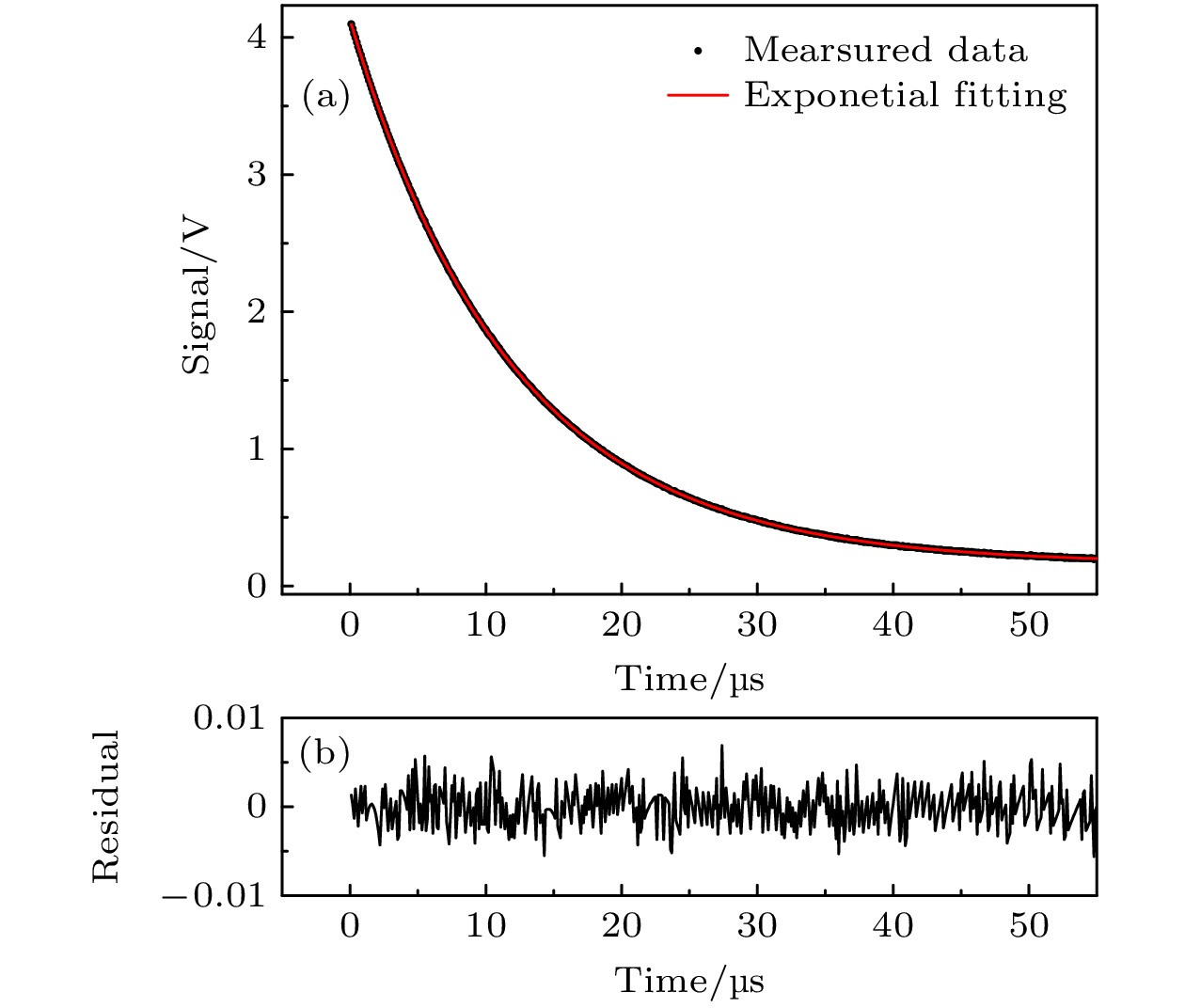
当从激光器锁定后, 使用该法布里-珀罗腔进行腔衰荡测试, 采集到的衰荡数据如图10(a)中黑点所示, 红线为使用e指数拟合获得的结果, 拟合获得的衰荡信号的信噪比为2000, 空腔衰荡时间为12.7 μs.
-
本文对中红外QCL作为从激光器的OPLL进行了研究, 测量了QCL的传递函数. 使用相位超前电路补偿QCL频率调制中出现的相位反转, 并且使用强光学反馈压窄从激光器线宽, 降低锁相难度. 系统锁定后, 功率谱中心窄拍频信号提高至66 dBm, 低频区域相位噪声被抑制到–81 dBc/Hz@2 kHz, 高频区域相位噪声被抑制到–101 dBc/Hz@2 MHz. 从激光器低频区域频率噪声与主激光器一致, 激光器线宽从MHz量级被压窄到和主激光器同等的Hz量级水平, 实现了良好的锁相. 下一步将该锁定后的激光应用于中红外腔衰荡放射性二氧化碳同位素精密光谱测量, 实现对14CO2的超高灵敏检测.
结合光学反馈以及光学锁相环的量子级联激光器线宽压窄和频率控制技术研究
Research on linewidth narrowing and frequency control technology of quantum cascade lasers based on optical feedback and optical phase-locked loops
-
摘要: 中红外波段缺乏窄线宽、可精确调谐的激光源, 限制了中红外精密光谱的发展. 本文介绍了一种结合强光学反馈和光学锁相环技术的量子级联激光器(QCL)频率控制技术, 通过强光学反馈先抑制QCL频率噪声中的高频成分, 再使用光学锁相环将激光频率偏频锁定到另外一个超稳中红外激光源上. 通过相位超前电路拓展锁定带宽, 系统锁定后, 将功率谱中心窄拍频信号提高66 dBm, 低频区域相位噪声抑制到–81 dBc/Hz@2 kHz, 高频区域相位噪声抑制到101 dBc/Hz@2 MHz, 激光器线宽从3.8 MHz被压窄到3 Hz. 最终, 利用该激光器进行腔衰荡光谱信号的测量, 相较于未锁定激光, 信号的信噪比提升了5倍.Abstract: The mid-infrared (MIR) spectral region, which corresponds to molecular vibrational and rotational energy level transitions, contains a wealth of molecular energy level information. By employing techniques such as cavity ring-down spectroscopy (CRDS), the MIR spectra can be precisely measured, thereby validating fundamental physical laws, the inversion of fundamental physical constants, and the detection of trace gases. However, technical noise from temperature fluctuations, mechanical vibrations, and current noise causes free-running quantum cascade laser (QCL) to suffer high-frequency noise, typically broadening the linewidth to the MHz range, thus reducing spectral resolution. Moreover, long-term drift in the laser frequency due to temperature and current fluctuations hinders high-precision spectroscopy, particularly for narrow-linewidth nonlinear spectroscopy, such as saturated absorption and multiphoton absorption spectroscopy. This work presents a method of combining optical feedback with an optical phase-locked loop (OPLL) for offset frequency locking, aiming to generate a mid-infrared (MIR) laser with excellent frequency characteristics. Strong optical feedback is employed to narrow the linewidth of the quantum cascade laser (QCL) acting as a slave laser, thereby alleviating the challenges associated with phase locking. The OPLL uses frequency-offset to lock the slave laser to the ultra-narrow laser. By adjusting the offset frequency, fine control of the slave laser is achieved. To ensure tight phase locking, the OPLL is based on the ADF4007, and combines a phase lead circuit to compensate for phase lag, effectively expanding the loop bandwidth of the system. In this work, the fundamental principles of the optical phase-locked loop are theoretically analyzed, and a basic model is established. The influence of loop bandwidth on locking performance is also investigated. Upon achieving phase locking using the combined optical feedback and OPLL system, the magnitude of the beat note of the two lasers is improved by 66 dBm, with phase noise suppressed to –81 dBc/Hz@2 kHz in the low-frequency region and -101 dBc/Hz@2MHz in the high-frequency region. The frequency noise power spectral density of both the master laser and slave laser is obtained via the error signal in the closed-loop system. Significant suppression of frequency noise is observed for the slave laser across both low- and high-frequency region, with suppression ratio reaching 86 dB at 100 Hz and 55 dB at 400 kHz. The frequency noise of the slave laser in the low-frequency domain is found to be comparable to that of the master laser. Based on the white noise response region in the frequency noise spectrum (from 200 Hz to 400 kHz), the locked slave laser linewidth is determined to be approximately 3 Hz, narrowing the initial MHz-level linewidth to match the Hz-level linewidth of the master laser. Finally, the locked laser is used to conduct cavity ring-down spectroscopy, achieving an improvement factor of 5 in the signal-to-noise ratio of the ringdown signal. This frequency-stabilized laser will be applied to high-precision spectroscopy for detecting radiocarbon isotopes in future.
-
Key words:
- quantum cascade laser /
- optical phase-locked loops /
- optical feedback .
-
-
图 4 (a)锁相环电路; (b)无源相位超前电路传递函数
Figure 4. (a) Phase-locked loop circuit; (b) transfer function of the passive phase lead circuit.
图 6 (a)不同锁定拍频功率谱; (b)拍频中心1 kHz范围功率谱
Figure 6. (a) Power spectral of beat frequencies under different conditions; (b) power spectral in the 1 kHz range at the center of beat frequencies.
图 8 主、从激光器频率噪声功率谱密度
Figure 8. Power spectral density of frequency noise of the master and slave laser.
图 9 (a)未锁定透射腔模; (b)锁定透射腔模
Figure 9. (a) Transmission cavity mode without locking; (b) transmission cavity mode without and with locking.
-
[1] Faist J, Capasso F, Sivco D L, Sirtori C, Hutchinson A L, Cho A Y 1994 Science 264 553 doi: 10.1126/science.264.5158.553 [2] Yao Y, Hoffman A J, Gmachl C F 2012 Nat. Photonics 6 432 doi: 10.1038/nphoton.2012.143 [3] Hvozdara L, Pennington N, Kraft M, Karlowatz M, Mizaikoff B 2002 Vib. Spectrosc. 30 53 doi: 10.1016/S0924-2031(02)00038-3 [4] Bartalini S, Borri S, Cancio P, Castrillo A, Galli I, Giusfredi G, Mazzotti D, Gianfrani L, De Natale P 2010 Phys. Rev. Lett. 104 083904 doi: 10.1103/PhysRevLett.104.083904 [5] Bartalini S, Borri S, Galli I, Giusfredi G, Mazzotti D, Edamura T, Akikusa N, Yamanishi M, De Natale P 2011 Opt. Express 19 17996 doi: 10.1364/OE.19.017996 [6] Genov G, Lellinger T E, Halfmann T, Peters T 2017 J. Opt. Soc. Am. B 34 2018 doi: 10.1364/JOSAB.34.002018 [7] Drever R W P, Hall J L, Kowalski F V, Hough J, Ford G M, Munley A J, Ward H 1983 Appl. Phys. B 31 97 doi: 10.1007/BF00702605 [8] Pound R V 1946 Rev. Sci. Instum. 17 490 doi: 10.1063/1.1770414 [9] Black E D 2001 Am. J. Phys. 69 79 doi: 10.1119/1.1286663 [10] Zhao G, Tian J F, Hodges J T, Fleisher A J 2021 Opt. Lett. 46 3057 doi: 10.1364/OL.427083 [11] Fasci E, Coluccelli N, Cassinerio M, Gambetta A, Hilico L, Gianfrani L, Laporta P, Castrillo A, Galzerano G 2014 Opt. Lett. 39 4946 doi: 10.1364/OL.39.004946 [12] Maisons G, Carbajo P G, Carras M, Romanini D 2010 Opt. Lett. 35 3607 doi: 10.1364/OL.35.003607 [13] Remillard J, Uy D, Weber W, Capasso F, Gmachl C, Hutchinson A, Sivco D, Baillargeon J, Cho A 2000 Opt. Express 7 243 doi: 10.1364/OE.7.000243 [14] 杨家齐, 赵刚, 焦康, 高健, 闫晓娟, 赵延霆, 马维光, 贾锁堂 2024 物理学报 73 014205 doi: 10.7498/aps.73.20231049 Yang J Q, Zhao G, Jiao K, Gao J, Yan X J, Zhao Y T, Ma W G, Jia S T 2024 Acta Phys. Sin. 73 014205 doi: 10.7498/aps.73.20231049 [15] Bordonalli A C, Walton C, Seeds A J 1999 J. Light. Technol. 17 328 doi: 10.1109/50.744252 [16] Satyan N, Liang W, Yariv A 2009 IEEE J. Quantum Electron. 45 755 doi: 10.1109/JQE.2009.2013120 [17] Steed R J, Pozzi F, Fice M J, Renaud C C, Rogers D C, Lealman I F, Moodie D G, Cannard P J, Lynch C, Johnston L, Robertson M J, Cronin R, Pavlovic L, Naglic L, Vidmar M, Seeds A J 2011 Opt. Express 19 20048 doi: 10.1364/OE.19.020048 [18] 王建, 陈迪俊, 蔡海文, 冯俊波, 郭进 2018 中国激光 45 0401001 doi: 10.3788/CJL201845.0401001 Wang J, Chen D J, Cai H W, Feng J B, Guo J 2018 Chin. J. Lasers 45 0401001 doi: 10.3788/CJL201845.0401001 [19] Wang F D, Ma W X, Mei F, Ji Z H, Su D Q, Zhao Y T, Xiao L T, Jia S T 2023 Appl. Opt. 62 7169 doi: 10.1364/AO.496663 [20] Qin J, Zhou Q, Xie W L, Xu Y, Yu S G, Liu Z W Y, Tong Y T, Dong Y, Hu W S 2015 Opt. Lett. 40 4500 doi: 10.1364/OL.40.004500 [21] Satyan N, Vasilyev A, Liang W, Rakuljic G, Yariv A 2009 Opt. Lett. 34 3256 doi: 10.1364/OL.34.003256 [22] Zhao B B, Wang X G, Wang C 2020 ACS Photonics 7 1255 doi: 10.1021/acsphotonics.0c00189 [23] Lang R, Kobayashi K 1980 IEEE J. Quantum Electron. 16 347 doi: 10.1109/JQE.1980.1070479 [24] Wang X G, Zhao B B, Grillot F, Wang C 2020 J. Appl. Phys. 127 073104 doi: 10.1063/1.5124521 [25] Domenico G D, Schilt S, Thomann P 2010 Appl. Opt. 49 4801 doi: 10.1364/AO.49.004801 [26] Fox R W, Oates C W, Hollberg L W 2003 Experimental Methods in the Physical Sciences (Vol. 40) (Amsterdam: Academic Press) pp1–46 [27] Kikuchi K 2012 Opt. Express 20 5291 doi: 10.1364/OE.20.005291 -
图( 10)
计量
- 文章访问数: 767
- HTML全文浏览数: 767
- PDF下载数: 5
- 施引文献: 0