腔光力学系统利用光的辐射压力来探索光与物质之间的相互作用, 已经成为研究量子和经典非线性现象的一个迷人的平台^[1–5]. 许多潜在的应用已经在一系列物理领域被发现, 包括光力诱导透明(OMIT)^[6–9] 、光学机械暗模式^[10]、片上纳米光子器件^[11]、机械双稳态^[12]、非互易传输^[13,14]、微波场的压缩^[15]. 此外, 腔光力学系统中存在的光力非线性也是研究光学边带效应的关键. 包括二阶边带^[16]、高阶边带^[17]以及和边带效应^[18], 并且这些边带效应的增强对于研究光操纵以及精密测量具有重要意义.

近年来, 复合光力系统的非线性现象越来越受到关注. 对于研究光力非线性, 腔-原子复合光力系统比典型的光力系统有着较为突出的有利条件. 由于光学腔与机械振子通过辐射压力产生光力耦合, 而与两能级原子通过电偶极相互作用耦合, 所以该复合光力系统结合了量子电动力学与腔光力学. 常见的复合腔光力系统有环形微波腔光力系统^[19,20]、拉盖尔-高斯(L-G)旋转腔光力系统^[21]、原子辅助腔光力系统^[22–26]等. 许多新的有趣现象已经被观察到, 例如, 正交模劈裂^[27,28]、量子相干耦合^[29–32]、光机械存储^[33–38]、二阶边带甚至高阶边带^[39–41]. 此外, 还包括原子系综或者玻色-爱因斯坦凝聚体 的复合光力系统^[42], 并且还存在原子-原子相互作用引起的另一种非线性^[43]. 这些腔光力系统中的发现可用于增强边带效应、操纵光传输等. 它们为信息传感器的制备提供了可能性, 并且有助于腔光力系统的发展.

和边带的生成是一种较为新颖的非线性光力现象. 通过双探测场入射到光力系统时, 双探测场之间产生相消干涉, 产生利于生成和边带频率分量的非线性频率. Xiong等^[18,44]首次揭示了在由多个探测场驱动的光力系统中和^[18]或差边带^[44]的存在. 然而由弱耦合引起的非线性相互作用不容易被检测. 为了提高和边带产生(SSG)的效率已经完成许多理论工作. 例如, Liu等^[45]提出了一种通过非线性和边带在色散光力系统中实现高灵敏度质量检测的理论方案. Wang等^[46]已经证明通过双声子过程的非线性光力相互作用, 使得上和边带的生成得到了新的匹配条件, 并且实现了对下和边带生成效率几个数量级的提高. 此外, Wu等^[47,48]提出了在L-G旋转系统和宇称-时间(PT)对称光力系统中生成和边带的方法. 最近, Liao等^[49]提出了在双辐射压力下的光力系统下和边带的产生与增强. 和边带信号的增强对于实现纳米级芯片等光传输器件的研究具有重要意义, 并且在量子信息处理等方面也具有十分重要的潜在应用.

在此基础上, 本文研究了含两能级原子系综的复合光力系统中的和边带效应. 复合原子光力系统展现出多重优势, 包括完美光力诱导透明及慢光效应^[50]、通过原子之间作用产生和调控纠缠^[51,52]以及产生和增强二阶边带^[53]. 因此, 我们可以预期在该系统增强和边带的产生. 本工作主要关注原子系综对和边带生成的影响, 并讨论了原子泵浦失谐、腔与原子系综之间的耦合强度以及原子衰减率等系统参数对SSG效率的影响. 结果表明, 通过调节耦合强度和原子泵浦失谐, SSG的效率可以显著提高.

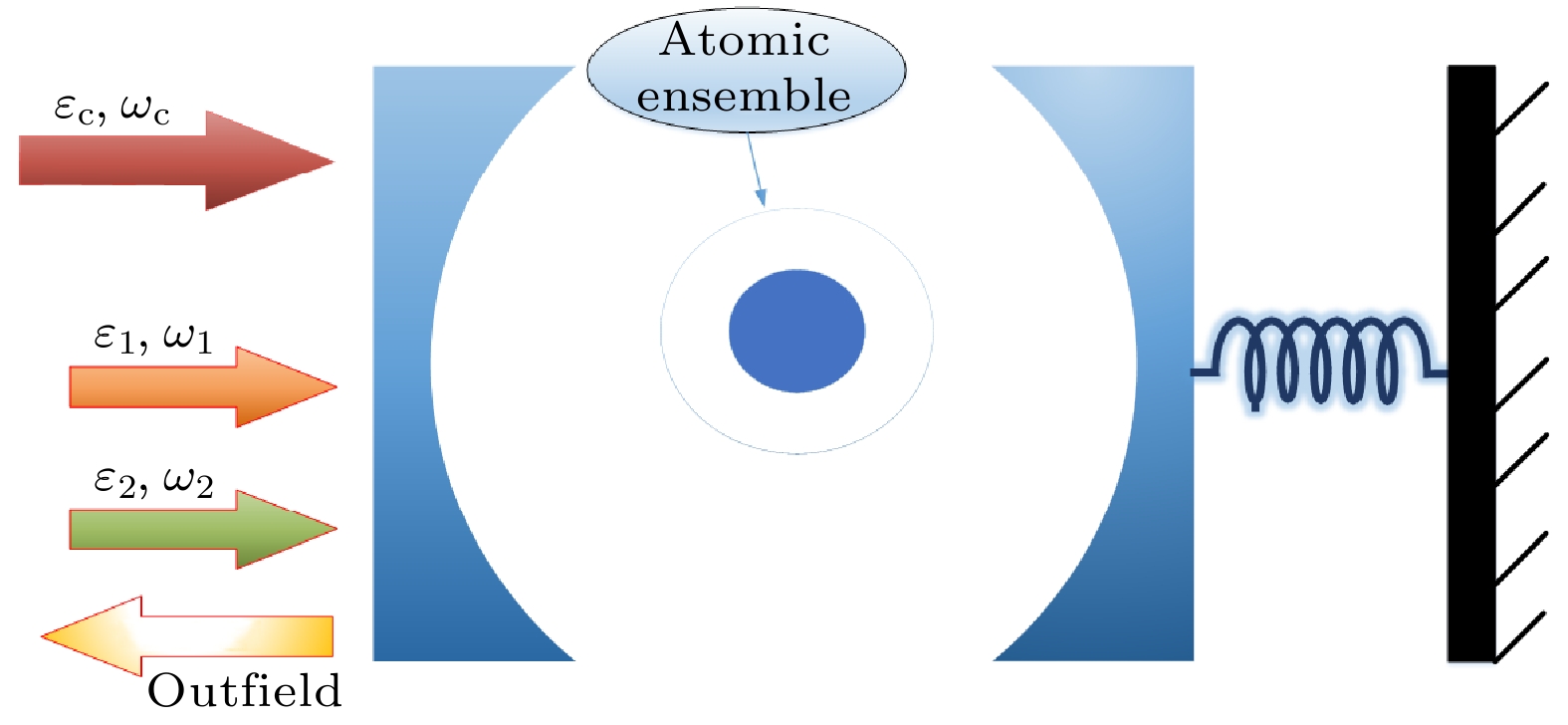
如图1所示, 该复合腔光力系统由放置在腔内的两能级原子、光学腔场和机械谐振器组成, 由频率为${\omega _{\text{c}}}$, 振幅为${\varepsilon _{\text{c}}}$的泵浦场和两个频率分别为${\omega _1}$和${\omega _2}$的相对较弱的探测场驱动, 同时与右侧机械振子耦合. 该系统支持3种不同类型的激发, 即光子、原子和声子. 在本文中, 考虑了两能级原子系综, 原子的集体自旋算符定义为${S_{z, + , - }} = \displaystyle\sum\nolimits_{i = 1}^N {\sigma _{z, + , - }^{\left( i \right)}} $, 定义原子的玻色子湮灭算符$c = {S_ - }/\left| {\sqrt {{S_z}} } \right|$, 满足$\left[ {c, {c^\dagger }} \right] = 1$. 则在${\omega _{\text{c}}}$的旋转框架下系统的哈密顿量如下:

其中$\varDelta = {\omega _{\text{c}}} - {\omega _0}$表示腔场与泵浦场的频率失谐; ${\varDelta _1} = {\omega _{\text{c}}} - {\omega _{\text{a}}}$表示两能级原子与泵浦场的频率失谐; ${\delta _i} = {\omega _1} - {\omega _{\text{c}}}~(i = 1, 2)$表示第一(二)探测场与泵浦场的频率失谐. ${\text{H}}{\text{.c}}{.}$表示$ {a^\dagger }{\varepsilon _1}{{\text{e}}^{ - {\text{i}}{\omega _1}t}} + {a^\dagger }{\varepsilon _2}{{\text{e}}^{ - {\text{i}}{\omega _2}t}} $的复共轭, $p$和$x$分别表示可移动镜子的动量算符和位移算符, $m$和${\omega _{\text{m}}}$分别为其有效质量和振动频率, $a$和${a^\dagger }$分别为腔场的湮灭算符和产生算符, 满足$\left[ {a, {a^\dagger }} \right] = 1$. 第1项$ \hbar \varDelta {a^\dagger }a $为此系统腔场的哈密顿量; 第2项$ {\varDelta _1}{c^\dagger }c $为两能级原子的哈密顿量; 第3项和第4项$ {{{p^2}} {/ } {2 m}} + {{m\omega _{\text{m}}^{2}{x^2}} {/ } 2} $为机械振子的哈密顿量; 第5项$ \hbar {g_{{\text{ac}}}}\left( {{a^\dagger }c + a{c^\dagger }} \right) $描述的是腔场和两能级原子相互作用的哈密顿量, 其中${g_{{\text{ac}}}}$为原子与腔场的耦合强度; 第6项$\left( { - {\lambda _0}x{a^\dagger }a} \right)$为腔场与机械振子相互作用的哈密顿量, 其中${\lambda _0} = - \hbar G$, $G$为光力耦合强度; 第7项$ {\text{i}}\hbar \sqrt {\eta \kappa } {\varepsilon _{\mathrm{c}}}\left( {{a^\dagger } - a} \right) $表示输入的强泵浦场的哈密顿量; 最后一项$ {\text{i}}\hbar \sqrt {\eta \kappa } [ ( {a^\dagger }{\varepsilon _1}{{\text{e}}^{ - {\text{i}}{\delta _1}t}} + {a^\dagger }{\varepsilon _2}{{\text{e}}^{ - {\text{i}}{\delta _2}t}} ) - {\text{H}}{\text{.c}}. ] $表示两个弱探测场的哈密顿量; 其中$\kappa $为腔场的耗散, 包括外部耗散${\kappa _{{\text{ex}}}}$和内部耗散${\kappa _0}$, 耦合参数$\eta = {\kappa _{{\text{ex}}}}/{\kappa _0}$, $\eta $通常取$1/2$; 表达式中的${\varepsilon _{\text{c}}}$, ${\varepsilon _1}$和${\varepsilon _2}$分别是强泵浦场和两个弱探测场的振幅, 各自输入功率关系为: $ \varepsilon_{\mathrm{c}}= \sqrt{P_{\mathrm{c}}/\hbar\omega_{\mathrm{c}}} $, ${\varepsilon _i} = \sqrt {{P_i}/\hbar {\omega _i}} \left( {i = 1, 2} \right)$.

基于系统总哈密顿量方程, 并且考虑到机械振子的热噪声${F_{{\text{th}}}}$和腔场的量子真空噪声${a_{{\text{in}}}}$, 系统的量子动力学可由海森伯-朗之万方程描述:

其中${g_0} = \sqrt N {g_{{\text{ac}}}}$和${s_{{\text{in}}}} = {\varepsilon _1}{{\text{e}}^{ - {\text{i}}{\delta _1}t}} + {\varepsilon _2}{{\text{e}}^{ - {\text{i}}{\delta _2}t}}$. 由于研究的是系统的平均响应, 因此将算符简化为它们的期望值, 即$a\left( t \right) = \left\langle {a\left( t \right)} \right\rangle $, ${a^ * }\left( t \right) = \left\langle {{a^\dagger }\left( t \right)} \right\rangle $, $x\left( t \right) = \left\langle {x\left( t \right)} \right\rangle $和$p\left( t \right) = \left\langle {p\left( t \right)} \right\rangle $. 并考虑到腔场的量子真空噪声和机械振子的热噪声项的平均值为零, 即$\left\langle {{F_{{\text{th}}}}} \right\rangle = 0$, $\left\langle {{a_{{\text{in}}}}} \right\rangle = 0$. 于是对系统的海森伯-朗之万方程整理得:

其中$ {\varDelta _x} = \varDelta + {\lambda _0}x/\hbar $. 将输入的弱探测场看作是对稳定系统的微扰, 考虑到系统产生扰动, 运用微扰法分析变化后的海森伯-朗之万方程即将每个算符分解为稳态项和涨落项之和: $a = \bar a + \delta a$, $x = \bar x + \delta x$, $c = \bar c + \delta c$. 即稳态项$\bar a$, $\bar x$和$\bar c$以及涨落项$\delta a$, $\delta x$和$\delta c$. 对(3)式进行简化计算, 忽略扰动项${s_{{\text{in}}}}$得到稳态项的表达式:

现在考虑由双探针场引起的扰动, 量子涨落的朗之万方程如下:

因此必须考虑非线性项${\text{i}}{\lambda _0}\delta x\delta a, {\lambda _0}\delta {a^*}\delta a$, 因为它们在和边带生成中起着重要的作用. 为了计算和边带的振幅, 通过引入以下忽略二阶和高阶项的方程来处理微扰状态下的SSG:

其中, $ \pm {\varOmega _ + } = \pm ({\delta _1} + {\delta _2})$的频率分量被称为和边带. 通过保留SSG分量的一阶分量和非线性二阶量, 并且忽略其他高阶非线性项来简化计算. 通过将(6)式代入(5)式, 可以得到两组代数方程.

1)第1组描述了频率为${\omega _1}({\omega _2})$的探针场的线性响应:

其中

2)第2组描述了SSG产生的过程:

第1组描述了探测场的线性响应. 方程(7)的解计算结果如下:

其中,

第2组对应于SSG过程. 在和边带处的频率分量的输出振幅以及机械振子和原子系综的振幅如下:

其中

根据输入-输出关系${s_{{\text{out}}}} = {s_{{\text{in}}}} - \sqrt {\eta \kappa } a$, 可以得到该复合光力系统在${\omega _{\text{c}}}$旋转框架下的输出场:

本节具体讨论复合光力系统中SSG的效率. 此外, 为了更系统地了解SSG的特性, 我们研究了系统参数对SSG的影响, 特别是两能级原子对于和边带效应的影响. 输入探针场1的振幅为${\varepsilon _1}$, 而具有上(下)和边带的输出场的振幅为$|\sqrt {\eta {\kappa _1}} a_{\text{s}}^{+}|(|\sqrt {\eta {\kappa _1}} a_{\text{s}}^{{ - }}|)$. 将无量纲$\eta _{\text{s}}^{+} = |\sqrt {\eta {\kappa _1}} a_{\text{s}}^{+}|\left( {\eta _{\text{s}}^{{ - }} = |\sqrt {\eta {\kappa _1}} a_{\text{s}}^{{ - }}|} \right)$定义为生成上(下)和边带的效率. 具体参数分别为^[43]: $ {\gamma }_{\text{m}}/(2\text{π)}=100\;\text{Hz} $, $ {\gamma }_{\text{a}}/(2\text{π)}=2.875\;\text{MHz} $, $ \kappa /(2\text{π)}= 2\;\text{MHz} $, $ {\omega }_{\text{m}}/(2\text{π)} = 10\;\text{MHz} $, ${P}_{1} = {P}_{2} = 0.5\;\text{μW} $, $ {P}_{\text{c}}= 5\;\text{mW} $, ${\lambda }_{\text{c}} = 794.98\;\text{nm}, $ $ m = 10\;\text{ng} $, $\dfrac{G}{2\text{π}} = 0.4\;\text{GHz}/\text{nm} $.

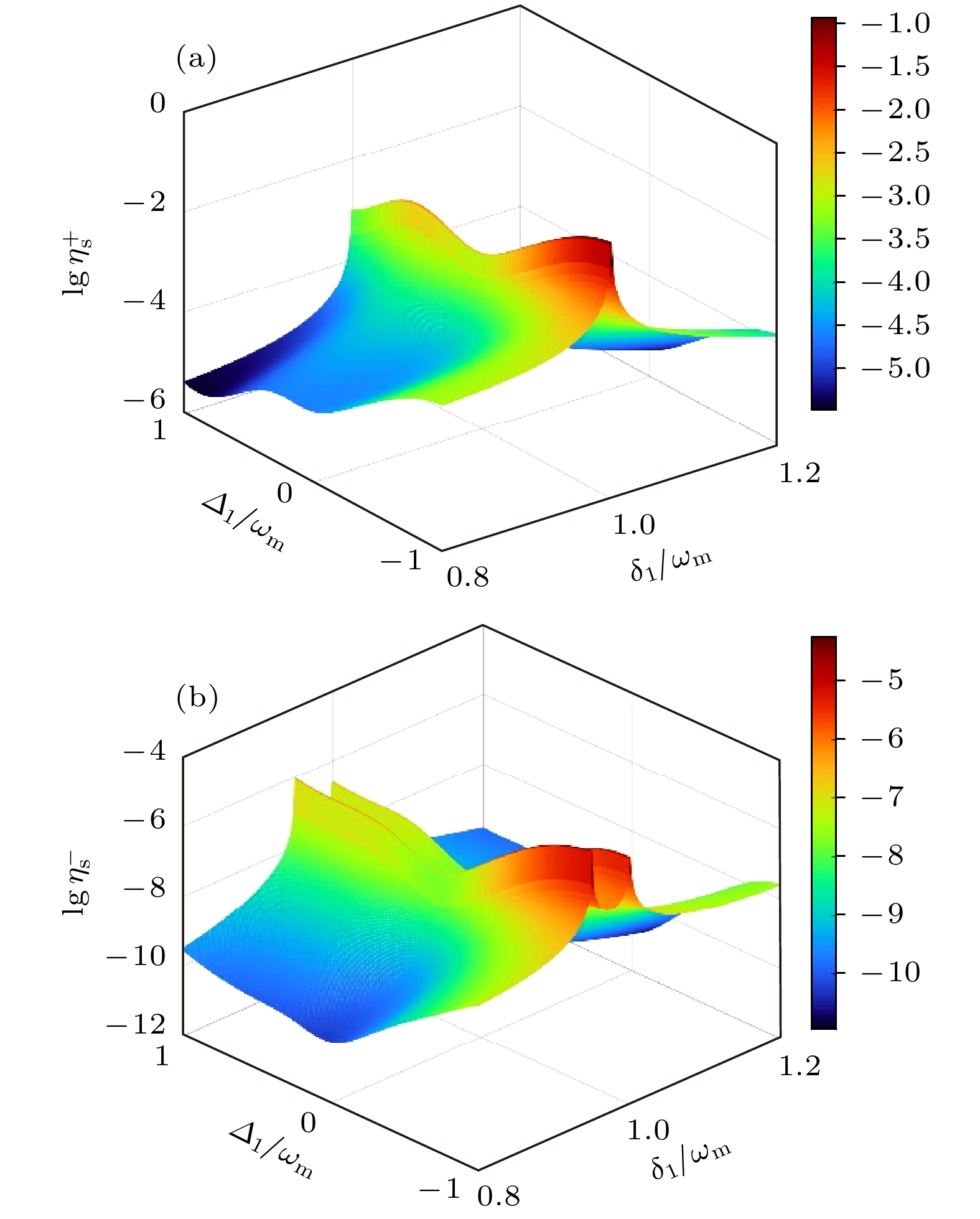
首先, 研究了两能级原子失谐频率和探测场失谐频率对和边带产生的影响. 为此, 在图2中绘制了和边带的效率$\lg \eta _{\text{s}}^{{ \pm }}$作为原子失谐${{{\varDelta _1}} {/ } {{\omega _{\text{m}}}}}$和探测失谐${{{\delta _1}} {/ } {{\omega _{\text{m}}}}}$的函数关系图. 从图2可以观察到, 和边带的效率谱在原子红失谐$\left( {{\omega _{\text{c}}} \leqslant {\omega _{\text{a}}}} \right)$下明显要比处于原子蓝失谐$\left( {{\omega _{\text{c}}} \geqslant {\omega _{\text{a}}}} \right)$下的颜色更鲜艳, 这表明在处于原子红失谐下, 和边带的效率要更高; 并且上、下和边带都在${\varDelta _1} = - {\omega _{\text{m}}}$获得最大生成效率. 如图2(a)所示, 上和边带的效率谱呈现单峰的峰值结构, 其只在${\delta _1} = {\omega _{\text{m}}}$出现一条类似山脉的凸起; 这也说明可以通过适当调节探测场的失谐频率${\delta _1}$增强和边带的产生效率. 值得注意的是, 原子失谐频率在$ - {\omega _{\text{m}}} < {\varDelta _1} < 0$范围内, 和边带信号急速下降; 而在原子蓝失谐下, 和边带的效率呈现先增后减的趋势, 并在大概${\varDelta _1} = 0.5{\omega _{\text{m}}}$处达到局部极大值. 这是因为原子从基态跃迁到激发态, 其跃迁频率高于泵浦场频率时, 由于此时原子的本征非线性较强, 以至于对于复合腔-原子系统中控制场的要求不高, 即使在弱驱动作用下也能产生极强的和边带. 如图2(b)所示, 与上和边带不同, 下和边带的效率谱出现双峰结构, 分别在${\delta _1} = 0.95{\omega _{\text{m}}}$和${\delta _1} = {\omega _{\text{m}}}$处出现增强峰; 并且其左侧峰值明显略高于右侧. 这表明两能级原子系综的介入, 可以改变下和边带产生的匹配条件. 下和边带的效率在原子红失谐下表现出下降的趋势, 而在原子蓝失谐下呈现效率上升. 需要留意的是, 上、下和边带的峰值结构在${\varDelta _1} = 0$处都出现了波谷, 产生这一物理现象也从侧面表明两能级原子系综的加入, 急剧增强了复合腔光力系统的非线性效应, 使得原本光学腔场和机械振子之间的弱光力耦合非线性作用增强, 从而提高了和边带产生的效率.

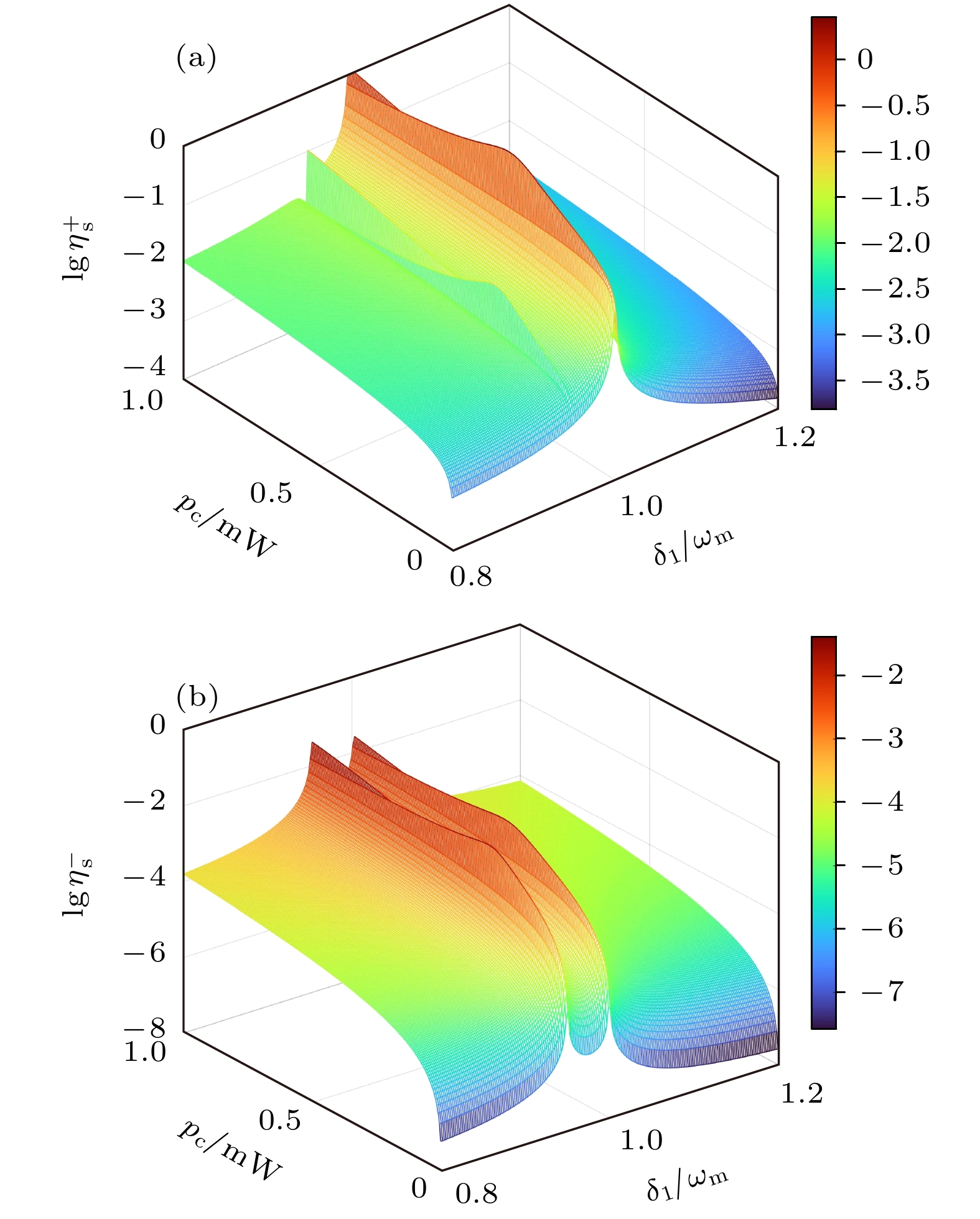
其次, 为了研究泵浦功率对于腔-原子复合系统中和边带的影响, 图3所示为和边带的效率谱$\lg \eta _{\text{s}}^{{ \pm }}$(对数形式)随着泵浦功率$ {p_{\text{c}}} $和探测失谐频率${\delta _1}$的变化情况. 由于传统的光力耦合非线性较弱, 所以输出场产生的和边带信号强度也非常小, 而泵浦功率作为驱动场, 是唯一可以通过直接调节的方式控制输出信号的. 从图3(a)可以观察到, 上和边带的效率谱随泵浦功率$ {p_{\text{c}}} $的增强而颜色逐渐变深, 这表明上和边带的效率$\lg \eta _{\text{s}}^{{ \pm }}$会随着泵浦功率的增大而近似单调增强. 但其在探测失谐频率为${\delta _1} = 0.95{\omega _{\text{m}}}$和${\delta _1} = {\omega _{\text{m}}}$时表现出不同的函数关系. 在${\delta _1} = 0.95{\omega _{\text{m}}}$处, 呈现出双峰结构, 当$0 < {p_{\text{c}}} < 0.5 \;{\text{mW}}$时, 上和边带的效率先递增后递减, 并在${p_{\text{c}}} \approx 0.3\; {\text{mW}}$时达到局部极大值; 而超过这一范围后, 上和边带的效率表现为单调递增. 其主峰结构位于${\delta _1} = {\omega _{\text{m}}}$, 与之前不同, 在该处上和边带的效率与泵浦功率之间表现出了极为复杂的线性关系, 当${p_{\text{c}}} \approx 0.5 \;{\text{mW}}$时, 获得局部极大效率值; 当${p_{\text{c}}} \approx 0.8\; {\text{mW}}$时达到局部极小值, 出现该抑制窗口的原因在于两束探测光通过不同的散射路径, 发生非相干叠加而产生干涉效应, 对该现象的物理解释是由于两条散射路径的频率差异足够小或为零, 它们在空间中相遇时会发生相互抵消或增强, 即存在明显的干涉效应. 这种零频差或极小频差是导致两条散射路径之间发生干涉的直接原因^[18,46]. 而当$ 0.8\; {\text{mW}} < {p_{\text{c}}} $后, 上和边带的效率值随泵浦功率$ {p_{\text{c}}} $的增大而迅速增大. 如图3(b)所示, 下和边带的峰值结构中两峰表现相同, 其与上和边带的主峰结构相似, 具有主峰近乎相同的线性函数关系, 只是下和边带的效率小于上和边带.

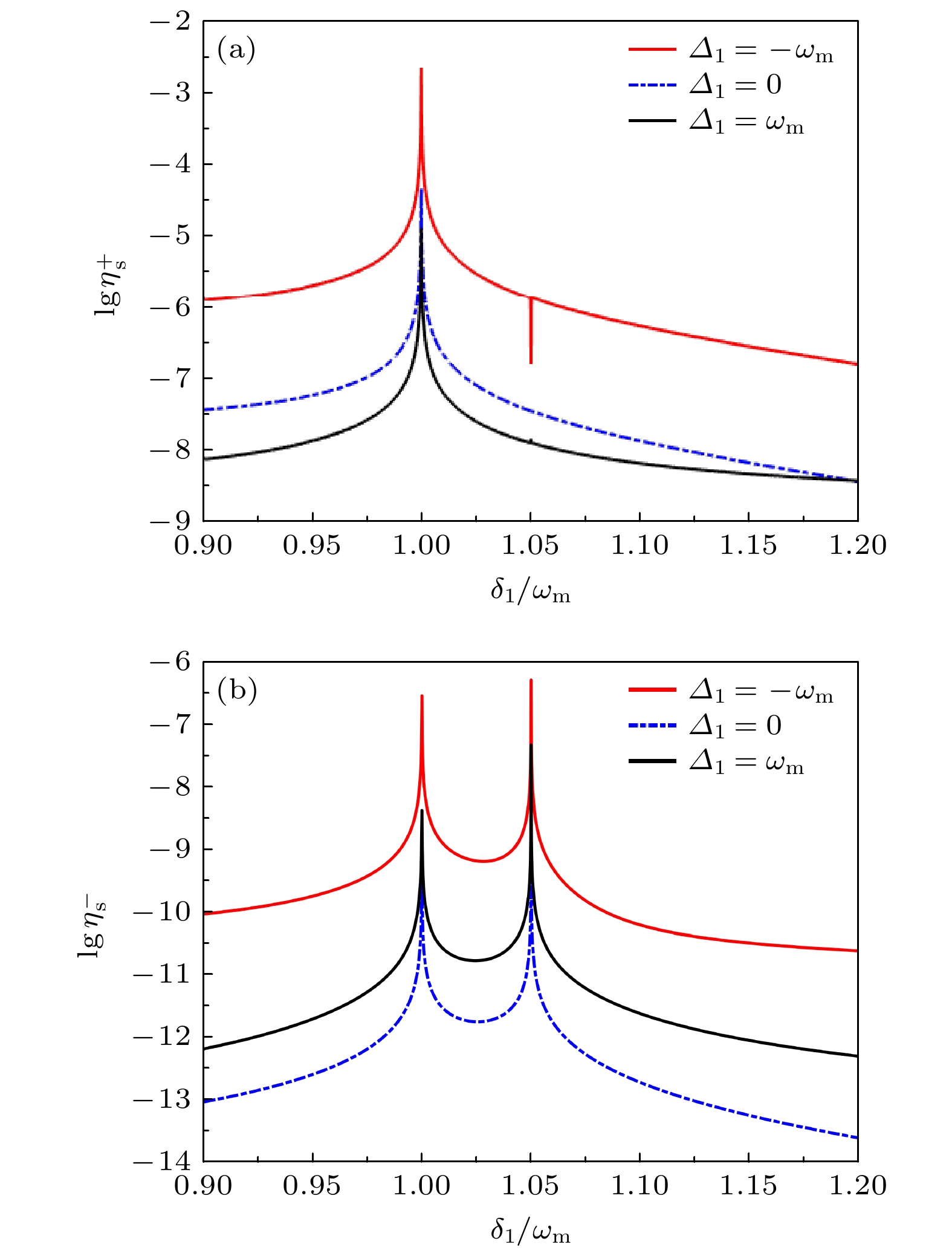
图4所示为在不同的原子失谐${\varDelta _1}$下, 输出场和边带的效率$\lg \eta _{\text{s}}^{{ \pm }}$与归一化失谐$ {{{\delta _1}} {/ } {{\omega _{\text{m}}}}} $的函数关系. 结果表明, 通过比较图4(a), (b)可以发现在原子红失谐下, 无论上、下和边带的效率都最大的. 而上和边带的效率在蓝失谐下表现出了抑制现象, 出现该物理行为的解释是蓝失谐下, 原子的跃迁频率不足以将原子由基态跃迁至激发态, 使得原子与腔内光子纠缠, 从而减少了与声子相互转化的光子数, 故而非线性和边带的产生受到抑制. 然而, 下和边带的效率由于二能级原子的介入, 不论在原子红失谐还是蓝失谐下都表现出增强的效果, 且红失谐状态下的效率更高. 通过测量和边带频率谱的峰值, 可以很容易地检测出原子的失谐频率. 当原子失谐${\varDelta _1} = - {\omega _{\text{m}}}$时, 上和边带在${\delta _1} = 1.05{\omega _{\text{m}}}$处差生一个吸收峰, 对这一现象的物理解释是满足共振条件${\varDelta _1} = - {\omega _{\text{m}}}$, 机械振荡器的激发引起了腔内探测场激发路径的相消干涉, 这种干涉效应导致了腔内探测场的透明窗口的产生^[8].

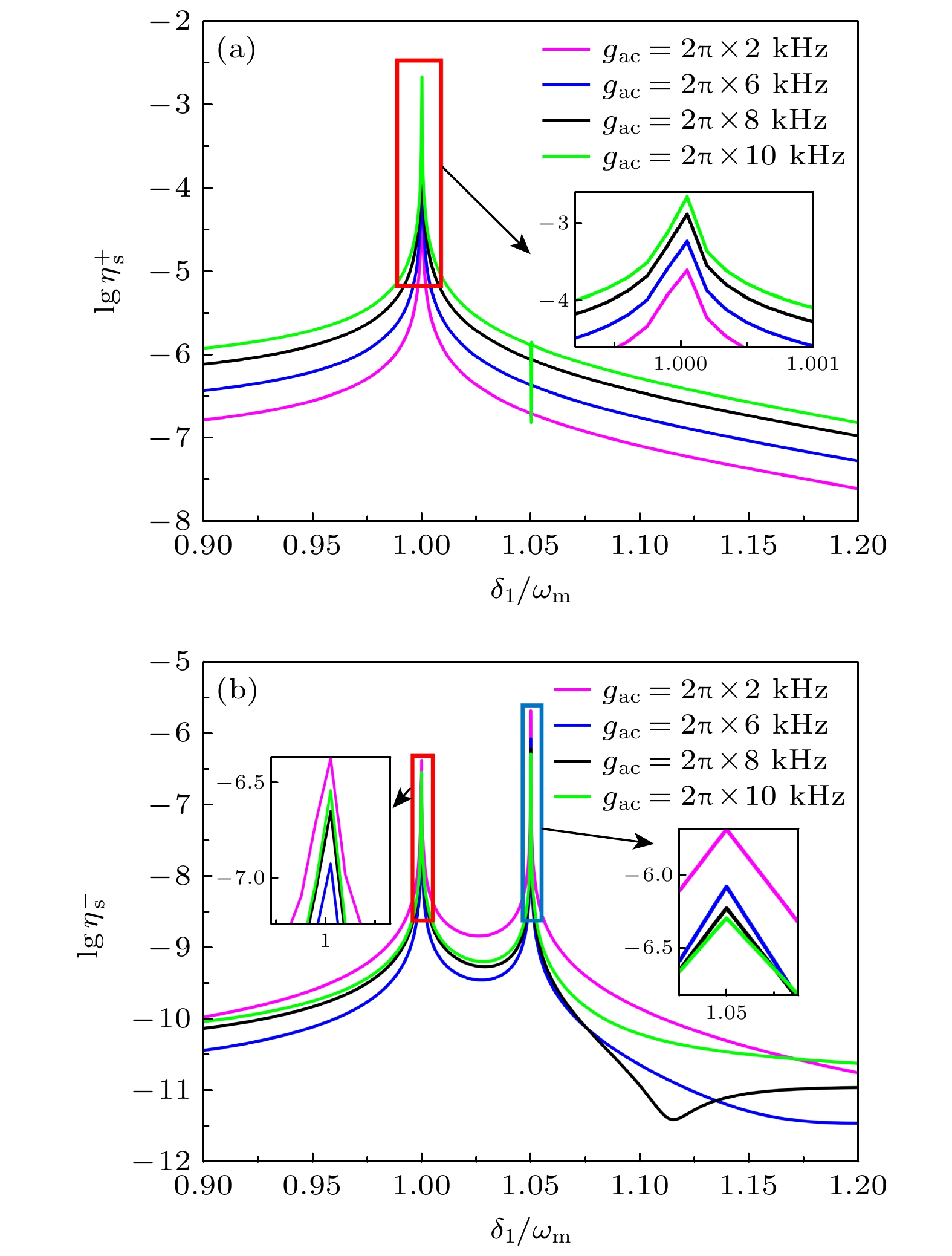
图5所示为通过设置不同腔-原子耦合强度${g_{{\text{ac}}}}$来研究对于腔-原子复合光力系统和边带效率的影响. 根据图5(a)可知, 随着腔-原子耦合强度${g_{{\text{ac}}}}$的增强, 上和边带的效率值$\lg \eta _{\text{s}}^{{ \pm }}$在急剧增大. 这反映了通过光学腔场与两能级原子系综的电偶极相互作用, 能够提高腔场和机械振子的纠缠, 增强二者之间的光力耦合非线性, 使得非线性相互作用占主导, 实现选择性特定频率的和边带产生, 而抑制其他频率边带的生成. 并且当$ {g_{{\text{ac}}}} = 2{\text{π}} \times 10\; {\text{kHz}} $时, 上和边带的效率在$ {{{\delta _1}} {/ } {{\omega _{\text{m}}}}} $处会产生一个吸收峰. 产生该现象的物理原因是因为在光学腔场的共振条件下, 当控制场的功率驱动一定值的腔场时, 系统产生相消干涉, 满足干涉条件$\varDelta = {\delta _1} + {\delta _2}$, 导致吸收峰的出现^[48]. 如图5(b)所示, 与上和边带相比, 下和边带的效率受腔-原子耦合强度的影响明显产生了抑制效果. 值得注意的是, 下和边带的效率在$ {{{\delta _1}} {/ } {{\omega _{\text{m}}}}} $存在阈值, 当$ {g_{{\text{ac}}}} < 2{\text{π}} \times 6\; {\text{kHz}} $时, 其随腔-原子耦合强度的增强而减小; 而当$ {g_{{\text{ac}}}} > 2{\text{π}} \times 6 \;{\text{kHz}} $时, 下和边带的效率才会逐渐增强. 然而, 其在${\delta _1} = 1.05{\omega _{\text{m}}}$附近的生成效率始终表现下降的趋势. 总体来说, 下和边带的效率随腔-原子耦合强度的增强会产生抑制现象. 这说明上和边带对于腔-原子耦合强度的依赖性更强. 在检测腔-原子的耦合强度时通过测量和边带频率谱峰值的方法, 可以很容易得到光学微腔与两能级原子间的电偶极耦合强度. 这为腔场与两能级原子之间耦合强度的精密测量提供了一种简单便捷的方法, 同时也为和边带信号传输的调控提供有益的借鉴.

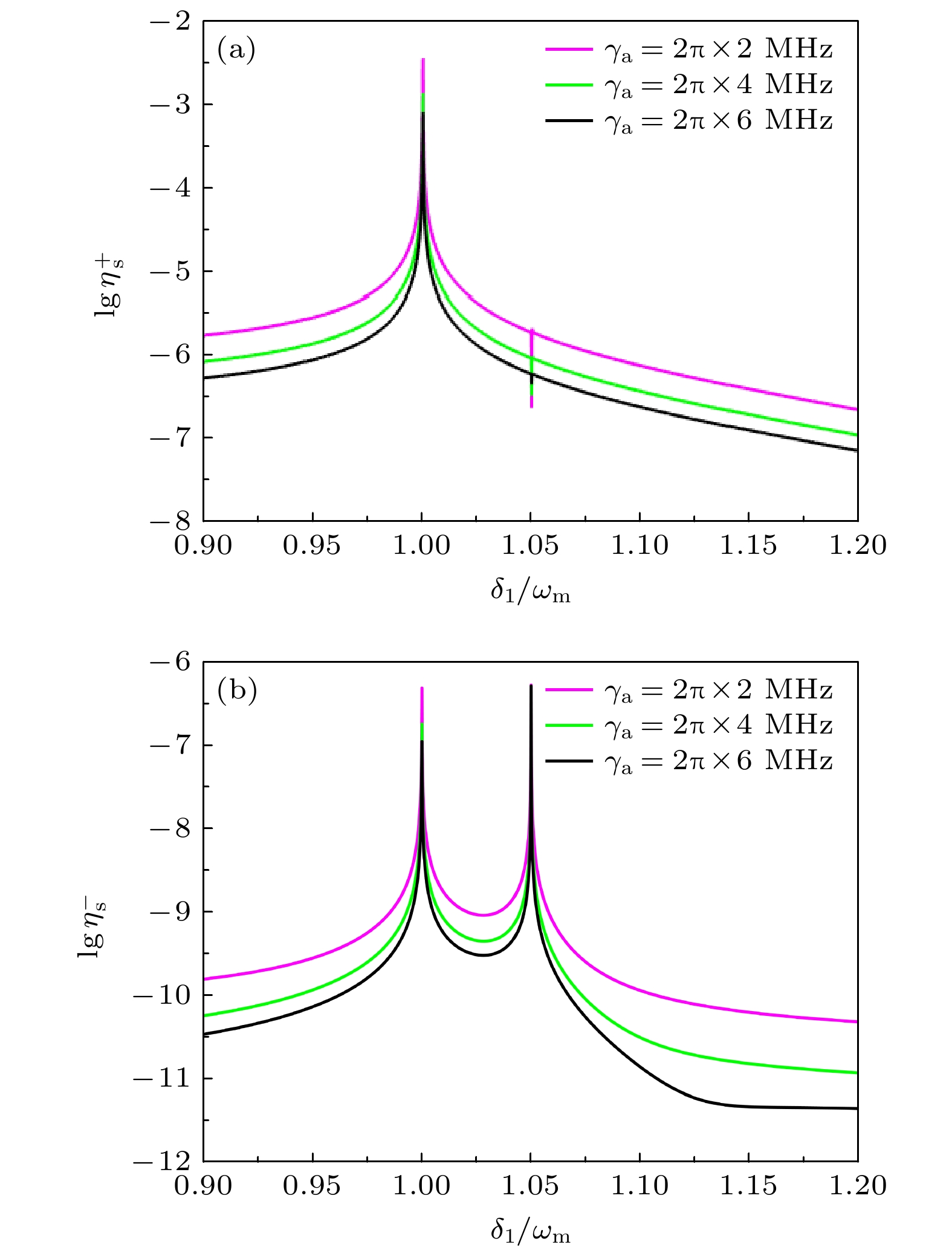
最后, 本文研究了两能级原子衰减率对于复合腔-原子系统中和边带信号产生的影响. 图6显示了在相同的腔-原子耦合强度$ {g_{{\text{ac}}}} = 2{\text{π}} \times 10\; {\text{kHz}} $的情况下, 和边带的效率在不同的原子衰减率${\gamma _{\text{a}}}$下的变化曲线. 结果表明, 无论上、下和边带, 其产生效率都会随原子衰减率的增大而下降. 说明两能级原子介质的引入可以提高复合腔场中光子与声子之间的转换率, 增强系统的光力非线性. 根据图6(a)所示, 上和边带信号在${\delta _1} = {\omega _{\text{m}}}$附近有明显的增强, 且当$ {\gamma _{\text{a}}} = 2{\text{π}} \times 2 \;{\text{MHz}} $时, 上和边带的效率值$\eta _s^ + $达到最大. 然而, 其效率值的变化曲线都会在${\delta _1} = 1.05{\omega _{\text{m}}}$附近产生吸收峰, 并且吸收峰的深度逐渐变深. 该现象的物理解释是, 随着原子衰减率的增大, 机械振子的共振吸收也随着增强, 从而导致光力效应被抵消, 产生的吸收峰程度变深. 根据图6(b), 下和边带的效率在${\delta _1} = {\omega _{\text{m}}}$附近与上和边带的变化趋势相同, 但其在${\delta _1} = 1.05{\omega _{\text{m}}}$表现出相反的变化情况. 产生这种现象的原因是因为衰变速率较低的原子处于高能态的时间较长, 能够有效增强原子-腔耦合作用, 使得原子向腔内发射光子的概率增大, 进而增强光力学非线性, 提高和边带的效率^[53]. 说明下和边带的效率在光学腔场的共振条件$\varDelta = {\omega _{\text{m}}}$周围对于原子衰减率的依赖程度更强. 同时也表明, 可以通过选取合适的原子介质调节输出和边带信号的强度.

本文分析了含有两能级原子系综的复合腔光力系统中和边带效应, 并且发现通过引入两能级原子系综可以实现光学和边带的选择性增强或抑制. 同时, 研究了原子系综的失谐频率对于和边带的产生效率的影响. 结果表明, 不论在原子红失谐还是蓝失谐下都可以使和边带的效率得到显著增强, 并且对于红失谐状态下的依赖性更大, 其增强的效果更加明显. 还考虑了泵浦功率的影响, 通过选择适当的泵浦功率可以有效的增强输出和边带信号的强度. 进一步讨论了腔-原子耦合强度与原子衰减率对于和边带信号的传输特性. 结果表明, 可以通过选取合适的原子介质调节输出和边带信号的强度. 此外, 上和边带对于腔-原子耦合强度的依赖程度更强, 其随腔-原子耦合强度的增大而增强. 然而, 下和边带会受到抑制. 在检测腔-原子的耦合强度时, 通过测量和边带频率谱峰值的方法, 进而可以得到光学微腔与两能级原子间的电偶极耦合强度. 这为腔场与两能级原子之间耦合强度的精密测量提供了一种简单便捷的方法, 同时也为输出场和边带信号传输的调控提供有益的借鉴.