首页
登录
注册
下载:
-
超表面具有结构简单、易于制造、便于集成 的特点[1–3], 能够灵活调控电磁波, 广泛应用于太 赫兹滤波器[4,5]、透镜[6,7]、偏振转换器[8,9]、波前调 控[10,11]和成像[12,13]等领域. 通过对不同振幅和相位的单元按照一定规律进行编码排布, 超表面可实现成像、聚焦、分束、涡旋等功能[14–16]. 如2022年, Li等[17]根据几何相位原理设计了一种左右圆极 化太赫兹多功能编码超表面, 实现对圆偏振入射波的分束与聚焦. 2023年, Liu等[18]基于几何相位 原理设计多功能超薄超表面, 实现了不同拓扑荷 数涡旋波束以及偏振波的汇聚. 同年, Fu等[19] 基于几何相位原理设计了涡旋波束发生器, 在26.5—40 GHz频段实现了拓扑荷数为–1的涡旋 波束. Sun等[20]提出自旋和空间复用的四通道 超表面, 通过改变单元尺寸和旋转角度实现非对称传输和四通道波前调控. 上述已报道的超表面均 按照几何相位和传输相位理论来实现相位调制, 但是几何相位本身具有自旋锁定特性, 当单元旋转一定角度时, 对左旋圆极化波(LCP波)和右旋圆极化波(RCP波)实现大小相等、符号相反的几何 相位, 两种圆极化波获得的几何相位是相互锁定的. 传输相位法实现的相位调控都是单频点. 已报道的编码超表面要同时利用几何相位和传输相 位方法实现相位调控则需要构建复合结构超表面, 且为窄频带工作. 针对上述问题, 本文提出了弧度与旋转共同诱导相位调控超表面, 只需要单一超表面结构就可以分别对LCP和RCP入射波的相位进行独立调控, 同时实现对超表面的几何相位和传输相位调控, 而且工作频带较宽. 最后通过相位卷积和共享孔径原理该超表面实现多通道涡旋、聚焦、完美涡旋等功能, 该结构具有结构简单、调控方式灵活便捷、尺寸小、实用性高等优点, 应用前景广阔.
-
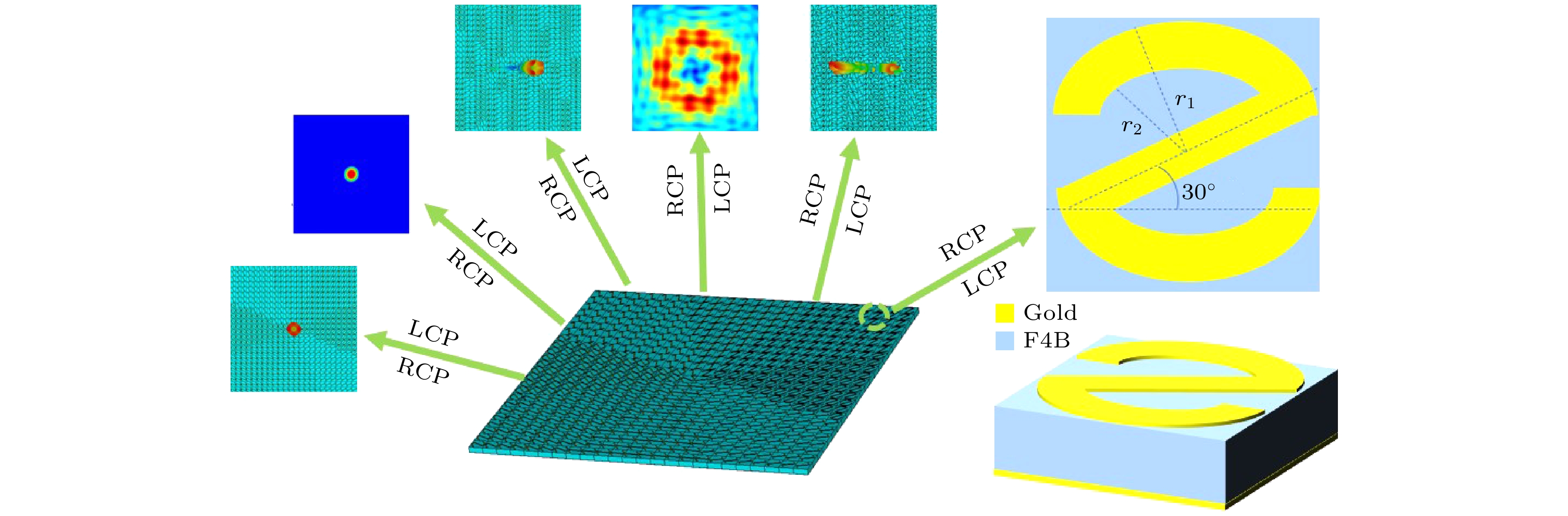
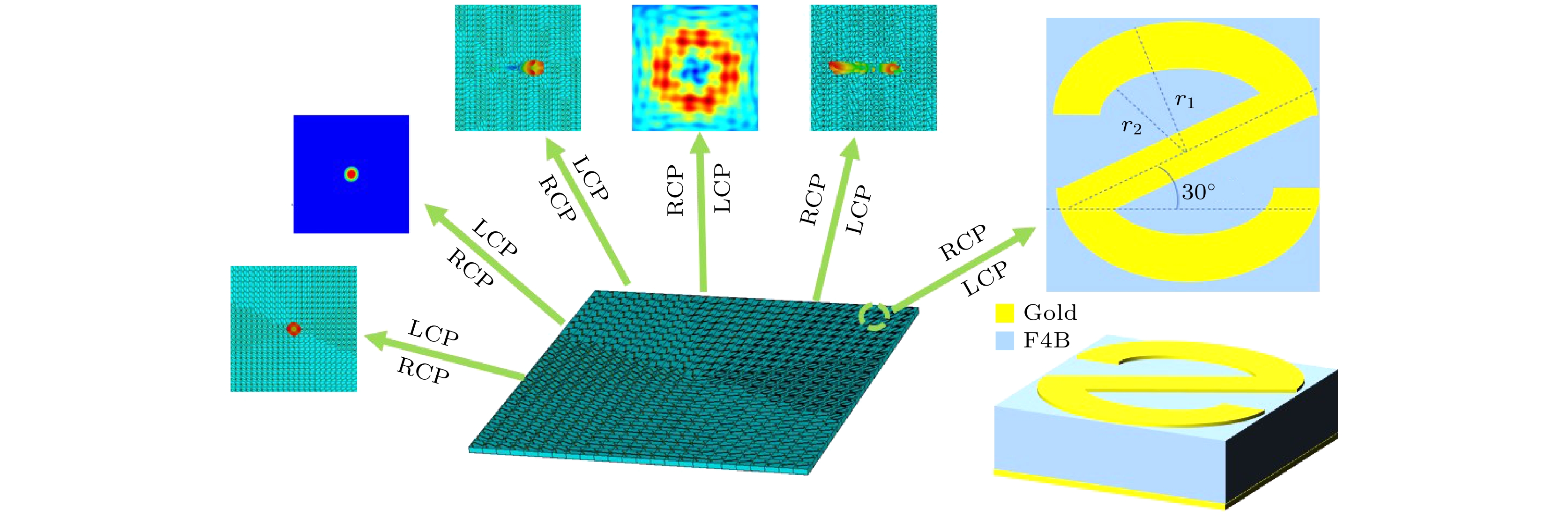
本文提出的弧度与旋转共同诱导相位调控超表面及其功能示意如图1所示. 顶层为“2”型金属图案, 金属图案呈中心对称, 金属圆弧外径r1 = 46 μm, 内径r2 = 39 μm; 金属矩形斜边长w = 46 μm, 宽d = 7 μm, 厚度为0.3 μm. 中间层为聚四氟乙烯(F4B)介质层, 介电常数为2.65, 损切角为0.001, 厚度为40 μm. 底层金属为金, 厚度为0.3 μm. 聚焦和涡旋的超表面仿真中, 超表面单元数量为24×24, 超表面单元周期为100 μm, 整体尺寸为2400 μm×2400 μm. 所设计超表面初步加工过程: 在介质层为40 μm厚的F4B介质层的底部和顶部利用磁控溅射方法制作厚度为0.3 μm金层, 然后通过光刻工艺在F4B介质顶部金层制作“2”字形结构, 最后完成超表面结构加工制作.
根据旋转诱导相位原理, 当一束平面波垂直照射到超表面单元结构上, 超表面单元的透射场与反射场可表示为[21]
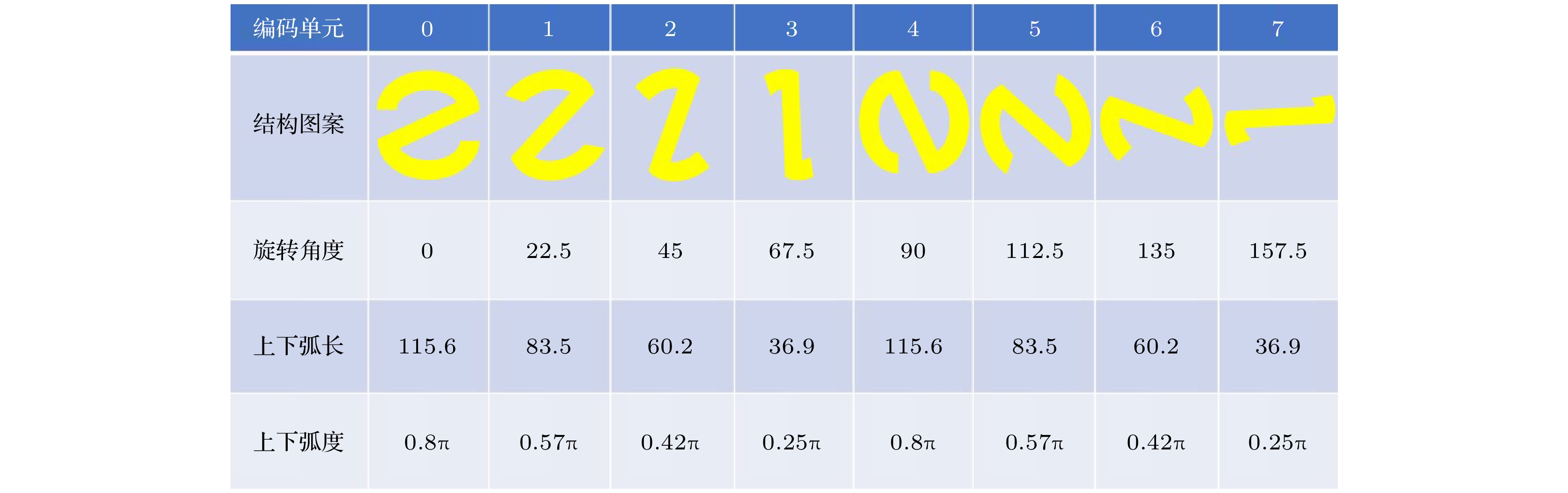
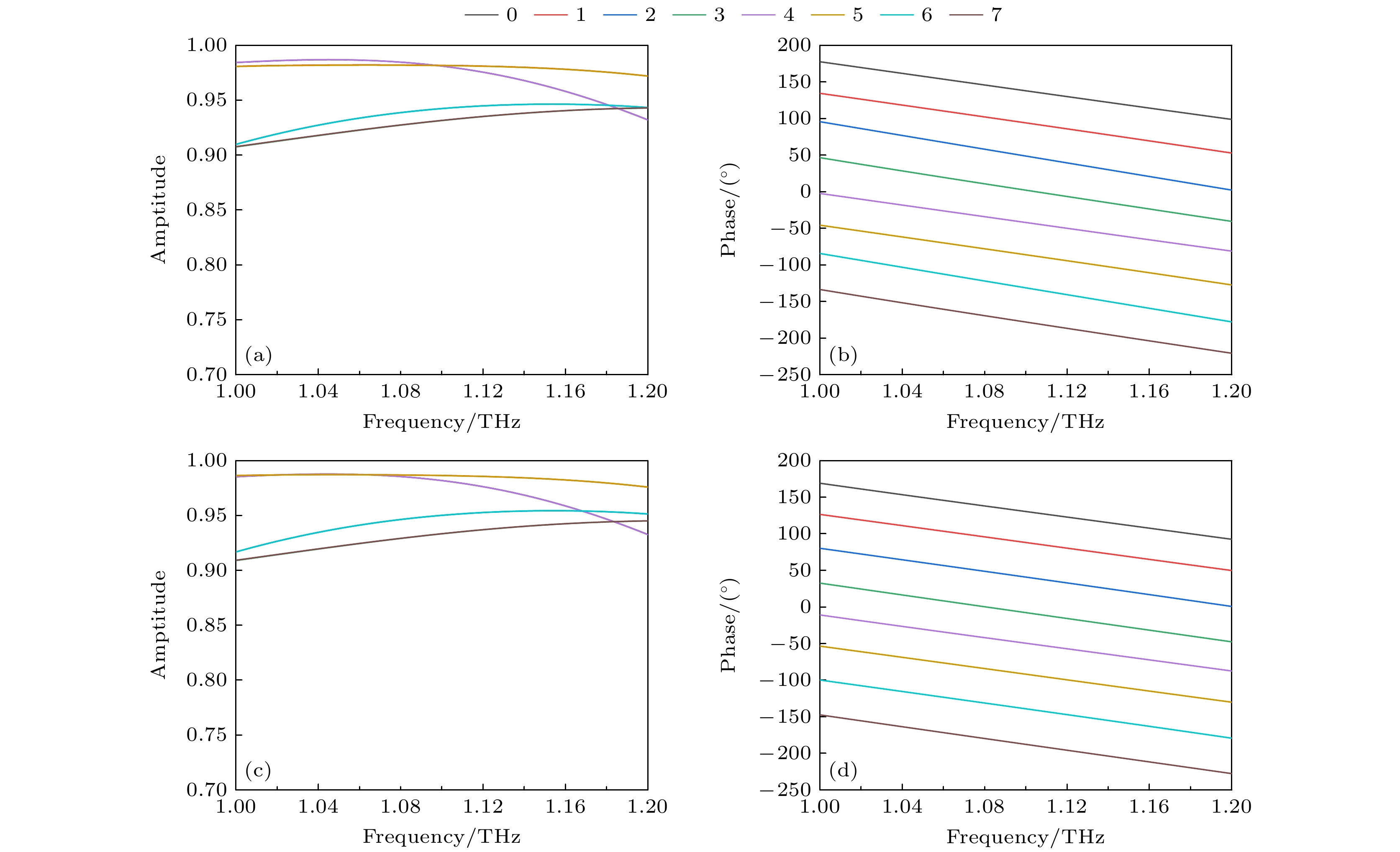
式中, txx, txy, tyx 和tyy是线偏振波的反射系数, 其中第1个下标是线偏振波的反射方向, 第2个下标是线偏振波的入射方向. 可见出射波第1项是未引入相位因子的共极化偏振波, 第2项是携带附加相位的交叉极化偏振波. 研究发现通过改变单元结构的弧度, 同样可以在LCP波和RCP波入射时实现相位调控, 这为相位调控提供了一种全新方式[22], 本文提出共同诱导超表面的相位调控. 通过旋转单元结构和改变上下圆弧的弧长, 获得超表面单元尺寸和旋转角度如图2所示, 对应的单元结构“0”, “1”, “2”, “3”, “4”, “5”, “6”, “7”的相位和反射系数图, 如图3所示. 在LCP波和RCP波入射下, 超表面单元在1—1.2 THz内, 反射系数均大于0.9, 相互之间保持近45°的相位差.
-
当圆极化波入射到超表面时, 其相位分布可以表示为[23]
式中, (x, y)为超表面单元在二维坐标系中的具体位置, l表示涡旋波束的拓扑荷数. 为简化排布和设计, 超表面可以划分为M个均匀的区域, 每个区域所需的梯度分布相位由(3)式计算得到:
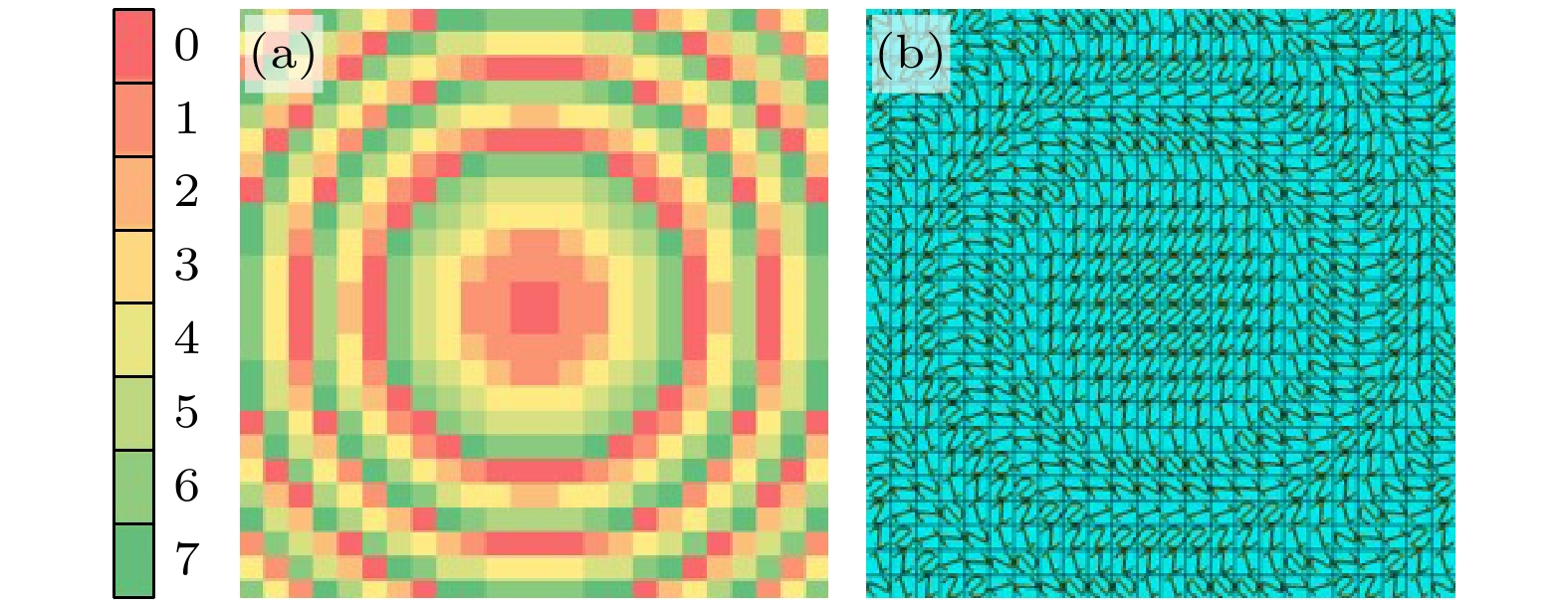
式中, M是超表面被划分的区域数. 图4(a), (c)分别表示拓扑荷数为l = 1和l = –1时涡旋超表面相位分布, 将单元结构按照相位分布进行排布获得超表面结构如图4(b), (d)所示.
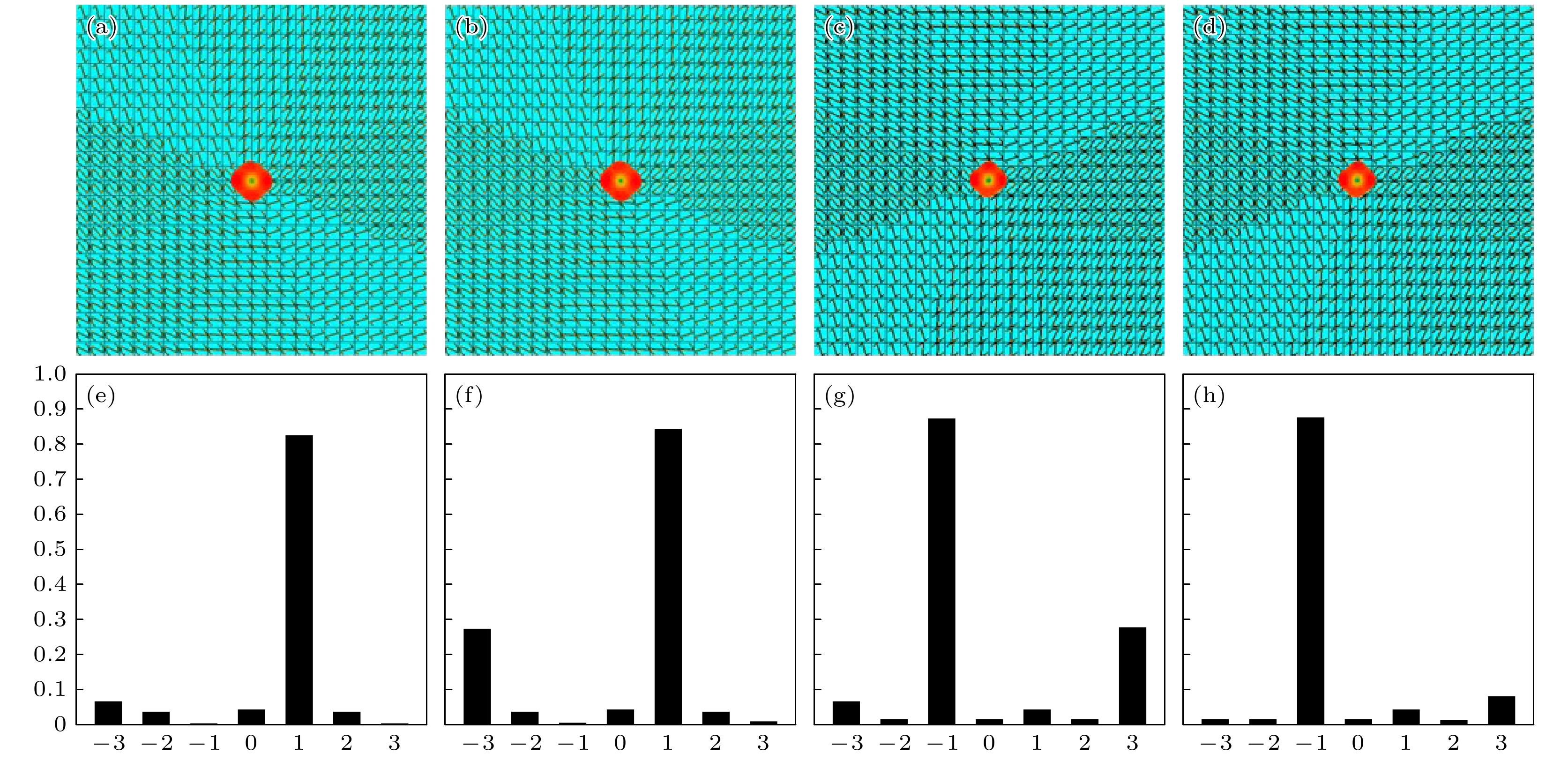
图5(a)—(d)给出了频率为1.1 THz时, LCP和RCP入射下超表面产生涡旋远场. 通过傅里叶变换可以计算具有不同拓扑荷的涡旋波束模式纯度:
式中exp(ilφm)是涡旋谐波, α(φm)是相位. 图5(e)—(h)表示超表面产生l = 1和l = –1涡旋波束的模式纯度分别为84.95%, 83.79%, 88.12%和87.55%.
根据聚焦理论, 对于具有给定焦距的超表面每个单元相移φf满足以下关系:
式中, zf是焦距, λ是波长. 本文设计了焦距为zf = 1500 μm的聚焦超表面, 其相位排布和超表面结构如图6所示.
计算得到在频率为1.1 THz处, LCP波入射下, zf = 1500 μm时的x-y截面电场如图7(a)所示, 可以观察到预设的焦点. 图7(b)表示y = 0 μm处x-z截面的聚焦, 模拟结果与预设焦点一致. 同理, RCP波入射下超表面产生聚焦结果如图7(c), (d)所示, 模拟结果与理论预测一致, 在zf = 1500 μm处有明显的聚焦效果.
-
编码超表面可以利用相位突变的梯度进行调控波束异常反射, 偏折角度可以表示为[23]
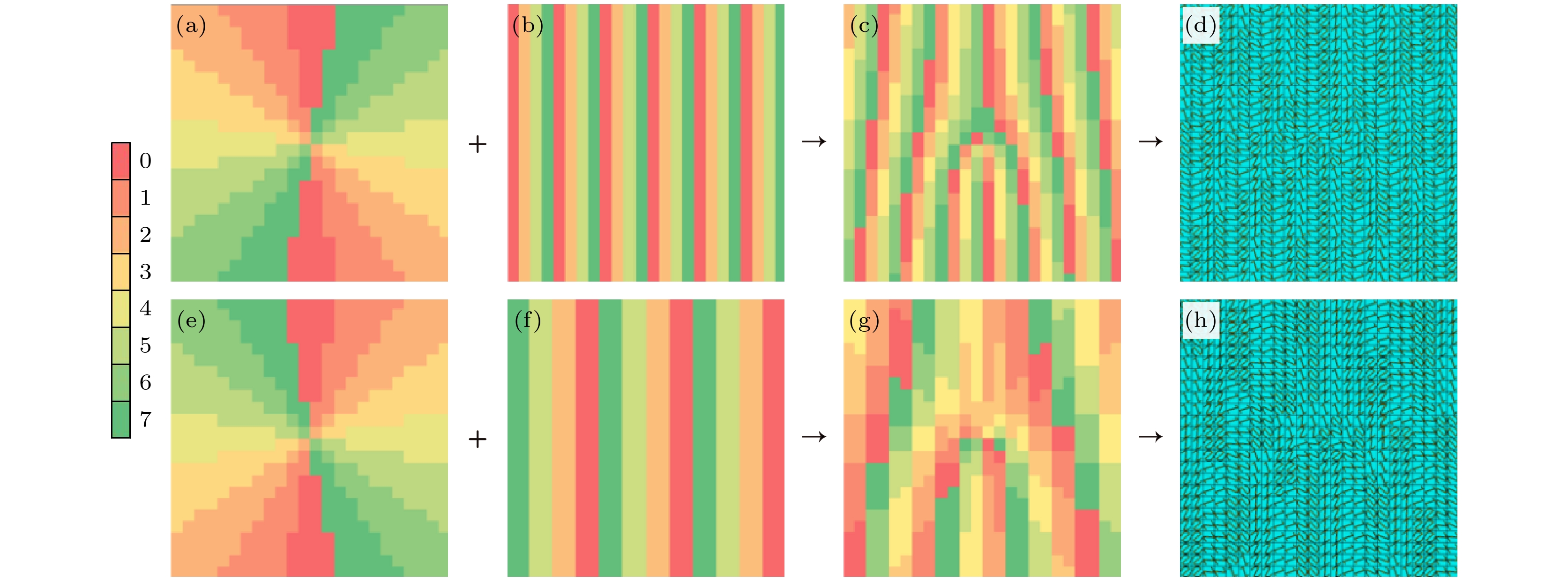
式中, τ是梯度编码序列的周期, λ是波长. 拓扑荷数分别为l = 2和l = –2时, 超表面的相位排布如图8(a), (e)所示. 将编码单元按序列“64206420…”和“0022446600224466…”沿x方向周期性排布, 每个超表面由24×24个单元组成, 排布结果如图8(b), (f)所示. 通过卷积运算将涡旋相位和偏折梯度相位叠加, 得到相位排布如图8(c), (g)所示, 最终得到超表面结构如图8(d), (h)所示.
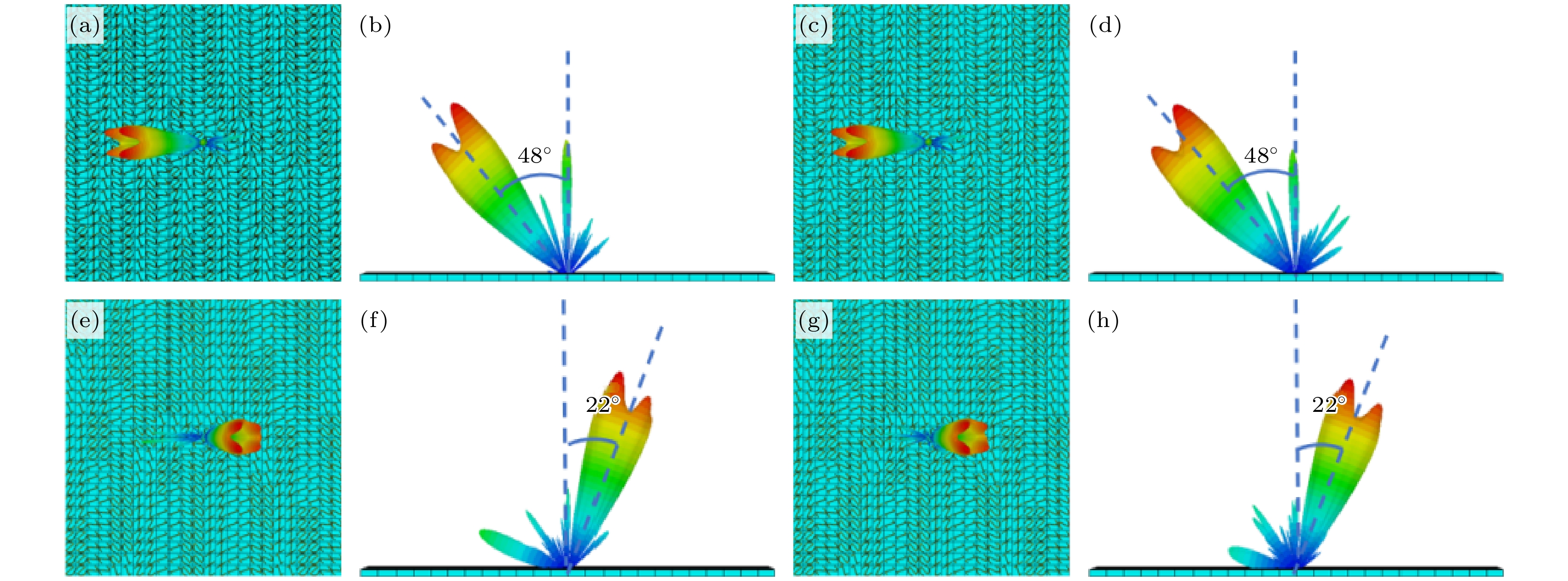
图9表示LCP波和RCP波入射时, 在频率为1.1 THz处涡旋远场, 仿真结果得到反射波束偏转角度分别为θ1 = 48°和θ2 = 22°, 利用(6)式计算得反射涡旋波束的偏角转为θ1 = 48.59°和θ2 = 22.02°. 仿真计算结果与理论预测相一致.
根据聚焦理论, 设计焦距为1500 μm的偏折聚焦超表面排布如图10所示, 将超表面按序列“02460246…”沿x方向周期性排布(如图10(b)所示), 通过卷积运算将聚焦相位和偏折梯度相位叠加得到相位如图10(c)所示, 最终得到超表面结构如图10(d)所示.
图11表示在LCP波和RCP波入射时, 在频率1.1 THz处, 距离超表面1500 μm时的x-y截面电场图如图10(a)所示, 可以观察到预设的焦点在x方向偏折显示出来. 图10(b)表示了y = 0 μm处x-z截面的聚焦, 模拟结果与理论预测一致, 在1500 μm处有明显的聚焦效果, 且偏折效果明显.
-
产生完美涡旋的相位轮廓可以由下式计算[24]:
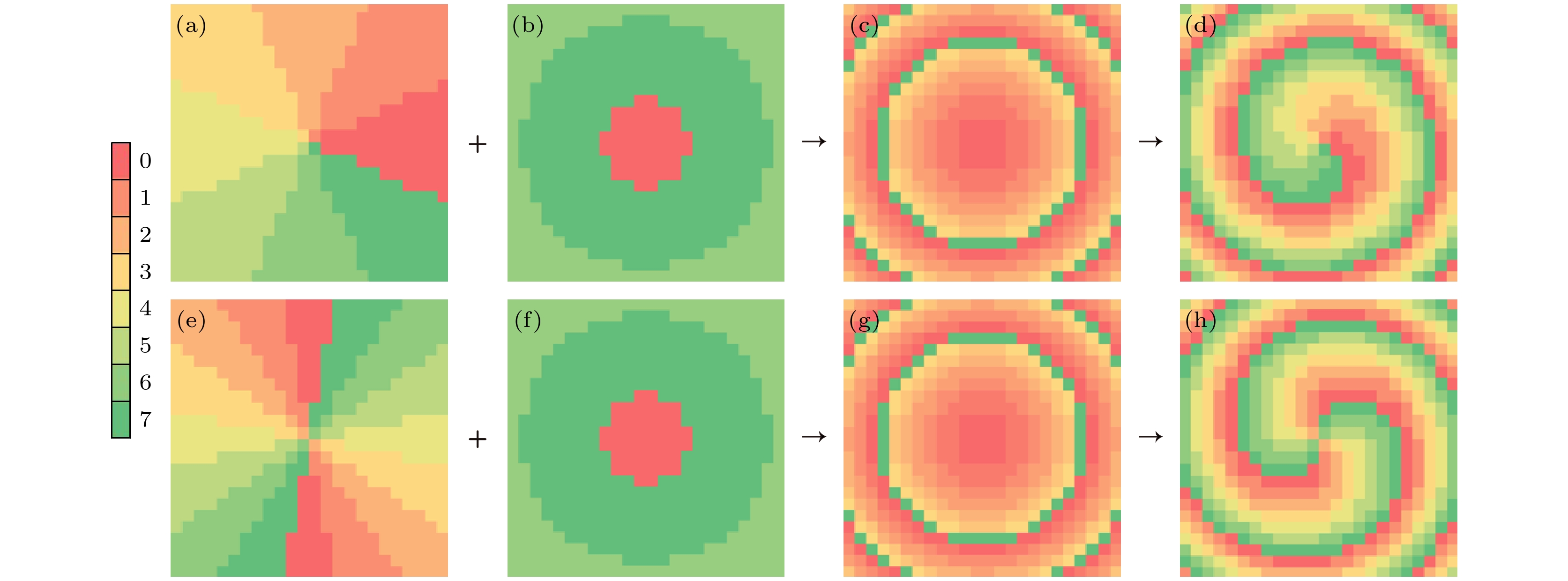
式中, x和y是空间坐标, Φvortex, Φnegative axion, Φlens分别是涡旋光束产生的相位分布、负轴向产生的反向贝塞尔光束的傅里叶变换相位分布和焦透镜的相位分布, l为涡旋波束拓扑荷数, D为编码单元周期, f是设置的焦距, λ是波长. 设计焦距为1500 μm的拓扑荷数为l = 1和l = 2的完美涡旋波束, 相位轮廓如图12所示.
图13表示当频率1.1 THz时, LCP波入射下, 超表面产生拓扑荷数为l = 1和l = 2的完美涡旋波束在聚焦平面1500 μm上的电场强度分布, 可以看出电场中均呈环形能量分布, 图13(a), (b)分别显示了具有不同拓扑荷数(l = 1, 2)的完美涡旋波束在聚焦平面1500 μm上沿x轴方向的归一化强度曲线, 可见在固定的焦透镜焦距下, 环形能量分布的半径没有明显变化, 表现出完美涡旋波束与拓扑荷数无关的特性.
-
当太赫兹波入射到共享孔径超表面上, 反射超表面的切向电场表示为[25]
式中, AR和ψR是(x, y, 0)位置处反射超表面所需的电场振幅和相位分布, Am和ψm是反射超表面产生具有OAM模式lm和N子阵列数量的涡旋波束所需的电场振幅和相位分布, ϕ(x, y)是反射超表面相应方位角位置, 两个子阵列的单元按照下式规则交错排列:
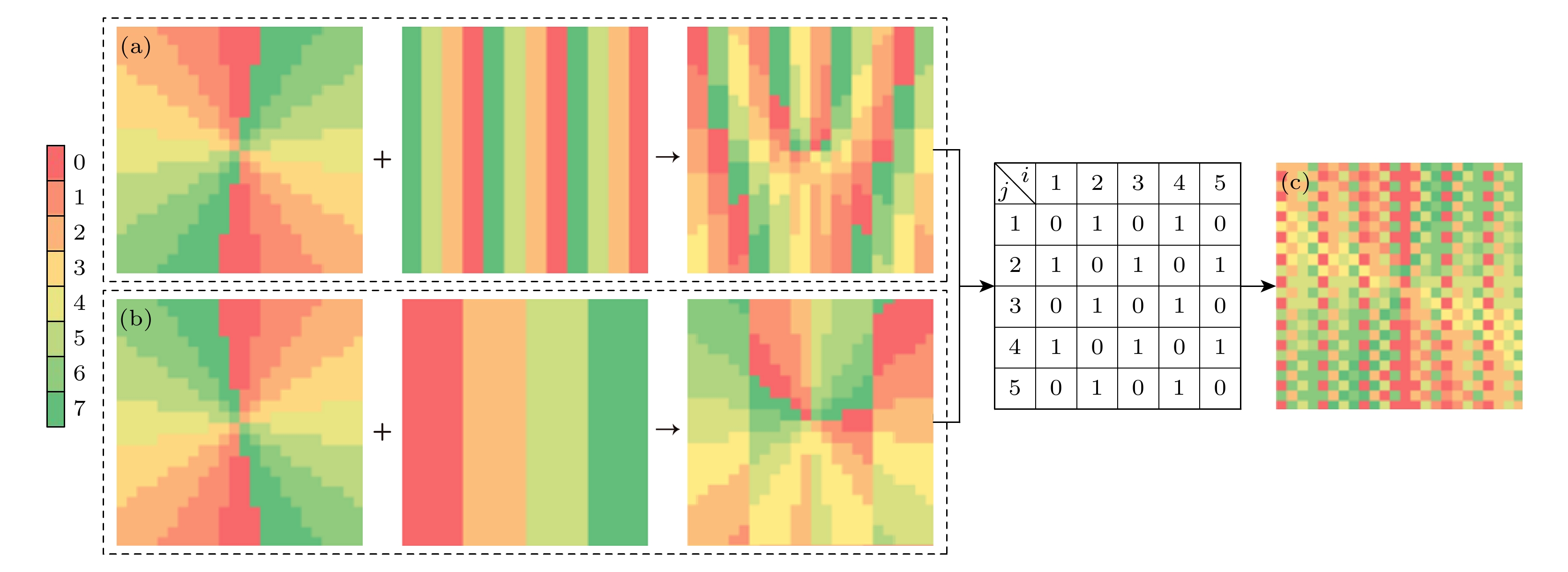
式中, N表示用于组成主阵列的子阵列数量, φ1—φN分别表示第1—N个子阵列的相位分布, i, j表示该相位对应单元在阵列中沿x轴和y轴的位置. 图14所示为具有不同拓扑荷双通道涡旋波束的超表面相位排布, 图14(a), (b)分别为左偏(l = 2)和右偏(l = –2)涡旋波束超表面相位分布图, 根据多通道传输原理排布, 图14(c)为双通道涡旋波束的超表面相位排布.
图15(a)所示为在频率1.1 THz处, LCP波入射, l = ±2双通道涡旋波束超表面的远场强度, 图15(b)所示为在频率1.1 THz处, RCP波入射, l = ±2双通道涡旋波束超表面的远场强度. 可看出, 该超表面将两个不同拓扑荷数和不同偏折角度的涡旋集成于一个超表面, 共享超表面的相同孔径.
-
本文提出弧度与旋转共同诱导相位调控超表面, 通过改变结构弧度尺寸和旋转单元结构, 对LCP波和RCP波的交叉极化反射相位进行独立调控, 根据相位卷积和共享孔径原理, 该超表面实现了多通道涡旋、聚焦、完美涡旋等功能, 有效提高了电磁空间的利用率, 对设计多功能超表面提供了一种方便有效的方法, 具有十分广阔的应用前景.
弧度与旋转共同诱导相位调控太赫兹超表面
Radian and rotation co-induced phase controlling terahertz metasurfaces
-
摘要: 传统编码超表面都是按照几何相位或传输相位理论来实现相位调控的, 然而几何相位具有自旋锁定特性, 传输相位具有单频特性, 限制了利用统一超表面同时调控几何相位和传输相位. 本文提出了一种弧度与旋转共同诱导相位调控超表面, 超表面单元能对左旋圆极化波(LCP波)和右旋圆极化波(RCP波)的交叉极化反射相位进行独立调控, 在1—1.2 THz范围内均满足要求. 通过相位卷积与共享孔径原理, 该超表面可以实现多通道涡旋、聚焦、完美涡旋等功能, 提高了电磁空间的利用率, 在未来太赫兹通信系统中具有广阔的应用前景.Abstract:
Metasurfaces have the characteristics of simple structure, easy fabrication, easy integration, etc., and can flexibly control electromagnetic waves. They are widely used in terahertz filters, lenses, polarization converters, wavefront adjustment and terahertz imaging and so on. By encoding and arranging unit cells with different amplitudes and phases according to a certain rule, the metasurfaces can achieve various functions such as imaging, focusing, beam splitting, and vortex beam. The reported coding metasurfaces are phase-modulated according to geometric phase or transmission phase theory. However, geometric phase has spin-locking property and transmission phase has single-frequency property, which hinder the applications of a unified metasurface in simultaneously regulating geometric phase and transmission phase. To address the above issues, in this work, we propose an radian and rotation co-induced phase modulation metasurface, whose unit cell independently modulates the cross-polarized reflection phases of LCP wave and RCP wave and has a certain bandwidth, which meets therequirement in a frequency region of 1–1.2 THz. Through the principle of phase convolution and shared aperture, the metasurface realizes the vortex beams with a topological charge of ±1, focusing with a focal length of 1500 μm, the deflected vortex beams with a topological charge of ±2, the quasi-perfect vortex beams, and the multichannel vortex beams. The structure has the advantages of simple structure, flexible and convenient regulation, and compact size, which improves the utilization of the electromagnetic space and has a broad application prospect in the future terahertz communication systems. -
Key words:
- terahertz metasurfaces /
- radian induction /
- geometrical phase /
- vortex /
- focus .
-
-
图 1 弧度与旋转共同诱导相位调控超表面及其功能示意图
Figure 1. Schematic diagram of the proposed metasurface and its function induced by both arc and rotation co-induced phase modulation.
图 3 超表面单元的反射系数与相位 (a) LCP入射下超表面单元反射系数; (b) LCP入射下超表面单元反射相位; (c) RCP入射下超表面单元反射系数; (d) RCP入射下超表面单元反射相位
Figure 3. Reflection coefficient and phase of the unit cells: (a) Reflection coefficients at LCP incidence; (b) reflection phases at LCP incidence; (c) reflection coefficients at RCP incidence; (d) reflection phases at RCP incidence.
图 4 (a) l = 1超表面相位分布; (b) l = 1的超表面排布; (c) l = –1超表面相位分布; (d) l = –1超表面排布
Figure 4. (a) The phase distribution of the metasurfaces at l = 1; (b) metasurfaces arrangement at l = 1; (c) the phase distribution of the metasurfaces at l = –1; (d) metasurfaces arrangement at l = –1.
图 5 (a), (e) LCP波入射下, l = 1涡旋波束远场图和模式纯度; (b), (f) RCP波入射下, l = 1涡旋波束远场图和模式纯度; (c), (g) LCP波下, l = –1涡旋波束远场图和模式纯度; (d), (h) RCP波入射下, l = –1涡旋波束远场图和模式纯度
Figure 5. (a), (e) Far-field patterns and mode purity of the vortex beam at l = 1 under LCP wave incidence; (b), (f) far-field patterns and mode purity of the vortex beam at l = 1 under RCP wave incidence; (c), (g) far-field patterns and mode purity of the vortex beam at l = –1 under LCP wave incidence; (d), (h) far-field patterns and mode purity of the vortex beam at l = –1 under RCP wave incidence.
图 6 (a) zf = 1500μm超表面聚焦相位排布; (b) 超表面结构
Figure 6. (a) Focusing phase arrangement of zf = 1500 μm metasurfaces; (b) metasurface structure.
图 7 (a) LCP波入射, zf = 1500 μm处x-y截面的二维电场; (b) LCP波入射, y = 0 μm处x-z截面的二维电场; (c) RCP波入射, zf = 1500 μm处x-y截面的二维电场; (d) RCP波入射, y = 0 μm处x-z截面的二维电场
Figure 7. (a) 2D electric field in x-y cross section at zf = 1500 μm under LCP wave incidence; (b) 2D electric field in x-z cross section at y = 0 under LCP wave incidence; (c) 2D electric field in x-y cross section at zf = 1500 μm under RCP wave incidence; (d) 2D electric field in the x-z cross section at y = 0 under RCP wave incidence.
图 8 (a) l = 2涡旋波束相位图; (b)“64206420…”偏折相位图; (c) l = 2偏折卷积涡旋波束相位图; (d) l = 2偏折涡旋波束超表面结构; (e) l = –2涡旋波束相位图; (f)“0022446600224466…”偏折相位图; (g) l = –2偏折卷积涡旋波束相位图; (h) l = –2偏折涡旋波束超表面结构
Figure 8. (a) Vortex beam phase diagram at l = 2; (b) ‘64206420…’ deflection phase diagram; (c) deflection convolution vortex beam phase diagram at l = 2; (d) deflection vortex beam metasurfaces structure at l = 2; (e) vortex beam phase diagram at l = –2, (f) ‘0022446600224466…’ deflected phase diagram; (g) deflected convolved vortex beam phase diagram at l = –2; (h) deflected vortex beam metasurfaces structure at l = –2.
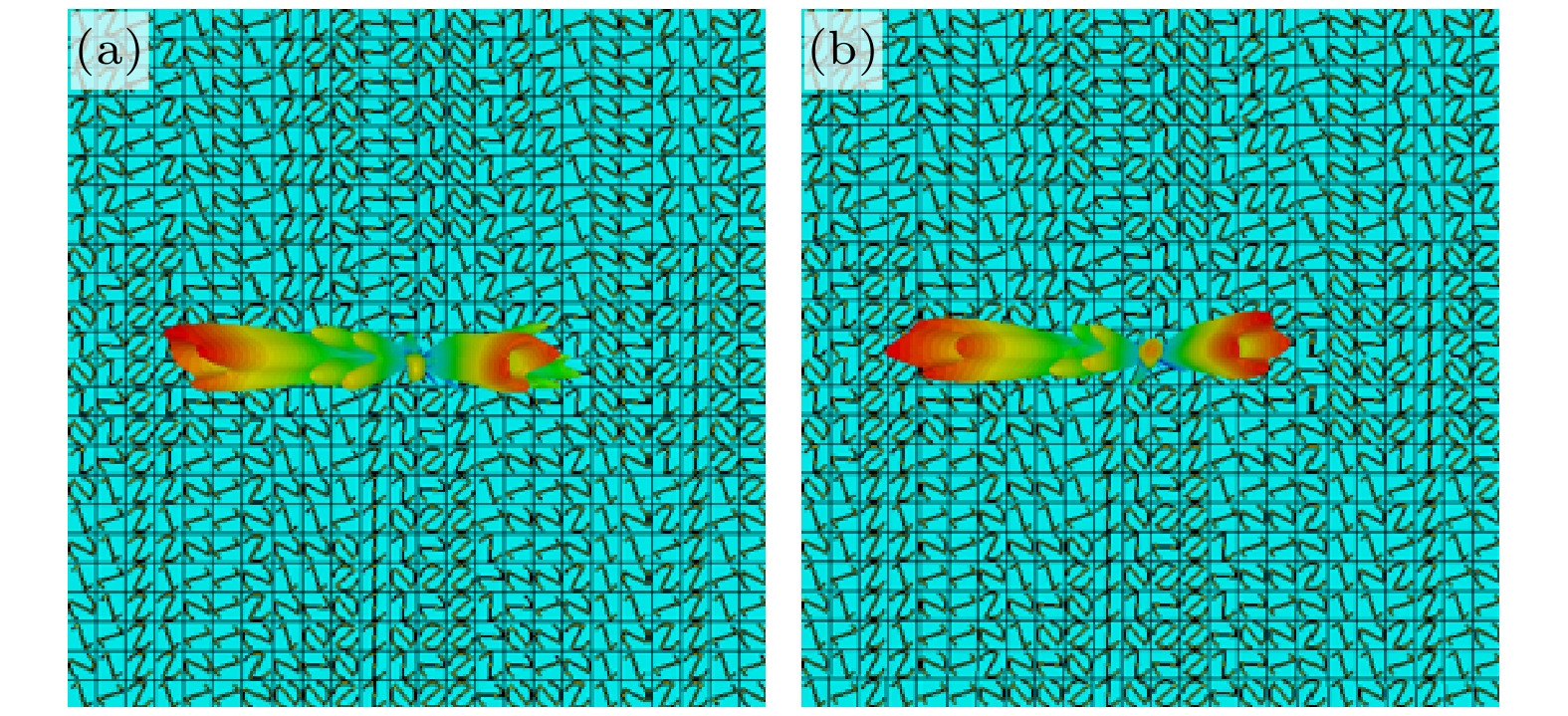
图 9 (a), (b) LCP波入射, l = 2偏折涡旋波束的远场和偏折角度; (c), (d) RCP波入射, l = 2偏折涡旋波束的远场和偏折角度; (e), (f) LCP波入射, l = –2偏折涡旋波束的远场和偏折角度; (g), (h) RCP波入射, l = –2偏折涡旋波束的远场和偏折角度
Figure 9. (a), (b) Far field and deflection angle of l = 2 deflected vortex beam under LCP wave incidence; (c), (d) far field and deflection angle of l = 2 deflected vortex beam under RCP wave incidence; (e), (f) far field and deflection angle of l = –2 deflected vortex beam under LCP wave incidence; (g), (h) far field and deflection angle of l = –2 deflected vortex beam under RCP wave incidence.
图 10 (a) zf = 1500 μm超表面聚焦相位; (b)“02460246…”偏折相位; (c)卷积后偏折聚焦相位; (d)偏折聚焦超表面结构
Figure 10. (a) zf = 1500 μm metasurfaces focusing phase, (b) ‘02460246…’ deflection phase, (c) deflection focusing phase after convolution, (d) deflection focusing metasurface structure
图 11 (a) LCP波入射, zf = 1500 μm处x-y截面的二维电场; (b) LCP波入射, y = 0 μm处x-z截面的二维电场; (c) RCP波入射, zf = 1500 μm处x-y截面的二维电场; (d) RCP波入射, y = 0 μm处x-z截面的二维电场
Figure 11. (a) 2D electric field in x-y cross section at zf = 1500 μm under LCP wave incidence, (b) 2D electric field in x-z cross section at y = 0 under LCP wave incidence, (c) 2D electric field in x-y cross section at zf = 1500 μm under RCP wave incidence, (d) 2D electric field in the x-z cross section at y = 0 under RCP wave incidence.
图 12 (a), (e)拓扑荷数为l = 1和 l = 2的涡旋相位排布; (b), (f)负轴向产生的反向贝塞尔光束的傅里叶变换相位排布; (c), (g) 焦透镜的相位排布; (d), (h) 拓扑荷数为l = 1和l = 2的完美涡旋相位排布
Figure 12. (a), (e) Vortex phase arrangement for the topological charges of l = 1 and l = 2; (b), (f) Fourier-transform phase arrangement of the inverted Bessel beam generated in the negative axial direction; (c), (g) phase arrangement of the focal lens; (d), (h) perfect vortex phase arrangement for the topological charges of l = 1 and l = 2.
图 13 (a) 拓扑荷数l = 1的完美涡旋波束电场强度分布; (b) 拓扑荷数l = 2的完美涡旋波束电场强度分布
Figure 13. (a) Electric field strength distribution of a perfect vortex beam for the topological charge of l = 1; (b) electric field strength distribution of a perfect vortex beam for the topological charge of l = 2.
图 14 (a)左偏 (l = 2) 涡旋波束的相位排布; (b) 右偏 (l = –2) 涡旋波束的相位排布; (c) 横向双通道涡旋波束的相位排布
Figure 14. (a) Phase arrangement of the left-biased vortex beam (l = 2); (b) phase arrangement of the right-biased vortex beam (l = –2); (c) phase arrangement of the transverse two-channel vortex beam.
图 15 (a) LCP波入射下, 频率1.1 THz处, l = ±2双通道涡旋波束的远场强度; (b) RCP波入射下, 频率1.1 THz处, l = ±2双通道涡旋波束的远场强度
Figure 15. (a) Far-field intensity of two-channel vortex beam (l = ±2) at 1.1 THz under LCP wave incidence; (b) far-field intensity of two-channel vortex beam (l = ±2) at 1.1 THz under RCP wave incidence.
-
[1] Feng C H, Otani C 2021 Crit. Rev. Food Sci. Nutr. 61 2523 doi: 10.1080/10408398.2020.1779649 [2] Song Z Y, Chen A P, Zhang J H 2020 Opt. Express 28 2037 doi: 10.1364/OE.376085 [3] Zhang Y B, Wu P H, Zhou Z G, Chen X F, Yi Z, Zhu J Y, Zhang T S, Ji H G 2020 IEEE Access 8 85154 doi: 10.1109/ACCESS.2020.2992700 [4] Hu X Z, Zheng D Y, Lin Y S 2020 Appl. Phys. A: Mater. Sci. Process. 126 110 doi: 10.1007/s00339-019-3274-5 [5] Liu X, Huang J, Chen H 2022 Photonics Res. 10 1090 doi: 10.1364/PRJ.451344 [6] Zhang Z, Wen D, Zhang C 2018 ACS Photonics 5 1794 doi: 10.1021/acsphotonics.7b01536 [7] Liu Y Q, Che Y X, Qi K N, Li L S, Yin H C 2020 Opt. Commun. 474 126061 doi: 10.1016/j.optcom.2020.126061 [8] Huang J, Fu T, Li H, Shou Z, Gao X 2020 Chin. Opt. Lett. 18 013102 doi: 10.3788/COL202018.013102 [9] Wang H, Zhang Z, Zhao K, Liu W, Wang P, Lu Y 2021 Chin. Opt. Lett. 19 053601 doi: 10.3788/COL202119.053601 [10] Ma Z J, Hanham S M, Gong Y D, Hong M H 2018 Opt. Lett. 43 911 doi: 10.1364/OL.43.000911 [11] Yang L J, Li J S, Yan D X 2022 Opt. Commun. 516 128234 doi: 10.1016/j.optcom.2022.128234 [12] Jiang Q, Jin G, Cao L 2019 Adv. Opt. Photonics 11 518 doi: 10.1364/AOP.11.000518 [13] Bao Y, Yan J, Yang X, Qiu C, Li B 2020 Nano Lett. 21 2332 doi: 10.1021/acs.nanolett.0c04485 [14] Gao P, Chen C, Dai Y W, Wang X L, Liu H 2023 Opt. Mater. 145 114448 doi: 10.1016/j.optmat.2023.114448 [15] Ma Z, Li P, Chen S, Wu X 2022 Nanophotonics 11 1847 doi: 10.1515/nanoph-2021-0714 [16] Zang X, Yao B, Chen L, Xie J, Guo X, Balakin A, Shkurinov A, Zhuang S 2021 Light: Adv. Manuf. 2 148 doi: 10.37188/lam.2021.010 [17] Li S, Li Z, Han B, Huang G, Liu X, Yang H, Cao X 2022 Front. Magn. Mater. 9 854062 doi: 10.3389/fmats.2022.854062 [18] Liu J, Cheng Y, Chen F, Luo H, Li X 2023 Infrared Laser Eng. 52 20220377 doi: 10.3788/IRLA20220377 [19] Fu C, Zhao J, Li F, Li H 2023 Micromachines 14 465 doi: 10.3390/mi14020465 [20] Sun S, Ma H F, Gou Y, Zhang T Y, Wu L W, Cui T J 2023 Adv. Opt. Mater. 11 2202275 doi: 10.1002/adom.202202275 [21] Fan J, Cheng Y 2020 J. Phys. D: Appl. Phys. 53 025109 doi: 10.1088/1361-6463/ab4d76 [22] Fu X M, Yang J, Wang J F, Ding C, Han Y J, Jia Y X, Liu T H, Zhu R C, Qu S B 2023 Laser Photonics Rev. 17 2200678 doi: 10.1002/lpor.202200678 [23] Zhang L, Liu S, Cui T 2017 Chin. Opt. 10 1 doi: 10.3788/co.20171001.0001b [24] Liu W, Yang Q, Xu Q, Jiang X, Wu T, Gu J, Han J, Zhang W 2022 Nanophotonics 11 3631 doi: 10.1515/nanoph-2022-0270 [25] Li J S, Guo F L, Chen Y 2023 Opt. Commun. 537 129428 doi: 10.1016/j.optcom.2023.129428 -
计量
- 文章访问数: 167
- HTML全文浏览数: 167
- PDF下载数: 3
- 施引文献: 0