非线性动力学作为一门研究非线性系统行为的学科, 近年来在科学与工程技术领域获得了广泛的应用^[1-4]. 相空间重构是非线性动力学研究的一个重要内容^[5]. 它为使用有限的一维时间序列数据分析复杂系统提供了基础. 对于一个非线性动力学系统, 随时间变化的系统状态是受整个系统的运动规律支配的. 由观测得到的一维时间序列隐含着整个系统的运动规律^[6-8]. 相空间重构就是利用这些一维时间序列重构非线性系统的动力学特性, 其依据是延迟嵌入维定理^[9]. 通过选择适当的时间延迟和嵌入维数, 将观测到的一维时间序列映射到高维相空间中^[10,11]. 相空间重构不仅可以帮助理解系统的演化轨迹和吸引子结构, 还可以为后续的动力学分析和系统特征参数计算提供基础. 传统的非线性特征算法由于观测得到的一维时间序列数据不足以完整描述系统的动力学特性, 因此需要借助相空间重构来弥补一维时间序列数据对系统描述不充分的问题, 从而对系统的动力学特性进行有效的表征^[12-14]. 通过对这些非线性特征参数进行计算和分析, 进而更全面地理解系统的动力学行为, 揭示系统内在的规律性和演化机制.

阵列技术在目标信号检测、方位估计等方面具有广泛应用^[15,16], 阵列技术的发展为非线性系统研究提供了新的思路. 利用多通道阵列数据可以对非线性系统进行更加准确的表征, 从而获得更加丰富的动力学信息. 然而, 在非线性动力学领域, 阵列数据对非线性特征的影响研究还有待深入. 从理论上分析, 虽然重构后的数据矩阵在结构上与阵列多通道数据相似, 但是相空间重构参数与阵列多通道数据之间的关系尚不明确. 多通道数据携带的更多信息是否可以给非线性特征参数的计算带来性能提升也值得研究.

本文选取多尺度样本熵^[17]与多尺度排列熵^[18]研究阵列数据对基于相空间重构的非线性算法的影响. 作为两种经典的非线性特征算法, 多尺度样本熵与多尺度排列熵分别从不同的角度对一维时间序列在时域上的结构特性进行了有效的表征. 随着研究的不断深入, 有学者对这两种算法进行了改进^[19,20], 改进后的算法被广泛应用于水声信号处理^[21]、机械故障诊断等领域^[22-24]. 虽然改进后的算法对信号结构特性的表征更加准确, 在对含噪信号的结构特性进行表征时具有更好的鲁棒性. 但是, 改进算法中复杂的预处理步骤会对熵值曲线产生干扰. 进而难以准确分析出阵列数据代替相空间重构对算法产生的影响.

本文首先从多通道数据结构的角度对相空间重构后的重构矩阵以及阵列数据进行了分析. 对比两种数据的数据结构, 给出了相空间重构中参数与阵列结构参数之间的对应关系. 具体来说, 对于阵列多通道数据, 阵元数与相空间重构中的嵌入维数是等价的. 而阵元间距、声速以及目标与阵列之间的夹角会对时间延迟产生影响. 进一步, 使用不同的仿真阵列数据与实际阵列数据, 分别使用其中一个通道的数据计算多尺度样本熵与多尺度排列熵结果. 再使用阵列数据直接代替相空间重构步骤计算对应熵值. 仿真与实际数据的分析结果表明, 使用阵列数据计算得到的多尺度样本熵曲线可以更好地对不同类型的信号进行区分. 而使用阵列数据计算得到的多尺度排列熵曲线可以更清晰地揭示信号在不同时间尺度上的复杂度结构特征, 证明了利用阵列数据代替相空间重构可以显著地提升非线性特征的性能. 本文的主要贡献如下: 1) 给出了相空间重构与阵列数据结构之间的关系; 2) 利用仿真实验分析证明了相空间重构后的数据结构与阵列数据结构之间的等效性; 3) 给出了一种新的基于阵列数据的非线性特征计算方法. 新计算方法不仅可以有效地提升不同类型信号的区分度, 还可以减少信号随尺度变化的波动, 更清晰地揭示信号随尺度变化的复杂度结构特征.

多尺度样本熵和多尺度排列熵是在样本熵和排列熵算法的基础上增加了粗粒化作为数据预处理步骤^[25,26]. 在样本熵算法中, 首先统计了时间序列中相似的两个长度为m的子序列, 再增加一个样本点后仍然保持相似的条件概率, 并计算了该条件概率的负自然对数作为时间序列复杂度的估计. 而排列熵算法则将数据重构为若干个长度为m的子序列, 并将这些子序列映射到m维序数模式空间中. 在序数模式空间中分析时间序列的结构特性, 以估计时间序列的复杂度.

给定一段长度为N的一维时间序列$ \{x_{i}\}, 1 \leqslant i \leqslant N $, 利用(1)式将$ \{x_{i}\} $分解到不同的时间尺度上:

式中, $ \{y_{i}^{(n)}\} $为粗粒化后的数据, 右上角标n为尺度因子, $ N_n $为$ N/n $向下取整. 下文中使用$ \{y_{i}\} $表示粗粒化后的数据, 省略尺度因子角标n.

得到粗粒化数据$ \{y_{i}\} $后, 给定嵌入维数m与时间延迟τ, 利用(2)式对粗粒化后的数据进行相空间重构:

对数据进行相空间重构得到$ {\boldsymbol{Y}}_{m}(i) $后, 定义相空间中任意两个不同向量之间的距离:

定义相空间中任意两向量之间的距离后, 设定$ {\mathrm{SD}}\times r $作为阈值, 其中r是阈值系数, $ {\mathrm{SD}} $是原始时间序列$ \{x_{i}\} $的标准差. 针对相空间中某一特定向量$ {\boldsymbol{Y}}_{m}(i) $, 计算其与相空间中其余向量之间的距离. 统计相空间中与向量$ {\boldsymbol{Y}}_{m}(i) $的距离小于给定阈值$ {\mathrm{SD}}\times r $的向量个数, 记为$ C^{m}_{i}(r) $. 利用(4)式即可计算出相空间中与向量$ {\boldsymbol{Y}}_{m}(i) $距离小于给定阈值的频率, 记为$ B^{m}_{i}(r) $:

在得到针对特定向量$ {\boldsymbol{Y}}_{m}(i) $的频率$ B^{m}_{i}(r) $后, 遍历相空间中的所有向量计算得到对应的$ B^{m}_{i}(r) $. 对所有的$ B^{m}_{i}(r) $求和取平均, 具体计算公式如下:

得到$ B^{m}(r) $后, 将嵌入维数由m变为m+1. 重复(2)式—(5)式计算得到对应的$ B^{m+1}(r) $. 则时间序列$ \{x_{i}\} $在尺度n上的样本熵值为

多尺度样本熵算法的计算步骤中, 分别重构了m维和m+1维相空间. 在重构出相空间后, 统计相空间中不同向量相似的频率. 最终计算的多尺度样本熵值本质上是两段长度为m的子序列在增加一个样本点后, 依然保持相似的条件概率的负自然对数. 由此可以看出, 多尺度样本熵表征的是时间序列在时域结构上的相关程度. 虽然这种时域结构上的相关程度可以在一定程度上侧面反映时间序列的复杂度, 但是并不能将两者混淆.

同样, 考虑长度为N的时间序列$ \{x_{i}\}, 1\leqslant i\leqslant N $, 利用(1)式对数据进行粗粒化处理后得到在尺度n上的粗粒化数据$ \{y_{i}\} $. 与多尺度样本熵算法类似, 给定嵌入维数m与时间延迟τ后, 利用(2)式进行相空间重构. 将相空间中所有向量中的各个元素按升序进行排列, 以向量$ {\boldsymbol{Y}}_{m}(i) $为例, 如(7)式所示:

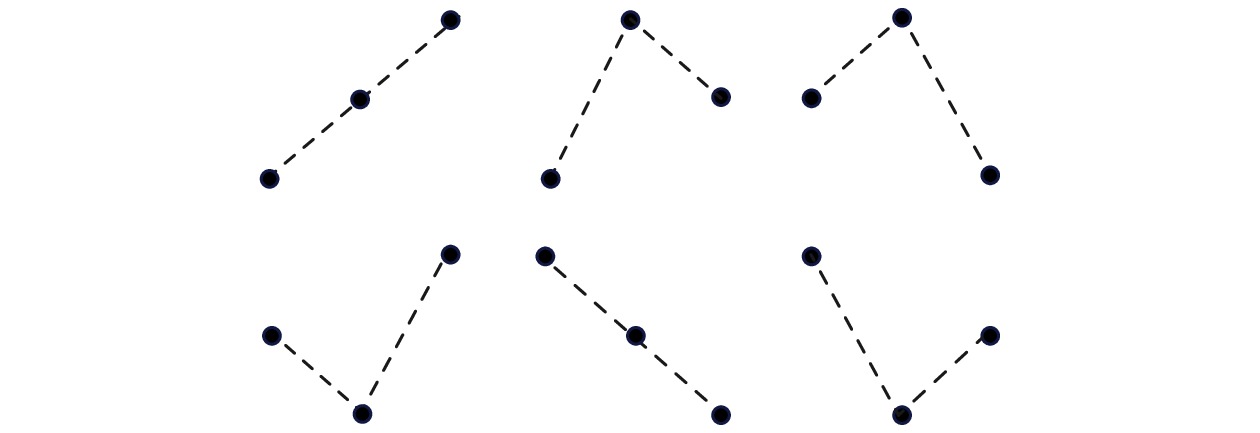
式中, $ k_1, k_2, \cdots, k_m $分别表示各元素的原始位置. 通过建立相空间中向量与序数模式$ \pi_{i} = [k_1, k_2, \cdots, k_m] $的对应关系, 将相空间中的所有向量映射到序数模式空间中. 一个m维的序数模式空间中共有$ m! $种可能的序数模式. 例如, 当$ m = 3 $时, 6种不同的序数模式的示意图如图1所示.

将相空间中所有向量映射到序数模式空间中后, 统计每种序数模式出现的频次$ h_l $, 并计算其出现的概率$ p_l = h_l/[N_n - (m - 1)\tau] $, 其中$ l = 1, 2, \cdots, m! $.

则多尺度排列熵的定义如下:

多尺度排列熵对不同时间尺度上时间序列的复杂程度进行了表征. 当相空间中仅存在一种序数模式时(时间序列单调递增或单调递减), 多尺度排列熵取最小值0; 当序数模式服从均匀分布时, $ p_l = 1/m!, \;l = 1, 2, \cdots, m! $, 多尺度排列熵取最大值$ \ln(m!) $. 因此在计算过程中, 可以对多尺度排列熵值进行归一化处理. 后文如无特殊说明, 多尺度排列熵值均为归一化后的结果.

由(2)式可知, 多尺度样本熵与多尺度排列熵算法在计算过程中将一维的时间序列重构为了一个$ m\times [N-(m-1)\tau] $的矩阵(尺度为1时). 将(2)式等号右侧展开如下:

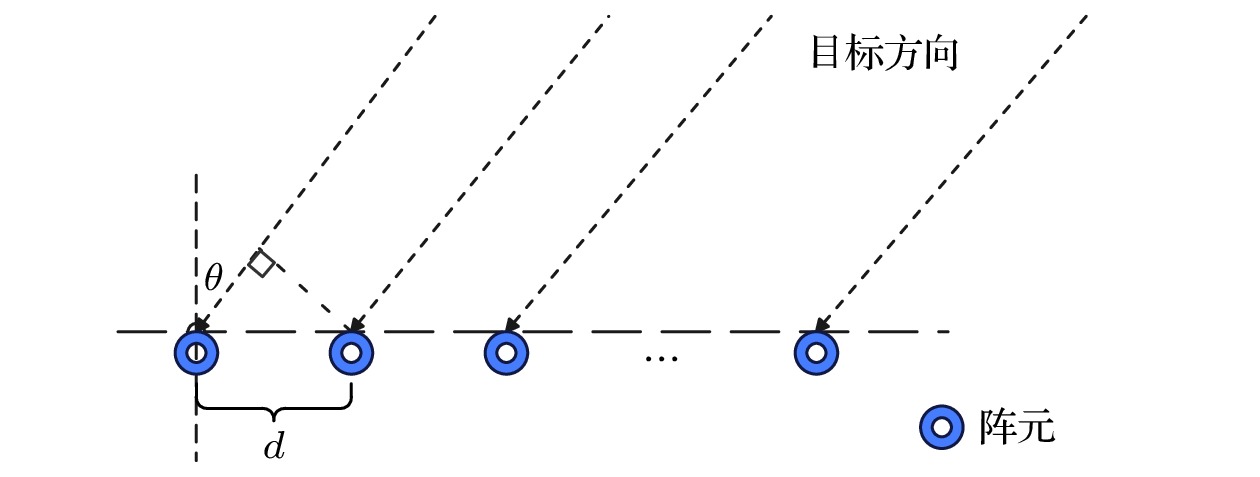
(9)式中的矩阵, 每一行是一个相空间中维数为m的向量, 而每一列则是时间序列$ \{y_i\} $的一段子序列. 并且在同一行中, 相邻两列的采样点相差固定的时间延迟τ. 这与由阵列采集到的多通道数据呈现出相似的结构特性. 以水下方位估计中的均匀线列阵为例, 假设阵元个数为$ m_{\mathrm{a}} $, 阵间距为d. 在远场条件下目标与阵列中心垂线的夹角为θ, 水下声速假设为c, 采样率为$ f_{\mathrm{s}} $. 线列阵结构示意图如图2所示.

由图2可以看出, 在远场条件下各个阵元的垂线方向与目标来波的方向夹角均为θ. 在阵间距、采样率和声速均已知的情况下, 可以根据(10)式求出相邻阵元之间的采样间隔$ \tau_{\mathrm{a}} $:

结合(9)式和图2, 可以观察到相空间重构后的数据结构与由均匀线列阵采集的数据结构相似. 需要特别注意的是, 与多尺度排列熵算法不同, 多尺度样本熵算法中包含了增加嵌入维数的步骤. 具体来说, 对于多尺度排列熵算法, 相空间重构中的参数m等效于均匀线列阵的阵元数$ m_{\mathrm{a}} $. 而对于多尺度样本熵算法, 初始相空间重构中的m与阵元个数$ m_{\mathrm{a}} $之间的关系是$ m = m_{\mathrm{a}}-1 $. 对于这两种熵算法来, 参数τ与阵间距d可以通过(10)式相互转化. 这意味着, 在多尺度样本熵和多尺度排列熵算法中, 相空间重构这一步骤本质上将一段一维的时间序列扩展为一个m维的阵列数据.

为了对比研究单通道数据与阵列数据对非线性特征参数的影响, 构造了由均匀线列阵采集到的远场多通道数据. 首先, 直接使用其中一个通道的数据, 并通过相空间重构技术将一维时间序列重构为多维相空间矩阵, 再计算其多尺度样本熵与多尺度排列熵. 接着, 跳过多尺度样本熵与多尺度排列熵算法中的相空间重构步骤. 直接使用阵列数据代替多维相空间矩阵, 再计算多尺度样本熵与多尺度排列熵值.

参考图2, 假设均匀线列阵阵元个数为5, 阵间距为5 m, 水中声速假设为1500 m/s, 目标信号假定为含有80 Hz, 210 Hz, 430 Hz线谱成分的连续波信号. 水听器采样率为5000 Hz, 目标与阵列垂直方向夹角设置为30°. 根据上述参数与(10)式的分析, 可以得出以下结论: 在使用多尺度样本熵时, 该均匀线列阵采集到的多通道数据与嵌入维数$ m = 4 $, 时间延迟$ \tau \approx 8 $的相空间重构数据具有相似的结构特征. 而在使用多尺度排列熵时, 该阵列数据与嵌入维数$ m = 5 $, 时间延迟$ \tau \approx 8 $的相空间重构数据具有相似的结构特征. 为了模拟实际环境, 在目标信号中加入高斯白噪声使信噪比为 0 dB. 分别使用多尺度样本熵与多尺度排列熵算法计算熵值, 并对比计算高斯白噪声的熵值, 以进行进一步的研究.

原始的多尺度样本熵和多尺度排列熵算法在计算过程中只需要使用单通道数据. 因此, 在第一组仿真实验中, 仅使用一个阵元采集到的一维时间序列进行分析. 相空间重构的参数设置遵循与实际阵列等效的参数设置, 即$ m_{{\mathrm{MSE}}} = 4,\; m_{{\mathrm{MPE}}} = 5, \tau = 8, r = 0.15 $. 其中$ m_{{\mathrm{MSE}}} $指多尺度样本熵算法中的嵌入维数, 而$ m_{{\mathrm{MPE}}} $指多尺度排列熵的嵌入维数. 数据长度为10000, 尺度因子范围为$ [1, 15] $. 对含噪信号和高斯白噪声分别独立重复进行10次试验, 得到多尺度样本熵与多尺度排列熵的误差图结果. 具体如图3所示.

从图3(a) 可以观察到, 在使用单通道数据计算多尺度样本熵时, 由于信噪比较低, 含噪目标信号的熵值曲线与高斯白噪声的熵值曲线相似. 随着尺度因子的增大, 两种曲线逐渐减小. 值得注意的是, 含噪信号的熵值结果方差明显大于高斯白噪声的熵值结果方差. 因此, 在计算多尺度样本熵时, 仅使用单通道数据难以有效区分两种不同的信号. 然而, 从图3(b) 的多尺度排列熵结果可以看出, 随着尺度因子的增大, 含噪目标信号的熵值出现明显的波动. 整体上, 含噪目标信号的熵值小于高斯白噪声的熵值. 因此, 多尺度排列熵能够有效地区分这两种信号.

在使用阵列数据计算多尺度样本熵和多尺度排列熵的结果时, 相较于直接使用单通道数据计算, 计算过程变得更为复杂. 从上述分析可以看出, 利用阵列数据可以直接替代原始多尺度样本熵和多尺度排列熵算法中的相空间重构步骤. 直观上, 这似乎只是一个简单的数据替代问题. 然而, 在仿真实验中, 还有以下几个问题需要额外关注.

1) 首先需要考虑的是加入高斯白噪声时遇到的问题. 在构造阵列仿真数据时, 我们要在目标信号中加入一定信噪比的高斯白噪声. 当仅使用一个通道的数据来计算多尺度样本熵和多尺度排列熵时, 可以直接将高斯白噪声加入生成的目标信号中. 然而, 在阵列数据的情况下, 构造仿真阵列数据的过程是先生成一段信号, 然后利用滑动窗口每隔时间间隔τ截取出每个通道的数据. 因此, 确定何时加入高斯白噪声变得尤为关键.

当使用相空间重构技术将一维数据扩展为阵列数据时, 由于一维数据事先已经加入了高斯白噪声, 因此在重构后的数据中相邻两列的采样点应严格满足关系$ y_{i+\tau, j} = y_{i, j+1} $. 其中, $ y_{i, j} $表示相空间重构后矩阵中第i行第j列的样本点(参考(9)式). 然而, 在实际阵列数据采集过程中, 每个通道接收到的高斯白噪声是相对独立的, 因此不满足上述关系. 为了更好地模拟实际采集到的阵列数据, 在构造阵列仿真数据时首先构造具有固定时间延迟的阵列数据, 然后为每一个通道分别加入相同功率的高斯白噪声.

2) 接下来需要考虑的是粗粒化过程. 在使用单通道数据计算多尺度样本熵和多尺度排列熵时, 首先对数据进行粗粒化处理, 将数据分解到不同的时间尺度. 然后, 在这些不同的时间尺度上进行相空间重构, 并计算相应的熵值. 然而, 在实际的阵列数据采集过程中, 首先获取整个阵列的数据, 接着需要对每一个通道的数据进行粗粒化预处理. 值得注意的是, 对于每个通道的数据, 在进行粗粒化处理之前, 需要先加入相应通道的高斯白噪声.

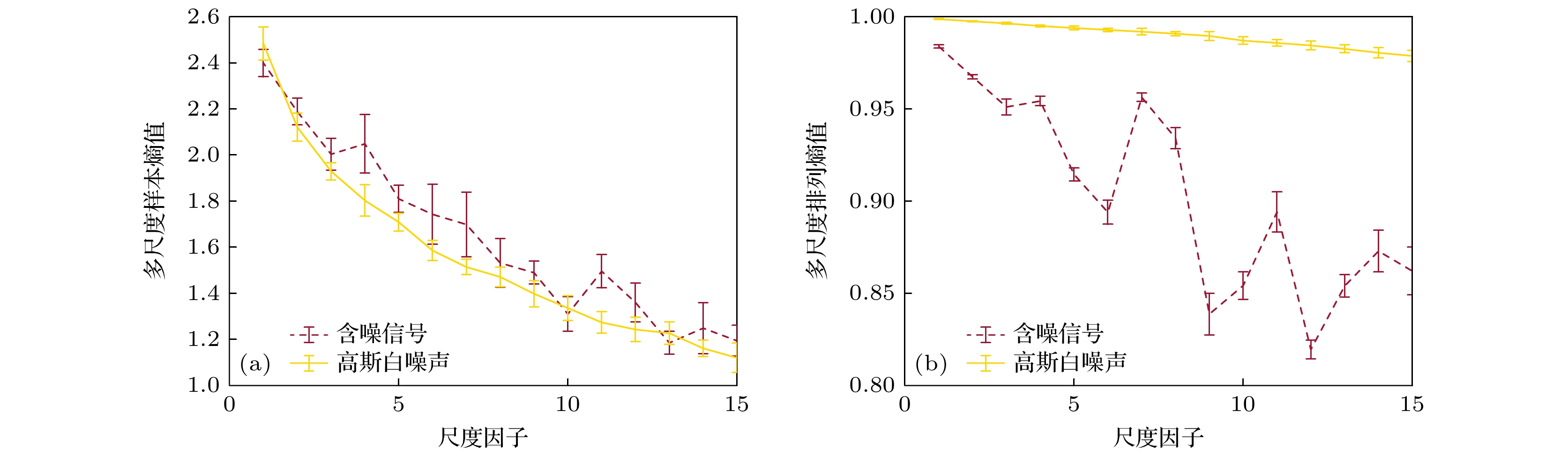
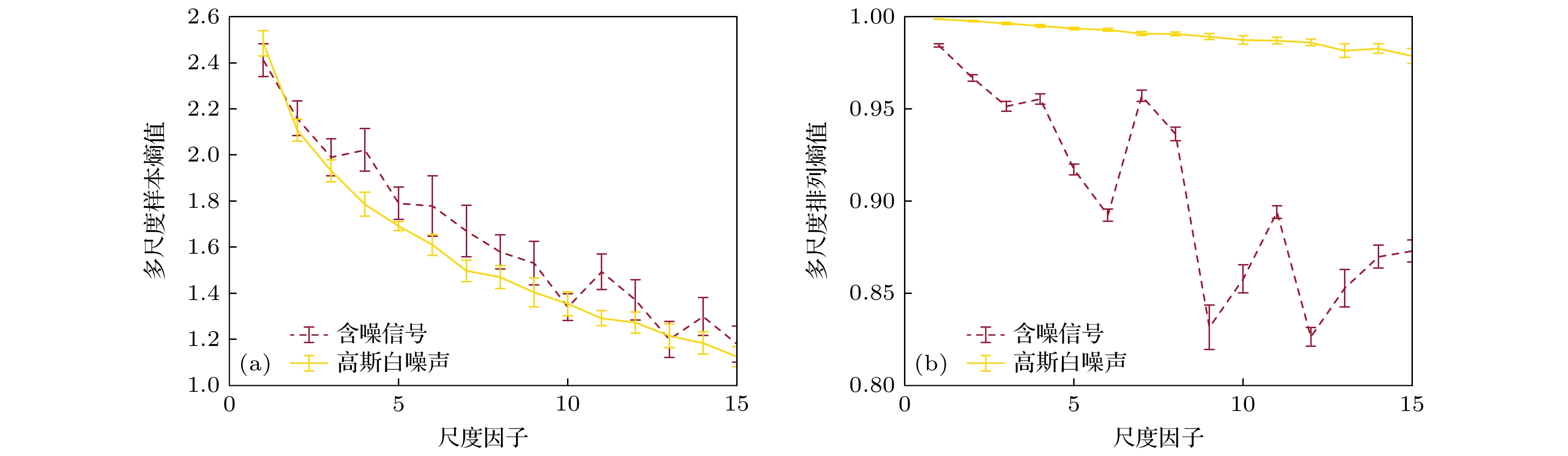
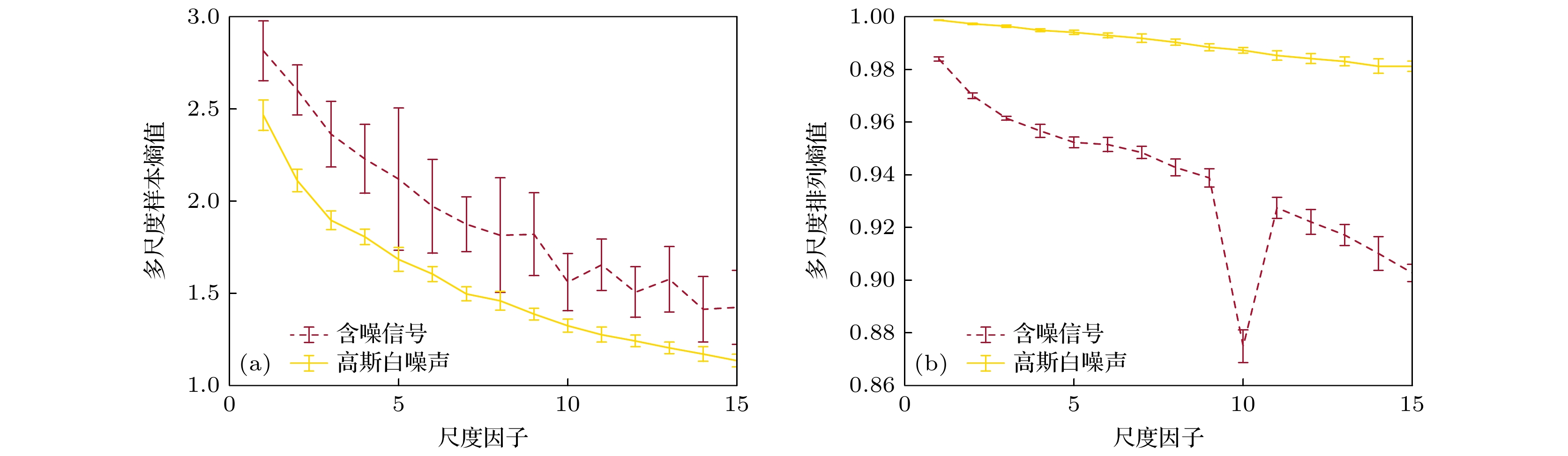
为了更好地对比使用单通道数据和仿真阵列多通道数据计算的熵结果, 设计了两组多通道数据的仿真实验. 第一组实验中的阵列多通道数据是按照相空间重构的逻辑严格构造的. 首先, 生成一个包含80 Hz, 210 Hz, 430 Hz线谱成分的连续波信号, 连续波信号的长度需大于10000. 在该信号中加入信噪比为0 dB的高斯白噪声. 接着, 按照不同的尺度因子n对一维数据进行粗粒化处理, 并使用长度为$ \lfloor 10000/n\rfloor $的滑动窗将一维数据转换为阵列多通道数据, $ \lfloor \cdot \rfloor $表示向下取整. 使用这些构造的阵列多通道数据替代多尺度样本熵算法和多尺度排列熵算法中的相空间重构步骤, 并计算相应的熵值. 其余未额外说明的计算参数与图3的仿真实验设置相同, 实验结果如图4所示. 将图4的结果与图3进行对比, 可以看出无论是多尺度样本熵还是多尺度排列熵, 其熵值曲线的整体趋势和波动都与单通道情况下的熵值曲线相一致. 通过对比图4与图3的结果, 证明了相空间重构技术本质上是将一维的时间序列重构为多维阵列数据, 从而弥补数据获取量不足的缺陷, 进而能够对复杂系统进行有效的非线性动力学分析.

第二组多通道数据的仿真实验在构造仿真阵列数据时, 采取了更符合实际情况的构造方法. 首先生成含有80 Hz, 210 Hz, 430 Hz线谱成分的一维连续波信号, 信号长度大于10000. 利用长度为10000的滑动窗将一维数据构造为阵列多通道数据, 给每个通道加入信噪比为 0 dB的高斯白噪声. 得到含噪的阵列连续波信号数据后, 利用粗粒化过程处理每一个通道的数据. 最后, 直接利用粗粒化后的多通道阵列数据计算对应的多尺度样本熵与多尺度排列熵结果. 其余计算参数均保持不变, 具体结果如图5所示. 图5(a)中的多尺度样本熵曲线与图4(a)中的多尺度样本熵曲线相比, 虽然含噪信号的方差增大, 但是含噪信号和高斯白噪声熵值曲线的均值差更大, 且熵值随尺度变化的趋势更加平缓, 从而更好地实现了对不同类型信号的区分. 而图5(b)中的多尺度排列熵曲线与图4(b) 中的多尺度排列熵曲线相比, 含噪信号的熵值曲线有较大差异. 虽然图4(b)和图5(b)中的含噪信号熵值曲线整体都呈现出下降的趋势, 但是图5(b) 中的曲线波动幅度更大. 且图5(b)中含噪信号的熵值曲线在尺度10出现局部极小值, 而在图4(b)中在尺度6, 9, 12处出现局部极小值. 两幅图并没有明显的对应关系.

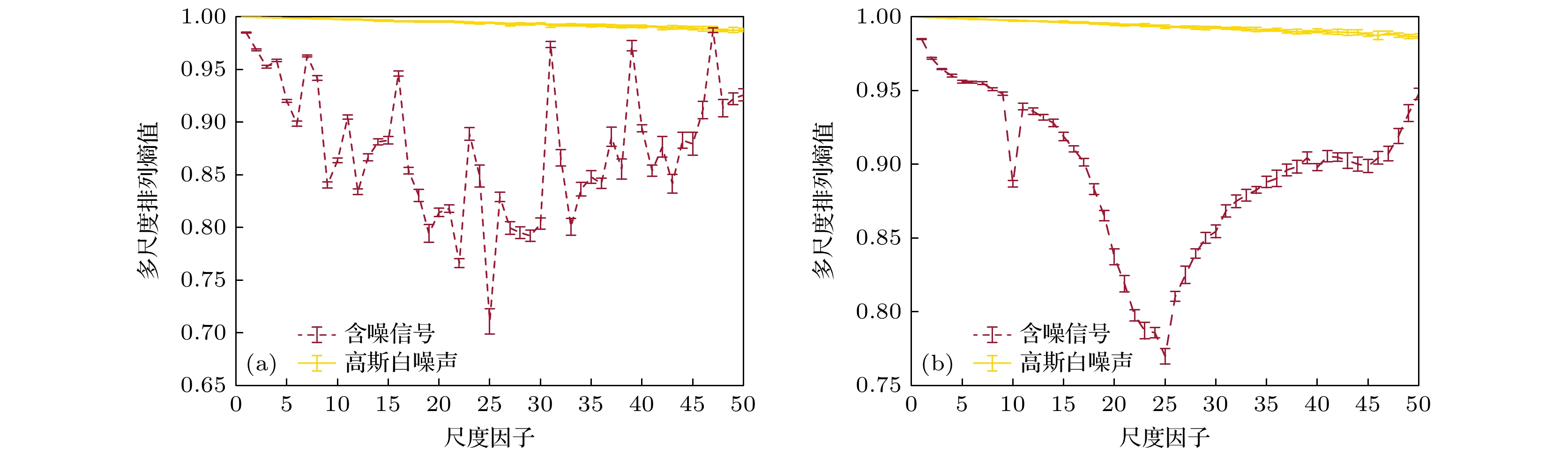
多尺度排列熵算法与多尺度样本熵算法相比, 对数据长度的要求更低. 因此在计算多尺度排列熵时, 通常可以选取较大的尺度范围从而更全面地分析数据在不同时间尺度上的复杂度结构特性. 因此, 本文分别在图4(b) 和图5(b) 的仿真实验基础上改变计算参数. 将每个通道的数据长度增大到50000, 尺度范围从$ [1, 15] $增大到$ [1, 50] $, 其余参数不变. 具体多尺度排列熵结果如图6所示.

对比图6的两个多尺度排列熵结果可以看出, 当尺度范围增大后, 信号在不同时间尺度上的结构特征被更完整的揭示出来. 图6(a), (b)的含噪信号多尺度排列熵结果曲线都呈现出先减小后增大的趋势. 在图6(b)中, 含噪信号的曲线在尺度$ [1, 9] $和$ [11, 24] $范围内逐渐减小, 在尺度$ [26, 44] $和$ [46, 50] $范围内逐渐增大. 并且, 曲线分别在尺度10, 25, 45处出现局部极小值. 反观基于相空间重构的多尺度排列熵曲线结果, 虽然整体上曲线的趋势也呈现出先减小后增大的特征, 并且在尺度25处出现局部极小值. 但是由于曲线整体不稳定导致无法有效的对数据在不同时间尺度上的结构特征进行分析, 并且无法清晰地观察到位于尺度10和45处的局部极小值.

本文使用3种由线列阵采集到的不同类型的实际多通道数据, 分别为两类不同的舰船辐射噪声和海洋背景噪声. 线列阵的阵元个数为5, 阵间距为5 m, 采样频率为9960 Hz. 由于实测数据无法精确获得目标与阵列垂直方向的夹角, 进而无法计算出理论上相邻阵元之间的时间延迟, 因此采用互相关函数计算两类舰船辐射噪声多通道数据中相邻阵元的时间延迟. 通过计算得到相邻通道间数据的互相关函数结果. 互相关函数取最大值时对应的时间延迟即认为是相邻阵元间的时间延迟. 表1列出了计算结果.

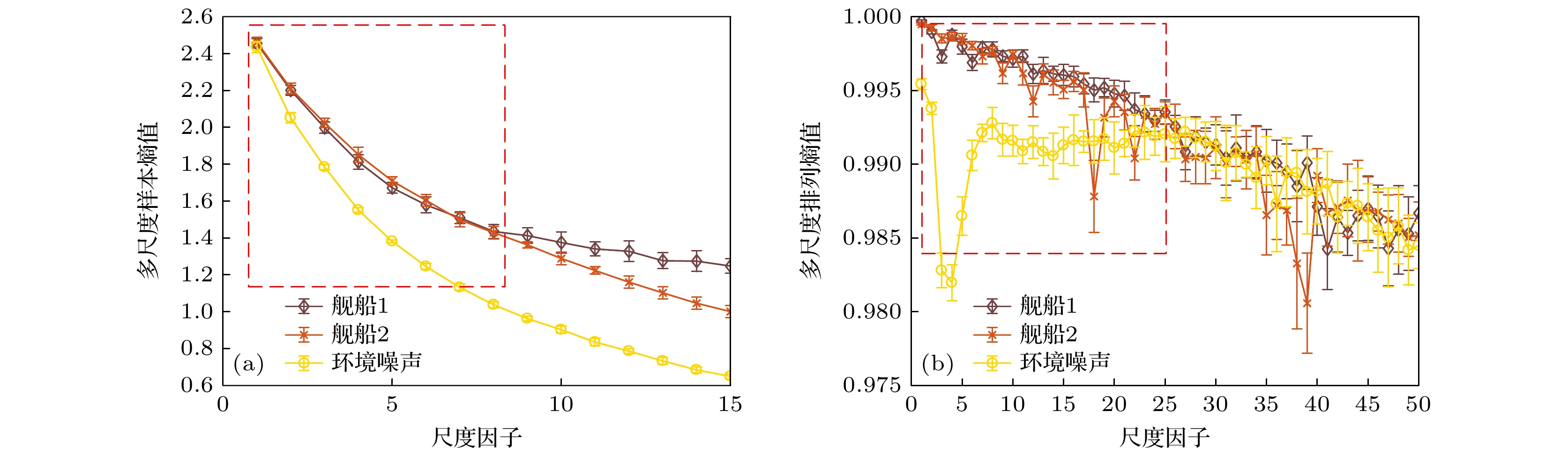
海浪波动以及人为测量误差等因素导致相邻通道之间的时间延迟不严格相等, 因此计算所有通道间时间延迟的均值并取整. 综上, 在计算多尺度样本熵时, 舰船1的阵列数据近似等效为嵌入维数$ m = 4 $, 时间延迟$ \tau \approx21 $的相空间重构后数据; 舰船2的阵列数据近似等效为嵌入维$ m = 4 $, 时间延迟$ \tau \approx 20 $的相空间重构后数据. 而在计算多尺度排列熵时, 舰船1的阵列数据近似等效为嵌入维数$ m = 5 $, 时间延迟$ \tau \approx21 $的相空间重构后数据; 舰船2的阵列数据近似等效为嵌入维$ m = 5 $, 时间延迟$ \tau \approx20 $的相空间重构后数据.

首先, 仅利用其中一个通道的数据直接计算多尺度样本熵与多尺度排列熵结果, 数据长度为20000, 多尺度样本熵的尺度因子范围为$ [1, 15] $, 多尺度排列熵的尺度因子范围为$ [1, 50] $. 相空间重构的参数设置遵循与实际阵列等效的参数设置, 即$ m_{{\mathrm{MSE}}} = 4, \;m_{{\mathrm{MPE}}} = 5, \;\tau_1 = 21,\; \tau_2 = 20,\; \tau_n = 1, r = 0.15 $. 其中, $ \tau_1 $是舰船1的时间延迟, $ \tau_2 $是舰船2的时间延迟, 而$ \tau_n $是环境噪声的时间延迟. 重复10次实验, 绘制多尺度样本熵与多尺度排列熵的误差图, 结果如图7所示.

图7(a) 的多尺度样本熵结果表明, 多尺度样本熵可以有效区分舰船与环境噪声. 然而, 仅依靠多尺度样本熵无法有效区分不同类型的舰船辐射噪声. 虽然当尺度大于8时, 两类舰船辐射噪声的多尺度样本熵曲线开始出现分离. 但由于两类舰船辐射噪声的多尺度样本熵曲线的整体均值过于相似, 在实际应用中, 仅使用一个通道的数据计算得到的多尺度样本熵曲线无法有效的对不同类型的舰船辐射噪声进行区分. 对于多尺度排列熵, 仅使用一个通道数据计算得到的多尺度排列熵曲线也同样并不理想. 信号的剧烈波动使得无法通过多尺度排列熵曲线区分两类不同的舰船. 虽然在低尺度下, 环境噪声与舰船辐射噪声的区别相对明显, 但随着尺度的增大, 无法有效区分舰船与环境噪声.

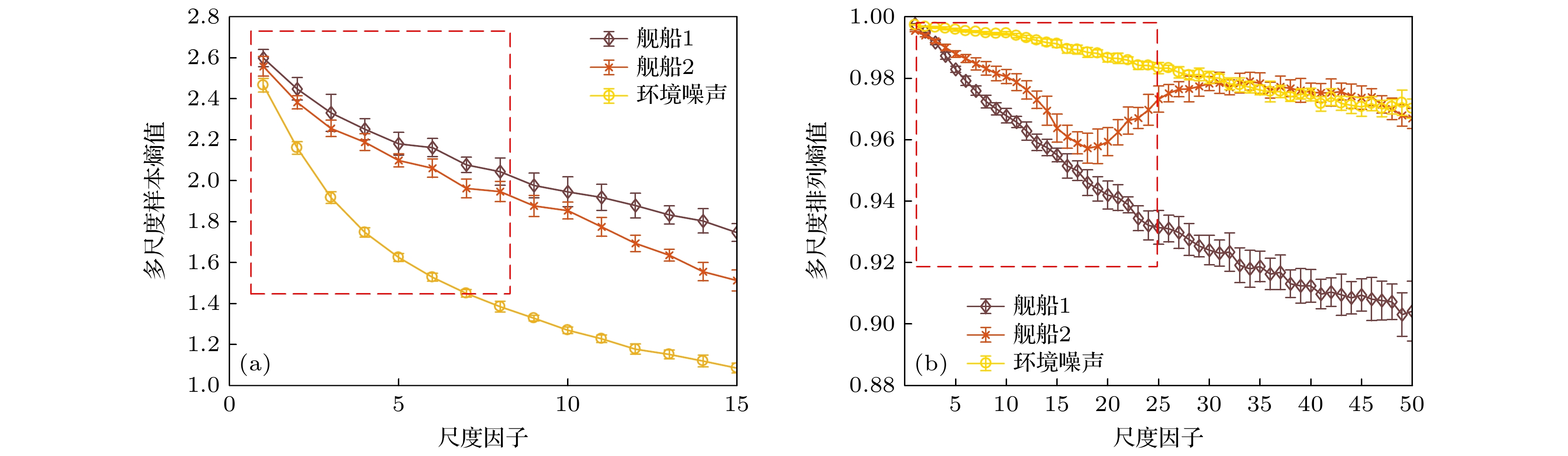
接下来, 使用由阵列采集到的多通道数据. 数据为5通道数据, 每个通道内有20000样本点. 采用与图5仿真实验相同的计算思路, 利用多通道数据代替多尺度样本熵与多尺度排列熵算法中的相空间重构步骤, 计算不同类型实际多通道数据的多尺度样本熵值与多尺度排列熵值. 多尺度样本熵尺度范围为$ [1, 15] $, 多尺度排列熵的尺度因子范围为$ [1, 50] $, 阈值系数$ r = 0.15 $. 重复进行10次实验, 结果如图8所示.

对比图8(a)与图7(a), 可以看到使用阵列数据计算得到的两类舰船辐射噪声的多尺度样本熵结果在尺度大于1时就有明显的区别. 在图8(a)的虚线矩形框中, 两种舰船辐射噪声的熵值曲线有明显区别. 而图7(a)中, 在尺度小于8时利用多尺度样本熵曲线是无法区分两种舰船辐射噪声的. 并且可以注意到, 图8(a)使用阵列数据计算得到的熵值曲线在均值、方差以及整体随尺度变化的趋势并没有出现明显变化的基础上对不同类型信号的区分度更好. 实测数据分析结果与仿真实验中的结果(图3(a), 图4(a), 图5(a))相一致. 这说明, 利用阵列数据代替相空间重构计算多尺度样本熵时, 阵列数据中更丰富的信息使得算法可以有效的对两种相似的信号进行区分. 而对比图8(b)与图7(b) 的多尺度排列熵曲线可以看出, 利用图8(b)的多尺度排列熵曲线可以有效区分舰船1, 舰船2与环境噪声. 图7(b)中两类舰船辐射噪声的熵值曲线近乎完全重叠, 并且随尺度变化出现了剧烈波动. 图8(b)中的熵值曲线明显比图7(b)的更加平稳. 在图8(b)的虚线框中, 三类信号的熵值曲线也有明显的差异. 这说明使用阵列数据计算得到的多尺度排列熵曲线对三类实测数据的区分度更高. 当尺度较大时, 虽然数据长度缩短, 但是使用阵列数据计算得到的多尺度排列熵曲线方差较小. 这也说明了使用阵列数据计算得到的多尺度排列熵结果更加稳定.

本文对比了相空间重构后的数据矩阵与阵列采集到的多通道数据在结构上的特征, 并定量分析了相空间重构参数与实际阵列参数之间的对应关系. 在仿真实验中, 首先利用仿真阵列数据的其中一个通道计算了多尺度样本熵和多尺度排列熵曲线. 结果显示, 当信噪比为0 dB时, 多尺度样本熵仅用一个通道数据难以有效区分含噪目标信号和高斯白噪声, 而多尺度排列熵由于与噪声曲线均值存在显著差异, 仅用一个通道数据即可有效区分两种不同的信号. 接下来, 构造了多通道仿真数据, 确保其与通过相空间重构生成的单通道数据在结构上保持一致. 将这些多通道数据直接代替了多尺度样本熵和多尺度排列熵算法中的相空间重构, 并计算了相应的熵值曲线. 结果证实了在特定条件下, 相空间重构技术与阵列采集的多通道数据是等价的. 进一步地, 构造了更符合实际情况的阵列数据, 并分别使用多尺度样本熵和多尺度排列熵算法计算了含噪目标信号与高斯白噪声的熵值. 对比分析表明, 由于阵列数据包含更多的目标系统信息, 使用阵列数据代替相空间重构步骤可以有效提升算法性能.

本文还使用了3组不同类型的多通道实际数据, 分别利用多尺度样本熵与多尺度排列熵进行分析. 结果表明, 仅使用单个通道数据计算得到的多尺度样本熵与多尺度排列熵曲线无法有效的对不同类型的实际数据进行区分. 而直接使用阵列数据代替相空间重构后, 多尺度样本熵和多尺度排列熵曲线均可以有效的区分不同类型的实际数据. 证明了多通道数据含有的丰富信息可以有效地提升传统基于单通道数据与相空间重构技术的非线性特征算法性能.