基于介观动理学理论的格子Boltzmann方程(LBE)方法是多相流模拟的一类有效研究手段, 如今已发展出多种有效的LBE模型^[1–4]. 然而, 常规多相LBE模型还存在一些根本问题, 如界面捕获不准确和虚假速度问题等. 理论上, 当系统达到平衡状态时, 化学势应为常数, 流体失去驱动力从而速度为零. 然而, 在现有许多多相LBE模型中, 界面附近的虚假速度无法完全消除^[5–13]. 一般情况下, 虚假速度远小于问题的特征速度, 对模拟的影响较小, 但在某些情况下, 虚假速度会导致数值不稳定和非物理现象, 例如, 伪势模型^[7,8]的两相密度分布会明显偏离麦克斯韦共存曲线, 相场模型^[9]中也观察到了类似的非物理现象.

为了确定虚假速度来源并减轻其影响, 人们已经做出了多种尝试. 例如, Cristea和Sofonea^[10]认为有限差分型LBE模型产生虚假速度的原因在于计算演化方程中空间导数的一阶迎风格式, 他们引入了一个修正力项用于解决这个问题. Wagner^[11]将虚假速度归因于作用力的离散化, 并指出使用势形式的表面张力可以消除虚假速度. 然而, 该方法存在数值不稳定问题, 需要加入与数值黏度和速度有关的校正项来改善. Shan^[12]指出伪势模型中的虚假速度来源于作用力项中梯度算子离散格式的各向同性不足. 基于这个观点, Sbragaglia等^[13]开发了高阶各向同性离散格式, 降低了伪势模型的虚假速度.

以往研究表明, LBE的虚假速度来源于离散误差产生的虚假力. Guo等^[14]对自由能LBE模型进行了严格的数学分析, 得出了总力不平衡方程. 结果表明, 理想气体压力梯度和表面张力在离散尺度上的不平衡导致了虚假速度. 随后Guo^[15]进一步得出了不平衡净力的结构, 提出了能完全消除虚假速度的精准平衡(well-balanced, WB) LBE模型. Zhang等^[16]在此基础上提出了改进模型, 提高了数值稳定性. 受WB-LBE模型的启发, Zheng 等^[17]提出了相场模型中平衡力的处理方式, 通过重构与Navier-Stokes方程对应的LBE, 建立了相场WB-LBE模型. 最近, Ju等^[18]通过分析发现, 相场LBE模型的虚假速度来自求解相场Cahn-Hilliard(CH)方程的LBE, 并重新设计了相应的LBE, 建立了另一种相场WB-LBE模型.

目前已有的相场WB-LBE模型已被证明能够很好地消除虚假速度. 然而, 上述相场WB-LBE模型都是基于不可压相场模型开发的, 当两种流体具有不同密度时, 无法保证局部质量守恒^[19]. Yang和Guo^[3]基于准不可压相场模型^[20]提出了能满足局部质量守恒的LBE模型, 但仍会产生较大的虚假速度. 因此, 本文的目的在于构建一个基于准不可压相场理论的WB-LBE模型.

本文安排如下. 第2节将简要介绍准不可压相场LBE模型; 第3节将分析虚假速度的来源, 提出精确平衡的LBE模型, 并通过Chapman-Enskog(CE)展开验证了所提出模型的平衡性质; 第4节将给出基础算例来验证我们的模型; 第5节为总结部分.

相场理论用自由能函数来描述两相系统的热力学行为, 它可以由标记不同相流体的序参数$ \phi $表示:

其中$ \psi \left(\phi \right) $是体相自由能密度, $ \kappa $是表面张力系数, $ \varOmega $是控制体积. 对于两相系统, 体相自由能密度可以采用双势阱的形式^[21]:

其中$ {\phi }_{1} $和$ {\phi }_{2} $分别为第1相和第2相的序参数, 一般有$ {\phi }_{1}=1 $和$ {\phi }_{2}=0$. $ \beta $是与$ \kappa $相关的常数, 它们满足以下关系:

其中$ \sigma $为表面张力, $ W $表示界面厚度. 根据自由能函数可以得到化学势$ \mu $, 即:

序参数的演化满足Cahn-Hilliard (CH)方程:

其中$ \boldsymbol{u} $是流体速度, $ \lambda $是迁移系数.

在不可压相场理论中, 描述流体的控制方程还包括不可压Navier-Stokes (NS)方程:

其中$ p $是动力学压力; $ \boldsymbol{F}={\boldsymbol{F}}_{{\mathrm{s}}}+\boldsymbol{G} $是总力, 包括表面张力$ {\boldsymbol{F}}_{{\mathrm{s}}} $和外部体积力$ \boldsymbol{G} $. Zhang等^[4]指出, 表面张力采用势能形式时, 可以得到更小的虚假速度. 因此, 如无特别说明, 我们在模拟中均使用$ {\boldsymbol{F}}_{{\mathrm{s}}}=-\phi {{\nabla}} \mu $形式的表面张力, 并利用各向同性中心差分格式(41)离散梯度算子. $ \rho $和$ \nu $分别是混合流体的密度和运动黏度, 采用线性混合规则可以表示为

其中$ {\rho }_{1} $和$ {\rho }_{2} $分别表示第1相和第2相流体的密度, $ {\nu }_{1} $和$ {\nu }_{2} $分别表示第1相和第2相流体的运动黏度. 由于$ \phi $的实际物理意义为第1相的体积分数, 根据密度的定义, 混合密度一般采用线性混合规则, 而黏度则可采用不同的混合方法, 如倒数规则、指数规则和阶跃规则等, 将在后文进行比较. 上述模型已在多相流领域得到广泛应用. 然而, 将(7)式和(9a)代入(6)式中会得到:

显然, 当$ {\rho }_{1}\ne {\rho }_{2} $时, 不可压相场模型无法保证局部质量守恒.

准不可压相场模型^[20]不再假设速度散度为0, 而是取

其中$ \gamma $是和两相密度相关的系数, 可表示为

将(9)式、(11)式和(12)式代入(6)式中, 可以得到:

这表明准不可压相场模型严格满足局部质量守恒.

Yang和Guo^[3]基于准不可压相场理论给出了相应的LBE模型, 使用两套分布函数分别描述流动和相场, 求解NS方程和CH方程的LBE分别为

式中$ {f}_{i}\left(\boldsymbol{x}, t\right) $和$ {g}_{i}\left(\boldsymbol{x}, t\right) $表示在$ t $时刻位于$ \boldsymbol{x} $处的$ i $方向的分布函数, 分别为压力分布函数和序参数分布函数; $ \tau_f $和$ \tau_g $分别是黏度和迁移系数相关的无量纲松弛时间; $ {f}_{i}^{{\mathrm{e}}{\mathrm{q}}} $和$ {g}_{i}^{{\mathrm{e}}{\mathrm{q}}} $为平衡态分布函数, 定义为

其中

这里$ \alpha $为可调参数, 一般取为1; $ {c}_{{\mathrm{s}}} = c/\sqrt{3} $是格子声速; $ {\omega }_{i} $为权系数; $ {\boldsymbol{e}}_{i} $是第$ i $个离散速度. 以D2Q9模型为例, 权系数为$ {\omega }_{0} = 4/9 $, $ {\omega }_{1-4} = 1/9 $和$ {\omega }_{5-8} = 1/36 $, 离散速度为$ {\boldsymbol{e}}_{0}=\left({\mathrm{0, 0}}\right) $, $ {\boldsymbol{e}}_{1-4}=c\left\{{\mathrm{cos}}\left[\left({\mathrm{i}}-1\right) {{\pi }}/ 2\right], {\mathrm{sin}}\left[\left({\mathrm{i}}-1\right){\mathrm{\pi }}/2\right]\right\} $以及$ {\boldsymbol{e}}_{5-8} = \sqrt{2}c\left\{{\mathrm{cos}}\left[\left(2{\mathrm{i}}-1\right) {\mathrm{\pi }}/4\right], \sin \left[\left(2{\mathrm{i}}-1\right){\mathrm{\pi }}/4\right]\right\} $, 其中$ c={\delta }_{x}/{\delta }_{t} $, $ {\delta }_{x} $和$ {\delta }_{t} $分别为空间和时间步长. $ {F}_{i} $和$ {G}_{i} $是源项, 定义为

宏观量包括压力$ p $、速度$ \boldsymbol{u} $和序参数$ \phi $, 可通过下式统计得到:

通过Chapman-Enskog (CE)展开, 模型可恢复宏观方程, 同时得到运动黏度和迁移系数的计算式:

为方便, 我们称上述LBE模型为YG-LBE模型.

与大多数两相LBE模型类似, YG-LBE模型也存在虚假速度. Ju等^[18]分析发现, 其根源在于求解CH方程的LBE中平衡态和源项在离散尺度上不平衡. 该模型通过CE展开所恢复的宏观方程为^[18]

其中

显然$ {\varGamma }_{1} $和$ {\varGamma }_{2} $的表达式相同, 通常可以认为它们相互抵消. 然而$ {\varGamma }_{1} $产生于LBE的碰撞迁移过程, 源于平衡态分布函数; 而$ {\varGamma }_{2} $是源项中的添加项, 目的是为了消除$ {\varGamma }_{1} $. 但二者实质上来源不同, 在数值网格上其离散模板不同, 因此会产生非零的化学势梯度, 从而导致虚假速度的出现.

上述分析表明, 产生$ {\varGamma }_{1} $和$ {\varGamma }_{2} $的根源在于平衡态分布函数(17)引入了$ {s}_{i}\left(\boldsymbol{u}\right) $来恢复CH方程中的对流项${{\nabla}} \cdot \left(\phi \boldsymbol{u}\right) $. ${s}_{i}\left(\boldsymbol{u}\right) $导致了$ {\varGamma }_{1} $的出现, 因此需要引入人工项$ {\varGamma }_{2} $来抵消它. 解决办法是^[18]移除平衡态分布函数中的$ {s}_{i}\left(\boldsymbol{u}\right) $, 通过重新设计源项来恢复准确的对流项. 这样$ {\varGamma }_{1} $不再出现, 也就不再需要人工项$ {\varGamma }_{2} $. 基于上述思路, 我们重新设计了求解CH方程的LBE, 发展了一个基于准不可压相场理论的精确平衡模型.

求解CH方程的新LBE为^[22]

其中平衡态分布函数不再包含$ {s}_{i}\left(\boldsymbol{u}\right) $, 定义为

为了准确恢复CH方程, 新的源项定义为

序参数的计算式为

为分析LBE (29)式对应的宏观方程, 对其进行CE分析. 首先引入如下的多尺度展开:

对(29)式应用Taylor展开, 可以得到:

其中$ {D}_{i}={\partial }_{t}+{\boldsymbol{e}}_{i}\cdot {{\nabla}} $. 将(33)式和(34)式代入(35)式中, 可以得到不同尺度上的方程:

根据(36b)式, 可将(36c)式写为

根据平衡态分布函数$ {g}_{i}^{{\mathrm{e}}{\mathrm{q}}} $和源项$ {G}_{i} $的定义, 可以得到如下的速度矩:

对(36b)式和(37)式求零阶矩, 并利用(38)式, 可以得到:

联立(39a)式和(39b)式, 得到如下的CH方程:

从上述推导中可以看到, 当前模型在恢复宏观方程的过程中避免了不平衡项的产生, 可以实现离散尺度上的精确平衡.

为了计算方便并保证二阶空间精度, 本文均采用各向同性中心差分格式来离散梯度算子和Laplace算子:

其中$ \phi $可以是任意物理量.

为方便, 本文称该模型为well-balanced (WB)-LBE模型.

本节将模拟几个典型算例, 验证WB-LBE的性能, 并与YG-LBE模型进行比较.

首先模拟了一个$ x{\text{-}}y $坐标系下的平界面问题. 计算区域是一个$ {L}_{x}\times {L}_{y}=30\times 128 $的矩形区域, $ {L}_{x} $和$ {L}_{y} $分别为区域宽度和高度. 计算网格为$ {N}_{x}\times {N}_{y}=30\times 128 $. 初始时第1相分布在中心区域, 其余空间充满第2相. 初始的序参数根据下式设置:

其中$ {y}_{1}={N}_{y}/4 $和$ {y}_{2}=3{N}_{y}/4 $分别是第1相所在区域的下边界和上边界; $ W $是界面厚度, 在本文中均设置为$ W=4 $. 模拟中, 四个边界均设置为周期边界. 第1相流体的密度和运动黏度分别为$ {\rho }_{1}=10 $和$ {\nu }_{1}=0.1 $, 而第2相流体的密度和运动黏度分别为$ {\rho }_{2}=1.0 $和$ {\nu }_{2}=0.1 $; 表面张力$ \sigma =0.005 $, 迁移系数$ \lambda =0.1 $.

为了便于比较, 我们用系统的总动能$ E $来表征虚假速度的大小, 总动能定义为

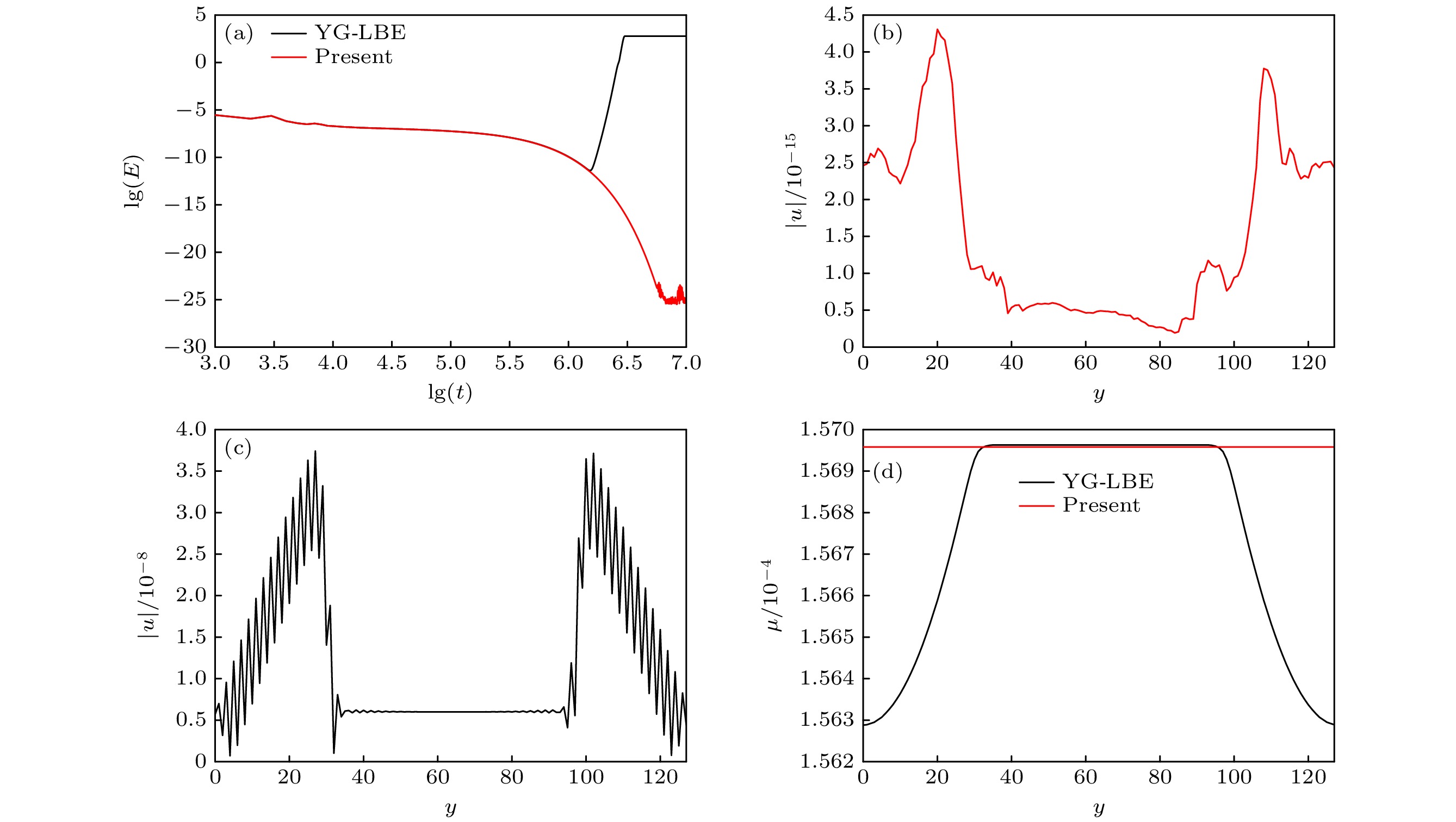
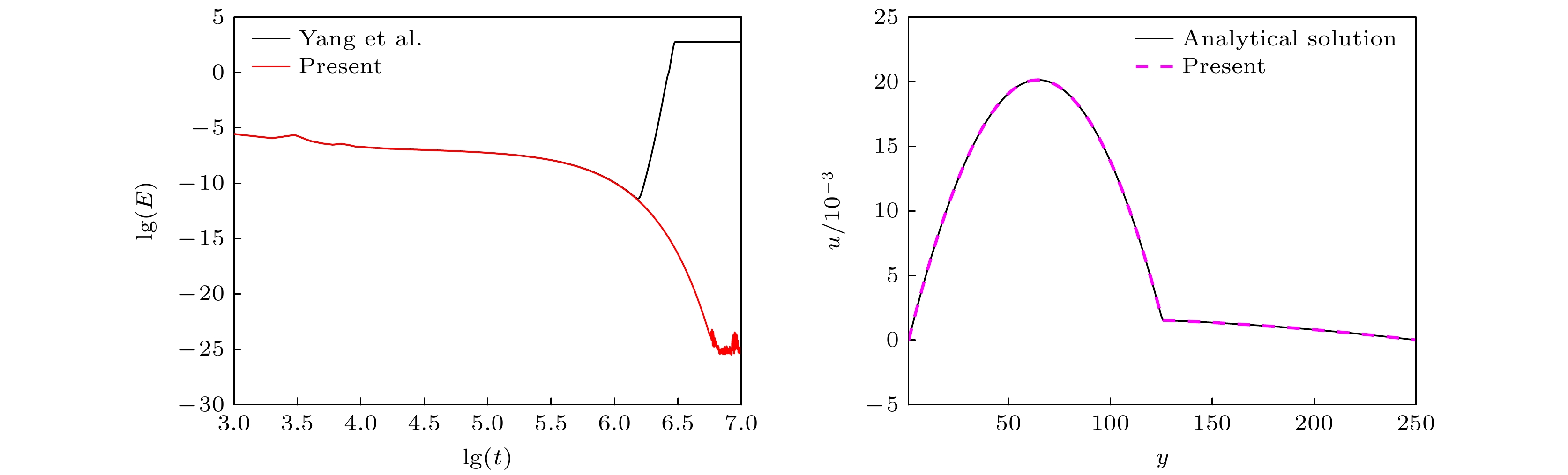
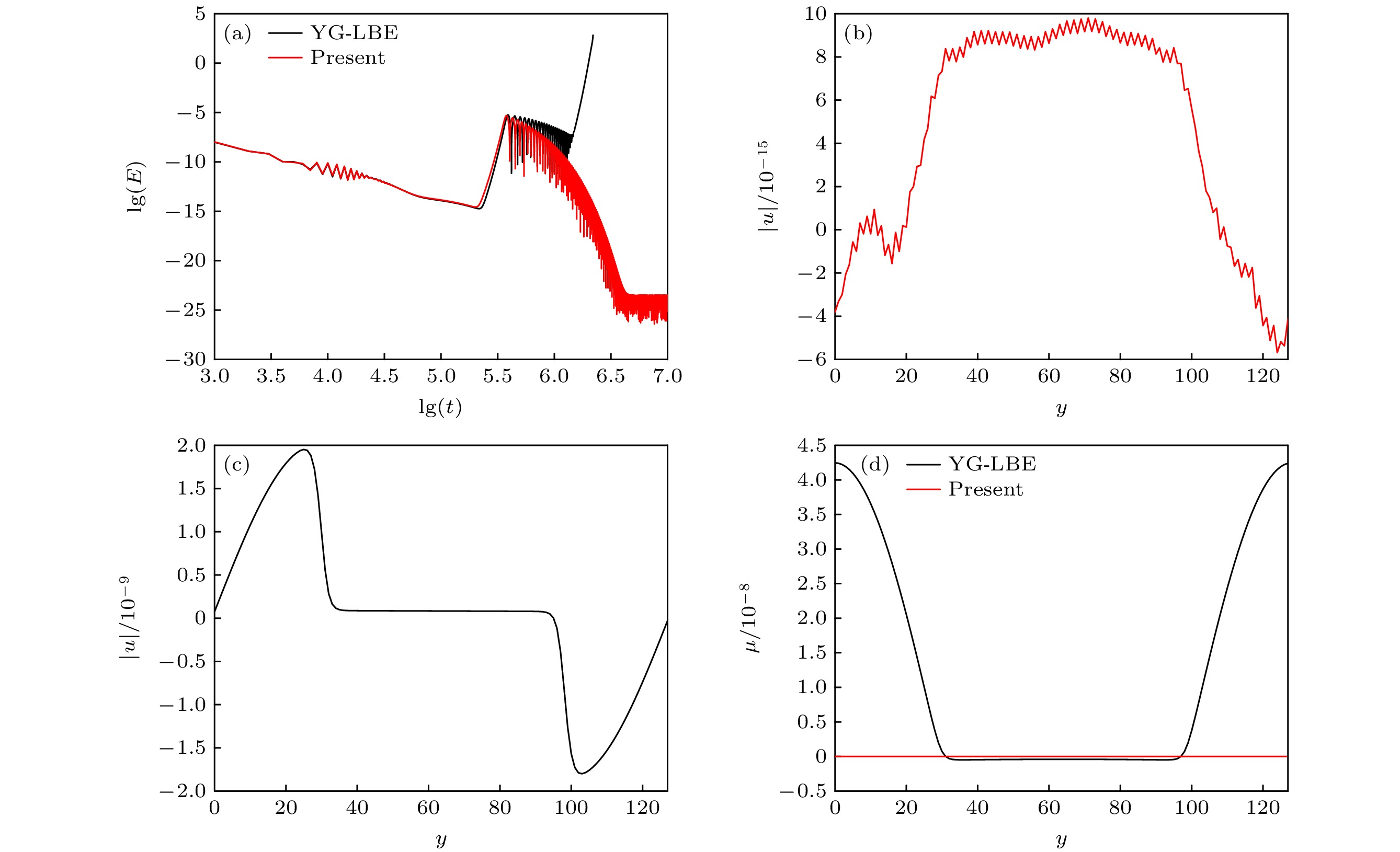
其中$ \varOmega $表示计算域. 图1给出了本文模型(WB-LBE)与YG-LBE模型的结果. 图1(a)给出了总动能$ E $随时间步$ t $的演化过程. 由图1(a)可以看出, 在大约$ t={10}^{6} $前, 二者的总动能变化趋势相同, 都是先随时间减小到约$ {10}^{-15} $量级, 再升高到约$ {10}^{-5} $量级, 然后开始随时间逐步减小. 然而在$ t={10}^{6}—{10}^{6.5} $之间某个时刻之后, YG-LBE的总动能再次迅速升高, 直到数值发散. 而WB-LBE总动能不断减小, 最终稳定在约$ {10}^{-25} $量级. 图1(b)给出了稳态时WB-LBE的速度分布. 由图1(b)可以发现, 虚假速度在$ {10}^{-15} $量级, 达到了机器精度. YG-LBE即使是在前期总动能降到最低的时刻(图1(c))其最大虚假速度仍然在$ {10}^{-9} $量级. 图1(d)给出了总动能达到最低时两个模型所得的化学势分布. 可以看到, YG-LBE模型的化学势有$ {10}^{-8} $量级的变化, 而本文模型的化学势基本保持常数, 其变化量级在$ {10}^{-15} $.

我们进一步模拟了一个二维稳态液滴问题. 液滴半径为$ R $, 计算域为$ {N}_{x}\times {N}_{y}=128\times 128 $. 用第1相表示液滴, 半径$ R={N}_{x}/4 $, 初始时置于计算域中心, 其他位置充满第2相流体. 序参数初始化为

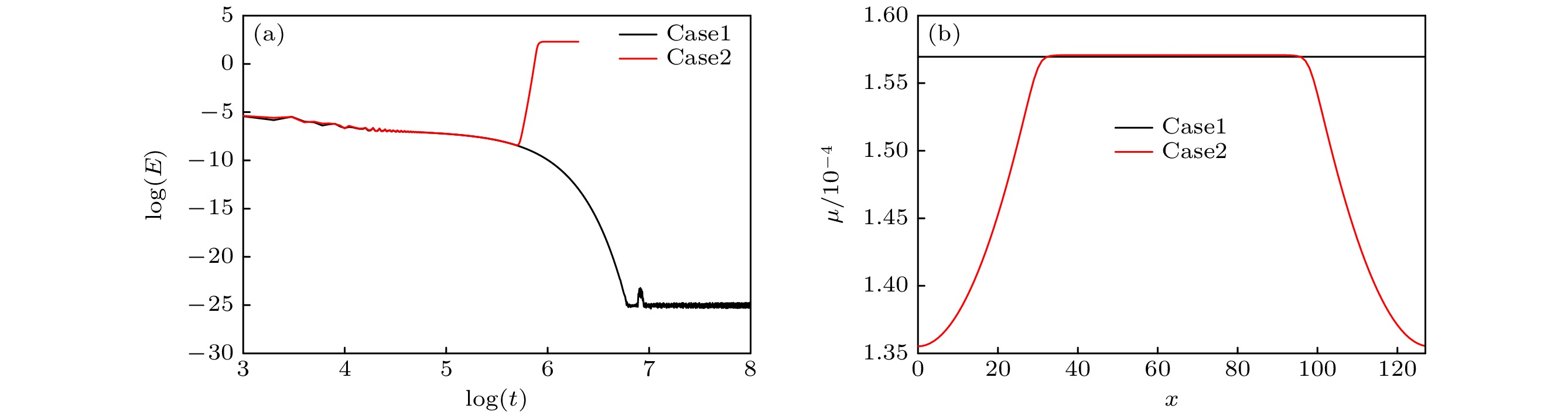
其中$ \left({x}_{{\mathrm{c}}}, {y}_{{\mathrm{c}}}\right)=\left({N}_{x}/2, {N}_{y}/2\right) $是初始时液滴圆心所在位置坐标. 模拟中, 对四个边界均采用周期边界, 其他参数和前述平界面问题一致.

我们比较了本文WB-LBE模型和YG-LBE模型的结果, 如图2所示. 图2(a)给出的总动能时间演化过程与平界面问题的有所不同, 不再有先减小后快速增大的阶段, 而是一个近乎单调下降的过程. 与平界面问题类似的是, 在$ t={10}^{6}—{10}^{6.5} $之间某个时刻之后, YG-LBE模型的结果中$ E $随时间快速增大, 直到稳定在$ {10}^{2} $量级, 此时虚假速度极大. 本文的WB-LBE模型计算的总动能$ E $则不断随时间减小, 最终稳定在约$ {10}^{-25} $量级. 从图2(b)给出的速度分布可以看出, 此时虚假速度在$ {10}^{-15} $量级, 达到了机器精度. 而在$ E $达到最低时, 图2(c)所展示的YG-LBE模型的虚假速度仍然在$ {10}^{-8} $量级. 从图2(d)给出的化学势分布还能发现, 在$ E $达到最低时, YG-LBE模型的化学势有$ {10}^{-7} $量级的变化, 而WB-LBE模型的化学势基本保持恒定. 上述比较均说明了当前模型可以达到精确平衡状态.

下面我们比较两种形式的表面张力对模型性能的影响. 这两种表面张力的表达式如下^[4]:

结果如图3所示, 其中case1和case2分别使用了(45a)式和(45b)式计算表面张力. 图3(a)给出了两种情况下总动能的时间演化过程. 由图3(a)可以看到, case1中总动能下降到了$ {10}^{-25} $量级, 而case2中总动能在中途突然升高, 最终稳定在较高水平. 这说明使用(45b)式形式的表面张力无法消除虚假速度. (45a)式和(45b)式这两种势能形式的表面张力通常被认为是等价的, 然而在平衡状态下, (45b)式无法保证化学势为常数, 从而无法实现精确平衡. 图3(b)给出了两种情况下的化学势分布, 可见case1中化学势为常数, 而case2中化学势有明显变化.

上述模拟均使用了线性黏度混合规则. 前面提到, 黏度的混合规则还包括倒数规则、指数规则和阶跃规则, 分别是

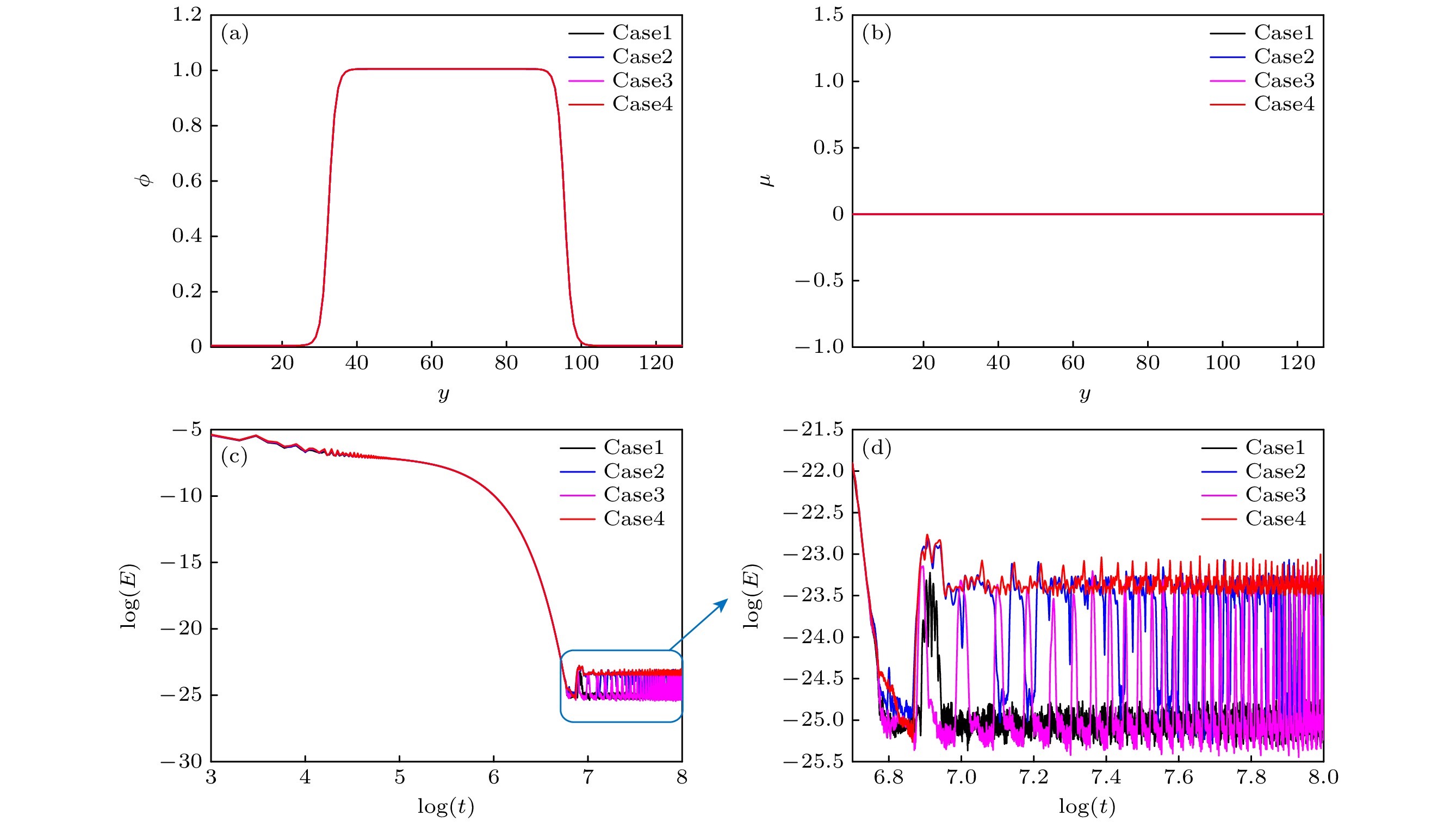
为了比较它们对模型性能的影响, 我们增大了黏度比, 令$ {\nu }_{1}=0.1 $, $ {\nu }_{2}=0.01 $, 其他参数保持不变. 图4比较了不同混合规则的结果, 其中case1—case4分别使用了(9b)式、(46a)式、(46b)式和(46c)式来计算混合黏度. 从图4(a)可以看到, 四种情况下的序参数分布完全一致, 说明不同黏度混合规则对于本问题的界面捕捉性能没有明显影响. 图4(b)给出了化学势的分布, 可以看到, 四种情况的化学势也均为常数, 且等于一个相同的值. 图4(c), (d)给出了总动能的时间演化及其局部放大图, 可以看到, 在虚假速度方面, 不同黏度混合规则展现出了一定的差别, case1和case4的总动能最终分别稳定在了$ {10}^{-25} $和$ {10}^{-23} $量级, case2和case3的总动能最终在$ {10}^{-25} $和$ {10}^{-23} $量级之间波动.

本节计算了分层泊肃叶流问题. 计算域设置为$ {N}_{x}\times {N}_{y}=64\times 250 $, 上下边界为无滑移固体边界, 使用修正反弹格式实现无滑移边界, 左右边界为周期边界. 计算域的上半部分充满第1相, 下半部分充满第2相. 流动由沿$ x $方向的恒定外力$ {G}_{x}={10}^{-7} $驱动. 模拟时, 设置两相密度为$ {\rho }_{1}={\rho }_{2}=1.0 $, 运动黏度分别为$ {\nu }_{1} = 1.0 $和$ {\nu }_{2} = 0.1 $, 表面张力$ \sigma = 0.005 $, 迁移系数$ \lambda =0.1 $, 界面厚度$ W=4.0 $. 该问题的$ x $方向速度沿$ y $方向的分布存在解析解:

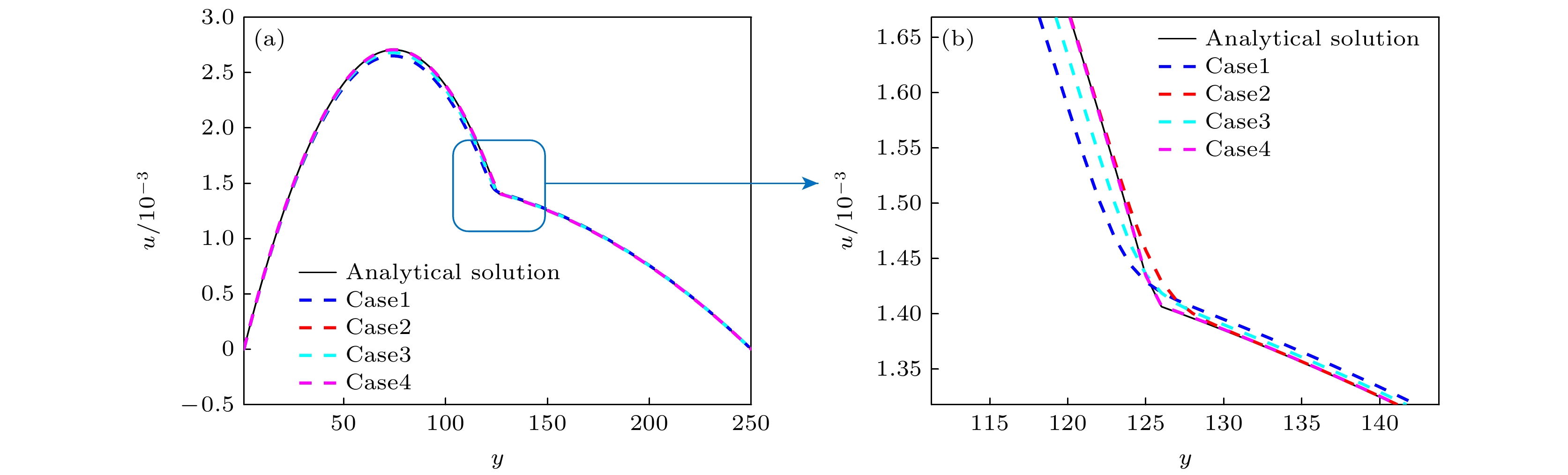
其中根据我们所取的网格数, $ h=124.5 $.

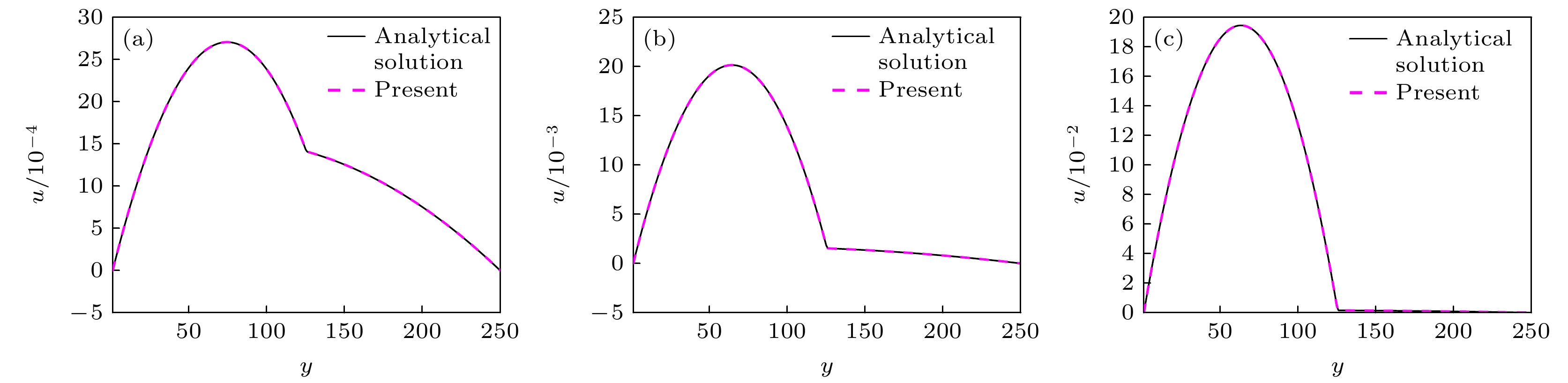
在4.2节中我们比较了不同黏度混合规则对静态液滴问题的影响, 下面将通过模拟该动态问题, 进一步比较它们之间的区别. 图5给出了$ x $方向速度沿$ y $方向的分布及其局部放大图, 其中case1—case4分别使用了(9b)式、(46a)式、(46b)式和(46c)式来计算混合黏度, 整体上看, case2和case4的结果与解析解吻合良好, 在界面附近, case4的结果与解析解更加一致. 因此, 模拟动态问题时, 使用(46c)式的阶跃混合规则计算混合黏度能得到更准确的结果.

为了进一步验证当前模型的准确性, 还模拟 了不同动力黏度比$ M=\dfrac{{\mu }_{1}}{{\mu }_{2}}=\dfrac{{\rho }_{1}{\nu }_{1}}{{\rho }_{2}{\nu }_{2}} $的情况. 我们使用(46c)式来计算混合黏度, 设置两相密度为$ {\rho }_{1}={\rho }_{2}=1.0 $, 固定$ {\nu }_{1}=1.0 $, 通过调整$ {\nu }_{2} $的大小来改变动力黏度比. 图6给出了和M = 10, 100, 1000时的速度分布, 模拟结果都和解析解吻合良好. 这证明了当前模型模拟动态问题及大黏度比问题的准确性.

本节将模拟一个两相分离问题, 并与基于不可压相场的LBE模型^[18]进行对比. 计算区域为$ {N}_{x}\times {N}_{y}=100\times 100 $的正方形区域, 初始时序参数包含一个小扰动, 即:

模拟时, 设置黏度比$ {\nu }_{1}/{\nu }_{2}=1 $, 表面张力$ \sigma =0.001 $, 松弛时间$ {\tau }_{f}={\tau }_{g}=1.0 $, 界面厚度$ W=4 $.

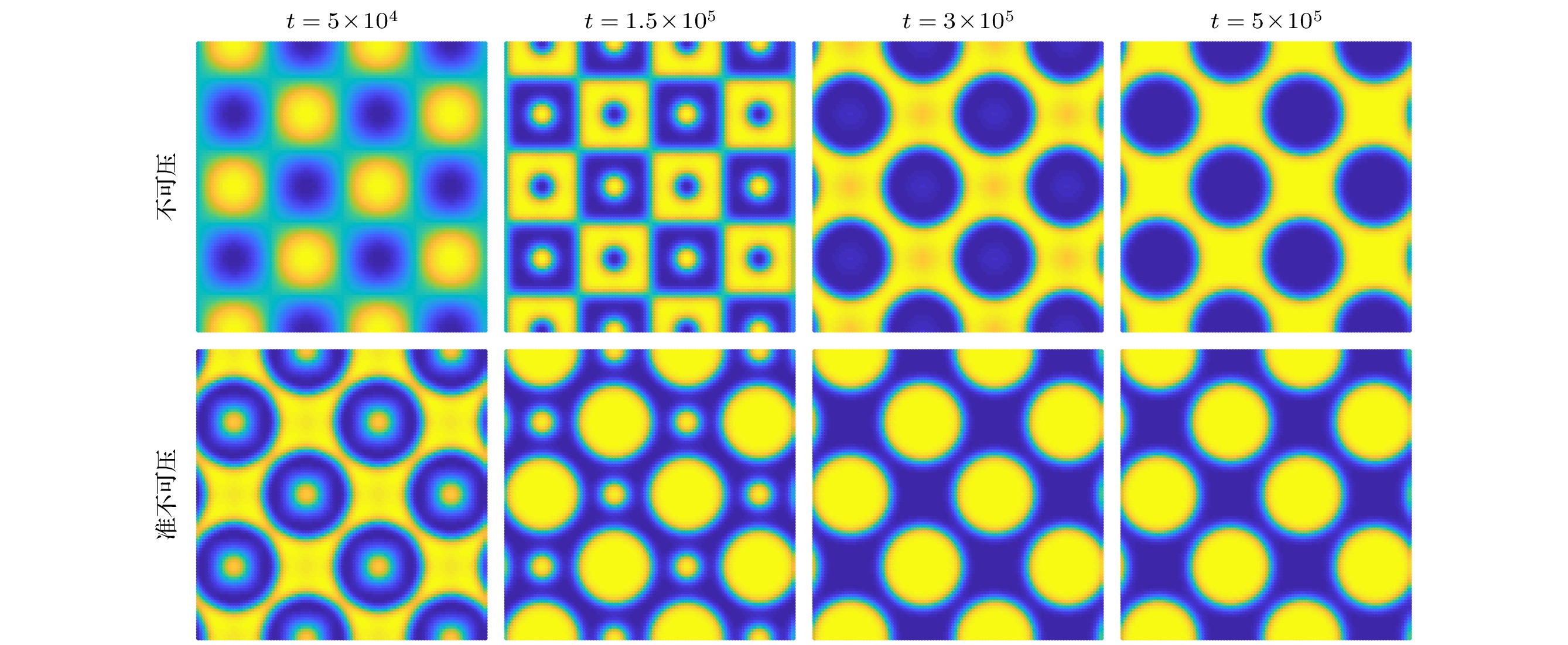
基于不可压相场的LBE模型^[18]中, 对应的连续方程为(7)式, 与准不可压连续方程(11)相比, 二者主要差异是右端项$ \gamma {{\nabla}} \cdot \left(\lambda {{\nabla}} \mu \right) $, 该项与参数$ \gamma $有关, 并且只在界面区起作用. 因此当$ \gamma =0 $时或在体相区, 两模型相同. 当$ \gamma $较大或界面占总体区域的比例较大时, 该项所起的作用越大, 模型差异也会明显. 本算例中我们取$ \gamma = 4 $, 密度比为$ {\rho }_{1}/{\rho }_{2} = 5 $. 同时, 由于初时时刻包含的两相界面较多, 因此两个模型的预测结果可能有较大差异.

图7给出了两个模型在不同时刻得到的相分布, 可以看到, 两个模型在相分离问题上展现出了较大的差异. 一方面, 准不可压模型结果的演化速度更快, 其预测的相分离要早于不可压模型; 另一方面, 两模型得到了相反的相分离结果, 在准不可压模型的结果中, 黄色表示的相为离散相, 蓝色为连续相, 而不可压模型的结果正好相反.

我们还统计了这个过程中两相的质量变化, 用下式计算各时刻单相总质量:

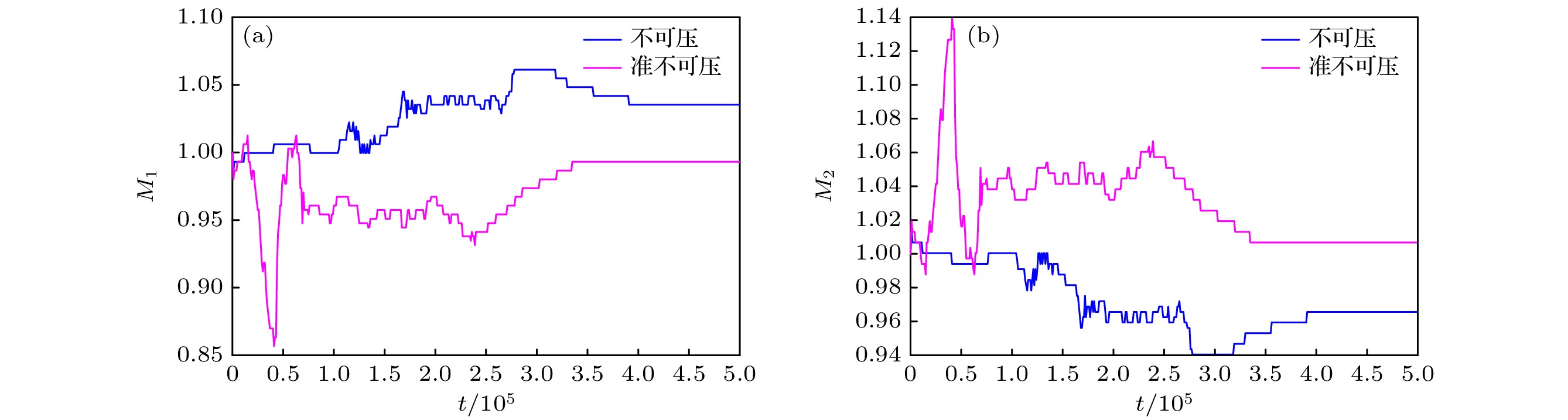
令$ M_1={m}_{1}\left(t\right)/{m}_{1}\left(0\right) $, $ M_2={m}_{2}\left(t\right)/{m}_{2}\left(0\right) $, 图8给出了M₁-t和M₂-t曲线. 可以看到, 稳定后, 不可压模型^[18]所得各相的质量均相对初始时有较大偏差, 相对误差为3.53%, 而准不可压模型的结果中质量偏差较小, 相对误差仅为0.67%.

基于准不可压相场理论, 本文提出了一种能够在离散尺度上达到精确平衡的两相LBE模型. 模拟了平界面问题和稳态液滴问题, 并与无精确平衡性质的准不可压相场YG-LBE模型^[3]进行了比较. 结果表明, 本文模型将虚假速度消除到了机器精度, 且得到了几乎恒定的化学势, 证明了当前模型的平衡性能. 模拟稳态液滴问题时, 还比较了不同表面张力形式和不同黏度混合规则的影响. 结果表明, (45b)式表示的表面张力形式不能保证化学势为常数, 无法实现精确平衡; 不同黏度混合规则在模拟静态问题时对模型没有明显影响. 进一步模拟了分层泊肃叶流, 比较了不同黏度混合规则的影响, 结果表明, 使用阶跃混合规则计算混合黏度可以得到更准确的结果. 还模拟了不同黏度比条件下的分层泊肃叶流, 结果均与解析解吻合良好, 证明了当前模型模拟动态问题及大黏度比问题的准确性. 此外, 还模拟了一个两相分离问题, 展示了准不可压模型和不可压模型的差异, 证明了本文模型能够保证局部质量守恒. 总之, 本文提出的精确平衡两相LBE模型解决了原始模型的虚假速度问题, 同时能够保证局部质量守恒.